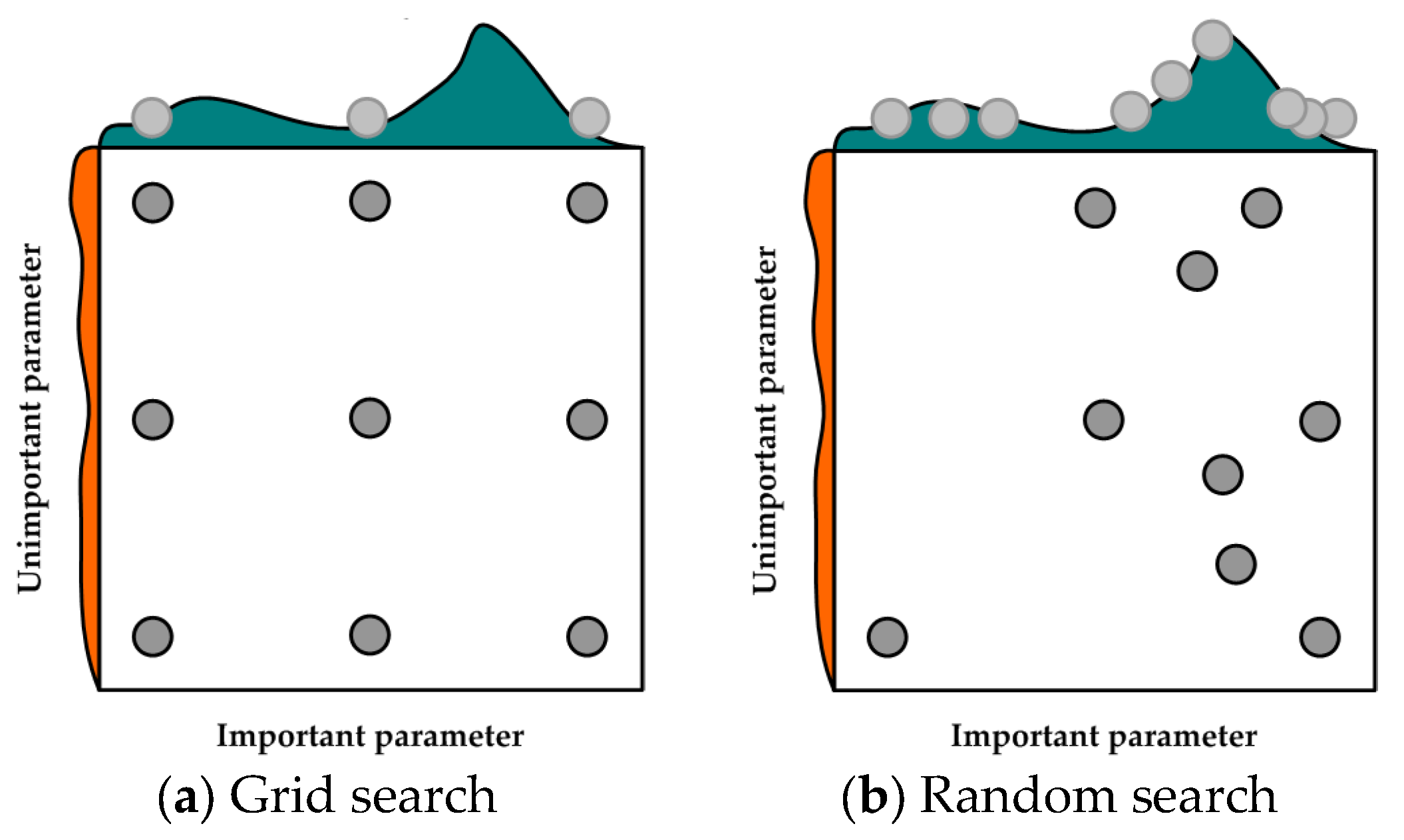
Figure 1.
Conceptual diagram of hyper-parameter optimization method.
Figure 1.
Conceptual diagram of hyper-parameter optimization method.
Figure 2.
Input data for mathematical model.
Figure 2.
Input data for mathematical model.
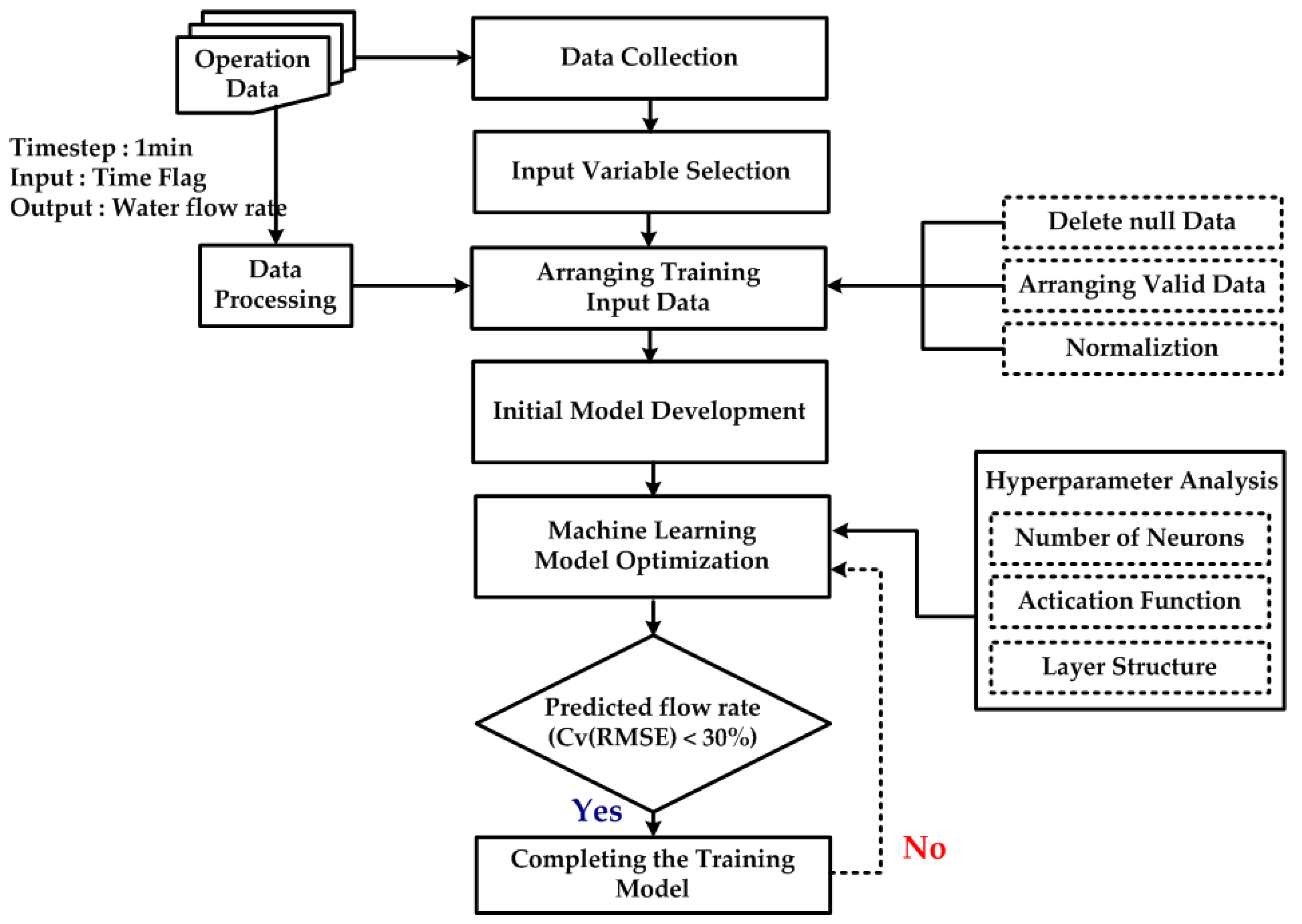
Figure 3.
Process of the development of the performance prediction model.
Figure 3.
Process of the development of the performance prediction model.
Figure 4.
Configuration of systems for operational data collection.
Figure 4.
Configuration of systems for operational data collection.
Figure 5.
View of systems installed in the target building.
Figure 5.
View of systems installed in the target building.
Figure 6.
Equipment for measuring coefficient of performance.
Figure 6.
Equipment for measuring coefficient of performance.
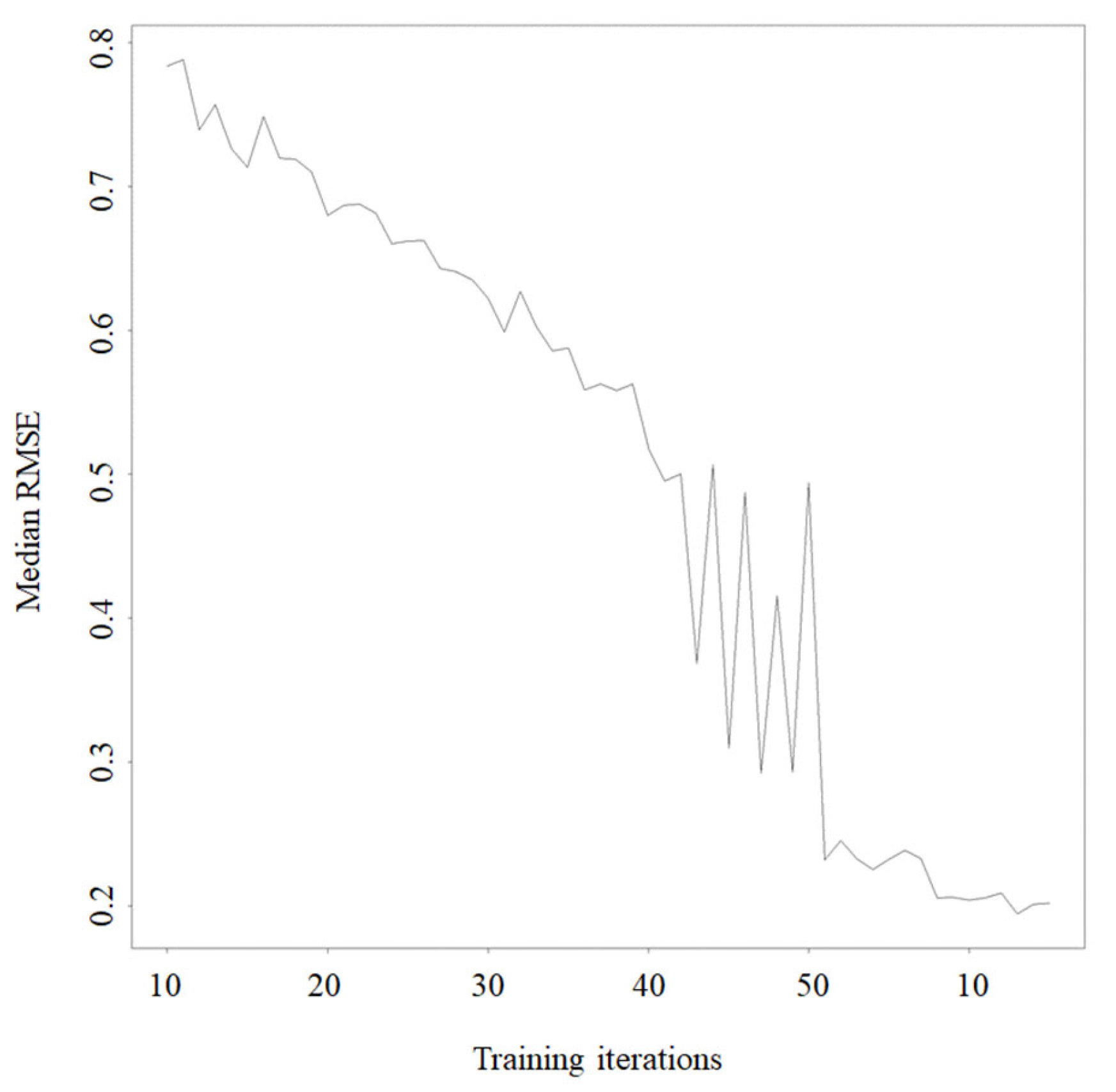
Figure 7.
Prediction model performance analysis for optimizing number of iterations.
Figure 7.
Prediction model performance analysis for optimizing number of iterations.
Figure 8.
Prediction model performance analysis for hidden layer structure.
Figure 8.
Prediction model performance analysis for hidden layer structure.
Figure 9.
Comparison of prediction performance of prediction model with hyper-parameter optimization.
Figure 9.
Comparison of prediction performance of prediction model with hyper-parameter optimization.
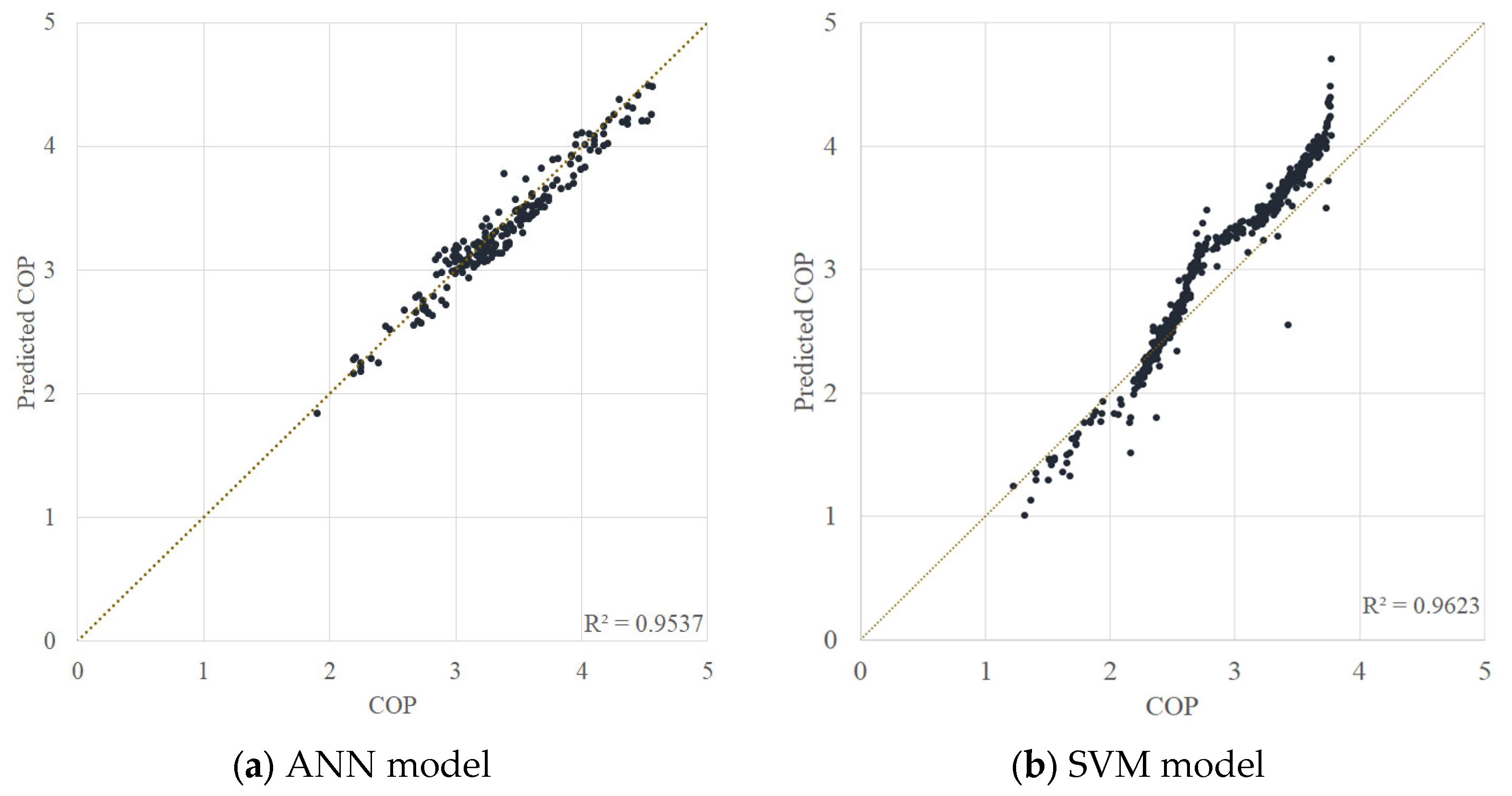
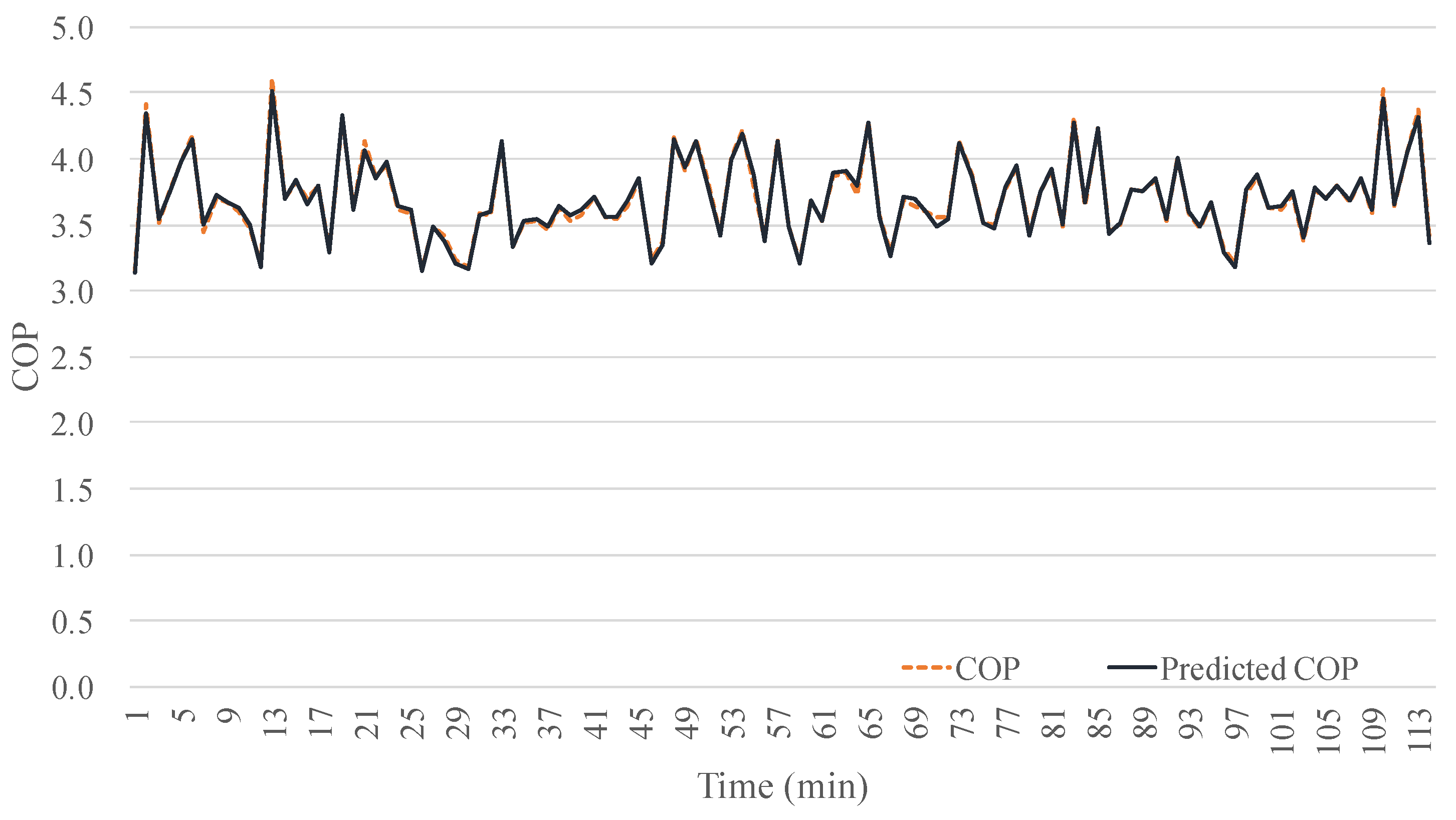
Figure 10.
Comparison of measured performance and prediction performance through an ANN model with optimal hyper-parameter.
Figure 10.
Comparison of measured performance and prediction performance through an ANN model with optimal hyper-parameter.
Table 1.
Type of hyper-parameter.
Table 1.
Type of hyper-parameter.
| Hyper-Parameter | Contents |
|---|
| Learning rate | A variable that determines how fast it will move in the gradient direction |
| Cost function | A function that estimates the difference between the expected value and the actual value according to the input |
| Regularization parameter | Using regularization method to avoid and solve overfitting problems |
| Mini-batch size | Splitting the entire training data to perform a batch set |
| Training loop | Variables that determine early termination of learning |
| Hidden unit | Learning Optimization Determinants on Training Data |
| Weight initialization | A determinant of performance |
Table 2.
Previous studies of performance prediction.
Table 2.
Previous studies of performance prediction.
| Category | Methods | Input | Author |
|---|
| Mathematical method | Polynomial | 7 point (Heating load, etc.) | Nam et al. |
| Machine learning | Random Forest | 9 point (Power consumption, etc.) | Cho |
| Recurrent Neural Networks | 12 point (Environmental variable, etc.) | Sun et al. |
| ANN | 5 point (Power consumption, etc.) | Benli |
| SVM | 8 points (Heating capacity, etc.) | Esen et al. |
| Adaptive neuro fuzzy inference system | 8 points (Heating capacity, etc.) | Kecman |
| ANN | 7 point (Power consumption, etc.) | Yilmaz |
| K-NN | 8 points (Water flow rate, etc.) | Akhlaghi |
| Random Forest | 12 point (Power consumption, etc.) | Swider |
| ANN | 29 point (Power consumption, etc.) | Park et al. |
| ANN | 5 point (Ground temperature, etc) | Esen et al. |
| ANN | 3 point (Ground temperature, etc) | Esen et al. |
| Back-propagation Neural Network | 23 point (Water flow rate, etc) | Yan et al. |
| Random Forest and Back propagation Neural Network | 16 point (Power consumption, etc.) | Lu et al. |
Table 3.
Overview of buildings for geothermal system operation data collection.
Table 3.
Overview of buildings for geothermal system operation data collection.
| Category | Contents |
|---|
| Building | Use | Office |
| Total floor area | 21,492 m2 |
| Size | B1/F9 |
| Geothermal system | Type | Vertical closed-loop |
| EA | 7 |
| Capacity (Cooling) | 105.6 kW |
| Capacity (Heating) | 101.4 kW |
| Number of borehole | 70 |
| Interval of borehole | 5 m |
| Period of data collection | 2014.02.05~2019.08.31 |
Table 4.
Overview of heat pump systems.
Table 4.
Overview of heat pump systems.
| Classification | Cooling | Heating |
|---|
| Capacity (kW) | 190.61 | 178.93 |
| Power (W) | 38.03 | 44.52 |
| Flow rate (LPM) | 600 | 600 |
| COP | 5.01 | 4.02 |
Table 5.
Overview of auxiliary systems.
Table 5.
Overview of auxiliary systems.
| Classification | Spec. | Contents |
|---|
| Heat source tank | 18.7 ton | Circulation flow rate on heat source side: 5~10 Ton |
| Load tank | 18.7 ton | Circulation flow rate on load side: 5~100 Ton |
| Auxiliary heat source | 10 HP | Air-cooled heat pump |
Table 6.
Overview of operation data collection.
Table 6.
Overview of operation data collection.
| Category | Building | Test-Bed |
|---|
| Data collection period | 1 January 2018~31 December 2018 | 25 August 2019~ 27 August 2019 |
| Data collection cycle | 3 h | 1 min |
| Data collection method | BAS | Measurement |
| Temperature range (cooling) | 24~43 °C | 20~49 °C |
| Temperature range (heating) | 11~24 °C | 8.1~26.8 °C |
Table 7.
Accuracy of the measurement devices.
Table 7.
Accuracy of the measurement devices.
| Measurement Device | Specific Information | Ranges | Accuracy |
|---|
| Temperature sensor (°C) | RTD (OMEGA) | −50~200 | ±0.15% |
| HOBO U12 (ONSET) | −20~70 | ±0.35% |
| Flow meter (m3/h) | FMAG 5000 (SIEMENS) | 0~400 | ±0.4% |
| Power meter | CW240 (YOKOGAWA) | 0~3000 | ±0.6% |
Table 8.
Operation data list.
Table 8.
Operation data list.
| Category | Unit | Symbol |
|---|
| Outdoor air temperature | °C | |
| Source side inlet temperature | °C | |
| Source side outlet temperature | °C | |
| Load side inlet temperature | °C | |
| Load side outlet temperature | °C | |
| Heat pump power | kW | |
| COP | - | |
| Pump power | kW | |
Table 9.
Measurement uncertainty.
Table 9.
Measurement uncertainty.
| Category | Uncertainty (%) |
|---|
| Temperature | 0.2 |
| Flow rate | 0.26~0.32 |
Table 10.
Correlation analysis between input data and output data.
Table 10.
Correlation analysis between input data and output data.
| Category | | |
|---|
| Outdoor air temperature | −0.72 | 0.52 |
| Source side inlet temperature | −0.76 | 0.58 |
| Source side outlet temperature | 0.59 | 0.35 |
| Load side inlet temperature | 0.60 | 0.39 |
| Load side outlet temperature | 0.32 | 0.10 |
Table 11.
Statistical analysis of ANN model.
Table 11.
Statistical analysis of ANN model.
| Variables | Statistical Parameters |
|---|
| Means | Standard Deviation | Minimum | Maximum |
|---|
| COP | Training | 2.90 | 0.71 | 1.17 | 5.46 |
| Testing | 2.76 | 0.55 | 1.22 | 3.77 |
| Load side inlet temperature | Training | 17.29 | 1.71 | 11.60 | 25.00 |
| Testing | 17.30 | 1.75 | 12.10 | 24.20 |
| Load side outlet temperature | Training | 16.02 | 2.12 | 9.00 | 24.40 |
| Testing | 15.99 | 2.16 | 9.10 | 23.60 |
| Source side inlet temperature | Training | 33.52 | 3.81 | 24.20 | 43.50 |
| Testing | 33.56 | 3.74 | 24.60 | 43.00 |
| Source side outlet temperature | Training | 37.52 | 3.81 | 28.20 | 47.50 |
| Testing | 37.56 | 3.74 | 28.60 | 47.00 |
| Outside temperature | Training | 25.43 | 2.21 | 22.90 | 33.70 |
| Testing | 2530 | 2.22 | 23.00 | 33.10 |
Table 12.
Statistical analysis of SVM model.
Table 12.
Statistical analysis of SVM model.
| Variables | Statistical Parameters |
|---|
| Means | Standard Deviation | Minimum | Maximum |
|---|
| COP | Training | 2.90 | 0.71 | 1.17 | 5.46 |
| Testing | 2.76 | 0.55 | 1.22 | 3.77 |
| Load side inlet temperature | Training | 17.29 | 1.71 | 11.60 | 25.00 |
| Testing | 17.30 | 1.75 | 12.10 | 24.20 |
| Load side outlet temperature | Training | 16.02 | 2.12 | 9.00 | 24.40 |
| Testing | 15.99 | 2.16 | 9.10 | 23.60 |
| Source side inlet temperature | Training | 33.52 | 3.81 | 24.20 | 43.50 |
| Testing | 33.56 | 3.74 | 24.60 | 43.00 |
| Source side outlet temperature | Training | 37.52 | 3.81 | 28.20 | 47.50 |
| Testing | 37.56 | 3.74 | 28.60 | 47.00 |
| Outside temperature | Training | 25.43 | 2.21 | 22.90 | 33.70 |
| Testing | 2530 | 2.22 | 23.00 | 33.10 |
Table 13.
Structure of initial ANN model.
Table 13.
Structure of initial ANN model.
| Category | Contents |
|---|
| Function | Activation | Sigmoid |
| Loss | Mean squared error |
| Optimization algorithm | Adam |
| Epoch | 5000 |
| Structure | Input layer | Number of layer | 1 |
| Number of neuron | 5 |
| Hidden layer | Number of layer | 1 |
| Number of neuron | 2 |
| Output layer | Number of layer | 1 |
| Number of neuron | 1 |
Table 14.
Structure of initial SVM model.
Table 14.
Structure of initial SVM model.
| Category | Contents |
|---|
| Type | Eps-regression |
| Kernel | Polynomial |
| Epsilon | 0.1 |
| Cost | 1 |
| Gamma | 1 |
Table 15.
Performance analysis of initial ANN model.
Table 15.
Performance analysis of initial ANN model.
| Category | Accuracy |
|---|
| R2 | CvRMSE | Error |
|---|
| ANN | 0.89 | 17.8 | −12~11 |
| SVM | 0.65 | 15.9 | −14~16 |
Table 16.
Computation time analysis of initial ANN model.
Table 16.
Computation time analysis of initial ANN model.
| Category | Normalization | Train Time
(s) |
|---|
| ANN | Min-Max | 1.43 |
| Standardization | 0.83 |
| SVM | Min-Max | 2.63 |
| Standardization | 6.64 |
Table 17.
Hyper-parameter optimization method.
Table 17.
Hyper-parameter optimization method.
| Machine Learning Model | Hyper Parameter | Optimization Method |
|---|
| ANN | Training iterations | Grid search |
| Number of hidden layer | Bayesian optimization |
| Number of hidden node | Bayesian optimization |
| SVM | Kernel | Grid search |
| Number of gamma | Random search |
| Number of cost | Random search |
Table 18.
Hyper-parameter for optimizing ANN model.
Table 18.
Hyper-parameter for optimizing ANN model.
| Category | Parameters |
|---|
| ANN | 1, 2, 3, 4 |
| SVM | 1~17 |
Table 19.
Hyper-parameter for optimizing SVM model.
Table 19.
Hyper-parameter for optimizing SVM model.
| Category | Parameters |
|---|
| Kernel | Radial, Linear, Polynomial, Sigmoid |
| Cost | 1, 2, 4, 8, 16 |
| Gamma | 0.00001, 0.0001, 0.001, 0.01, 0.1, 0 |
Table 20.
Prediction model performance analysis according to hyper-parameter (SVM model 1).
Table 20.
Prediction model performance analysis according to hyper-parameter (SVM model 1).
| Category | Cost |
|---|
| Gamma | 1 | 2 | 4 | 8 | 16 |
|---|
| 0.00001 | 49.6 | 47.0 | 43.9 | 41.4 | 39.6 |
| 0.0001 | 39.3 | 38.5 | 37.9 | 37.7 | 36.5 |
| 0.001 | 36.5 | 34.1 | 29.7 | 26.5 | 24.7 |
| 0.01 | 20.4 | 12.3 | 5 | 2.6 | 1.7 |
| 0.1 | 3.2 | 4.4 | 1.9 | 2.4 | 2.5 |
| 0 | 5.2 | 3.1 | 2.5 | 1.2 | 0.8 |
Table 21.
Prediction model performance analysis according to hyper-parameter (SVM model 2).
Table 21.
Prediction model performance analysis according to hyper-parameter (SVM model 2).
| Category | Cost |
|---|
| Gamma | 1 | 2 | 4 | 8 | 16 |
|---|
| 0.00001 | 2.334 | 2.334 | 2.313 | 2.310 | 2.310 |
| 0.0001 | 2.334 | 2.334 | 2.313 | 2.310 | 2.310 |
| 0.001 | 2.334 | 2.334 | 2.313 | 2.310 | 2.310 |
| 0.01 | 2.334 | 2.334 | 2.313 | 2.310 | 2.310 |
| 0.1 | 2.334 | 2.334 | 2.313 | 2.310 | 2.310 |
| 0 | 2.334 | 2.334 | 2.313 | 2.310 | 2.310 |
Table 22.
Prediction model performance analysis according to hyper-parameter (SVM model 3).
Table 22.
Prediction model performance analysis according to hyper-parameter (SVM model 3).
| Category | Cost |
|---|
| Gamma | 1 | 2 | 4 | 8 | 16 |
|---|
| 0.00001 | 51.21 | 47.00 | 50.05 | 51.05 | 53.05 |
| 0.0001 | 40.70 | 39.20 | 38.30 | 49.60 | 47.00 |
| 0.001 | 50.47 | 49.69 | 48.22 | 46.50 | 44.63 |
| 0.01 | 52.99 | 52.94 | 52.85 | 53.03 | 53.02 |
| 0.1 | 15.31 | 20.84 | 18.38 | 16.38 | 14.95 |
| 0 | 11.52 | 13.52 | 13.41 | 20.28 | 15.31 |
Table 23.
Prediction model performance analysis according to hyper-parameter (SVM model 1).
Table 23.
Prediction model performance analysis according to hyper-parameter (SVM model 1).
| Category | Cost |
|---|
| Gamma | 1 | 2 | 4 | 8 | 16 |
|---|
| 0.00001 | 51.21 | 49.55 | 47.00 | 43.92 | 41.41 |
| 0.0001 | 43.07 | 40.78 | 39.25 | 38.46 | 37.89 |
| 0.001 | 24.70 | 20.84 | 32.85 | 33.78 | 26.47 |
| 0.01 | 38.27 | 37.65 | 36.12 | 46.72 | 53.05 |
Table 24.
Construction of an ANN model with hyper-parameter optimization.
Table 24.
Construction of an ANN model with hyper-parameter optimization.
| Category | Contents |
|---|
| Function | Activation | Sigmoid |
| Loss | Mean squared error |
| Optimization algorithm | Adam |
| Epoch | 5000 |
| Structure | Input layer | Number of layer | 1 |
| Number of neuron | 4 |
| Hidden layer | Number of layer | 2 |
| Number of neuron | 11 |
| Output layer | Number of layer | 1 |
| Number of neuron | 1 |
Table 25.
Construction of a SVM model with hyper-parameter optimization.
Table 25.
Construction of a SVM model with hyper-parameter optimization.
| Category | Contents |
|---|
| Type | Eps-regression |
| Kernel | Radial |
| Epsilon | 16 |
| Cost | 0 |
| Gamma | 0.1 |
| Number of support vector | 1116 |
Table 26.
Performance analysis of prediction model with hyper-parameter optimization.
Table 26.
Performance analysis of prediction model with hyper-parameter optimization.
| Category | Accuracy |
|---|
| MBE | RMSE | CvRMSE | R2 |
|---|
| ANN | −3.6% | 15.96% | 5.4% | 0.953 |
| SVM | −9.8% | 43.96% | 8.10% | 0.962 |