Reliability Estimation Using EM Algorithm with Censored Data: A Case Study on Centrifugal Pumps in an Oil Refinery

Abstract

Centrifugal pumps are widely employed in the oil refinery industry due to their efficiency and effectiveness in fluid transfer applications. The reliability of pumps plays a pivotal role in ensuring uninterrupted plant productivity and safe operations. Analysis of failure history data shows that bearings have been identified as critical components in oil refinery pump groups. Analyzing historical failure data for such systems is a complex task due to censored data and missing information. This paper addresses the complexity of estimating the Weibull distribution parameters using the maximum likelihood method under these conditions. The likelihood equation lacks an explicit analytical solution, necessitating numerical methods for resolution. The proposed approach presented in this article leverages the expectation maximization (EM) algorithm for estimating the Weibull distribution parameters in a real-world case study of a complex engineering system. The results demonstrate the superior performance of the EM algorithm with censored data, showcasing its ability to overcome the limitations of traditional methods and provide more accurate estimates for reliability metrics. This highlights the importance of obtaining results through these methodologies in the analysis of reliability and in facilitating more informed decision making in complex systems.

1. Introduction

The growing demand for effective and secure systems has led to the development of operational maintenance processes to improve system availability and operational safety while achieving cost effectiveness. Predictive maintenance is one such process, which utilizes data analytics and machine-learning algorithms to predict potential failures before they occur [1,2]. This approach has widespread adoption in the manufacturing, energy, and transportation industries. Predictive maintenance can identify patterns and anomalies indicative of impending issues by analyzing real-time data obtained from sensors and other sources. This enables maintenance teams to take proactive measures, such as replacing faulty components or adjusting operating conditions, thereby preventing failures [3,4].

Unexpected and untimely failures remain a significant challenge for maintenance practices today. Depending on the severity of the failure, it can disrupt the proper functioning of a manufacturing line or, in more severe cases, lead to a complete shutdown, resulting in substantial expenses ranging from the procurement of spare components to equipment replacement. Hence, it becomes crucial to comprehend the behavior of equipment [5]. Such understanding forms a solid foundation for determining optimal maintenance policies tailored to each piece of equipment and its components. This leads to significant cost savings by optimizing inspection frequencies, reducing component replacements and stocking, improving pre-maintenance work, and minimizing repair times.

To predict the future behavior of equipment and components, it is valuable to employ a tool, which fits theoretical models to the dataset to identify potential failures accurately and rapidly. Analysis and estimation processes are supported by statistical techniques, methods, and procedures, which facilitate modeling the system by adjusting predefined distributions or calculating customized distribution functions [6,7]. These statistical techniques offer valuable tools for data-driven decision making, enabling the identification of underlying patterns and trends in complex systems.

Statistical techniques prove beneficial in predicting future trends and outcomes. Analyzing historical data allows statisticians to develop models and predictions for strategic decision making. By leveraging statistical techniques, it becomes possible to forecast when the equipment will require repair or replacement and allocate resources accordingly, thus saving time, money, and preventing unplanned downtime. Furthermore, statistical analysis can optimize maintenance schedules and identify opportunities for improving maintenance processes [8,9].

In some cases, estimating statistical distribution parameters can be challenging to solve [10,11,12]. This article presents a procedure for resolving such difficulties, employing the expectation maximization (EM) algorithm. The proposed procedure offers a structured and practical approach to estimating Weibull distribution parameters, even in challenging scenarios, where conventional methods may fail. By leveraging the EM algorithm, the estimation process becomes more precise and reliable, enhancing decision-making capabilities. This method helps estimate distribution parameters in realistic situations.

The remainder of this paper is organized as follows. Section 2 highlights the main practical problems, which are generally associated with the analysis of data from the historical record of mechanical equipment failures, namely the existence of censored data.

Section 3 provides an overview of the concepts and theoretical foundations underlying the method for determining Weibull distribution parameters. Since maximum likelihood equations often lack analytical solutions due to their complexity, the expectation maximization (EM) algorithm is presented as a resolution technique. The EM algorithm analysis is performed in the presence of censored data, aligning with their application in the case study.

Section 4 showcases the real-world application of the proposed methodology. The study focuses on a system comprising five centrifugal pumps in the petrochemical industry. Weibull distribution parameters are estimated using the maximum likelihood method through the EM algorithm. The confidence interval of the estimated parameters, obtained via the bootstrap method, is presented.

Section 5 concludes the paper by summarizing the essential findings and highlighting the significance of the proposed methodology in improving maintenance practices and system reliability.

2. Reliability Analysis with Censored Data

The Weibull distribution is widely utilized in reliability studies, survival analysis, and various other fields due to its versatility. It is commonly employed for modeling the failure rates of components and systems and estimating their lifetimes. The Weibull distribution can effectively fit data from diverse sources, including laboratory tests, field data, and warranty claims. Estimating its parameters can be accomplished through methods such as maximum likelihood estimation, enabling the development of models, which facilitate the predictions of future failures and reliability comparisons among different products or designs.

Maximum likelihood estimation (MLE) is fundamental for estimating unknown parameters in statistical models [13,14]. This approach involves determining the parameter values, which maximize the likelihood function, constructed based on the observed data and the parameters. The resulting estimates are frequently employed for making predictions and inferences about the underlying population from which the data were sampled.

The likelihood function is established by considering the joint probability distribution of the observed data. In simpler terms, it quantifies the probability of obtaining the observed data for various parameter values [15]. The maximum likelihood estimation method seeks to identify the parameter values, which maximize this likelihood function, thereby providing the most plausible parameter estimates (Equation (1)).

$$\max L\left({\theta }_1,{\theta }_2,\dots ,{\theta }_n\right)=max\prod _{i=1}^{n}f\left(\theta |x_i\right),$$

(1)

where x_i = x₁, x₂, …, x_n is a sample of n independent observations of the random variable X from a distribution with probability density function f(x, θ), and θ_i = θ₁, θ₂, …, θ_n is the vector of unknown parameters.

In practical applications, maximizing the log-likelihood function is often more convenient than the likelihood directly [16,17]. The log-likelihood function offers several advantages, as it is a monotonically increasing function of the likelihood and simplifies mathematical calculations. Consequently, the maximum likelihood estimation (MLE) problem can be transformed into a maximization problem of the log likelihood.

Assuming that each failure time (t_i = t₁, t₂, …, t_n) represents an independent data point from the same representative population following the Weibull distribution with scale parameter η and shape parameter β, the log-likelihood function for the Weibull distribution with complete data is expressed as follows (Equation (2)) [18]:

$$\ln L\left(\eta ,\beta \right)=\eta ln\beta -\eta \beta ln\eta +\left(\beta -1\right)\sum _{i=1}^n\left(ln{t}_i\right)-\sum _{i=1}^n{\left(\frac{t_i}{\eta }\right)}^{\beta }$$

(2)

Once the log-likelihood function is defined, various optimization techniques, including numerical optimization algorithms, can be employed to identify the maximum function. The parameter values corresponding to this maximum are considered the maximum likelihood estimation (MLE) estimates. These estimates represent the most likely values for the parameters given in the observed data. By maximizing the log-likelihood function, we obtain parameter estimates, which provide the best fit to the data according to the Weibull distribution model.

Historical failure data, documenting past failures, hold significant importance in reliability analysis, guiding the decision making related to maintenance strategies, equipment replacement or refurbishment, spare part stocking, and warranty policies. Through data analysis, optimal maintenance intervals can be determined, critical components that frequently fail can be identified, and the cost effectiveness of different maintenance approaches can be assessed.

Historical fault data can be categorized into two types based on the availability of information: complete data and censored data [10,19].

Complete data refers to records where the exact failure or event occurrence time is known without uncertainty. In other words, no censoring is present in the data, and the failure times are fully observed. Complete data provide precise information about when the failure event occurred, enabling accurate analysis of the reliability metrics and statistical modeling.

On the other hand, censored data refers to observations where the exact failure or event occurrence time is either unknown or partially known. Censoring occurs in different forms:

• Left censoring occurs when the event of interest (failure) has occurred before the study started, and only the time since the event is known. In such cases, the data provide a lower bound for the failure time, but the exact time remains unknown.
• Right censoring occurs when the event of interest (failure) has not occurred by the end of the observation period or study duration. The data indicate that the failure event will occur at some point in the future, but the exact time is unknown. Right censoring often occurs in reliability tests, where a specified number of units are tested until the end of the study period, and the unfailing units are right censored.
• Interval censoring arises when the exact failure time is unknown, but it is known that the failure occurred within a specific time interval. This form of censoring provides information about a range of possible failure times.

Understanding the type of censoring present in the data is crucial for appropriate data analysis and modeling, as different techniques are employed to handle each type. By properly accounting for censored data, a more accurate and comprehensive reliability analysis can be performed, facilitating informed decision making in maintenance and operational strategies. Censoring data are denoted by the δ_i variable to indicate that the event is censored, that is (Equation (3)) [20]

$${\delta }_i=\left\{\begin{array}{c}1,\mathrm{for}\mathrm{uncensored}\mathrm{data}\hfill \\ 0,\mathrm{for}\mathrm{censored}\mathrm{data}\hfill \end{array}\right.$$

(3)

Censored data pose a challenge in statistical analysis, as they contain incomplete information and introduce uncertainty in the failure times. Specialized statistical methods are necessary to appropriately handle censored data, accounting for the missing information and capturing uncertainty. By employing these methods, more accurate predictions and informed decisions can be made based on the available data.

Censored data are frequently encountered in reliability studies when analyzing the historical failure data of equipment. Therefore, a comprehensive understanding of censored data and their impact on reliability analysis is crucial to ensure the accuracy and reliability of the results. Researchers can obtain more robust and trustworthy findings by applying appropriate statistical techniques for censored data, enabling effective decision making in reliability and maintenance practices.

3. Expectation Maximization Algorithm

Estimating Weibull distribution parameters in the presence of censored data often poses challenges, as closed-form analytical solutions for the maximum likelihood equations are typically unavailable. Explicit formulae to directly solve parameter estimates are not feasible in this case.

When dealing with censored data, the likelihood function becomes more intricate, incorporating both observed failure times and censored observations. The likelihood function includes terms representing the probabilities of observed failure times and the probabilities of failure times being censored.

Due to the complexity of the problem, analytical solutions for the maximum likelihood equations are not viable. Instead, numerical methods and iterative algorithms are commonly employed to estimate the parameters, which maximize the likelihood function [21]. These methods iteratively update the parameter estimates until convergence is achieved, searching for the values that optimize the likelihood function.

In this work, the expectation maximization (EM) algorithm was chosen among other numerical methods due to its demonstrated effectiveness in producing reliable results [22,23]. The EM algorithm, introduced by Dempster, Laird, and Rubin in 1977, is an iterative optimization algorithm [24]. It is widely used in reliability and survival analysis, as well as in other fields, such as machine learning, data mining, and bioinformatics [25,26,27]. The EM algorithm is a powerful statistical tool for estimating parameters in complex models, particularly in situations involving incomplete or censored data, where analytical solutions are challenging [28,29]. The algorithm alternates between two steps: the E-step (expectation step) and the M-step (maximization step). In the E-step, the algorithm calculates the expected value of the log-likelihood function based on the current parameter estimates. In the M-step, it maximizes the expected value of the log-likelihood function concerning the parameters [24,30].

The log-likelihood function for the complete data set X is denoted as l_c(x, θ). When incomplete data are present, certain events are unknown, and the observed data set is represented as Y, while Z represents the unknown data. Consequently, X can be expressed as a function of (y, z).

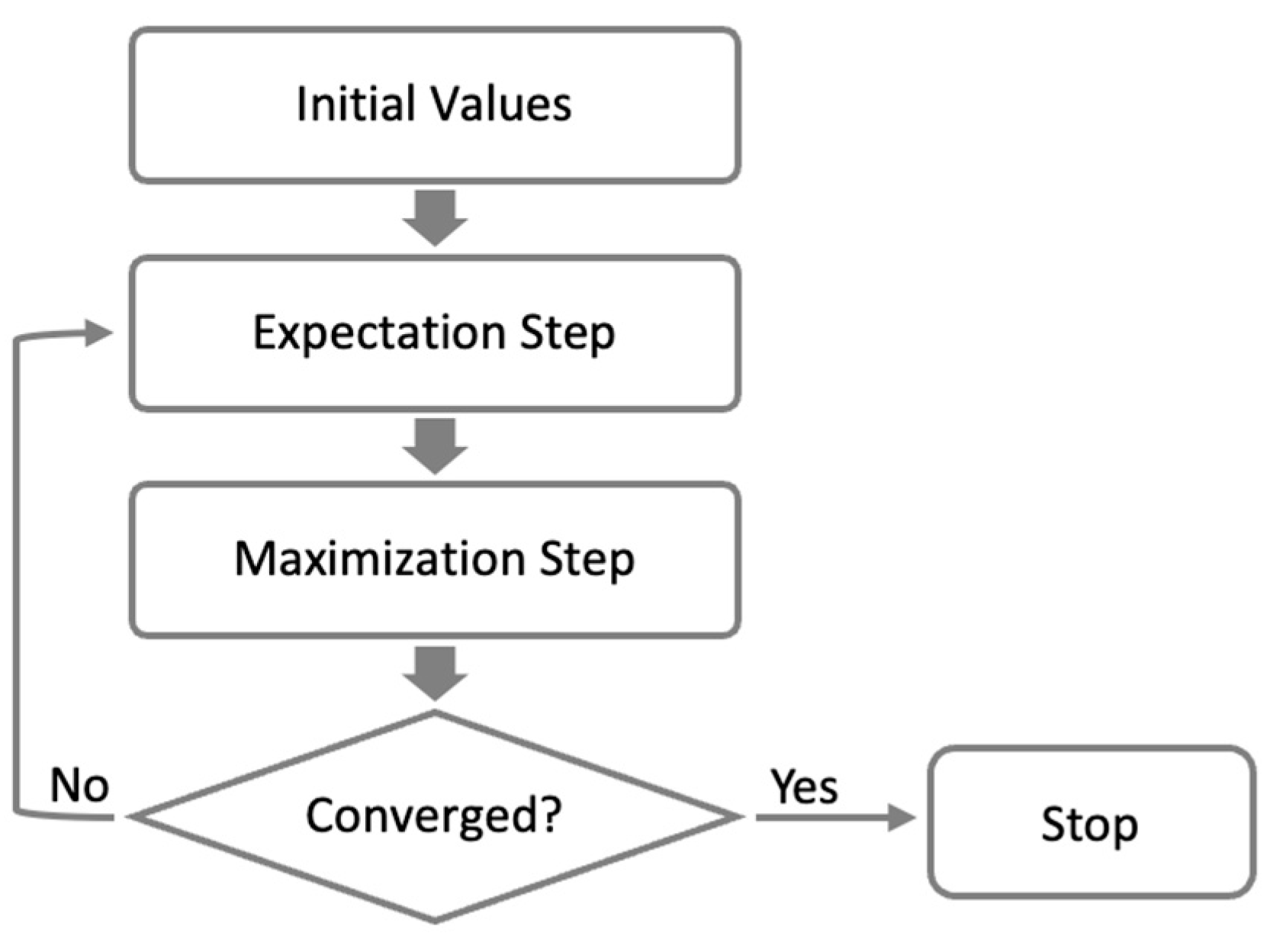
The EM algorithm with the presence of incomplete data can be summarized as follows:

• Initialization: The algorithm begins by initializing the model’s parameters, denoted as θ⁽⁰⁾. This initialization can be conducted randomly or with reasonable initial values. It is crucial to pay attention to the choice of initial values, as poor selection can result in slow algorithm convergence. Additionally, since the maximum likelihood equation can have multiple solutions corresponding to local maxima, the choice of initial values becomes significant. A comparative study on different strategies for choosing initial values was conducted by Ref [31], highlighting the dependence of the strategy on the selection of initial solutions.
• E-step (expectation step): The algorithm calculates the expected values of the missing or unobserved data in the E-step, given the current parameter estimates. This step involves computing the posterior probability distribution of the missing data, which represents the uncertainty about their values. The expectation is made concerning the conditional distribution of the missing data, conditioned on the observed data and the current parameter estimates.
  To perform the E-step, the algorithm typically utilizes the complete data likelihood function, which incorporates both the observed and missing data. However, since the missing data are unavailable, the algorithm computes the expectation of the complete data log likelihood instead. This expectation is often referred to as the “Q-function” (Equation (4)) [24].

  $$Q\left(\theta ,{\theta }^k\right)=E_{{\theta }^k}\left(l_c\left(x,\theta \right)|y,\delta ,{\theta }^{k-1}\right)$$

  (4)
• M-step (maximization step): In the M-step, the algorithm updates the parameter estimates to maximize the expected log likelihood computed in the E-step. It treats the expected values of the missing data as if they were observed and finds the parameter values that maximize the log likelihood of the complete data.
  To maximize the expected log likelihood, the algorithm employs standard optimization techniques, such as gradient descent or closed-form solutions tailored to specific models. The M-step involves solving the optimal values of the parameters by maximizing the Q-function for the parameters. This can be achieved through numerical optimization methods, which iteratively update the parameter estimates until convergence is reached. Gradient-based methods estimate the log-likelihood gradient for the parameters and adjust the parameter values in the direction of the steepest ascent. On the other hand, closed-form solutions exploit the specific structure of the model to derive explicit expressions for the optimal parameter estimates (Equation (5)).

  $$Q^{k+1}=\arg \max Q\left(\theta ,{\theta }^k\right)$$

  (5)
  The choice of the optimization technique depends on the complexity of the model and the computational efficiency required. Gradient-based methods are widely used due to their versatility and ability to handle many models. However, for simpler models, closed-form solutions may offer faster and more efficient estimation. The M-step has a crucial role in refining the parameter estimates by iteratively improving their values based on the available data. By maximizing the log likelihood of the complete data, the algorithm finds parameter values that optimize the fit between the model and the observed and expected data. This step is essential for obtaining accurate and reliable parameter estimates in the presence of incomplete data.
• Iteration: After completing the E-step and M-step, the algorithm checks for convergence. If the change in the log-likelihood or the parameter estimates falls below a certain threshold, the algorithm terminates. Otherwise, it continues to iterate by returning to the E-step and repeating the process until convergence is achieved.

The convergence guarantees of the EM algorithm ensure that the likelihood of the model increases or remains constant with each iteration. However, it is essential to note that the algorithm may converge to a local maximum of the likelihood function rather than the global maximum. This behavior arises due to the inherent non-convex nature of the likelihood function. Consequently, running the algorithm multiple times with different initializations is often recommended [31]. This strategy helps mitigate the risk of getting trapped in suboptimal solutions and increases the chances of finding the global maximum.

Figure 1 illustrates the interactive process of the EM algorithm, demonstrating how the algorithm iteratively updates the parameter estimates and improves the likelihood of the model. The stepwise nature of the algorithm is evident, with the E-step estimating the missing data and the M-step refining the parameter estimates based on the complete data. The iteration continues until convergence, resulting in optimized parameter estimates, which maximize the likelihood of the complete data.

The iterative nature of the EM algorithm allows it to handle complex models and effectively accommodate incomplete or censored data. The algorithm refines the parameter estimates by leveraging the E-step and M-step iteratively, improving the overall fit between the model and the observed data. Convergence serves as a criterion for determining when the algorithm has reached a stable solution, ensuring the reliability and accuracy of the estimated parameters.

Reliability studies often involve analyzing data where the failure times of equipment or systems are subject to right censoring. Right censoring occurs when the study’s duration limits the observed failure times, and failures beyond that duration are not observed. The EM algorithm is a practical approach to addressing the challenge of right censored data in reliability analysis.

The EM algorithm offers a robust framework for estimating the parameters of a chosen reliability model when working with censored data. In the case of right censored data, the algorithm employs an iterative process. It imputes the unobserved failure times based on the current parameter estimates and updates them using the imputed failure times. This iterative process enables the incorporation of censored data and enhances parameter estimation accuracy.

During the E-step of the EM algorithm for right censored data in reliability studies, the survival probabilities are computed using the current parameter estimates for each observation. These survival probabilities represent the probability of survival beyond the censoring time for each observation. Subsequently, the survival probabilities are utilized to impute the failure times for the censored observations.

The Q-equation, which characterizes the E-step in the EM algorithm for right censored data, can be expressed as follows, as presented in Ref. [18] (Equation (6)):

$$\begin{gathered} Q\left(\theta ,{\theta }^k\right)=nln\beta -n\beta ln\eta +\left(\beta -1\right)\sum _{i=1}^n\left[{\delta }_{i}ln{y}_i+\left(1-{\delta }_i\right)\left\{ln{y}_i+\frac{1}{{\beta }^k}exp{\left(\frac{y_i}{{\eta }^k}\right)}^{{\beta }^k}\Gamma \left[0,{\left(\frac{y_i}{{\eta }^k}\right)}^{{\beta }^k}\right]\right\}\right] \\ -\frac{1}{{\eta }^{\beta }}\sum _{i=1}^n\left\{{\delta }_i{y}_i^{\beta }+\left(1-{\delta }_i\right)\left[y_i^{{\beta }^k}+{\left({\eta }^k\right)}^{{\beta }^k}\right]\right\} \end{gathered}$$

(6)

where

$$\Gamma \left(p,x\right)=\underset{x}{\overset{\infty }{\int }}{u}^{p-1}{e}^{-u}du,\mathrm{is}\mathrm{the}\mathrm{incomplete}\mathrm{gamma}\mathrm{function}.$$

This equation estimates the missing failure times based on the available survival probabilities. By imputing the failure times for the censored observations, the algorithm iteratively refines the parameter estimates, progressively improving the fit between the reliability model and the right censored data.

As seen above, the M-step is designed to find the solution θ^k+1, which maximizes Q(θ, θ^k+1). Once the failure times are imputed, the M-step of the EM algorithm proceeds to update the parameter estimates. In this step, the algorithm maximizes the expected complete data log likelihood, incorporating both observed and imputed failure times. By incorporating the imputed failure times, the algorithm effectively accounts for the censored information and provides more accurate parameter estimates.

When applied to right censored data, the EM algorithm offers a robust approach for estimating reliability parameters in the presence of censored observations. It overcomes the limitations imposed by censoring, such as incomplete failure time information. It ensures that the analysis incorporates all available data to make reliable inferences about the reliability characteristics of the system or equipment under study.

It is important to note that the specific implementation of the EM algorithm for censored data in reliability studies relies on the chosen reliability model, such as the Weibull distribution, and the assumptions made about the underlying distribution.

Using appropriate statistical techniques can significantly enhance the analysis and estimation process. These procedures enable the modeling of the system based on the fit of a predefined distribution. In the following section, a case study will be presented to demonstrate the effectiveness of this approach in a real-world scenario.

4. Case Study

One of the objectives of this case study is to apply the EM algorithm to find the solution of the function obtained by the maximum likelihood method in the parameter estimation of the Weibull distribution using right censored data. The case study analyzes the failure history of five centrifugal pumps used by a petrochemical company for pumping similar density oil, specifically emphasizing bearing failures. Over seven years, these pumps experienced recurrent failures, resulting in significant downtime and a decrease in the overall reliability of the pumping system.

Centrifugal pumps play a critical role in various industries by transporting fluids. Their design allows them to handle various fluid viscosities and temperatures, making them versatile for different applications.

Reliability is essential for ensuring the efficient and uninterrupted operation of these pumps. The bearing system within centrifugal pumps is particularly crucial, as its performance directly impacts the overall reliability of the pump.

The collected data revealed that bearing failures accounted for significant failures, representing approximately 38%. This highlights the importance of investigating and addressing bearing failures to improve the reliability and performance of the pumping system.

Bearing failures can have severe consequences, including costly downtime, repairs, safety hazards, and environmental risks. Estimating the parameters of the Weibull distribution based on limited and censored data enables plant operators to proactively monitor and maintain critical components such as bearings to ensure continuous and safe operations. The failure data collected were analyzed to determine the frequency of each failure mode over the seven years. This analysis provides insights into the relative importance of each failure mode in contributing to the overall failure rate.

Failures between regular inspections conducted by the maintenance staff, which occur at least every 8 h, were considered complete data. Hence, it was assumed that the exact moment of failure was well known, as the time between inspections was relatively short compared to the total observed time.

The last recorded data point for each pump represents the end of the study rather than an actual failure. This type of situation, as mentioned earlier, is known as right censored data, where the observed data are incomplete due to the study ending without observing all potential failures.

Treating the last recorded time for each pump as right censored data is a good approach, since it indicates that the failure times for those pumps are unknown, as they were still operating when the study concluded.

The expectation maximization algorithm was employed to estimate the parameters of the Weibull distribution using the maximum likelihood method with right censored data. The iterative process was implemented using the R statistical program.

The least squares method [32] was utilized to determine the initial solution θ⁽⁰⁾. The iterative method terminated when the difference between iteration k + 1 and k was smaller than 0.1.

Table 1. The expected value for β and η for the bearings of five centrifugal pumps obtained by EM algorithm and respective confidence interval obtained by the bootstrap-T method.

Bearings		β
1	5.67	8.34	14.34
2	4.15	7.22	12.75
3	7.19	9.98	15.11
4	3.91	6.97	11.86
5	2.77	5.74	10.78
Bearings		η
1	544.75	584.81	626.10
2	476.28	509.95	551.36
3	579.78	601.29	631.04
4	493.96	529.86	572.89
5	611.07	656.96	701.03

presents the expected values for β and η for the bearings of the five analyzed centrifugal pumps obtained through the EM algorithm. The confidence intervals for each parameter are also provided.

Given the small data sample size, the bootstrap-t method was employed to determine the confidence intervals, with a confidence level of 95% [33].

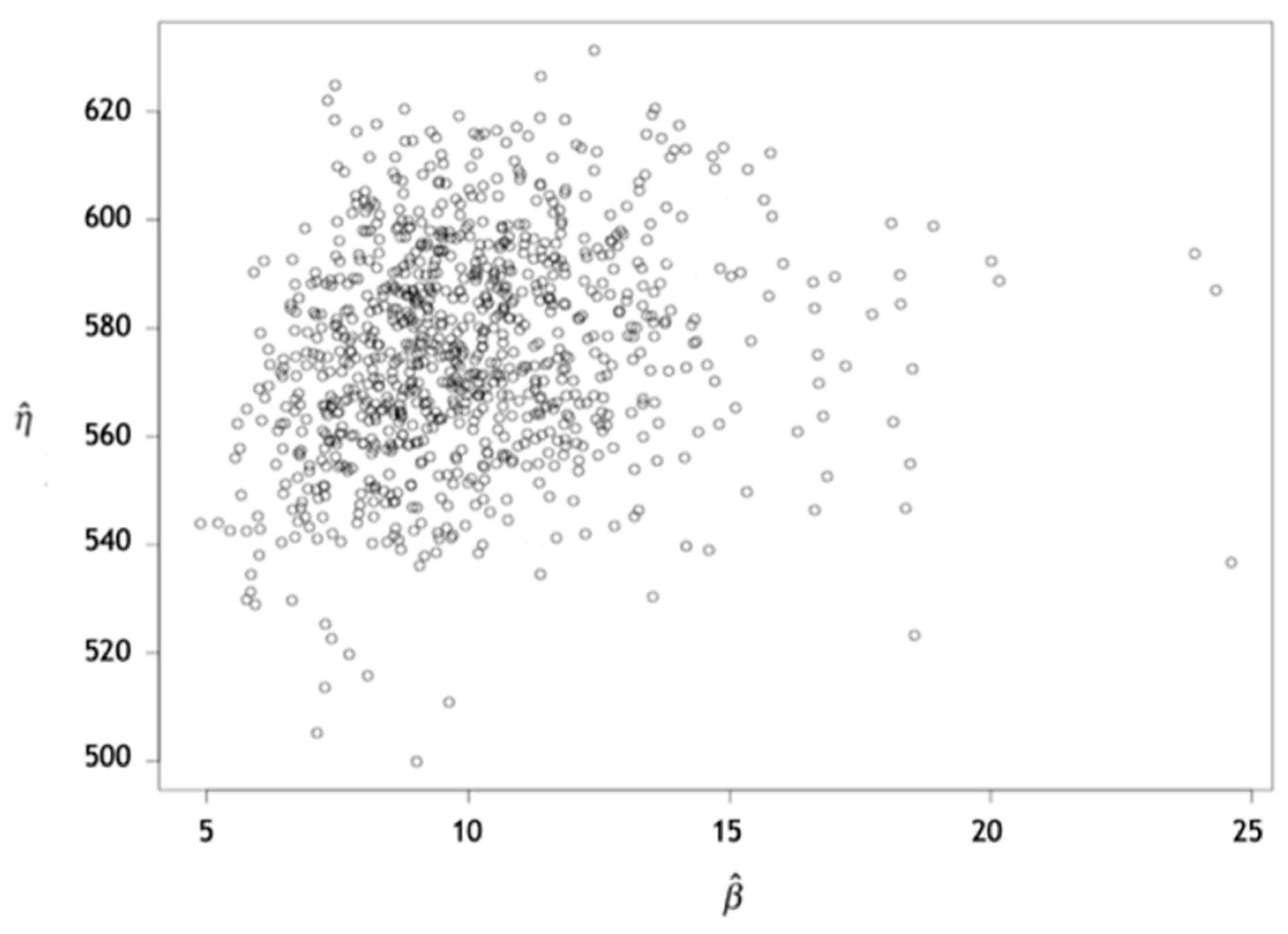
For all bearings, the shape parameter β was found to be greater than 1. The scale parameter η exhibited values ranging between 509.95 and 656.96 operation days. In the bootstrap method, 1000 resampling iterations were performed to obtain reliable estimates. Figure 2 visually presents the confidence interval of the estimated parameters of the Weibull distribution specifically for bearing 1. These intervals were derived from the information obtained through the bootstrap method.

Various tests are available for assessing the fit quality between the data and the theoretical distribution. In this study, the Kolmogorov–Smirnov (K-S) test was chosen due to its simplicity and reliable results, especially for data sets with limited data.

The K-S test involves three steps:

• Formulation of hypotheses:
  The null hypothesis (H₀) states that the population from which the data are derived follows the Weibull distribution. The alternative hypothesis (H₁) suggests that the population does not follow the Weibull distribution.
• Determination of the D value:
  The D value is calculated as the maximum absolute difference between the sample distribution function F(t_i) and the population distribution function F(t). This value is compared to the critical value, which depends on the sample size (n) and the chosen significance level (α). Additionally, the critical value is adjusted based on the shape parameter value (β):
  K = 0.70 (β > 3.0);
  K = 0.75 (1.5 < β < 3);
  K = 0.8 (β < 1.5).
• Comparison:
  If the test statistic D is greater than or equal to the corrected critical value (D ≥ k x critical value), the null hypothesis is rejected (Reject H₀). The p-value also provides insight into the quality of the fit. The p-value represents the probability of observing results as extreme as those obtained if the null hypothesis is true. A large p-value supports H₀, while a small p-value indicates evidence against H₀. If the p-value is greater than 0.05, there is no evidence against H₀. For bearing 1, with a sample size of n = 6 and a significance level of α = 5%, the following results were obtained:
  D = 0.218 < 0.363 (0.70 × 0.519);
  p-value = 0.5294 > 0.05.

Based on these results, the null hypothesis is not rejected, indicating that the population from which the data are derived follows the Weibull distribution. Similar results were obtained for the other bearings.

Estimating the parameters of the Weibull distribution allows for comprehensive reliability analysis of industrial equipment, specifically in centrifugal pumps. By understanding failure patterns through parameter estimation, system designs can be optimized, appropriate materials can be selected, and maintenance intervals can be determined. Reliability estimates derived from Weibull analysis serve as a quantitative basis for decision making, facilitating efficient resource allocation, reducing downtime, and improving system performance.

Furthermore, Weibull analysis enables comparative failure data analysis from different systems, components, or designs. The relative reliability of various products or configurations can be assessed by comparing the estimated parameters.

5. Conclusions

In this study, we addressed the challenge of estimating reliability in industrial equipment, focusing on the example of centrifugal pumps in an oil refinery. Analyzing historical failure data for such systems is a complex task due to censored data and missing information. However, accurate reliability estimation is crucial for effective maintenance and system monitoring.

To overcome the limitations of traditional methods, we proposed the use of the expectation maximization (EM) algorithm as a solution for parameter estimation. The EM algorithm demonstrated its effectiveness in handling limited and censored data, providing accurate estimates of reliability parameters. By applying the EM algorithm, significant cost savings and improved safety can be achieved in critical industries, such as oil refining.

The increasing complexity and criticality of modern systems make accurate reliability estimation more important than ever. The use of advanced statistical methods, such as the EM algorithm, is essential in achieving this goal. For example, in an oil refinery, failure in a pump bearing can lead to costly shutdowns and hazardous accidents. By employing the EM algorithm to estimate Weibull distribution parameters based on limited and censored data, plant operators can proactively monitor and maintain critical components such as bearings, ensuring continuous and safe operations.

Integrating the reliability estimation results from the EM algorithm into maintenance decision-making processes would be a valuable extension. Developing optimization models that consider the estimated failure rates and probabilities could help determine optimal maintenance policies and resource allocation strategies. This integration would contribute to improving maintenance practices, reducing costs, and enhancing system reliability.

Furthermore, the proposed methodology is not limited to the oil industry but can be applied to other sectors, including aerospace, automotive, and healthcare, where limited and censored failure data are common. It is important to acknowledge that the predictions of the EM algorithm will be more accurate with larger amounts of data and higher data quality.