SFBKT: A Synthetically Forgetting Behavior Method for Knowledge Tracing

Abstract

Knowledge tracing (KT) aims to model students’ knowledge levels based on their historical learning records and predict their future learning performance, which constitutes an essential component of intelligent education. Learning and forgetting are closely related, and forgetting can often interfere with the learning process. Prior research has employed diverse techniques to address the issue of interference caused by forgetting factors in predictions, yet many of these methods fail to fully leverage the forgetting information contained within learning records. This paper proposes a synthetically forgetting behavior knowledge tracing (SFBKT) model that comprehensively models a student’s knowledge level by considering both individual forgetting factors and group status. Specifically, the model initially extracts forgetting information from exercise records in the input module, then updates the student’s knowledge state through an improved continuous-time long short-term memory network (CTLSTM), and finally combines the individual state with the group state using collaborative filtering to predict the student’s ability to correctly answer the next exercise. Our predictive model has been evaluated using four public education datasets. The experimental results indicate that our model’s predictions are effective and outperform other existing methods.

1. Introduction

Smart learning and education are new concepts of technology-enhanced learning [1]. In the past three decades, as intelligent education has continued to advance, numerous online education platforms have emerged as a supplement to the limitations of traditional education methodologies [2]. Online education emphasizes the importance of customized instruction that accommodates the unique abilities of individual students and recommends appropriate learning resources based on their knowledge levels. A student’s knowledge level is shaped by their learning stage and cognitive capacity and constantly evolves throughout the learning process. Consequently, real-time monitoring of students’ knowledge levels is indispensable for personalized online education [3]. To gain insight into students’ knowledge proficiency and provide individualized guidance, knowledge tracing (KT) has garnered considerable attention from researchers. Knowledge tracing can generate models of students’ knowledge states based on their past practice, analyze their interactions with online learning materials, identify patterns in their knowledge progression, and predict their future learning outcomes [4]. Specifically, knowledge tracing encompasses two primary objectives: modeling students’ knowledge status and predicting their future performance. The precision of knowledge tracing is directly correlated with the relevance and efficacy of the system’s provided content [5]. In contrast, a user study has shown that presenting content and questions that are excessively challenging or easy for students diminishes their engagement [6]. Therefore, it is essential to create accurate models of students’ knowledge to increase their learning efficiency and satisfaction with the online education system.

The notion of knowledge tracing was initially introduced by Anderson et al. in a technical report in 1986 to facilitate cognitive modeling and intelligent tutoring [7]. Subsequently, a variety of approaches have been devised to tackle the knowledge-tracing challenge. Initially, researchers employed Bayesian inference methods [8,9], which often involved simplifying model assumptions (e.g., assuming only one skill) to render posterior computation more feasible. Subsequently, with the advent of classical machine learning methods, parametric factor analysis methods emerged as the dominant approach to knowledge tracing. Various factors, including those related to students, study materials, and the environment, are modeled by these methods to track students’ knowledge status and make answer predictions [10,11,12]. Moreover, psychological research on students’ learning and forgetting behavior has provided new insights into modeling students’ knowledge state [13,14]. These studies suggest that forgetting is a critical factor that affects a student’s knowledge state over time.

Deep learning techniques have made significant breakthroughs in recent years and have been applied extensively in various fields [15], leading to the rapid emergence of deep learning knowledge tracing models. Piech et al. were the pioneers in this research direction and demonstrated the superior performance of deep learning techniques for knowledge tracing [16]. Over time, numerous knowledge tracing methods have incorporated diverse neural network architectures to enhance their efficacy by considering the unique features of the learning sequence. For instance, graph-based knowledge tracing approaches have utilized graph neural networks to model the knowledge structure in knowledge concept (KC) [17]. Attention-based knowledge tracing techniques have integrated the attention mechanism to capture dependencies among learning interactions [18]. In addition, CKT has incorporated convolutional neural networks (CNNs) to analyze the personalized phased learning patterns of students and predict their learning outcomes [19]. In real-world scenarios, forgetting is an inevitable consequence of learning [20]. According to the Ebbinghaus forgetting curve theory, students’ knowledge proficiency can decline over time due to forgetting [21]. Thus, it is unreasonable to assume that a student’s knowledge state will remain constant over time. Moreover, the incorporation of the forgetting factor into knowledge tracing has advanced with the development of deep learning techniques. To account for the intricate forgetting behavior, the DKT + forgetting model [22] integrates forgetting into deep knowledge tracing through the consideration of three types of side information associated with forgetting. Notably, the HawkesKT model proposes an explicit modeling of temporal cross-effects inspired by point processes, which takes into account the varying impacts of previous interactions [23]. HawkesKT is the pioneering model that incorporates the Hawkes process for the simulation of temporal cross-effects in knowledge tracing; this characteristic facilitates the more effective integration of students’ forgetting behavior into the learning process. Additionally, AKT is an attention-based neural network model that utilizes distance-aware exponential decay with a global decay rate, which also integrates temporal information into the model to compute attention weights [24].

Over the past few years, there have been attempts to incorporate forgetting factors into knowledge tracing. However, the methods proposed so far have relied on either manually designed forgetting features or oversimplified process assumptions, such as fixed time intervals and global decay functions. According to temporal cross-effect theory [23] and temporal point process theory [25], every student’s interaction with an exercise will significantly influence their knowledge states. Figure 1 illustrates how the impacts of different exercises on knowledge states can vary over time. Previous studies’ methods have not been able to fully utilize forgotten information, resulting in a failure to capture dynamic changes in knowledge states. To address this problem, we propose a neural time series point process and a collaborative filtering-based forgetting behavior knowledge tracing model. Building on the ideas of DKT + forgetting [22], neural hawkes process [25], and collaborative filtering (CF) [26], our model considers several factors, including practice records before learning, lag time after learning, and the hidden forgetting factor in the group state. These factors are all essential to effectively capturing students’ forgetting behaviors and improving the accuracy of the model’s forecasts. In particular, we modify the memory cells within the network based on the lag time after learning. This gradual alteration over time serves to mitigate the effects of mutations resulting from interactions. As a result, the training process of the model becomes more akin to the natural forgetting process of students, as opposed to abrupt and drastic changes. Specifically, we first extract three types of forgetting-related information from practice records, which are then combined with the records as joint input data. The forgetting information consists of repetition intervals, sequence intervals, and past practice times. The joint data are fed into the Continuous-Time LSTM network to generate a knowledge state that changes dynamically over time. Lastly, cosine similarity is employed to assess the similarity of the knowledge state, which is then combined with neighbor information for prediction.

In summary, our main contributions are as follows:

• Our study proposes the Synthetically Forgetting Behavior Knowledge Tracing model, which aims to comprehensively model students’ knowledge levels by incorporating pre-training forgetting information, post-training forgetting behavior, and a group forgetting state. This approach allows for a better prediction of students’ performance in the next stage.
• The Neural Hawkes Process is a seminal article in the field of time series point processes. In this study, we enhance it and transfer the improved model to the field of knowledge tracing as part of SFBKT. This enables us to fully consider the forgetting information implicit in students’ training records, even during irregular continuous time periods. By using the self-exciting multivariate point process, the knowledge levels of students obtained by the neural network dynamically change over time, better aligning with the law of human forgetting.
• Our approach employs the expressive power of neural networks to model individual training records while utilizing traditional collaborative filtering to account for similarities in knowledge levels among groups of students. This approach enables us to combine individual student status with group status and avoid ignoring students’ social attributes.
• We tested our model on four widely used public education datasets, and the results indicate that it outperformed the standard methods used for comparison in all four datasets.

The remainder of the article is organized as follows: First, Section 2 provides a brief summary of the research on knowledge tracing and its underlying reasons. Then, in Section 3, our paper offers a precise explanation of the issue that the knowledge tracing task aims to solve. Additionally, we discuss the various components that comprise the SFBKT model structure and provide comprehensive information on its implementation. In Section 4, we compare the experimental outcomes of SFBKT with various baseline methods and variants of the SFBKT model in four public datasets. Finally, in Section 5, we conclude the paper and discuss potential research opportunities in the future.

2. Related Work and Motivation

Research on knowledge tracing can be broadly classified into two phases: the development of KT models based on traditional research methods and the development of KT models based on deep learning. Traditionally, Bayesian knowledge tracing and factor analysis models have been the two primary areas of research in KT. However, in recent years, KT based on deep learning has incorporated various advanced techniques to improve its performance.

Table 1. An overview of knowledge tracing models.

Model	Method	Deep Learning
BKT	Bayesian Knowledge Tracing	×
IRT	Factor Analysis Models	×
AFM
PFA
KTM
DKT	Sequence Modeling KT Models	√
EERNN	Text-Aware KT Models	√
EKT
SAKT	Attentive KT Models	√
AKT
SSAKT
RKT
GKT	Graph-Based KT Models	√
GIKT
SKT
DKT + Forgetting	Forgetting-Aware KT Models	√
KPT
HawkesKT
DGMN
DKVMN	Memory-Augmented KT Models	√
SKVMN

presents an overview of the principal knowledge tracing models that have been developed in the KT literature.

Bayesian knowledge tracing is based on the principles of mastery learning, which assumes that students can attain mastery of a skill through practice if two conditions are met: (a) knowledge is represented as a hierarchical structure of skills, and (b) the learning experiences are structured such that students can master lower-level skills before progressing to higher-level ones [2]. The BKT approach usually employs probabilistic graphical models, such as Hidden Markov Models [8] and Bayesian Belief Network [9], to monitor how students’ knowledge states evolve while they practice various skills. The BKT model posits a uniform level of prior knowledge and learning rate for all students with regard to any skill, failing to personalize model parameters for individual students. Consequently, the model may provide inaccurate estimates of learning performance, with such estimates tending to skew toward the mean. Subsequent studies have primarily focused on enhancing the BKT model from two key perspectives: incorporating individualized parameters for each student and modeling the interplay between various skills. Bayes’ theorem is a fundamental tool in these models that describes the relationship between two events, A and B, as follows:

$$\mathrm{p}\left(\left.\mathrm{A}\right|\mathrm{B}\right)=\frac{\mathrm{p}\left(\left.\mathrm{B}\right|\mathrm{A}\right)\mathrm{p}\left(\mathrm{A}\right)}{\mathrm{p}\left(\mathrm{B}\right)}$$

(1)

Factor analysis models in education are based on Item Response Theory (IRT) [27], which has made significant contributions to educational measurement. IRT typically constructs a function that estimates the performance of students based on the various factors involved in their learning processes. Although the original IRT was only capable of modeling single-skill problems, subsequent research has enabled it to model problems involving multiple skills. In such cases, the relationship between skills and items is commonly expressed using a $Q$-matrix, where each entry $q_{jk}$ is set to 1 if item $j$ involves skill $k$ and 0 otherwise. The $Q$-matrix is often used as an additional source of information in these models. Psychometric models can be well understood from a psychological perspective, but their ability to encode complex features is limited by simplistic parameter settings.

Deep Knowledge Tracing (DKT) is an innovative knowledge tracing model that utilizes deep learning to predict learning performance. To overcome the limitations of DKT, a range of knowledge tracing models have been developed using it as a foundation. For instance, the Extended-DKT model represents an improvement over the original DKT model by incorporating both student and exercise features. The model leverages student features, such as prior knowledge, answer rate, and practice time, as well as exercise features, such as textual information, question difficulty, skill level, and skill dependency [28]. To enhance the capacity of the original loss function and mitigate inconsistencies in answering predictions for questions that share similar knowledge components (KC), the DKT+ model introduces two regularization terms [29]. Furthermore, to capture the intricate KCs that students learn, key-value memory has been introduced as a representation of the knowledge state, inspired by memory-augmented neural networks [30]. The use of an external memory structure provides greater representational power than the hidden variables used in the original DKT model, thus enhancing the model’s ability to indicate proficiency. Several studies have endeavored to integrate attention mechanisms into KT models by adopting the Transformer architecture [31]. The common goal of these studies is to optimize prediction performance by redistributing the attention weight of the problem. Although each work adopts a unique approach to incorporating the attention mechanism, the underlying idea remains consistent [18,32,33]. Moreover, graph-based KT models utilize graph neural networks to model the interrelatedness and interdependence among KCs. Despite some previous research addressing the limitations of existing KT models and advancing the field of deep learning-based KT, the feature extraction methods used in these models have tended to be relatively simplistic, resulting in suboptimal utilization of student practice record information.

Table 2. Comparison of previous main research in KT. The “Learning Model” column means the main machine learning or deep learning techniques used, the “Knowledge State” column means how the obtained student knowledge level is stored, and the “Forgetting” column indicates whether the mode takes forgetting information into account.

KT Model	Year	Learning Model	Knowledge State	Forgetting
IRT	1993	LR	Real-valued vector	×
BKT	1994	HMM	Binary scalar	×
AFM	2008	LR	Real-valued vector	×
DKT	2015	RNN/LSTM	Vector	×
DKVMN	2017	MVNN	matrix	×
KTM	2019	FM	Real-valued vector	×
DKT + Forgetting	2019	RNN/LSTM	Vector	√
GKT	2019	GNN	Vector	×
AKT	2020	FFN + MSA	Vector	√
HawkesKT	2021	FM	Real-valued vector	√

provides a summary of the key descriptive features of the main KT methods employed in the field.

Based on current knowledge, it appears that students’ learning sequences are embedded with complex information forgetting. The probability of a student providing a correct answer in the next exercise is influenced not only by their learning history but also by the time lag of the previous exercise. Traditional knowledge tracing models and deep knowledge tracing models have rarely comprehensively considered forgetting behavior. Most models only account for forgetting factors in past exercise records, such as the DKT-forgetting model, and ignore the forgetting process after practice. The introduction of the neural Hawkes process is a significant step in addressing this issue, as it expands the traditional multivariate Hawkes process by incorporating the time decay effects of past times and LSTM nodes [25]. Building on this concept, we aim to combine traditional forgetting factors with the Hawkes process to enable dynamic changes in students’ knowledge states over time while also considering past practice records, which align more closely with the forgetting curve. Collaborative filtering can further enhance the full utilization of information by better integrating individual and group data.

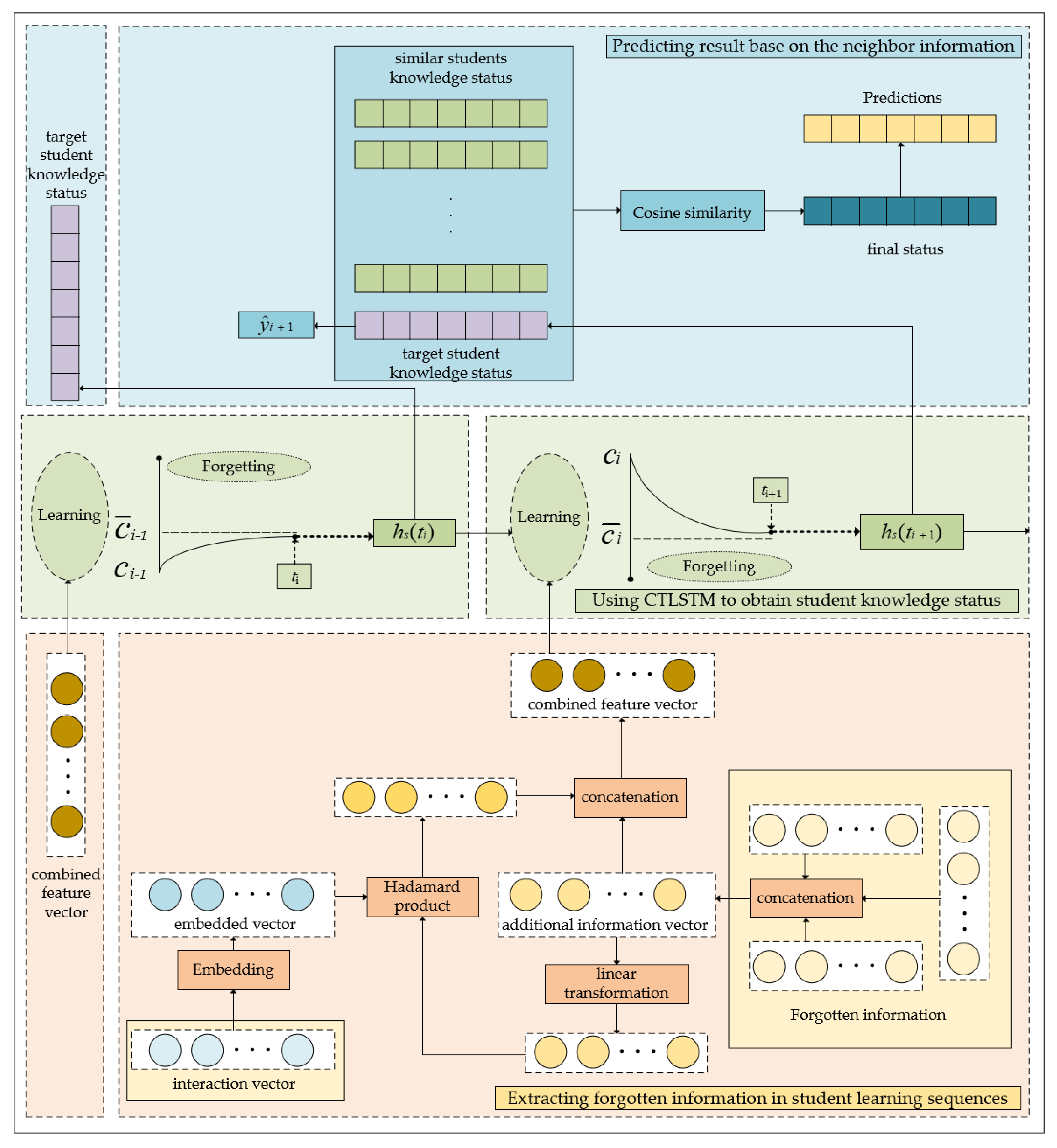
3. Proposed Method

3.1. Problem Definition

Given a student’s interaction sequence $S_t=\left\{k_0,k_1,\cdots k_n\right\}$, knowledge tracing aims to assess the student’s knowledge state and predict whether they can answer the next interaction $k_{n+1}$ correctly. In the learning sequence, $k_i$ is defined as a tuple $\left(q_i,t_i,a_i\right)$, which includes the question $q_i$ that the student attempts to answer at timestamp $t_i$, and the corresponding response $a_iϵ\left\{0,1\right\}$ indicates whether the exercise $q_i$ has been answered correctly (1 stands for correct, and 0 represents wrong).

3.2. Model Architecture

The Synthetically Forgetting Behavior Knowledge Tracing model comprises three primary components. The first component extracts forgotten information from a student’s learning sequences. This process involves integrating additional information related to forgetting from the student’s sequence of interactions with their interaction sequence. The second part involves obtaining the student’s knowledge status through a continuous-time long short-term memory network (CTLSTM), which captures changes in the student’s knowledge state throughout the learning process. Finally, the third component predicts the student’s performance in the next time slice by leveraging neighbor information and using cosine similarity to determine the similarity of different students’ knowledge states. The model combines individual and group information to determine the student’s knowledge state and predict their performance.

The SFBKT model is an improvement over existing models such as DKT-forgetting [22] and HawkesKT [23] as it considers forgetting as a critical factor in student learning and uses continuous-time LSTM networks to capture changes in student knowledge states over time. Figure 2 demonstrates how the SFBKT model enhances the model structures of DKT-forgetting and HawkesKT.

DKT-forgetting integrates practice sequences and additional forgetting information in the data processing stage and uses LSTM networks for feature extraction to obtain the student’s knowledge status. However, DKT-forgetting assumes that the knowledge state remains unchanged until the next exercise, which contradicts the law of forgetting. SFBKT improves upon DKT-forgetting in two primary ways. First, the SFBKT model enhances the LSTM network to capture the change in the knowledge state over time. This improvement addresses the inadequacy of the DKT-forgetting model by incorporating the forgetting curve into the learning process, where the students’ mastery of exercises gradually declines over time [34]. Second, the SFBKT model leverages group information to improve prediction accuracy. Since students often learn together in groups rather than independently, combining the knowledge state of the group helps to reduce interference from incorrect information recorded in the dataset. This approach combines information from students with similar knowledge states with the student being predicted, resulting in a more precise assessment of the student’s knowledge state.

HawkesKT represents the first model to incorporate the Hawkes process for simulating temporal cross-effects in knowledge tracing, serving as an inspiration for our work. Nevertheless, HawkesKT employs an exponential function as a kernel function to approximate the forgetting curve, which only crudely simulates the average knowledge state of students and cannot be customized for individual students. In contrast, we integrate the CTLSTM network with the Hawkes process to model student knowledge, thereby facilitating the personalized tracing of forgetting patterns for each student. This approach yields more precise and dependable predictions of students’ knowledge states over time.

3.2.1. Extracting Forgotten Information in Student Learning Sequences

Given the proven effectiveness of the method of extracting forgotten information proposed by DKT-forgetting, we adopted this method in our work and improved upon it. However, we differ from DKT-forgetting in that our SFBKT approach requires the extracted features to be fed into the CTLSTM network instead of the RNN network. We proceed as follows:

• Extracting information related to memory retention from learning sequences. Previous studies have confirmed the existence of temporal cross-effects, which means that each previous interaction has a time-sensitive effect on mastery of the target skill. In our approach, we extract three pieces of information from a student’s learning sequence: the time interval of the same skill, the time interval of the previous skill, and the number of attempts at the same skill in the past.
• Incorporate information into the input space of the model. To model the knowledge acquisition process of students, we utilize a trainable embedding matrix A to calculate the embedding vector $v_i$ of the interaction vector $k_i$ at time $i$, instead of assigning arbitrary values. The above process can be summarized as follows:

$$k_i=\left(q_i,a_i\right)$$

(2)

$$v_i=k_i\times A$$

(3)

The information’s three characteristics are expressed as one-hot vectors and subsequently merged. Before entering the CTLSTM module, the embedding vector $v_i$ and additional information vector $p_i$ are combined into $x_i$ and fed into the network. Specifically, $p_i$ is created by concatenating three one-hot vectors and transforming them using a trainable transformation matrix $C$ to match the dimensions of $v_i$. Then, a Hadamard product operation is performed on $v_i$ and the transformed $p_i$, resulting in a vector that is connected with $p_i$ to form the combined feature vector $x_i$. The above process can be summarized as follows:

$$x_i={\theta }^{in}\left(v_i,p_i\right)=\left[v_i⨀{Cp}_i;p_i\right]$$

(4)

3.2.2. Using CTLSTM to Obtain Student Knowledge Status

In continuous-time LSTM, the knowledge state vector is dependent on the memory unit vector $c_t$ as the lstm network. The key difference is that each memory unit $c$ decays exponentially at a rate $\delta$ towards a steady-state value $\stackrel{-}{c}$ in subsequent time intervals after the event. Formula (5) depicts how the hidden states $h_t$ are continually obtained from the memory cells $c_t$ as the cells decay, where $O_i$ is the output gate following the $\mathrm{i}-th$ event. $h_t$ is analogous to $h_i$ in an LSTM language model [35], summarizing the past knowledge state changes caused by learning sequences $\left\{k_0,k_1,\cdots ,k_{i-1}\right\}$. Afterwards, the model predicts the probabilities of answering correctly for all skills, based on the hidden states $h\left(t_{i+1}\right)$. The resulting output $\widehat{Y}\left(t_{i+1}\right)$ is a vector of equal length to the number of questions. Each entry in $\widehat{Y}\left(t_{i+1}\right)$ represents the predicted probability that the student answered a specific question correctly. Therefore, the prediction ${\widehat{y}}_{i+1}$ for question $q_{i+1}$ can be obtained from the entry corresponding to $q_{i+1}$ in $\widehat{Y}\left(t_{i+1}\right)$. The above can be summarized as follows:

$$h\left(t\right)=O_i\odot \left(2\sigma \left(2c\left(t\right)\right)-1\right)fortϵ\left(t_i,\right.\left.t_{i+1}\right]$$

(5)

$$\widehat{Y}\left(t_{i+1}\right)=\sigma \left(W^{out}h\left(t_{i+1}\right)+b^{out}\right)$$

(6)

In our model, $h_t$ also reflects memory decay caused by the time interval $t_i-t_{i-1}$ between the current event and the last event. This interval $\left(t_{i-1},\right.\left.t_i\right]$ ends when the next event $k_i$ occurs stochastically at some time $t_i$. At this point, the continuous-time LSTM reads $\left(k_{\dot{i}},t_i\right)$ and updates the current (decayed) hidden cells $c_{\left(t\right)}$ to new initial values $c_{i+1}$, based on the current (decayed) hidden state $h\left(t_i\right)$. When information is input at time $t_i$, the update formula of the model is similar to traditional LSTM. The overall process is illustrated in Formulas (7)–(13).

$$i_{i+1}\leftarrow \sigma \left(W_i{x}_i+U_{i}h\left(t_i\right)+d_i\right)$$

(7)

$$f_{i+1}\leftarrow \sigma \left(W_f{x}_i+U_{f}h\left(t_i\right)+d_f\right)$$

(8)

$$z_{i+1}\leftarrow 2\sigma \left(W_z{x}_i+U_{z}h\left(t_i\right)+d_z\right)-1$$

(9)

$$o_{i+1}\leftarrow \sigma \left(W_o{x}_i+U_{o}h\left(t_i\right)+d_o\right)$$

(10)

$$c_{i+1}\leftarrow f_{i+1}\odot c\left(t_i\right)+i_{i+1}\odot z_{i+1}$$

(11)

$${\stackrel{-}{c}}_{i+1}\leftarrow {\stackrel{-}{f}}_{i+1}\odot {\stackrel{-}{c}}_i+{\stackrel{-}{i}}_{i+1}\odot z_{i+1}$$

(12)

$${\delta }_{i+1}\leftarrow f\left(W_d{x}_i+U_{d}h\left(t_i\right)+d_d\right)$$

(13)

The vector $x_i$ is derived from Formulas (2)–(4), which represents the new exercise item information combined with the forgotten factor in the input module. The symbol $\sigma$ is the logistic sigmoid function, and $i$, $f$, $o$, $c$ are respectively the input gate, forget gate, output gate and cell activation vectors. The upright-font subscripts $i$, $f$, $z$, $c$ and $o$ are not variables but constant labels that distinguish different $W$, $U$ and $d$ tensors. The $\stackrel{-}{f}$ and $\stackrel{-}{i}$ in Formula (12) are defined analogously to $f$ and $i$ but with different weights. The key difference between this method and the traditional LSTM is that the update depends not only on the knowledge state at $t_{i-1}$ time, but also on the time interval between this time and the last practice, which affects the update of the knowledge state. As time progresses, the memory cell vector changes according to Formula (14). Specifically, the memory cell vector at the moment when a new practice occurs continues to decay deterministically from $c_{i+1}$ to the target ${\stackrel{-}{c}}_{i+1}$ at different rates. In other words, on the interval $\left(t_i,t_{i+1})\right.$, $c_{\left(t\right)}$ follows an exponential curve that begins at $c_{i+1}$ (in the sense that $\underset{t\to t_i^{+}}{\lim }c\left(t\right)=c_{i+1}$) and decays toward ${\stackrel{-}{c}}_{i+1}$ (which it would approach as $t\to \infty$, if extrapolated).

$$c\left(t\right)\stackrel{\mathrm{def}}{=}{\stackrel{-}{c}}_{i+1}+(c_{i+1}-{\stackrel{-}{c}}_{i+1})\exp \left(-{\delta }_{i+1}\left(t-t_i\right)\right)fortϵ\left(t_i,\right.\left.t_{i+1}\right]$$

(14)

The aforementioned scenario pertains to situations wherein a new test question is answered correctly, resulting in a sudden increase followed by decay in the memory unit vector $c_t$. Similarly, when the response is incorrect, $c_t$ undergoes a sudden decrease, followed by an increase, and the formula remains the same as in the case of a correct response.

3.2.3. Predicting Results Based on Neighbor Information

The SFBKT network is utilized to calculate the knowledge state vector of each student, resulting in the acquisition of the knowledge state vector matrix $U\left(m\times n\right)$ representing all students. Cosine similarity is employed to determine the similarity between the vectors $U_i$ and $U_j$. Assuming that $U_i=\{a_1,a_2,\dots ,a_n\}$ and $U_j=\{b_1,b_2,\cdots ,b_n\}$, the cosine similarity between $U_i$ and $U_j$ is defined by Formula (15).

$$\cos \left(\theta \right)=\frac{U_i\cdot U_j}{\parallel U_i\parallel \parallel U_j\parallel }=\frac{\sum _{i=1}^n{a}_i\cdot b_i}{\sqrt{\sum _{i=1}^n{\left(a_i\right)}^2}\times \sqrt{\sum _{i=1}^n{\left(b_i\right)}^2}}$$

(15)

Through the ranking of cosine similarity, students whose scores are above a certain threshold (0.9 in the experiment) are selected as similar users. For the target student $i$, the final knowledge state vector is predicted using Formula (16). In this equation, $U_i$ represents the knowledge level vector of the target student, while $average\left(N_i\right)$ is the average knowledge level vector of the similar students. The parameter $\rho$ is used to adjust the proportion of the individual knowledge level of students and the common knowledge level between students when using $f_i$ to predict. The value range of $\rho$ is $[0,1]$. As $\rho$ increases, the influence of the individual knowledge level of students also increases. Specifically, when $\rho =0$, $f_i$ represents the average knowledge level of neighboring students without considering the individual state of the target student. On the other hand, when $\rho =1$, $f_i$ represents solely the personal knowledge level vector output by the SFBKT model.

$$f_i=\rho \cdot U_i+\left(1-\rho \right)\cdot average\left(N_i\right)$$

(16)

3.3. Optimization

All parameters of SFBKT are obtained by training on the student practice sequence. A cross-entropy loss function and Adam optimizer are employed to optimize the model. Specifically, ${\hat{y}}_t^s$ represents the model’s prediction for the performance of student $s$ at time $t$, while $y_t^s$ represents the actual performance of the student. The loss function used is formulated as follows:

$$\mathcal{L}=-\sum _S\sum _t\left(y_t^{s}log{\hat{y}}_t^s+(1-y_t^s)\mathrm{l}\mathrm{o}\mathrm{g}(1-{\widehat{y}}_t^s)\right)$$

(17)

4. Experiments

4.1. Experimental Datasets

To ensure an equitable comparison of our model with other knowledge-tracing models, we conducted experiments using identical public datasets to evaluate our model’s performance. Specifically, we used four datasets, namely ASSISTment09-10, ASSISTment12-13, ASSISTment17, and Slepemapy.cz. ASSISTments is an online tutoring system specifically designed to provide mathematical instruction to students. We selected three publicly available datasets from different time periods. For the Slepemapy.cz4 dataset, which comes from an online geography practice system, we defined the skill ID as ‘place_asked’ to maintain consistency.

Utilizing the previously mentioned datasets necessitates consideration of student records that have insufficient practice data, as such records may not accurately reflect the actual learning progression of the students and could be unsuitable for implementation in time series models [36]. Therefore, we removed student records with fewer than five practice records from the sample set. Additionally, we only considered the first 50 interactions of each user, as predictive performance is more important when there is little user history. Furthermore, the ASSISTment09-10 dataset is devoid of timestamps for each interaction. Consequently, we made the working assumption that users responded to questions with an identical time interval of 1 s.

Table 3. Introduction of the datasets.

Dataset	Students	Skills	Records
ASSISTment09-10	3700	111	110,200
ASSISTment12-13	25,300	245	879,500
ASSISTment17	1700	102	9,786,500
Slepemapy.cz	81,700	1473	2,877,500

presents the descriptive statistics for all four datasets post-preprocessing.

4.2. Experimental Environment

The success of a model analysis experiment is critically dependent on the availability of an appropriate hardware and software environment.

Table 4. Description of the experimental environment.

Configuration Environment	Configuration Parameters
Operating System	Windows 10 64-bit
GPU	RTX 3070
CPU	R7 5800H
Memory	16 GB
Programming language	Python3.6
Deep learning framework	Pytorch 1.7.1
Python library	Scikit-learn, Numpy, Pandas

presents an overview of the key hardware and software environment configurations utilized in this study.

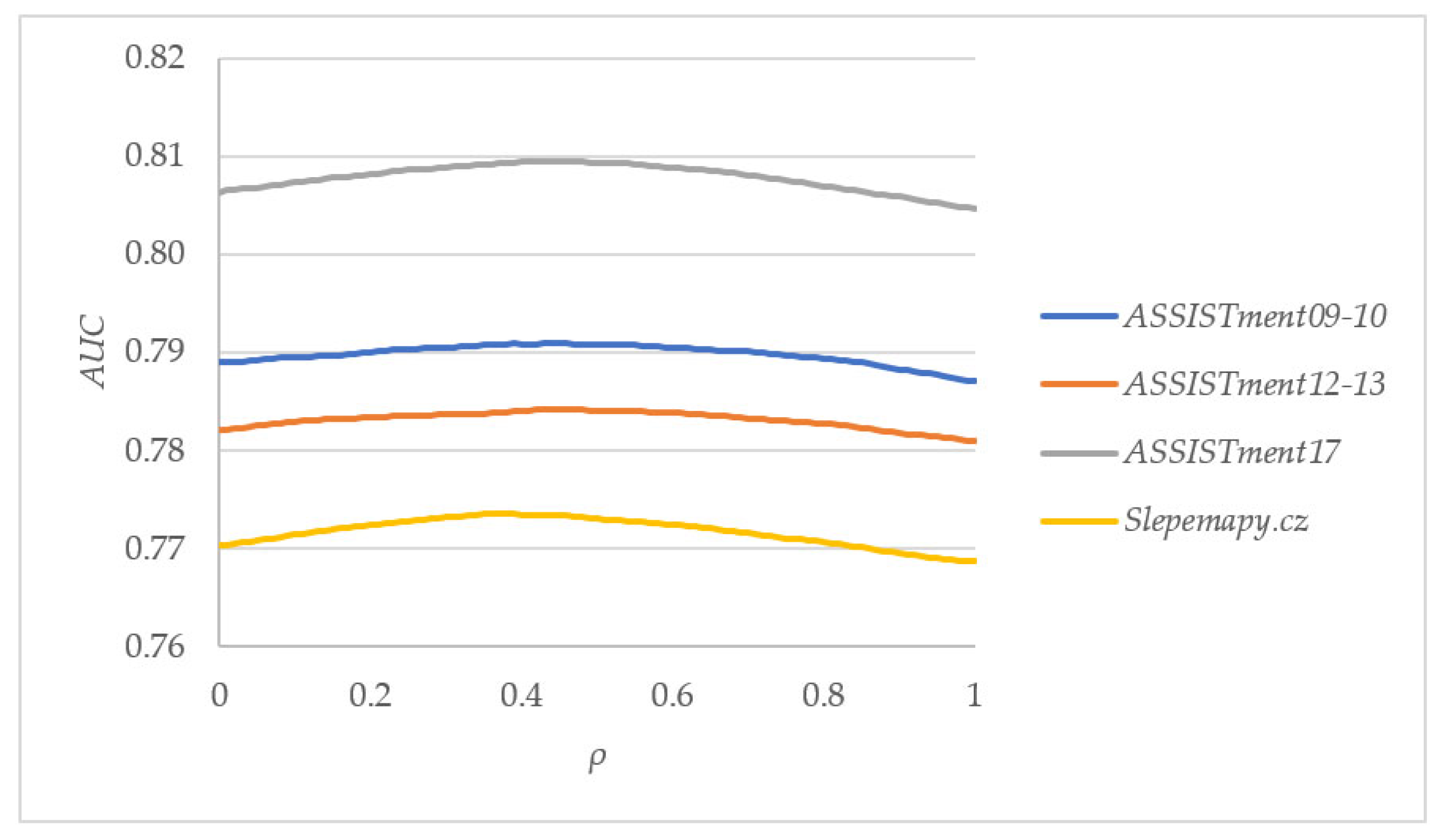
4.3. Results and Discussion

We conducted 5-fold cross-validation in our experiments. For each fold, we divided the dataset into three parts: the training set, the validation set, and the test set, accounting for 70%, 10%, and 20%, respectively. Area under the curve (AUC) and accuracy (ACC) were used as evaluation indices to assess the model’s performance. In order to strike a balance between prediction accuracy and computational resources, we established the hyperparameters, as presented in

Table 5. Hyperparameters of the SFBKT.

Hyperparameters	Value
Learning rate	0.001
Batch size	1
Hidden size	64
Embed size	64
Epochs	100
Early stop	5
K-Fold	5

. It is worth mentioning that, irrespective of the available computational resources, the SFBKT model can achieve even more accurate predictions by adjusting its hyperparameters.

Furthermore, in the collaborative filtering component of our model, the parameter $\rho$ is utilized to adjust the proportion of influence of individual knowledge levels of students and the common knowledge level of the student group on the recommendation results. The value range of $\rho$ is $[0,1]$. When $\rho$ is smaller, the predicted exercise score vector is closer to that of the knowledge state of the student group, similar to the target students. On the other hand, when the value of $\rho$ is closer to 1, the final vector is more similar to the students’ personal knowledge status vector. Figure 3 illustrates the relationship between AUC and $\rho$ when the SFBKT method predicts varying $\rho$ across the four datasets. The experimental results indicate that $\rho$ has a significant impact on prediction effectiveness. For all four datasets, $\rho$ between 0.4 and 0.5 yielded the highest AUC values, suggesting a strong correlation between individual student states and the group’s state.

Baseline comparison. To evaluate the performance of our synthetically forgetting behavior knowledge tracing method, we selected five classic models for comparative experiments, including:

• DKT. It was the first to employ deep learning methods to trace knowledge progression. By utilizing the long short-term memory model, it has the capability to monitor changes in students’ proficiency levels over an extended period. This is a conventional technique that has been refined by numerous models in recent years.
• DKT + Forgetting. Although several models have explored the concept of forgetting behaviors in knowledge tracing, DKT-Forgetting stands out as the pioneer in integrating forgetting-related information into deep learning.
• KTM. It employs Factorization Machines to model the interplay between features. The characteristics taken into account in this approach comprise question ID, skill ID, previous responses to diverse skills, and temporal features within DKT + Forgetting.
• HawkesKT. It represents a pioneering category of knowledge-tracing methodologies that resulted from the integration of temporal point processes and knowledge-tracing studies. This approach builds upon the observed temporal crossover effects in the data, where each historical interaction has a continuously changing effect on the target skill, offering fresh perspectives on the incorporation of forgetting behavior.
• AKT. It employs a novel attention mechanism that links a student’s forthcoming responses with their previous responses. This attention mechanism calculates attention weights through exponential decay and a context-sensitive relative distance metric, as well as the resemblance between the questions.

Table 6. AUC and ACC of all methods on the four datasets (higher is better), the best results are in bold face, and the best baseline is underlined.

Method	ASSISTment 09-10	ASSISTment 12-13	ASSISTment17	Slepemapy.cz
Metrics	ACC    AUC	ACC    AUC	ACC    AUC	ACC    AUC
DKT	0.7396   0.7508	0.7275    0.7314	0.6981    0.7273	0.7971   0.7421
DKT + Forgetting	0.7402   0.7537	0.7388   0.7457	0.6993   0.7302	0.8009   0.7498
KTM	0.7327   0.7415	0.7439   0.7532	0.6935   0.7237	0.7967   0.7415
HawkesKT	0.7472   0.7623	0.7513   0.7663	0.7063   0.7487	0.8028   0.7523
AKT-R	0.7375   0.7462	0.7452   0.7552	0.7174   0.7583	0.7986   0.7462
SFBKT	0.7593   0.7909	0.7544   0.7842	0.7404   0.8095	0.8087   0.7736

presents a performance comparison of our SFBKT model with five classic models. As the DKT model outperforms traditional KT methods significantly, we only select models that appear after DKT as baseline methods. Figure 4 visualizes the AUC results of all models on the four datasets in the form of histograms, providing an intuitive comparison of their predictive effects.

Among these methods, the extent of the considered forgetting factors positively correlates with their predictive performance. DKT and KTM do not consider forgetting factors, resulting in lower performance than the other three methods that incorporate forgetting behaviors. HawkesKT performs best on most datasets by deeply considering the time cross-effect in the learning sequence. However, our SFBKT model outperforms other models in both ACC and AUC for all datasets. Specifically, in the ASSISTment09-10 dataset, SFBKT achieves an ACC of 0.7593 and an AUC of 0.7909, which are 1.21% and 2.86% higher than the best results among the five baseline methods, respectively. On the ASSISTment12-13 dataset, SFBKT achieves an ACC of 0.7544 and an AUC of 0.7842, which are 0.31% and 1.79% higher than the best results among the five baseline methods, respectively. On the ASSISTment17 dataset, SFBKT achieves an ACC of 0.7404 and an AUC of 0.8095, which are 2.30% and 5.12% higher than the best results among the five baseline methods, respectively. On the Slepemapy.cz dataset, SFBKT achieves an ACC of 0.8087 and an AUC of 0.7736, which are 0.59% and 2.13% higher than the best results among the five baseline methods, respectively. Therefore, SFBKT can better classify the prediction results of students’ correctness.

Ablation Study. We conduct a series of ablation experiments to evaluate the performance of individual components in SFBKT, thereby enabling us to assess the effectiveness of each component and determine its impact on the overall system. Since the model consists of three modules, we remove one module in turn to observe its impact on the prediction.

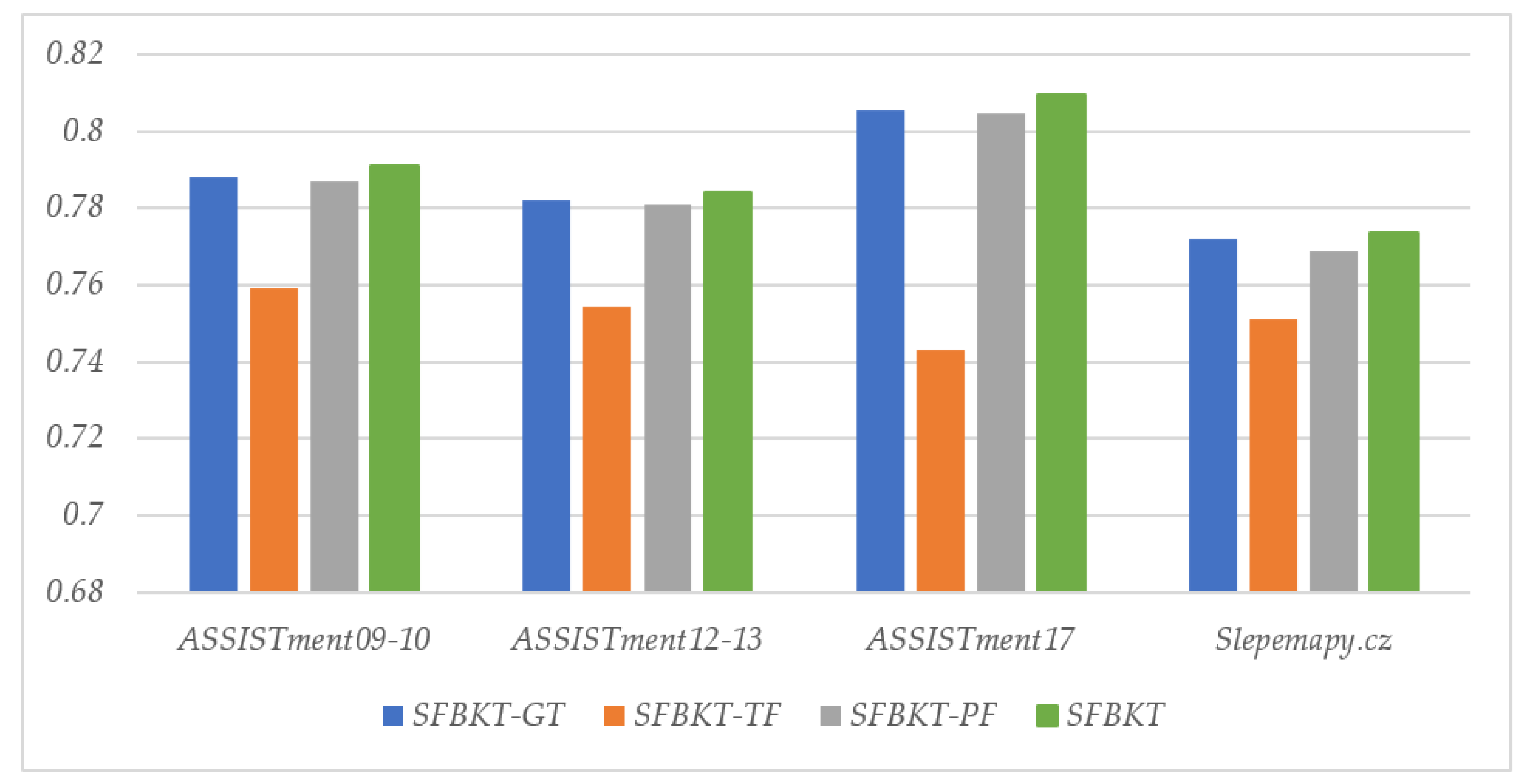
• SFBKT-GF. The SFBKT-Group Forgetting variant model is used to study the influence of personal forgetting information processing in the SFBKT model on prediction. In the input module of SFBKT-GF, the part of extracting students’ past forgetting records is removed. Thus, the variant model maintains the network module and output module of the SFBKT model, while reducing the input data of the CTLSTM network to a series of student exercises. SFBKT-GF can effectively reflect the degree of influence of students’ personal forgotten information on predictions.
• SFBKT-TF. To study the importance of the continuous-time long short-term memory network in the SFBKT model for prediction performance, the SFBKT-TF variant model removes it and compares it with the original model. At this time, the second part of the model becomes the traditional LSTM network, which is called the SFBKT-Traditional Forgetting variant model.
• SFBKT-PF. To investigate how group forgetting impacts the predictive accuracy of the SFBKT model, the SFBKT-Personal Forgetting variant model removes the part of collaborative filtering by considering the state of group knowledge from the SFBKT model. Specifically, the SFBKT-PF model first integrates the students’ forgetting information and the record of doing questions as input. Then, through the CTLSTM network, the time feature is extracted to obtain the student’s knowledge status and predict the result based on this output.

Table 7. Comparison of the experimental results among the SFBKT and variants of SFBKT.

Method	ASSISTment 09-10	ASSISTment 12-13	ASSISTment17	Slepemapy.cz
Metrics	ACC     AUC	ACC     AUC	ACC     AUC	ACC     AUC
SFBKT-GF	0.7581   0.7883	0.7535   0.7822	0.7361   0.8057	0.8064   0.7721
SFBKT-TF	0.7423   0.7592	0.7448   0.7544	0.7036   0.7431	0.8001   0.7512
SFBKT-PF	0.7566   0.7870	0.7518   0.7810	0.7345   0.8046	0.8026   0.7688
SFBKT	0.7593   0.7909	0.7544   0.7842	0.7404   0.8095	0.8087   0.7736

presents the prediction performance of SFBKT and its variants (SFBKT-GF, SFBKT-TF, and SFBKT-PF) on four datasets, namely, ASSISTment09-10, ASSISTment12-13, ASSISTment17, and Slepemapy.cz. Notably, different models based on the same hyperparameters were used in experiments on the same datasets. The other modules within SFBKT maintained identical configurations, with the only variation being the structure of the module in each individual experiment. To facilitate a more intuitive comparison between the original model and its variants, the histograms in Figure 5 display the AUC outcomes for SFBKT and its variant models on the four datasets.

Among the various model variants, the SFBKT-TF model performed the worst, which suggests that the CTLSTM network played a crucial role in improving model performance. Although the AUC of the other two variant models was similar to the original model, subtle differences still existed, reflecting certain underlying rules. Specifically, the SFBKT-GF model performed better than the SFBKT-PF model, which could be attributed to two factors. First, although the former eliminated the artificial integration of personal information, the CTLSTM network in the model still captured and processed personal forgetting information, thereby reducing the impact of deleted modules on prediction. Second, the collaborative filtering module fused similar students’ knowledge states with the target students’ knowledge states, thereby mitigating the influence of unreasonable data collected in individual practice sequences and enhancing the weight of effective data in the process of knowledge state formation. These two reasons contributed to the excellent performance of the SFBKT-GF model.

By conducting ablation experiments, we assessed the importance of each module of the model in enhancing its performance. The most crucial module was found to be the improved network module. When this module was removed and the original RNN network was restored, the prediction accuracy of the model was significantly reduced. Specifically, the AUC of the SFBKT-TF variant model on the ASSISTment09-10 dataset decreased by 3.17% when compared with the original model. Similar outcomes were observed in other datasets, which further underscores the importance of this module in improving model performance. Our findings demonstrate the feasibility of integrating the theory of neurally self-modulating multivariate point processes into the field of knowledge tracing and the promising results that can be achieved. Additionally, the other two modules played significant roles and contributed to the improvement of the model’s performance.

The experimental results presented above demonstrate that SFBKT outperforms previous knowledge tracing methods in terms of predictive performance, with each module playing its due role. This indicates that our consideration of the forgetting factor is more profound than previous models, effectively capturing the forgetting behavior of students in the learning sequence. The practical significance of our model is twofold: for students, it reduces the number of useless exercises and promotes more efficient learning, while for teachers, it enhances their work efficiency, enabling personalized education for each student. Overall, through its innovative design and implementation, it has demonstrated the ability to effectively optimize learning outcomes and improve the quality of education. Our SFBKT model can contribute significantly to the advancement of intelligent education.

5. Conclusions

To address the limitations of the existing Knowledge Tracing model, and completely consider the forgotten information in the student learning sequence, we propose a synthetically forgetting behavior knowledge tracing model (SFBKT). SFBKT comprises three modules to process forgetting information and to better analyze the forgetting behavior of students in the learning sequence. First, SFBKT identifies the learning characteristics related to forgetting from the learning records before learning. Second, the jointly learned features are input into the CTLSTM network. Lastly, collaborative filtering is combined with the learning status of similar students to predict whether the students can answer the questions correctly. We verify the prediction performance of the SFBKT model on four public datasets, and the experimental results demonstrate that SFBKT’s prediction effect is superior to that of the five classic knowledge tracing models. Therefore, SFBKT can effectively utilize forgotten information in the student learning sequence and improve prediction accuracy. Additionally, we conduct multiple experiments comparing the predictive performance of SFBKT with its variant models and identifying the role of each module.

As part of our future research objectives, we plan to utilize the findings from this study to investigate the forgetting patterns of individual students, with the ultimate goal of enabling more personalized and targeted instruction. Additionally, we intend to enhance the scalability of SFBKT by incorporating supplementary side information, such as skill dependencies and the role of group size, individual age, and gender on the model’s performance, to improve the accuracy of our predictions.