EC-GAN: Emotion-Controllable GAN for Face Image Completion

Abstract

Image completion methods based on deep learning, such as Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs), have succeeded in producing semantically plausible results. However, existing facial image completion methods can either produce only one result or, although they can provide multiple results, cannot attribute particular emotions to the results. We propose EC-GAN, a novel facial Emotion-Controllable GAN-based image completion model that can infer and customize generative facial emotions. We propose an emotion inference module that infers the emotions of faces based on the unmasked regions of the faces. The emotion inference module is trained in a supervised manner and enforces the encoder to disentangle the emotion semantics from the native latent space. We also developed an emotion control module to modify the latent codes of emotions, moving the latent codes of the initial emotion toward the desired one while maintaining the remaining facial features. Extensive experiments were conducted on two facial datasets, CelebA-HQ and CFEED. Quantitative and qualitative results indicate that EC-GAN produces images with diverse desired expressions even when the main features of the faces are masked. On the other hand, EC-GAN promotes semantic inference capability with irregularly masked holes, resulting in more natural facial expressions.

1. Introduction

Image completion [1,2] (also known as image inpainting) is the task of filling in the missing parts of an image with visually realistic and semantically plausible content. As a low-level vision application, it has been extensively studied and applied in unwanted object removal [3,4] and image synthesis [5,6]. As one example, the completion of face images has been an active research topic since it has the potential to benefit a wide range of applications, such as old facial photo restoration, portrait image editing, and face beautification. In order to capture the high-level semantics while maintaining consistency near the borders of the regions to be completed, the current mainstream methods are based on two types of deep learning generative models, namely, Variational Autoencoders(VAEs) [7] and Generative Adversarial Networks (GANs) [8,9], conditioned on known image regions. A typical strategy is to feed corrupted images into an encoder–decoder network, generating a photorealistic image similar to the ground truth and then filling the corrupted areas with the corresponding content [10]. There have been tremendous advances in image completion with the proper design of networks and loss functions [11,12,13].

Due to the diversity in facial expressions and the subjective nature of human vision, one of the main challenges in the completion of face images is that a single corrupted face can produce numerous reasonable results [14,15,16]. However, previous research still has its limitations. Concretely speaking, (1) the majority of groundbreaking works, such as GLCIC [17], DeepFill [16], Partial Convolution (PConv) [15], EdgeConnect [18], PEN-Net [12], and CR-Fill [19], aim to obtain only one desirable result for each image, and thus are incapable of generating a wide variety of completions. (2) Other methods, such as PIC-Net [13], PD-GAN [20], UCTGAN [21], and PUT [22], can produce diverse results by generating from the random samplings of the latent spaces [23]. However, these methods do not have the ability to control and customize the completion results. Thus, imagine that we want an angry face rather than a smiling one. A post-processing step is inevitable after image completion, which means either manually selecting one among numerous pluralistic results or further utilizing an emotion recognition system to pick out the desired one. The two methods outlined above are both labor-intensive and inefficient in practice.

In order to bridge the gap between the controllability and diversity during face image completion, we propose an Emotion-Controllable GAN (EC-GAN), a novel face completion model that can infer and customize the emotion based on the information of the unmasked parts. EC-GAN utilizes the CVAE-GAN [23] architecture as the completion network. To embed the expected image prior to the generation process, we first designed an encoder based on the CVAE pipeline since it has excellent performances in learning the structured representation, including expected semantics for real images [24]. Several advanced losses [13,25] were also introduced to ensure the fidelity and realism of the completed results.

We have proposed an emotion inference module to infer approximate emotion from unmasked regions of human faces. Following the usual practice [26], we used seven common categories of facial emotions, namely, neutral, happy, sad, angry, disgusted, surprised, and fearful.

The emotion inference module is trained to learn the emotion semantics in a supervised manner and it enforces the encoder to disentangle the emotion semantics from the native latent space. To customize a desired emotion, we propose an emotion control module to modify the corresponding emotion semantics in the latent space. In this way, we established our Emotion-Controllable GAN image completion framework. The sub-modules in our model were trained simultaneously in an end-to-end manner, and the model can correctly complete facial images with the emotions designated by users.

We summarize our contributions as follows:

• We present a novel emotion-controllable image completion framework. In contrast to randomly generating diverse results, our model is capable of explicitly inferring reasonable facial expressions from masked faces, guaranteeing visually realistic and semantically plausible results.
• For large-size masked face images, we propose a strategy to control the image completion process and to customize different facial expressions, resulting in a more practical approach to face completion and editing. For small-size, irregularly masked face images, our model can also infer reasonable emotions from the visible parts, thereby enhancing semantic inferences for facial features during completion.
• We conducted comprehensive experiments on two face benchmark datasets, CelebA-HQ [11] and CFEED [27]. Experimental results demonstrate that for an image with the whole face corrupted (center-masked), our model can produce results with reliable, diverse desired expressions, which is beyond the capabilities of other comparison methods. For an image with irregular masks, our model accurately infers the emotion of the target image and obtains completed results with more natural facial expressions.

2. Related Work

In this section, we only focus on these deep-learning-based methods, which are technically related to our work.

2.1. Image Completion with Single Result

Typically, the image completion methods with only one result generally use encoder–decoder architectures to visualize meaningful semantic content with properly designed reconstruction losses. For the photorealistic rendering of the generated image, an adversarial discriminator is usually added to the decoder during training. Context-Encoder (CE) [14] is the first GAN-based image completion network in which the encoder takes in the corrupted image and the decoder creates the missing image content. Based on CE, GLCIC [17] employs dilated convolutions and the global and local discriminators to inpaint random holes. This idea is followed by DeepFill [16]. DeepFill V1 [16] introduces a contextual attention layer in a feed-forward generative network, and DeepFill V2 [28] presents gated convolution to dynamically select features for each channel and improves color consistency for free masks. In PConv [15], a partial convolution is used to ensure that only valid pixels are covered to obtain a more accurate prediction. Zeng et al. [12] proposed a Pyramid-Context Encoder Network (PEN-Net). PEN-Net adds an attention transfer network, combining high-level feature maps between the visible and invisible areas to ensure the consistency at visual and semantic levels. A more recent network, RFR-Net [29] exploits the correlation between pixels and develops a Knowledge Consistent Attention module in order to produce detailed results. CR-Fill [19] adds a contextual reconstruction branch to train an attention-free generator. EdgeConnect [18] and CTSDG [30] use the edge information to guide the reconstruction of image structures. MISF [31] proposes a kernel prediction model to learn the multi-level features of images. AOT-GAN [32] adopts information from distant contexts and rich patterns of interest for context reasoning. Although these methods are capable of producing one determined result for a given image, they cannot generate other possible results that also match the style and semantics of the given image.

2.2. Image Completion with Diverse Results

Image completion can be viewed as an ill-posed inverse problem with no determined solution, and for face images, it seems more reasonable to obtain multiple results. Diverse image completion methods have been studied in several recent studies. PIC-Net [13] develops a probabilistic principled framework with two parallel paths, utilizing prior conditional lower bound coupling to provide multiple diverse results with reasonable content for a single masked input. By learning the image mapping between the instance image space and the conditional completion image space, UCTGAN [21] yields a variety of completion results. PD-GAN [20] samples random latent vectors from the standard Gaussian distribution to generate different images. By separating the structural and textural information, VQ-VAE [33] constructs an autoregressive model for discrete distributions over the structural features, thus obtaining samples with different structural characteristics. ICT [34] and PUT [22] introduce the transformer [35] to their autoencoder pipelines to reduce the loss of information during the encoding process. Even though these methods have successfully generated multiple results, they are incapable of producing images that are semantically specific or have controllable expressions since they are based on random sampling from the latent space.

Our work is mainly inspired by PIC-Net [13], and we have made significant improvements. In contrast to the methods mentioned above that generate multiple images at random, our method is intended to complete images with the specified expression semantics or correctly inferred emotions.

2.3. Facial Expression Inference and Editing

There has been considerable research in computer vision related to facial expression inference and editing. Recent work reveals that GANs can generate designated images, such as smiling faces, by sampling from a specific latent space. InfoGAN [36] and Elastic-InfoGAN [37] obtain divisibility in latent space by maximizing the mutual information of categories between the truth and the generated image, which enables their networks to handle extra condition information. InterFaceGAN [38] adopts a specific linear transformation on latent codes to implement smiling faces from neutral faces. In-Domain GAN inversion [39] designs a domain-guided encoder to invert the real images into the semantically meaningful latent space and then set it as a regularizer to add other semantics into the latent codes. However, the editing method used in InterFaceGAN is non-local and may result in changes to other image content. Furthermore, most of the previous methods require a pre-trained generative model such as PG-GAN [11] or styleGAN [40], so they cannot be directly applied for the emotion-controllable image completion.

Inspired by the above work, we designed an emotion control module that allows us to disentangle the emotion semantics from the native latent space in a supervised manner, therefore providing diverse choices for facial expression generation without requiring pre-trained generation models. Our model also offers a broader range of expression options for the single image to be inpainted, such as sad, angry, disgusted, and so on, rather than the single choice of smiling or not smiling.

3. Proposed Approach

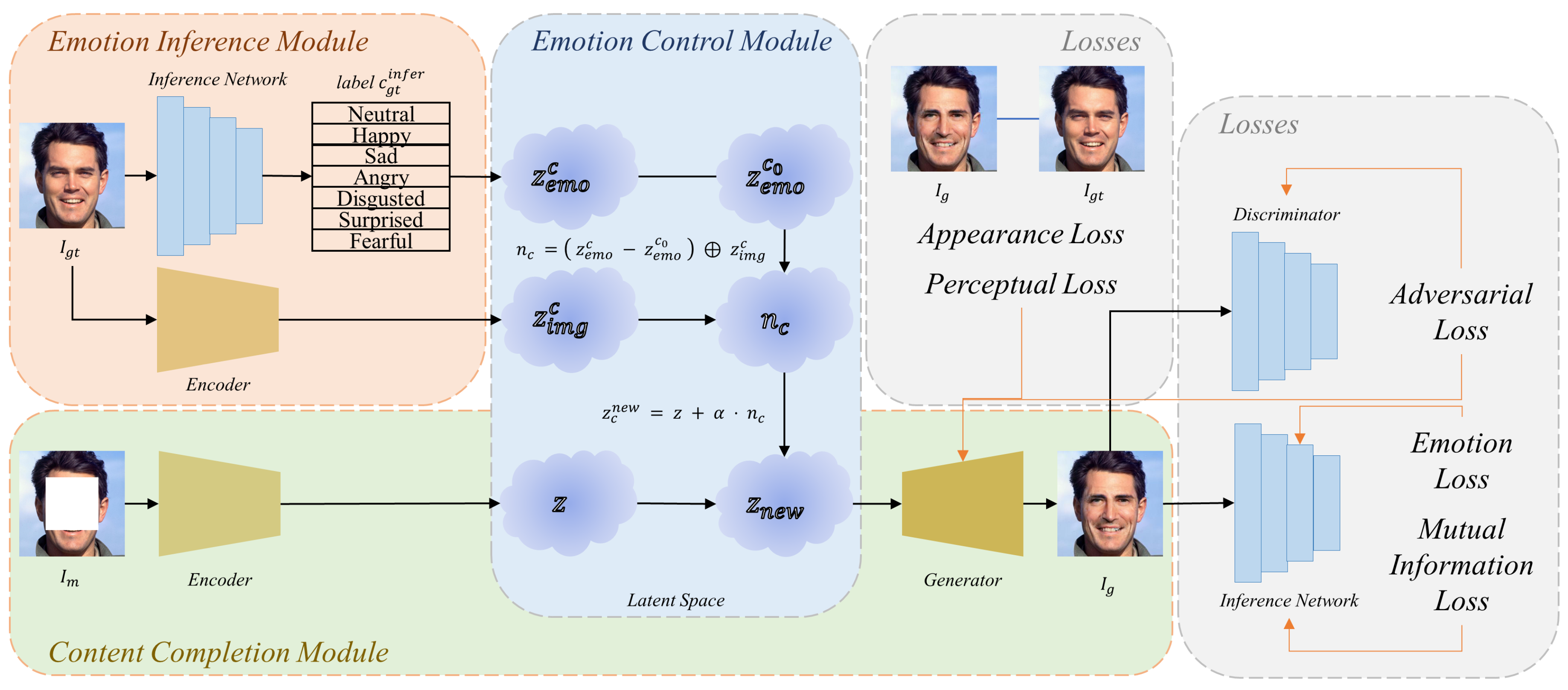
In this section, we first present a brief introduction to our overall EC-GAN architecture. Then, we describe the method for the disentanglement of latent space and facial expression control. Finally, we describe the loss functions applied in EC-GAN.

In general cases, the dataset contains two parts: a ground truth face image $I_{gt}$ and its corresponding emotion label $c_{gt}$. We denote the partially masked version as $I_m$. M is a binary matrix; 1 indicates the observed region and 0 indicates the missed region to be inpainted; thus, $I_m=I_{gt}\odot M$, where ⊙ represents the Hadamard product. The generated image in our model is denoted by $I_g$ and the final completed result $I_{out}$ is calculated by

$$I_{out}=M\odot I_{gt}+(1-M)\odot I_g.$$

(1)

3.1. EC-GAN Overall Image Completion Framework

The overview architecture of EC-GAN is illustrated in Figure 1. The content completion module (with a pale green background) contains an encoder E and a generator G. The main network of our generator is similar to PIC-Net [13], but we modify the encoder and generator to enable them to deal with extra-label information. The encoder maps the visible parts $I_m$ into the native latent space, and the corresponding latent codes are denoted by z. The generator reconstructs the image from z.

To disentangle the emotion semantics from the native latent space, we propose the emotion inference module (with a light orange background in Figure 1), which contains two parallel paths, one for the emotion semantics path and one for the image content path. The emotion semantics path designs an inference network to infer the emotion labels $c_{gt}^{infer}$ of the ground truth and calculates the information entropy of the emotion noted as $z_{emo}^c$, while the image content path maps the ground truth $I_{gt}$ to the latent codes of content $z_{img}^c$. Once the generator G produces a result sample $I_g$, the emotion semantics path maximizes the mutual information between the inferred truth emotion labels $c_{gt}^{infer}$ and the generated sample $I_g$, resulting in the disentanglement of the emotion semantics from the latent space (disentanglement between $z_{emo}^c$ and $z_{img}^c$).

Then the final latent codes $z^c$ are obtained by combining $z_{emo}^c$ and $z_{img}^c$ together in the emotion control module (with a pale blue background Figure 1). Therefore, our model can calculate the emotion vectors $n_c$, which are utilized to move the latent codes in the content completion module from z to $z_{new}$ by the emotion control module. More details will be introduced in Section 3.3.

The encoder E in the content completion module is optimized by minimizing the following loss function:

$$L_{\mathrm{CVAE}}=-E_{q\left(z\right|x)}[\log p\left(c\right|x,z)]+\mathrm{KL}\left[q\left(z\right|x,c)\right|\left|p\left(z\right|x)\right]$$

(2)

where x is the data sample from the generative distribution $p\left(x\right|z)$ and z is the latent variable extracted from the prior distribution $p\left(z\right|x)$. In our EC-GAN model, the input data sample x is the truth image sample $I_{gt}$, and the label c is the inferred truth emotion label $c_{gt}^{infer}$. The generator G and the discriminator D of GAN try to minimize the loss functions $L_G$ and $L_D$, respectively:

$$L_D=-E_{x\sim P_{data}}[\log D\left(x\right)]-E_{z\sim P_z}[\log (1-D\left(G\left(z\right)\right))],$$

(3)

$$L_G=-E_{z\sim P_z}[1-\log D\left(G\left(z\right)\right)].$$

(4)

Therefore, the combined loss function of our content completion module is:

$$L_{\mathrm{VG}}=L_{\mathrm{CVAE}}+L_D+L_G.$$

(5)

3.2. The Disentangled Emotion Inference Module

Since the encoder E is constructed by multiple convolutional layers with different scales, it mashes up all the facial features in the latent space, which makes the generator G fail to extract the emotion information from the latent codes. To generate images with customized emotions, we need to disentangle the emotion semantics from the latent space [37]. To address this problem, we designed an emotion inference module which utilizes the mutual information [41] to achieve the independent encoding of emotion semantics in the latent space.

The emotion inference module contains two parallel paths. One path is the inference network designed to infer the labels of images and then calculate the entropy of emotions, and the other is the encoder aiming to embed the remaining image information into the latent space. The outputs of the two paths are combined in the emotion control module, which will be interpreted in Section 3.3. The emotion inference network is always trained from scratch for different quantities of emotions. Meanwhile, in order to save calculation costs, the emotion inference module shares the same architecture and parameters with the discriminator D, except for the last output layer.

First, the emotion inference network tries to obtain the inferred emotion labels $c_{gt}^{infer}$ of the ground truth $I_{gt}$ and the inferred generation labels $c_g^{infer}$ of the constructed image $I_g$. To obtain the emotion semantics, we optimized the inference network in a supervised manner. By using the given emotion label $c_{gt}$, we can utilize the L-1 loss function to optimize the emotion loss of the inference module:

$$L_E=\parallel c_{gt}^{infer}-c_{gt}{\parallel }_1+\parallel c_g^{infer}-c_{gt}{\parallel }_1.$$

(6)

Next, according to information theory, mutual information measures the reduction in uncertainty between two random variables. If the two variables are independent, the mutual information becomes zero. In contrast, if two variables are strongly correlated, then one of them can be predicted from the other. Consequently, we propose to maximize the mutual information $I(c;G(z,c\left)\right)$ between the inferred emotion labels c and the generation distribution $G(z,c)$ to strengthen their correlation. In the next parts, $c_{gt}^{infer}$ is replaced with c for convenience.

We set the inferred emotion labels c as part of the input of generator G and note this part as the emotion entropy or latent codes of emotion semantics $z_{emo}^c$ in advance. The latent codes of emotions $z_{emo}^c$ are calculated by a replication strategy in which we expand the $c^{m\times 1}$ dimension to match the latent space dimension, which is noted as the mapping function:

$$f:c^{m\times 1}\stackrel{}{\to }{z}_{m\times n\times n}^c.$$

(7)

where m is the number of emotion categories and $n\times n$ is the dimension of the latent space. By doing so, the generator G can produce samples containing the information from the inferred emotion labels c and will change expressions as c changes. Then, we can calculate the mutual information $I(c;G(z,c\left)\right)$.

However, the mutual information term $I(c;G(z,c\left)\right)$ is hard to maximize directly as it requires the posterior information $P\left(c\right|x)$[36]. Therefore, we utilize a lower bound of it to approximate $P\left(c\right|x)$ by defining an auxiliary distribution $Q\left(c\right|x)$:

$$\begin{array}{cc}\hfill I(c;G(z,c\left)\right)& =H\left(c\right)-H\left(c\right|G(z,c))\hfill \\ \hfill & =E_{x\sim G(z,c)}\left[E_{c^{\prime }\sim P\left(c\right|x)}[\log P\left(c^{\prime }\right|x)]\right]+H\left(c\right)\hfill \\ \hfill & =E_{x\sim G(z,c)}[D_{KL}(P\left(c\right|x)\parallel Q\left(c\right|x))+E_{c^{\prime }\sim P\left(c\right|x)}[\log Q\left(c^{\prime }\right|x)]]+H\left(c\right)\hfill \\ \hfill & \ge E_{x\sim G(z,c)}\left[E_{c^{\prime }\sim P\left(c\right|x)}[\log Q\left(c^{\prime }\right|x)]\right]+H\left(c\right).\hfill \end{array}$$

(8)

In fact, the entropy of the inferred emotion labels $H\left(c\right)$ can be treated as a constant in that it highly relies on the truth labels $c_{gt}$. Thus, the mutual information loss can be defined as follows and be minimized during training:

$$L_{\mathrm{MI}}=-I(c;G(z,c)).$$

(9)

With the above analysis, we can divide the latent space into two independent parts; one represents the emotion semantics $z_{emo}^c$, which is from the inference module, and the other represents the remaining image semantics $z_{img}^c$, which is from the encoder. The visualization process is shown in Figure 2.

3.3. Emotion Control Module

Now that the emotion inference module has disentangled the emotion semantics from the native latent space, we can edit and modify these semantics independently. To do this, we propose an emotion control module to customize the expression of the generated face.

During training, the latent codes of each emotion from the emotion inference module are recorded as $z_{emo}^{c_i}$, $i=0,1,2,\cdots ,m$, and the neutral expression codes are denoted by $z_{emo}^{c_0}$. Take the emotion happy as an example; when the smile gradually fades from the face, it presents a calm face, which is considered neutral. Thus, we regard the neutral expression as the start point for all other expressions. Then, the emotion vector can be calculated by:

$$n_{c_i}=(z_{emo}^{c_i}-z_{emo}^{c_0})\oplus z_{img}^{c_i}.$$

(10)

As a result, we can conveniently edit the original latent codes z using the following linear transformation:

$$z_{new}^{c_i}=z+\alpha n_{c_i}$$

(11)

where setting the directional parameters $\alpha >0$ will make the generation move in the positive direction, e.g., from neutral to smiling. Unlike InterFaceGAN, our model only changes the latent codes of emotions, which were separated from the native latent space in Section 3.2. At the same time, the other parts of the facial semantics are preserved. The visualization process is shown in Figure 3.

3.4. Loss Function

In this section, we summarize the losses utilized in our model during the training process. The joint loss is composed of five parts. In addition to the content completion loss $L_{\mathrm{VG}}$, the emotion inference loss $L_E$, and the mutual information loss $L_{\mathrm{MI}}$ described earlier, we also introduce the appearance loss [13] $L_{\mathrm{A}}$ and perceptual loss [25] $L_{\mathrm{PL}}$ to further improve the photorealism and the local semantic consistency of completed results during training. Concretely, $L_{\mathrm{VG}}$ regularizes the consistency between pairs of distributions, $L_E$ ensures the correctness of the emotion inference, and $L_{\mathrm{MI}}$ encourages the encoder to disentangle the latent space. $L_{\mathrm{A}}$ adds more fidelity to the generation outputs, and $L_{\mathrm{PL}}$ measures the distance between the features of ground truth and those of generated images.

The appearance loss is calculated as

$$L_{\mathrm{A}}=\parallel (1-M)\odot (I_t-I_{out}){\parallel }_1.$$

(12)

and the perceptual loss is calculated as follows

$$L_{\mathrm{PL}}=\sum _l\frac{1}{H_l{W}_l}\sum _{h,w}\parallel {\omega }_l\odot (y_{hw}^l-y_{0hw}^l){\parallel }_2^2.$$

(13)

where $y_{hw}^l$ and $y_{0hw}^l$ are the extracted feature stacks for layer l.

The full loss in our model is

$$L=L_{\mathrm{VG}}+{\lambda }_E{L}_E+{\lambda }_{\mathrm{MI}}{L}_{\mathrm{MI}}+{\lambda }_{\mathrm{A}}{L}_{\mathrm{A}}+{\lambda }_{\mathrm{PL}}{L}_{\mathrm{PL}}.$$

(14)

4. Experiments

4.1. Implementation Details and Datasets

Our EC-GAN is implemented with Pytorch v1.9.0 and CUDA v11.0. We trained our model on NVIDIA GeForce RTX 2080 (8GB). For the weights of different losses, we first referred to PEN-Net (2019) [12], DeepFill V1 [16] and PIC-Net (2019) [13] to determine their approximate ranges and proportional relationships. Then, we selected 10 combinations for hyperparameter search by training EC-GAN on 100 images, using FID, IS, and SSIM as indicators to select the optimal combination. The weights of different losses were finally set to $\alpha =1$, ${\lambda }_{\mathrm{VG}}={\lambda }_{\mathrm{MI}}=20$, ${\lambda }_E=5$, and ${\lambda }_{\mathrm{app}}={\lambda }_{\mathrm{PL}}=1$. Meanwhile, we used an Adam optimizer with ${\beta }_1=0$ and ${\beta }_2=0.999$, and the learning rate was fixed as $\lambda ={10}^{-4}$.

We trained the network separately on two different facial datasets, CelebA-HQ [11] and CFEED [27]. The CelebA-HQ dataset contains 30,000 colored face images with 40 binary attribute vectors. In our experiment, we used one specific attribute: smiling or not. For CelebA-HQ, we used the same split strategy as in [16], i.e., 28,000 images for training and 2000 images for testing. CFEED contains human faces with 22 categories of emotions—7 for basic emotions and 15 for compound emotions—and each category contains 230 face images. For CFEED, we used seven independent expressions, namely, neutral, happy, sad, angry, surprised, disgusted, and fearful, and set 1660 images for training and 180 images for testing. Images in the two datasets were resized to a 256 × 256 resolution. The center mask used in the training was generated by the model, and the random irregular masks were provided by Liu et al. [15]. The models for the center mask and random masks were trained separately. For single-image completion during the testing, we implemented a GUI program to conveniently customize free-form masks using the mouse.

4.2. Experiments on CELEBA-HQ

4.2.1. Qualitative Comparisons of the Emotion Controllability for Single-Image Completion

To evaluate the performance of the emotion controllability of our model, we first utilized a 128 × 120 center mask to cover the main facial components. In this way, the eyes, nose, mouth, and ears are essentially invisible, so it seems more plausible to obtain diverse results with different expressions. We compared our model with five representative state-of-the-art methods, including PEN-Net (2019) [12], MISF (2022) [31], AOT-GAN (2022) [32], PIC-Net (2019) [13], and VQ-VAE (2021) [33]. Among them, the first three methods produced one single result for one image, and the last two yielded multiple results.

For CelebA-HQ [11], since there only exists the ”smiling or not” label among all the attribute labels, we completed images with a label, 1 indicating a smiling expression and 0 indicating neutral. Figure 4 shows some comparative experiment results of faces with various skin tones, expressions, and facial postures.

The visual inspection reveals that although PIC-Net [13] and VQ-VAE [33] can provide many results, the expressions are not controllable, so for each image, it takes approximately 2 min to manually select two results with clearly contrasting expressions, which is time consuming and impractical. Moreover, the faces generated by PIC-Net [13] are slightly stiff, whereas VQ-VAE [33] produces faces with distortions in the five facial features. Additionally, VQ-VAE [33] is unstable during testing. In contrast, EC-GAN can produce visually natural and realistic faces with two obviously different emotions. Additionally, our model manages to transform the happy face into a neutral one with lifelike expressions and rich details. Meanwhile, the expressions generated by EC-GAN are more natural than those produced by PIC-Net [13] and VQ-VAE [33].

The remaining three methods (producing only one result for one image without emotion controllability) behave differently. PEN-Net [12] yields soft results lacking texture details, MISF [31] produces faces with unnatural expressions (especially in the mouth areas), and AOT-GAN [32] generates results with apparent inconsistencies along the boundaries. We also noticed that the completed faces from PEN-Net [12], MISF [31], and AOT-GAN [32] are slightly blurred. This experiment shows that the completion of facial images with large-size missing areas remains challenging.

4.2.2. Qualitative Comparisons of Emotion Inference

To demonstrate the emotion inference capacity of our model, we carried out an experiment with small-sized irregular masks. In this case, we purposely created random masks to cover the areas around critical facial landmarks, such as the eyes, the nose, and the mouth. Our motivation is that, for the area to be inpainted, the content should be consistent with the semantics and expression of the visible part. Therefore, a competent method must be able to deduce the emotion of a face based on the visible portion and complete it with desired content. In this experiment, although EC-GAN can produce multiple results, these results contain subtle differences (we will explain in Section 4.3.3), which is why we illustrate only one result for one image. Results by PIC-Net [13] and VQ-VAE [33] were selected based on the highest scores defined in their papers.

Figure 5 illustrates some comparison results. Specifically, Figure 5a shows that all methods are capable of inferring the semantic information to some extent, despite the fact that PEN-Net [12] generates teeth that are slightly inconsistent with the unmasked part, AOT-GAN [32] generates inconsistent skin color boundaries, and VQ-VAE [33] generates eyes and eyebrows that are asymmetrical to unmasked ones. Figure 5f further illustrates that all the methods can generate satisfactory nasolabial furrows that are semantically coherent with the visible part, despite the fact that AOT-GAN [32] still suffers from inconsistent skin tones, and the result of VQ-VAE [33] is slightly discontinuous around the beard area. Figure 5b,c show that MISF [31] and AOT-GAN [32] generate unnatural mouths compared with PIC-Net [13] and VQ-VAE [33]. Additionally, the generated region from PIC-Net [13] does not match the surrounding skin tone, and the result from PEN-Net [12] loses texture details of teeth. MISF [31] generates teeth whose posture is frontal, which is inconsistent with the context of the ground truth. In Figure 5d,e, all models manage to generate appropriate eyes, but MISF [31], AOT-GAN [32], and VQ-VAE [33] fail to restore the eyebrows, thus achieving unnatural results. Our model, on the other hand, is able to infer the emotion of the faces by learning emotion semantics from visible regions. When considering all results together, our model successfully fills the missing part with expressions closest to the ground truth.

4.2.3. Quantitative Comparisons of Emotion Controllability and Inference

We evaluated the mean performance of different image completion methods on the testing dataset for CelebA-HQ [11]. Four types of quality metrics, namely, the Fréchet Inception Distance score (FID) [42], Inception Score (IS) [43], Structural Similarity Index (SSIM) [44], Peak Signal-to-noise Ratio (PSNR) [16], and Mean Absolute Error (MAE), were adopted in our experiments since the ground truth images were available.

Table 1. Quantitative results for center masks on CelebA-HQ [11]; ↓ means lower number is better.

Method	FID ↓	IS ↑	SSIM ↑	PSNR ↑	MAE ↓
PEN-Net [12]	20.18	22.12	0.85	19.73	1.87
MISF [31]	25.61	21.36	0.81	21.12	1.44
AOT-GAN [32]	23.34	22.78	0.79	20.64	2.08
PIC-Net [13]	19.19	23.29	0.86	20.78	1.52
VQ-VAE [33]	19.34	22.97	0.76	20.86	1.27
EC-GAN(ours)	18.81	23.36	0.88	20.97	1.39

and

Table 2. Quantative results for random masks on CelebA-HQ [11].

Method	FID ↓	IS ↑	SSIM ↑	PSNR ↑	MAE ↓
PEN-Net [12]	8.44	26.89	0.92	32.25	1.32
MISF [31]	7.97	28.27	0.94	33.48	1.26
AOT-GAN [32]	10.32	24.61	0.93	30.87	1.43
PIC-Net [13]	8.13	27.16	0.94	33.47	1.29
VQ-VAE [33]	8.01	26.99	0.91	33.54	1.31
EC-GAN(ours)	7.51	27.24	0.94	33.83	1.21

present the completion results under the center mask and random masks, respectively. As shown in Table 1, our model outperforms other models, especially in terms of FID, IS, and SSIM. Since our generator is similar to that of PIC-Net [13], the scores of EC-GAN and PIC-Net [13] are extremely similar. Our model, however, still performs better due to the fact that EC-GAN is equipped with an emotion inference module, resulting in more photorealistic and visually natural images. Table 2 further demonstrates that our model surpasses other models in terms of mean FID, SSIM, PSNR, and MAE. This further proves that our model can capture the emotion semantics more accurately than other methods.

4.3. Experiments on CFEED

In order to further evaluate the expression controllability and the effectiveness of emotion inference in our proposed method, we conducted two experiments on the CFEED dataset [27]. This is because CFEED [27] contains more face emotion categories. Therefore, our model is capable of producing more diverse results with obviously different expressions from the ground truth. However, previous work mainly focuses on the quality and precision of completion results rather than on the customization of emotions, so, to the best of our knowledge, we have not found an image completion method implemented on CFEED [27]; thus, we did not perform comparative experiments on this dataset. However, as an alternative, we utilized a state-of-the-art face recognition network provided by Microsoft Azure [45] to verify our completion results of multi-emotion.

4.3.1. Qualitative Results of Controllability

We first carried out an experiment with the center mask. In accordance with Equation (11), we performed seven linear transformations of different emotion semantics over the target image, which shifted the original emotion latent codes to the desired one. Then, our EC-GAN model managed to fill the missing areas with the semantics indicated by the new latent codes and thus customize various expressions. In Figure 6, for each image to be inpainted, we present the completion results with four typical emotions, namely, happy, angry, disgusted, and surprised. Other customized emotion results are presented in Figure A1, including neutral, sad, and fearful. It can be seen that each completion result has a natural and plausible expression that is consistent with the designed emotion. In particular, angry faces pull their brows down and press their lips together, while happy faces raise the corners of their lips with apparently deepened nasolabial furrows; surprised faces raise their eyebrows with eyes and mouths open wide. This experiment shows that our method can obtain diverse meaningful results with customized emotions for a face with most of its features invisible, which is beyond the reach of other image completion methods.

For each person, CFEED [27] provides different faces with various emotions. For comparison, in Figure 6 and Figure A1, we also present the corresponding images in the dataset with the same emotion labels that EC-GAN designed. It can be observed that the emotions produced by EC-GAN are also consistent with the corresponding ground truth emotions of the same person, but EC-GAN presents another plausible outcome. This fact also demonstrates that face image completion for large masks should be of diverse results, and EC-GAN is competent to customize the same emotion but with different details.

4.3.2. Emotion Recognition Results for Customized Emotions on CFEED

To quantitatively estimate the effectiveness of the emotion customization ability of EC-GAN, we further utilized the off-the-shelf Microsoft Azure Cognitive Service [45] to distinguish the expressions of our completion results on CFEED [27] for the center mask.

Table 3. Emotion recognition results by Azure congitive service [45] for images in Figure 6 and Figure A1.

Image	Neutral	Happy	Sad	Angry	Disgusted	Surprised	Fearful
Figure 6a Our Results	1.00	1.00	0.85	0.97	0.61	1.00	0.96
Figure 6a Dataset Images	1.00	1.00	0.90	0.83	0.74	0.98	0.89
Figure 6b Our Results	1.00	0.99	0.98	0.78	0.77	1.00	0.98
Figure 6b Dataset Images	0.99	1.00	1.00	0.88	0.94	1.00	0.99
Figure 6c Our Results	1.00	0.98	0.74	0.88	0.86	1.00	0.89
Figure 6c Dataset Images	1.00	0.97	0.74	0.77	0.83	0.96	0.78
Figure 6d Our Results	0.95	1.00	0.99	0.86	0.99	1.00	0.71
Figure 6d Dataset Images	0.99	1.00	0.87	0.71	0.82	1.00	0.69
Figure 6e Our Results	1.00	0.99	0.99	0.99	0.62	0.99	0.58
Figure 6e Dataset Images	1.00	1.00	0.98	0.92	0.51	1.00	0.60
Figure 6f Our Results	1.00	1.00	0.97	0.98	0.93	1.00	0.63
Figure 6f Dataset Images	1.00	0.99	0.75	0.89	0.59	1.00	0.54

records the highest emotion probability (score) for each of the result images and the ground truth images in Figure 6 and Figure A1. It shows that the emotion of each result image has been correctly recognized since all the probabilities are higher than 0.5; additionally, the scores are close to the ground truth, which further justifies the effectiveness of expression controllability proposed in our model.

At last, for each image in the testing set (including 25 images for each emotion), we obtained seven completion results with designed emotions for the center mask. We also used Microsoft Azure Cognitive Service [45] to calculate the emotion scores for both our results and the stand images in the testing set. Figure 7 illustrates the box plot of these scores. It is obvious that our designed emotions are reliable since the statistics data of each type of emotion are very close to that of the ground truth.

4.3.3. Qualitative Results of Emotion Inference

To further evaluate the emotion inference ability, we also carried out an experiment with irregular masks on CFEED [27]. For each original image, we masked five different individual parts and used the emotion control module to modify the emotion semantics of the same masked images.

As shown in Figure 8, our model can not only capture the semantics of happy or neutral, but successfully infer other emotion semantics like sad, angry, surprised, disgusted, and fearful. We observed that the mouth and nasolabial furrows are restored for the smiling faces (Figure 8a), while a downward curved mouth and furrowing of the eyebrows are evident for the sad faces (Figure 8b). In Figure 8c, the surprised results open the mouths and eyes widely. In the meantime, all the expressions from our results are natural and gentle, and the textural details and postures of the five senses have been well preserved.

It is noteworthy that all five completion results are similar to the ground truth, despite the inpainting areas varying dramatically. This means when we attempt to customize multiple emotions, the results yield only slight variations. Experiments carried out on CelebA-HQ [11] for free masks show a similar phenomenon (reported in Section 4.2.2). This is because when the masks are smaller, the encoder obtains more determinant facial semantics from the visible regions, which decreases the proportion of the completion loss ( $L_{\mathrm{VG}}$) in the overall loss, whereas the proportion of the inference and perception loss ($L_E$ and $L_{\mathrm{MI}}$) increases relatively. Therefore, to obtain face expressions with reasonable semantics for small-size masked image completion tasks, the expression inference power of EC-GAN dominates. Thus, the expression control has only a minor change in the results; this phenomenon is consistent with our common sense.

4.3.4. Quantitative Results of Emotion Inference

Scores of each quantitative term are shown in

Table 4. Quantitative results for random masks on CFEED [27].

Method	FID ↓	IS ↑	SSIM ↑	PSNR ↑	MAE ↓
EC-GAN	5.47	24.58	0.93	28.01	0.94

. All scores in the experiment on CFEED [27] are close to those in the experiment on CelebA-HQ [11]. This reflects that EC-GAN can accurately capture the emotion from the unmask region of the face, further indicating the excellent emotion inference ability of EC-GAN.

4.4. Ablation Study

In order to study the contributions of our emotion inference module, we conducted an ablation study on the CFEED dataset [27]. EC-GAN models are trained and tested with and without the emotion inference module for the center-missing case, aiming to complete an image with diverse emotions. We named them model I (with the emotion inference module, it is also the EC-GAN model) and model II (without the emotion inference module), respectively. Figure 9 shows some completion results.

It can be observed that Model I (EC-GAN) is capable of customizing the same emotion semantics as the ground truths. Meanwhile, it also customizes different expressions while preserving other facial semantics successfully. On the other hand, Model II can also generate the correct facial expressions, but other important facial features are altered in the meantime. As shown in Figure 9, the male images appear to have feminine attributes after the completion. Additionally, the face tones of some images also change significantly.

We attribute this result to the disentanglement functionality of our proposed emotion inference module. As described in Section 3.2, the emotion inference module disentangles the emotion semantics from the native latent space, enabling the emotion control module to manipulate the latent codes of emotions independently. By contrast, without the emotion inference module, the control module can only manipulate the composite latent codes, resulting in the simultaneous alteration of all facial features.

We also evaluated the results in the testing set (containing 180 images) using five quantitative terms. The completed results were compared with images that have the same emotions in the dataset.

Table 5. Quantitative results for ablation study of emotion inference module on CFEED [27].

Method	FID ↓	IS ↑	SSIM ↑	PSNR ↑	MAE ↓
Model I	20.61	28.14	0.89	25.76	1.24
Model II	21.35	28.09	0.85	23.92	1.33

presents the evaluation results. It is obvious that EC-GAN with the emotion inference module outperforms EC-GAN without the emotion inference module. This is because the emotion inference module learns different emotion semantics of the face and promotes the model to generate more realistic expression content for the corrupt images.

Furthermore, we carried out a quantitative experiment to validate the contributions of the appearance and perceptual losses used in EC-GAN. Three models were trained and compared with the completed EC-GAN model, evaluated using three terms (FID, IS, and SSIM).

Table 6. Quantitative results for ablation study of the appearance and perceptual losses on CFEED [27].

Appearance Loss	Perceptual Loss	FID ↓	IS ↑	SSIM ↑
		22.17	25.66	0.81
✓		21.92	26.93	0.84
	✓	21.43	27.08	0.87
✓	✓	20.61	28.14	0.89

shows the result, where “✓” means the model utilizes the loss item. We can see that EC-GAN with both appearance loss and perceptual loss surpasses other models in all metrics, demonstrating that both losses make positive contributions to the final image completion quality and precision.

5. Conclusions

This paper presents an Emotion-Controllable GAN model for customized realistic face completion. With the contribution of the emotion inference module and emotion control module, EC-GAN enables the emotion semantics to be disentangled from the native latent space and be modified independently, resulting in diverse expressions without affecting other facial features. In addition, the proposed EC-GAN correctly infers emotions and provides natural and plausible content for facial images where key regions are covered. Comprehensive experiments conducted on two publicly available face datasets establish that EC-GAN is capable of inferring emotions and controlling them more effectively than other state-of-the-art models. However, our model does not involve the control of the intensity of the generated expressions. We will conduct further research focusing on this problem and expect our EC-GAN to inspire new insights. Among future directions, one particularly interesting direction is to extend our model to the control of other attributions, such as hair color, makeup style, etc.