Impact of Mass-Gap on the Dispersion Interaction of Nanoparticles with Graphene out of Thermal Equilibrium
Abstract
1. Introduction
2. Nonequilibrium Dispersion Force on a Nanoparticle on the Source Side of Gapped Graphene
3. Polarization Tensor in the Area of Evanescent Waves
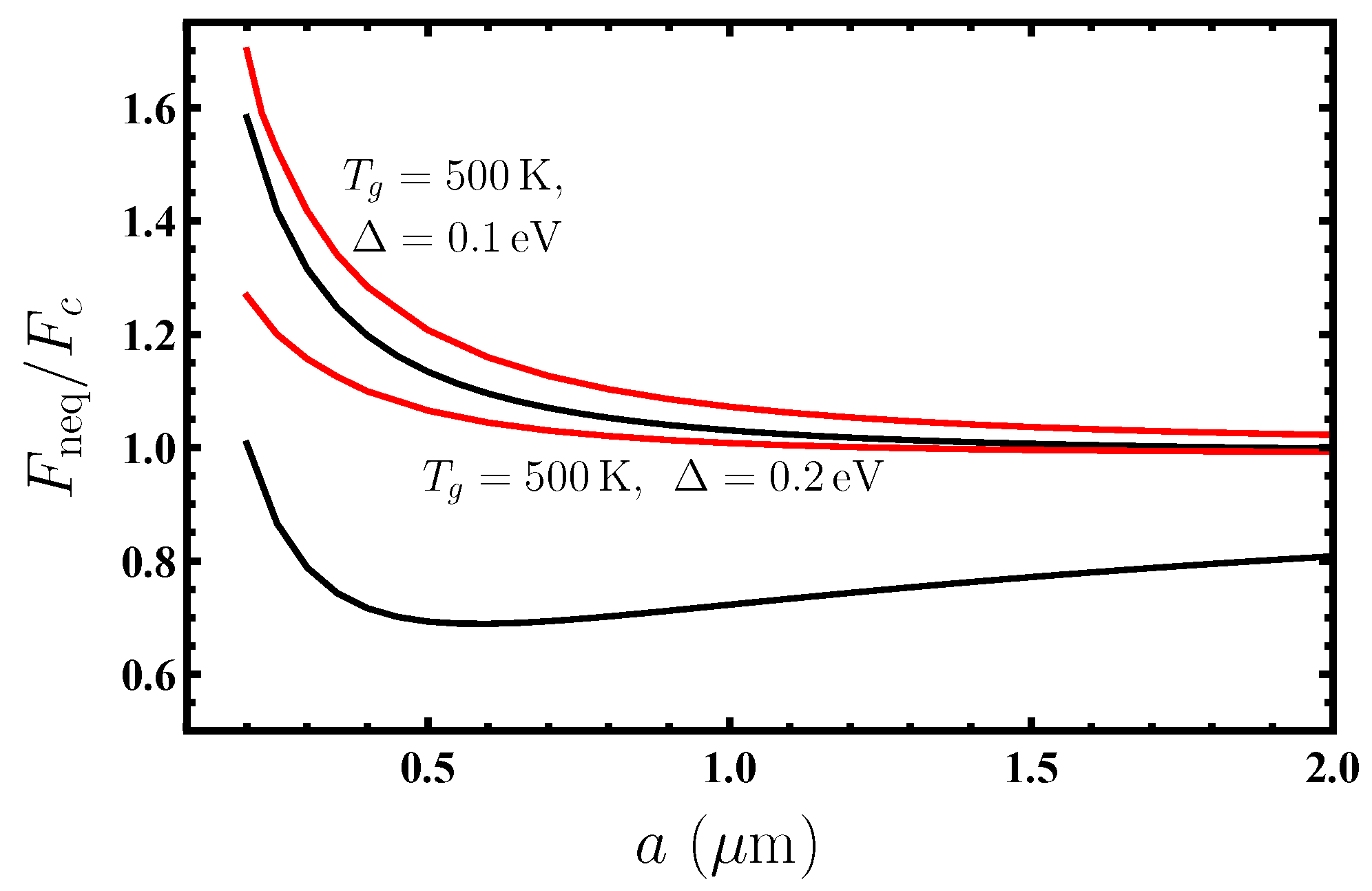
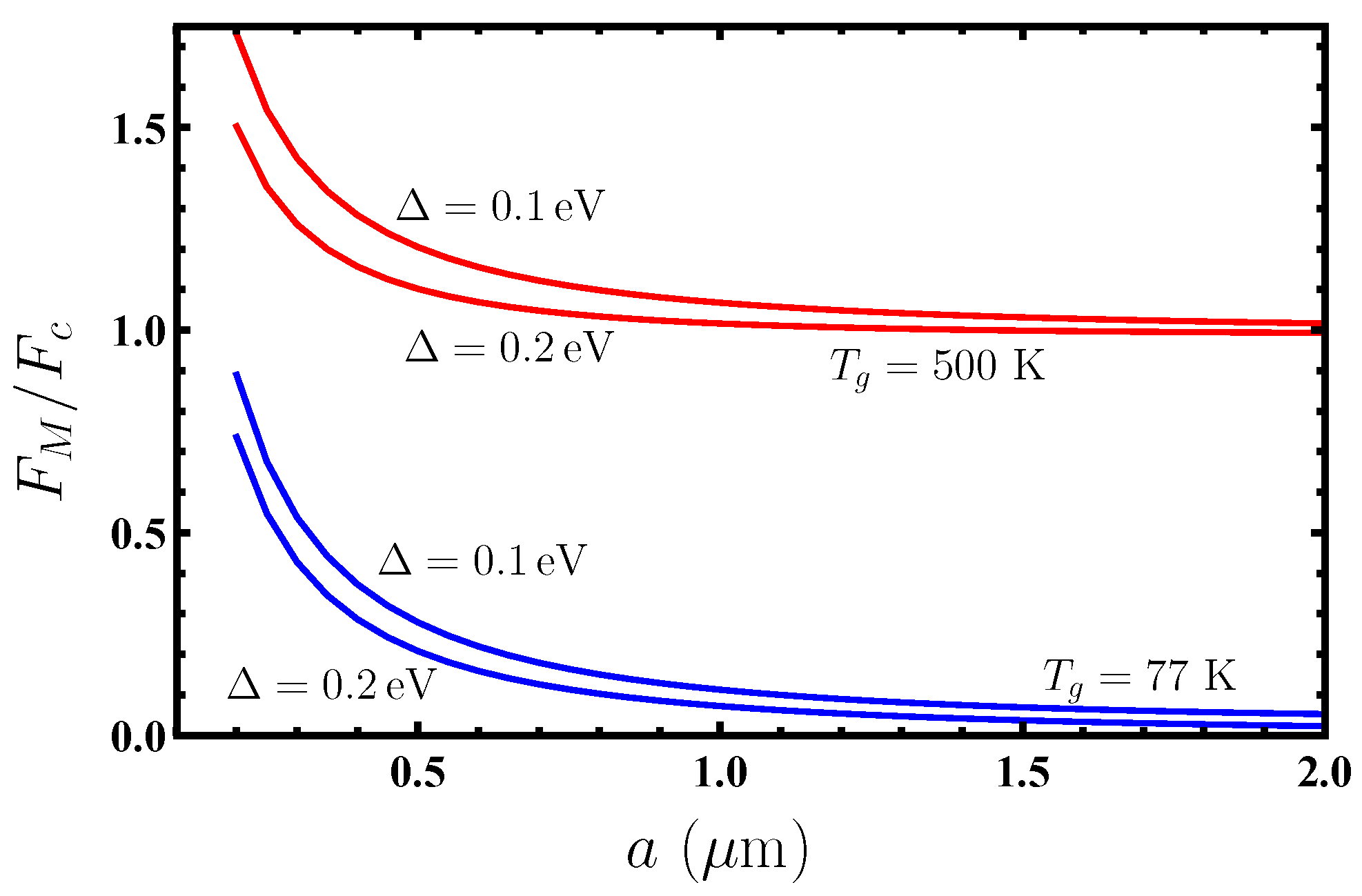
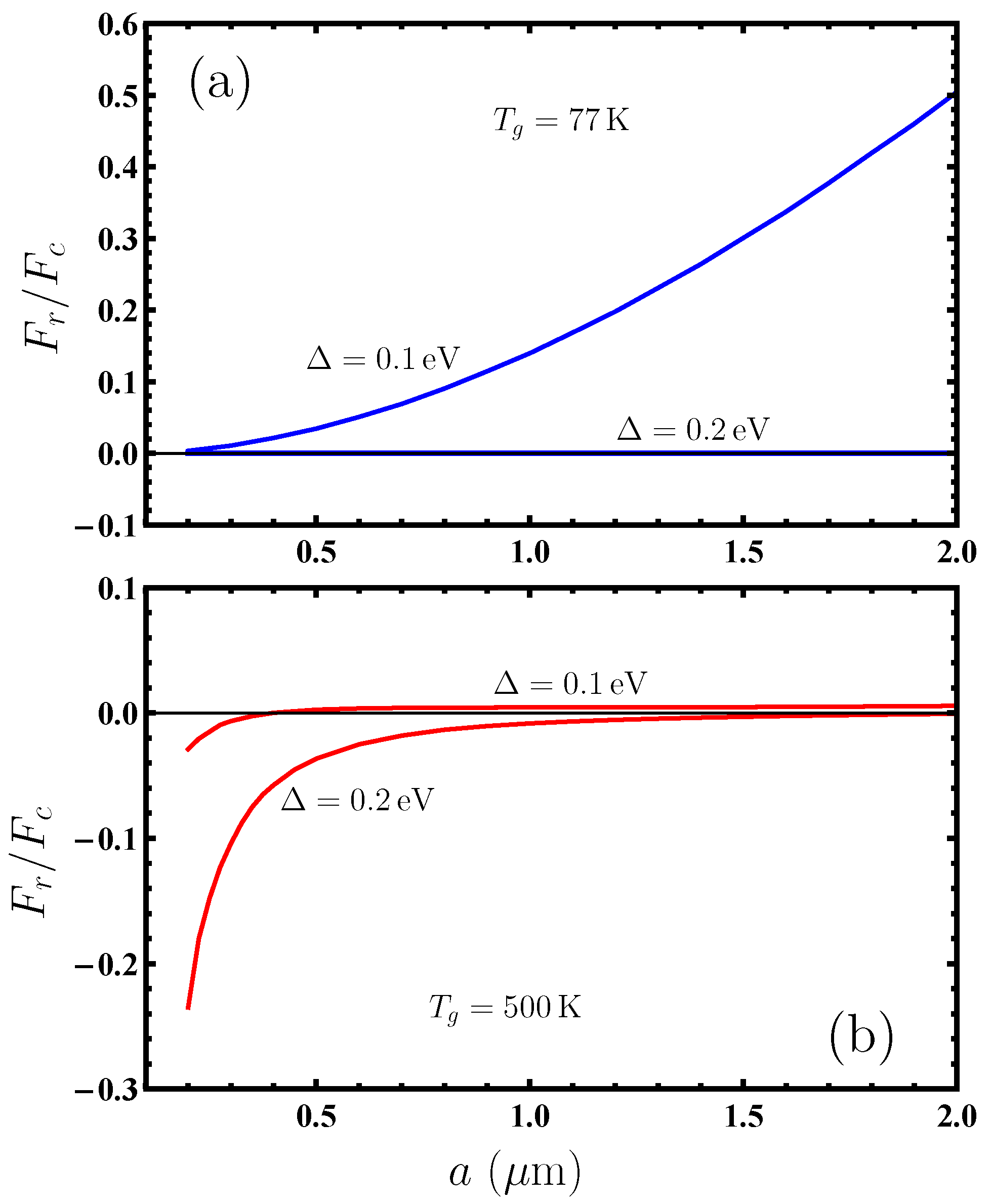
4. Computational Results for the Dispersion Force on Nanoparticles from Graphene
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kysylychyn, D.; Piatnytsia, V.; Lozovski, V. Electrodynamic interaction between a nanoparticle and the surface of a solid. Phys. Rev. E 2013, 88, 052403. [Google Scholar] [CrossRef]
- Ma, C.; Huangfu, X.; He, Q.; Ma, J.; Huang, R. Deposition of engineered nanoparticles (ENPs) on surfaces in aquatic systems: A review of interaction forces, experimental approaches, and influencing factors. Environ. Sci. Pollut. Res. 2018, 25, 33056–33081. [Google Scholar] [CrossRef]
- Summueang, C.; Boonchui, S. Electrical interaction between nanoparticle and surface of material. IOP Conf. Ser. Mater. Sci. Eng. 2019, 526, 012016. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; Zeng, S.; Shen, C.; Jin, C.; Huang, Y. Interactions between nanoparticles and fractal surfaces. Water Res. 2019, 151, 296–309. [Google Scholar] [CrossRef]
- Andrén, D.; Länk, N.O.; Šípová-Jungová, H.; Jones, S.; Johansson, P.; Käll, M. Surface Interactions of Gold Nanoparticles Optically Trapped against an Interface. J. Phys. Chem. C 2019, 123, 16406–16414. [Google Scholar] [CrossRef]
- Luo, X.; Morrin, A.; Killard, A.J.; Smyth, M.R. Application of Nanoparticles in Electrochemical Sensors and Biosensors. Electroanalysis 2006, 18, 319–326. [Google Scholar] [CrossRef]
- Willner, I.; Baron, R.; Willner, B. Integrated nanoparticle-biomolecule systems for biosensing and bioelectronics. Biosens. Bioelectron. 2007, 22, 1841–1852. [Google Scholar] [CrossRef] [PubMed]
- Lynch, I.; Dawson, K.A. Protein-nanoparticle interactions. Nanotoday 2008, 3, 40–47. [Google Scholar] [CrossRef]
- Verma, A.; Stellacci, F. Effect of Surface Properties on Nanoparticle-Cell Interactions. Small 2010, 6, 12–21. [Google Scholar] [CrossRef] [PubMed]
- Saptarshi, S.R.; Duschl, A.; Lopata, A.L. Interaction of nanoparticles with proteins: Relation to bio-reactivity of the nanoparticle. J. Nanobiotechnol. 2013, 11, 26. [Google Scholar] [CrossRef]
- Dyubo, D.; Tsybin, O.Y. Particles-on-surface sensor with potential barriers embedded in a semiconductor target. J. Phys. Conf. Ser. 2019, 1326, 012003. [Google Scholar] [CrossRef]
- Perera, Y.R.; Hill, R.A.; Fitzkee, N.C. Protein Interactions with Nanoparticle Surfaces: Highlighting Solution NMR Techniques. Isr. J. Chem. 2019, 59, 962–979. [Google Scholar] [CrossRef] [PubMed]
- Park, S.J. Protein-Nanoparticle Interaction: Corona Formation and Conformational Changes in Proteins on Nanoparticles. Int. J. Nanomed. 2020, 15, 5783–5802. [Google Scholar] [CrossRef] [PubMed]
- Dyubo, D.; Tsybin, O.Y. Computer Simulation of a Surface Charge Nanobiosensor with Internal Signal Integration. Biosensors 2021, 11, 397. [Google Scholar] [CrossRef]
- González-García, L.E.; MacGregor, M.N.; Visalakshan, R.M.; Lazarian, A.; Cavallaro, A.A.; Morsbach, S.; Mierczynska-Vasilev, A.; Mailänder, V.; Landfester, K.; Vasilev, K. Nanoparticles Surface Chemistry Influence on Protein Corona Composition and Inflammatory Responses. Nanomaterials 2022, 12, 682. [Google Scholar] [CrossRef]
- de Macedo, E.F.; Santos, N.S.; Nascimento, L.S.; Mathey, R.; Brenet, S.; de Moura, M.S.; Hou, Y.; Tada, D.B. Interaction between Nanoparticles, Membranes and Proteins: A Surface Plasmon Resonance Study. Int. J. Mol. Sci. 2023, 24, 591. [Google Scholar] [CrossRef]
- Vilquin, A.; Bertin, V.; Raphaël, E.; Dean, D.S.; Saler, T.; McGraw, J.D. Nanoparticle Taylor Dispersion Near Charged Surfaces with Open Boundary. Phys. Rev. Lett. 2023, 130, 038201. [Google Scholar] [CrossRef]
- Sun, W. Interaction forces between a spherical nanoparticle and a flat surface. Phys. Chem. Chem. Phys. 2014, 16, 5846–5854. [Google Scholar] [CrossRef]
- Moreno, F.; García-Cámara, B.; Saiz, J.M.; González, F. Interaction of nanoparticles with substrates: Effects on the dipolar behaviour of the particles. Opt. Express 2008, 16, 12487–12504. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Aoki, H.; Dresselhaus, M.S. (Eds.) Physics of Graphene; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Katsnelson, M.I. The Physics of Graphene; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Judd, T.E.; Scott, R.G.; Martin, A.M.; Kaczmarek, B.; Fromhold, T.M. Quantum reflection of ultracold atoms from thin films, graphene and semiconductor heterostructures. New J. Phys. 2011, 13, 083020. [Google Scholar] [CrossRef]
- Chaichian, M.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Tureanu, A. Thermal Casimir-Polder interaction of different atoms with graphene. Phys. Rev. A 2012, 86, 012515. [Google Scholar] [CrossRef]
- Arora, B.; Kaur, H.; Sahoo, B.K. C3 coefficients for the alkali atoms interacting with a graphene and carbon nanotube. J. Phys. B 2014, 47, 155002. [Google Scholar] [CrossRef]
- Kaur, K.; Kaur, J.; Arora, B.; Sahoo, B.K. Emending thermal dispersion interaction of Li, Na, K and Rb alkali-metal atoms with graphene in the Dirac model. Phys. Rev. B 2014, 90, 245405. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Impact of graphene coating on the atom-plate interaction. Phys. Rev. A 2014, 89, 062508. [Google Scholar] [CrossRef]
- Cysne, T.; Kort-Kamp, W.J.M.; Oliver, D.; Pinheiro, F.A.; Rosa, F.S.S.; Farina, C. Tuning the Casimir-Polder interaction via magneto-optical effects in graphene. Phys. Rev. A 2014, 90, 052511. [Google Scholar] [CrossRef]
- Kaur, K.; Arora, B.; Sahoo, B.K. Dispersion coefficients for the interactions of the alkali-metal and alkaline-earth-metal ions and inert-gas atoms with a graphene layer. Phys. Rev. A 2015, 92, 032704. [Google Scholar] [CrossRef]
- Henkel, C.; Klimchitskaya, G.L.; Mostepanenko, V.M. Influence of the chemical potential on the Casimir-Polder interaction between an atom and gapped graphene or a graphene-coated substrate. Phys. Rev. A 2018, 97, 032504. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Kashapov, R.; Woods, L.M. Casimir-Polder effect for a stack of conductive planes. Phys. Rev. A 2016, 94, 012513. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Kashapov, R.; Woods, L.M. Thermal Casimir and Casimir-Polder interactions in N parallel 2D Dirac materials. 2D Mater. 2018, 5, 035032. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Nernst heat theorem for an atom interacting with graphene: Dirac model with nonzero energy gap and chemical potential. Phys. Rev. D 2020, 101, 116003. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Emelianova, N. The Low-Temperature Expansion of the Casimir-Polder Free Energy of an Atom with Graphene. Universe 2021, 7, 70. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L. The Casimir-Polder interaction of an atom and real graphene sheet: Verification of the Nernst heat theorem. Mod. Phys. Lett. A 2020, 35, 2040004. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir and Casimir-Polder Forces in Graphene Systems: Quantum Field Theoretical Description and Thermodynamics. Universe 2020, 6, 150. [Google Scholar] [CrossRef]
- Das, B.; Choudhury, B.; Gomathi, A.; Manna, A.K.; Pati, S.K.; Rao, C.N.R. Interaction of Inorganic Nanoparticles with Graphene. ChemPhysChem 2011, 12, 937–943. [Google Scholar] [CrossRef]
- Biehs, S.-A.; Agarwal, G.S. Anisotropy enhancement of the Casimir-Polder force between a nanoparticle and graphene. Phys. Rev. A 2015, 90, 042510, Erratum in 2015, 91, 039901. [Google Scholar] [CrossRef]
- Devi, J.M. Simulation Studies on the Interaction of Graphene and Gold Nanoparticle. Int. J. Nanosci. 2018, 17, 1760043. [Google Scholar] [CrossRef]
- Low, S.; Shon, Y.-S. Molecular interactions between pre-formed metal nanoparticles and graphene families. Adv. Nano Res. 2018, 6, 357–375. [Google Scholar] [PubMed]
- Huang, L.-W.; Jeng, H.-T.; Sua, W.-B.; Chang, C.-S. Indirect interactions of metal nanoparticles through graphene. Carbon 2021, 174, 132. [Google Scholar] [CrossRef]
- Williams, G.; Kamat, P.V. Graphene-Semiconductor Nanocomposites: Excited-State Interactions between ZnO Nanoparticles and Graphene Oxide. Langmuir 2009, 25, 13869–13873. [Google Scholar] [CrossRef]
- Donnelly, M.; Mao, D.; Park, J.; Xu, G. Graphene field-effect transistors: The road to bioelectronics. J. Phys. D Appl. Phys. 2018, 51, 493001. [Google Scholar] [CrossRef]
- Puigpelat, E.; Ignés-Mullol, J.; Sagués, F.; Reigada, R. Interaction of Graphene Nanoparticles and Lipid Membranes Displaying Different Liquid Orderings: A Molecular Dynamics Study. Langmuir 2019, 35, 16661–16668. [Google Scholar] [CrossRef]
- Liu, H.; Hao, C.; Zhang, Y.; Yang, H.; Sun, R. The interaction of graphene oxide-silver nanoparticles with trypsin: Insights from adsorption behaviors, conformational structure and enzymatic activity investigations. Coll. Surf. B Biointerf. 2021, 202, 111688. [Google Scholar] [CrossRef] [PubMed]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Velichko, E.N. Casimir pressure in peptide films on metallic substrates: Change of sign via graphene coating. Phys. Rev. B 2021, 103, 245421. [Google Scholar] [CrossRef]
- Lifshitz, E.M. The theory of molecular attractive forces between solids. Zh. Eksp. Teor. Fiz. 1955, 29, 94–110, Translated: Sov. Phys. JETP 1956, 2, 73–83.. [Google Scholar]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. The general theory of van der Waals forces. Usp. Fiz. Nauk 1961, 73, 381–422, Translated: Adv. Phys. 1961, 10, 165–209.. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics, Part II; Pergamon: Oxford, UK, 1980. [Google Scholar]
- Bordag, M.; Fialkovsky, I.V.; Gitman, D.M.; Vassilevich, D.V. Casimir interaction between a perfect conductor and graphene described by the Dirac model. Phys. Rev. B 2009, 80, 245406. [Google Scholar] [CrossRef]
- Fialkovsky, I.V.; Marachevsky, V.N.; Vassilevich, D.V. Finite-temperature Casimir effect for graphene. Phys. Rev. B 2011, 84, 035446. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Petrov, V.M. Quantum field theoretical description for the reflectivity of graphene. Phys. Rev. D 2015, 91, 045037, Erratum in Phys. Rev. D 2016, 93, 089907.. [Google Scholar] [CrossRef]
- Bordag, M.; Fialkovskiy, I.; Vassilevich, D. Enhanced Casimir effect for doped graphene. Phys. Rev. B 2016, 93, 075414, Erratum in Phys. Rev. B 2017, 95, 119905.. [Google Scholar] [CrossRef]
- Henkel, C.; Joulain, K.; Mulet, J.P.; Greffet, J.J. Radiation forces on small particles in thermal near fields. J. Opt. A Pure Appl. Opt. 2002, 4, S109–S114. [Google Scholar] [CrossRef]
- Antezza, M.; Pitaevskii, L.P.; Stringari, S. New Asymptotic Behavior of the Surface-Atom Force out of Thermal Equilibrium. Phys. Rev. Lett. 2005, 95, 113202. [Google Scholar] [CrossRef]
- Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Svetovoy, V.B. Casimir-Lifshitz force out of thermal equilibrium. Phys. Rev. A 2008, 77, 022901. [Google Scholar] [CrossRef]
- Bimonte, G. Scattering approach to Casimir forces and radiative heat transfer for nanostructured surfaces out of thermal equilibrium. Phys. Rev. A 2009, 80, 042102. [Google Scholar] [CrossRef]
- Messina, R.; Antezza, M. Scattering-matrix approach to Casimir-Lifshitz force and heat transfer out of thermal equilibrium between arbitrary bodies. Phys. Rev. A 2011, 84, 042102. [Google Scholar] [CrossRef]
- Krüger, M.; Bimonte, G.; Emig, T.; Kardar, M. Trace formulas for nonequilibrium Casimir interactions, heat radiation, and heat transfer for arbitrary bodies. Phys. Rev. B 2012, 86, 115423. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Krüger, M.; Kardar, M. Dilution and resonance-enhanced repulsion in nonequilibrium fluctuation forces. Phys. Rev. A 2011, 84, 042503. [Google Scholar] [CrossRef]
- Krüger, M.; Emig, T.; Bimonte, G.; Kardar, M. Non-equilibrium Casimir forces: Spheres and sphere-plate. Europhys. Lett. 2011, 95, 21002. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sedmik, R.I.P. Casimir pressure between metallic plates out of thermal equilibrium: Proposed test for the relaxation properties of free electrons. Phys. Rev. A 2019, 100, 022511. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir-Polder Interaction of an Atom with a Cavity Wall Made of Phase-Change Material out of Thermal Equilibrium. Atoms 2020, 9, 4. [Google Scholar] [CrossRef]
- Ingold, G.-L.; Klimchitskaya, G.L.; Mostepanenko, V.M. Nonequilibrium effects in the Casimir force between two similar metallic plates kept at different temperatures. Phys. Rev. A 2020, 101, 032506. [Google Scholar] [CrossRef]
- Khandekar, C.; Buddhiraju, S.; Wilkinson, P.R.; Gimzewski, J.K.; Rodriguez, A.W.; Chase, C.; Fan, S. Nonequilibrium lateral force and torque by thermally excited nonreciprocal surface electromagnetic waves. Phys. Rev. B 2021, 104, 245433. [Google Scholar] [CrossRef]
- Castillo-López, S.G.; Esquivel-Sirvent, R.; Pirruccio, G.; Villarreal, C. Casimir forces out of thermal equilibrium near a superconducting transition. Sci. Rep. 2022, 12, 2905. [Google Scholar] [CrossRef] [PubMed]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Tsybin, O.Y. Casimir-Polder attraction and repulsion between nanoparticles and graphene in out-of-thermal-equilibrium conditions. Phys. Rev. B 2022, 105, 195430. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. On the universal ac optical background in graphene. New J. Phys. 2009, 11, 095013. [Google Scholar] [CrossRef]
- Pyatkovsky, P.K. Dynamical polarization, screening, and plasmons in gapped graphene. J. Phys. Condens. Matter 2009, 21, 025506. [Google Scholar] [CrossRef] [PubMed]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sernelius, B.E. Two approaches for describing the Casimir interaction with graphene: Density-density correlation function versus polarization tensor. Phys. Rev. B 2014, 89, 125407. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Korikov, C.C.; Petrov, V.M. Theory of reflectivity properties of graphene-coated material plates. Phys. Rev. B 2015, 92, 125419, Erratum in 2016, 93, 159906.. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Reflectivity properties of graphene with nonzero mass-gap parameter. Phys. Rev. A 2016, 93, 052106. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Optical properties of dielectric plates coated with gapped graphene. Phys. Rev. B 2017, 95, 035425. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Maximum reflectance and transmittance of films coated with gapped graphene in the context of the Dirac model. Phys. Rev. A 2018, 97, 063817. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Conductivity of pure graphene: Theoretical approach using the polarization tensor. Phys. Rev. B 2016, 93, 245419. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Quantum electrodynamic approach to the conductivity of gapped graphene. Phys. Rev. B 2016, 94, 195405. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Petrov, V.M. Conductivity of graphene in the framework of Dirac model: Interplay between nonzero mass gap and chemical potential. Phys. Rev. B 2017, 96, 235432. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Kramers-Kronig relations and causality conditions for graphene in the framework of Dirac model. Phys. Rev. D 2018, 97, 085001. [Google Scholar] [CrossRef]
- Zhu, T.; Antezza, M.; Wang, J.-S. Dynamical polarizability of graphene with spatial dispersion. Phys. Rev. B 2021, 103, 125421. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Y.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of Unusual Thermal Effect in the Casimir Force from Graphene. Phys. Rev. Lett. 2021, 126, 206802. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Y.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Experimental and theoretical investigation of the thermal effect in the Casimir interaction from graphene. Phys. Rev. B 2021, 104, 085436. [Google Scholar] [CrossRef]
- Bordag, M.; Pirozhenko, I.G. Surface plasmon on graphene at finite T. Int. J. Mod. Phys. B 2016, 30, 1650120. [Google Scholar] [CrossRef]
- Obrecht, J.M.; Wild, R.J.; Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Cornell, E.A. Measurement of the temperature dependence of the Casimir-Polder force. Phys. Rev. Lett. 2007, 98, 063201. [Google Scholar] [CrossRef]
- Galassi, M.; Davies, J.; Theiler, J.; Gough, B.; Gungman, G.; Alken, P.; Booth, M.; Rossi, F.; Ulerich, R. GNU Scientific Library Reference Manual. 2021. Available online: Https://www.gnu.org/software/gsl/doc/latex/gsl-ref.pdf (accessed on 8 May 2023).
- Boost C++ Libraries. Available online: Https://www.boost.org (accessed on 8 May 2023).
- Boost Multiprecision Library. Available online: Https://github.com/boostorg/multiprecision (accessed on 8 May 2023).
- OpenMP Application Programming Interface. Available online: Https://www.openmp.org/specifications (accessed on 8 May 2023).
- Cahangirov, S.; Topsakal, M.; Aktürk, E.; Sahin, H.; Ciraci, S. Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium. Phys. Rev. Lett. 2009, 102, 236804. [Google Scholar] [CrossRef]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-Like Two-Dimensional Materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef]
- Yuhara, J.; Fujii, Y.; Nishino, K.; Isobe, N.; Nakatake, M.; Xian, L.; Rubio, A.; Le Lay, G. Large area planar stanene epitaxially grown on Ag(1 1 1). 2D Mater. 2018, 5, 025002. [Google Scholar] [CrossRef]
- Mu, X.; Yu, W.; Yuan, J.; Lin, S.; Zhang, G. Interface and surface engineering of black phosphorus: A review for optoelectronic and photonic applications. Mater. Futures 2022, 1, 012301. [Google Scholar] [CrossRef]
- Xu, R.; Guo, J.; Mi, S.; Wen, H.; Pang, F.; Ji, W.; Cheng, Z. Advanced atomic force microscopies and their applications in two-dimensional materials: A review. Mater. Futures 2022, 1, 032302. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, H.; Yang, Z.; Ji, C.; Zhang, G.; Tu, Y.; Du, G.; Cai, S.; Lin, S. Emerging Two-Dimensional Tellurene and Tellurides for Broadband Photodetectors. Small 2022, 18, 2200016. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimchitskaya, G.L.; Korikov, C.C.; Mostepanenko, V.M.; Tsybin, O.Y. Impact of Mass-Gap on the Dispersion Interaction of Nanoparticles with Graphene out of Thermal Equilibrium. Appl. Sci. 2023, 13, 7511. https://doi.org/10.3390/app13137511
Klimchitskaya GL, Korikov CC, Mostepanenko VM, Tsybin OY. Impact of Mass-Gap on the Dispersion Interaction of Nanoparticles with Graphene out of Thermal Equilibrium. Applied Sciences. 2023; 13(13):7511. https://doi.org/10.3390/app13137511
Chicago/Turabian StyleKlimchitskaya, Galina L., Constantine C. Korikov, Vladimir M. Mostepanenko, and Oleg Yu. Tsybin. 2023. "Impact of Mass-Gap on the Dispersion Interaction of Nanoparticles with Graphene out of Thermal Equilibrium" Applied Sciences 13, no. 13: 7511. https://doi.org/10.3390/app13137511
APA StyleKlimchitskaya, G. L., Korikov, C. C., Mostepanenko, V. M., & Tsybin, O. Y. (2023). Impact of Mass-Gap on the Dispersion Interaction of Nanoparticles with Graphene out of Thermal Equilibrium. Applied Sciences, 13(13), 7511. https://doi.org/10.3390/app13137511







