Effective Quantization Evaluation Method of Functional Movement Screening with Improved Gaussian Mixture Model

Abstract

Background: Functional movement screening (FMS) allows for the rapid assessment of an individual’s physical activity level and the timely detection of sports injury risk. However, traditional functional movement screening often requires on-site assessment by experts, which is time-consuming and prone to subjective bias. Therefore, the study of automated functional movement screening has become increasingly important. Methods: In this study, we propose an automated assessment method for FMS based on an improved Gaussian mixture model (GMM). First, the oversampling of minority samples is conducted, the movement features are manually extracted from the FMS dataset collected with two Azure Kinect depth sensors; then, we train the Gaussian mixture model with different scores (1 point, 2 points, 3 points) of feature data separately; finally, we conducted FMS assessment by using a maximum likelihood estimation. Results: The improved GMM has a higher scoring accuracy (improved GMM: 0.8) compared to other models (traditional GMM = 0.38, AdaBoost.M1 = 0.7, Naïve Bayes = 0.75), and the scoring results of improved GMM have a high level of agreement with the expert scoring (kappa = 0.67). Conclusions: The results show that the proposed method based on the improved Gaussian mixture model can effectively perform the FMS assessment task, and it is potentially feasible to use depth cameras for FMS assessment.

1. Introduction

Functional Movement Screening (FMS) is a widely recognized and highly regarded screening instrument used to assess an individual’s exercise capacity and identify the potential risks of sports injuries. It involves a comprehensive evaluation of fundamental movement patterns, including deep squat, hurdle step, in-line lunge, shoulder mobility, active straight leg raise, trunk stability push-up, and rotary stability. FMS also examines mobility, stability, and asymmetries in the body, utilizing a standardized scoring system to assess movement quality and identify areas of concern. FMS has gained immense popularity in recent years due to its holistic approach to assessing movement quality and injury risk. By analyzing deviations from ideal movement patterns, FMS provides valuable insights into an individual’s functional movement capabilities, including strength, flexibility, and motor control. This information is instrumental in guiding injury prevention strategies, training programs, and rehabilitation protocols. The application of FMS extends to various domains, including sports training, injury prevention, and rehabilitation. Numerous studies have demonstrated its effectiveness in evaluating sports performance and reducing the incidence of musculoskeletal injuries. For example, Sajjad et al. utilized FMS to assess sports performance and musculoskeletal pain in college students, highlighting its utility in identifying areas for improvement and addressing potential injury risks [1]. Similarly, Li et al. successfully employed FMS assessment to reduce knee injuries among table tennis players, showcasing the role of FMS in optimizing movement patterns and minimizing the risk of sports-related injuries [2]. By identifying limitations and imbalances in movement patterns, FMS enables targeted interventions to address specific areas of concern. This comprehensive approach helps individuals improve their functional movement, enhance athletic performance, and minimize the risk of sports injuries. Indeed, FMS has become a valuable tool in optimizing physical well-being and promoting long-term athletic success. On-site evaluation is the most common method in FMS. An expert observes each subject’s movement. However, on-site evaluation is time-consuming and labor-intensive, and the subjectivity of expert affects the accuracy of the results.

Researchers have experimented with other functional movement data collection methods to address these issues. Shuai et al. used seven nine-axis inertial measurement units (IMUs) method to collect joint angle information of functional movements [3]; Vakanski et al. used a Vicon motion capture system to collect joint angle and joint position information of functional movements [4]; and Wang et al. collect video data of FMS assessment movements by using two 2D cameras with different viewpoints [5]. Although these devices have high-precision motion capture capabilities and enable fast and accurate assessments by analyzing large amounts of motion data, traditional motion capture systems such as IMU, Vicon, and OptiTrack require invasive operations such as tagging or wearing sensors on the subject [6,7,8], which are not only tedious but may also interfere with the subject’s movements. At the same time, the high price of these devices limits their popularity and diffusion in fields such as sports medicine and rehabilitation therapy [9]. As the field of movement quality assessment continues to evolve, some methods of data acquisition using depth cameras are beginning to emerge. Cuellar et al. used a Kinect V1 depth camera to collect 3D skeletal data for standing shoulder abduction, leg lift, and arm raise [10]. Capecci et al. used a Kinect V2 depth camera to capture 3D skeletal data and videos of healthy subjects and patients with motor disabilities performing squats, arm extensions, and trunk rotations [11]. Depth cameras are able to measure the depth information (RGB-D) of each pixel and use depth information to generate 3D scene models compared with conventional 2D cameras. This makes depth cameras more precise in distance measurement and spatial analysis; therefore, it is more suitable for fields such as human activity recognition and movement quality assessment. In addition, depth cameras are also affordable and have the advantages of being non-invasive, portable, and low cost [12].

In recent years, with the continuing progress and development of artificial intelligence, some automated FMS measurement methods have emerged. Andreas et al. proposed a CNN-LSTM model to achieve the classification of functional movements [13]. Duan et al. used a CNN model to classify the electromyographic (EMG) signals of functional movements, in which the classification accuracies of squat, stride, and straight lunge squat were $91\%$, $89\%$, and $90\%$, respectively, [14]. Deep learning algorithms can automatically extract a set of movement features, which can improve the accuracy of activity recognition. However, they require large amounts of training data, which is time-consuming, and the network structures of deep learning models are more complex and less interpretable. Meanwhile, better results have been achieved in the field of movement quality assessment by training multiple weak classifiers to form a strong classifier in machine learning methods. An automated FMS assessment method based on the AdaBoost.M1 classifier was proposed by Wu et al. [15]. FMS assessment can be achieved by training weak classifiers and combining them into a strong classifier. Bochniewicz et al. used a random forest model to assess the arm movements of stroke patients by randomly selecting samples to form multiple classifiers [16]. The classification labels were then predicted by a voting method using a minority–majority approach. This method requires a smaller amount of data and is based on the interpretability of a machine learning method with manually extracted features.

In summary, we propose an automated FMS assessment method based on an improved Gaussian mixture model in this study. First, we perform feature extraction on the FMS dataset collected with two Azure Kinect depth sensors; then, the features with different scores (1 point, 2 points, or 3 points) are trained separately in a Gaussian mixture model. Finally, FMS assessment can be achieved by performing maximum likelihood estimation. The results show that the improved Gaussian mixture model has better performance compared to the traditional Gaussian mixture model. It provides fast and objective evaluation with real-time feedback. In addition, we further explore the application of datasets acquired using depth cameras in the field of FMS and validate the feasibility of FMS assessment based on depth cameras.

This research makes a significant contribution to the field by introducing an automated FMS assessment method and exploring the potential of depth cameras in enhancing the evaluation process. These advancements overcome the limitations of traditional methods by providing an objective and efficient FMS assessment method. The implications of our findings extend to various domains, including sports medicine, rehabilitation therapy, and performance optimization.

2. Materials and Methods

2.1. Manual Features in FMS Assessment

Manual feature extraction is a common approach in machine-learning-based movement quality assessment; it transforms raw data into a set of representative features for machine learning algorithms. Manual feature extraction usually requires the knowledge and experience of domain experts to select features relevant to the target task, converted into numerical or discrete variables for training and classification of machine learning algorithms. Manual feature extraction has many advantages. First, because human-selected features are highly interpretable, they can provide meaningful references for subsequent data analysis. Second, manual feature extraction is controllable and can be adjusted according to actual requirements, thus improving movement classification accuracy and generalization ability [17].

In our study, we performed manual feature extraction based on the functional movement screening method and scoring criteria developed by Gray Cook and Lee Burton, as well as input from our school’s team of biomechanical experts [18,19,20]. We manually selected a comprehensive set of informative and easily interpretable features by leveraging these well-established methodologies. These features encompass the key motion characteristics of each functional movement, such as joint angles and joint spacing, which are critical in the development of effective machine-learning-based FMS assessment models. Figure 1 visually illustrates the skeletal joint points, while the subsequent section provides a detailed description of the calculation method for automatic evaluation metrics associated with each movement.

Overall, manual feature extraction plays a pivotal role in bridging the gap between domain-specific knowledge and deep-learning-based automatic feature extraction, ultimately enhancing the performance and robustness of machine-learning-based FMS assessment.

2.1.1. Deep Squat

The angle between the thigh and the horizontal plane is defined as the angle between the vector along the left thigh hip joint point to the knee joint point and the horizontal plane during movement.The thigh angle is calculated as the angle between a vector connecting the left thigh hip joint and knee joint and a horizontal vector. $K(X_k,Y_k,Z_k)$ and $H(X_h,Y_h,Z_h)$ represent the 3D coordinates of the knee joint and hip joint. $\alpha$ is shown in Figure 2a.

$$\begin{array}{c}\hfill \overrightarrow{KH}=\left(X_k-X_h,Y_k-Y_h,Z_k-Z_h\right)\end{array}$$

(1)

The thigh angle is given by

$$\begin{array}{c}\hfill \alpha =arccos\frac{\overrightarrow{KH}·\overrightarrow{h}}{|\overrightarrow{KH}\left|\right|\overrightarrow{h}|}\end{array}$$

(2)

where $\overrightarrow{KH}$ is the left thigh vector (joint 12, joint 13) and $\overrightarrow{h}=(1,0,0)$ is the horizontal vector.

2.1.2. Hurdle Step

The raised leg angle is calculated as the angle between a vector connecting the raised leg hip joint and knee joint and a normal vector. $H(X_h,Y_h,Z_h)$ and $A(X_a,Y_a,Z_a)$ represent the 3D coordinates of the hip joint and ankle joint. $\alpha$ is shown in Figure 2b.

$$\begin{array}{c}\hfill \overrightarrow{HA}=\left(X_a-X_h,Y_a-Y_h,Z_a-Z_h\right)\end{array}$$

(3)

The raised leg angle is given by

$$\begin{array}{c}\hfill \alpha =arccos\frac{\overrightarrow{HA}·\overrightarrow{V}}{|\overrightarrow{HA}\left|\right|\overrightarrow{V}|}\end{array}$$

(4)

where $\overrightarrow{HA}$ is the raised leg vector (joint 12, joint 14) and $\overrightarrow{V}=(0,1,0)$ is the vertical vector.

2.1.3. In-Line Lunge

The trunk angle is calculated as the angle between a vector connecting the spine chest joint and pelvis joint and a normal vector. $S(X_s,Y_s,Z_s)$ and $P(X_p,Y_p,Z_p)$ represent the 3D coordinates of the spine chest joint and pelvis joint. $\alpha$ is shown in Figure 2c.

$$\begin{array}{c}\hfill \overrightarrow{SP}=\left(X_p-X_s,Y_p-Y_s,Z_p-Z_s\right)\end{array}$$

(5)

The trunk angle is given by

$$\begin{array}{c}\hfill \alpha =arccos\frac{\overrightarrow{SP}·\overrightarrow{V}}{|\overrightarrow{SP}\left|\right|\overrightarrow{V}|}\end{array}$$

(6)

where $\overrightarrow{SP}$ is the trunk vector (joint 2, joint 0) and $\overrightarrow{V}=(0,1,0)$ is the vertical vector.

2.1.4. Shoulder Mobility

The wrist distance is the minimum distance between the left wrist joint and the right wrist joint. ${\mathrm{W}}_l\left(X_l,Y_l,Z_l\right)$ and ${\mathrm{W}}_r\left(X_r,X_r,X_r\right)$ represent the 3D coordinates of the left wrist joint and the right wrist joint. d is shown in Figure 2d. The wrist distance is given by

$$\begin{array}{c}\hfill d=\sqrt{{\left(X_r-X_l\right)}^2+{\left(Y_r-Y_l\right)}^2+{\left(Z_r-Z_l\right)}^2}\end{array}$$

(7)

2.1.5. Active Straight Leg Raise

The raised leg angle is calculated as the angle between a vector connecting the hip joint and ankle joint and a horizontal vector. $H(X_h,Y_h,Z_h)$ and $A(X_a,Y_a,Z_a)$ represent the 3D coordinates of the hip joint and ankle joint. $\alpha$ is shown in Figure 2e.The raised leg angle is given by

$$\begin{array}{c}\hfill \alpha =arccos\frac{\overrightarrow{HA}·\overrightarrow{h}}{|\overrightarrow{HA}\left|\right|\overrightarrow{h}|}\end{array}$$

(8)

2.1.6. Trunk Stability Push-Up

The angle between trunk and thigh is calculated as the angle between a vector connecting the spine chest joint and pelvis joint and a vector connecting the hip joint and ankle joint. $\alpha$ is shown in Figure 2f. The angle between trunk and thigh is given by

$$\begin{array}{c}\hfill \alpha =arccos\frac{\overrightarrow{PS}·\overrightarrow{HA}}{|\overrightarrow{PS}\left|\right|\overrightarrow{HA}|}\end{array}$$

(9)

2.1.7. Rotary Stability

The distance between the elbow joint and the ipsilateral or contralateral knee joint is the distance between the moving elbow joint and the moving knee joint.

$E_l\left(X_{el},Y_{el},Z_{el}\right)$, $K_l\left(X_{kl},Y_{kl},Z_{kl}\right)$, and $K_r\left(X_{kr},Y_{kr},Z_{kr}\right)$ represent the 3D coordinates of the left elbow joint, left knee joint, and right knee joint, respectively. d is shown in Figure 2g. The distance between the elbow joint and the ipsilateral knee joint is given by

$$\begin{array}{c}\hfill d=\sqrt{{\left(X_{kl}\left(X_{kr}\right)-X_{el}\right)}^2+{\left(Y_{kl}\left(Y_{kr}\right)-Y_{el}\right)}^2+{\left(Z_{kl}\left(Z_{kr}\right)-Z_{el}\right)}^2}\end{array}$$

(10)

2.2. Improved Gaussian Mixture Model

The Gaussian mixture model (GMM) is composed of k sub-Gaussian distribution models, which are the hidden variables of the mixture model, and the probability density function of the Gaussian mixture model is formed by the linear summation of these Gaussian distributions [21,22]. A model is chosen randomly among the k Gaussian models according to the probability. The probability distribution of the Gaussian mixture model can be described as follows:

$$\begin{array}{c}\hfill p\left(x\right)=\sum _{K=1}^K{\phi }_{i}N\left(x\mid {\mu }_i,{\sigma }_i\right)\end{array}$$

(11)

where ${\phi }_i$ is the coefficient $({\phi }_i⩾0,{\sum }_{K=1}^K{\phi }_i=1)$. $N(x\mid {\mu }_i)$ is the probability density function of the Gaussian distribution, and the associated parameters indicate that there are k Gaussian models, each with 3 parameters, namely, the mean ${\mu }_i$, the variance ${\sigma }_i$, and the generation probability ${\phi }_i$. The sample data are generated by their Gaussian probability density function $N(x\mid {\mu }_i)$ after model selection.

$$\begin{array}{c}\hfill N\left(x\mid {\mu }_i,{\sigma }_i\right)=\frac{1}{{\sigma }_i\sqrt{2\pi }}exp\left(-\frac{{\left(x-{\mu }_i\right)}^2}{2{\sigma }_i^2}\right)\end{array}$$

(12)

The maximum likelihood function method is used to train the Gaussian mixture model. The likelihood function can be expressed as follows:

$$\begin{array}{c}\hfill L=\prod _{i=1}^{L}p\left(x_i\mid \phi \right)\end{array}$$

(13)

where L is the number of samples in the dataset, x is the data object $(i=1,2,3\cdots \mathrm{N})$, and p(x) denotes the probability of data sample generation in the Gaussian mixture model. The mixed model with maximum likelihood is calculated as follows:

$$\begin{array}{c}\hfill logL=\sum _{i=1}^{N}P\left(x_i\mid \phi \right)=\sum _{i=1}^{N}log\left(\sum _{k=1}^K{\alpha }_{i}N\left(x\mid {\phi }_i\right)\right)\end{array}$$

(14)

The Gaussian mixture model cannot acquire the derivative, and the EM algorithm is used to solve the best parameters of the model according to the maximized likelihood function in the training phase of the GMM model; the mixture probability, ${\phi }_k$; the mean, ${\mu }_k$; and the covariance, ${\sigma }_i$, until the convergence of the model.

However, the use of a single GMM as a classifier in movement quality assessment has certain drawbacks. First, it may oversimplify the complexity of motion data and affect the model performance [23,24]. Second, the sensitivity to noisy data and statistics outliers is a weak feature of a single Gaussian mixture model, which reduces the model accuracy [25]. Meanwhile, promising results have been achieved in movement quality assessment by combining weak classifiers into a strong classifier in machine learning methods. Several studies have confirmed the validity of this method. For example, Wu proposed an automated FMS assessment method based on an AdaBoost.M1 classifier, which trains different weak classifiers for the FMS dataset collected by IMU and then combines these weak classifiers to form a powerful classifier for FMS [15]. In addition, Bochniewicz evaluated the arm movements of stroke patients using a random forest model with randomly selected samples to form multiple classifiers, and then used a minority–majority approach to predict the classification labels through a voting method [16]. Therefore, we proposed an automated FMS assessment method based on the idea of combining three Gaussian mixture models into a strong classifier in this study.

As shown in Figure 3, firstly, a Gaussian mixture model is trained separately for the movement features with different scores to obtain the Gaussian mixture model probability distributions of 1 point, 2 points, and 3 points ($p_1\left(x\right)$, $p_2\left(x\right)$, $p_3\left(x\right)$, respectively). Next, the feature data with unknown scores are modeled using each of the 3 Gaussian mixture models, and finally, maximum likelihood estimation is performed to obtain the evaluation results. We evaluated the performance of the new classifier by comparing it with three basic classifiers, including the traditional Gaussian mixture model [26], Naïve Bayes [27], and AdaBoost.M1 classifier [15].

2.3. Statistical Analysis

In this experiment, we contrasted three traditional machine learning methods (GMM, Naïve Bayes, AdaBoost.M1) to evaluate the scoring ability of the improved GMM. Due to the analysis of the experimental results, we used scoring accuracy, confusion matrix, and kappa statistic to evaluate the performance of our proposed models. For the task of FMS movement assessment, scoring accuracy can visually reflect the scoring performance of each model. The confusion matrix can show the difference between the predicted results and the expert scores, the diagonal element values of the matrix represent the consistency between the prediction results and the actual measurements, and the non-diagonal element values of the matrix denote wrong predictions. The kappa coefficient is used to assess the degree of agreement between the model scoring results and the expert scoring results [28].

$$\begin{array}{c}\hfill k=\frac{P_o-P_e}{1-P_e}\end{array}$$

(15)

where $P_o$ is defined as the sum of the number of samples correctly in each category divided by the total number of samples, which is the overall classification accuracy. We assume the number of correctly samples in each category $\left(a_1,a_2\cdots ,a_{\mathrm{m}}\right)$, and the number of predicted samples in each category $\left(a_1,a_2\cdots ,a_{\mathrm{m}}\right)$. The total number of samples is n, and $P_e$ is obtained by dividing the sum of the “product of the actual value and predicted value” for all categories by the square of the total number of samples.

$$\begin{array}{c}\hfill P_e=\frac{a_1\times b_1+a_2\times b_2+\cdots +a_m\times b_m}{n\times n}\end{array}$$

(16)

The value of kappa usually lies between 0 and 1. Typically, kappa values of 0.0–0.2 are considered in slight agreement, 0.2–0.4 in fair agreement, 0.4–0.6 in moderate agreement, 0.6–0.8 in substantial agreement, and >0.8 in almost perfect agreement.

For the evaluation of the performance on different movements, we also used the F1-Measure to evaluate the performance of the model, we adopted the micro-averaged F1 (miF1), macro-averaged F1 (maF1), and weighted-F1 simultaneously.

3. Results and Discussion

We conducted an experimental study using a dataset acquired by a depth camera to validate the effectiveness of the proposed improved Gaussian mixture model. First, the used dataset was introduced. Then, we contrasted three classifiers to evaluate the performance of the improved Gaussian mixture model. (Traditional Gaussian mixture model, Naïve Bayes, and AdaBoost.M1). Finally, we analyzed the effect of skeleton data and feature data on FMS assessment.

3.1. Dataset

This study used the FMS dataset proposed by Xing et al. [29]. This dataset was collected from 2 Azure Kinect depth cameras and covered 45 subjects between the ages of 18 and 59 years. The dataset consists of functional movement data, which are divided into left and right side movements, including deep squat, hurdle step, in-line lunge, shoulder mobility, active straight leg raise, trunk stability push-up, and rotary stability. In order to improve the accuracy and stability of the data, the researcher used two depth cameras with different viewpoints to collect the movement data of the subjects. The dataset contains both skeletal data and image information.

The Azure Kinect depth sensor provides better quality and accuracy of data compared to depth cameras, such as Kinect V1, Kinect V2, and Real Sense; thus, it offers the possibility of machine learning and other methods for tasks such as human motion recognition and movement assessment [30,31,32,33,34]. In addition, the dataset not only provides strong support for functional movement assessment and rehabilitation training, but also provides technical support and data sources for research and applications in the fields of intelligent fitness and virtual reality.

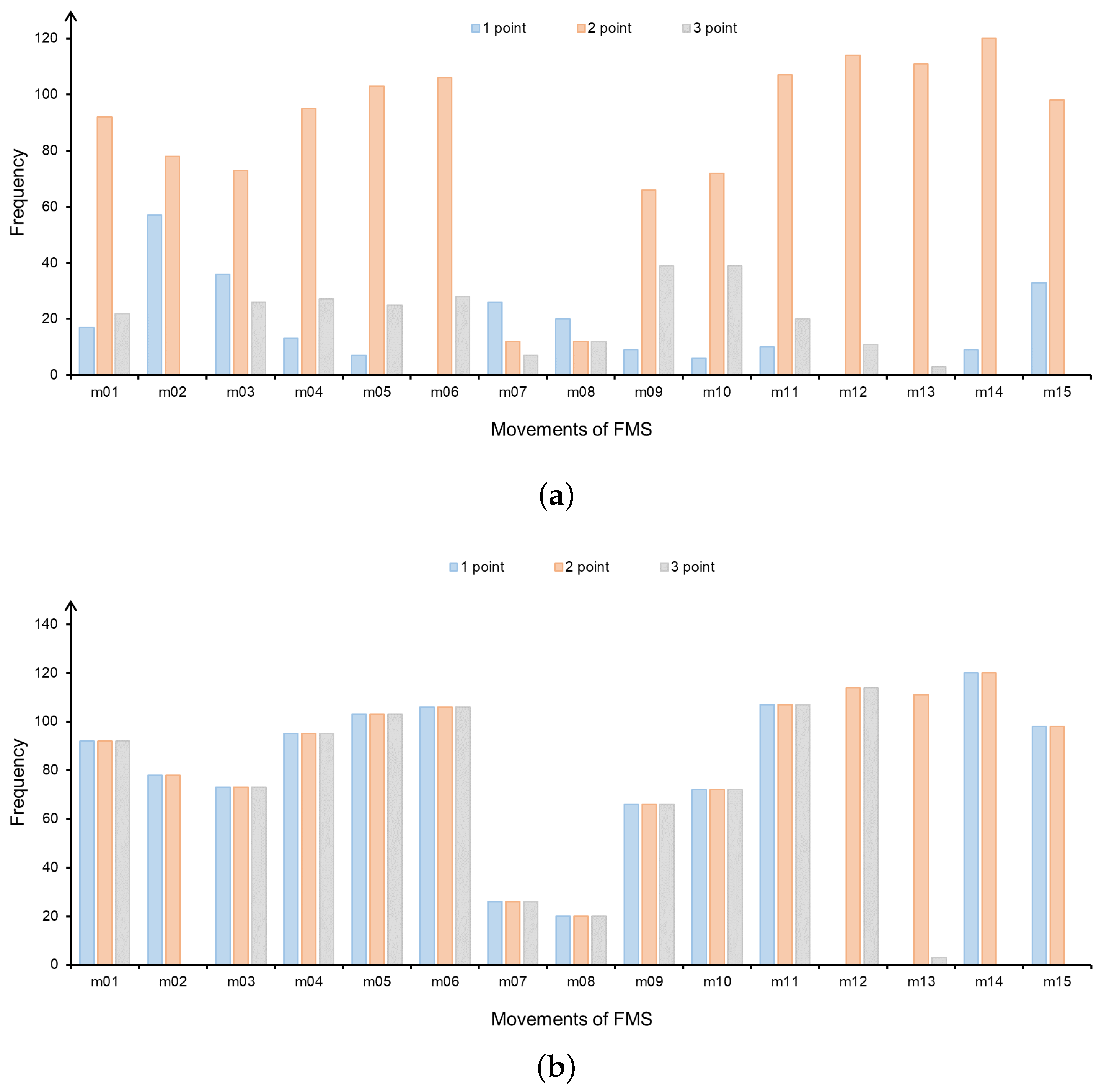
The 3D skeleton data acquired by the frontal depth camera were used in this experiment. The score distribution of each movement is shown in Figure 4a.

As shown in Figure 4a, for example, the number of 2 score is much larger than the number of 1 and 3 scores in m11, due to the uneven distribution of FMS scores, which may decrease the performance of some machine learning models. Although the model has a high overall accuracy rate, 1 point and 3 points have low accuracy rates. Therefore, in order to avoid this situation, the problem of unequal distribution of each movement in the dataset needs to be addressed. This experiment used the Borderline SMOTE oversampling algorithm, which is a variant of SMOTE algorithm [35]. This algorithm synthesizes new samples using only the minority boundary samples and considers the category information of the neighbor samples, avoiding the poor classification results caused by the overlapping phenomenon in the traditional SMOTE algorithm. The Borderline SMOTE method divides the minority samples into three categories (Safe, Danger, and Noise) and oversamples only the minority samples of the Danger category.

After Borderline SMOTE pre-processing, the expert score uniform distribution of FMS movements is also realized, as shown in Figure 4b. However, the distribution of m13 is still uneven. In order to avoid impacts on the experimental results, m13 was not tested in the subsequent experiments. The movements in the dataset are divided into the left side and the right side except for m01, m02, and m11, both sides have the same movement type and movement repetitions. In order to facilitate the targeted analysis and processing of the movement data, we only analyzed the movements on the left side of the body. In summary, the movements used for this experiment included m01, m03, m05, m07, m09, m11, m12, and m14.

3.2. Evaluation of the Performance on Different Methods

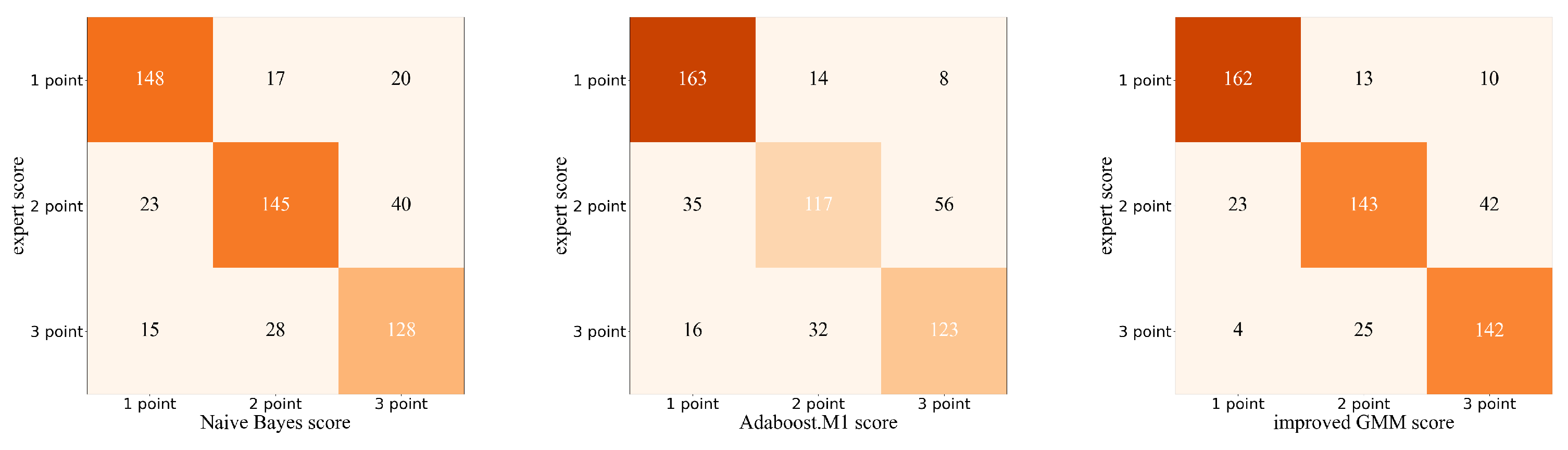
The machine learning model can predict each test action as a score of 1–3. To analyze more detailed results about the scoring performance of the improved GMM, we further visualized the confusion matrix based on expert scoring and automatic scoring. Figure 5 shows the confusion matrix obtained by the Naïve-Bayes-based method, AdaBoost.M1-based method, and improved GMM-based method. In this study, we consider expert scoring as the gold standard, and we combined the scoring results for each test action. From Figure 5, we can observe that the misclassified samples are prone to be predicted as a score close to its true score, 1-point samples are more likely to be wrongly predicted as 2 points than 3 points, and 3 points samples are more likely to be wrongly predicted as 2 points than 1 point; among these, the most errors occur when 2-point samples are predicted as 3-point samples.

Table 1. Overall comparisons of different methods in FMS assessment.

Methods	Accuracy	maF1	Weighted-maF1	Kappa	Level of Agreement
Naïve Bayes	0.75	0.75	0.71	0.6	Moderate
AdaBoost.M1	0.72	0.7	0.71	0.55	Moderate
Traditional GMM	0.38	0.34	0.35	0.1	Poor
Improved GMM	0.8	0.77	0.79	0.67	Good

shows the scoring of the Naive Bayes, AdaBoost.M1, improved Gaussian mixture model (GMM), and traditional GMM. The accuracy of improved GMM is higher than Naïve Bayes, AdaBoost.M1, and traditional GMM, and the improved GMM has the highest agreement. In general, the FMS assessment based on the improved GMM model outperformed Naïve Bayes and AdaBoost.M1. The results indicate that the improved GMM yields considerable improvement over the traditional GMM.

3.3. Evaluation of the Performance on Different Movements

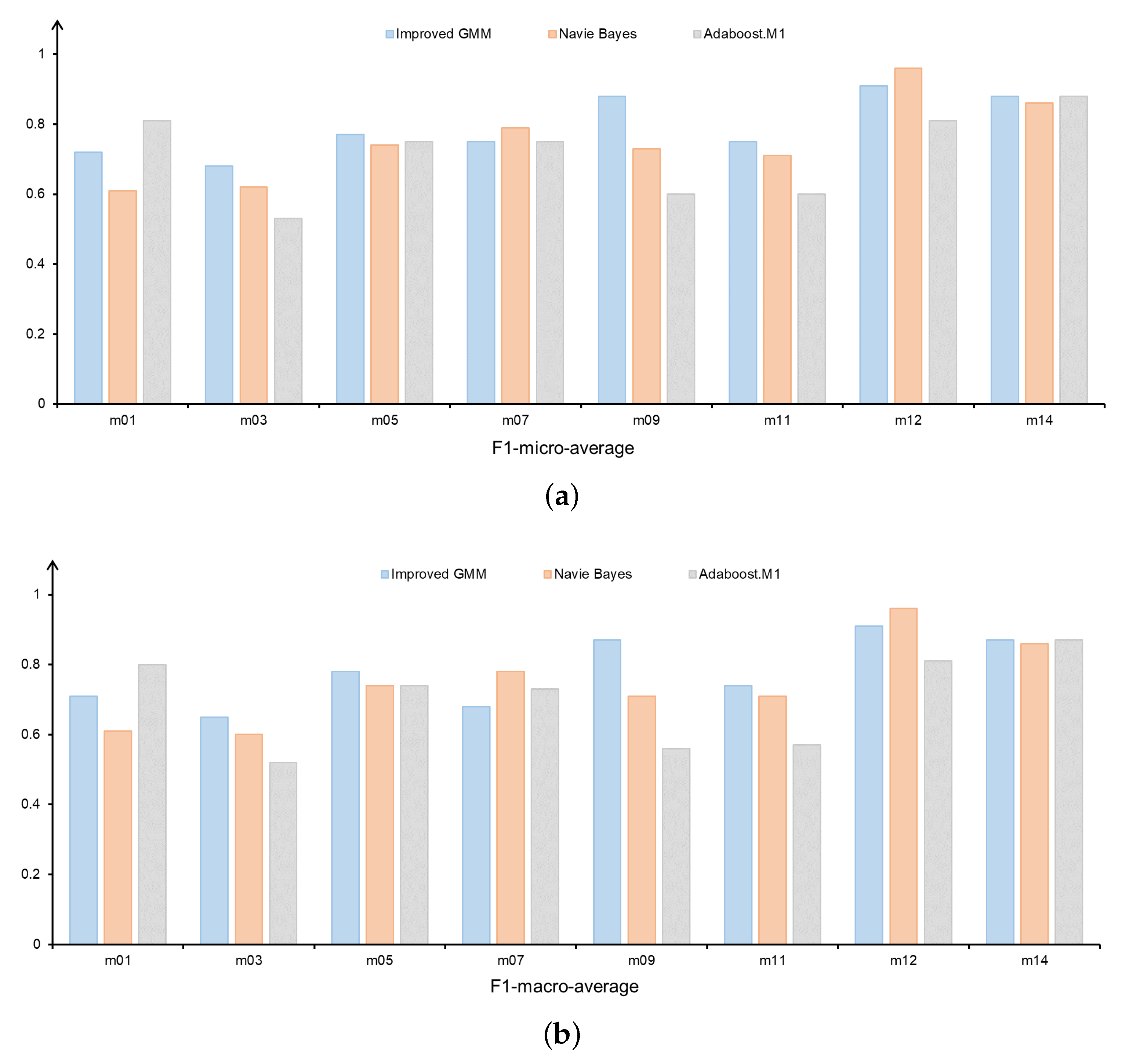
We further investigated the model performance for each FMS test individually. Figure 6a,b show the F1-micro-average and F1-macro-average for FMS movements on different methods. For all three models, we found that improved GMM-based model has better overall performance compared to the Naïve-Bayes-based model and AdaBoost.M1-based model. Specifically, the improved GMM-based model performs better than the other methods across the four movements (m03, m05, m09, and m11); the performance of the three methods is essentially the same across the two movements (m07 and m14).

3.4. Comparison of Accuracy before and after Data Balancing

We also compared FMS performance using the original unbalanced feature data (Figure 4a) and balanced feature data after oversampling pre-processing (Figure 4b) in this research. As shown in

Table 2. Improved GMM scoring accuracy before and after data balancing.

	Feature Data before Balance			Feature Data after Balance
ID	1	2	3	1	2	3
m01	0.86	0.48	0.25	0.86	0.63	0.71
m03	0.45	0.49	0.57	0.77	0.37	0.88
m05	0	0.67	0.29	0.97	0.69	0.68
m07	1	0	0	0.5	0.56	1
m09	0.8	0.74	0.64	0.95	0.8	0.89
m11	0.67	0.69	0	0.85	0.56	0.84
m12		0.8	0.67		0.88	0.94
m14	0.5	0.83		0.92	0.83
Averge accuracy		0.62			0.8

, the average accuracy of balanced distribution of feature data is 0.8, while the average accuracy of unbalanced distribution of feature data is only 0.62, which indicates that the balanced features perform better in the FMS assessment. The scoring accuracy of the balanced movement features is greatly improved compared with the unbalanced movement features. This imbalance will cause the performance of the classifier to be biased towards the majority samples due to the unbalanced sample size. Using sampling processing can improve the balance of the training data by increasing the number of samples, thus effectively avoiding this bias. The balanced features after oversampling pre-processing not only reflect the FMS movement quality more comprehensively, but also the accuracy of the classifier is significantly improved.

3.5. Comparison of Performance between Features and Skeleton Data

In the present study, we compared the performance of the manual feature extraction method and the skeleton-data-based method in FMS assessment. As shown in

Table 3. Improved GMM scoring accuracy based on skeleton data.

m01	m03	m05	m07	m09	m11	m12	m14	Average Accuracy
0.36	0.39	0.68	0.7	0.44	0.73	0.88	0.86	0.63

, the manual feature extraction method has better performance in FMS assessment. Compared with the skeleton-data-based method, the manual feature extraction method can capture the key features of the FMS movement more accurately, thus assessing the quality of the movement more accurately. The manual feature extraction method circumvents the impact of skeleton data quality differences on action scoring to a certain extent because the skeleton data are screened and cleaned through bespoke processing. In addition, the manual feature extraction method has good interpretability, which helps us better understand the FMS movement quality. Specifically, the manual feature extraction method generally scores each action with higher accuracy than the skeleton-data-based method; for example, the scoring accuracy of m09 improved from 0.44 to 0.88. The average accuracy of the manual feature extraction method is 0.8, while the average accuracy of the skeleton-data-based method is only 0.63, indicating that the manual feature extraction method has better performance in FMS assessment.

3.6. Limitations and Future Work

It is important to acknowledge the limitations of this study and consider future research directions in Functional Movement Screening (FMS).

One limitation is the small dataset used in this study. Future research should aim to expand the dataset with a larger sample size to improve the performance and generalizability of machine learning models in FMS assessment. Additionally, exploring different populations, such as pathological or elite athletes, would help validate the reliability and applicability of the proposed method. Another aspect for future research is refining depth-camera-based FMS assessment. Despite the advantages of depth cameras in precise distance measurement and spatial analysis, they may have limitations in capturing fine-grained movement details, especially under challenging conditions or when certain body parts are occluded. Investigating techniques, such as advanced image processing algorithms or multimodal sensor fusion, could enhance the accuracy and robustness of depth-camera-based FMS assessment. Lastly, this method should be tested on different datasets to improve the performance of machine learning methods and achieve more accurate prediction results in future studies. Future research in FMS should focus on expanding the dataset, refining depth-camera-based assessment, and exploring alternative classifiers. These endeavors will advance FMS assessment methods and contribute to more accurate predictions in future studies.

4. Conclusions

Based on the experimental results, our proposed automated FMS assessment method utilizing the improved Gaussian mixture model (GMM) achieved a scoring accuracy of 0.8, outperforming the other models. The high agreement between the scoring results and expert scoring (kappa = 0.67) demonstrates the effectiveness of the improved GMM-based method in accurately assessing FMS. In conclusion, the high scoring accuracy and agreement with expert scoring support its value in accurately assessing functional movement patterns. Our study validates the efficacy of the proposed method based on the improved GMM for FMS assessment. Moreover, the successful implementation of depth cameras for FMS assessment holds great promise in fields such as sports performance analysis, rehabilitation programs, and personalized movement assessments. These advancements have the potential to enhance injury prevention strategies and optimize training protocols. Further exploration and integration of depth-camera-based FMS assessment methods will contribute to the advancement in these areas, benefiting athlete performance, reducing injury risks, and improving overall well-being.