Optimal Control Algorithm for Subway Train Operation by Proximal Policy Optimization

Abstract

With the increasing scale of the urban subway, the total energy consumption of the subway has increased dramatically and poses a great challenge to the comfort of passengers and the punctuality of train operation. In order to ensure on-time train operation and passenger comfort, and at the same time reduce the energy consumption of subway operation, this paper proposes a Proximal Policy Optimization (PPO)-based optimization algorithm for the optimal control of subway train operation. Firstly, a reinforcement learning architecture for optimal control of subway train operation is constructed with the position and speed of train operation as the reinforcement learning state, energy consumption and comfort as the optimization objectives, and train operation time as the constraint. The proposed reinforcement learning model is trained by the PPO algorithm, and the reward scaling is added to the training process to accelerate the training speed and improve the efficiency of the algorithm. The experimental results show that the proposed PPO with reward scaling algorithm can effectively reduce train energy consumption and improve passenger comfort while ensuring on-time train operation.

1. Introduction

The urban subway is the main line of urban public transportation and the main artery of passenger flow. It is a key system project for the rapid and smooth operation of urban traffic. It plays an important role in improving the happiness index and promoting social and economic development. With the rapid development of urban subways and the continuous expansion of network scale, the sustainable development of urban subways has attracted more and more attention. Although urban subways use less energy per unit of traffic than other forms of public transportation, they are massive. With the continuous expansion of urban subways, total energy consumption has increased dramatically. Among them, the traction energy consumption of train operation accounts for a relatively high proportion. Urban subway trains use on-board inverters to convert the DC power in the power supply system into AC power for the traction motor to drive the train, which requires a lot of power consumption. At the same time, auxiliary facilities such as lighting, air conditioning, and electric heating inside the carriage also require energy from the traction power supply system. In this situation, optimizing train operation energy consumption while maintaining comfort and punctuality is crucial for train operations.

At present, many scholars have carried out relevant research on the train operation optimization problem by using heuristic methods such as genetic algorithms and differential evolution. The optimization process is roughly divided into two steps: first, optimize the train speed profiles, and then track the optimized speed profiles. Manual tuning, speed profiles, and operational constraints have been considered in existing work in order to improve performance. However, these solutions may lead to a gap between the control model and the actual operating process, thereby affecting the accuracy of the control model [1]. The emergence of reinforcement learning has found a feasible solution to this problem. It can directly optimize the train operation control strategy without the train speed profiles, to get rid of the limitations of the offline speed profiles and the precise model information of the train.

In this thesis, we propose an optimal control algorithm for subway train operation based on Proximal Policy Optimization (PPO) to reduce train operation energy consumption, ensure passenger comfort, and at the same time meet the requirements of the train schedule for train operation time. In this paper, the position and speed of the train are used as the reinforcement learning state, the energy consumption and comfort are the optimization goals, the train running time is strongly constrained, and the output sequence of the train operation control is optimized based on PPO.

This study is organized as follows: Section 2 presents a literature review about optimal control algorithms for subway train operation from the perspective of heuristic methods and reinforcement learning methods. Section 3 introduces the optimal control algorithm for subway train operation based on PPO, including the original PPO algorithm and the combination between PPO and the train operation model. Section 4 discusses the results of the PPO-based optimal control algorithm for subway train operation based on real data. Section 5 summarizes the innovation of this study and provides directions for future research.

2. Literature Review

Since the 1960s, foreign scholars have begun to study the energy-saving operation optimization of trains [2,3]. These research results laid the foundation for the follow-up research in the field of train operation control optimization. However, due to the limited computing resources at that time, and the relatively simple model construction at that time, the information extraction and construction of the actual operating environment were not sufficient. The research results cannot be widely used in the actual train operation control.

With the development of technology, the operation control of subway trains has gradually evolved from the fixed block non-automatic train operation mode to semi-automatic train operation, manned train automatic operation, and unattended train automatic operation. Among them, the automatic speed control of the train is one of the core technologies for the automatic operation of subway trains. At present, automatic train operation (ATO) technology is applied in the subway train system. It first generates the speed profiles used to guide the train operation according to the safety constraints and the basic information of the line, and then uses the speed tracking technology to generate the speed profiles, combined with the current train running state (speed, position, etc.), calculates the control quantity that the train traction drive system needs to output under the current running state, and outputs it to the train interface unit to complete the operation of the train.

In this case, many scholars have carried out relevant research on the train operation optimization problem from the perspective of optimizing speed profiles. Gao et al. [4] systematically introduced the energy-saving approaches of the urban subway system from three aspects: train speed profiles optimization, renewable energy utilization, and train schedule optimization with speed profiles, and clarified the future research direction for the field of urban subway energy conservation. Ahmadi et al. [5] proposed an energy-saving solution that satisfies the constraints related to the operation. Firstly, the optimal speed distribution of a single train is given by taking the net energy consumption of the train and the travel time between stations as the objective function. Then by allocating travel time among stations and adopting a predetermined optimal speed distribution, the total grid input power is minimized. De Martinis et al. [6] proposed an optimization framework for the definition and evaluation of energy-saving speed curves based on supply design models, considering the possible impact of speed profiles on subway flow. This makes it possible to fully consider the business requirements of the service when evaluating the optimal speed profiles. Amrani et al. [7] proposed a speed profiles optimization scheme based on a genetic algorithm, taking into consideration the train physical constraints and train operation constraints. On the premise of considering the utilization of renewable energy, Zhou et al. [8] proposed an improved train control model to obtain the train speed optimization profiles by combining the optimization of the operation diagram with the optimization of the operation of a single vehicle considering the change of train quality caused by passengers getting on and off the train. Anh et al. used the optimization method based on Pontryagin’s maximum principle in their literature [9,10], which can not only find the optimal switching points in the three operating stages of acceleration, coasting, and braking but also determine the optimal switching point from these switching points. It has excellent speed profiles, but also ensures a fixed travel time. To use nonlinear programming to determine the travel time, the Lagrangian multiplier $\lambda$ is introduced into the objective function as a time constraint. Considering the longitudinal section design, Kim et al. [11] proposed a multi-stage decision-making model to jointly optimize the longitudinal section design profiles, cruising speed, and inert speed conversion point of the route to optimize the energy saving of urban subway operation. Sandidzadeh et al. [12] used the Second Tabu Search (TS) algorithm to optimize the train speed profiles. Scheepmaker et al. based on the optimal allocation of running time at multiple stations of a single vehicle [13], combined with regenerative braking and mechanical braking, derived the optimal control structure and studied the impact of different speed limits on different driving strategies [14]. De Sousa et al. [15] proposed a metro energy regeneration model based on controlling stops and train departures throughout the journey and using energy from regenerative braking in the drive system, to optimize power consumption and improve efficiency.

In terms of train speed profile optimization, there are also many scholars conducting research from other angles. Considering the actual location of the substation, Chen et al. [16] modeled the traction power supply system and combined it with the optimal speed profiles of the train and the travel time distribution between stations to minimize the energy consumption at the substation level. Su et al. [17] considered the speed tracking problem for multi-objective speed profiles optimization and proposed a numerical algorithm for solving the train energy consumption control problem with a given travel time. On this basis, based on the ATO control principle, the target speed profiles optimization method guides the train to output the optimal control sequence. Pu et al. [18] constructed a comprehensive optimization method for train speed tracking through speed profiles and fuzzy PID controller design and combined it with the NSGA-II algorithm. Based on the analysis of train operating conditions and the operating environment, Zhu et al. [19] established a multi-objective model of train automatic operation by using a multi-objective decision-making method with a penalty function. They also used genetic algorithms to solve the model, and then designed a fuzzy controller, to achieve speed tracking control. Wu et al. [20] proposed an improved traction energy consumption evaluation model for the traction system considering the working efficiency of the traction motor under different working conditions and the efficiency of the inverter and gearbox, and then transformed the speed profiles optimization into a multi-decision problem, which is solved by a dynamic programming method. Liu et al. [21] designed a moving horizon optimization algorithm that can obtain the speed profile online and applied sequential quadratic programming (SQP) to a multi-objective optimization problem with several nonlinear constraints, which can realize online optimization of speed profiles. In most urban subway operation optimization problems, the train operation model is considered based on a single particle. Wang et al. [22] proposed a multi-particle train model for the optimization of the urban rail train speed profiles, taking the train length factor into account. In addition, some scholars have carried out research on the optimization of train operation profiles [23,24,25,26,27].

3. Methodology

In this section, we build the train dynamic model including the traction/breaking characteristics of the subway train. Subsequently, we propose an optimal control algorithm for subway train operation based on PPO. This algorithm aims to optimize the operation control by utilizing the dynamic model and considering parameters of the operating environment, such as the line slope.

3.1. The Train Dynamic Model

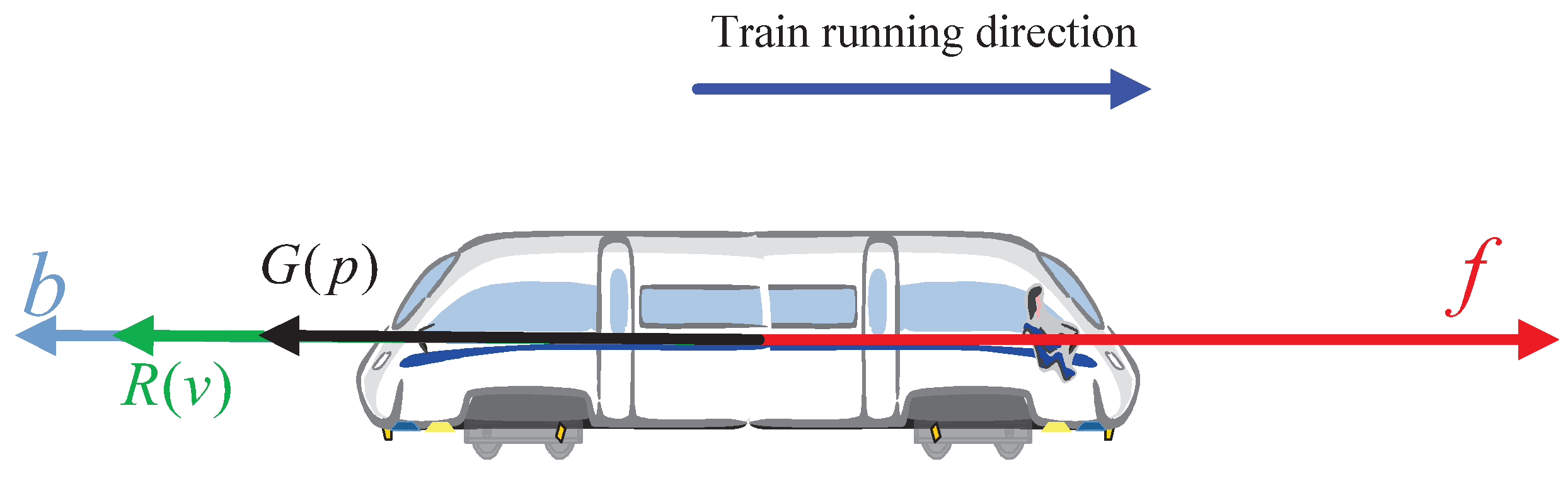
Figure 1 shows the force analysis while the train is running. f is the traction force output by the train’s traction systems. $G\left(p\right)$ represents the additional gradient resistance due to the gradient on the line track while p represents the position of the railway track. $R\left(v\right)$ is the resistance produced by friction while v is the running speed of the train. b is the braking force generated by the braking system of the train.

As shown in Figure 1, when the train is running, the resistance it receives includes $G\left(p\right)$ and $R\left(v\right)$. Taking the train traction and braking forces into account, the kinematic equation is shown in Equation (1).

$$\left\{\begin{array}{c}\frac{dv}{dt}=\frac{f-b-R\left(v\right)-G\left(p\right)}{(1+\tau M)}\\ \frac{dp}{dt}=v\end{array}\right.$$

(1)

while M is the train mass and $\tau$ represents the rotation mass coefficient of the train, and its value is determined by the total mass of the train and the converted mass of the rotation part.

The energy consumption is calculated by Equation (2).

$$E\left(T\right)=\frac{{\int }_0^{T}fv\left(t\right)dt}{{\eta }_f}+{\int }_0^T{P}_{au}\left(t\right)dt-{\eta }_b{\int }_0^{T}bv\left(t\right)dt$$

(2)

In Equation (2), T is the travel time of the train, and $P_{au}\left(t\right)$ is the power of train auxiliary systems, such as lights and air conditioners, at time t. ${\eta }_f$ is the efficiency of converting electrical energy into mechanical energy when the train traction system is working. ${\eta }_b$ is the efficiency of converting mechanical energy into electrical energy during the regenerative braking of the train.

The first part of Equation (2) represents the electric energy consumed by the traction system of the train; the second part is the energy consumed by auxiliary systems of the train, and the third part is the energy generated by train regenerative braking. Compared with the energy consumed by the traction system, the proportion of auxiliary energy consumption in the process of train operation is very small, so this paper takes the energy consumed by the train traction drive system as the optimization object. That is, the optimization objective of the optimization problem is obtained by Equation (3).

$$E\left(T\right)=\frac{{\int }_0^{T}fv\left(t\right)dt}{{\eta }_f}-{\eta }_b{\int }_0^{T}bv\left(t\right)dt$$

(3)

The additional gradient resistance $G\left(p\right)$ and the resistance produced by friction $R\left(v\right)$ are calculated by Equations (4) and (5), respectively.

$$G\left(p\right)=Mgsin\left(\theta \right(p\left)\right)$$

(4)

$$R\left(v\right)=r_0+r_{1}v+r_2{v}^2$$

(5)

while g is the gravitational acceleration; $\theta \left(p\right)$ is the gradient of the line on position p; $r_0$, $r_1$ and $r_2$ are basic resistance coefficients.

In Equation (4), the gradient $\theta \left(p\right)$ is measured by radians. To ensure the safety of train operation, the gradient of the line is strictly limited within a certain range, that is, the slope is at a small value. We can thus make the following approximation.

$$sin\left(\theta \right(p\left)\right)\approx \theta \left(p\right)$$

(6)

Then we can change Equation (4) into Equation (7) for more convenient calculation.

$$G\left(p\right)=Mg\theta \left(p\right)$$

(7)

In addition to energy consumption, passenger comfort is defined by the negative integral of jerk rate over time as another optimization object, and it is defined by Equation (8).

$$C\left(T\right)=-{\int }_0^T\left|\frac{du}{dt}\right|dt$$

(8)

while u is the acceleration of the train.

Equations (3) and (8) are the objects to be optimized. There are additional constraints to consider, such as travel time and speed limitations, in addition to the dynamic characteristics of the subway train as depicted in Equation (1). Then we have the multi-objective optimization function for train operation, as shown in Equation (9).

$$\begin{array}{c}minOp\left(E\right(T),C)\\ \\ s.t.\begin{array}{c}\left\{\begin{array}{c}\frac{dv}{dt}=\frac{f-b-R\left(v\right)-G\left(p\right)}{(1+\tau M)}\\ \frac{dp}{dt}=v\end{array}\right.\\ v\left(0\right)=v\left(T\right)=0\\ t\in [0,T]\\ v\left(t\right)\in [0,v_{max}\left(t\right)]\end{array}\end{array}$$

(9)

while $Op(·)$ represents the optimization function and $v_{max}\left(t\right)$ is the maximum speed at time t.

3.2. Optimization Model of Train Operation Based on Reinforcement Learning

This subsection presents the reinforcement learning (RL) modules for train operation.

The RL architecture includes the following items: $agent$, $environment$, $action$, $state$, and $reward$. $agent$ obtains $state$ from $environment$, and executes $action$. Then, $action$ is output into $environment$, which can cause the transfer of $state$ and $reward$ generated by $environment$ to $agent$. RL aims to obtain as much $reward$ as possible from $environment$.

Agent: As the output module of the train operation control command, the ATO subsystem plays the role of the agent in the RL architecture, which controls the speed and position of the train by changing the output level of the traction system.

Action Space: During the operation of the train, the output level of the traction/braking system is the only way to control the change in speed and position. Changes in traction/brake levels will result in corresponding changes in train speed and position. The traction and brake output of subway trains are continuous variables, and when the traction/brake reach the maximum, it will output the max traction/braking force (represented by $f_{max}$ and $b_{max}$, respectively). So, we can define the action space in the RL architecture as $[-1,1]$, and the action $a_t$ taken by the agent at time t conforms to Equation (10). If $a_t>0$, the train is under the traction condition with traction power $a_t\times f_{max}$, and the train is under the brake condition with brake force $a_t\times b_{max}$ if $a_t<0$. If $a_t=0$, the train is under the coasting condition.

$$a_t\in [-1,1]$$

(10)

State Space: Two crucial elements describe the operation characteristic of the train: speed and position. When the agent, known as the ATO system, takes an action, the speed and position of the train will be changed immediately. We define the speed and position of the train as the state of RL architecture, and the state $s_t$ at time t can be described as Equation (11). Note that the speed and the position are bounded within a certain range, shown in Equation (12).

$$s_t=(v_t,p_t)$$

(11)

$$\left\{\begin{array}{c}{v}_t\in [0,v_{max}\left(t\right)]\\ p_t\in [0,P]\end{array}\right.$$

(12)

Environment: The environment in the RL architecture requires an accurate relationship between the agent’s output and the state transfer. In this paper, the purpose of the environment is to describe the relationship between the output level of the train traction system and the speed and position of the train, i.e., to construct an accurate train dynamics model with the control level as the independent variable.

We assumed that at time t, the speed and the position of the train are $v_t$ and $p_t$, respectively. Meanwhile, the agent takes an action $a_t$. The traction force and brake force are calculated by Equations (13) and (14), respectively.

$$f_t=\left\{\begin{array}{cc}{a}_t\times f_{max}& a_t>0\\ 0& a_t\le 0\end{array}\right.$$

(13)

$$b_t=\left\{\begin{array}{cc}{a}_t\times b_{max}& a_t<0\\ 0& a_t\ge 0\end{array}\right.$$

(14)

Then, we can get the acceleration of the train $u_t$ using Equations (1), (5) and (7). After that, the state of RL architecture $(v_t,p_t)$ is transferred to $(v_{t+\Delta t},p_{t+\Delta t})$ by Equation (15) (assuming that the action execution time is $\Delta t$).

$$\left\{\begin{array}{c}{v}_{t+\Delta t}=v_t+u_t\Delta t\\ p_{t+\Delta t}=p_t+v_t\Delta t+0.5u_t{\Delta t}^2\end{array}\right.$$

(15)

Reward: The reward of RL architecture comprises three components: the reward of energy saving, the reward of comfort, and the penalty term of time exceeded. We define the reward $r\left(t\right)$ at time t as Equation (16).

$$r\left(t\right)=-{\mu }_{1}E\left(t\right)+{\mu }_{2}C\left(t\right)$$

(16)

where $E\left(t\right)$ and $C\left(t\right)$ are calculated by Equations (3) and (8), respectively, and ${\mu }_1$ and ${\mu }_2$ are the coefficients of the reward of energy saving and the reward of comfort. In practice, we expect to minimize energy consumption and maximize comfort. And in RL architecture, we always expect to maximize the expectation of accumulative rewards. Therefore, ${\mu }_1$ and ${\mu }_2$ are all positive values.

When the train arrives at the destination station, the total reward is calculated by Equation (17).

$$r\left(T\right)=\left\{\begin{array}{cc}-{\mu }_{1}E\left(T\right)+{\mu }_{2}C\left(T\right)& \left|T-T_{timetable}\right|\le T_d\\ -P_{en}& \left|T-T_{timetable}\right|\ge T_d\end{array}\right.$$

(17)

where $P_{en}$ is a large positive number, $T_{timetable}$ is the expected operating time, and $T_d$ is the expected deviation between the real operating time and the expected operating time.

3.3. Proximal Policy Optimization Method

Proximal Policy Optimization Method [28] is one of the policy gradient methods which work by computing an estimator of the policy gradient and plugging it into a stochastic gradient ascent algorithm. The most commonly used gradient estimator has the form of Equation (18).

$$\widehat{g}={\widehat{\mathbb{E}}}_t[{\nabla }_{\theta }log{\pi }_{\theta }\left(a_t\right|s_t){\widehat{A}}_t]$$

(18)

And $\widehat{g}$ is obtained by differentiating the objective function shown as Equation (19).

$$L^{PG}\left(\theta \right)={\widehat{\mathbb{E}}}_t[log{\pi }_{\theta }\left(a_t\right|s_t){\widehat{A}}_t]$$

(19)

where ${\pi }_{\theta }$ is a stochastic policy, $a_t$ and $s_t$ are the action and state at time t, respectively, ${\widehat{A}}_t$ is an estimator of the advantage function.

PPO is optimized from the Trust Region Policy Optimization (TRPO) and in TRPO, the objective function is maximized subject to a constraint on the size of the policy update shown in Equation (20) [29].

$$\begin{array}{cc}{\displaystyle \underset{\theta }{max}}& {\widehat{\mathbb{E}}}_t\left[\frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{\pi }_{{\theta }_{old}}\left(a_t\right|s_t)}{\widehat{A}}_t\right]\\ s.t.& {\widehat{\mathbb{E}}}_t\left[KL\left[{\pi }_{{\theta }_{old}}(·|s_t),{\pi }_{\theta }(·|s_t)\right]\right]\le \delta \end{array}$$

(20)

where ${\theta }_{old}$ is the parameters before the update. In TRPO, the optimization problem (20) is solved by using a penalty instead of the constraint. But it is hard and complicated for TRPO to implement. There are two ways to make the implementation easier: adaptive KL penalty coefficient and clipped surrogate objective [28]. In this paper, we focus on the clipped surrogate objective due to its simplicity and accuracy.

We denote the objective function in Equation (20) as follows:

$$L^{CPI}\left(\theta \right)={\widehat{\mathbb{E}}}_t\left[\frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{\pi }_{{\theta }_{old}}\left(a_t\right|s_t)}{\widehat{A}}_t\right]$$

(21)

where $CPI$ represents the conservative policy iteration [30].

In PPO, a hyper-parameter $ϵ$ is introduced to limit the distance between old and new strategies to a specific range shown as Equation (22), where $radi{o}_t\left(\theta \right)=\frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{\pi }_{{\theta }_{old}}\left(a_t\right|s_t)}$. The first part is the probability ratio multiplied by the advantage function that is the unclipped objective $L^{CPI}$. The second part of Equation (22) is to limit the probability ratio $radi{o}_t\left(\theta \right)$ to the interval $[1-ϵ,1+ϵ]$ which is the clipped objective. At last, we take the minimum of the unclipped and clipped objective to calculate $L^{CLIP}\left(\theta \right)$.

$$L^{CLIP}\left(\theta \right)={\widehat{\mathbb{E}}}_t\left[min(radi{o}_t\left(\theta \right){\widehat{A}}_t,clip(radi{o}_t\left(\theta \right),1-ϵ,1+ϵ){\widehat{A}}_t)\right]$$

(22)

In order to speed up the training process and improve the efficiency of the PPO algorithm, we adopted Reward Scaling [31] in the training process, shown in Equation (23).

$$R\left(t\right)=\frac{R\left(t\right)}{St{d}_R+\xi }$$

(23)

where $St{d}_R$ is the standard deviation of rewards R and $\xi$ is a very small positive number to prevent a zero denominator.

The optimal control process for subway train operation based on PPO with reward scaling is shown as Algorithm A1 in Appendix A. The comparison between the PPO algorithm with and without Reward Scaling is described in detail in Section 4.

4. Case Study

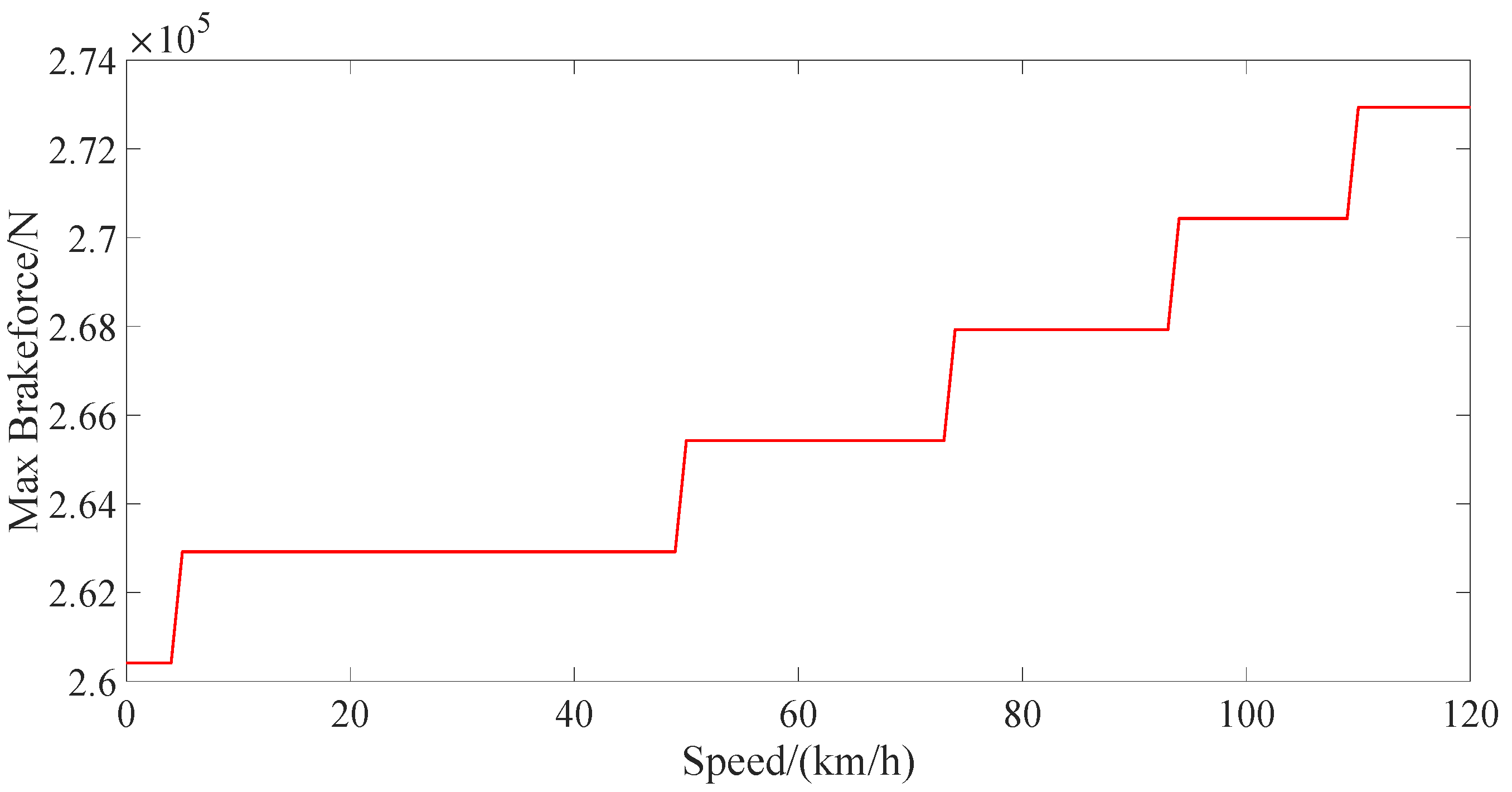
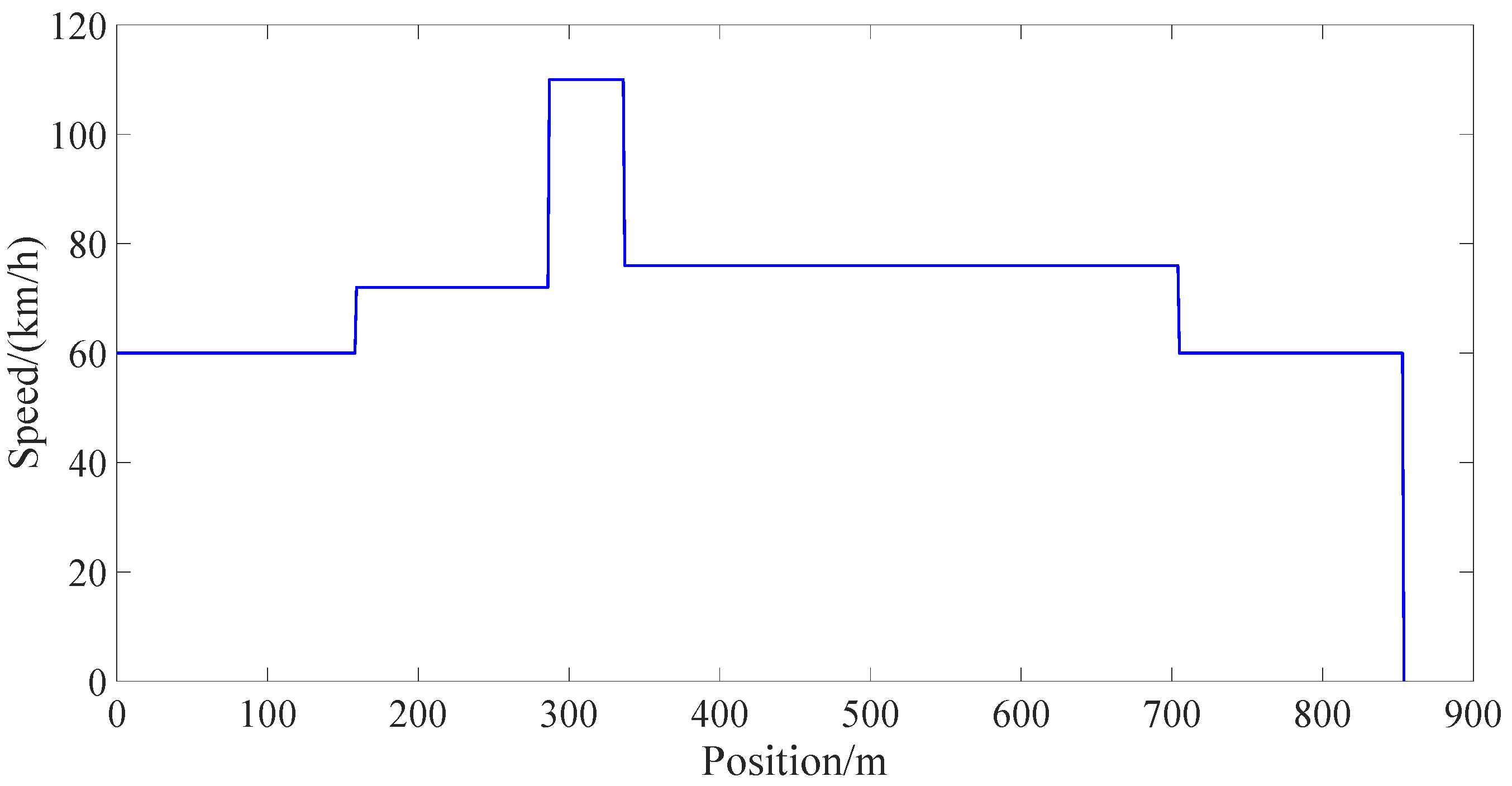
This section carried out the simulation results of several algorithms applied to the subway operation control including Deep Deterministic Policy Gradient (DDPG), PPO, and PPO with rewards scaling. The simulations are based on the actual track and train conditions in Beijing. The traction/breaking characteristics are shown in Figure 2 and Figure 3. The track speed limitation is shown in Figure 4. Other parameters of the simulation are shown in

Table 1. Parameters of the simulation.

Parameter Names	Parameters
Operating mileage/m	854
Train mass/t	234.4
Rotation mass coefficient	1.068
Max speed/(km/h)	110
Max traction power/kN	282
Operation time/s	80
${\mu }_1$	2/3
${\mu }_2$	1/3

.

Due to the difference between the three algorithms, the training steps differ, but the numbers of training episodes are all around 20,000 episodes. We carried out simulations through these aspects as follows: convergence of the rewards, the loss, and the indicators of train operation.

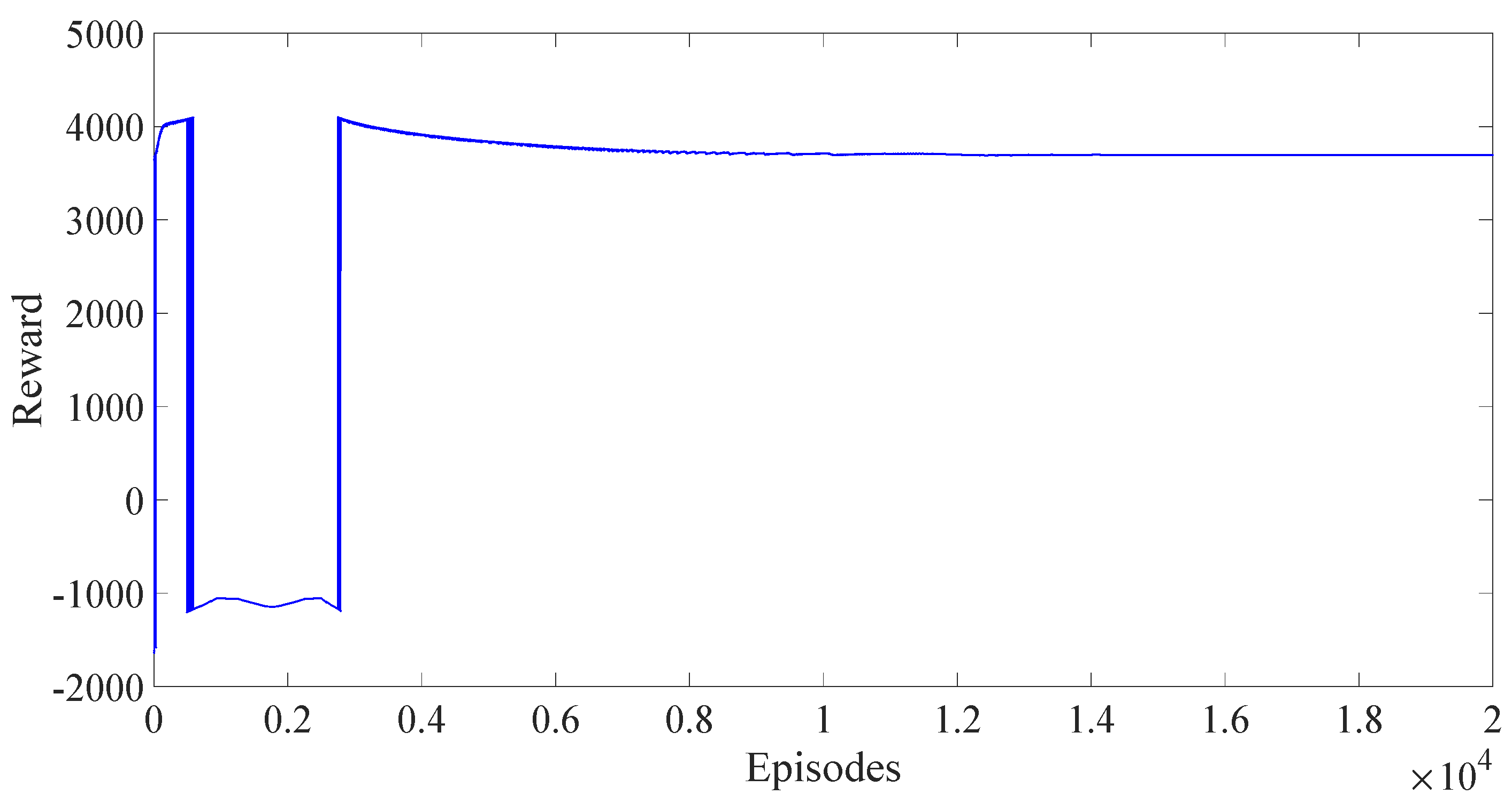
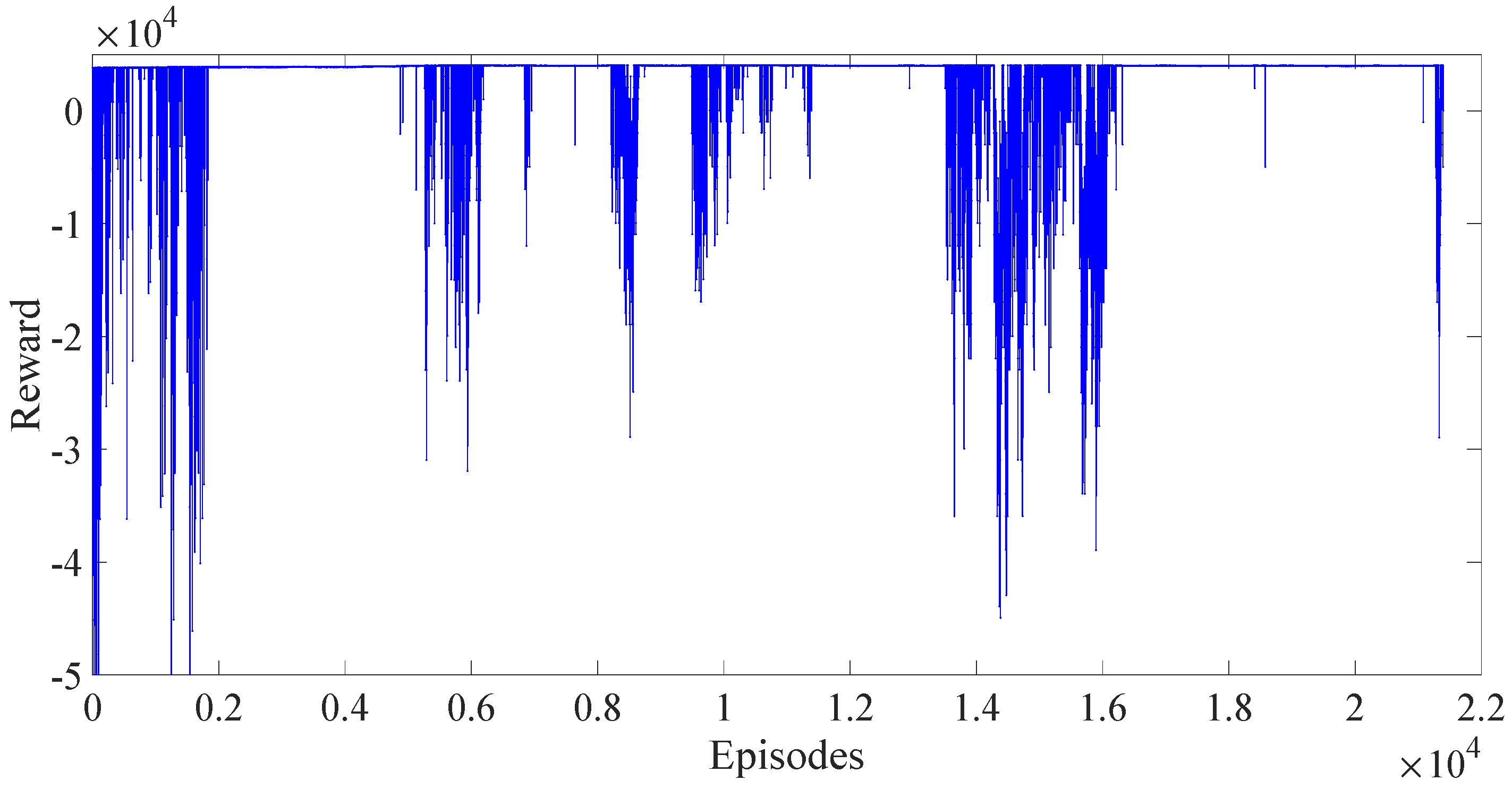
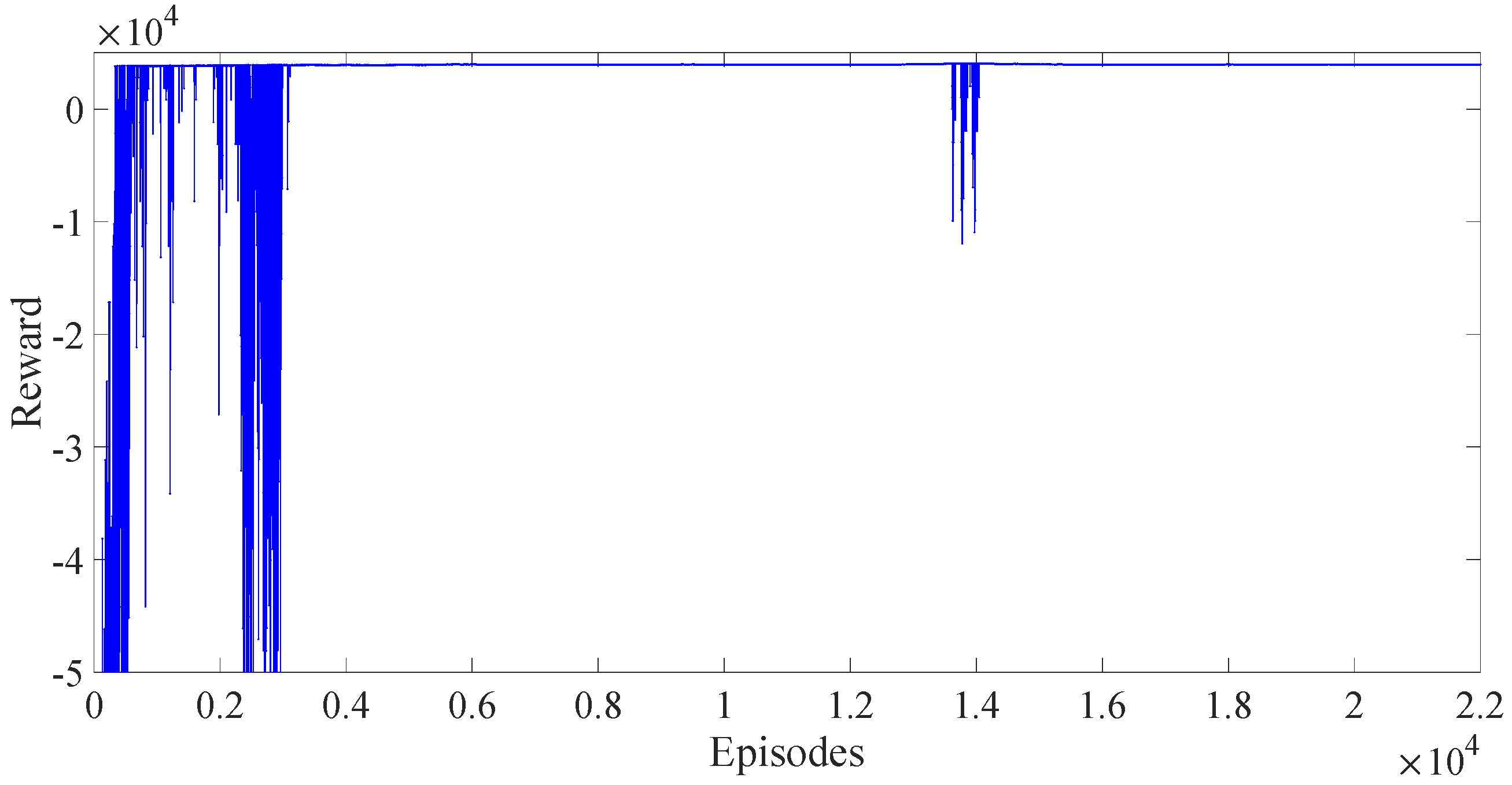
Figure 5, Figure 6 and Figure 7 are the variations of rewards with the episodes in three algorithms. In Figure 5, we can find that the reward of DDPG reaches a stable state around the 3000th episode. The reward of PPO fluctuates greatly and has not yet converged over 21,000 episodes. After adding the reward scaling, the reward of the PPO algorithm converged at about the 3000th episode. Despite the small data jump at the 4000th time, the reward converges back quickly. The DDPG algorithm and the PPO with reward scaling both have better results than the conventional PPO from the analysis of the change in reward only.

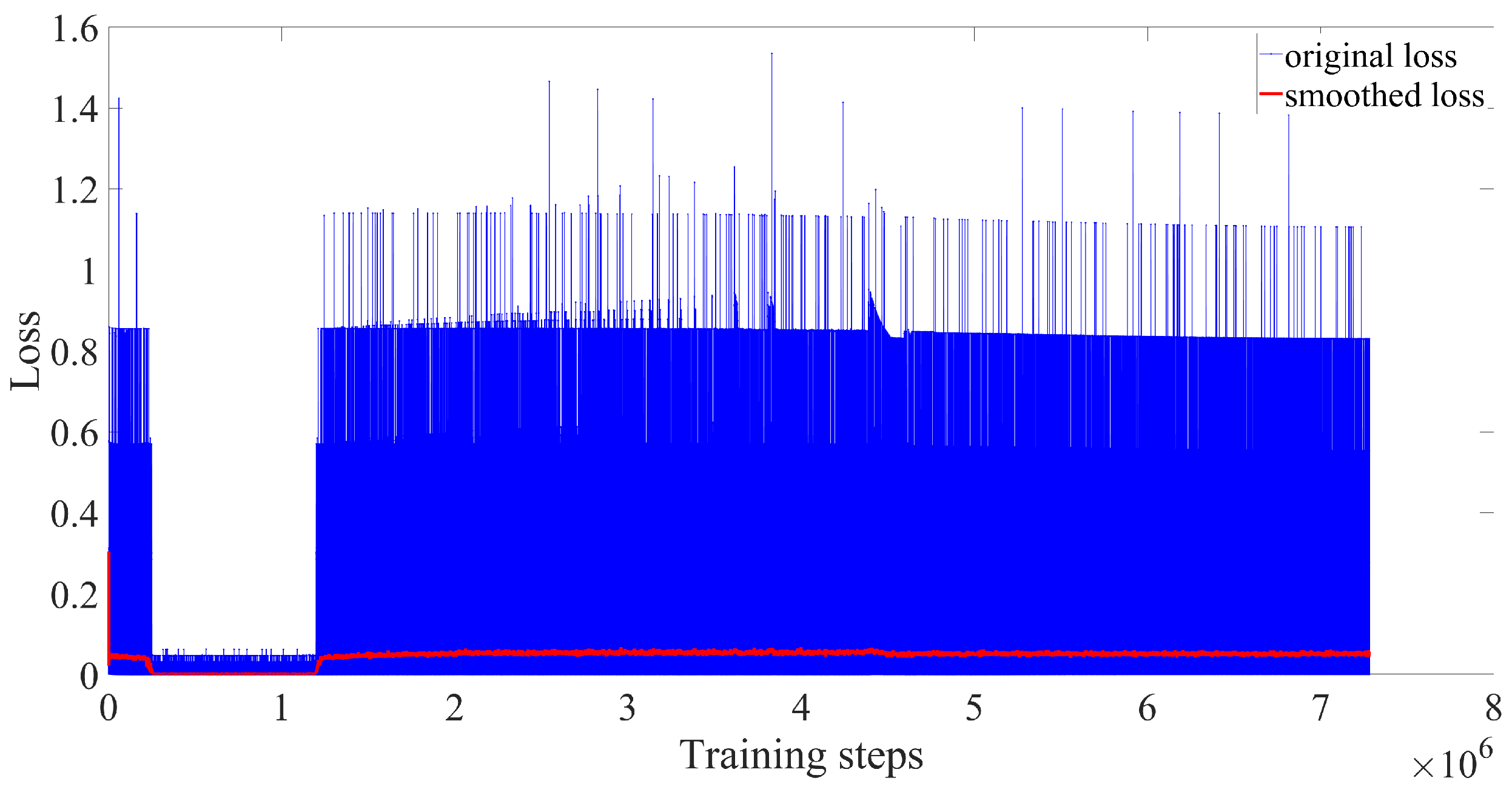
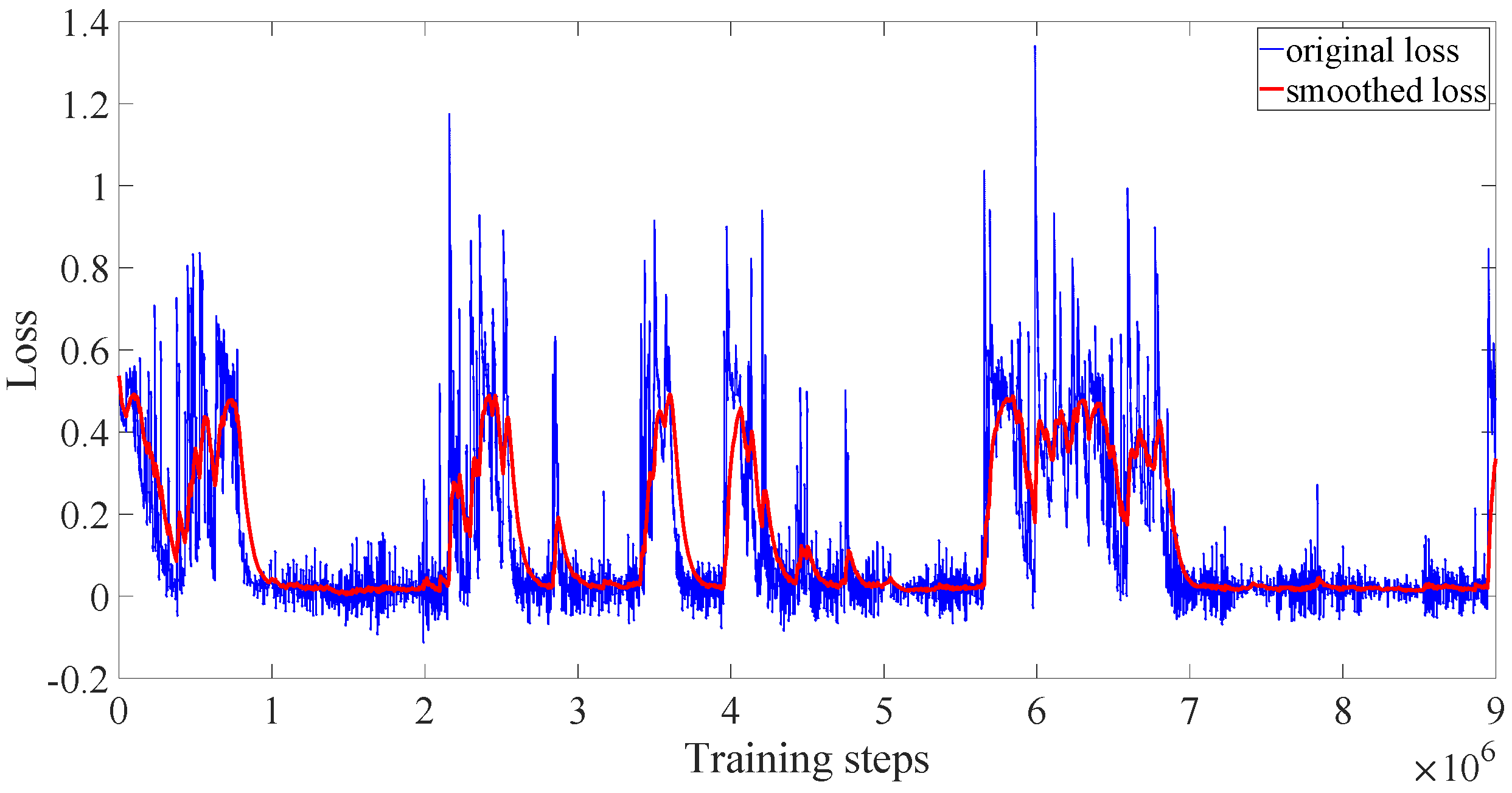
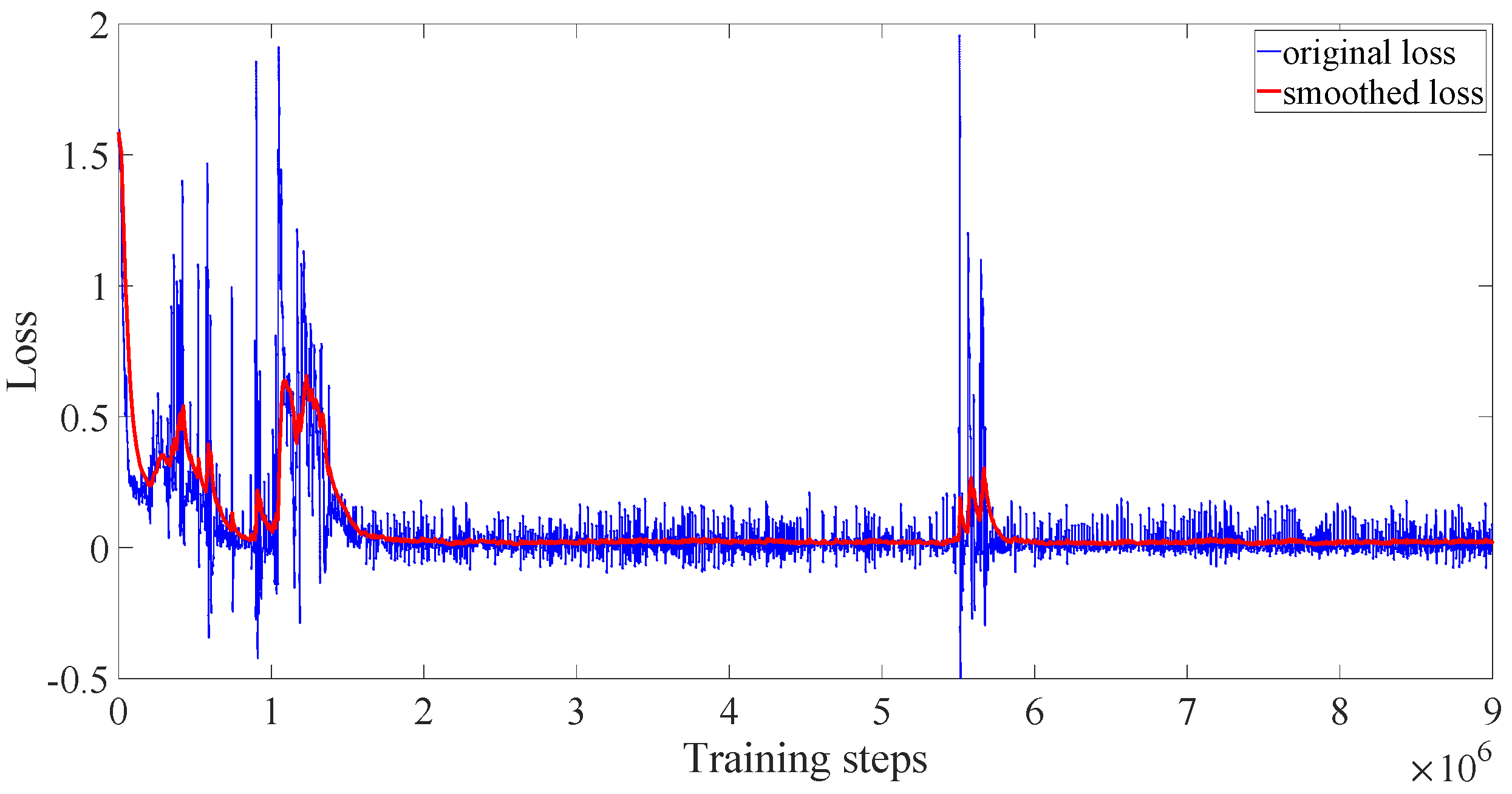
Figure 8, Figure 9 and Figure 10 represent the variation trend of training losses in three algorithms, respectively. The loss of DDPG jumps between very large and very small values, which means after 20,000 episodes (for about $7.2\times {10}^6$ training steps) the algorithm still does not converge. As for the conventional PPO, the training does not converge due to the dispersion of the loss every few episodes, which can also be proved by Figure 6. In Figure 10 we can find that the loss of PPO with reward scaling converges to a small range at about $2\times {10}^6$ training steps corresponding to about the 3000th episode. Despite the data jumping around a few training steps, the loss remains in the small range, which means the training of PPO with reward scaling converges. From Figure 8, Figure 9 and Figure 10, we can see that although the reward of the DDPG algorithm reaches a stable state around the 3000th episode, its training loss does not converge. Only PPO with reward scaling performs the best among these three algorithms.

From the above analysis, it can be seen that, among the three algorithms, the conventional PPO algorithm has the worst effect. Although it may converge if the training continues, it will consume a lot of time and computational resources. The DDPG algorithm’s reward will reach a stable state, but from the loss analysis, it has not yet reached a stable convergence state. The PPO with reward scaling algorithm has the fastest convergence speed and is more stable. However, there are still other indicators that are also important to the operation of the subway train.

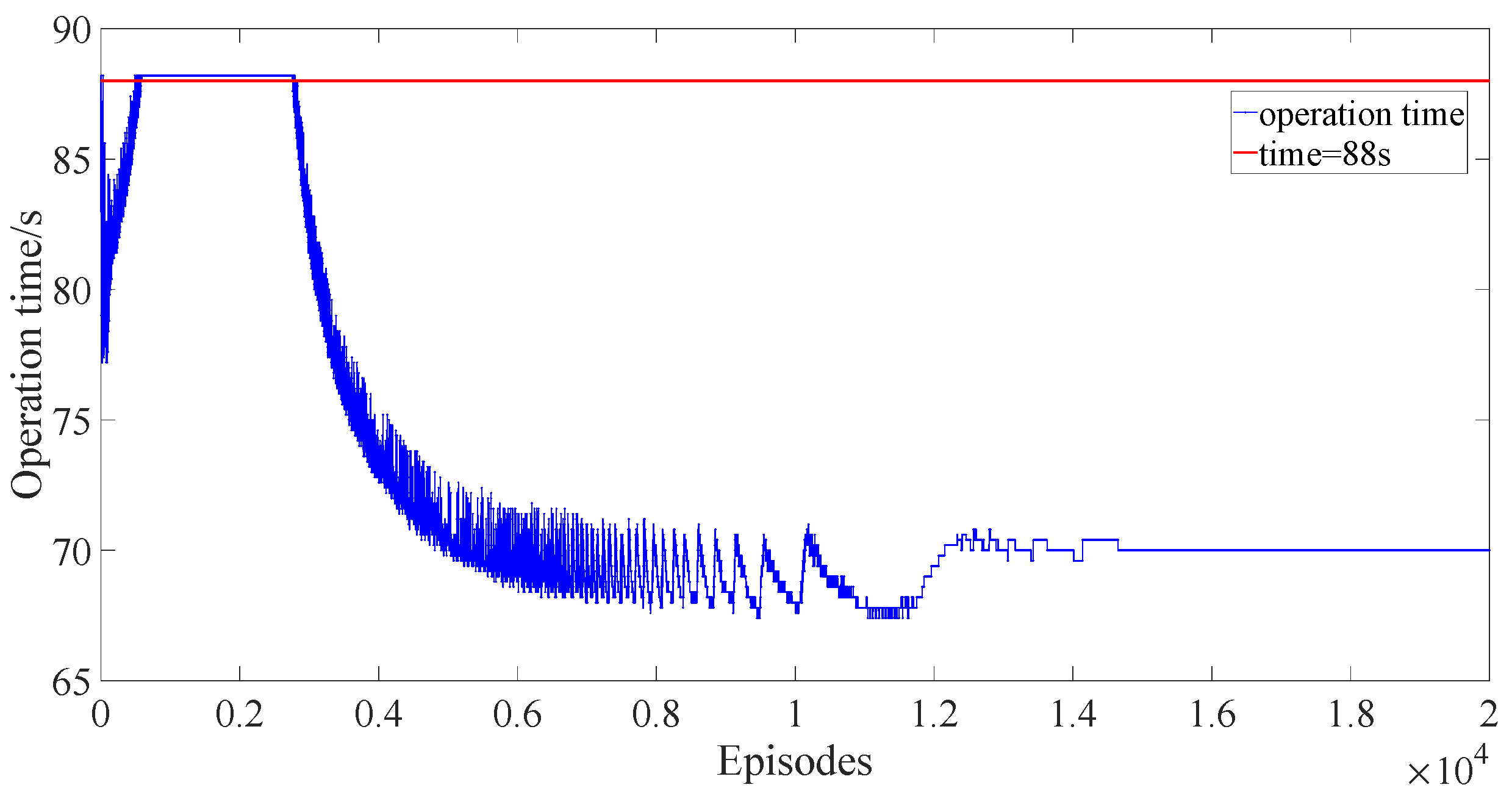
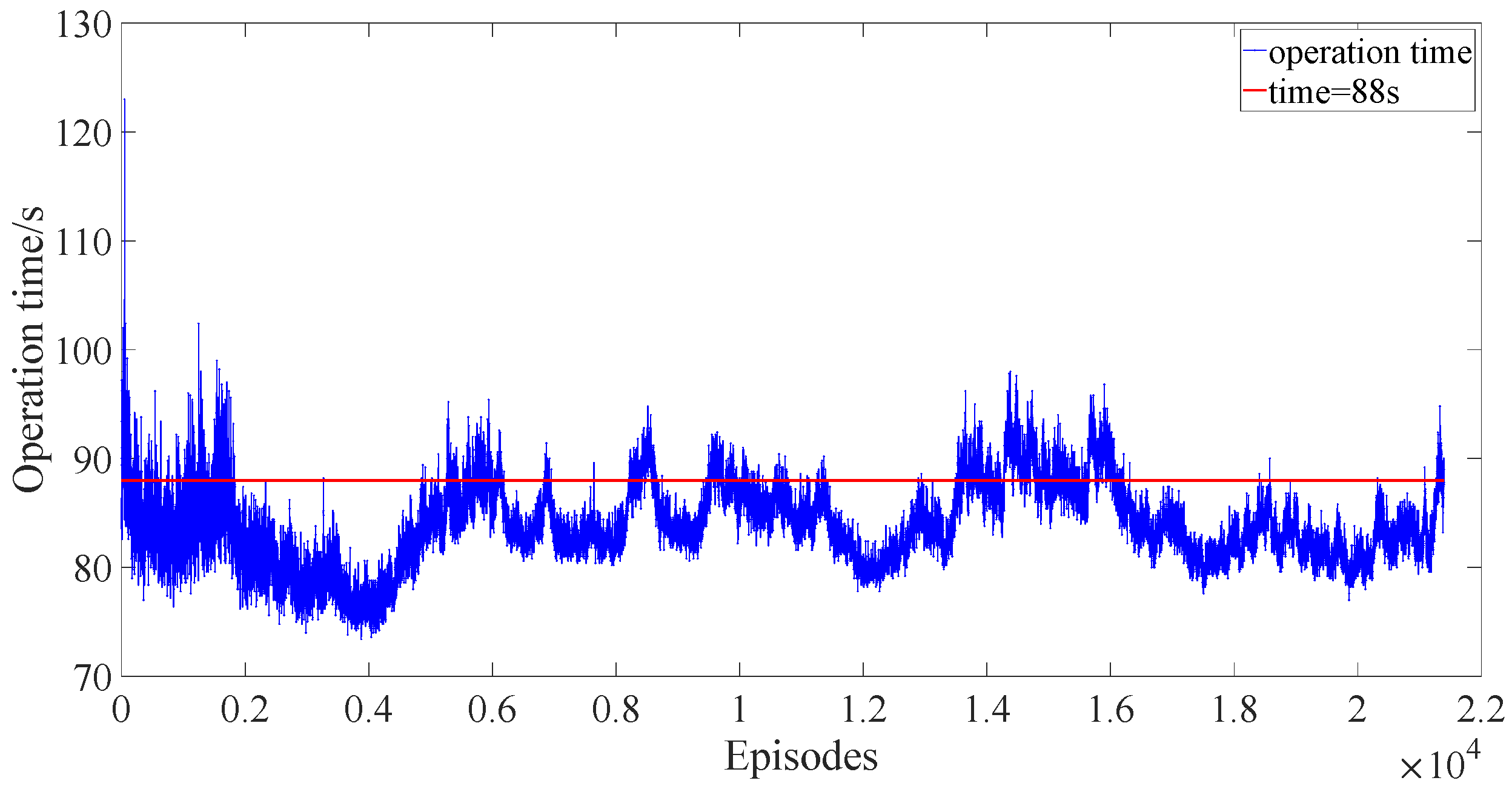
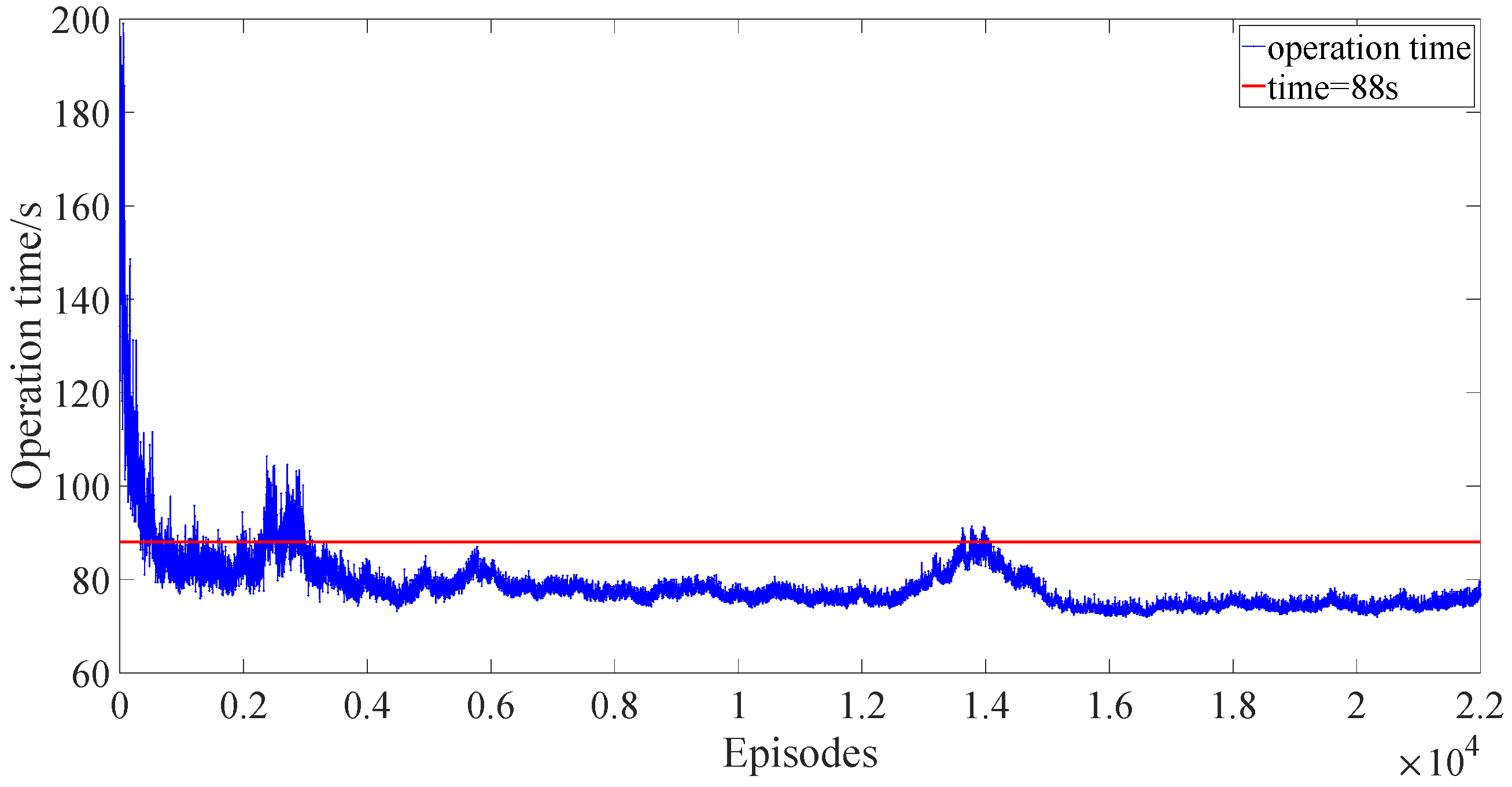
The operation time is an important indicator in the subway system. In this paper, we select 110% of the prescribed operation time (shown in Table 1), which is 88 s, as the threshold of the operation time. The results are shown in Figure 11, Figure 12 and Figure 13, respectively.

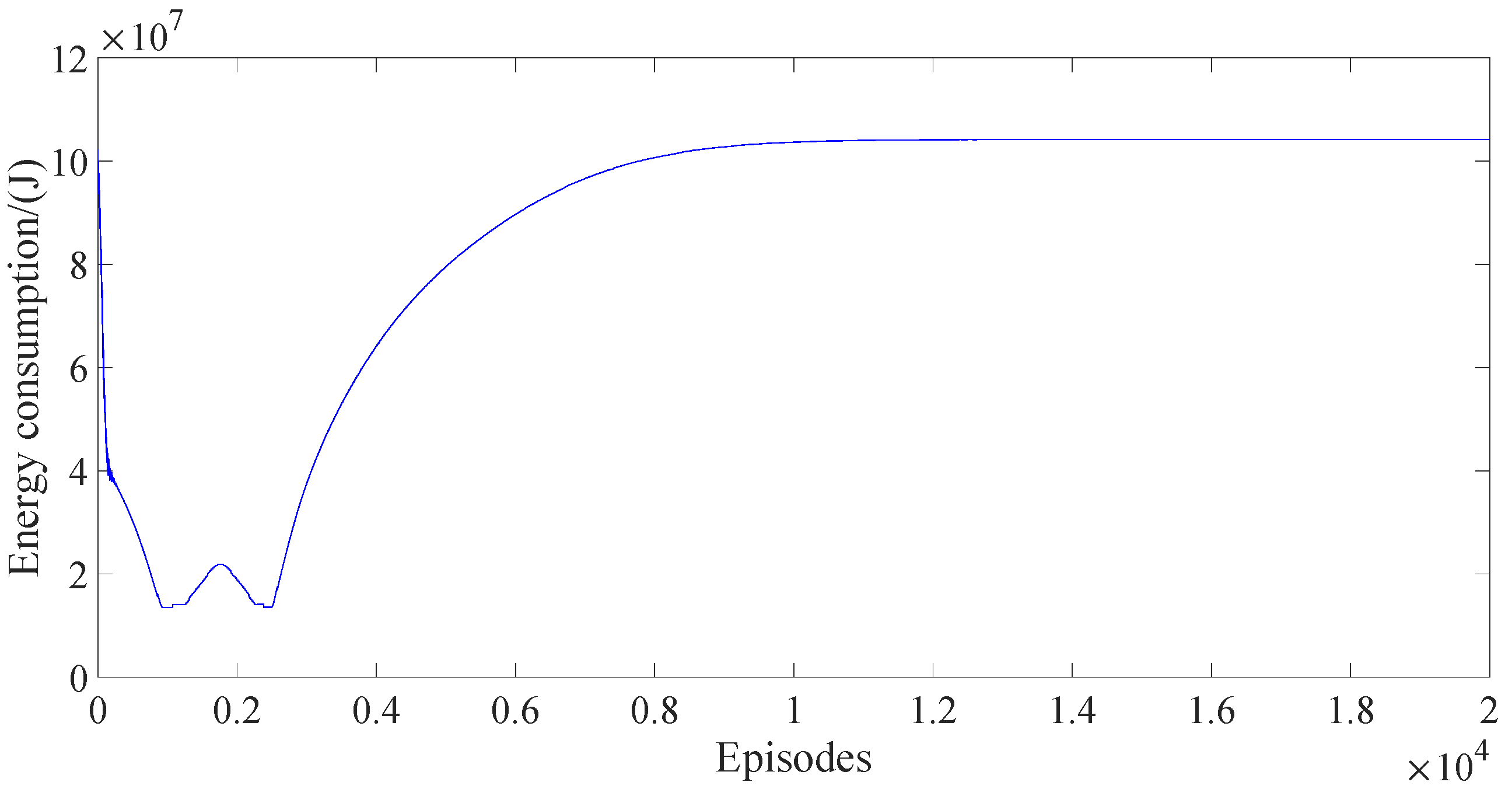
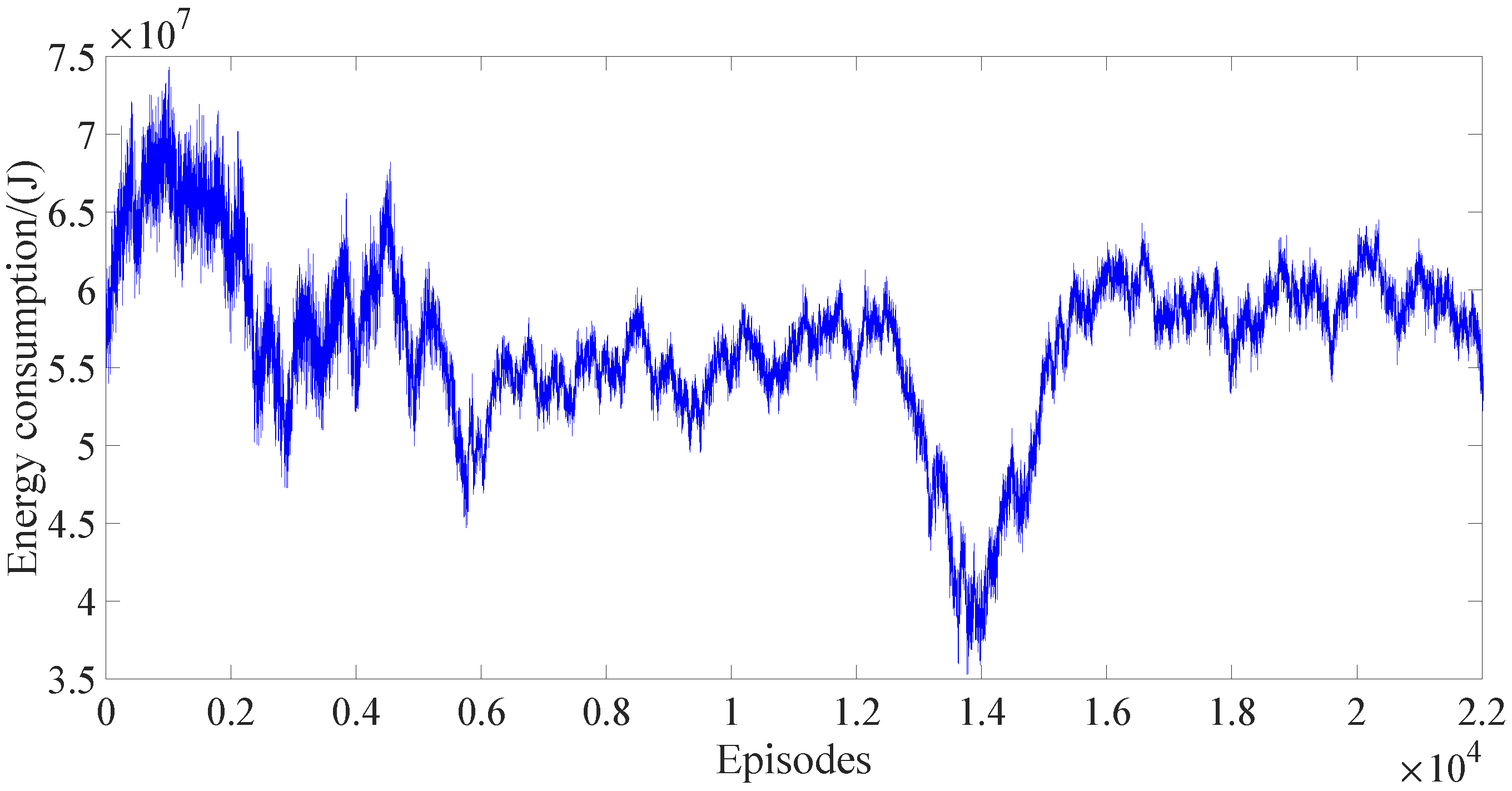
From Figure 11, Figure 12 and Figure 13, we can find that after 4000 episodes, the operation time in DDPG and PPO with reward scaling meets the requirements of the operation (only small episodes whose operation times exceed the threshold but converge quickly) while the operation time in the conventional PPO exceeds the threshold for many episodes. Although the operation time in DDPG is lower than that in PPO with reward scaling, the energy consumed in DDPG is much higher than that in PPO with reward scaling shown in Figure 14 and Figure 15. The energy consumed in the conventional PPO is lower than that of the PPO with reward scaling because of more time consumed in the conventional PPO shown in Figure 15 and Figure 16; however, this does not meet the demand of subway operation.

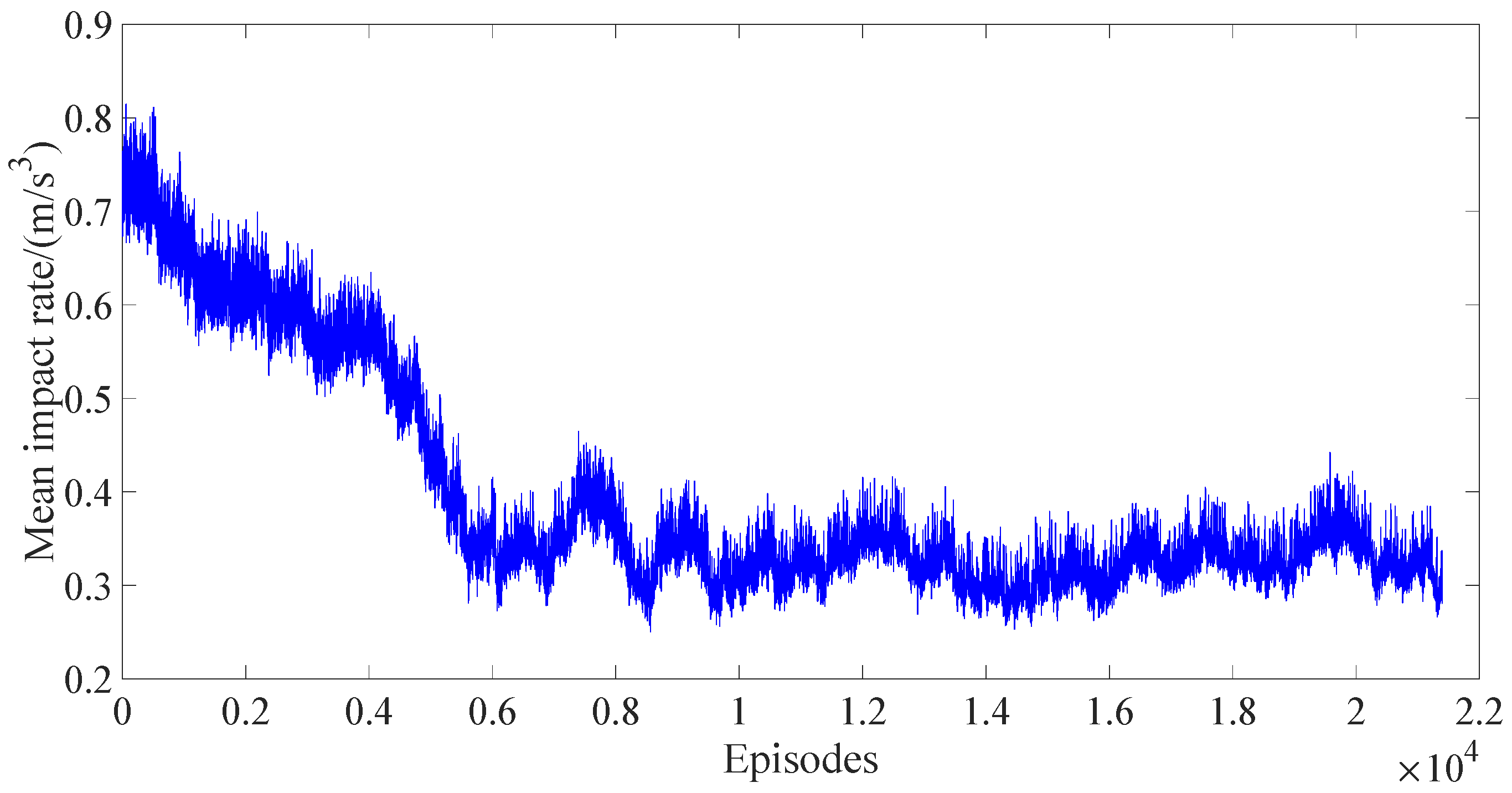
The mean impact rates of the three algorithms are shown in Figure 17, Figure 18 and Figure 19. Here, it can be observed that, at the end of training, the mean impact rate of the PPO with reward scaling is lower than that of DDPG. Similarly, the mean impact rate of the conventional PPO is lower than that of the PPO with reward scaling because the conventional PPO consumes more time in operation, which does not meet the demand of subway operation.

From the above analysis, it can be seen that PPO with reward scaling has the fastest convergence speed and is the most stable after convergence. Compared with DDPG, it performs better in terms of operation time, energy consumption, and comfort. The conventional PPO may require more computing resources to achieve a stable convergence state. Although it performs better in terms of energy consumption and comfort than PPO with reward scaling in some episodes, it does not meet the requirements of the subway operating timetable.

5. Conclusions

With the increasing scale of the urban subway, the total energy consumption of the subway has increased dramatically and poses a great challenge to the comfort of passengers and the punctuality of train operation. In order to ensure on-time train operation and passenger comfort, and at the same time reduce the energy consumption of subway operation, this paper proposes a Proximal Policy Optimization (PPO)-based optimization algorithm for the optimal control of subway train operation. Firstly, a reinforcement learning architecture for optimal control of subway train operation is constructed with the position and speed of train operation as the reinforcement learning state, energy consumption and comfort as the optimization objectives, and train operation time as the constraint. The proposed reinforcement learning model is trained by the PPO algorithm, and the reward scaling is added to the training process to accelerate the training speed and improve the efficiency of the algorithm. Finally, the algorithm proposed in this paper is compared with the Deep Deterministic Policy Gradient (DDPG) algorithm and the conventional PPO, and the superiority of the algorithm is verified.

The research in this paper can provide new ideas for the optimal control direction of train operation. It can directly optimize the train operation control strategy without the train speed profiles, to get rid of the limitations of the offline speed profiles and the precise model information of the train. In addition, the research content of this paper can provide the basic control method selection for the multi-train tracking model, but the train operation model still needs to be improved according to the constraints of multi-train tracking. This is also the content of the author’s future research.