Research on Tracking Control of Urban Rail Trains Based on Improved Disturbance Observer
Abstract
:1. Introduction
- (1)
- In this paper, to more accurately describe the motion state of the URTs and improve the control accuracy, consider the coupling force between carriages to establish the multiple point-mass model. An expression for the state space form with partial actuator failure is also given.
- (2)
- In order to enhance the anti-disturbance ability of the URTs system, an improved disturbance observer is proposed for unknown external disturbances to estimate and attenuate the unknown disturbances online. The proposed disturbance observer-based controller has high control accuracy and anti-disturbance capability.
- (3)
- The proposed disturbance observer in this paper does not require a priori knowledge of unknown disturbances and can estimate attenuation for more types of disturbances. The strict condition that the rate of change of disturbance is equal to zero is also removed, which aligns better with the actual scenario of URTs operation.
2. Problem Statement
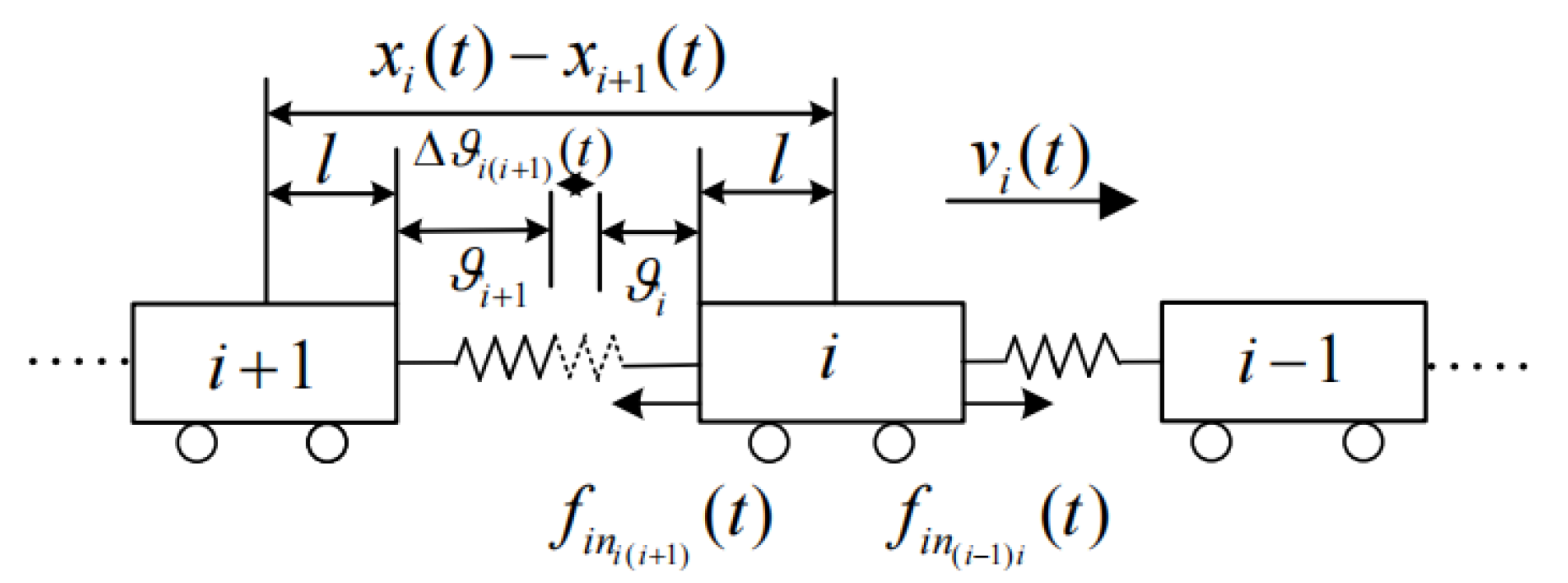
2.1. The In-Train Force and Running Resistance of the URTs
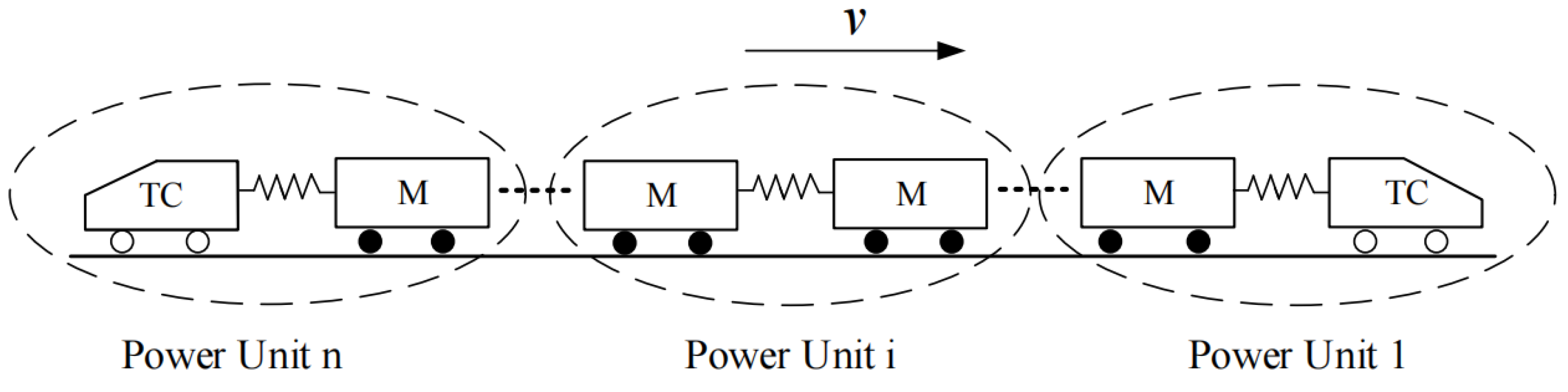
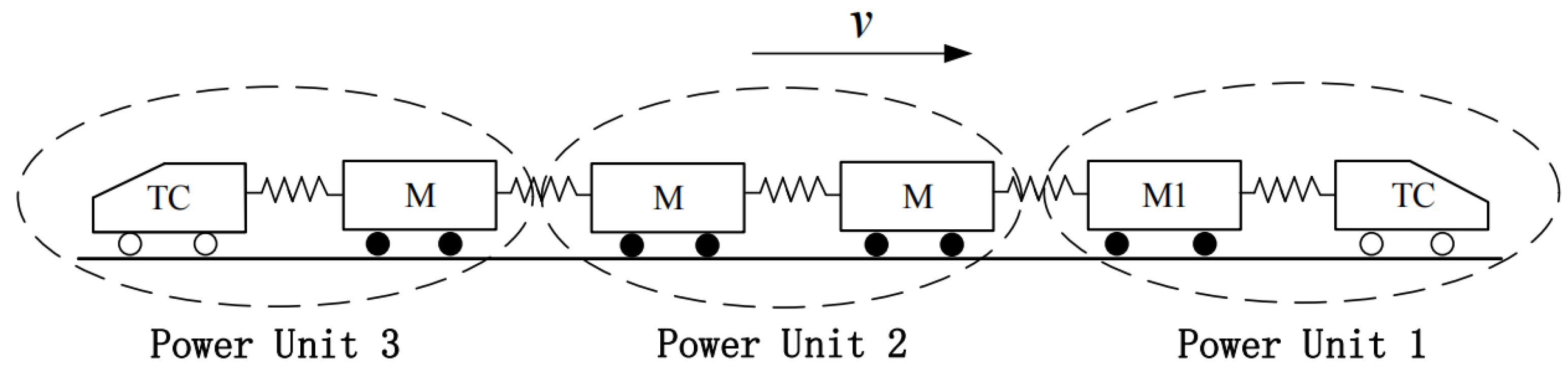
2.2. The Multiple Point-Mass Model of the URTs
3. Main Results
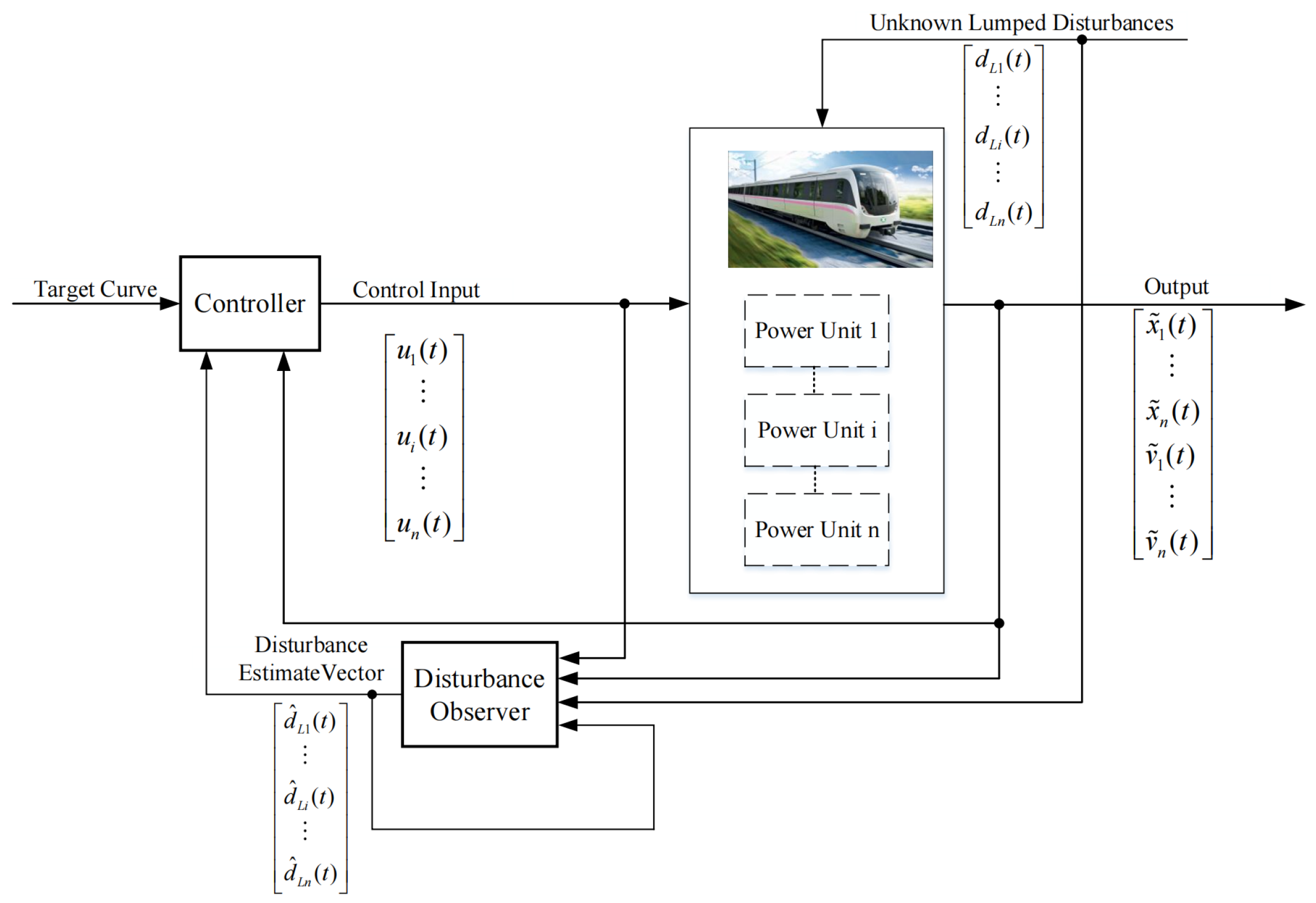
3.1. The Improved Disturbance Observer Design
3.2. Controller Design and Stability Proof Based on Improved Disturbance Observer
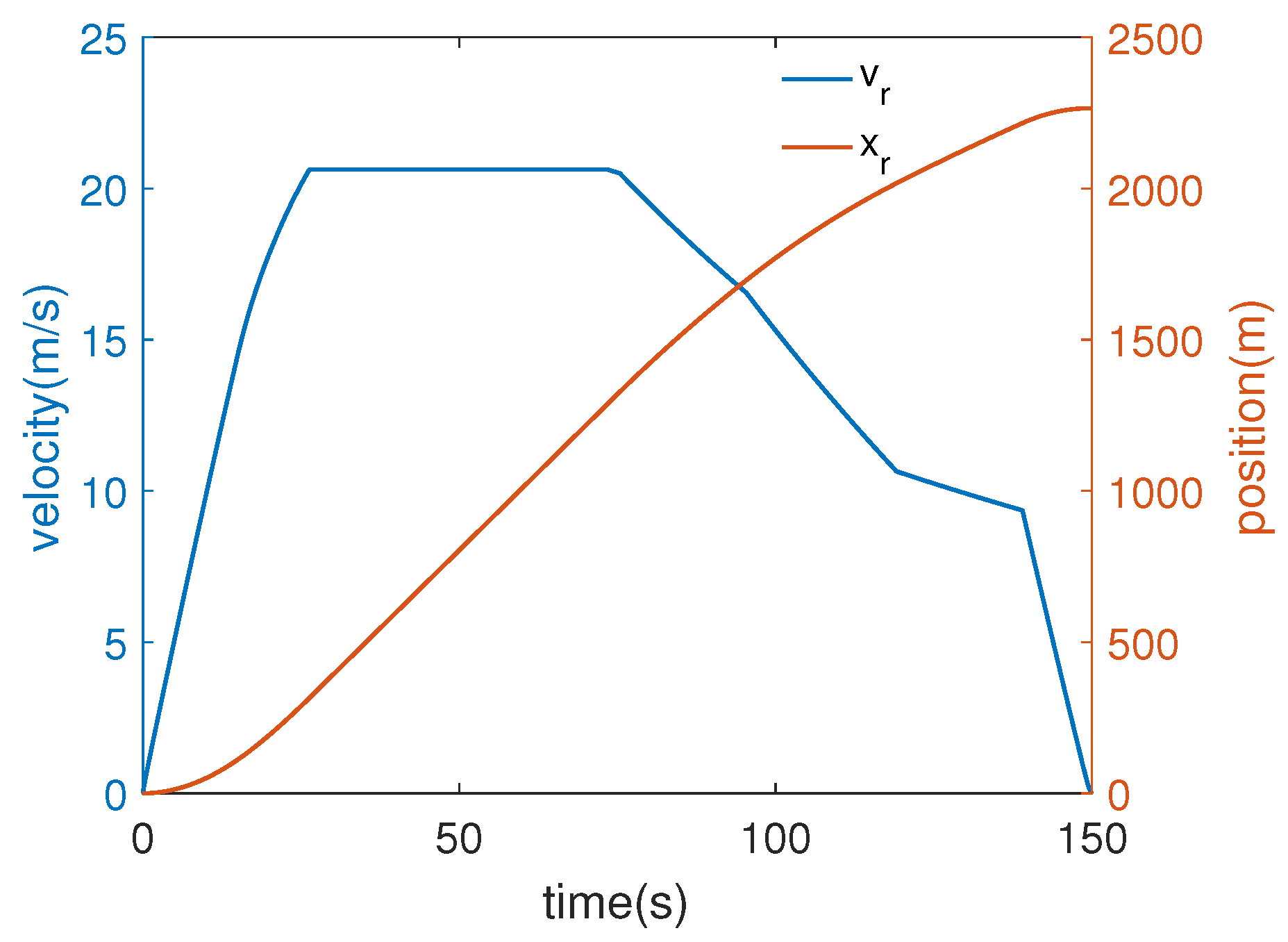
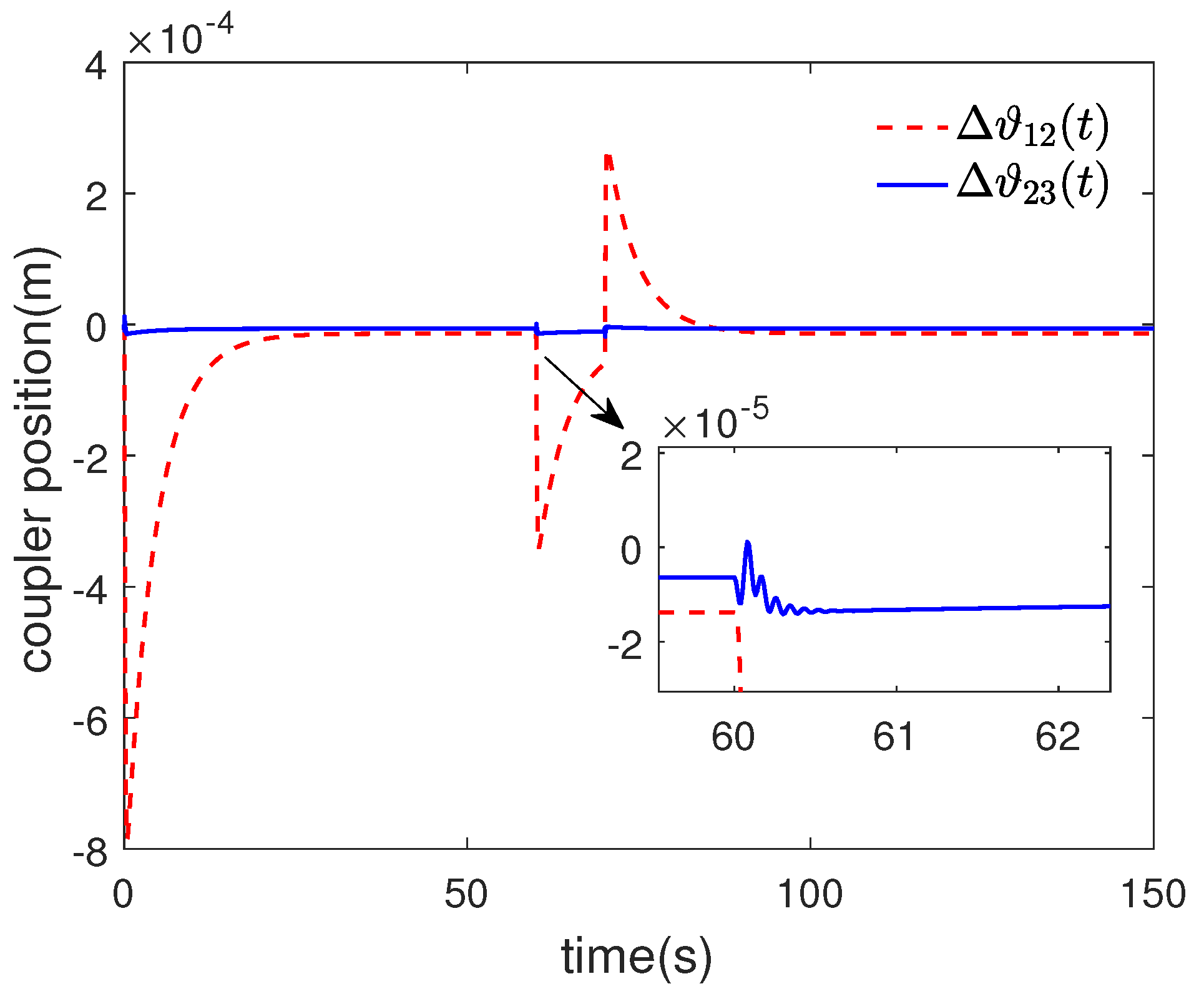
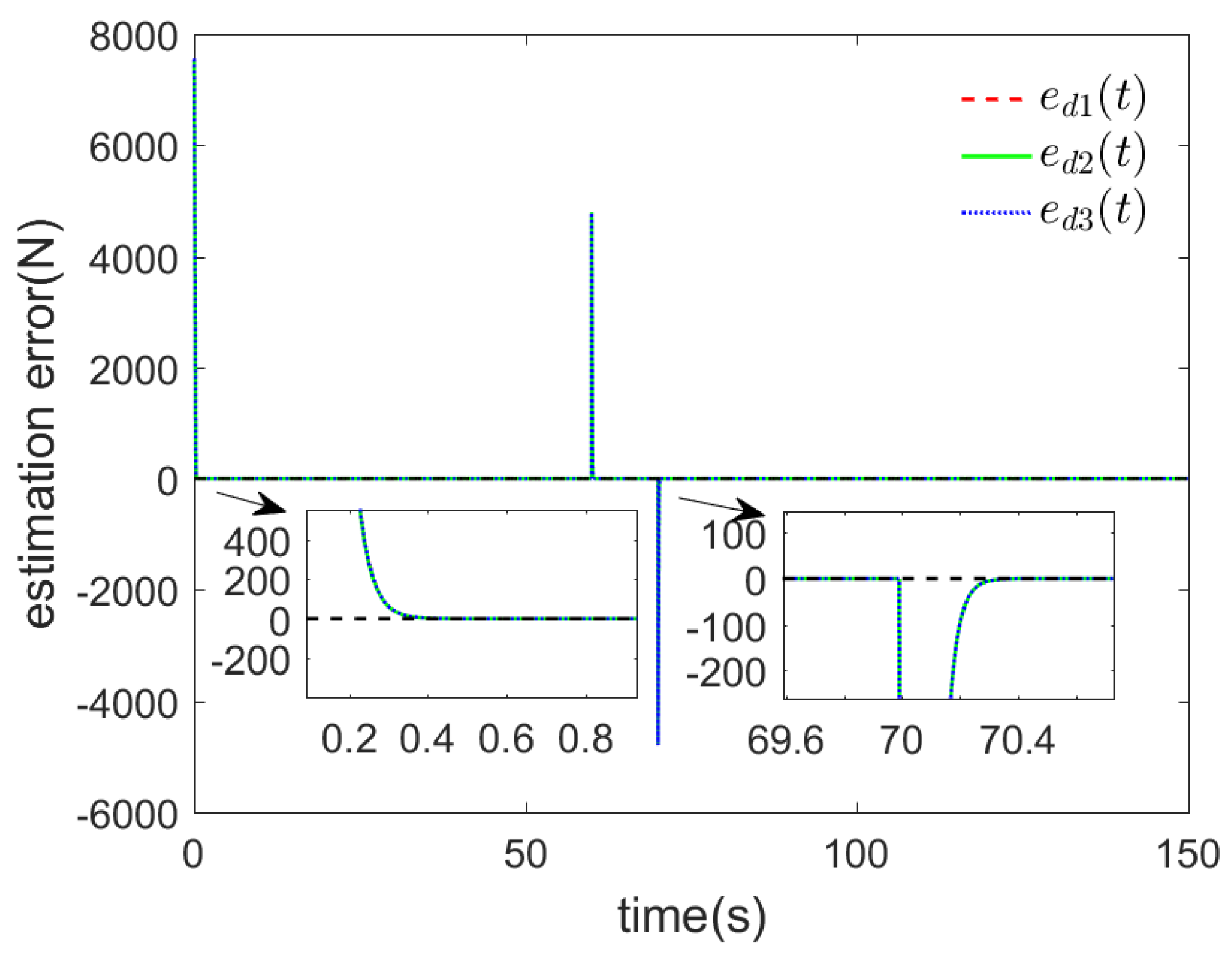
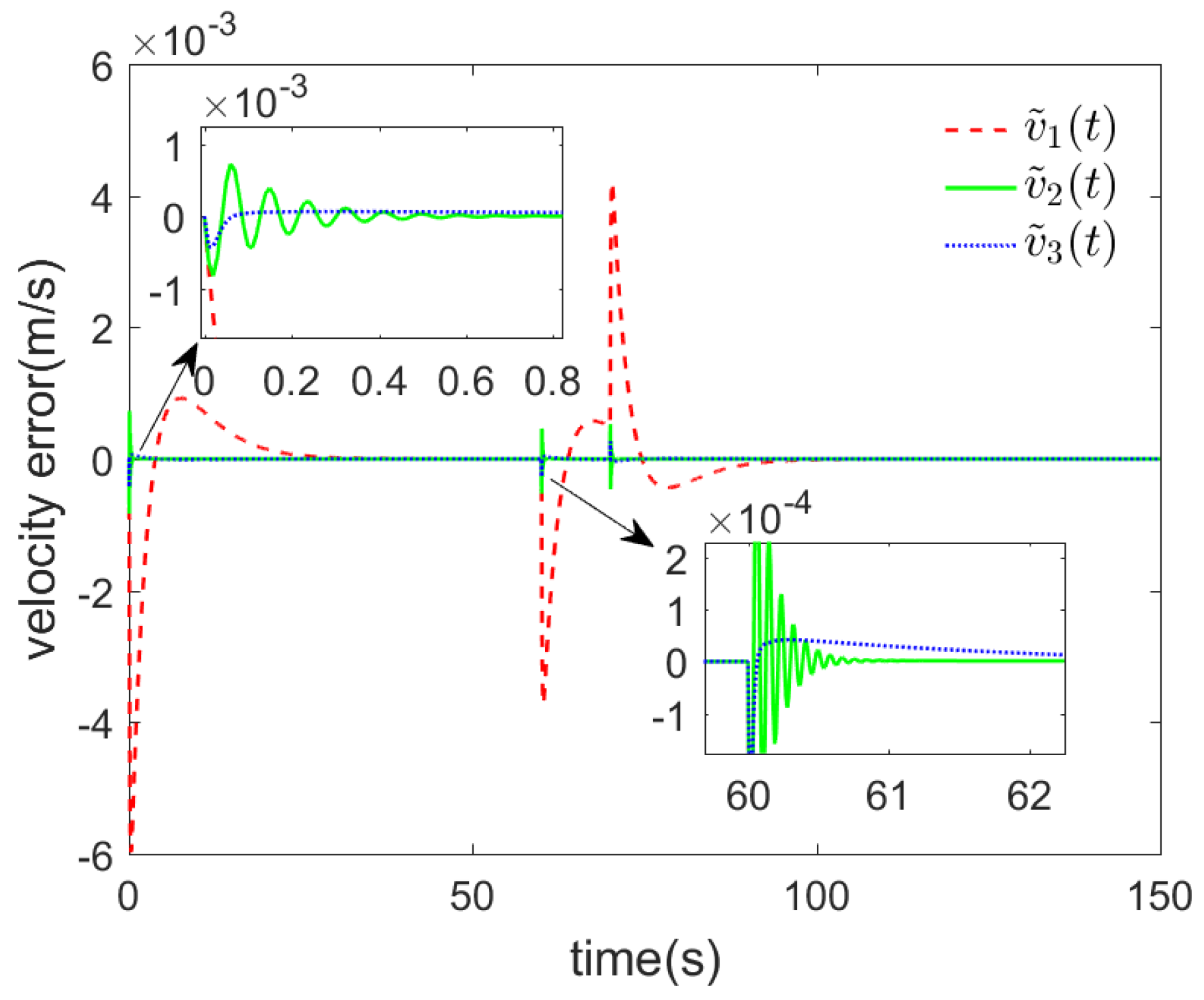
4. Simulation Verification and Results Analysis
5. Conclusions
- (1)
- It exhibits higher tracking accuracy in terms of displacement and velocity, and the tracking error is in the range of m and m/s, which meets the punctual operation requirement of the UTRs.
- (2)
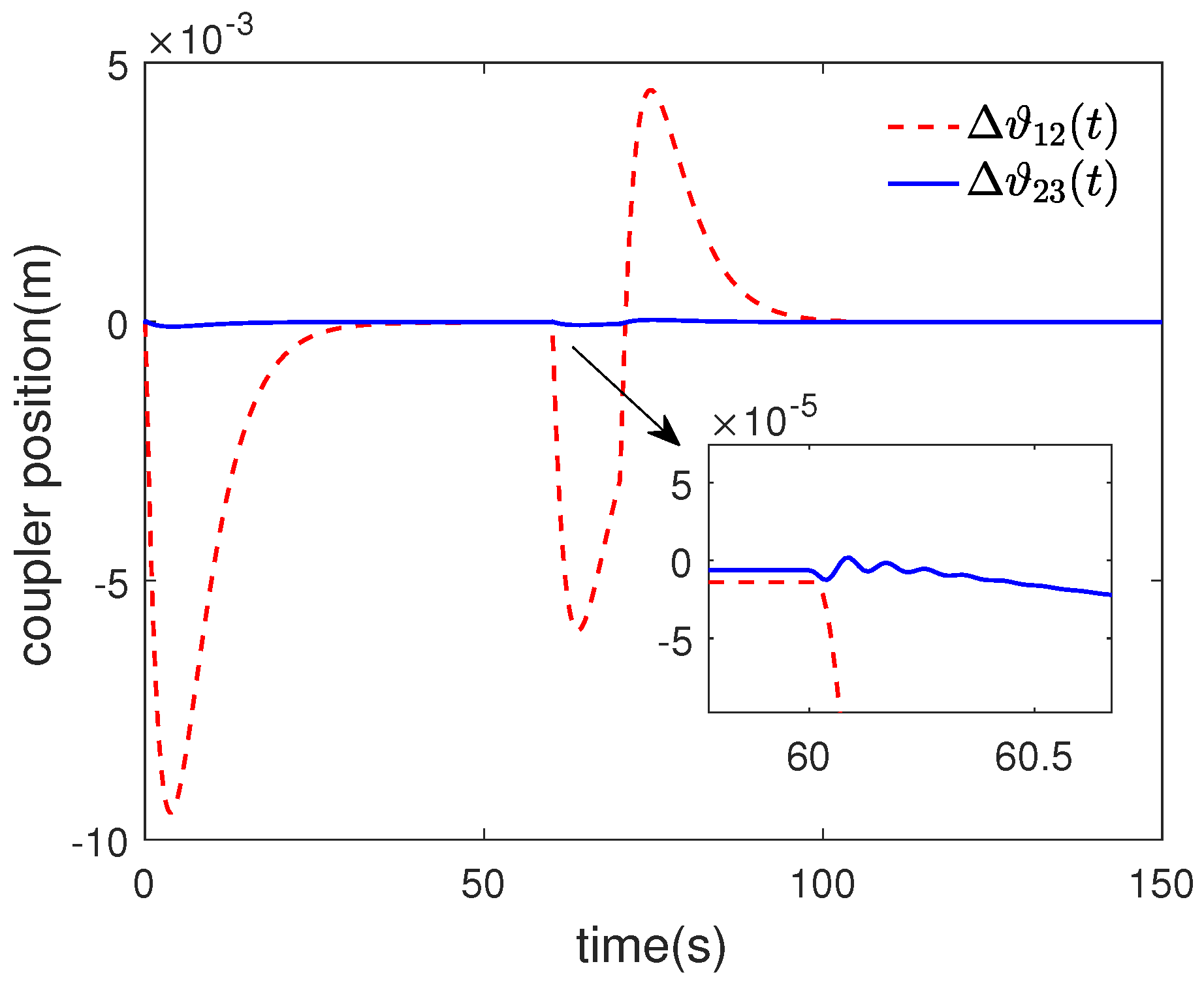
- With a smaller coupler displacement, which meets safety specifications and ensures safer train operation.
- (3)
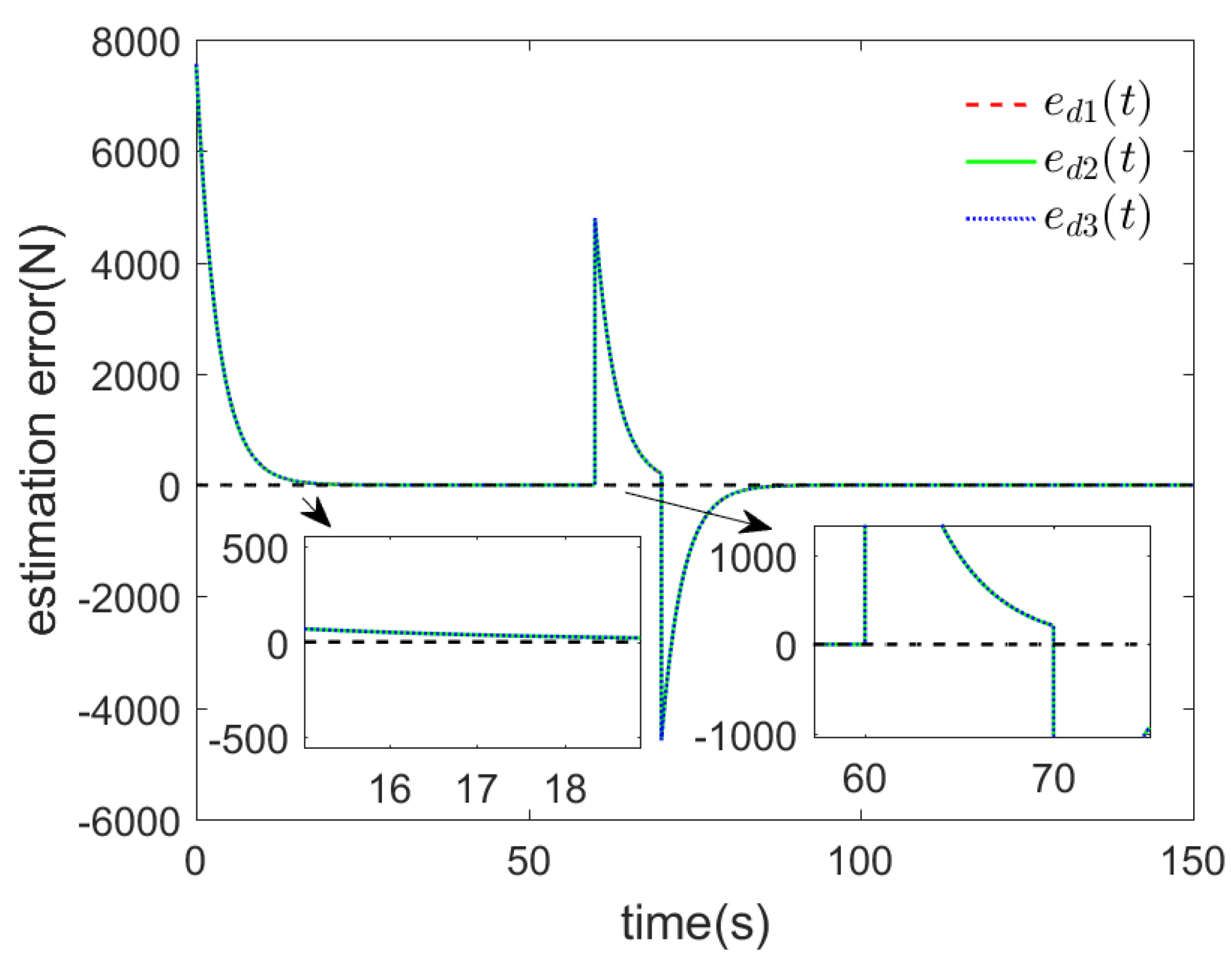
- With stronger anti-disturbance capability, the error converges to zero faster after suffering external disturbance, which can make the URTs have better tracking performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bao, X.D. Urban rail transit present situation and future development trends in China: Overall analysis based on national policies and strategic plans in 2016–2020. Urban Rail Transit 2018, 4, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.N.; Ma, W.G.; Xie, G.; Hei, X.H.; Wang, F.; Tan, S.Y. A survey of control algorithm for automatic train operation. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 2405–2410. [Google Scholar]
- Dong, H.R.; Ning, B.; Cai, B.G.; Hou, Z.S. Automatic train control system development and simulation for high-speed railways. IEEE Circuits Syst. Mag. 2010, 10, 6–18. [Google Scholar] [CrossRef]
- Domínguez, M.; Fernández-Cardador, A.; Cucala, A.P.; Gonsalves, T.; Fernández, A. Multi objective particle swarm optimization algorithm for the design of efficient ATO speed profiles in metro lines. Eng. Appl. Artif. Intell. 2014, 29, 43–53. [Google Scholar] [CrossRef]
- Yin, J.T.; Chen, D.W.; Li, L.X. Intelligent train operation algorithms for subway by expert system and reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2561–2571. [Google Scholar] [CrossRef]
- Lin, W.S.; Sheu, J.W. Optimization of train regulation and energy usage of metro lines using an adaptive-optimal-control algorithm. IEEE Trans. Autom. Sci. Eng. 2011, 8, 855–864. [Google Scholar] [CrossRef]
- Liu, J.Q.; Guo, H.L.; Yu, Y.X. Research on the cooperative train control strategy to reduce energy consumption. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1134–1142. [Google Scholar] [CrossRef]
- Keskin, K.; Karamancioglu, A. Energy-efficient train operation using nature-inspired algorithms. J. Adv. Transp. 2017, 2017, 6173795. [Google Scholar] [CrossRef] [Green Version]
- Pu, Q.; Zhu, X.M.; Zhang, R.T.; Liu, J.; Cai, D.B.; Fu, G.H. Speed profile tracking by an adaptive controller for subway train based on neural network and PID algorithm. IEEE Trans. Veh. Technol. 2020, 69, 10656–10667. [Google Scholar] [CrossRef]
- Yang, H.; Fu, Y.T.; Wang, D.H. Multi-ANFIS model based synchronous tracking control of high-speed electric multiple unit. IEEE Trans. Fuzzy Syst. 2017, 26, 1472–1484. [Google Scholar] [CrossRef]
- Liu, H.E.; Yang, H.; Wang, D.H. Robust speed prediction of high-speed trains based on improved echo state networks. Neural Comput. Appl. 2021, 33, 2351–2367. [Google Scholar] [CrossRef]
- Li, S.K.; Yang, L.X.; Li, K.P. Robust output feedback cruise control for high-speed train movement with uncertain parameters. Chin. Phys. B 2014, 24, 010503. [Google Scholar] [CrossRef]
- Yao, X.M.; Park, J.H.; Dong, H.R.; Guo, L.; Lin, X. Robust adaptive nonsingular terminal sliding mode control for automatic train operation. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 2406–2415. [Google Scholar] [CrossRef]
- Rui, S.; Shi, G. Robust control for T-S fuzzy multi-particle model of high-speed train with disturbances and time-varying delays. Int. J. Control Autom. Syst. 2022, 20, 3063–3074. [Google Scholar]
- Sariyildiz, E.; Oboe, R.; Ohnishi, K. Disturbance observer-based robust control and its applications: 35th anniversary overview. IEEE Trans. Ind. Electron. 2019, 67, 2042–2053. [Google Scholar] [CrossRef] [Green Version]
- Vo, A.T.; Truong, T.N.; Kang, H.J. A novel tracking control algorithm with finite-time disturbance observer for a class of second-order nonlinear systems and its applications. IEEE Access 2021, 9, 31373–31389. [Google Scholar] [CrossRef]
- Benevides, J.R.; Paiva, M.A.; Simplício, P.V.; Inoue, R.S.; Terra, M.H. Disturbance observer-based robust control of a quadrotor subject to parametric uncertainties and wind disturbance. IEEE Access 2022, 10, 7554–7565. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, L.; Ji, W. Improved non-singular fast terminal sliding mode control with disturbance observer for PMSM drives. IEEE Trans. Transp. Electrif. 2021, 7, 2753–2762. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, L.; Wang, H.W.; Tang, T.; Li, K.C. Robust distributed cruise control of multiple high-speed trains based on disturbance observer. IEEE Trans. Intell. Transp. Syst. 2019, 22, 267–279. [Google Scholar] [CrossRef]
- Leng, P.; Yu, P.; Gao, M.; Li, J.; Li, Y. Optimal Control Scheme of Maglev Train Based on The Disturbance Observer. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1935–1940. [Google Scholar]
- Chen, B.; Zhang, R.; Zhou, F.; Du, W. An Observer-Driven Distributed Consensus Braking Control Method for Urban Railway Trains with Unknown Disturbances. Actuators 2023, 12, 111. [Google Scholar] [CrossRef]
- Chen, D. Derailment risk due to coupler jack-knifing under longitudinal buff force. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2010, 224, 483–490. [Google Scholar] [CrossRef]
- Xu, C.F.; Chen, X.Y.; Wang, L. Model-independent adaptive fault-tolerant tracking control for high-speed trains with actuator saturation. Appl. Sci. 2019, 9, 4146. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Li, Z.Q.; Yang, H.; Fu, Y.T.; Yan, Y. Data-driven model-free adaptive sliding mode control based on FFDL for electric multiple units. Appl. Sci. 2022, 12, 10983. [Google Scholar] [CrossRef]
- Yang, C.D.; Sun, Y.P. Mixed H2/H cruise controller design for high speed train. Int. J. Control 2001, 74, 905–920. [Google Scholar] [CrossRef]
- Zhong-Qi, L.; Hui, Y.; Zhang, K.P.; Ya-Ting, F. Distributed model predictive control based on multi-agent model for electric multiple units. Acta Autom. Sin. 2014, 40, 2625–2631. [Google Scholar]
- Yang, J.; Chen, W.H.; Li, S.H. Non-linear disturbance observer-based robust control for systems with mismatched disturbances/uncertainties. IET Control Theory Appl. 2011, 5, 2053–2062. [Google Scholar] [CrossRef] [Green Version]
- Khalil, H.K. Nonlinear Control; Pearson: New York, NY, USA, 2015. [Google Scholar]
- Cao, Y.; Wang, Z.C.; Liu, F.; Li, P.; Xie, G. Bio-inspired speed curve optimization and sliding mode tracking control for subway trains. IEEE Trans. Veh. Technol. 2019, 68, 6331–6342. [Google Scholar] [CrossRef]
- Liu, G.F.; Hou, Z.S. Adaptive iterative learning control for subway trains using multiple-point-mass dynamic model under speed constraint. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1388–1400. [Google Scholar] [CrossRef]



| Symbol | Description |
|---|---|
| ,, and | Position, speed, and acceleration of carriage |
| The control input of carriage | |
| Coupling forces between ith and th carriage | |
| Coupler deformation length | |
| The elastic coupling coefficient | |
| S | The sum of the original length of the carriage and coupler |
| The mass of ith carriage | |
| ,, and | The Davis coefficients |
| , | The length and center angle of the curve |
| The slope angle | |
| The tunnel Length | |
| The running resistance of ith carriage | |
| The additional resistance of ith carriage | |
| The unknown external disturbance of ith carriage | |
| The lumped disturbance of ith carriage | |
| , | The target position and speed |
| ,, and | The position, speed, and control input error of ith carriage |
| L | The observer gain matrix |
| K | The controller gain matrix |
| The estimate of lumped disturbance | |
| The disturbance estimation error | |
| The actuator health factor | |
| , | The maximum and minimum singular values of the |
| The Euclidean norm of the matrix | |
| The matrix and its transpose sum | |
| dimensional unit matrix | |
| ∗ | The symmetric part of the matrix |
| Parameter Symbols (i = 1, 2, 3) | Parameter Value |
|---|---|
| kg | |
| kg | |
| kg | |
| 2.031 N/kg | |
| 0.0622 Ns/mkg | |
| 0.00187 | |
| N/m | |
| 23 m | |
| 0.6 m |
| Strategy | MPE (m) | MNE (m) | MAE (m) |
|---|---|---|---|
| IDOBC | |||
| TDOBC |
| Strategy (m/s) | MPE (m/s) | MNE (m/s) | MAE (m/s) |
|---|---|---|---|
| IDOBC | 0.0018 | −0.0035 | |
| TDOBC | 0.0042 | −0.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Zhang, J.; Yang, H. Research on Tracking Control of Urban Rail Trains Based on Improved Disturbance Observer. Appl. Sci. 2023, 13, 7403. https://doi.org/10.3390/app13137403
Zhou Y, Zhang J, Yang H. Research on Tracking Control of Urban Rail Trains Based on Improved Disturbance Observer. Applied Sciences. 2023; 13(13):7403. https://doi.org/10.3390/app13137403
Chicago/Turabian StyleZhou, Yanli, Jianping Zhang, and Hui Yang. 2023. "Research on Tracking Control of Urban Rail Trains Based on Improved Disturbance Observer" Applied Sciences 13, no. 13: 7403. https://doi.org/10.3390/app13137403
APA StyleZhou, Y., Zhang, J., & Yang, H. (2023). Research on Tracking Control of Urban Rail Trains Based on Improved Disturbance Observer. Applied Sciences, 13(13), 7403. https://doi.org/10.3390/app13137403






