Real-Time Anomaly Detection with Subspace Periodic Clustering Approach

Abstract

Finding real-time anomalies in any network system is recognized as one of the most challenging studies in the field of information security. It has so many applications, such as IoT and Stock Markets. In any IoT system, the data generated is real-time and temporal in nature. Due to the extreme exposure to the Internet and interconnectivity of the devices, such systems often face problems such as fraud, anomalies, intrusions, etc. Discovering anomalies in such a domain can be interesting. Clustering and rough set theory have been tried in many cases. Considering the time stamp associated with the data, time-dependent patterns including periodic clusters can be generated, which could be helpful for the efficient detection of anomalies by providing a more in-depth analysis of the system. Another issue related to the aforesaid data is its high dimensionality. In this paper, all the issues related to anomaly detection are addressed, and a clustering-based approach is proposed for finding real-time anomalies. The method employs rough set theory, a dynamic k-means clustering algorithm, and an interval superimposition approach for finding periodic, partially periodic, and fuzzy periodic clusters in the subspace of the dataset. The data instances are thought to be anomalous if they either belong to sparse clusters or do not belong to any clusters. The efficacy of the method can be assessed by means of both time-complexity analysis and comparative studies with existing clustering-based anomaly detection algorithms on a synthetic and a real-life dataset. It can be found experimentally that our method outperforms others and runs in cubic time.

1. Introduction

1.1. Origin of the Problem

Due to the extensive use of computers, networks, and databases, they are exposed to various types of attacks. The attacks may be in the form of hacking, intruding, etc. The term “anomalous activity” has been used for this, and any data instance associated with such attacks is known as “anomaly”. Finding such anomalies is one of the hot areas of research in modern times. It has so many applications, such as IoT, the stock market, banking, security, defense, etc. Over the past few years, Internet of Things (IoT) networks have brought significant changes to individual lives, society, and industry [1,2]. The IoT devices consist of a huge number of sensors generating data over time [3], and as a result, the availability of streaming time-series data is expanding exponentially. As a result of the involvement of a wide range of information and communication technologies, IoT networks are exposed to various types of security threats [4,5]. In other words, any system that relies on the IoT faces huge security and privacy challenges [6,7]. The challenges are in the form of anomalies, intrusions, or any other illegitimate activities that jeopardize the security of the system [8]. Although the system can be protected to some extent by the defense mechanisms currently in place, malicious attackers are becoming more skilled at breaking networks. Again, in an event such as an inside attack, it is more challenging to prevent it in real-time. Therefore, identifying such real-time attacks can provide actionable information in dire situations for which there are no trustworthy solutions [9,10,11,12,13,14,15,16,17,18]. Here, a new and reliable clustering-based method is put forth to address the problem.

Unsupervised learning techniques such as clustering [19] are widely used to determine the distribution of data and patterns. It has recently been employed in anomaly detection as well as other branches such as psychology and social science, where it has long been extensively used [20,21]. Static clustering and dynamic clustering are the two primary categories of clustering techniques. Static clustering primarily targets static datasets that are prepared before the algorithm is applied. Dynamic clustering is necessary in some applications using real-time data, such as cloud computing, IoT, finance, and stock markets. A hierarchical approach that may be applied to both static and dynamic datasets was proposed by the authors in [22]. Several incremental clustering algorithms were put forth by the authors in [23] in order to process new records or data instances as and when they are added.

There are mainly two problems encountered while dealing with anomalies in any IoT-based system: the high dimensionality of the data and the real-time detection of anomalies. Anomalies are often hard to find at high dimensionality. For that reason, more data are necessary to properly generalize as the number of attributes or features rises, which results in data sparsity. Data sparsity is brought on by these additional attributes or a sizable amount of noise from several irrelevant attributes that obscure the real anomalies. The term “curse of dimensionality” [24,25] is a well-known one used to describe the issue. As a result, it has been discovered that numerous traditional anomaly detection methods [26,27,28] are inappropriate for high-dimensional data because they lose their effectiveness. In [29], the authors suggested a method for high-dimensional and categorical data anomaly detection. Similar works were presented in [30,31,32,33]. Again, any IoT system generates real-time data. In such systems, anomalies can be temporal or contextual [34] in nature, where the temporal order of the data is significant. To put it another way, a data instance can only be anomalous within a particular temporal context, or more accurately, within a timeframe. Some of these anomalies can be periodic in nature, i.e., they occur after a certain interval of time. These anomalies are difficult to detect. The development of an early warning system is one of the key applications of such abnormalities. In view of the above scenario, it is necessary to design an effective algorithm that locates clusters in the subspace of high-dimensional real-time data and detects anomalies in real-time.

Pawlak proposed rough set theory [35] to address the ambiguity and uncertainty that can be found in any dataset. Thivagar et al. [36,37] gave the notion of nano topological space in terms of the two approximations and generated CORE, a subset of conditional attributes used for medical diagnosis. The same notion can be used for generating a subset of high-dimensional real-time data. A comparison of five time-series anomaly detection techniques was conducted by the authors of [38]. Similar efforts were mentioned in [39,40,41,42,43,44,45,46,47]. The insider threat, which creates significant issues for the cyber security of industrial control systems, was addressed by the authors of [48]. A random forest-based strategy for online anomaly detection was presented by Zhao et al. [49]. In [50,51,52], the authors offered fuzzy-based approaches for real-time anomaly detection. In [53], the authors suggested a fuzzy neural network approach with the goal of identifying anomalies in significant cyberattacks. An effective real-time clustering-based anomaly detection system was described by the authors in [54].

As mentioned earlier, while detecting anomalies in most cases, two problems are frequently encountered, namely the high dimensionality of the data and the temporal reference of the detected anomaly. High dimensionality is a serious issue that reduces the efficacy of any anomaly detection method. Also, the temporal reference of the anomaly is important as it gives the time of occurrence of the anomalous data, which can be useful for the design of an early warning system. Though several methods tried to address the aforesaid problems, only a few successfully addressed one or another. So, there is enough scope to work on these problems.

1.2. Motivation and Contribution

Most of the algorithms discussed above have some limitations. For example, some are inefficient at finding anomalies in high-dimensional data, and others are unable to find real-time anomalies. Although there exist many algorithms [7,8,9,15,18,29,34,38,42,43] for efficient detection of real-time anomalies, only a few actually address the periodicity in the real-time data. In real-time data such as sensors, IT monitoring applications generate huge volume of data continuously over a period of time, which is the lifespan of the dataset. Over the lifespan of the dataset, there may be data instances of similar nature that occur periodically. Considering the time attribute associated with such data as calendar dates (year_month_day_hour_minute_second), periodic clusters can be generated where the period of a cluster can be represented as a sequence of lifespans of clusters. In other words, in such a system, it would be interesting to observe whether the clusters or anomalies generated are of a periodic nature or not. This information can be useful for predicting anomalies. In [55], the authors proposed calendar-based periodic patterns from supermarket datasets. With the help of an interval superimposition operation [56,57,58], the algorithm finds a match ratio to generate fully, partially, and fuzzy [59] periodic patterns.

In this article, the problems of high-dimensionality, real-time detection of anomalies, and periodicity have been efficiently addressed—and a method is proposed that can generate fully periodic, partially periodic, and fuzzy periodic clusters. It is named the RADSPCA. The method uses the notion of rough set theory and the k-means clustering algorithm to generate clusters along with their sequence of lifespans, and then the interval superimposition is applied to the lifespans to generate the periodicity of the clusters. The objective of the paper is as follows:

Firstly, a dominance relation is defined on the dataset [60].

Secondly, an interval superimposition operation is defined, and a match ratio in terms of interval superimposition is also defined.

Finally, a new clustering-based method is proposed to generate periodic, partially periodic, and fuzzy periodic clusters in the subspace of the dataset.

Thus, the RADSPCA first uses a rough set theoretic approach to find a lower-dimensional space by removing the irrelevant attributes. Then, the dynamic k-means clustering algorithm is applied to it to find the clusters along with their list of lifespans. At the end of this stage, each cluster will have a list of lifespans describing its period. Then the interval superimposition operation is applied to the list of lifespans to generate superimposed time-intervals along with their match ratio [55,56]. The match ratio will determine whether the corresponding cluster is fully or partially periodic. Also, by applying a nice method [56,57] on superimposed intervals, fuzzy time intervals can be generated. This way, from each fully or partially periodic cluster fuzzy periodic clusters can be generated. Then, RADSPCA’s complexity is estimated. Lastly, a detailed comparative analysis is conducted with existing well-known clustering-based methods [9,10,19,46,54,61,62,63] using a MATLAB implementation with first KDDCUP’99 [64] and then Kitsune Network Attack [65] datasets. The results effectively validate our technique.

The structure of the paper is as follows: In Section 2, it is discussed how this field has recently advanced. In Section 3, the problem definition is presented. Section 4 covers the proposal method (RADSPCA). Section 5 discusses the time-complexity. Section 6 of the paper contains the experiments, results, and analysis, and Section 7 of the paper contains the conclusions, limitations, and future directions.

2. Related Works

Anomaly detection is the search for patterns that differ from previously known ones. It is useful for obtaining sufficient information about the system that generates, processes, or transmits the data. Since the last couple of years, sensors and application-based IoT networks have become popular to substantially upgrade the standard of individual life by contributing to the development of society and industry [1,2]. Such systems generate data exponentially over time [3]. However, due to the involvement of the Internet and other communication technologies, the networks are always open to various security threats [4,5,6]. So, for such a system, the security and privacy challenges [7] are major causes of concern. Some of the common challenges are anomalies, fraud, intrusion, or any other illegitimate activities that jeopardize the system’s reliability [8]. Currently, the protection of networks exists to a reasonable extent, but malicious attackers are becoming smart enough to break into the networks again and again. In [9], the authors proposed a hybrid approach using both partitioning and an agglomerative hierarchical clustering algorithm for real-time anomaly detection. Using a unified metric [9] defined on both numeric and categorical attributes, a distance function and similarity measure are expressed which are then used for generating clusters on fuzzy time intervals. However, the above method did not supply periodic clusters and periodic anomalies. In [10], the author used a merge function in the k-means algorithm to generate anomalies from a mixed attribute dataset. Though the work of [10] is quite similar to [9], the later method supplies real-time anomalies, which the former does not. In [11], the authors put forward an agglomerative hierarchical model for the detection of anomalies in a network dataset. [12] built a rough set-based classification model for anomaly detection. Applying automatic labeling for supervised learning, an anomaly detection scheme was proposed in [13]. In [14], an unsupervised deep learning approach was proposed that can detect the potential correlation features among multi-dimensional sensor data and find out the anomalies in public transportation and facilities in smart cities. The work of [14] efficiently addressed some of the issues, such as the multi-dimensionality and the periodicity of the real-life data. However, the periodicity of clusters or anomalies was not addressed. In [15], the authors offered both semi-supervised and supervised approaches for real-time anomaly detection in a high-dimensional data stream. In [16], the authors used correlation laws to detect anomalies. In [17], the authors proposed a new method incorporating neural processes into a semi-supervised anomaly detection model. In [18], the authors conducted a detailed review on anomaly detection paradigms based on offline-learning, semi-online learning and online-learning. in high-velocity data streams.

Cheng et al. [20], proposed a unified metric defined by mixed attributes to generate clusters. In [21], the authors offered an agglomerative hierarchical model for clustering periodic patterns, where a pattern is said to be periodic if it occurs repeatedly after a certain period of time. There are mainly two problems encountered while dealing with anomalies in any real-time data, namely, the high dimensionality and the real-time detection of anomalies. In [24], the authors tried to address the ‘curse of dimensionality issue effectively and used a one-class support vector machine for the effective detection of anomalies from high-dimensional data. In [25], the authors introduced a survey on contemporary anomaly detection paradigms. Kaya et al. [26] analyzed different methodologies for communication pattern recognition. Considering the fact that the sparsity of data in high-dimensional spaces leads to the failure of the effectiveness of any anomaly detection method in [27], the authors suggested an efficient scheme for detecting high-dimensional anomalies. In [28] the authors addressed the high dimensionality and proposed an unsupervised method for anomaly detection in such data. In [32], the authors presented a hybrid approach consisting of a semi-supervised approach for anomaly detection in high-dimensional data. In [33], the authors proposed a mixed approach consisting of rough set theory and a density-based clustering algorithm for anomaly detection in high-dimensional data. In [34], the authors addressed the issue of the temporality of anomalies and proposed a clustering-based system for real-time anomaly detection in streaming data. Most of the aforesaid methods tried to address high dimensionality efficiently but the periodicity of clusters or anomalies was not discussed.

Rough set theory as a tool to deal with the ambiguity and uncertainty occurring in any real system was proposed by Pawlak [35]. In [36], the authors applied the rough set theory to produce nano topology. In [37], the authors applied the notion of nano topology for medical diagnosis. The same notion can be used for attribute reduction in high-dimensional data [33]. Halstead et al. [44], proposed a method using diverse meta-features for identifying recurring concepts of drift in data streams. In [45], the authors put forward a two-layered classification model for the online anomaly detection of highly unreliable data. In [46], the authors presented a scheme for the online detection of anomalies in data streams. In [47], the authors proposed to evaluate cyber risk for operation technology systems. In [48], the authors discussed insider threat, which creates significant issues for the cyber security of industrial control systems. Zhao et al. [49] presented an online anomaly detection model based on a random forest method. Izakian et al. [50] proposed to introduce fuzzy in anomaly detection by proposing a fuzzy c-means-based technique. Souza et al. [53] presented a fuzzy neural network-based approach for detecting anomalies in massive cyberattacks. In [54], the authors presented an effective clustering-based real-time anomaly detection system. Mahanta et al. [55] proposed a calendar-based periodic pattern from supermarket datasets. In [56], the authors used an interval operation called interval superimposition to find the solution of a fuzzy linear equation. In [58], the authors proposed a lemma called the Glivenko–Cantelli lemma. Using the lemma on superimposed intervals [56], fuzzy intervals [57,59] can be generated. In [60], the authors proposed a dominance relation on conditional attributes to generate set-valued ordered information systems which can be used for attribute reduction in the dataset. In most of the anomaly detection cases discussed above, the methods tried to propose effective ways to deal with either high-dimensionality or real-time issues. However, a few were able to deal with both effectively. Also, no algorithms have addressed the periodicity of clusters or anomalies in the datasets. However, the periodicity of the clusters or anomalies can be very useful in designing early warning systems. In this article, we propose to address all the aforesaid issues effectively and present a suitable solution for them.

3. Problem Definitions

In below, we present some important terms and definitions used in this paper.

Definition 1. 

Let U be a non-empty finite set of objects, A, a finite set of attributes, and V = ∪ V_a, where V_a is the domain of the attribute a ∈ A, then quadruple S = (U, A, V, f) defines a set-valued information system [60]. A function f:U × A→V is defined as 1 ≤ f(x, a) ∈ V_a, ∀ x ∈ U, a ∈ A. Also, we take the attribute set A = {C∪{d}; C∩{d} = ϕ; C, the set of conditional and {d} the decision attributes}.

Definition 2. 

If the domain of a conditional attribute in C can be arranged in ascending or descending order of preference, then such attribute is called as criterion [36]. If every conditional attribute of C is a criterion, then the information system is known as the set-valued ordered information system [60].

Definition 3. 

The attribute is an inclusion criterion if the values of some objects in U under a conditional attribute of C can be sorted according to inclusion increasing or decreasing preferences [60].

Definition 4. 

Let us define a relation ${\mathit{R}}_{\mathit{A}}^{\ge }$  on a set-valued ordered information system [60] with inclusion increasing preference as, [see e.g., [46]]

$$R_A^{\ge }=\left\{\left(y,x\right)\in U\times U:f\left(y,a\right)\ge f\left(x,a\right)\forall a\in A\right\}$$

(1)

then     $R_A^{\ge }$  is said to be the dominance relation on U. When    ${(y,x)\in R}_A^{\ge }$  then    $y{\ge }_{A}x$  , that means y is at least as good as x with reference to A.

Property 1. 

The inclusion dominance relation  ${\mathit{R}}_{\mathit{A}}^{\ge }$  [60] is (i) reflexive, (ii) unsymmetric, and (iii) transitive.

Definition 5. 

For x ∈ U, the dominance class [36,37] of x is defined as

$$[{x]}_A^{\ge }=\{yϵU:\left(y,x\right)ϵR_A^{\ge }\}=\{yϵU:f\left(y,a\right)\ge f\left(x,a\right),\forall aϵU\}$$

(2)

where  $U_A^{\ge }=\{{\left[x\right]}_A^{\ge }:xϵU\}$  is the family of dominance classes.

Remark 1. 

   ${\mathit{U}}_{\mathit{A}}^{\ge }$  is not a partition of U, rather it creates a covering of U, that is U = ∪ $[{\mathit{x}]}_{\mathit{A}}^{\ge }$ .

Definition 6. 

For any set-valued ordered information system S = {U, A, V, f} and for a given X ⊆ U, the upper approximation, lower approximation and boundary regions of X are respectively expressed as [36,37]

$${\mathit{U}}_{\mathit{A}}^{\ge }\left(\mathit{X}\right)=\left\{\mathit{x}\mathit{ϵ}\mathit{U}:{\left[\mathit{x}\right]}_{\mathit{A}}^{\ge }\cap \mathit{X}\ne \mathit{\varphi }\right\}$$

(3)

$${\mathit{L}}_{\mathit{A}}^{\ge }\left(\mathit{X}\right)=\{\mathit{x}\mathit{ϵ}\mathit{U}:[{\mathit{x}]}_{\mathit{A}}^{\ge }\subseteq \mathit{X}\}$$

(4)

$${\mathit{B}}_{\mathit{A}}^{\ge }\left(\mathit{X}\right)={\mathit{U}}_{\mathit{A}}^{\ge }\left(\mathit{X}\right)-{\mathit{L}}_{\mathit{A}}^{\ge }\left(\mathit{X}\right)$$

(5)

Definition 7. 

For a set-valued ordered information system, S = {U, A, V, f}, B (⊆ A) is termed as criterion reduction of S if ${\mathit{R}}_{\mathit{A}}^{\ge }={\mathit{R}}_{\mathit{B}}^{\ge }$  and ${\mathit{R}}_{\mathit{M}}^{\ge }\ne {\mathit{R}}_{\mathit{A}}^{\ge }$  for any M ⊆ A. On the other way, a minimal attribute set B is a criterion reduction of S if ${\mathit{R}}_{\mathit{A}}^{\ge }={\mathit{R}}_{\mathit{B}}^{\ge }$  [36,37].

Definition 8. 

A CORE is a minimal subset of attributes such that none of its elements can be removed without violating the nano topology generated by the lower and upper approximations. The CORE(A) is given by CORE(A) =    $\{\mathit{a}\mathit{ϵ}\mathit{A}:{\mathit{R}}_{\mathit{A}}^{\ge }\ne {\mathit{R}}_{\mathit{A}-\left\{\mathit{a}\right\}}^{\ge }\}$  [see e.g., [36,37]].

Definition 9. 

Let    ${\mathit{R}}_{\mathit{C}}^{\ge }$  be a dominance relation on U, then    ${\mathit{\tau }}_{\mathit{C}}^{\ge }\left(\mathit{X}\right)=\{\mathit{U},\mathit{\varphi },{\mathit{U}}_{\mathit{C}}^{\ge }\left(\mathit{X}\right),{\mathit{L}}_{\mathit{C}}^{\ge }\left(\mathit{X}\right),{\mathit{B}}_{\mathit{C}}^{\ge }\left(\mathit{X}\right)\}$  forms a nano topology [36,37] on U with respect to X. As well,    ${\mathit{\beta }}_{\mathit{C}}^{\ge }\left(\mathit{X}\right)=\{\mathit{U},{\mathit{U}}_{\mathit{C}}^{\ge }\left(\mathit{X}\right),{\mathit{L}}_{\mathit{C}}^{\ge }\left(\mathit{X}\right)\}$  is the basis for    ${\mathit{\tau }}_{\mathit{C}}^{\ge }\left(\mathit{X}\right)$. Furthermore, CORE(C) =    $\{\mathit{a}\mathit{ϵ}\mathit{C}:{\mathit{\beta }}_{\mathit{C}}^{\ge }\ne {\mathit{\beta }}_{\mathit{C}-\left\{\mathit{a}\right\}}^{\ge }\}$  =    $\cap$  red(C) where red(C) denotes the criterion reduction.

Definition 10. 

Consider an information system S = (U, A, V, f) consisting of m entities or objects a₁, a₂, ..., a_m. Let the attribute set A have n members. Then, S is expressed as an m×n matrix with rows as objects and columns as attributes. Attributes can be designated as dimensions and each a_i = (a_i1, a_i2, …, a_in); i = 1, 2, …, m will be a point in n-dimensional space S.

Definition 11. 

Let us consider a_i = (a_i1, a_i2, …, a_in), being the points in n-dimensional space, then the distance d(a_i, C_j) between a_i; i = 1, 2, ..., n and cluster C_j; j = 1, 2, …, k is defined as follows.

$$d(a_i,C_j)=\frac{{}^{{\left|\left|a_i-c_j\right|\right|}^2}}{{\displaystyle \sum _{t=1}^k{\left|\left|a_i-c_t\right|\right|}^2}}\hspace{0.17em}\hspace{0.17em}$$

(6)

where c_j is the C_j,’s centroid and d(a_i,C_j) ∈ [0, 1].

Definition 12. 

Support and core of a fuzzy set. The support of a fuzzy set A in X is the crisp set containing every element of X with membership grades greater than zero in A and is denoted by S(A) = {x ∈ X; μ_A(x) > 0}, whereas the core of A in X is the crisp set containing every element of X with membership grades equal to 1 in A [see e.g., [59]]. Obviously, core [t₁, t₂] = [t₁, t₂], since a closed interval [t₁, t₂] is an equi-fuzzy interval with membership 1 [see e.g., [56,57,58,59]].

Definition 13. 

Set Superimposition. Set superimposition (S), an operation, was proposed in [56] as follows;

A₁ (S) A₂ = (A₁ − A₂)^(1/2) (+) (A₁∩ A₂)⁽¹⁾ (+)(A₂ − A₁)^(1/2)

(7)

where (A₁ − A₂)^(1/2) and (A₂ − A₁)^(1/2) are fuzzy sets [57,59] with constant membership value (1/2), and (+) signifies a union of disjoint sets. To elaborate it, let A₁ = [s₁, t₁] and A₂ = [s₂, t₂] are two real intervals such that when A₁ ∩ A₂ ≠ ϕ, we will obtain a superimposed part. When two intervals are superimposed, each interval contributes half of its value to the superimposed interval, so from Equation (7) we obtain:

[s₁, t₁](S)[s₂, t₂] = [s₍₁₎,t₍₂₎]^(1/2) (+) [s₍₂₎,t₍₁₎]⁽¹⁾ (+) (s₍₁₎,t₍₂₎]^(1/2)

(8)

where s₍₁₎ = min(s₁, s₂), s₍₂₎ = max(s₁, s₂), t₍₁₎ = min(t₁, t₂), and t₍₂₎ = max(t₁, t₂). The superimposition process is presented using Figure 1, Figure 2 and Figure 3 below.

Similarly, three intervals [s₁, t₁], [s₂, t₂], and [s₃, t₃], (with non-empty intersection) are superimposed to obtain the following expression.

[s₁, t₁](S)[s₂, t₂](S)[s₃,t₃] = [s₍₁₎,s₍₂₎]^(1/3) (+)[s₍₂₎,s₍₃₎]^(2/3) (+) [s₍₃₎,t₍₁₎]⁽¹⁾ (+) [t₍₁₎,t₍₂₎]^(2/3) (+)[t₍₂₎,t₍₃₎]^(1/3)

(9)

where the sequence {s_(i); i = 1, 2, 3} is arranged from {s_i; i = 1, 2, 3} in an increasing order of magnitude and {t_(i); i = 1, 2, 3} is also arranged from {t_i; i = 1, 2, 3} in the similar fashion. Let [s_i, t_i], i = 1,2,…,n, be n real intervals with    ${\displaystyle \underset{i=1}{\overset{n}{\cap }}\left[s_i,t_i\right]}$ ≠ ϕ. Using generalization (9) gives as follows.

[s₁, t₁](S) [s₂, t₂](S) ... (S)[s_n, t_n] = [s₍₁₎, s₍₂₎]^(1/n) (+) [s₍₂₎, s₍₃₎]^(2/n) (+) ... (+) [s_(r), s_(r+1)]^(r/n) (+) ... (+) [s_(n),t₍₁₎]⁽¹⁾(+)[t_(1),t₍₂₎]^((n−1)/n)(+)...(+)[t_(n-r),t_(n-r+1)]^(r/n)(+)...(+)[t_(n-2),t_(n-1)]^(2/n)(+)[t_(n-1),t_(n)]^(1/n)

(10)

In (10), the sequence {s_(i)} is organized from {s_i} in increasing order of magnitude for i = 1,2, …, n and similarly {t_(i)} is also organized from {t_i} in increasing order of magnitude [57]. It is to be noted here that the membership functions are a mixture of an empirical probability distribution function and a complementary probability distribution function given, as follows:

$${\gamma }_1(x)=\left\{\begin{array}{cc}\hfill 0,& \hfill x<s\left(1\right)\\ \frac{r-1}{m},& s\left(r-1\right)<x<s\left(r\right)\\ \hfill 1,& x>s\left(m\right)\hfill \end{array}\right.$$

(11)

And

$${\gamma }_2(x)=\left\{\begin{array}{cc}1,& \hfill x<t\left(1\right)\\ 1-\frac{r-1}{n},& t\left(r-1\right)<x<t\left(r\right)\\ 0,& x>t\left(n\right)\hfill \end{array}\right.$$

(12)

The membership function of the fuzzy interval [57,59]will be provided for us by Equations (11) and (12), which together use the Glivenko-Cantelli Lemma of order statistics [58].

Definition 14. 

Match ratio. If n be the number of periods in the lifespan of a dataset (no. of years/months/days etc.) and m be the number of time-intervals in the list of lifespans of any cluster, then m/n is called the match ratio of the cluster. Obviously, 0 ≤ m/n ≤ 1.

Definition 15. 

Fully/Partially periodic cluster. A cluster with a superimposed time interval is said to be full periodic if its match ratio is equal to 1. Otherwise, it is partially periodic.

Definition 16. 

Fuzzy periodic cluster. Since using the Glivenko–Calntelli lemma of order-statistics [58] on superimposed time intervals, fuzzy time intervals [57,59] can be found, the cluster associated with the superimposed time-intervals is known as a fuzzy periodic cluster.

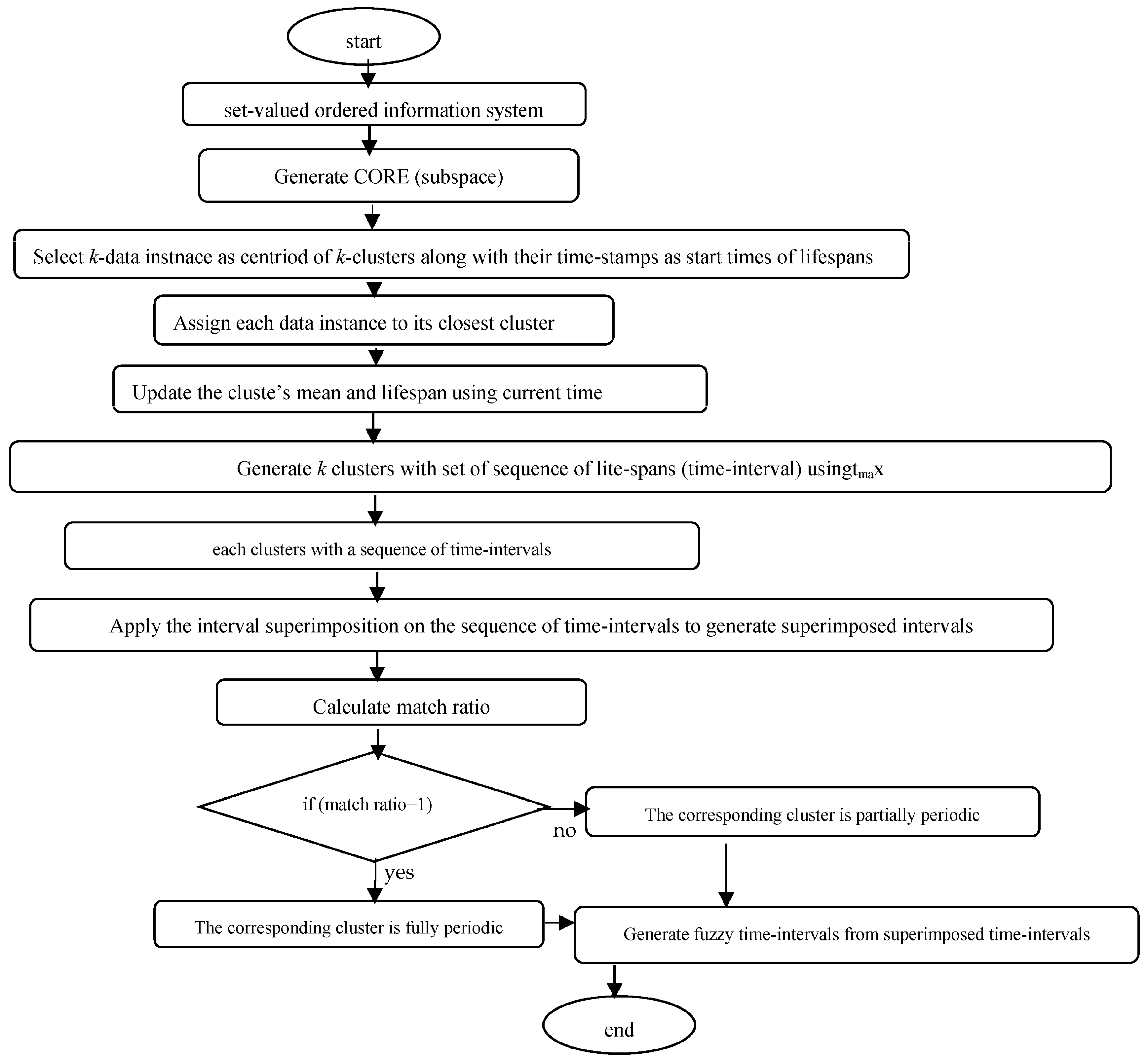
4. Proposed Algorithm

For detecting anomalies, a partitioning subspace clustering approach is employed. The method first uses a rough set theoretic approach for attribute or dimension reduction and then uses a dynamic k-means clustering approach for finding clusters along with their lifespans. Each cluster will have a sequence of time intervals representing its lifespan. Then, an interval superimposition-based approach is employed to find the periodic clusters along with the noises. The proposed method is described as follows. Here the dataset S = (U, A) is an information system consisting of both conditional attributes and decision attributes. First of all, the data pre-processing techniques are employed to convert the information system into a set-valued ordered information system. Then, a dominance relation is generated on the ordered information system. With reference to the dominance relation, a nano topology and its basis is generated. Then the criterion reduction process is used to generate CORE(A) as a subset of attribute set A and the new information system E = (U, CORE(A)) on U is formed, which is a lower dimensional space. The pseudocode of the Algorithm 1 for the criterion reduction is given below.

Algorithm 1: Subspace Generation

Input: (U, A): the information system, where the attribute set A is divided into C-conditional attributes and D-decision attributes, consisting of n objects, Output: Subspace of (U, A)  Step 1. Generate a dominance relation    $R_C^{\ge }$  on U corresponding to C and X ⊆ U.  Step 2. Generate the nano topology    ${\tau }_C^{\ge }\left(X\right)$  and its basis    ${\beta }_C^{\ge }\left(X\right)$   Step 3. for each x ∈ $C, \mathrm{find} {\tau }_{C-\left\{x\right\}}^{\ge }\left(X\right)$  and  ${\beta }_{C-\left\{x\right\}}^{\ge }\left(X\right)$   Step 4. if ( ${\beta }_C^{\ge }\left(X\right)={\beta }_{C-\left\{x\right\}}^{\ge }\left(X\right)$ )  Step 5.  then drop x from C,  Step 6. else form criterion reduction  Step 7.  end for  Step 8. generate CORE(C) = ∩ {criterion reductions}  Step 9. Generate subspace of the given information system.

The above algorithm supplies the CORE of the attribute set by removing insignificant attributes which gives us a subspace E = (U, CORE(A)) of the given information system S = (U, A). Then a dynamic k-means is applied to E. The following is an explanation of the algorithm: First of all, it randomly picks first k–data instances from the CORE(A) as k-clusters-centroids with associated timestamps (times of generation) as the start-time of their lifespans. For each cluster, a last-time and a list are maintained to keep the last timestamp and lifespan of each cluster, respectively. Initially start-time = last-time. If a data instance is added to a cluster based on how far away from the cluster centroid it is, its current time-stamp (current-time) is added to the lifespan to obtain an updated life span, provided that the time gap between the cluster’s last-time and the data instance current-time is within a predetermined range, such as t_max. Otherwise, a new life-span will start by setting the current-time as a start-time and the previous life-span of the cluster will be closed with last-time as the end of the life-span. The lifespan of the cluster will be put on the list maintained for it if its length is greater than a specified length (say t_min). The lifespans of the earlier and later clusters are updated if a data instance switches from one cluster to another during the execution process. For instance, if the time stamp on the outgoing data instance is either the start-time or end-time of the preceding cluster, the lifespan of the prior cluster is updated by using the next or previous cluster time-stamps respectively. Updates are made to the cluster-centroids as well. Again, the lifespans of the former and later clusters will not change if the time stamp of the outgoing data instance falls within those lifespans, but the cluster centroids will be modified. Similar to this, if the time stamp of a data instance migrating from one cluster to another falls outside the later cluster’s lifespan, the cluster-centroid is updated and the later cluster’s life-span is updated as well, provided that the time gap between the two clusters is within a certain limit (t_max). The pseudocode of the algorithm is given below.

Here each output cluster in the final output cluster set has a sequence of time intervals describing its lifespan. It should be noted that only clusters with lifespans of at least t_min are provided by Algorithm 2.

Algorithm 2: Dynamic k-means clustering algorithm

Input: E: Information system consisting n objects and attribute set CORE(A) ⊆ A, tmax: the maximum time-gap of consecutive time-stamp, tmin: the minimum length of lifespan. Output: Set of clusters where each cluster is associated with a sequence of time intervals as its lifespans  Step 1. Given d1-dimensional dataset CORE(A)  Step 2. Select C[i] = {x[i], tp[i]}; i = 1, 2, …, k, where x[i] be the data instances or means of clusters, tp[i] points to list of time-intervals each maintained for every cluster contains time-stamps (start-time) of x[i] and start-time = last-time initially  Step 3. for each incoming data instance x with current time-stamp current-time  Step 3.  {if d(x, Cj) ≤ d(x, Ci), i ≠ j; i = 1, 2, …, k  Step 4.   {Add x to Cj  Step 5.   Update mean(Cj)  Step 6.   if (|current-time − last-time[j]|≤ tmax)  Step 7.   {if(last-time[j] ≤ current-time)  Step 8.   extend lifespan(Cj) by setting last-time[j] = current-time  Step 9. else go to Step3  Step 10. }  Step 11. else if|last-time[j] − start-time|≥ tmin  Step 12.  {Add [start-time[j], last-time[j]] to tp[j]  Step 13. set last-time[j] = start-time[j] = current-time  Step 14.  }  Step 15. }  Step 16. }  Step 17. if (assign does not occur) go to step19  Step 18. else go to Step3  Step 19. Output cluster set

For each cluster with a sufficient number of time intervals as its lifespans, the following procedure is applied to find periodic clusters from the interval list. The interval superimposition operation is to keep the information about the periods (time interval associated with a cluster). The interval superimposition is used only if the intervals have overlapping or non-empty intersections. Throughout Algorithm 3 execution, a list of superimposed time intervals is maintained. The total number of time intervals of any clusters is taken as n (number of Years/Months etc.). To determine whether a new crisp time-interval can be superimposed on an already superimposed time-interval or not. it is checked whether the interval has a non-empty intersection with the core of the superimposed time interval or not (the definition of core is given in Section 3). If it has, then the superimposition process is computed to get a new superimposed time interval and membership values are reconstructed accordingly. The list of superimposed time intervals is initially empty. A full pass through the time interval list of a cluster is conducted during Algorithm 3 execution. When it switches to a new time interval, it determines if it can be superimposed on any of the previously obtained superimposed intervals. If so, the superimposition process is performed, which updates the relevant superimposed time interval. This time interval is added as a new entry to the list if it is not superimposed with any of the previously acquired superimposed time intervals (kept as a list). Finally, each superimposed time interval is examined to determine the number of time intervals superimposed in one place and kept using a counter (m). At the beginning of the superimposition process of a time interval, the value of m is taken as 1. If a time interval is superimposed on the time interval, then m is updated by adding 1 to it. After the execution, the match ratio for a cluster is obtained with the help of m and n. If the match ratio is found to be 1, the corresponding cluster is fully periodic, else partially periodic. Each superimposed time interval produces a fuzzy time interval. This way, the fuzzy periodic clusters can be obtained. The pseudocode for the process is given below.

Algorithm 3: Algorithm for finding periodic (fully/partially) and fuzzy periodic clusters

Input: Set of clusters along with their lifespans (set of sequence of time intervals). Output: Set of fuzzy periodic clusters  Step 1. For each cluster c with list of linespans L.  Step 2. initially Lc=null//Lc is the list of superimposed intervals  Step 3. lt = L.get() //lt points to the 1st time interval (lifespan) in L  Step 4. Lc = append(lt)  Step 5. m = 1 //m = number of intervals superimposed  Step 6. while((lt=L.get())!=null)  Step 7.   {flag = 0  Step 8.    while ((lct =L.get())!=null)  Step 9.    if (compsuperimp(lt, lct)  Step 10.   flag =1  Step 11. if (flag == 0)  Step 12. Lc.append(lt) }  Step 13. }  Step 14.  }  Step 15. compsupeimp(lt, lct)  Step 16.  if(|intersect(lct, lt)!=null)|  Step 17. { superimp(lct, lt)  Step 18. m++  Step 19. return 1  Step 20. }  Step 21. return 0  Step 22. Compute match ratio = m/n  //n = number periods in the whole dataset.  Step 23. if (match = 1)  Step 24. the cluster c is fully periodic  Step 25. else partially periodic  Step 26. generate fuzzy time intervals from superimposed time intervals to get fuzzy periodic clusters.  Step 27. End

The function compsuperimp(lt, lct) initially finds the intersection between lt and the core of lct. If it is found to be non-empty, the function computes the superimposition process by reconstructing the membership values. If lt has been superimposed on lct it returns 1, otherwise it returns 0. get () and append () are functions operating on time interval lists to obtain a pointer to the next time interval in a list and to append a time interval, into a list, respectively. For each cluster, a counter (m) is also kept in order to keep track of how many time intervals are superimposed in one place. The match ratio is computed with the help of m. If the match ratio is found to be 1, the corresponding cluster is fully periodic, else partially periodic. Finally, the fuzzy intervals can be generated with the help of superimposed intervals to get fuzzy periodic patterns. The flowchart for the proposed method is described in Figure 4 below.

Anomalies are data instances or groups of data instances that either belong to sparse clusters or don’t fit the defined lifespans. As a result, a data instance may be anomalous depending on both its generation time and its distance from clusters.

5. Complexity Analysis

For generating dominance classes and corresponding classes, the algorithm needs to compare the values of all the possible pairs of objects from U in all dimensions, there can be at most |U| × |U| × |C| number of comparisons. So, the computational complexity for step1 is O(n².d), where |U| = n, and |C| = d. For generating the nano topology, the lower approximation and approximation of the set has to be generated, which takes computational time O(|X|.|U|). So the total computational cost of step1 and step2 is O(n².d+|X|.|U|)= O(n².d) which is the worst-case complexity. From step3 for loop starts it runs over at most all the attributes of the attribute set. The computation from step 4 to step7 takes constant time, say O(k₁), where k₁ = constant. Therefore, the computational cost from step3 to step8 is O(k₁d). Similarly, that of step9 and 10 is also constant, say O(k₂), where k₂ = constant. The overall complexity of algorithm1 is O(n².d + k₁d+ k₂) = O(n².d). For finding the complexity of Algorithm2, the following steps are taken. Let k(≤ n) be the number of clusters. The computational cost of a centroid is O(n + n.k.d₁) = O(n.k.d₁), where d₁ (≤d), is the dimension of the CORE. Also, O(2n.k) = O(n.k) is the time required compute the minimum distance and time-gap for each cluster. The cost of updating cluster-mean and lifespan is O(2k). The total cost of algorithm2 is O(i(n.k.d₁ + n.k + k)) = O(i.n.k.d₁) = O(n³) as i(≤ n), the number of iterations, k ≤ n, and d₁ is considerably small. The worst-case complexity of the whole method is O(n².d + n³). For finding the time-complexity of Algorithm 3, we proceed as follows. Let n₁ be the size of the sequence of time intervals associated with a cluster and n₂ be the average number of time intervals superimposed. For each time interval of a cluster, it is required to make a pass through the list of superimposed time intervals to check whether the corresponding time interval can be superimposed on any of the available superimposed time intervals or not. For this, the intersection of the current time-interval with the core of the superimposed time interval is computed, which requires O(1) time. If the current time interval is superimposed, then its boundaries have to be inserted into two sorted arrays used to keep the end points of the superimposed time-intervals (one sorted array for left end points and other for right end points). Now, searching in a sorted array requires O(log n₁) time and insertion needs O(n₁) time. The two end points require O(2(log n₁ + n₁)) = O(n₁) time. For one cluster, the process requires O(n₁.p.n₂) time, where p is the size of the list of superimposed time intervals. On the other hand, p = O(n₁), and n₂ = O(n₁); the overall time-complexity in the worst-case is O(n₁³). For k clusters, the total time-complexity in worst-case is O(k.n₁³). Therefore, the worst-case complexity of the whole method is O((n².d + n³) + k.n₁³). Also k = O(n), which gives the time-complexity, as O(n².d + n³ + n.n₁³) = O(n³ + n.n₁³), as d ≤ n, which is the time-complexity of the method in worst-case. Since the time-complexity of the method depends on n and n_1, and not on d (dimension), the worst-case complexity of the method can be rewritten as O(n³). Thus, the method runs in cubic time.

6. Experimental Analysis and Results

In this Section the experimental studies are conducted and comparative analysis of the proposed method is performed against ten different clustering-based anomaly detection algorithms [see e.g., Table 3], namely k-means [19], IF (Isolation Forest) [61,62], SC (Spectral Clustering) [54], HDBSCAN (hierarchical density-based spatial clustering of applications with noise) [63], ACA (Agglomerative Clustering Algorithm) [54], LOF (Local Outlier Factor) [54], SSWLOFCC (streaming sliding window local outlier factor coreset clustering algorithm) [54], PCM (Partitioning Clustering with Merging) [10], OnCAD (Online Clustering and Anomaly Detection) [46], and MCA (Mixed Clustering Algorithm) [9]. The dataset employed for the experiment is Kitsune Network Attack dataset [64] and KDDCUP’99 dataset [64], collected through the UCI machine repository. The Kitsune Network attack dataset [65] is a multi-variate, sequential, time-series dataset with real and temporal attributes. It has 27,170,754 data instances and its number of attributes is 115. It is a collection of nine network attack datasets each containing network packets and various cyberattacks, collected from an IoT-based network system or commercial IP-based surveillance system. The dataset, KDDCUP’99 [64] is a multi-variate dataset with numeric, categorical and temporal attributes. It has 4,898,431 data instances with 37 numeric, 3 categorical and 1 temporal (time-stamp) attributes.

The proposed method (RADSPCA) is first implemented with the KDDCUP’99 [64] dataset, using MATLAB. The implementation process consists of three stages: the input data pre-processing, periodic subspace clustering, and testing. First of all, the method accepts the input data and converts it to a set-valued matrix. The matrix representation of the dataset is the information system. Since the rough set can’t deal with continuous attributes, so they are discretized at the same time. The Algorithm 1 is then applied to find the subset of the attribute set by removing the insignificant attributes and by using the concept of dominance relation, nano topology and its basis. The algorithm1 gives the subset as CORE of the attribute set. Then Algorithm 2 is applied on the CORE to find clusters along with the set of sequence time-intervals where each cluster is associated with a sequence of time intervals describing its lifespan. For the efficient implementation, two parameters, namely t_min (minimum length of a lifespan = 180 min) and t_max (maximum time-gap between two consecutive time-stamps associated with a cluster = 20 min) are to be specified. Then the Algorithm 3 is applied to the clusters to generate periodic, partially periodic, and fuzzy periodic clusters. The performances of the proposed method along with the afore-mentioned methods are recorded. The performance is measured using the following evaluation metrics.

$$\mathrm{Recall}=\frac{True Positive}{True Positive+False Negative}$$

$$\mathrm{Precision}=\frac{True Positive}{True Positive+False Positive}$$

$$\mathrm{F}1-\mathrm{score}=\frac{2\ast (Precision\ast Recall)}{Precision+Recall}$$

The details of the outcomes of the investigations are presented in tabular form in

Table 1. Comparative performances analysis of RADSPCA with some well-known existing methods using KDDCUP’99 [64] dataset.

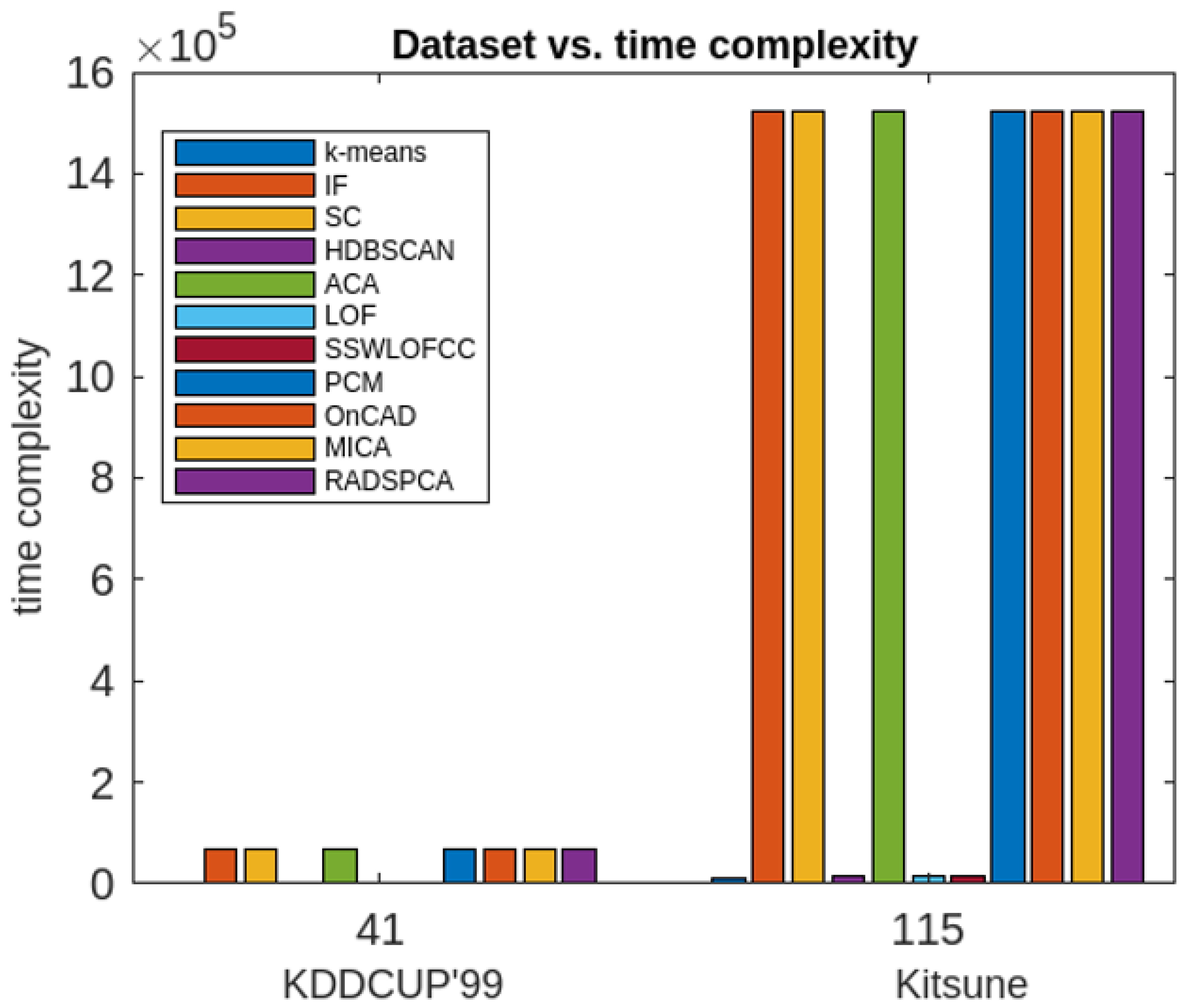
Algorithms		Evaluation Metrics			Execution Time (in Seconds)	Periodic Clusters Obtained
		Recall	Precision	F1-Score
1	k-means	0.9605	0.9400	0.9500	28	×
2	IF model	0.8301	0.850	0.8400	19	×
3	SC	0.6220	0.6004	0.6110	44	×
4	HDBSCAN	0.2530	0.2300	0.2410	95	×
5	ACA	0.8400	0.8010	0.8200	16	×
6	LOF	0.9550	0.9390	0.9470	14	×
7	SSWLOFCC	0.9665	0.9460	0.9560	12	×
8	PCM	0.8800	0.8420	0.8600	26	×
9	OnCAD	0.9751	0.9650	0.9700	30	×
10	MICA	0.9822	0.9780	0.9800	28	×
11	Proposed Approach (RADSPCA)	0.9812	0.9790	0.9800	58	√

below.

Similarly, the proposed method (RADSPCA) is also implemented with the Kitsune Network attack dataset [64] and the results were recorded in tabular form in

Table 2. Comparative performances analysis of RADSPCA with some well-known existing methods using Kitsune [65] dataset.

Algorithms		Evaluation Metrics			Execution Time (in Seconds)	Periodic Clusters Obtained
		Recall	Precision	F1-Score
1	k-means	0.8701	0.8501	0.8600	95	×
2	IF model	0.7300	0.7502	0.7400	64.5	×
3	SC	0.6645	0.6420	0.6530	149.5	×
4	HDBSCAN	0.3899	0.3793	0.3850	150	×
5	ACA	0.7410	0.7010	0.7200	54.4	×
6	LOF	0.90401	0.9000	0.9020	47.6	×
7	SSWLOFCC	0.9280	0.9499	0.9390	40	×
8	PCM	0.7430	0.7810	0.7600	88	×
9	OnCAD	0.8450	0.8353	0.8400	102	×
10	MICA	0.9832	0.9770	0.9800	68	×
11	Proposed Approach (RADSPCA)	0.9860	0.9801	0.9830	88.5	√

below.

The following observations can be drawn from the obtained results.

The k-means algorithm is quite good as per as the values of the evaluation metrics are concerned. However, it is sensitive to both the dataset and the dimensions. It is also sensitive to the distribution of the dataset in the plane. It cannot supply periodic clusters.

The IF model is reasonably good; however, it is efficient up to a certain dimensional dataset, beyond which its efficacy decreases rapidly. It cannot supply periodic clusters.

The SC and HDBSCAN algorithms are poor in both performance and execution times. Though. HDBSCAN works very well with lower-dimensional data, but its performance decreases proportionately with the increase in the dimension of the dataset. Both algorithms are not capable of finding periodic clusters.

The ACA is reasonably good as far as performance and execution time are concerned. However, it is very sensitive to the order of input to the algorithm. It is not useful for determining periodic clusters.

Though the LOF algorithm performs well, it has similar issues as the k-means algorithm.

The SSWLOFCC performs better, and its performance does not depend much on the size of the dataset. However, its execution time increases with the increment of the dimension as well as the size of the dataset. It cannot extract periodic clusters.

The PCM is an algorithm consisting of both k-means and hierarchical agglomerative approaches. However, its performance decreases with the increase in size and dimension of the dataset. It cannot be used for finding periodic clusters.

OnCAD has a problem with dimensionality. Its accuracy and execution time fall rapidly with the increase in data size and dimensions. It cannot find periodic clusters.

The MICA is very good as far as accuracy is concerned. It has recalls of 0.9822 and 0.9832, precisions of 0.978 and 0.977, and F1-scores of 98% and 98% with the KDDCUP’99 [65] and the Kitsune [64] datasets, respectively, which is quite impressive. Its execution time is also quite good. However, it cannot be used for finding periodic clusters.

The proposed algorithm (RADSPCA) is better as far as performance is concerned. It has recall, precision, and F1-score values that are almost the same for both datasets. It has recall 0.9812, 0.9860, precision 0.979, 0.9801, and F1-score 0.98, 0.983, with the datasets KDDCUP’99 [64] and Kitsune [65], respectively. It has the ability to extract periodic clusters, which others do not. Though its execution time is a little longer than that of others, the rate of increase is quite low. The extra is the time spent finding subspace and extracting periodicity. Thus, the execution time of RADSPCA depends mostly on the dataset sizes and the number of periods associated with a cluster in its lifespan.

Moreover, the RADSPCA’s execution time in seconds is compared against that of k-means [19], IF model [61,62], SC Algorithm [54], HDBSCAN algorithm [63], ACA Algorithm [54], LOF algorithm [54], SSWLOFCC algorithm [54], PCM algorithm [10], OnCAD algorithm [46], and MCA Algorithm [9] and the results are presented using a bar diagram in Figure 5.

It has been found from Figure 5 that most of the aforesaid algorithms depend not only on dataset sizes but also on dimensions, and some are inefficient with high-dimensional data. However, RADSPCA is less dependent on the dimension of the dataset and is a bit dependent on the sequence of time intervals associated with every cluster, which is a negligible factor. In fact, Figure 6 and Figure 7 further validate that the RADSPCA’s execution time grows linearly with respect to the increase in dimension if the dataset size is kept constant. Also, RADSPCA runs in cubic time.

7. Conclusions, Limitations and Lines for Future Works

7.1. Conclusions

In this article, a clustering-based method for finding real-time anomalies in a subspace is given. The method first uses a nano-topology-based attribute reduction approach for finding subspace as the core of an attribute set. Then, a dynamic k-means clustering approach is employed to find k-clusters in the subspace. It is to be mentioned here that the clusters obtained by the aforesaid approach will have a k-number of sequences of time intervals, and each cluster will be associated with a sequence of time intervals describing its lifespan. Then, using an interval superimposition method, a superimposed time interval is obtained, and a match ratio for each cluster is also computed. The match ratio determines whether the cluster is fully or partially periodic. Further, from each superimposed time interval, a fuzzy time interval can be computed, and the cluster associated with the fuzzy time interval is termed a fuzzy periodic cluster. At the end, the method supplies fuzzy periodic clusters in the subspace. Since the obtained clusters are periodic in nature, they provide more detailed information about the nature of the data instances. The anomalies would be mostly doubtful instances that either belong to sparse clusters or do not belong to any of the periodic clusters.

The time-complexity of the method is computed and found to be O(n³ + n.n₁³) in the worst-case, where n = the number of instances and n₁ = the maximum number of intervals associated with any cluster. Obviously, n₁ is very small in comparison to n. Therefore, the method runs in cubic time. Further, it has also been found that RADSPCA runs linearly with respect to the dimension of the datasets.

To find efficacy further, ten well-known clustering-based algorithms were taken, and a detailed comparative analysis was conducted against RADSPCA, first using the KDDCUP’99 [64] dataset and then the Kitsune [65] network attack dataset. Experimentally, RADSPCA is found to be more efficient than others in terms of recall, precision, and F1-score in high-dimensional data.

7.2. Limitations and Future Directions of Work

The proposed RADSPCA has some limitations. Firstly, it is unable to deal with continuous data, as a rough set is inefficient to handle continuous data. Secondly, the method uses the k-means algorithm. It has the following issues with finding anomalies: For example, the centroid of any cluster can be pulled by anomalies, or there may be a cluster of anomalies extracted by the method that looks such as a normal cluster. Finally, the method cannot detect anomalies from temporal interval data.

Future works could be possible in the following lines.

Methods other than the k-means approach can be employed for efficient anomaly detection.

An effective method can be proposed to deal with continuous attributes or temporal interval datasets.

Table 3. Acronym table.

Acronym	Full Form and Purpose
IF	Isolation Forest: It is an anomaly detection using binary tree.
SC	Spectral Clustering: It has been used as an outlier detection algorithm many times
HDBSCAN	Hierarchical Density-based Spatial Clustering of Applications with Noise: It is a density–based hierarchical clustering approach that has been used for anomaly detection many times with less efficacies
ACA	Agglomerative Clustering Algorithm: It is a hierarchical clustering approach for anomaly detection.
LOF	Local Outlier Factor: It is an algorithm to identify outliers based on local neighborhood.
SSWLOFCC	Streaming Sliding Window Local Outlier Factor Coreset Clustering Algorithm: It focuses on real-time detection of anomalies using big data technologies.
PCM	Partitioning Clustering with Merging: It is an algorithm for finding anomalies which uses both partitioning and Hierarchical approaches
OnCAD	Online Clustering and Anomaly Detection: It is a clustering-based anomaly detection approach in data streams that considers the temporal as well as spatial proximity of observations to detect the real-time anomaly.
MICA	Mixed Clustering Algorithm: It is an algorithm for finding real-time anomalies using both partitioning and Hierarchical approaches
RADSPSCA	Real-time Anomaly Detection with Subspace Periodic Clustering Approach is the method proposed in this article.

shows acronyms and their full form and purpose.