Gas Turbine Off-Design Performance Adaption Based on Cluster Sampling
Abstract
:1. Introduction
- (1)
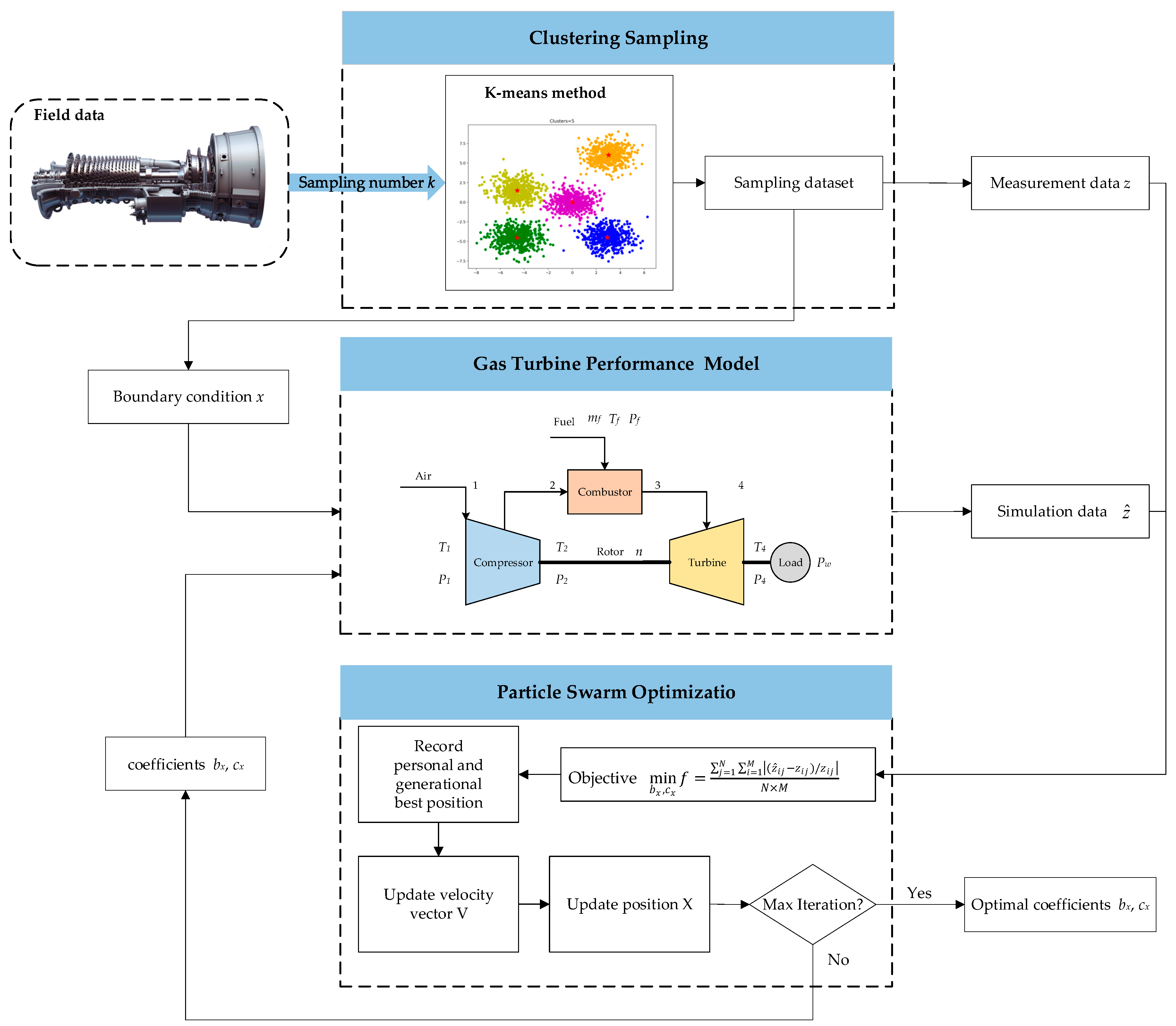
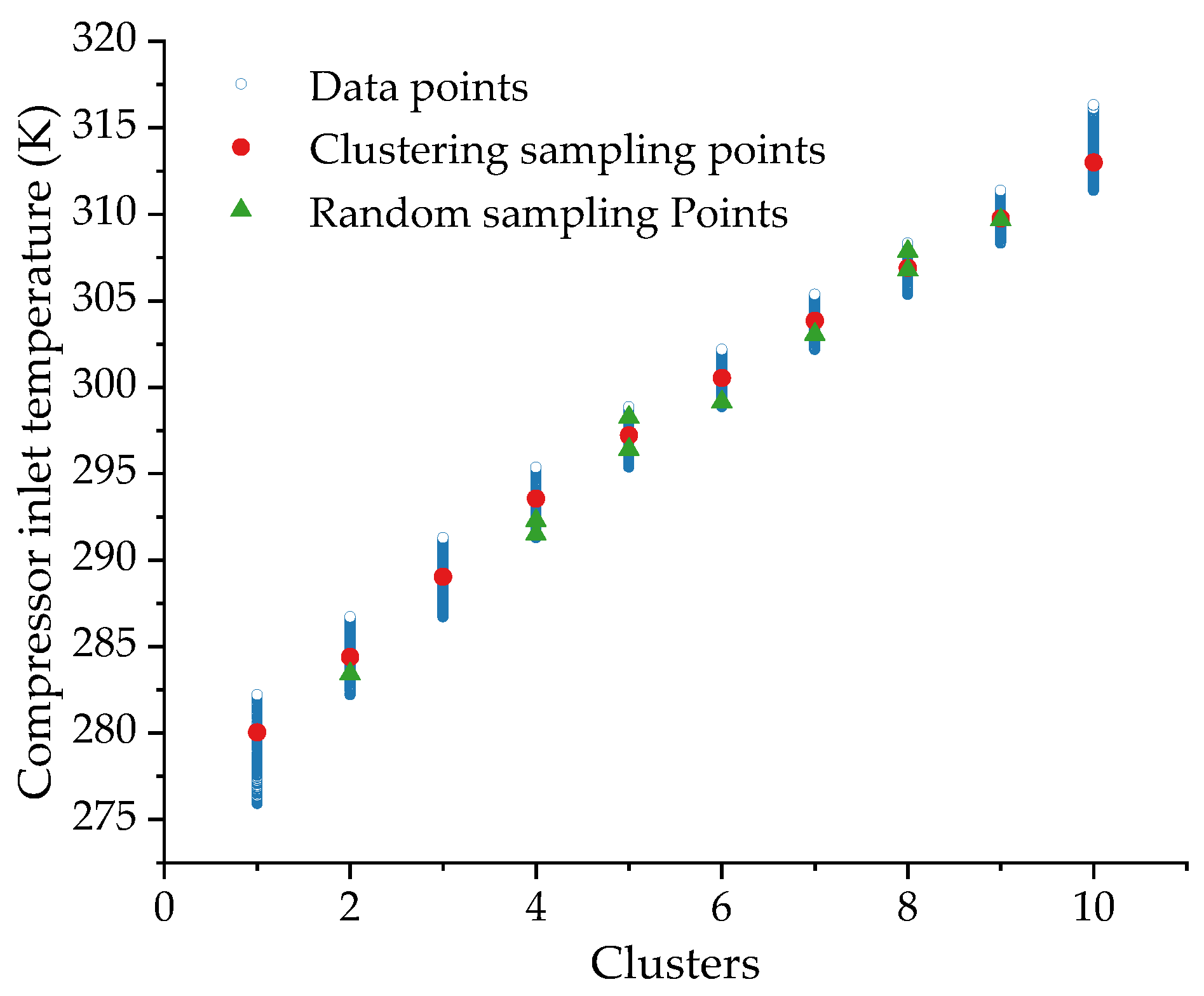
- The proposed cluster sampling method divides all operating points into categories and selects the points closest to the cluster centers. Compared with random sampling, it can enhance the coverage and dispersion (representing the degree of sample difference) of the sampling set and enhance the representativeness of the sampling set.
- (2)
- Compared with the performance model before adaption, the accuracy of the performance model tuned by the particle swarm optimization algorithm (PSO) is increased.
- (3)
- The proposed method was applied on a real E-class gas turbine power station and compared with the performance adaption based on the random sampling method.
- (4)
- Compared with the model based on the random sampling method, the proposed method has a higher accuracy in the entire field dataset, especially the overlooked random sampling conditions.
2. Methodology
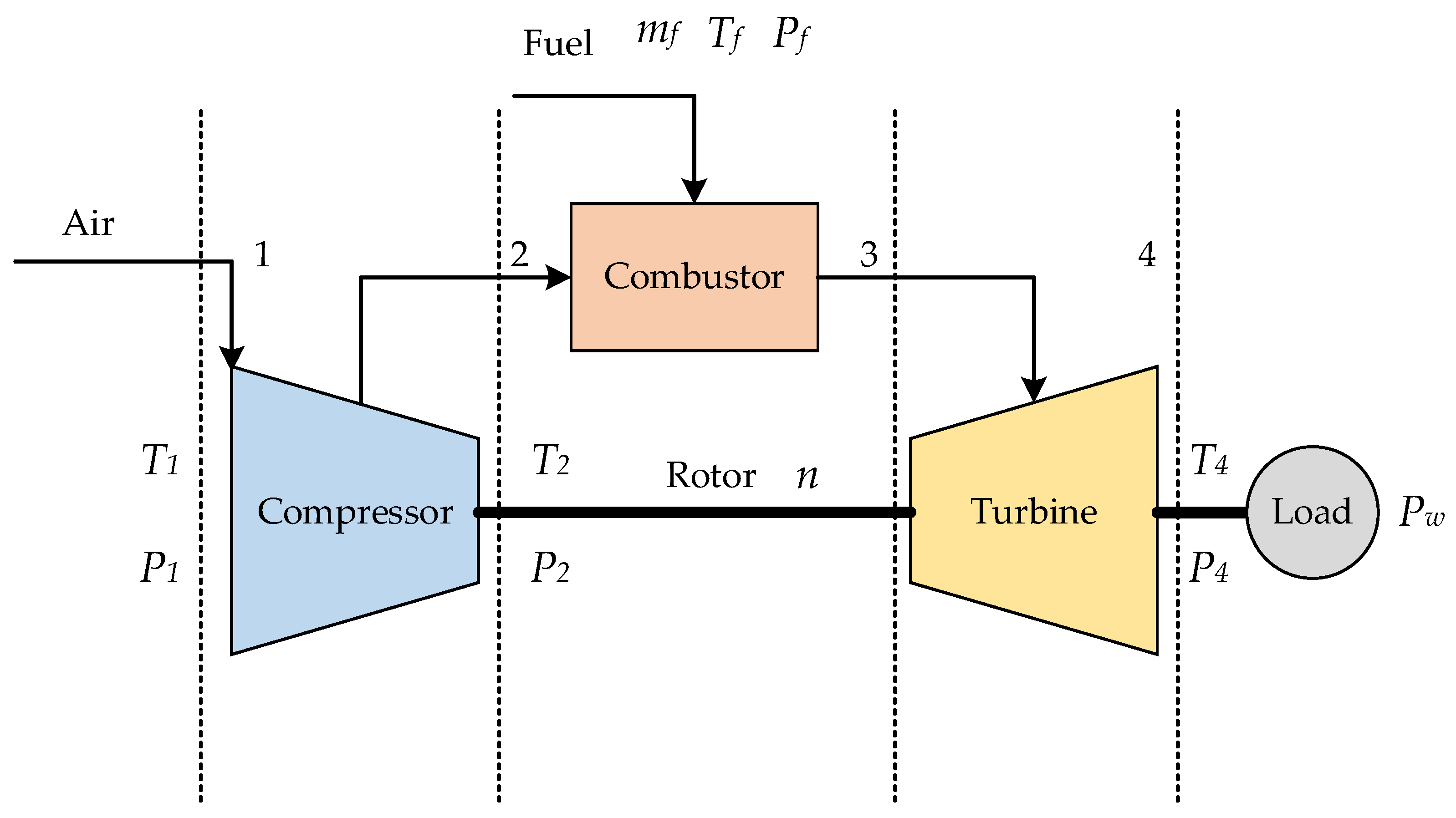
2.1. Performance Model of the Gas Turbine
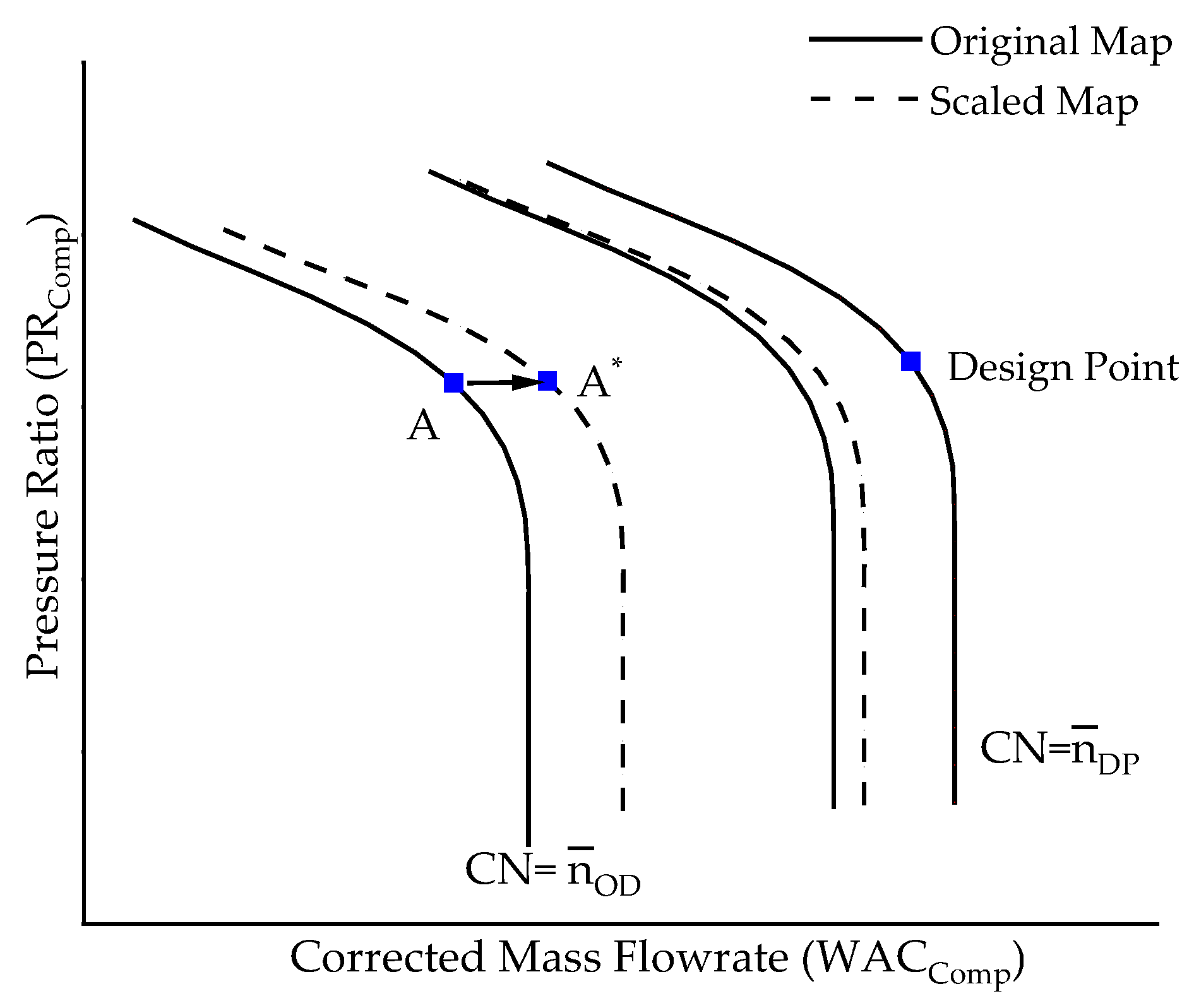
2.2. Performance Adaption
2.3. Data Clustering for Sampling
- Randomly select k points, , ,…, , as initial centroids.
- In the tth iteration step, calculate the distance from each point to the k centroids according to Equation (7), and assign them to the nearest cluster.
- Calculate the mean of the points in each cluster and update the centroids by Equation (8).
- Repeat steps 2 and 3, until the difference between two consecutive centroids is smaller than a predefined threshold or the max iteration step is achieved.
2.4. Particle Swarm Optimization (PSO)
3. Results and Discussion
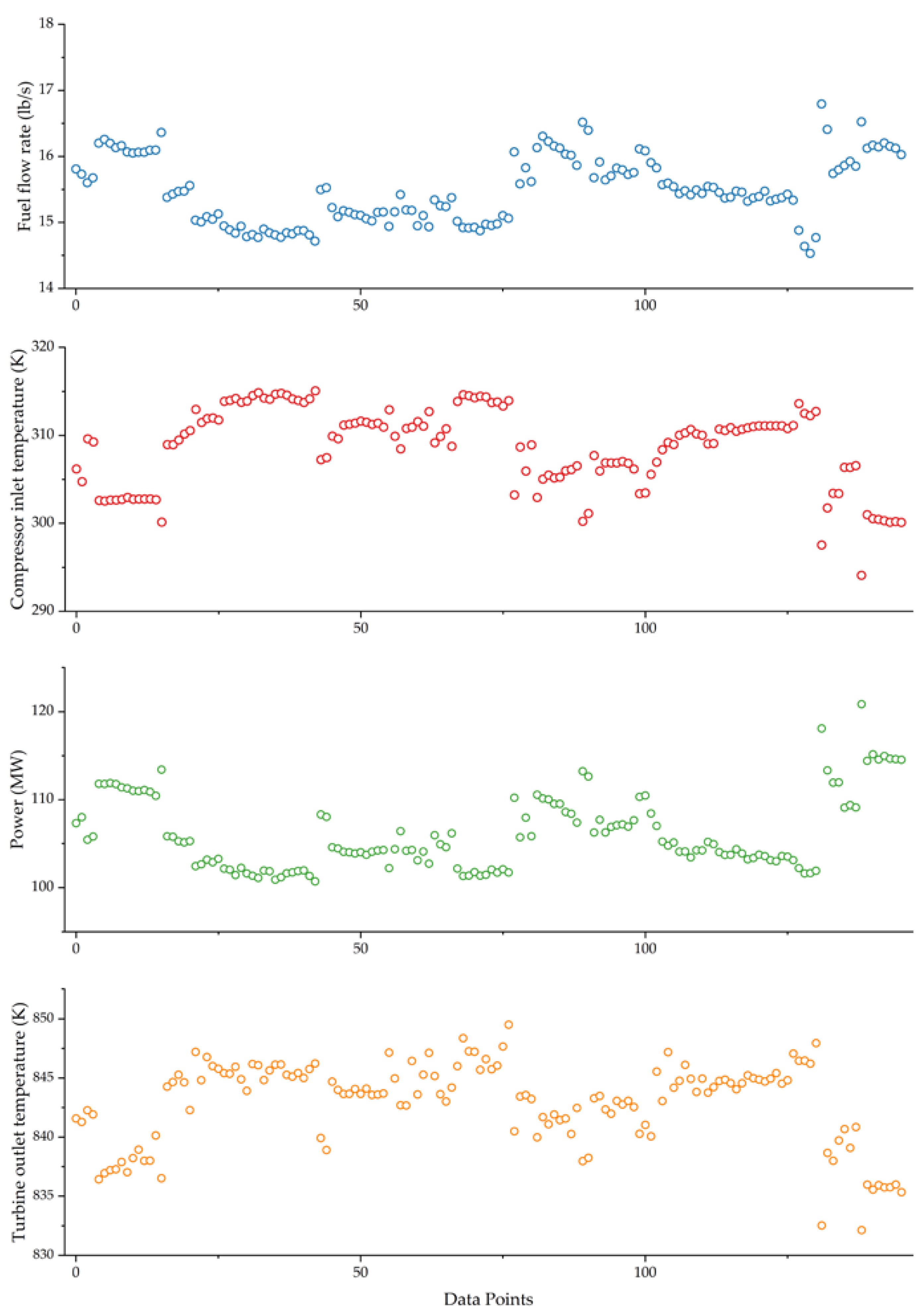
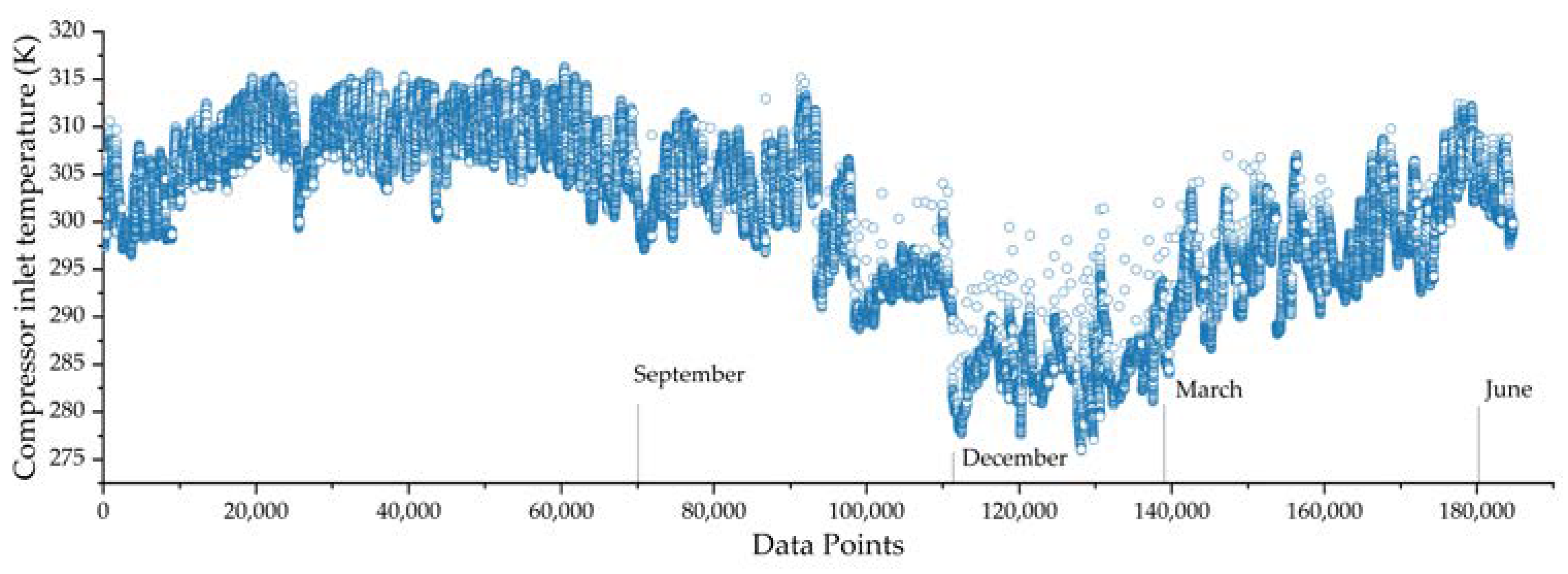
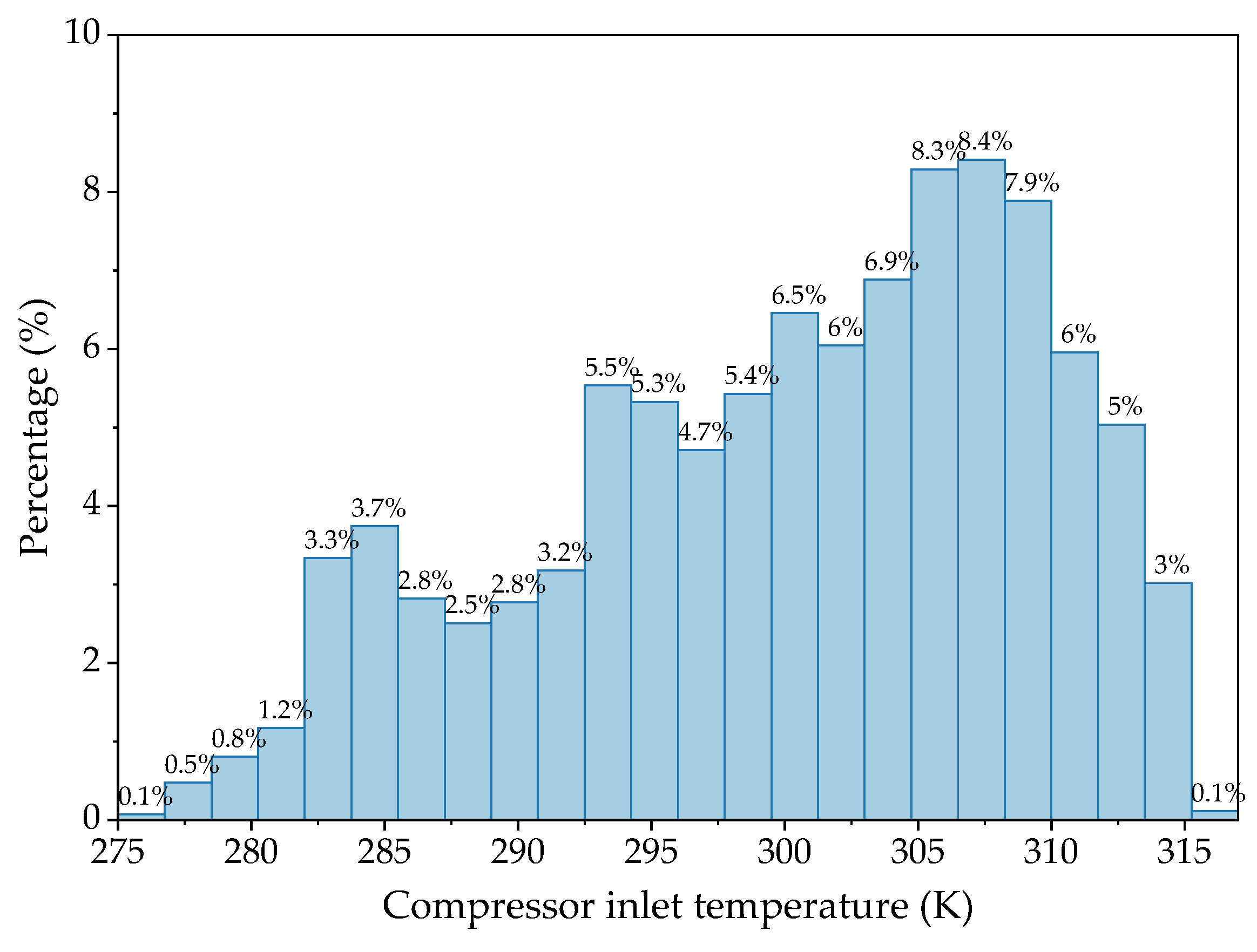
3.1. Application
3.2. Comparison of Random Sampling and Cluster Sampling
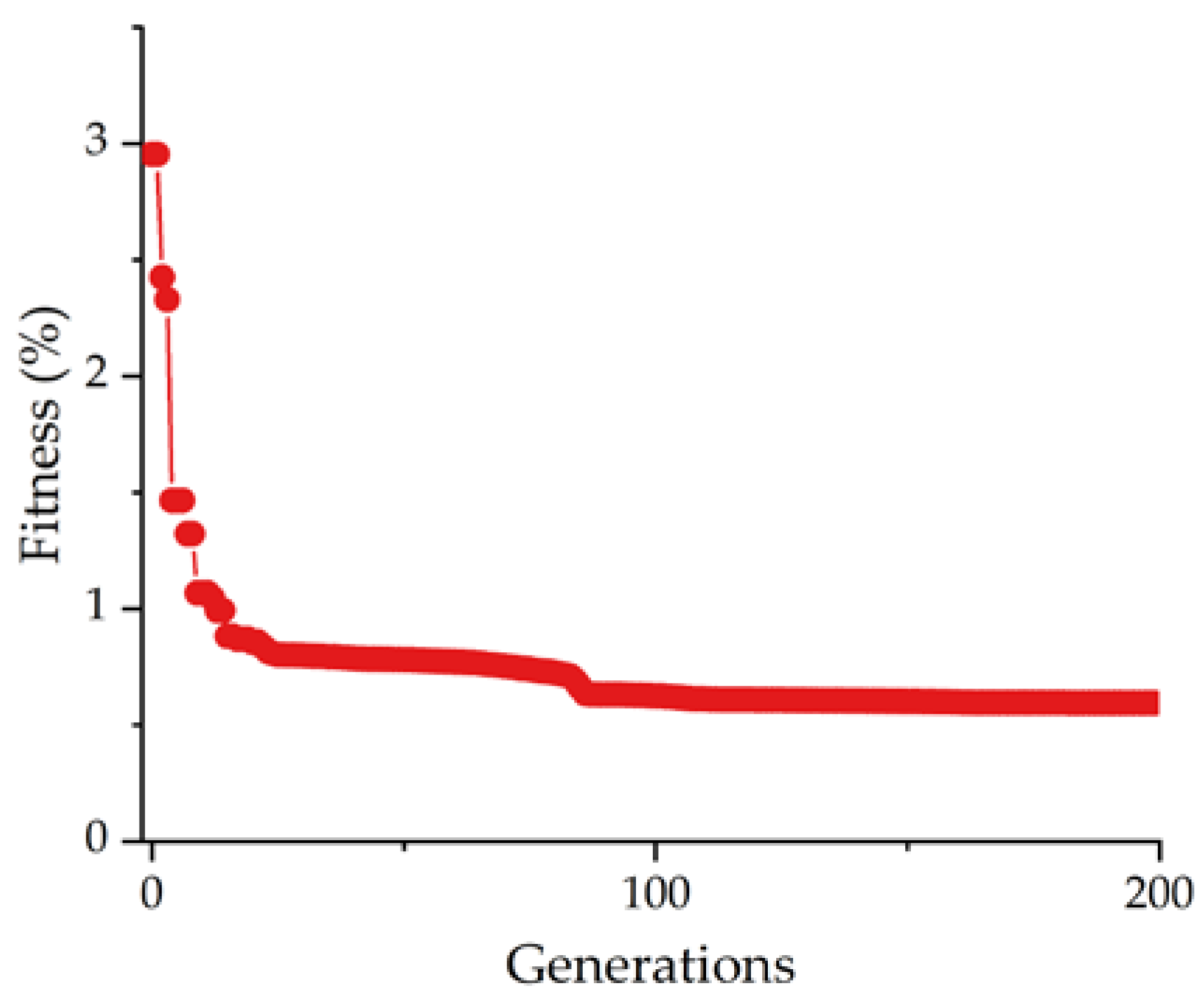
3.3. Optimization Results
3.4. Comparison of the Prediction Using Random Sampling and Cluster Sampling
3.5. Discussion of Random Sampling and Cluster Sampling for a Long Period
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| Compressor inlet temperature, K | |
| Compressor inlet pressure, kPa | |
| Compressor outlet temperature, K | |
| Compressor outlet pressure, kPa | |
| Fuel mass flow, lb/s | |
| Fuel temperature, K | |
| Fuel pressure, kPa | |
| Turbine outlet temperature, K | |
| Turbine outlet pressure, kPa | |
| Power output, MW | |
| Rotor speed | |
| Corrected relative non-dimensional rotational speed | |
| WAC | corrected mass flowrate |
| PR | Pressure ratio |
| ETA | Isentropic efficiency |
| SF | Scaling factor |
| The first-order coefficient | |
| The second-order coefficient | |
| Number of targeted off-design points | |
| M | Number of performance measurements |
| Predicted performance measurements | |
| Actual performance measurements | |
| Subscript | |
| 1 | Inlet of compressor |
| 2 | Outlet of compressor |
| 3 | Outlet of burner |
| 4 | Outlet of turbine |
| Comp | Compressor |
| OD | Off-design point |
| DP | Design point |
| x | One of the characteristic parameters, WAC, PR, or ETA |
| Abbreviations | |
| GA | Genetic algorithm |
| CN | Corrected relative non-dimensional rotational speed |
| PSO | Particle swarm optimization algorithm |
| CV | Coefficient of variation |
References
- Polyzakis, A.L.; Koroneos, C.; Xydis, G. Optimum gas turbine cycle for combined cycle power plant. Energy Convers. Manag. 2008, 49, 551–563. [Google Scholar] [CrossRef]
- Vyncke-Wilson, D. Advantages of Aeroderivative Gas Turbines: Technical & Operational Considerations on Equipment Selection. In Proceedings of the 20th Symposium of the Industrial Application of Gas Turbines Committee, Banff, AB, Canada, 21–23 October 2013. [Google Scholar]
- Haglind, F. A Review on the Use of Gas and Steam Turbine Combined Cycles as Prime Movers for Large Ships. Part I: Background and Design. Energy Convers. Manag. 2008, 49, 3458–3467. [Google Scholar] [CrossRef]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Karim, Z.A. Performance-Based Health Monitoring, Diagnostics and Prognostics for Condition-Based Maintenance of Gas Turbines: A Review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.G. Aero Gas Turbine Flight Performance Estimation Using Engine Gas Path Measurements. J. Propuls. Power 2015, 31, 851–860. [Google Scholar] [CrossRef] [Green Version]
- Gu, C.; Wang, H.; Ji, X.; Li, X. Development and Application of a Thermodynamic-Cycle Performance Analysis Method of a Three-Shaft Gas Turbine. Energy 2016, 112, 307–321. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. Transient Gas Turbine Performance Diagnostics through Nonlinear Adaptation of Compressor and Turbine Maps. J. Eng. Gas Turbines Power 2015, 137, 091201. [Google Scholar] [CrossRef]
- Yang, X.; Guo, X.; Dong, W. On-Line Component Map Adaptive Procedure Based on Sensor Data. In Proceedings of the ASME Turbo Expo 2020, Virtual, 21–25 September 2020. [Google Scholar]
- Lo Gatto, E.; Li, Y.G.; Pilidis, P. Gas Turbine Off-Design Performance Adaptation Using a Genetic Algorithm; American Society of Mechanical Engineers Digital Collection; ASME: New York, NY, USA, 2008; pp. 551–560. [Google Scholar]
- Alberto Misté, G.; Benini, E. Turbojet Engine Performance Tuning With a New Map Adaptation Concept. J. Eng. Gas Turbines Power 2014, 136, 071202-1–071202-8. [Google Scholar] [CrossRef]
- Stamatis, A.; Mathioudakis, K.; Papailiou, K.D. Adaptive simulation of gas turbine performance. ASME J. Eng. Gas Turbines Power 1990, 112, 168–175. [Google Scholar] [CrossRef]
- Lambiris, B.; Mathioudakis, K.; Stamatis, A.; Papailiou, K. Adaptive modeling of jet engine performance with application to condition monitoring. J. Propuls. Power 1994, 10, 890–896. [Google Scholar] [CrossRef]
- Kong, C.; Ki, J.; Kang, M. A new scaling method for component maps of gas turbine using system identification. J. Eng. Gas Turbines Power 2003, 125, 979–985. [Google Scholar] [CrossRef]
- Kong, C.; Kho, S.; Ki, J. Component map generation of a gas turbine using genetic algorithms. J. Eng. Gas Turbines Power 2006, 128, 92–95. [Google Scholar] [CrossRef]
- Kong, C.; Ki, J. Components map generation of gas turbine engine using genetic algorithms and engine performance deck data. J. Eng. Gas Turbines Power 2007, 129, 312–317. [Google Scholar] [CrossRef]
- Li, Y.G.; Pilidis, P.; Newby, M.A. An adaptation approach for gas turbine design-point performance simulation. J. Eng. Gas Turbines Power 2006, 128, 789–795. [Google Scholar] [CrossRef]
- Li, Y.G.; Marinai, L.; Gatto, E.L.; Pachidis, V.; Philidis, P. Multiple-point adaptive performance simulation tuned to aeroengine test-bed data. J. Propuls. Power 2009, 25, 635–641. [Google Scholar] [CrossRef]
- Li, Y.G.; Ghafir, M.F.; Wang, L.; Singh, R.; Huang, K.; Feng, X. Nonlinear multiple points gas turbine off-design performance adaptation using a genetic algorithm. J. Eng. Gas Turbines Power 2011, 133, 071701-1–071701-9. [Google Scholar] [CrossRef]
- Li, Y.G.; Ghafir, M.F.; Wang, L.; Singh, R.; Huang, K.; Feng, X.; Zhang, W. Improved multiple point nonlinear genetic algorithm based performance adaptation using least square method. J. Eng. Gas Turbines Power 2012, 134, 031701-1–031701-10. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Li, Y.G.; Pilidis, P.; Newby, M. Part-Load Performance of Gas Turbines: Part I—A Novel Compressor Map Generation Approach Suitable for Adaptive Simulation. In Proceedings of the ASME 2012 Gas Turbine India Conference, Mumbai, Maharashtra, India, 1 December 2012. [Google Scholar]
- Tsoutsanis, E.; Li, Y.G.; Pilidis, P.; Newby, M. Part-Load Performance of Gas Turbines: Part II—Multi-Point Adaptation with Compressor Map Generation and GA Optimization; American Society of Mechanical Engineers Digital Collection; ASME: New York, NY, USA, 2013; pp. 743–751. [Google Scholar]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. A Component Map Tuning Method for Performance Prediction and Diagnostics of Gas Turbine Compressors. Appl. Energy 2014, 135, 572–585. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Li, S.; Cao, Y. A New Component Map Generation Method for Gas Turbine Adaptation Performance Simulation. J. Mech. Sci. Technol. 2017, 31, 1947–1957. [Google Scholar] [CrossRef]
- Li, S.Y.; Li, Z.; Li, S.Y. Improved Method for Gas-Turbine Off-Design Performance Adaptation Based on Field Data. J. Eng. Gas Turbines Power 2020, 142, 041001-1–041001-12. [Google Scholar] [CrossRef]
- Yan, B.; Hu, M.; Feng, K.; Jiang, Z. Enhanced Component Analytical Solution for Performance Adaptation and Diagnostics of Gas Turbines. Energies 2021, 14, 4356. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November 1995. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar]



| No. | Measurable Parameters | No. | Measurable Parameters |
|---|---|---|---|
| 1 | Compressor inlet temperature | 7 | Fuel pressure |
| 2 | Compressor inlet pressure | 8 | Turbine outlet temperature * |
| 3 | Compressor outlet temperature * | 9 | Turbine outlet pressure |
| 4 | Compressor outlet pressure * | 10 | Power output * |
| 5 | Fuel mass flow | 11 | Rotor speed |
| 6 | Fuel temperature |
| Parameters | Value |
|---|---|
| Output power (MW) | 127.6 |
| System efficiency (%) | 33.6 |
| Compressor pressure ratio | 12.75 |
| Turbine inlet temperature (K) | 1397.15 |
| Turbine outlet temperature (K) | 821.55 |
| Measurements | Before Adaption | After Adaption |
|---|---|---|
| Power | 3.316% | 0.497% |
| Compressor Outlet Temperature | 3.716% | 0.316% |
| Compressor Outlet Pressure | 3.359% | 0.469% |
| Turbine Outlet Temperature | 1.396% | 1.159% |
| Four Measurements | 2.947% | 0.610% |
| Measurements | Error Type | Model 1 | Model 2 |
|---|---|---|---|
| Power | Average | 1.111% | 0.552% |
| Maximum | 2.847% | 1.654% | |
| Compressor Outlet Temperature | Average | 0.235% | 0.249% |
| Maximum | 0.880% | 1.068% | |
| Compressor Outlet Pressure | Average | 0.713% | 0.411% |
| Maximum | 2.287% | 1.246% | |
| Turbine Outlet Temperature | Average | 0.586% | 0.650% |
| Maximum | 3.027% | 2.037% | |
| Four Measurements | Average | 0.661% | 0.466% |
| Maximum | 1.552% | 1.088% |
| Measurements | Error Type | Dataset 1 | Dataset 2 | ||
|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 1 | Model 2 | ||
| Power | Average | 0.938% | 0.567% | 1.712% | 0.501% |
| Maximum | 2.585% | 1.654% | 2.847% | 1.307% | |
| Compressor Outlet Temperature | Average | 0.235% | 0.243% | 0.235% | 0.271% |
| Maximum | 0.880% | 1.068% | 0.616% | 0.744% | |
| Compressor Outlet Pressure | Average | 0.572% | 0.392% | 1.204% | 0.474% |
| Maximum | 1.731% | 1.246% | 2.287% | 1.041% | |
| Turbine Outlet Temperature | Average | 0.432% | 0.645% | 1.118% | 0.670% |
| Maximum | 2.320% | 2.037% | 3.028% | 1.894% | |
| Four Measurements | Average | 0.544% | 0.462% | 1.067% | 0.479% |
| Maximum | 1.238% | 1.088% | 1.552% | 0.887% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, J.; Yu, W.; Chen, J.; Zhang, H. Gas Turbine Off-Design Performance Adaption Based on Cluster Sampling. Appl. Sci. 2023, 13, 7352. https://doi.org/10.3390/app13137352
Kong J, Yu W, Chen J, Zhang H. Gas Turbine Off-Design Performance Adaption Based on Cluster Sampling. Applied Sciences. 2023; 13(13):7352. https://doi.org/10.3390/app13137352
Chicago/Turabian StyleKong, Jing, Wei Yu, Jinwei Chen, and Huisheng Zhang. 2023. "Gas Turbine Off-Design Performance Adaption Based on Cluster Sampling" Applied Sciences 13, no. 13: 7352. https://doi.org/10.3390/app13137352
APA StyleKong, J., Yu, W., Chen, J., & Zhang, H. (2023). Gas Turbine Off-Design Performance Adaption Based on Cluster Sampling. Applied Sciences, 13(13), 7352. https://doi.org/10.3390/app13137352






