A Decomposition Algorithm for Dynamic Car Sequencing Problems with Buffers
Abstract
1. Introduction
- Pull-out buffer: Cars at any position in the car sequence can be removed and placed in the backward buffer, and then inserted into the appropriate position as the car sequence advances, so that cars can be moved to any position later in the sequence, and the advancement of the car sequence is limited by the number of cars allowed out of the column.
- Ring buffer: Multiple cars can be selected from the car sequence into the ring buffer, and cars from any position in the ring buffer can be put back into the sequence.
- Automated storage and retrieval system (AS/RS): Consisting of hundreds of buffer points, each buffer point can be accessed individually to generate the desired sequence of cars, and the flexibility of car sequencing is influenced by the number of buffer point locations.
- Parallel buffer: It consists of multiple parallel lanes (Figure 1), where cars from the upstream workshop are put into the parallel lanes, and then the first car of a lane is selected to join the downstream car production sequence according to the needs of the downstream workshop, and cars can only move in one direction in the lane, following the “FIFO” principle.
2. Literature Review
3. Problem Description and Mathematical Model
- 1.
- Each car takes the same amount of time to move one space in either lane of the buffer and can only move in one direction.
- 2.
- The buffer continues to function normally, regardless of fault conditions.
4. DCSPwB Decompositional Algorithm
4.1. Simple Rule-Based Heuristic Entry Algorithm
- 1.
- Select the lane with the best match.
- 2.
- Select the lane with the largest remaining capacity.
- 3.
- Select the lane that takes the shortest amount of time to enter the buffers.
| Algorithm 1: Heuristic storage algorithm for simple rules |
 |
4.2. Dynamic Genetic Algorithm
4.2.1. Encoding Method of Solution with Population Initialization
4.2.2. Selection
| Algorithm 2: GA TS |
|
Input: Num of chromosomes in the population n, vector of chromosomes fitness values v, number of parental chromosomes m. return idx |
4.2.3. Dynamic Crossover Algorithm
4.2.4. Dynamic Mutation Algorithm
4.3. Greedy Algorithm for Postponed Car Release
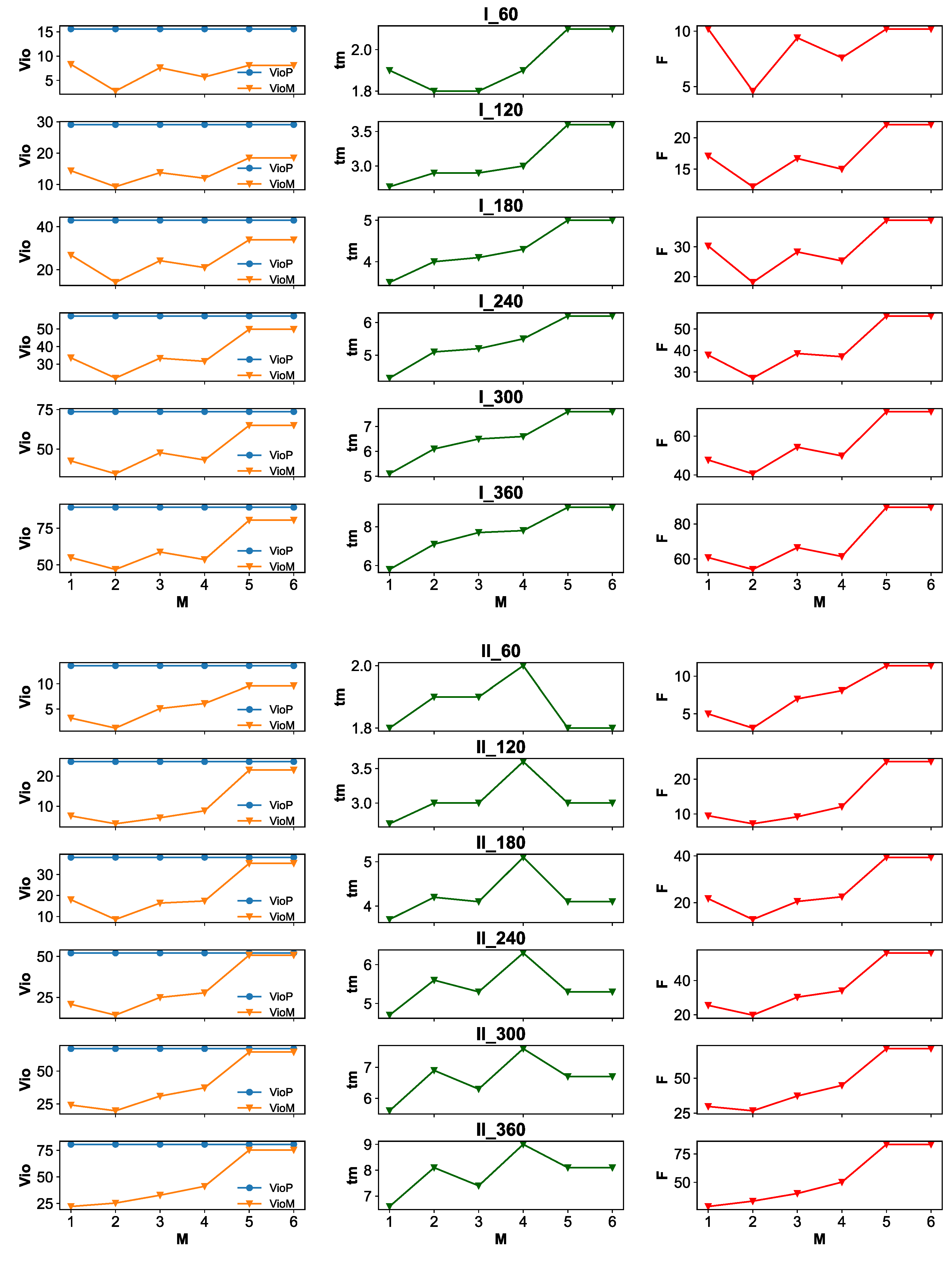
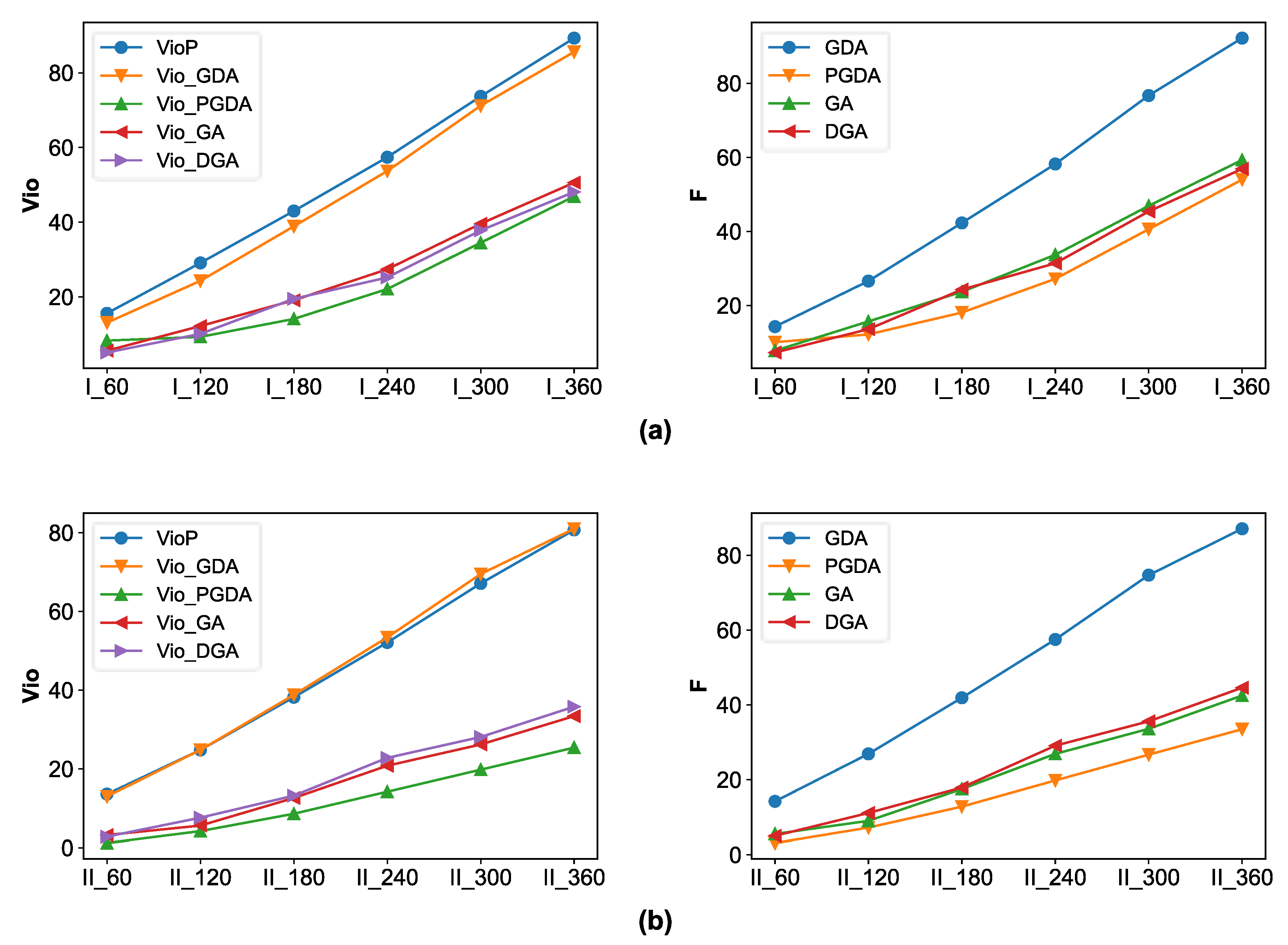
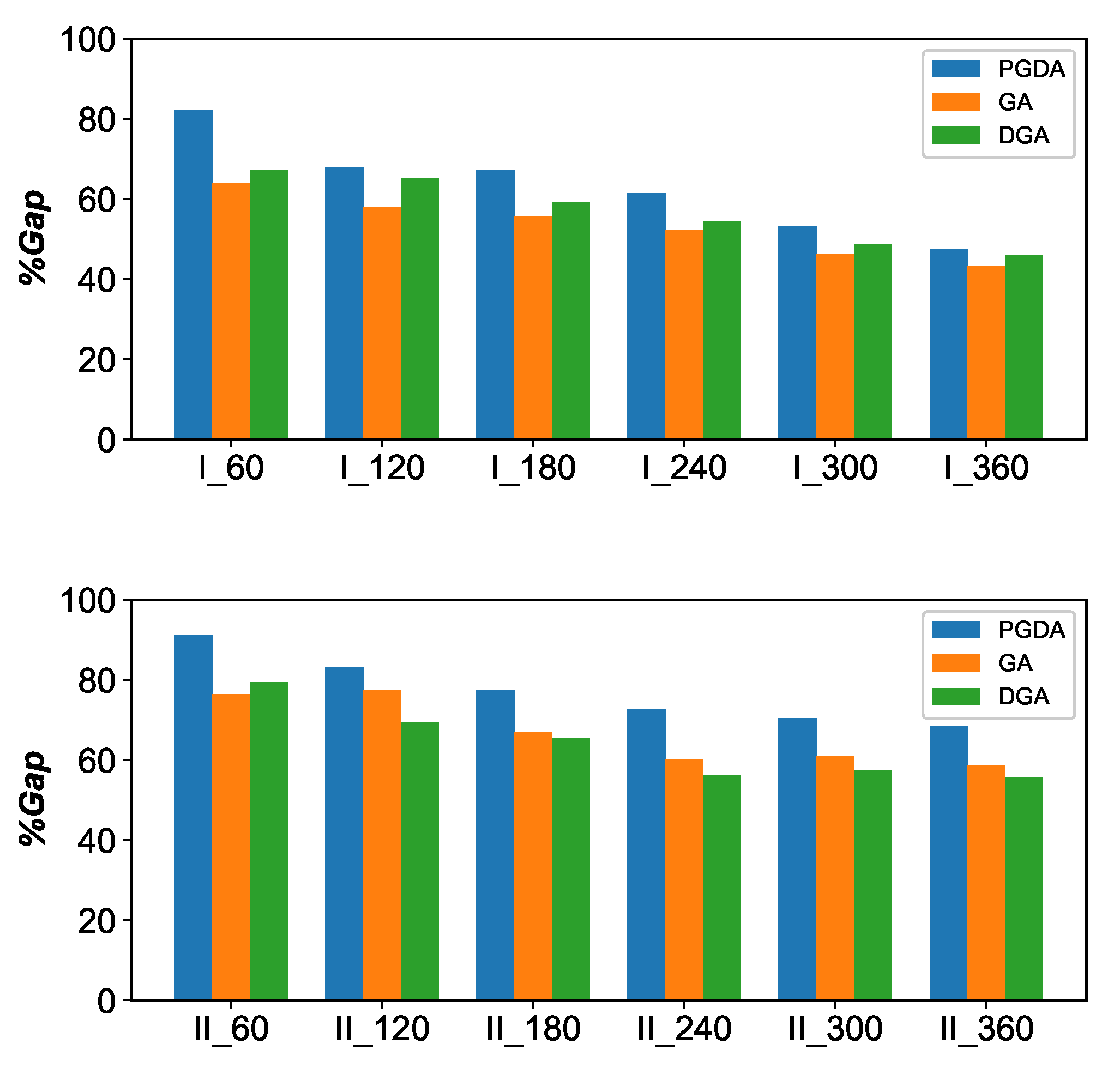
5. Experiments and Results
5.1. Dataset
5.2. Experimental and Computational Results
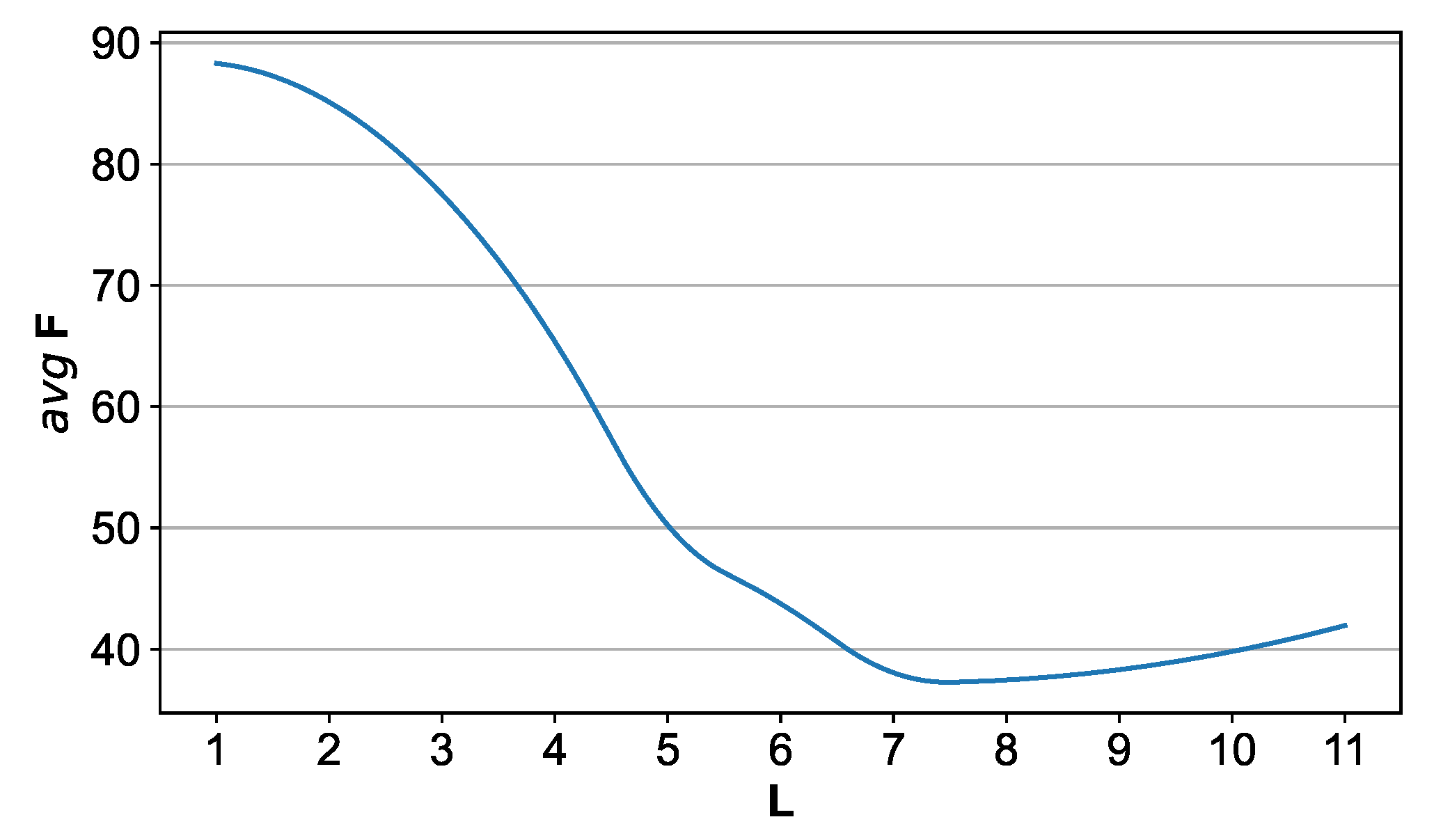
5.3. The Effect of Buffer Capacity on Car Resequence
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boysen, N.; Fliedner, M.; Scholl, A. Sequencing mixed-model assembly lines: Survey, classification and model critique. Eur. J. Oper. Res. 2009, 192, 349–373. [Google Scholar] [CrossRef]
- Baybars, I. A survey of exact algorithms for the simple assembly line balancing problem. Manag. Sci. 1986, 32, 909–932. [Google Scholar] [CrossRef]
- Becker, C.; Scholl, A. A survey on problems and methods in generalized assembly line balancing. Eur. J. Oper. Res. 2006, 168, 694–715. [Google Scholar] [CrossRef]
- Yurtkuran, A.; Yagmahan, B.; Emel, E. A novel artificial bee colony algorithm for the workforce scheduling and balancing problem in sub-assembly lines with limited buffers. Appl. Soft Comput. 2018, 73, 767–782. [Google Scholar] [CrossRef]
- Zhu, X.; Hu, S.J.; Koren, Y.; Marin, S.P. Modeling of Manufacturing Complexity in Mixed-Model Assembly Lines. J. Manuf. Sci. Eng. 2008, 130, 649–659. [Google Scholar] [CrossRef]
- Takai, S. An Approach to Integrate Product and Process Design Using Augmented Liaison Diagram, Assembly Sequencing, and Assembly Line Balancing. J. Mech. Des. 2021, 143, 1–24. [Google Scholar] [CrossRef]
- Lahmar, M.; Ergan, H.; Benjaafar, S. Resequencing and feature assignment on an automated assembly line. IEEE Trans. Robot. Autom. 2003, 19, 89–102. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Laporte, G.; Pasin, F. Iterated tabu search for the car sequencing problem. Eur. J. Oper. Res. 2008, 191, 945–956. [Google Scholar] [CrossRef]
- Gagné, C.; Gravel, M.; Price, W.L. Solving real car sequencing problems with ant colony optimization. Eur. J. Oper. Res. 2006, 174, 1427–1448. [Google Scholar] [CrossRef]
- Mansouri, S.A. A multi-objective genetic algorithm for mixed-model sequencing on JIT assembly lines. Eur. J. Oper. Res. 2005, 167, 696–716. [Google Scholar] [CrossRef]
- Prandtstetter, M.; Raidl, G.R. An integer linear programming approach and a hybrid variable neighborhood search for the car sequencing problem. Eur. J. Oper. Res. 2008, 191, 1004–1022. [Google Scholar] [CrossRef]
- McMullen, P.R.; Tarasewich, P.; Frazier, G.V. Using genetic algorithms to solve the multi-product JIT sequencing problem with set-ups. Int. J. Prod. Res. 2000, 38, 2653–2670. [Google Scholar] [CrossRef]
- Boysen, N.; Scholl, A.; Wopperer, N. Resequencing of mixed-model assembly lines: Survey and research agenda. Eur. J. Oper. Res. 2012, 216, 594–604. [Google Scholar] [CrossRef]
- Wortmann, D.; Spieckermann, S. Manufacturing line simulation of automotive industry to enhance productivity and profitability. Automot. Simul. 1995, 95, 91–106. [Google Scholar]
- Parrello, B.D.; Kabat, W.C.; Wos, L. Job-shop scheduling using automated reasoning: A case study of the car-sequencing problem. J. Autom. Reason. 1986, 2, 1–42. [Google Scholar] [CrossRef]
- Kis, T. On the complexity of the car sequencing problem. Oper. Res. Lett. 2004, 32, 331–335. [Google Scholar] [CrossRef]
- Solnon, C.; Nguyen, A.; Artigues, C.; Van Cung, D. The car sequencing problem: Overview of state-of-the-art methods and industrial case-study of the ROADEF’2005 challenge problem. Eur. J. Oper. Res. 2008, 191, 912–927. [Google Scholar] [CrossRef]
- Drexl, A.; Kimms, A. Sequencing JIT mixed-model assembly lines under station-load and part-usage constraints. Manag. Sci. 2001, 47, 480–491. [Google Scholar] [CrossRef]
- Thiruvady, D.; Morgan, K.; Amir, A.; Ernst, A.T. Large neighbourhood search based on mixed integer programming and ant colony optimisation for car sequencing. Int. J. Prod. Res. 2020, 58, 2696–2711. [Google Scholar] [CrossRef]
- Estellon, B.; Gardi, F.; Nouioua, K. Two local search approaches for solving real-life car sequencing problems. Eur. J. Oper. Res. 2008, 191, 928–944. [Google Scholar] [CrossRef]
- Gavranović, H. Local search and suffix tree for car-sequencing problem with colors. Eur. J. Oper. Res. 2008, 191, 972–980. [Google Scholar] [CrossRef]
- Siala, M.; Hebrard, E.; Huguet, M.J. A study of constraint programming heuristics for the car-sequencing problem. Eng. Appl. Artif. Intell. 2015, 38, 34–44. [Google Scholar] [CrossRef]
- Bulgak, A. Analysis and design of split and merge unpaced assembly systems by metamodelling and stochastic search. Int. J. Prod. Res. 2006, 44, 4067–4080. [Google Scholar] [CrossRef]
- Muhl, E.; Charpentier, P.; Chaxel, F. Optimization of physical flows in an automotive manufacturing plant: Some experiments and issues. Eng. Appl. Artif. Intell. 2003, 16, 293–305. [Google Scholar] [CrossRef]
- Spieckermann, S.; Gutenschwager, K.; Voß, S. A sequential ordering problem in automotive paint shops. Int. J. Prod. Res. 2004, 42, 1865–1878. [Google Scholar] [CrossRef]
- Yu, D.Y.; Zhang, S.Q.; Shao, X.Y.; Liu, S.Q.; Tian, Y.H. A gravity-like mechanism for car sequencing problem with multistage sequencing buffer. In Advanced Materials Research; Trans Tech Publications: Stafa-Zurich, Switzerland, 2011; Volume 314, pp. 2232–2237. [Google Scholar] [CrossRef]
- Moon, D.H.; Song, C.; Ha, J.H. A dynamic algorithm for the control of automotive painted body storage. Simulation 2005, 81, 773–787. [Google Scholar] [CrossRef]
- Pereira, J.; Vilà, M. An exact algorithm for the mixed-model level scheduling problem. Int. J. Prod. Res. 2015, 53, 5809–5825. [Google Scholar] [CrossRef]
- Son, B.; Kim, J.W.; Lee, D.; Jung, S.Y. Genetic algorithm with species differentiation based on kernel support vector machine for optimal design of wind generator. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Schoen, M.P.; Hoover, R.C.; Chinvorarat, S.; Schoen, G.M. System identification and robust controller design using genetic algorithms for flexible space structures. J. Dyn. Syst. Meas. Control 2009, 131, 304–314. [Google Scholar] [CrossRef]
- Xidias, E.; Moulianitis, V.; Azariadis, P. Optimal robot task scheduling based on adaptive neuro-fuzzy system and genetic algorithms. Int. J. Adv. Manuf. Technol. 2021, 115, 927–939. [Google Scholar] [CrossRef]
- Knust, J.; Podszus, F.; Stonis, M.; Behrens, B.A.; Overmeyer, L.; Ullmann, G. Preform optimization for hot forging processes using genetic algorithms. Int. J. Adv. Manuf. Technol. 2017, 89, 1623–1634. [Google Scholar] [CrossRef]
- Zhengdong, Z.; Yuanhua, C.; Dongdong, W.; Zili, Y. Reconstruction of the linac photon spectrum based on prior knowledge and the genetic algorithm. J. Southeast Univ. (Engl. Ed.) 2014, 30, 311–314. [Google Scholar]
- Singh, P.; Singh, R.K.; Joshi, D.; Bathla, G. Knowledge Application to Crossover Operators in Genetic Algorithm for Solving the Traveling Salesman Problem. Int. J. Softw. Innov. (IJSI) 2022, 10, 1–20. [Google Scholar] [CrossRef]
- Mehta, C.; Patil, L.; Dutta, D. An approach to determine important attributes for engineering change evaluation. J. Mech. Des. 2013, 135, 041003. [Google Scholar] [CrossRef]
- Malhan, R.; Jomy Joseph, R.; Bhatt, P.M.; Shah, B.; Gupta, S.K. Algorithms for improving speed and accuracy of automated three-dimensional reconstruction with a depth camera mounted on an industrial robot. J. Comput. Inf. Sci. Eng. 2022, 22, 031012. [Google Scholar] [CrossRef]
- Gottlieb, J.; Puchta, M.; Solnon, C. A study of greedy, local search, and ant colony optimization approaches for car sequencing problems. In Proceedings of the Applications of Evolutionary Computing: EvoWorkshops 2003: EvoBIO, EvoCOP, EvoIASP, EvoMUSART, EvoROB, and EvoSTIM, London, UK, 14–16 April 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 246–257. [Google Scholar]

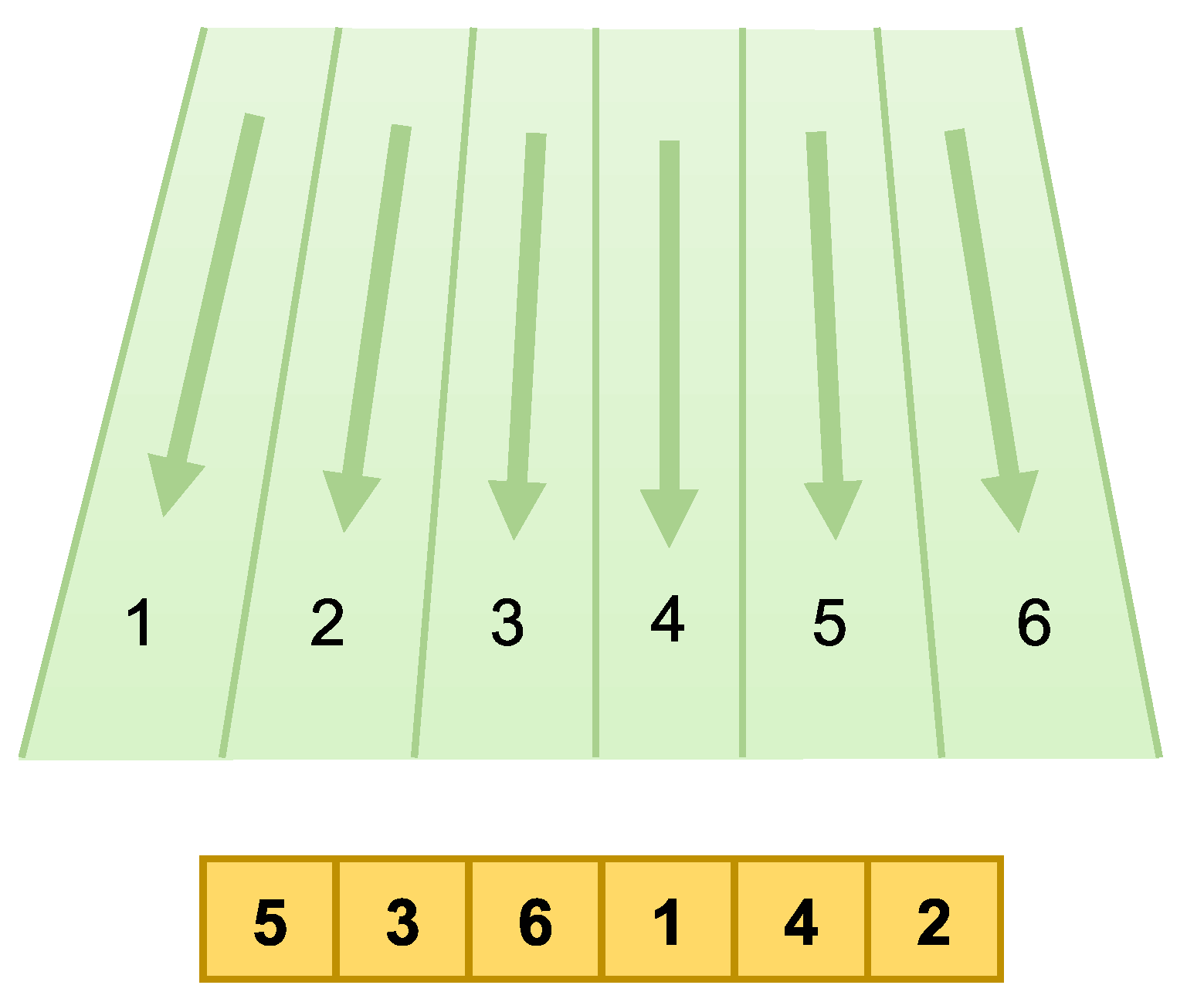
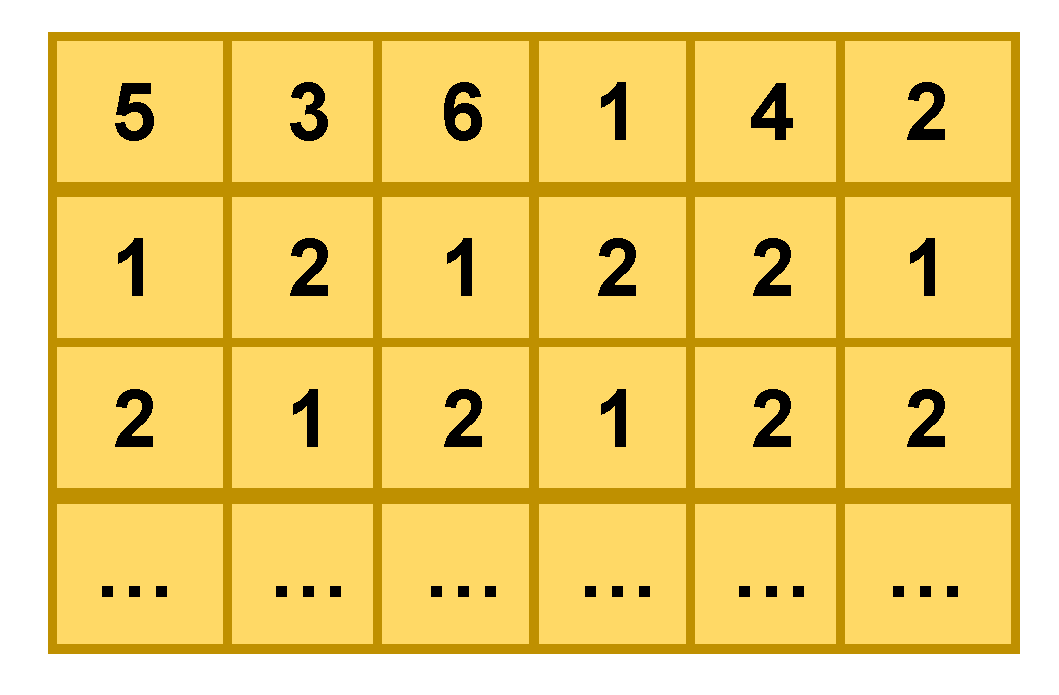



| Car Type | A | B | C | D | |
|---|---|---|---|---|---|
| ✓ | ✓ | ||||
| ✓ | ✓ | ✓ | |||
| Amount | 2 | 1 | 1 | 1 |
| N | Total number of cars, index i. |
| O | Collection of options, index o. |
| L | Number of lanes in the buffer, index l. |
| V | Capacity per lane. |
| Option weights. | |
| A continuous sequence of cars, some of which require the option o. | |
| The maximum number of cars with option o allowed in a continuous sequence of cars . | |
| Capacity constraint, i.e., the maximum number of cars with option o allowed in a continuous sequence of cars . | |
| Binary variable: 1, if the car sequence starting from position j satisfies the constraint , 0, otherwise. | |
| M | Scaling for (). |
| Binary variables: 1, if car i is in lane l, 0, otherwise. | |
| Binary variables: 1, if car i is in position j of the sequence, 0, otherwise. | |
| Large integers. | |
| Binary variables: 1, if car i needs option o, 0, otherwise. | |
| The time it takes for a car to move one space in the buffer lane. | |
| Time it takes for a car to enter the buffer lane l. | |
| Time it takes for a car to exit from the buffer lane l. |
| Order of Entering the Car | Car Type | |||
|---|---|---|---|---|
| 1 | K1 | ✓ | ||
| 2 | K2 | ✓ | ✓ | |
| 3 | K2 | ✓ | ✓ | |
| 4 | K1 | ✓ | ||
| … | … | … | … | … |
| 22 | K3 | ✓ | ||
| 23 | K1 | ✓ | ||
| … | … | … | … | … |
| Parameters | Value | Unit |
|---|---|---|
| L | 6 | |
| V | 10 | |
| 9 | s | |
| [18, 12, 6, 0, 12, 18] | s | |
| [18, 12, 6, 0, 12, 18] | s |
| Example | VoiP | GDA | PGDA | GA | DGA | ||||
|---|---|---|---|---|---|---|---|---|---|
| I_60 | 15.6 | 13.1 | 1.2 | 8.3 | 1.8 | 5.6 | 2.2 | 5.1 | 2.2 |
| I_120 | 29.1 | 24.3 | 2.3 | 9.3 | 2.9 | 12.2 | 3.5 | 10.1 | 3.5 |
| I_180 | 43 | 38.9 | 3.4 | 14.1 | 4.0 | 19.1 | 4.6 | 19.5 | 4.8 |
| I_240 | 57.4 | 53.7 | 4.5 | 22.1 | 5.1 | 27.4 | 6.3 | 25.2 | 6.2 |
| I_300 | 73.7 | 71.2 | 5.5 | 34.5 | 6.1 | 39.6 | 7.3 | 37.8 | 7.6 |
| I_360 | 89.3 | 85.6 | 6.6 | 46.9 | 7.1 | 50.6 | 8.7 | 48.1 | 8.8 |
| II_60 | 13.6 | 13 | 1.2 | 1.2 | 1.9 | 3.2 | 2.3 | 2.8 | 2.2 |
| II_120 | 24.8 | 24.8 | 2.1 | 4.2 | 3.0 | 5.6 | 3.4 | 7.6 | 3.5 |
| II_180 | 38.2 | 38.8 | 3.1 | 8.6 | 4.2 | 12.6 | 4.9 | 13.2 | 4.7 |
| II_240 | 52.1 | 53.4 | 4.1 | 14.2 | 5.6 | 20.8 | 6.1 | 22.8 | 6.3 |
| II_300 | 67.1 | 69.5 | 5.2 | 19.8 | 6.9 | 26.2 | 7.4 | 28.1 | 7.5 |
| II_360 | 80.7 | 81 | 6.1 | 25.4 | 8.1 | 33.4 | 9.1 | 35.8 | 8.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ding, W. A Decomposition Algorithm for Dynamic Car Sequencing Problems with Buffers. Appl. Sci. 2023, 13, 7336. https://doi.org/10.3390/app13127336
Zhang H, Ding W. A Decomposition Algorithm for Dynamic Car Sequencing Problems with Buffers. Applied Sciences. 2023; 13(12):7336. https://doi.org/10.3390/app13127336
Chicago/Turabian StyleZhang, Haida, and Wensi Ding. 2023. "A Decomposition Algorithm for Dynamic Car Sequencing Problems with Buffers" Applied Sciences 13, no. 12: 7336. https://doi.org/10.3390/app13127336
APA StyleZhang, H., & Ding, W. (2023). A Decomposition Algorithm for Dynamic Car Sequencing Problems with Buffers. Applied Sciences, 13(12), 7336. https://doi.org/10.3390/app13127336





