Upper Bound Solution Analysis of the Ultimate Bearing Capacity of Two–Layered Strip Foundation Based on Improved Radial Movement Optimization

Abstract

Considering the change of different soil layer parameters of a two–layered strip foundation, a planar kinematically permissible multi–block failure mechanism of a two–layered strip foundation under vertical uniform load is formulated. Based on upper–bound limit analysis theorem, the solution process of ultimate bearing capacity of a two–layered strip foundation is proposed. The improved radial movement optimization (IRMO) could search the critical slip surface of the foundation and calculate associated ultimate bearing capacity. On this basis, analyze the influence parameters. The results show that the IRMO algorithm is feasible, stable, and efficient in solving the ultimate bearing capacity. With the increase in the internal friction angle and cohesion of the two–layered strip foundation, the critical slip surface will expand more deeply, and the ultimate bearing capacity will increase. The influence of upper soil parameters on the calculation results is greater than that of lower soil. For the case with upper–hard soil, the ultimate bearing capacity of it increases gradually with the increase in the H/B ratio. For the upper–soft case, the ultimate bearing capacity of it decreases gradually with the increase in the H/B ratio. Moreover, the increase of ground overload will also cause a linear–increasing in the ultimate bearing capacity.

1. Introduction

Numerous practical projects widely use two–layered strip foundations. To reasonably determine the ultimate bearing capacity of two–layered strip footing, scholars have conducted many studies on the solution methods, such as the diffusion angle method [1], the Hanson weighted average method [2], shear failure theory [3,4], and the limit analysis method [5,6,7]. These methods only take into account the velocity model and soil energy dissipation when applying the upper–bound limit analysis theorem. With this approach, the ultimate load can be solved immediately without the complex elastic–plastic body being deformed. The upper–bound limit analysis theory has nonetheless been adopted by numerous researchers due to its simplicity even if it frequently somewhat overestimates the ultimate load. Two–layered soils differ mechanically from homogeneous soil foundations in that they have more complex failure modes and bearing processes. The ultimate carrying capability of a layered soil foundation must therefore be determined differently. Determining the ultimate bearing capacity of a two–layered foundation is crucial in both theory and practice. Scholars have relatively limited research on the critical sliding surface of double–layer foundations. Therefore, studying the ultimate bearing capacity of double–layer foundations has great practical significance. How to determine the critical sliding surface of double–layer foundations and calculate the corresponding ultimate bearing capacity of foundations to reasonably evaluate the safety status of foundations is still a subject that needs to be continuously improved.

With the development of numerical methods, the finite element method is more and more used to study the ultimate bearing capacity of foundation. Lee [8] used FEM to calculate the numerical results of the undrained vertical bearing capacity of a rough ring foundation on two layers of clay, and compared the small displacement finite element prediction with existing experience, analysis, and numerical solutions to determine the coupling effects of the dimensionless parameters. Tootoonchi [9] proposed a smooth spread method based on enrichment elements for numerical modeling of regions including weak and strong discontinuities. The triangular background grid is used to discretize the region. Kalourazi [10] mainly studied the influence of shear strength anisotropy on the bearing capacity of surface foundation near the slope. The lower limit analysis method is used with finite element and linear programming techniques to predict the limit pressure. Experimental methods can also be used to analyze the mechanical properties of layered soil. Jiao [11] analyzed the mechanical properties of backfill soil when the bedding plane is inclined, and as the dip angle of the interlayer increases, the crack distribution of the fine filler becomes more concentrated.

Numerous studies have been conducted recently on various optimization techniques to locate the crucial slip surface and ascertain the ultimate bearing capacity of the foundation. Based on the limit analysis, Lin et al. [12] created an optimization model of the two–layered clay foundation through the rigid block discrete system, then used the dichotomy method to find the critical slip surface and determine the ultimate bearing capacity. By using an updated Hoek–Brown failure criterion, Hazim AIKhafaji [13] examined the bearing capacity of a shallow rigid foundation on rock mass under horizontal seepage. Yang XL [14] used the upper–bound theorem in conjunction with the spatial discretization technique to calculate the ultimate bearing capacity of the foundation in nonhomogeneous and anisotropic clays. For the reinforced foundation under the strip footing, Liu [15,16] combined the critical sliding field method with the limit equilibrium slice method to locate the critical slip surface and compute the related ultimate bearing capacity. The ultimate bearing capacity of a cohesionless soil foundation was calculated by Zhang R [17] using the multi expression programming method. Jin et al. have investigated the critical slip surface and associated ultimate bearing capacity for unsaturated soil foundations (Jin and Pan [18], Jin and Zhang [19]), nonhomogeneous clay foundation adjacent to slopes (Jin and Feng [20]), and strip footing on sands (Jin and Zhang [21]) using the IRMO algorithm. In the analysis of the ultimate bearing capacity of double–layer foundation, due to the different parameters of each soil layer, the upper bound method is used to consider the more complex velocity field of the maneuvering permission, and a more precise analysis of the velocity field is needed to reduce errors in calculating the ultimate bearing capacity of the foundation.

The difference of the two–layered strip foundation soils mechanical characteristics give rise to more complex rigid block partitioning situations, which usually result in more complex computing procedures and more computations. Based on the upper–bound limit analysis theorem, this study develops a multi–block failure mechanism that is planarly kinematically acceptable. The IRMO algorithm is used to compute the ultimate bearing capacity of a two–layered strip foundation while simultaneously identifying a crucial slip surface and optimizing both procedures. It is also examined how the characteristics of the soil layers, the thickness of the upper soil, and overload affect the critical slip surface and the ultimate bearing capacity.

2. Multi Rigid Block Failure Mechanism

2.1. Two–Layered Strip Foundation Failure Mode

In terms of the different soil characteristics of a two–layered strip foundation, this paper makes the following assumptions before analyzing the bearing capacity of the foundation:

• The two–layered soils are assumed as elastic–perfectly plastic material, and the soils above the base level are simplified as overload q on both sides of the foundation.
• Two–layered soils are subjected to the associated flow rule and Mohr–Coulomb yield criterion.
• The foundation is assumed to be relatively still, and its base surface is assumed to be completely rough.
• The foundation moves downward at an assumed vertical speed $v_0$.

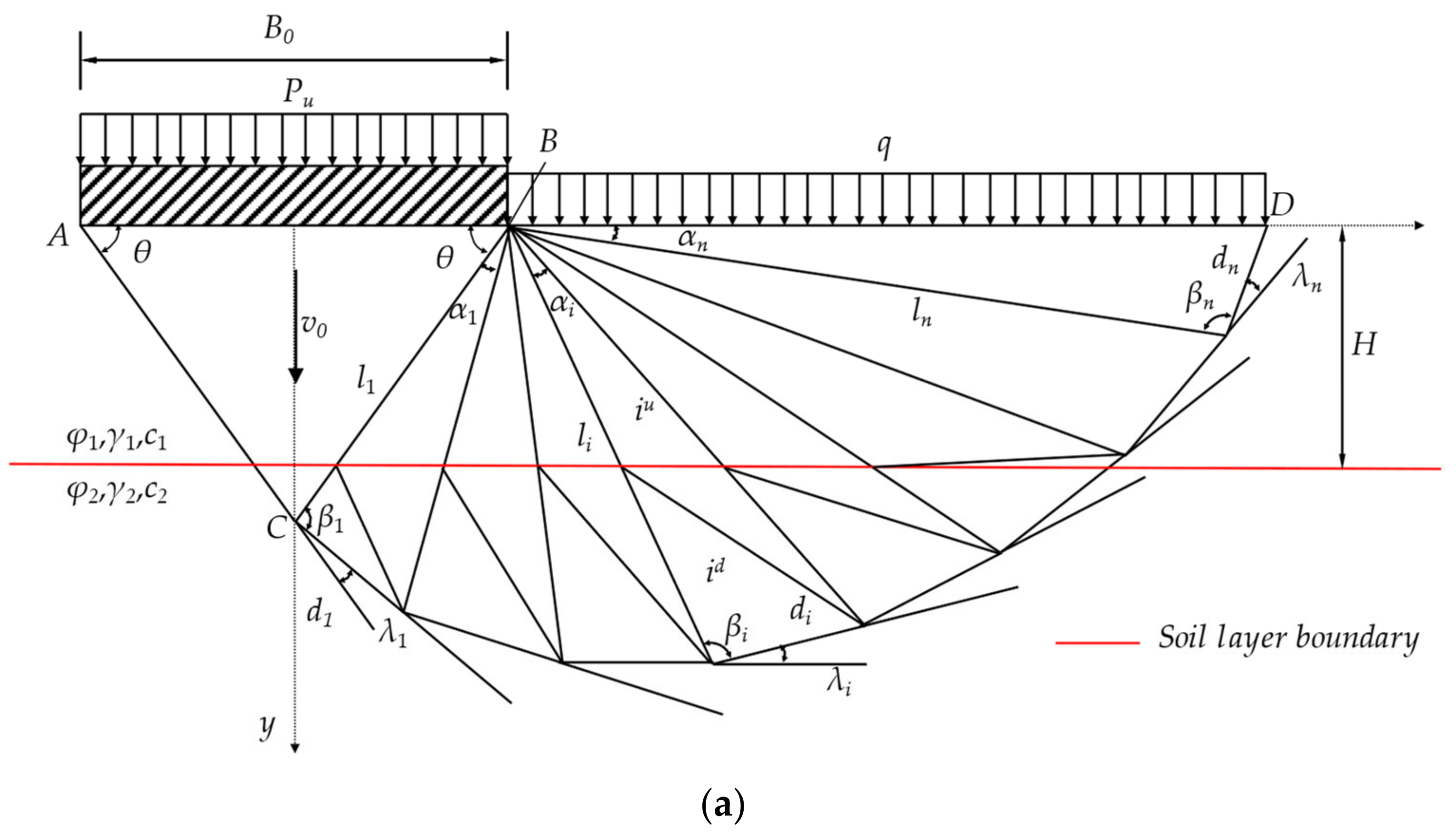
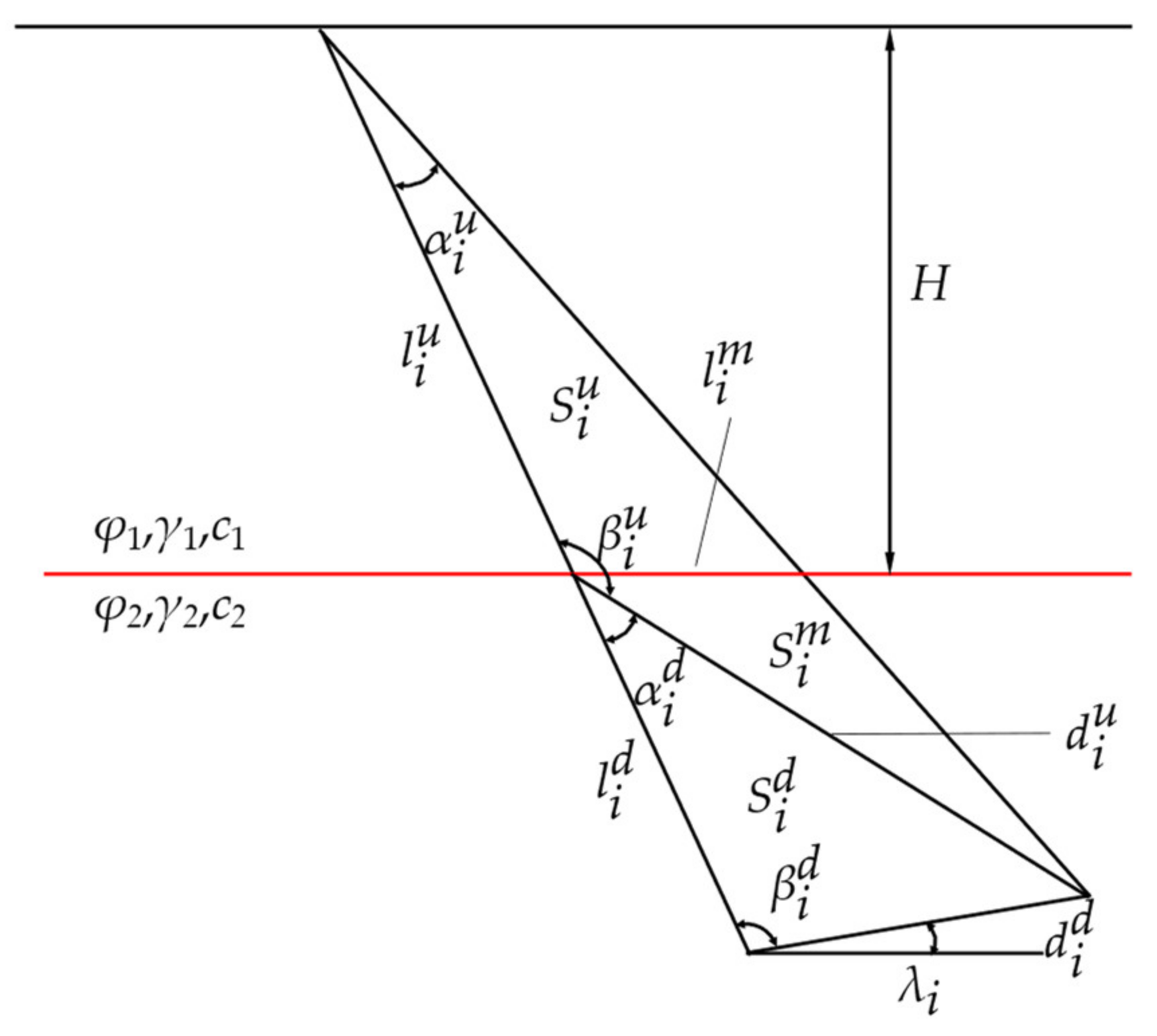
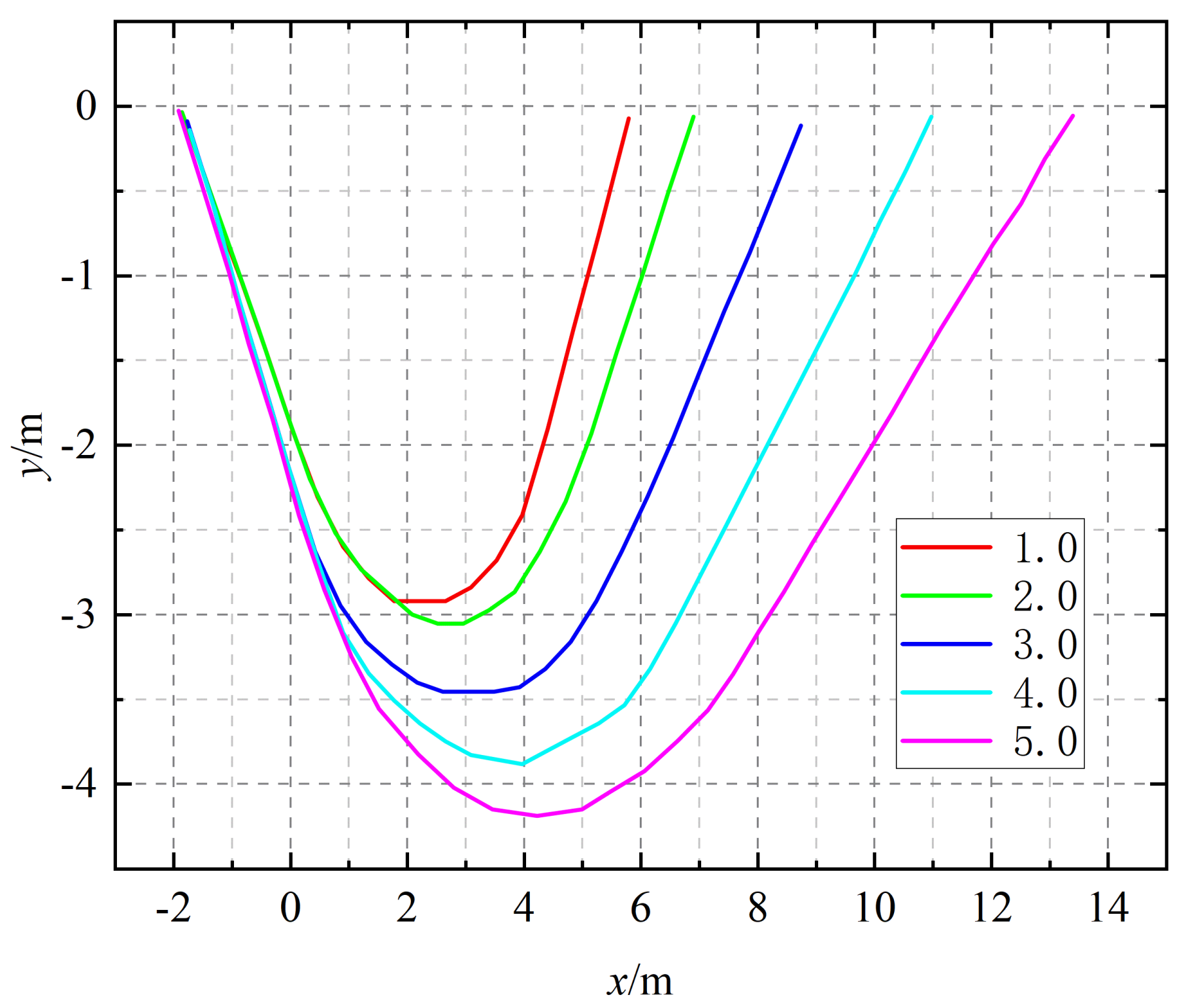
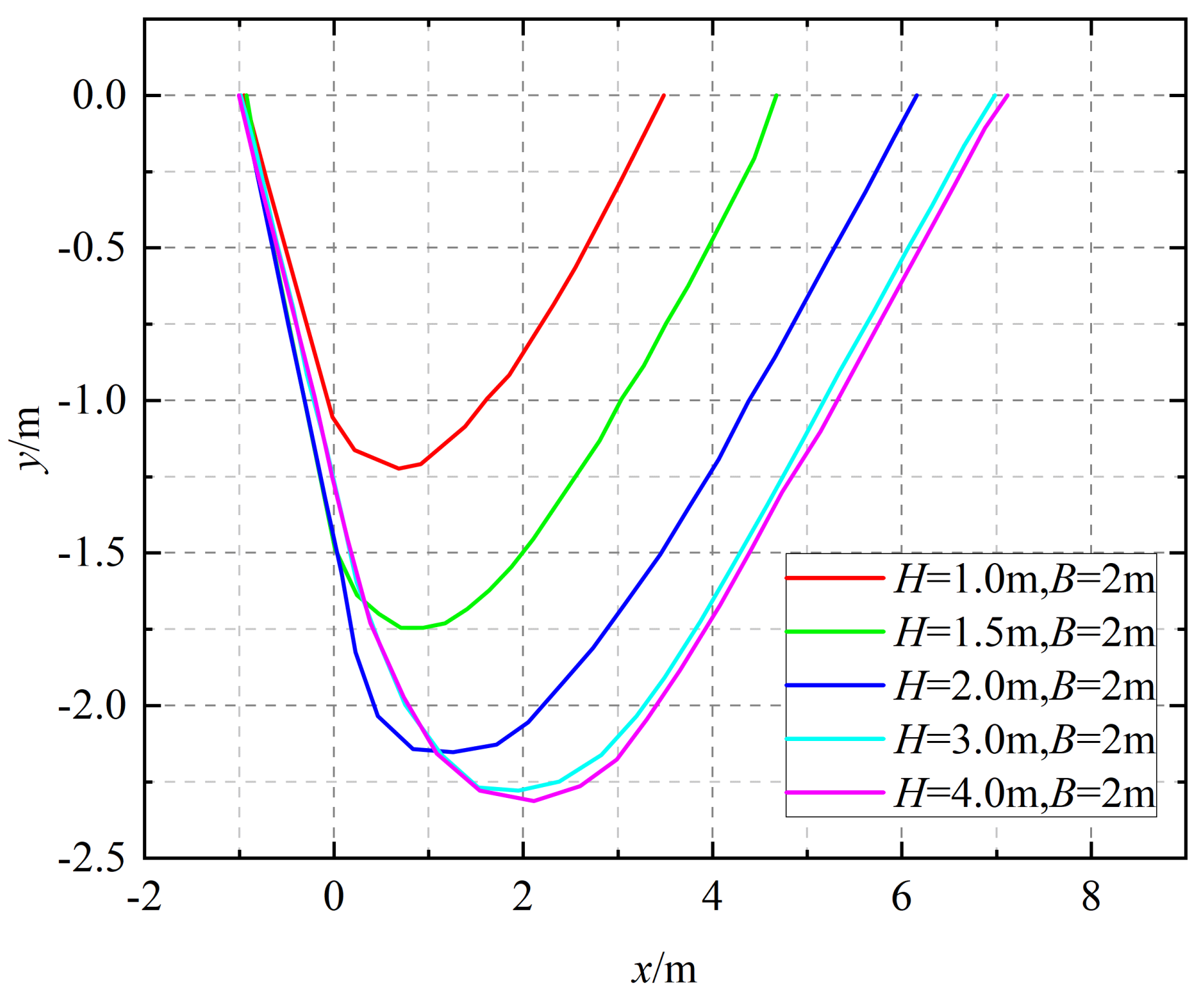
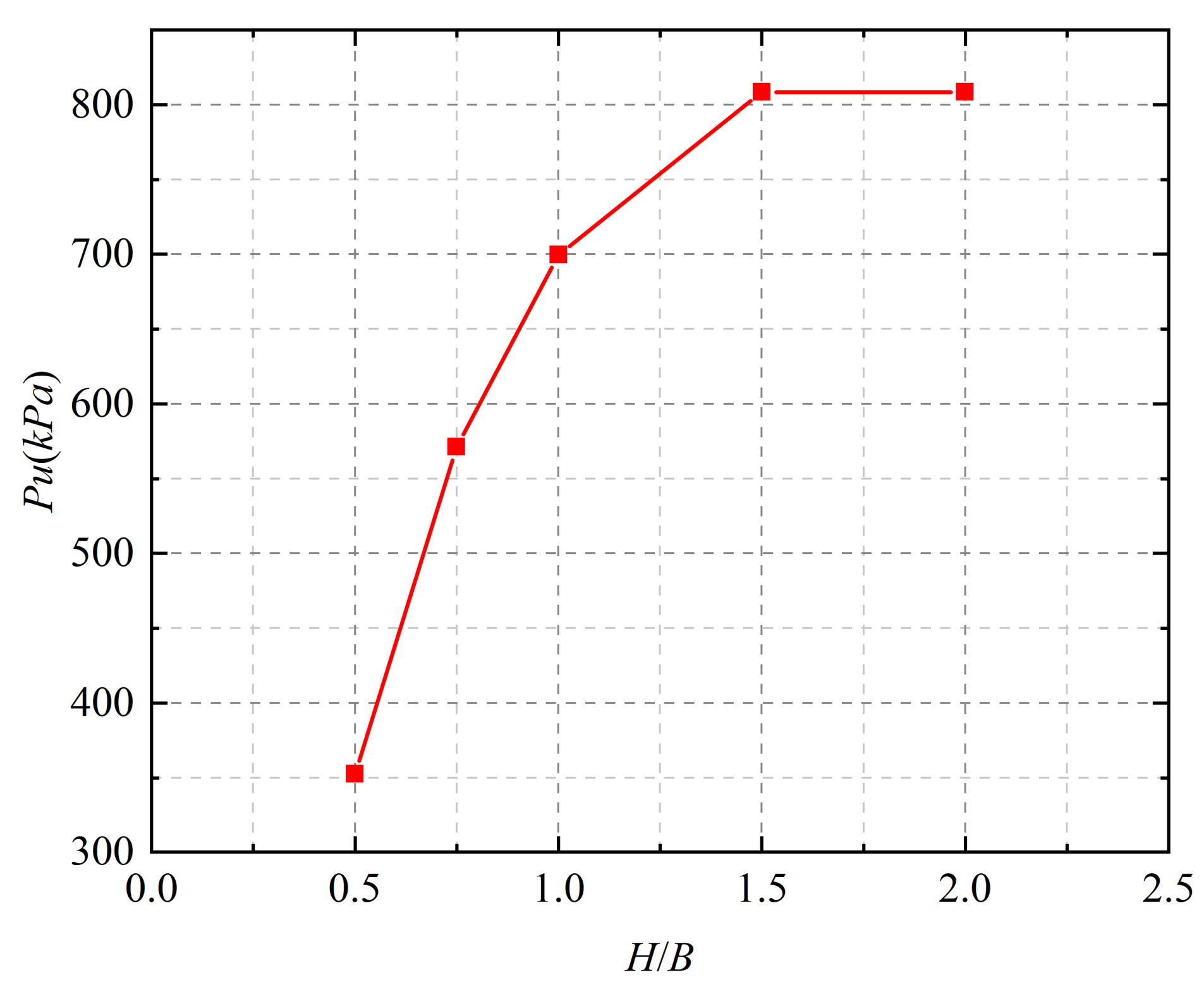
Based on the above assumptions, a planar kinematically permissible multi–block failure mechanism under vertical uniform load is established (Take the right half for a diagram), as shown in Figure 1a. B₀ is the width of the strip footing, H is the thickness of the upper soil, P_u is the vertical uniformly distributed load, q is the overload on both sides, and v₀ is the vertical downward speed of the strip foundation. ${\phi }_1$, ${\gamma }_1$, $c_1$ and ${\phi }_2$, ${\gamma }_2$, $c_2$ are the internal friction angle, soil weight, and cohesion of the upper and lower soil, respectively. In this model, the base angle of the isosceles triangle is marked as θ, and base edge length is B₀. Starting from the rigid block ABC, the remaining rigid blocks are numbered to the nth block in turn from the left to right. For each rigid block, its angle variable is recorded as ${\alpha }_i$ (i = 1, 2, 3, …, n), ${\beta }_i$ (i = 1, 2, 3, …, n), and the side length is recorded as $l_i$ (i = 1, 2, 3, …, n), $d_i$ (i = 1, 2, 3, …, n). The side length can be calculated through the geometric relationship of triangles, and the area of each rigid block is recorded as $S_{\mathit{ABC}}$, $S_i$ (i = 1, 2, 3, …, n). It should be mentioned that, due to the uncertain position of the soil layer boundary, the multi–rigid block failure mechanisms for the two–layered strip foundation are discussed with three cases herein. The soil layer boundary passes through the stiff block ABC in the first case, which is depicted in Figure 1a. 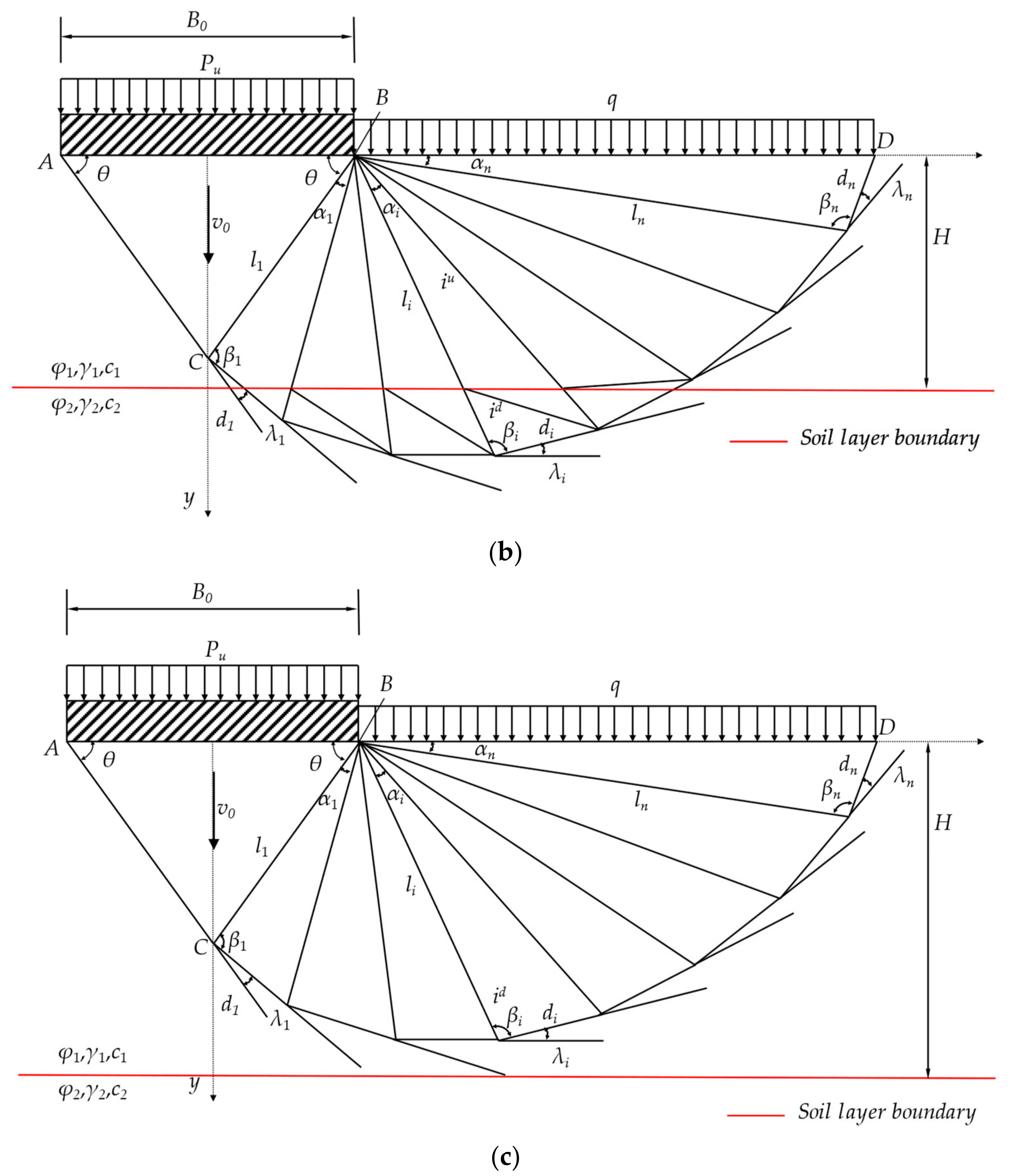The second case is that the soil layer boundary line does not pass through rigid block ABC but passes through some subsequent rigid blocks, which is depicted in Figure 1b. The third case is that the soil layer boundary is completely placed under the foundation failure mechanism, as shown in Figure 1c.

Since the weight of the upper and lower soil layers is different, it is necessary to calculate the gravity of the rigid block of different soil layers. Thus, the superscripts u (up), m (middle), and d (down) are used to differ the variables of the rigid block in the upper and lower soil layers, respectively.

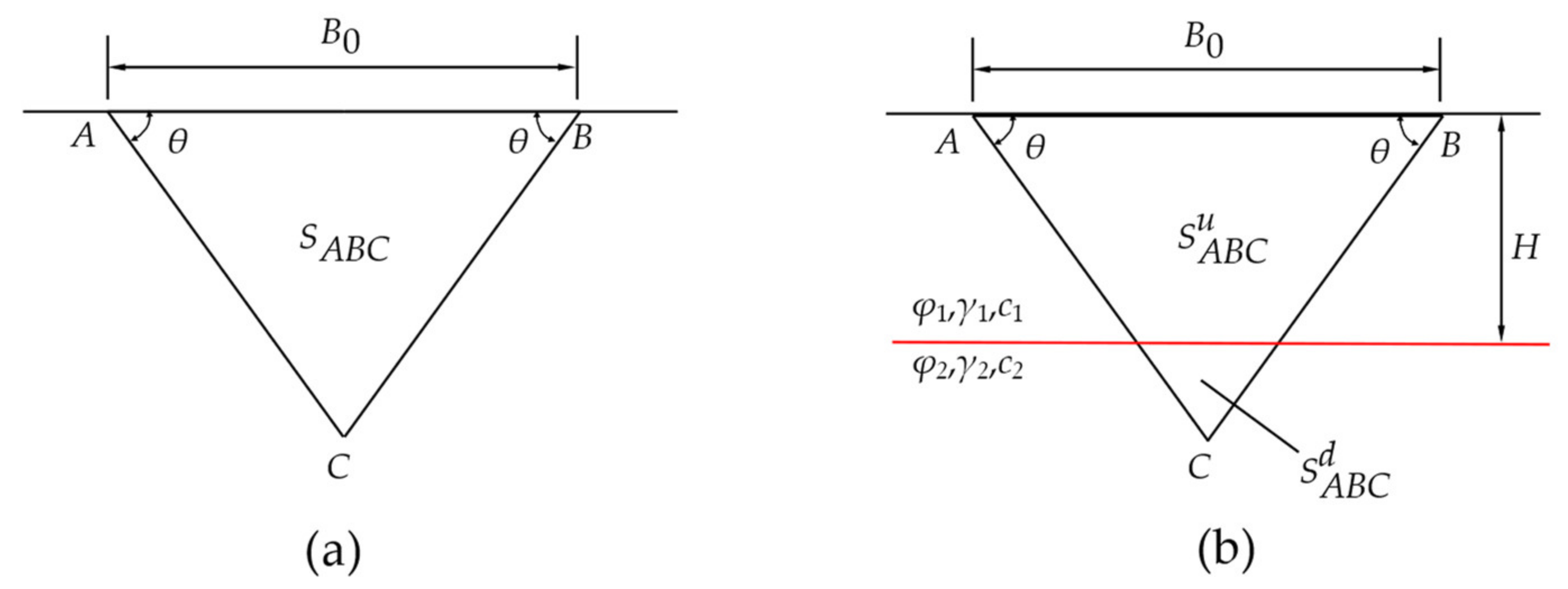
The rigid blocks in the multi–rigid block failure mechanism of the two–layered strip foundation are divided into three types to calculate their area. The rigid block ABC is Type I. The failure mechanism of a stiff block of Type II only penetrates the top layer of soil, while that of Type III penetrates two soil layers.

(1)

Type I

When calculating Type I, there are two cases, that is, whether Type I passes through the upper and lower soil layers at the same time, as shown in Figure 2a,b.

It is necessary to determine whether the rigid block ABC passes through the two layers soil by Equation (1). If Equation (1) is valid, Type I passes through the two–layered soil, and is calculated according to Figure 2a. The area expression is shown in Equation (2), otherwise, Type I does not pass through the two–layered soil. It is calculated according to Figure 2b, and the area expression is shown in Equation (3).

$$\frac{B_0}{2} \times \tan \theta > H$$

(1)

$$S_{\mathit{ABC}}=\left(\frac{B_0^2}{2}\right)\tan \theta$$

(2)

$$\left.\begin{array}{c}{S}_{\mathit{ABC}}^u=H\left(B_0-\frac{H}{\tan \theta }\right)\\ S_{\mathit{ABC}}^d={\left(\frac{B_0}{2}\right)}^2\tan \theta -S_{\mathit{ABC}}^u\end{array}\right\}$$

(3)

where $S_{\mathit{ABC}}$ represents the area of the rigid block in Figure 2a. $S_{\mathit{ABC}}^u$ represents the area containing only upper soil in Figure 2b. $S_{\mathit{ABC}}^d$ represents the area of the lower triangle in Figure 2b.

(2)

Type II and Type III

For other rigid blocks i except for Type I, it is necessary to determine whether the rigid block belongs to Type II or Type III by Equation (4). When Equation (4) is valid, it means that the rigid block i passes through the two–layered soil, which belongs to Type III. The rigid block needs to be divided into two rigid blocks, namely, i^u and i^d, for calculation. Otherwise, it means that the rigid block i belongs to Type II, which can be calculated directly.

$$l_i \times \sin \left(\theta +{\displaystyle \sum }_{i=1}^{i-1}{\alpha }_i\right) > H$$

(4)

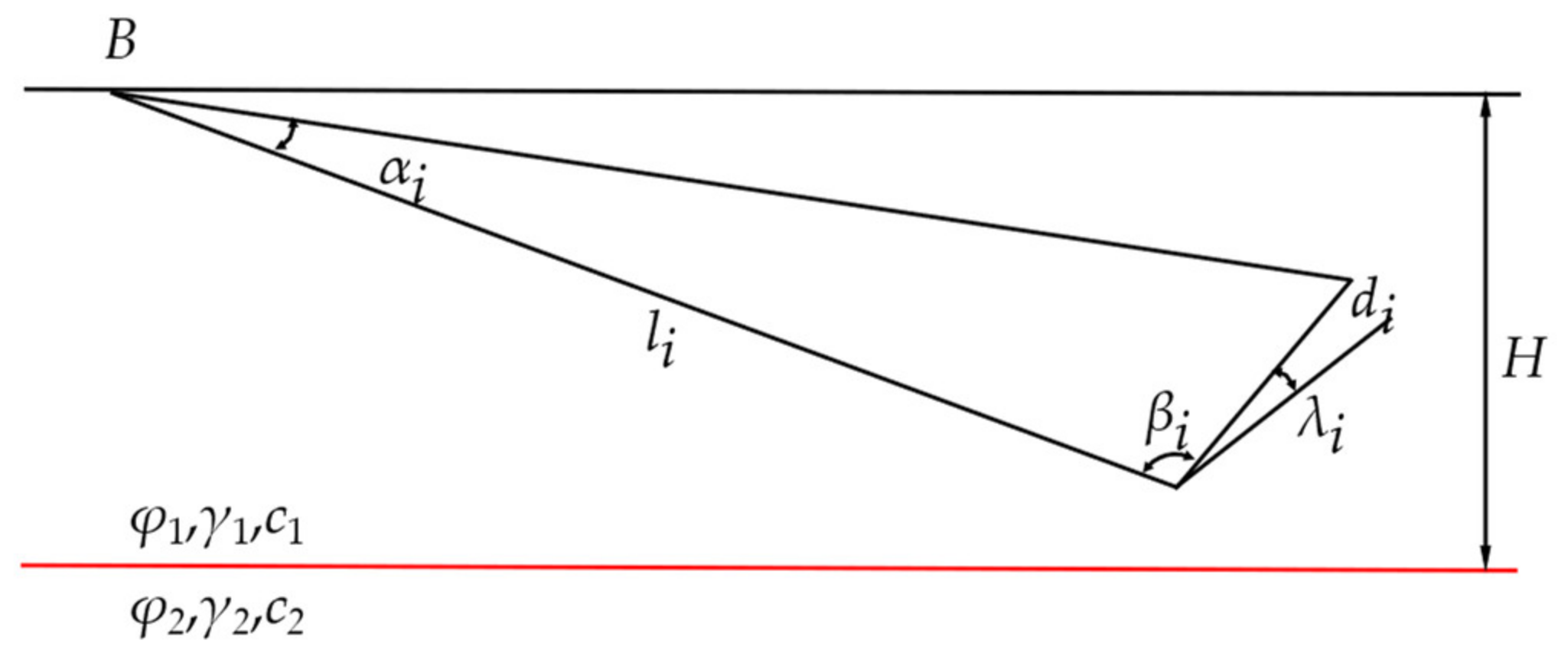
The triangular rigid block i of Type II is shown in Figure 3, and its variable expression is shown in Equation (5):

$$S_i=\frac{1}{2}{l}_i{d}_i{\sin \beta }_i$$

(5)

where l_i and d_i represent the two side lengths of the rigid block i, and S_i represents the area of the rigid block i.

For the triangular rigid block of Type III, the rigid block i^d is composed of a triangle. Since the rigid block i^u is in two layers of soil, it will be divided into two areas, namely, $S_i^u$ and $S_i^m$, as shown in Figure 4. The area expression such as Equations (6)–(8):

$$S_i^u=\frac{1}{2}{l}_i^u{l}_i^m\sin \left(\theta +{\displaystyle \sum }_{i=1}^{i-1}{\alpha }_i^u\right)$$

(6)

$$S_i^m=\frac{1}{2}{d}_i^u{l}_i^m\sin \left(\beta -\theta -{\displaystyle \sum }_{i=1}^{i-1}{\alpha }_i^u\right)$$

(7)

$$S_i^d=\frac{1}{2}{d}_i^d{l}_i^d\sin \left({\beta }_i^d\right)$$

(8)

where the parameters with superscripts u and d represent the parameters on the corresponding small rigid block after the rigid block of Type III is divided into upper and lower rigid blocks i^u and i^d. $l_i^m$ is the length of the soil layer boundary line passing through the $i^u$ rigid block. $S_i^u$ refers to the area where the $i^u$ rigid block belongs to the upper soil. $S_i^m$ is the area of the i^u rigid block that belongs to the subsoil. $S_i^d$ is the area of the i^d rigid block.

The transition of two types of different rigid blocks needs to be calculated separately, as shown in Figure 5. It means that the area formula will be different from the above situation when the type III rigid block is transformed into a Type II rigid block. $S_i^m$ means that the soil layer where the area is located has changed, but the solution idea is similar, so it will not be repeated here.

2.2. Establishment of the Permissible Velocity Field

To do an upper-bound analysis of strip footing under vertical uniform load, a flexible permitted velocity field must be created for each rigid block. The allowable velocity field can be determined using the triangular geometric relationship of the allowable velocity field. The absolute and relative velocity vectors of three types of rigid blocks are analyzed and solved, respectively:

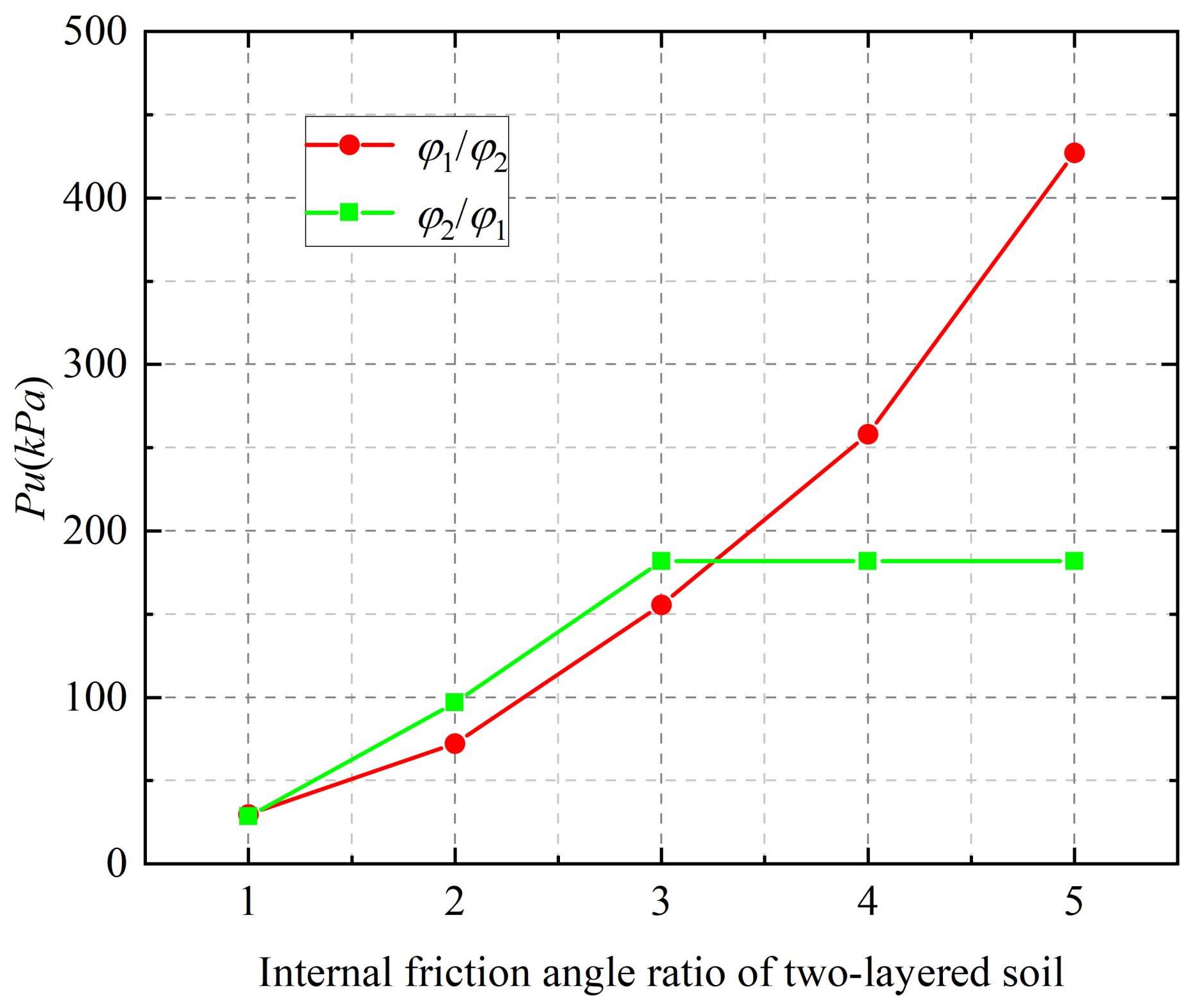
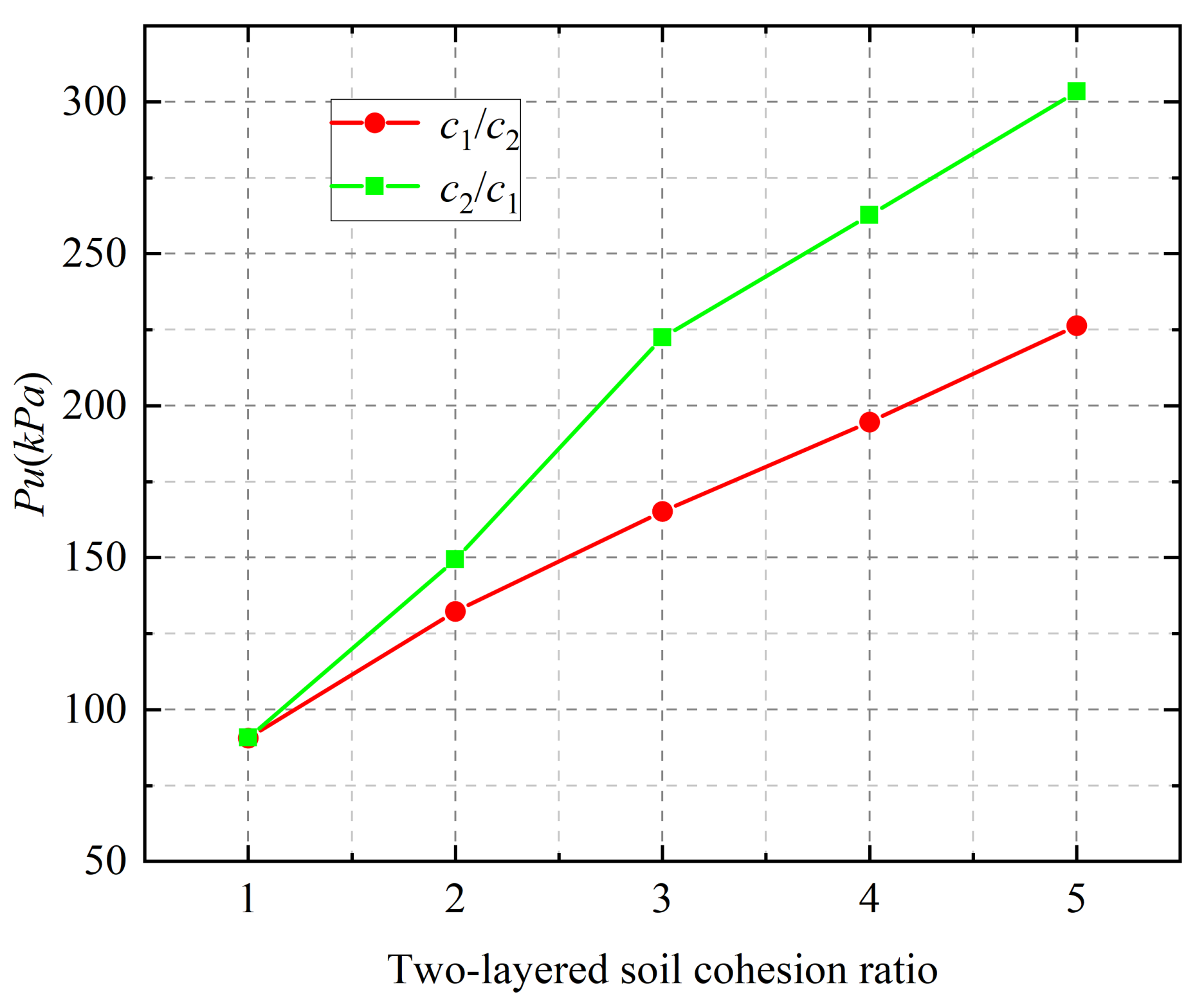
In Equations (9)–(33), the internal friction angle of the upper soil is φ₁. The internal friction angle of the soil is φ₂. θ is the bottom angle of rigid block ABC. ${\displaystyle \sum }_{i=1}^{i-1}{\alpha }_i$ is the sum of i − 1 triangle the rigid block’s top angle ${\alpha }_1$ before rigid block i. ${\beta }_i^u$ is the bottom angle β of rigid block i^u. ${\theta }_i^u$, ${\theta }_{i^d}^v$ and ${\theta }_{i^u}^v$ represents the absolute velocity vector direction angle of rigid block i, rigid block i^d, and rigid block i^u, where ${\theta }_i^v$ is determinable. $v_i$, $v_{i^d}$ and $v_{i^u}$ represents the absolute velocity vector of rigid block i, rigid block i^d, and rigid block i^u. The relative speed between the two rigid blocks, i − 1 and i, is represented by $v_{i-1,i}$. The expression of relative velocity between the other rigid blocks is similar, so it will not be repeated.

• For rigid block: Type I

When the two–layered strip foundation fails, rigid block ABC of Type I is designed to travel vertically downward at a speed of v₀.

• For rigid block: Type II

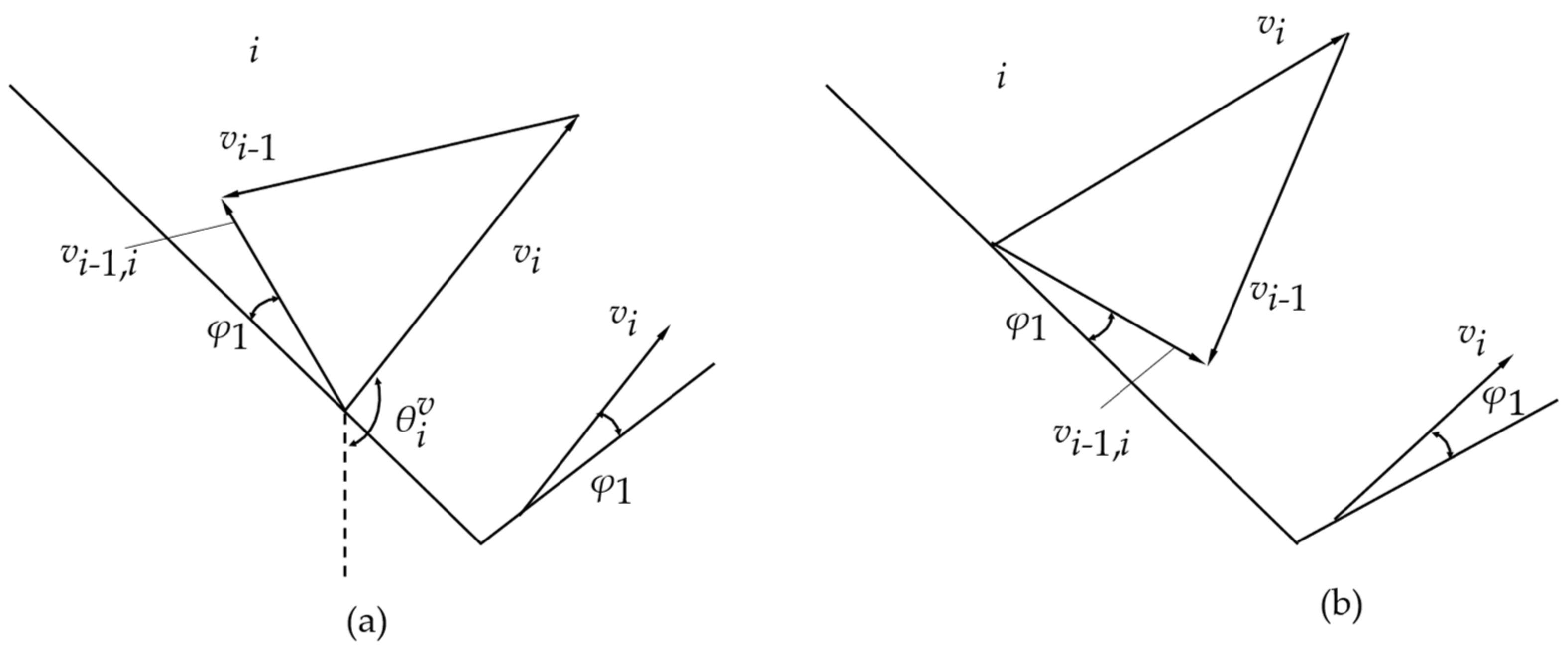
During the analysis of Type II, due to the uncertainty of the relative motion direction between rigid blocks, there are two cases of compatible velocity relationship between rigid blocks i and rigid blocks i − 1, as shown in Figure 6.

According to the compatible velocity vector triangle in two cases, we can calculate v_i−1,i using the Equations (9) and (10) or the Equations (11) and (12).

• Case: II–1: (Figure 6a)

For Figure 6a, the relative velocity $v_{i-1,i}$ between rigid blocks i and i − 1 face upwards along the velocity discontinuity and form an angle φ₁.

$$v_i=\frac{\sin \left(\frac{\pi }{2}{+\phi }_1{+\theta }_{i-1}^v-\theta -{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i\right)}{\sin \left(-\frac{\pi }{2}-{\phi }_1-{\theta }_i^v+\theta +{{\displaystyle \sum }}_1^{i-1}{\alpha }_i\right)}{v}_{i-1}$$

(9)

$$v_{i-1,i}=\frac{\sin \left({\theta }_i^v-{\theta }_{i-1}^v\right)}{\sin \left(-\frac{\pi }{2}-{\phi }_1-{\theta }_i^v+\theta +{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i\right)}{v}_{i-1}$$

(10)

Equation (11) applies to case: II −1: (Figure 6a):

$$\left.\begin{array}{c}{\theta }_i^v>{\theta }_{i-1}^v\\ -\frac{\pi }{2}{<\phi }_1{+\theta }_{i-1}^v-\theta -{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i<\frac{\pi }{2}\\ \frac{\pi }{2}<-{\phi }_1-{\theta }_i^v+\theta +{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i<\frac{3\pi }{2}\end{array}\right\}$$

(11)

• Case: II–2: (Figure 6b)

In the second case in Figure 6b, the relative velocity v_i−1,i between rigid blocks i − 1 and i face downward along the velocity discontinuity φ₁.

$$v_i=\frac{\sin \left(\frac{\pi }{2}{+\phi }_1-{\theta }_{i-1}^v+\theta +{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i\right)}{\sin \left(\frac{\pi }{2}-{\phi }_1{+\theta }_i^v-\theta -{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i\right)}{v}_{i-1}$$

(12)

$$v_{i-1,i}=\frac{\sin \left({\theta }_{i-1}^v-{\theta }_i^v\right)}{\sin \left(\frac{\pi }{2}-{\phi }_1{+\theta }_i^v-\theta -{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i\right)}{v}_{i-1}$$

(13)

To make Equations (12) and (13) work, the following requirements need to be met:

$$\left.\begin{array}{c}{\theta }_i^v{ < \theta }_{i-1}^v\\ -\frac{\pi }{2}{<\phi }_1-{\theta }_{i-1}^v+\theta +{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i<\frac{\pi }{2}\\ -\frac{\pi }{2}<-{\phi }_1{+\theta }_i^v-\theta -{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i<\frac{\pi }{2}\end{array}\right\}$$

(14)

It should be noted that when the rigid block (i − 1) belongs to Type III, that is, at the joint of two types of rigid blocks, $v_{i-1}{, \theta }_{i-1}^v{ \mathrm{and} v}_{i-1,i}$ in the above formula should be changed to $v_{i-1^u}{, \theta }_{i-1^u}^v{ \mathrm{and} v}_{i-1^u,i}$ for calculation.

• For rigid block: TypeIII

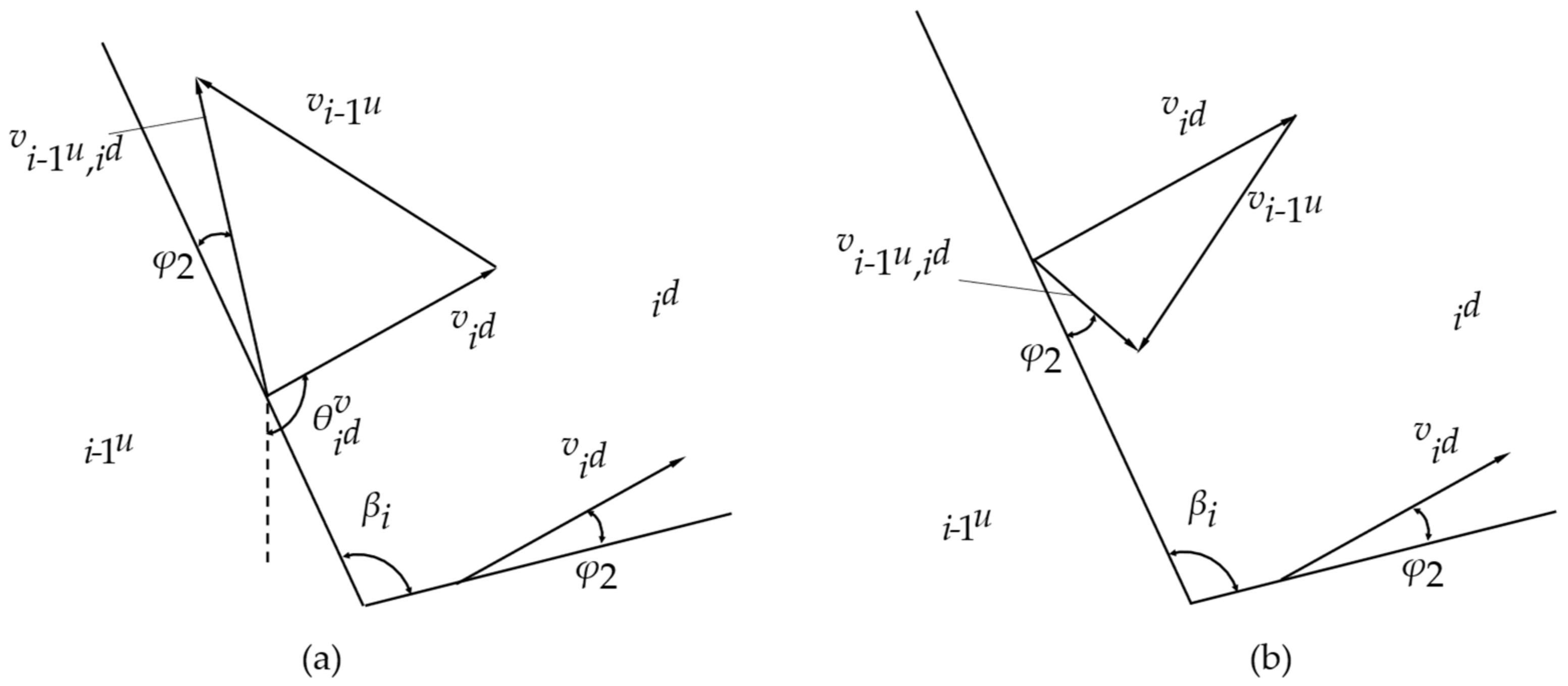
The velocity vector solution of Type III shall be divided into two rigid blocks: i^u and i^d. Rigid block i^u and i^d are, respectively, the upper and the lower parts of each rigid block i of Type III separated by the intersection of the boundary line of the foundation soil layer and the triangle edge connecting the vertex of the triangle. In the calculation process, it is necessary to analyze the permissible velocity relationship between rigid block i − 1^u and rigid block i^d, rigid block i − 1^u and rigid block i^u, rigid block i^d and rigid block i^u. Then, the relative velocity of rigid block i^u and i^d are solved simultaneously through the permissible velocity relation.

Type III–i^d:

According to the relationship of permissible velocity between rigid block i − 1^u and i^d, the direction angle of the velocity vector of rigid block i^d can be obtained as Equation (15).

$${\theta }_{i^d}^v=\frac{\pi }{2}-{\beta }_{i^d}{+\phi }_2+\theta +{\displaystyle \sum }_{i=1}^{i-1}{\alpha }_i^u$$

(15)

As shown in Figure 7, there are two cases of permissible velocity relationship between rigid block $i-1^u$ and i^d:

According to the compatible velocity vector triangle in two cases:

• Case: III–i^d rigid block −1 (Figure 7a)

For Figure 7a, the relative velocity $v_{i-1^u{,i}^d}$ between the rigid block i − 1^u and i^d face upwards along the velocity discontinuity and forms an angle φ₂.

$$v_{i^d}=\frac{\sin (\frac{\pi }{2}{+\phi }_2{+\theta }_{i-1^u}^v-\theta -{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i^u)}{\sin (\frac{\pi }{2}-{\phi }_2-{\theta }_{i^d}^v+\theta +{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i^u)}{v}_{i-1^u}$$

(16)

$$v_{i-1^u{,i}^d}=\frac{{\sin (\theta }_{i^d}^v-{\theta }_{i-1^u}^v)}{\sin (\frac{\pi }{2}-{\phi }_2-{\theta }_{i^d}^v+\theta +{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i^u)}{v}_{i-1^u}$$

(17)

Requirements of Equations (16) and (17):

$$\left.\begin{array}{c}{\theta }_{i^d}^v{>\theta }_{i-1^u}^v\\ -\frac{\pi }{2}{<\phi }_2{+\theta }_{i-1^u}^v-\theta -{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i^u<\frac{\pi }{2}\\ -\frac{\pi }{2}<-{\phi }_2-{\theta }_{i-1^u}^v+\theta +{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i^u<\frac{\pi }{2}\end{array}\right\}$$

(18)

• Case: III–i^d rigid block −2 (Figure 7b)

The relative velocity $v_{i-1^u{,i}^d}$ between the rigid block $i-1^u$ and $i^d$ in Figure 7b face downward along the velocity discontinuity and forms an angle φ₂.

$$v_{i^d}=\frac{\sin (\frac{\pi }{2}{+\phi }_2-{\theta }_{i-1^u}^v+\theta +{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i^u)}{\sin (\frac{\pi }{2}-{\phi }_2{+\theta }_{i^d}^v-\theta -{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i^u)}{v}_{i-1^u}$$

(19)

$$v_{i-1^u{,i}^d}=\frac{{\sin (\theta }_{i-1^u}^v-{\theta }_{i^d}^v)}{\sin (\frac{\pi }{2}-{\phi }_2{+\theta }_{i^d}^v-\theta -{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i^u)}{v}_{i-1^u}$$

(20)

Requirements of Equations (19) and (20)

$$\left.\begin{array}{c}{\theta }_{i^d}^v{<\theta }_{i-1^u}^v\\ -\frac{\pi }{2}{<\phi }_2-{\theta }_{i-1^u}^v+\theta +{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i^u<\frac{\pi }{2}\\ -\frac{\pi }{2}<-{\phi }_2{+\theta }_{i^d}^v-\theta -{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i^u<\frac{\pi }{2}\end{array}\right\}$$

(21)

Since the direction angle ${\theta }_{i^d}^v$ of the rigid block is known, it is possible to calculate the absolute and relative velocity vectors of the rigid block $i^d$ directly for the identified multi–rigid block failure mechanism.

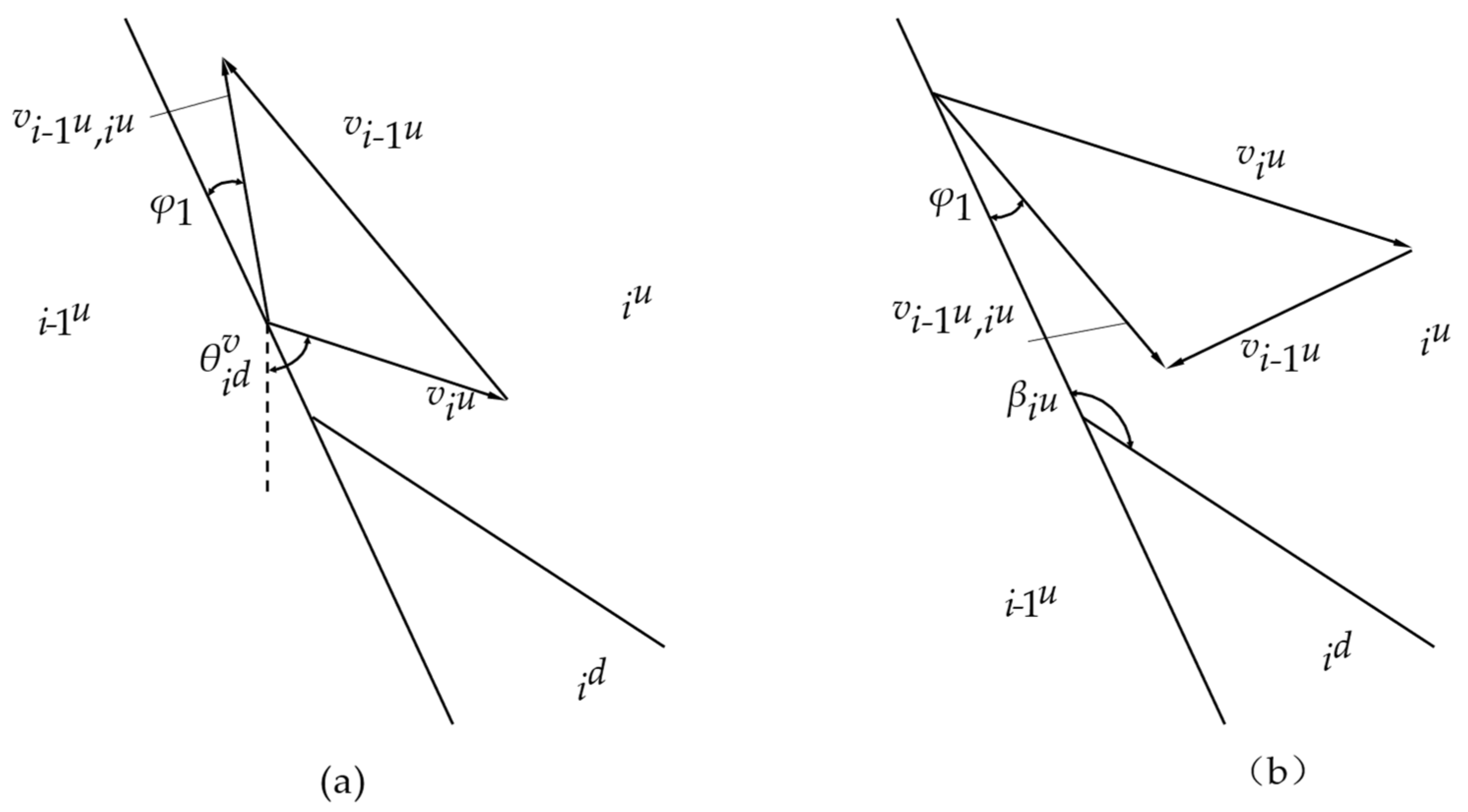
Type III–i^u:

For rigid block i^u, since the direction angle ${\theta }_{i^u}^v$ of its absolute velocity vector cannot be determined directly, it is necessary to analyze the compatible velocity relationship between rigid block i − 1^u and i^u, rigid block i^d and i^u, and perform simultaneous solution.

(1)

Type Ⅲ–ⅰ^u rigid block and i − 1^u rigid block:

The compatible velocity relationship of rigid block $i^u \mathrm{and} i-1^u$, as shown in Figure 8:

Case: 1 (Figure 8a)

For Figure 8a, the relative velocity $v_{i-1^u{,i}^u}$ between the rigid block i − 1^u and i^u face upwards along the velocity discontinuity and forms an angle φ₁

$$v_{i^u}=\frac{\sin (\frac{\pi }{2}{+\phi }_1{+\theta }_{i-1^u}^v-\theta -{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i^u)}{\sin (\frac{\pi }{2}-{\phi }_1-{\theta }_{i^u}^v+\theta +{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i^u)}{v}_{{i-1}^u}$$

(22)

$$v_{i-1^u{,i}^u}=\frac{{\sin (\theta }_{i^u}^v-{\theta }_{i-1^u}^v)}{\sin (\frac{\pi }{2}-{\phi }_1-{\theta }_{i^u}^v+\theta +{{\displaystyle \sum }}_{i=1}^{i-1}{\alpha }_i^u)}{v}_{i-1^u}$$

(23)

Requirements of Equations (22) and (23):

$$\left.\begin{array}{c}{\theta }_{i^u}^v{>\theta }_{i-1^u}^v\\ -\frac{\pi }{2}{<\phi }_1{+\theta }_{i-1^u}^v-\theta -{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i^u<\frac{\pi }{2}\\ -\frac{\pi }{2}<-{\phi }_1-{\theta }_{i^u}^v+\theta +{\displaystyle \sum _{i=1}^{i-1}}{\alpha }_i^u<\frac{\pi }{2}\end{array}\right\}$$

• Case: 2 (Figure 8b)

The relative velocity $v_{i-1^u{,i}^u}$ between the rigid block in Figure 8b face downward along the velocity discontinuity and forms an angle φ₁.

$$v_{i^u}=\frac{\sin (\frac{\pi }{2}{+\phi }_1-{\theta }_{i-1^u}^v+\theta +{{\displaystyle \sum }}_1^{i-1}{\alpha }_i^u)}{\sin (\frac{\pi }{2}-{\phi }_1{+\theta }_{i^u}^v-\theta -{{\displaystyle \sum }}_1^{i-1}{\alpha }_i^u)}{v}_{i-1^u}$$

(24)

$$v_{i-1^u{,i}^u}=\frac{{\sin (\theta }_{i-1^u}^v-{\theta }_{i^u}^v)}{\sin (\frac{\pi }{2}-{\phi }_1{+\theta }_{i^u}^v-\theta -{{\displaystyle \sum }}_1^{i-1}{\alpha }_i^u)}{v}_{i-1^u}$$

(25)

Requirements of Equations (24) and (25):

$$\left.\begin{array}{c}{\theta }_{i^u}^v{<\theta }_{i-1^u}^v\\ -\frac{\pi }{2}{<\phi }_1-{\theta }_{i-1^u}^v+\theta +{\displaystyle \sum _1^{i-1}}{\alpha }_i^u<\frac{\pi }{2}\\ -\frac{\pi }{2}<-{\phi }_1{+\theta }_{i^u}^v-\theta -{\displaystyle \sum _1^{i-1}}{\alpha }_i^u<\frac{\pi }{2}\end{array}\right\}$$

(26)

(2)

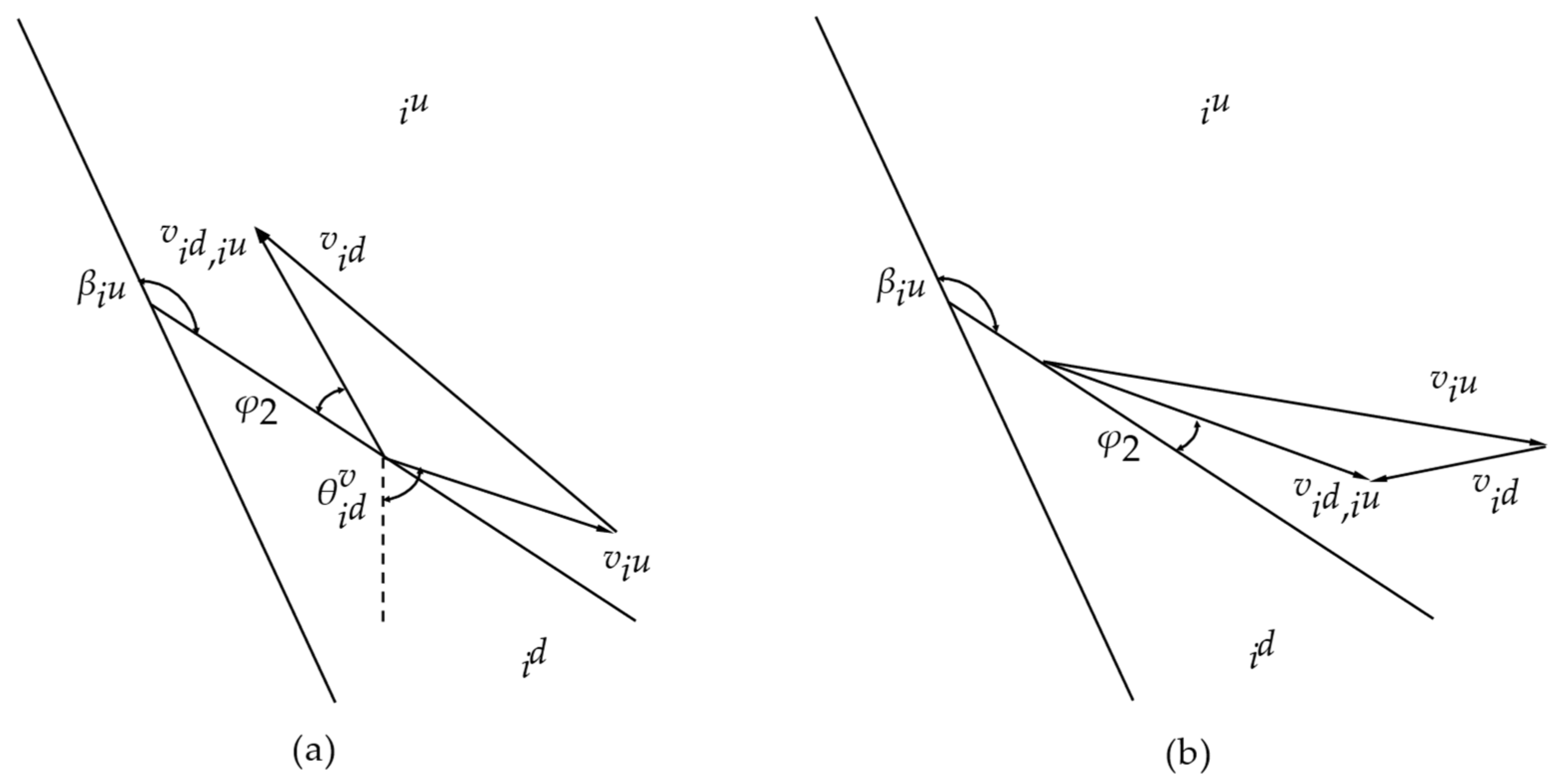
Type III–ⅰ^u and i^d:

The possibility of two compatible velocity relationships between rigid block $i^u$ and $i^d$ is shown in Figure 9:

• Case: 3 (Figure 9a)

For Figure 9a, the relative velocity $v_{i^d{,i}^u}$ between the rigid block i^d and i^u face upwards along the velocity discontinuity and forms an angle φ₂.

$$v_{i^u}=\frac{\sin (-\frac{\pi }{2}{+\phi }_2{+\beta }_i^u{+\theta }_{i^d}^v-\theta -{{\displaystyle \sum }}_1^{i-1}{\alpha }_i^u)}{\sin (\frac{3\pi }{2}-{\phi }_2-{\beta }_i^u-{\theta }_{i^u}^v+\theta +{{\displaystyle \sum }}_1^{i-1}{\alpha }_i^u)}{v}_{i^d}$$

(27)

$$v_{i^d{,i}^u}=\frac{{\sin (\theta }_{i^u}^v-{\theta }_{i^d}^v)}{\sin (\frac{3\pi }{2}-{\phi }_2-{\beta }_i^u-{\theta }_{i^u}^v+\theta +{{\displaystyle \sum }}_1^{i-1}{\alpha }_i^u)}{v}_{i^d}$$

(28)

Requirements of Equations (27) and (28):

$$\left.\begin{array}{c}{\theta }_{i^u}^v{>\theta }_{i^d}^v\\ \frac{\pi }{2}{<\phi }_2{+\beta }_i^u{+\theta }_{i^d}^v-\theta -{\displaystyle \sum _1^{i-1}}{\alpha }_i^u<\frac{3\pi }{2}\\ -\frac{3\pi }{2}<-{\phi }_2-{\beta }_i^u-{\theta }_{i^u}^v+\theta +{\displaystyle \sum _1^{i-1}}{\alpha }_i^u<-\frac{\pi }{2}\end{array}\right\}$$

(29)

• Case: 4 (Figure 9b)

The relative velocity $v_{i^d{,i}^u}$ between the rigid block in Figure 9b faces downward along the velocity discontinuity and forms an angle φ₂.

$$v_{i^u}=\frac{\sin (\frac{3\pi }{2}{+\phi }_2-{\beta }_i^u-{\theta }_{i^d}^v+\theta +{{\displaystyle \sum }}_1^{i-1}{\alpha }_i^u)}{\sin (-\frac{\pi }{2}-{\phi }_2{+\beta }_i^u{+\theta }_{i^u}^v-\theta -{{\displaystyle \sum }}_1^{i-1}{\alpha }_i^u)}{v}_{i^d}$$

(30)

$$v_{i^d{,i}^u}=\frac{{\sin (\theta }_{i^d}^v-{\theta }_{i^u}^v)}{\sin (-\frac{\pi }{2}-{\phi }_2{+\beta }_i^u{+\theta }_{i^u}^v-\theta -{{\displaystyle \sum }}_1^{i-1}{\alpha }_i^u)}{v}_{i^d}$$

(31)

Requirements of Equations (30) and (31):

$$\left.\begin{array}{c}{\theta }_{i^u}^v{<\theta }_{i^d}^v\\ -\frac{3\pi }{2}{<\phi }_2-{\beta }_i^u-{\theta }_{i^d}^v+\theta +{\displaystyle \sum _1^{i-1}}{\alpha }_i^u<-\frac{\pi }{2}\\ \frac{\pi }{2}{<\phi }_2-{\beta }_i^u-{\theta }_{i^d}^v+\theta +{\displaystyle \sum _1^{i-1}}{\alpha }_i^u<\frac{3\pi }{2}\end{array}\right\}$$

(32)

To solve the velocity vector of rigid block i^u, it can be seen from the above that there are four cases (2*2). For example, we can get ${\theta }_{i^u}^v$ by Equations (22) and (27) and then get each velocity vector by substituting Equations (22), (23), (27) and (28). The other three cases are also considered similar.

When calculating the velocity vector of Type III rigid blocks, there will be two types of connections in the two–layered strip foundation multi–rigid block failure mechanism. If the rigid block i − 1 is Type II, it is only necessary to replace all rigid blocks i − 1^u in the above calculation formula with rigid block i − 1 to calculate normally.

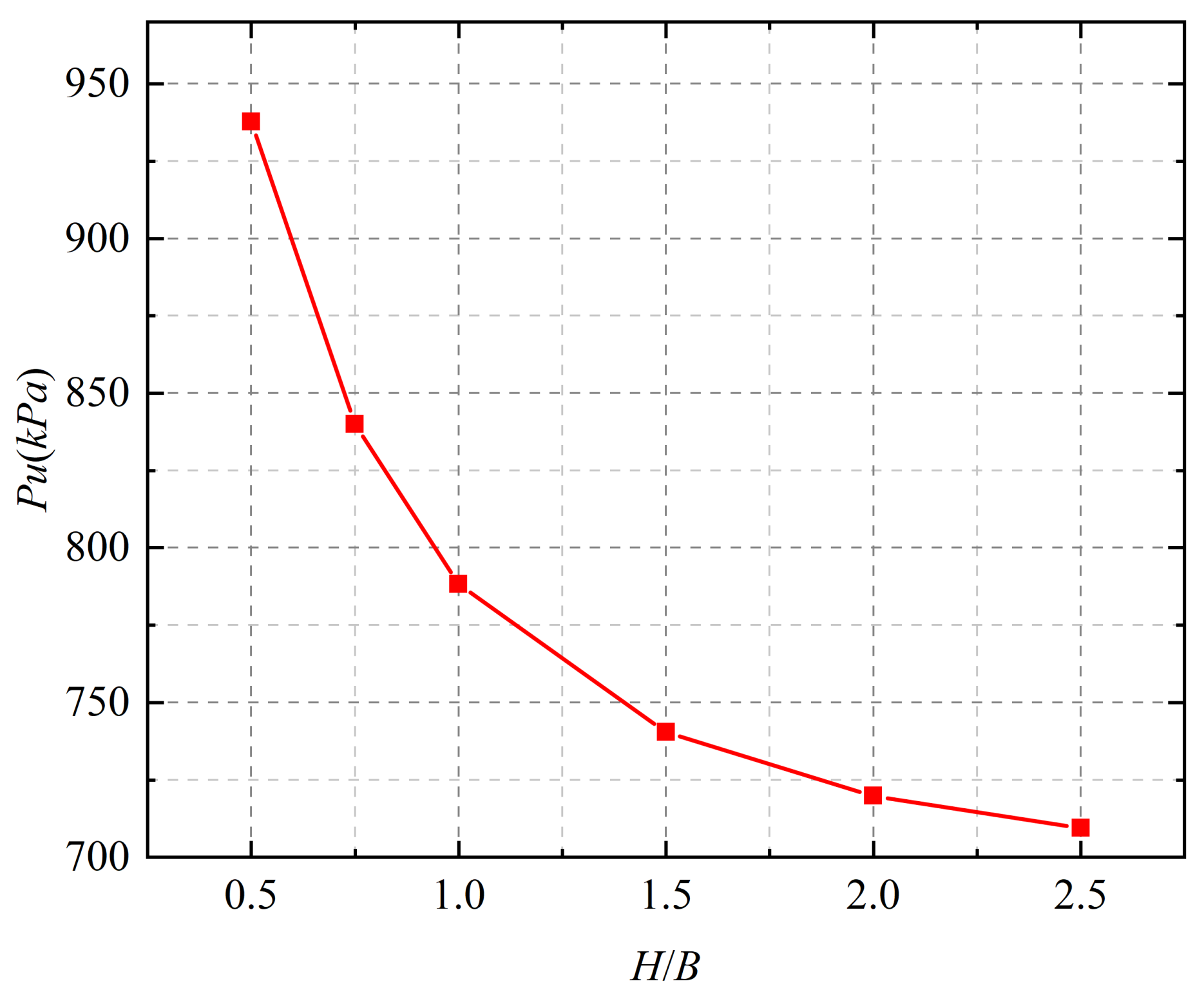
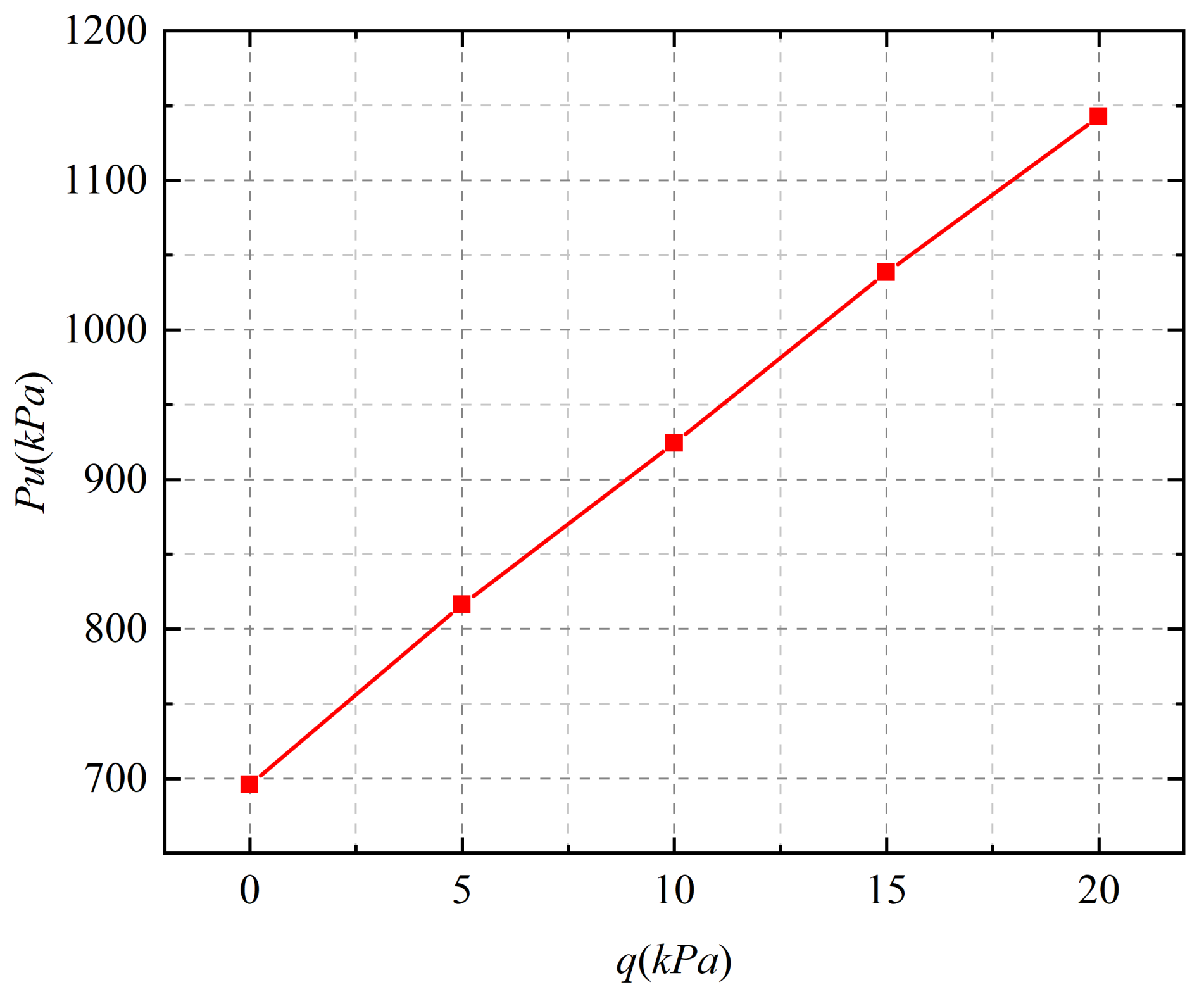
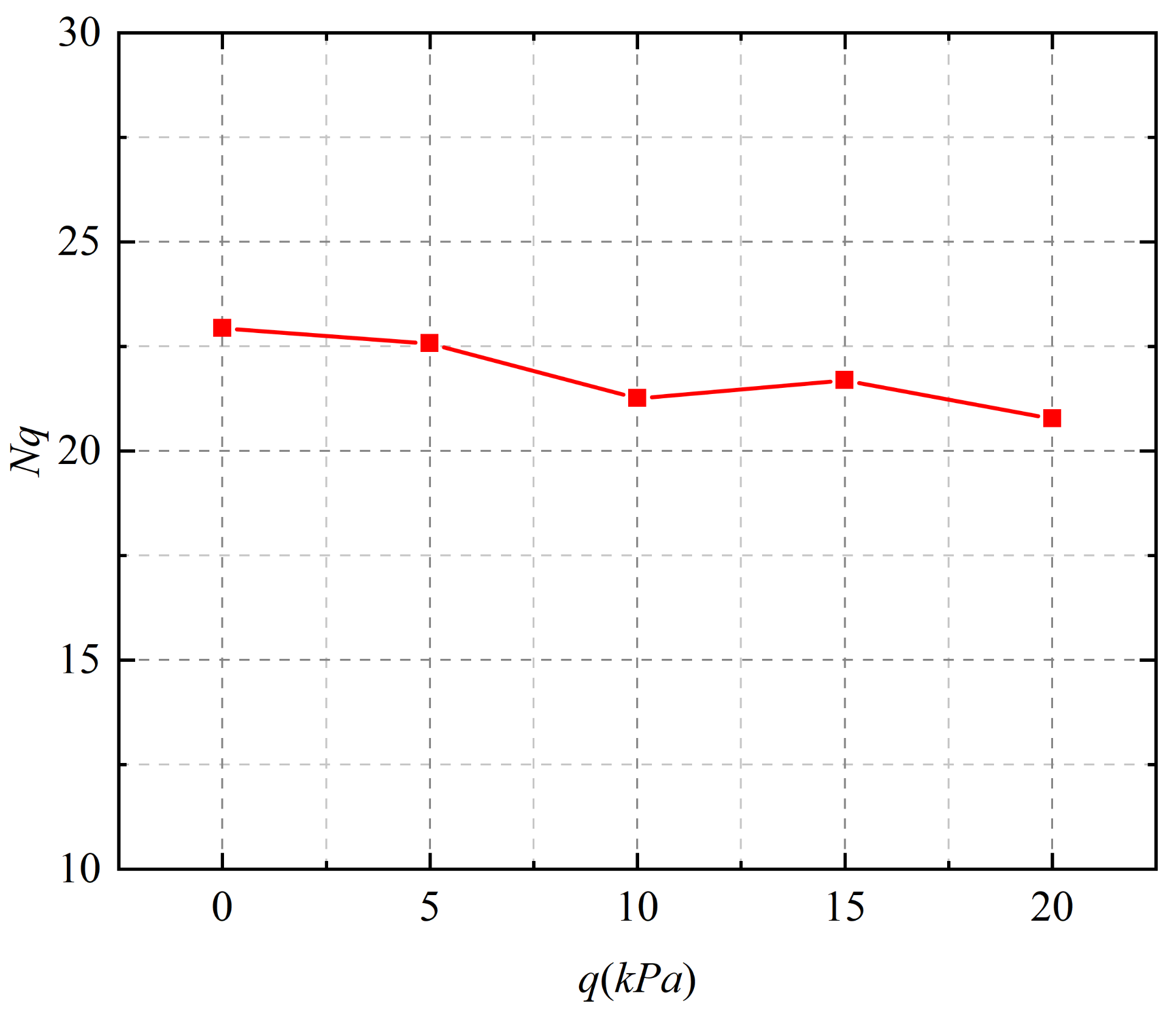
2.3. Upper Limit Solution of Ultimate Bearing Capacity of Two–Layered Foundation

The virtual work theory serves as the foundation for the upper−bound limit analysis theorem. According to the virtual work concept, the elastic−plastic material deforms with a little displacement (virtual displacement). According to Equation (33), under the influence of this virtual displacement, the virtual external power produced by the external force acting on the elastic−plastic material is equal to the virtual internal power produced by the system’s internal virtual strain.

$${{\displaystyle \int }}_V{F}_i{\mathit{du}}_i{d}_V+{{\displaystyle \int }}_S{T}_i{\mathit{du}}_i\mathit{dS}={{\displaystyle \int }}_V{\mathsf{\sigma }}_{\mathit{ij}}{d\mathsf{\epsilon }}_{\mathit{ij}}\mathit{dV}$$

(33)

In the multi–rigid block failure mechanism of the two–layered strip foundation, the work performed by the external force includes: the power ${\dot{W}}_{\mathit{Pu}}$ made by the ultimate load Pu of the foundation, the power ${\dot{W}}_q$ made by the overload q on both sides of the foundation, and the power $G_i$ made by the gravity of each rigid block. Where ${\dot{W}}_{\mathit{ABC}}$ represents gravity work of No.0 rigid block, ${\dot{W}}_{i^u}$ and ${\dot{W}}_{i^d}$ represent gravity work of rigid block $i^u$ and $i^d$, and ${\dot{W}}_i$ represents gravity work of rigid block i. The expressions of each external force power are as follows: Equations (35)–(40).

$${\dot{W}}_{\mathit{Pu}}=B_0\cdot P_u{v}_0$$

(34)

$${\dot{W}}_{\mathit{ABC}}={(S}_{\mathit{ABC}}^u\cdot {\gamma }_1{+S}_{\mathit{ABC}}^d\cdot {\gamma }_2)$$

(35)

$${\dot{W}}_i=S_i\cdot {\gamma }_1\cdot v_i\cdot {\theta }_i^v$$

(36)

$${\dot{W}}_i^u={(S}_i^u\cdot {\gamma }_1{+S}_i^m\cdot {\gamma }_2)\cdot v_{i^u}\cdot {\cos \theta }_{i^u}^v$$

(37)

$${\dot{W}}_i^d=S_i^d\cdot {\gamma }_2\cdot v_{i^d}\cdot {\cos \theta }_{i^d}^v$$

(38)

$${\dot{W}}_q=2\cdot q\cdot \frac{l_n{\sin \beta }_n}{\sin (\pi -{\alpha }_n-{\beta }_n)}\cdot v_n{\cos \theta }_n^v$$

(39)

At the connection of different types of rigid blocks, the division of the area of the rigid blocks will be different. It is necessary to recalculate the gravity work $\dot{W_i}$ of its rigid block i, which is similar to the above expression and will not be introduced in detail.

The soil mass does not experience internal plastic deformation according to the upper bound theory of limit analysis, and the internal force energy consumption only happens on the velocity discontinuities $l_i$, $d_i$ (including $l_i^u$, $l_i^d$, $d_i^u$, $d_i^d$, but excluding $l_i^m$, because $l_i^m$ does not belong to the interface of rigid blocks) between adjacent rigid blocks. The internal force energy consumption expression is shown in Equations (40)–(43).

• Type II rigid block:

$$\dot{W_{l_i}}=c_1{l}_i{v}_{i-1,i}\cos \phi$$

(40)

$$\dot{W_{d_i}}=c_1{d}_i{v}_i{\cos \phi }_1$$

(41)

• Type III rigid block:

$$W_{l_i}=c_1{l}_i^u{v}_{i-1^u{,i}^u}{\cos \phi }_1{+c}_2{l}_i^d{v}_{i-1^u{,i}^d}{\cos \phi }_2$$

(42)

$$W_{d_i}=c_2{d}_i^u{v}_{i^d{,i}^u}{\cos \phi }_2{+c}_2{d}_i^d{v}_{i^d}{\cos \phi }_2$$

(43)

where $\dot{W_{l_i}}$ and $\dot{W_{d_i}}$ refer to the internal force energy consumption on the velocity discontinuity between each rigid block in the failure mechanism, and the subscripts l and d correspond to the side lengths L and D of the rigid block in the failure mechanism.

At the connection of different types of rigid blocks, such as Type Ⅲ rigid blocks connected to type Ⅱ rigid blocks, the corresponding c₁ and φ₁ should be used for the calculation of the velocity discontinuity plane $d_i^u$ in Equation (43). Other calculation methods are the same.

According to the principle of virtual work, in the assumed failure model, the external force power and internal energy consumption are equal, then the expression of ultimate bearing capacity Pu can be deduced according to Equation (44).

$$\mathit{Pu}=\frac{\dot{W_l}+\dot{W_d}-{\dot{W}}_{\mathit{soil}}-\dot{W_q}}{B_0\cdot v_0}$$

(44)

3. Improved Radial Movement Optimization (IRMO) Algorithm

The IRMO algorithm [22] can be summarized as the situation that a group of articles moves to seek the global optimal solution in the search space that is shrinking with the change of algebra. After setting a strict and reasonable objective function F and variable value range, the IRMO algorithm starts to randomly generate multiple particles, which are recorded as the initial particle swarm $X_i^1$. The objective function expression F could be used to evaluate the fitness value of each particle, then the particle with the best fitness value is chosen as the central particle of the initial particle swarm and recorded as Center¹ (Center¹ is the first generation of central particles). When generating a new generation particle swarm $Y_i^k$, two additional parameters h₁ and h₂ will be used to decide whether each of the new particles is generated by a central particle or just inherit the particle information from the last generation. As the location information of particles is updated from generation to generation, the search space is shrinking, and its center will move toward the direction of the global optimal solution to the set final generation. Currently, the search space is close to a point, and the corresponding particle location information is the global optimal solution.

3.1. IRMO Algorithm

Based on the radial movement algorithm (RMO), the enhanced radial movement optimization (IRMO) is a global optimization algorithm. The phenomena of a set of particles travelling in a search space that continuously contracts with algebra to find the overall optimal solution can be summed up as the IRMO algorithm. By setting a more strict and reasonable objective function expression F and variable value range, the IRMO algorithm starts to randomly generate multiple particles, denoted as the first–generation particle swarm $X_i^1$. The objective function expression F evaluates the fitness of each particle and takes the best particle as the first–generation central particle, recorded as Center¹. When generating a new generation of particle swarm $Y_i^k$, The IRMO algorithm not only relies on the central particle alone, but also determines that some particles directly inherit the particle information of the adjacent generation according to the control parameters h₁ and h₂. As generations continue to update the position information of particles, the search space continues to shrink, and its center will move towards the direction of the global optimal solution. By the end of the set generation, the search space has approached a point, and the corresponding particle position information is recorded as the global optimal position. The objective function value is the global optimal solution. Figure 10 shows the implementation of the IRMO algorithm [23].

3.2. Implementation of IRMO

According to the above two–layered strip foundation multi–rigid block failure mechanism, for the determination of the critical sliding surface, only the bottom angle θ and bottom edge B₀ of the rigid block ABC and the angle variables α_i, ${\mathsf{\lambda }}_i$, and side length l_i of the ith rigid block can determine a unique critical sliding surface. A particular collection of variables for the foundation’s critical sliding surface corresponds to a solution vector in matrix X. The IRMO algorithm could automatically search the critical sliding surface of the foundation and calculate the corresponding ultimate bearing capacity.

Combined with the implementation process of the IRMO algorithm, each generation of particle swarm generates N particles in total, representing N critical sliding surfaces of the two–layered strip foundation. Equation (45) implements the application of the IRMO algorithm to the calculation of the ultimate bearing capacity of the two–layered strip foundation in the analysis of the ultimate bearing capacity of the two–layered strip foundation.

$$X=\left[\begin{array}{cccccc}{\theta }_{1,1}& {\alpha }_{1,2}^1& {\mathsf{\lambda }}_{1,3}^1& \cdots & {\alpha }_{1,M-1}^n& {\mathsf{\lambda }}_{1,M}^n\\ {\theta }_{2,1}& {\alpha }_{2,2}^1& {\mathsf{\lambda }}_{2,3}^1& \cdots & {\alpha }_{2,3}^1& {\mathsf{\lambda }}_{2,M}^n\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ {\theta }_{N,1}& {\alpha }_{N,2}^1& {\mathsf{\lambda }}_{N,3}^1& \cdots & {\alpha }_{N,M-1}^n& {\mathsf{\lambda }}_{N,M}^n\end{array}\right]$$

(45)

The variable in the matrix must adhere to the geometric restrictions in Equation (46) in order to guarantee that the critical sliding surface can be located within a tolerable range and that the ultimate bearing capacity of the two–layered strip foundation can be calculated:

$$\left.\begin{array}{c}0<\theta <\frac{\pi }{2}\\ \theta +{\displaystyle \sum _{i=1}^n}{\alpha }_i=\pi \\ {\beta }_{i+1}{<\alpha }_i{+\beta }_i<\pi \\ {\alpha }_1+2\theta -{\pi <\mathsf{\lambda }}_1<2\theta -{2\phi }_{\max }\\ {\mathsf{\lambda }}_i>0\\ {\alpha }_i{+\alpha }_{i-1}{+\beta }_{i-1}-{\pi <\mathsf{\lambda }}_i{<\alpha }_{i-1}{+\beta }_{i-1}-{2\phi }_{\max }\end{array}\right\}$$

(46)

where φ_max refers to the maximum value of the two–layered strip foundation soil layer parameters φ₁ and φ₂.

According to the above basic variable matrix X and geometric constraints, all the codes and procedures were realized by the commercial software Matlab2021b. In the specific engineering example following, the basic parameters c₁, c₂, φ₁, φ₂, γ₁, and γ₂ of the two–layered soil and the parameters N, M, G, max x_j, min x_j of the IRMO algorithm are set in advance, so that the location of the critical slip surface of the two–layered foundation under vertical uniform load can be searched and the corresponding ultimate bearing capacity can be determined simultaneously.

4. Example Calculation and Comparative Analysis

This section discusses the viability of using the IRMO algorithm to determine the ultimate bearing capacity of a two–layered strip foundation and verifies the IRMO algorithm’s effectiveness and stability in searching for the critical slip surface of a two–layered strip foundation and calculating the upper bound solution of the corresponding ultimate bearing capacity.

4.1. Example 1

The strip foundation of example 1 is located at a two–layered soil with an upper sand soil layer and a lower clay layer. The foundation width of the two–layered strip foundation is 2 m, regardless of the ground overload. The soil parameters are listed in

Table 1. Soil layer parameter information of calculation example.

Soil Layer Classification	H (m)	φ (°)	c (kPa)	γ (kN/m3)
Upper soil	4	35	0	17
Lower soil	−	−	50	19

. The angle of internal friction is not considered for the clay layer, and the clay weight is taken as 19 kN/m³. The parameters of the IRMO algorithm are N = 50, M = 51, and G = 500.

The ultimate bearing capacity of the foundation calculated by the IRMO algorithm in this paper is compared with the corresponding calculation results of predecessors (Michalowski and Shi [24] and Qin Huilai [25]), as shown in

Table 2. Foundation ultimate bearing capacity Q_u of different scholars.

Literature	Computing Method	Qu/kPa
Michalowski and Shi [24]	Upper−bound limit analysis theorem	764.16
Qin Huilai [25]	Upper−bound limit analysis theorem	660.69
This Study	Upper−bound limit analysis theorem	810.74

. The solution in this paper is higher than Michalowski’s, Shi’s, and Qin Huilai’s solutions. The reason for this kind of deviation may be that although the three solutions are the same upper bound solution of limit analysis, the specific optimization algorithms implemented are different. For example, the IRMO algorithm is used in this paper to search and solve, and there are 25 rigid blocks for calculation. Qin Huila uses the Monte Carlo optimization method to solve, and the rigid block division is not as detailed as in this paper, resulting in different calculation results. Therefore, the comparative analysis in this example verifies the feasibility of the IRMO algorithm in calculating the ultimate bearing capacity of a two–layered foundation.

After repeated calculation 20 times in this example, the search results of the critical sliding surface of the two–layered foundation were obtained by running the IRMO algorithm 20 times, as shown in Figure 11. The corresponding upper limit solution of the ultimate bearing capacity of the two–layered foundation is shown in Figure 12.

Figure 11 shows that the results of 20 searches of the IRMO algorithm almost overlap, the relative error control between the calculation results of each generation is quite small. Figure 12 shows that the standard deviation is 0.2599, and the average is 810.7433 (the position of the red line in the figure). Therefore, it demonstrates the great stability of the algorithm in determining the critical sliding surface of the two–layered strip foundation and calculating the corresponding ultimate bearing capacity.

Figure 13 shows the convergence of the upper limit solution of the ultimate bearing capacity of the two–layered strip foundation with the number of iterations after the algorithm has been run three times under the same conditions. The IRMO algorithm has gradually become stable after 250 generations. The convergence rate of the proposed algorithm is compared with the convergence generations of Wu [26] which shows that the algorithm in this paper is efficient and has an ideal convergence efficiency.

4.2. Example 2

This paper also compared the upper bound solution of IRMO with three commonly used calculation methods for the ultimate bearing capacity of the two–layered strip foundation in China—the diffusion angle method [1], Hansen’s weighted average method [2], and Meyerhof and Hannah’s shear failure theory [3,4], respectively. Moreover, the results in Xiao [27] carried out by using a large load plate test are compared herein as well. The test is carried out by loading a square load plate with different widths of 0.707 m, 1 m, and 2 m. The soil layer parameters of example 2 are shown in

Table 3. Parameters of each soil layer.

Soil Layer	H (m)	c (kPa)	φ (°)	γ (kN/m3)
Hard soil layer	0.75	7.0	19.5	19
Soft soil layer	−	5.0	10	17

.

Table 4. Result comparison of example 2.

B (m)	Diffusion Angle Method (kPa)	Hansen Weighted Average Method (kPa)	Meyerhof and Hannah’s Shear Failure Theory (kPa)	Large Load Plate Test [27] (kPa)	This Study
0.707	151.83	176.17	132.47	150	146.71
1.0	116.28	169.36	118.58	120	126.51
2.0	79.70	126.73	103.40	80	109.28

shows the comparison between the results of the ultimate bearing capacity obtained by the IRMO algorithm and other methods of this example. The B − P_u relationship diagram of the ultimate bearing capacity of the two–layered foundation is obtained by various calculation methods under the above load plates with different widths, as shown in Figure 14.

It can be seen from the data and corresponding charts that the calculation results of this IRMO algorithm for the ultimate bearing capacity of a two–layered foundation are basically consistent with the actual field test values when the width is small. As shown in Figure 13, with the width of the load plate expanding, errors occur. The reason for the errors is that the jack is generally used to apply pressure on the square plate in the field test, which is somewhat different from the uniform load of the strip foundation considered in this calculation. Considering that the upper−bound limit analysis theorem is adopted in this study, the calculated load is always greater than the real load. Therefore, it is reasonable that the result of the IRMO algorithm is larger than the actual test result, which shows that the IRMO algorithm strives to be correct and effective in solving the ultimate bearing capacity of the two–layered strip foundation.

4.3. Example 3

Xu Yang [6] adopted the slip line theory and assumed the shape of the slip line in the composite double−layer foundation, and derived a calculation method for its ultimate bearing capacity. The following examples are compared with the upper limit solution calculation of limit analysis for the double−layer foundation in this article, as shown in

Table 5. Soil parameter.

Soil Layer Classification	φ (°)	H (m)	c (kPa)	γ (kN/m3)
Upper soil	22	2	20	19.5
Lower soil	22	−	20	19.5

. At present, the internal friction angle of the current upper soil φ₁ = 22°, 25°, 30°, 35°, respectively.

The calculation results of the two methods are shown in Figure 15. It can be seen that the solution to the ultimate bearing capacity of the double−layer foundation is similar to the upper limit analysis method used in this article and Xu Yang’s slip line method. As the internal friction angle of the upper soil increases, there is a gradual gap between the two due to the different calculation methods used.

5. Analysis of Influence Parameters

This section discusses the influence of internal friction angle φ₁, φ₂, cohesion c₁, c₂, the thickness of upper soil H, and ground overload q of two–layered soil on the ultimate bearing capacity of a two–layered strip foundation.

5.1. Internal Friction Angle φ₁, φ₂

Before parameter analysis, it is uniformly stipulated that the foundation width is 4 m and the upper soil height is 2 m, regardless of the ground overload. The soil parameters of the two–layered foundation are shown in

Table 6. Soil parameter.

Soil Layer Classification	φ (°)	H (m)	c (kPa)	γ (kN/m3)
Upper soil	15	2	5	10
Lower soil	5	−	5	10

(except for specific modifications). The internal friction angle of foundation soil reflects its shear strength. At present, the internal friction angle of the current upper soil φ₁ = 10°, internal friction angle of subsoil φ₂ = 10°, 20°, 30°, 40°, and 50°, respectively, then φ₁/φ₂ is 1, 2, 3, 4, 5 in turn; retrieving φ₂ = 10°, φ₁ = 10°, 20°, 30°, 40°, and 50°, respectively, then the ratio φ₂/φ₁ is 1, 2, 3, 4, 5 in turn.

The crucial sliding surface of the internal friction angle between the top soil and the lower soil is shown by Figure 16 in the ratio φ₁/φ₂. Figure 17 shows the influence of the internal friction angle ratio of two–layered soil on the ultimate bearing capacity of the foundation.

It is discovered that the essential sliding surface under search would deepen and expand when the internal friction angle ratio rises (Figure 16). In order to expand the area of the soil affected by the foundation and drive more soil to contribute to the instability of the foundation, the internal friction angle must be increased. This will raise the foundation’s overall bearing capacity. As shown in Figure 17, when the internal friction angle of the subsoil is fixed, the internal friction angle of the upper soil increases, enhancing the ultimate bearing capacity of the foundation. The ultimate bearing capacity of the double−layer foundation will initially increase and then essentially remain unchanged when the internal friction angle of the upper soil is fixed and the value of the internal friction angle of the lower soil is continuously increased. Therefore, in the actual project, appropriate measures should be taken to increase the ratio of the internal friction angle between the upper soil and the lower soil, so as to improve the ultimate bearing capacity of the foundation.

5.2. Analysis on the Influence of Cohesive Force c₁ and c₂ of Two–Layered Soil

The cohesion of the soil layer is another important characteristic relating to the shear strength of the soil. The cohesion c₁ is taken as 10 kPa, and c₂ is taken as 10 kPa, 20 kPa, 30 kPa, 40 kPa, and 50 kPa, respectively, so c₁/c₂ is taken as 1, 2, 3, 4, and 5 in turn; then take c₂ as 10 kPa, c₁ as 10 kPa, 20 kPa, 30 kPa, 40 kPa, and 50 kPa, respectively, then c₂/c₁ is 1, 2, 3, 4 and 5 in turn. Other soil parameters are shown in Table 6. The method in this paper is used to solve the ultimate bearing capacity of the two–layered foundation under different cohesion ratios. The specific data changes are shown in Figure 18.

As shown in Figure 18, the ultimate bearing capacity of the two–layered foundation gradually increases as the cohesion ratios c₁/c₂ and c₂/c₁ of the upper soil and lower soil increase from 1 to 5. However, the change in c₁/c₂ has a more noticeable impact on the ultimate bearing capacity of the foundation, meaning that the cohesion of the upper soil has a greater impact.

5.3. Analysis of the Influence of Upper Soil Thickness H

In the calculation of the ultimate bearing capacity of the two–layered foundation, the thickness of upper soil H has a significant influence on the results. The soil parameters of the two–layered foundation in Example 1 are adopted. The fixed foundation width B is 2 m, and the thickness H of the upper layer soil is 1 m, 1.5 m, 2 m, 3 m, and 4 m, respectively. To determine the ultimate bearing capacity of a two–layered foundation, the IRMO algorithm is employed. The comparison of the ultimate bearing capacity of the foundation under different H/B ratios is shown in Figure 19. And Figure 20 shows the corresponding search result of the critical sliding surface of the two–layered foundation.

It can be seen that for the two–layered foundation with a hard upper layer and soft lower layer, when the value of H/B ranges from 0.5 to 1.5, both upper and lower layers of soil participate in the foundation failure, so the ultimate bearing capacity of the foundation increases gradually, and the critical sliding surface of the foundation also gradually expands. When the value of H/B changes from 1.5 to 2, the ultimate bearing capacity of the foundation almost does not change, and the critical sliding surface is close to coincidence. This is because when the value of H/B is 1.5, only the upper layer of the foundation soil is involved in the foundation damage, and further increasing the thickness of the upper layer of the foundation will not have a great impact.

On the contrary, if the upper and lower soil layers in Example 1 are interchanged, that is, the upper soft and lower hard two–layered foundation is formed. The fixed foundation width B is 2 m, and the thickness H of the upper soil is taken as 1 m, 1.5 m, 2 m, 3 m, 4 m, and 5 m, respectively. The ultimate bearing capacity of the foundation under different H/B ratios is solved by IRMO algorithm, as shown in Figure 21.

It can be found that the ultimate bearing capacity of the two–layered strip foundation tends to decrease with the increasing H/B value. After the H/B value is greater than 2, only the upper soil will participate in the foundation damage, so the variation of the foundation bearing capacity in this example is relatively small. Therefore, in the actual project, the H/B value can be appropriately increased to improve the ultimate bearing capacity of the two–layered foundation.

5.4. Analysis of the Influence of Overload q

The soil parameters in Example 1 are also used. Considering that the upper and lower soil layers are affected together, H = 2 m is selected for analysis. At this time, the upper and lower soil layers are involved in the foundation damage. Keep other parameters unchanged, the overload q = 0 kPa, 5 kPa, 10 kPa, 15 kPa, 20 kPa, and calculate the ultimate bearing capacity and bearing capacity coefficient N_q of the foundation.

Figure 22 shows the change of the ultimate bearing capacity of the foundation with different overloads q. It can be seen that the ultimate bearing capacity of the foundation increases gradually with the increase in overloads q, and the trend is close to the linear increase. The variation in bearing capacity coefficient Nq with various overloads q is shown in Figure 23. As can be observed, the bearing capacity coefficient Nq varies slightly in value.

6. Conclusions

A planar kinematically allowed multi−block failure mechanism and the flexible permissible velocity field are established based on the upper−bound limit analysis theorem. Based on this, the IRMO algorithm, which offers a new calculation method for figuring out the critical slip surface and the ultimate bearing capacity of a two–layered strip foundation, is used to optimize the ultimate bearing capacity of the two–layered strip foundation.

(1)

The IRMO algorithm can accurately and stably search the critical slip surface of the two–layered strip foundation and calculate the corresponding ultimate bearing capacity of the foundation. This study demonstrates the feasibility, stability, and efficiency of the IRMO algorithm in solving the ultimate bearing capacity of a two–layered strip foundation by two examples. Example 1 shows that the IRMO algorithm has great stability in global optimization since the contact ratio of the crucial slip surface, which is searched 20 times, is high and the standard deviation is 0.2599. The comparative analysis of Example 2 demonstrates the viability of using IRMO to determine the ultimate bearing capacity of a two–layered strip foundation.

(2)

The critical slip surface and ultimate bearing capacity of the two–layered strip foundation are significantly impacted by the soil parameters and overloads. The ultimate bearing capacity of the foundation will rise regardless of whether the internal friction angle or cohesiveness of the top and lower layers of soil are enhanced. Additionally, the area of soil involved in destroying the foundation will grow, and the upper layer of soil will ultimately improve the foundation’s carrying capacity more than the lower layer. With the increase in overload q, the ultimate bearing capacity of the foundation gradually increases linearly, but the bearing capacity coefficient N_q is kept to a constant level.

(3)

Considering the strip foundation fixed on upper−soft and lower−hard soils, the ultimate bearing capacity of the upper−hard and lower−soft foundation gradually increases with the increase in the H/B ratio. When the ratio increases to a certain level, the ultimate bearing capacity of the strip foundation tends to be stable, and the critical slip surfaces almost coincide. While the analysis results of the strip foundation fixed on upper−soft and lower−hard soils are opposite. With the increase in the H/B, the ultimate bearing capacity of the strip foundation decreases, and it will also tend to a certain level eventually.