A Graph Neural Network Node Classification Application Model with Enhanced Node Association
Abstract
1. Introduction
- ENode-GAT is a node classification model for graph neural networks that improves the connections between nodes. This model is applicable to several emerging disciplines, including the classification of citation networks, stocks, tender documents, news, and government announcements;
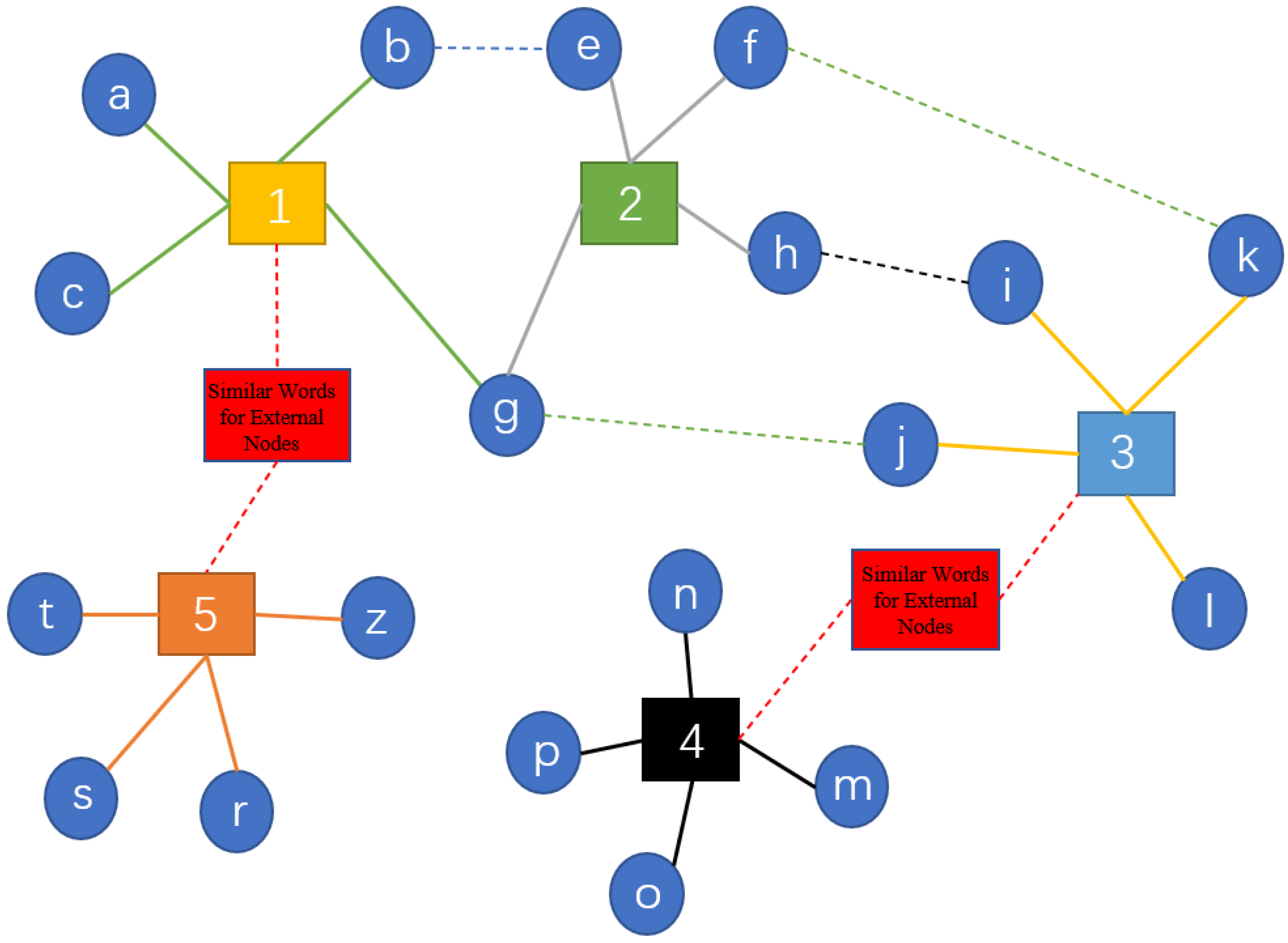
- By introducing similar terms to external nodes, the graph structure at the input side of the model is reconstructed and a small sample classification dataset is generated;
- The model effectively combines a graph convolutional neural network, a graph attention mechanism, an early stop algorithm, and a Dropout algorithm, and uses the reconstructed graph structure as model input for classification experiments, which demonstrate that ENode-GAT has distinct advantages over other classification models.
2. Related Work
2.1. Graph Neural Network
2.2. Classification of Graph Neural Network Nodes
3. Model Analysis
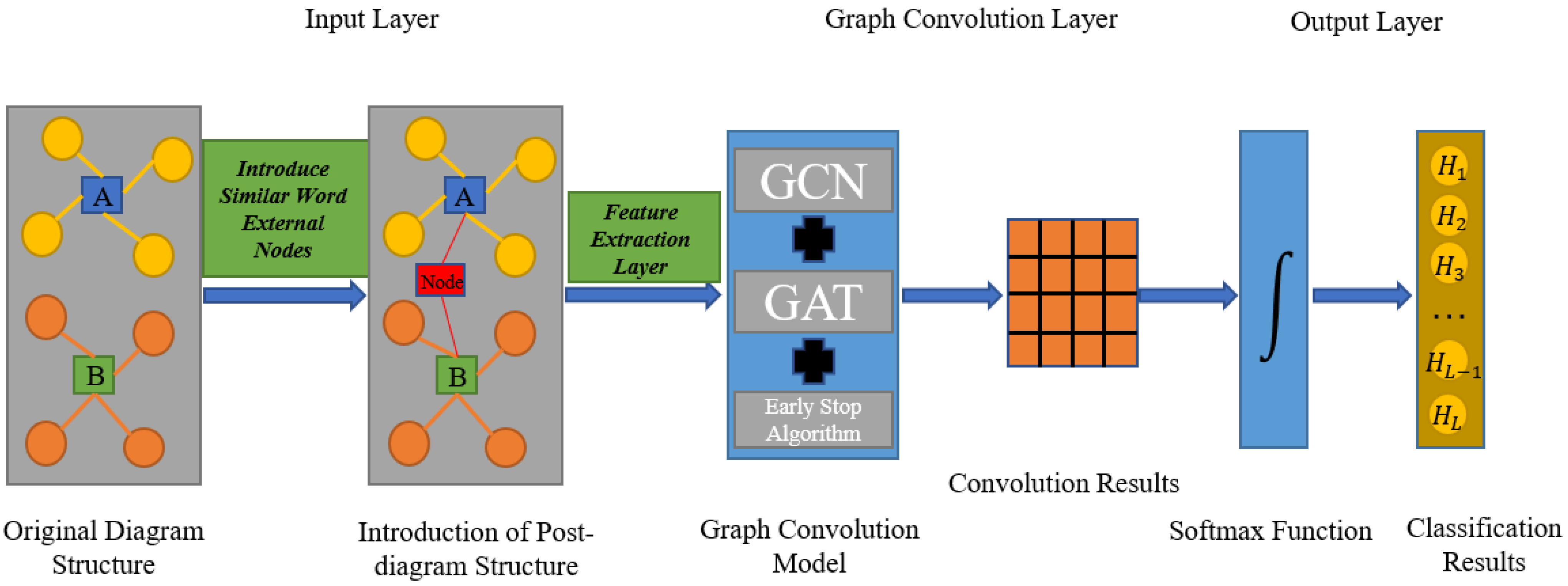
3.1. ENode-GAT Model
3.1.1. Input Layer
3.1.2. Feature Extraction Layer
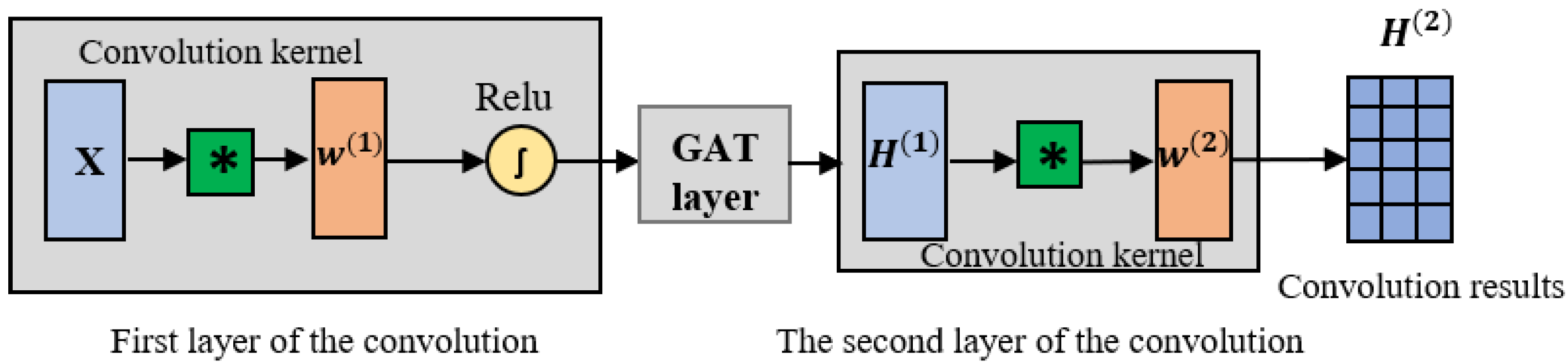
3.1.3. Graph Convolution Layer
3.1.4. Output Layer
4. Data Preparation
4.1. Dataset Selection
4.2. Dataset Processing
5. Experiment and Result Analysis
5.1. Experimental Dataset Partitioning
5.2. Model Parameter Setting
5.3. Analysis of the Over-Fitting Phenomenon
5.4. Model Comparison Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, A.; Singh, S.; Singh, K.; Biswas, B. Link prediction techniques, applications, and performance: A survey. Phys. Stat. Mech. Appl. 2020, 553, 124289. [Google Scholar] [CrossRef]
- Hong, X.; Zhang, T.; Cui, Z. Variational Gridded Graph Convolution Network for Node Classification. J. Autom. Engl. Ed. 2021, 8, 12. [Google Scholar] [CrossRef]
- Kipf, T.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Lyu, Z.; Aziguli, W.; Zhang, D. Geometry-V-Sub: An Efficient Graph Attention Network Struct Based Model for Node Classification. Appl. Sci. 2022, 12, 7246. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Maurya, S.; Liu, X.; Murata, T. Simplifying approach to Node Classification in Graph Neural Networks. J. Comput. Sci. 2022, 62, 101695. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, J.; Zhang, W. Bag of Tricks for Node Classification with Graph Neural Networks. arXiv 2021, arXiv:2103.13355. [Google Scholar]
- Qin, A.; Shang, Z.; Tian, J. Spectral–spatial graph convolutional networks for semisupervised hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 16, 241–245. [Google Scholar] [CrossRef]
- Huang, Z.; Tang, Y.; Chen, Y. A graph neural network-based node classification model on class-imbalanced graph data. Knowl. Based Syst. 2022, 244, 108538. [Google Scholar] [CrossRef]
- Gao, J.; Hao, L. Graph Neural Network and its applications. J. Phys. Conf. Ser. 2021, 1994, 012004. [Google Scholar] [CrossRef]
- Zhang, C. Research on Classification of Hyperspectral Remote Sensing Images Based on Graph Neural Network. Ph.D. Thesis, University of Chinese Academy of Sciences, Bejing, China, 2022. [Google Scholar] [CrossRef]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A. The graph neural network model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A. Spectral Networks and Locally Connected Networks on Graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Zhang, G.; He, H.; Katabi, D. Circuit-GNN: Graph Neural Networks for Distributed Circuit Design. PMLR 2019, 97, 7364–7373. [Google Scholar]
- Bai, B.; Liu, Y.; Ma, C. Graph Neural Networks. Sci. China Math. 2020, 50, 367–384. [Google Scholar]
- Ma, S.; Liu, J.; Zuo, X. Overview of graph neural networks. Comput. Res. Dev. 2022, 59, 47–80. [Google Scholar]
- Wang, J.; Kong, L.; Huang, Z. A review of graph neural networks. Comput. Eng. 2021, 47, 1–12. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, Q. A Review of Large-Scale Graph Neural Network Systems. J. Softw. 2022, 33, 150–170. [Google Scholar] [CrossRef]
- Li, Q.; Han, Z.; Wu, X. Deeper insights into graph convolutional networks for semi-supervised learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 3. [Google Scholar]
- Hu, F.; Zhu, Y.; Wu, S. Hierarchical graph convolutional networks for semi-supervised node classification. arXiv 2019, arXiv:1902.06667. [Google Scholar]
- Zeng, J.; Wang, P. A node-embedding enhancement model for graph neural networks oriented to node classification. J. Zhejiang Univ. Eng. Ed. 2023, 57, 219–225. [Google Scholar]
- Guo, M. An integrated graph neural network model for imbalanced node classification. Mod. Inf. Technol. 2023, 7, 29–32. [Google Scholar] [CrossRef]
- Jang, Y.; Won, K.; Choi, H.-d.; Shin, S.Y. Classification of Research Papers on Radio Frequency Electromagnetic Field (RF-EMF) Using Graph Neural Networks (GNN). Appl. Sci. 2023, 13, 4614. [Google Scholar] [CrossRef]
- Gong, L.; Cheng, Q. Exploiting edge features for graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9211–9219. [Google Scholar]
- Yang, Y.; Li, D. Nenn: Incorporate node and edge features in graph neural networks. In Proceedings of the 12th Asian Conference on Machine Learning, Bangkok, Thailand, 18–20 November 2020; pp. 593–608. [Google Scholar]
- Jiang, X.; Ji, P.; Li, S. CensNet: Convolution with Edge-Node Switching in Graph Neural Networks. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, Macao, China, 10–16 August 2019; pp. 2656–2662. [Google Scholar]
- Xiao, B.; Tseng, C.; Lee, S. A Hypergraph Convolutional Neural Network for Node Classification of Citation Network Data. In Proceedings of the 2022 IEEE International Conference on Consumer Electronics—Taiwan, Taipei, Taiwan, 6–8 July 2022; pp. 243–244. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Y.; Ma, T. A classification model for academic papers based on an improved graph neural network. Data Anal. Knowl. Discov. 2022, 2022, 1–14. Available online: http://kns.cnki.net/kcms/detail/10.1478.G2.20220413.1113.012.html (accessed on 10 May 2023).
- Qiang, C.; Li, X.; Ma, X. Application of graph neural network in classification of bidding documents. J. Chin. Comput. Syst. 2022, 1–7. Available online: http://kns.cnki.net/kcms/detail/21.1106.TP.20211112.1908.002.html (accessed on 10 May 2023).
- Xu, H.; Zhang, Y.; Xu, Y. Promoting Financial Market Development—Financial Stock Classification Using Graph Convolutional Neural Networks. IEEE Access 2023, 11, 49289–49299. [Google Scholar] [CrossRef]
- Li, X.; Wen, L.; Deng, Y. Graph Neural Network with Curriculum Learning for Imbalanced Node Classification. arXiv 2022, arXiv:2202.02529. [Google Scholar]
- Martineau, J.; Finin, T. Delta tfidf: An improved feature space for sentiment analysis. In Proceedings of the International AAAI Conference on Web and Social Media, San Hose, CA, USA, 17–20 May 2009; Volume 3. [Google Scholar]
- Wu, Z.; Zhu, M. Center-guided relation-aware network for cross-domain object detection. J. Chin. Comput. Syst. 2021, 42, 1066–1070. [Google Scholar]
- Xue, Y.; Ju, Z. Method for recognizing indoor scene classification based on fusion deep neural network with attention mechanism. J. Chin. Comput. Syst. 2021, 42, 1022–1028. [Google Scholar]
- Sen, P.; Namata, G.; Bilgic, M. Collective classification in network data. AI Mag. 2008, 29, 93. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y. Enhancement Economic System Based-Graph Neural Network in Stock Classification. IEEE Access 2023, 11, 17956–17967. [Google Scholar] [CrossRef]
| Number of nodes | 2708 |
| Number of sides | 5429 |
| Initial feature dimension | 1433 |
| Classifying categories | 7 |
| Category | Case-based, genetic algorithms, neural networks, probabilistic methods reinforcement learning, rule-based learning, theoretical |
| Is there a class imbalance | No |
| Number of nodes | 273 |
| Number of sides | 1452 |
| Initial feature dimension | 368 |
| Classifying categories | 8 |
| Category | Pharmaceutical manufacturing, computer technology, equipment manufacturing, material manufacturing, metal manufacturing, electrical machinery, environmental protection, rubber-plastic manufacturing. |
| Is there a class imbalance | No |
| Basic Information | Original Dataset after Expansion | ENode-GAT Model after the Introduction of External Nodes |
|---|---|---|
| Number of nodes | 380 | 380 |
| Number of sides | 2152 | 4329 |
| Initial feature dimension | 368 | 368 |
| Classifying categories | 8 | 8 |
| Category | Pharmaceutical manufacturing, computer technology, equipment manufacturing, material manufacturing, metal manufacturing, electrical machinery, environmental protection, rubber-plastic manufacturing. | |
| Is there a class imbalance | No | No |
| Experimental Dataset | Training Set | Validation Set | Test Set |
|---|---|---|---|
| Cora dataset | 200 | 300 | 1000 |
| Stock dataset | 40 | 40 | 300 |
| Split Ratio | 1:2:5 | 2:3:3 | 1:4:3 | 6:1:1 | |
|---|---|---|---|---|---|
| ENode-GAT-Cora | Training Accuracy | 0.8500 | 0.8350 | 0.8500 | 0.8258 |
| Validation Accuracy | 0.8233 | 0.8600 | 0.8375 | 0.8800 | |
| Test Accuracy | 0.8510 | 0.8460 | 0.8480 | 0.8800 | |
| Rounds | 270 | 298 | 299 | 295 | |
| ENode-GAT-Stock | Split ratio | 1:1:8 | 6:1:3 | 2:6:2 | 5:2:3 |
| Training Accuracy | 0.9000 | 0.9045 | 0.8625 | 0.9000 | |
| Validation Accuracy | 0.8750 | 0.8750 | 0.8250 | 0.9000 | |
| Test Accuracy | 0.8533 | 0.8767 | 0.8682 | 0.8912 | |
| Rounds | 287 | 296 | 290 | 292 |
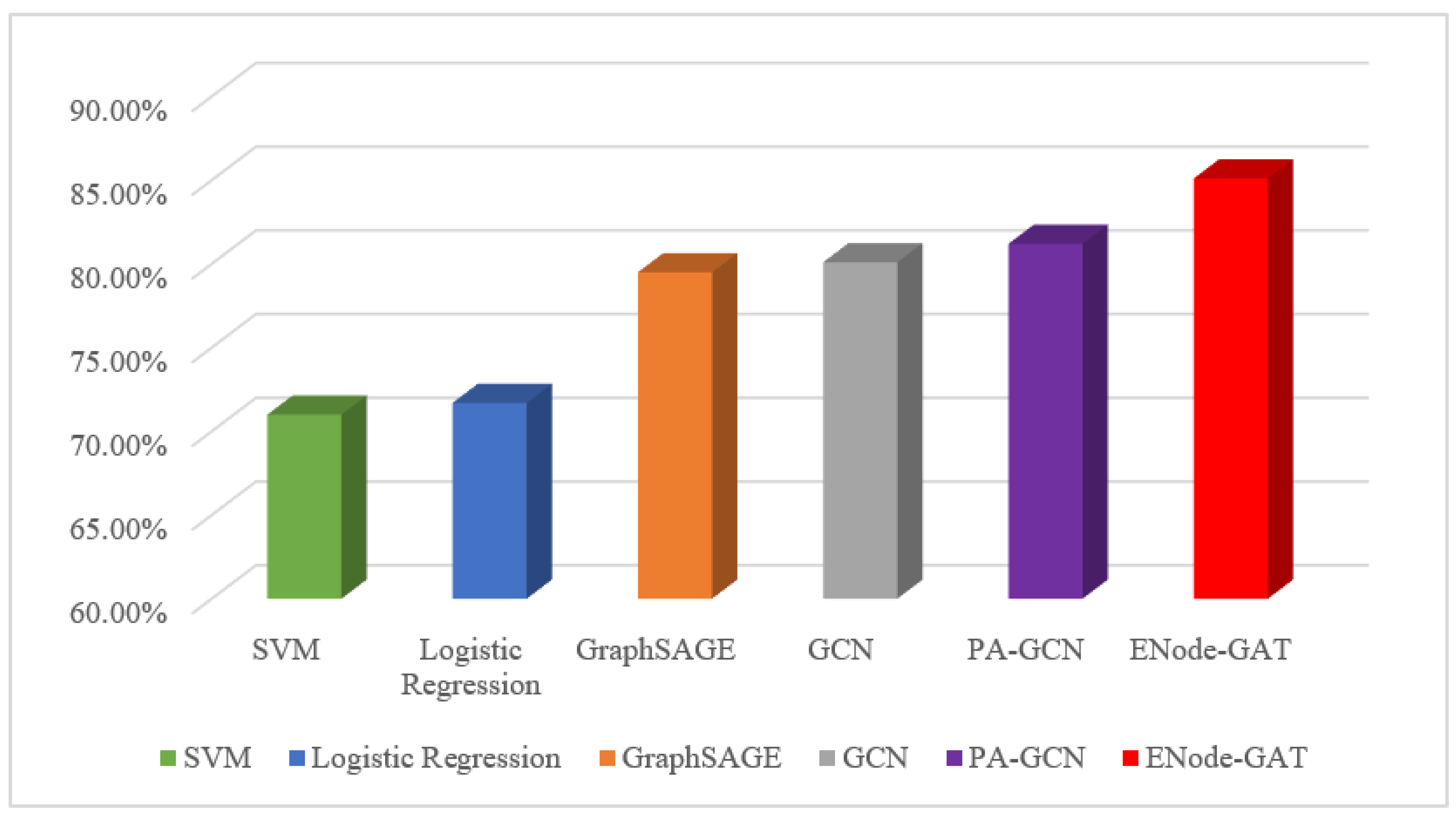
| Classification Method | Accuracy |
|---|---|
| SVM | 71.0% |
| Logistic Regression | 71.7% |
| GraphSAGE | 79.5% |
| GCN | 80.1% |
| PA-GCN [37] | 81.2% |
| ENode-GAT | 85.1% |
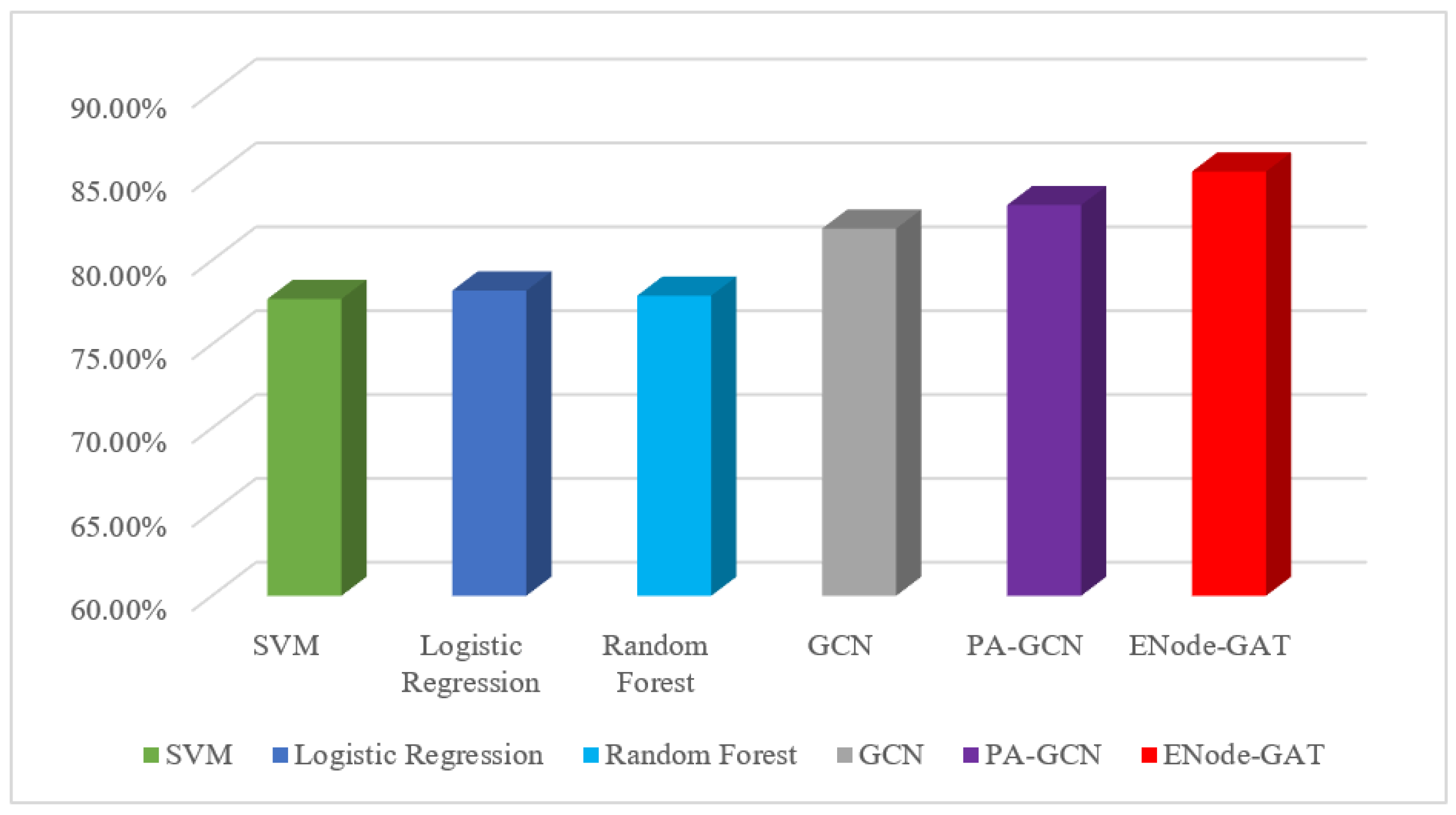
| Classification Method | Accuracy |
|---|---|
| SVM | 77.7% |
| Logistic Regression | 78.2% |
| Random Forest | 77.9% |
| GCN | 81.9% |
| PA-GCN | 83.3% |
| ENode-GAT | 85.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xu, Y.; Zhang, Y. A Graph Neural Network Node Classification Application Model with Enhanced Node Association. Appl. Sci. 2023, 13, 7150. https://doi.org/10.3390/app13127150
Zhang Y, Xu Y, Zhang Y. A Graph Neural Network Node Classification Application Model with Enhanced Node Association. Applied Sciences. 2023; 13(12):7150. https://doi.org/10.3390/app13127150
Chicago/Turabian StyleZhang, Yuhang, Yaoqun Xu, and Yu Zhang. 2023. "A Graph Neural Network Node Classification Application Model with Enhanced Node Association" Applied Sciences 13, no. 12: 7150. https://doi.org/10.3390/app13127150
APA StyleZhang, Y., Xu, Y., & Zhang, Y. (2023). A Graph Neural Network Node Classification Application Model with Enhanced Node Association. Applied Sciences, 13(12), 7150. https://doi.org/10.3390/app13127150





