Abstract
This paper proposes a novel hardware design for a compact crypto processor devoted to elliptic-curve point multiplication over . We focus on minimizing hardware usage, which we obtain using an iterative bit–serial finite field modular multiplier for polynomial coefficient multiplication. The same multiplier is also used for modular squares and inversion computations, further optimizing the hardware footprint. Our design offers flexibility by permitting users to load different curve parameters and secret keys while keeping a low-area hardware design. To efficiently generate the control signals, we utilize a finite-state-machine-based controller. We have implemented the proposed crypto processor on Virtex-6 and Virtex-7 FPGA devices, and we have evaluated its performance at clock frequencies of 100, 50, and 10 MHz. Specifically, for one point multiplication computation on Virtex-7 FPGA, our crypto processor uses 391 slices, attains a maximum frequency of 161 MHz, has a latency of 4.45 ms, and consumes 77 mW of power. These results, along with a comparison to state-of-the-art designs, clearly demonstrate the practicality of our crypto processor for applications requiring efficient and compact cryptographic computations.
1. Introduction
Elliptic curve cryptography (ECC) and Rivest–Shamir–Adleman (RSA) are two well-known public-key cryptography (PKC) schemes. ECC, described by Victor Miller [1], offers comparable security to RSA but with shorter key lengths [2]. For instance, a 233 bit ECC key provides similar protection to a 2048 bit RSA key. The advantage of ECC lies in its ability to achieve security with shorter key sizes, resulting in lower power consumption, reduced channel bandwidth requirements, and more efficient use of hardware resources; on the other hand, the longer key lengths are advantageous for maximizing security. However, challenges arise when implementing longer ECC key lengths while minimizing area utilization, especially in designs optimized for securing area-constrained applications.
For security purposes, various applications demand area-optimized implementations of cryptographic algorithms, such as wireless sensor nodes [3,4], radio-frequency-identification (RFID) networks [5], and secure robotics communication [6,7]. Using shorter ECC key lengths than RSA helps protect these applications with minimum area utilization and is the main focus of this work.
The National Institute of Standards and Technology (NIST) has standardized ECC for prime and binary fields (i.e., and ) to maintain security standards for efficient communications [8]. More precisely, NIST has recommended specific field lengths for and , such as 192, 224, 256, 384, and 521 for , and 163, 233, 283, 409, and 571 for [8,9]. ECC employs a four-layer model to implement NIST’s suggested prime and binary field lengths. Therefore, the foremost layer ensures encryption/decryption, signature generation/verification, secret-key authentication, and other similar functions. The essential operation in ECC is point multiplication (PM), which involves point addition (PA) and point double (PD) operations for computations—these operations are the second layer of the ECC model. Modular arithmetic operators (such as adder, square, multiplier, and inversion) show the layer one ECC operations. ECC’s PM operation efficiency depends on implementing these modular arithmetic operators efficiently.
Two alternatives to implement ECC are software-based implementations on microcontrollers and hardware accelerators on field-programmable gate arrays (FPGA) and application-specific integrated circuits (ASIC). Although software-based implementations offer greater flexibility, they provide limited throughput [2,10,11]. Conversely, hardware accelerators offer higher throughput but with lower flexibility [2,10]. Therefore, the implementation choice relies on the platform used. The fields are beneficial for hardware acceleration due to their carry-free additions, whereas fields are more advantageous for software platforms [10,12]. In addition, ECC offers a polynomial and normal basis for point representation [9]. The polynomial basis is more practical for efficient modular multiplications, and the normal basis is helpful for frequent modular square computations [12]. Two coordinates, i.e., affine, and projective, used in ECC also affect performance. The affine coordinate is more computationally expensive, requiring an inversion operation during each PA and PD computation. In contrast, the projective coordinate is more suitable to maximize the performance of the ECC accelerators [9,12,13]. Based on this compliance, binary fields, projective coordinates, and polynomial basis representations are chosen in this study due to the focus on accelerating ECC on a hardware platform.
1.1. Low-Area Hardware Implementations with Limitations
Concerning the aforementioned selections, several PM ECC designs exist in the literature; however, we preferred to include only those implemented and optimized for area-efficient realizations. Examples of the most recent hardware accelerators are available in [12,13,14,15,16,17,18]. A two-stage pipelined PM architecture of ECC is described in [12], where pipelining is utilized to decrease the critical path delay and carefully schedule the computations associated with PA and PD to reduce the number of clock cycles required; these two characteristics combine to decrease the time needed for a single PM operation, and the minimum utilization of area results in a higher throughput/area ratio. For , the implementation results on Virtex-7 demonstrate that their design can operate at frequencies of up to 369, 357, and 337 MHz for m = 163, 233, and 283 bit key lengths, respectively. Similarly, another two-stage pipelined architecture is designed in [13] to reduce overall computation time by rescheduling PA and PD instructions. The hardware resources are reduced by efficiently utilizing memory locations and employing a digit-serial multiplier with a digit length of 41 bits. The FPGA and ASIC implementation results are provided and compared to state-of-the-art implementations, demonstrating their proposed accelerator’s significance in latency and area.
An efficient hardware implementation of a 256 bit ECC processor over a is presented in [14], where Jacobian coordinates have been utilized to avoid the costly modular inversion operation. In addition, an interleaved modular multiplier reduces the area and delay in modular multiplication. The PA and PD design is realized with the minimum arithmetic unit, utilizing the efficient modular multiplier algorithm. The implementation results are reported on FPGA.
A low-area efficient implementation of ECC over is described in [15], where authors investigate area–time and area–2-time performances utilizing a digit serial multiplier architecture on different FPGA devices. Moreover, an 8 bit input–output interface is utilized for low-cost cryptographic applications and can easily be embedded with 8 bit processors. Their Montgomery PM implementation on Virtex-5 shows the best result, achieving 0.11 ms using only 473 slices in the area. Another low-area PM implementation is illustrated in [16], where a Lopez Dahab PM algorithm is used over . On different FPGA devices, they have realized low area using a bit parallel hybrid Karatsuba multiplier; they implemented the hybrid multiplier using a simple Karatsuba multiplier for multiplying longer bits, whereas they generated simple partial products to execute multiplication on smaller bits.
Specific to wireless sensor nodes, we found an interesting work in [17], where an ECC-based crypto engine is described over . The crypto engine targets digit-by-digit computations to execute finite field arithmetic operations of ECC. In addition, they have reused the hardware resources of the targeted FPGA device to keep less area. The crypto engine has been validated through hardware/software codesign of the Diffie–Hellman key exchange protocol deployed in the IoT MicroZed FPGA board. For PM computation over 233 bit key length, their design utilizes 442 slices and executes one PM computation in 15,53,782 clock cycles at 190 MHz. We found another compelling work in [18], where the authors utilize a coprocessor design technique to obtain the advantages of symmetric and PKC simultaneously. More precisely, an advanced encryption standard (AES-128 [19]) algorithm is incorporated to perform the symmetric cryptography; ECC over is utilized to operate elliptic-curve operations for PKC; and a secure hash algorithm (SHA-256) is considered to perform a hash computation for digital signature, authentication, and random-keys generation—they used a MicroBlaze processor to supervise these coprocessors.
Instead of the ECC-based PKC schemes, NIST is progressing with a quantum-resistant cryptographic protocols contest to standardize new standards for securing future communications [20]. Even if we are not dealing with quantum-resistant algorithms in this work, it is essential to highlight that the respective community is progressing well in this domain, and it seems to be a part of the systems being developed shortly. Some recent examples include quantum processors designed by IBM [21] and Google [22]. Another example consists of an experimental quantum secure network presented in [23], where digital signatures and encryption operations are operated at the same time. Moreover, from a hardware perspective, a systematic study of several quantum algorithms is performed in [24,25], where the cost of various building blocks is evaluated.
Although several low-area realizations of ECC PM designs have already been reported [15,18], these hardware architectures utilize lower binary field 163 bit key length. Other low-area PM designs of [12,13,14,16,17] are impressive, but they consider different design parameters (such as throughput and area) for realizations at the same time. Although flexibility allows multiple cryptographic algorithms to operate in a same design as implemented in [18], the design uses considerable hardware resources and also reduces the performance. Therefore, this work aims to realize area-efficient implementation of PM computation of ECC for various constrained cryptographic applications.
1.2. Novelty and Contributions
Novelty yields a flexible crypto processor design with efficient control functionalities to obtain the area-efficient implementation of PM operation. Towards our contribution, we have proposed an area-efficient elliptic-curve PM-based hardware crypto processor architecture over , where we implemented a bit-serial finite field modular multiplier to keep hardware resources lower. For further area optimizations, we computed the square and modular inversion operations using the implemented bit-serial multiplier; this approach results in lower hardware resource utilization with throughput or performance overhead. Moreover, keeping low-area PM design, users can load different curve parameters to infer data memory of the proposed crypto processor design and secret key into the corresponding buffer, enabling flexibility. Finally, we implemented a finite-state-machine (FSM) based controller for providing efficient control functionalities.
1.3. Main Findings and Significance
We implemented our crypto processor in Verilog (HDL) programming language using the Vivado IDE tool. We show the implementation results over as a trend after the post-place-and-route level on Virtex-6 and Virtex-7 FPGA devices. The trend has been shown for operating frequencies of 100, 50, and 10 MHz, showing that decreasing clock frequency increases the computation time or latency. Moreover, the higher frequencies consume more power. Our crypto processor outperforms in hardware resources and consumes power on modern (28 nm) Virtex-7 FPGA devices. On identical FPGA, it utilizes 391 slices, achieves a maximum 161 MHz frequency, takes 4.45 ms latency, and consumes 77 mW when computing one ECC PM operation. Results and comparisons indicate that our crypto processor design benefits applications that demand low area and less power for cryptographic computations.
2. Background
Section 2.1 presents the mathematical background essential for implementing the PM operation of ECC over . In contrast, Section 2.2 provides design rationales that gradually show how we reach our proposed crypto processor design.
2.1. ECC over
Projective coordinates represent the affine x and y coordinates of a point P over field in a triplet, i.e., . Therefore, for a field, a Lopez Dahab projective form of the ECC curve is defined by Equation (1), where the variables X, Y, and Z are the Lopez Dahab projective elements of point , , a and b are the curve constants, and :
To implement Equation (1), it is necessary to utilize PA and PD operations for evaluating the PM operation of ECC. Let us illustrate ECC’s PA, PD, and PM operations through an example: suppose we have two points (P and Q) on an ECC curve. Performing a PA results in , where R represents the resultant point. Similarly, adding two identical points on the ECC curve, denoted as , corresponds to a PD operation. By employing the definitions of PA and PD operations in ECC, the PM operation involves the addition of k instances of PA and PD on the specified ECC curve. This can be computed using Equation (2):
Here, P is an initial point; k is a scalar multiplier; and Q denotes a resultant point in Equation (2). Several PM algorithms exist in literature to implement Equation (2). A comparison of hardware implementations of several PM algorithms is described in [2]. The research presented in [2] suggests that a Montgomery PM algorithm is more practical for implementing side-channel resistant ECC. This algorithm exhibits similarities in instructions used for both PA and PD computations. Therefore, in this study, Algorithm 1, a Montgomery PM algorithm, is employed to develop a hardware implementation of ECC that offers robust side-channel protection.
| Algorithm 1 Montgomery PM algorithm [12] | |
| 1 | Input: with , |
| 2 | Output: |
| 3 | Set, , and |
| 4 | for (i from m−2 down to 0) do |
 | |
| 39 | , |
| 40 | |
Algorithm 1 bears an initial point P and a binary sequence denoting a scalar multiplier k as inputs. Its output is the final point Q with x and y coordinates. The first line of Algorithm 1 determines the operations for converting between affine and projective (Lopez Dahab) coordinates. Similarly, the loop runs the PM operation in the Lopez Dahab coordinates. The and statements used inside the loop direct to PA and PD operations, respectively. Particularly, instructions from to computes PA, whereas to perform PD. The choice between the execution of and instructions depends on the value of inspected one bit scalar multiplier. The final two lines of Algorithm 1 consist of instructions for converting the Lopez Dahab projective coordinates back to affine coordinates.
2.2. Design Rationales
This section sets the design settings based on the underlying principles, justifications, and explanations that tell the designers about the decisions (that we made) to implement this crypto processor for PM computation of ECC. Therefore, multiple architectural styles have been employed in literature to implement ECC’s PM operation, including crypto processors, crypto co-processors, and multicore crypto processors [2]. Comparatively, multicore processors are beneficial to maximize the performance of PM computation; conversely, the co-processors offer higher flexibility—where a host processor (such as microcontroller or microprocessor) needs to integrate with the crypto processor design [26,27]. The host processor controls the integrated crypto processor, and the crypto processor implements the cryptographic operations for higher speedups. Therefore, rather than the crypto co-processors and multicore crypto processors, a crypto processor implementation style is selected in this work to accelerate the PM operation of ECC on FPGA. The arithmetic operations in ECC can be employed differently to compute PA and PD operations. For example, multiple finite field arithmetic operators are used in [28,29] to maximize the performance of ECC; conversely, single finite field arithmetic operators are utilized in [12,13,16] to minimize the hardware resources. Hence, our objective is to realize area-efficient PM computation of ECC; we preferred single arithmetic operators. Fewer ECC designs [12,13] even adopted one adder and one modular multiplier, then use multiplier for both square and inversion computations. We also utilize the same strategy but with a different modular multiplier.
3. Proposed Crypto Processor Design
Generally, a crypto processor design contains an arithmetic and logic unit (ALU), a control unit, and an instance of data memory [2]. The ALU executes required arithmetic operations such as addition, subtraction, multiplication, inversion, etc.; data memory keeps the initial, intermediate, and final results; the control unit generates the control signals for efficient control functionalities. Our proposed crypto processor design over for PM computation of ECC contains three identical blocks of ALU, control unit, and data memory, as shown in Figure 1. The control unit takes the inputs from outside and also produces outputs. The inputs are , , , , , , , and ; the outputs are and . As the names imply, the and signals determine the clock and reset behavior of the proposed design. The and signals specify load data and key, respectively. The signal shows input data to the crypto processor. The specifies the start signal to the processor. Read/write addresses to load/store data to/from memory are specified by the corresponding and signals. The signal shows the processor output, and a signal determines the completion of the PM computation of ECC. Despite these I/O signals, the red dotted lines in Figure 1 determine the control signals that the control unit generates. Additionally, a KeyReg in Figure 1 is a 233 bit buffer that keeps the secret key or the scalar multiplier, i.e., k, to implement PM Algorithm 1. Below, we describe three blocks (data memory, ALU, and control unit) of our proposed crypto processor design over for PM computation of ECC.
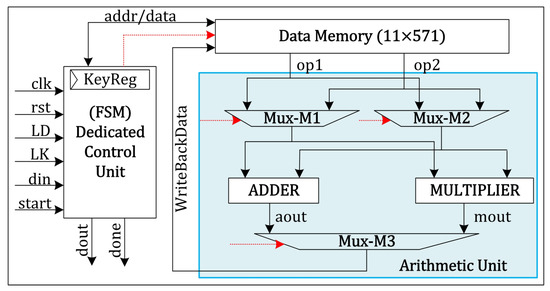
Figure 1.
Proposed crypto processor architecture for PM computation of binary ECC field over : LD/LK shows load data and key, din presents data in, start is a start signal to ensure computations begin, addr/data determines addr/data signals to/from memory, dout shows processor data as an output, done means computation has been finished.
3.1. Data Memory
The data memory benefits keeping the initial, intermediate, and final generated results during and after the computation. In Figure 1, we used an size of a register array as a data memory, where 11 shows the total number of addresses and m specifies the number of bits stored on each address. Out of the eleven addresses, three addresses keep ECC curve parameters, i.e., , , and b, where is the x coordinate of initial point P, is the y coordinate of initial point P, and b is the curve constant. In comparison, the remaining eight addresses hold the intermediate and final results to implement instructions of Algorithm 1. The inner structure of the data memory comprises two sizes of multiplexers and one size of a demultiplexer. The multiplexers read two 233 bit operands from the data memory, and a demultiplexer updates the value of the specified register for writing back. The control unit is responsible for managing the control signals in read/write operations. Note that the utilized data memory makes our architecture flexible, as users can load different curve parameters, i.e., , , and b, and a scalar multiplier to our proposed processor for PM computation. In addition, the corresponding values or curve parameters for , , and b buffers are selected from a standardized NIST document [8].
3.2. Arithmetic Unit
To perform modular finite field operations, an arithmetic unit is required to perform essential functions such as addition, multiplication, square, reduction, and inversion. The blue color portion in Figure 1 shows the arithmetic unit, which comprises three multiplexers (M1, M2, and M3) for routing purposes, an adder, and a polynomial multiplier unit. The routing multiplexers select appropriate operands for the arithmetic operators (adder and multiplier) and data memory. The M1 and M2 multiplexers select operands for the adder and multiplier units. The M3 multiplexer is leveraged to choose the outputs of these modular operators to be written back on the data memory. The control unit generates the related control signals for operating M1, M2, and M3 multiplexers. Below, we describe the arithmetic operators required to implement ECC’s PM operation.
Implementing a modular adder over the field is straightforward, requiring only bitwise exclusive (OR) gates, as shown in Figure 2. For example, adding two 233 bit input operands a and b, two-input 233 exclusives (OR) gates are needed [12,13,18]. Implementation of an adder is a combinational circuit; therefore, one polynomial addition over binary field results in one clock cycle.
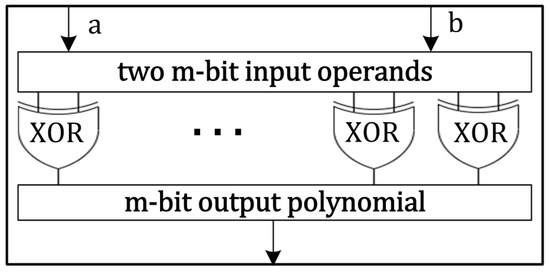
Figure 2.
Modular adder over .
Let us discuss polynomial multiplication approaches. According to the study in [30], four commonly utilized methods are bit-serial, digit-serial, bit-parallel, and digit-parallel multiplication. Another resource, [31], presents an open-source tool that can generate Verilog HDL implementations of different modular multipliers, such as schoolbook, Booth, 2-way Karatsuba, 3-way Toom–Cook, and 4-way Toom–Cook. These multiplication methods have their unique benefits and weaknesses. For example, bit and digit-serial methods help implement area and power-optimized circuits [15,32]. Conversely, bit-parallel and digit-parallel multipliers for high-performance implementations are more suitable [12,13,30]. It is important to note that the computational cost of these methods can vary. For instance, for two m bit sizes of polynomial operands as input, the bit-serial multipliers require cycles; on the other hand, the digit-serial approach requires cycles, where m is the operand length and n is the digit size. The computational cost of digit and bit-parallel approaches is one clock cycle with additional area and power overheads. There is always a tradeoff between design parameters (such as area, power, and performance). We recommend [30,31] for a more comprehensive comparison of different multiplication architectures.
Our design premise is an area-efficient realization of PM implementation of ECC; hence, we have implemented a bit-serial multiplication method, as presented in Figure 3. It comprises two multiplexers, a one bit shift towards the right (≪), an exclusive (OR) gate (XOR), and a 233 bit accumulator register (ACC). The multiplexers help to generate the partial products depending on the value of and b, where is the ith value of the operand a and b is the second operand. The symbol ≪ in Figure 3 shows a one bit shift right. The exclusive (OR) or XOR performs the corresponding operation on shifted and accumulated results. The ACC accumulates the results to keep the final result. The multiplier takes m bit a and b as inputs, resulting in bits out as output. Similarly, we used the same multiplier design by providing identical inputs to perform the modular square instructions of Algorithm 1. Note that the multiplier produces output in bits; therefore, a polynomial reduction is essential to perform over bit polynomial to get the result back into m bit polynomial. The literature contains several polynomial reduction approaches; hence, we preferred modular reduction over recommended by NIST, which is shown in Algorithm 2. For 233 bit key length, the computational cost of the adder and multiplier units is one and 233 clock cycles, respectively.

Figure 3.
Bit-serial polynomial multiplier over .
In Algorithm 1, the final two lines involve the computation of modular inversion. Numerous methods for modular inversion exist in the literature, but not all are suitable for hardware platforms due to varying mathematical structures [9]. In our design for an accelerator, we have utilized a square version of the Itoh–Tsujii algorithm [33], which requires squares equivalent to the field length followed by ten modular multiplications over the field. The modular inversion unit is not explicitly spotlighted in Figure 1, as the Itoh–Tsujii inversion algorithm leverages square and multiplication circuits commonly employed in PM architectures [12,13]. As a result, this approach reduces both hardware costs and power consumption. As described, for a 233 bit key length, one square and multiplier circuit cost one and 233 clock cycles, respectively. Thus, implementing the Itoh–Tsujii algorithm for modular inversion over requires clock cycles for square computations; this means that 232 square operations are needed, and each needs 233 clock cycles. On the other hand, clock cycles are necessary for modular multiplication, which means that ten multiplications are required to implement inversion, and each needs 233 clock cycles. Thus, the total clock cycles for one modular inversion computation is 56,386 (54,056 for square operations and 2330 for 10 multiplications).
| Algorithm 2 Polynomial reduction over (algorithm 2.42 of [9]) | |
| 1 | Input: Polynomial, with bit length |
| 2 | Output: Polynomial, with m bit length |
| |
3.3. Control Unit and Clock Cycles Calculation
An FSM-based dedicated controller is implemented in this work to execute Algorithm 1 for PM computation. Before implementing it, we need to load the initial point P coordinates (i.e., , ), a curve constant b, and a value of the scalar multiplier (k) as input, as shown in Algorithm 1. Based on a one bit signal , the corresponding data values will be loaded into the related data memory addresses; in other words, the signal triggers the proposed crypto processor to load curve input parameters (, , and b). Similarly, when a one bit signal, , becomes 1, a secret key or scalar multiplier k must be loaded into a KeyReg, as shown in Figure 1. The interface of the proposed crypto processor architecture only supports 8 bit data loading using an 8 bit ; therefore, the 233 bit ECC parameters, including , , b, and a secret key k, must be loaded in 8 bit form. Hence, loading a 233 bit secret key into the corresponding KeyReg buffer needs 32 clock cycles, and loading , , and b into the data memory addresses requires 3 × 32 clock cycles. Next, after loading the input parameters, the PM computation is essential to execute; hence, to do so, FSM goes through multiple states for affine to projective conversions, PM computation in projective coordinates, and re-conversion back from projective to affine coordinates; details about these states are as follows.
The first line in Algorithm 1 applies initializing or converting coordinates from affine to projective form. Due to our implementation of modular operators, an adder unit takes one clock cycle for computation, and a multiplier unit needs 233 clock cycles for a 233 bit key length. As can be observed from the first line of Algorithm 1, there are four instructions to execute: (i) , (ii) , (iii) , and (iv) . Using our architecture, and take two clock cycles to execute. Recalling again that we executed square instructions by providing identical inputs to the multiplier unit, takes 233 clock cycles, as the supported key length is 233 bits. Similarly, to compute , 234 clock cycles are needed; there are 233 cycles for computation of and one clock cycle for adding curve constant b. Overall, the affine to projective coordinate takes 469 clock cycles to implement.
A loop in Algorithm 1 determines the PM computation in Lopez Dahab projective form. The and statements (within the loop) incorporate instructions for executing PA and PD operations, respectively. The – are for PA, whereas – are for PD. Implementing the or portions of Algorithm 1 relies on the value of the one bit scalar multiplier ; when , the statements will be implemented; otherwise, the portion will be implemented. Note that the and parts comprise fourteen instructions; eleven are for square and multiplier computations, and three are for modular addition. Hence, and statements require 2563 clock cycles for square and multiplier units and three clock cycles for addition computations. This is the cost for one PA and PD computation; the total clock cycle cost to process 233 bit key length is 233 × 2566, equivalent to 597,878.
The final two lines of Algorithm 1 generate the x and y coordinates of the resultant point Q on the curve. These two lines determine re-conversion from Lopez Dahab projective to affine coordinates; as noted, these lines need two modular inverse operations and some addition and multiplication operations, as shown in Algorithm 1. Recalling again, in the Itoh–Tsujii inversion algorithm, squares followed by ten modular multiplications are needed to compute each inversion operation. As we reported earlier, we utilized an iterative schoolbook modular multiplier for both polynomial multiplication and square computations; hence, the Itoh–Tsujii inversion algorithm is implemented using the multiplier unit of Figure 3. For squares computation, our design utilizes 54,056 clock cycles, and for ten modular multiplication computations, it takes 2330 cycles; overall, 56,386 clock cycles are needed to implement the Itoh–Tsujii inversion algorithm for one modular inverse computation. As noted, the last two lines of Algorithm 1 involve two modular inverse computations; therefore, 2 × 56,386 clock cycles are needed to implement two modular inverse operations. Instead of the modular inverse computations, several square, multiplication, and addition operations are required to implement the last line of Algorithm 1; hence, an additional 5340 clock cycles are needed to execute these operations. Subsequently, 118,112 clock cycles are needed to implement the Lopez Dahab projective to affine conversions.
As summarized, Algorithm 1 bears a total of 716,459 clock cycles to compute one PM in . The distribution of these clock cycles comprises 469 cycles for affine to Lopez Dahab conversion, 597,878 cycles for PM computation in Lopez Dahab projective coordinates, and 118,112 clock cycles for re-conversion (from Lopez Dahab projective to affine coordinates).
4. Results and Comparison
Section 4.1 describes the implementation results of the proposed crypto processor design. We compare the results of our crypto processor with state-of-the-art hardware designs in Section 4.2.
4.1. Results
We have used the Vivado IDE tool to implement our proposed crypto processor design over . Moreover, we have implemented a register-transfer-level (RTL)-design in a Verilog HDL. The input parameters, namely the x and y coordinates of an initial point P and the curve constant b, were selected from the NIST recommended document [8]. We developed a reference model of Algorithm 1 using C/C++ programming language. Then, we compared the behavioral and post-place-and-route simulated models, written in Verilog HDL, of Algorithm 1 with the C/C++ reference design to ensure correctness. We summarize the implementation results in Table 1, representing the outcomes obtained after the post-place-and-route stage on Virtex-6 and Virtex-7 FPGA devices. The first column indicates the specific implementation device, whereas columns two to three display area information regarding slices and look-up tables (LUTs). Similarly, columns four to six provide timing results in clock cycles, operating frequency (Freq), and latency. The circuit frequency is measured in megahertz (MHz), whereas latency represents the computation time for one PM execution, which we calculated in microseconds (s). The last column of Table 1 presents the total power consumption of the design, which is the combined static and dynamic power. Furthermore, the area, operating frequency, and power values were obtained from the synthesis tool, ahd we calculated the latency using Equation (3):

Table 1.
Implementation results for on Xilinx FPGA devices.
The proposed ECC design can operate on a maximum of 129 and 161 MHz on Virtex-6 and Virtex-7 FPGA devices, respectively. These higher frequencies require additional hardware resources and consume more power, making our design inappropriate for WSN and RFID-related applications. The timing constraints were met until these frequencies (129 and 161 MHz), meaning the design has the worst-negative-slack of 0. Therefore, our objective was to obtain an area-optimized ECC implementation on FPGA, and hence in Table 1, we show a trend on Virtex-6 and Virtex-7 FPGA devices for operating frequencies of 100, 50, and 10 MHz. Consequently, this trend reveals that decreased clock frequency increases the computation time or latency. Moreover, the higher frequencies consume more power, as illustrated in the last column of Table 1.
Considering the results for Virtex-6 and Virtex-7 FPGA devices, the proposed crypto processor utilizes 407 slices and 2442 LUTs on Virtex-6 devices and 391 slices and 2346 LUTs on Virtex-7 FPGA. It takes 716,459 clock cycles for one PM computation. The reason for requiring higher clock cycle utilization is the use of a bit-serial modular multiplier for square, multiplication, and inverse computations. Using separate units for square and inversion reduces clock cycle overhead but significantly increases the amount of hardware resources and also raises the power consumption. Instead of using separate square and inversion blocks, faster modular multiplication methods can be employed, such as bit-parallel (Karatsuba, Toom–Cook), and digit-parallel; these also effect both hardware resources and power consumption of the crypto processor.
For Virtex-6 and Virtex7 FPGA devices at 100, 50, and 10 MHz, our crypto processor takes 7.16, 14.32, and 71.64 ms time for one PM computation, but the power consumption is different. For Virtex-6 devices, our crypto processor consumes 73, 39, and 7 mW power on identical 100, 50, and 10 MHz clock frequencies during one PM execution. Similarly, for Virtex-7 FPGA devices at 100, 50, and 10 MHz, our crypto processor consumes 51, 28, and 4 mW power during one PM execution. Notice that the proposed crypto processor outperforms hardware resources and power consumption on modern (28 nm) Virtex-7 FPGA devices. In addition, we have reported our results on Virtex-7 FPGA at a maximum 161 MHz frequency, where our processor takes 4.45 ms latency and consumes 77 mW for the execution of one PM operation of ECC; this higher power consumption is due to a maximum circuit frequency.
4.2. Comparisons
We show comparisons with state-of-the-art designs in Table 2, where the first column indicates the reference design (Ref. #). The second column displays the employed PM algorithm or computation method, and the third column specifies the implementation device. Columns four and five exhibit the area results regarding slices and LUTs. The number of clock cycles required for one PM computation is displayed in the sixth column. The operating frequency of the state-of-the-art PM designs is provided in the seventh column. The computation time or latency for a single PM execution is shown in the eighth column. The total power consumption of the designs is presented in the ninth column. Finally, the last column (ten) gives the architectural details of the hardware designs.

Table 2.
Comparison to state-of-the-art hardware designs of PM.
Column two of Table 2 shows that the reference designs of [12,13] implement the Montgomery PM algorithm; we also implement the same PM algorithm. If we compare the slices and LUTs of [12] for 163 bit binary field on the same Virtex-7 FPGA devices, our crypto processor design is 5.64 (ratio of 2207 to 391) and 4.24 (ratio of 9965 to 2346) times more efficient. Similarly, if we compare the slices and LUTs of [12] for 233 bit binary field on the same Virtex-7 FPGA devices, our crypto processor design is 13.09 (ratio of 5120 to 391) and 8.07 (ratio of 18,953 to 2346) times more efficient. We utilize a bit-serial modular multiplier, whereas the reference design uses a digit-parallel multiplier. On the other hand, the reference design takes fewer clock cycles than ours (see column six of Table 2). Columns seven and eight of Table 2 show that the reference design over and fields operates on higher circuit frequency and requires less computation time than this work because the reference design uses pipeline registers in the data path, which shortens the critical path delay and improves the circuit frequency. Overall the improvement in circuit frequency decreases the computation time.
Similar to [12], another pipelined PM design is described in [13]. If we compare only the slices over and fields, the proposed crypto processor is 3.91 (ratio of 1529 to 391) and 5.23 (ratio of 2048 to 391) times more efficient, respectively. Similarly, if we compare LUTs over and fields, the proposed crypto processor is 1.77 (ratio of 4162 to 2346) and 2.73 (ratio of 6407 to 2346) times more efficient, respectively. The reason includes the use of bit-serial multiplier architecture in our work, whereas a digit-parallel multiplier is used in [13]. Based on column six in Table 2, the reference design requires fewer clock cycles than ours. Additionally, the results displayed in columns seven and eight demonstrate that the reference design operates at a higher circuit frequency and demands less computation time over and fields. This is because the reference design incorporates pipeline registers in the data path, which minimizes the critical path delay and improves the circuit frequency. Hence, the improvement in circuit frequency leads to a reduction in computation time.
An accurate comparison is difficult to provide as the reference design of [14] targeted the prime field, i.e., with , for implementation, whereas we adopted a binary field, i.e., with . Moreover, the supported key lengths differ; the reference design uses 256 bits, whereas we utilized 233 bits. Despite the field selections and supported key lengths, the implemented PM algorithms also differ; we incorporated the Montgomery algorithm, whereas the reference design utilizes the double and add PM algorithm. Comparatively, our design utilizes 21.64 (ratio of 50,789 to 2346) times fewer LUTs and is 1.76 (ratio of 161 to 91) times more efficient in clock frequency. On the other hand, the reference design employs an interleaved modular multiplier, which takes fewer clock cycles (shown in column six of Table 2) and (also) utilizes lower computation time (shown in column eight of Table 2) than ours, where we used a bit-serial multiplier design.
As shown in Table 2, the performance of three PM algorithms (Binary, Frobenius Map, and Lopez Dahab) are compared in [15] on Virtex-5 FPGA. For all the PM algorithms implemented in [15], our crypto processor design outperforms in slices on identical Virtex-5 FPGA. The reason is the use of a digit-serial multiplier in the reference design of [15], whereas we preferred to use a bit-serial multiplier. The comparison to LUTs, clock cycles, and power cannot be provided, as the relevant information is not provided in the reference implementation (see the corresponding columns in Table 2). The reference design outperforms ours if we examine the frequency and latency columns in Table 2. Our objective was to realize an area-efficient ECC implementation, and our design outperforms in slices; therefore, there is always a trade-off.
A Lopez Dahab-based PM design over is described in [16] on Virtex-7 FPGA. On an identical Virtex-7 FPGA, our proposed crypto processor over is 9.35 (ratio of 3657 to 391) and 4.31 (ratio of 10,128 to 2346) times more efficient in slices and LUTs. One reason is the use of a bit-parallel hybrid Karatsuba multiplier in the reference design, whereas we used a bit-serial modular multiplier. Another reason is the use of a separate modular multiplier for polynomial multiplications and a square for polynomial square computations in the reference design. At the same time, we incorporated only one modular multiplier for polynomial multiplications and square computations. Similarly, column seven of Table 2 shows that our design outperforms in frequency compared to the reference PM implementation. On the other hand, using a faster hybrid Karatsuba multiplier in [16] results in lower clock cycles (see column six) as compared to ours; the lower clock cycles achieve lower computation time (see column eight) in [16]. There is always a trade-off.
The PM designs for wireless sensor nodes are described in [17,18], and implementations are carried out on Artix-7 FPAG (see column three of Table 2). We implemented our crypto processor design on Virtex-7 FPGA. The Artix-7 and Virtex-7 devices are built on 28 nm process technology [34]. Therefore, we compared our Virtex-7 implemented results to Artix-7 FPGA reference designs of [17,18]. Regarding slices, the most efficient area-optimized implementation on 28 nm technology [17] utilizes 442 slices on Artix-7 FPGA, which is comparatively 1.13 (ratio of 442 to 391) times higher than this work, where we implemented the design on Virtex-7 FPGA; the reason is the use of a digit-by-digit modular multiplier in the reference design, whereas we used a bit-serial multiplier. The LUTs comparison is impossible, as the related data are unavailable in the reference design. Comparing the clock cycles and latency, the proposed crypto process is 2.16 (ratio of 1,553,782 to 716,459) and 1.83 (ratio of 8177 to 4450) times more efficient than [17]. However, digit-by-digit multiplication style in [17] results in a higher operating frequency of 190 MHz, whereas our design achieves a maximum of 161 MHz. Even if the reference design operates at a higher clock frequency, overall, our crypto processor outperforms in computation time (or latency). Comparing our results to the Artix-7 implementation of [18] is a bit hard, as the reference design implemented three cryptographic algorithms to simultaneously obtain the advantages of symmetric and PKC. An advance encryption standard (AES-128) algorithm is incorporated to perform the symmetric cryptography; ECC over is utilized to operate elliptic-curves operations for PKC; and a secure hash algorithm (SHA-256) is considered to perform hash computation for digital signature, authentication, and random-keys generation. On the other hand, we have implemented only a Montgomery PM algorithm for the PM computation of ECC. Therefore, column five of Table 2 confirms the higher LUTs utilization in the reference design than our implementation. Slices cannot be compared, as the reference design does not provide this information. In clock cycles and computation time, the reference design is more efficient, but our crypto processor design is faster in clock frequency and consumes less power than the reference design (see columns six to nine in Table 2).
Regarding the power comparison, column nine of Table 2 show that most state-of-the-art designs lack discussion over power results, and we show a hyphen symbol in the corresponding column. Therefore, this comparison to our results is impossible.
5. Conclusions
This article has presented a crypto processor design for elliptic curve PM computation over with an aim of reducing hardware resources. In this regard, a bit-serial finite field modular multiplier has been implemented, which is also employed for the computation of modular squares, modular multiplication, and modular inversion operations, minimizing a significant amount of hardware resources. Moreover, on Virtex-6 and Virtex-7 FPGA devices, we found that the decrease in clock frequency shows an increase in the computation time or latency. In addition, higher circuit frequencies consume more power. For on Virtex-7 FPGA, our crypto processor utilizes 391 slices, achieves a maximum frequency of 161 MHz, takes 4.45 ms latency, and consumes 77 mW power for one PM execution. Moreover, the proposed design uses less area and consumes less power than state-of-the-art designs. Our results demonstrate that the proposed crypto processor design is beneficial for applications that need low hardware area and less power for cryptographic computations.
Author Contributions
Conceptualization, M.R., S.S.J. and A.A.; methodology, A.R.A. and M.A.; software, D.J.A.; validation, M.R. and S.S.J.; formal analysis, A.A. and A.R.A.; investigation, M.R. and S.S.J.; resources, D.J.A.; data curation, A.A.; writing—original draft preparation, A.R.A. and A.A.; writing—review and editing, M.R., S.S.J. and M.A.; visualization, A.A.; supervision, A.A. and M.R. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at University of Tabuk for funding this work through Research no. S-0151-1443.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Miller, V.S. Use of Elliptic Curves in Cryptography. In Proceedings of the Advances in Cryptology—CRYPTO ’85 Proceedings, Linz, Austria, 9–11 April 1985; Williams, H.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 417–426. [Google Scholar]
- Rashid, M.; Imran, M.; Jafri, A.R.; Al-Somani, T.F. Flexible Architectures for Cryptographic Algorithms—A Systematic Literature Review. J. Circuits Syst. Comput. 2019, 28, 1930003. [Google Scholar] [CrossRef]
- Abella, C.S.; Bonina, S.; Cucuccio, A.; D’Angelo, S.; Giustolisi, G.; Grasso, A.D.; Imbruglia, A.; Mauro, G.S.; Nastasi, G.A.M.; Palumbo, G.; et al. Autonomous Energy-Efficient Wireless Sensor Network Platform for Home/Office Automation. IEEE Sens. J. 2019, 19, 3501–3512. [Google Scholar] [CrossRef]
- Oladipupo, E.T.; Abikoye, O.C.; Imoize, A.L.; Awotunde, J.B.; Chang, T.Y.; Lee, C.C.; Do, D.T. An Efficient Authenticated Elliptic Curve Cryptography Scheme for Multicore Wireless Sensor Networks. IEEE Access 2023, 11, 1306–1323. [Google Scholar] [CrossRef]
- Ibrahim, A.A.A.; Nisar, K.; Hzou, Y.K.; Welch, I. Review and Analyzing RFID Technology Tags and Applications. In Proceedings of the 2019 IEEE 13th International Conference on Application of Information and Communication Technologies (AICT), Baku, Azerbaijan, 23–25 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Hu, S.; Chen, Y.; Zheng, Y.; Xing, B.; Li, Y.; Zhang, L.; Chen, L. Provably Secure ECC-Based Authentication and Key Agreement Scheme for Advanced Metering Infrastructure in the Smart Grid. IEEE Trans. Ind. Informatics 2023, 19, 5985–5994. [Google Scholar] [CrossRef]
- Jain, S.; Nandhini, C.; Doriya, R. ECC-Based Authentication Scheme for Cloud-Based Robots. Wirel. Pers. Commun. 2021, 117, 1557–1576. [Google Scholar] [CrossRef]
- NIST. Recommended Elliptic Curves for Federal Government Use. 1999. Available online: https://csrc.nist.gov/csrc/media/publications/fips/186/2/archive/2000-01-27/documents/fips186-2.pdf (accessed on 11 April 2023).
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography. 2004, pp. 1–311. Available online: https://link.springer.com/book/10.1007/b97644 (accessed on 27 March 2023).
- Lara-Nino, C.A.; Diaz-Perez, A.; Morales-Sandoval, M. Elliptic Curve Lightweight Cryptography: A Survey. IEEE Access 2018, 6, 72514–72550. [Google Scholar] [CrossRef]
- Mondal, S.; Patkar, S. Hardware-Software Hybrid Implementation of Non-Deterministic ECC over Curve-25519 for Resource Constrained Devices. In Proceedings of the 2021 Asian Conference on Innovation in Technology (ASIANCON), Pune, India, 27–29 August 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M.; Jafri, A.R.; Kashif, M. Throughput/area optimised pipelined architecture for elliptic curve crypto processor. IET Comput. Digit. Tech. 2019, 13, 361–368. [Google Scholar] [CrossRef]
- Imran, M.; Pagliarini, S.; Rashid, M. An Area Aware Accelerator for Elliptic Curve Point Multiplication. In Proceedings of the 2020 27th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 23–25 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Rahman, M.S.; Hossain, M.S.; Rahat, E.H.; Dipta, D.R.; Faruque, H.M.R.; Fattah, F.K. Efficient Hardware Implementation of 256 bit ECC Processor Over Prime Field. In Proceedings of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Khan, Z.U.A.; Benaissa, M. Low area ECC implementation on FPGA. In Proceedings of the 2013 IEEE 20th International Conference on Electronics, Circuits, and Systems (ICECS), Abu Dhabi, United Arab Emirates, 8–11 December 2013; pp. 581–584. [Google Scholar] [CrossRef]
- Imran, M.; Shafi, I.; Jafri, A.R.; Rashid, M. Hardware Design and Implementation of ECC Based Crypto Processor for Low-Area-Applications on FPGA. In Proceedings of the 2017 International Conference on Open Source Systems & Technologies (ICOSST), Lahore, Pakistan, 18–20 December 2017; pp. 54–59. [Google Scholar] [CrossRef]
- Morales-Sandoval, M.; Flores, L.A.R.; Cumplido, R.; Garcia-Hernandez, J.J.; Feregrino, C.; Algredo, I. A Compact FPGA-Based Accelerator for Curve-Based Cryptography in Wireless Sensor Networks. J. Sens. 2021, 2021, 8860413. [Google Scholar] [CrossRef]
- Toubal, A.; Bengherbia, B.; Zmirli, M.O.; Guessoum, A. FPGA implementation of a wireless sensor node with built-in security coprocessors for secured key exchange and data transfer. Measurement 2020, 153, 107429. [Google Scholar] [CrossRef]
- FIPS PUB 197. Advanced Encryption Standard (AES), National Institute of Standards and Technology, U.S. Department of Commerce, November 2001. Available online: http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf (accessed on 8 June 2023).
- NIST. Computer Security Resource Centre: PQC Standardization Process, Round 4 Submissions. Available online: https://csrc.nist.gov/Projects/post-quantum-cryptography/round-4-submissions (accessed on 24 May 2023).
- IBM. IBM Unveils Breakthrough 127-Qubit Quantum Processor. Available online: https://newsroom.ibm.com/2021-11-16-IBM-Unveils-Breakthrough-127-Qubit-Quantum-Processor (accessed on 22 May 2023).
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.L.; Fu, Y.; Li, C.L.; Weng, C.X.; Li, B.H.; Gu, J.; Lu, Y.S.; Huang, S.; Chen, Z.B. Experimental quantum secure network with digital signatures and encryption. Natl. Sci. Rev. 2022, 10, nwac228. [Google Scholar] [CrossRef] [PubMed]
- Imran, M.; Abideen, Z.U.; Pagliarini, S. An Experimental Study of Building Blocks of Lattice-Based NIST Post-Quantum Cryptographic Algorithms. Electronics 2020, 9, 1953. [Google Scholar] [CrossRef]
- Soni, D.; Karri, R. Efficient Hardware Implementation of PQC Primitives and PQC algorithms Using High-Level Synthesis. In Proceedings of the 2021 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Tampa, FL, USA, 7–9 July 2021; pp. 296–301. [Google Scholar] [CrossRef]
- Imran, M.; Almeida, F.; Basso, A.; Roy, S.S.; Pagliarini, S. High-speed SABER Key Encapsulation Mechanism in 65nm CMOS. J. Cryptogr. Eng. 2023. [Google Scholar] [CrossRef]
- Ghosh, A.; Mera, J.; Karmakar, A.; Das, D.; Ghosh, S.; Verbauwhede, I.; Sen, S. A 334 μW 0.158 mm2 Saber Learning with Rounding based Post-Quantum Crypto Accelerator. In Proceedings of the 2022 IEEE Custom Integrated Circuits Conference (CICC), Newport Beach, CA, USA, 24–27 April 2022; pp. 1–2. [Google Scholar] [CrossRef]
- Basu Roy, D.; Mukhopadhyay, D. High-Speed Implementation of ECC Scalar Multiplication in GF(p) for Generic Montgomery Curves. IEEE Trans. Very Large Scale Integr. Syst. 2019, 27, 1587–1600. [Google Scholar] [CrossRef]
- Hu, X.; Li, X.; Zheng, X.; Liu, Y.; Xiong, X. A high speed processor for elliptic curve cryptography over NIST prime field. IET Circuits Devices Syst. 2022, 16, 350–359. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M. Architectural Review of Polynomial Bases Finite Field Multipliers Over GF(2m). In Proceedings of the 2017 International Conference on Communication, Computing and Digital Systems (C-CODE), Islamabad, Pakistan, 8–9 March 2017; pp. 331–336. [Google Scholar] [CrossRef]
- Imran, M.; Abideen, Z.U.; Pagliarini, S. An Open-source Library of Large Integer Polynomial Multipliers. In Proceedings of the 2021 24th International Symposium on Design and Diagnostics of Electronic Circuits & Systems (DDECS), Vienna, Austria, 7–9 April 2021; pp. 145–150. [Google Scholar] [CrossRef]
- Sutter, G.D.; Deschamps, J.P.; Imana, J.L. Efficient Elliptic Curve Point Multiplication Using Digit-Serial Binary Field Operations. IEEE Trans. Ind. Electron. 2013, 60, 217–225. [Google Scholar] [CrossRef]
- Itoh, T.; Tsujii, S. A fast algorithm for computing multiplicative inverses in GF (2m) using normal bases. Inf. Comput. 1988, 78, 171–177. [Google Scholar] [CrossRef]
- XILINX. 7 Series FPGAs Data Sheet: Overview. Available online: https://docs.xilinx.com/v/u/en-US/ds180_7Series_Overview (accessed on 19 April 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).