The Applicability of Machine Learning Methods to the Characterization of Fibrous Gas Diffusion Layers
Abstract
1. Introduction
2. Methods and Data
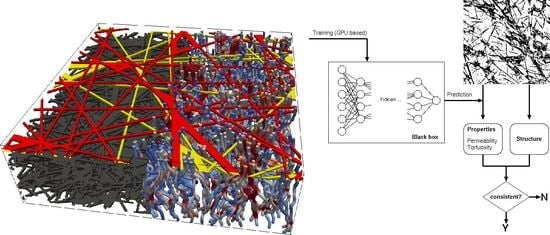
2.1. An Overview on the Machine Learning Model
2.2. Convolutional Neural Network Model
2.3. Lattice–Boltzmann Simulations
2.4. Basic Data
- the number of the realizations of the fiber geometry: 25;
- the number of parameters used for different binder distributions: 4;
- the number of compression levels, where six steps from 0% (uncompressed) to 50%—in steps of 10%—were used.
2.5. Real Data
- R1
- R2
- R3
- one without (Figure 5).



2.6. Evaluation of the Predictions
3. Data Preparation
3.1. Domain Size Normalization
3.2. Real Data
4. Validation
- (A)
- permeability ;
- (B)
- tortuosity ;
- (C)
- permeability ;
- (D)
- tortuosity .
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ye, D.H.; Gauthier, E.; Cheah, M.J.; Benziger, J.; Pan, M. The Effect of Gas Diffusion Layer Compression on Gas Bypass and Water Slug Motion in Parallel Gas Flow Channels. AIChE J. 2015, 61, 355–367. [Google Scholar] [CrossRef]
- Ryan, E.M.; Mukherjee, P.P. Mesoscale modeling in electrochemical devices—A critical perspective. Prog. Energy Combust. Sci. 2019, 71, 118–142. [Google Scholar] [CrossRef]
- Holzer, L.; Pecho, O.; Schumacher, J.; Marmet, P.; Stenzel, O.; Büchi, F.; Lamibrac, A.; Münch, B. Microstructure-property relationships in a gas diffusion layer (GDL) for Polymer Electrolyte Fuel Cells, Part I: Effect of compression and anisotropy of dry GDL. Electrochim. Acta 2017, 227, 419–434. [Google Scholar] [CrossRef]
- Zenyuk, I.V.; Parkinson, D.Y.; Connolly, L.G.; Weber, A.Z. Gas-diffusion-layer structural properties under compression via X-ray tomography. J. Power Sources 2016, 328, 364–376. [Google Scholar] [CrossRef]
- Bao, Z.; Li, Y.; Zhou, X.; Gao, F.; Du, Q.; Jiao, K. Transport properties of gas diffusion layer of proton exchange membrane fuel cells: Effects of compression. Int. J. Heat Mass Transf. 2021, 178, 121608. [Google Scholar] [CrossRef]
- Bosomoiu, M.; Tsotridis, G.; Bednarek, T. Study of effective transport properties of fresh and aged gas diffusion layers. J. Power Sources 2015, 285, 568–579. [Google Scholar] [CrossRef]
- Mukherjee, M.; Bonnet, C.; Lapique, F. Estimation of through-plane and in-plane gas permeability across gas diffusion layers (GDLs): Comparison with equivalent permeability in bipolar plates and relation to fuel cell performance. Int. J. Hydrogen Energy 2020, 45, 13428–13440. [Google Scholar] [CrossRef]
- Leonard, D.; Babu, S.K.; Baxter, J.; Meyer, H.M.; Cullen, D.; Borup, R. Natural fiber-derived gas diffusion layers for high performance, lower cost PEM fuel cells. J. Power Sources 2023, 564, 232619. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, L.; Harandi, H.B.; Duan, K.; Zeis, R.; Sui, P.C.; Chuang, P.Y.A. Microstructure reconstruction of the gas diffusion layer and analyses of the anisotropic transport properties. Energy Convers. Manag. 2021, 241, 114293. [Google Scholar] [CrossRef]
- Yin, Y.; Qu, Z.; Prodanović, M.; Landry, C.J. Identifying the dominant transport mechanism in single nanoscale pores and 3D nanoporous media. Fundam. Res. 2022, 3, 409–421. [Google Scholar] [CrossRef]
- Ding, R.; Zhang, S.; Chen, Y.; Rui, Z.; Hua, K.; Wu, Y.; Li, X.; Duan, X.; Wang, X.; Li, J.; et al. Application of Machine Learning in Optimizing Proton Exchange Membrane Fuel Cells: A Review. Energy AI 2022, 9, 100170. [Google Scholar] [CrossRef]
- Froning, D.; Wirtz, J.; Hoppe, E.; Lehnert, W. Flow Characteristics of Fibrous Gas Diffusion Layers Using Machine Learning Methods. Appl. Sci. 2022, 12, 12193. [Google Scholar] [CrossRef]
- Cawte, T.; Bazylak, A. A 3D convolutional neural network accurately predicts the permeability of gas diffusion layer materials directly from image data. Curr. Opin. Electrochem. 2022, 35, 101101. [Google Scholar] [CrossRef]
- Wang, Y.D.; Chung, T.; Armstrong, R.T.; Mostaghimi, P. ML-LBM: Predicting and Accelerating Steady State Flow Simulation in Porous Media with Convolutional Neural Networks. Transp. Porous Media 2021, 138, 49–75. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, H.; Brandon, N.P. Gas diffusion layer degradation in proton exchange membrane fuel cells: Mechanisms, characterization techniques and modelling approaches. J. Power Sources 2021, 513, 230560. [Google Scholar] [CrossRef]
- Jafarizadeh, A.; Ahmadzadeh, M.; Mahmoudzadeh, S.; Panjepour, M. A New Approach for Predicting the Pressure Drop in Various Types of Metal Foams Using a Combination of CFD and Machine Learning Regression Models. Transp. Porous Media 2023, 147, 59–91. [Google Scholar] [CrossRef]
- Santos, J.E.; Yin, Y.; Jo, H.; Pan, W.; Kang, Q.; Viswanathan, H.S.; Prodanović, M.; Pyrcz, M.J.; Lubbers, N. Computationally Efficient Multiscale Neural Networks Applied to Fluid Flow in Complex 3D Porous Media. Transp. Porous Media 2021, 140, 241–272. [Google Scholar] [CrossRef]
- Yeh, R.; Hasegawa-Johnson, M.; Do, M.N. Stable and symmetric filter convolutional neural network. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 2652–2656. [Google Scholar] [CrossRef]
- Li, H.W.; Liu, J.N.; Yang, Y.; Lu, G.L.; Qiao, B.X. Coupling flow channel optimization and Bagging neural network to achieve performance prediction for proton exchange membrane fuel cells with varying imitated water-drop block channel. Int. J. Hydrogen Energy 2022, 47, 39987–40007. [Google Scholar] [CrossRef]
- Shum, A.D.; Liu, C.P.; Lim, W.H.; Parkinson, D.Y.; Zenyuk, I.V. Using Machine Learning Algorithms for Water Segmentation in Gas Diffusion Layers of Polymer Electrolyte Fuel Cells. Transp. Porous Med. 2022, 144, 715–737. [Google Scholar] [CrossRef]
- Zhu, G.; Chen, W.; Lu, S.; Chen, X. Parameter study of high-temperature proton exchange membrane fuel cell using data-driven models. Int. J. Hydrogen Energy 2019, 44, 28958–28967. [Google Scholar] [CrossRef]
- Buchaniec, S.; Gnatowski, M.; Brus, G. Integration of Classical Mathematical Modeling with an Artificial Neural Network for the Problems with Limited Dataset. Energies 2021, 14, 5127. [Google Scholar] [CrossRef]
- Yasuda, T.; Ookawara, S.; Yoshikawa, S.; Matsumoto, H. Materials processing model-driven discovery framework for porous materials using machine learning and genetic algorithm: A focus on optimization of permeability and filtration efficiency. Chem. Eng. J. 2023, 453, 139540. [Google Scholar] [CrossRef]
- Arigbe, O.D.; Oyeneyin, M.B.; Arana, I.; Ghazi, M.D. Real-time relative permeability prediction using deep learning. J. Petrol. Explor. Prod. Technol. 2018, 9, 1271–1284. [Google Scholar] [CrossRef]
- Hurtz, S. Brettspiel Go: Hobbyspieler Schlägt “übermenschliche” KI. Available online: https://www.sueddeutsche.de/wirtschaft/go-ki-kellin-pelrine-lee-sedol-alphago-hobbyspieler-1.5754972 (accessed on 20 February 2023).
- Froning, D.; Brinkmann, J.; Reimer, U.; Schmidt, V.; Lehnert, W.; Stolten, D. 3D analysis, modeling and simulation of transport processes in compressed fibrous microstructures, using the Lattice Boltzmann method. Electrochim. Acta 2013, 110, 325–334. [Google Scholar] [CrossRef]
- Galeone, P. Hands-On Neural Networks with TensorFlow 2.0; Packt Publishing: Birmingham, UK, 2019. [Google Scholar]
- Froning, D.; Gaiselmann, G.; Reimer, U.; Brinkmann, J.; Schmidt, V.; Lehnert, W. Stochastic Aspects of Mass Transport in Gas Diffusion Layers. Transp. Porous Media 2014, 103, 469–495. [Google Scholar] [CrossRef]
- Froning, D.; Yu, J.; Gaiselmann, G.; Reimer, U.; Manke, I.; Schmidt, V.; Lehnert, W. Impact of compression on gas transport in non-woven gas diffusion layers of high temperature polymer electrolyte fuel cells. J. Power Sources 2016, 318, 26–34. [Google Scholar] [CrossRef]
- Koponen, A.; Kataja, M.; Timonen, J. Tortuous flow in porous media. Phys. Rev. E 1996, 54, 406–410. [Google Scholar] [CrossRef]
- Krause, D.; Thörnig, P. JURECA: Modular supercomputer at Jülich Supercomputing Centre. J. Large-Scale Res. Facil. JLSRF 2018, 4, A132. [Google Scholar] [CrossRef]
- Thiedmann, R.; Fleischer, F.; Hartnig, C.; Lehnert, W.; Schmidt, V. Stochastic 3D Modeling of the GDL Structure in PEMFCs Based on Thin Section Detection. J. Electrochem. Soc. 2008, 155, B391–B399. [Google Scholar] [CrossRef]
- Wang, Y.; Cho, S.; Thiedmann, R.; Schmidt, V.; Lehnert, W.; Feng, X. Stochastic modeling and direct simulation of the diffusion media for polymer electrolyte fuel cells. Int. J. Heat Mass Transf. 2010, 53, 1128–1138. [Google Scholar] [CrossRef]
- Lintermann, A.; Schröder, W. Lattice–Boltzmann simulations for complex geometries on high-performance computers. CEAS Aeronaut. J. 2020, 11, 745–766. [Google Scholar] [CrossRef]
- Hoppe, E. Kompressionseigenschaften der Gasdiffusionslage einer Hochtemperatur-Polymerelektrolyt-Brennstoffzelle. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2021. [Google Scholar]
- Tomadakis, M.M.; Robertson, T.J. Viscous Permeability of Random Fiber Structures: Comparison of Electrical and Diffusional Estimates with Experimental and Analytical Results. J. Compos. Mater. 2005, 39, 163–188. [Google Scholar] [CrossRef]
- The ImageMagick Development Team. ImageMagick. Available online: https://imagemagick.org (accessed on 4 January 2021).
- Nguyen, A.; Yosinski, J.; Clune, J. Understanding Neural Networks via Feature Visualization: A Survey. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 55–76. [Google Scholar] [CrossRef]
- El-Amir, H.; Hamdy, M. Deep Learning Pipeline; Apress: Berkeley, CA, USA, 2020. [Google Scholar] [CrossRef]
- Thiedmann, R.; Hartnig, C.; Manke, I.; Schmidt, V.; Lehnert, W. Local Structural Characteristics of Pore Space in GDLs of PEM Fuel Cells Based on Geometric 3D Graphs. J. Electrochem. Soc. 2009, 156, B1339. [Google Scholar] [CrossRef]
- Mangal, P.; Pant, L.M.; Carrigy, N.; Dumontier, M.; Zingan, V.; Mitra, S.; Secanell, M. Experimental study of mass transport in PEMFCs: Through plane permeability and molecular diffusivity in GDLs. Electrochim. Acta 2015, 167, 160–171. [Google Scholar] [CrossRef]
- Feser, J.; Prasad, A.; Advani, S. Experimental characterization of in-plane permeability of gas diffusion layers. J. Power Sources 2006, 162, 1226–1231. [Google Scholar] [CrossRef]
- Hoppe, E.; Janßen, H.; Müller, M.; Lehnert, W. The impact of flow field plate misalignment on the gas diffusion layer intrusion and performance of a high-temperature polymer electrolyte fuel cell. J. Power Sources 2021, 501, 230036. [Google Scholar] [CrossRef]
- Zou, W.; Froning, D.; Shi, Y.; Lehnert, W. Working zone for a least-squares support vector machine for modeling polymer electrolyte fuel cell voltage. Appl. Energy 2021, 283, 116191. [Google Scholar] [CrossRef]











| Series | No. | Comp. % | No. of Images | Dimensions |
|---|---|---|---|---|
| R1 | 1 | 0 | 200 | 1250 × 1250 |
| R2 | 1 | 6 | 40 | 694 × 670 |
| 2 | 8 | 22 | 671 × 688 | |
| 3 | 11 | 27 | 697 × 661 | |
| 4 | 13 | 40 | 684 × 673 | |
| 5 | 16 | 22 | 682 × 682 | |
| 6 | 18 | 40 | 673 × 687 | |
| 7 | 19 | 21 | 685 × 680 | |
| 8 | 21 | 40 | 688 × 677 | |
| 9 | 24 | 40 | 670 × 685 | |
| 10 | 29 | 40 | 670 × 685 | |
| R3 | 1 | 7 | 40 | 760 × 310 |
| 2 | 10 | 40 | 760 × 310 | |
| 3 | 11 | 40 | 760 × 310 | |
| 4 | 14 | 40 | 760 × 310 | |
| 5 | 18 | 40 | 760 × 310 | |
| 6 | 19 | 40 | 760 × 310 | |
| 7 | 24 | 40 | 760 × 310 | |
| 8 | 28 | 40 | 760 × 310 | |
| 9 | 30 | 40 | 760 × 310 | |
| 10 | 31 | 40 | 760 × 310 |
| TP | IP | |||||
|---|---|---|---|---|---|---|
| min | 8.89 | 1.17 | 11.73 | 17.44 | 1.07 | 19.23 |
| max | 11.94 | 1.36 | 15.18 | 19.82 | 1.14 | 22.02 |
| average | 10.54 | 1.27 | 13.43 | 18.83 | 1.10 | 20.80 |
| median | 10.54 | 1.28 | 18.85 | 1.10 | ||
| std. deviation | 0.62 | 0.038 | 0.75 | 0.56 | 0.014 | 0.69 |
| variance | 0.38 | 0.32 | ||||
| var. coeff. | ||||||
| average (B) in [26] | 11.18 | 1.27 | 17.98 | 1.11 | ||
| average (C) in [26] | 10.51 | 1.29 | 17.81 | 1.11 | ||
| favored: | C | B | B | B, C | ||
| Series | No. | Comp. | Porosity | TP | IP | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % | ||||||||||||
| R2 | 1 | 6 | 0.688 | 7.12 | 1.22 | 1.26 | 6.01 | 8.18 | 1.01 | 18.20 | ||
| 2 | 8 | 0.666 | 6.38 | 1.13 | 1.17 | 5.91 | 6.97 | 1.01 | 15.97 | |||
| 3 | 11 | 0.678 | 6.72 | 1.15 | 1.28 | 6.07 | 7.03 | 1.01 | 16.31 | |||
| 4 | 13 | 0.669 | 6.74 | 1.23 | 1.27 | 4.65 | 6.82 | 1.04 | 16.10 | |||
| 5 | 16 | 0.669 | 6.74 | 1.11 | 1.35 | 6.98 | 6.25 | 1.05 | 16.09 | |||
| 6 | 18 | 0.669 | 6.59 | 1.25 | 1.27 | 4.36 | 6.05 | 1.07 | 15.37 | |||
| 7 | 19 | 0.680 | 6.05 | 1.12 | 1.26 | 5.49 | 5.91 | 1.07 | 14.09 | |||
| 8 | 21 | 0.644 | 6.42 | 1.26 | 1.27 | 3.46 | 5.86 | 1.03 | 13.35 | |||
| 9 | 24 | 0.640 | 6.41 | 1.27 | 1.27 | 3.23 | 5.12 | 1.02 | 12.25 | |||
| 10 | 29 | 0.640 | 6.41 | 1.27 | 1.28 | 3.23 | 4.59 | 1.04 | 11.05 | |||
| R3 | 1 | 7 | 0.685 | 7.61 | 1.18 | 1.13 | 7.46 | 7.65 | 1.08 | 16.23 | ||
| 2 | 10 | 0.709 | 7.91 | 1.15 | 1.19 | 9.46 | 7.21 | 1.09 | 16.19 | |||
| 3 | 11 | 0.669 | 7.02 | 1.20 | 1.13 | 5.39 | 6.94 | 1.07 | 15.08 | |||
| 4 | 14 | 0.666 | 6.86 | 1.20 | 1.16 | 5.01 | 6.46 | 1.09 | 14.18 | |||
| 5 | 18 | 0.678 | 6.91 | 1.18 | 1.20 | 5.68 | 6.08 | 1.08 | 14.13 | |||
| 6 | 19 | 0.685 | 6.89 | 1.18 | 1.22 | 6.54 | 1.11 | 14.45 | ||||
| 7 | 24 | 0.597 | 4.61 | 1.08 | 5.15 | 1.04 | 10.79 | |||||
| 8 | 28 | 0.555 | 4.84 | 0.98 | 3.75 | 1.04 | 7.97 | |||||
| 9 | 30 | 0.570 | 6.69 | 1.19 | 3.80 | 1.12 | 7.38 | |||||
| 10 | 31 | 0.592 | 8.87 | 1.25 | 4.09 | 1.17 | 8.68 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Froning, D.; Hoppe, E.; Peters, R. The Applicability of Machine Learning Methods to the Characterization of Fibrous Gas Diffusion Layers. Appl. Sci. 2023, 13, 6981. https://doi.org/10.3390/app13126981
Froning D, Hoppe E, Peters R. The Applicability of Machine Learning Methods to the Characterization of Fibrous Gas Diffusion Layers. Applied Sciences. 2023; 13(12):6981. https://doi.org/10.3390/app13126981
Chicago/Turabian StyleFroning, Dieter, Eugen Hoppe, and Ralf Peters. 2023. "The Applicability of Machine Learning Methods to the Characterization of Fibrous Gas Diffusion Layers" Applied Sciences 13, no. 12: 6981. https://doi.org/10.3390/app13126981
APA StyleFroning, D., Hoppe, E., & Peters, R. (2023). The Applicability of Machine Learning Methods to the Characterization of Fibrous Gas Diffusion Layers. Applied Sciences, 13(12), 6981. https://doi.org/10.3390/app13126981