Mesh-Free MLS-Based Error-Recovery Technique for Finite Element Incompressible Elastic Computations
Abstract
1. Introduction
2. Finite-Element Incompressible Elastic Formulation
3. Finite-Element-Solution Effectivity and Accuracy
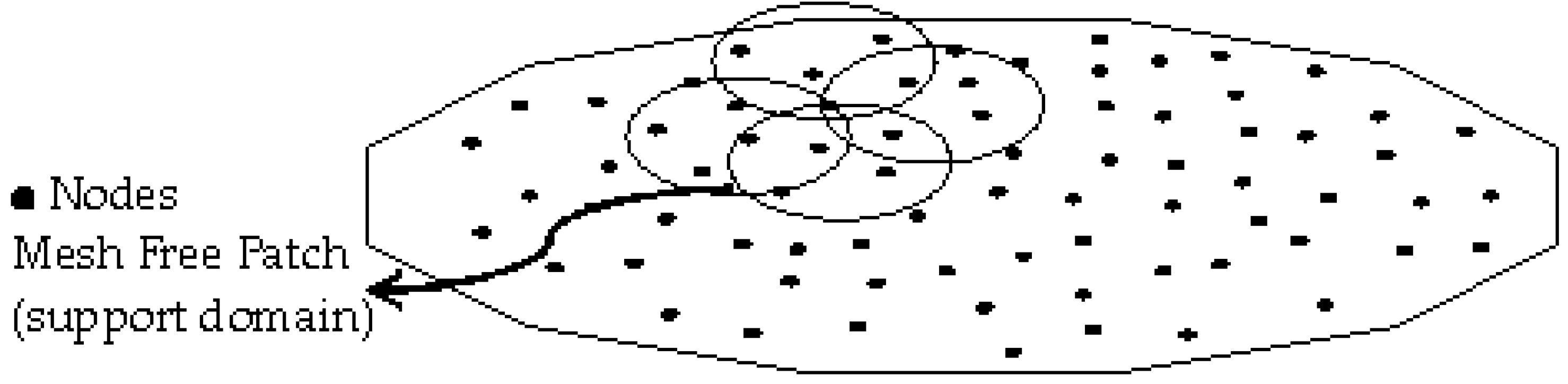
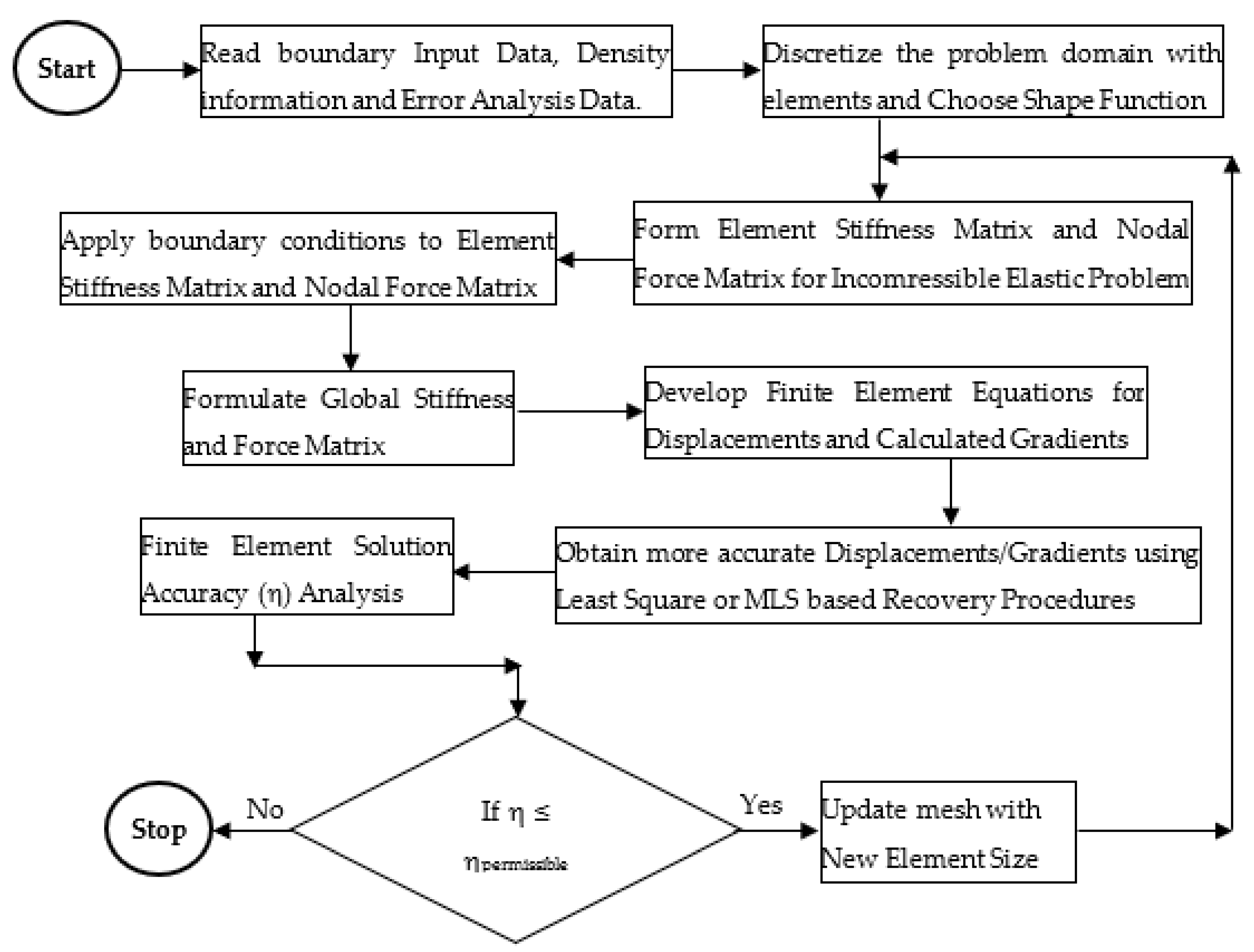
4. MLS-Procedure-Based Mesh-Free Error Recovery
5. Illustrative Applications
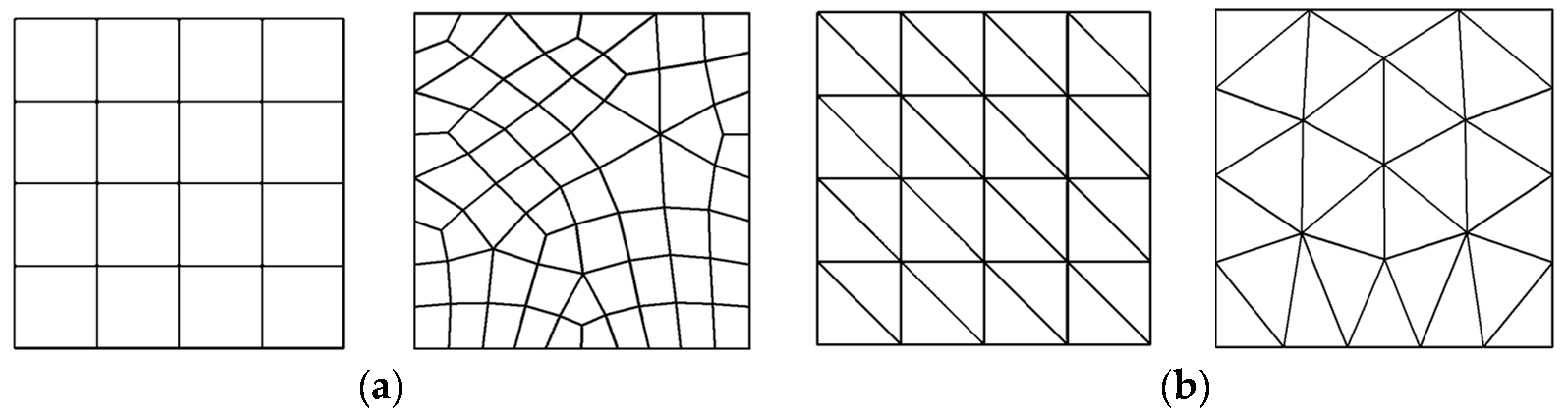
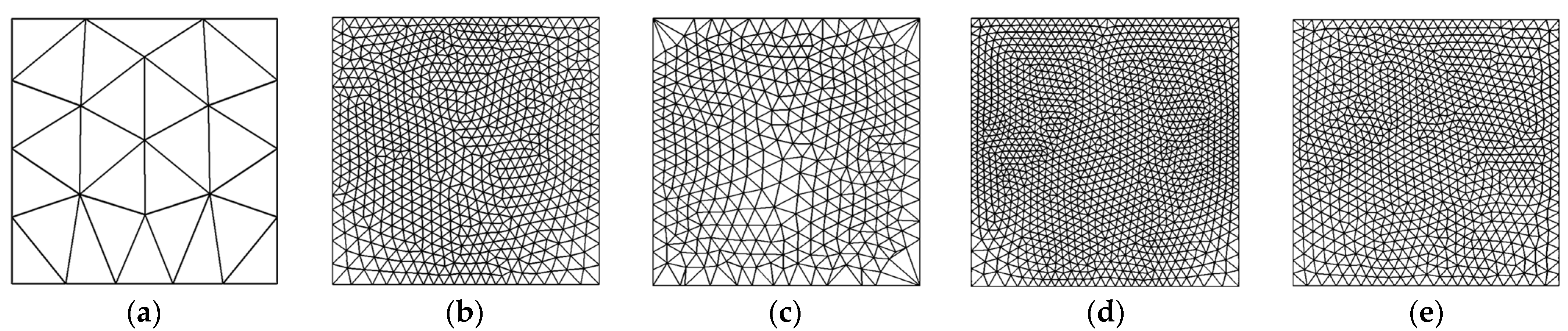
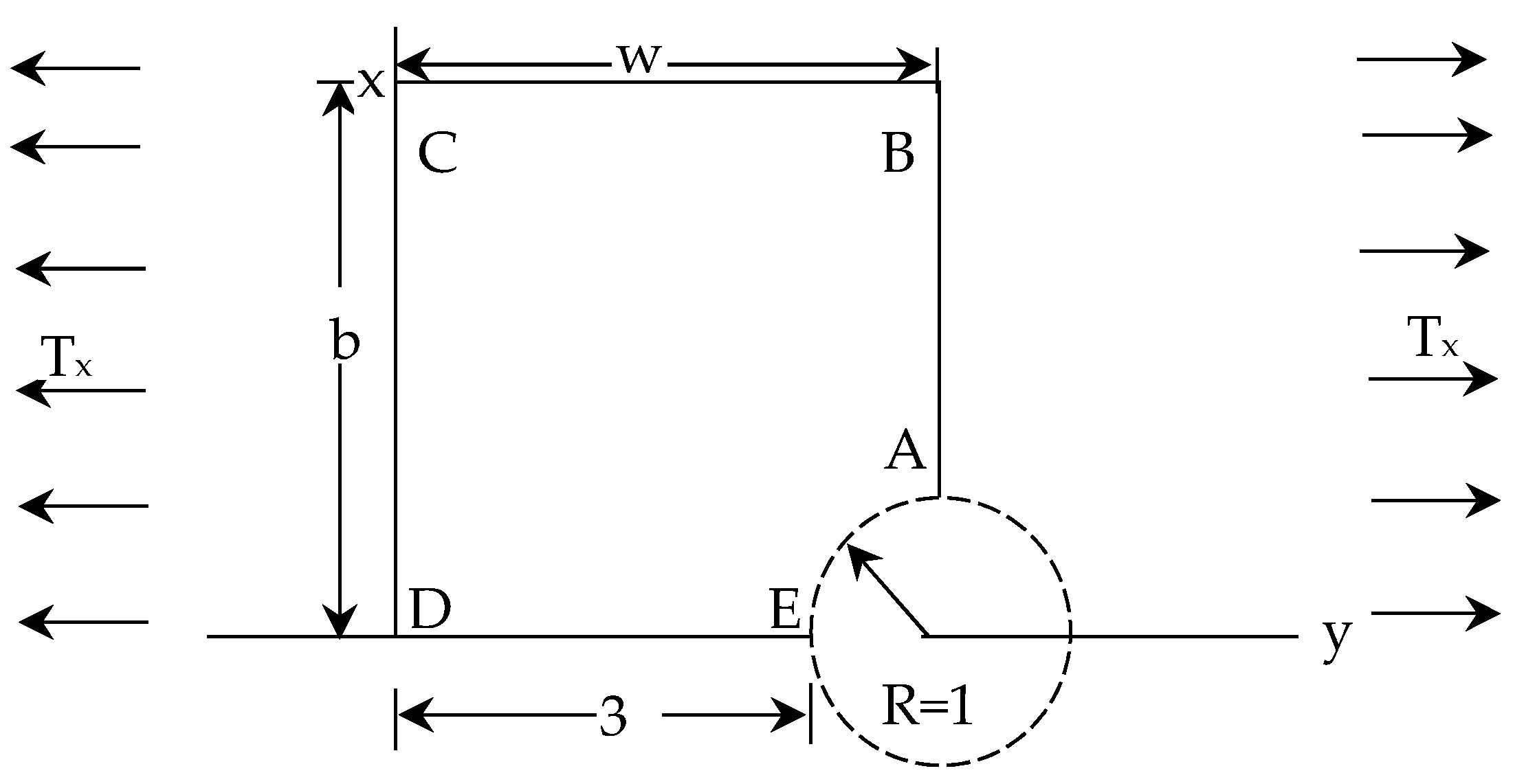
5.1. Incompressible Infinite Square Elastic Plate
Effect of Patch Formation on Error Recovery
5.2. Infinite Incompressible Elastic Plate with Rigid Inclusion
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cen, S.; Wu, C.J.; Li, Z.; Shang, Y.; Li, C. Some advances in high-performance finite element methods. Eng. Comput. 2019, 36, 2811–2834. [Google Scholar] [CrossRef]
- Gratsch, T.; Bathe, K. A posteriori error estimation technique in practical finite element analysis. Comput. Struct. 2005, 83, 75–90. [Google Scholar] [CrossRef]
- Chen, J.-S.; Hillman, M.M.; Chi, S.-W. Meshfree Methods: Progress Made after 20 Years. J. Eng. Mech. 2017, 143, 04017001. [Google Scholar] [CrossRef]
- Babuska, I.; Banerjee, U.; Kergrene, K. Strongly stable generalized finite element method: Application to interface problems. Comput. Methods Appl. Mech. Eng. 2017, 327, 58–92. [Google Scholar] [CrossRef]
- Yu, P.; Hao, Q.; Wang, X.; Yu, Y.; Zhan, Z. Mixed Integration Scheme for Embedded Discontinuous Interfaces by Extended Finite Element Method. Front. Earth Sci. 2022, 9, 829203. [Google Scholar] [CrossRef]
- Lee, C.-K.; Mihai, L.A.; Hale, J.S.; Kerfriden, P.; Bordas, S.P.A. Strain smoothing for compressible and nearly-incompressible finite elasticity. Comp. Struct. 2017, 182, 540–555. [Google Scholar] [CrossRef]
- Tong, Z.; Peng, Z.; Yue, Y.; Chen, Z. A SPH-GFDM Coupled Method for Elasticity Analysis. Symmetry 2021, 13, 1774. [Google Scholar] [CrossRef]
- Baek, J.; Chen, J.; Susuki, K. A neural network-enhanced reproducing kernel particle method for modeling strain localization. Int. J. Numer. Methods Eng. 2022, 123, 4422–4454. [Google Scholar] [CrossRef]
- Xiang, H.; Chen, B. A moving particle semi-implicit method for free surface flow: Improvement in inter-particle force stabilization and consistency restoring. Numer. Methods Fluids 2017, 84, 409–442. [Google Scholar] [CrossRef]
- Brink, U.; Stein, E. On some mixed finite element methods for incompressible and nearly incompressible finite elasticity. Comput. Mech. 1996, 19, 105–119. [Google Scholar] [CrossRef]
- Zeng, W.; Liu, G.R. Smoothed Finite Element Methods (S-FEM): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2018, 25, 397–435. [Google Scholar] [CrossRef]
- Farrell, P.E.; Gaticay, L.F.; Lamichhanez, B.; Oyarzua, R.; Ruiz-Baier, R. Mixed Kirchhof stress-displacement—Pressure formulations for incompressible hyper elasticity. Comput. Methods Appl. Mech. Eng. 2021, 374, 113562. [Google Scholar] [CrossRef]
- Karabelas, E.; Haase, G.; Plank, G.; Augustin, C.M. Versatile stabilized finite element formulations for nearly and fully incompressible solid mechanics. Comput. Mech. 2020, 65, 193–215. [Google Scholar] [CrossRef]
- Doll, S.; Schweizerhof, K.; Hauptmann, R.; Freischläger, C. On volumetric locking of low order solid and solid shell elements for finite elasto-viscoplastic deformations and selective reduced integration. Eng. Comput. 2000, 17, 874–902. [Google Scholar] [CrossRef]
- Boffi, D.; Stenberg, R. A remark on finite element schemes for nearly incompressible elasticity. Comput. Math. Appl. 2017, 74, 2047–2055. [Google Scholar] [CrossRef]
- Nemer, R.; Larcher, A.; Coupez, T.; Hachem, E. Stabilized finite element method for incompressible solid dynamics using an updated Lagrangian formulation. Comput. Methods Appl. Mech. Eng. 2021, 384, 113923. [Google Scholar] [CrossRef]
- Gültekin, O.; Dal, H.; Holzapfel, G.A. On the quasi-incompressible finite element analysis of anisotropic hyperelastic materials. Comput. Mech. 2019, 63, 443–453. [Google Scholar] [CrossRef]
- Jarak, T.; Jalušić, B.; Sorić, J. Mixed Meshless Local Petrov-Galerkin Methods for Solving Linear Fourth-Order Differential Equations. Trans. Famena 2020, 44, 1–12. [Google Scholar] [CrossRef]
- Saikia, B.B.; Nath, D.; Gautam, S.S. Application of machine learning in efficient stress recovery in finite element analysis. Mater. Today Proc. 2023, 78, 359–363. [Google Scholar] [CrossRef]
- Ahmed, M.; Singh, D. An adaptive parametric study on mesh refinement during adaptive finite element simulation of sheet forming operations. Turk. J. Eng. Environ. Sci. 2008, 32, 163–175. [Google Scholar]
- Cai, D.; Cai, Z. Hybrid a posteriori error estimator for conforming finite element approximations. Comput. Methods Appl. Mech. Eng. 2018, 339, 320–340. [Google Scholar] [CrossRef]
- Gabriel, N.G.; Luis, F.G.; Filánder, A.S. A reliable and efficient residual-based a posteriori error estimator for the mixed finite elements scheme. Comput. Math. Appl. 2016, 71, 585–614. [Google Scholar] [CrossRef]
- Li, W.; Thanh, N.N.; Huanga, J.; Zhoua, K. Adaptive analysis of crack propagation in thin-shell structures via an isogeometric mesh free moving least-squares approach. Comput. Methods Appl. Mech. Eng. 2020, 358, 112613. [Google Scholar] [CrossRef]
- Bird, R.E.; Giani, S.; Coombs, W.M. A posteriori discontinuous Galerkin error estimator for linear elasticity. Appl. Math. Comput. 2019, 344–345, 78–96. [Google Scholar] [CrossRef]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Lee, C.K.; Zhou, C.E. On error estimation and adaptive refinement for element free Galerkin method: Part I: Stress recovery and a posteriori error estimation. Comput. Struct. 2004, 82, 413–428. [Google Scholar] [CrossRef]
- Khan, A.; Powell, C.E.; Silvester, D.J. Robust a posteriori error estimators for mixed approximation of nearly incompressible elasticity. Int. J. Numer. Methods Eng. 2019, 119, 18–37. [Google Scholar] [CrossRef]
- Ahmed, M.; Singh, D.; AlQadhi, S.; Kahla, N.B. L2-Norm based a-Posteriori Error Estimates of Compressible and Nearly-Incompressible Elastic Finite Element Solutions. Appl. Sci. 2022, 12, 3999. [Google Scholar] [CrossRef]
- Kumor, D.; Rademacher, A. Goal-Oriented a Posteriori Error Estimates in Nearly Incompressible Linear Elasticity. In Proceedings of the European Conference on Numerical Mathematics and Advanced Applications ENUMATH 2017, Voss, Norway, 25–29 September 2017; Radu, F.A., Kumar, K., Berre, I., Nordbotten, J., Pop, I., Eds.; Lecture Notes in Computational Science and Engineering 126. Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Ahmed, M.; Singh, D.; AlQadhi, S.; Thanh, N.V. Moving Least Squares Interpolation Based A-Posteriori Error Technique in Finite Element Elastic Analysis. CMES-Comput. Model. Eng. Sci. 2021, 129, 168–188. [Google Scholar] [CrossRef]
- Karvonen, T.; Cirak, F.; Girolami, M. Error Analysis for a Statistical Finite Element Method. arXiv 2022. [Google Scholar] [CrossRef]
- Vogl, C.J.; Joseph, I.; Holec, M. Mesh Refinement for Anisotropic Diffusion in Magnetized Plasmas. arXiv 2022. [Google Scholar] [CrossRef]
- Katiyar, V.; Gupta, A.; Tounsi, A. Microstructural/geometric imperfection sensitivity on the vibration response of geometrically discontinuous bi-directional functionally graded plates (2D-FGPs) with partial supports by using FEM. Steel Compos. Struct. 2022, 45, 621–640. [Google Scholar]
- Vinh, P.V.; Chinh, N.V.; Tounsi, A. Static bending and buckling analysis of bi-directional functionally graded porous plates using an improved first-order shear deformation theory and FEM. Eur. J. Mech.—A/Solids 2022, 96, 104743. [Google Scholar] [CrossRef]
- Kahla, N.B.; AlQadhi, S.; Ahmed, M. Radial Point Interpolation-Based Error Recovery Estimates for Finite Element Solutions of Incompressible Elastic Problems. Appl. Sci. 2023, 13, 2366. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Lui, Y.C.; Huang, G.C. Error Estimates and convergence rate for various incompressible elements. Int. J. Numer. Meth. Eng. 1989, 28, 2192–2202. [Google Scholar] [CrossRef]
- Onate, E.; Perazzo, F.; Miquel, J. A finite point method for elasticity problems. Comput. Struct. 2001, 79, 2151–2163. [Google Scholar] [CrossRef]
- Szabó, B.A.; Babuška, I.; Chayapathy, B.K. Stress computations for nearly incompressible materials by the p-version of the finite element method. Int. J. Numer. Meth. Eng. 1989, 28, 2175–2190. [Google Scholar] [CrossRef]


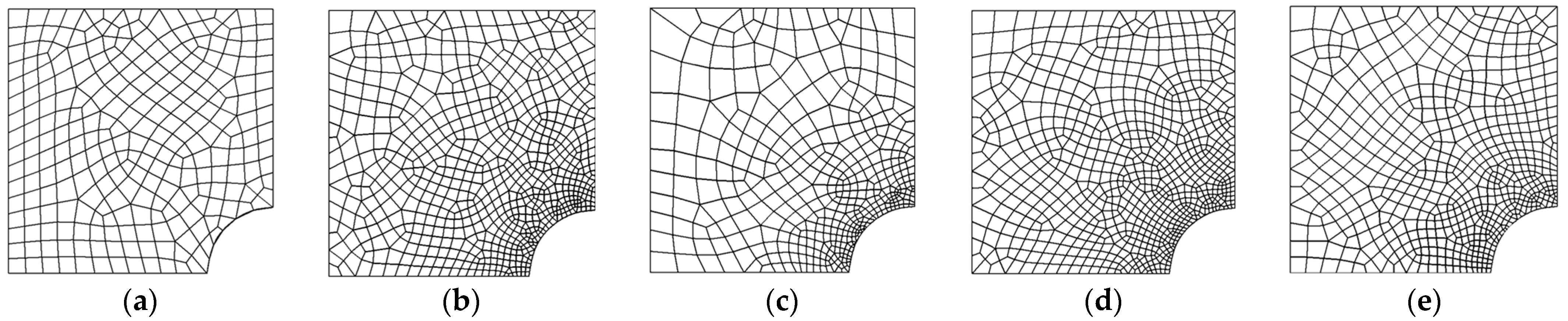
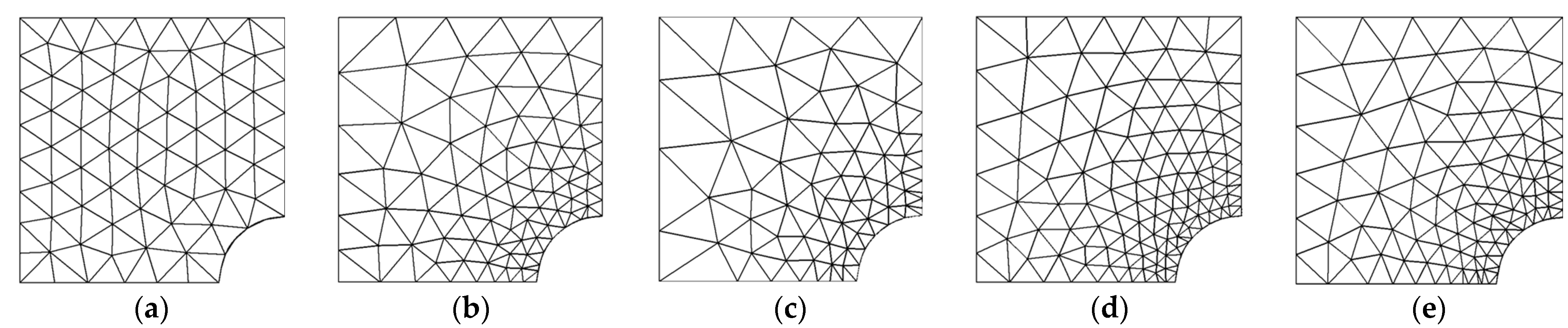
| Mesh Size (1/h) | Mesh-Free Patch | Mesh-Dependent Patch | |||||||
|---|---|---|---|---|---|---|---|---|---|
| FEM Error (×10−3) | Displacement Recovery | Stress Recovery | Displacement Recovery | Stress Recovery (ZZ) | |||||
| Error (×10−3) | θ | Error (×10−3) | Θ | Error (×10−3) | θ | Error (×10−3) | Θ | ||
| 1/4 | 29.44 | 15.87 | 0.8174 | 22.77 | 0.8890 | 18.23 | 0.8788 | 22.74 | 0.9573 |
| 1/16 | 7.69 | 0.66 | 0.9838 | 2.35 | 2.1200 | 2.05 | 0.9992 | 3.36 | 1.0264 |
| 1/32 | 3.85 | 0.15 | 0.9956 | 0.36 | 1.1855 | 0.57 | 1.0004 | 0.92 | 1.0080 |
| Convergence Rate | 0.9777 | 2.2501 | 2.0012 | 1.6710 | 1.5436 | ||||
| Mesh Size (1/h) | Mesh-Free Patch | Mesh-Dependent Patch | |||||||
|---|---|---|---|---|---|---|---|---|---|
| FEM Error (×10−3) | Displacement Recovery | Stress Recovery | Displacement Recovery | Stress Recovery (ZZ) | |||||
| Error (×10−3) | θ | Error (×10−3) | Θ | Error (×10−3) | θ | Error (×10−3) | Θ | ||
| 1/4 | 40.20 | 23.89 | 1.0135 | 20. 52 | 1.0022 | 18.88 | 0.9304 | 21.58 | 0.8843 |
| 1/12 | 14.11 | 2.27 | 0.9879 | 2.98 | 0.9815 | 2.19 | 0.9655 | 4.22 | 0.9712 |
| 1/24 | 7.02 | 0.57 | 0.9929 | 0.99 | 0.9904 | 0.65 | 0.9715 | 1.48 | 0.9870 |
| Convergence Rate | 0.9736 | 2.0869 | 1.6931 | 1.8806 | 1.4973 | ||||
| Elements | DOF | Mesh-Free Patch | Mesh-Dependent Patch | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FEM Error (×10−3) | Displacement Recovery | Stress Recovery | Displacement Recovery | Stress Recovery (ZZ) | ||||||
| Error (×10−3) | θ | Error (×10−3) | Θ | Error (×10−3) | θ | Error (×10−3) | Θ | |||
| 64 | 162 | 18.00 | 8.97 | 0.8602 | 8.60 | 0.8841 | 11.04 | 0.9555 | 14.32 | 1.0206 |
| 702 | 1514 | 5.02 | 0.96 | 0.9763 | 0.66 | 0.7432 | 1.25 | 1.0002 | 1.94 | 1.0004 |
| 1212 | 2566 | 3.67 | 0.47 | 0.9882 | 0.48 | 0.7812 | 0.69 | 1.0012 | 1.37 | 1.0134 |
| Elements | DOF | Mesh-Free Patch | Mesh-Dependent Patch | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FEM Error (×10−3) | Displacement Recovery | Stress Recovery | Displacement Recovery | Stress Recovery (ZZ) | ||||||
| Error (×10−3) | θ | Error (×10−3) | Θ | Error (×10−3) | θ | Error (×10−3) | Θ | |||
| 28 | 146 | 35.23 | 23.54 | 0.5717 | 29.64 | 0.7046 | 22.62 | 0.5817 | 21.08 | 0.4905 |
| 340 | 1470 | 6.31 | 1.97 | 0.9077 | 2.47 | 0.9008 | 1.57 | 0.8710 | 2.04 | 0.8347 |
| 580 | 2462 | 2.20 | 1.13 | 0.8750 | 1.16 | 0.8889 | 1.21 | 0.8118 | 1.31 | 0.7814 |
| Meshing Scheme | Initial Mesh | Mesh-Free Patch | Mesh-Dependent Patch | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Displac. Recovery | Stress Recovery | Displac. Recovery | Stress Recovery | |||||||
| N | DOF | N | DOF | N | DOF | N | DOF | N | DOF | |
| Quadrilateral | 64 | 162 | 9209 | 19,766 | 2222 | 4584 | 11,283 | 22,926 | 14,658 | 29,730 |
| Triangular | 28 | 146 | 1439 | 5936 | 791 | 3280 | 2577 | 10,540 | 1767 | 7264 |
| Mesh-Dependent Patch-MLS (4-Node) | Mesh-Dependent Patch-MLS (6-Node) | ||||||
|---|---|---|---|---|---|---|---|
| Mesh Size (1/h) | FEM Error (×10−3) | Displacement Recovery | Mesh Size (1/h) | FEM Error (×10−3) | Displacement Recovery | ||
| Error (×10−3) | Θ | Error (×10−3) | Θ | ||||
| 1/4 | 29.44 | 16.54 | 0.7234 | ¼ | 40.20 | 18.71 | 0.9409 |
| 1/16 | 7.69 | 0.99 | 0.9677 | 1/12 | 14.11 | 2.94 | 0.9811 |
| 1/32 | 3.85 | 0.24 | 0.9909 | 1/24 | 7.02 | 0.89 | 0.9859 |
| Convergence Rate | 0.9777 | 2.0253 | 0.9736 | 1.7001 | |||
| Elements | DOF | Mesh-Free Patch | Mesh-Dependent Patch | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FEM Error (×10−3) | Displacement Recovery | Stress Recovery | Displacement Recovery | Stress Recovery | ||||||
| Error (×10−3) | θ | Error (×10−3) | θ | Error (×10−3) | θ | Error (×10−3) | θ | |||
| 266 | 594 | 157.20 | 90.10 | 0.8989 | 123.04 | 1.7373 | 123.63 | 1.1371 | 148.44 | 1.1276 |
| 793 | 1698 | 91.17 | 31.40 | 0.9212 | 43.18 | 1.7426 | 51.56 | 1.0264 | 65.40 | 1.0214 |
| 1842 | 3854 | 67.81 | 22.71 | 0.8972 | 19.45 | 0.9901 | 26.84 | 0.9587 | 37.62 | 0.9270 |
| Elements | DOF | Mesh-Free Patch | Mesh-Dependent Patch | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FEM Error (×10−3) | Displacement Recovery | Stress Recovery | Displacement Recovery | Stress Recovery | ||||||
| Error (×10−3) | θ | Error (×10−3) | θ | Error (×10−3) | Θ | Error (×10−3) | θ | |||
| 124 | 558 | 150.98 | 104.88 | 0.7295 | 93.95 | 0.6296 | 133.92 | 0.9637 | 137.51 | 0.8937 |
| 373 | 1604 | 73.53 | 40.66 | 0.7791 | 40.66 | 0.6626 | 65.97 | 1.0426 | 67.65 | 0.9273 |
| 874 | 3666 | 40.52 | 36.41 | 1.0168 | 25.23 | 0.6304 | 21.14 | 0.8994 | 23.00 | 0.8181 |
| Meshing Scheme | Initial Mesh | Mesh-Free Patch | Mesh-Dependent Patch | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Displac. Recovery | Stress Recovery | Displac. Recovery | Stress Recovery | |||||||
| N | DOF | N | DOF | N | DOF | N | DOF | N | DOF | |
| Quadrilateral | 266 | 594 | 694 | 1490 | 419 | 926 | 760 | 1622 | 609 | 1314 |
| Triangular | 124 | 558 | 151 | 676 | 121 | 548 | 218 | 962 | 188 | 842 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kahla, N.B.; AlQadhi, S.; Ahmed, M. Mesh-Free MLS-Based Error-Recovery Technique for Finite Element Incompressible Elastic Computations. Appl. Sci. 2023, 13, 6890. https://doi.org/10.3390/app13126890
Kahla NB, AlQadhi S, Ahmed M. Mesh-Free MLS-Based Error-Recovery Technique for Finite Element Incompressible Elastic Computations. Applied Sciences. 2023; 13(12):6890. https://doi.org/10.3390/app13126890
Chicago/Turabian StyleKahla, Nabil Ben, Saeed AlQadhi, and Mohd. Ahmed. 2023. "Mesh-Free MLS-Based Error-Recovery Technique for Finite Element Incompressible Elastic Computations" Applied Sciences 13, no. 12: 6890. https://doi.org/10.3390/app13126890
APA StyleKahla, N. B., AlQadhi, S., & Ahmed, M. (2023). Mesh-Free MLS-Based Error-Recovery Technique for Finite Element Incompressible Elastic Computations. Applied Sciences, 13(12), 6890. https://doi.org/10.3390/app13126890








