Injection Harmonic Current Differential Protection Based on Control-Protection Synergy for Distribution Networks with IBDGs
Abstract
1. Introduction
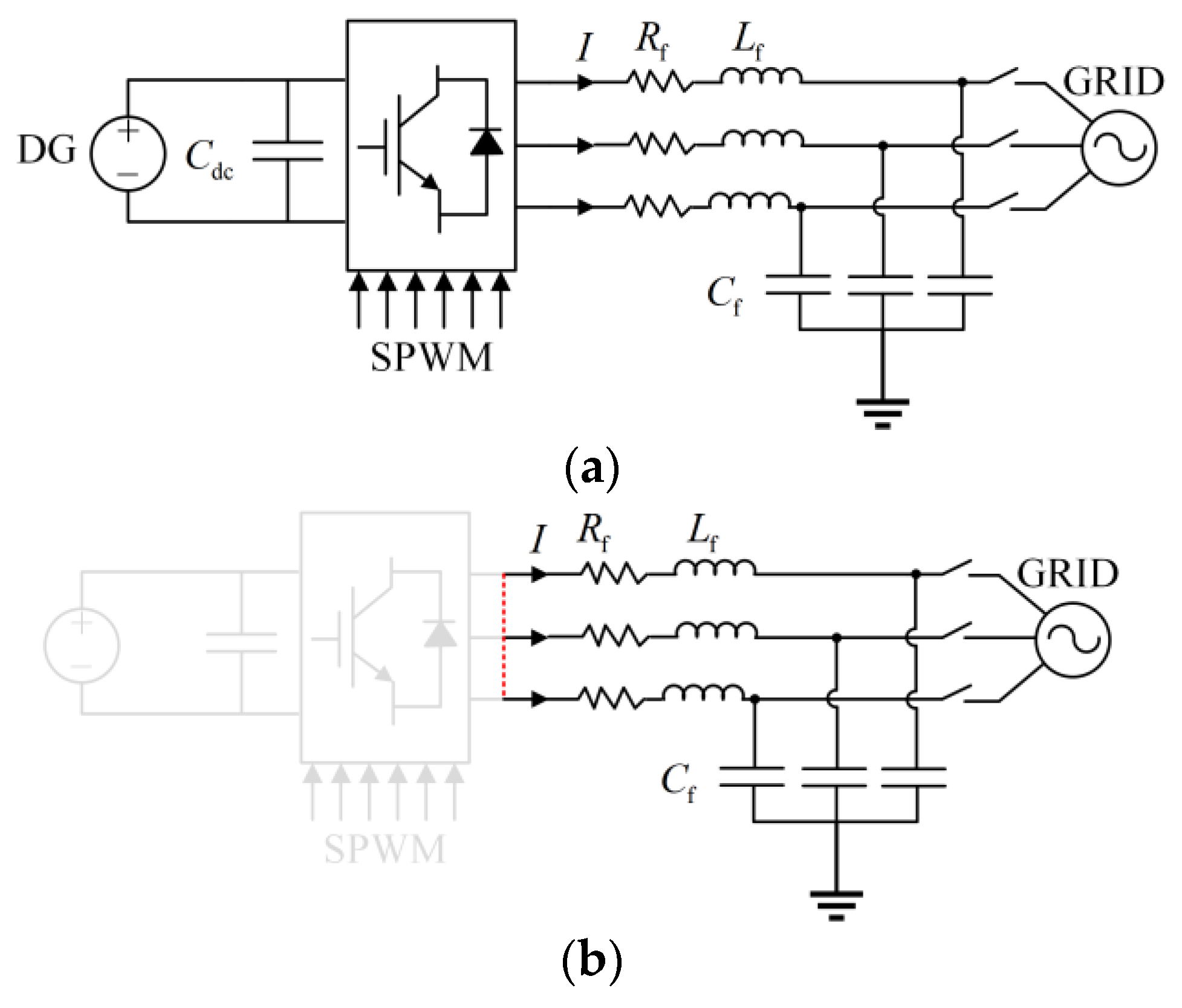
2. Equivalence Model of IBDG
2.1. Typical Structure of IBDG
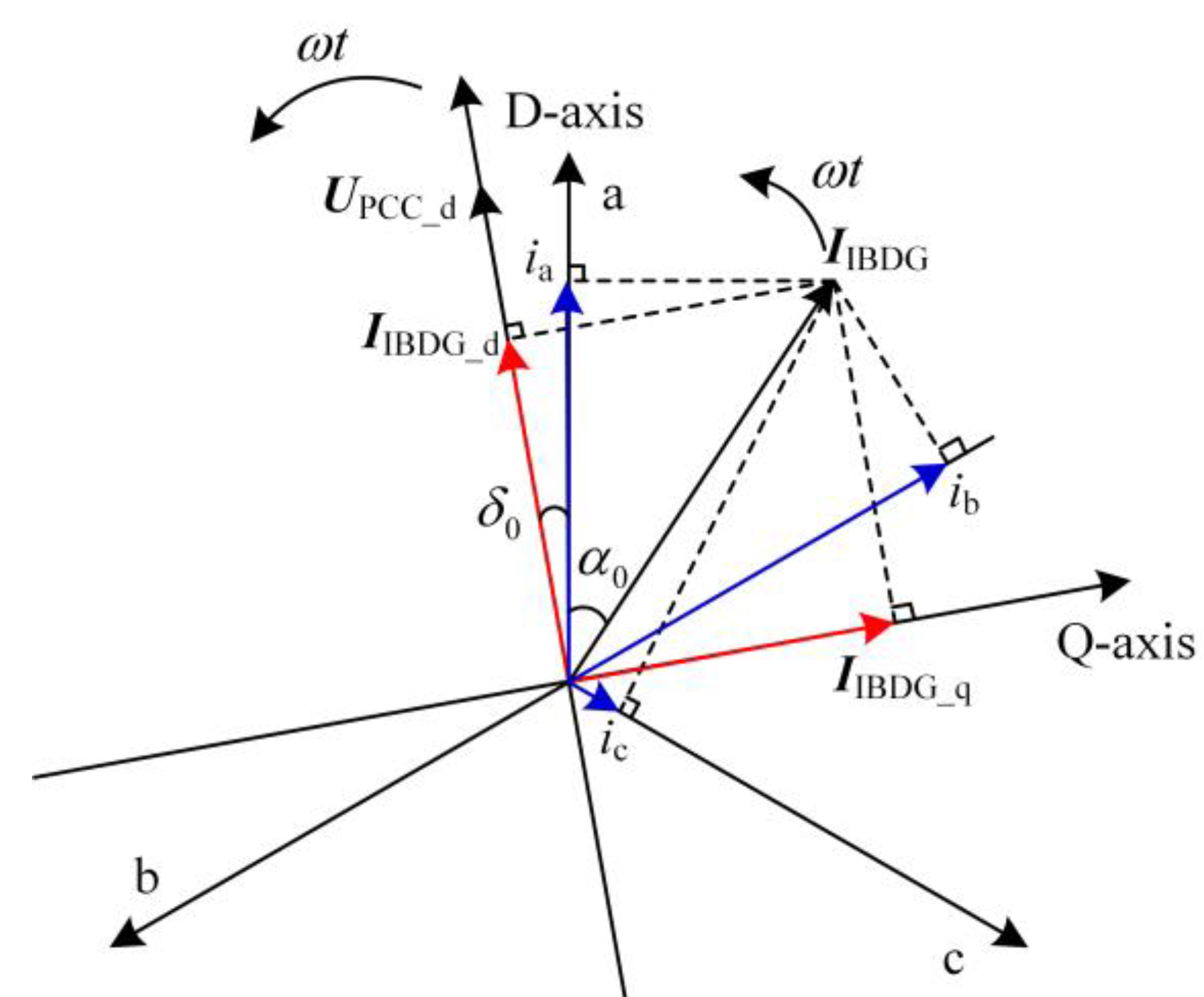
2.2. PQ Control Strategy of IBDGs
2.3. Control Characteristics of Low Voltage Ride-Through
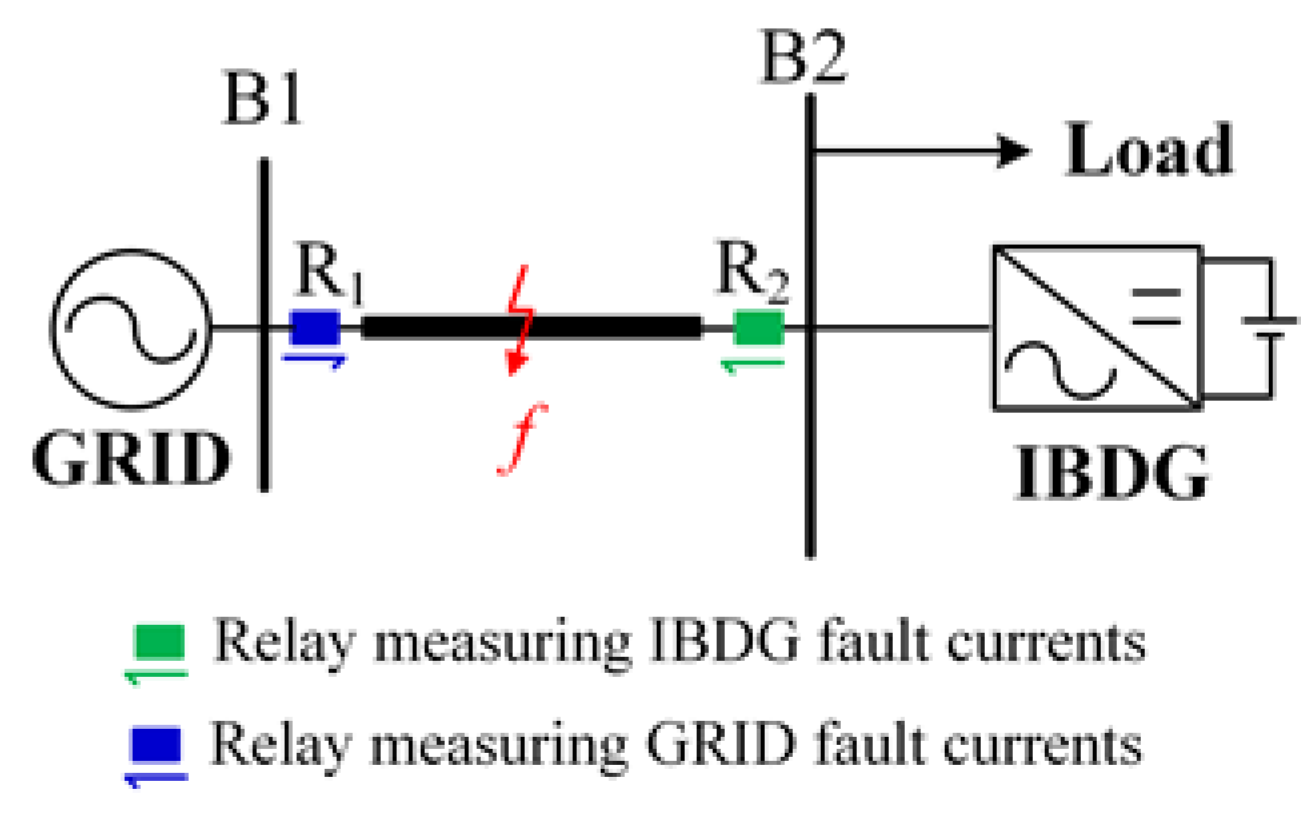
3. Analysis of Output Short-Circuit Currents of IBDG
3.1. Analysis of Output Fundamental Frequency Short-Circuit Currents
3.2. Analysis of Output Short-Circuit Currents after Injection
4. Principle of Characteristic Harmonic Current Differential Protection
- In the case of asymmetrical faults:
- In the case of symmetrical faults:
5. Implementation Scheme of Injection Harmonic Current Differential Protection
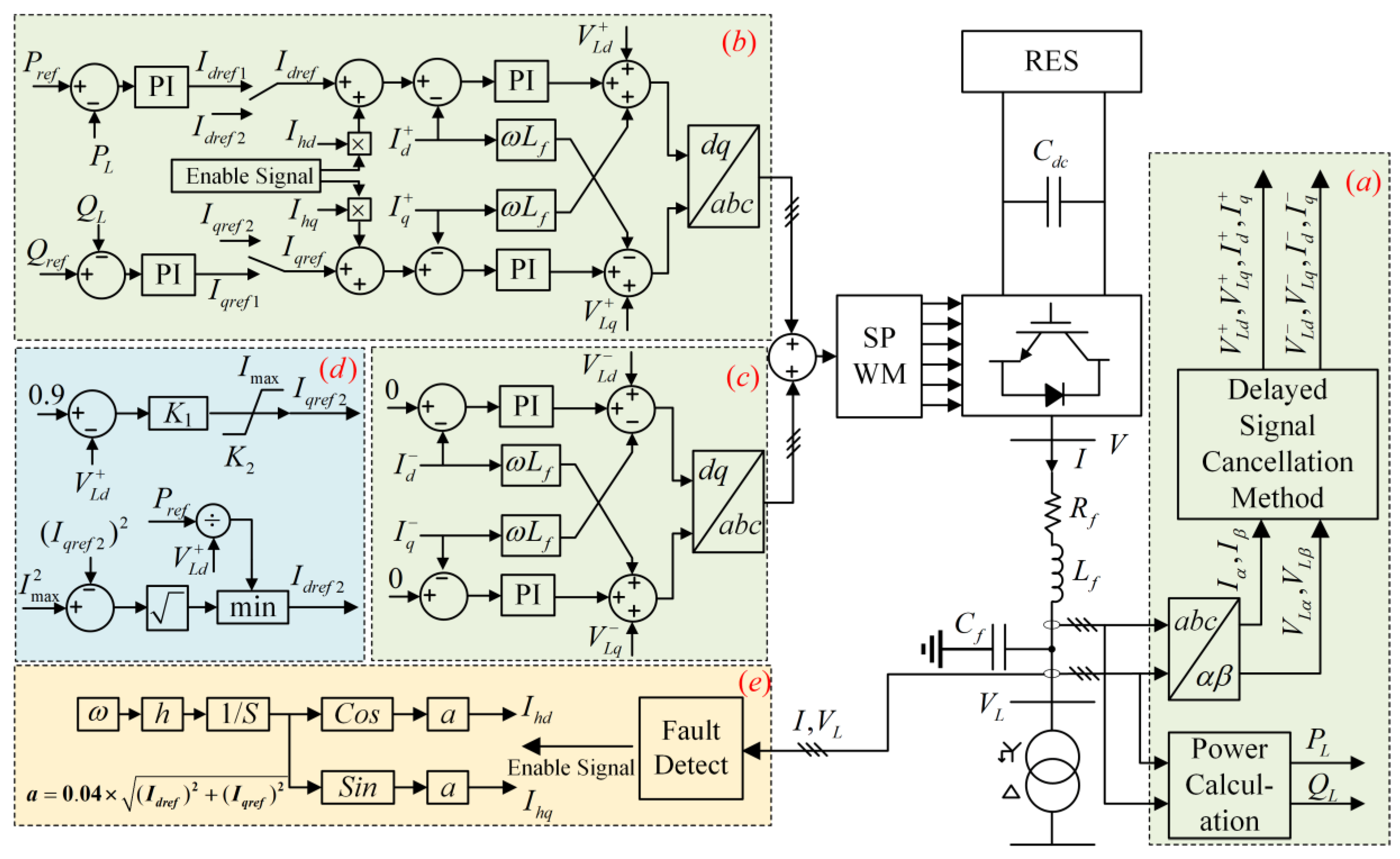
5.1. Selection of the Frequency and Amplitude of the Characteristic Harmonic Current
- The characteristic frequency should not exceed ten times the fundamental frequency. The resonant frequencies of IBDG filters are generally widely distributed from 10 times the fundamental frequency to 0.5 times the carrier frequency. The characteristic frequency is less than ten times the fundamental frequency, which can avoid the resonance of CHCs with IBDG filters and thus ensure the safe and stable operation of IBDG. In order to suppress the shunting effect of the non-injected source IBDG on CHCs, the characteristic frequency cannot be much smaller than the resonant frequency.
- The characteristic frequency should be as far from the fundamental frequency as possible. When the distribution network is disturbed, or after a fault occurs, the harmonics will inevitably be generated, mainly low-order harmonics. If the characteristic frequency is far from the fundamental frequency, it can minimize the interference of the generated harmonics to the injection protection.
- The characteristic frequency should be taken as an integer multiple of the fundamental frequency. The selection of integer multiples of the fundamental frequency facilitates the extraction, analysis, and processing of the Fast Fourier Transform (FFT), wavelet transform, and other standard time-frequency analysis methods, shortens the signal processing delay, and improves the engineering practicality of the injection protection method.
5.2. Principle of Injection Starting of Characteristic Harmonic Currents
5.3. Total Control System of IBDG with the CHC Injection
6. Simulation and Analysis
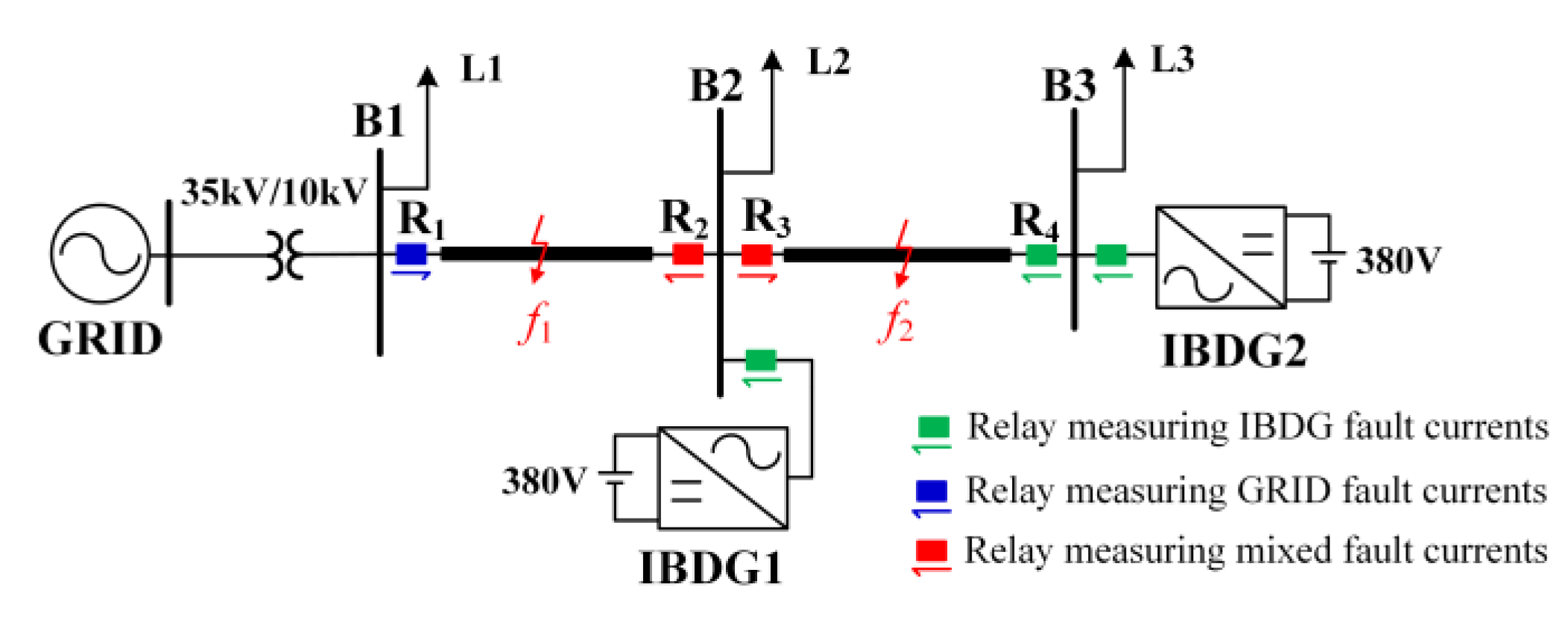
6.1. Test System under Study
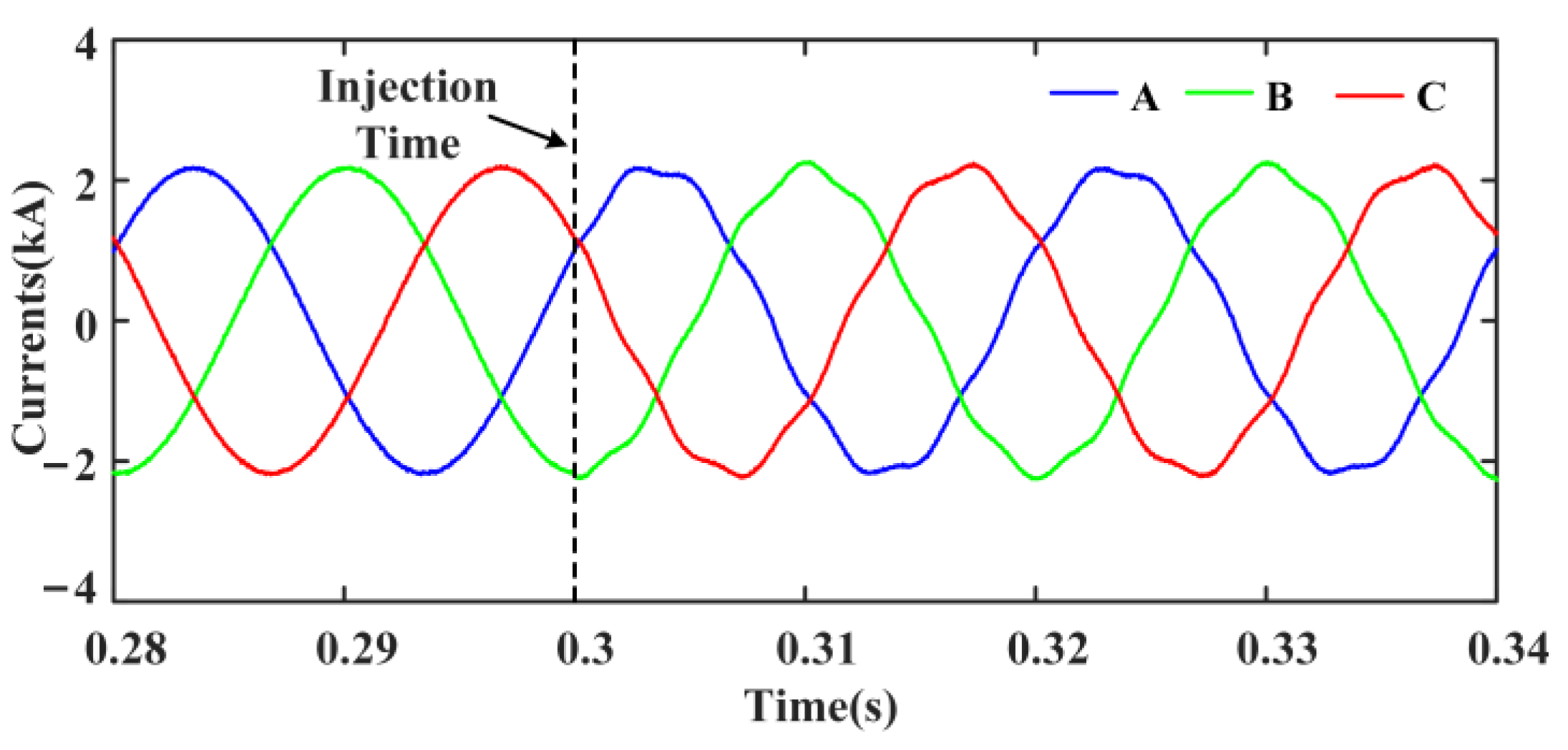
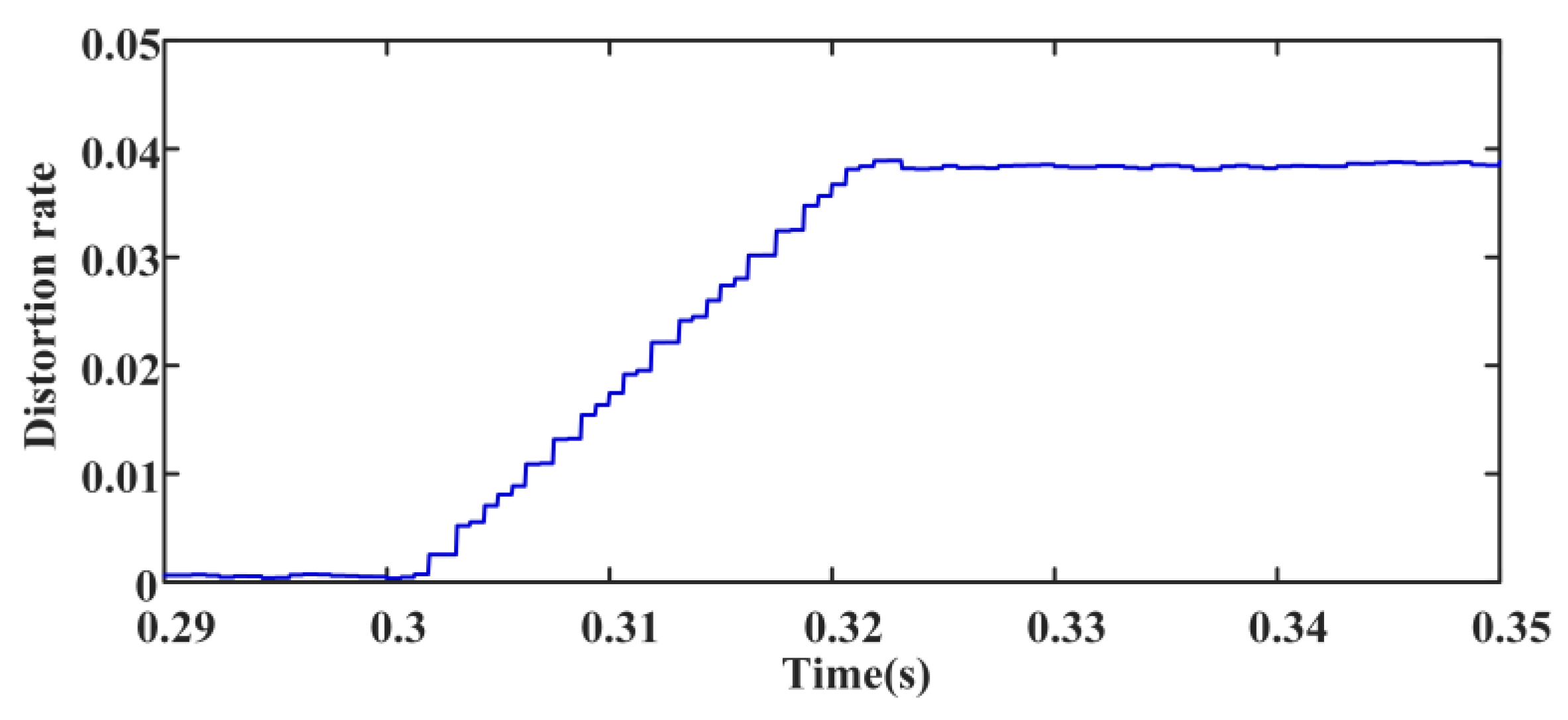
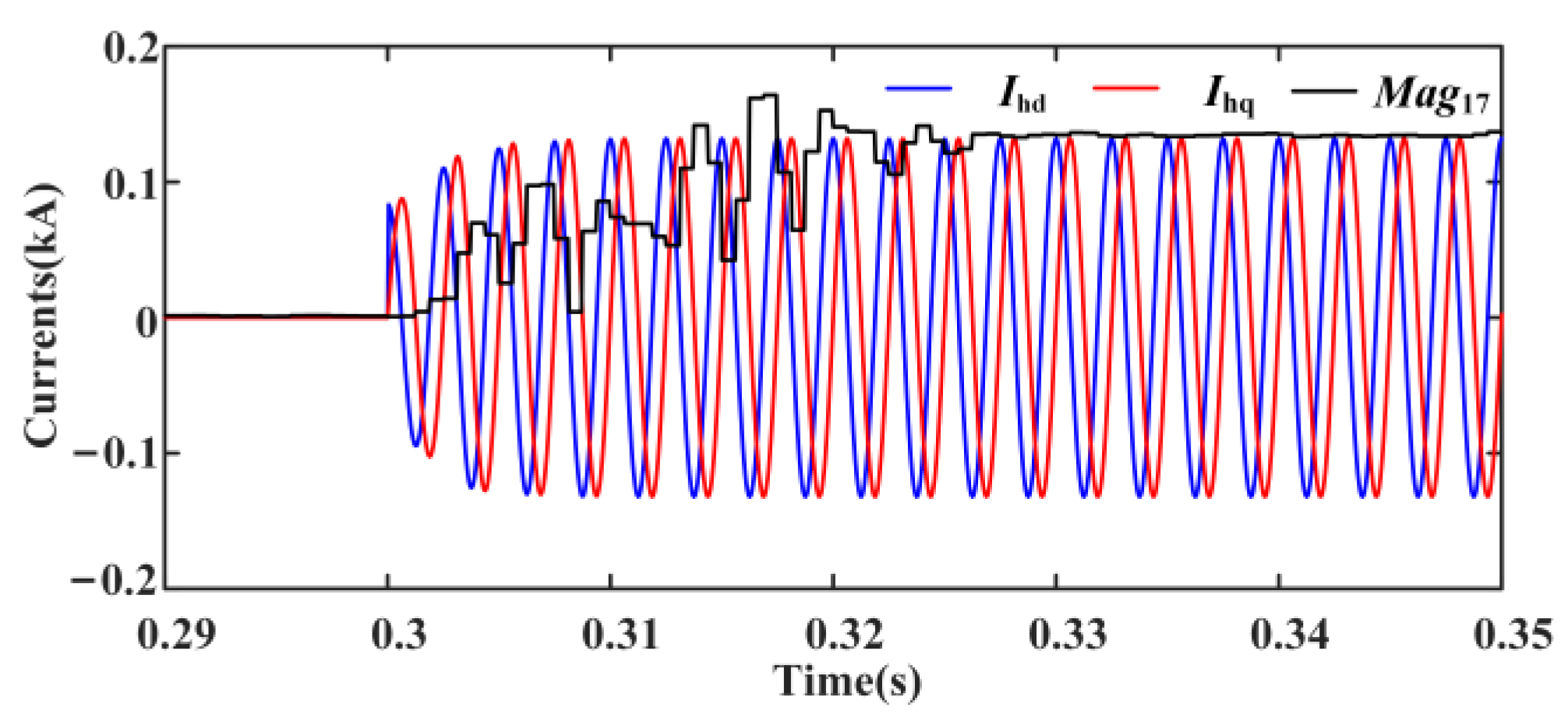
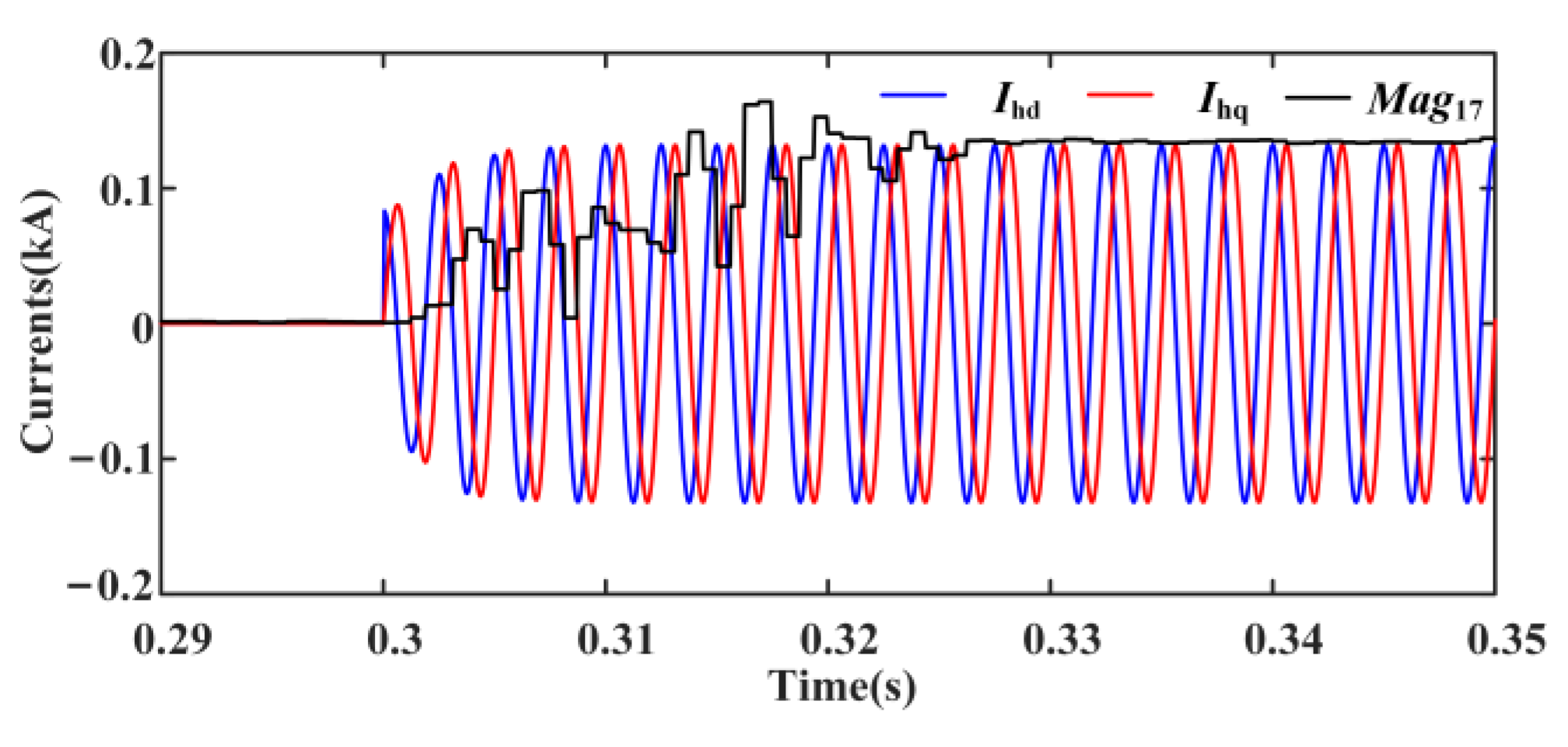
6.2. Verifying the Correctness of CHCs Injection
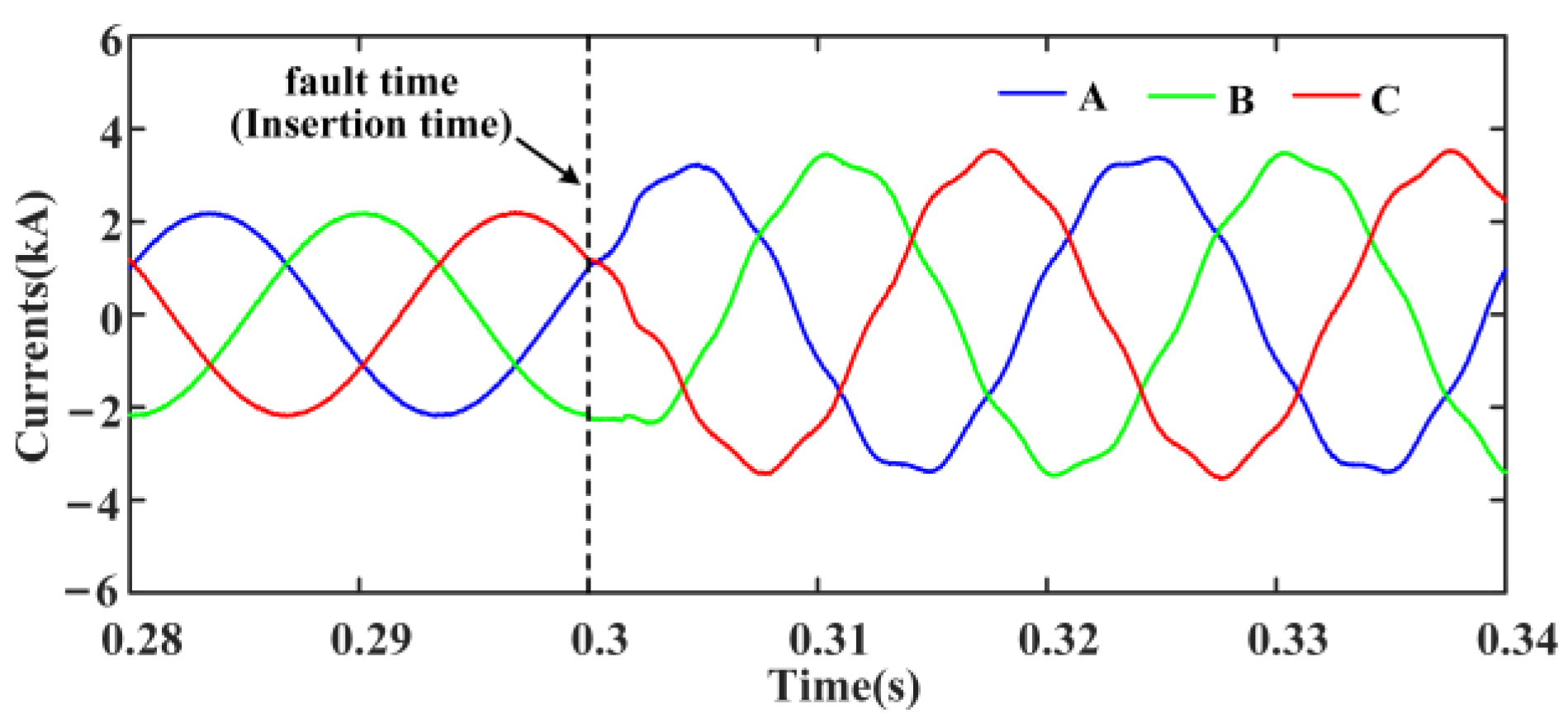
6.2.1. During Normal Operation, CHCs Are Artificially Injected at 0.3 s
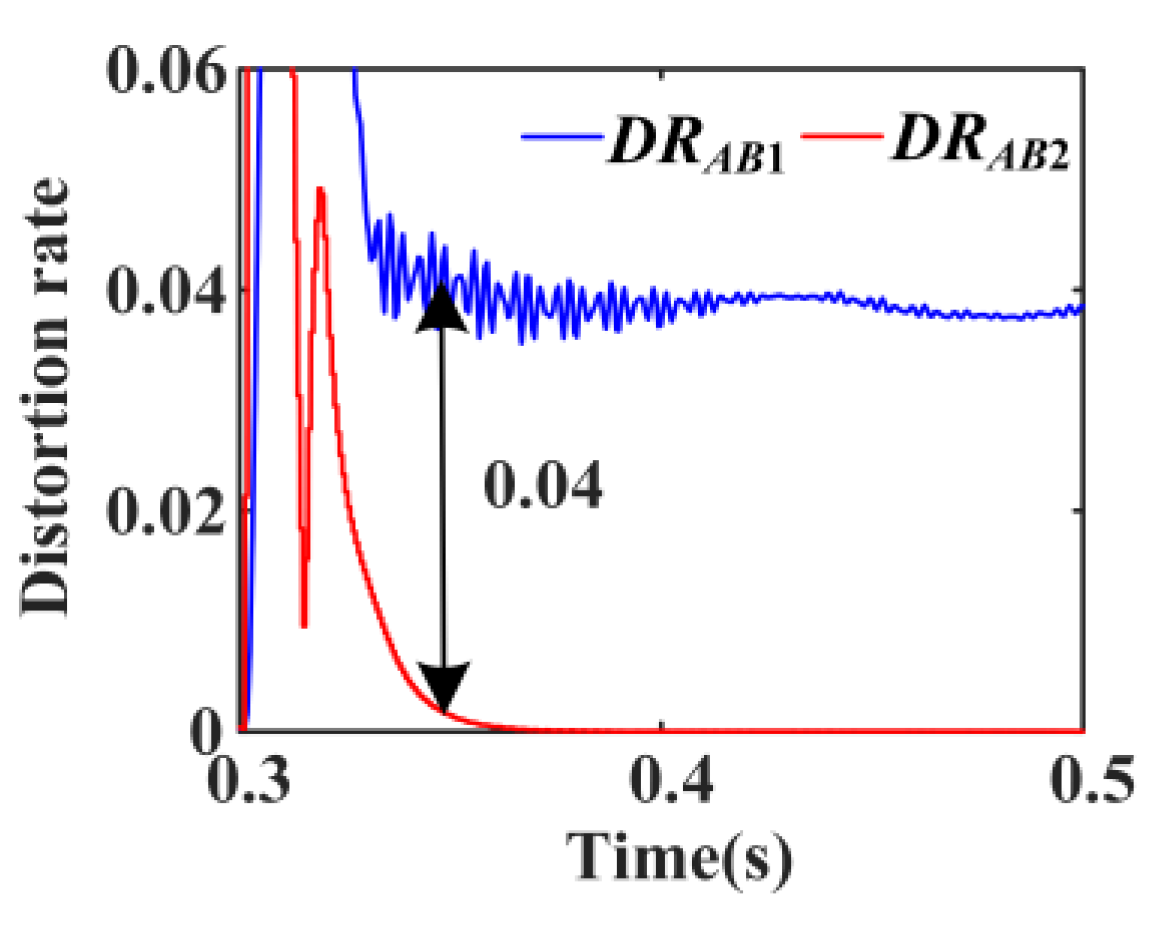
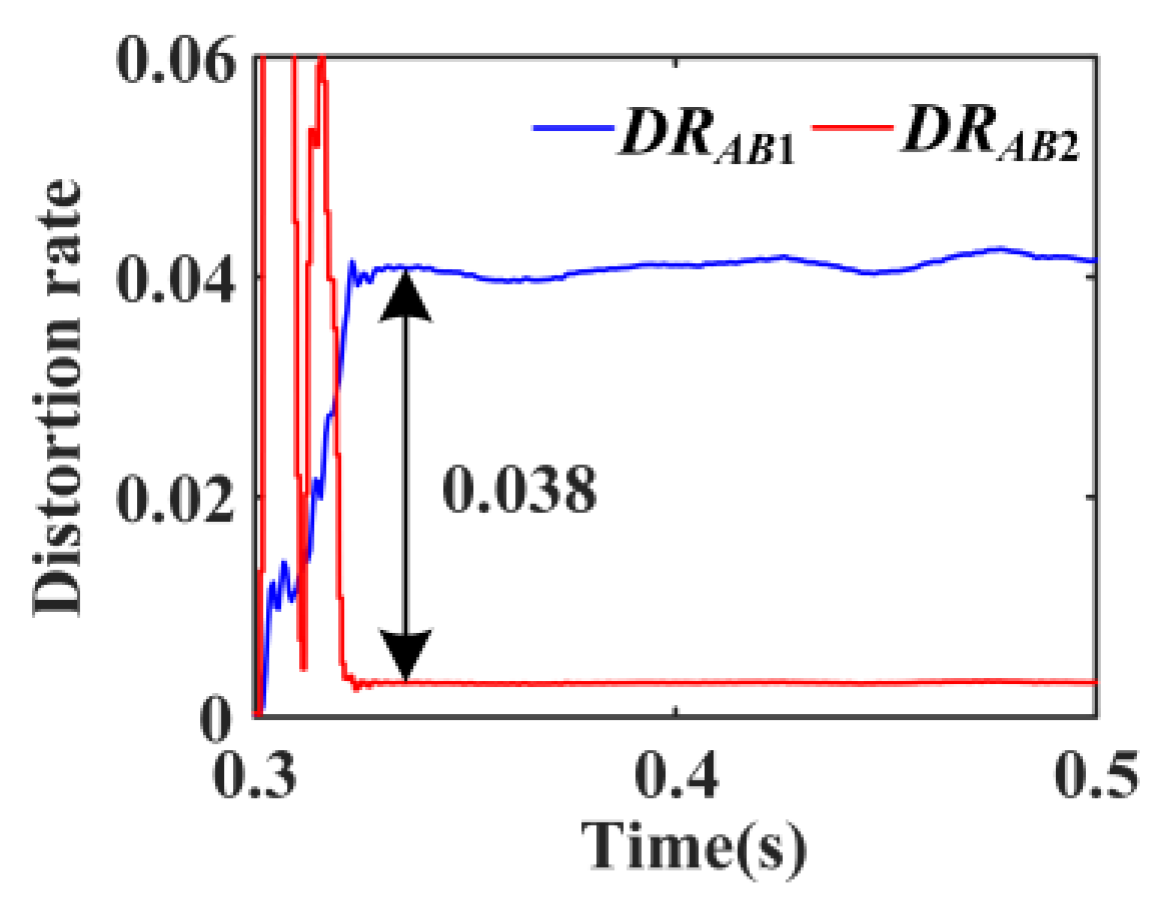
6.2.2. Phase-to-Phase (A–B) Faults with 0.1 Ω Fault Resistance Occur at f2
6.3. Verifying the Correctness of IHCDP
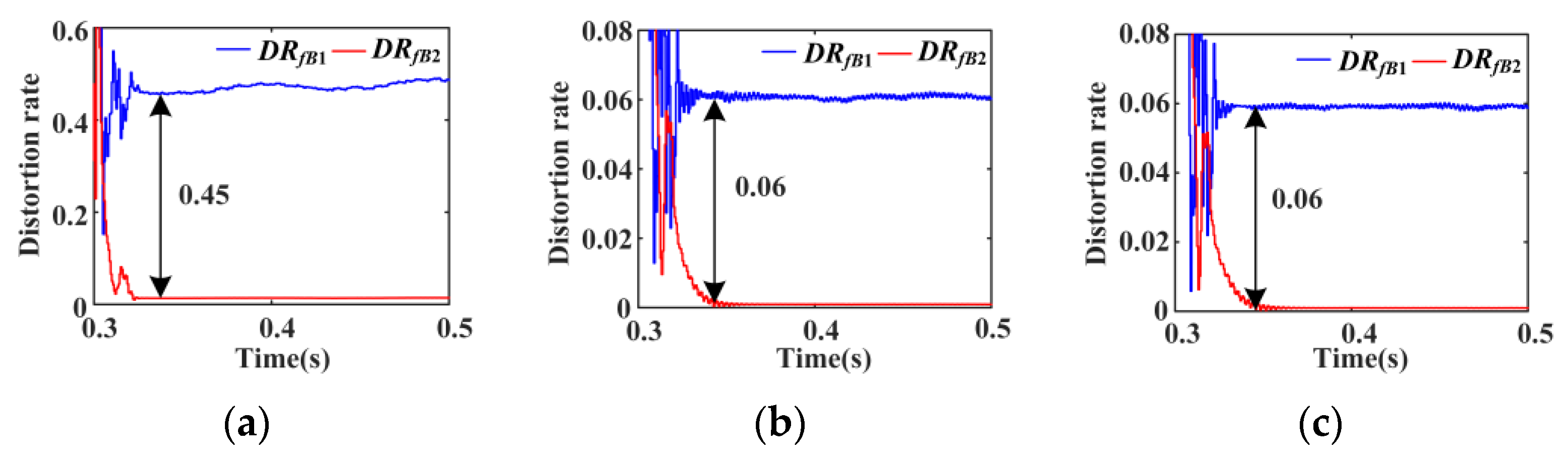
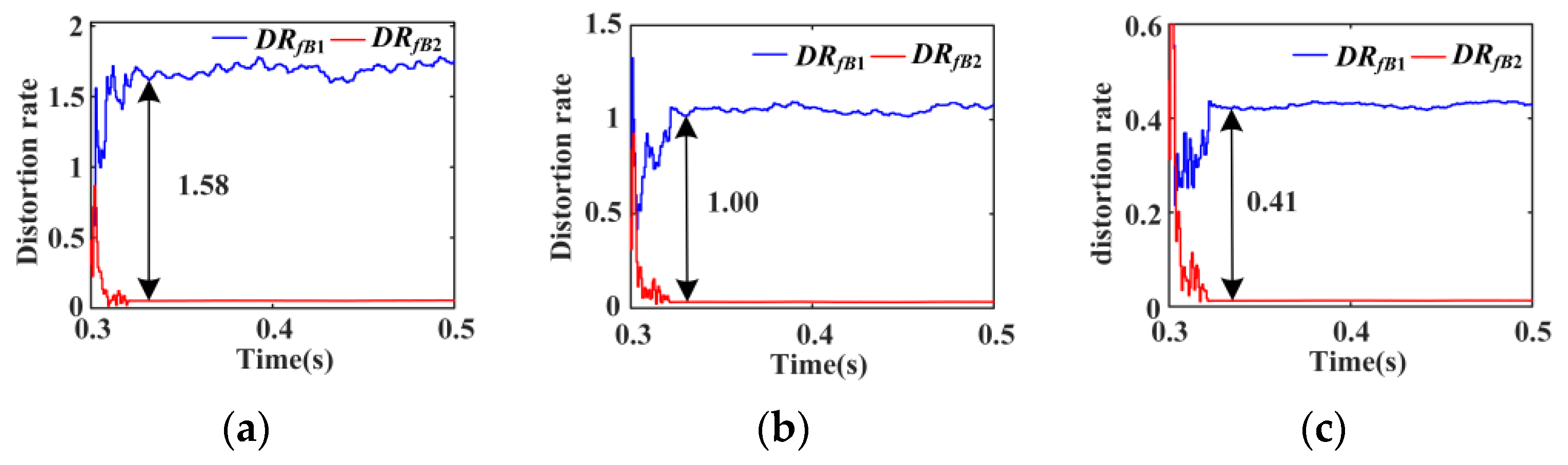
6.3.1. Case 1: Asymmetrical Short-Circuit Faults with 0.1 Ω Fault Resistance Occur at f1
6.3.2. Case 2: Symmetrical Short-Circuit Faults with 0.1 Ω Fault Resistance Occur at f1
6.3.3. Case 3: Asymmetrical Short-Circuit Faults with 20 Ω Fault Resistance Occur at f1
6.3.4. Case 4: Symmetrical Short-Circuit Faults with 20 Ω Fault Resistance Occur at f1
7. Conclusions
- (1)
- The CHC injection-control strategy of IBDG based on the d-axis and q-axis is proposed. Injection starting criteria are established based on the mutation of phase current and voltage.
- (2)
- The fault characteristics of CHCs after injection are analyzed. For asymmetrical short-circuit faults, a differential protection criterion based on the distortion rate of NSCCHCs is proposed; for symmetrical short-circuit faults, the proposed differential protection criterion utilizes the distortion rate of A-phase CHCs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barani, M.; Aghaei, J.; Akbari, M.A.; Niknam, T.; Farahmand, H.; Korpas, M. Optimal Partitioning of Smart Distribution Systems into Supply–Sufficient Microgrids. IEEE Trans. Smart Grid 2019, 10, 2523–2533. [Google Scholar] [CrossRef]
- Telukunta, V.; Pradhan, J.; Agrawal, A.; Singh, M.; Srivani, S.G. Protection Challenges Under Bulk Penetration of Renewable Energy Resources in Power Systems: A Review. CSEE J. Power Energy Syst. 2017, 3, 365–379. [Google Scholar] [CrossRef]
- Jamali, S.; Borhani–Bahabadi, H. Protection Method for Radial Distribution Systems with DG Using Local Voltage Measurements. IEEE Trans. Power Del. 2019, 34, 651–660. [Google Scholar] [CrossRef]
- Zhang, F.; Mu, L.; Wang, Z.; Zhou, H.; Zhang, X. Optimal Fault Control Strategy of Master–slave Controlled Islanding Microgrid. Proc. CSEE 2020, 40, 1241–1248. [Google Scholar]
- Eskandari, M.; Savkin, A.V. On the Impact of Fault Ride–Through on Transient Stability of Autonomous Microgrids: Nonlinear Analysis and Solution. IEEE Trans. Smart Grid 2021, 12, 999–1010. [Google Scholar] [CrossRef]
- Coffele, F.; Booth, C.; Dysko, A. An Adaptive Overcurrent Protection Scheme for Distribution Networks. IEEE Trans. Power Del. 2015, 30, 561–568. [Google Scholar] [CrossRef]
- Kumar, D.S.; Srinivasan, D.; Reindl, T. A Fast and Scalable Protection Scheme for Distribution Networks with Distributed Generation. IEEE Trans. Power Del. 2016, 31, 67–75. [Google Scholar] [CrossRef]
- Shen, S.; Lin, D.; Wang, H.; Hu, P.; Jiang, K.; Lin, D.; He, B. An Adaptive Protection Scheme for Distribution Systems with DGs Based on Optimized Thevenin Equivalent Parameters Estimation. IEEE Trans. Power Del. 2017, 32, 411–419. [Google Scholar] [CrossRef]
- Darabi, A.; Bagheri, M.; Gharehpetian, G.B. Highly reliable overcurrent protection scheme for highly meshed power systems. Int. J. Electr. Power Energy Syst. 2020, 119, 105874. [Google Scholar] [CrossRef]
- Ma, J.; Liu, J.; Yang, G.; Phadke, A.G. Research on regional centralized protection scheme for distribution network integrated with electric vehicles. Int. J. Electr. Power Energy Syst. 2020, 119, 105903. [Google Scholar] [CrossRef]
- Ghotbi–Maleki, M.; Chabanloo, R.M.; Zeineldin, H.H.; Miangafsheh, S.M.H. Design of Setting Group–Based Overcurrent Protection Scheme for Active Distribution Networks Using MILP. IEEE Trans. Smart Grid 2021, 12, 1185–1193. [Google Scholar] [CrossRef]
- Mirshekali, H.; Dashti, R.; Keshavarz, A.; Torabi, A.J.; Shaker, H.R. A Novel Fault Location Methodology for Smart Distribution Networks. IEEE Trans. Smart Grid 2021, 12, 1277–1288. [Google Scholar] [CrossRef]
- Jamali, S.; Borhani–Bahabadi, H. Non–communication protection method for meshed and radial distribution networks with synchronous–based DG. Int. J. Electr. Power Energy Syst. 2017, 93, 468–478. [Google Scholar] [CrossRef]
- Jia, K.; Bi, T.; Ren, Z.; Thomas, D.W.P.; Sumner, M. High Frequency Impedance Based Fault Location in Distribution System with DGs. IEEE Trans. Smart Grid 2018, 9, 807–816. [Google Scholar] [CrossRef]
- Chen, G.; Liu, Y.; Yang, Q. Impedance Differential Protection for Active Distribution Network. IEEE Trans. Power Del. 2020, 35, 25–36. [Google Scholar] [CrossRef]
- Sharma, N.K.; Samantaray, S.R. PMU Assisted Integrated Impedance Angle–Based Microgrid Protection Scheme. IEEE Trans. Power Del. 2020, 35, 183–193. [Google Scholar] [CrossRef]
- Gao, H.; Li, J.; Xu, B. Principle and Implementation of Current Differential Protection in Distribution Networks with High Penetration of DGs. IEEE Trans. Power Del. 2017, 32, 565–574. [Google Scholar] [CrossRef]
- Zhou, C.; Zou, G.; Du, X.; Zang, L. Adaptive current differential protection for active distribution network considering time synchronization error. Int. J. Electr. Power Energy Syst. 2022, 140, 108085. [Google Scholar] [CrossRef]
- Laaksonen, H.J. Protection Principles for Future Microgrids. IEEE Trans. Power Electron. 2010, 25, 2910–2918. [Google Scholar] [CrossRef]
- Azzouz, M.A.; Hooshyar, A. Dual Current Control of Inverter–Interfaced Renewable Energy Sources for Precise Phase Selection. IEEE Trans. Smart Grid 2019, 10, 5092–5102. [Google Scholar] [CrossRef]
- Song, G.; Wang, T.; Zhang, B.; Dong, X.; Kang, X. Analysis and Prospect of Detective Fault Identification Technologies Using Power Electronic Device. Autom. Electr. Power Syst. 2020, 44, 173–188. [Google Scholar]
- Soleimanisardoo, A.; Karegar, H.K.; Zeineldin, H.H. Differential Frequency Protection Scheme Based on Off–Nominal Frequency Injections for Inverter–Based Islanded Microgrids. IEEE Trans. Smart Grid 2019, 10, 2107–2114. [Google Scholar] [CrossRef]
- El–Sayed, W.T.; Azzouz, M.A.; Zeineldin, H.H.; El–Saadany, E.F. A Harmonic Time–Current–Voltage Directional Relay for Optimal Protection Coordination of Inverter–Based Islanded Microgrids. IEEE Trans. Smart Grid 2021, 12, 1904–1917. [Google Scholar] [CrossRef]
- Guo, W.; Mu, L.; Zhang, X. Fault Models of Inverter-Interfaced Distributed Generators within a Low-Voltage Microgrid. IEEE Trans. Power Del. 2017, 32, 453–461. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Power Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, Z.; Yin, X.; Wang, F.; He, M. Study on Fault Current Characteristics and Fault Analysis Method of Power Grid with Inverter Interfaced Distributed Generation. Proc. CSEE 2013, 33, 65–74. [Google Scholar]
- Zhang, F.; Mu, L. A Fault Detection Method of Microgrids with Grid–Connected Inverter Interfaced Distributed Generators Based on the PQ Control Strategy. IEEE Trans. Smart Grid 2019, 10, 4816–4826. [Google Scholar] [CrossRef]
- Bae, Y.; Trung–Kien, V.; Kim, R. –Y. Implemental Control Strategy for Grid Stabilization of Grid–Connected PV System Based on German Grid Code in Symmetrical Low–to–Medium Voltage Network. IEEE Trans. Energy Convers. 2013, 28, 619–631. [Google Scholar] [CrossRef]
- China National Standard GB/T 19964–2012; Technical Requirements for Connecting Photovoltaic Power Station to Power System. Standardization Administration of China: Beijing, China, 2012.
- Zhao, F.; Meng, Z.; Li, Y.; Liu, C. Pilot Protection Scheme for Active Distribution Network Based on Fault Components. High Volt. Eng. 2019, 45, 3092–3100. [Google Scholar]
- Han, H.; Mu, L.; Zhang, F.; Guo, W. Microgrid Protection Considering Low Voltage Ride-through of IIDG. Proc. CSEE 2017, 37, 110–119. [Google Scholar]
- Han, B.; Li, H.; Wang, G.; Zeng, D.; Liang, Y. A Virtual Multi–Terminal Current Differential Protection Scheme for Distribution Networks with Inverter–Interfaced Distributed Generators. IEEE Trans. Smart Grid 2018, 9, 5418–5431. [Google Scholar] [CrossRef]
- China National Standard NB/T 32004–2018; Technical Specification of PV Grid–Connected Inverter. Standardization Administration of China: Beijing, China, 2018.
- Svensson, J.; Bongiorno, M.; Sannino, A. Practical implementation of delayed signal cancellation method for phase–sequence separation. IEEE Trans. Power Del. 2007, 22, 18–26. [Google Scholar] [CrossRef]
- China National Standard GB/T 156-2017; Standard Voltages. Standardization Administration of China: Beijing, China, 2017.



| Parameters | Values |
|---|---|
| Capacity of IBDG1 and IBDG2 | 1 MW |
| Capacity of L1, L2 and L3 Length of feeder sections B1B2 and B2B3 | 2 MVA 4 km |
| Positive-sequence impedance of feeder sections B1B2 and B2B3 Negative-sequence impedance of feeder sections B1B2 and B2B3 | (0.13 + j0.402) Ω/km (2.00 + j0.400) Ω/km |
| Fault Resistance | Fault Type | Distortion Rate Difference Values | Trip or Not |
|---|---|---|---|
| 0.1 Ω | A–G | 0.18 | Yes |
| AB–G | 0.06 | Yes | |
| A–B | 0.055 | Yes | |
| ABC | 0.04 | Yes | |
| 20 Ω | A–G | 0.52 | Yes |
| AB–G | 0.34 | Yes | |
| A–B | 0.15 | Yes | |
| ABC | 0.035 | Yes | |
| 50 Ω | A–G | 1.14 | Yes |
| AB–G | 0.87 | Yes | |
| A–B | 0.33 | Yes | |
| ABC | 0.036 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Gao, Z.; Liu, Z.; Tao, Z. Injection Harmonic Current Differential Protection Based on Control-Protection Synergy for Distribution Networks with IBDGs. Appl. Sci. 2023, 13, 6725. https://doi.org/10.3390/app13116725
Yu C, Gao Z, Liu Z, Tao Z. Injection Harmonic Current Differential Protection Based on Control-Protection Synergy for Distribution Networks with IBDGs. Applied Sciences. 2023; 13(11):6725. https://doi.org/10.3390/app13116725
Chicago/Turabian StyleYu, Chengao, Zhanjun Gao, Zhao Liu, and Zhengchen Tao. 2023. "Injection Harmonic Current Differential Protection Based on Control-Protection Synergy for Distribution Networks with IBDGs" Applied Sciences 13, no. 11: 6725. https://doi.org/10.3390/app13116725
APA StyleYu, C., Gao, Z., Liu, Z., & Tao, Z. (2023). Injection Harmonic Current Differential Protection Based on Control-Protection Synergy for Distribution Networks with IBDGs. Applied Sciences, 13(11), 6725. https://doi.org/10.3390/app13116725




