An Innovative System of Deep In Situ Environment Reconstruction and Core Transfer
Abstract
Featured Application
Abstract
1. Introduction
2. Related Works
3. Design of the SERCT
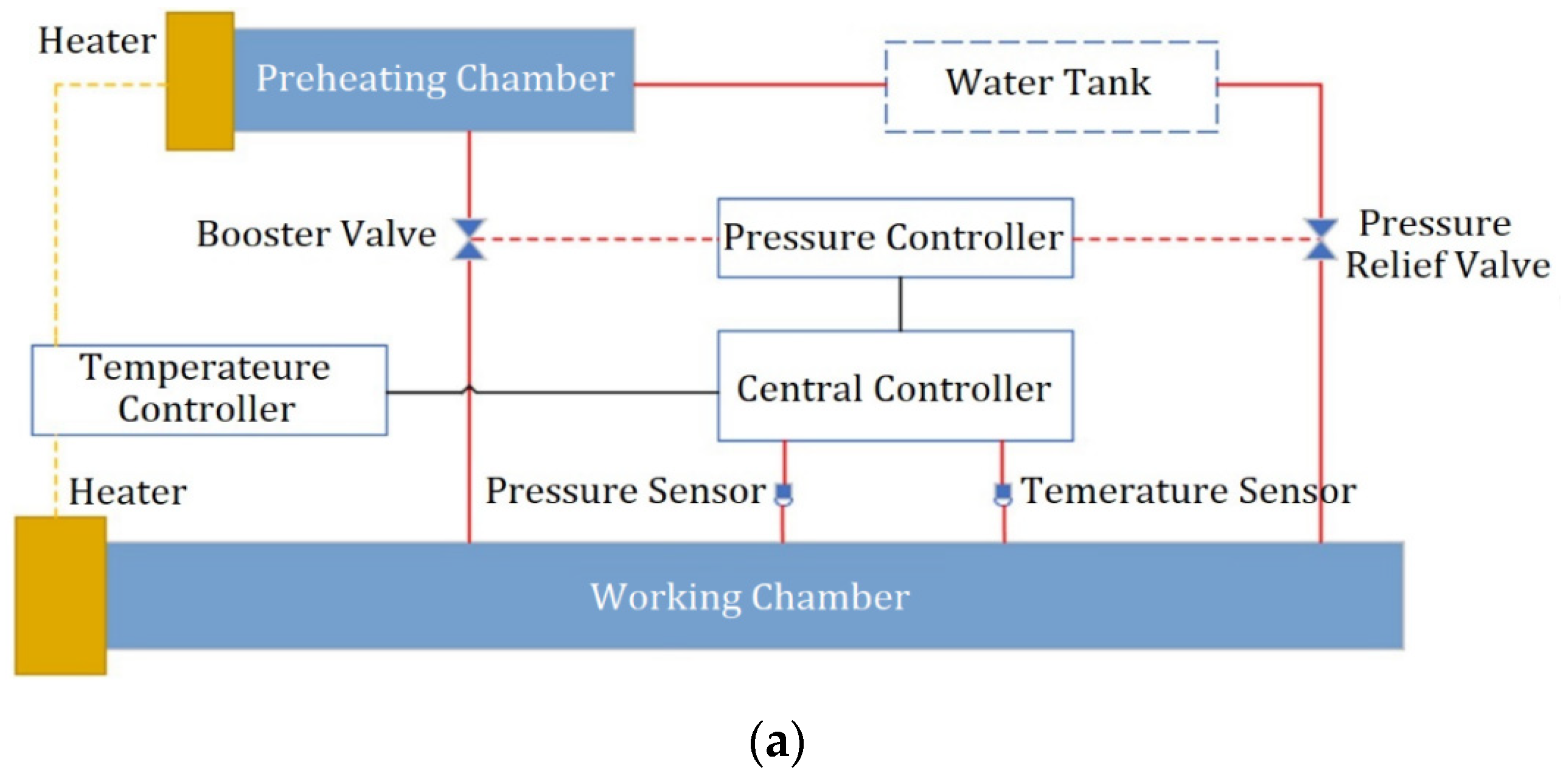
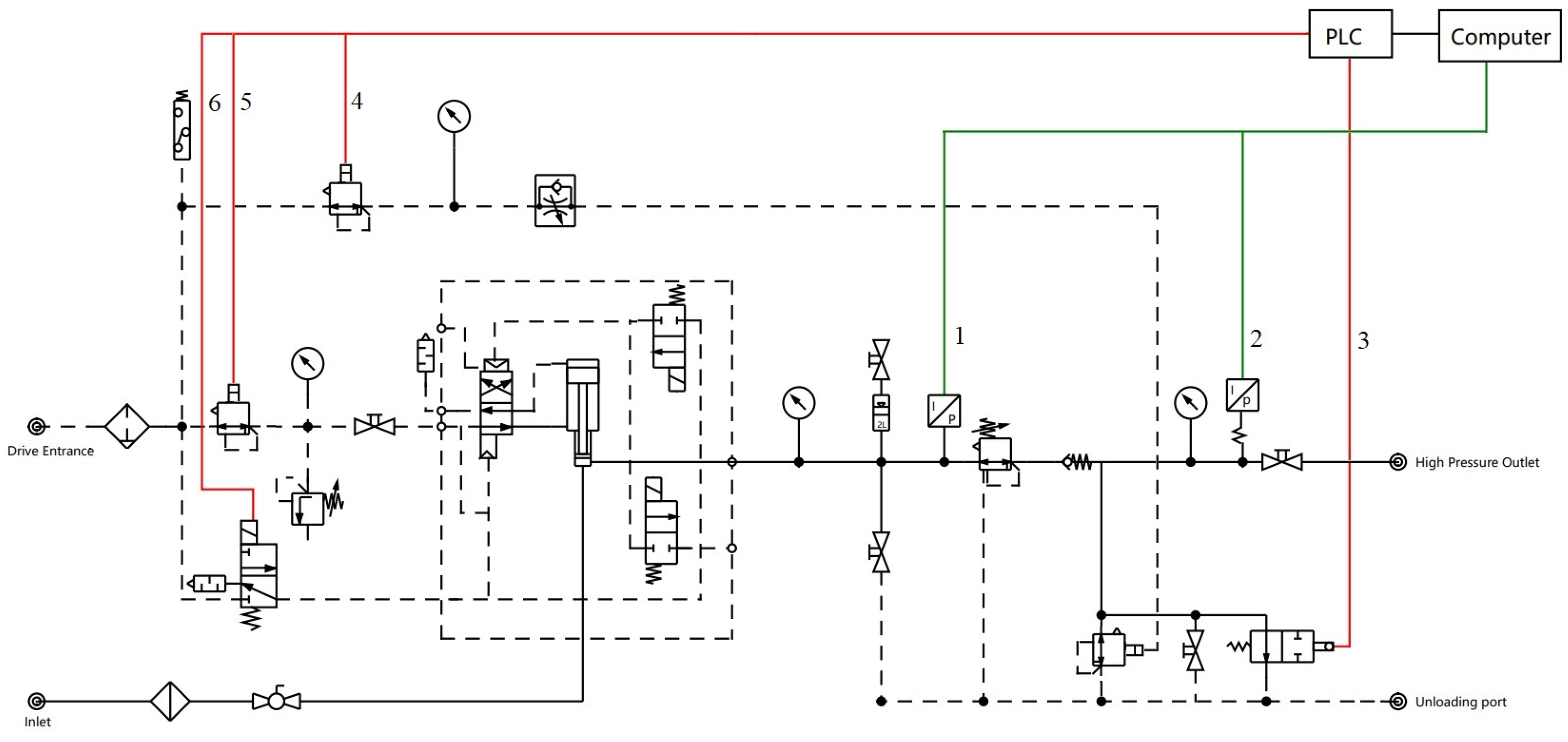
3.1. System Functions and Composition
3.2. The Temperature and Pressure Decoupling Control System
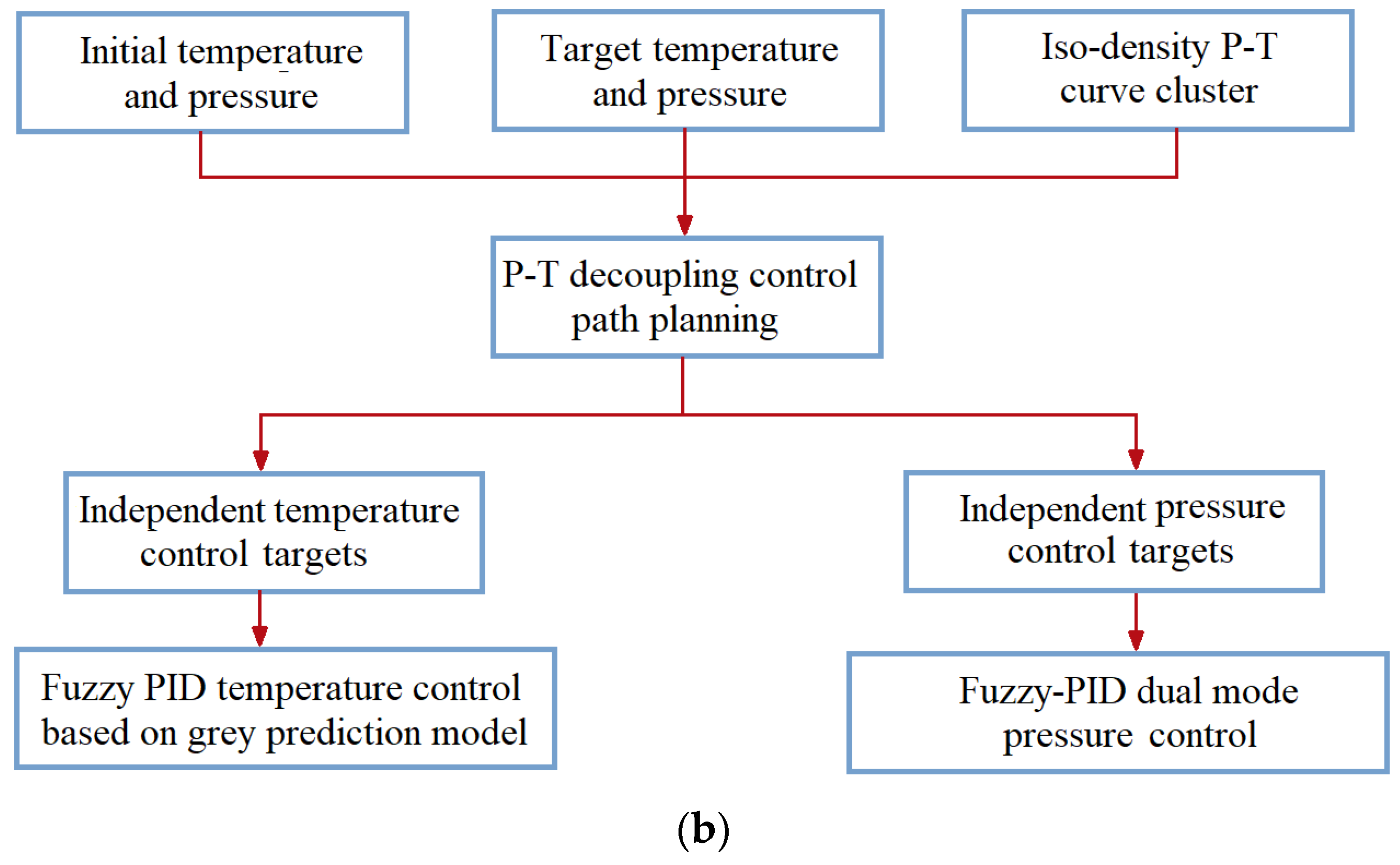
4. Temperature and Pressure Decoupling Control Based on the Iso–Density Curves of Water
4.1. State Surface of Water
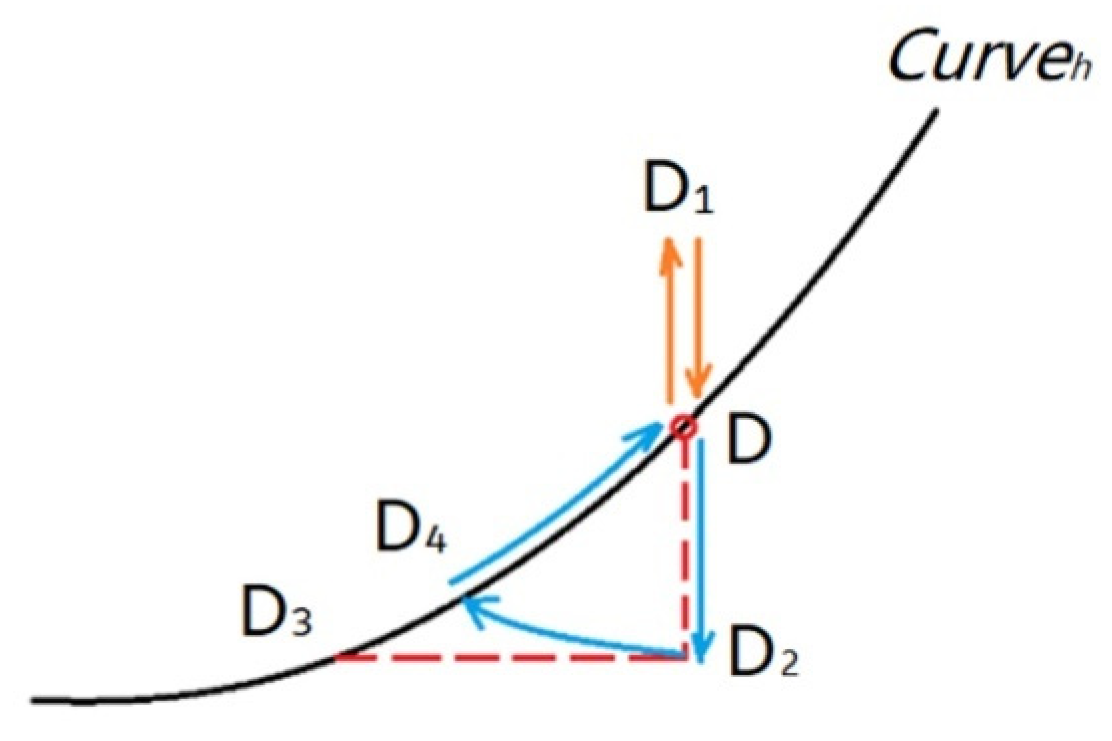
4.2. Digitization of the Iso–Density Curves of Water
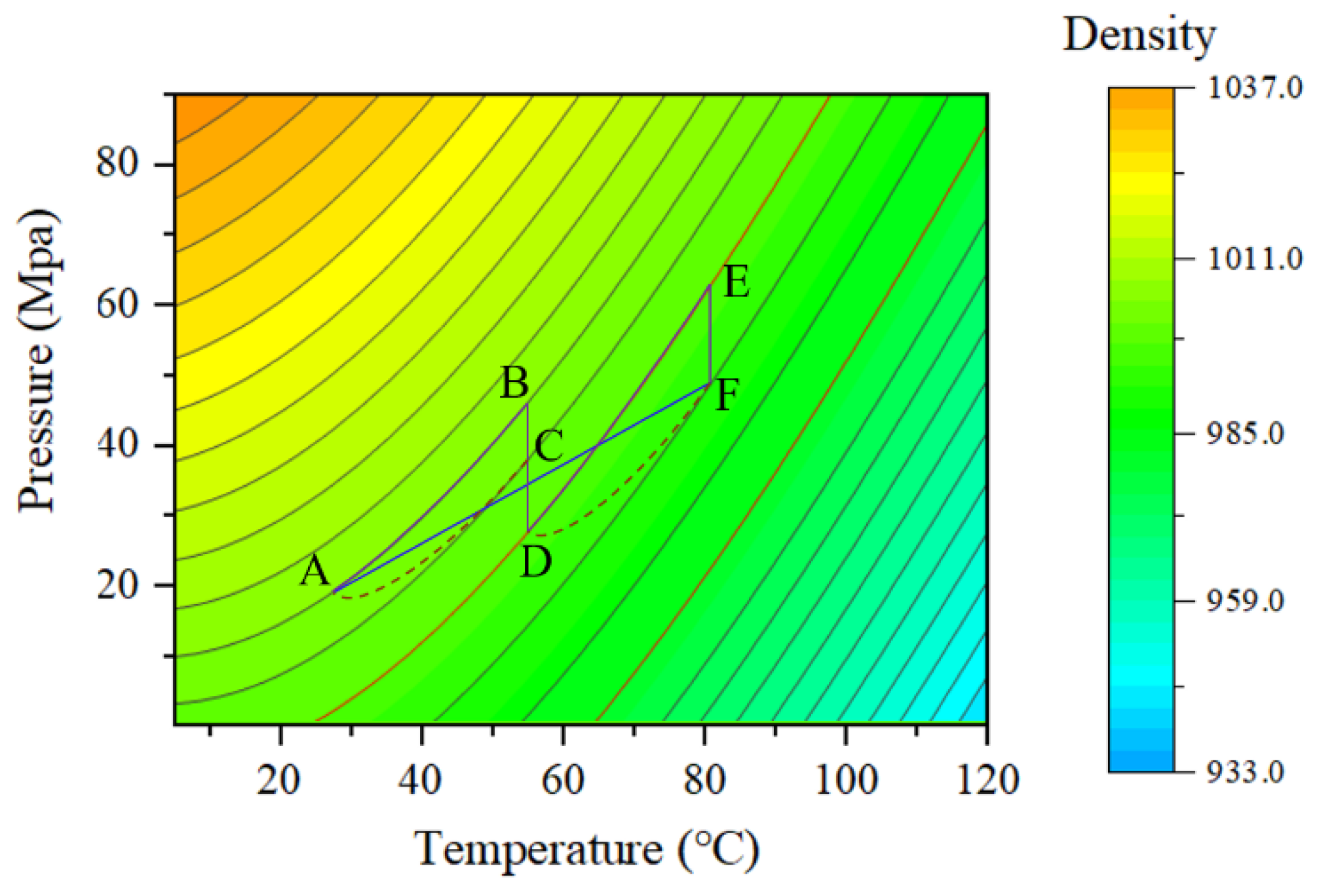
4.3. Initial Environment Reconstruction
4.4. P-T Preservation
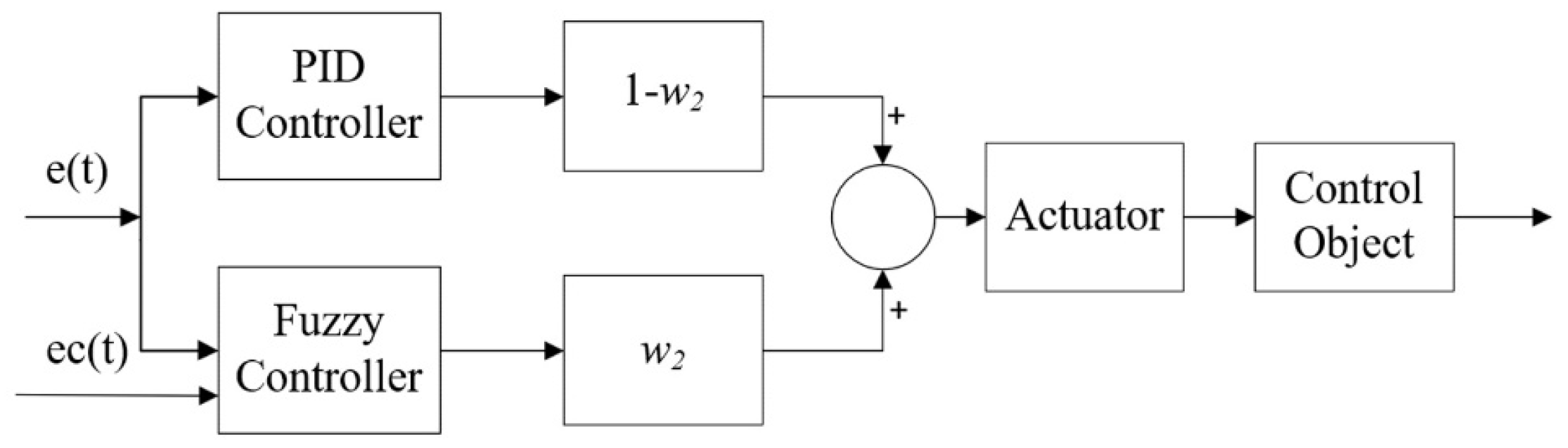
5. Fuzzy-PID Dual Mode Pressure Control
- Define E in the domain of discourse of fuzzy discrete set to represent the deviation, EC to represent the deviation change, and U to represent the output;
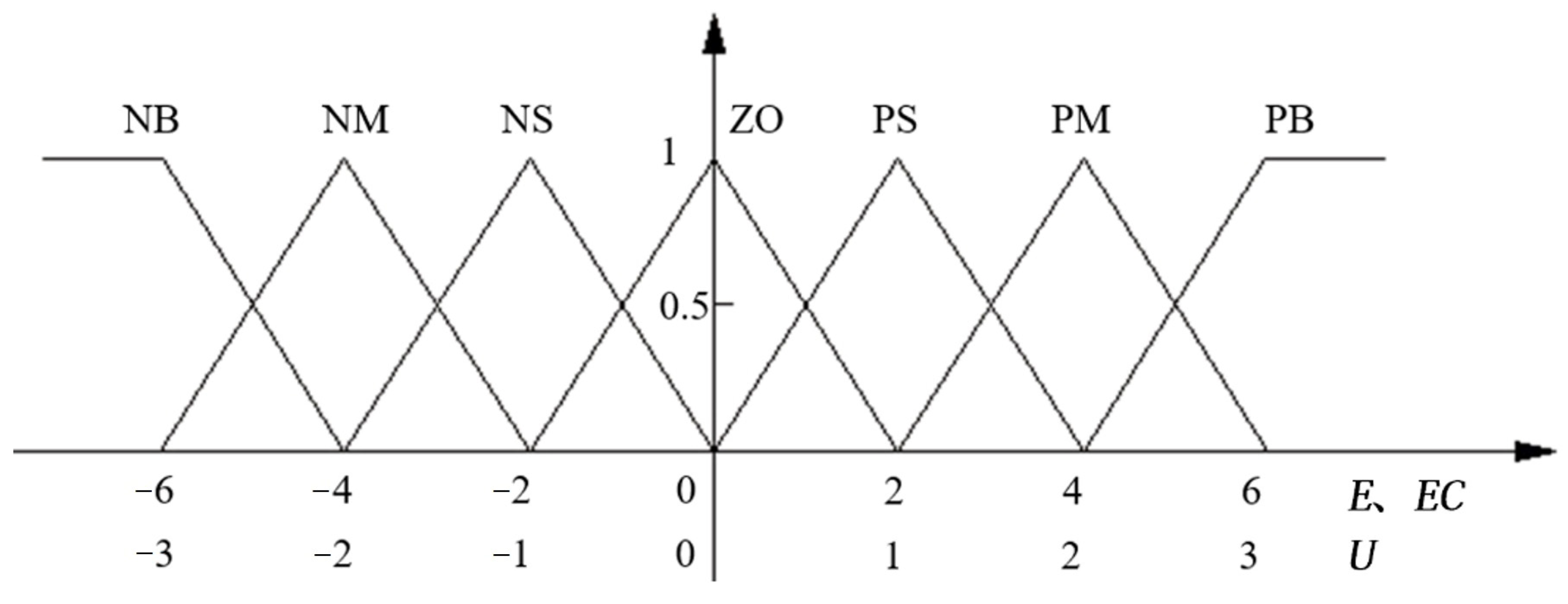
- Set the domain of discourse of E and EC as {−6, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, 6}, and the domain of discourse of U as {−3, −2.5, −2, −1.5, −1.0, −0.5, 0, 0.5, 1.0, 1.5, 2.0, 2.5, 3};
- Seven fuzzy linguistic variables are used, namely PB (positive big), PM (positive middle), PS (positive small), ZO (zero), NS (negative small), NM (negative middle) and NB (negative big);
- Triangular membership function is adopted, as shown in Figure 8;
- The main principles for determining U according to E and EC are as follows:
- (a)
- When E is big, U should be big to speed up the system response;
- (b)
- When E is medium and EC is small, U should be medium to slow down the control;
- (c)
- When E and EC are both small, U should be small.
- 6.
- Center-of-gravity defuzzification is used on U to get its precise output.
6. Fuzzy PID Temperature Control Based on Grey Prediction Model
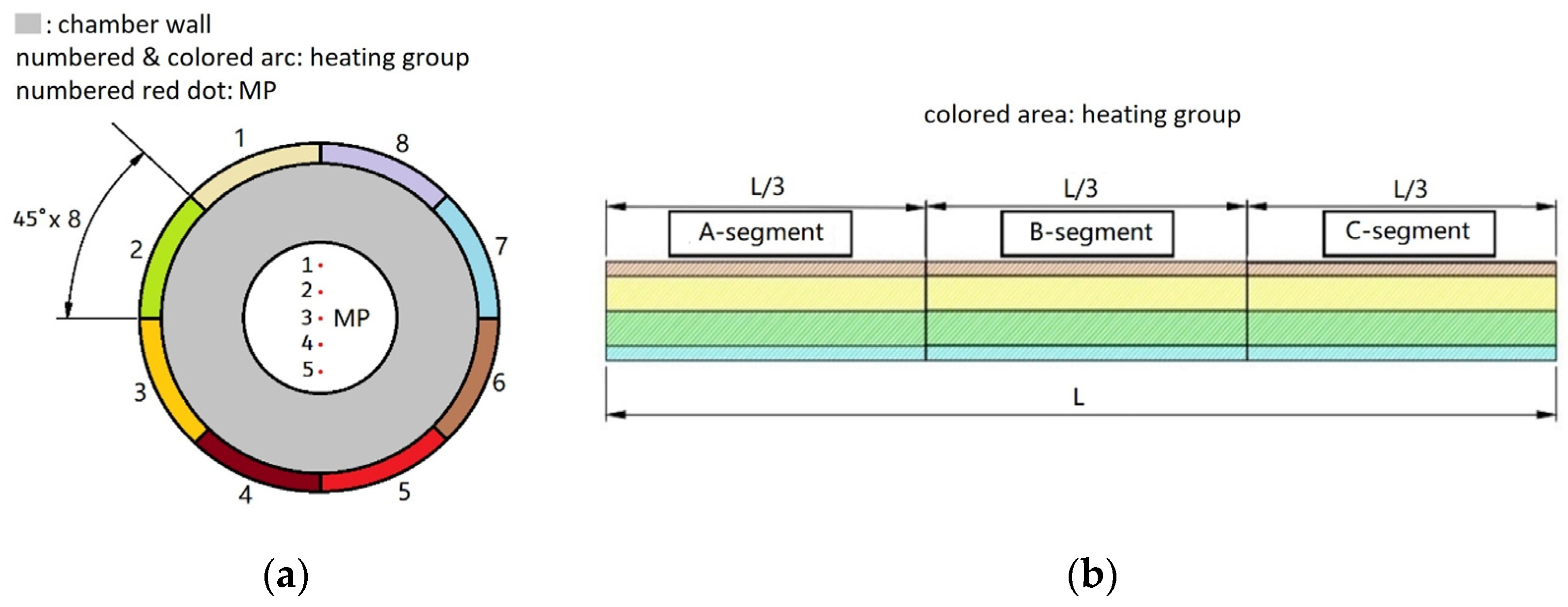
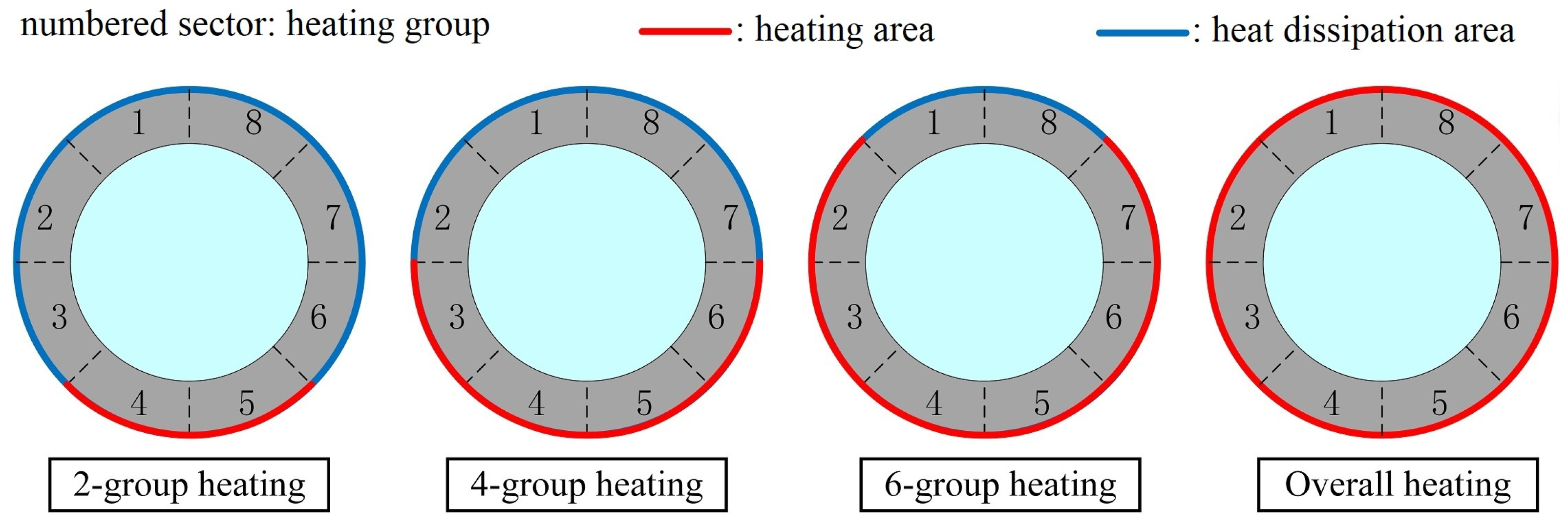
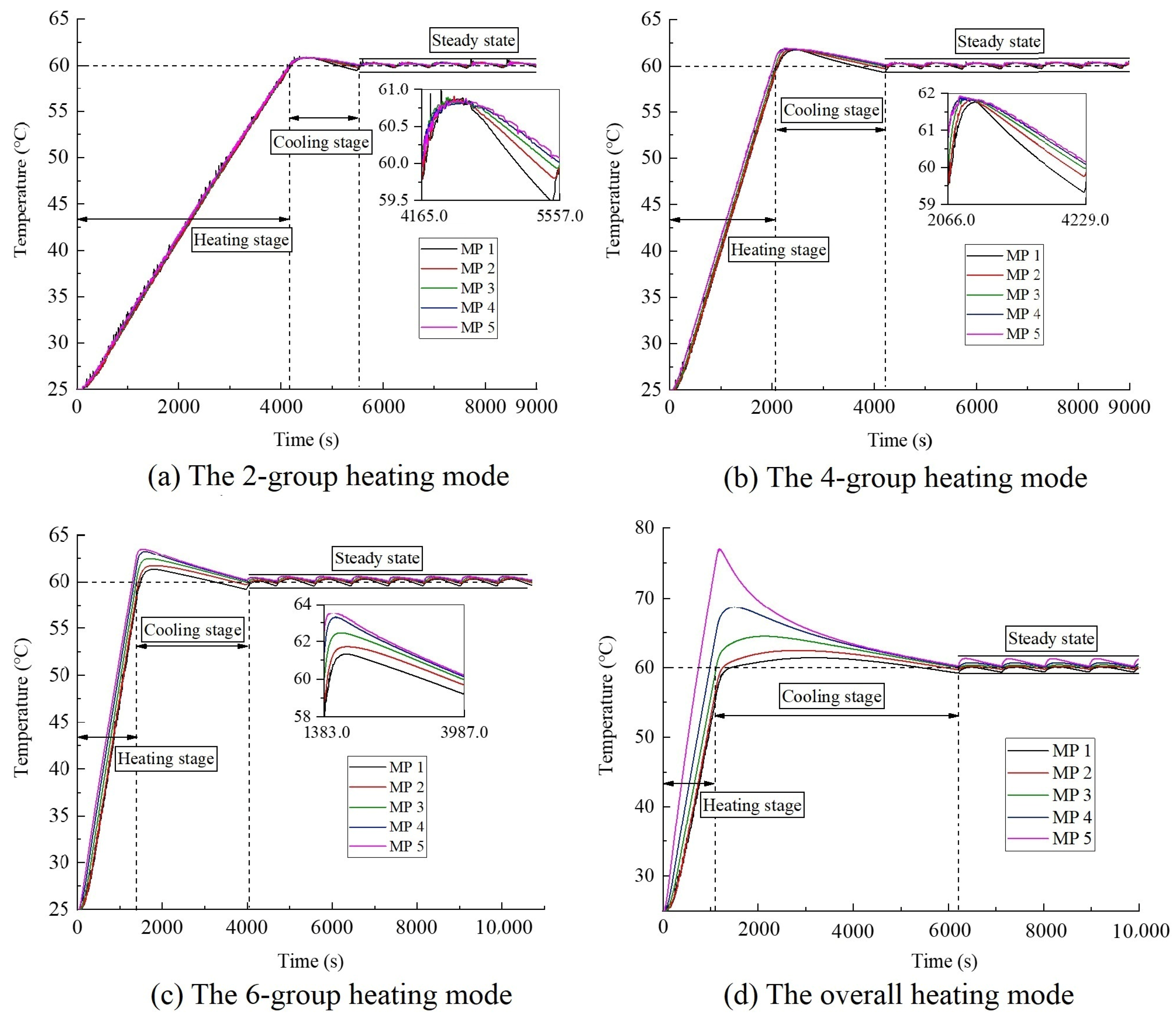
6.1. Study on Uniformity of Electric Heating Temperature Field
6.2. Simulation of Electric Heating Temperature Field
- In the heating stage, the less the heating groups, the better the temperature uniformity. The temperature field uniformity of the 2-group heating mode is the best, while that of the overall heating mode is the worst. In the steady state, the uniformities of temperature field of different heating modes are all improved, and the 4-group heating mode has the best result;
- The more the heating groups, the longer the cooling duration is;
- 4-group heating mode has a better overall performance in terms of temperature uniformity and cooling speed.
6.3. Fuzzy PID Temperature Control Based on Grey Prediction Model
6.3.1. Grey Prediction Model
6.3.2. Grey-Prediction-Based Fuzzy PID Controller
Ki = K′i + ΔKi
Kd = K′d + ΔKd
7. Experiment Results and Discussion
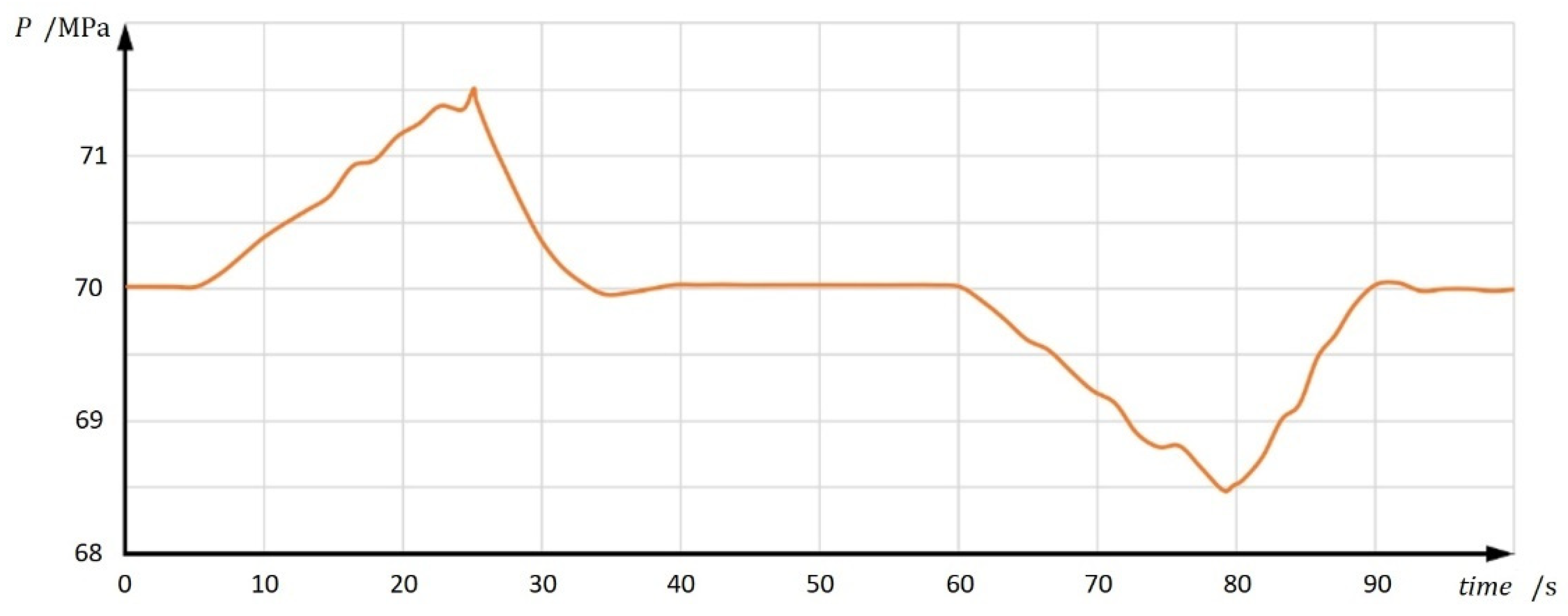
7.1. Experiment of the Fuzzy-PID Dual Mode Pressure Control
7.2. Experiment of the Uniformity of Temperature Field
7.3. Experiment of the Fuzzy PID Temperature Control Based on Grey Prediction Model
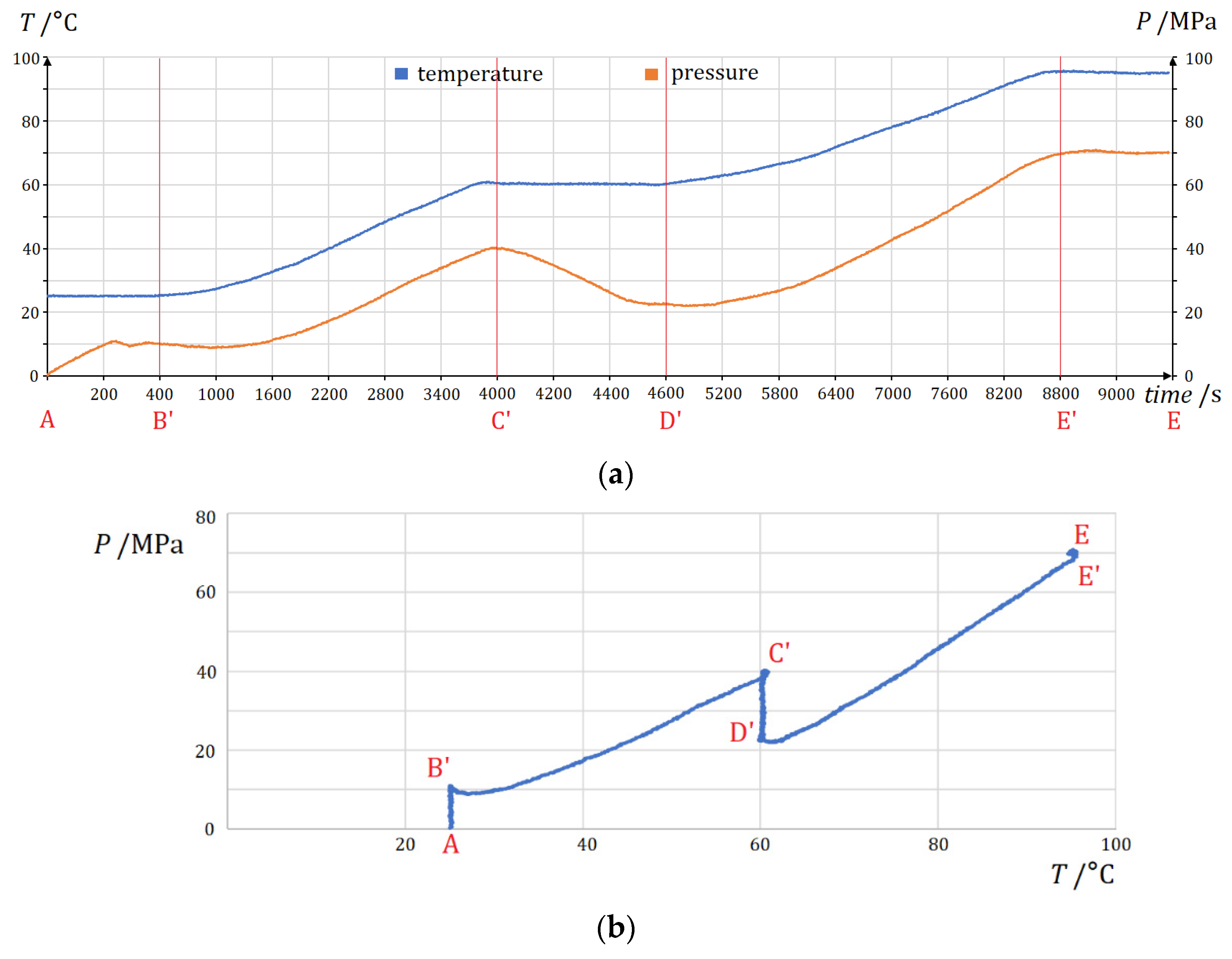
7.4. Experiment of the Temperature and Pressure Decoupling Control
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, Y.C.; He, Z.Q.; Wang, Y.W.; Dai, Z.X.; Wang, Z.J. Mining-induced mechanics behavior in the deep mine with an overkilometer depth. J. China Coal Soc. 2019, 44, 1326–1336. [Google Scholar]
- Xie, H.P.; Li, C.B.; Gao, M.Z.; Zhang, R.; Gao, F.; Zhu, J.B. Conceptualization and preliminary research on deep in situ rock mechanics. Chin. J. Rock Mech. Eng. 2021, 40, 217–232. [Google Scholar]
- Zhang, Z.P.; Xie, H.P.; Zhang, R.; Zhang, Z.T.; Gao, M.Z.; Jia, Z.Q.; Xie, J. Deformation damage and energy evolution characteristics of coal at different depths. Rock Mech. Rock Eng. 2019, 52, 1491–1503. [Google Scholar] [CrossRef]
- Xie, H.P.; Gao, M.Z.; Zhang, R.; Chen, L.; Liu, T.; Li, C.B.; Li, C.; He, Z.Q. Study on concept and progress of in situ fidelity coring of deep rocks. Chin. J. Rock Mech. Eng. 2020, 39, 865–876. [Google Scholar]
- Li, C. Reliability Analysis of Deep-Sea Ultra-High Pressure Environment Simulation System; SOA: Beijing, China, 2013. [Google Scholar]
- Zhang, J.N. Study on Acoustic Testing System for Pressure Environment Simulation of Seabed Sediment. Master’s Thesis, Guangdong University of Technology, Guangzhou, China, 2021. [Google Scholar]
- Molfino, P.; Nervi, M.; Rossi, M.; Malgarotti, S.; Odasso, A. Design and development of a module for the construction of reversible HVDC submarine deep-water sea electrodes. IEEE Trans. Power Deliv. 2017, 32, 1682–1687. [Google Scholar] [CrossRef]
- Gauthey, J.R.; Ventriglio, F.J. Naval Ship Systems Command Research and Development Program on Pollution Abatement; American Society of Mechanical Engineers: New York, NY, USA, 1973; Volume 95, p. 69. [Google Scholar]
- McInroy, J.E.; Neat, G.W.; O’Brien, J.F. A robotic approach to fault-tolerant, precision pointing. IEEE Robot. Autom. Mag. 1999, 6, 24–31. [Google Scholar] [CrossRef]
- AMSTEC. Facilities and Equipment in Yokosuka Headquarters. 2003. Available online: https://www.jamstec.go.jp/e/about/equipment/yokosuka/chugata_kouatsu_jikken.html (accessed on 22 May 2023).
- Qing, X. Design and Finite Element Analysis of a Super High Pressure Cylinder. Master’s Thesis, Sichuan University, Chengdu, Chian, 2017; pp. 3–40. [Google Scholar]
- Wang, W.T. Study on Pressure Retaining Transfer Device for Deep-Sea Sediments. Master’s Thesis, Zhejiang University, Hangzhou, China, 2015. [Google Scholar]
- Zeng, R.Y.; Chan, Z.H. Progress in research and development techniques on deep sea microorganism resource. Chin. Bull. Life Sci. 2012, 24, 991–996. [Google Scholar]
- Ross, P.S.; Bourke, A.; Fresia, B. A multi-sensor logger for rock cores: Methodology and preliminary results from the Matagami mining camp, Canada. Ore Geol. Rev. 2013, 53, 93–111. [Google Scholar] [CrossRef]
- Schultheiss, P.J.; Francis, T.J.G.; Holland, M.; Roberts, J.A.; Amann, H.; Thjunjoto, R.J.; Parkes, R.J.; Martin, D.; Rothfuss, M.; Tyunder, F.; et al. Pressure Coring, Logging and Subsampling with the Hyacinth System; Geological Society: London, UK, 2006; Volume 267, pp. 151–163. [Google Scholar]
- Liu, J.B. Study on Pressure Maintaining System of Gas Hydrate Transfer Device. Master’s Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Liu, H.; Lee, J.C.; Li, B.R. High precision pressure control of a pneumatic chamber using a hybrid fuzzy PID controller. Int. J. Precis. Eng. Manuf. 2007, 8, 8–13. [Google Scholar]
- Yu, L.; Lim, J.G.; Fei, S.M. An improved single neuron self-adaptive PID control scheme of superheated steam temperature control system. Int. J. Syst. Control. Inf. Process. 2017, 2, 1–13. [Google Scholar] [CrossRef]
- Chew, I.M.; Wong, F.; Bono, A.; Nan, D.J.; Wong, K.I. Genetic algorithm optimization analysis for temperature control system using cascade control loop model. Int. J. Comput. Digit. Syst. 2020, 9, 119–128. [Google Scholar]
- Shakeri, E.; Latif-Shabgahi, G.; Abharian, A.E. Design of an intelligent stochastic model predictive controller for a continuous stirred tank reactor through a Fokker-Planck observer. Trans. Inst. Meas. Control. 2018, 40, 3010–3022. [Google Scholar] [CrossRef]
- Shi, H.Y.; Li, P.; Wang, L.M.; Su, C.L.; Yu, J.X.; Cao, J.T. Delay-range-dependent robust constrained model predictive control for industrial processes with uncertainties and unknown disturbances. Complexity 2019, 2019, 2152014. [Google Scholar] [CrossRef]
- Aguilar-López, R.; Mata-Machuca, J.L.; Godinez-Cantillo, V. A tito control strategy to increase productivity in uncertain exothermic continuous chemical reactors. Processes 2021, 9, 873. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.B.; Chen, W.N.; Wang, X.D.; Wang, D.C. Overview of Pressure Control System Based on PID Algorithm. Proc. First Pearl River Sci. Assoc. Forum 2011, 128–132. [Google Scholar]
- Qian, X.; Huang, K.J.; Jia, S.K.; Chen, H.S.; Yuan, Y.; Zhang, L.; Wang, S.F. Temperature difference control and pressure-compensated temperature difference control for four-product extended Petlyuk dividing-wall columns. Chem. Eng. Res. Des. 2019, 146, 263–276. [Google Scholar] [CrossRef]
- Pan, H.; Wu, X.; Qiu, J.; He, G.C.; Ling, H. Pressure compensated temperature control of Kaibel divided-Wall column. Chem. Eng. Sci. 2019, 203, 321–332. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Liu, M.; Wu, H.; Wang, J. Temperature and Pressure Dynamic Control for the Aircraft Engine Bleed Air Simulation Test Using the LPID Controller. Aerospace 2021, 8, 367. [Google Scholar] [CrossRef]
- The International Association for the Properties of Water and Steam, IAPWS R6-95(2018), Revised Release on the IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use, 2018. Available online: http://www.iapws.org/relguide/IAPWS-95.html (accessed on 22 May 2023).
- Li, X.J.; Wu, M.W.; Wan, L.H.; Wu, J.J.; Zhang, H.Y. Simulation and experimental study of uniformity of temperature field of water by electric heating. J. Shenzhen Univ. Sci. Eng. 2022, 39, 314–323. [Google Scholar] [CrossRef]
- Ghani, A.A.; Farid, M.M. Numerical simulation of solid-liquid food mixture in a high pressure processing unit using computational fluid dynamics. J. Food Eng. 2007, 80, 1031–1420. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Wei, Z.Y.; Lin, Q.Y.; Zhang, L.; Xu, J. MBD of gray prediction fuzzy-PID irrigation control technology. Desalination Water Treat. 2018, 110, 328–336. [Google Scholar] [CrossRef]
- Kayacan, E.; Kaynak, O. An adaptive gray PID-type fuzzy controller design for a non-linear liquid level system. Trans. Inst. Meas. Control. 2009, 31, 33–49. [Google Scholar] [CrossRef]







| U | EC | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | ||
| E | NB | PB | PB | PM | PM | PS | ZO | ZO |
| NM | PB | PB | PM | PS | PS | ZO | NS | |
| NS | PM | PM | PM | PS | ZO | NS | NS | |
| ZO | PM | PM | PS | ZO | NS | NM | NM | |
| PS | PS | PS | ZO | NS | NS | NM | NM | |
| PM | PS | ZO | NS | NM | NM | NM | NB | |
| PB | ZO | ZO | NM | NM | NM | NB | NB | |
| Heating Mode | UI/% | Duration of Cooling Stage/min | |
|---|---|---|---|
| Heating Stage | Steady State | ||
| 2-group | 98.29 | 99.66 | 27.88 |
| 4-group | 97.36 | 99.71 | 44.52 |
| 6-group | 93.24 | 99.51 | 55.21 |
| overall | 84.75 | 98.96 | 98.26 |
| U (ΔKp/ΔKi/ΔKd) | EC | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | ||
| E | NB | PB/NB/PS | PB/NB/NS | PM/NM/NB | PM/NM/NB | PS/NS/NB | ZO/ZO/NM | ZO/ZO/PS |
| NM | PB/NB/PS | PB/NB/NS | PM/NM/NB | PS/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/ZO/ZO | |
| NS | PM/NB/ZO | PM/NM/NS | PM/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/PS/NS | NS/PS/ZO | |
| ZO | PM/NM/ZO | PM/NM/NS | PS/NS/NS | ZO/ZO/NS | NS/PS/NS | NM/PM/NS | NM/PM/ZO | |
| PS | PS/NM/ZO | PS/NS/ZO | ZO/ZO/ZO | NS/PS/ZO | NS/PS/ZO | NM/PM/ZO | NM/PB/ZO | |
| PM | PS/ZO/PM | ZO/ZO/PS | NS/PS/PS | NM/PS/PS | NM/PM/PS | NM/PB/PS | NB/PB/PS | |
| PB | ZO/ZO/PB | ZO/ZO/PM | NM/PS/PM | NM/PM/PM | NM/PM/PS | NB/PB/PS | NB/PB/PS | |
| Heating Mode | UI/% | Duration/min | ||
|---|---|---|---|---|
| Heating Stage | Steady State | Heating Stage | Cooling Stage | |
| 2-group | 99.20 | 99.12 | 90.23 | 23.54 |
| 4-group | 99.07 | 99.23 | 43.50 | 44.52 |
| 6-group | 98.14 | 98.96 | 30.24 | 71.15 |
| overall | 91.30 | 98.46 | 32.23 | 79.71 |
| Target Temp. | Performance | Fuzzy PID | Grey Prediction Based Fuzzy PID | ||||
|---|---|---|---|---|---|---|---|
| Sect. A | Sect. B | Sect. C | Sect. A | Sect. B | Sect. C | ||
| 75 °C | Overshoot/% | 0.14 | 0.25 | 0.48 | 0.07 | 0.10 | 0.13 |
| Steady-state error/°C | −0.20 | 0.28 | 0.17 | 0.10 | −0.11 | 0.12 | |
| 85 °C | Overshoot/% | 0.19 | 0.19 | 0.14 | 0.09 | 0.14 | 0.18 |
| Steady-state error/°C | 0.29 | 0.25 | 0.13 | 0.13 | −0.10 | −0.10 | |
| 95 °C | Overshoot/% | 0.28 | 0.29 | 0.20 | 0.17 | 0.22 | 0.10 |
| Steady-state error/°C | 0.33 | −0.26 | 0.14 | 0.13 | 0.12 | 0.13 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Li, X.; Yang, S.; Wu, J.; Wu, M.; Wan, L.; Zhang, H.; Xie, H. An Innovative System of Deep In Situ Environment Reconstruction and Core Transfer. Appl. Sci. 2023, 13, 6534. https://doi.org/10.3390/app13116534
Peng X, Li X, Yang S, Wu J, Wu M, Wan L, Zhang H, Xie H. An Innovative System of Deep In Situ Environment Reconstruction and Core Transfer. Applied Sciences. 2023; 13(11):6534. https://doi.org/10.3390/app13116534
Chicago/Turabian StylePeng, Xiaobo, Xiongjun Li, Shigang Yang, Jinjie Wu, Mingwei Wu, Langhui Wan, Huaiyu Zhang, and Heping Xie. 2023. "An Innovative System of Deep In Situ Environment Reconstruction and Core Transfer" Applied Sciences 13, no. 11: 6534. https://doi.org/10.3390/app13116534
APA StylePeng, X., Li, X., Yang, S., Wu, J., Wu, M., Wan, L., Zhang, H., & Xie, H. (2023). An Innovative System of Deep In Situ Environment Reconstruction and Core Transfer. Applied Sciences, 13(11), 6534. https://doi.org/10.3390/app13116534





