Study on Damage Behavior and Its Energy Distribution of Deep Granite at High-Temperature Conditions
Abstract
1. Introduction
2. Acoustic Emission Test of Fractured Rock under Triaxial Loading
2.1. Instrument and Control Method
- (1)
- PCI-II acoustic emission test system: In order to reduce the interference of environmental noise during the test, the preamplifier gain and trigger threshold value were set to 40 dB, and the sampling frequency was 0.5 MHz. For the uniaxial compression test, an acoustic emission sensor (Micro 30) was placed in the middle of the rock sample, and vaseline was coated between the rock sample and the sensor to provide good acoustic coupling.
- (2)
- For the tubular high-temperature furnace, we used the programmable high-temperature furnace from the Metallurgical Laboratory of University of Science and Technology Beijing, as shown in Figure 1. The highest heating temperature of the high-temperature furnace is 1000 °C. Temperature control precision is less than 2 °C. The display precision is 1 °C, and the heating rate is controllable at 1 °C/min.
- (3)
- The pressure chamber can apply a radial force of 200 MPa, and can monitor the compression deformation of samples in real time. The maximum pressure of the high-precision oil pressure control system is 200 MPa, precision is 0.01 MPa, directly connected with the high-pressure chamber; the three-way valve system is mainly for loading and unloading of oil inlet valve and oil return valve control, control precision is 0.05 MPa; the ultra-high pressure hand pump can apply the maximum pressure is 200 MPa. Three kinds of confining pressures (0 MPa, 10 MPa, and 20 MPa) are designed. The loading was similar to the conventional triaxial test, and the axial pressure and confining pressure were loaded alternately with a gradient of 5 MPa each time. When it reached the design value, the axial loading rate was 0.02 mm/min to failure.
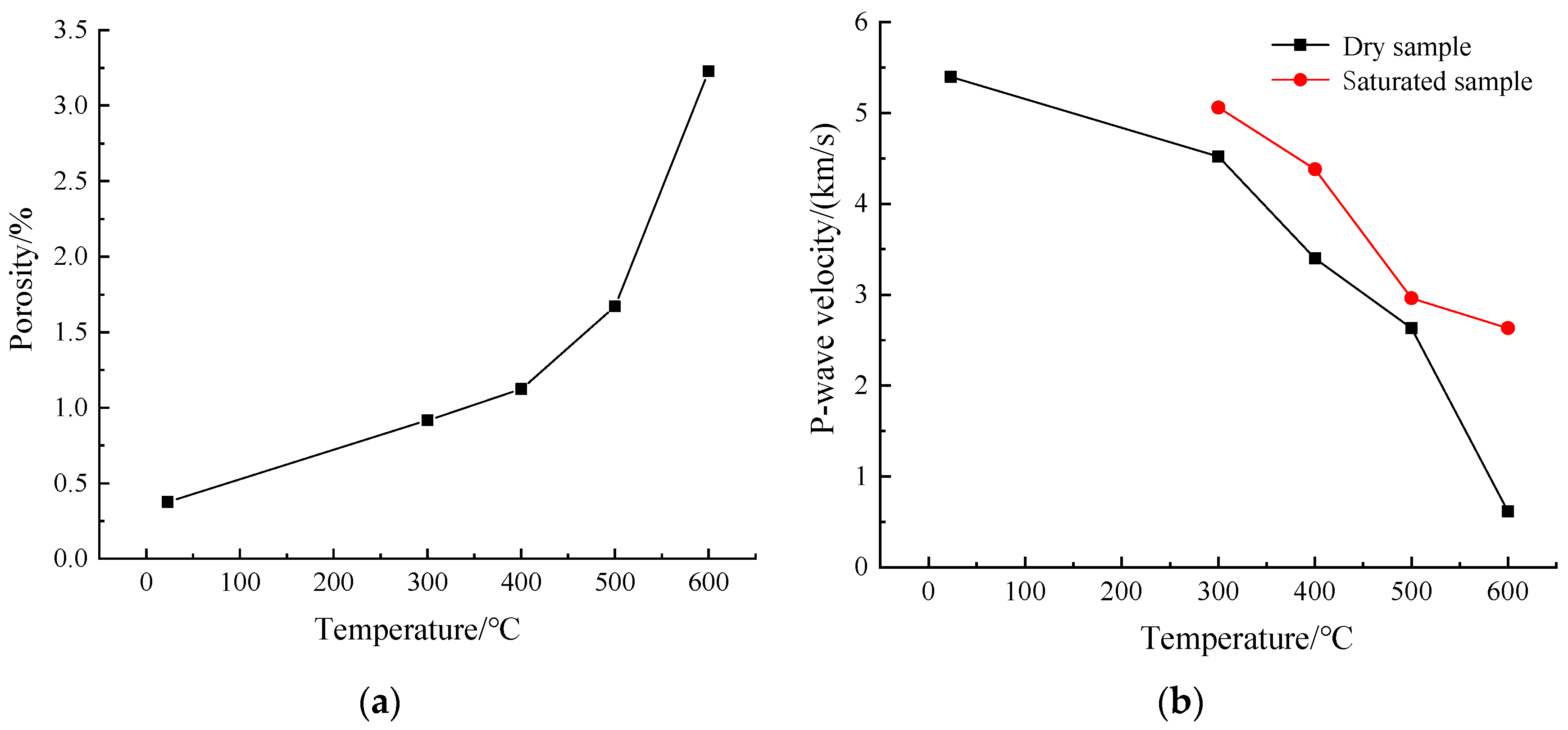
2.2. High-Temperature Damage Test and Analysis of Rock
3. Acoustic Emission Test Results and Analysis of Fractured Rock under Triaxial Loading
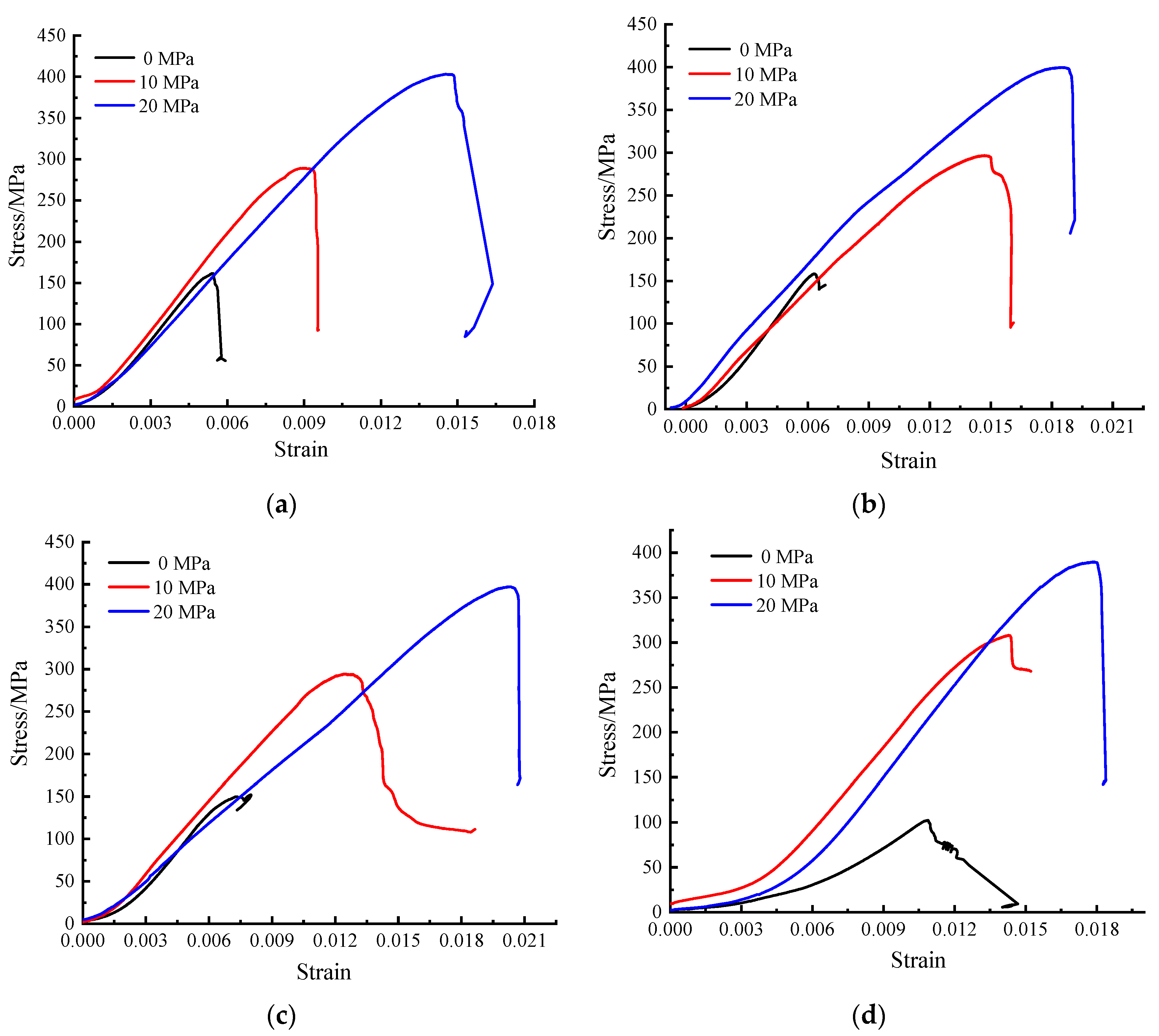
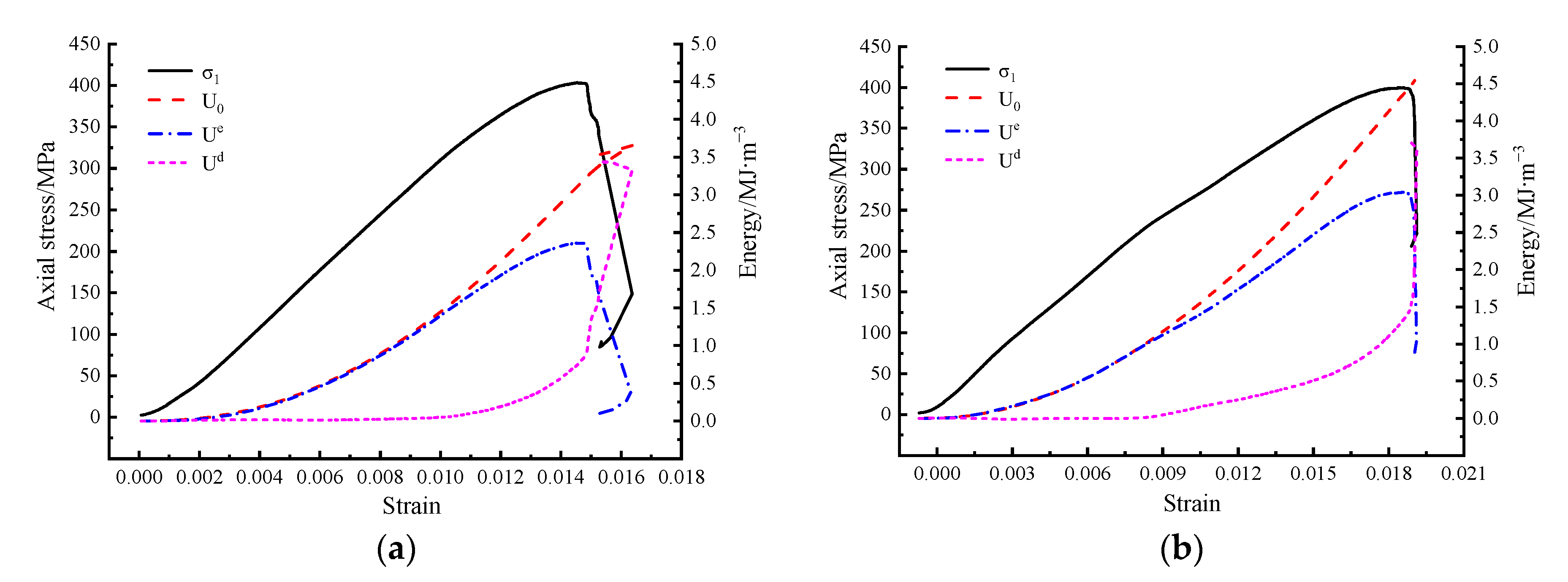
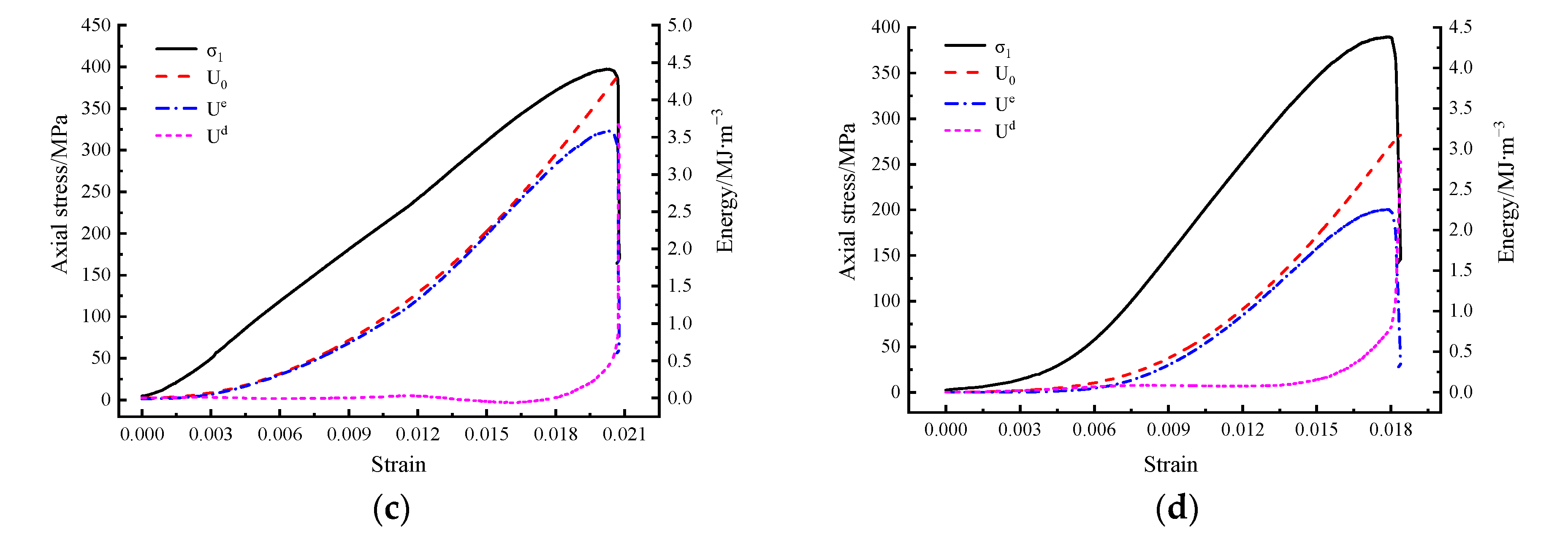
3.1. Total Stress–Strain Curve and Failure Mode
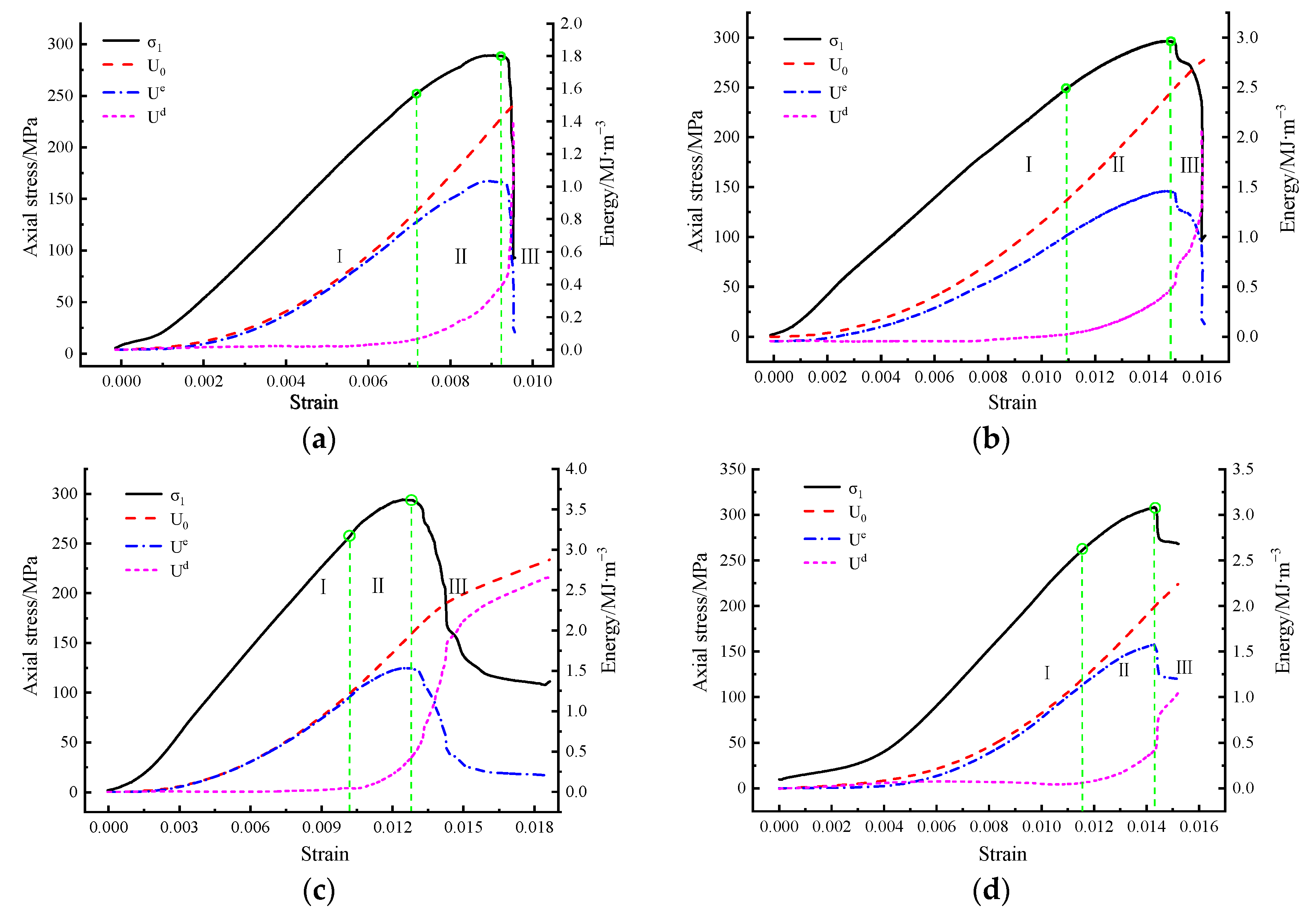
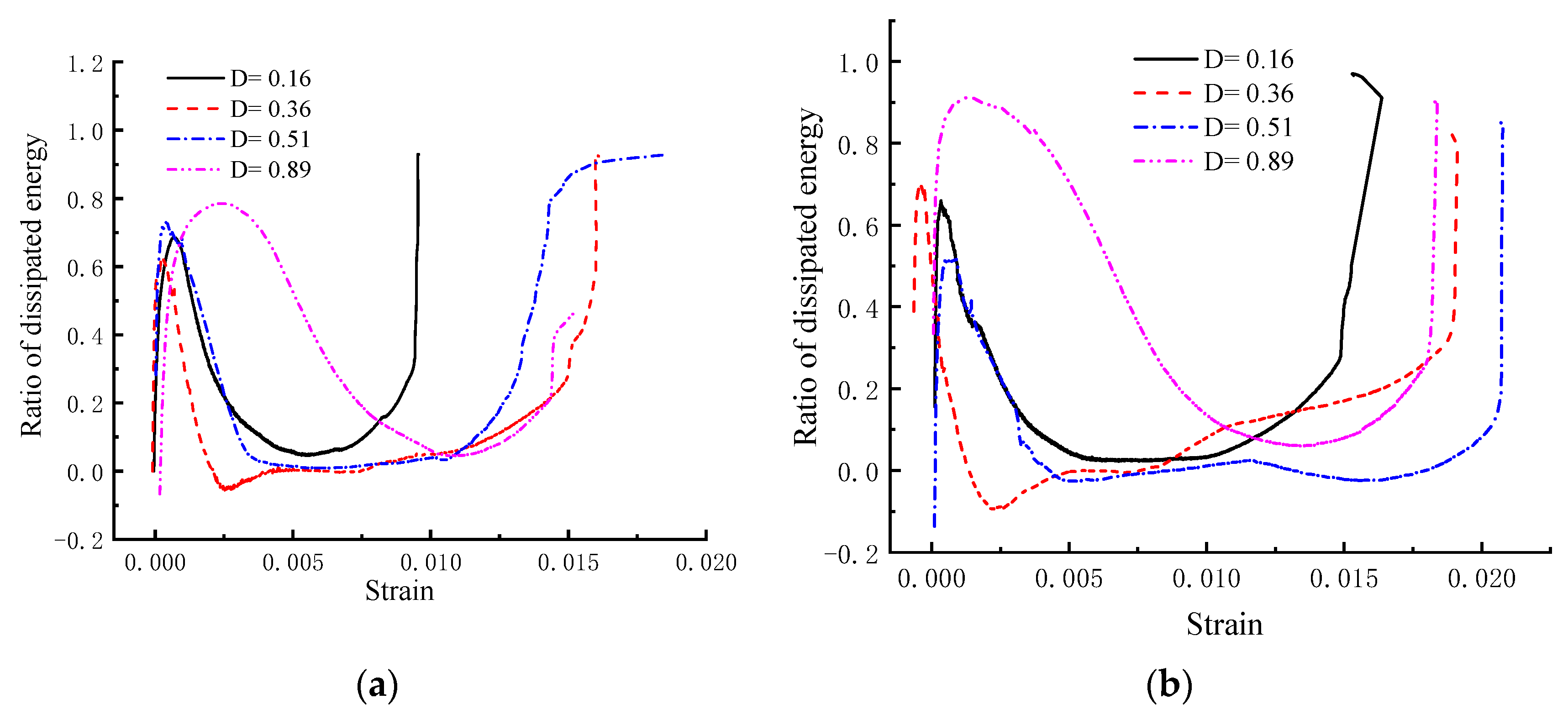
3.2. Effect Analysis of Equivalent Damage Factors on Rock Energy Evolution
4. Discussion
- (1)
- In the research of rock mass engineering, the primary task is to obtain the distribution characteristics of anisotropic crack in rock mass by using ultrasonic borehole television technology. Using borehole TV, the crack dip angle in the scanning area is segmented statistics, so as to obtain the distribution law of crack occurrence. Secondly, by analyzing the relationship between crack tendency and crack depth, the statistical data of the dominant crack surface are obtained. Then, the number of fracture surfaces within each unit distance is counted to obtain the density distribution characteristics of the fracture surface. These steps are the basis for the study of fractured surrounding rock.
- (2)
- Because the failure of the granite specimens is sudden, the damage is gradual in the specimen before the failure. When the fissure degree in the rock develops to a certain extent, the fissure changes from a stable expansion to an unstable expansion, and then the fissure quickly passes through the rock, causing damage. Therefore, for brittle hard rock, if the support can be carried out before the fissure instability expansion, the development of fissure can be effectively controlled. For example, Wei et al. [41] has carried out 3D network simulation based on deep rock joint of borehole TV, hoping to achieve the purpose of evaluating the stability of surrounding rock by simulating and exploring the distribution law of fracture space. Therefore, the fissure degree corresponding to the inflection point of maximum dissipated energy is finally adopted in this paper as the target factor to measure the support time.
- (3)
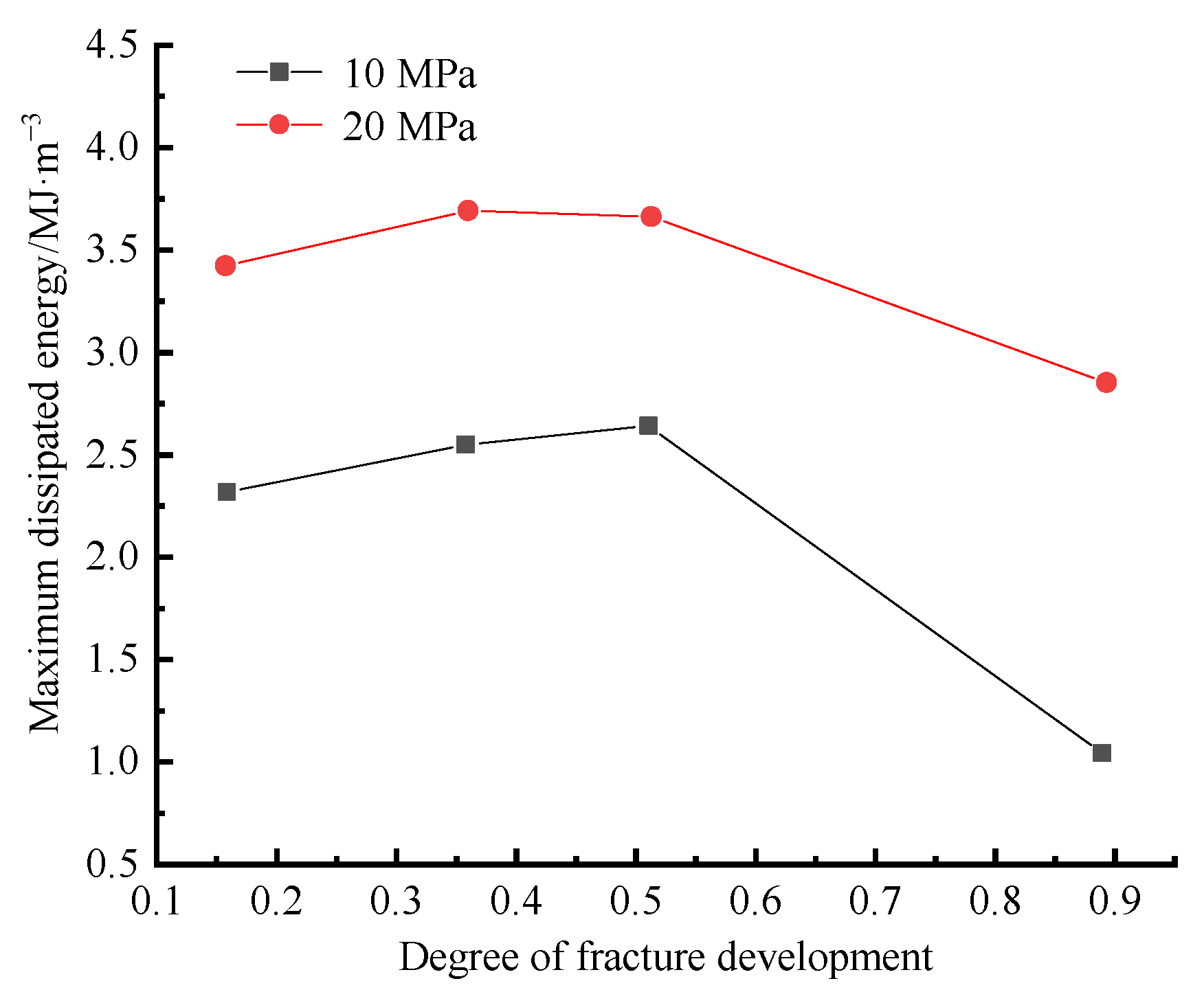
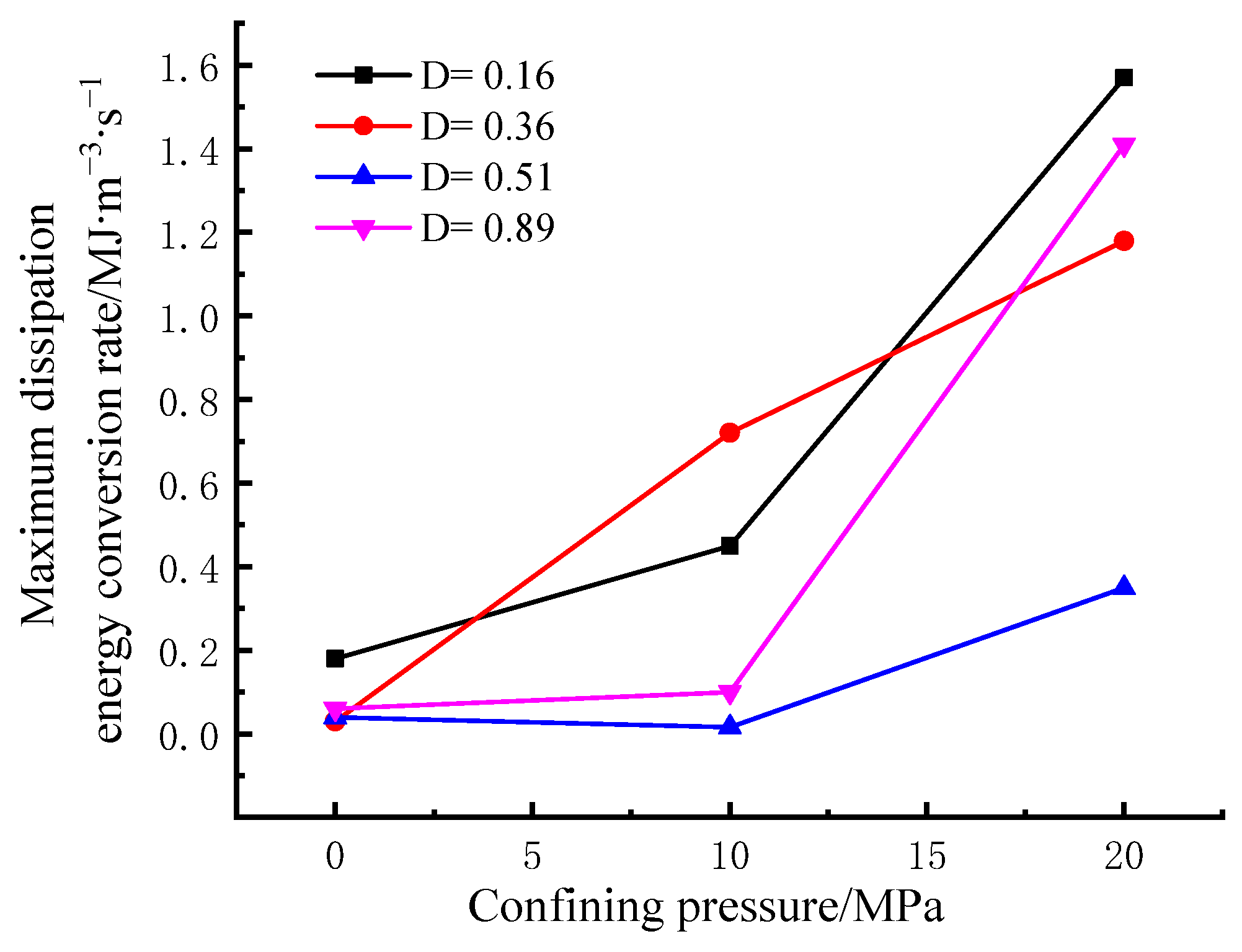
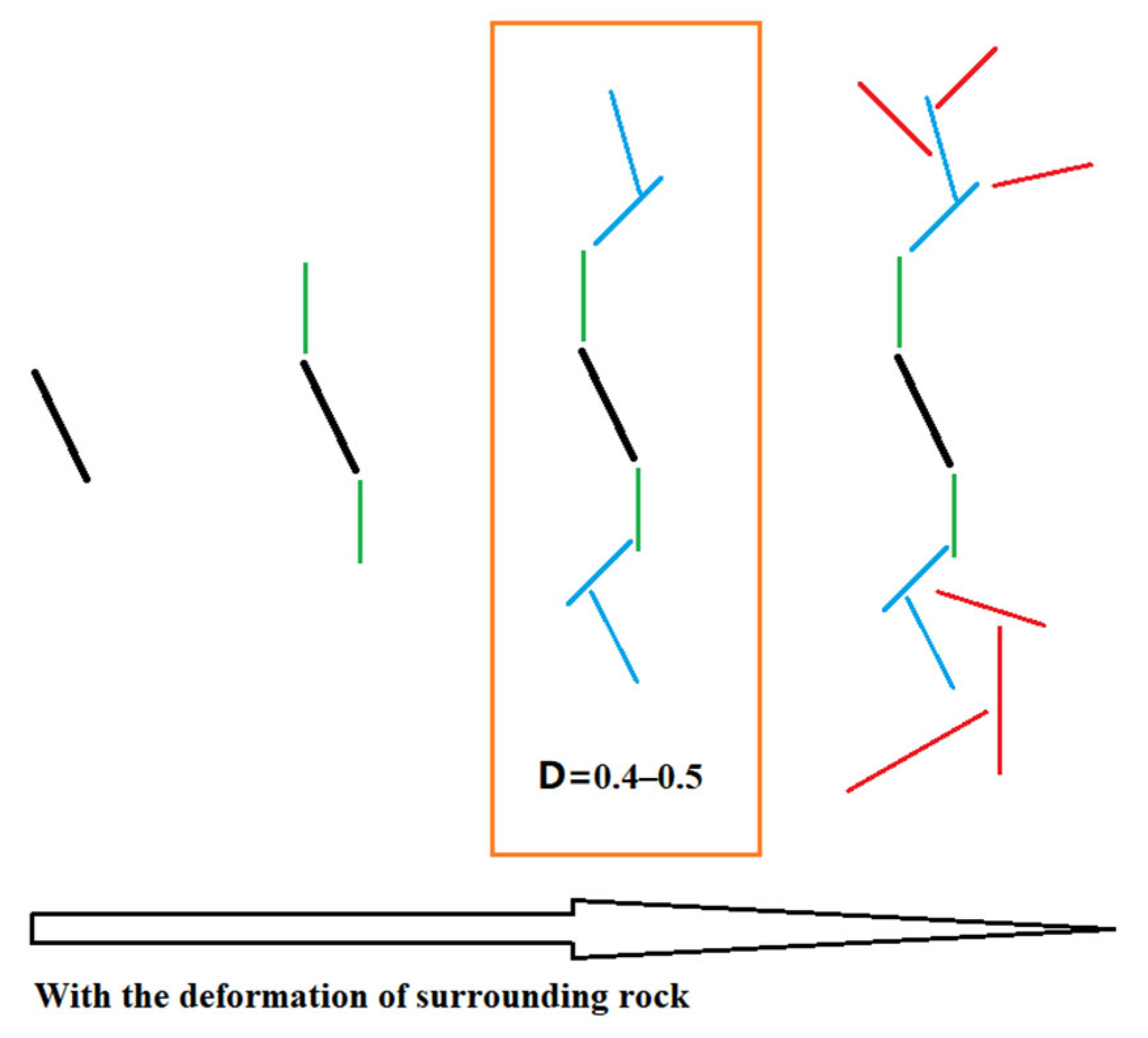
- In the study of fractured rocks, the current research is more inclined to simplify fractures into one, two, or more visible artificial fractures [26,27,28,37,38,39], and then analyze the influence of the number of artificial fractures on rock mass deformation and failure, which can reflect the influence of fractures to a certain extent on the macro level. However, this simplified process completely ignores the influence of the interaction between disordered fractures on the evolution of rock deformation energy. Therefore, this paper adopts thermal damage to create this disordered fracture, and replaces the traditional fracture number with the crack degree. The results show that there is an inflection point of maximum dissipated energy change at the fissure degree D = (0.4~0.5). Before the inflection point, the maximum dissipated energy gradually increases, but the variation amplitude is small. This is because the consumption of plastic deformation energy at the crack tip increases during the deformation process, and the fracture development can reduce the brittleness of the sample and make the fracture in the rock more fully developed. After the inflection point, the maximum dissipated energy decreases rapidly, which is due to the development of fractures in the rock mass, which reduces the bearing capacity of the internal structure damage. Figure 12 shows the schematic diagram of the internal fracture degree of rock mass with surrounding rock deformation. Therefore, in engineering support, when the internal fracture degree of rock mass D = (0.4~0.5), the support can be used as the basis for the identification of critical support for key parts.
5. Conclusions and Future Work
- (1)
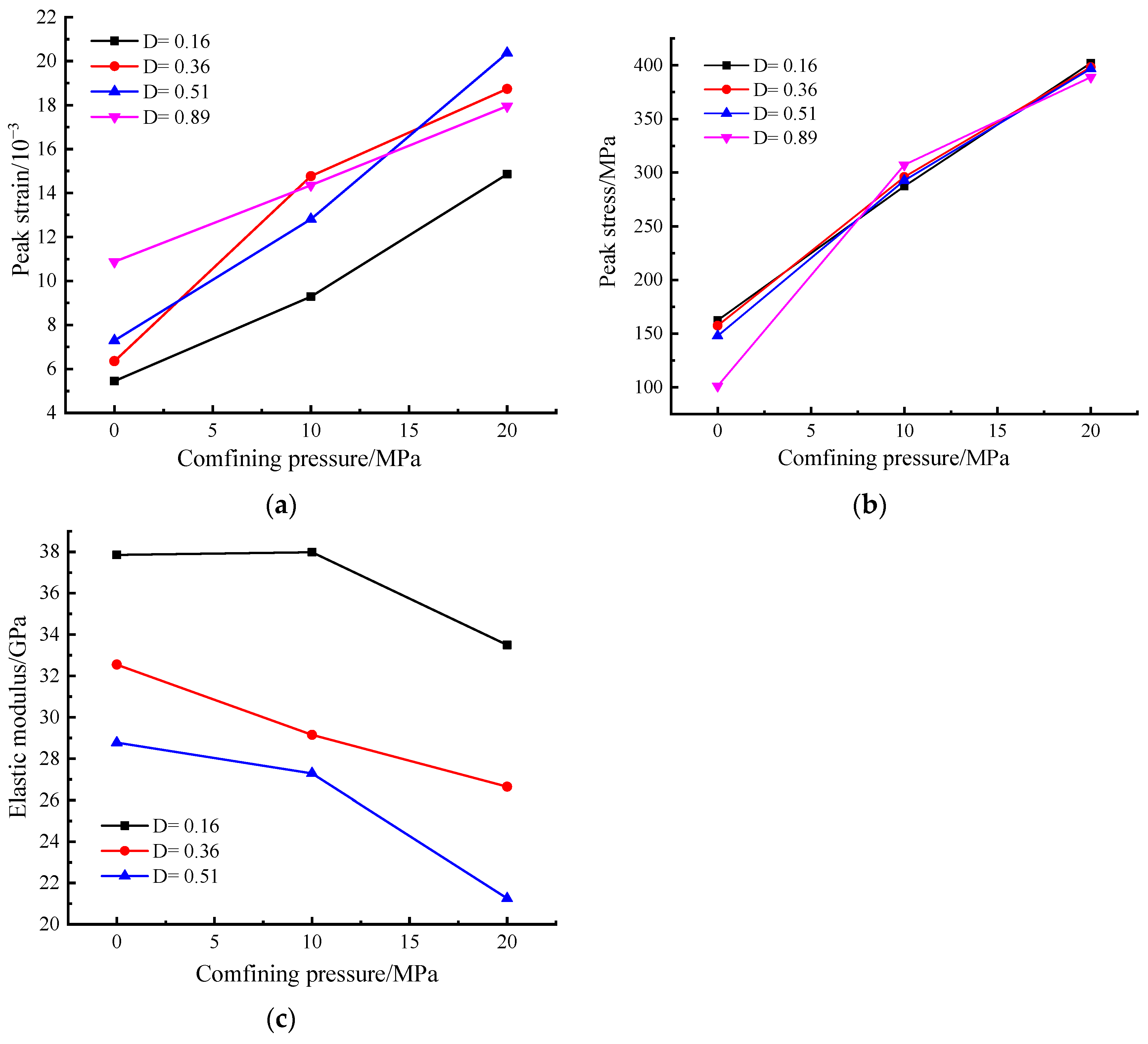
- With the increase in confining pressure, the peak stress and corresponding strain of rock samples with similar equivalent damage factors increase. However, compared with the same confining pressure rock specimens of different initial thermal damage found that when the confining pressure is the same, the greater the confining pressure, the difference in peak stress of different initial thermally damaged samples becomes smaller and smaller, when the confining pressure is 0 MPa, the maximum difference of peak stress is 6 MPa, but when the confining pressure is 10 MPa and 20 MPa, the peak stress is almost identical, and the difference of corresponding peak strain does not decrease with the increase in confining pressure, and is always stable between 0.006 and 0.007. The results show that the peak stress is sensitive to confining pressure and the peak strain is sensitive to the equivalent fracture damage factor.
- (2)
- For rocks with similar equivalent damage factors, the greater the confining pressure, the less the influence of equivalent damage factors inside the rock mass on the failure mode. The evolution of dissipated energy ratio of specimens with different initial thermal damage is similar in the compression deformation failure process under different confining pressures, and all specimens experience four stages, rapid increase → rapid decline → steady at a certain value → rapid rise. In addition, the proportion of dissipated energy of samples with equivalent damage factor D = 0.89 is significantly higher than that of other damaged samples, indicating that the development of internal cracks in granite samples is mutational, and the internal cracks in rock develop rapidly when the thermal stress reaches the threshold value of crack propagation.
- (3)
- Under the same fracture degree, the maximum energy dissipation changes greatly with the increase in confining pressure. Under the same confining pressure, the maximum energy dissipated during rock failure increases slowly first and then decreases rapidly with the increase in fracture degree. Taking 20 MPa as an example, the maximum dissipated energy density remains stable at 3.5–3.6 MJ∙m-3 at D = (0.4~0.5). Before this, the dissipated energy density increases monotonically, and then slowly decreases. Therefore, there is a maximum inflection point at the fissure D = (0.4~0.5). So, when the internal fracture degree of rock mass D = (0.4~0.5), it can be used as the discriminant basis for critical support in engineering support.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Sun, Z.; Xie, T.; Li, X.; Ranjith, P.G. Energy evolution characteristics of hard rock during triaxial failure with different loading and unloading paths. Eng. Geol. 2017, 228, 270–281. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, G.; Meng, X.; Zhang, R.; Dong, C.; Xu, W. Energy Analysis Method for Uniaxial Compression Test of Sandstone under Static and Quasi-Dynamic Loading Rates. Adv. Mater. Sci. Eng. 2021, 2021, 9933243. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, M.; Han, L.; Pu, H.; Nie, T. Effects of acoustic emission and energy evolution of rock specimens under the uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 2016, 49, 3873–3886. [Google Scholar] [CrossRef]
- Yan, Z.; Dai, F.; Zhu, J. Dynamic cracking behaviors and energy evolution of multi-flawed rocks under static pre-compression. Rock Mech. Rock Eng. 2021, 54, 5117–5139. [Google Scholar] [CrossRef]
- Yang, Y.S.; Cheng, W.; Zhang, Z.R.; Tian, H.Y.; Li, K.Y.; Huang, C.P. Energy Evolution Law of Marble Failure Process Under Different Confining Pressures Based on Particle Discrete Element Method. Front. Mater. 2021, 8, 665955. [Google Scholar] [CrossRef]
- Yang, D.; Hu, J.; Wen, G.; Zeng, P. Analysis of fracture deformation field and energy evolution of granite after high confining pressure cyclic load pre-damage. R. Soc. Open Sci. 2021, 8, 201966. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, Z.H.; Wang, C.S.; Liu, J.F. On acoustic emission and post-peak energy evolution in Beishan granite under cyclic loading. Rock Mech. Rock Eng. 2019, 52, 283–288. [Google Scholar] [CrossRef]
- Cook, N.G.W. The basic mechanics of rockbursts. J. S. Afr. Inst. Min. Metall. 1963, 64, 71–81. [Google Scholar]
- Walsh, J.B. Energy changes due to mining. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1977, 14, 25–33. [Google Scholar] [CrossRef]
- Salamon, M.D.G. Energy considerations in rock mechanics: Fundamental results. J. S. Afr. Inst. Min. Metall. 1984, 84, 233–246. [Google Scholar]
- Dai, B.; Zhao, G.Y.; Konietzky, H.; Wasantha, P.L.P. Experimental investigation on damage evolution behaviour of a granitic rock under loading and unloading. J. Cent. South Univ. 2018, 25, 1213–1225. [Google Scholar] [CrossRef]
- Dong, X.; Karrech, A.; Basarir, H.; Elchalakani, M.; Qi, C. Analytical solution of energy redistribution in rectangular openings upon in-situ rock mass alteration. Int. J. Rock Mech. Min. Sci. 2018, 106, 74–83. [Google Scholar] [CrossRef]
- Luo, J.A.; Wang, L.L. Study on Energy Evolution and Damage Constitutive Model of Sandstone under Cyclic Loading and Unloading. Appl. Sci. 2023, 13, 1690. [Google Scholar] [CrossRef]
- Pei, F.; Ji, H.; Zhang, T.; Su, X. Acoustic Emission Characteristics and Energy Evolution of Granite Subjected to Uniaxial Compression. IOP Conf. Ser. Earth Environ. Sci. 2019, 218, 012081. [Google Scholar] [CrossRef]
- Qin, T.; Duan, Y.; Sun, H.; Liu, H.; Wang, L. Energy evolution and acoustic emission characteristics of sandstone specimens under unloading confining pressure. Shock Vib. 2019, 2019, 1612576. [Google Scholar] [CrossRef]
- Wen, T.; Tang, H.; Wang, Y. Brittleness evaluation based on the energy evolution throughout the failure process of rocks. J. Pet. Sci. Eng. 2020, 194, 107361. [Google Scholar] [CrossRef]
- Yang, S.; Wang, J.; Ning, J.; Qiu, P. Experimental Study on Mechanical Properties, Failure Behavior and Energy Evolution of Different Coal-Rock Combined Specimens. Appl. Sci. 2019, 9, 4427. [Google Scholar] [CrossRef]
- Zhang, M.; Meng, Q.; Liu, S. Energy evolution characteristics and distribution laws of rock materials under triaxial cyclic loading and unloading compression. Adv. Mater. Sci. Eng. 2017, 2017, 5471571. [Google Scholar] [CrossRef]
- Wong, N.Y. Crack Coalescence in Molded Gypsum and Carrara Marble. Massachusetts Institute of Technology. 2008. Available online: https://dspace.mit.edu/handle/1721.1/42927 (accessed on 7 March 2023).
- Bobet, A. Fracture Coalescence in rock materials: Experimental observations and numerical predictions. Massachusetts Institute of Technology. 1997. Available online: https://www.researchgate.net/publication/279823677 (accessed on 8 March 2023).
- Huang, D.; Wang, J.; Liu, S. A comprehensive study on the smooth joint model in DEM simulation of jointed rock masses. Granul. Matter 2015, 17, 775–791. [Google Scholar] [CrossRef]
- Sagong, M.; Bobet, A. Coalescence of multiple flaws in a rock-model material in uniaxial compression. Int. J. Rock Mech. Min. Sci. 2002, 39, 229–241. [Google Scholar] [CrossRef]
- Park, C.H.; Bobet, A. Crack initiation, propagation and coalescence from frictional flaws in uniaxial compression. Eng. Fract. Mech. 2010, 77, 2727–2748. [Google Scholar] [CrossRef]
- Ferro, G.; Carpinteri, A. Effect of specimen size on the dissipated energy density in compression. J. Appl. Mech. 2008, 75, 041003. [Google Scholar] [CrossRef]
- Zhong, P.; Li, J.; Zhou, X.; Xiao, H.; Yue, S.; Zhang, P.; Wang, Y. Study of Energy Evolution Law and Damage Characteristics during Uniaxial Cyclic Loading and Unloading of Sandstone. Appl. Sci. 2022, 12, 9985. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Gong, X.F.; Gu, X.B. Mechanical Properties and Energy Evolution Law of Fractured Coal under Low Confining Pressure. Appl. Sci. 2022, 12, 12422. [Google Scholar] [CrossRef]
- Liu, X.Q.; Wang, G.; Wen, Z.; Wang, D.; Song, L.; Lin, M.; Chen, H. The Transient Unloading Response of a Deep-Buried Single Fracture Tunnel Based on the Particle Flow Method. Sustainability 2023, 15, 6840. [Google Scholar] [CrossRef]
- Duan, Y.W.; Zhang, G.H.; Qin, T. Analysis of Crack-Characteristic Stress and Energy Characteristics of Sandstone under Triaxial Unloading Confining Pressure. Appl. Sci. 2023, 13, 2671. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, M.; Zhang, Z.; Han, L.; Pu, H. Research on non-linear characteristics of rock energy evolution under uniaxial cyclic loading and unloading conditions. Environ. Earth Sci. 2019, 78, 650. [Google Scholar] [CrossRef]
- Pan, J.; Wu, X.; Guo, Q.; Xi, X.; Cai, M. Uniaxial experimental study of the deformation behavior and energy evolution of conjugate jointed rock based on AE and DIC methods. Adv. Civ. Eng. 2020, 2020, 8850250. [Google Scholar] [CrossRef]
- Ping, Q.; Zhang, C.; Su, H.; Zhang, H. Experimental study on dynamic mechanical properties and energy evolution characteristics of limestone specimens subjected to high temperature. Adv. Civ. Eng. 2020, 2020, 8875568. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, F. Energy evolution mechanism in process of Sandstone failure and energy strength criterion. J. Appl. Geophys. 2018, 154, 21–28. [Google Scholar] [CrossRef]
- Zhao, H.; Song, Z.; Zhang, D.; Liu, C.; Yu, B. True triaxial experimental study on mechanical characteristics and energy evolution of sandstone under various loading and unloading rates. Geomech. Geophys. Geo-Energy Geo-Res. 2021, 7, 22. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, S.; Sun, B. Energy evolution of rock under different stress paths and establishment of a statistical damage model. KSCE J. Civ. Eng. 2019, 23, 4274–4287. [Google Scholar] [CrossRef]
- Lu, J.; Yin, G.; Zhang, D.; Gao, H.; Li, C.; Li, M. True triaxial strength and failure characteristics of cubic coal and sandstone under different loading paths. Int. J. Rock Mech. Min. Sci. 2020, 135, 104439. [Google Scholar] [CrossRef]
- Zhang, J.; Song, Z.; Wang, S. Experimental investigation on permeability and energy evolution characteristics of deep sandstone along a three-stage loading path. Bull. Eng. Geol. Environ. 2021, 80, 1571–1584. [Google Scholar] [CrossRef]
- Zhang, L.; Cong, Y.; Meng, F.; Wang, Z.; Zhang, P.; Gao, S. Energy evolution analysis and failure criteria for rock under different stress paths. Acta Geotech. 2021, 16, 569–580. [Google Scholar] [CrossRef]
- Enfedaque, A.; Romero, H.L.; Gálvez, J.C. Fracture energy evolution of two concretes resistant to the action of freeze-thaw cycles. Mater. Constr. 2014, 64, 420–431. [Google Scholar] [CrossRef]
- Lin, B.; Liu, T.; Zou, Q.; Zhu, C.; Yan, F.; Zhang, Z. Crack propagation patterns and energy evolution rules of coal within slotting disturbed zone under various lateral pressure coefficients. Arab. J. Geosci. 2015, 8, 6643–6654. [Google Scholar]
- Matallah, M.; Farah, M.; Grondin, F.; Loukili, A.; Rozière, E. Size-independent fracture energy of concrete at very early ages by inverse analysis. Eng. Fract. Mech. 2013, 109, 1–16. [Google Scholar] [CrossRef]
- Wei, X.; Hou, Z.K. 3D Network Simulation of Deep Rock Joints Based on Borehole TV. J. Jilin Univ. Earth Sci. Edit. 2021, 51, 1605–1612. [Google Scholar]

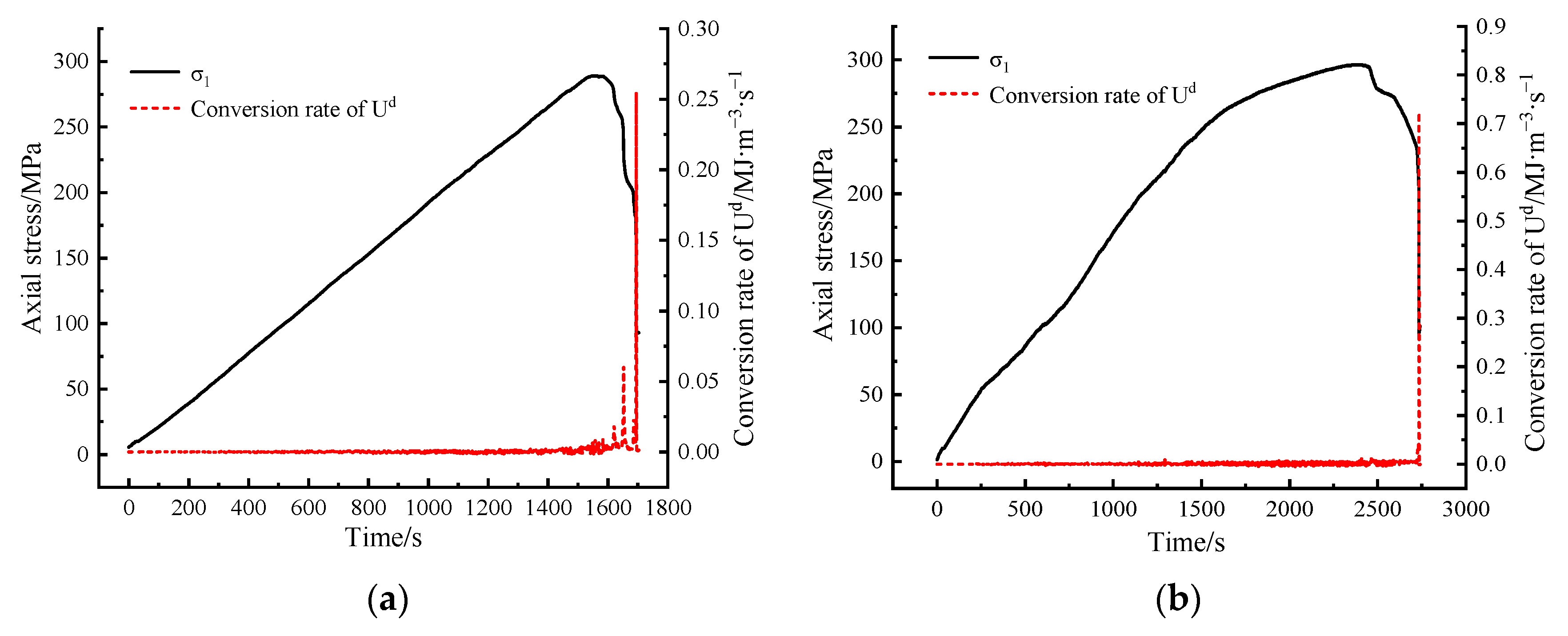
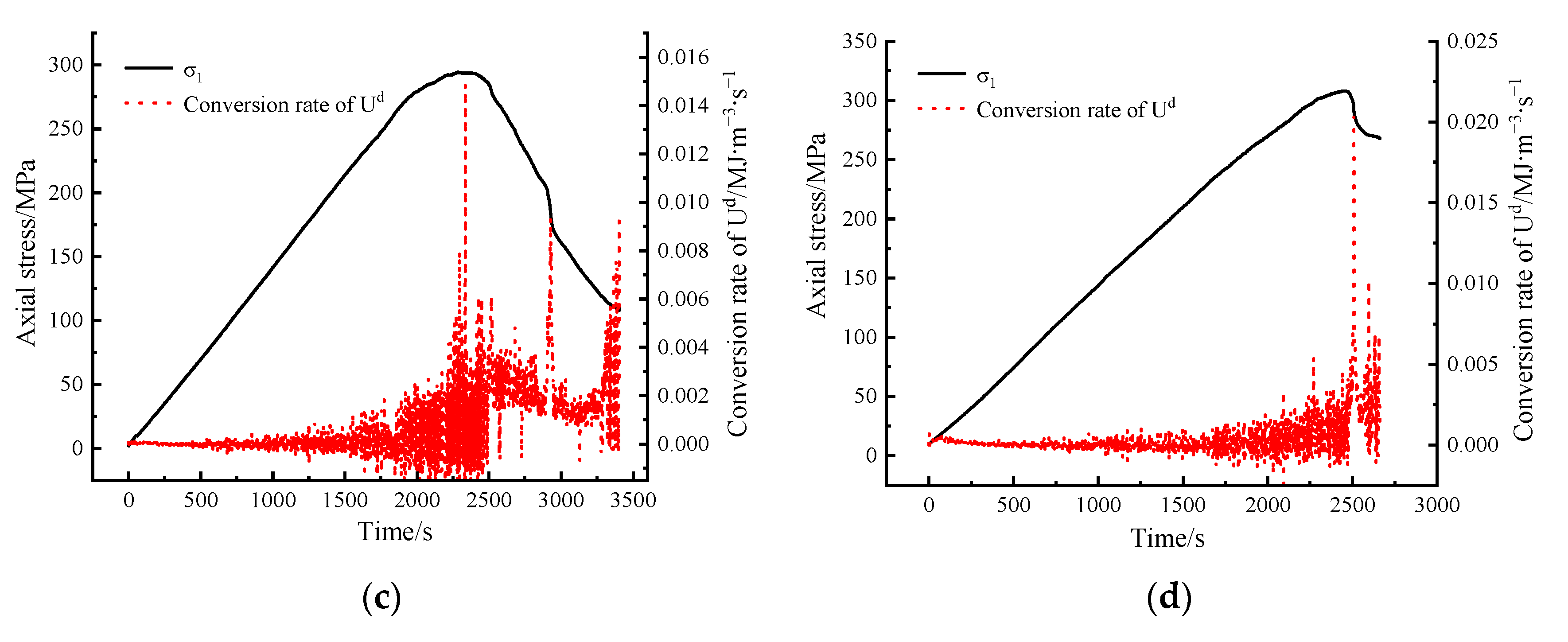
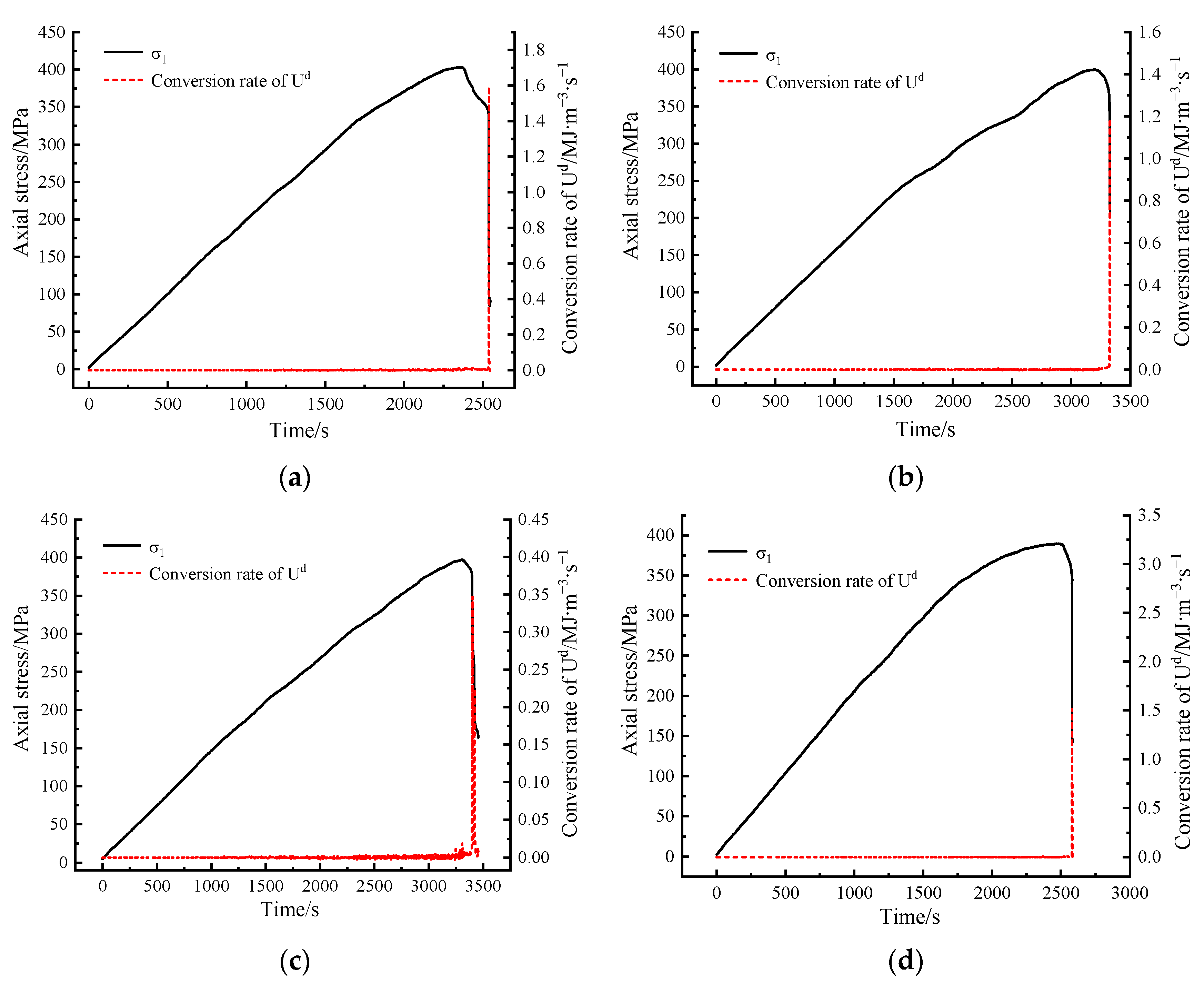
| Confining Pressure/MPa | Equivalent Damage Factor (D) | |||
|---|---|---|---|---|
| D = 0.16 | D = 0.36 | D = 0.51 | D = 0.89 | |
| 0 MPa |  |  |  |  |
| 10 MPa |  |  |  |  |
| 20 MPa |  |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Qiao, L.; Li, Q.; Yang, J. Study on Damage Behavior and Its Energy Distribution of Deep Granite at High-Temperature Conditions. Appl. Sci. 2023, 13, 6498. https://doi.org/10.3390/app13116498
Zhou M, Qiao L, Li Q, Yang J. Study on Damage Behavior and Its Energy Distribution of Deep Granite at High-Temperature Conditions. Applied Sciences. 2023; 13(11):6498. https://doi.org/10.3390/app13116498
Chicago/Turabian StyleZhou, Ming, Lan Qiao, Qingwen Li, and Jianming Yang. 2023. "Study on Damage Behavior and Its Energy Distribution of Deep Granite at High-Temperature Conditions" Applied Sciences 13, no. 11: 6498. https://doi.org/10.3390/app13116498
APA StyleZhou, M., Qiao, L., Li, Q., & Yang, J. (2023). Study on Damage Behavior and Its Energy Distribution of Deep Granite at High-Temperature Conditions. Applied Sciences, 13(11), 6498. https://doi.org/10.3390/app13116498






