Distributed GNE-Seeking under Partial Information Based on Preconditioned Proximal-Point Algorithms

Abstract

This paper proposes a distributed algorithm for games with shared coupling constraints based on the variational approach and the proximal-point algorithm. The paper demonstrates the effectiveness of the proximal-point algorithm in distributed computing of generalized Nash equilibrium (GNE) problems using local data and communication with neighbors in any networked game. The algorithm achieves the goal of reflecting local decisions in the Nash–Cournot game under partial-decision information while maintaining the distributed nature and convergence of the algorithm.

1. Introduction

The problem of finding a generalized Nash equilibrium (GNE) for networked systems has gained significant interest recently owing to its applicability to multi-agent decision-making scenarios, such as demand-side management in intelligent grids [1], demand response in competitive markets [2], and electric vehicle charging [3]. In such systems, the agents aim to minimize cost functions under joint feasibility constraints with non-cooperative settings. They cannot reduce their local costs by unilaterally changing their decisions but by relying on the decisions of the other agents. The GNE is a self-executing outcome, and once computed, all agents execute it to achieve their own minimum cost. In these systems, each user has a local cost function to minimize, which is a function of their own and other users’ decisions. Moreover, each user’s feasible decision set is coupled with other users’ decisions due to the limited network resources. A natural solution concept for such systems is the GNE, which captures the non-cooperative behavior of multiple interacting agents. A GNE is a vector of decisions such that no user can reduce their local cost by unilaterally deviating from it, given the decisions of other users. Hence, a GNE is a self-enforcing outcome that all agents will implement once computed, as it achieves their individual minimum costs.

To compute GNE introspectively, most algorithms for finding Nash equilibrium require a central information center to collect and store all game information such as cost functions, coupling constraints, and feasible local sets in a traditional computing environment. However, this approach is not suitable for large-scale network games because it is difficult to observe the true decisions of all other players in this type of game. Additionally, having a central coordinator node may be impractical due to technical, geographical, or game-related reasons. In this case, each player needs to compute their local decision corresponding to GNE in a distributed way by utilizing their local objective function, local feasible set, and possibly local data related to the coupling constraints and communicating with their neighbors. Therefore, our goal is to develop a distributed algorithm that estimates the strategies of all other agents only by communicating with adjacent agents. This algorithm can achieve the goal of reflecting local decisions in the absence of global information and eventually reconstructing actual value.

The proximal-point algorithm has been widely used in distributed computing of GNE problems. In our study, we demonstrate that it can achieve the goal of reflecting local decisions in the absence of global information while maintaining the distributed nature and convergence of the algorithm. That is to say, in the absence of a central coordinator, the generalized Nash equilibrium point is calculated by each participant using local information and communication with neighbors. This approach enables each player to compute a local decision corresponding to GNE by utilizing its local objective function, local feasible set, and possibly local data related to the coupling constraints and communicating with its neighbors. By continuously updating the proximal point, the proximal-point algorithm can achieve the convergence of restricted monotone and Lipschitz continuous pseudo-gradient games under appropriate fixed step size conditions. Our study proposes a new distributed GNE algorithm for games with shared biomimetic coupling constraints, which is based on the variational GNE approach and the proximal-point algorithm. Our results demonstrate the effectiveness of the proposed algorithm in achieving GNE in a distributed manner in the presence of shared constraints.

1.1. Literature Review

The research of GNE was initiated by the seminal works of [4,5]. In recent years, the computation of distributed GNE in monotone games has received considerable interest. However, most existing studies rely on the assumption that every agent in the system has access to the decision information of other agents, i.e., by employing a central node coordinator to orchestrate the information processing. The initial approach was based on the variational inequality method [6]. The variational inequality framework for generalized Nash equilibrium problems established in [6] has been extended to more general settings, such as time-dependent or stochastic problems in [7]. Ref. [8] developed a Tikhonov-regularized primal-dual algorithm, and [9] devised a primal-dual gradient method, which can reduce the compensation and assumed that it can acquire the decisions of all adversaries that influence each cost. In ref. [10], a payoff-based GNE algorithm was introduced, which has a diminishing step size and converges to a class of convex games. Recently, an operator-splitting method has emerged as a very powerful design technique, which ensures global convergence and features a fixed step size and succinct convergence analysis. However, most GNE application scenarios are aggregative games, such as [3,11,12,13,14]. In refs. [12,13], the algorithms are semi-decentralized, requiring a central node to disseminate the common multipliers and aggregate variables, thus resulting in a star topology. In ref. [14], this is relaxed by a projection gradient algorithm based on two-layer consensus, both of which are only suitable for aggregative games.

In networked non-cooperative games, a distributed forward-backward operator-splitting algorithm for seeking the GNE has been proposed by Yi and Pavel [15], based on the convex analysis framework of Bauschke and Combettes [16]. Under partial information, the algorithm requires only local objective function, feasible set, and block of affine constraints for each agent. It also introduces a local estimate of all agents’ decisions. They further extended their algorithm to an asynchronous setting by using auxiliary variables associated with Graphology [17]. In this setting, each agent uses private data and delay information from their neighbors’ latency information to iterate asynchronously. They proved the convergence and effectiveness of their algorithm under mild assumptions. Ref. [18] investigated a generalized Nash equilibrium problem in which players are modeled as nodes of a network and each player’s utility function depends on its own and its neighbors’ actions, and derived a variational decomposition of the game under a quadratic reference model with shared constraints, which is illustrated with numerical examples. Bianchi et al. [19] has developed a novel algorithm that differs from the existing projective pseudo gradient dynamics in that it is fully distributed, one-layer, and uses a proximal best response with consensus terms. It can overcome the limitations of double-layer iterations or conservative step sizes of the gradient-based methods. It can also extend the applicability of the proximal point method by analyzing the restricted monotonicity property. Pavel [20] applied a preconditioned proximal point algorithm (PPPA) that decomposes the merit-seeking task into Nash equilibrium (NE) computation of regularised subgame sequences based on local information. The PPPA also performs distributed updates of multipliers and auxiliary variables, which require multiple communications among agents to solve the subgame. For games with general coupling costs and affine coupling constraints, [15,21] adopt operator methods to perform distributed decentralized GNE optimization: forward-backward optimization algorithm for strongly monotone games [15] and preconditioned proximal optimization algorithm for monotone games [21]. The players exchange local multipliers over the network with arbitrary topology, but each user can access all the agent decisions that affect its cost, thus obtaining complete decision information.

1.2. Contributions

Compared with most existing distributed optimization algorithms, the main contributions of this paper are summarized as follows:

• The proposal of a GNE algorithm for games with shared biomimetic coupling constraints. The algorithm is based on the variational GNE approach and the proximal-point algorithm, and is improved by introducing two choice matrices to enhance its accuracy, as in [22,23], where we design a novel preconditioning matrix to distribute the computation and obtain a single-layer iteration. Each player has an auxiliary variable to estimate the decisions of other agents. The algorithm is distributed, where each player only utilizes its local objective function, local feasible set, and local data related to the coupling constraints, and there is no centralized coordinator to update and propagate dual variables.
• An original dual analysis of the Karush–Kuhn–Tucker (KKT) conditions of the variational inequality (VI) is conducted, which introduces a local copy of the multiplier and an auxiliary variable for each player. It is observed that the KKT conditions mandate consensus among all agents on the multiplier for shared constraints. By reformulating the original problem as finding the zero point of a monotone operator that includes the Laplacian matrix of the connected graph, the consistency of local multipliers is enhanced.

This paper presents global and distributed methods for finding GNE in games with shared affine coupling constraints under partial decision information. Section 2 introduces the game model and formulates the GNE problem. Section 3 proposes a global GNE-seeking method based on the proximal-point algorithm with global information. Section 4 develops a distributed GNE-finding method with partial information and proves its convergence and implementation feasibility. Section 5 illustrates the performance of our methods through numerical simulations. Finally, Section 6 concludes the paper and discusses some future work directions.

2. Game Formulation

We study a non-cooperative generalized game with a crowd of agents. Each agent $i\in \mathcal{I}(\mathcal{I}=1,\dots ,N)$ has a local decision set ${\Omega }_i\subseteq {\mathbb{R}}^{n_i}$ and chooses its own decision $x_i\in {\Omega }_i$, where $\mathbb{R}$ is the set of real numbers and $n_i$ is the dimension of agent i’s decision-making. The global decision space is $\Omega ={\prod }_{i=1}^N{\Omega }_i\subset {\mathbb{R}}^n$ where $n={\displaystyle \sum _{i=1}^N}{n}_i$ and the stacked vector of all agents’ decisions is $\mathit{x}=col\left({\left(x_i\right)}_{i\in \mathcal{I}}\right)$. Let ${\mathit{x}}_{-i}=col\left({\left(x_j\right)}_{j\in \mathcal{I},j\ne i}\right)$ denote the decision profile of all other agents except for agent i, then $\mathit{x}=\left(x_i,{\mathit{x}}_{-i}\right)$. The feasible set for any agent depends on the coupling constraints shared with other agents and their own decisions. Each agent aims to minimize its objective function over this feasible set as follows:

$$\begin{array}{c}\hfill \underset{x_i}{min}{J}_i\left(x_i,{\mathit{x}}_{-i}\right):=f_i\left(x_i,{\mathit{x}}_{-i}\right)+g_i\left(x_i\right).\end{array}$$

(1)

The objective function (1) can describe how multiple participants can optimize their interests in a non-cooperative situation while being affected by sharing constraints. This model can be applied to a variety of practical scenarios, such as smart grids, competitive markets, and electric vehicle charging.

Assumption 1. 

The cost functions $f_i$ and $g_i$ of each agent $i\in \mathcal{I}$ are convex. The common cost function $f_i$ is continuously differentiable and the local idiosyncratic cost function $g_i$ is lower semicontinuous. ${\Omega }_i$ is bounded and closed for any $i\in \mathcal{I}$.

We denote $A:=\left[A_1,\dots ,A_N\right]$ and $b:={\sum }_{i=1}^N{b}_i$, where $A_i\in {\mathbb{R}}^{m\times n_i}$ and $b_i\in {\mathbb{R}}^m$ are local parameters. By the affine function above, the set of overall feasible decisions via affine coupling constraints and cost functions is denoted as follows:

$$\mathcal{X}:=\Omega \bigcap \left\{\mathit{x}\in {\mathbb{R}}^{nN}\mid A\mathit{x}-b\le {\mathbf{0}}_m\right\}\subseteq {\mathbb{R}}^{nN},$$

(2)

where $\mathcal{X}$ is a closed and convex set of decisions that is nonempty. It is used to simulate some phenomena in nature, such as group behavior, competition, and cooperation. Such constraints can reflect the interactions and dependencies among participants, making the game more complex and interesting.

Assumption 2. 

Slater’s constraint qualification holds for the collective set $\mathcal{X}$. Therefore, each agent $i\in \mathcal{I}$ in the generalized game tries to solve this interdependent optimization problem as follows:

$$\forall i\in \mathcal{I}:\left\{\begin{array}{cc}\underset{x_i\in {\Omega }_i}{min}& J_i\left(x_i,{\mathit{x}}_{-i}\right)\hfill \\ \mathrm{s}.\mathrm{t}.& A_i{x}_i\le b-{\displaystyle \sum _{j\ne i}^N}{A}_j{x}_j.\hfill \end{array}\right.$$

(3)

To obtain the primal-dual characterization of each agent $i\in \mathcal{I}$, we define a Lagrangian function with dual variable multiplier ${\lambda }_i\in {\mathbb{R}}_{+}^m$ as follows:

$$\begin{array}{c}\hfill {\mathcal{L}}_i\left(x_i,{\mathit{x}}_{-i};{\lambda }_i\right):=f_i\left(x_i,{\mathit{x}}_{-i}\right)+g_i\left(x_i\right)+{\lambda }_i^{\mathrm{T}}\left({\displaystyle \sum _{i=1}^N}\left(A_i{x}_i-b_i\right)\right).\end{array}$$

(4)

We call a decision $x^{*}\in \mathcal{X}$ that satisfies (3) a GNE of the game. This implies that for any agent $i\in \mathcal{I}$,

$$J_i\left(x_i^{*},{\mathit{x}}_{-i}^{*}\right)\le inf\left\{J_i\left(y,{\mathit{x}}_{-i}^{*}\right)\mid y\in {\mathcal{X}}_i\left({\mathit{x}}_{-i}^{*}\right)\right\},$$

(5)

where ${\mathcal{X}}_i\left({\mathit{x}}_{-i}\right):=\left\{y_i\in {\Omega }_i\mid A_i{y}_i\le b-{\displaystyle \sum _{j\ne i}^N}{A}_j{x}_j\right\}$.

If $x_i^{*}\in {\Omega }_i$ satisfies the KKT conditions below with ${\lambda }_i^{*}\in {\mathbb{R}}_{+}^m$, then it is an optimal solution to (3).

$$\forall i\in \mathcal{I}:\left\{\begin{array}{c}{\nabla }_{x_i}{\mathcal{L}}_i\left(x_i^{*},{\mathit{x}}_{-i}^{*}\right)=\mathbf{0}\hfill \\ 〈{\lambda }_i^{*},A{x}^{*}-b〉=\mathbf{0}\hfill \\ -\left(A{x}^{*}-b\right)\ge \mathbf{0}\hfill \\ {\lambda }_i^{*}\ge 0.\hfill \end{array}\right.$$

(6)

We reformulate the KKT condition using the normal cone operator as follows:

$$\left\{\begin{array}{c}0\in {\nabla }_{x_i}{f}_i\left(x_i^{*},x_{-i}^{*}\right)+\partial g_i\left(x_i^{*}\right)+A_i^{\mathrm{T}}{\lambda }_i^{*}\hfill \\ 0\in {\displaystyle \sum _{i=1}^N}{A}_i{x}_i^{*}-{\displaystyle \sum _{i=1}^N}{b}_i-{\mathrm{N}}_{{\mathbb{R}}_{⩾0}^m}\left({\lambda }_i^{*}\right).\hfill \end{array}\right.$$

(7)

We denote the pseudogradient of $f_i\left(x_i,{\mathit{x}}_{-i}\right)$ as $\mathbb{F}\left(\mathit{x}\right)=col{\left({\nabla }_{x_i}{f}_i\left(x_i,{\mathit{x}}_{-i}\right)\right)}_{i\in \mathcal{I}}\in {\mathbb{R}}^n$. Denote the pseudogradient of $g_i\left(x_i\right)$ as $g\left(\mathit{x}\right)={\displaystyle \sum _{i=1}^N}{g}_i\left(x_i\right)$.

Let $\mathsf{\lambda }=col{\left({\lambda }_i\right)}_{i\in N}$ denote the vector of Lagrangian multipliers associated with each agent $i\in N$. A variational GNE is a decision ${\mathit{x}}^{*}\in \mathcal{X}$ that satisfies the variational inequality problem $\mathrm{VI}(\mathbb{F},\mathcal{X})$ and has equal Lagrangian multipliers (${\lambda }_1=\dots ={\lambda }_N$).

$$\begin{array}{cc}\hfill & \mathrm{find}{\mathit{x}}^{*}\in \mathcal{X}=\left\{\mathit{x}\in {\mathbb{R}}^n\mid {\displaystyle \sum _{i=1}^N}{A}_i{x}_i\le {\displaystyle \sum _{i=1}^N}{b}_i\right\},\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.〈\mathbb{F}\left({\mathit{x}}^{*}\right),\mathit{x}-{\mathit{x}}^{*}〉+g\left(\mathit{x}\right)\ge 0,\forall \mathit{x}\in \mathcal{X}.\hfill \end{array}$$

(8)

Under Assumption 1, $J_i$ is a continuous and convex function, and ${\Omega }_i$ is a bounded local decision set. These ensure that $\mathrm{VI}(\mathbb{F},\mathcal{X})$ has a solution. Let ${\mathit{x}}^{*}$ be such a solution. Then it satisfies (7) with equal Lagrange multipliers ${\mathsf{\lambda }}^{*}$. Therefore, ${\mathit{x}}^{*}$ is a variational GNE for (3).

3. Iterative Algorithms with Global Information

We propose a distributed algorithm based on preconditioned proximal-point algorithms that use full-decision information. This means that every agent can access the decisions of all other agents that affect its local objective function directly.

3.1. Communication Graph

Let $\left|\mathcal{N}\right|=N$ and $\left|\mathcal{E}\right|=M$. We define ${\mathcal{E}}_i$ as the set of edges adjacent to i, which consists of ${\mathcal{E}}_{i^{\mathrm{in}}}$ (the incoming edges) and ${\mathcal{E}}_{i^{\mathrm{out}}}$ (the outgoing edges). Let $W={\left[w_{i,j}\right]}_{i,j\in \mathcal{I}}\in {\mathbb{R}}^{N\times N}$ be the symmetric weight matrix of $\mathcal{G}$, where $w_{i,j}>0$ if $(i,j)\in \mathcal{E}$ and $w_{i,j}=0$ otherwise. We also set $w_{i,i}=0$ for all agents. The Laplacian matrix of $\mathcal{G}$ is denoted by $L:=D-W$, where $D:=diag\left({\left(d_i\right)}_{i\in \mathcal{I}}\right)$ is the degree matrix and $d_i:={\sum }_{j=1}^N{w}_{i,j}$ for all $i\in \mathcal{I}$.

Assumption 3. 

$\mathcal{G}$ is a connected and undirected graph.

3.2. Algorithm Development

Assumption 4. 

$\mathbb{F}\left(\mathit{x}\right)$ is a μ-strongly monotone function, meaning that $\langle \mathbb{F}\left(\mathit{x}\right)-\mathbb{F}\left(\mathit{y}\right),\mathit{x}-\mathit{y}\rangle \ge {\mu |\mathit{x}-\mathit{y}|}_2^2,\forall \mathit{x},\mathit{y}\in \Omega$, and a ${\theta }_0$-Lipschitz continuous function, implying that ${|\mathbb{F}\left(\mathit{x}\right)-\mathbb{F}\left(\mathit{y}\right)|}_2\le {\theta }_0{|\mathit{x}-\mathit{y}|}_2,\forall \mathit{x},\mathit{y}\in \Omega$.

The strong monotonicity of $\mathbb{F}$ implies that a v-GNE exists and is unique. We can write the variational problem for the original game problem as follows:

$$\begin{array}{cc}\hfill \underset{x\in {\mathbb{R}}^n}{min}& 〈\mathbb{F}\left({\mathit{x}}^{*}\right),\mathit{x}〉+g\left(\mathit{x}\right),\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& {\displaystyle \sum _{i=1}^N}{A}_i{x}_i\le {\displaystyle \sum _{i=1}^N}{b}_i.\hfill \end{array}$$

(9)

The objective function is defined by the following Lagrangian function:

$$\begin{array}{c}\hfill \tilde{\mathcal{L}}\left(\mathit{x},{\lambda }_g\right):=〈\mathbb{F}\left({\mathit{x}}^{*}\right),\mathit{x}〉+g\left(\mathit{x}\right)+{\lambda }_g^{\mathrm{T}}\left({\displaystyle \sum _{i=1}^N}\left(A_i{x}_i-b_i\right)\right).\end{array}$$

(10)

Let ${\lambda }_g\in {\mathbb{R}}^m$ be a global Lagrangian multiplier. To design distributed optimization algorithms, we impose the consistency constraints ${\lambda }_i={\lambda }_j,\forall (i,j)\in \mathcal{E}$, i.e., $\left(L\otimes I_m\right)\mathsf{\lambda }=0$, where $I_m$ is an identity matrix of order m. Define $\mathbb{G}\left(\mathit{x}\right)=col{\left(\partial g_i\left(x_i\right)\right)}_{i\in \mathcal{I}}\in {\mathbb{R}}^n$, $\mathsf{\lambda }=col\left({\lambda }_1,\dots ,{\lambda }_N\right)=col\left({\lambda }_i\right)\in {\mathbb{R}}^m$, $\mathit{A}=\left[A_1,\dots ,A_N\right]\in {\mathbb{R}}^{m\times n}$, and $\mathbf{b}=col\left(b_i\right)\in {\mathbb{R}}^m$. Then,

$$\begin{array}{c}\hfill {\mathcal{L}}_1(\mathit{x},\mathsf{\lambda }):=〈\mathbb{F}\left({\mathit{x}}^{*}\right),\mathit{x}〉+g\left(\mathit{x}\right)+{\mathsf{\lambda }}^{\mathrm{T}}(\mathit{A}\mathit{x}-\mathbf{b}).\end{array}$$

(11)

Its corresponding saddle point problem would be

$$\begin{array}{cc}\hfill \underset{\lambda }{max}\underset{\mathit{x}}{min}& 〈\mathbb{F}\left({\mathit{x}}^{*}\right),\mathit{x}〉+g\left(\mathit{x}\right)+{\mathsf{\lambda }}^{\mathrm{T}}(\mathit{A}\mathit{x}-\mathbf{b}),\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(L\otimes I_m\right)\mathsf{\lambda }=0.\hfill \end{array}$$

(12)

Let $\mathbf{L}=\left(L\otimes I_m\right)$, $\mathbf{W}=\left(W\otimes I_m\right)$ and $\mathbf{D}=\left(D\otimes I_m\right)$, the Lagrangian function that defines this saddle point problem is ${\mathcal{L}}_2(\mathit{x},\mathsf{\lambda },\mathit{z})=〈\mathbb{F}\left({\mathit{x}}^{*}\right),\mathit{x}〉+g\left(\mathit{x}\right)+{\mathsf{\lambda }}^{\mathrm{T}}(\mathit{A}\mathit{x}-\mathbf{b})+{\mathit{z}}^{\mathrm{T}}\mathbf{L}\mathsf{\lambda }$. The optimal conditions for this problem are obtained by sequentially finding the partial derivatives of the variables $\mathit{x}$, $\mathit{y}$, and $\mathit{z}$ as follows:

$$\left\{\begin{array}{c}0\in \mathbb{F}\left(\mathit{x}\right)+\mathbb{G}\left(\mathit{x}\right)+{\mathit{A}}^{\mathrm{T}}\mathsf{\lambda }\hfill \\ 0=\mathbf{L}\mathsf{\lambda }\hfill \\ 0\in \mathbf{b}+\mathbf{L}\mathsf{\lambda }+{\mathrm{N}}_{{\mathbb{R}}_{\ge 0}^{Nm}}\left(\mathsf{\lambda }\right)-\mathit{A}\mathit{x}-\mathbf{L}\mathit{z}.\hfill \end{array}\right.$$

(13)

It follows from Lagrange’s dual theorem that the variational problem has an optimal solution ${\mathit{x}}^{*}=\left(x_i^{*},{\mathit{x}}_{-i}^{*}\right)$ only when ${\lambda }_g^{*}\in {\mathbb{R}}^m$ satisfies the KKT conditions (13).

Lemma 1. 

If Assumptions 1–3 hold, then (13) implies (7).

Let $v=col(\mathit{x},\mathit{z},\mathsf{\lambda })$ and consider the following operator:

$$\mathcal{A}\left[\begin{array}{c}\mathit{x}\\ \mathit{z}\\ \mathsf{\lambda }\end{array}\right]=\left[\begin{array}{c}\mathbb{F}\left(\mathit{x}\right)\\ \mathbf{0}\\ \mathbf{b}\end{array}\right]+\left[\begin{array}{c}\mathbb{G}\left(\mathit{x}\right)\\ \mathbf{0}\\ N_{{\mathbb{R}}_{\ge 0}^{Nm}}\left(\mathsf{\lambda }\right)\end{array}\right]+\left[\begin{array}{c}{\mathit{A}}^{\mathrm{T}}\mathsf{\lambda }\\ \mathbf{L}\mathsf{\lambda }\\ -\mathit{A}\mathit{x}-\mathbf{L}\mathit{z}\end{array}\right].$$

(14)

We regard the iterative algorithm as a special case of proximal-point algorithms (PPA) [16] for finding a zero of $\mathcal{A}$. The general form of PPA can be written as

$$v^{k+1}\in {\mathrm{J}}_{\mathcal{A}}\left(v^k\right),$$

(15)

where ${\mathrm{J}}_{\mathcal{A}}\left(v^k\right)\ne ⌀$.

We apply the interaction rule (9) to the operator ${\Phi }^{-1}\mathcal{A}$, where $\Phi$ is defined as the following:

$$\Phi =\left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& -{\mathbf{A}}^{\mathrm{T}}\\ \mathbf{0}& \mathbf{0}& -\mathbf{L}\\ -\mathbf{A}& -\mathbf{L}& \mathbf{0}\end{array}\right]+\left[\begin{array}{ccc}{\alpha }^{-1}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\tau }^{-1}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\gamma }^{-1}\end{array}\right].$$

(16)

We choose the step sizes $\alpha =diag\left({\alpha }_i{I}_{n_i}\right)$, $\tau =diag\left({\tau }_i{I}_m\right)$ and $\gamma =diag\left({\gamma }_i{I}_m\right)$ such that $\Phi >0$.The next lemma provides sufficient conditions for $\Phi >0$ based on Gershgorin’s circle theorem.

Lemma 2. 

For any agent $i\in \mathcal{I}$ and any $\delta >0$, the preconditioning matrix Φ in (16) is positive definite if

$$\begin{array}{cc}\hfill & 0<{\alpha }_i\le {\left(\underset{j\in \left\{1,\dots ,n_i\right\}}{max}{\displaystyle \sum _{k=1}^m}\left|{\left[A_i^{\top }\right]}_{jk}\right|+\delta \right)}^{-1},\hfill \\ \hfill & 0<{\tau }_i\le {\left(2d_i+\delta \right)}^{-1},\hfill \\ \hfill & 0<{\gamma }_i\le {\left(\underset{j\in \{1,\dots ,m\}}{max}{\displaystyle \sum _{k=1}^{n_i}}\left|{\left[A_i\right]}_{jk}\right|+2d_i+\delta \right)}^{-1}.\hfill \end{array}$$

(17)

Assuming that $\Phi >0$ for all chosen step sizes, we can state the following results.

Lemma 3. 

The iterative algorithm is equivalent to the following:

$$(\forall k\in \mathbb{N})v^{k+1}\in {\mathrm{J}}_{{\Phi }^{-1}\mathcal{A}}\left(v^k\right),$$

(18)

where $\mathcal{A}$ is given by (14), Φ is given by (16).

Proof of Lemma 3. 

We use the definition of the inverse operator and obtain that

$$\begin{array}{cc}\hfill & v^{k+1}\in {\left(\mathrm{Id}+{\Phi }^{-1}\mathcal{A}\right)}^{-1}\left(v^k\right)\hfill \\ \hfill \iff & \mathbf{0}\in {\Phi }^{-1}\mathcal{A}\left(v^{k+1}\right)-v^k+v^{k+1}\hfill \\ \hfill \iff & \mathbf{0}\in \Phi \left(v^{k+1}-v^k\right)+\mathcal{A}\left(v^{k+1}\right).\hfill \end{array}$$

(19)

Substituting $\mathcal{A}$ and $\Phi$ into (19) and simplifying them, we obtain that

$$\begin{array}{cc}\hfill & {\mathit{x}}_{k+1}+\alpha \mathbb{F}\left({\mathit{x}}_{k+1}\right)+\alpha G\left({\mathit{x}}_{k+1}\right)=-\alpha {\mathit{A}}^{\mathrm{T}}{\mathsf{\lambda }}_k+{\mathit{x}}_k,\hfill \\ \hfill & {\mathit{z}}_{k+1}=-\tau \mathbf{L}{\mathsf{\lambda }}_k+{\mathit{z}}_k,\hfill \\ \hfill & {\mathsf{\lambda }}_{k+1}+{\mathrm{N}}_{{\mathbb{R}}_{\ge 0}^{Nm}}\left({\mathsf{\lambda }}_{k+1}\right)=-\gamma \mathit{A}{\mathit{x}}_k-\gamma \mathbf{L}{\mathit{z}}_k+{\mathsf{\lambda }}_k+2\gamma \mathit{A}{\mathit{x}}_{k+1}+2\gamma \mathbf{L}{z}_{k+1}-\gamma \mathbf{b}.\hfill \end{array}$$

(20)

Using the definition of the proximal operator [16], we can write (20) as

$$\begin{array}{cc}\hfill & {\mathit{x}}_{k+1}=arg\underset{x}{min}\left(\frac{1}{2}{∥\mathit{x}-{\mathit{x}}_k∥}^2+〈\mathit{x},\alpha {\mathit{A}}^{\mathrm{T}}{\mathsf{\lambda }}_k〉+\alpha f\left(\mathit{x}\right)+\alpha g\left(\mathit{x}\right)\right),\hfill \\ \hfill & {\mathit{z}}_{k+1}=-\tau \mathbf{L}{\mathsf{\lambda }}_k+{\mathit{z}}_k,\hfill \\ \hfill & {\mathsf{\lambda }}_{k+1}={proj}_{{\mathbb{R}}_{\ge 0}^{Nm}}({\mathsf{\lambda }}_k-\gamma \mathit{A}{\mathit{x}}_k-\gamma \mathbf{L}{\mathit{z}}_k+2\gamma \mathit{A}{\mathit{x}}_{k+1}+2\gamma \mathbf{L}{\mathit{z}}_{k+1}-\gamma \mathbf{b}).\hfill \end{array}$$

(21)

   □

4. Distributed Algorithm with Partial Information

In a distributed setting, it is challenging to access the decisions of all other agents requiring a central coordinator to collect and deliver information from all participants, as assumed in the previous section. The global information assumptions in Section 3 are relaxed in this section, allowing each participant to iteratively update their decisions, multipliers, and auxiliary variables using only their own local information and the estimates exchanged with their neighbors. Therefore, this section proposes a distributed GNE-seeking algorithm that uses partial information based on the preconditioned proximal-point algorithm.

4.1. Algorithm Development

This section presents an algorithm for GNE-seeking in game (3) in a fully distributed manner.

Each agent i has a cost function $J_i$ and a feasible set ${\Omega }_i$ but does not know the full state $x_{-i}$ of other agents. Agent i can only exchange information with its neighboring agents over a network $\mathcal{G}(\mathcal{I},\mathcal{E})$. The edge $(i,j)$ belongs to $\mathcal{E}$ if agents i and j can exchange information mutually. ${\mathit{x}}^i:=col\left({\left({\mathit{x}}_j^i\right)}_{j\in \mathcal{I}}\right)\in {\mathbb{R}}^n$ is defined as agent i’s estimate of agent j’s decision. Then ${\mathit{x}}_i^i:=x_i$ and ${\mathit{x}}_{-i}^j:=col\left({\left({\mathit{x}}_{\ell }^j\right)}_{\ell \in \mathcal{I}\backslash \left\{i\right\}}\right)$ denotes j’s estimate of all other agents except i. If ${\mathit{x}}^i={\mathit{x}}^j$, we can replace the cost function of agent i with $J_i\left({\mathit{x}}_i^i,{\mathit{x}}_{-i}^i\right)$. Then, we equivalently transform the game (3) as the following:

$$\begin{array}{cc}\underset{x^i}{\min }\hfill & J_i\left({\mathit{x}}_i^i,{\mathit{x}}_{-i}^i\right)=f_i\left({\mathit{x}}_i^i,{\mathit{x}}_{-i}^i\right)+g_i\left({\mathit{x}}_i^i\right),\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & {\mathit{x}}_i^i\in {\tilde{\mathcal{X}}}_i,\hfill \\ \hfill & {\mathit{x}}^i={\mathit{x}}^j,\forall j\in \mathcal{I}.\hfill \end{array}$$

(22)

It is worth noting that problems (3) and (22) are equivalent under a certain condition. We will explain this point below.

Let ${\tilde{\mathcal{X}}}_i=\left\{x\in {\Omega }_i\mid A_i{x}_i^i+{\displaystyle \sum _{j\ne i}}{A}_j{x}_j^i\le {\displaystyle {\displaystyle \sum _{i=1}^m}}{b}_i\right\}$ be the set of feasible solutions for agent i under a consistency constraint. Then, agent i’s cost function $J_i$ only depends on its own local information ${\mathit{x}}^i$.

We introduce matrices ${\mathcal{R}}_i$ and ${\mathcal{S}}_i$ to develop a distributed algorithm that uses partial decision information for game (22).

$${\mathcal{R}}_i:=\left[\begin{array}{ccc}{\mathbf{0}}_{n_i\times n_{<i}}\hfill & I_{n_i}\hfill & {\mathbf{0}}_{n_i\times n_{>i}}\hfill \end{array}\right],$$

(23)

$${\mathcal{S}}_i:=\left[\begin{array}{ccc}{I}_{n<i}& {\mathbf{0}}_{n<i\times n_i}& {\mathbf{0}}_{n<i\times n>i}\\ {\mathbf{0}}_{n>i\times n<i}& {\mathbf{0}}_{n>i\times n_i}& I_{n>i}\end{array}\right].$$

(24)

where $n_{<i}:={\sum }_{j=1}^{i-1}{n}_j,n_{>i}:={\sum }_{j=i+1}^N{n}_j$. Then, ${\mathcal{R}}_i{\mathit{x}}_i={\mathit{x}}_i^i=x_i$ and ${\mathcal{S}}_i{\mathit{x}}_i={\mathit{x}}_{-i}^i$. Let $\mathcal{R}:=diag\left({\left({\mathcal{R}}_i\right)}_{i\in \mathcal{I}}\right)$, $\mathcal{S}:=diag\left({\left({\mathcal{S}}_i\right)}_{i\in \mathcal{I}}\right)$. Hence $\mathcal{R}x=x$ and $\mathcal{R}x=col\left({\left({\mathit{x}}_{-i}^i\right)}_{i\in \mathcal{I}}\right)\in {\mathbb{R}}^{(N-1)n}$. Moreover, $\mathit{x}={\mathcal{R}}^{\top }x+{\mathcal{S}}^{\top }\mathcal{S}\mathit{x}$.

Similar to (13), we design sufficient conditions of (22) as follows:

$$\left\{\begin{array}{c}0\in {\mathcal{R}}^{\mathrm{T}}\widehat{\mathbb{F}}\left({\widehat{\mathit{x}}}^{*}\right)+{\mathcal{R}}^{\mathrm{T}}\mathbb{G}\left({\mathcal{R}}^{*}{\widehat{\mathit{x}}}^{*}\right)+{\mathcal{R}}^{\mathrm{T}}{\mathit{A}}^{\mathrm{T}}{\mathsf{\lambda }}^{*}+c\widehat{\mathbf{L}}{\widehat{\mathit{x}}}^{*}\hfill \\ 0=\mathbf{L}{\mathsf{\lambda }}^{*}\hfill \\ 0\in \mathit{A}\mathcal{R}{\widehat{\mathit{x}}}^{*}-\mathbf{b}+\mathbf{L}{\mathit{z}}^{*}-{\mathrm{N}}_{{\mathbb{R}}_{\ge 0}^{Nm}}\left({\mathsf{\lambda }}^{*}\right),\hfill \end{array}\right.$$

(25)

where $\widehat{\mathbf{L}}=\left(L\otimes I_n\right)\in {\mathbb{R}}^{Nn\times Nn}$, $\mathcal{R}=diag\left\{{\mathcal{R}}_i\right\}$, $\mathbb{F}\left(\mathit{x}\right)=col{\left({\nabla }_{x_i^i}{f}_i\left(x_i^i,{\mathit{x}}_{-i}^i\right)\right)}_{i\in I}\in {\mathbb{R}}^n$, $\mathbb{G}\left(\mathit{x}\right)=col{\left(\nabla g_i\left(x_i^i\right)\right)}_{i\in I}\in {\mathbb{R}}^n$, Moreover, c is a parameter about the dual variable associated with the constraint $0=-\widehat{L}{x}^{*}$.

Define the following operator:

$$\begin{array}{c}\hfill \overline{\mathbb{A}}:\left[\begin{array}{c}\widehat{\mathit{x}}\hfill \\ \mathit{z}\hfill \\ \mathsf{\lambda }\hfill \end{array}\right]\mapsto \left[\begin{array}{l}{\mathcal{R}}^{\mathrm{T}}\widehat{\mathbb{F}}\left(\widehat{\mathit{x}}\right)+{\mathcal{R}}^{\mathrm{T}}\mathbb{G}\left(\mathcal{R}\widehat{\mathit{x}}\right)+{\mathcal{R}}^{\mathrm{T}}{\mathit{A}}^{\mathrm{T}}\mathsf{\lambda }+c\widehat{\mathbf{L}}\widehat{\mathit{x}}\hfill \\ \mathbf{L}\mathsf{\lambda }\\ -\mathit{A}\mathcal{R}\widehat{\mathit{x}}+\mathbf{b}-\mathbf{L}\mathit{z}+{\mathrm{N}}_{{\mathbb{R}}_{\ge 0}^{Nm}}\left(\mathsf{\lambda }\right)\end{array}\right],\end{array}$$

(26)

$$\Phi =\left[\begin{array}{ccc}c\widehat{\mathbf{W}}& \mathbf{0}& -{\mathcal{R}}^{\mathrm{T}}{\mathbf{A}}^{\mathrm{T}}\\ \mathbf{0}& \mathbf{0}& -\mathbf{L}\\ -\mathbf{A}\mathcal{R}& -\mathbf{L}& \mathbf{0}\end{array}\right]+\left[\begin{array}{ccc}{\alpha }^{-1}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\tau }^{-1}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\gamma }^{-1}\end{array}\right].$$

(27)

The variables $\mathit{x},\mathit{z}$ and $\mathsf{\lambda }$ satisfy condition (25) if $\mathbf{0}\in \overline{\mathbb{A}}v$ where $v={\left[{\widehat{\mathit{x}}}^{\mathrm{T}},{\mathit{z}}^{\mathrm{T}},{\mathsf{\lambda }}^{\mathrm{T}}\right]}^{\mathrm{T}}$.

Lemma 4. 

Algorithm 1 is equivalent to the following:

$$(\forall k\in \mathbb{N})v^{k+1}\in {\mathrm{J}}_{{\Phi }^{-1}\overline{\mathbb{A}}}\left(v^k\right).$$

(28)

Let $\overline{\mathbb{A}}$ be defined as in (26) and Φ as in (27). Then, Algorithm 1 generates a sequence $\left({\mathit{x}}^k,{\mathit{z}}^k,{\mathsf{\lambda }}^k\right)$ for $k\in \mathbb{N}$ and any initial condition $v^0=$$col\left({\mathit{x}}^0,{\mathit{z}}^0,{\mathsf{\lambda }}^0\right)$.

Proof of Lemma 4. 

By applying the definition of inverse operations, we obtain that

$$\begin{array}{cc}\hfill & {\mathit{v}}^{k+1}\in {\left(Id+{\Phi }^{-1}\overline{\mathbb{A}}\right)}^{-1}\left({\mathit{v}}^k\right)\hfill \\ \hfill \iff & \mathbf{0}\in {\Phi }^{-1}\overline{\mathbb{A}}\left({\mathit{v}}^{k+1}\right)-{\mathit{v}}^k+{\mathit{v}}^{k+1}\hfill \\ \hfill \iff & \mathbf{0}\in \Phi \left({\mathit{v}}^{k+1}-{\mathit{v}}^k\right)+\overline{\mathbb{A}}\left({\mathit{v}}^{k+1}\right)\hfill \\ \hfill \iff & \left\{\begin{array}{cc}\hfill \mathbf{0}\in & {\alpha }^{-1}\left({\widehat{\mathit{x}}}_{k+1}-{\widehat{\mathit{x}}}_k\right)+c\widehat{\mathbf{W}}{\widehat{\mathit{x}}}_{k+1}-c\widehat{\mathbf{W}}{\widehat{\mathit{x}}}_k+c\widehat{\mathbf{L}}{\widehat{\mathit{x}}}_{k+1}-{\mathcal{R}}^{\top }{\mathit{A}}^{\top }{\mathsf{\lambda }}_{k+1}+{\mathcal{R}}^{\top }{\mathit{A}}^{\top }{\mathsf{\lambda }}_k\hfill \\ \hfill & +{\mathcal{R}}^{\mathrm{T}}\widehat{\mathbb{F}}\left({\widehat{\mathit{x}}}_{k+1}\right)+{\mathcal{R}}^{\mathrm{T}}G\left(\mathcal{R}{\widehat{\mathit{x}}}_{k+1}\right)-{\mathcal{R}}^{\top }{\mathit{A}}^{\top }{\mathsf{\lambda }}_{k+1}\hfill \\ \hfill \mathbf{0}\in & {\tau }^{-1}\left({\mathit{z}}^{k+1}-{\mathit{z}}^k\right)+\mathbf{L}{\mathsf{\lambda }}_{k+1}+\mathbf{L}{\mathsf{\lambda }}_k-\mathbf{L}{\mathsf{\lambda }}_{k+1}\hfill \\ \hfill \mathbf{0}\in & {\gamma }^{-1}\left({\mathsf{\lambda }}_{k+1}-{\mathsf{\lambda }}_k\right)+{\mathrm{N}}_{{\mathbb{R}}_{\ge 0}^{mN}}\left({\mathsf{\lambda }}^{k+1}\right)+\mathbf{b}-\mathit{A}\mathcal{R}\left(2{\widehat{\mathit{x}}}_{k+1}-{\widehat{\mathit{x}}}_k\right)+\mathbf{L}\left(2{\mathit{z}}_{k+1}-{\mathit{z}}_k\right).\hfill \end{array}\right.\hfill \end{array}$$

(29)

By $\widehat{\mathbf{L}}=\widehat{\mathbf{D}}-\widehat{\mathbf{W}}$, $\mathcal{R}\alpha {\mathcal{R}}^{\mathrm{T}}=\tilde{\alpha },\mathcal{S}\alpha {\mathcal{R}}^{\mathrm{T}}=\mathbf{0},\mathcal{R}\alpha \widehat{\mathbf{L}}=\tilde{\alpha }\mathcal{R}\widehat{\mathbf{L}}$, and $\mathcal{S}\alpha \widehat{\mathbf{L}}=\widehat{\alpha }\widehat{\mathcal{S}}$, we have

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}\hfill 0\in & \mathcal{S}\left(\left(I+c\widehat{\alpha }\widehat{\mathbf{D}}\right){\mathit{x}}_{k+1}-{\mathit{x}}_k-c\widehat{\alpha }\widehat{\mathbf{W}}{\mathit{x}}_k\right)\hfill \\ \hfill 0\in & \mathcal{R}\left(\left(I+c\tilde{\alpha }\widehat{\mathbf{D}}\right){\mathit{x}}_{k+1}-{\mathit{x}}_k-c\tilde{\alpha }\widehat{\mathbf{W}}{\mathit{x}}_k\right)+\tilde{\alpha }\widehat{\mathbb{F}}\left({\widehat{\mathit{x}}}_{k+1}\right)+\tilde{\alpha }\mathbb{G}\left(\mathcal{R}{\mathit{x}}_{\mathbf{k}+\mathbf{1}}\right)+\tilde{\alpha }{\mathit{A}}^{\mathrm{T}}{\mathsf{\lambda }}_k\hfill \end{array}\right.\hfill \\ \hfill \underset{\forall i\in \mathcal{I}}{\iff }& \left\{\begin{array}{c}{\mathit{x}}_{-i,k+1}^i=\frac{1}{1+c{\alpha }_i{d}_i}\left({\mathit{x}}_{-i,k}^i+{\alpha }_{i}c{\displaystyle \sum _{j=1}^N}{w}_{ij}{\mathit{x}}_{-i,k}^j\right)\hfill \\ 0_{n_i}\in {\partial }_{x_i^{k+1}}(\frac{1}{2}{\parallel x-x_{i,k}\parallel }^2+{\alpha }_i{x}^{\mathrm{T}}{A}_i^{\mathrm{T}}{\mathsf{\lambda }}_{i,k}+\frac{c}{2}{\alpha }_i{d}_i\parallel x-\frac{1}{d_i}{\displaystyle \sum _{j=1}^N}{w}_{ij}{x}_{i,k+1}^j{\parallel }^2\hfill \\ +{\alpha }_i{f}_i\left(x,{\mathit{x}}_{-i,k+1}^i\right)+{\alpha }_i{g}_i\left(x\right)).\hfill \end{array}\right.\hfill \end{array}$$

(30)

Hence, by the property that the subdifferential of a convex function contains only zeros at its minima [16], we can reformulate (30) as follows.

$$\begin{array}{cc}\hfill & \forall i\in \mathcal{I}:\left\{\begin{array}{c}{\mathit{x}}_{-i,k+1}^i=\frac{1}{1+{\tau }_i{d}_i}\left({\mathit{x}}_{-i,k}^i+{\tau }_i{\displaystyle \sum _{j=1}^N}{w}_{i,j}{\mathit{x}}_{-i,k}^j\right)\hfill \\ x_{i,k+1}=\underset{x}{argmin}(\frac{1}{2}{\parallel x-x_{i,k}\parallel }^2+{\alpha }_i{x}^{\mathrm{T}}{A}_i^{\mathrm{T}}{\mathsf{\lambda }}_{i,k}+{\alpha }_i{f}_i\left(x,{\mathit{x}}_{-i,k+1}^i\right)\hfill \\ +{\alpha }_i{g}_i\left(x\right)+\frac{c}{2}{\alpha }_i{d}_i\parallel x-\frac{1}{d_i}{\displaystyle \sum _{j=1}^N}{w}_{ij}{x}_{i,k+1}^j{\parallel }^2),\hfill \end{array}\right.\hfill \\ \hfill & {\mathit{z}}_{k+1}=-\tau \mathbf{L}{\mathsf{\lambda }}_k+{\mathit{z}}_k,\hfill \\ \hfill & {\mathsf{\lambda }}_{k+1}={\mathrm{proj}}_{{\mathbb{R}}_{\ge 0}^{mN}}\left(\begin{array}{c}{\mathsf{\lambda }}_k+\gamma \mathit{A}\mathcal{R}\left(2{\widehat{\mathit{x}}}_{k+1}-{\widehat{\mathit{x}}}_k\right)+2\gamma \mathbf{L}{\mathit{z}}_{k+1}-\gamma \mathbf{L}{\mathit{z}}_k-\gamma \mathbf{b}\end{array}\right).\hfill \end{array}$$

(31)

   □

Write (31) as a distributed algorithm as Algorithm 1.

4.2. Convergence Analysis

In this section, we will prove that Algorithm 1 applying the game (22) converges to the variational GNE through a rigorous mathematical analysis. We show that any limit point of Algorithm 1 satisfies $\mathbf{0}\in {\Phi }^{-1}\overline{\mathbb{A}}$ and has certain properties. Moreover, we demonstrate that every such zero is in the consensus subspace and solves $\mathrm{VI}(\mathbb{F},\mathcal{X})$.

Algorithm 1. Distributed Algorithm with Partial Information

Initialize:   For all $i\in \mathcal{I}$, set $x_{i,0}\in {\Omega }_i$,$x_{-i,0}^i\in {\mathbb{R}}^{n-n_i}$, ${\lambda }_{i,0}\in {\mathbb{R}}_{+}^m$, $z_{i,0}\in {\mathbb{R}}^m$

for $k=1,2,3,\dots$do

${\mathit{x}}_{-i,k+1}^i=\frac{1}{1+{\tau }_i{d}_i}\left({\mathit{x}}_{-i,k}^i+{\tau }_i{\sum }_{j=1}^N{w}_{i,j}{\mathit{x}}_{-i,k}^j\right)$

$x_{i,k+1}=\underset{x}{argmin}(\frac{1}{2}{\parallel x-x_{i,k}\parallel }^2+{\alpha }_i{x}^{\mathrm{T}}{A}_i^{\mathrm{T}}{\lambda }_{i,k}+\frac{c}{2}{\alpha }_i{d}_i\parallel x-\frac{1}{d_i}{\sum }_{j=1}^N{w}_{ij}{x}_{i,k+1}^j{\parallel }^2$

$+{\alpha }_i{f}_i\left(x,{\mathit{x}}_{-i,k+1}^i\right)+{\alpha }_i{g}_i\left(x\right))$

$z_{i,k+1}=z_{i,k}-{\tau }_i{\sum }_{j=1}^N{w}_{ij}({\lambda }_{i,k}-{\lambda }_{j,k})$

${\lambda }_{i,k+1}={\mathrm{prox}}_{{\mathbb{R}}_{\ge 0}^m}\left({\lambda }_{i,k}+2{\gamma }_i{A}_i{x}_{i,k+1}-{\gamma }_i{A}_i{x}_{i,k}+2{\gamma }_i{\sum }_{j=1}^N{w}_{ij}(z_{i,k+1}-z_{i,k+1})-{\gamma }_i{b}_i\right)$

end for

Retuen: The sequence ${\left(x_{i,k}\right)}_{k=1}^{\infty }$ will eventually approximate the optimal solution.

Assumption 5. 

$\mathbb{F}$ is a Lipschitz continuous mapping, which implies that there exists a positive constant θ such that for any $\mathit{x}$ and $\mathit{y}$, we have $\left.|\mathbb{F}\left(\mathit{x}\right)-\mathbb{F}\left(\mathit{y}\right)\right|\le \theta |\mathit{x}-\mathit{y}|$.

Define the operator:

$${\mathit{F}}_{\mathrm{c}}\left(\mathit{x}\right):={\mathcal{R}}^{\mathrm{T}}\widehat{\mathbb{F}}\left(\mathit{x}\right)+{\mathcal{R}}^{\mathrm{T}}\mathbb{G}\left(\mathcal{R}\mathit{x}\right)+c\widehat{\mathbf{L}}\mathit{x}.$$

(32)

From (26), we know

$$\overline{\mathbb{A}}\left[\begin{array}{c}\mathit{x}\\ \mathit{z}\\ \mathsf{\lambda }\end{array}\right]=\left[\begin{array}{c}{\mathit{F}}_{\mathrm{c}}\left(\widehat{\mathit{x}}\right)\\ \mathbf{0}\\ \mathbf{b}\end{array}\right]+\left[\begin{array}{c}{\mathcal{R}}^{\mathrm{T}}{\mathit{A}}^{\mathrm{T}}\mathsf{\lambda }\\ \mathit{L}\mathsf{\lambda }\\ -\mathit{A}\mathcal{R}\widehat{\mathit{x}}-\mathbf{L}\mathit{z}\end{array}\right]+\left[\begin{array}{c}\mathbf{0}\\ \mathbf{0}\\ {\mathrm{N}}_{{\mathcal{R}}_{\ge 0}^{Nm}}\left(\mathsf{\lambda }\right)\end{array}\right].$$

(33)

Lemma 5. 

Define $c_{min}=\frac{{\left(\theta +{\theta }_0\right)}^2}{4\mu s_2\left(L\right)}+\frac{\theta }{s_2\left(L\right)}$.

$$\mathsf{\Psi }=\left[\begin{array}{cc}\frac{\mu }{N}& -\frac{\theta +{\theta }_0}{2\sqrt{N}}\\ -\frac{\theta +{\theta }_0}{2\sqrt{N}}& c{s}_2\left(L\right)-\theta \end{array}\right],{\mu }_{{\mathbf{F}}_c}=s_{min}\left(\mathsf{\Psi }\right).$$

(34)

When $c>c_{\min }$, we have ${\mu }_{{\mathbf{F}}_c}=s_{min}\left(\mathsf{\Psi }\right)>0$ and $\overline{\mathbb{A}}$ is restricted monotone if Assumptions 1–5 hold.

Proof of Lemma 5. 

Let $v^{*}=col\left({\mathit{x}}^{*},{\mathit{z}}^{*},{\mathsf{\lambda }}^{*}\right)\in zer\left(\overline{\mathbb{A}}\right)$ be any zero of $\overline{\mathbb{A}}$, which exists by Lemma 4. From (33), we can decompose $\overline{\mathbb{A}}$ as a sum of three operators, two of which are monotone. Moreover, for any $c>c_{\min }$, we have $\mathsf{\Psi }⩾0$ for all $\mathit{x}\in {\mathbb{R}}^{Nn}$ by Lemma 1. Then,

$$〈\mathit{x}-{\mathit{x}}^{*}\mid {\mathit{F}}_{\mathrm{c}}\left(\mathit{x}\right)-{\mathit{F}}_{\mathrm{c}}\left({\mathit{x}}^{*}\right)〉\ge {\mu }_{{\mathit{F}}_{\mathrm{c}}}{∥\mathit{x}-{\mathit{x}}^{*}∥}^2.$$

(35)

Hence, for any $(v,u)\in gra\left(\overline{\mathbb{A}}\right)$, with $v=col(\mathit{x},\mathit{z},\mathsf{\lambda })$, we obtain $〈v-v^{*}\mid u-\mathbf{0}〉\ge {\mu }_{{\mathbf{F}}_{\mathrm{c}}}{∥\mathit{x}-{\mathit{x}}^{*}∥}^2\ge 0$. □

Lemma 6. 

Define $\mathcal{B}:{\mathbb{R}}^q\rightrightarrows {\mathbb{R}}^q$ as a restricted monotone in ${\mathcal{H}}_{\Phi }$ and ${\mathrm{J}}_{\mathcal{B}}$ is firmly quasinonexpansive in ${\mathcal{H}}_{\Phi }$, where ${\mathcal{H}}_{\Phi }$ is the Hilbert space induced by the inner product ${\langle ·,·\rangle }_{\Phi }$. Then for any $(v,u)\in gra\left({\mathrm{J}}_{\mathcal{B}}\right)$, $v^{*}\in zer\left(\mathcal{B}\right)=fix\left({\mathrm{J}}_{\mathcal{B}}\right)$, it holds that

$${〈v-u\mid v-v^{*}〉}_{\Phi }-{\parallel u-v\parallel }_{\Phi }^2={〈v-u\mid u-v^{*}〉}_{\Phi }\ge 0.$$

(36)

Proof of Lemma 6. 

We use the definition of resolvent: $v^{*}\in {\mathrm{J}}_{\mathcal{B}}\left(v^{*}\right)\iff v^{*}+\mathcal{B}{v}^{*}\ni$$v^{*}\iff$$\mathbf{0}\in \mathcal{B}\left(v^{*}\right)$. Moreover, for any $(v,u)\in gra\left({\mathrm{J}}_{\mathcal{B}}\right)$, we have $v-u\in \mathcal{B}\left(u\right)$. Therefore, (36) follows from the restricted monotonicity of $\mathcal{B}$ and some simple algebra. Finally, setting $v=v^{*}$ in (36), we obtain that $J_{\mathcal{B}}$ is single-valued. □

Lemma 7. 

Let $zer\left(\mathcal{B}\right)\ne ⌀$ by Lemma 6. For $k\in \mathbb{N}$,we assume that ${\beta }^k\in [0,2]$ and $e^k\in {\mathbb{R}}^q$ such that ${\beta }^k{∥e^k∥}_P\in {\ell }^1$. If $v^0\in {\mathbb{R}}^q$,

$$(\forall k\in \mathbb{N})v^{k+1}=v^k+{\beta }^k\left(u^k-v^k+e^k\right),u^k\in {\mathrm{J}}_{\mathcal{B}}\left(v^k\right).$$

(37)

Then we obtain Algorithm 1 by applying (13) to the operator ${\Phi }^{-1}\overline{\mathbb{A}}$, where

$$\Phi =\left[\begin{array}{ccc}c\widehat{\mathbf{W}}& \mathbf{0}& -{\mathcal{R}}^{\mathrm{T}}{\mathit{A}}^{\mathrm{T}}\\ \mathbf{0}& \mathbf{0}& -\mathbf{L}\\ -\mathit{A}\mathcal{R}& -\mathbf{L}& \mathbf{0}\end{array}\right]+\left[\begin{array}{ccc}{\alpha }^{-1}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\tau }^{-1}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\gamma }^{-1}\end{array}\right]$$

(38)

is called a preconditioning matrix. It ensures that the agents will be able to compute the resulting iteration in a fully distributed manner.

We choose the step sizes $\alpha =diag\left({\alpha }_i{I}_{n_i}\right)$, $\tau =diag\left({\tau }_i{I}_m\right)$ and $\gamma =diag\left({\gamma }_i{I}_m\right)$ such that $\Phi >0$. This implies that $zer\left({\Phi }^{-1}\overline{\mathbb{A}}\right)=zer\left(\overline{\mathbb{A}}\right)$. The next lemma provides sufficient conditions for $\Phi >0$ based on Gershgorin’s circle theorem.

Lemma 8. 

For any agent $i\in \mathcal{I}$ and any $\delta >0$, the preconditioning matrix Φ in (38) is positive definite if

$$\begin{array}{cc}\hfill & 0<{\alpha }_i\le {\left(\underset{j\in \left\{1,\dots ,n_i\right\}}{max}{\displaystyle \sum _{k=1}^m}\left|{\left[A_i^{\top }\right]}_{jk}\right|+\delta \right)}^{-1},\hfill \\ \hfill & 0<{\tau }_i\le {\left(2d_i+\delta \right)}^{-1},\hfill \\ \hfill & 0<{\gamma }_i\le {\left(\underset{j\in \{1,\dots ,m\}}{max}{\displaystyle \sum _{k=1}^{n_i}}\left|{\left[A_i\right]}_{jk}\right|+2d_i+\delta \right)}^{-1}.\hfill \end{array}$$

(39)

Using Lemma 4 and Assumption 4, we can show that ${\mathrm{J}}_{{\Phi }^{-1}\overline{\mathbb{A}}}$ is single-valued by applying Equation (28) to ${\Phi }^{-1}\overline{\mathbb{A}}$.

Lemma 9. 

Let $c>c_{\min },c_{\min }$ as in Lemma 3. Then ${\Phi }^{-1}\overline{\mathbb{A}}$ is restricted monotone in ${\mathcal{H}}_{\Phi }$.

It means that finding a zero point of $\overline{\mathbb{A}}$ is equivalent to finding a variational GNE for problem (3). Moreover, since $\Phi >0$, we have $zer\left(\overline{\mathbb{A}}\right)=zer\left({\Phi }^{-1}\overline{\mathbb{A}}\right)$ by Lemma 9. Therefore, finding a zero point of ${\Phi }^{-1}\overline{\mathbb{A}}$ is also equivalent to finding a variational GNE for problem (3). This establishes the equivalence between problems (3) and (22) under the condition that $c>c_{\min },c_{\min }$ as in Lemma 3.

Theorem 1. 

Assume that $c>c_{\min },c_{\min }$ are as defined in Lemma 8 and that the step sizes $\alpha ,\tau ,\gamma$ satisfy Lemma 5. Then, Algorithm 1 generates a sequence ${\left({\mathit{x}}^k,{\mathit{z}}^k,{\mathsf{\lambda }}^k\right)}_{k\in \mathbb{N}}$ that converges to an equilibrium $\left({\mathit{x}}^{*},{\mathit{z}}^{*},{\mathsf{\lambda }}^{*}\right)$.

Proof of Theorem 1. 

The set of inequalities (29) is equivalent to Equation (37) when ${\beta }^k=1$, $e^k=0$ for all $k\in \mathbb{N}$. By applying Lemma 9, we deduce that ${\Phi }^{-1}\overline{\mathbb{A}}$ is restricted monotone on ${\mathcal{H}}_{\Phi }$. Then, we define

$$u^k={\mathrm{J}}_{{\Phi }^{-1}\overline{\mathbb{A}}}\left(v^k\right).$$

(40)

By Lemma 9, ${\Phi }^{-1}\overline{\mathbb{A}}$ is restricted monotone in ${\mathcal{H}}_{\Phi }$, which implies $u^k=v^{k+1}$.

Let $h^k:=v^k+{\beta }^k\left(u^k-v^k\right)$, so that $v^{k+1}=h^k+{\beta }^k{e}^k$. For all $k\in \mathbb{N}$,

$$\begin{array}{c}\hfill {∥h^k-v^{*}∥}_{\Phi }^2={∥v^k-v^{*}∥}_{\Phi }^2-2{\beta }^k{〈v^k-u^k\mid v^k-v^{*}〉}_{\Phi }+{\left({\beta }^k\right)}^2{∥u^k-v^k∥}_{\Phi }^2\end{array}.$$

(41)

Then by Lemma 7, we have

$$\begin{array}{c}\hfill {∥h^k-v^{*}∥}_{\Phi }^2\le {∥v^k-v^{*}∥}_{\Phi }^2-{\gamma }^k\left(2-{\beta }^k\right){∥u^k-v^k∥}_{\Phi }^2\end{array}.$$

(42)

By the Cauchy–Schwarz inequality, it holds that

$${∥h^k-v^{*}∥}_{\Phi }\le {∥v^k-v^{*}∥}_{\Phi }.$$

(43)

By (43), the sequence ${\left({\mathit{v}}^k\right)}_{k\in \mathbb{N}}$ is bounded so that there is at least one cluster point such as $\overline{v}$. Define:

$$\overline{{\mathbb{A}}_1}\left[\begin{array}{c}\mathit{x}\\ \mathit{z}\\ \mathsf{\lambda }\end{array}\right]=\left[\begin{array}{c}{\mathit{F}}_{\mathrm{c}}\left(\widehat{\mathit{x}}\right)\\ 0\\ \mathbf{b}\end{array}\right]+\left[\begin{array}{c}{\mathit{R}}^{\mathrm{T}}{\mathit{A}}^{\mathrm{T}}\mathsf{\lambda }\\ \mathit{L}\mathsf{\lambda }\\ -\mathit{A}\mathit{R}\widehat{\mathit{x}}-\mathit{L}\mathit{z}\end{array}\right].$$

(44)

$\overline{{\mathbb{A}}_1}$ consists of the sum of the first two equations of $\overline{\mathbb{A}}$. By (29) and (44), it holds that

$$\left.〈\overline{{\mathbb{A}}_1}\left(u^k\right)+\Phi \left(u^k-v^k\right)\right|v-u^k〉\ge 0.$$

(45)

Let $\eta :={sup}_{k\in \mathbb{N}}{∥v^k-v^{*}∥}_{\Phi }<\infty$ and ${ϵ}^k:=2\eta \left({\beta }^k{∥e^k∥}_{\Phi }\right)+{\left({\beta }^k{∥e^k∥}_{\Phi }\right)}^2$, for all $k\in \mathbb{N}$. Then, ${\left({ϵ}^k\right)}_{k\in \mathbb{N}}\in {\ell }^1$. Moreover, for all $k\in \mathbb{N}$ we have

$$\begin{array}{cc}\hfill & {∥v^{k+1}-v^{*}∥}_{\Phi }^2\hfill \\ \hfill \le & {\left({∥h^k-v^{*}∥}_{\Phi }+{\beta }^k{∥e^k∥}_{\Phi }\right)}^2\hfill \\ \hfill \le & {∥v^k-v^{*}∥}_{\Phi }^2-{\beta }^k\left(2-{\beta }^k\right){∥u^k-v^k∥}_{\Phi }^2+{ϵ}^k.\hfill \end{array}$$

(46)

Followed by recursion, it holds that

$${\left({\beta }^k\left(2-{\beta }^k\right){∥u^k-v^k∥}_{\Phi }^2\right)}_{k\in \mathbb{N}}\in {\ell }^1.$$

(47)

By (47), $u^k-{\mathit{v}}^k$ converges to 0 as $k\to \infty$. Let $l_k$ be a divergent subsequence such that $v^{l_k}\to \overline{v}$. Then, for any $v\in \Omega \times {\mathbb{R}}^m\times {\mathbb{R}}_{\ge 0}^m$, we have $〈\overline{{\mathbb{A}}_1}\left(\overline{v}\right)\mid v-\overline{v}〉\ge 0$ by continuity of $\overline{{\mathbb{A}}_1}$, which means $\overline{v}\in zer\left(\overline{\mathbb{A}1}\right)=fix\left({\mathrm{J}}_{{\Phi }^{-1}}\overline{{\mathbb{A}}_1}\right)$. By Lemma 6, any cluster point of $v^k$ belongs to C. Hence, $v^k$ converges to an equilibrium of (29). □

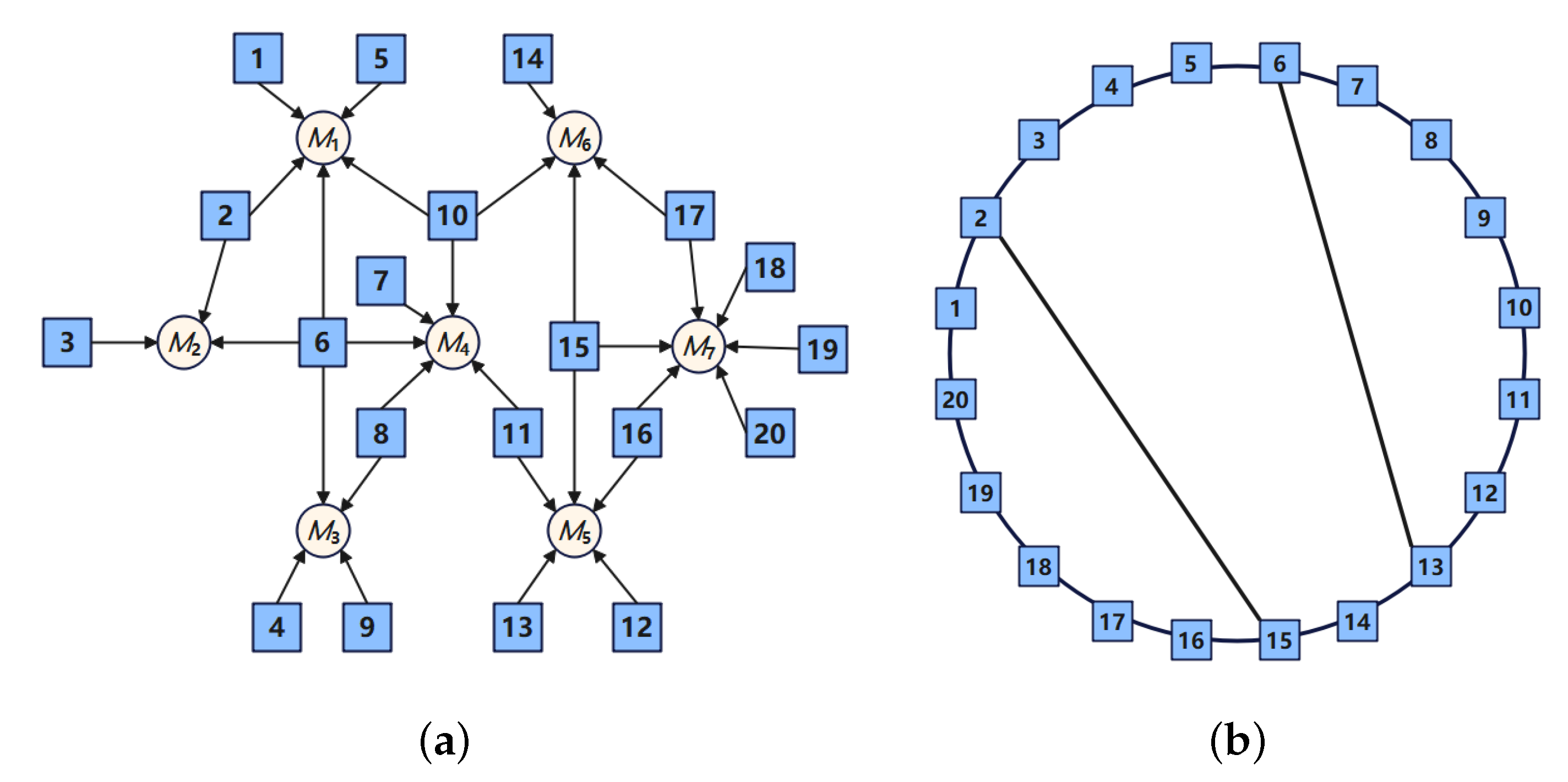
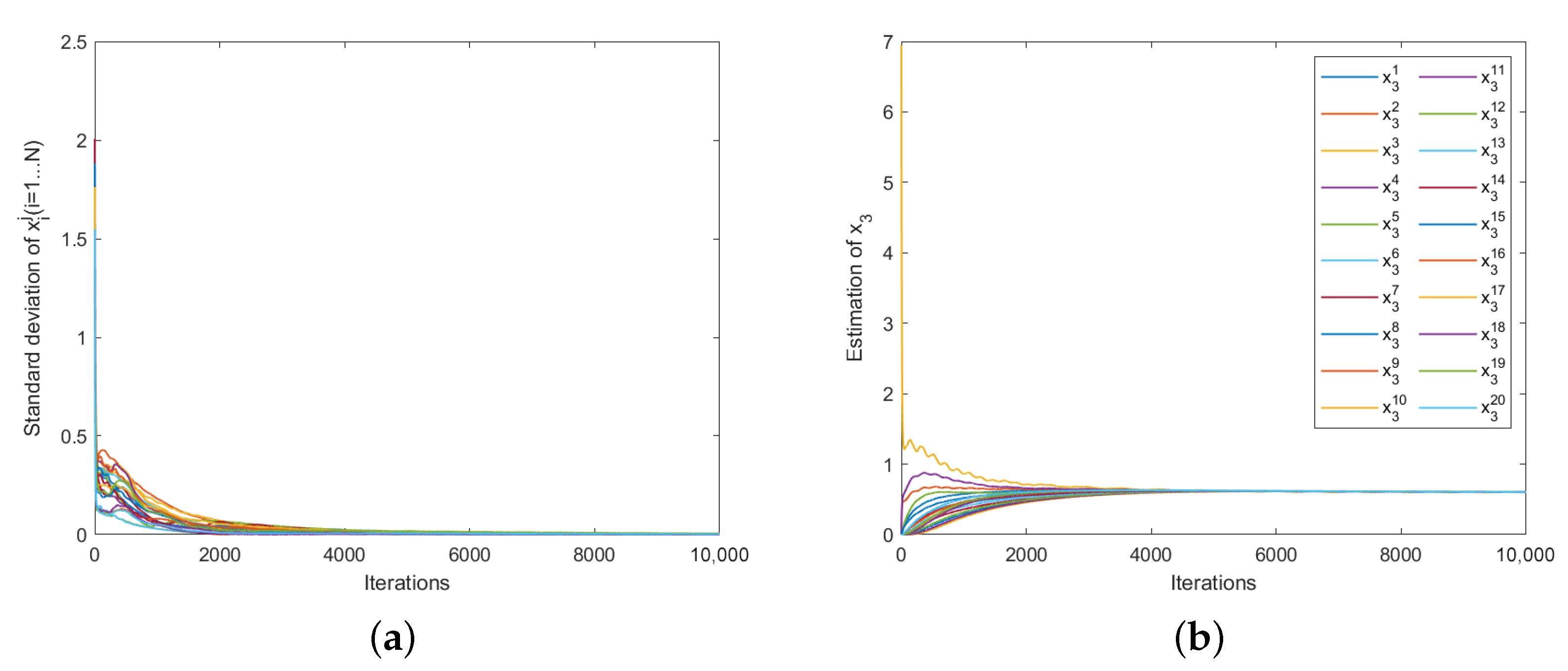
5. Numerical Studies

In this section, we will explore a network-based Nash–Cournot game [21] that is used to model the competition between N companies in m markets. This game is of particular interest because it has been shown to be an effective tool for analyzing competition between companies. The markets have shared affine constraints or equivalent global coupling affine constraints, which makes it possible to model the interactions between the companies in a realistic way. It is important to note that in this game, the agents can only communicate with their neighbors, and there is no central node with bidirectional communication to all participants. This makes the game even more challenging, as the agents must rely on their own resources to make decisions.

Although this game has been applied in networked Cournot games [15], it is worth noting that it assumes that the agents’ decision information is global. However, in contrast, our work considers network structure and partial decision information, which leads to a more accurate representation of the real-world dynamics of competition between companies. This means that our research is more relevant to the real world, and can help us gain a deeper understanding of the complex interactions between the agents. By incorporating the network structure and partial decision information, we are able to gain a deeper understanding of the complex interactions between the agents, which can have significant implications for the overall performance of the companies in the markets. Additionally, our research can help to inform future policy decisions, as it provides a more accurate picture of the dynamics of competition between companies in networked markets.

5.1. Cournot Market Competition

Each firm i decides the quantity $x_i\in {\mathbb{R}}^{n_i}$ of the commodity for $n_i\le m$ markets, subject to ${\mathbf{0}}^{n_i}\le x_i\le X_i$. The maximum capacity of each market $l=1,\dots ,m$ is $r_l$. Hence, we have a shared affine constraint $Ax\le r$, where $r=col\left({\left(r_k\right)}_{l=1,\dots ,m}\right)$ and $A=\left[A_1\dots A_N\right]$. The matrix $A_i\in {\mathbb{R}}^{m\times n_i}$ indicates which markets firm i enters. Specifically, ${\left[A_i\right]}_{l,j}=1$ if firm i enters market l, and ${\left[A_i\right]}_{l,j}=0$ otherwise, for all $j=1\dots ,n_i$ and $l=1,\dots ,m$.The profit function of each firm i is $J_i\left(x_i,{\mathit{x}}_{-i}\right)=f_i\left(x_i,{\mathit{x}}_{-i}\right)+g_i\left(x_i\right)$, where $f_i\left(x_i,x_{-i}\right)=p{\left(Ax\right)}^{\top }{A}_i{x}_i$ and $g_i\left(x_i\right)=-x_i^{\top }{Q}_i{x}_i-q_i^{\top }{x}_i$. $g_i\left(x_i\right)$ is the production cost of firm i, and $Q_i\in {\mathbb{R}}^{n_i\times n_i},$$Q_i>0$$,q_i\in {\mathbb{R}}^{n_i}$ are given parameters. The market price for each market and $l=1,\dots ,m$ is given by ${\left[p\left(x\right)\right]}_l={\overline{P}}_l-{\chi }_l{\left[Ax\right]}_l$, where ${\overline{P}}_l,{\chi }_l>0$ are constants.

In this simulation, we set the total number of participants to 20 and the number of markets to 7, i.e., $N=20,m=7$. We defined the market structure using Figure 1a, which does not show the actual spatial relationships and distances among markets and firms. We also set $n_i=1$ for all $i\in \mathcal{I}$. Then the arrows in Figure 1a represent only the participation of firms in the markets; therefore, we have $x=col{\left(\left(x_i\right)\right)}_{i\in \mathcal{I}}\in {\mathbb{R}}^n$.

We considered m markets distributed across seven continents. Individual firms could not communicate with all other firms because of geographical location, communication technology, or company systems. The firms could communicate only with their neighbors on the communication graph ${\mathcal{G}}_c$, shown in Figure 1b. Only connected firms i and j in the undirected communication graph ${\mathcal{G}}_c$ could exchange their information. We randomly selected $r_l\in [1,2]$, Q with diagonal elements in [1,8], $q_i\in [1,2]$, ${\overline{P}}_l\in [10,20]$, ${\chi }_l\in [1,3]$, and $X_i\in [5,10]$ for all $i\in \mathcal{I}$ and $l=1,\dots ,m$.

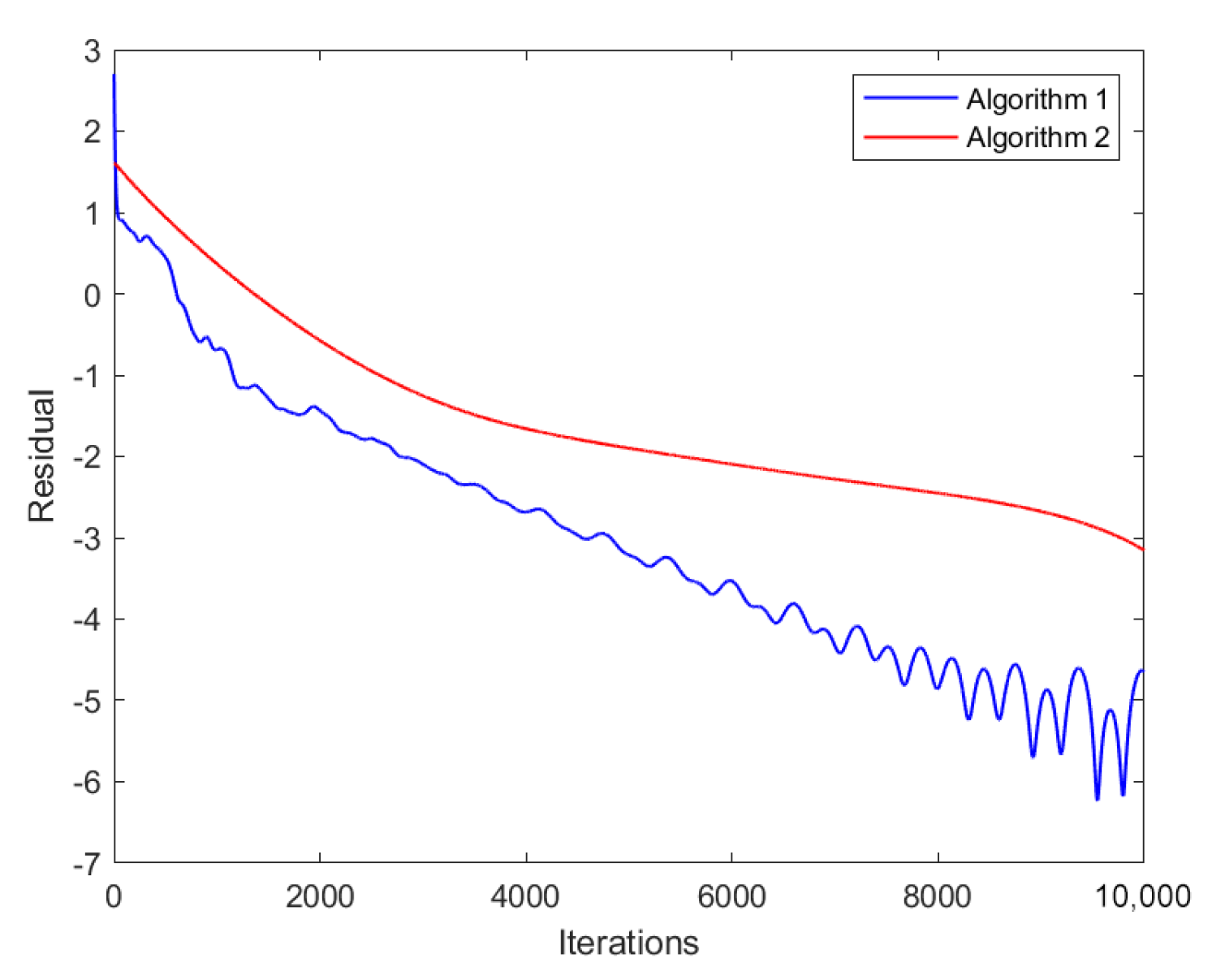
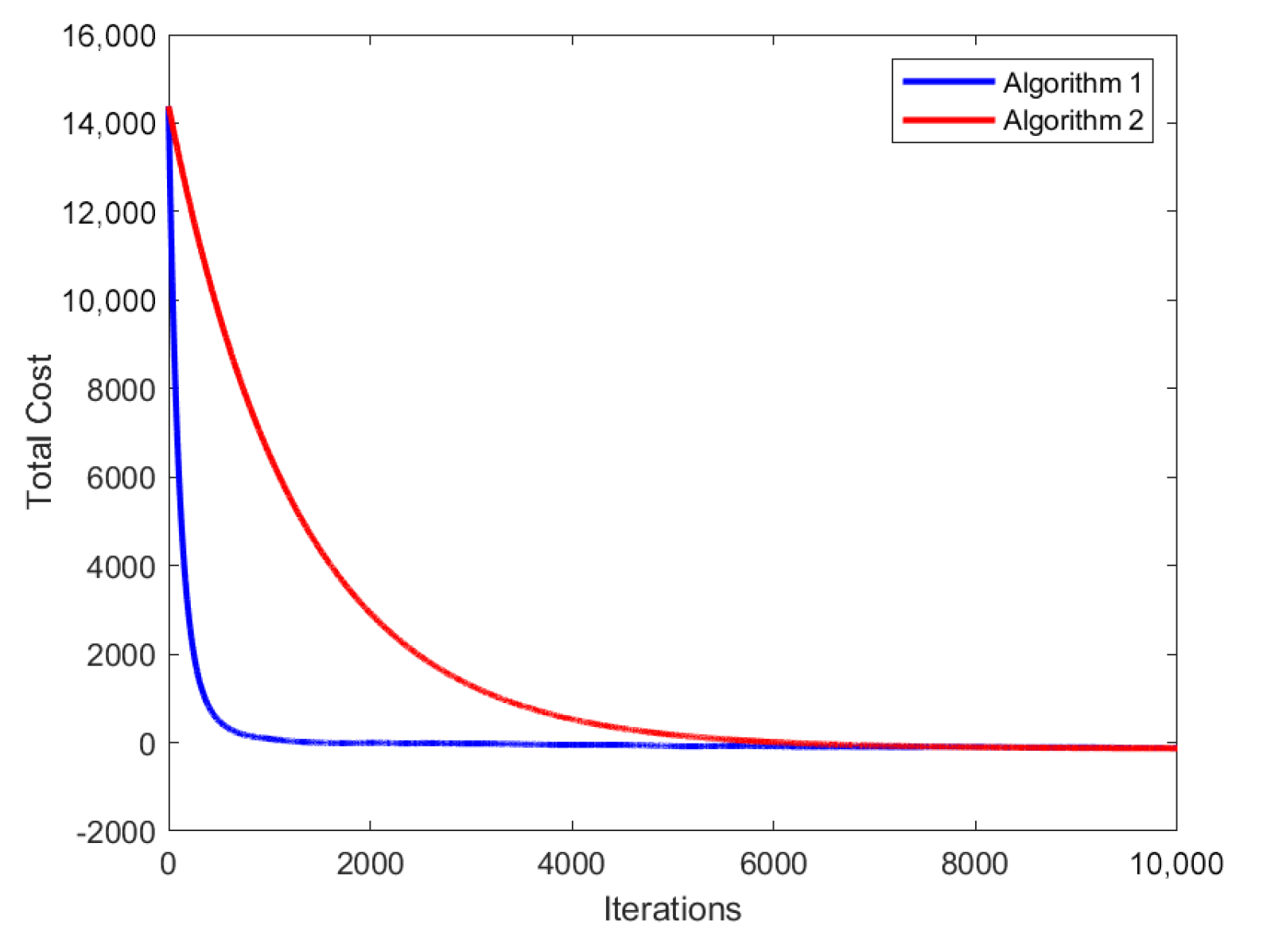
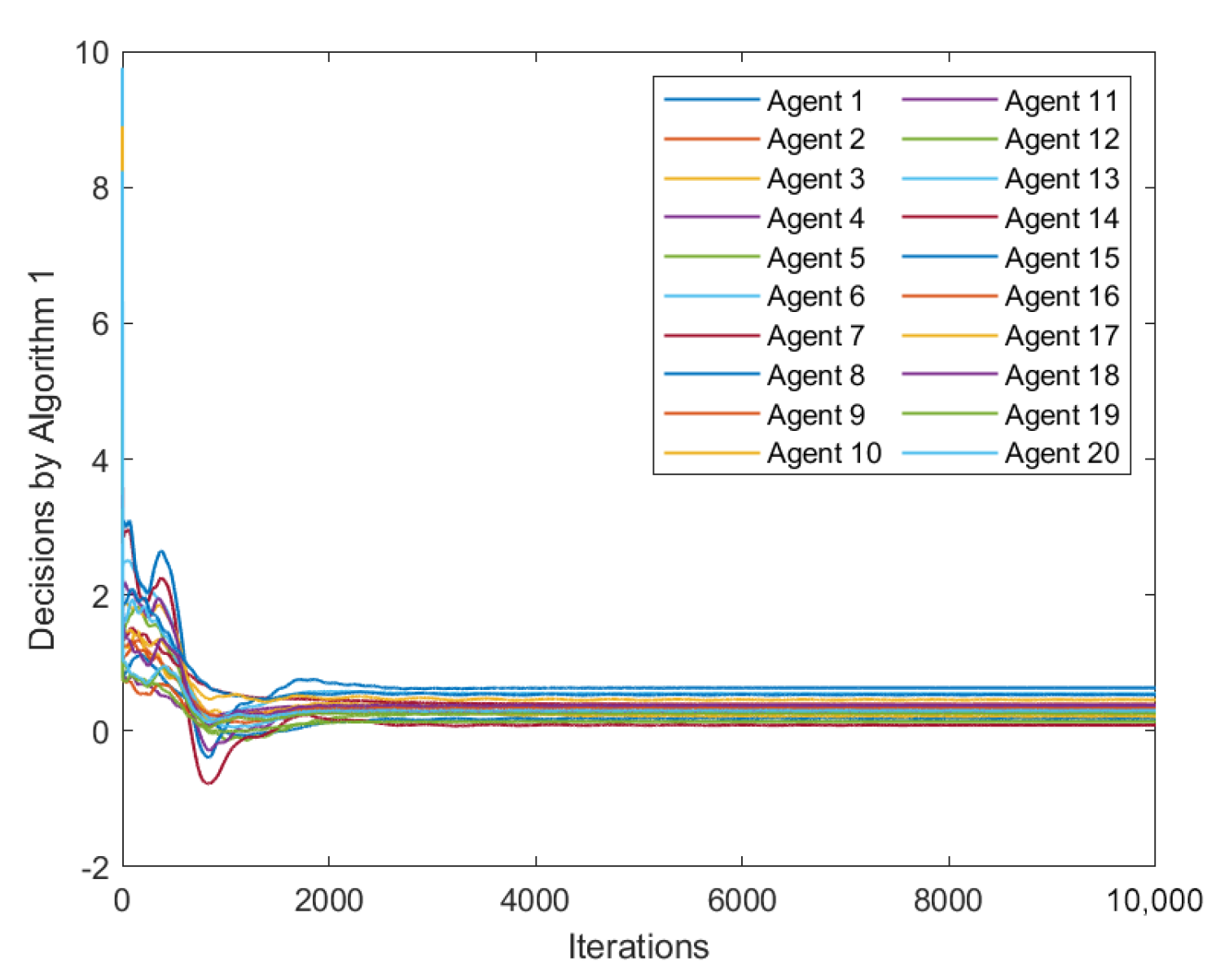
5.2. Numerical Results

The experimental settings described above satisfy all assumptions presented in [21]. We selected the step size in Lemma 8 to fulfill all conditions required by Theorem 1. To compare the performance of Algorithm 1 and the algorithm in [21], we conducted experiments using the same random initial condition for both algorithms. As shown in Figure 2 and Figure 3, Algorithm 1 proposed in this paper converges faster than the algorithm in [21], which is referred to as Algorithm 2 in the following text.

Figure 2 compares the convergence of the two algorithms under the partial decision setting by plotting the relative error of their decisions. The results show that Algorithm 1 has smaller relative errors than Algorithm 2 (the algorithm in [21]) for the same number of iterations, indicating a faster convergence rate for Algorithm 1.

Figure 3 illustrates the trajectory of the total cost of all agents in the market corresponding to Algorithm 1 and Algorithm 2 (the algorithm in [21]), where the total cost is generated by ${\displaystyle \sum _{i=1}^N}{J}_i\left(x_i,{\mathit{x}}_{-i}\right)$. The trajectory eventually converges to the same minimum value, indicating the correctness and accuracy of Algorithm 1. Furthermore, the convergence of the trajectory represents the effectiveness of the algorithm in terms of optimizing the total cost of all agents in the market.

In Figure 4, we can observe the trajectory of each agent’s decision in the Cournot market game, which has been solved by Algorithm 1. As we can see from the graph, the decision trajectories of all agents converge, which is a strong indication that the GNE obtained by executing Algorithm 1 can effectively minimize the cost incurred by each agent. It is worth noting that the convergence of decision trajectories is a critical aspect of the game theory that is often used to evaluate the effectiveness of a given algorithm. Therefore, the observed convergence in Figure 4 is an encouraging sign that Algorithm 1 can be a viable approach for solving similar problems in the future.

During the iterative process of Algorithm 1, the estimated value of each agent’s decision for all other agents is first obtained according to the formula ${\mathit{x}}_{-i,k+1}^i=\frac{1}{1+{\tau }_i{d}_i}\left({\mathit{x}}_{-i,k}^i+{\tau }_i{\sum }_{j=1}^N{w}_{i,j}{\mathit{x}}_{-i,k}^j\right)$. This formula is used to compute the value of ${\mathit{x}}_{-i,k+1}^i$. Subsequently, the estimated decision value is used for the iteration of $\left(\mathit{x},\mathit{z},\mathsf{\lambda }\right)$, which is a mathematical notation used to represent the values of the decision variables. When the algorithm converges, i.e., when the GNE is obtained, the estimated decision value of each agent for $x_i$ is equal to the actual decision value of $x_i$, i.e., $x_i^j=x_i^i$ for $j=1,\dots ,N$. Figure 5a shows the trajectory of the standard deviation of each agent’s estimated decision set for $x_i$ with increasing iteration times, which is generated by $\sqrt{\frac{1}{N}{\displaystyle {\displaystyle \sum _{j=1}^N}}{(x_i^j-{\displaystyle {\displaystyle \sum _{j=1}^N}}{x}_i^j)}^2}$ for $j=1,\dots ,N$. It can be seen that the standard deviation of the estimated decision set for each agent eventually converges to 0. This indicates that the results satisfy the condition that the estimated value of each agent’s decision for $x_i$ is equal to the actual decision value of $x_i$. As shown in Figure 5b, taking agent 3 as an example, the trajectory plot of all agents’ estimated decision values for agent 3 is displayed, where $x_3^3$ represents the actual value of agent 3’s decision. The trajectory plot eventually converges to the same value, visually confirming the accuracy of Algorithm 1.

6. Conclusions

In this paper, we propose a distributed algorithm for games with shared coupling constraints based on the preconditioned proximal-point algorithm under partial decision information, which can converge with a fixed step size on arbitrarily connected graphs and is successfully applied to the GNE computation of the Cournot Market competition under partial decision information with a relatively fast convergence rate. A possible direction for future work is to study partial decision information sets and their impact on the memory efficiency of the algorithm. We will also explore how to predict only a subset of agents’ decisions rather than all agents’ decisions and study the convergence properties of the algorithm. Future work will further investigate this direction.