Autonomous Driving Decision Control Based on Improved Proximal Policy Optimization Algorithm
Abstract
1. Introduction
2. Reinforcement Learning
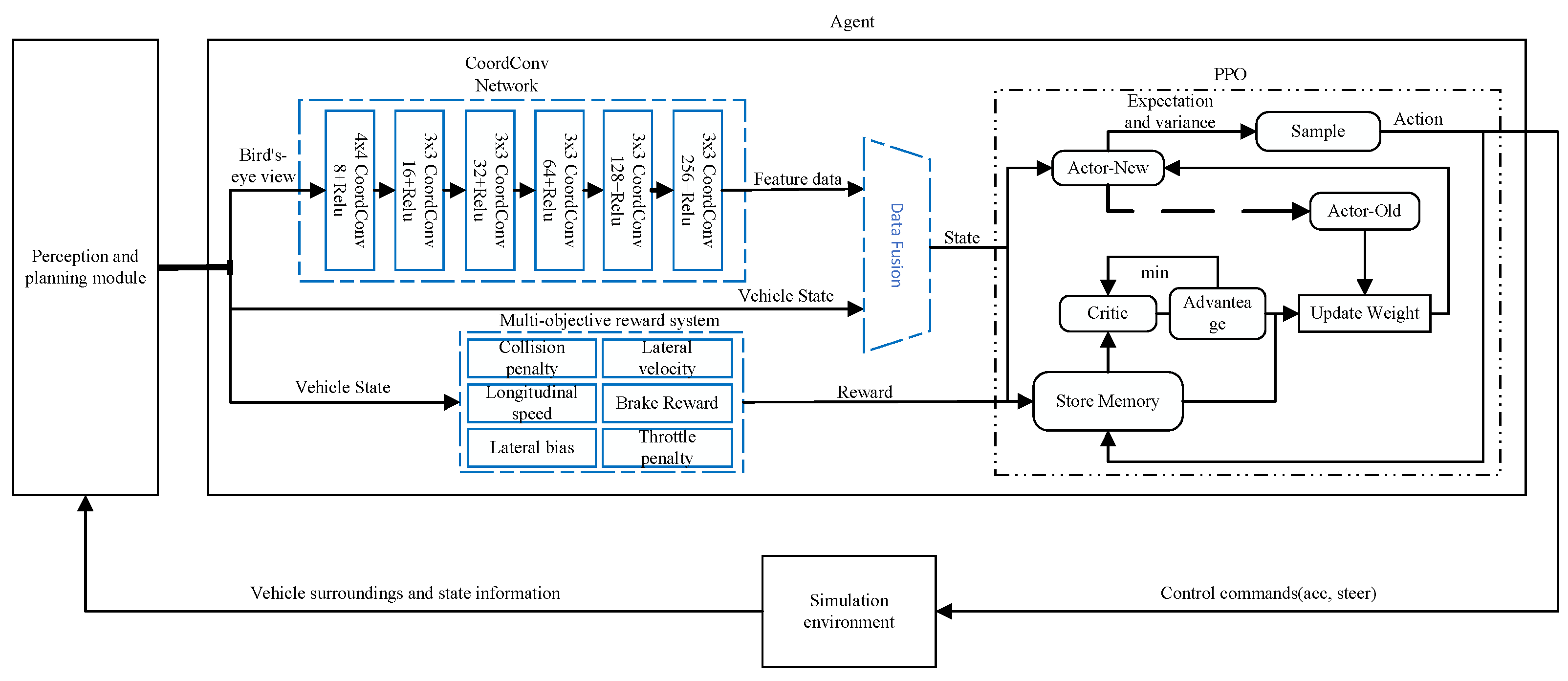
3. Method
3.1. State Space
3.2. Action Space
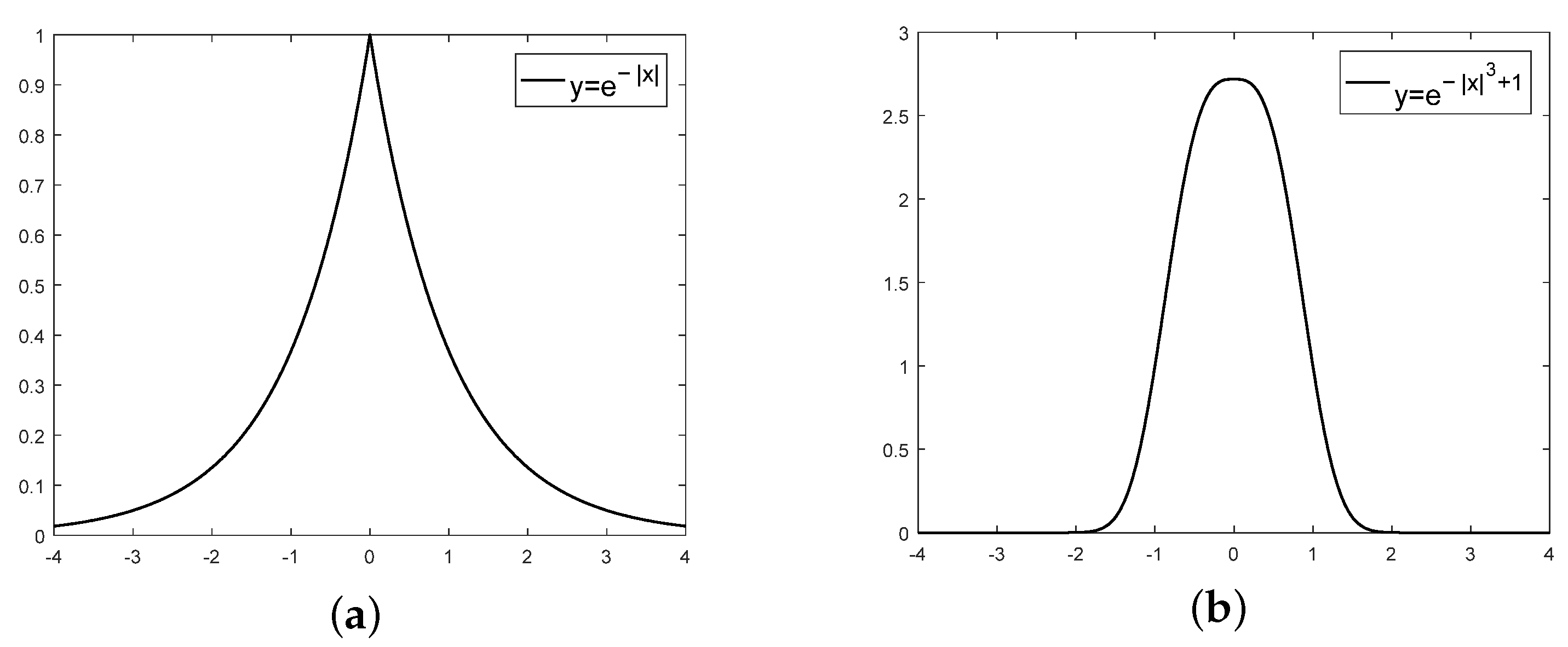
3.3. Reward Function
3.3.1. Collision Penalty
3.3.2. Longitudinal Speed
3.3.3. Lane Departure
3.3.4. Lateral Speed
3.3.5. Brake Reward
3.3.6. Throttle Penalty
3.4. Policy and Value Function as Neural Networks
3.5. Termination Conditions
3.5.1. Specify the Number of Steps to Perform in the Episode
3.5.2. Out of Lane
3.5.3. Collision Occurs
4. Results and Discussion
4.1. Experimental Environment
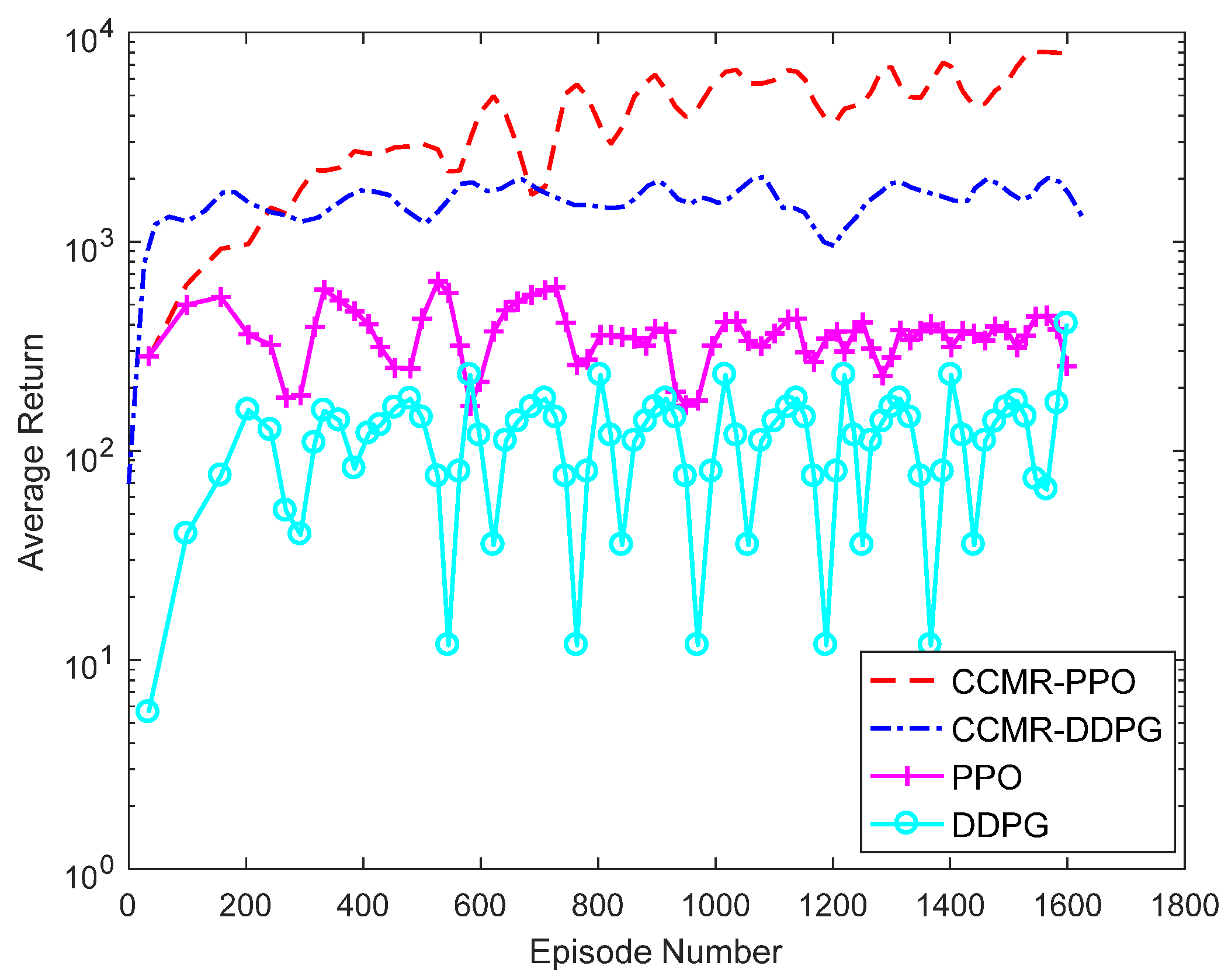
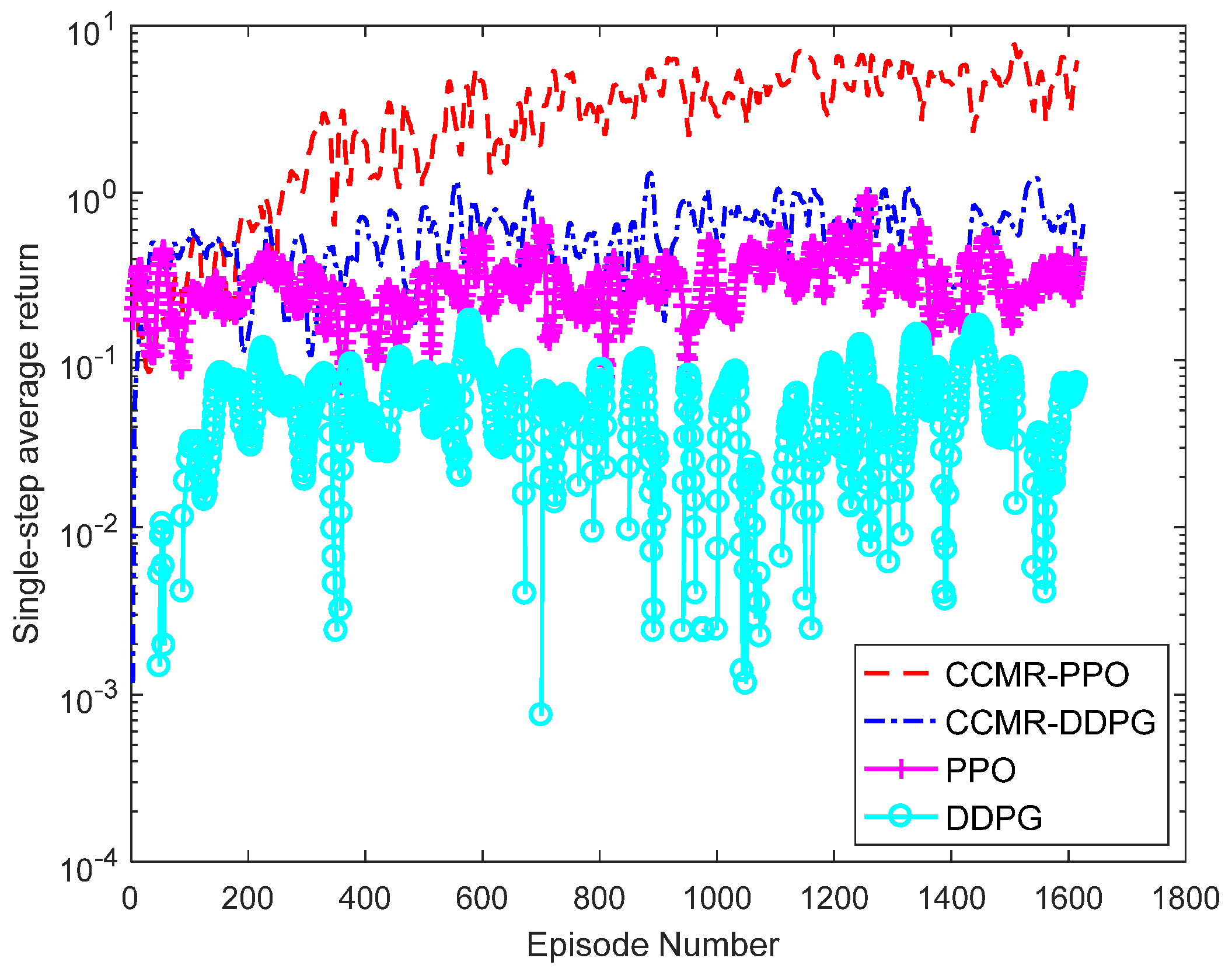
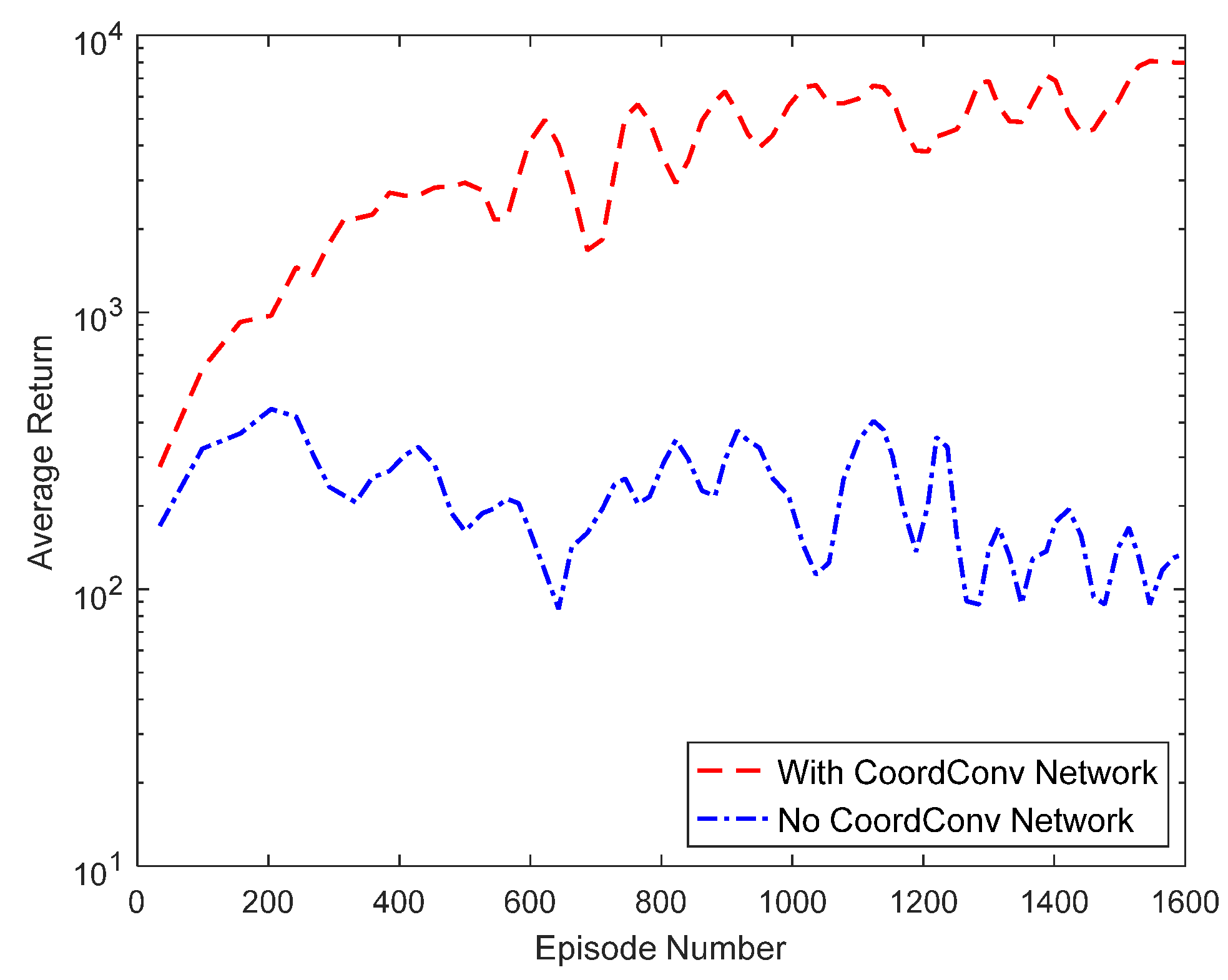
4.2. Comparative Analysis of Algorithms
4.2.1. Analysis of Training Results
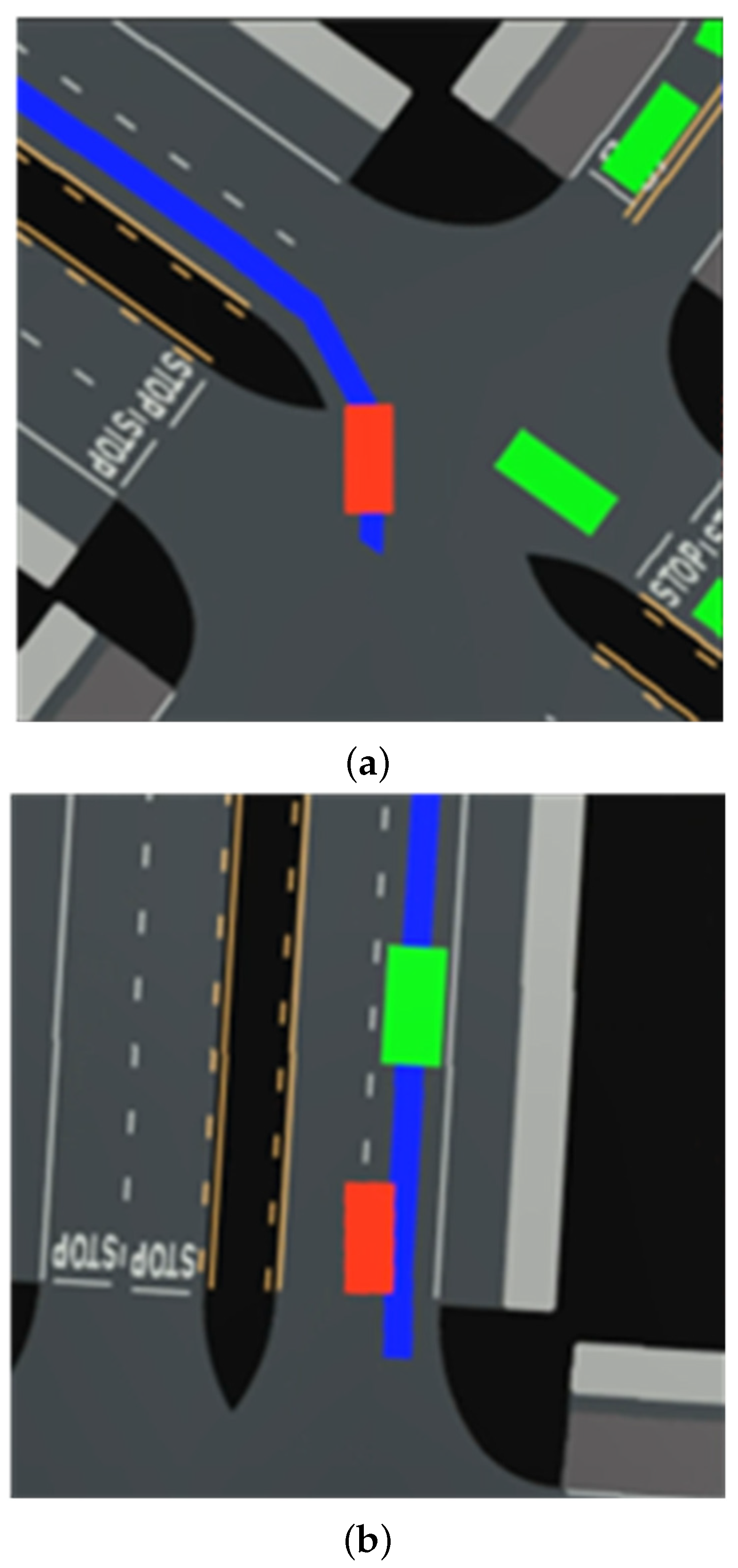
4.2.2. Analysis of Test Results
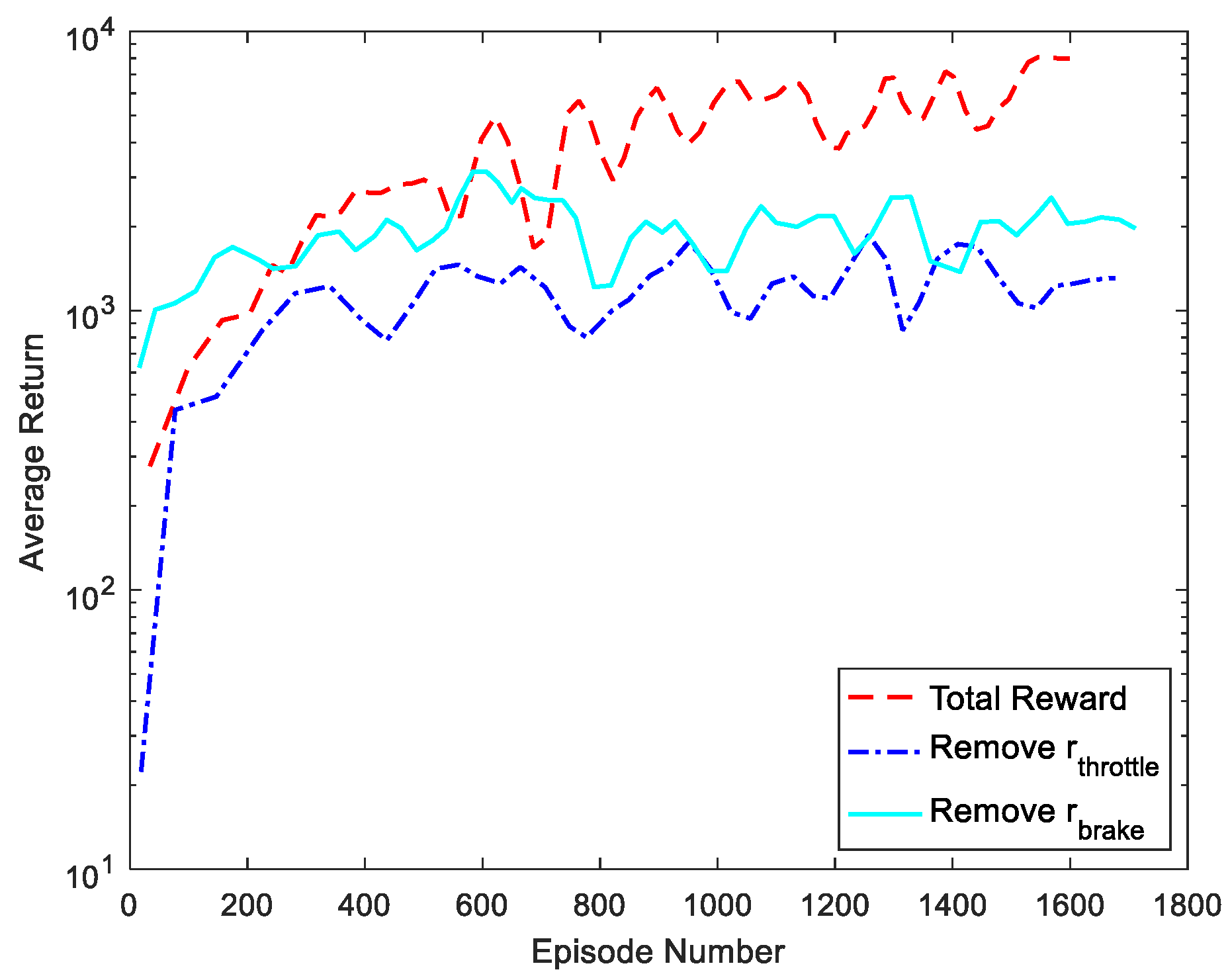
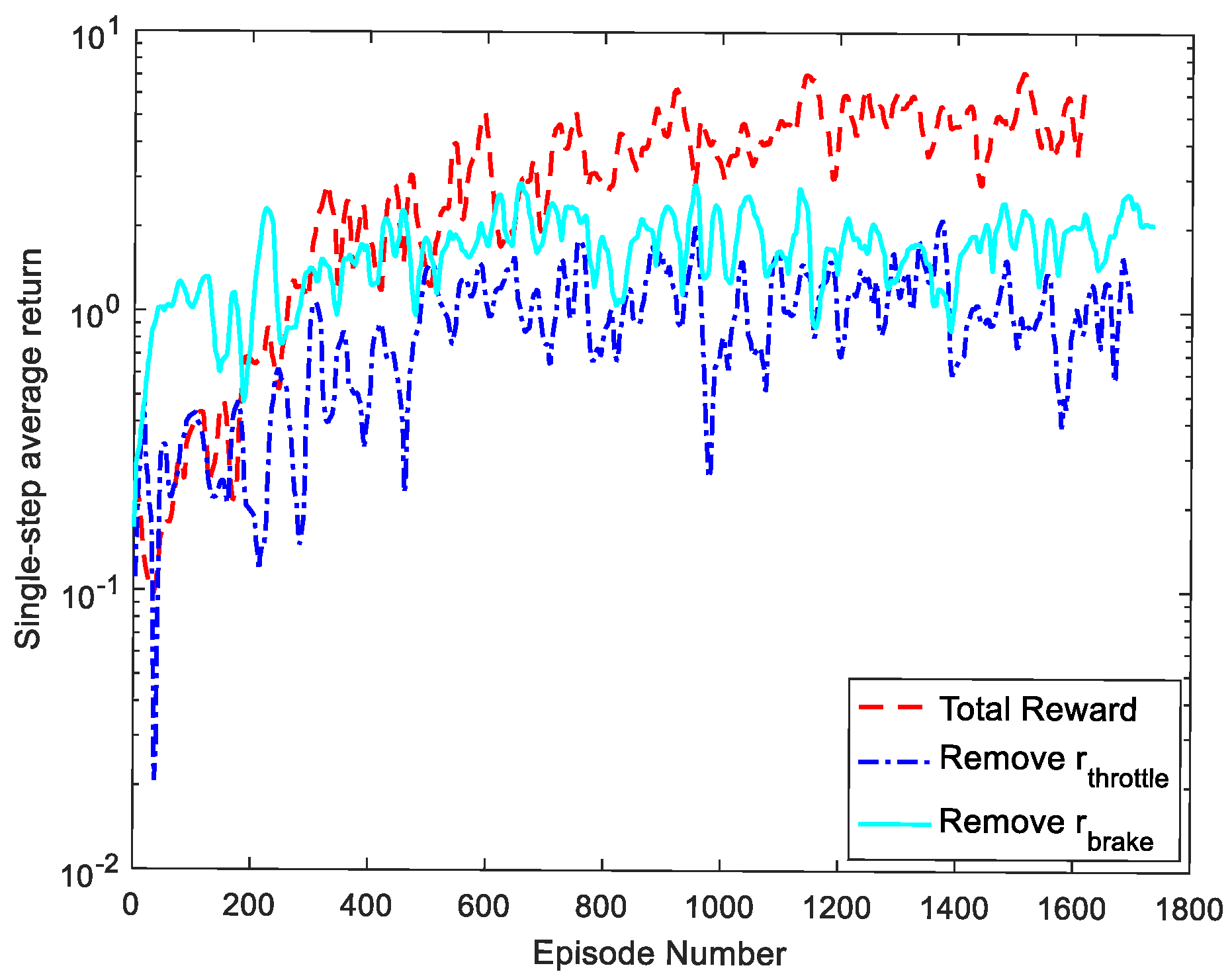
4.3. Ablation Study
4.3.1. Analysis of Training Results
4.3.2. Analysis of Test Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, L.; Xiong, L.; Xia, X.; Lu, Y.; Yu, Z.; Khajepour, A. Improved Vehicle Localization Using On-Board Sensors and Vehicle Lateral Velocity. IEEE Sens. J. 2022, 22, 6818–6831. [Google Scholar] [CrossRef]
- Xia, X.; Hashemi, E.; Xiong, L.; Khajepour, A. Autonomous Vehicle Kinematics and Dynamics Synthesis for Sideslip Angle Estimation Based on Consensus Kalman Filter. IEEE Trans. Control. Syst. Technol. 2022, 31, 179–192. [Google Scholar] [CrossRef]
- Liu, W.; Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Automated Vehicle Sideslip Angle Estimation Considering Signal Measurement Characteristic. IEEE Sens. J. 2021, 21, 21675–21687. [Google Scholar] [CrossRef]
- Xiong, G.; Li, Y.; Wang, S. Behavior prediction and control method based on FSM for intelligent vehicles in an intersection. Behavior 2015, 35, 34–38. [Google Scholar]
- Wu, L. Research on Environmental Information Extraction and Movement Decision-Making Method of Unmanned Vehicle. Ph.D. Dissertation, Chang’an University, Xi’an, China, 2016. [Google Scholar]
- Liu, W.; Hua, M.; Deng, Z.; Huang, Y.; Hu, C.; Song, S.; Xia, X. A systematic survey of control techniques and applications: From autonomous vehicles to connected and automated vehicles. arXiv 2023, arXiv:2303.05665. [Google Scholar]
- Chen, G.; Hua, M.; Liu, W.; Wang, J.; Song, S.; Liu, C. Planning and Tracking Control of Full Drive-by-Wire Electric Vehicles in Unstructured Scenario. arXiv 2023, arXiv:2301.02753. [Google Scholar]
- Gutiérrez-Moreno, R.; Barea, R.; López-Guillén, E.; Araluce, J.; Bergasa, L.M. Reinforcement Learning-Based Autonomous Driving at Intersections in CARLA Simulator. Sensors 2022, 22, 1424–8220. [Google Scholar] [CrossRef]
- Yu, W.; Qian, Y.; Xu, J.; Sun, H.; Wang, J. Driving Decisions for Autonomous Vehicles in Intersection Environments: Deep Reinforcement Learning Approaches with Risk Assessment. World Electr. Veh. J. 2023, 14, 2032–6653. [Google Scholar] [CrossRef]
- Xia, X.; Meng, Z.; Han, X.; Li, H.; Tsukiji, T.; Xu, R.; Ma, J. Automated Driving Systems Data Acquisition and Processing Platform. arXiv 2022, arXiv:2211.13425. [Google Scholar]
- Liu, W.; Quijano, K.; Crawford, M.M. YOLOv5-Tassel: Detecting Tassels in RGB UAV Imagery with Improved YOLOv5 Based on Transfer Learning. IEEE J. Sel. Top. Appl. Earth Obs.Remote Sens. 2022, 15, 8085–8094. [Google Scholar] [CrossRef]
- Tampuu, A.; Aidla, R.; van Gent, J.A.; Matiisen, T. LiDAR-as-Camera for End-to-End Driving. Sensors 2023, 23, 1424–8220. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Yuan, B.; Tomizuka, M. Deep imitation learning for autonomous driving in generic urban scenarios with enhanced safety. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 2884–2890. [Google Scholar]
- Toromanoff, M.; Wirbel, E.; Wilhelm, F.; Vejarano, C.; Perrotton, X.; Moutarde, F. End to end vehicle lateral control using a single fisheye camera. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3613–3619. [Google Scholar]
- Geng, G.; Wu, Z.; Jiang, H.; Sun, L.; Duan, C. Study on Path Planning Method for Imitating the Lane-Changing Operation of Excellent Drivers. Appl. Sci. 2018, 8, 2076–3417. [Google Scholar] [CrossRef]
- Li, D.; Zhao, D.; Zhang, Q.; Chen, Y. Reinforcement learning and deep learning based lateral control for autonomous driving [application notes]. IEEE Comput. Intell. Mag. 2019, 14, 83–98. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, H. A Survey of Deep RL and IL for Autonomous Driving Policy Learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14043–14065. [Google Scholar] [CrossRef]
- Park, M.; Lee, S.Y.; Hong, J.S.; Kwon, N.K. Deep Deterministic Policy Gradient-Based Autonomous Driving for Mobile Robots in Sparse Reward Environments. Sensors 2022, 22, 1424–8220. [Google Scholar] [CrossRef] [PubMed]
- Kendall, A.; Hawke, J.; Janz, D.; Mazur, P.; Reda, D.; Allen, J.M.; Shah, A. Learning to drive in a day. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8248–8254. [Google Scholar]
- Qiao, Z.; Muelling, K.; Dolan, J.M.; Palanisamy, P.; Mudalige, P. Automatically generated curriculum based reinforcement learning for autonomous vehicles in urban environment. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1233–1238. [Google Scholar]
- Isele, D.; Rahimi, R.; Cosgun, A.; Subramanian, K.; Fujimura, K. Navigating Occluded Intersections with Autonomous Vehicles Using Deep Reinforcement Learning. In Proceedings of the IEEE international conference on robotics and automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2034–2039. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Hassabis, D. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; López, A.; Koltun, V. CARLA: An Open Urban Driving Simulator. In Proceedings of the 1st Conference on Robot Learning, Mountain View, CA, USA, 13–15 November 2017; pp. 1–16. [Google Scholar]
- Plappert, M.; Andrychowicz, M.; Ray, A.; McGrew, B.; Baker, B.; Powell, G.; Schneider, J.; Tobin, J.; Chociej, M.; Welinder, P.; et al. Multi-Goal Reinforcement Learning: Challenging Robotics Environments and Request for Research. arXiv 2018, arXiv:1802.09464. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Bansal, M.; Krizhevsky, A.; Ogale, A. Chauffeurnet: Learning to drive by imitating the best and synthesizing the worst. arXiv 2018, arXiv:1812.03079. [Google Scholar]
- Liu, R.; Lehman, J.; Molino, P.; Such, F.P.; Frank, E.; Sergeev, A.; Yosinski, J. An intriguing failing of convolutional neural networks and the coordconv solution. In Proceedings of the 32st International Conference on Neural Information Processing Systems (NIPS 2018), Montréal, QC, Canada, 2–8 December 2018; pp. 9605–9616. [Google Scholar]
- Chen, J.; Yuan, B.; Tomizuka, M. Model-free deep reinforcement learning for urban autonomous driving. In Proceedings of the IEEE intelligent transportation systems conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 2765–2771. [Google Scholar]




| Name of Network | Network Dimension | Activation Function |
|---|---|---|
| Input layer | 256 + 4 | / |
| Fully connected layer1 | 100 | tanh |
| Fully connected layer2 | 100 | soft plus |
| Output layer | 2 | / |
| Name of Network | Network Dimension | Activation Function |
|---|---|---|
| Input layer | 256 + 4 | / |
| Fully connected layer1 | 100 | tanh |
| Fully connected layer2 | 100 | tanh |
| Output layer | 1 | / |
| Parameter | Value |
|---|---|
| Sampling time (s) | |
| CoordConv network initial learning rate | |
| Actor network initial learning rate | |
| Critic network initial learning rate | |
| Discount factor | 0.99 |
| Clip parameter | 0.2 |
| GAE parameter | 0.95 |
| Batch size | 64 |
| Number of Episodes | 1600 |
| Algorithms | Straight-Road | Curve-Road | Crossroad | T-Junction | Roundabout | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CT | CL | CO | CT | CL | CO | CT | CL | CO | CT | CL | CO | CT | CL | CO | |
| CCMR-PPO | 10 | 0 | 0 | 10 | 0 | 0 | 10 | 1 | 0 | 6 | 5 | 4 | 10 | 2 | 0 |
| CCMR-DDPG | 10 | 3 | 0 | 8 | 5 | 1 | 6 | 2 | 2 | 4 | 4 | 3 | 8 | 5 | 0 |
| cPPO | 6 | 3 | 4 | 4 | 3 | 0 | 5 | 3 | 3 | 2 | 6 | 2 | 2 | 5 | 2 |
| DDPG | 2 | 10 | 0 | 0 | 10 | 0 | 3 | 10 | 2 | 0 | 10 | 0 | 1 | 10 | 0 |
| Crossroad | Roundabout | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Reward | Turn Left | Turn Right | Inner Circle | Outer Circle | |||||||||
| CT | CL | CO | CT | CL | CO | CT | CL | CO | CT | CL | CO | ||
| Total reward | 10 | 0 | 0 | 8 | 2 | 1 | 10 | 0 | 0 | 10 | 0 | 0 | |
| Remove | 7 | 3 | 1 | 6 | 4 | 4 | 9 | 1 | 0 | 8 | 3 | 0 | |
| Remove | 8 | 1 | 2 | 6 | 3 | 2 | 10 | 2 | 0 | 10 | 1 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Q.; Liu, Y.; Lu, M.; Zhang, J.; Qi, H.; Wang, Z.; Liu, Z. Autonomous Driving Decision Control Based on Improved Proximal Policy Optimization Algorithm. Appl. Sci. 2023, 13, 6400. https://doi.org/10.3390/app13116400
Song Q, Liu Y, Lu M, Zhang J, Qi H, Wang Z, Liu Z. Autonomous Driving Decision Control Based on Improved Proximal Policy Optimization Algorithm. Applied Sciences. 2023; 13(11):6400. https://doi.org/10.3390/app13116400
Chicago/Turabian StyleSong, Qingpeng, Yuansheng Liu, Ming Lu, Jun Zhang, Han Qi, Ziyu Wang, and Zijian Liu. 2023. "Autonomous Driving Decision Control Based on Improved Proximal Policy Optimization Algorithm" Applied Sciences 13, no. 11: 6400. https://doi.org/10.3390/app13116400
APA StyleSong, Q., Liu, Y., Lu, M., Zhang, J., Qi, H., Wang, Z., & Liu, Z. (2023). Autonomous Driving Decision Control Based on Improved Proximal Policy Optimization Algorithm. Applied Sciences, 13(11), 6400. https://doi.org/10.3390/app13116400








