Numerical Study on Vibration Response of Compressor Stator Blade Considering Contact Friction of Holding Ring
Abstract
1. Introduction
2. Numerical Methods
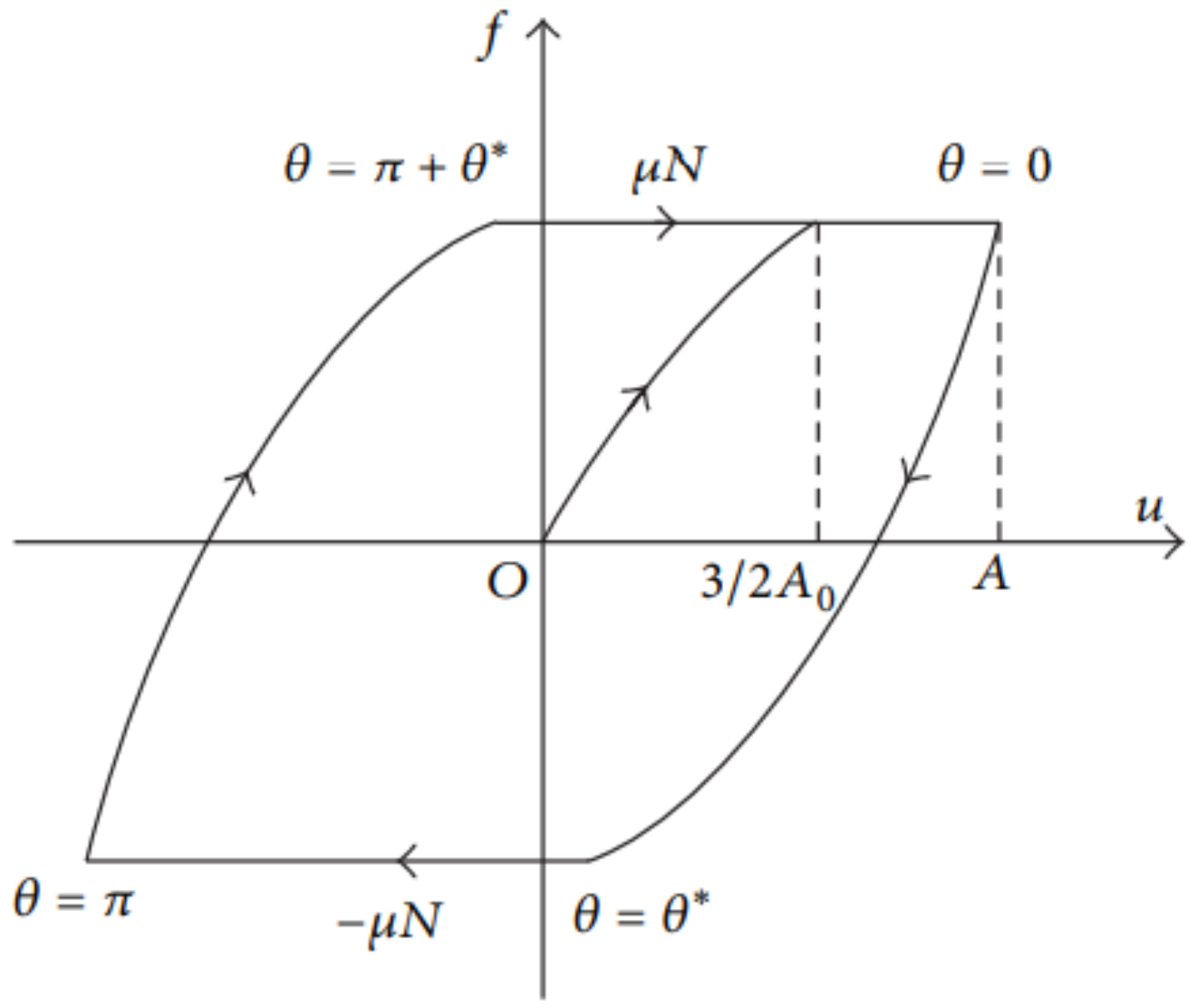
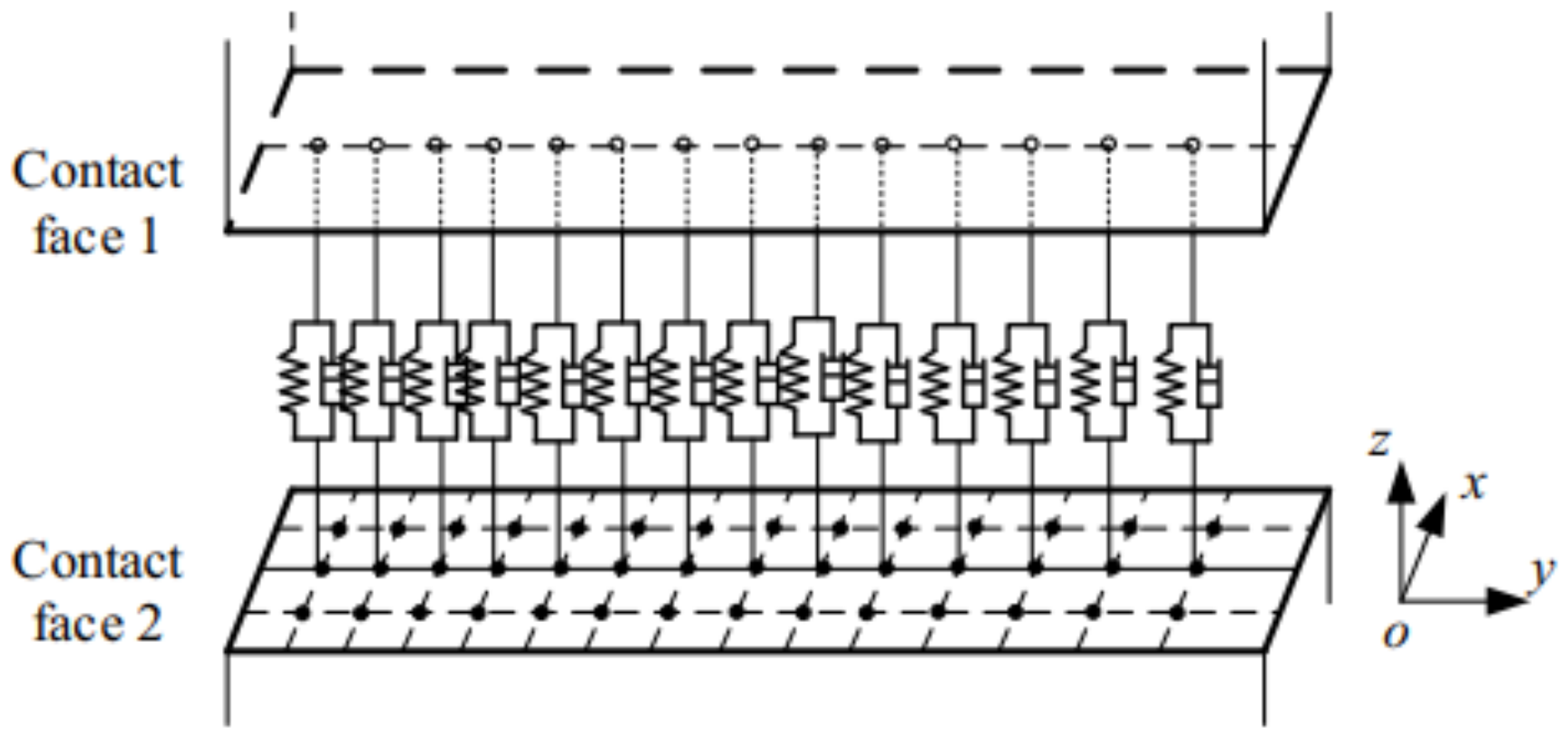
2.1. Frictional Contact Model
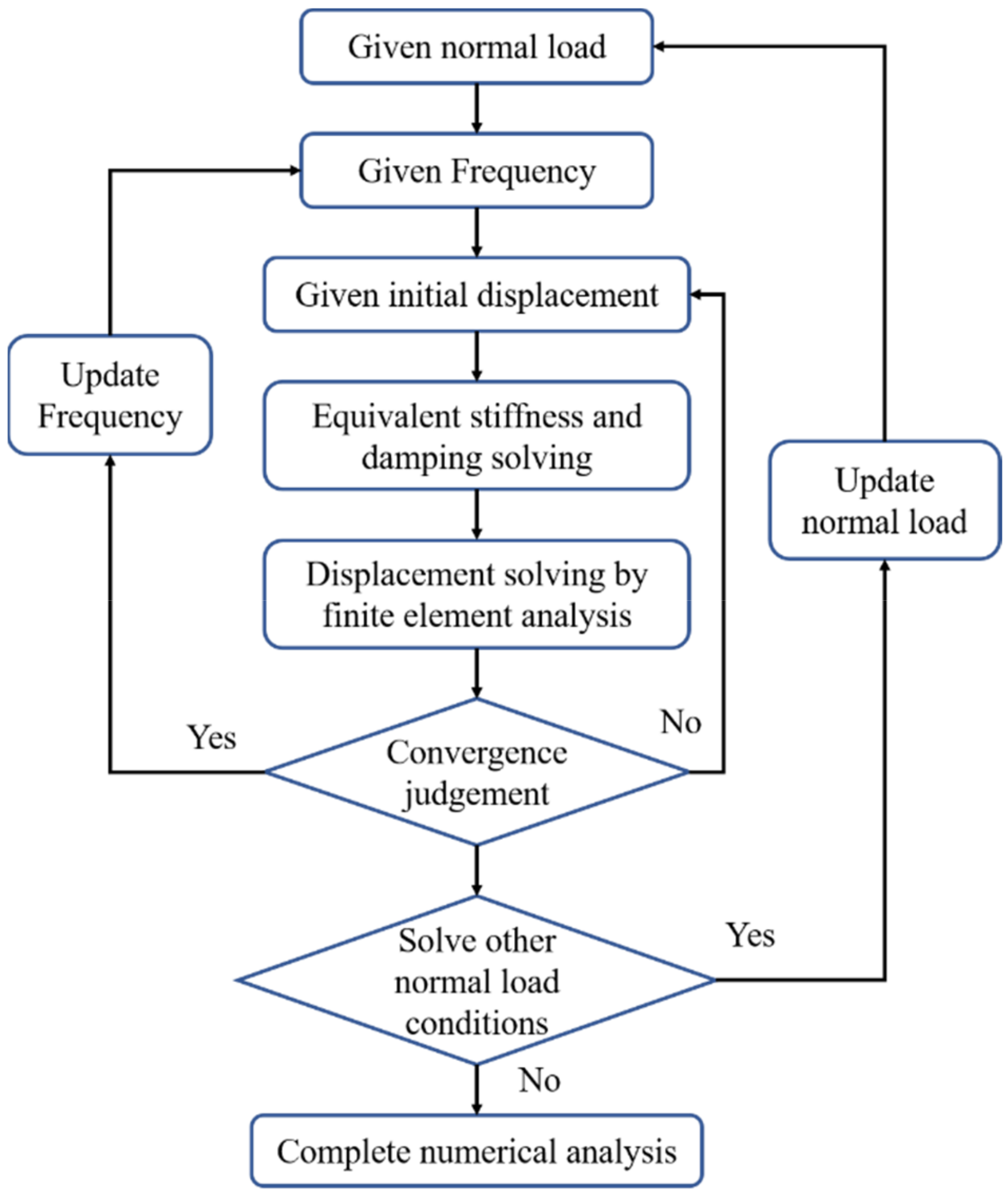
2.2. Vibration Response Analysis Method
2.3. Airflow Load Analysis
3. Computational Model
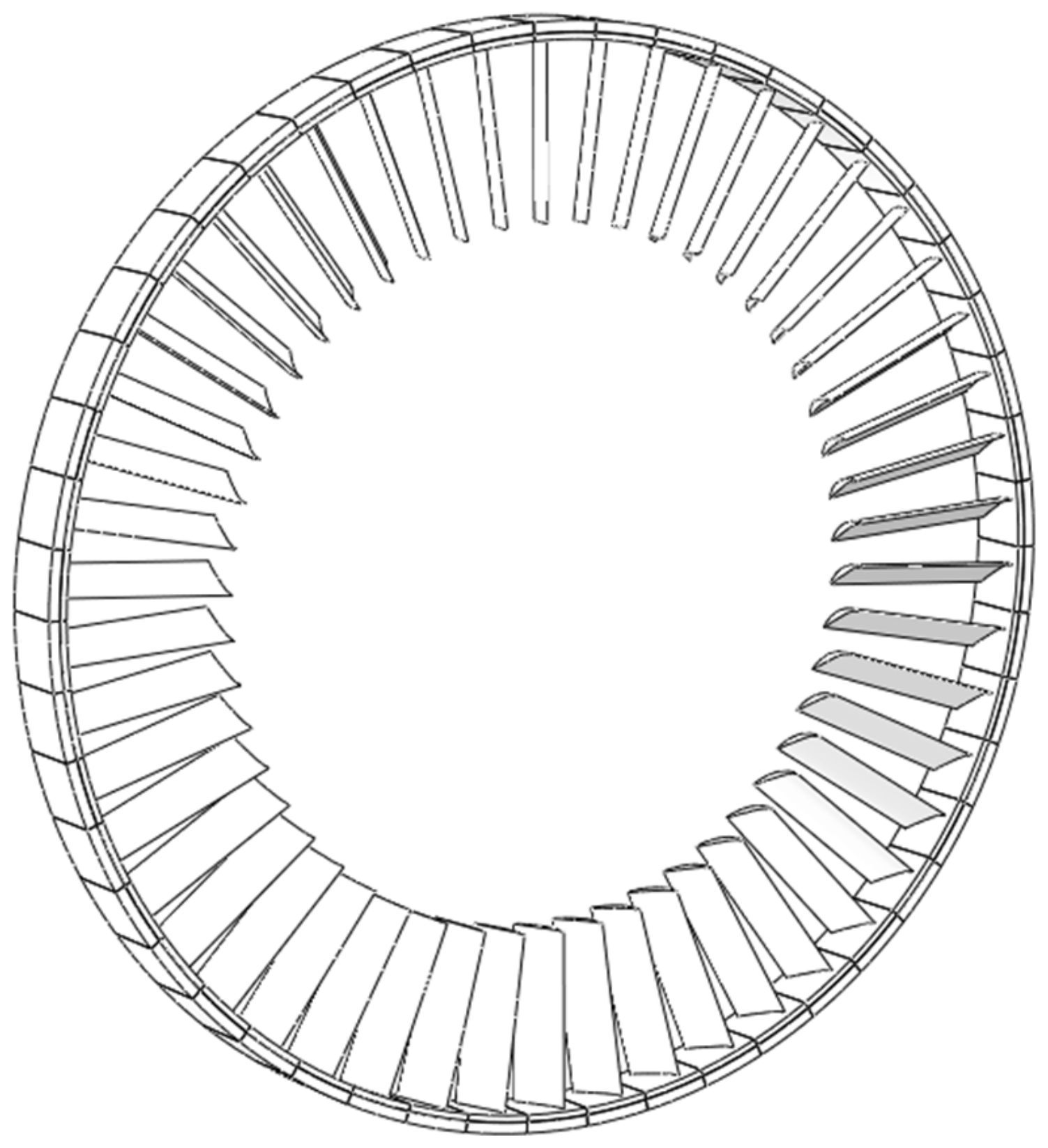
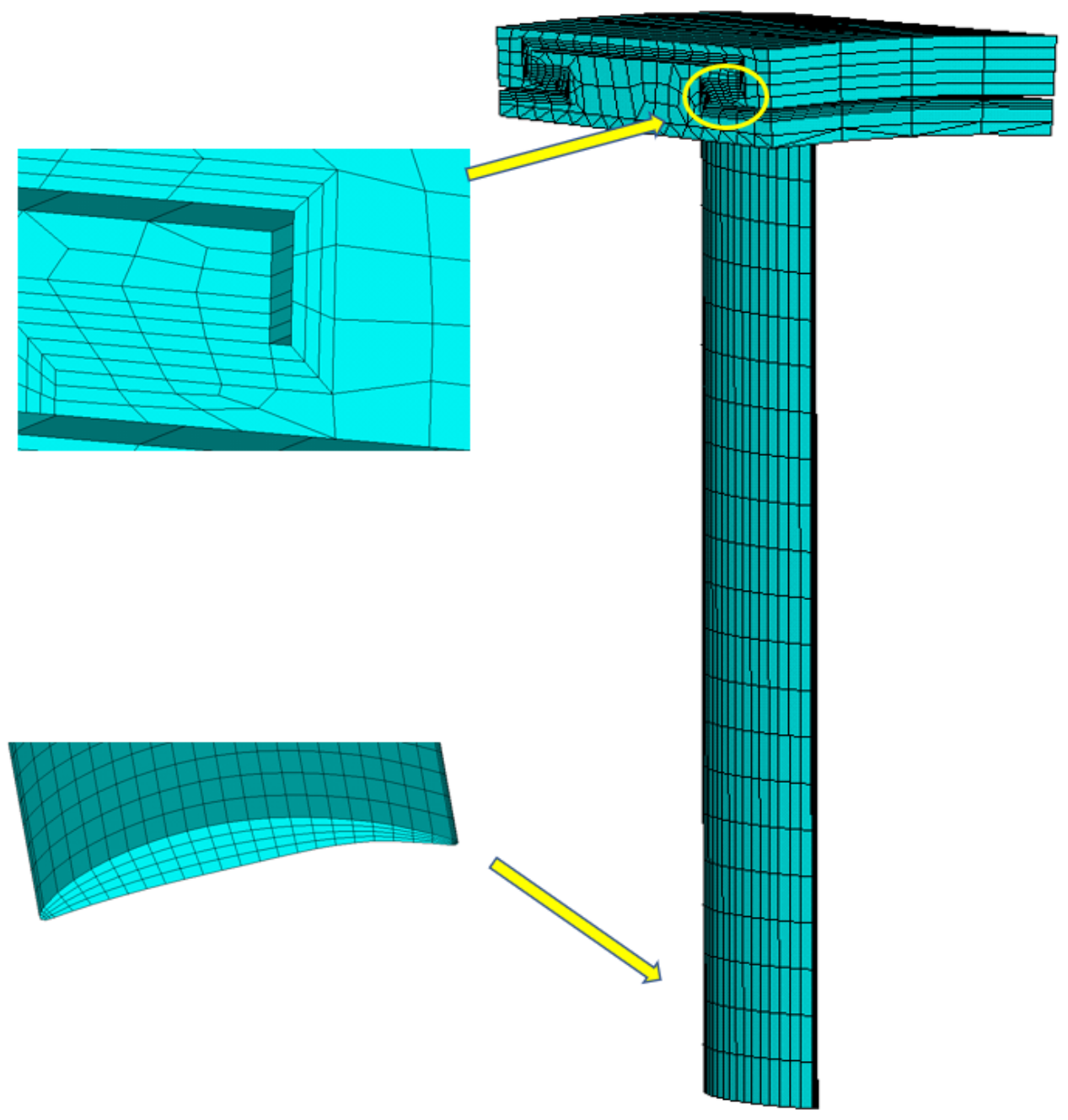
3.1. Finite Element Model of Compressor Stator Blade
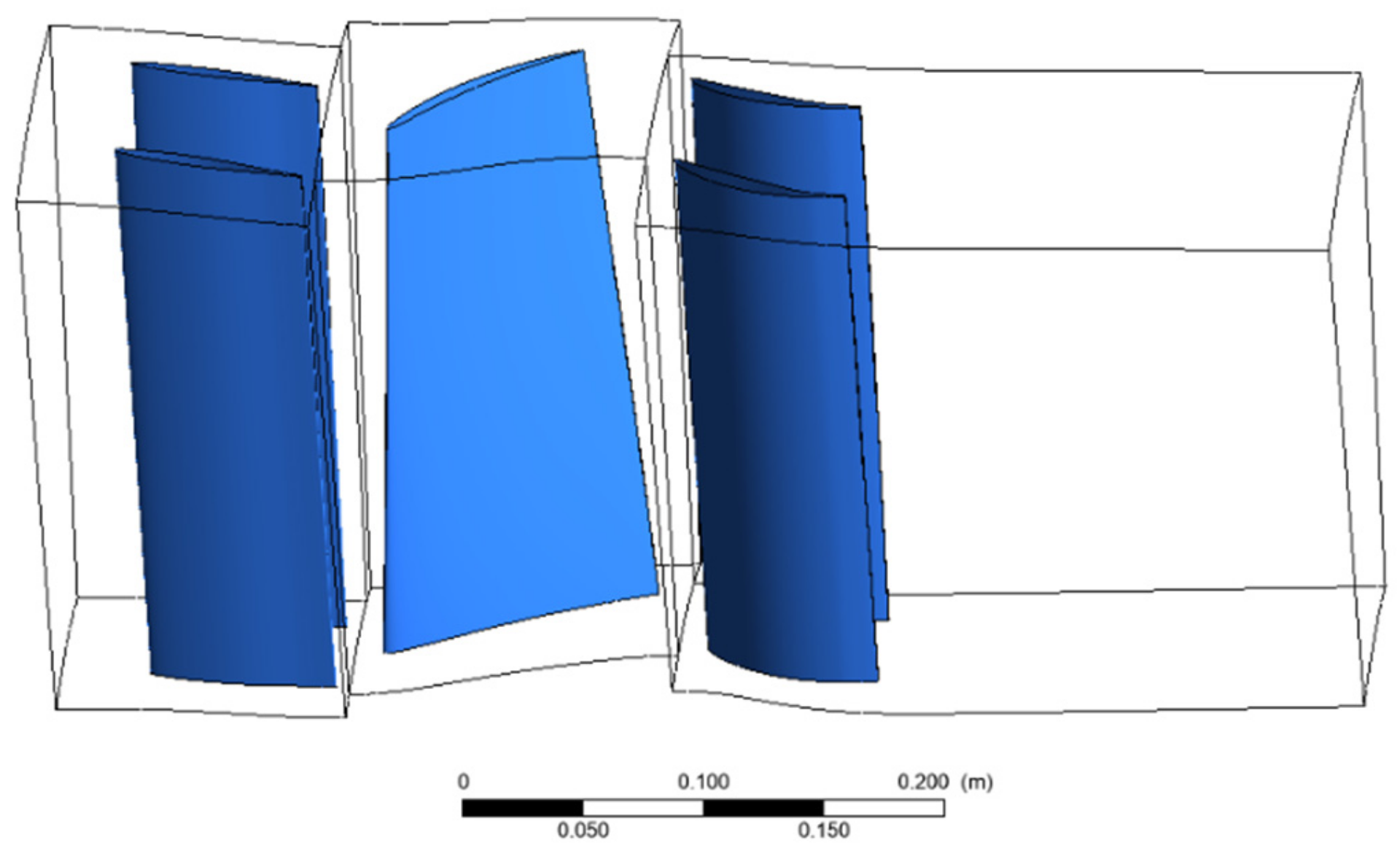
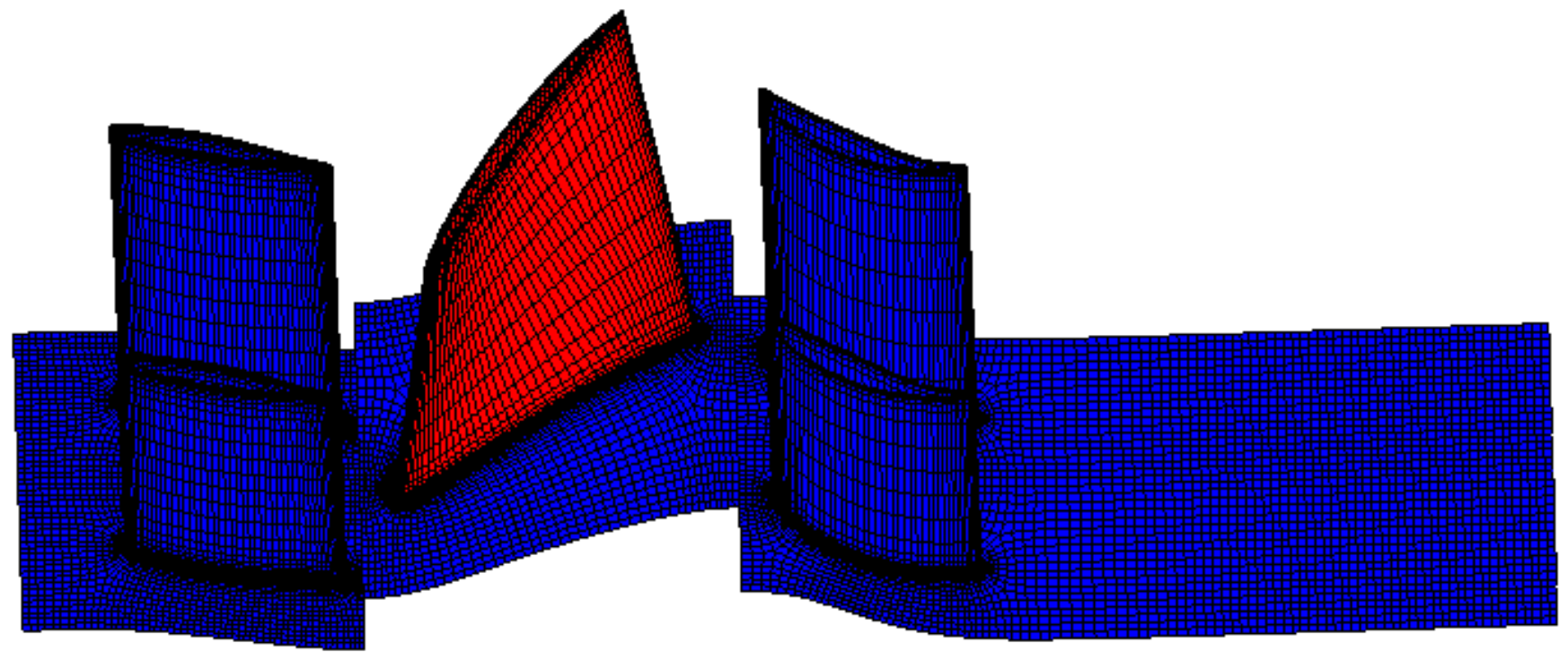
3.2. Stator Blade Load Analysis Model
4. Results and Discussion
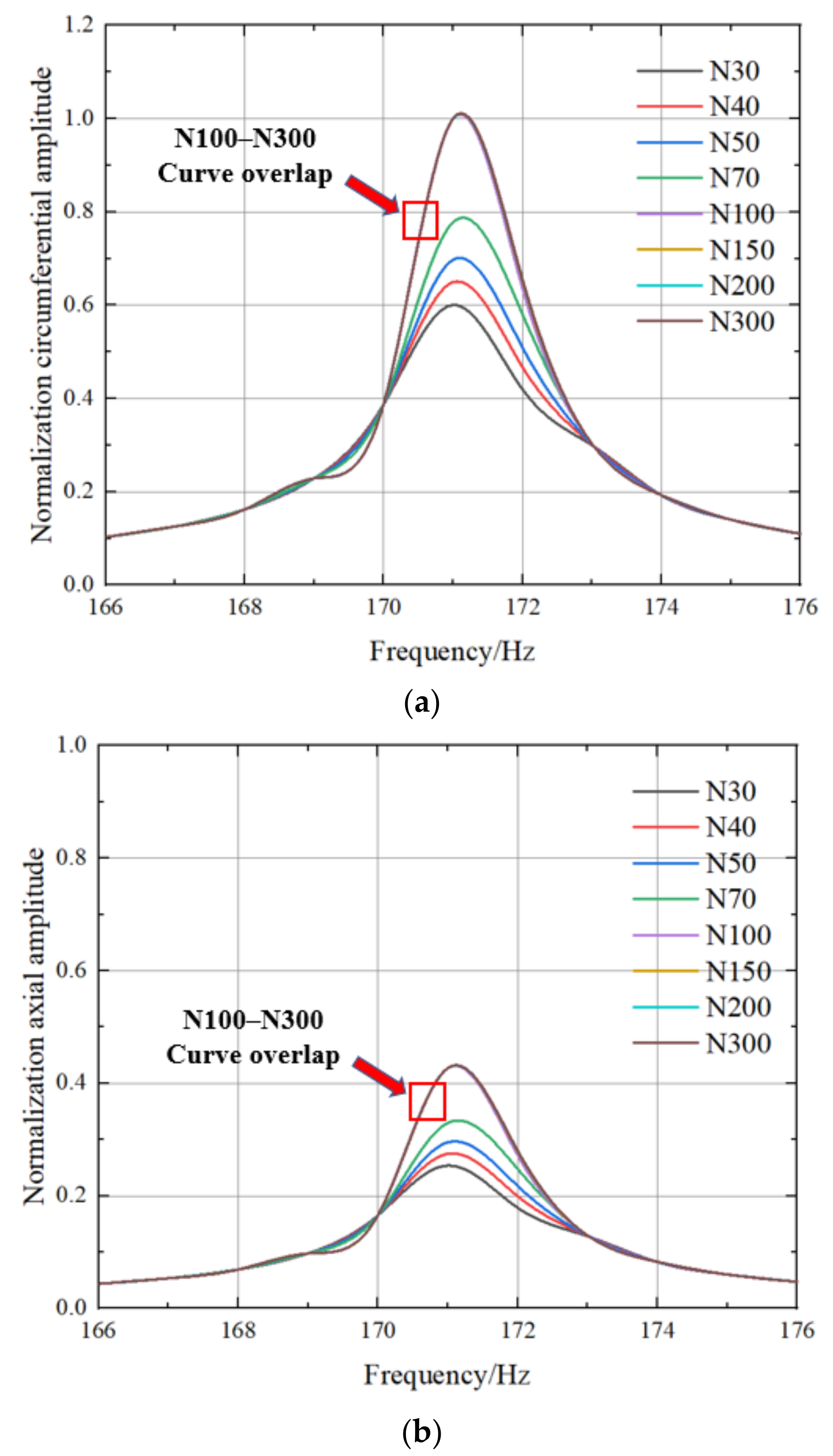
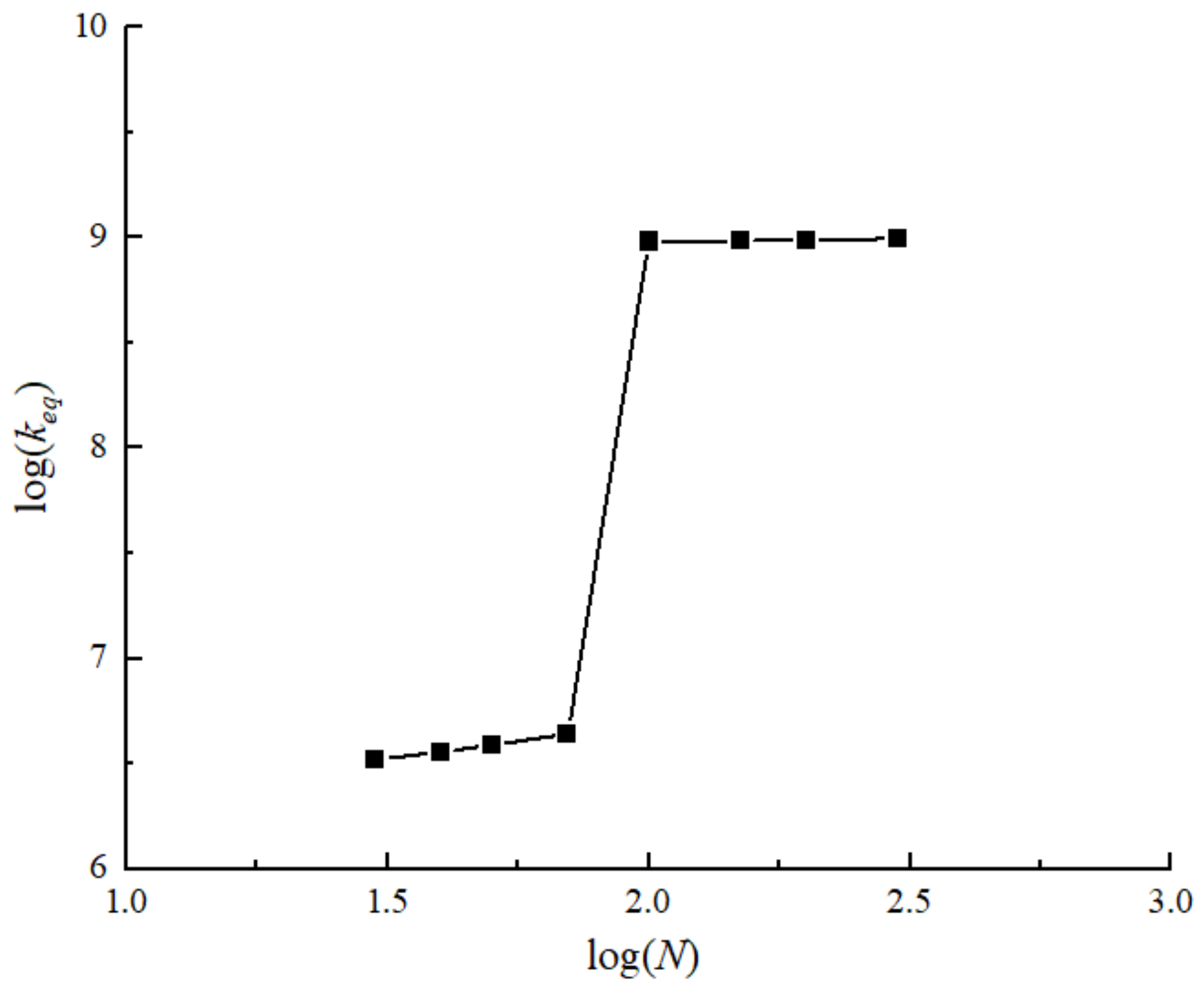
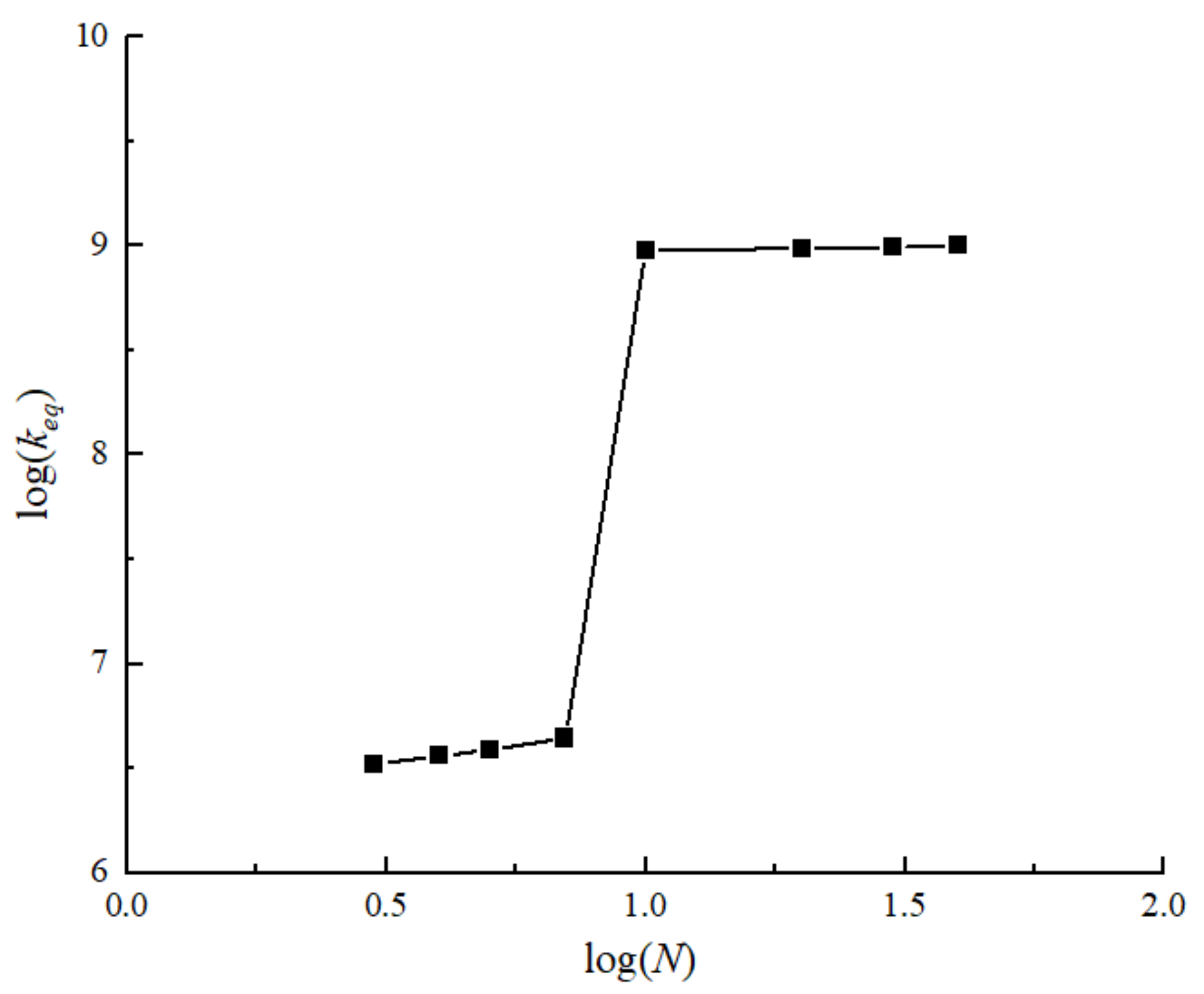
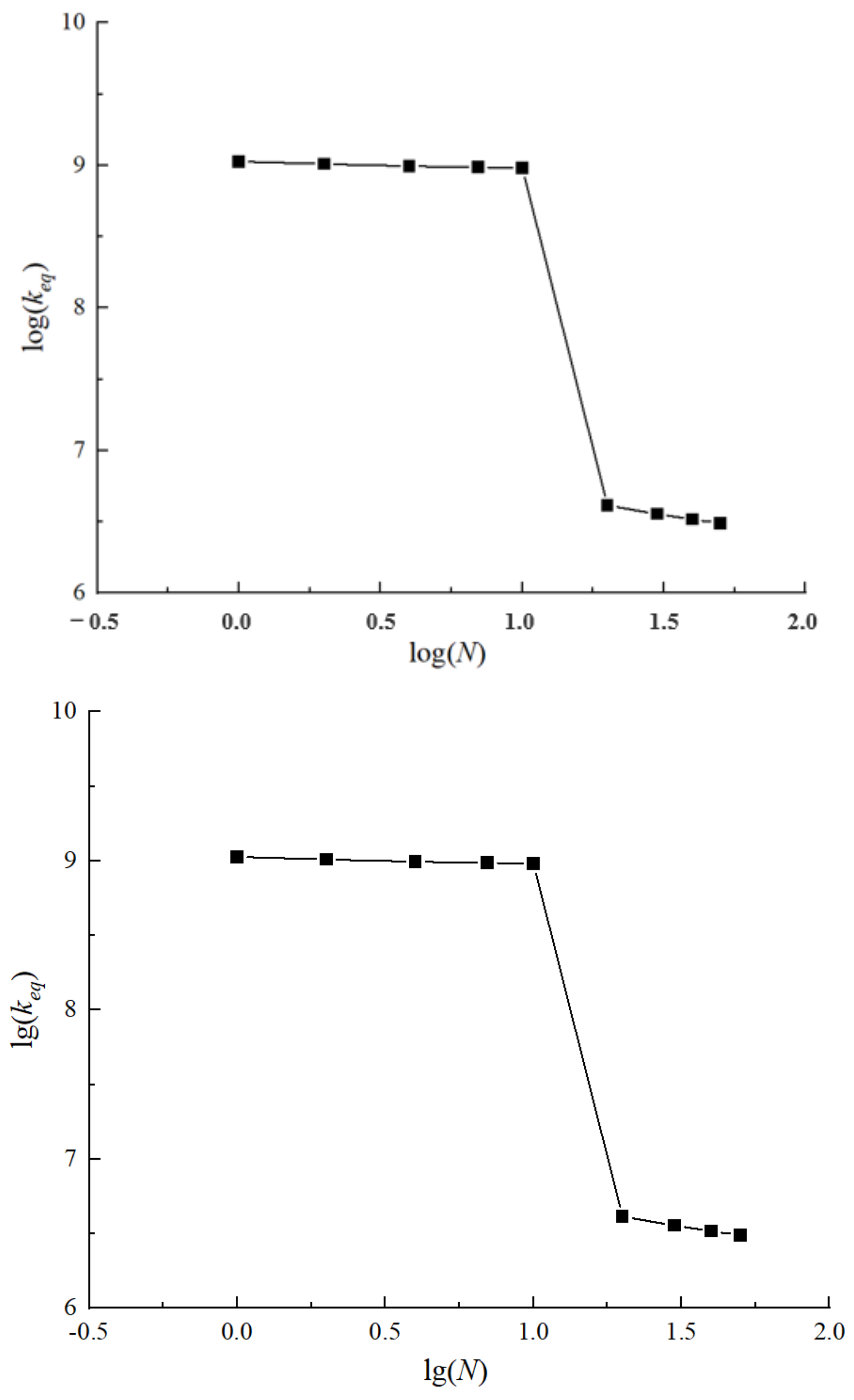
4.1. Nonlinear Vibration Results of Different Models
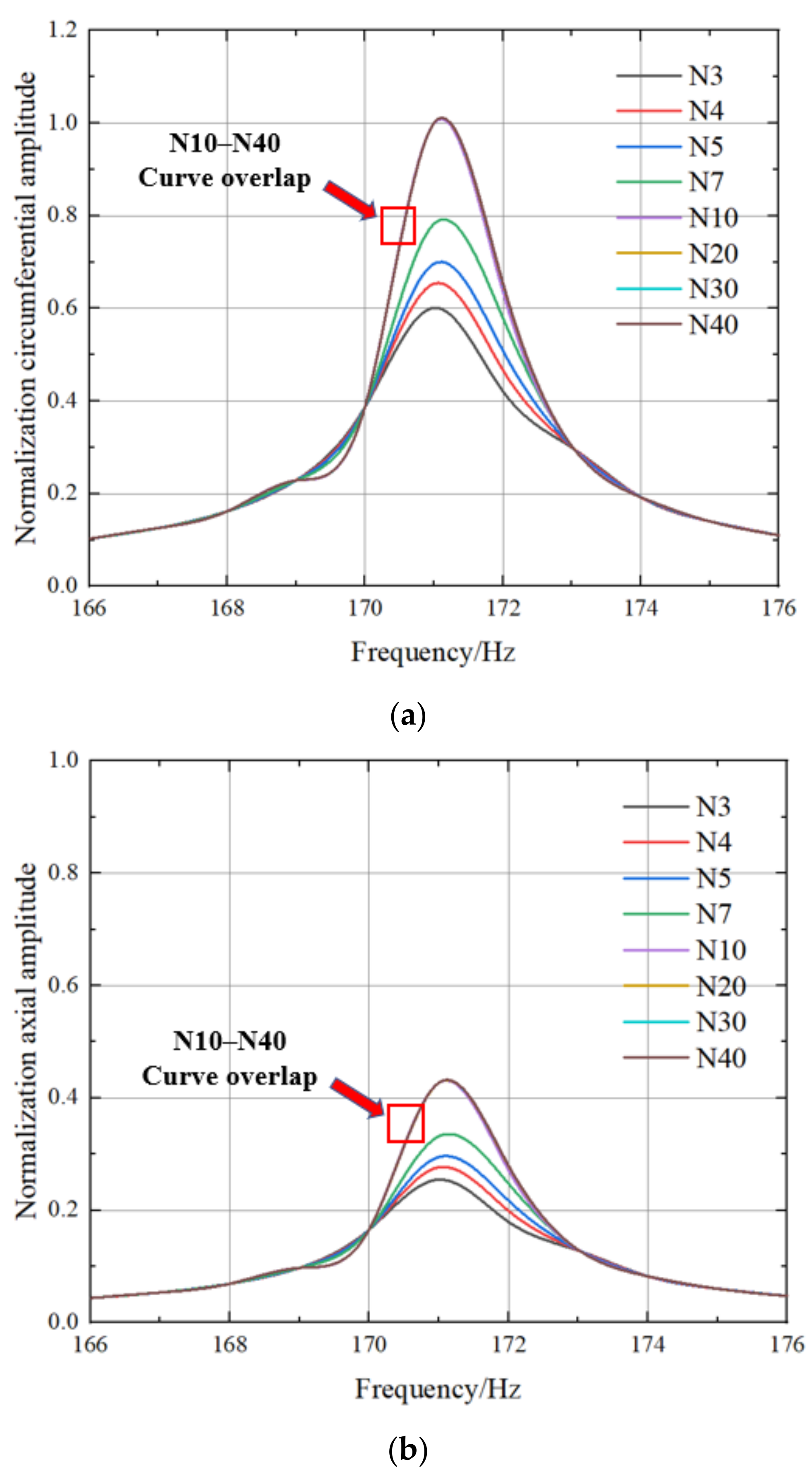
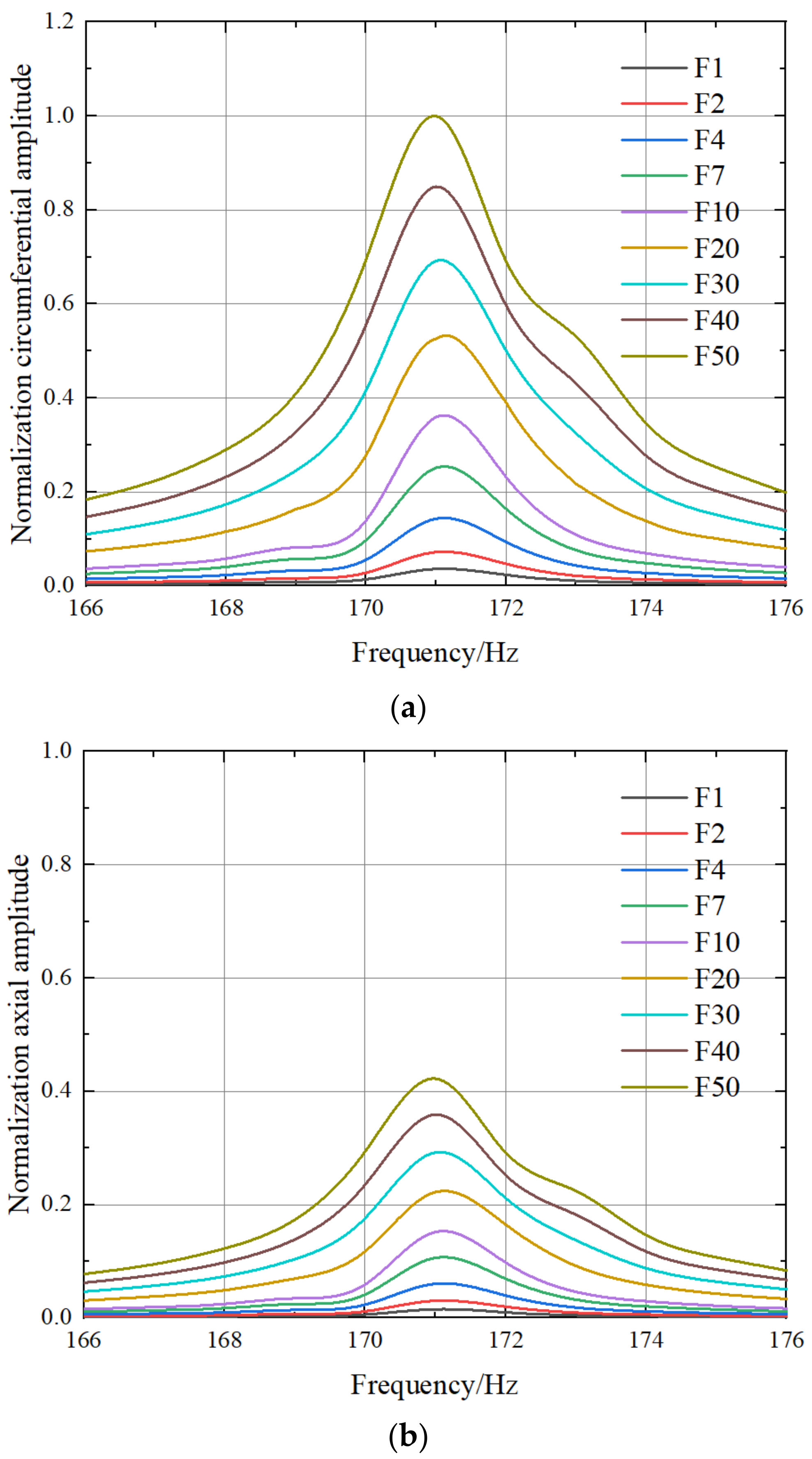
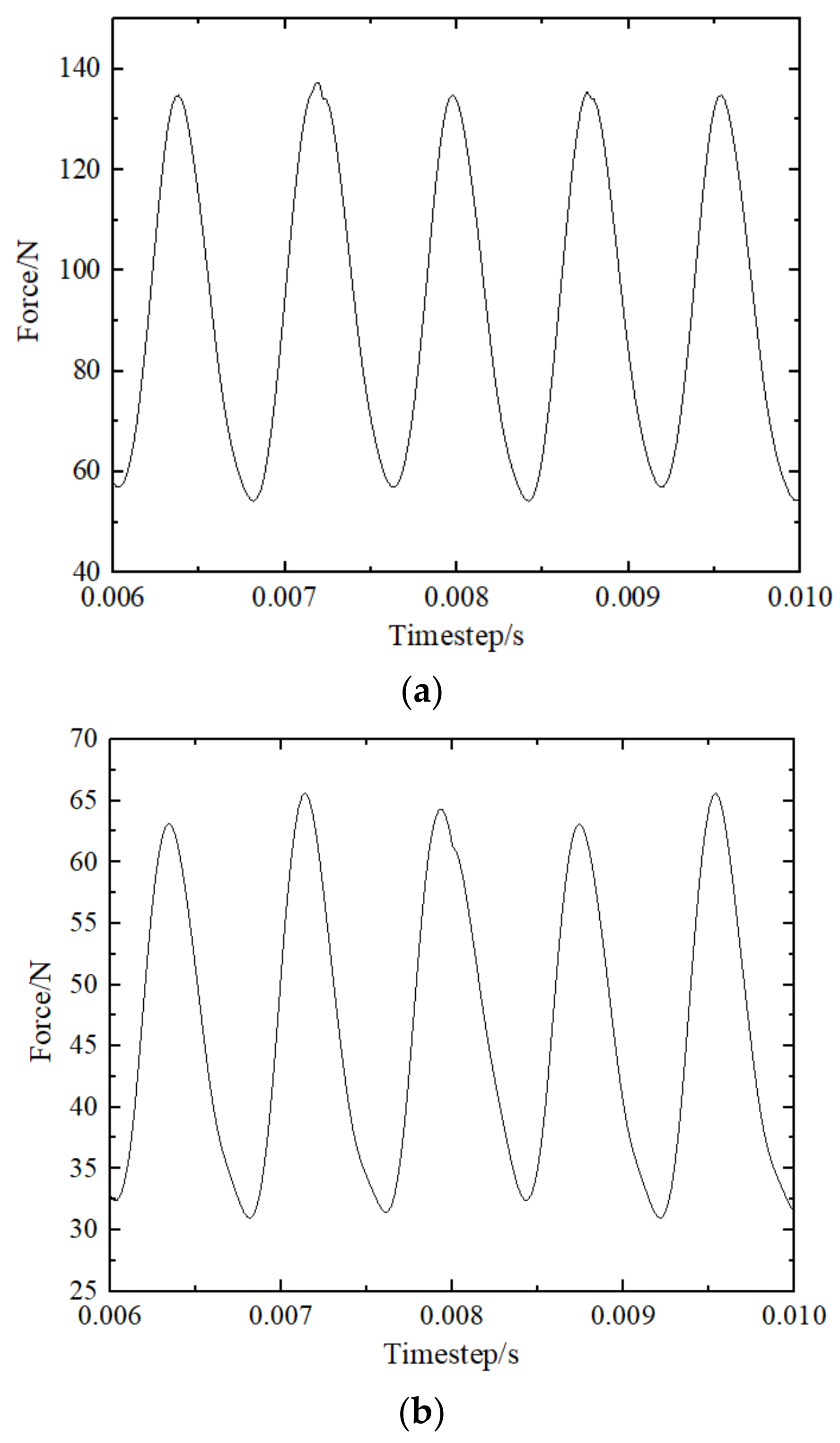
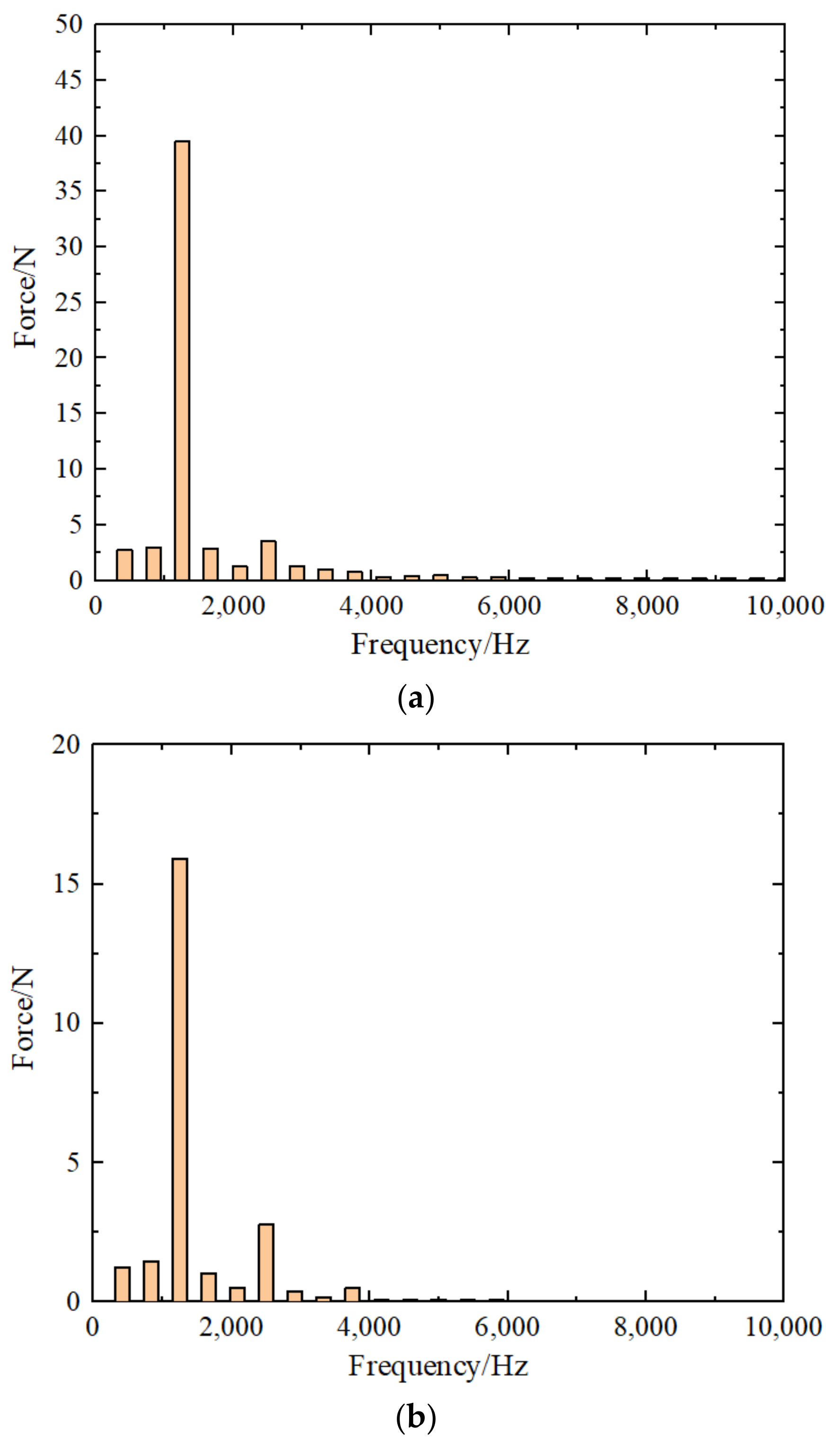
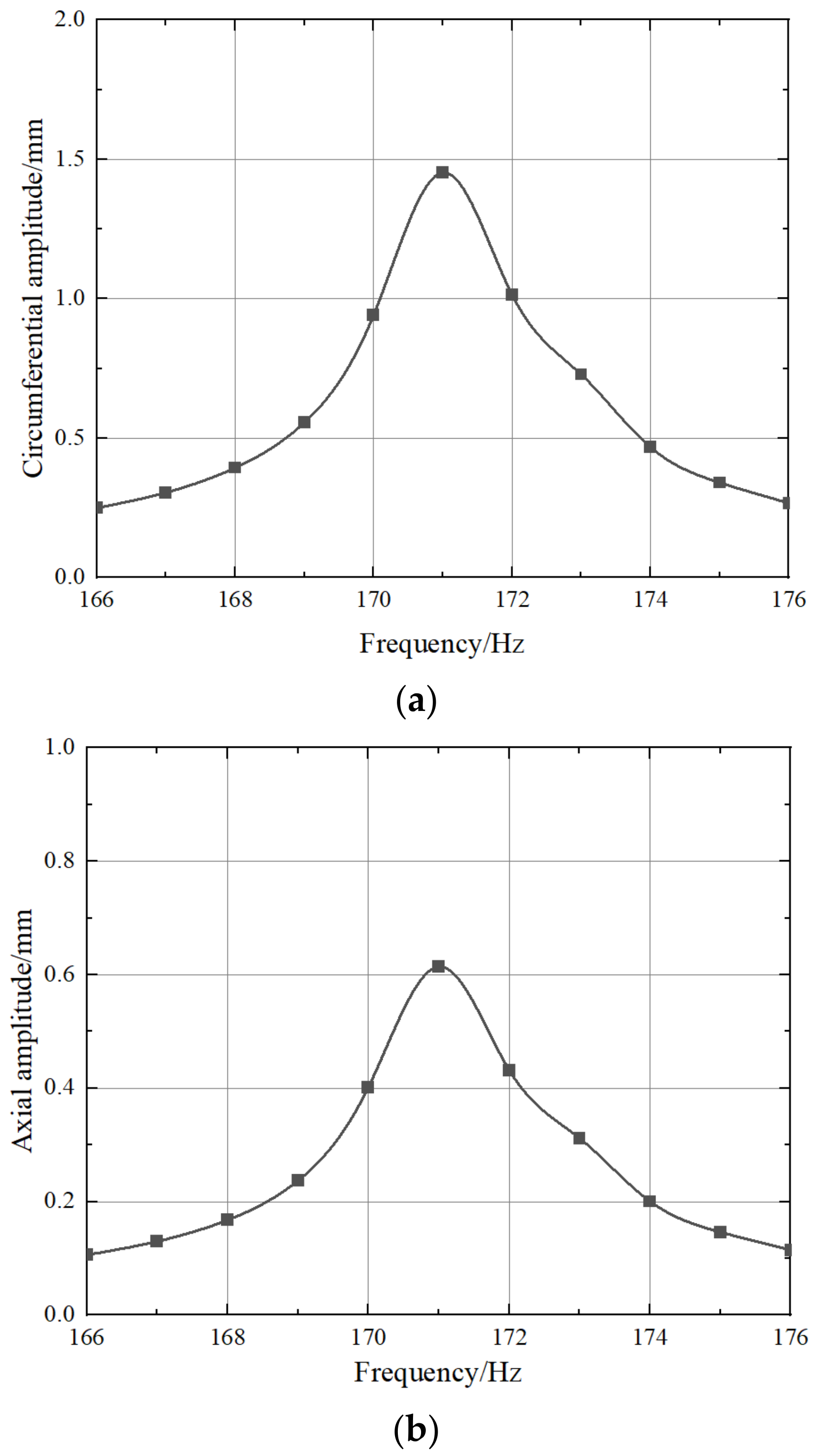
4.2. Vibration Response under a Particular Exciting Force
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sakulkaew, S.; Tan, C.S.; Donahoo, E.; Cornelius, C.; Montgomery, M. Compressor efficiency variation with rotor tip gap from vanishing to large clearance. J. Turbomach. 2013, 135, 031030. [Google Scholar] [CrossRef]
- Piollet, E.; Nyssen, F.; Batailly, A. Blade/casing rubbing interactions in aircraft engines: Numerical benchmark and design guidelines based on NASA rotor 37. J. Sound Vib. 2019, 460, 114878. [Google Scholar] [CrossRef]
- Nyssen, F.; Tableau, N.; Lavazec, D.; Batailly, A. Experimental and numerical characterization of a ceramic matrix composite shroud segment under impact loading. J. Sound Vib. 2020, 467, 115040. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, L.; Liu, Y.; Xu, L. Numerical Investigation and Optimization on Inlet Guide Vane Resonance of High-Pressure Compressor Caused by Wake Effect of Intermediate Case Strut in Multi-Stage Environment. J. Propuls. Technol. 2022, 43, 210098. [Google Scholar]
- Ozoliņš, Ē.; Ozoliņš, I.; Ramāna, L. Turbine Blade of Gas Turbine Engine Additional Unloading by Changing the Layout of the Gravity Centre of the Shroud Shelf. Transp. Aerosp. Eng. 2019, 7, 14–23. [Google Scholar] [CrossRef]
- Liu, L.L.; Liu, H.Z.; Wu, Z.Y.; Wang, Z.M. Research progress of friction model in mechanical system. J. Adv. Mech. 2008, 2, 201–213. [Google Scholar]
- Yang, B.D.; Chu, M.L.; Menq, C.H. Stick–slip–separation analysis and non-linear stiffness and damping characterization of friction contacts having variable normal load. J. Sound Vib. 1998, 210, 461–481. [Google Scholar] [CrossRef]
- Chen, J.J.; Yang, B.D.; Menq, C.H. Periodic forced response of structures having three-dimensional frictional constraints. J. Sound Vib. 2000, 229, 775–792. [Google Scholar] [CrossRef]
- Petrov, E.P. A method for use of cyclic symmetry properties in analysis of nonlinear multiharmonic vibrations of bladed disks. J. Turbomach. 2004, 126, 175–183. [Google Scholar] [CrossRef]
- Petrov, E.P. Explicit finite element models of friction dampers in forced response analysis of bladed disks. J. Eng. Gas Turbines Power 2008, 130, 022502. [Google Scholar] [CrossRef]
- Burdekin, M.; Cowley, A.; Back, N. An elastic mechanism for the micro-sliding characteristics between contacting machined surfaces. J. Mech. Eng. Sci. 1978, 20, 121–127. [Google Scholar] [CrossRef]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Cha, D.; Sinha, A. Statistics of responses of a mistuned and frictionally damped bladed disk assembly subjected to white noise and narrow band excitations. Probabilistic Eng. Mech. 2000, 21, 384–396. [Google Scholar] [CrossRef]
- Sinclair, G.B.; Cormier, N.G. Contact stresses in dovetail attachments: Physical modeling. J. Eng. Gas Turbines Power 2000, 124, 325–331. [Google Scholar] [CrossRef]
- Sinclair, G.B.; Cormier, N.G.; Griffin, J.H.; Meda, G. Contact stresses in dovetail attachments: Finite element modeling. J. Eng. Gas Turbines Power 2002, 124, 182–189. [Google Scholar] [CrossRef]
- Sinclair, G.B.; Cormier, N.G. Contact stresses in dovetail attachments: Alleviation via precision crowning. J. Eng. Gas Turbines Power 2003, 125, 1033–1041. [Google Scholar] [CrossRef]
- Ciğeroğlu, E.; Özgüven, H.N. Nonlinear vibration analysis of bladed disks with dry friction dampers. J. Sound Vib. 2006, 295, 1028–1043. [Google Scholar] [CrossRef]
- Wang, H.J.; He, E.M.; Yu, S.X. Forced response characteristics of bladed disks with disordered dry friction. J. Aerosp. Power 2006, 21, 711–715. [Google Scholar]
- Firrone, C.M.; Zucca, S.; Gola, M.M. The effect of under platform dampers on the forced response of bladed disks by a coupled stator/dynamic harmonic balance method. Int. J. Non-Linear Mech. 2011, 46, 363–375. [Google Scholar] [CrossRef]
- Zhang, L.; Yuan, H.Q.; Han, Q.K.; Yang, S.M.; Song, L.; Li, Y. Vibration analysis of mistuned bladed disk system based on microslip friction model. J. Vib. Eng. 2012, 25, 289–293. [Google Scholar]
- Ma, H.; Wang, D.; Neng, H.Q.; Tai, X.Y. Contact characteristic analysis of a compressor disc dovetail structure. J. Northeast. Univ. 2015, 36, 109–113. [Google Scholar]
- Peng, M.L.; Yang, Z.C.; Cao, Y.Y. Analysis on the influences of the contact gap on the contact response of turbine disc-blade structures. J. Aerosp. Power 2011, 26, 779–786. [Google Scholar]
- Wang, S.F.; Wen, Z.X.; Gao, Y.F. Effects of contact gap on contact properties of turbine blade tenon /mortise. J. Propuls. Technol. 2015, 36, 112–118. [Google Scholar]
- Chen, Z.Y.; Wang, C.; Zhou, P. Research on Robust Optimization of Fatigue Life for Blade-Disk Considering Contact Gap between Tenon and Mortise. J. Propuls. Technol. 2018, 39, 857–864. [Google Scholar]
- Zeng, H.N.; Cao, S.Q.; Su, Y.L. Vibration localization of a mistuned bladed disk system with friction and gap. J. Vib. Shock 2016, 35, 82–90. [Google Scholar]
- Wu, J.; Yuan, R.; He, Z.; Zhang, D.; Xie, Y. Experimental study on dry friction damping characteristics of the steam turbine blade material with nonconforming contacts. Adv. Mater. Sci. Eng. 2015, 2015, 849253. [Google Scholar]
- Zhao, W.; Zhang, D.; Sun, L.; Xie, Y. Nonlinear dynamics analysis of mistuned turbine bladed disks with damped shrouds. In Proceedings of the ASME Power Conference; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 57618, p. V002T11A011. [Google Scholar]
- Ma, J.; Liu, Z.; Li, Y.; Xie, Y. Prediction Method of Unsteady Flow Load of Compressor Stator under Working Condition Disturbance. Appl. Sci. 2022, 12, 11566. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Liu, Z.; Zhang, D.; Xie, Y. Numerical Study on Vibration Response of Compressor Stator Blade Considering Contact Friction of Holding Ring. Appl. Sci. 2023, 13, 6380. https://doi.org/10.3390/app13116380
Ma J, Liu Z, Zhang D, Xie Y. Numerical Study on Vibration Response of Compressor Stator Blade Considering Contact Friction of Holding Ring. Applied Sciences. 2023; 13(11):6380. https://doi.org/10.3390/app13116380
Chicago/Turabian StyleMa, Jiaobin, Zhufeng Liu, Di Zhang, and Yonghui Xie. 2023. "Numerical Study on Vibration Response of Compressor Stator Blade Considering Contact Friction of Holding Ring" Applied Sciences 13, no. 11: 6380. https://doi.org/10.3390/app13116380
APA StyleMa, J., Liu, Z., Zhang, D., & Xie, Y. (2023). Numerical Study on Vibration Response of Compressor Stator Blade Considering Contact Friction of Holding Ring. Applied Sciences, 13(11), 6380. https://doi.org/10.3390/app13116380




