A Comprehensive Methodology for Investment Project Assessment Based on Monte Carlo Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Problem Description
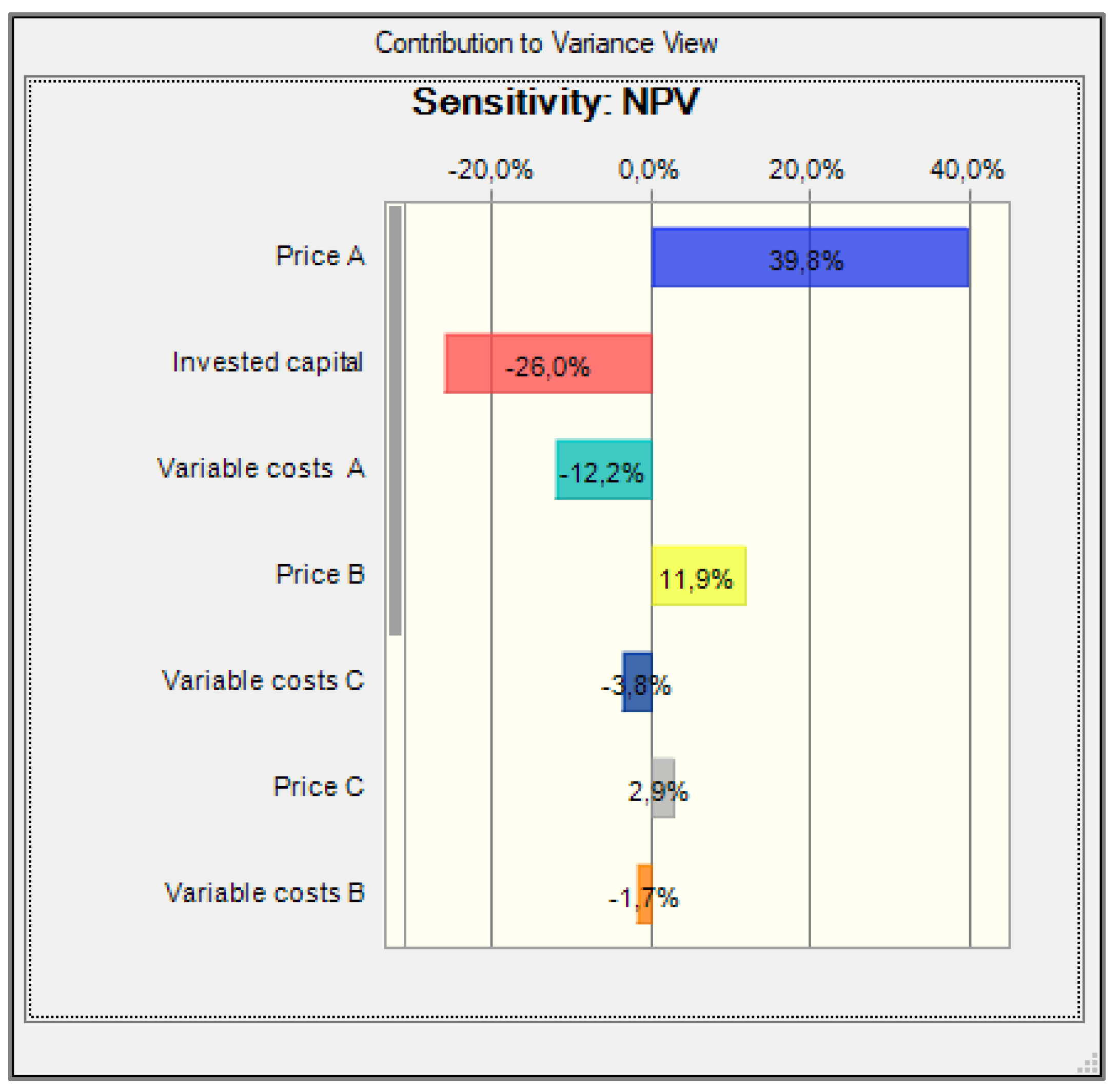
- First, it concerns the selection of input variables and the definition of their relationship to overall economic efficiency. Many input variables are stochastic, and the numerical value we consider in the calculation has a direct and significant impact on the forecast of investment profitability. Here, if their development in the past is known, we can use time series forecasting methods to forecast their future evolution; it can be the development of demand, the prices of essential materials and energy inputs, the selling price of products, etc.
- The second step is the choice of a financial indicator for assessing profitability and its calculation. It is essentially a forecast variable that can be calculated deterministically or, if the input variables are stochastic, by Monte Carlo simulations.
- The third step is to assess the result of the simulations in terms of risk and optimize the production program concerning the requirement—maximum profitability at an acceptable level of risk.
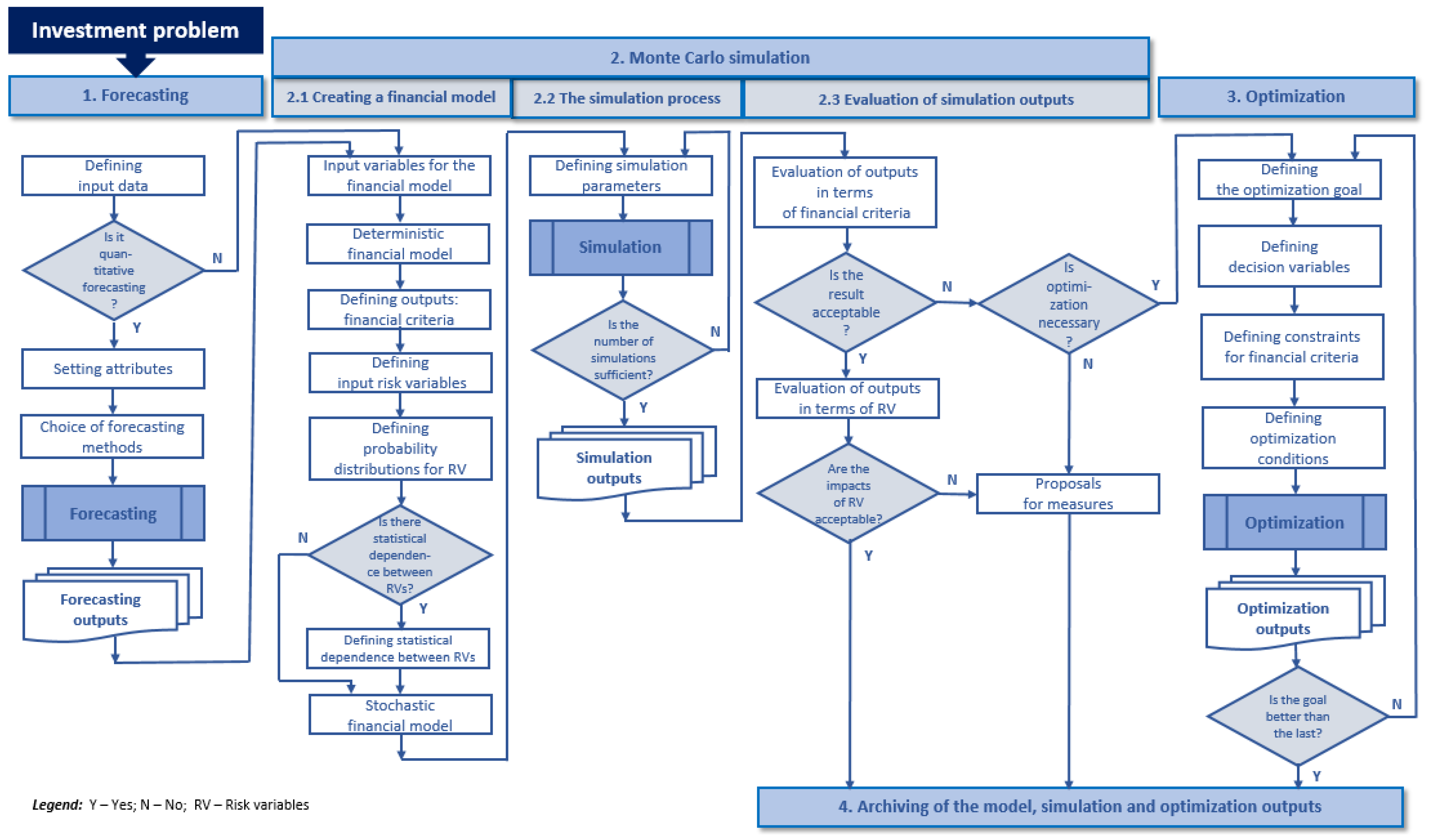
2.2. Methodology for Investment Assessment
3. Application of the Methodology on a Virtual Investment Project
3.1. Investment Project Description
- optimal use of the line time,
- maximization of the economic efficiency of the investment using the NPV financial criterion,
- minimization of the investment risk (i.e., achieving an acceptable level of risk while simultaneously maximizing the economic efficiency of the investment).
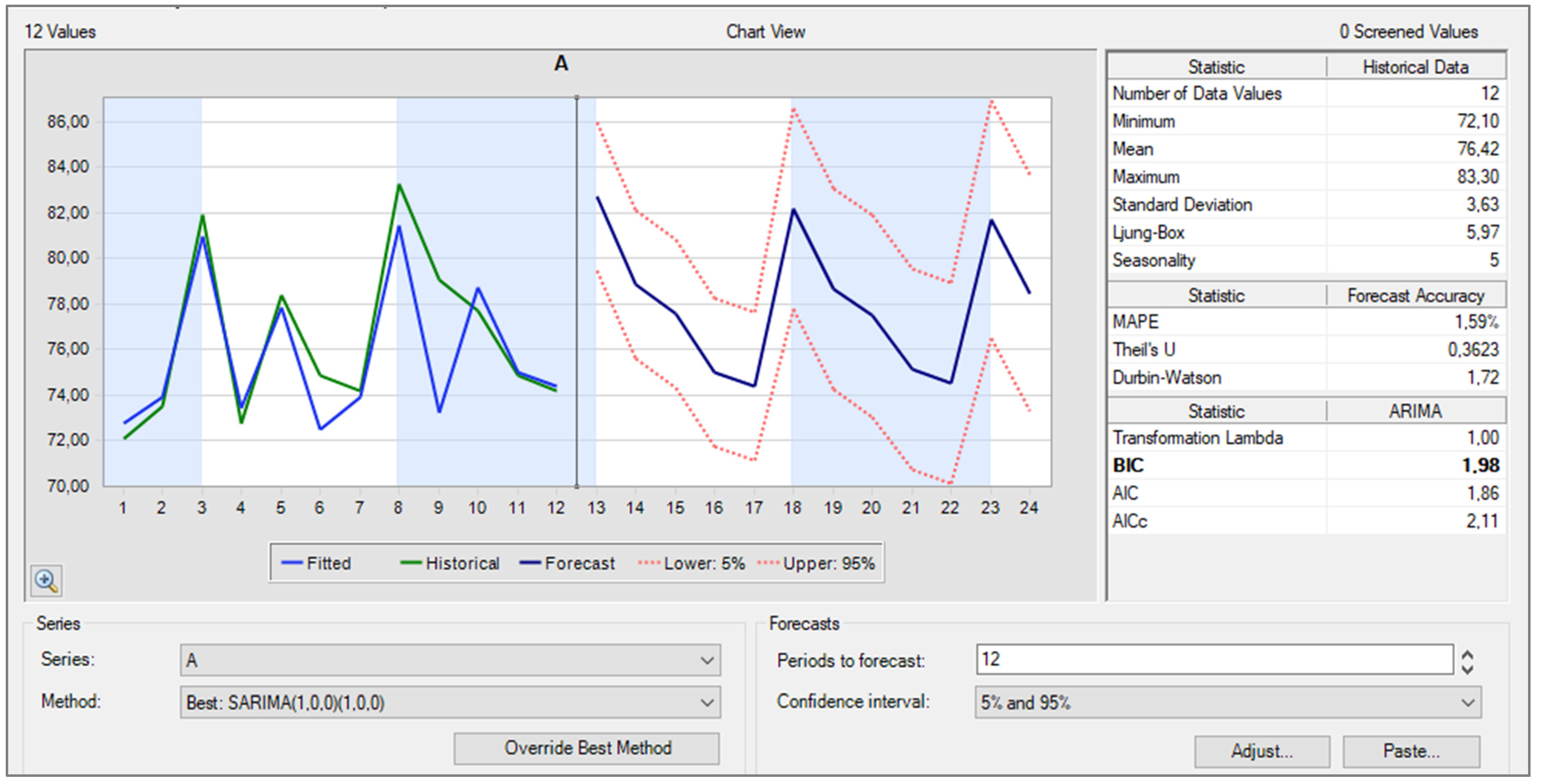
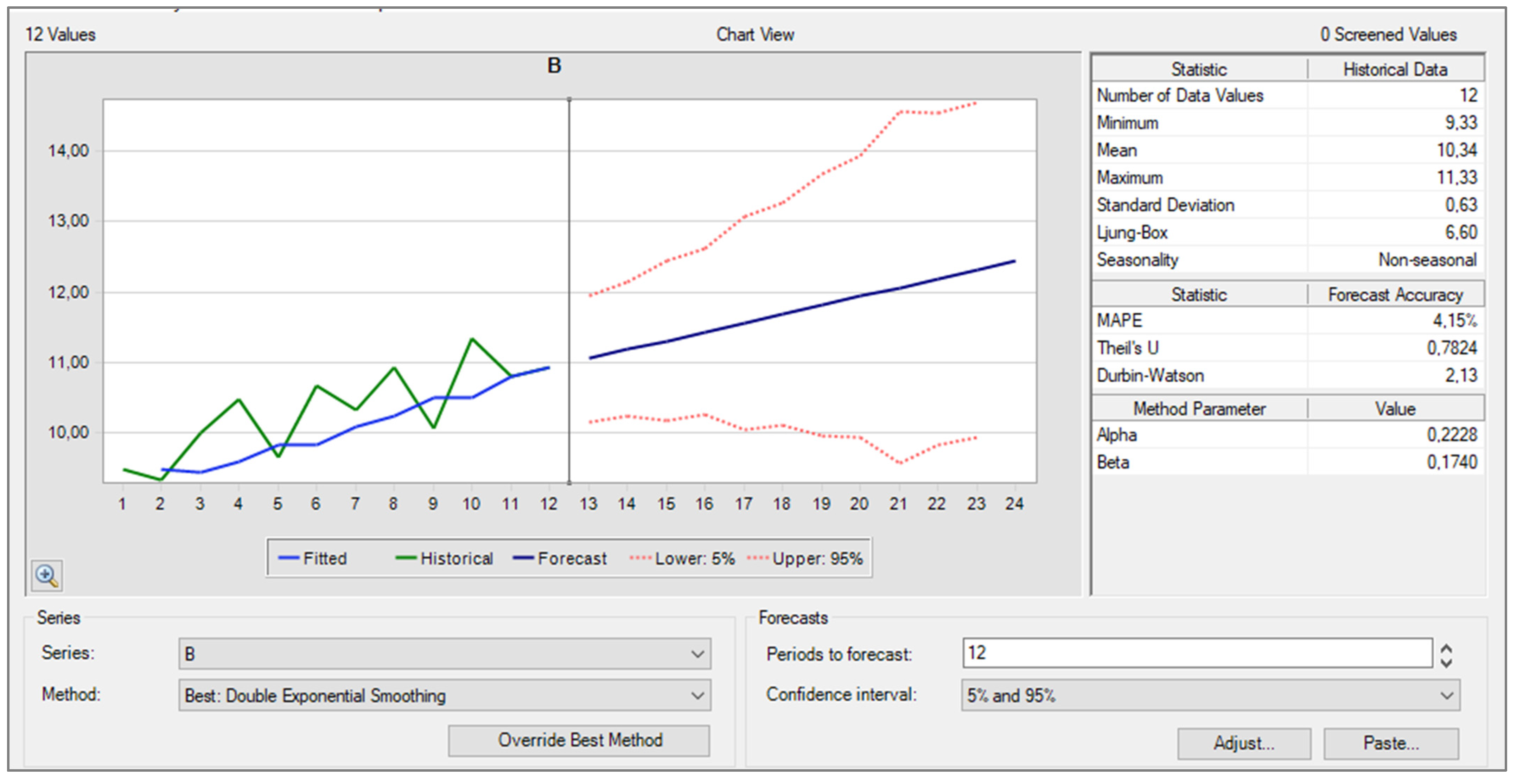
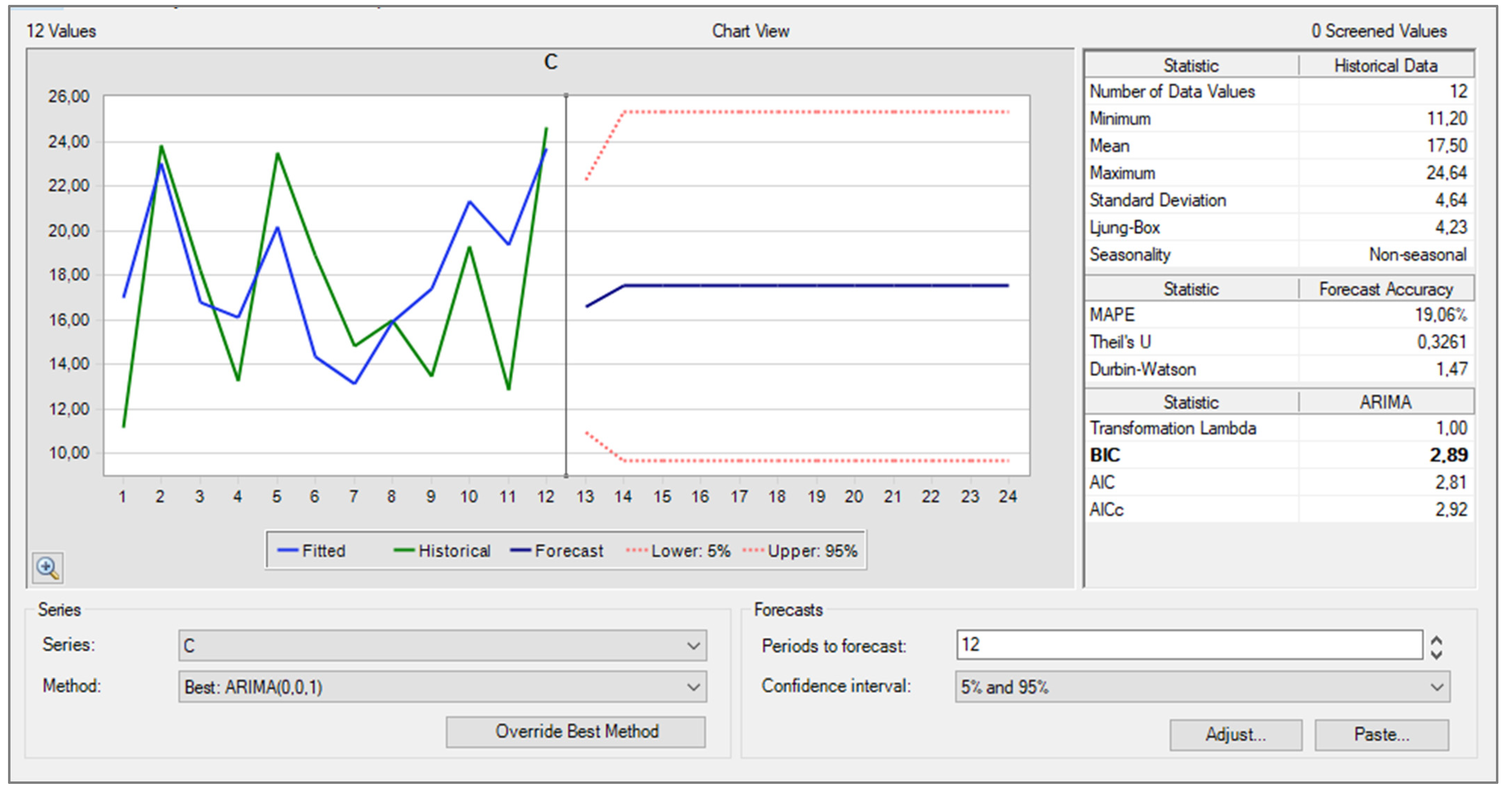
3.2. Timeseries Forecasting of Demand for Products A, B, C
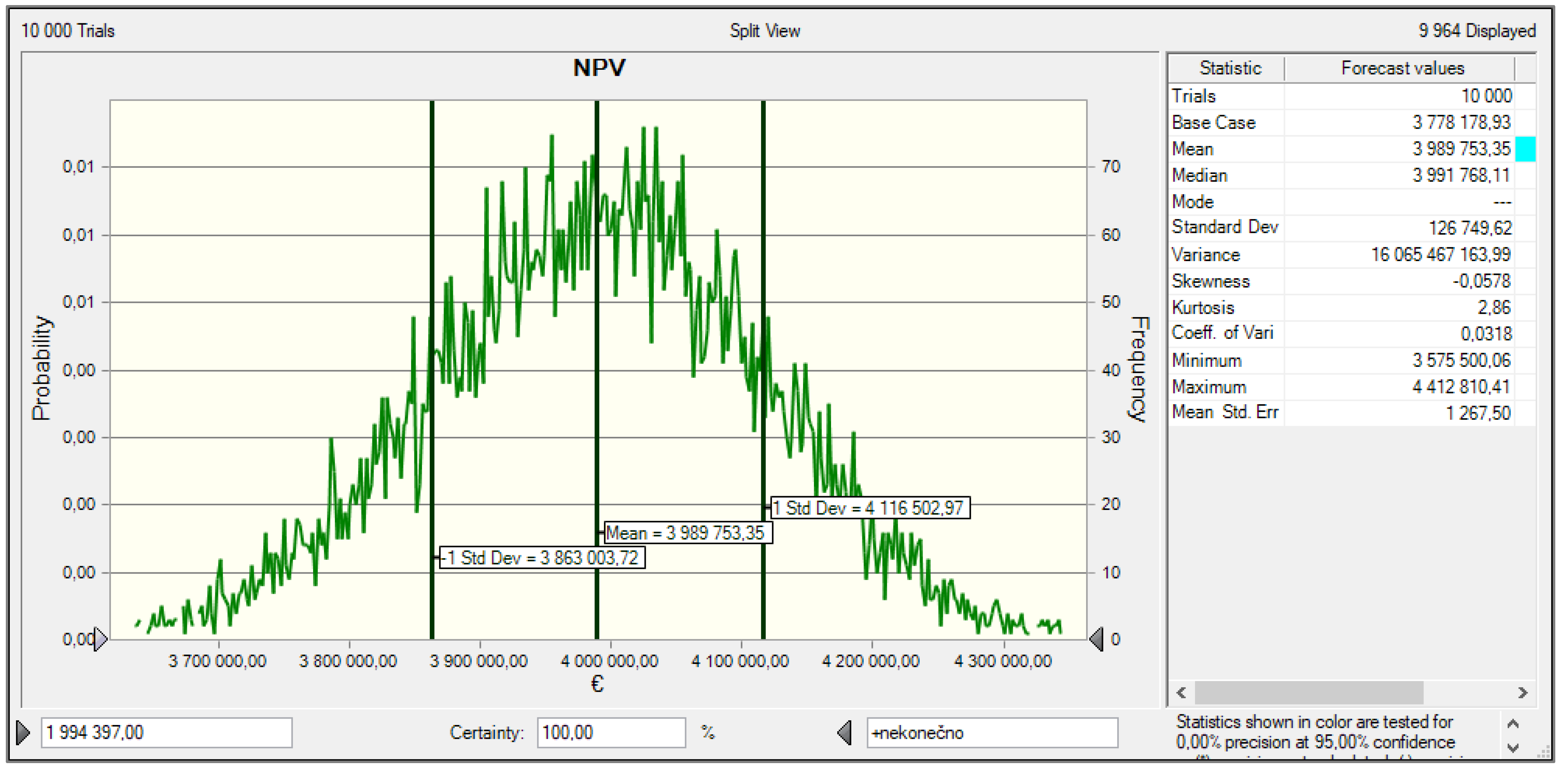
3.3. Creating a Financial Model and Calculating NPV Deterministically
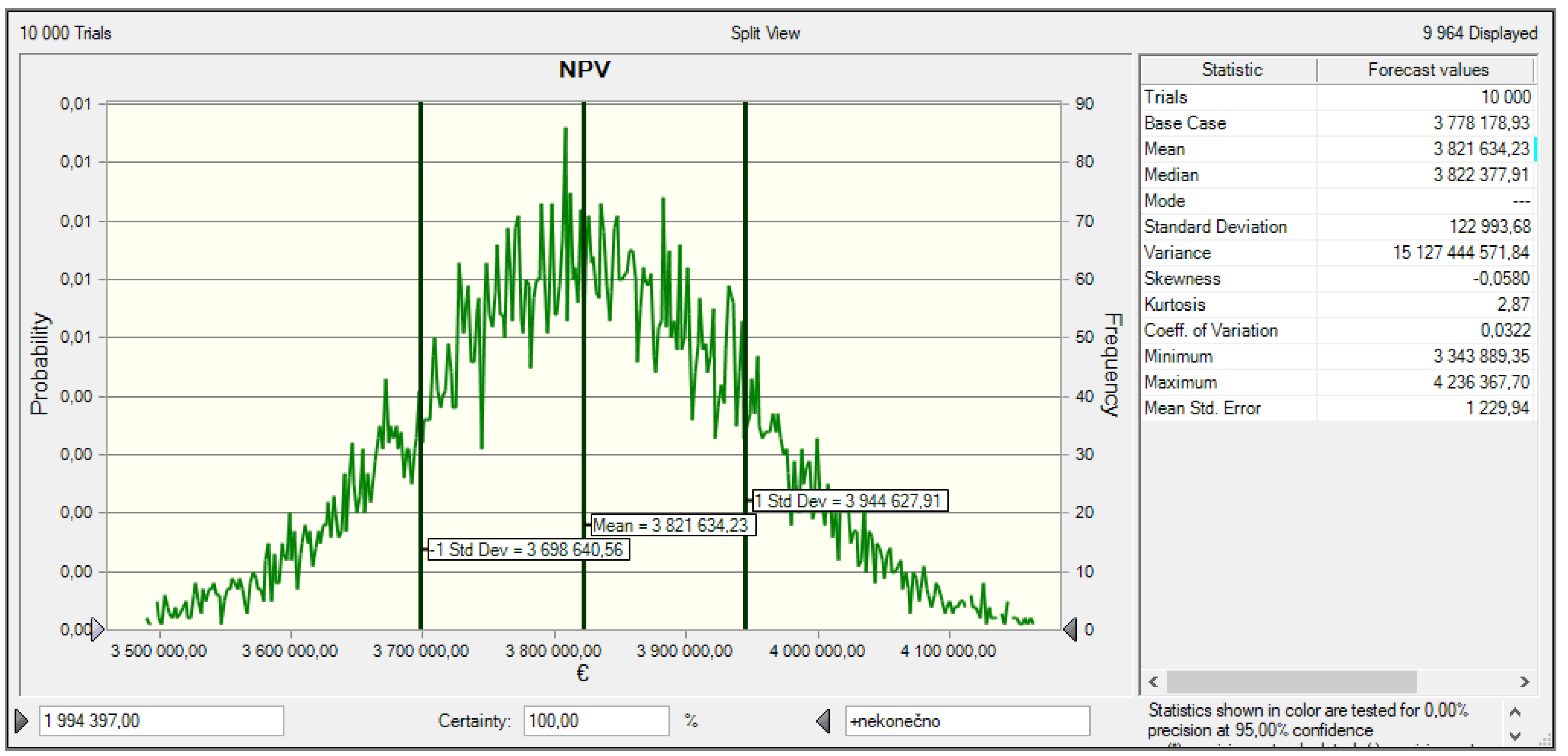
3.4. Simulation of NPV by Monte Carlo Method
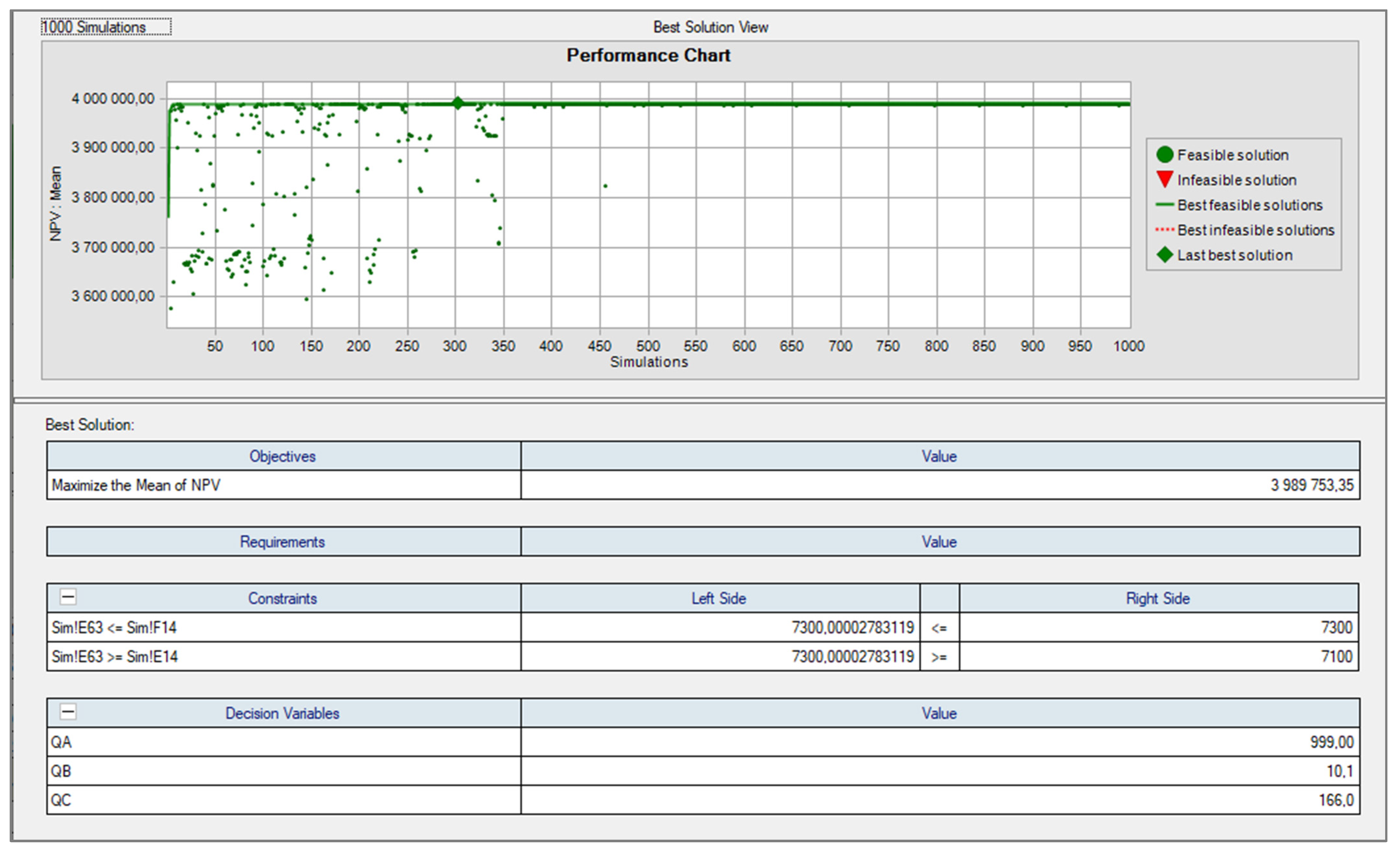
3.5. Optimization of the Production Plan
- The objective of the optimization is to maximize the mean NPV.
- Restriction for optimization:
- ○
- Constraints in the use of the time of the production line. Minimum use of 7100 h and maximum available line time capacity of 7300 h.
- ○
- The production volume of product A is limited to a minimum of 700 t/year due to the contracts.
- ○
- For the controlled variables (production volumes A, B, C), a minimum volume of 10 t/year was set (because at least a minimum production would be available and the product would not be dropped from the production program), and a maximum volume of 1000 t/year (which was only a theoretical limitation—such a volume would not be sold on the market due to the demand forecast).
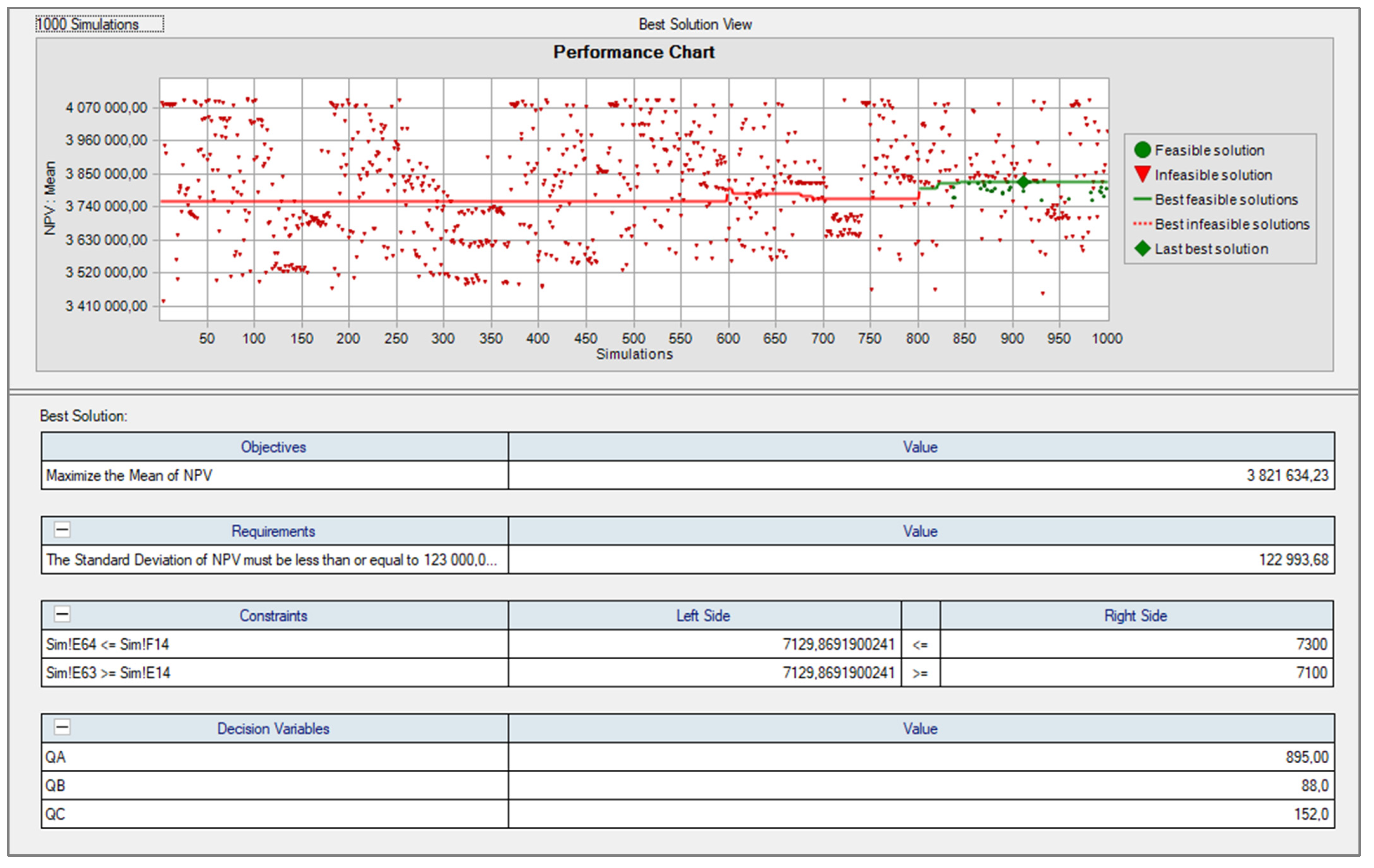
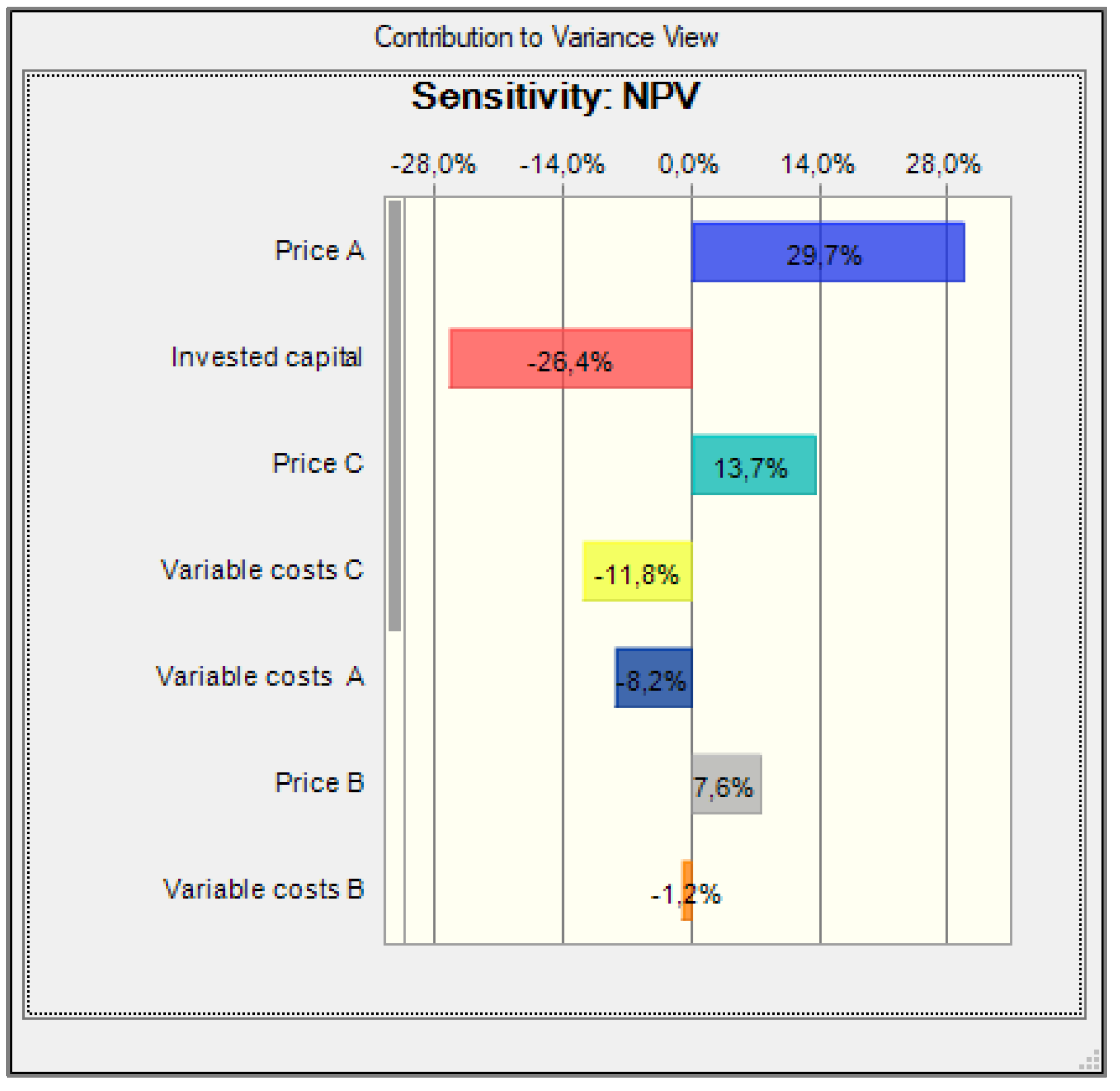
3.6. Optimization of the Production Plan Taking Risk into Account
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grzeszczyk, T.A.; Waszkiewicz, M. Sustainable Investment Project Evaluation. Entrep. Sustain. Issues 2020, 7, 2363–2381. [Google Scholar] [CrossRef] [PubMed]
- Suhanyiova, A.; Suhanyi, L. Analysis of depreciation of intangible and tangible fixed assets and the impact of depreciation on the profit or loss and on the tax base of the enterprise. In Proceedings of the 18th International Scientific Conference on International Relations—Current Issues of World Economy and Politics, Smolenice, Slovakia, 30 November–1 December 2017; pp. 939–950. [Google Scholar]
- Song, Y.; Li, X.Y.; Li, Y.; Hong, X. Risk investment decisions within the deterministic equivalent income model. Kybernetes 2021, 50, 616–632. [Google Scholar] [CrossRef]
- Froot, K.A.; Scharfstein, D.S.; Stein, J.C. Risk Management: Coordinating Corporate Investment and Financing Policies. J. Financ. 1993, 48, 1629–1658. [Google Scholar] [CrossRef]
- Feng, Z. Financial risks from three dimensions and risk identification model of enterprise. Int. J. Manag. Sci. Eng. Manag. 2011, 6, 71–80. [Google Scholar] [CrossRef]
- Tobisova, A.; Senova, A.; Rozenberg, R. Model for Sustainable Financial Planning and Investment Financing Using Monte Carlo Method. Sustainability 2022, 14, 8785. [Google Scholar] [CrossRef]
- Chung, S.H.; Lee, A.H.I.; Pearn, W.L. Product mix optimization for semiconductor manufacturing based on AHP and ANP analysis. Int. J. Adv. Manuf. Technol. 2005, 25, 1144–1156. [Google Scholar] [CrossRef]
- Aryanezhad, M.B.; Komijan, A.R. An improved algorithm for optimizing product mix under the theory of constraints. Int. J. Prod. Res. 2004, 42, 4221–4233. [Google Scholar] [CrossRef]
- Janekova, J.; Fabianova, J.; Izarikova, G.; Onofrejova, D.; Kovac, J. Product mix optimization based on Monte Carlo simulation: A case study. Int. J. Simul. Model 2018, 17, 295–307. [Google Scholar] [CrossRef]
- Dranka, G.G.; Cunha, J.; de Lima, J.D.; Ferreira, P.V. Economic evaluation methodologies for renewable energy projects. AIMS Energy 2020, 8, 339–364. [Google Scholar] [CrossRef]
- Dheskali, E.; Koutinas, A.A.; Kookos, I.K. Risk assessment modeling of bio-based chemicals economics based on Monte-Carlo simulations. Chem. Eng. Res. Des. 2020, 163, 273–280. [Google Scholar] [CrossRef]
- Cunha, J.C.; Demirdal, B.; Gui, P. Use of quantitative risk analysis for uncertainty quantification on drilling operationsreview and lessons learned. SPE Lat. Am. Caribb. Pet. Eng. Conf. Proc. 2005; Epub ahead of print. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Z.; Zhang, S.; Chen, Y. Investment decision making along the b&r using critic approach in probabilistic hesitant fuzzy environment. J. Bus Econ. Manag. 2020, 21, 1683–1706. [Google Scholar]
- Harris, C.; Roark, S. Cash flow risk and capital structure decisions. Financ. Res. Lett. 2019, 29, 393–397. [Google Scholar] [CrossRef]
- da Silva Pereira, E.J.; Pinho, J.T.; Galhardo, M.A.B.; Macêdo, W.N. Methodology of risk analysis by Monte Carlo Method applied to power generation with renewable energy. Renew. Energy 2014, 69, 347–355. [Google Scholar] [CrossRef]
- Arnold, U.; Yildiz, Ö. Economic risk analysis of decentralized renewable energy infrastructures—A Monte Carlo Simulation approach. Renew. Energy 2015, 77, 227–239. [Google Scholar] [CrossRef]
- Ng, G.H.; Tiong, R.L.K. Model on cash flow forecasting and risk analysis for contracting firms. Int. J. Proj. Manag. 2002, 20, 351–363. [Google Scholar]
- Zhang, R.; Langrené, N.; Tian, Y.; Zhu, Z.; Klebaner, F.; Hamza, K. Skewed target range strategy for multiperiod portfolio optimization using a two-stage least squares Monte Carlo method. J. Comput. Financ. 2019, 23, 97–127. [Google Scholar] [CrossRef]
- Homem-de-Mello, T.; Bayraksan, G. Monte Carlo sampling-based methods for stochastic optimization. Surv. Oper. Res. Manag. Sci. 2014, 19, 56–85. [Google Scholar] [CrossRef]
- Popescu, C.; Gheorghiu, S.A. Economic Analysis and Generic Algorithm for Optimizing the Investments Decision-Making Process in Oil Field Development. Energies 2021, 14, 6119. [Google Scholar] [CrossRef]
- Koroteev, M.; Romanova, E.; Korovin, D.; Shevtsov, V.; Feklin, V.; Nikitin, P.; Makrushin, S.; Bublikov, K.V. Optimization of Food Industry Production Using the Monte Carlo Simulation Method: A Case Study of a Meat Processing Plant. Informatics 2022, 9, 5. [Google Scholar] [CrossRef]
- Kooros, S.K.; McManis, B.L. A Multiattribute Optimization Model for Strategic Investment Decisions. Can. J. Adm. Sci. Rev. Can. Des Sci. L’Adm. 1998, 15, 152–164. [Google Scholar] [CrossRef]
- Tobisova, A.; Senova, A.; Izarikova, G.; Krutakova, I. Proposal of a Methodology for Assessing Financial Risks and Investment Development for Sustainability of Enterprises in Slovakia. Sustainability 2022, 14, 5068. [Google Scholar] [CrossRef]
- Marzouk, M. Fuzzy Monte Carlo simulation optimization for selecting materials in green buildings. J. Environ. Eng. Landsc. Manag. 2020, 28, 95–104. [Google Scholar] [CrossRef]
- Yang, J.; Xiang, Y.; Wang, Z.; Dai, J.; Wang, Y. Optimal Investment Decision of Distribution Network with Investment Ability and Project Correlation Constraints. Front. Energy Res. 2021, 9, 380. [Google Scholar] [CrossRef]
- Geng, D.; Zhang, S.M.; Wang, D.G.; Gao, J.; Dai, L.S. The Optimization Analysis of Equipment Maintenance Based on Monte-Carlo Simulation. Adv. Mater. Res. 2011, 189–193, 424–427. [Google Scholar] [CrossRef]
- Lampa, M.; Samolejová, A. Fleet optimization based on the Monte Carlo algorithm. Acta Logist. 2020, 7, 17–21. [Google Scholar] [CrossRef]
- Cho, T.M.; Lee, B.C. Reliability-based design optimization using convex linearization and sequential optimization and reliability assessment method. Struct. Saf. 2011, 24, 42–50. [Google Scholar] [CrossRef]
- Zhang, K.; Song, Y. A new multi-objective optimization algorithm based on combined swarm intelligence and Monte Carlo simulation. Inf. Sci. 2022, 610, 759–776. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D. An Improved SPEA2 Algorithm with Local Search for Multi-Objective Investment Decision-Making. Appl. Sci. 2019, 9, 1675. [Google Scholar] [CrossRef]
- Vrecko, I.; Kovac, J.; Rupnik, B.; Gajsek, B. Using queuing simulation model in production process innovations. Int. J. Simul. Model 2019, 18, 47–58. [Google Scholar] [CrossRef]

| Period (month) | Products (t/month) | ||
|---|---|---|---|
| A | B | C | |
| 1 | 72.1 | 9.5 | 11.2 |
| 2 | 73.5 | 9.3 | 23.8 |
| 3 | 81.9 | 10.0 | 18.2 |
| 4 | 72.8 | 10.5 | 13.3 |
| 5 | 78.4 | 9.7 | 23.5 |
| 6 | 74.9 | 10.7 | 18.9 |
| 7 | 74.2 | 10.3 | 14.8 |
| 8 | 83.3 | 10.9 | 16.0 |
| 9 | 79.1 | 10.1 | 13.4 |
| 10 | 77.7 | 11.3 | 19.3 |
| 11 | 74.9 | 10.8 | 12.9 |
| 12 | 74.2 | 10.9 | 24.6 |
| Total | 91.0 | 124.0 | 210.0 |
| Preliminary production plan | 850 | 130 | 140 |
| Month | Forecast: Products Demand (t/month) | ||
|---|---|---|---|
| A | B | C | |
| 13 | 82.71 | 11.06 | 16.60 |
| 14 | 78.88 | 11.18 | 17.50 |
| 15 | 77.59 | 11.31 | 17.50 |
| 16 | 75.03 | 11.44 | 17.50 |
| 17 | 74.38 | 11.56 | 17.50 |
| 18 | 82.19 | 11.69 | 17.50 |
| 19 | 78.67 | 11.81 | 17.50 |
| 20 | 77.50 | 11.94 | 17.50 |
| 21 | 75.14 | 12.06 | 17.50 |
| 22 | 74.55 | 12.19 | 17.50 |
| 23 | 81.71 | 12.31 | 17.50 |
| 24 | 78.48 | 12.44 | 17.50 |
| Total | 936.84 | 140.99 | 209.10 |
| Method | Forecast Accuracy | ||
|---|---|---|---|
| A | B | C | |
| MAPE | 1.59% | 4.15% | 19.06% |
| RMSE | 1.97 | 0.54 | 3.4 |
| MAD | 1.24 | 0.44 | 2.8 |
| Input Variables | Unit | Value | ||
|---|---|---|---|---|
| A | B | C | ||
| Planned production | t/year | 850 | 130 | 140 |
| Average production time | h/t | 6.0 | 7.6 | 7.5 |
| Price | EUR/t | 1300 | 1600 | 1800 |
| Variable costs | EUR/t | 370 | 550 | 650 |
| Nominal time of the line | h/year | 8760 | ||
| Loss times (repairs, cleaning, and others) | h/year | 460 | ||
| Operating time of the line | h/year | 7300 | ||
| Number of shifts | day | 3 | ||
| The length of a shift | h/shift | 8 | ||
| Fixed costs personal (2% annual increase from year 2) | EUR/year | 120,000 | ||
| Fixed costs other (3% from investment costs) | EUR/year | 43,896 | ||
| Income tax | % | 21 | ||
| Discount rate | % | 3.5 | ||
| Investment costs | EUR | 1,463,190 | ||
| NPV | EUR | 3,778,179 | ||
| Variable | Unit | Statistical Characteristics | Distribution Function |
|---|---|---|---|
| Revenue Variables | |||
| Price A | EUR/t | Likeliest 1300; Min. 1250; Max. 1330 | Triangular |
| Price B | EUR/t | Likeliest 1600; 5% 1500; 95% 1700 | Triangular |
| Price C | EUR/t | Likeliest 1800; Min. 1720; Max. 1880 | BetaPERT |
| Cost Variables | |||
| Variable costs A | EUR/t | Likeliest 370; 5% 350; 95% 380 | Triangular |
| Variable costs B | EUR/t | Likeliest 550; Min. 495; Max. 605 | Triangular |
| Variable costs C | EUR/t | Likeliest 1800; Min. 1720; Max. 1880 | BetaPERT |
| Personal costs | EUR | Likeliest 40,000; Min. 39,000; Max. 43,000 | BetaPERT |
| Other fixed costs | EUR | Mean 123,500; 90% 135,000 | Normal |
| Investment costs | EUR | Likeliest 1,339,690; 5% 1,248,086; 95% 1,431,294 | Triangular |
| Time Variables | |||
| Average production time A | h/t | Mean 6; Std. Dev. 0.2 | Normal |
| Average production time B | h/t | Mean 7.6; Std. Dev. 0.76 | Normal |
| Average production time C | h/t | Mean 7.5; Std. Dev. 0.3 | Normal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabianová, J.; Janeková, J.; Fedorko, G.; Molnár, V. A Comprehensive Methodology for Investment Project Assessment Based on Monte Carlo Simulation. Appl. Sci. 2023, 13, 6103. https://doi.org/10.3390/app13106103
Fabianová J, Janeková J, Fedorko G, Molnár V. A Comprehensive Methodology for Investment Project Assessment Based on Monte Carlo Simulation. Applied Sciences. 2023; 13(10):6103. https://doi.org/10.3390/app13106103
Chicago/Turabian StyleFabianová, Jana, Jaroslava Janeková, Gabriel Fedorko, and Vieroslav Molnár. 2023. "A Comprehensive Methodology for Investment Project Assessment Based on Monte Carlo Simulation" Applied Sciences 13, no. 10: 6103. https://doi.org/10.3390/app13106103
APA StyleFabianová, J., Janeková, J., Fedorko, G., & Molnár, V. (2023). A Comprehensive Methodology for Investment Project Assessment Based on Monte Carlo Simulation. Applied Sciences, 13(10), 6103. https://doi.org/10.3390/app13106103









