BILSTM-Based Deep Neural Network for Rock-Mass Classification Prediction Using Depth-Sequence MWD Data: A Case Study of a Tunnel in Yunnan, China
Abstract
1. Introduction
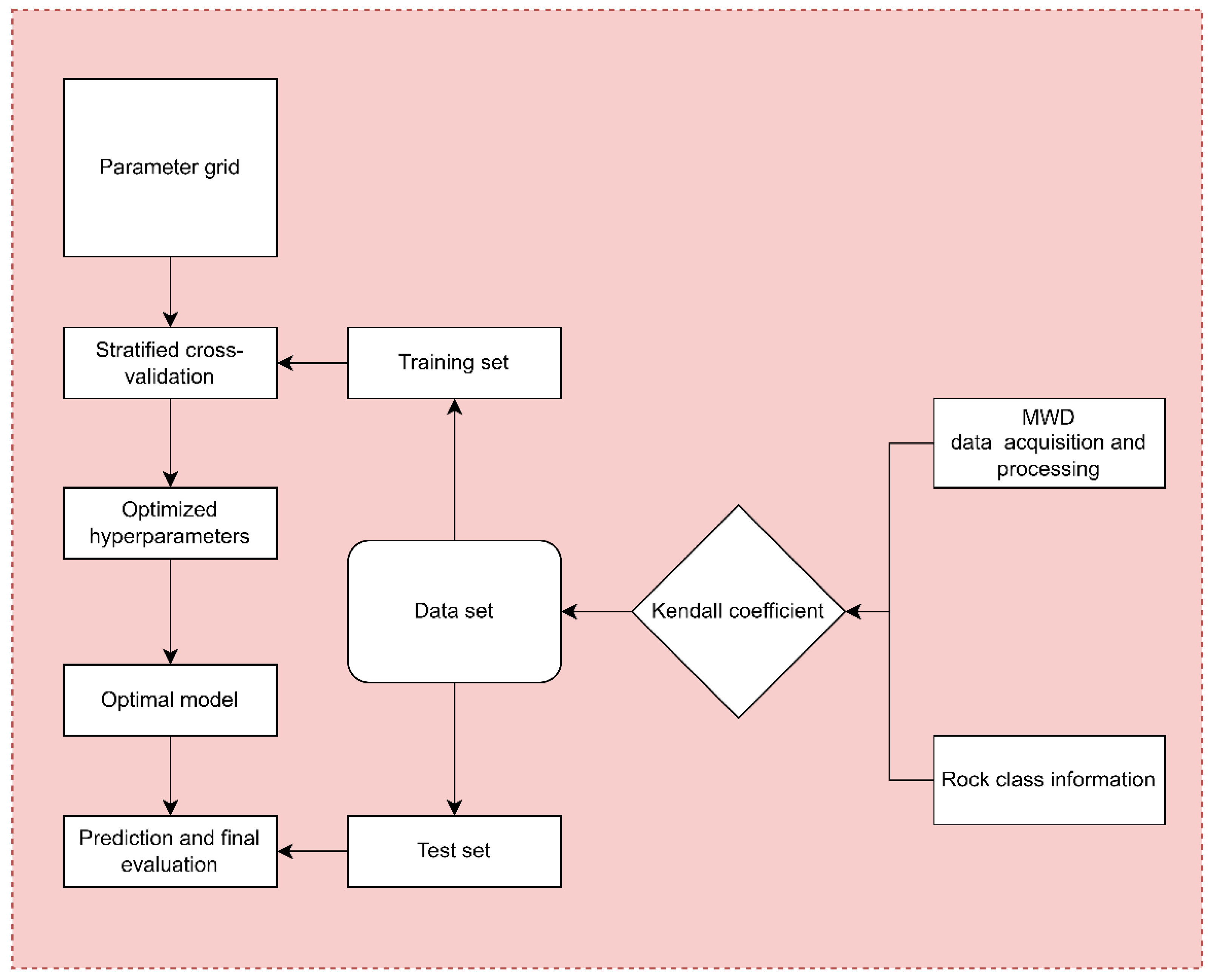
2. Dataset Establishment and Preprocessing
2.1. Dataset Source
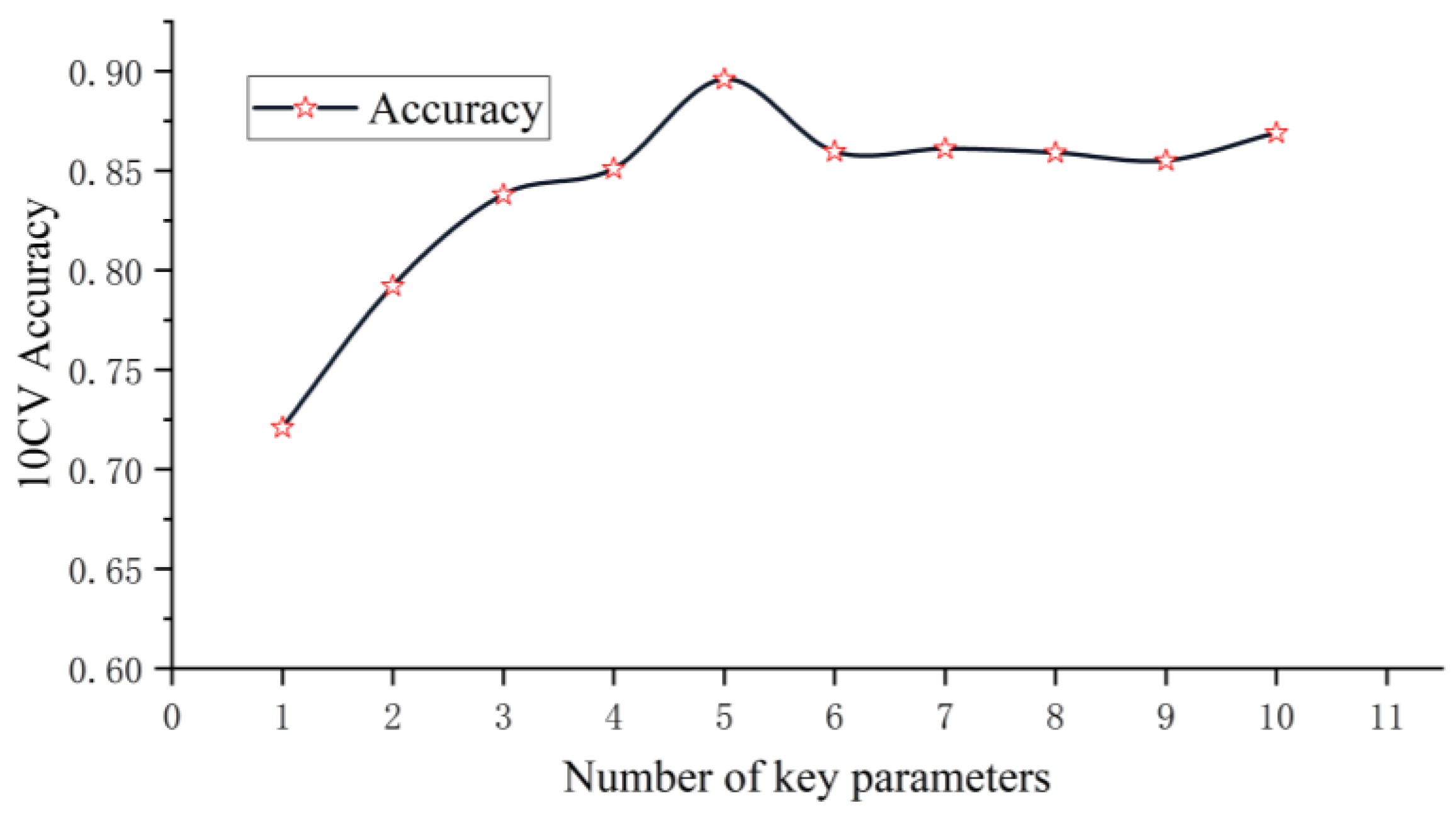
2.2. Key Drilling-Parameter Selection
2.3. Dataset Division
3. BILSTM-Based Deep Neural Network Rock-Mass Classification Method
3.1. Deep Neural Network Structure
3.1.1. BILSTM Neural Network
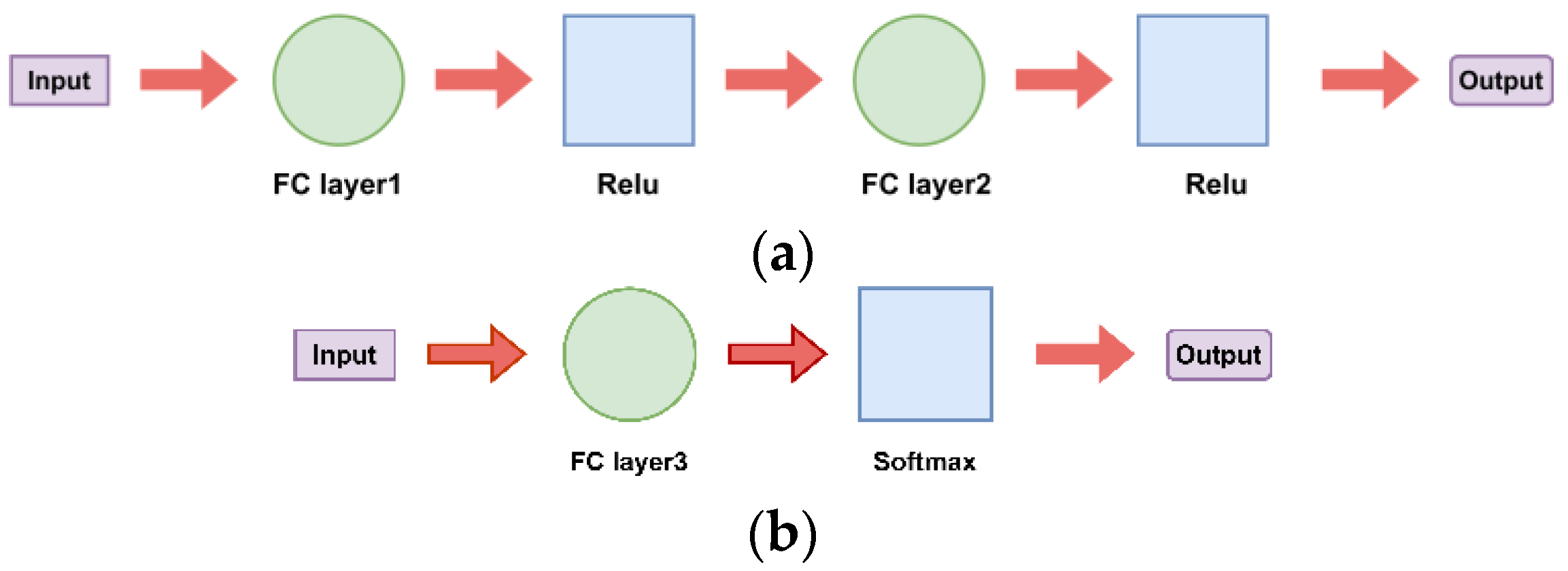
3.1.2. Fully Connected Layer
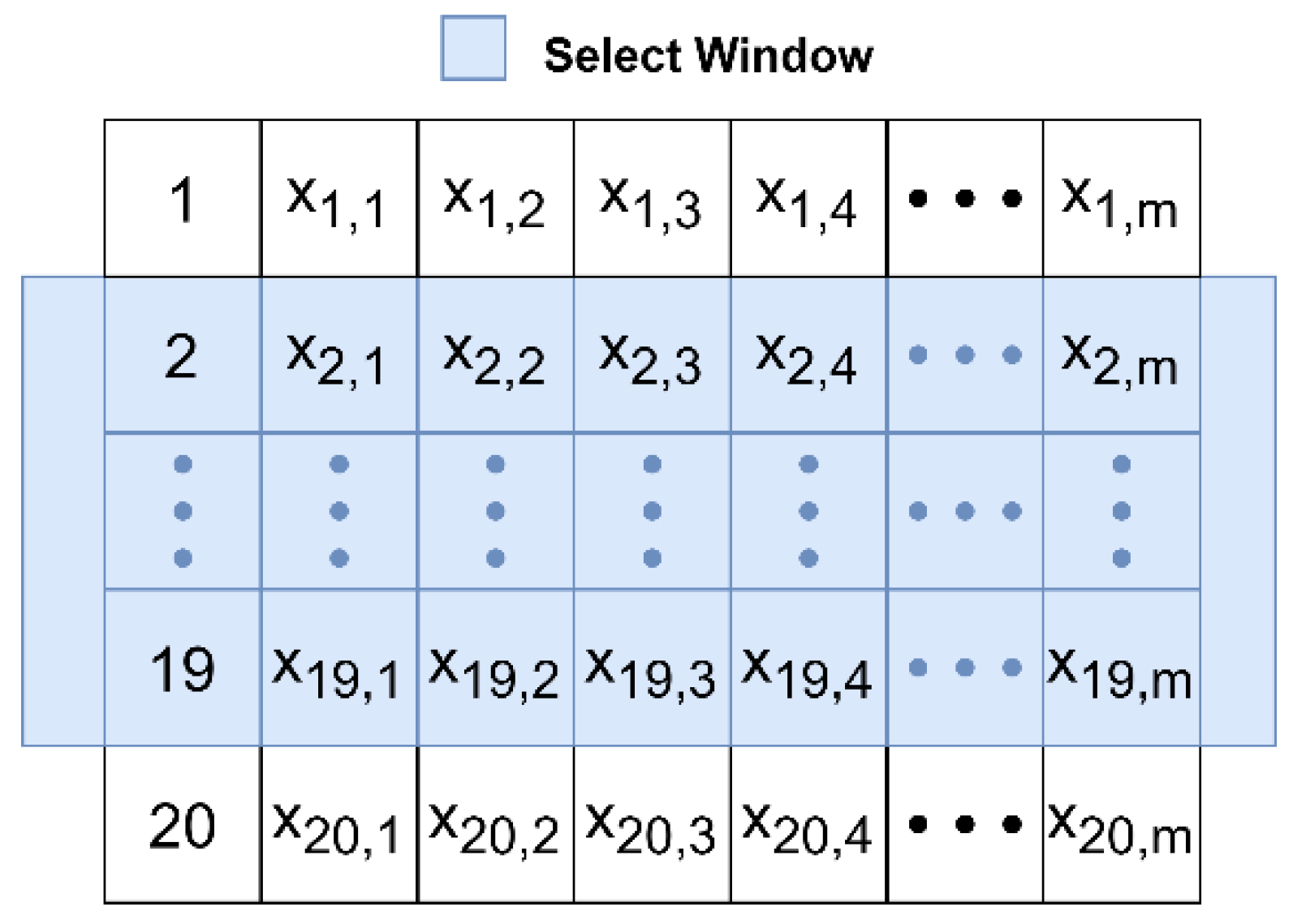
3.1.3. Window Selector and Voter
3.1.4. BILSTM-Based Deep Neural Network Structure Design
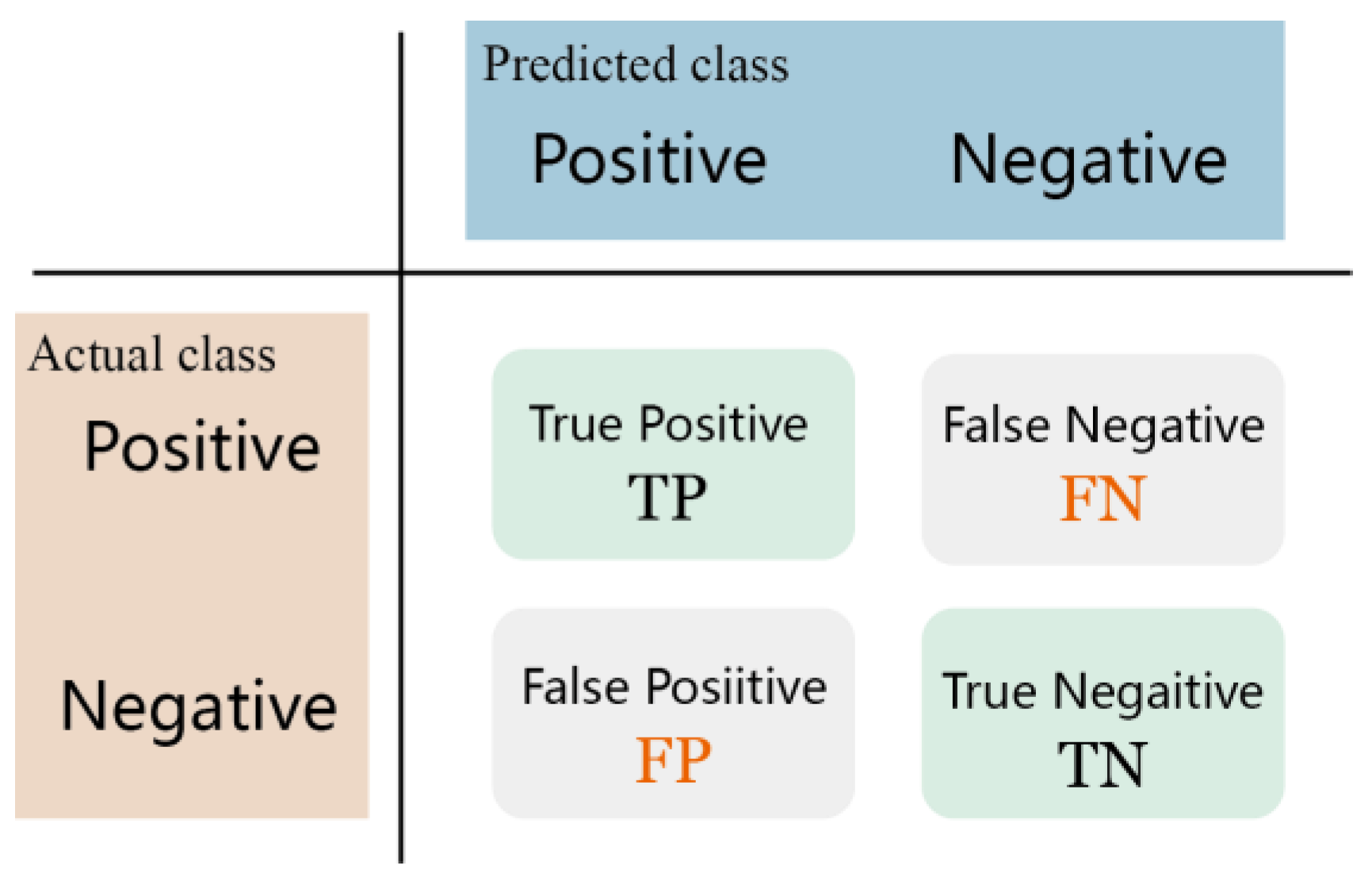
3.2. Evaluation Metrics
4. Engineering Case Application
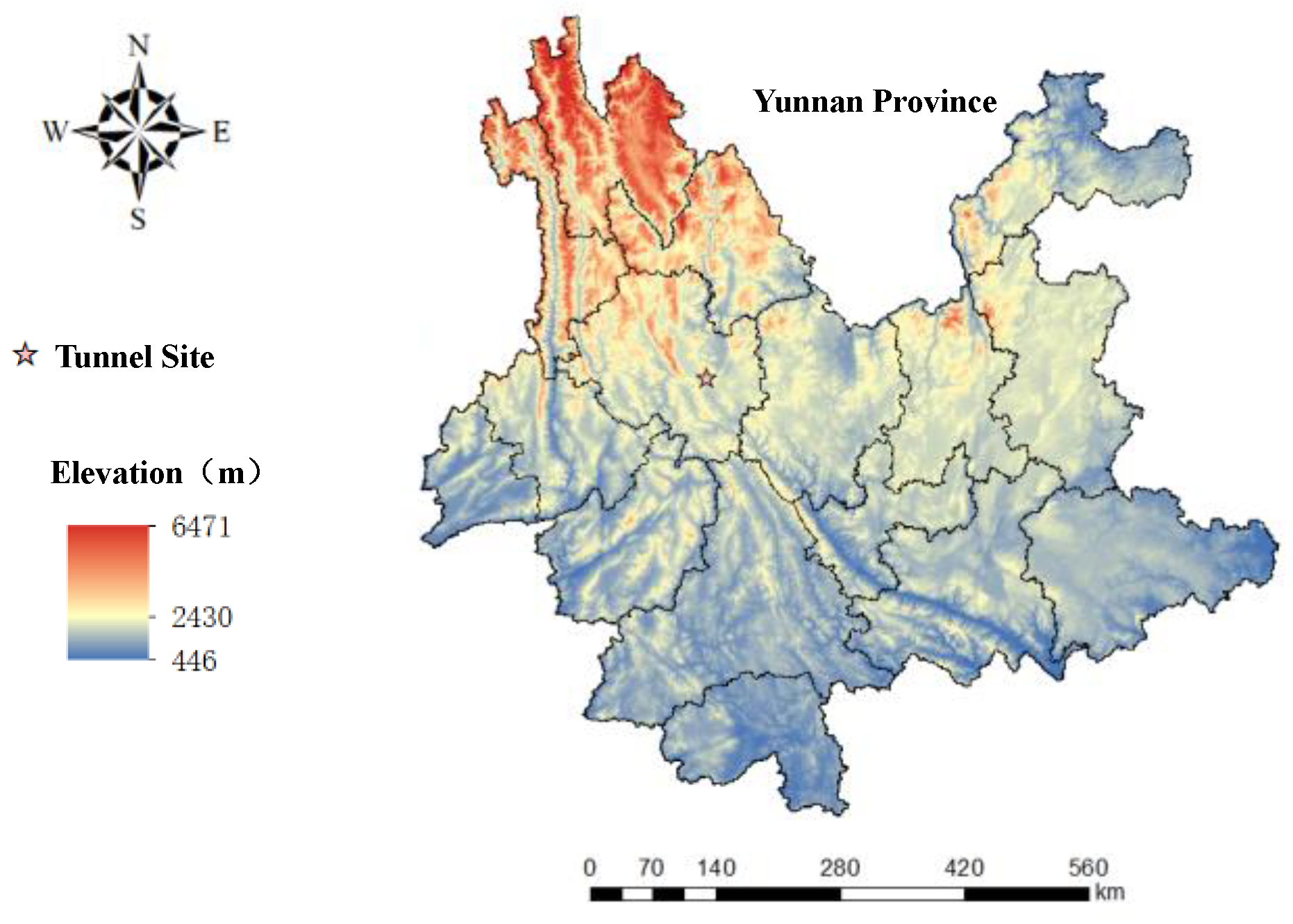
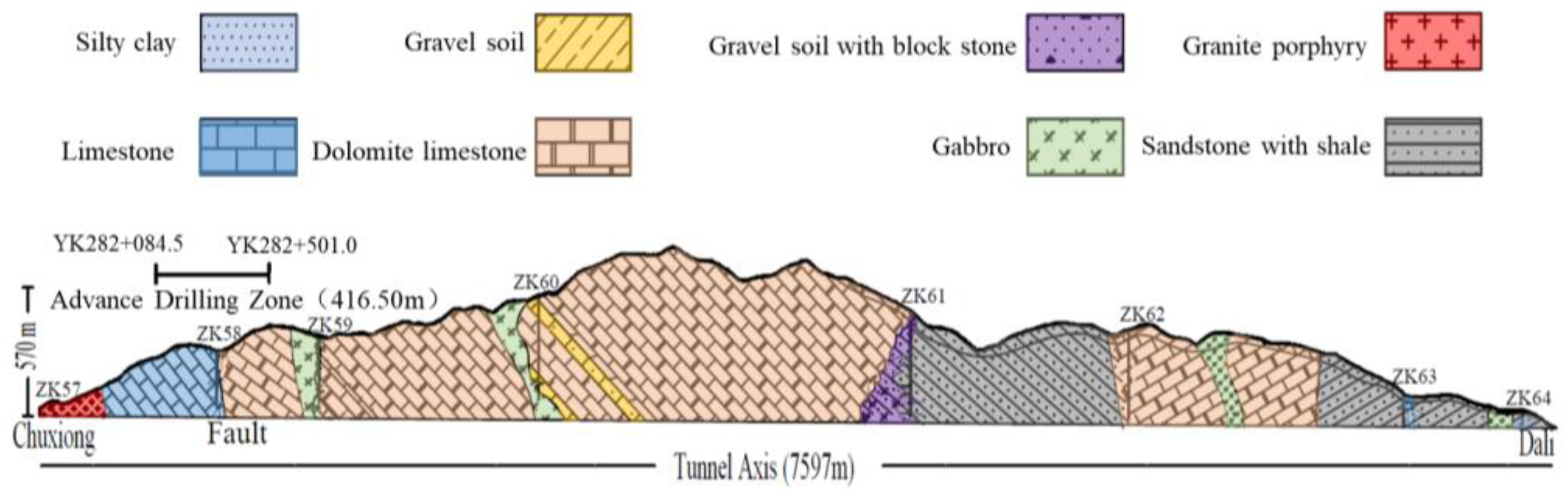
4.1. Project Overview
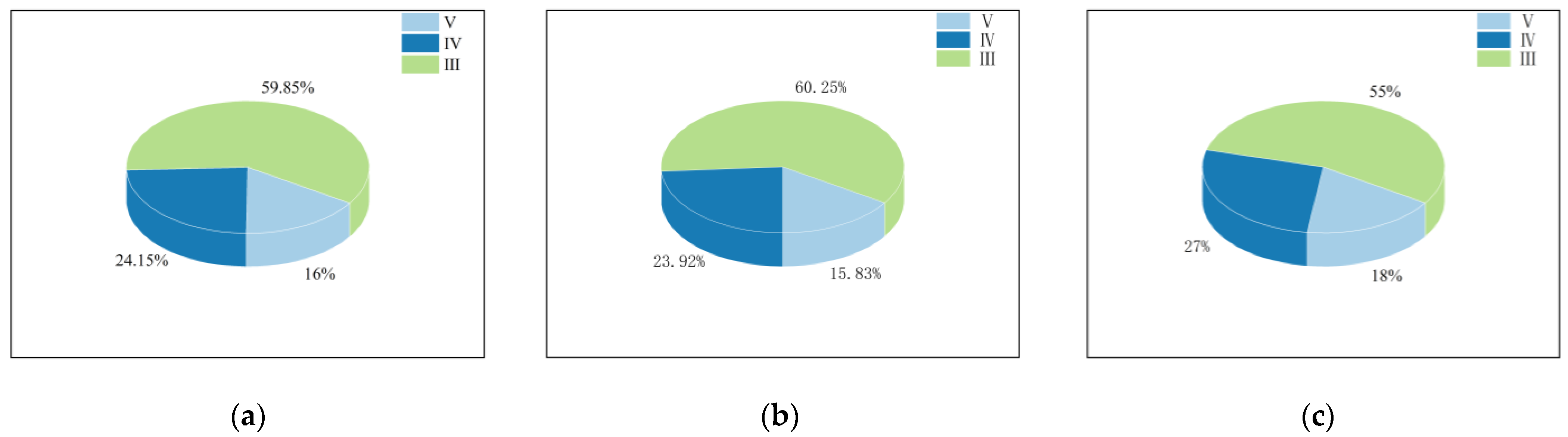
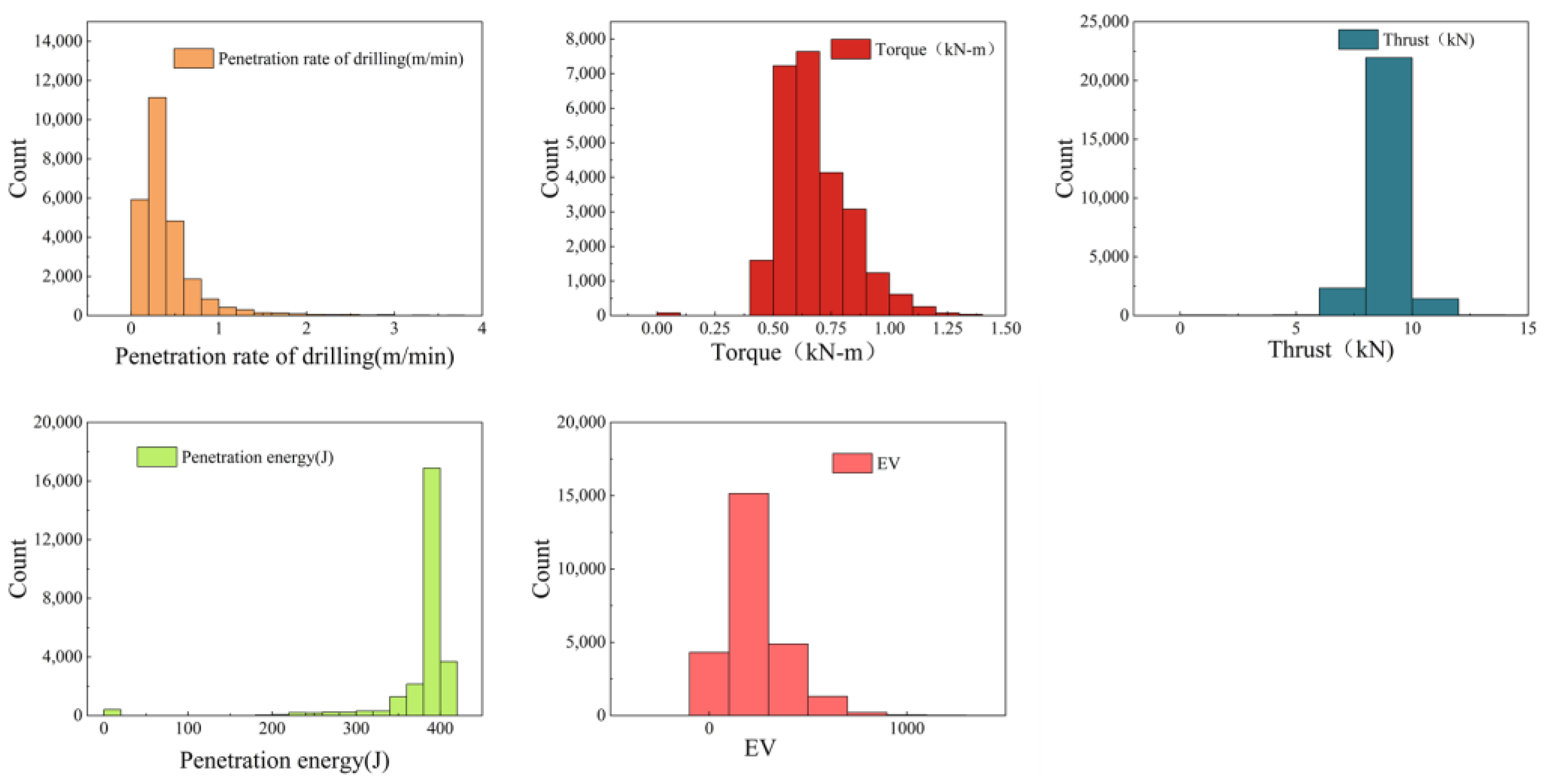
4.2. Dataset Creation
4.3. Rock-Mass Classification Prediction
5. Conclusions
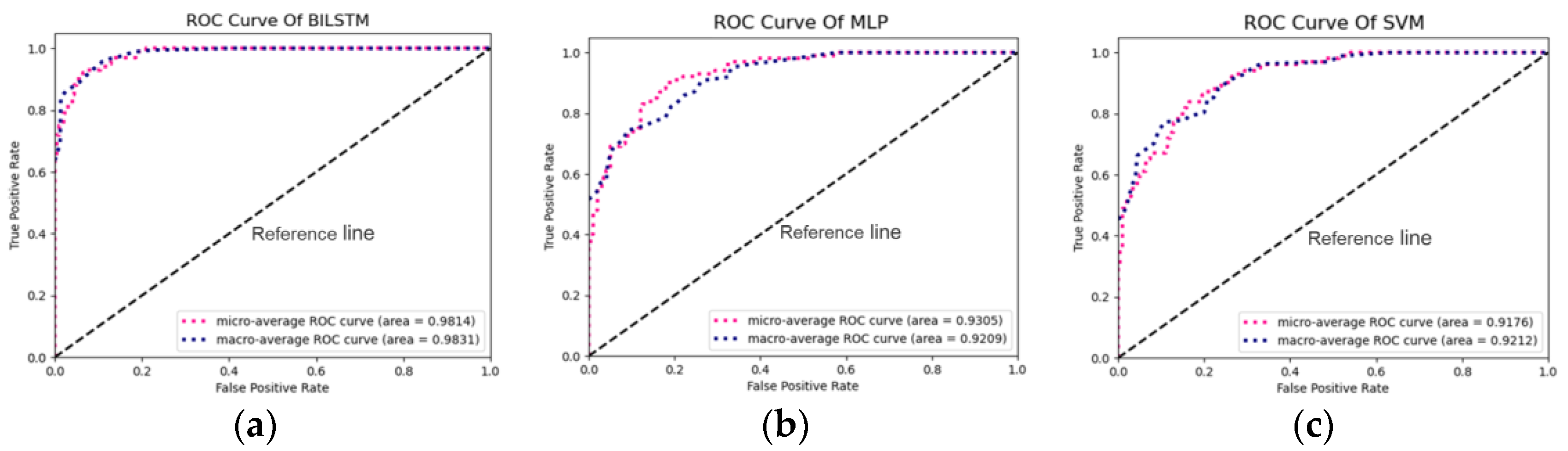
- Compared with the MLP and SVM models, the BILSTM model has the best prediction ability, with the results of each metric being , , , , , , , i.e., all significantly higher than those of the MLP and SVM models.
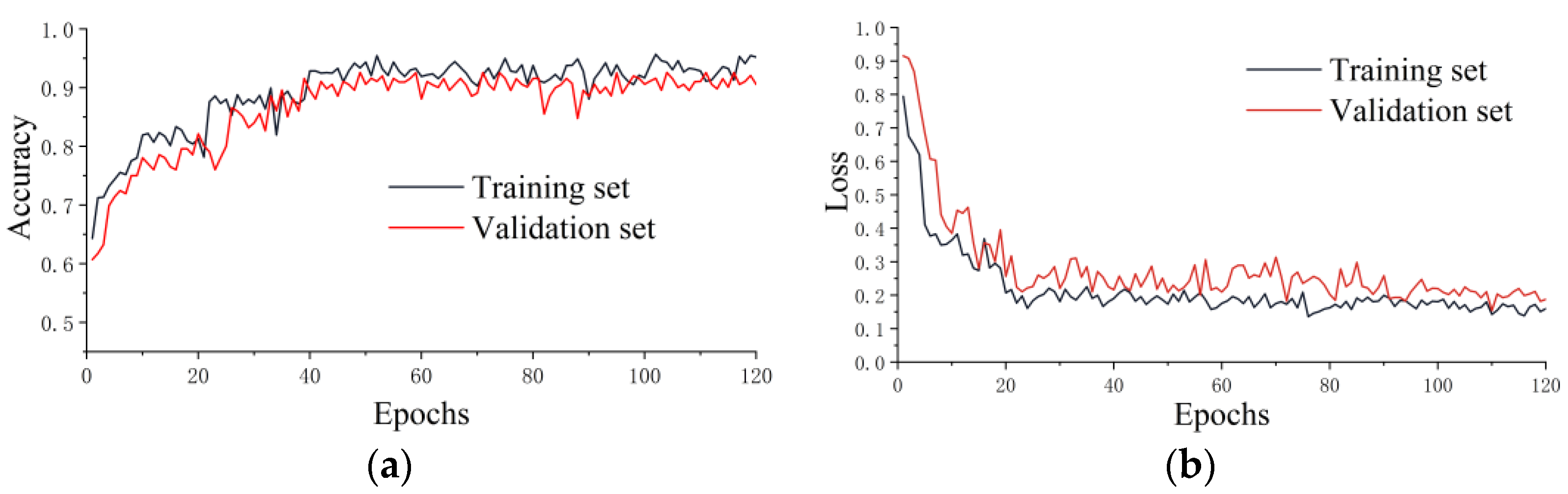
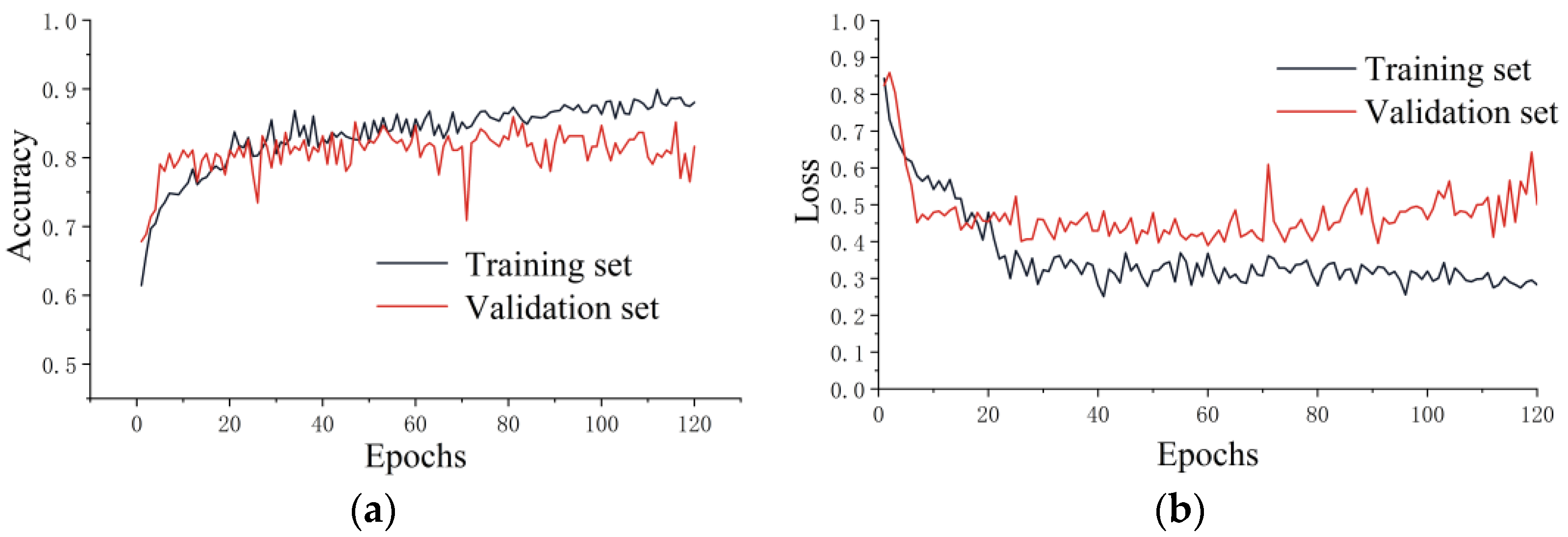
- The accuracies of the BILSTM model were 0.954 and 0.900 in the training and test sets, respectively, with the difference being 0.054. The difference of the BILSTM model was the smallest compared with those of the MLP and SVM models, meaning that it had the best generalization performance. The other two methods performed well in the training set but poorly in the test set, with poor generalization and overfitting.
- The average 10-fold CV accuracy of the BILSTM model was slightly lower than that in the test set. This is because the data in the training, validation, and test sets all came from the same tunnel, with the dataset being homogeneous. The results for the validation set were that the average of the 10-fold CV accuracy and the generalization of the BILSTM model were high, while the results for the test set were only single results; it is reasonable that they were slightly higher than the average 10-fold CV accuracy.
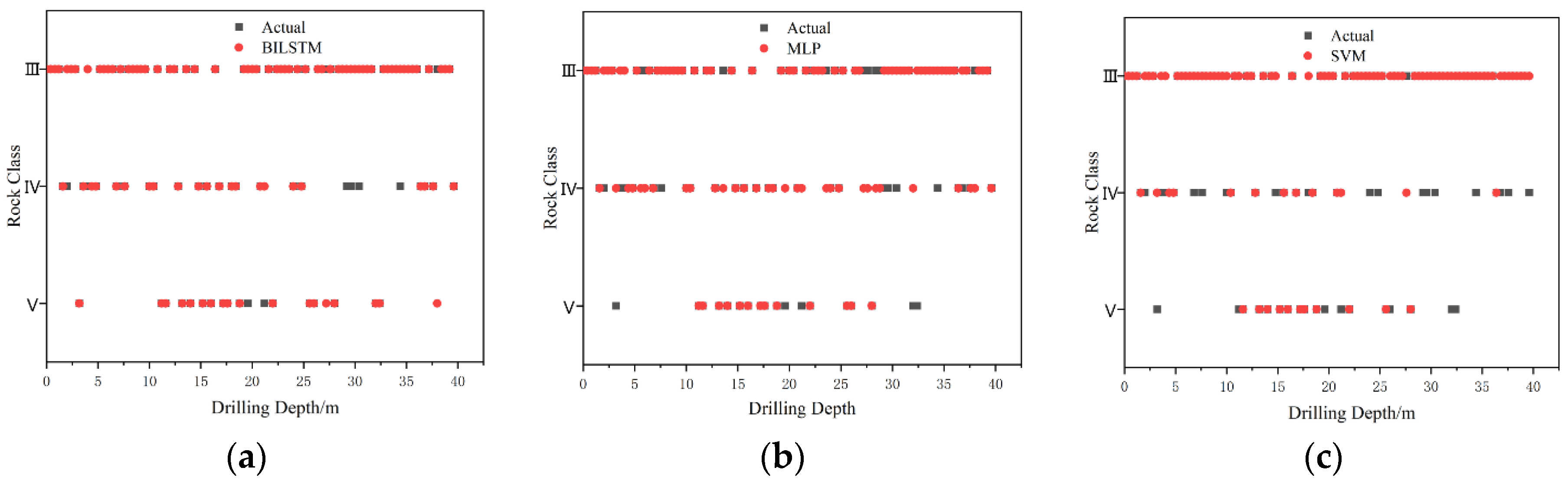
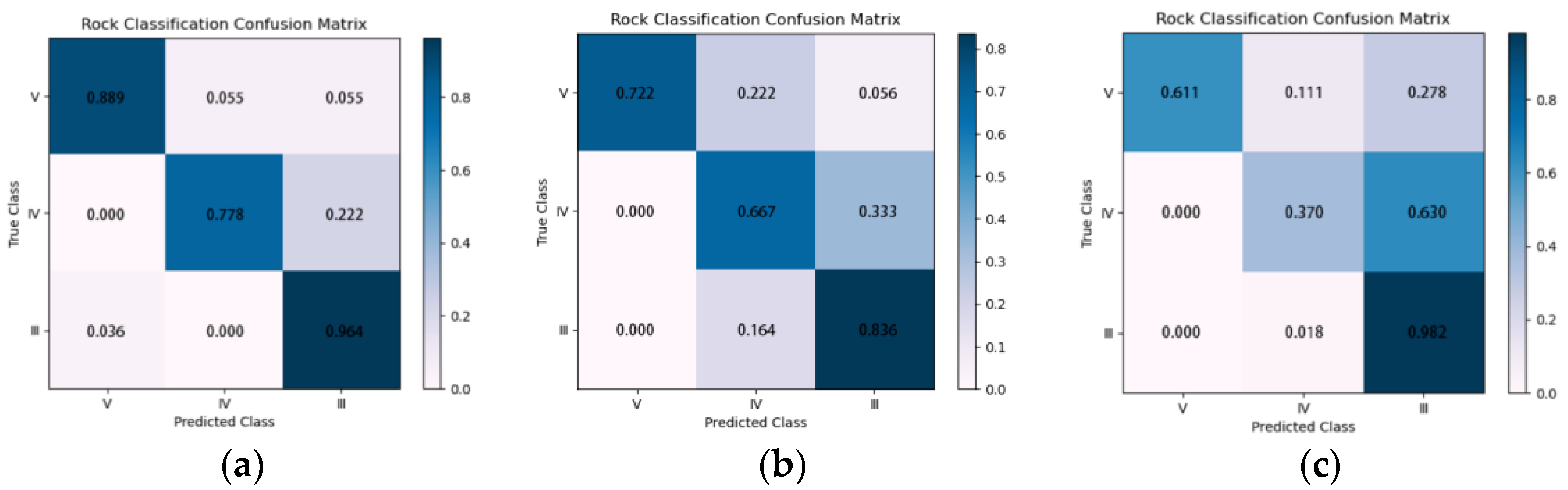
- For class III surrounding rocks, with a large number of samples, all three methods exhibited high accuracies; for classes IV and V, with a small number of samples, the accuracies of all three methods decreased, but that of the BILSTM model was significantly higher than those of the other two methods, indicating that it has the best processing capability for unbalanced datasets.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, X.J.; Zhang, P.L.; Guo, X.; Liu, B.; Chen, L.; Zhang, Q.S.; Nie, L.C.; Zhang, Y. A case study of seismic forward prospecting based on the tunnel seismic while drilling and active seismic methods. Bull. Eng. Geol. Environ. 2021, 80, 3553–3567. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, Z.; Fang, Q. Scientific problems and research proposals for Sichuan–Tibet railway tunnel construction. Undergr. Space 2022, 7, 419–439. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Tootoonchi, H.; Jahed Armaghani, D.; Tonnizam Mohamad, E.; Hedayat, A. Application of deep neural networks in predicting the penetration rate of tunnel boring machines. Bull. Eng. Geol. Environ. 2019, 78, 6347–6360. [Google Scholar] [CrossRef]
- Kitchah, F.; Benmebarek, S.; Djabri, M. Numerical assessment of tunnel collapse: A case study of a tunnel at the East–West Algerian highway. Bull. Eng. Geol. Environ. 2021, 80, 6161–6176. [Google Scholar] [CrossRef]
- Ren, Q.; Xu, L.; Zhu, A.; Shan, M.; Zhang, L.; Gu, J.; Shen, L. Comprehensive safety evaluation method of surrounding rock during underground cavern construction. Undergr. Space 2021, 6, 46–61. [Google Scholar] [CrossRef]
- Hassanpour, J.; Rostami, J.; Khamehchiyan, M.; Bruland, A.; Tavakoli, H.R. TBM performance analysis in pyroclastic rocks: A case history of Karaj water conveyance tunnel. Rock Mech. Rock Eng. 2010, 43, 427–445. [Google Scholar] [CrossRef]
- Li, S.C.; Liu, B.; Xu, X.J.; Nie, L.C.; Liu, Z.Y.; Song, J.; Sun, H.F.; Chen, L.; Fan, K. An overview of ahead geological prospecting in tunneling. Tunn. Undergr. Space Technol. 2017, 63, 69–94. [Google Scholar] [CrossRef]
- Panthi, K.K.; Nilsen, B. Uncertainty analysis of tunnel squeezing for two tunnel cases from Nepal Himalaya. Int. J. Rock Mech. Min. 2007, 44, 67–76. [Google Scholar] [CrossRef]
- Somerton, W.H. A laboratory study of rock breakage by rotary drilling. Trans. Aime 1959, 216, 92–97. [Google Scholar] [CrossRef]
- Hamelin, J.P.; Levallois, J.; Pfister, P. Drilling parameters recording: New developments. In Bulletin of the International Association of Engineering Geology-Bulletin de l’Association Internationale de Géologie de l’Ingénieur; Springer: Berlin/Heidelberg, Germany, 1982; Volume 26, pp. 83–88. [Google Scholar]
- Schunnesson, H. RQD predictions based on drill performance parameters. Tunn. Undergr. Space Technol. 1996, 11, 345–351. [Google Scholar] [CrossRef]
- Yue, Z.Q.; Lee, C.F.; Law, K.T.; Tham, L.G. Automatic monitoring of rotary-percussive drilling for ground characterization—Illustrated by a case example in Hong Kong. Int. J. Rock Mech. Min. 2004, 41, 573–612. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, H.K.; Yu, H.C.; Jiang, B.; Liu, B.H. Method for measuring rock mass characteristics and evaluating the grouting-reinforced effect based on digital drilling. Rock Mech. Rock Eng. 2019, 52, 841–851. [Google Scholar] [CrossRef]
- Liang, D.C.; Tang, H.; Wu, Z.J.; Zhang, Y.H.; Fang, Y.W. Stratum identification based on multiple drilling parameters and probability classification. Rock Soil Mech. 2022, 43, 1123–1134. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, S.; Li, S.; He, M.; Gao, H.; Jiang, B.; Jiang, Y. Upper bound analytic mechanics model for rock cutting and its application in field testing. Tunn. Undergr. Space Technol. 2018, 73, 287–294. [Google Scholar] [CrossRef]
- Bo, Y.; Liu, Q.; Huang, X.; Pan, Y. Real-time hard-rock tunnel prediction model for rock mass classification using CatBoost integrated with Sequential Model-Based Optimization. Tunn. Undergr. Space Technol. 2022, 124, 104448. [Google Scholar] [CrossRef]
- Lu, J.; Guo, W.; Liu, J.; Zhao, R.; Ding, Y.; Shi, S. An Intelligent Advanced Classification Method for Tunnel-Surrounding Rock Mass Based on the Particle Swarm Optimization Least Squares Support Vector Machine. Appl. Sci. 2023, 13, 2068. [Google Scholar] [CrossRef]
- Benemaran, R.S.; Esmaeili-Falak, M.; Javadi, A. Predicting resilient modulus of flexible pavement foundation using extreme gradient boosting based optimised models. Int. J. Pavement Eng. 2022, 1–20. [Google Scholar] [CrossRef]
- Esmaeili-Falak, M.; Benemaran, R.S. Ensemble deep learning-based models to predict the resilient modulus of modified base materials subjected to wet-dry cycles. Geomech. Eng. 2023, 32, 583–600. [Google Scholar]
- LaBelle, D. Lithological Classification by Drilling. Thesis Proposal, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, USA, 2001. [Google Scholar]
- Gao, H.K.; Wang, Q.; Jiang, B.; Zhang, P.; Jiang, Z.H.; Wang, Y. Relationship between rock uniaxial compressive strength and digital core drilling parameters and its forecast method. Int. J. Coal Sci. Technol. 2021, 8, 605–613. [Google Scholar] [CrossRef]
- Ameur-Zaimeche, O.; Kechiched, R.; Heddam, S.; Wood, D.A. Real-time porosity prediction using gas-while-drilling data and machine learning with reservoir associated gas: Case study for Hassi Messaoud field, Algeria. Mar. Pet. Geol. 2022, 140, 105631. [Google Scholar] [CrossRef]
- Kadkhodaie-Ilkhchi, A.; Monteiro, S.T.; Ramos, F.; Hatherly, P. Rock recognition from MWD data: A comparative study of boosting, neural networks, and fuzzy logic. IEEE Geosci. Remote Sens. Lett. 2010, 7, 680–684. [Google Scholar] [CrossRef]
- Fang, Y.W.; Wu, Z.J.; Sheng, Q.; Tang, H.; Liang, D.C. Tunnel geology prediction using a neural network based on instrumented drilling test. Appl. Sci. 2020, 11, 217. [Google Scholar] [CrossRef]
- Klyuchnikov, N.; Zaytsev, A.; Gruzdev, A.; Ovchinnikov, G.; Antipova, K.; Ismailova, L.; Koroteev, D. Data-driven model for the identification of the rock type at a drilling bit. J. Petrol. Sci. Eng. 2019, 178, 506–516. [Google Scholar] [CrossRef]
- Romanenkova, E.; Zaytsev, A.; Klyuchnikov, N.; Gruzdev, A.; Antipova, K.; Ismailova, L.; Koroteev, D. Real-time data-driven detection of the rock-type alteration during a directional drilling. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1861–1865. [Google Scholar] [CrossRef]
- Gupta, I.; Tran, N.; Devegowda, D.; Jayaram, V.; Rai, C.; Sondergeld, C.; Karami, H. Looking ahead of the bit using surface drilling and petrophysical data: Machine-learning-based real-time geosteering in Volve field. SPE J. 2020, 25, 990–1006. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Matwin, S.; Mielniczuk, J. Challenges in Computational Statistics and Data Mining; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Xiao, H.H.; Yang, W.K.; Hu, J.; Zhang, Y.P.; Jing, L.J.; Chen, Z.Y. Significance and methodology: Preprocessing the big data for machine learning on TBM performance. Undergr. Space 2022, 7, 680–701. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Di Martino, M.; Fernández, A.; Iturralde, P.; Lecumberry, F. Novel classifier scheme for imbalanced problems. Pattern Recogn. Lett. 2013, 34, 1146–1151. [Google Scholar] [CrossRef]
- Industrial Standard of the People’s Republic of China. Specifications for Design of Highway Tunnels Section 1 Civil Engineering: JTG 3370. 1-2018; China Communications Press: Beijing, China, 2018; ISBN 978-7-114-14639-8. [Google Scholar]
- TensorFlow Developers. TensorFlow (v2.12.0). Zenodo. 2023. Available online: https://doi.org/10.5281/zenodo.7764425 (accessed on 23 March 2023).
- Yan, T.; Shen, S.L.; Zhou, A.; Chen, X. Prediction of geological characteristics from shield operational parameters by integrating grid search and K-fold cross validation into stacking classification algorithm. J. Rock Mech. Geotech. 2022, 14, 1292–1303. [Google Scholar] [CrossRef]
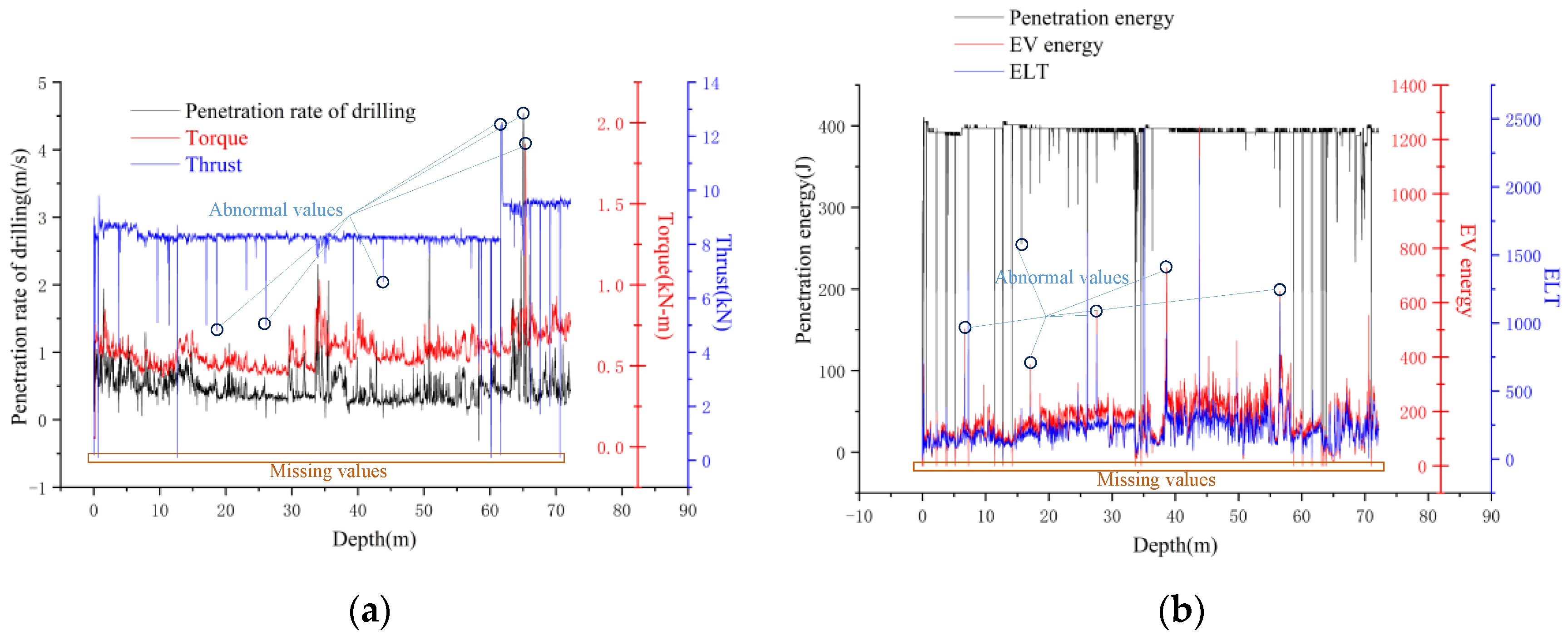
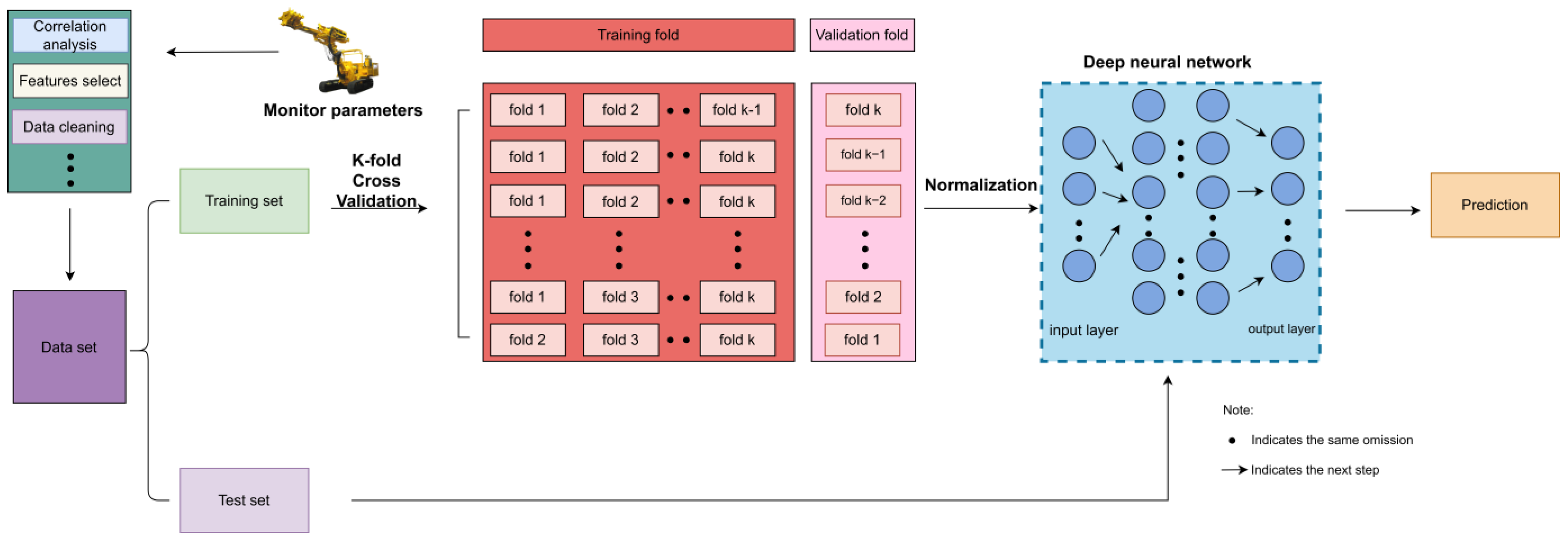
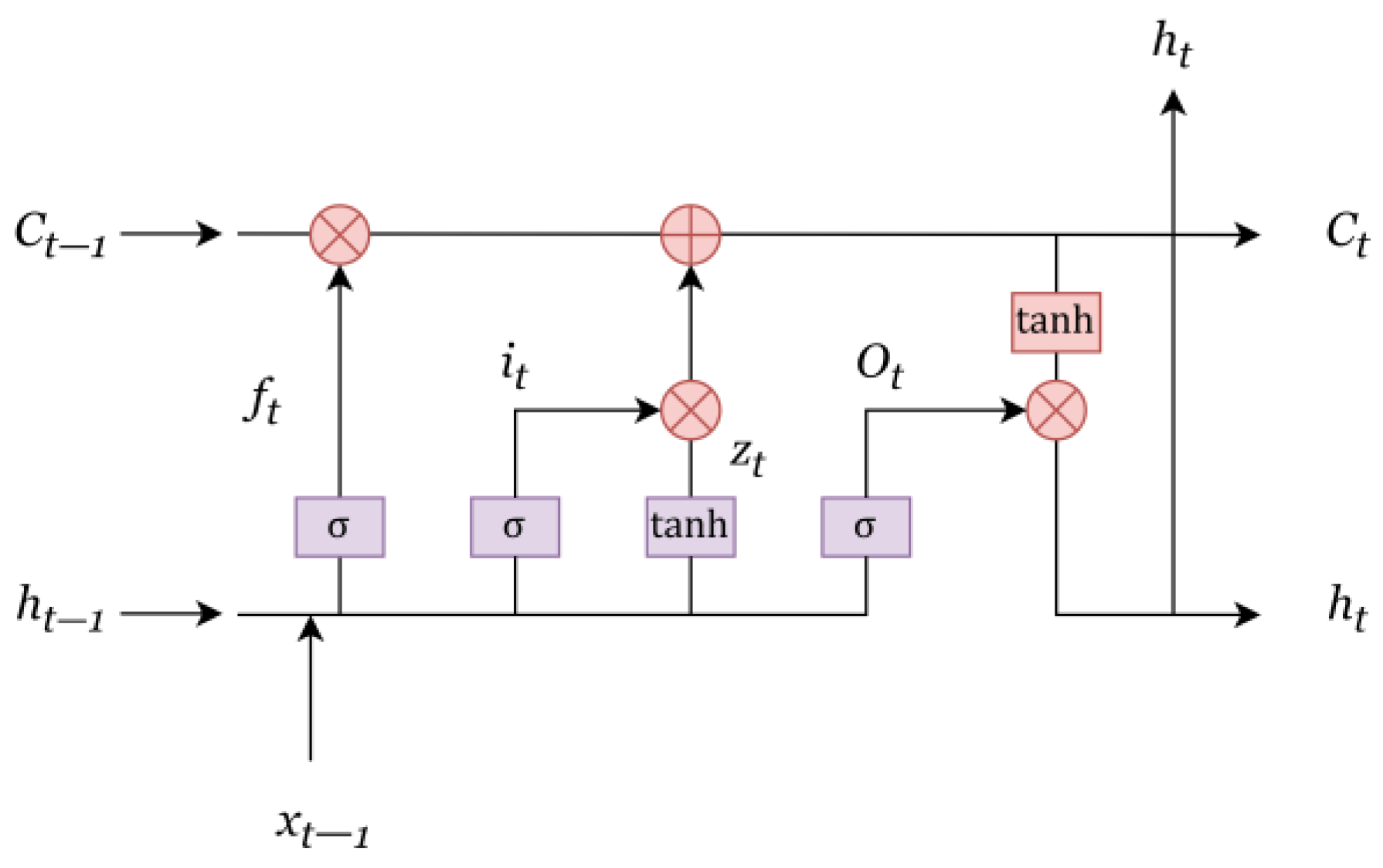
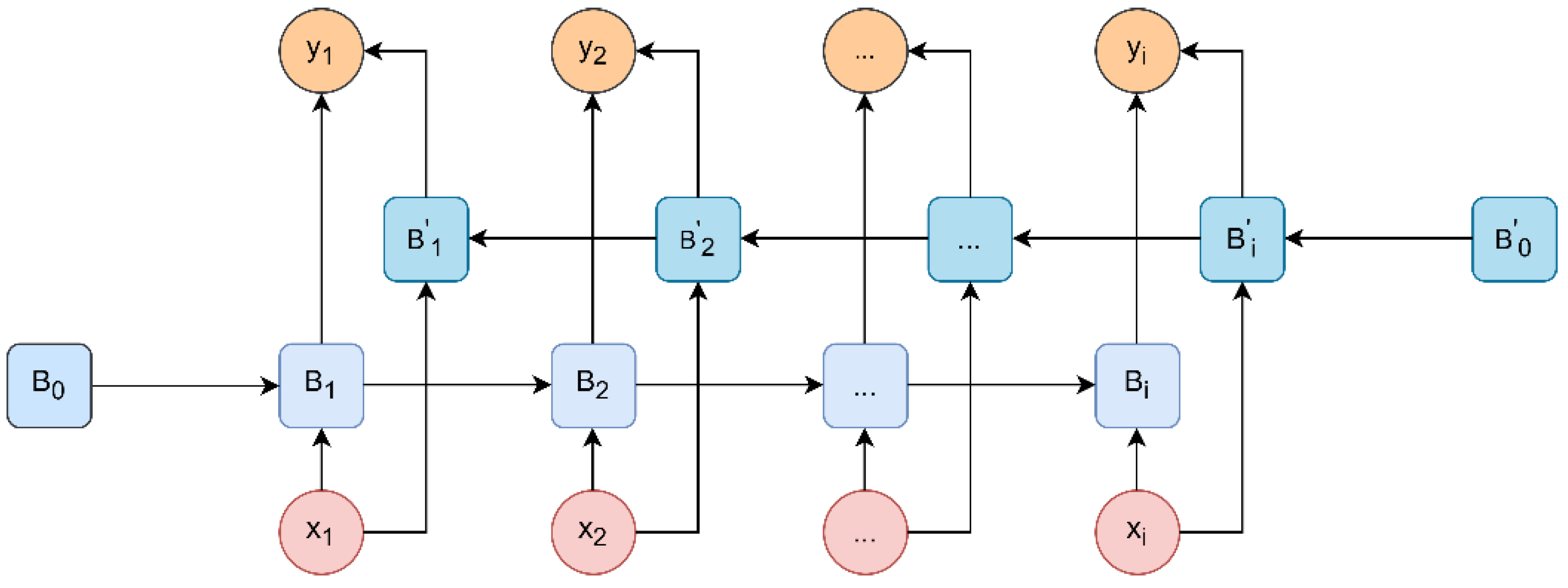





| Drilling Parameter | Unit | Drilling Parameter | Unit |
|---|---|---|---|
| Depth | m | Water supply pressure | MPa |
| Torque | kN-m | Water supply rate | L/min |
| Rotation Speed | rpm | Drainage pressure | MPa |
| Percussive force | kN | Drainage rate | L/min |
| Beat per minute | bpm | EV | J/m3 |
| Thrust | kN | ELT | - |
| p-Value | Coincidence Probability | Null Hypothesis | Statistical Significance |
|---|---|---|---|
| p > 0.05 | Coincidence probability greater than 5% | Cannot refuse | No significant difference |
| p ≤ 0.05 | Coincidence probability less than 5% | Refuse | Significant difference |
| p ≤ 0.01 | Coincidence probability less than 1% | Refuse | Very significant difference |
| Penetration Rate of Drilling | Torque | Rotation Speed | Thrust | Penetration Energy | Beat Per Minute | Water Supply Rate | Water Supply Pressure | EV | ELT | Rock Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Penetration Rate of Drilling | 1.000 | 0.268 | −0.008 | −0.255 | 0.028 | 0.028 | 0.042 | −0.025 | −0.916 | −0.948 | −0.406 |
| Torque | 0.268 | 1.000 | 0.070 | −0.074 | −0.134 | −0.134 | −0.108 | 0.295 | −0.289 | −0.253 | −0.242 |
| Rotation Speed | −0.008 | 0.070 | 1.000 | −0.013 | 0.059 | 0.059 | −0.103 | 0.081 | 0.012 | 0.012 | −0.002 |
| Thrust | −0.255 | −0.074 | −0.013 | 1.000 | 0.096 | 0.096 | −0.034 | 0.019 | 0.274 | 0.311 | 0.167 |
| Penetration Energy | 0.028 | −0.134 | 0.059 | 0.096 | 1.000 | 1.000 | 0.046 | −0.131 | 0.074 | −0.014 | 0.136 |
| Beat Per Minute | 0.028 | −0.134 | 0.059 | 0.096 | 1.000 | 1.000 | 0.046 | −0.131 | 0.074 | −0.014 | 0.136 |
| Water Supply Rate | 0.042 | −0.108 | −0.103 | −0.034 | 0.046 | 0.046 | 1.000 | −0.096 | −0.046 | −0.043 | −0.001 |
| Water Supply Pressure | −0.025 | 0.295 | 0.081 | 0.019 | −0.131 | −0.131 | −0.096 | 1.000 | 0.025 | 0.034 | −0.083 |
| EV | −0.916 | −0.289 | 0.012 | 0.274 | 0.074 | 0.074 | −0.046 | 0.025 | 1.000 | 0.900 | 0.433 |
| ELT | −0.948 | −0.253 | 0.012 | 0.311 | −0.014 | −0.014 | −0.043 | 0.034 | 0.900 | 1.000 | 0.403 |
| Rock Class | −0.406 | −0.242 | −0.002 | 0.167 | 0.136 | 0.136 | −0.001 | −0.083 | 0.433 | 0.403 | 1.000 |
| Key Drilling Parameters | Unit | Max | Min | Mean | Median |
|---|---|---|---|---|---|
| Penetration rate of drilling | m/min | 4.96 | 0.00 | 0.42 | 0.31 |
| Torque | kN-m | 1.87 | 0.02 | 0.68 | 0.65 |
| Thrust | kN | 36.30 | 0.00 | 8.93 | 8.80 |
| Penetration energy | J | 423.00 | 0.00 | 376.05 | 392.00 |
| EV | \ | 6448.00 | 0.00 | 239.98 | 201.00 |
| Key Drilling Parameters | Unit | Max | Min | Mean | Median |
|---|---|---|---|---|---|
| Penetration rate of drilling | m/min | 3.69 | 0.00 | 0.47 | 0.32 |
| Torque | kN-m | 1.72 | 0.05 | 0.65 | 0.62 |
| Thrust | kN | 21.00 | 0.00 | 8.79 | 8.60 |
| Penetration energy | J | 410.00 | 0.00 | 378.83 | 388.00 |
| EV | \ | 6448.00 | 0.00 | 227.87 | 198.00 |
| Model | Optimized Hyperparameters |
|---|---|
| BILSTM | learning_rate = 0.01; epoch = 120; drop_out = 0.3; l2_regularization = 5 × 10−5; layer_1_units = 20; layer_2_units = 20; LSTM_hidden_units = 32. |
| SVC | C = 7; kernel = ‘rbf’; gamma = 47. |
| MLP | learning_rate = 0.01; epoch = 120; drop_out = 0.3; l2_regularization = 5 × 10−5; hidden_layer_1_units = 20; hidden_layer_2_units = 20. |
| Method | Rock Mass Class | Accuracy | Precision | Recall | F1 | Support |
|---|---|---|---|---|---|---|
| BILSTM | III | 0.883 | 0.964 | 0.922 | 55 | |
| IV | 0.955 | 0.778 | 0.857 | 27 | ||
| V | 0.889 | 0.889 | 0.889 | 18 | ||
| Overall | 0.900 | 0.904 | 0.898 | 0.900 | 100 | |
| MLP | III | 0.821 | 0.836 | 0.828 | 55 | |
| IV | 0.581 | 0.667 | 0.621 | 27 | ||
| V | 1.000 | 0.722 | 0.839 | 18 | ||
| Overall | 0.770 | 0.789 | 0.774 | 0.770 | 100 | |
| SVM | III | 0.711 | 0.982 | 0.825 | 55 | |
| IV | 0.769 | 0.370 | 0.500 | 27 | ||
| V | 1.000 | 0.611 | 0.759 | 18 | ||
| Overall | 0.750 | 0.778 | 0.725 | 0.750 | 100 |
| Method | Macro_Average_AUC | Micro_Average_AUC | Difference |
|---|---|---|---|
| BILSTM | 0.9831 | 0.9814 | 0.0017 |
| MLP | 0.9209 | 0.9305 | −0.0096 |
| SVM | 0.9212 | 0.9176 | 0.0036 |
| Method | Training-Set Accuracy | Test-Set Accuracy | Difference |
|---|---|---|---|
| BILSTM | 0.954 | 0.900 | 0.054 |
| MLP | 0.886 | 0.770 | 0.116 |
| SVM | 0.844 | 0.750 | 0.094 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.; Tang, H.; Wu, Z.; Liang, D.; Xie, Y. BILSTM-Based Deep Neural Network for Rock-Mass Classification Prediction Using Depth-Sequence MWD Data: A Case Study of a Tunnel in Yunnan, China. Appl. Sci. 2023, 13, 6050. https://doi.org/10.3390/app13106050
Cheng X, Tang H, Wu Z, Liang D, Xie Y. BILSTM-Based Deep Neural Network for Rock-Mass Classification Prediction Using Depth-Sequence MWD Data: A Case Study of a Tunnel in Yunnan, China. Applied Sciences. 2023; 13(10):6050. https://doi.org/10.3390/app13106050
Chicago/Turabian StyleCheng, Xu, Hua Tang, Zhenjun Wu, Dongcai Liang, and Yachen Xie. 2023. "BILSTM-Based Deep Neural Network for Rock-Mass Classification Prediction Using Depth-Sequence MWD Data: A Case Study of a Tunnel in Yunnan, China" Applied Sciences 13, no. 10: 6050. https://doi.org/10.3390/app13106050
APA StyleCheng, X., Tang, H., Wu, Z., Liang, D., & Xie, Y. (2023). BILSTM-Based Deep Neural Network for Rock-Mass Classification Prediction Using Depth-Sequence MWD Data: A Case Study of a Tunnel in Yunnan, China. Applied Sciences, 13(10), 6050. https://doi.org/10.3390/app13106050






