1. Introduction
Material manufacturing processes are not defect free and nondestructive testing techniques (NDT) are required to ensure quality standards. Driven by low costs and inspection times, ultrasonic testing (UT) is one of the most widely used types of NDT. It consists of the transmission of ultrasonic waves through the component. Any defect that is present produces a reflected wave that can be measured at the electronic transducer. The signal produced by the propagation of the ultrasonic wave is called A-scan, and its analysis can provide relevant information about the defect, the component or the material. B-scan refers to the image produced when the data collected from an ultrasonic inspection is plotted on a cross-sectional view of the component. The cross-section will normally be the plane through which the individual A-scans have been collected. C-scan refers to the image produced when the data collected from an ultrasonic inspection is plotted on a plan view of the component. A C-scan does not have to be a single cross-section. Indeed, it often shows a combination of measurements obtained across the whole thickness. B-scan and C-scan representations are often used because ultrasonic signals are hard to interpret.
Defect detection and measurement of defects from ultrasonic data is a manual task. Therefore, it calls for skilled technicians and is a time-consuming process subject to human error. The successful application of machine learning, and more specifically deep learning in the field of computer vision, within different neural networks architectures [
1,
2,
3,
4,
5] and object detection [
6,
7,
8] has increased the interest in models to automatically detect defects in ultrasonic data. Xiao et al. [
9] developed support vector machines to identify defects. Ye and Toyama [
10] created a dataset of ultrasonic images, benchmarked several object detection deep learning architectures, and publicly shared the data and codes. Latête et al. [
11] used a convolutional neural network (CNN) to identify and size up defects in phased array data. Medak et al. [
12] proved that EfficientDET [
13] was better at detecting defects than RetinaNet [
14], and YOLOv3 [
7]. They suggested a novel procedure for calculating anchors. Furthermore, they developed a large dataset of phased array ultrasonic images, which they were able to use to conduct a robust validation of their results using a 5-fold cross-validation. In a more recent work [
15], Medak et al. developed two approaches to incorporate the A-scan signal surrounding a defect area into the detection architecture. One approach was based on model expansion, the second method extracts the features separately, and they are then merged in the detection head. Virkkunen et al. [
16] developed a data augmentation technique adapted to the ultrasonic NDT domain to train another CNN, based on the architecture of VGG [
2]. The above works have several points in common: inspections are carried out on metal materials, defects (side-drilled holes, flat bottom holes, thermal fatigue cracks, mechanical fatigue cracks, electric discharge machined notches...) are artificially introduced, and detection/segmentation are performed in the B-scan mode.
Today, composite materials, in particular carbon fiber reinforced polymers (CFRP), are increasingly used in the aerospace, automotive, and construction industries in order to create lightweight structures and achieve more efficient transportation mechanisms. CFRP are inhomogeneous materials. This poses an obstacle to the application of automatic defect detection models due to noise artefacts [
17]. In spite of this, automatic defect detection tasks are possible. Meng et al. [
18] developed a convolutional neural network together with wavelet transformations to classify A-scan signals that correspond to defects inserted at different depths during manufacturing. In addition, they developed a post-processing scheme to interpret the classifier outputs and visualize the locations of defects using a 3D model. Caizhi Li et al. [
19] developed 1D-YOLO, a network based on the use of dilated convolutions, the Recursive Feature Pyramid [
20] and the R-CNN [
21] to detect damage on aircraft composite materials using a fusion of C-scan and ultrasonic A-scan data with an accuracy of 94.5% and a mean average precision of 80%. This combination of signal and image detection and classification has potential as a method for achieving production-level defect ultrasonic detection applied to composites.
However, current ultrasonic techniques do not provide enough information about some of the most common manufacturing defects of composite materials, e.g., porosity, 3-D maps of fiber volume fraction, out-of-plane wrinkling, in-plane fiber waviness, ply-drop, ply-overlap location, and ply stacking sequence, which are not fully detectable or measurable [
22]. In these cases, a different NDT technique would be required to label data and develop datasets for supervised learning tasks. One option is the use of X-ray computed tomography (XCT) because it enables the 3D reconstruction of the internal microstructure of a sample. It has been widely used to perform quantitative analysis on metal [
23,
24] and composite materials [
25,
26]. However, its use in in-service environments has a number of limitations. For example, there needs to be access to the item under inspection from all angles (360º), the use of ionizing radiation generates safety concerns, the equipment is costly, and inspection times can be protracted. In addition, X-ray images tend to have low brightness; a possible solution could be found by improving visual effects [
27,
28]. On the other hand, XCT is one of the few techniques that provides a full 3D picture of the microstructure of the inspected item with sufficient spatial resolution (1000 times higher than UT).
Thus, XCT and UT data fusion is an opportunity: automatic defect detection algorithms could be developed for ultrasonic data using the XCT data as ground truth. One example is the work of Sparkman et al. [
29] on the improvement of delamination characterization. Accordingly, labeling is possible in the cases where current UT techniques are unable to detect defects, or fail to provide enough information to this end or in the presence of noisier data. Furthermore, detection models may be developed from any component, and not only from demo components with known inserted defects. In other words, XCT and ultrasounds fusion enables the development of automatic detection/segmentation in ultrasonic data for cases where UT alone is not enough to perform labeling.
As mentioned above, porosity is one type of defect for which UT techniques do not provide enough information. It is also one of the most common manufacturing defects of composite materials. The appearance of voids is random, and there is currently no manufacturing method that is consistently free from porosity. Usually, a threshold of 2% void volume fraction is set as acceptance criteria. However, the estimation of void volume fraction using UT is highly dependent on material, manufacturing process, and inspection equipment [
30]. The void size, shape, and distribution have an impact on the estimation of the void volume fraction [
31,
32], and on the mechanical properties [
33]. Bhat et al. examine the performance of ultrasonic array imaging in distinguishing non-sharp defects, assuming that all defects are crack-like. However, they state that such an approach could be over-conservative and lead to pessimistic assessments of structural components [
34]. Therefore, current UT methods are capable of detecting porosity, but do not provide relevant information about its quantity, shape, and size [
30,
31,
32]. In addition, it is challenging to detect a flaw near another flaw or structure because the resulting waves usually overlap. In composite materials, the main impact of this effect is on close-proximity flaws and at the edges of the part under inspection [
35].
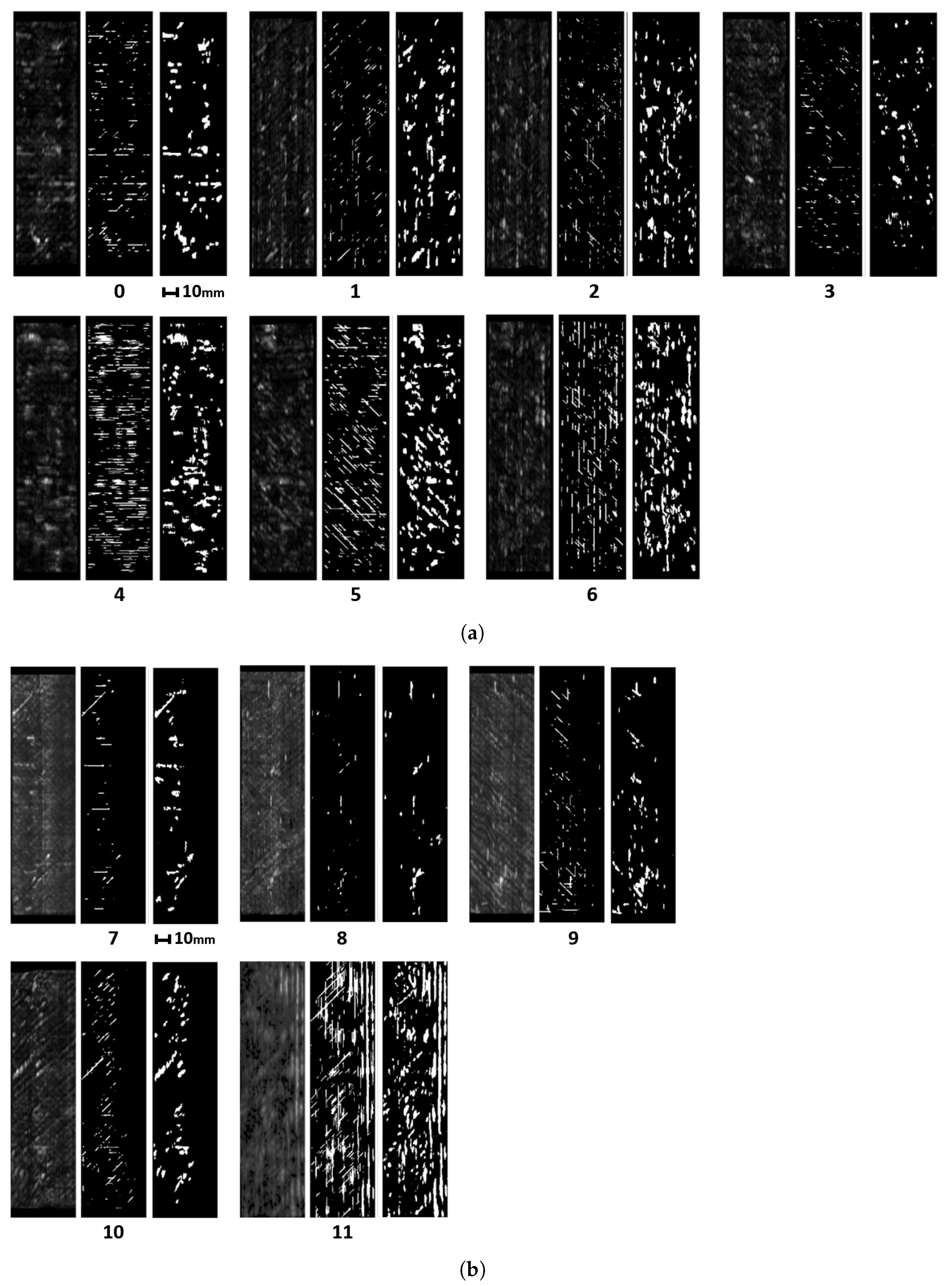
In this article, we develop a methodology for XCT and ultrasonic data fusion that trains a CNN to segment porosity. This would provide a 3D representation of porosity from ultrasonic data and improve the information on the impact of porosity on manufacturing, increasing quality and facilitating efficiency. To do this, phased array (PA) UT was used to obtain the best porosity images, XCT inspections were performed, and a labeled dataset of porosity defects was built and applied to train a convolutional neural network to segment the voids using UT images as input and XCT data as the ground truth. The dataset consists of several C-scans with different cases of void structures. The idea was to train a CNN on 2D cases, evaluated on a 2D test set, and use the trained network to infer ultrasonic 3D data as a sequence of C-scans, long the lines of the approach using B-scans reported in [
15]. Experiments were performed on two 150 × 40 × 5 mm
CFRP coupons. The main contributions of the research are:
A methodology to use ultrasonic and XCT data and its application for porosity assessment, which is a use-case where UT data would not enable the formation of a supervised dataset;
the construction of a dataset of ultrasonic porosity images;
the optimization of phased array ultrasonic inspections enhances the detail level in the analysis of porosity, and void shape, size and distribution;
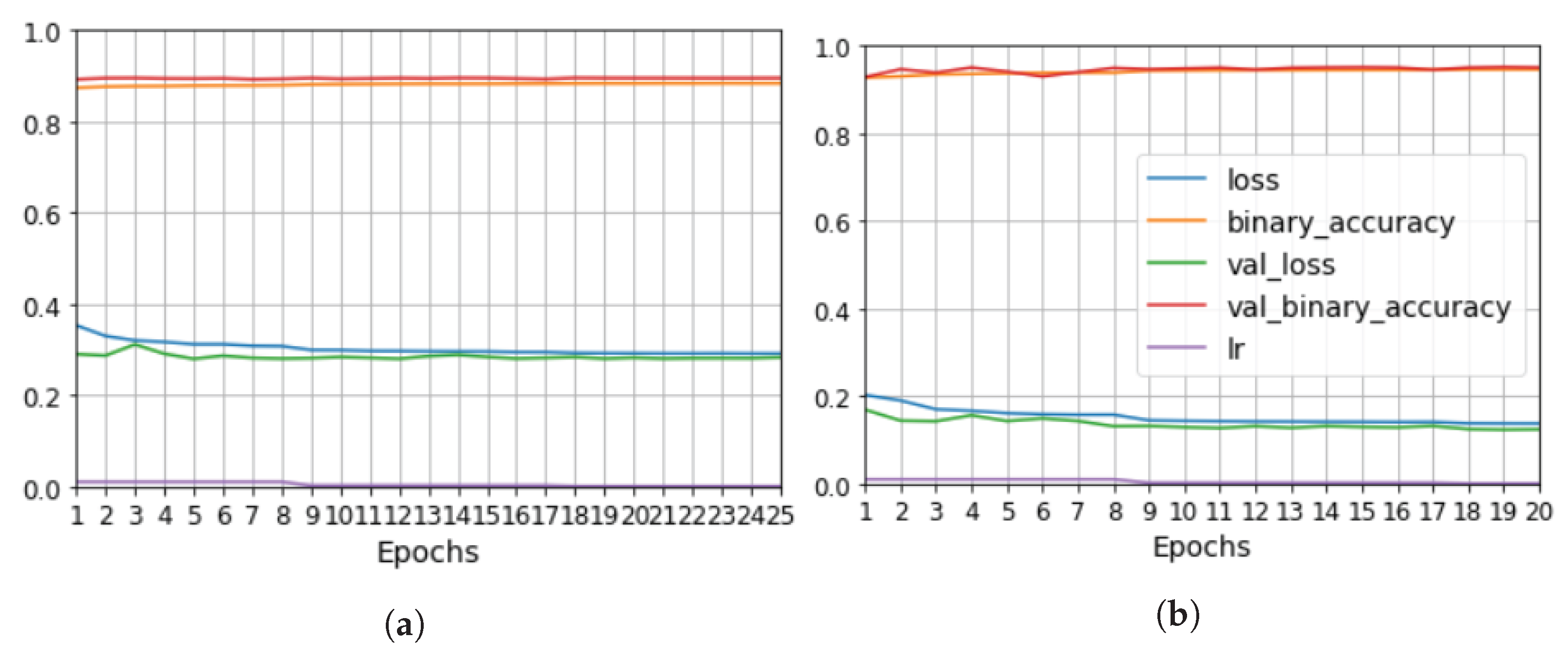
the evaluation of model performance depending on which data were used for training or testing, equal to an F1 of 0.6–0.7 and a IoU of 0.4–0.5 for the test data. Furthermore, the results proved to be robust, since the segmentation was equivalent for data that were part of the training and the test datasets in different training processes.
5. Conclusions and Future Work
We developed a methodology to semi-automatically segment defects in 3D ultrasonic data using a convolutional neural network (CNN). The methodology consists of X-ray computed tomography and phased-array ultrasonic testing data fusion. Supervised classification was then used to train the CNN with 2D images. The use of this approach makes it possible to measure evaluation metrics such as precision, recall, F1 and IoU. The CNN results were compared to the outcomes of applying global thresholds to the phased array. According to the metrics implemented, CNN clearly outperformed the global threshold.
One of the most challenging tasks is data fusion. The proposed solution is an image registration process for 2D images output by each technique, as 3D registration was found not to be accurate enough to train the CNN. In the absence of an algorithm to find common keypoints or any similarity measure between the two data sources, however, registration is not fully automated. This is a future line of work, where the application of deep learning based on the manually annotated data reported here could prove to be useful.
We explored the use of two ground truths: XCT segmented voids and manual labels. The use of the XCT labels was found to output data that were too noisy for CNN training, and manual labels provided more robust training. The evaluation metrics for manual labels were twice as good. The network results—an F1 for test data equal to 0.63 and IoU equal to 0.5—were better than outcomes for the global thresholds. However, CNN is not able to distinguish between echoes produced by defects such as porosity and echoes produced by microstructural elements such as resin-rich areas. Future works should improve the signal-to-noise ratio, increase the dataset, and integrate more information from ultrasonic signals and C-scan representations.