1. Introduction
The ride comfort of vehicles has continuously improved in response to the diverse needs of consumers over the years. Previously, in degraded road environments, ride comfort was evaluated according to the behavior of a vehicle traveling on an uneven road surface. However, in recent years, when the road environment has improved, the behavior of the vehicle based on the steering wheel operation of the driver on a uniform road surface has also had a significant influence on the evaluation of riding comfort. To satisfy the riding comfort performance with the conditions mentioned above and consumers’ demand, automobile manufacturers have continuously conducted driving tests using numerous test vehicles from the past and have evaluated and improved ride comfort through the analysis of driving test results. However, the driving test process is time-consuming and expensive and involves the vehicle design stage, developing a prototype, and preparing and performing the test. In addition, variables such as external environmental factors during the driving test and the driver’s driving condition may adversely affect the reliability of the test. Therefore, to address the shortcomings and limitations of these driving tests, various studies are being conducted to establish a vehicle dynamics model and evaluate and improve riding comfort through simulations.
Vehicle dynamics have been studied by several researchers. Genta [
1] presented the dynamic modeling of a vehicle and the dynamic behavior of the vehicle in some driving conditions, while Gillespie [
2] presented the vehicle dynamics and balanced engineering with practical explanations of the performance of an automotive vehicle. Gillespie and Karamihas [
3] examined the factors that must be considered in developing a simplified dynamic model for truck response to road roughness inputs. Meanwhile, the dynamics of tires and suspensions, which are vehicle parts, were also studied. Pacejka and Bakker [
4] provided a set of mathematical formulae that accurately describe measured tire behavior and contain physically based formulations to calculate the forces and moments acting from road to tire during longitudinal, lateral, and camber slips. Dixon [
5] provided comprehensive coverage of the design, installation, and utilization of a vehicle’s shock absorbers.
Based on the procedures of various driving tests, studies have been conducted to analyze ride comfort through the simulation of vehicle models. Accordingly, some notable studies related to driving tests are summarized. Choi et al. [
6] experimentally measured and evaluated the vertical direction (bounce) and front-rear tilting (pitch) behavior of a vehicle body, which occurs predominantly when the vehicle passes through an uneven road surface during the test. Jonsson and Johansson designed a suspension system that can control bounce and pitch behavior to improve riding comfort [
7]. On the other hand, the left and right tilting (roll) behavior of the vehicle body while turning on a flat road surface is also very important, considering ride comfort and stability. In this regard, Uys et al. [
8] experimentally evaluated the roll behavior caused by changing the steering wheel of a driving vehicle. Additionally, Darling and Hickson [
9] developed an anti-roll suspension system that can improve riding comfort by controlling roll behavior. Further, Choi et al. [
10] performed an experiment suggesting a method to control the damping characteristics of the suspension. This method takes into account the distinct body bounce, pitch, and roll behaviors, which were previously examined individually in separate studies.
Several studies have been published on the analysis of ride comfort, utilizing simulation techniques that simplify vehicle systems into basic dynamic models These studies predominantly focus on the quarter-car model, which solely considers the vertical behavior of the vehicle body. Sun et al. [
11] established a two-degree-of-freedom vehicle model with vertical road surface excitation and derived the equation of motion using the Lagrange equation. Subsequently, the vertical vibration of the vehicle body according to the change in parameters such as mass, stiffness, and damping ratio in the model was analyzed through numerical analysis. Georgiou et al. [
12] presented an optimization technique for deriving optimum values of damping and stiffness of suspension for improved ride comfort with vehicle models, including manual and semi-active suspension. Singh et al. [
13,
14] established a model by additionally considering a seat and a human body in a quarter-car model that depicts only existing vehicles. They proposed a methodology to improve ride comfort through vibration responses from seats or body parts according to vertical road excitation.
After that, the vehicle model was expanded from the existing quarter-car model to the half-car model to consider the tilting behavior of the car body. Some studies that analyzed ride comfort using this model are as follows: Sun et al. [
15] derived the equations of motion for a vehicle model with four degrees of freedom that can consider the bounce and pitch of the vehicle body traveling on a rough road. They analyzed various responses in the time and frequency domains for the change in model parameters. Zhu et al. [
16] obtained frequency response functions for random road excitation through a vehicle model considering the pneumatically interconnected suspension (PIS) system and compared and analyzed them with the vehicle model without the PIS system. On the other hand, Hudha et al. [
17] were interested in the roll behavior of the vehicle body. They established a vehicle model with the effects of the anti-roll bar and the control arm and presented a suspension control system that can control the roll of the vehicle body caused by road excitation. Gosselin-Brisson et al. [
18] proposed an active anti-roll bar system that can effectively control the roll motion of the vehicle body caused by lateral acceleration under vehicle turning conditions.
Recent studies analyzed the riding comfort of a full-size car model to better understand the behavior of the actual vehicle. Abu Bakar et al. [
19] proposed a full car model with seven degrees of freedom that can analyze ride comfort. To verify the validity of the proposed model, the similarity between the simulation and experimental results was shown in the pitch mode test condition of the vehicle body that occurs when passing through a bump. Palli et al. [
20] and Sentilkumar et al. [
21] established a full vehicle model with seven degrees of freedom considering active suspension and found that active suspension improves riding comfort by preventing vehicle resonance that may occur due to road excitation. On the other hand, Ghike and Shim [
22] proposed a full car model with 14 degrees of freedom that can analyze the rolling behavior of a turning vehicle according to steering conditions. He also showed the limitations of his model and demonstrated its excellence and validity.
On the other hand, vehicle dynamics can be analyzed by using commercial multi-body dynamics software packages such as ANSYS-Motion [
23], RecurDyn [
24], MSC/Adams [
25], and Simpack [
26]. These commercial packages provide the advantage of easily constructing detailed vehicle models. However, they require a lot of experience and skill in constructing the model, assigning boundary conditions/constraints, and often requiring long computation times. On the contrary, concentrated mass models are difficult to apply to complex systems. However, it is relatively easy to analyze the influence of various parameters of the model and requires shorter computation times.
With improvements in the road environment and recent developments in the vehicle industry, vehicle consumers are demanding improvements in ride comfort performance according to the driver’s steering conditions rather than solely focusing on ride comfort performance against irregular road surface disturbances. In this regard, various vehicle manufacturers have attempted to analyze and improve ride comfort through driving tests. However, a time-efficient and affordable method is needed for driving tests to quickly respond to consumer demands. Therefore, building a simple mathematical model of a vehicle that can analyze the riding comfort of a vehicle driven by steering input through simulation is desired.
However, most of the previous studies investigated by the authors tend to focus on vehicle models for analyzing ride comfort under disturbance conditions, such as uneven road surfaces or irregularities. In addition, several studies have been published to analyze the behavior of the vehicle body by establishing a vehicle model for turning conditions. However, they have used a method to obtain a response generated by inputting an arbitrary lateral acceleration into the vehicle body. Since lateral acceleration is a variable determined by the change in steering angle input by the driver, it is limited as an actual input condition for a turning vehicle. In summary, the limitation of vehicle models in the previous studies is that they cannot analyze the dynamic responses of a turning vehicle according to the vehicle speed and steering angle controlled by a driver. Therefore, this study introduces a full-car model that can analyze the dynamic behavior of a turning vehicle according to the change in steering angle, which is the driver’s input condition. The new 7-DOF full-car model proposed in this study is valuable in that the simulation and driving test results for various steering conditions have been comparatively verified. The main contribution of this study is to present a full car model encompassing an anti-roll bar that can analyze the dynamic behavior of the variation of the steering angle controlled by a driver.
The remainder of this paper is organized as follows: In
Section 2, a dynamic vehicle model that can analyze the behavior of a driving passenger car is developed. A vehicle model with seven degrees of freedom was established, considering the centrifugal force acting on the vehicle during turning and the torsional stiffness of the anti-roll bar. Based on this model, the equations of motion are derived using Lagrange’s equation. In
Section 3, the established vehicle model is verified by comparing the vertical suspension deformations computed with the vehicle model with the deformations measured through actual vehicle driving tests. For comparison, three driving tests were performed: the slalom, double lane change, and step steer tests. In
Section 4, the natural frequencies and mode shapes of the dynamic vehicle model are computed and analyzed using the developed vehicle model. Furthermore, the effects of changes in the design parameters on the dynamic response of the vehicle model were investigated. The considered design parameters were suspension stiffness, suspension damping, and anti-roll bar torsional stiffness. Finally, conclusions and a summary of this study’s results are presented in
Section 5.
2. Dynamic Vehicle Model
In this section, a dynamic model of a vehicle that can analyze the behavior of a driving passenger car is presented. This study assumes that the speed of the vehicle is kept constant, and the driving direction of the vehicle is changed by the steering wheel. Under these assumptions, the vehicle does not accelerate in the longitudinal direction (direction of travel), but only in the lateral direction perpendicular to the traveling direction. This lateral acceleration imparts a centripetal force to the vehicle and maintains it on a turning trajectory.
The centrifugal force acting on the vehicle during turning is given by the following equation:
where
is the total mass of the vehicle,
is the speed of the vehicle, and
is the turning radius. When the vehicle is traveling at a constant speed, as long as the mass
and speed
are constant, the centrifugal force
is determined by the turning radius
.
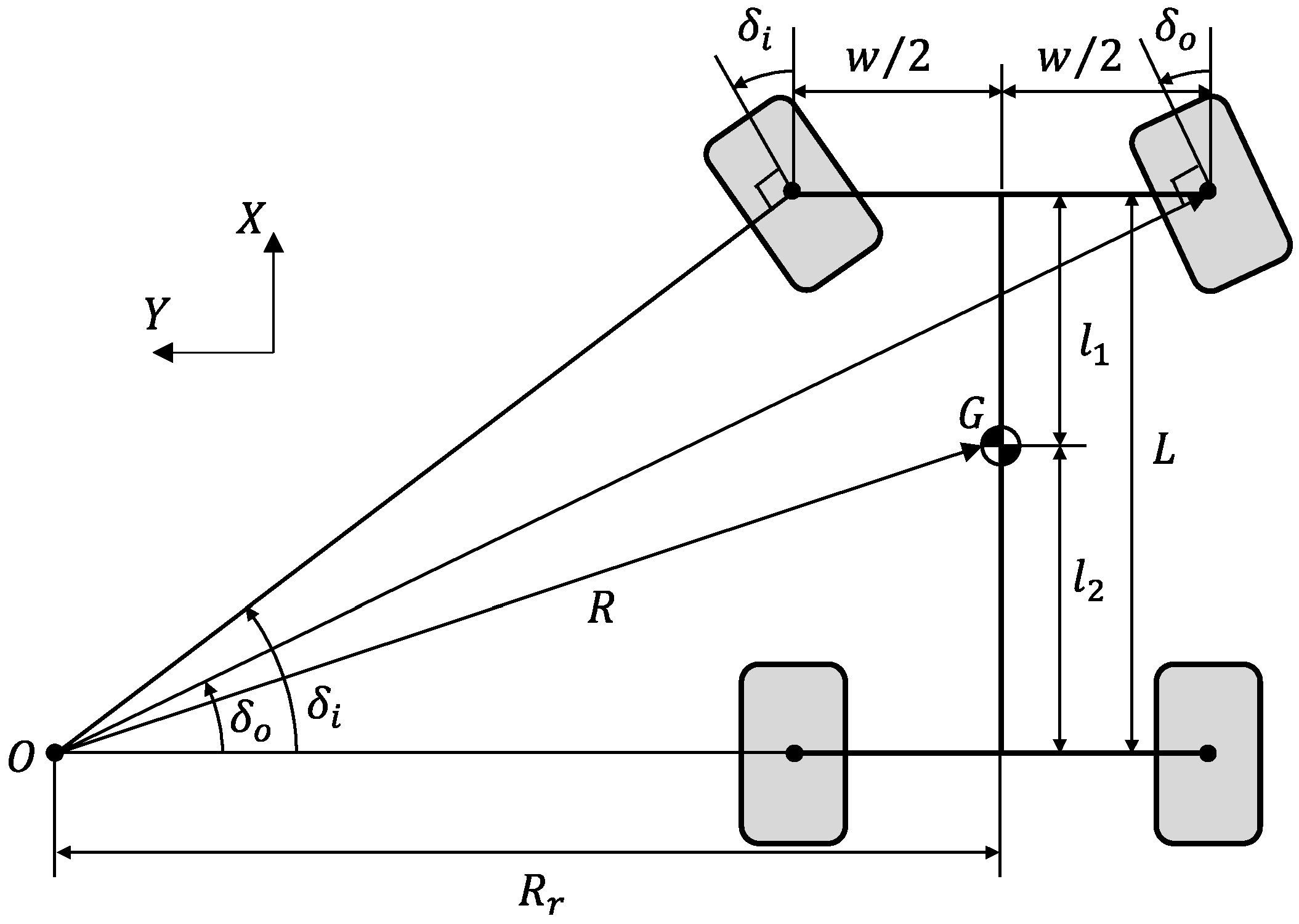
The relationship between the turning radius of the vehicle and the steering angle of the steering wheel was analyzed. First, the relationship between the vehicle’s turning radius and the steering angles of the front wheels can be derived from the Ackermann steering geometry [
27], as shown in
Figure 1. In
Figure 1, point
is the instantaneous turning center,
is the center of mass of the vehicle, and
and
are the distances from the center of mass to the front and rear wheels, respectively.
is the distance between the centers of the left and right wheels, and
is the distance from the front wheel to the rear wheel. As shown in this figure, the position of the turning center
coincides with the intersection of the extension line of the rear axle and the vertical lines inside and outside the front wheels. Accordingly, the steering angle of the inner front wheel,
is formed by the extension line of the rear axle and a line perpendicular to the inner front wheel. Additionally, the steering angle of the outer wheel,
is formed by the extension line and a line perpendicular to the outer front wheel. The distance
from the turning center
to the vehicle center of mass
is called the turning radius, and the distance from the turning center
to the center of the rear axle is expressed as
.
Thus, if the instantaneous turning center is determined geometrically, the turning radius
can be expressed as the inner and outer front wheel steering angles,
and
. The relationship between the steering angles of the inner and outer front wheels, the distance from the turning center to the center of the rear wheel axle, and the distance between the left and right wheels can be expressed by the following equations:
In general, as the steering angle is not large when the vehicle is traveling, the steering angles
and
are assumed to be small, and the turning radius
is very large compared to the distance w between the centers of the left and right wheels. Therefore, in Equations (2) and (3),
and
can be approximated by
and
, the distance from the turning center to the center of the rear wheel axle,
can be replaced by the turning radius
, and the distance between the left and right wheels
can be neglected. Denoting the average steering angles of the inner and outer front wheels by
, that is,
, the turning radius of the vehicle is given by:
This equation implies that the turning radius is determined by the average steering angle of the front wheels and wheelbase distance .
The centrifugal force applied to a turning vehicle can be obtained by substituting Equation (4) with Equation (1).
The average steering angle of the front wheels is determined by the steering ratio and steering wheel angle, which can be expressed by the following equation [
28]:
where
is the angle of the steering wheel and
is the steering ratio of the steering wheel angle to the steering angle of the front wheels. The steering angle ratio
is determined by the gear ratio of the steering linkage connecting the steering wheel and the front wheel, which is 15 for the target vehicle of this study. Finally, the centrifugal force applied to a turning vehicle is expressed as follows: vehicle mass
, vehicle speed
, wheelbase distance
, steering wheel angle
, and steering ratio
.
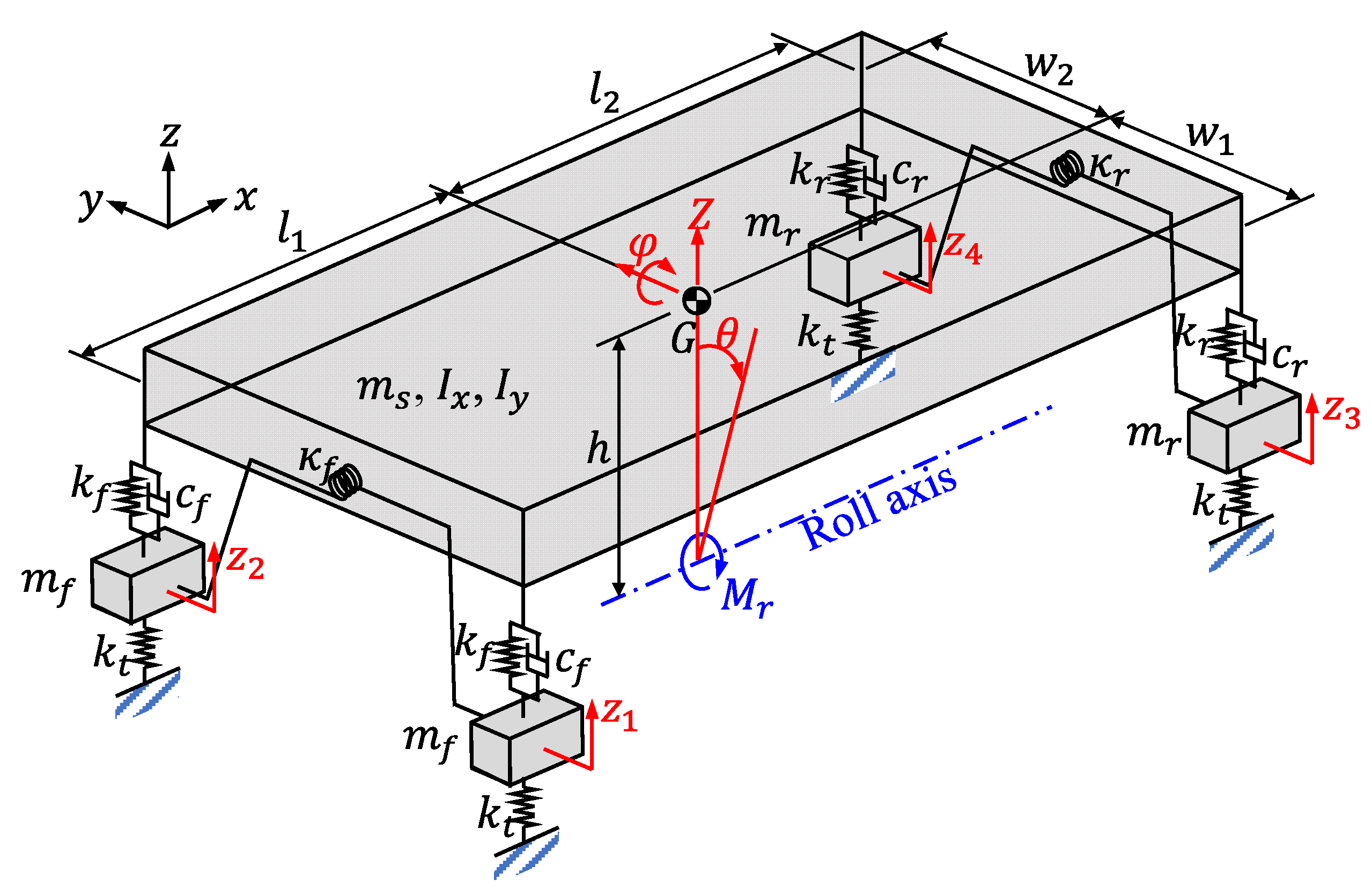
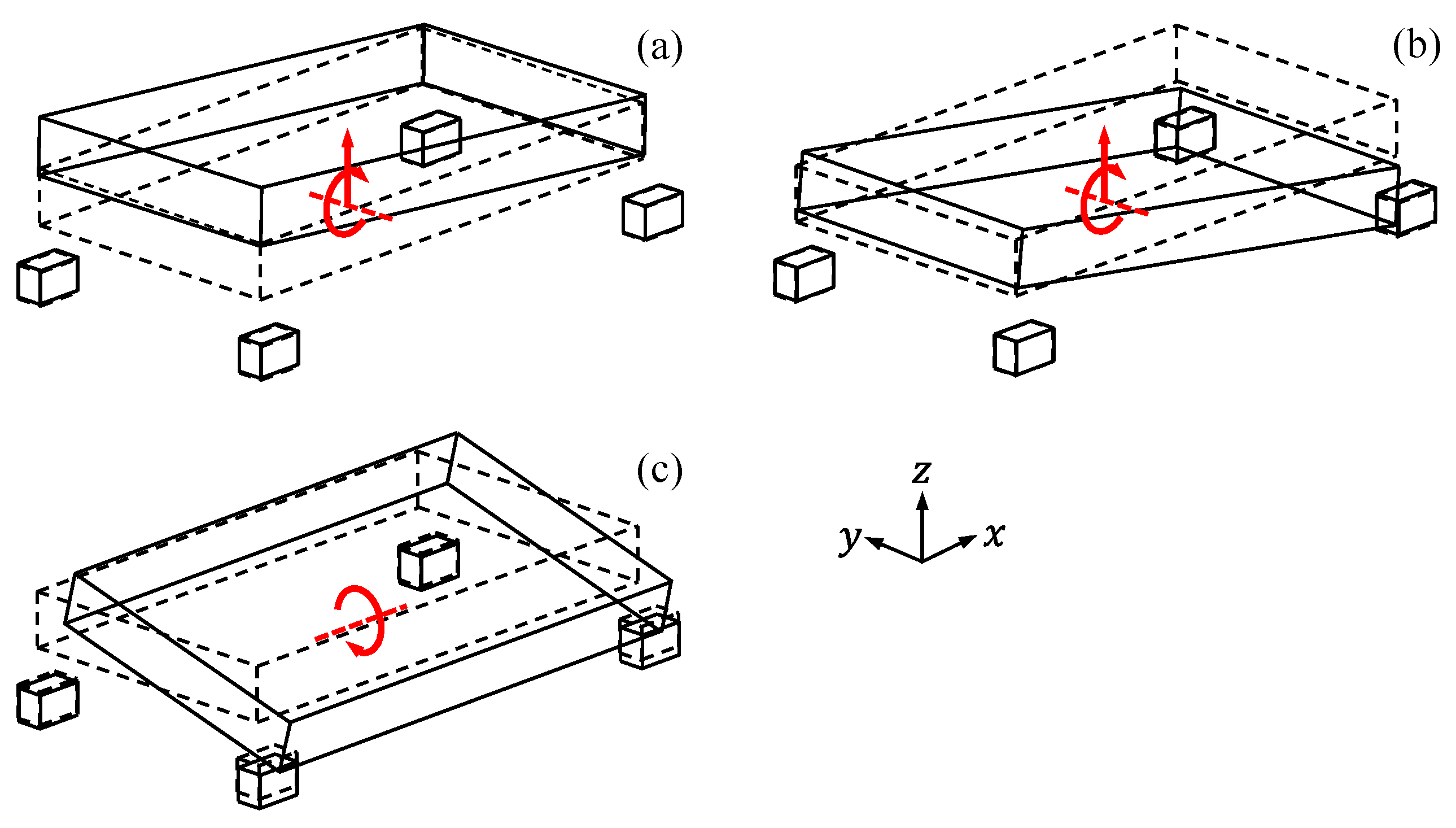
Next, a dynamic vehicle model with seven degrees of freedom was established to analyze the behavior of a driving vehicle. As shown in
Figure 2, the vehicle was modeled with one sprung mass and four unsprung masses, for a total of five rigid bodies, and the suspension, anti-roll bar, and tires were modeled as springs and dampers. In
Figure 2, the vehicle’s forward direction is the negative
x-axis direction. In addition, the
y- and
z-axes are parallel to the left and right directions and the up and down directions of the vehicle, respectively. The sprung mass is the total mass of a vehicle supported by the suspension, which includes the body, frame, engine, transmission, and internal components. The unsprung mass includes wheel axles, wheel bearings, wheel hubs, tires, drive shafts, springs, shock absorbers, and suspension links. The motion of the sprung mass is described by the bounce displacement of the mass center
, the pitch angle
, and the roll angle
, while the motions of the unsprung masses are described by the vertical displacements of
,
,
and
. In this study, the x-direction motion of the sprung mass is defined as a constant vehicle speed
. Since the vibration and yaw motion in the
x and
y directions are ignored, the motion of the sprung mass is defined by the bounce displacement, pitch angle, and roll angle.
As shown in
Figure 2, the sprung mass has a roll motion that rotates about a roll axis parallel to the
x-axis at a distance
mm vertically from the center of mass [
29]. This considers the phenomenon that the lateral centrifugal force acting on the center of mass of the vehicle body located at a distance
from the roll axis generates a roll moment for the vehicle body when the vehicle turns to the right. The position of the roll axis changes with a very complex mechanism depending on the kinematics of the suspension links. However, in this study, the relative position of the roll axis to the body is considered fixed to establish a simple and efficient model. Therefore, the roll moment
shown in
Figure 2 is expressed as the product of the centrifugal force
applied to the vehicle and the distance
from the roll axis to the mass center, that is,
.
The sprung mass has mass
, mass moment of inertia about the center of mass
, and mass moment of inertia about the
y-axis
. The mass center of the sprung mass
is located at a distance
from the front of the vehicle,
from the rear,
from the left end of the vehicle, and
from the right end of the vehicle. The front unsprung masses with mass
have vertical displacements
and
, while the rear unsprung masses with mass
have displacements
and
. However, experimentally obtaining the mass and mass moment of inertia values of various parts to calculate the inertia parameters of the model shown in
Figure 2 is a time-consuming and complicated procedure. Therefore, in this study, the inertial values of the sprung and unsprung masses for the dynamic vehicle model were extracted from the 3-D solid model of the vehicle using commercial CAD software. These are the values:
kg,
kg,
kg,
kg·m
2, and
kg·m
2. The products of inertia were neglected in this study because they were relatively small.
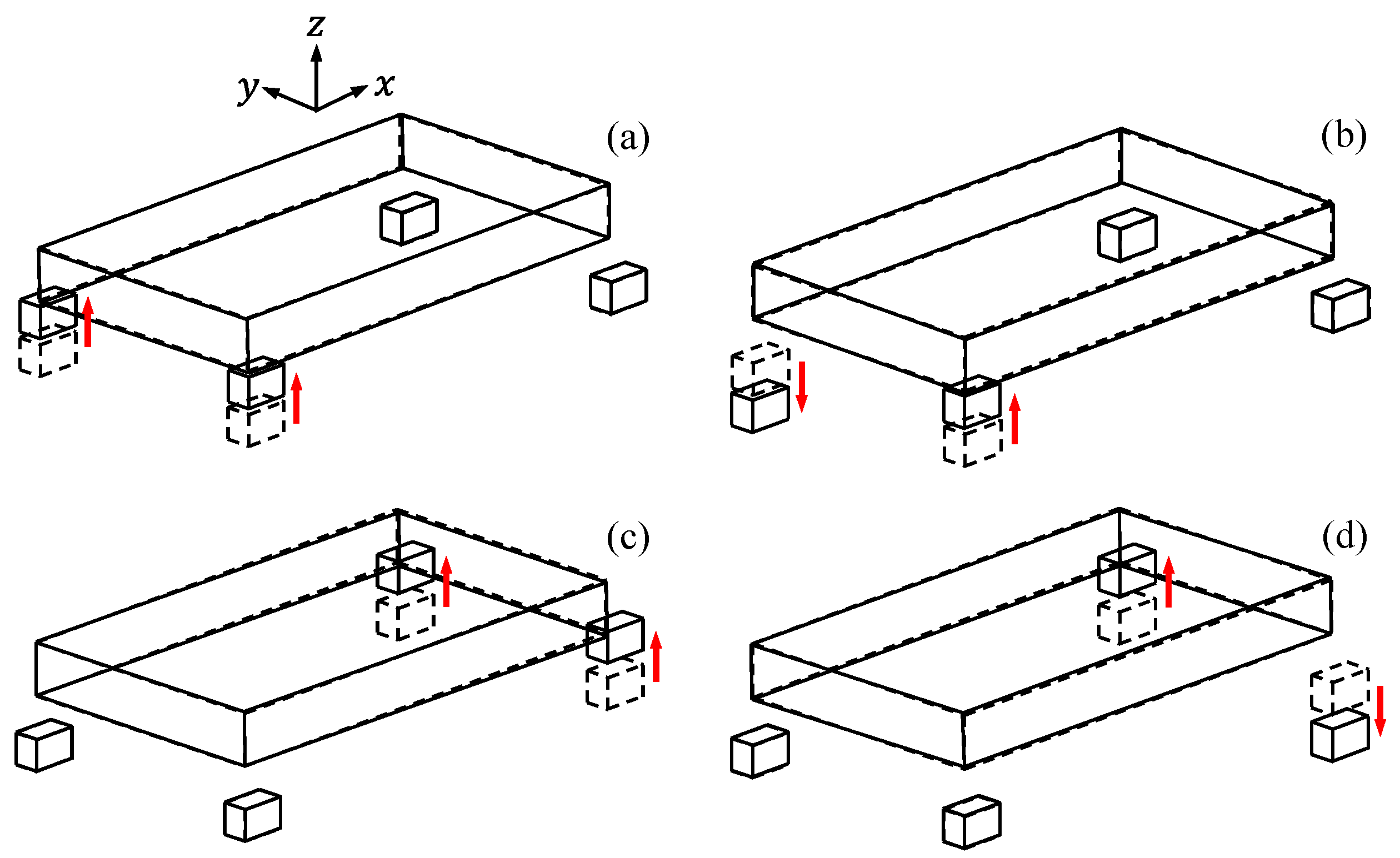
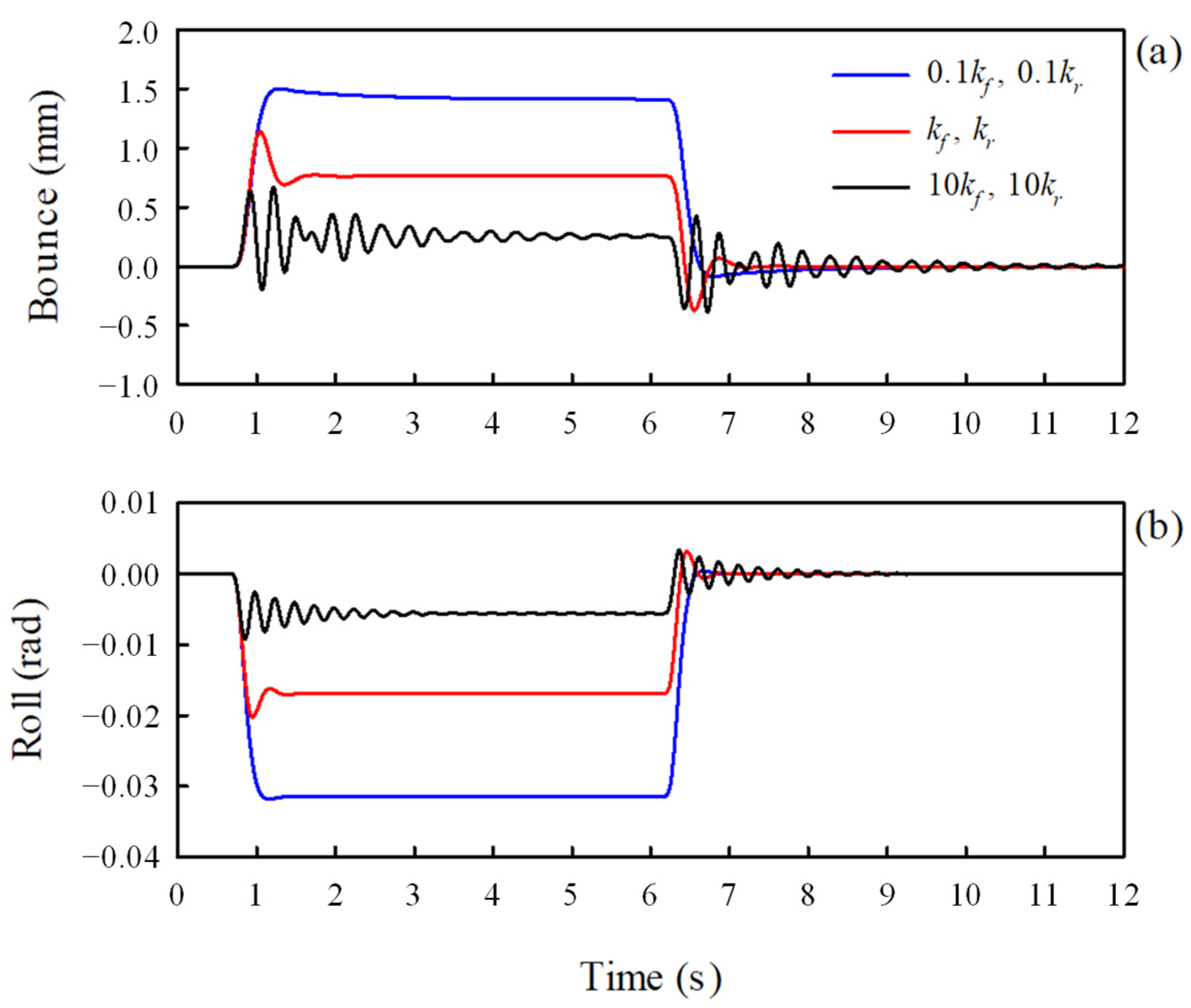
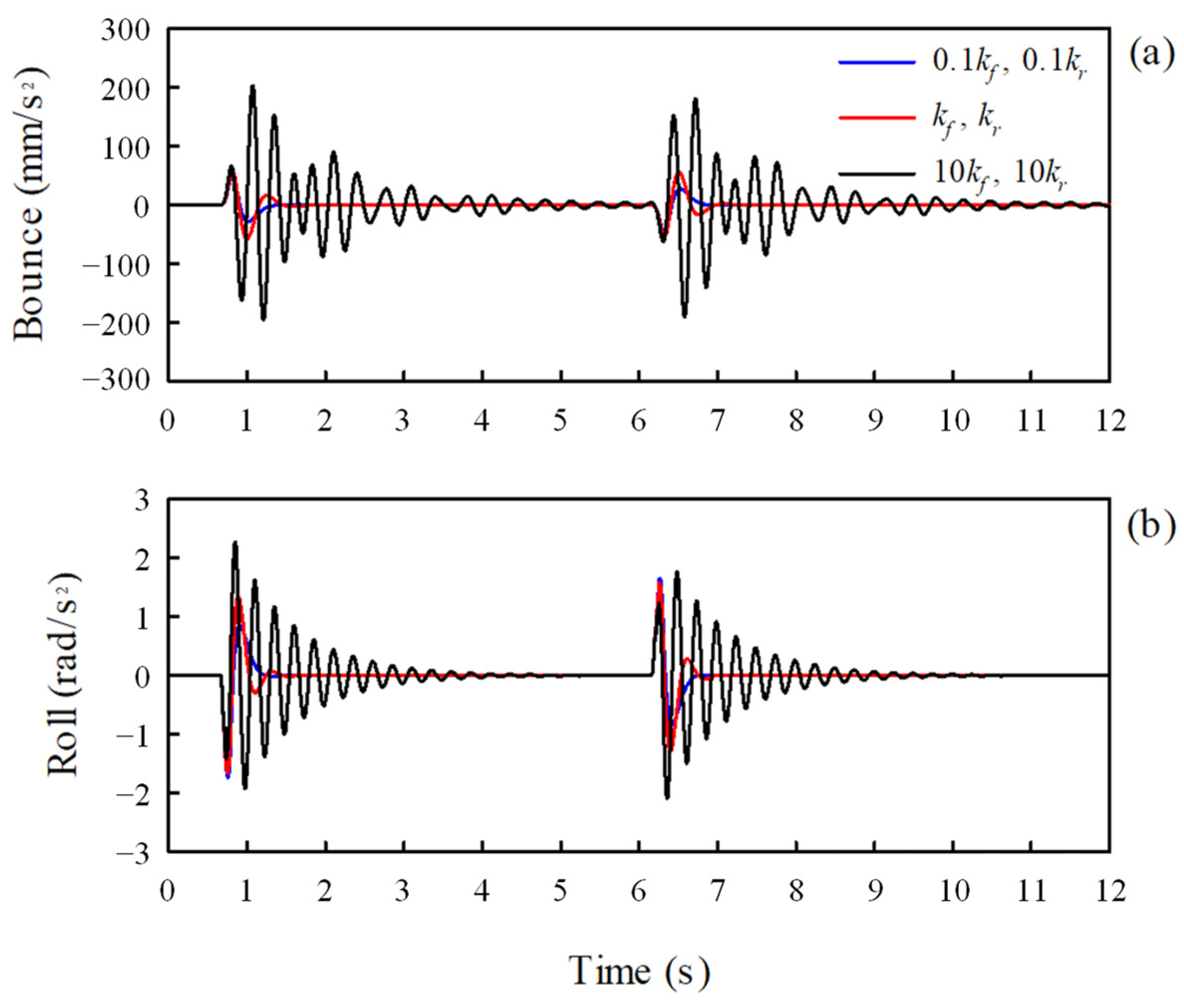
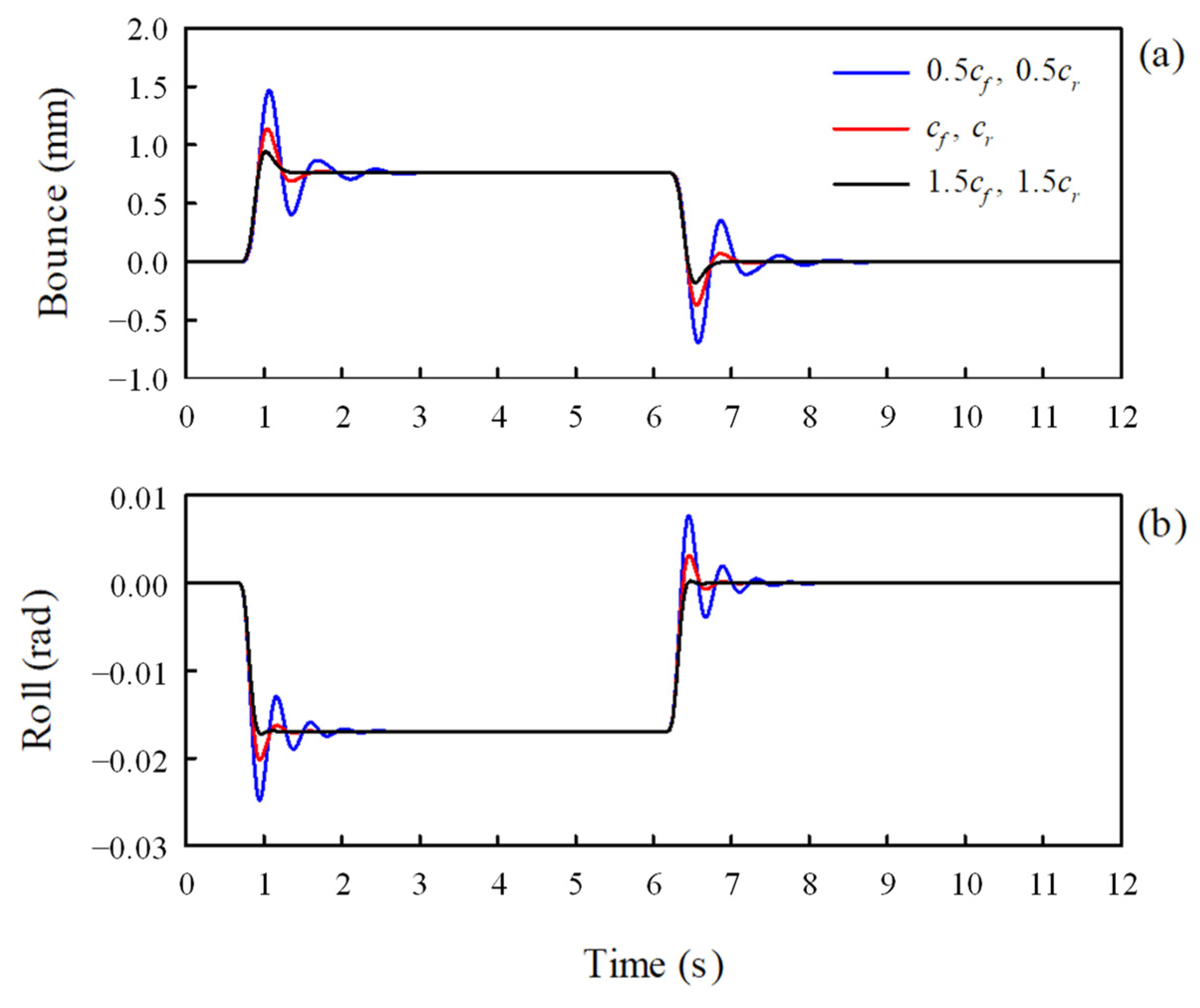
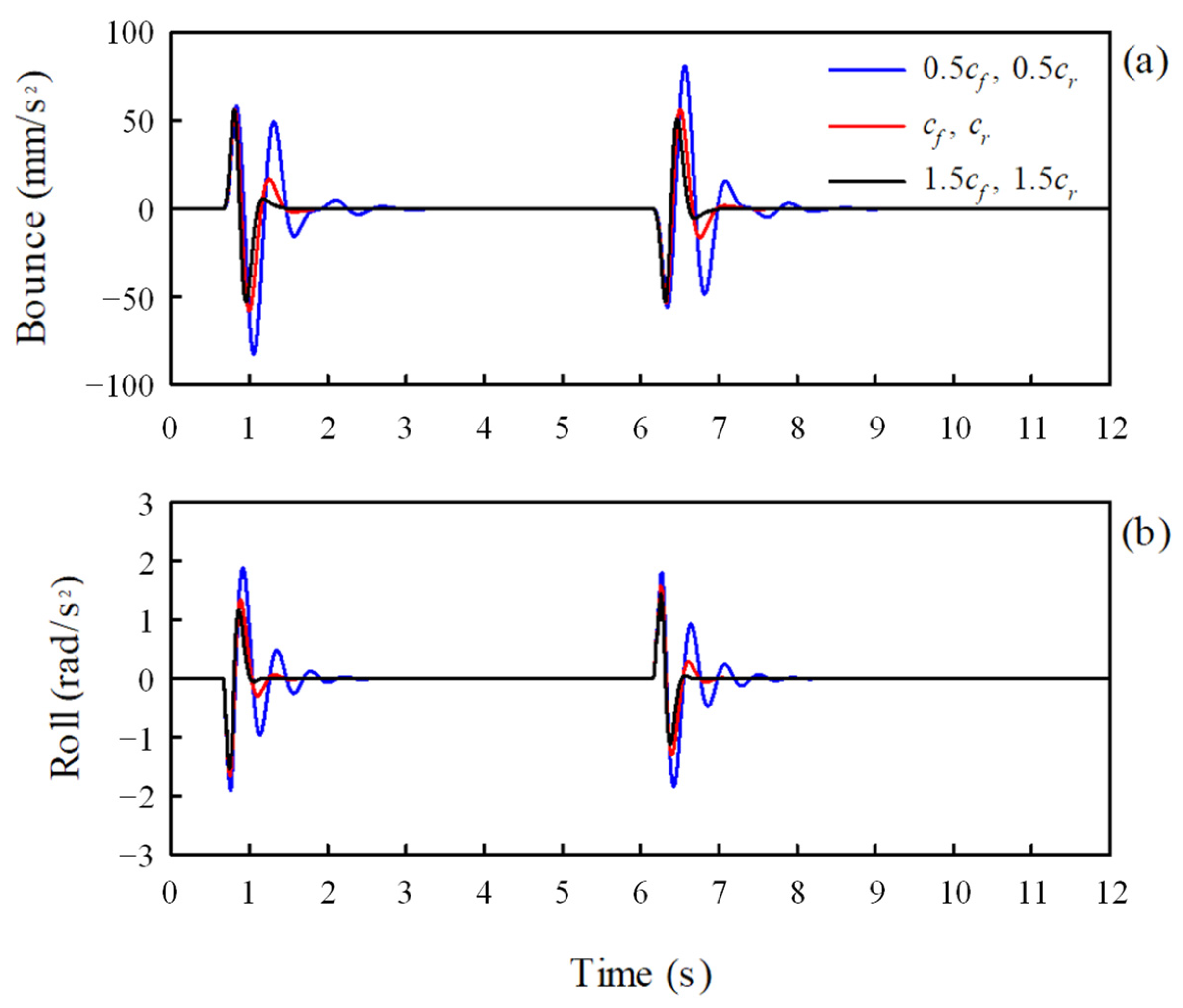
The suspension, tire, and anti-roll bar that connect the rigid body and ground defined above were modeled with linear equivalent springs and dampers. The front suspensions vertically connected between the sprung mass and front unsprung masses were modeled with an equivalent stiffness and an equivalent damping coefficient . Additionally, the rear suspension vertically connected between the sprung mass and rear unsprung masses was modeled with an equivalent stiffness and equivalent damping coefficient . As the tires between the ground and the unsprung masses have very high stiffness, they are modeled with an equivalent stiffness without damping.
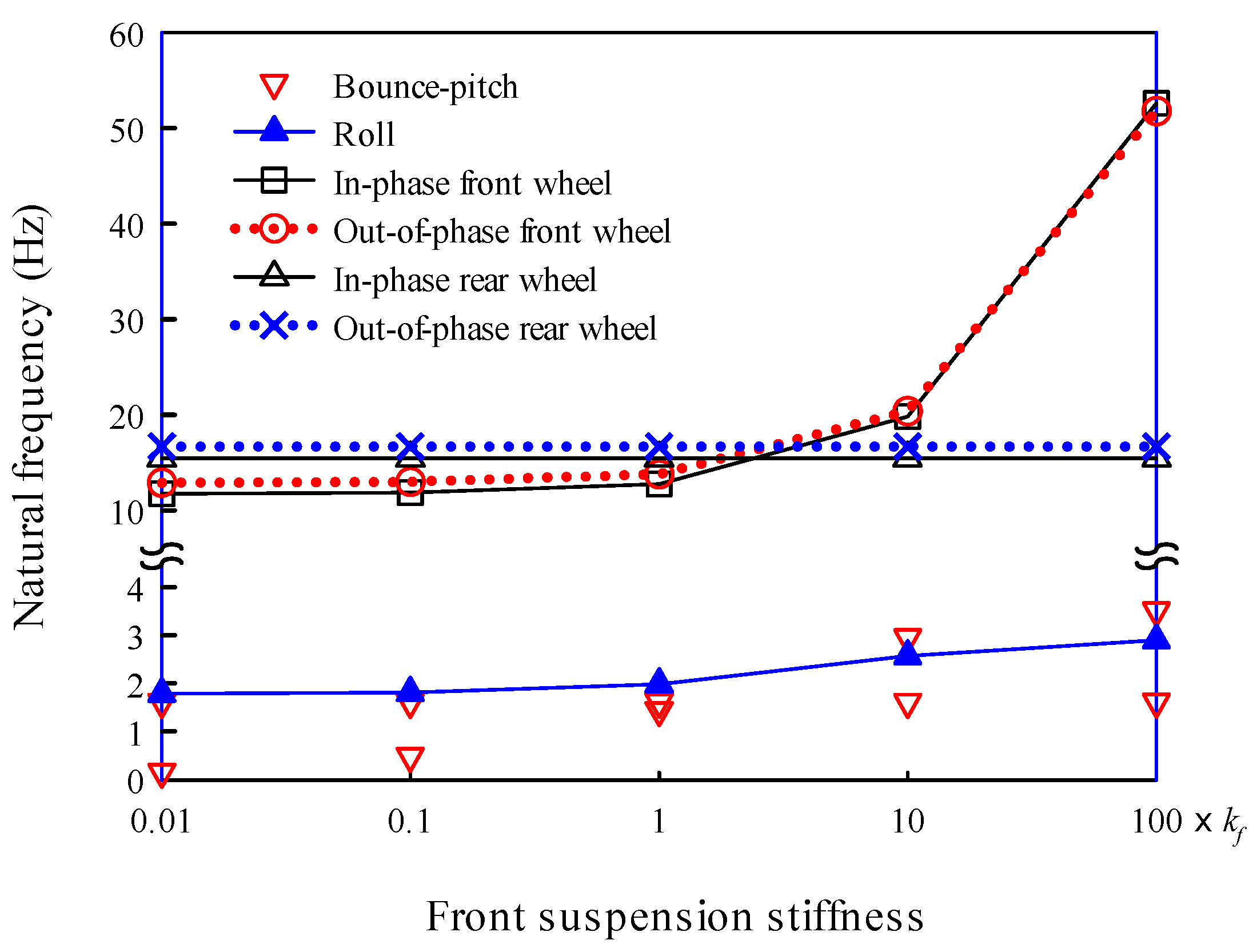
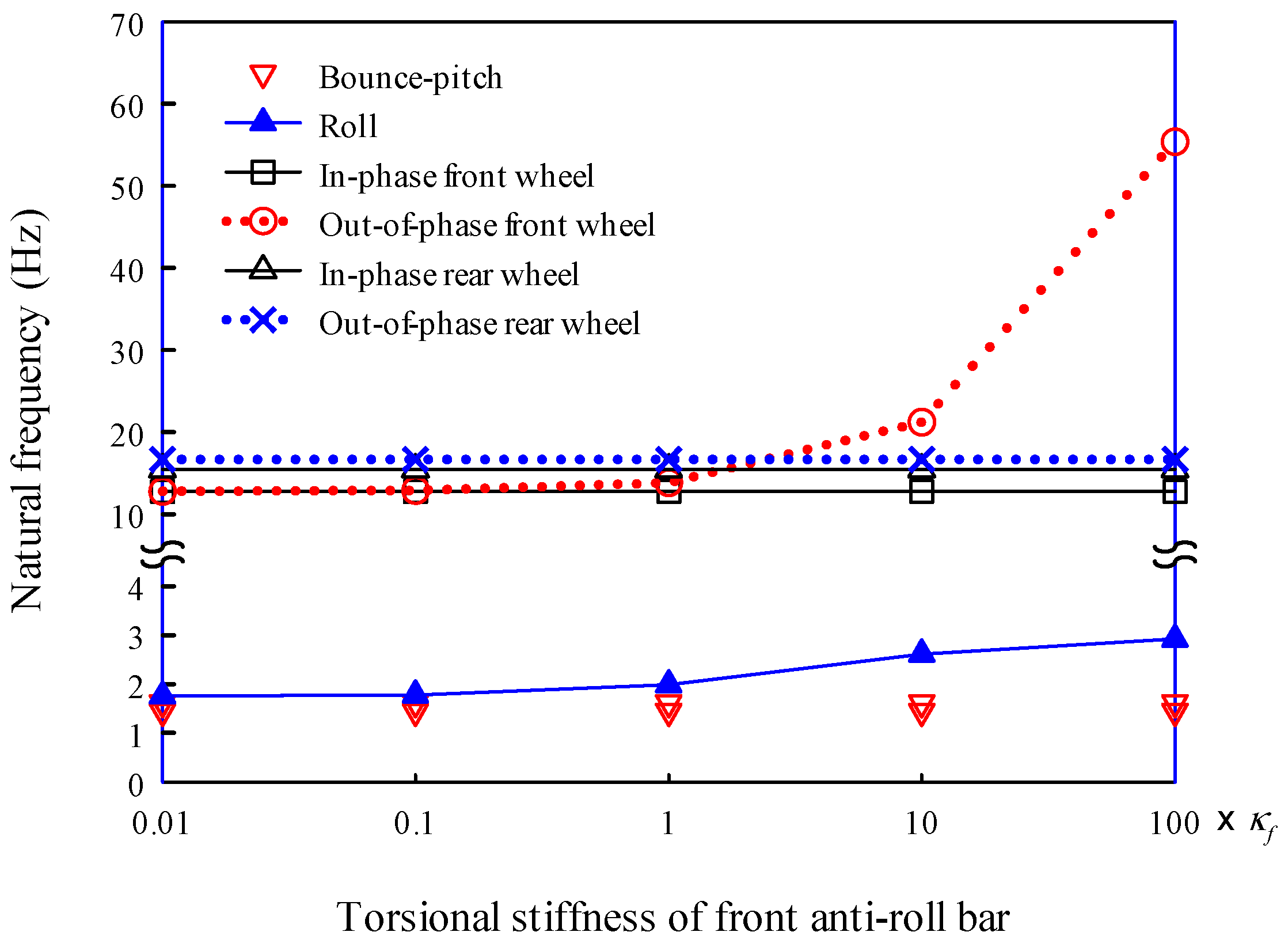
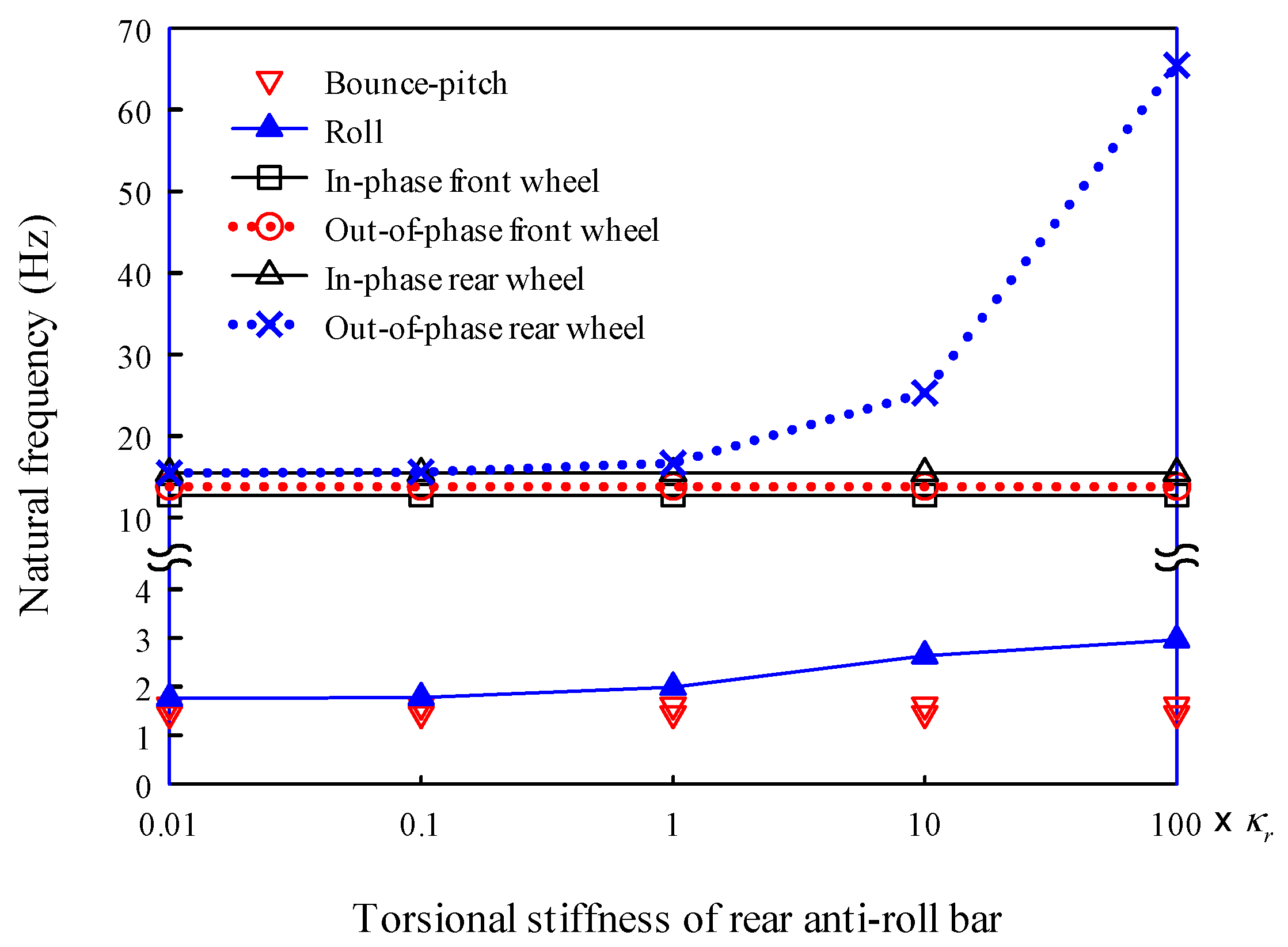
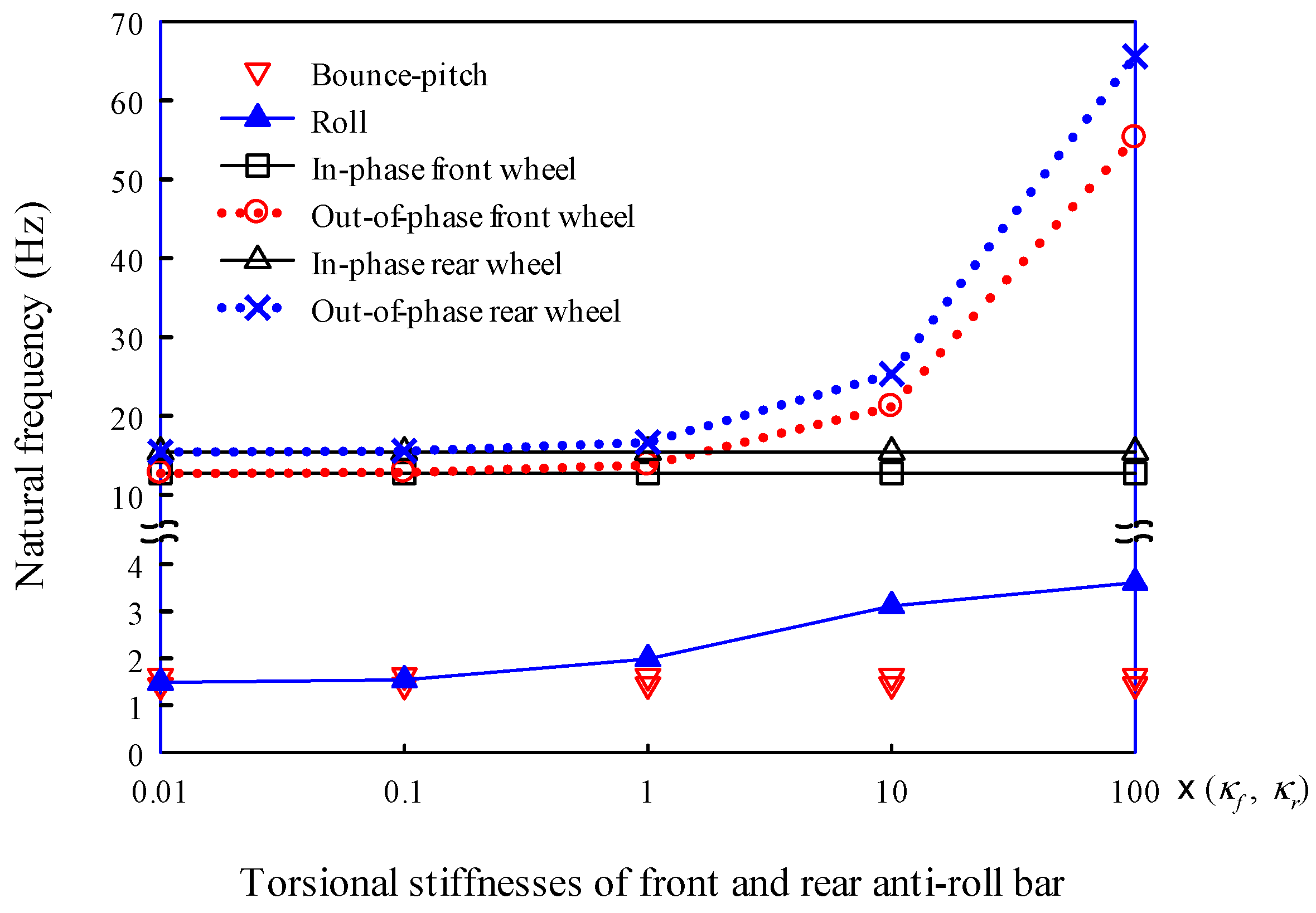
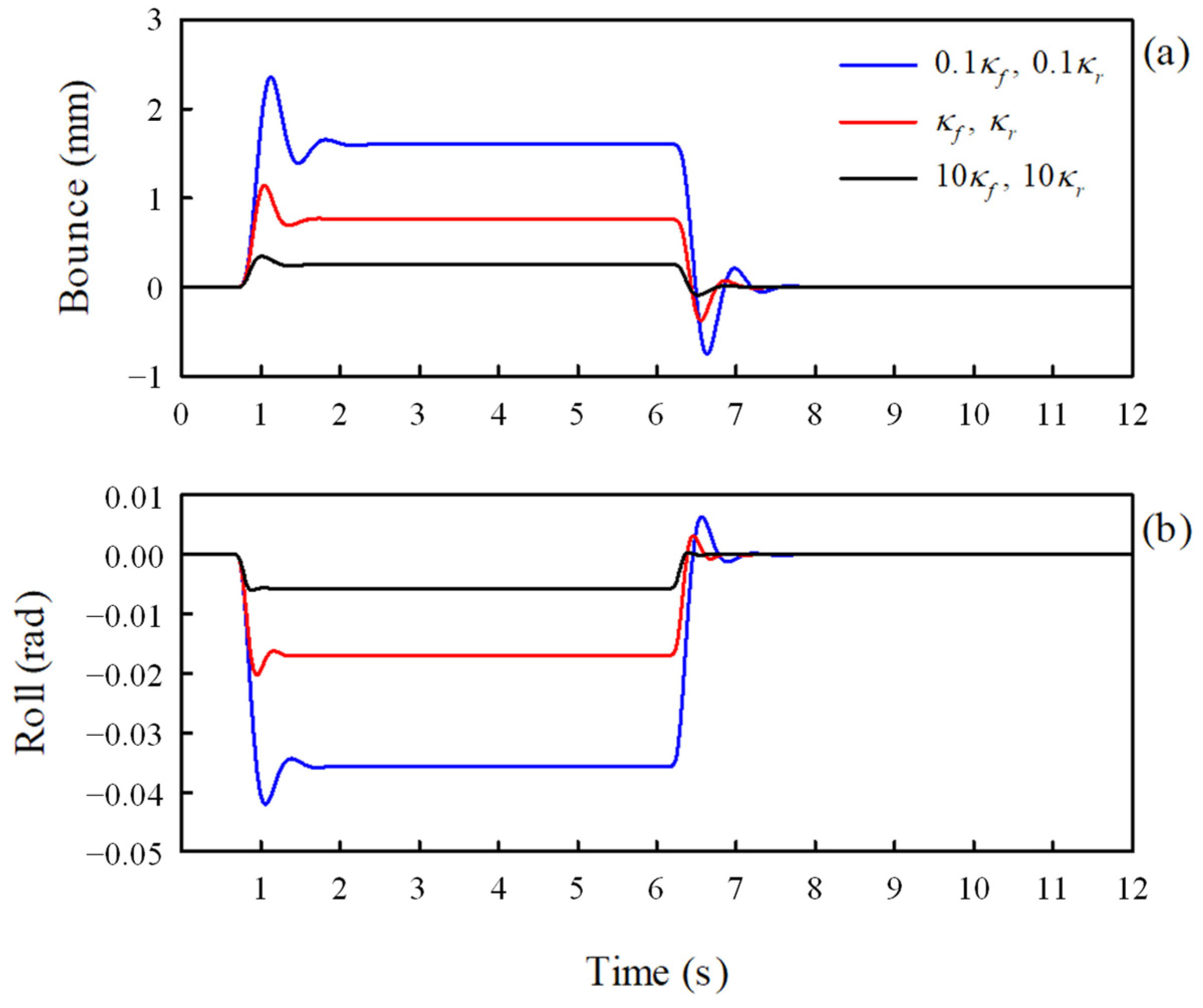
On the other hand, anti-roll bars, which help reduce vehicle body roll in fast cornering or on irregular roads, are modeled as torsion springs. The bars are long U-shaped metals with hollow cross sections that join the suspensions on the right and left sides of an axle. They are usually attached to the chassis at two points using rubber bushings. The torsional stiffnesses of the front and rear anti-roll bars were assumed to be
and
, respectively [
30]. The twist angles of the anti-roll bars were determined by the angular displacements of the axel shafts relative to the sprung mass. The axle shaft has an angular displacement owing to the difference between the right and left wheels. To help understand this, a dynamic vehicle model viewed from the front is shown in
Figure 3 as an example.
As the front left and right unsprung masses have vertical displacements
and
, respectively, the angular displacement of the front axle shaft is computed as
. Therefore, the twist angle of the front anti-roll bar
, is given by
Similarly, the twist angle of the rear anti-roll bar can be expressed as
The equivalent stiffness and damping coefficients presented above were calculated using an experimental method. The equivalent stiffness values of the suspensions and tires were obtained through static vertical load-deflection tests [
31,
32]. Similarly, the equivalent torsional stiffness values of the anti-roll bars were obtained through torsional load-torsion angular deformation tests. The values for the various equivalent stiffness, equivalent torsional stiffness, and damping coefficients obtained by the tests were as follows:
N/m,
N/m,
N/m,
N·m/rad,
N·m/rad, and
N·s/m.
The equations of motion for the driving vehicle were derived using the following Lagrange equation:
where the superposed dot represents differentiation with respect to time;
stands for the seven generalized coordinates;
,
,
and
are the kinetic energy, potential energy, Rayleigh’s dissipation function, and generalized force, respectively. Among the generalized coordinates, the three coordinates (
,
, and
) are for the motion of the sprung mass, whereas the four coordinates (
,
,
,
) are for the motions of the unsprung masses.
First, the kinetic energy of the dynamic vehicle model can be expressed as the following equation:
where the first term is for the translational motion of the sprung mass, the second and third terms are for the rotational motion of the sprung mass, and the fourth and fifth terms are for the translational motions of the unsprung masses.
Next, the potential energy owing to the deformations of the springs and torsional springs in the dynamic vehicle model may be given by
where the first term is the potential energy of the tire, the second and third terms are the potential energies of the suspensions, and the fourth and fifth terms are the potential energies of the anti-roll bars. In the second and third terms,
,
,
, and
are the suspension deformations at the left front wheel, right front wheel, left rear wheel, and right rear wheel, respectively.
The suspension deformation at each wheel,
for
i = 1, 2, 3, 4, is determined by subtracting the displacement of the unsprung mass from the
z-directional displacement of the sprung mass at the point corresponding to each suspension. The displacement of the sprung mass at the left–front suspension,
, displacement at the right–front suspension,
, displacement at the left–rear suspension,
, and displacement at the right–rear suspension,
, can be determined by
where
is the displacement of the mass center of the sprung mass,
is the position vector of the point on the spring mass corresponding to each suspension, and
and
are the rotation matrices about the
and
axes, respectively. The vectors and matrices in Equation (13) are given by
In other words, the suspension deformations were obtained by subtracting the displacements of the corresponding unsprung mass
from the
z-directional components of
. Consequently, the suspension deformations can be expressed as
On the other hand, Rayleigh’s dissipation function for the vehicle model can be represented by
where
(
,
,
,
) are the time derivatives of the suspension deformations given by Equation (16). Finally, the non-conservative generalized forces of Equation (10) are given by
As shown in these equations, there are no generalized forces except for , and this generalized force is the roll moment described above.
The equations of motion were obtained by substituting the kinetic energy (Equation (11)), potential energy (Equation (12)), Rayleigh’s dissipation function (Equation (17)), and generalized forces (Equation (18)) into the Lagrange equation (Equation (10)). The derived equations are nonlinear ordinary differential equations for generalized coordinates. Assuming that the roll and pitch angles are small, the nonlinear equation can be linearized. The linearized equations of motion can be written as a matrix–vector equation as follows:
where the superposed dot represents differentiation with respect to time,
is the displacement vector defined by
,
,
,
,
,
,
,
is the mass matrix,
is the damping matrix,
is the stiffness matrix, and
is the load vector defined by
.
3. Dynamics Model Verification
To verify the dynamic vehicle model proposed in this study, the vertical suspension deformations computed using the vehicle model were compared with the deformations measured through actual vehicle driving tests. The vehicle for the driving tests was a semi-midsize hatchback-type passenger car with the specifications mentioned above. This vehicle, with one driver on board, was driven at a constant speed of 100 km/h on an outdoor proving ground with a dry and flat road surface. Three types of driving tests were conducted according to ISO standards: the slalom test [
33], the double lane change test [
34], and the step steer test [
35]. These tests are performed for three steering wheel angle variations, the details of which will be discussed later.
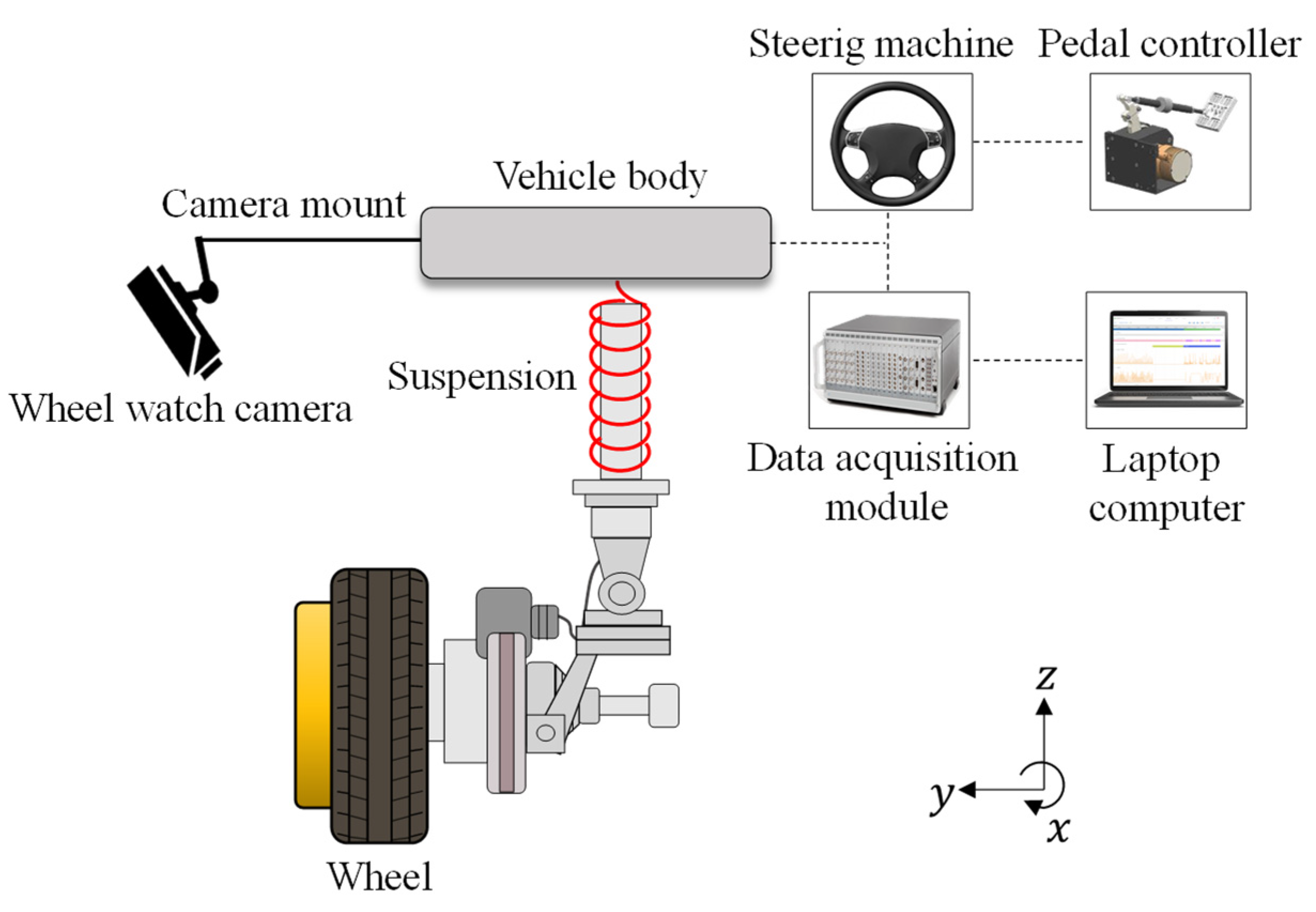
The experimental setup for measuring suspension deformations is shown in
Figure 4. The pedal controller was used to maintain the vehicle’s speed at 100 km/h. The steering machine provides steering wheel angle variations for driving tests according to the steering wheel angle pattern entered in advance. Four wheel-watch cameras were installed on the exterior of the vehicle to measure the suspension deformations under the dynamic condition of the vehicle. These cameras were mounted on camera mounts that extended approximately 300 mm outward and transversely from the vehicle body on the tops of the four wheels and measured the relative motions of the wheels in the longitudinal, lateral, and vertical directions with respect to the vehicle body. The data on suspension deformations measured by the cameras were stored in the data acquisition module, and a laptop computer was installed to monitor these data in real-time.
First, the suspension deformations were experimentally measured while performing the slalom test and compared with the deformations from the simulation using the dynamic model established in the previous section. For the slalom test, six cones were installed at equal intervals of 45 m on a flat road, and the test vehicle was driven zigzag between the cones at a constant speed of 100 km/h. The steering wheel angle variation for zigzag driving, as shown in
Figure 5, was imposed on the vehicle. Note that the positive direction of the steering wheel angle is clockwise.
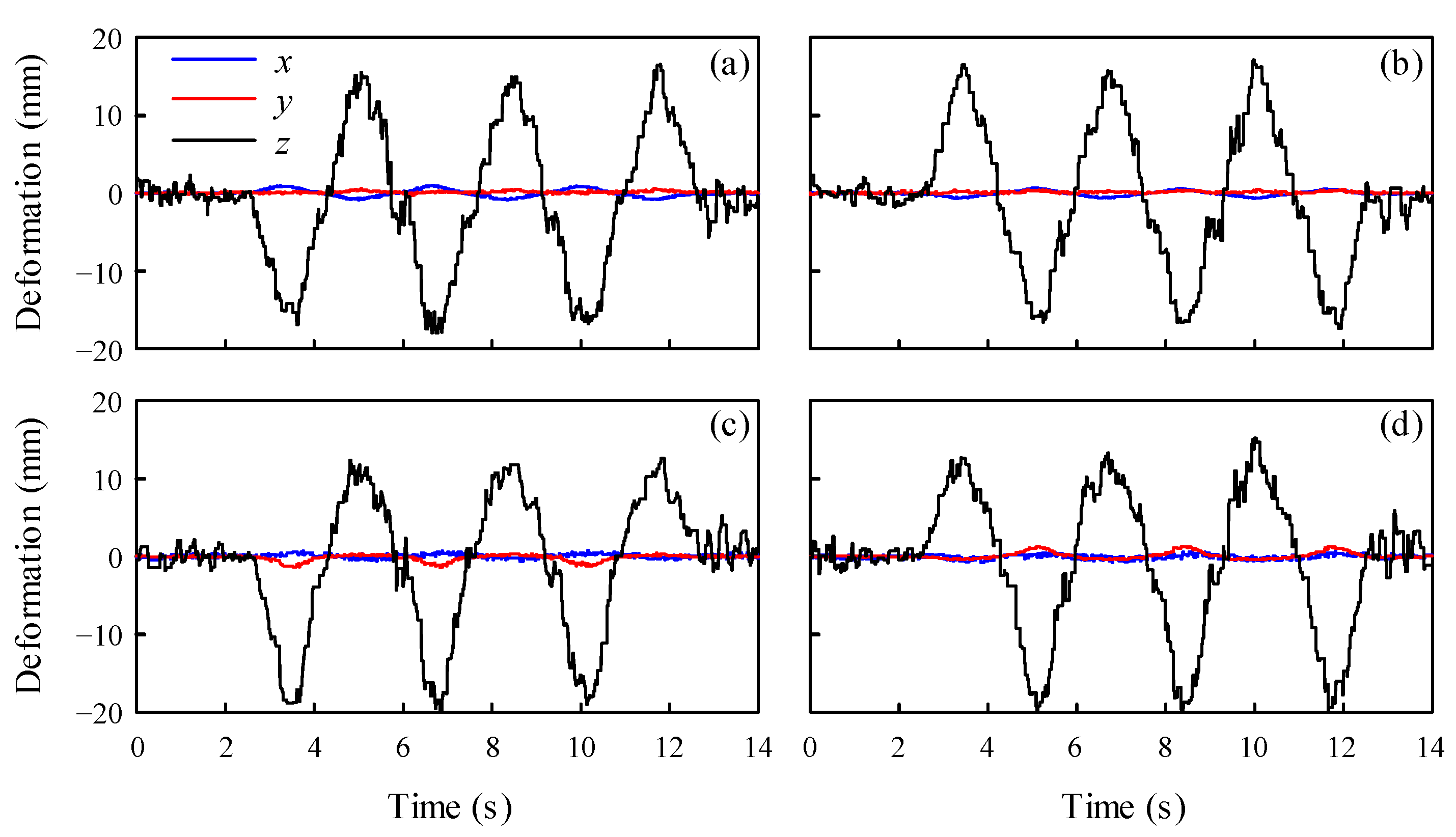
The suspension deformations measured during the slalom test are shown in
Figure 6.
Figure 6a shows the deformation at the left front wheel.
Figure 6b shows the deformation at the right front wheel.
Figure 6c shows the deformation at the left rear wheel.
Figure 6d shows the deformation at the right rear wheel. In
Figure 6, the blue, red, and black lines represent the deformations in the directions of the
x,
y, and
z axes, respectively, which are the forward-rearward, left–right, and down–up directions with respect to the vehicle. The vertical deformations of the left suspensions of the vehicle (
Figure 6a,c) have opposite phases to those of the right suspensions (
Figure 6b,d). This is because the vehicle body rolls about the
x-axis during turning, causing compressive deformation on the left side of the suspension and tensile deformation on the right side. The deformations in the
z-direction are much larger than those in the
x- and
y-directions. This implies that the suspensions, which are connected in a nearly vertical position between the wheels and body, are vertically tensioned or compressed. Therefore, only the
z-directional suspension deformations were considered in the comparison between the simulation and experimental results.
Simulations were performed with the dynamic vehicle model expressed as the equations of motion derived in the previous section. After obtaining the roll moment
using the centrifugal force computed with the steering wheel angle for the slalom test shown in
Figure 5, it was substituted into the equations of motion given by Equation (19). Applying the Newmark time integration method [
36] with a time step size of 0.005 s to the equations of motion, the time histories of the bounce displacement (
), pitch angle (
), roll angle (
), and vertical displacements of the unsprung masses (
,
,
,
) were computed. Using these time histories, the vertical suspension deformations at the four wheels were computed from the following linearized deformations:
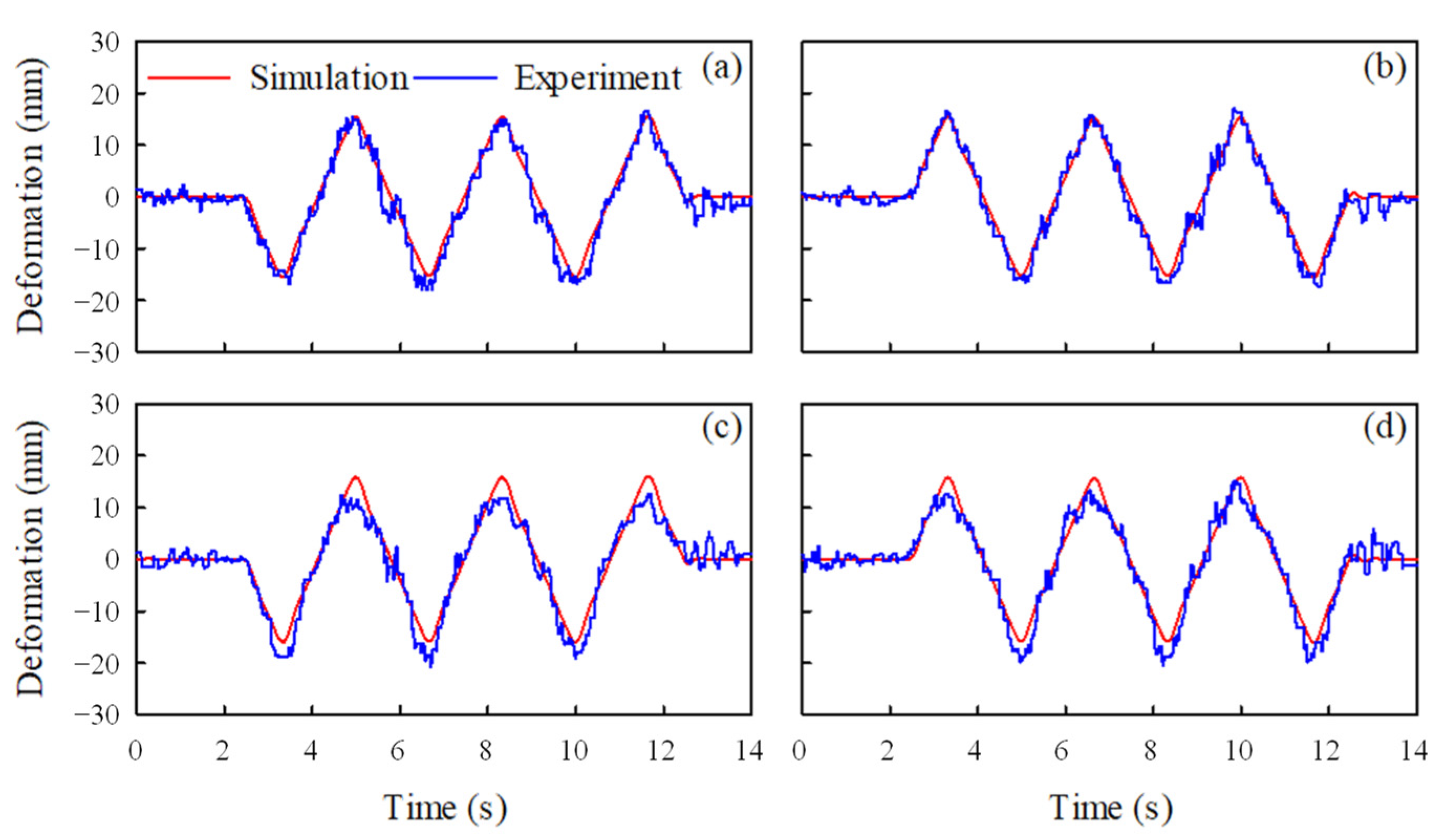
The dynamic responses of the suspension deformations by simulation and experiment during the slalom test for 14 s are shown in
Figure 7.
Figure 7a represents the left front wheel;
Figure 7b corresponds to the right front wheel;
Figure 7c illustrates the left rear wheel; and
Figure 7d depicts the right rear wheel. In
Figure 7, the red and blue solid lines represent the simulated and experimental results, respectively.
Figure 7 shows that the overall behaviors of the simulation are very similar to those of the experiment. This implies that the vehicle dynamics model presented in this study can be used to predict the behavior of a vehicle during a slalom test. However, the experimental results for the suspension deformations at all wheels had high-frequency vibrations compared with the simulation results. This is because, unlike the vehicle dynamic model, real vehicles have high-frequency components of vibration in suspension deformations. These high-frequency components are caused by wheel vibrations owing to the uneven road surface and the vibrations of various power transmission system components.
Next, while the steering wheel angle shown in
Figure 8 was imposed on the vehicle, the suspension deformations were measured during the double lane change test. These measured deformations were compared with the simulated deformations to validate the vehicle dynamic model. The double-lane change test was performed by maintaining the vehicle speed constant at 100 km/h. Similar to the slalom test, the suspension deformations in the horizontal directions of the vehicle (
x and
y directions) were very small compared to the deformations in the vertical direction (the
z direction). Therefore, the deformations in only the vertical direction were compared between the simulation and the experiment.
Figure 9 compares the results of the simulation and experiment for suspension deformations during the 7 s double lane change test. The suspension deformations at the four wheels are shown in
Figure 9a–d, where the red and blue lines represent the simulation and experiment results, respectively. For the double-lane change test, the suspension deformations obtained by simulation using the vehicle dynamic model presented in this study followed the deformations measured through the experiment. However, slightly larger overshoots are observed in the simulation results compared to the experimental results at approximately 4.09 s in
Figure 9a,c and 2.08 s in
Figure 9d. This implies that the simplified and linearized vehicle dynamic model proposed in this study does not sufficiently reflect the complex kinematic and nonlinear elements of an actual vehicle. The numerical calculation errors may be attributable to the modeling of the nonlinear suspension system with variable stiffness and damping as a linear system. Nevertheless, the suggested model simulates the overall vehicle behavior relatively well while performing the double-lane change test.
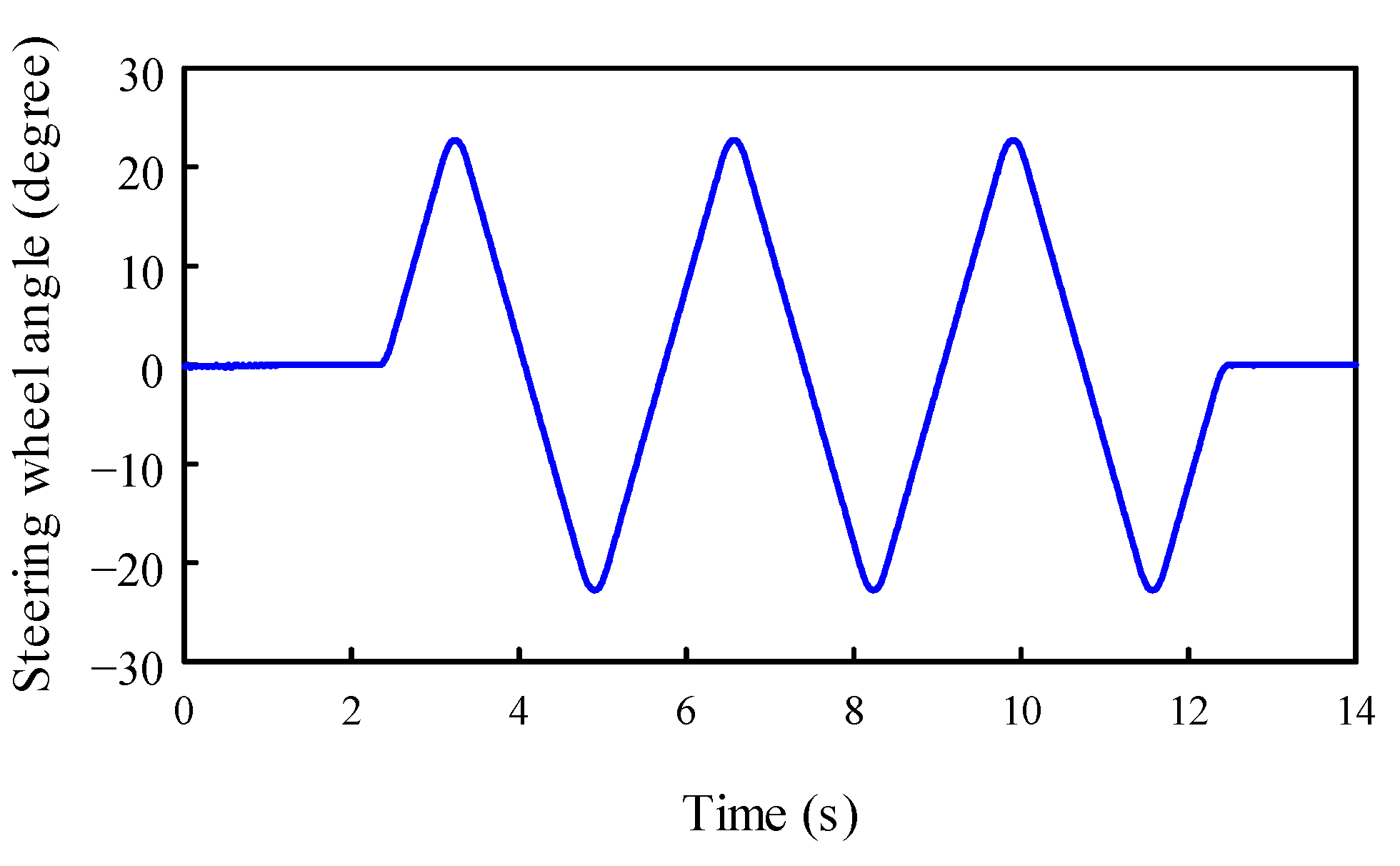
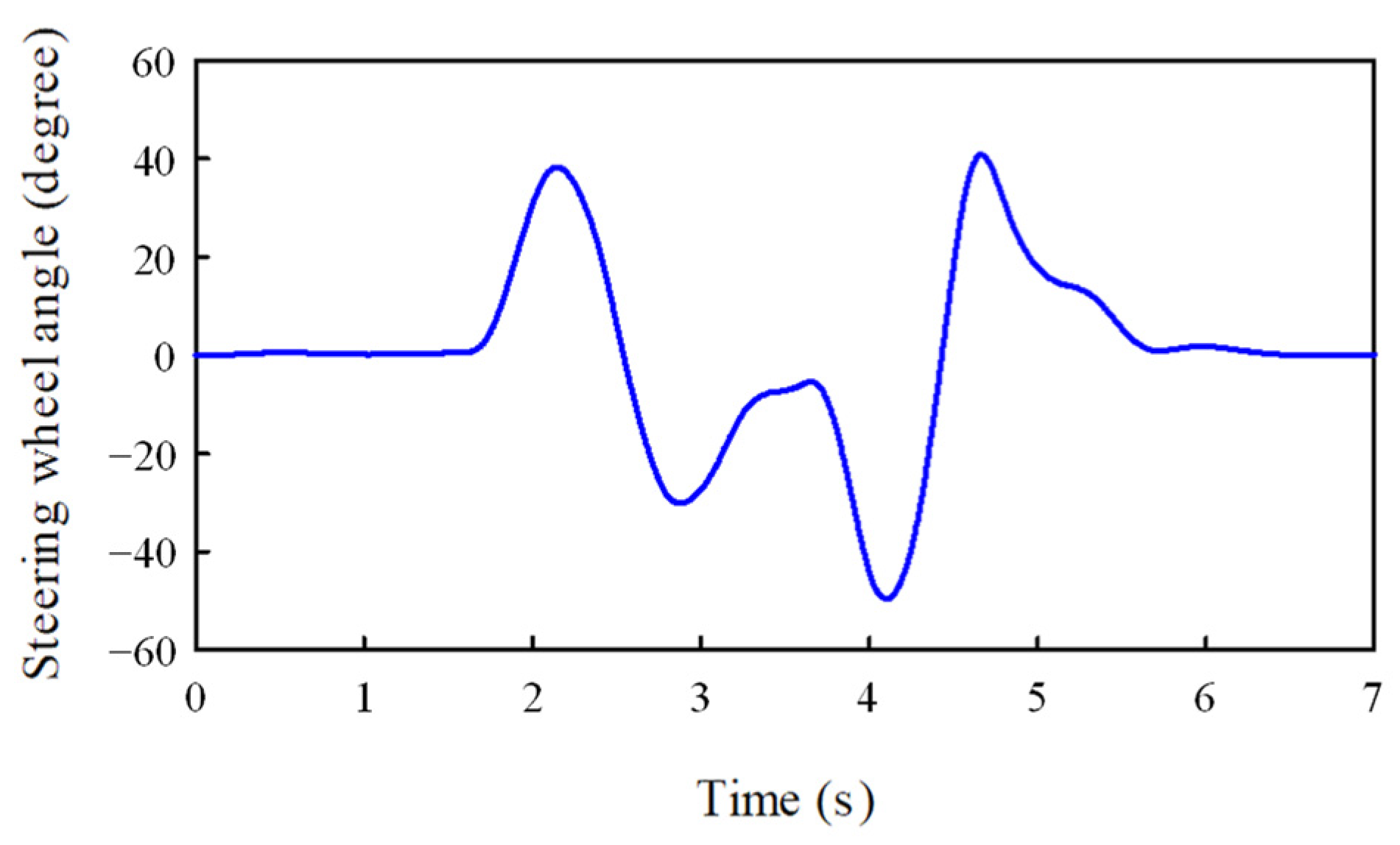
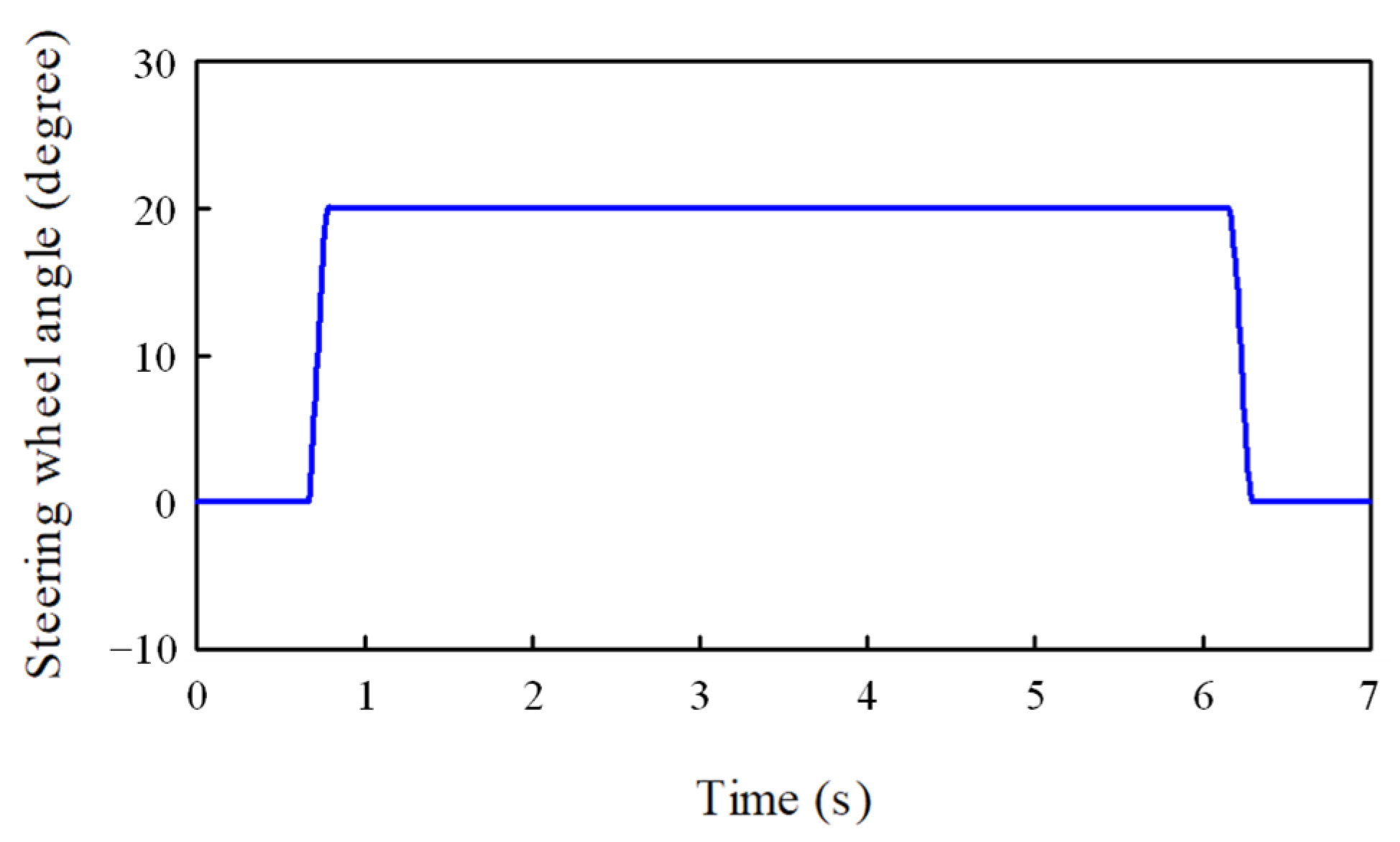
Finally, the validity of the vehicle model was further confirmed through a step steer test. This involved comparing the suspension deformations measured on the actual vehicle in motion with the deformations calculated in the simulation using the presented model. The step steer test, often referred to as the J-turn test, involves applying a fast steering-wheel input to a fixed magnitude of the steering wheel angle while the vehicle moves along a straight path at a constant speed. While maintaining the vehicle speed at 100 km/h, the steering wheel angle, shown in
Figure 10, was imposed on the vehicle.
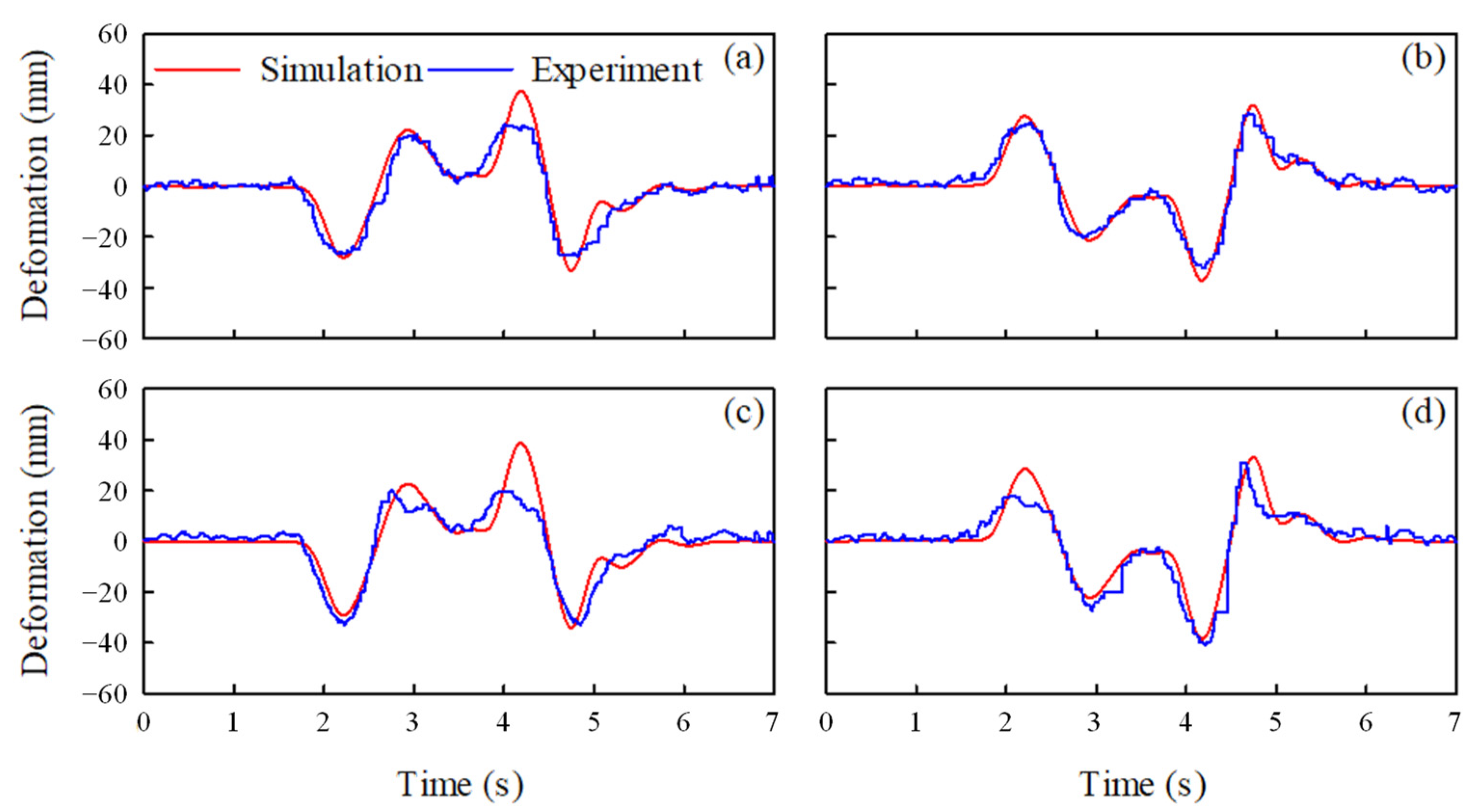
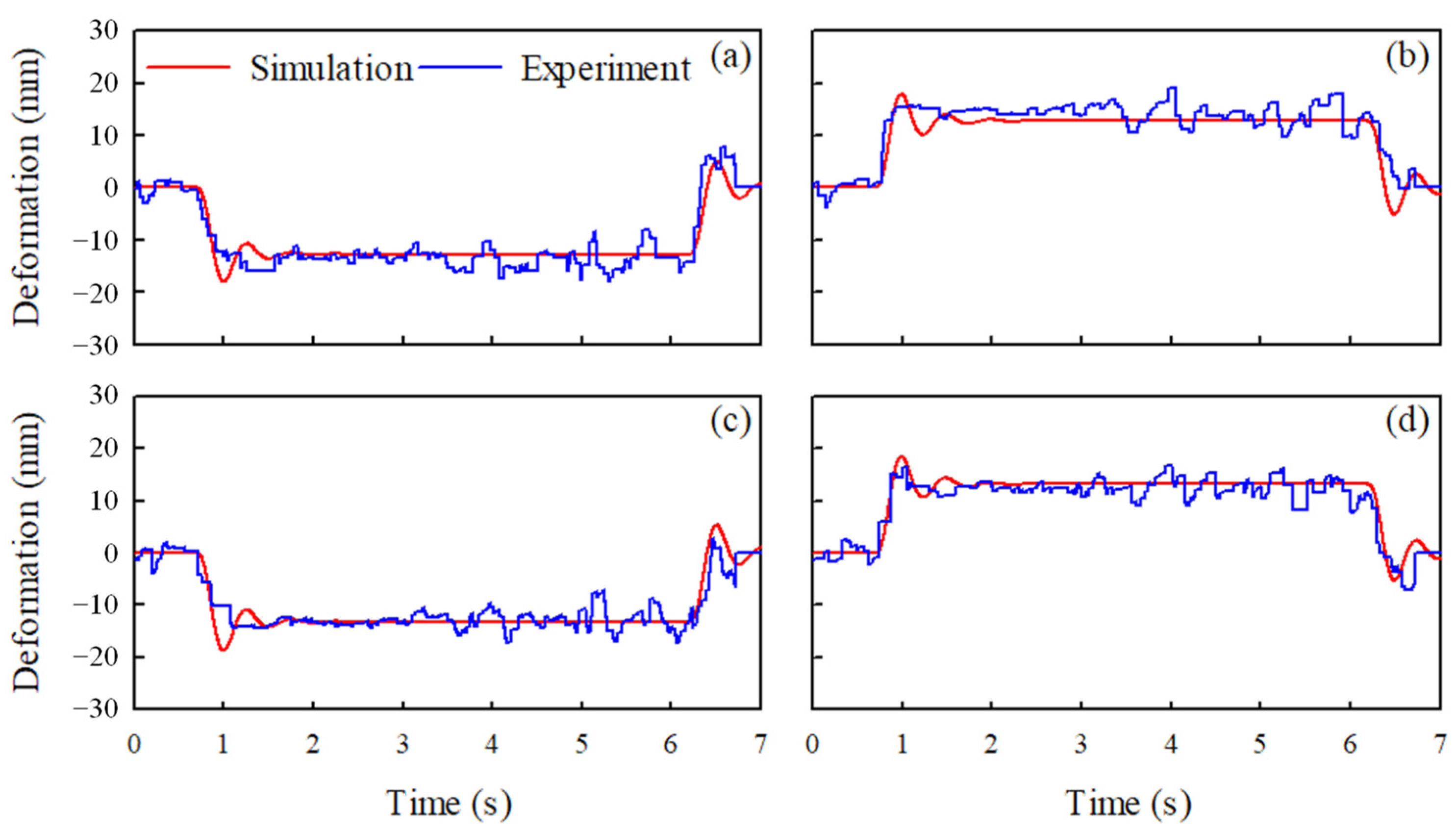
The suspension deformations for the step steer test by simulation and measurement are shown in
Figure 11. This figure shows that the suspension deformations obtained by the simulation, indicated by the red line, were in good overall agreement with the deformations measured by the experiment, indicated by the blue line. The high-frequency components in the time responses of suspension deformations, which were shown in the experimental results of the slalom test above, were also observed in the experimental results of the step steer test. Consequently, the simulations using the vehicle dynamic model proposed in this study provide reasonable computations of the suspension deformations for the three tests: the slalom, double lane change, and step steer.