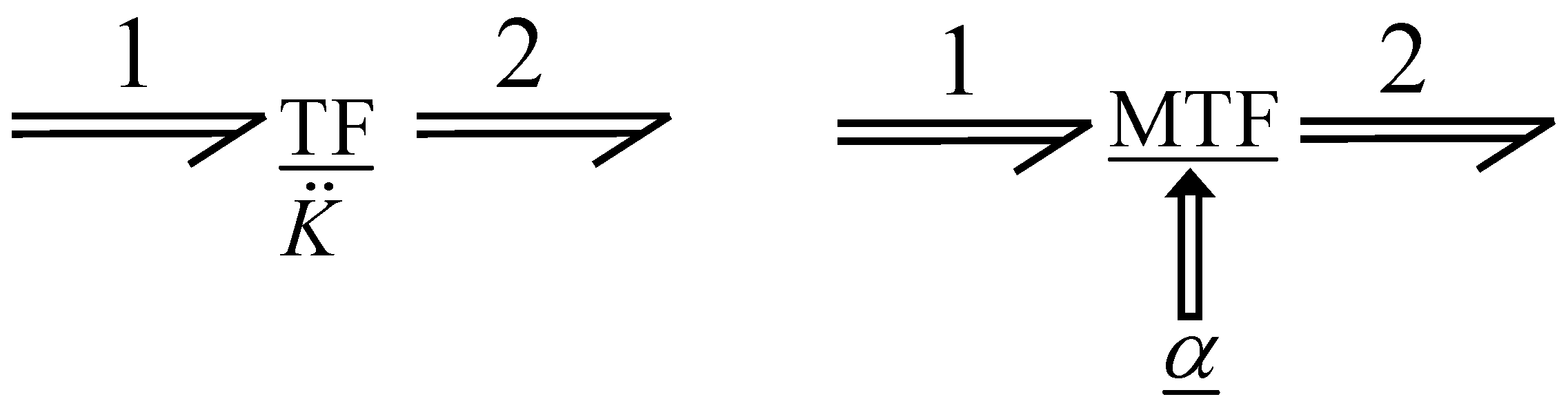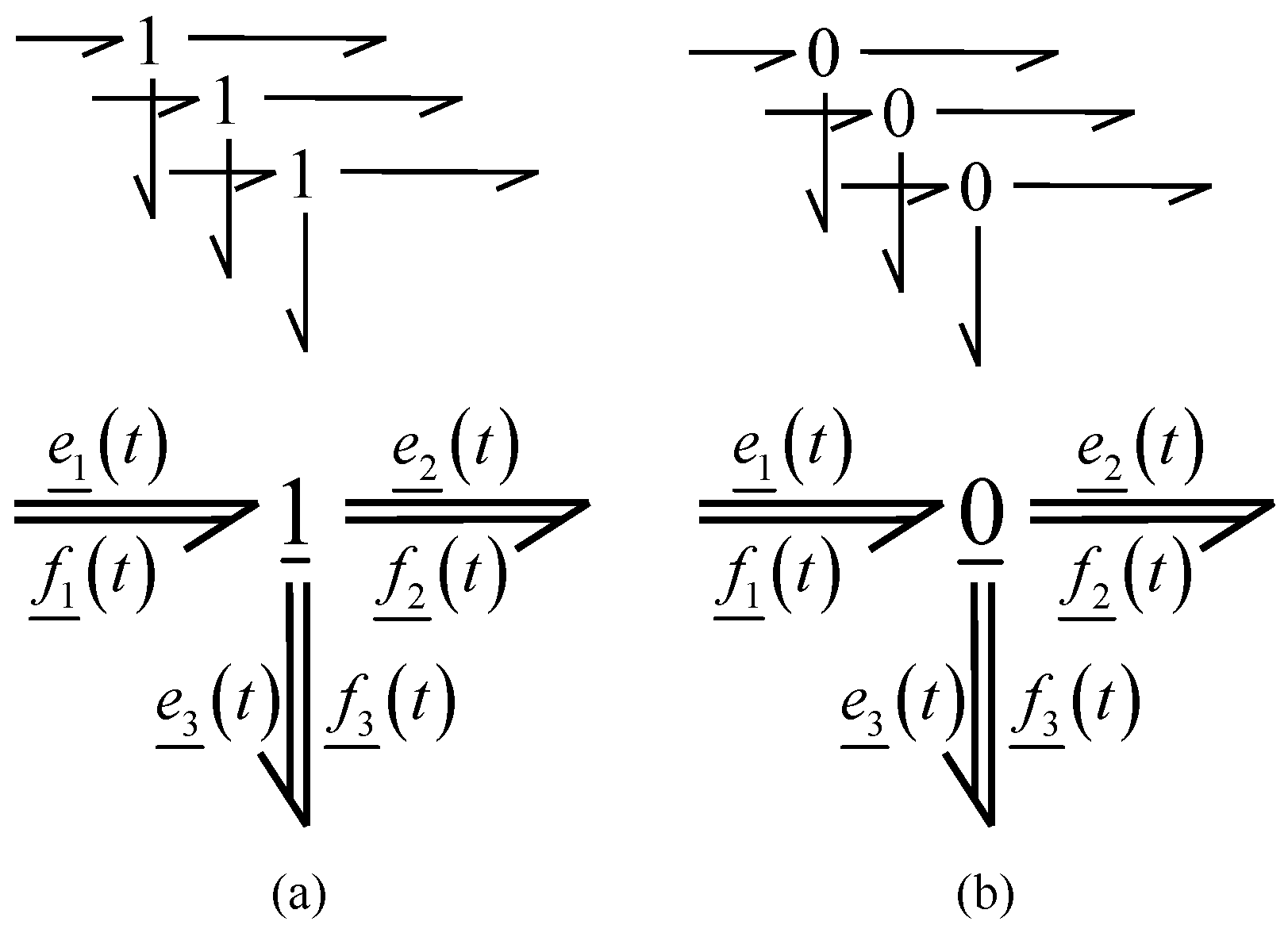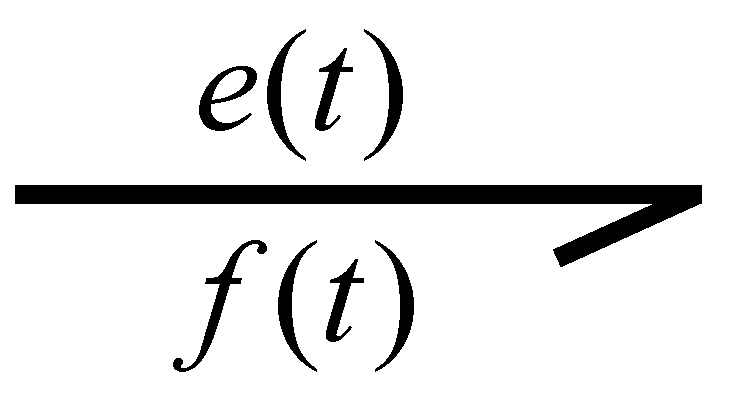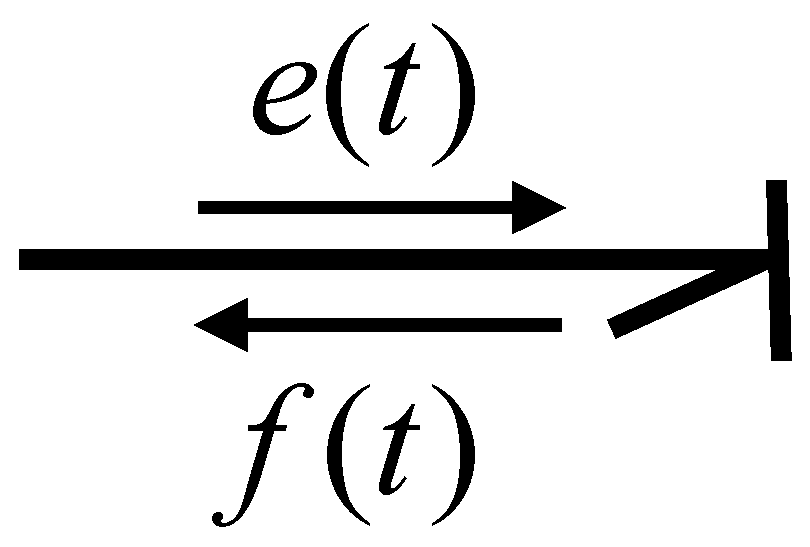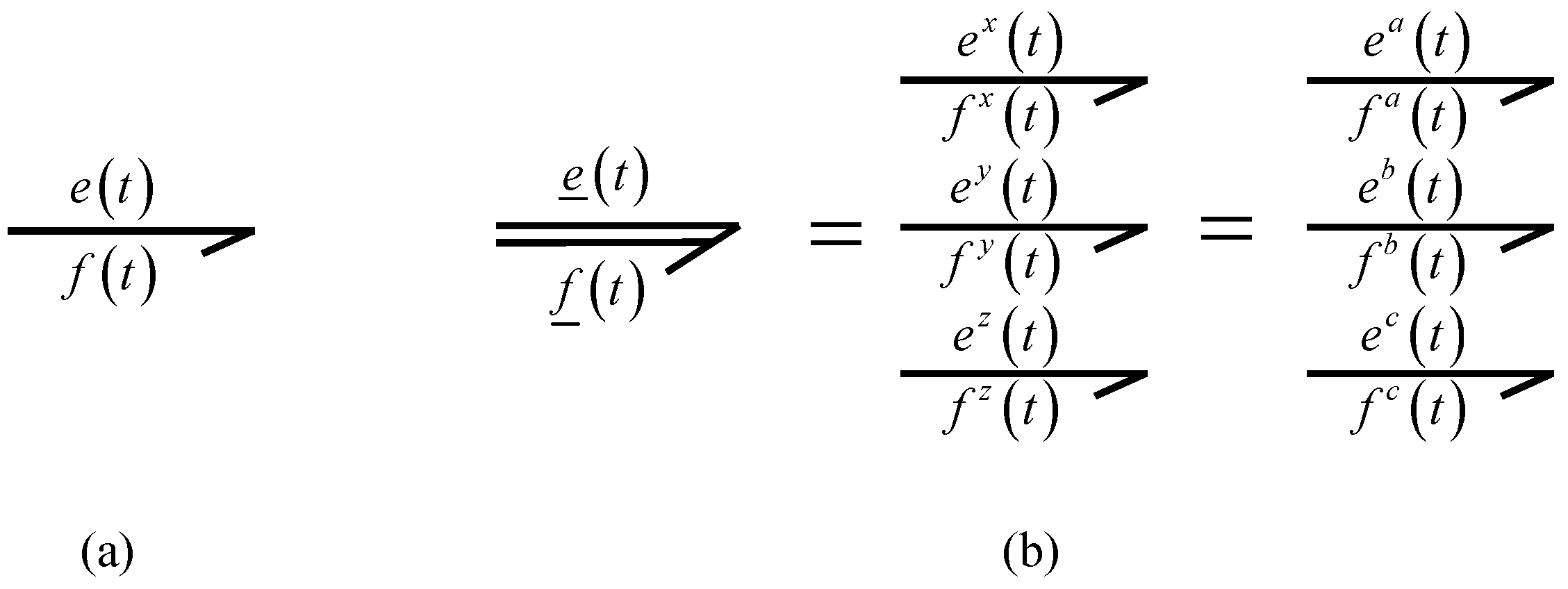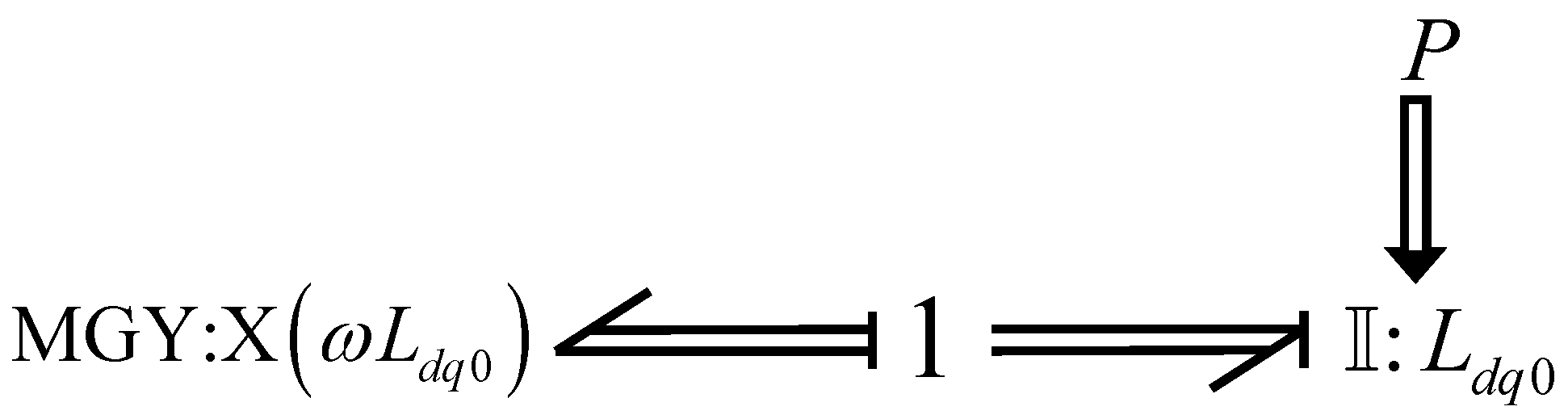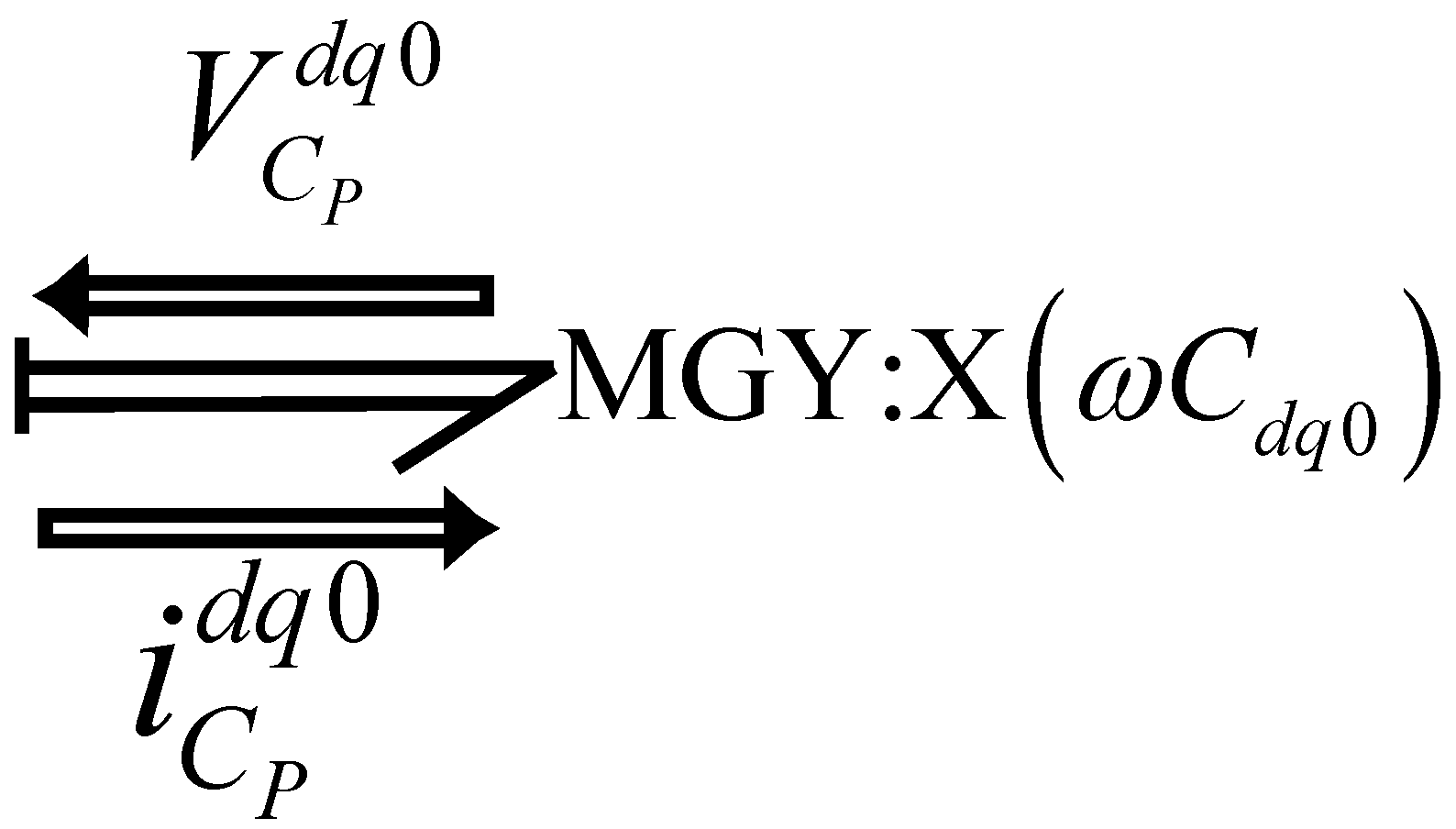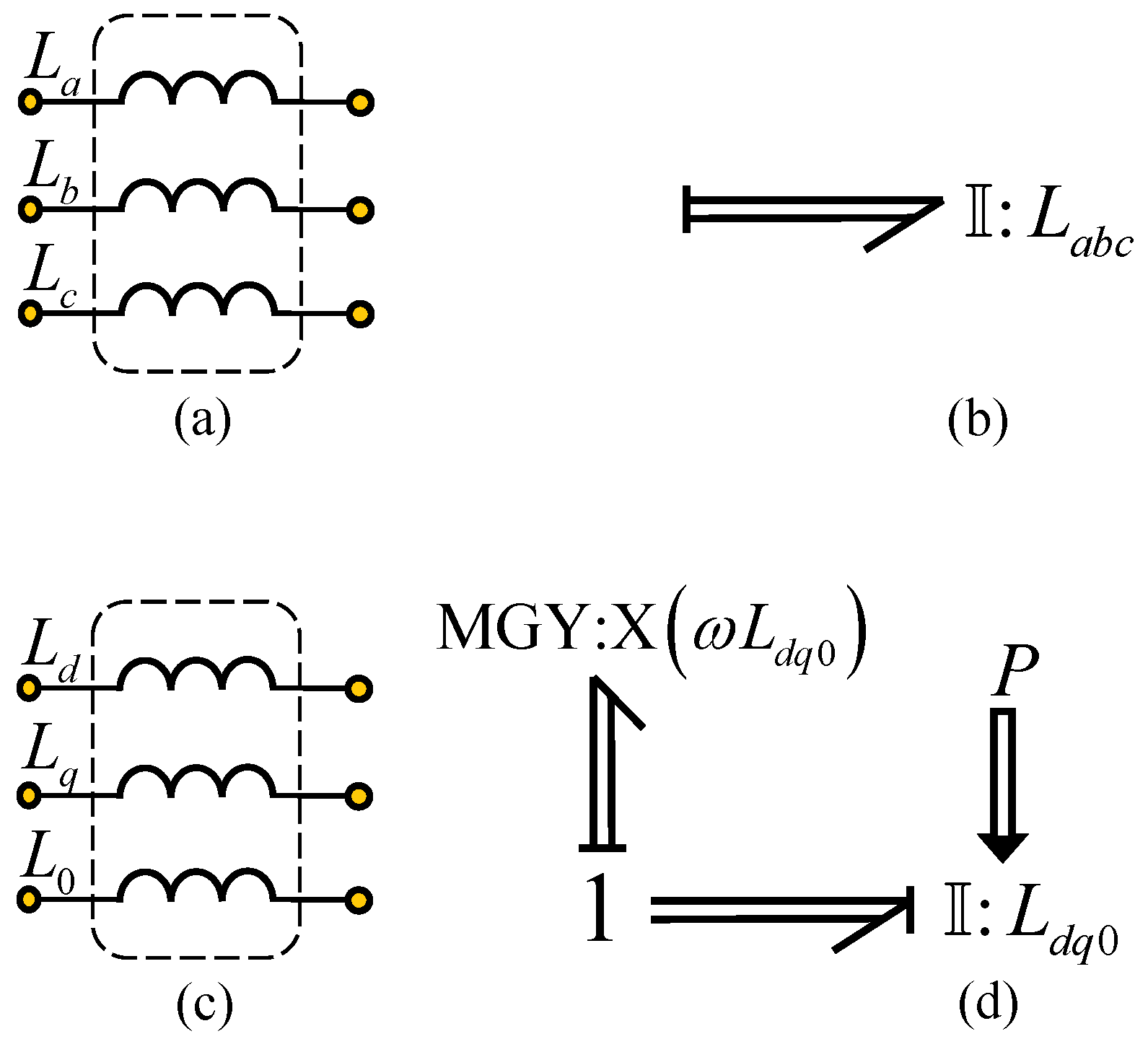Modeling and Simulation in Multibond Graphs Applied to Three-Phase Electrical Systems

Abstract

The modeling of three-phase electrical systems in the coordinates $\left(d,q,0\right)$ in a simple and direct way in a multibond graph approach is presented. From the graphical model obtained, a mathematical model in state space can be determined. Thus, studies of the electromagnetic transients of electrical systems can be analyzed. Likewise, this modeling in the physical domain can be applied to balanced or unbalanced systems and the storage elements (inductances and capacitances) can be connected to be linearly independent or dependent. Structural properties such as stability, controllability, observability or controller design can be analyzed in multibond graphs. The proposed methodology is applied to two examples and the simulation results are shown using 20-Sim software.

1. Introduction

The mathematical modeling of three-phase electrical systems to evaluate electromagnetic transients in the different equipment and devices that are part of these systems is determined by high-order, nonlinear and time-varying models and generally complicated systems.

The mathematical model for an electrical power system using field approaches was developed in [1]; here, the model of the transmission lines are obtained by partial differential equations and the equation of the supply to the transmission line uses two first-order differential equations. The real-time simulation of a transmission line with the objective of knowing the behavior of harmonic signals in line transients is presented in [2], and the dynamic domain is also applied to the transmission line, which allows the visualization of the steady state and the transient condition. Different configurations of power transmission lines are simulated in [3], however, here, a negative capacitance is added in parallel with the inductance in the $\pi$ equivalent circuit that allows one to improve the simulation of transmission lines. The study of the available transfer capability in a transmission system to know the transient stability is proposed in [4], performing network analysis with ultra-high-voltage lines. The stability control in long transmission lines can incorrectly operate the equipment, which is simulated and analyzed in [5]. A three-phase power transformer is modeled and simulated with a digital implementation in [6], and the transformer model is verified with experiments carried out on a 6 kVA transformer.

Recently, with the supply of electrical energy from renewable energy sources such as wind turbines and photovoltaic panels, electrical system modeling includes elements and equipment that these new electrical power generation systems require. In [7], the modeling and simulation of a photovoltaic power system is proposed that is connected to the network with a three-phase power of 8kW for at home purposes with a PQ controller. The modeling of a wind turbine for harmonic analysis with different switching techniques is proposed in [8] where doubly-fed induction generators are connected to the back-to-back power converter. The modeling and simulation of a photovoltaic system using Matlab with the aim of considering the irradiance and analyzing the power quality was found in [9]; in addition, the behavior of a three-phase system with different inverter control techniques is described when the PV system is generating energy. Likewise, the simulation of a distributed generation model with the use of multi-energy sources for three-phase stability studies was developed in [10], wherein a unified interface model for a synchronous generator and inverter that applies to different types of energy—electric, heat and hydrogen—was proposed.

The difficulty in the modeling, analysis and control of three-phase electrical systems has become one of the reasons for the use of various software such as in [9], wherein Matlab software is used. The application of the Multisim software in the simulation of three-phase electrical circuits was found in [11]. Furthermore, the study of electromagnetic transients in three-phase electrical systems for transmission and distribution models using the EMTP software was proposed in [12].

Other interesting references with the application of coordinate transformations applied to electrical systems are the following: the comparison of current regulators in three-phase electrical systems in the reference frames: (1) natural $\left(a,b,c\right)$, (2) orthogonal stationary $\left(\alpha ,\beta \right)$ and (3) orthogonal stationary $\left(d,q\right)$ were presented in [13]. A new reference frame, called a reduced reference frame, which can be used for unbalanced three-phase systems, was proposed in [14]. The properties of three transients with unbalanced sources were investigated in [15], where the Clarke and Park transformations are used. The energy management architecture model using a complete supervisory control and data acquisition system in a educational building was presented in [16]. An energy management system applied to isolated micro grids was proposed in [17], wherein they apply a PID controller which contains coordinate transformations from $\left(a,b,c\right)$ to $\left(d,q\right)$.

When considering a renewable power system and its control, full modeling can be challenging because the system will have different energy domains. For example, if the system is the interconnection of thermoelectric, hydroelectric, wind turbines and photovoltaic panels as sources of generation, their transmission and distribution to electrical loads, then there are electrical, mechanical, thermal and hydraulic subsystems, subsystems for control as well as three-phase systems, due to which factors the bond graph is a system modeling methodology that can be applied to the systems formed by different energy domains. Likewise, the analysis and control of systems in the bond graph are direct and physically achievable. In addition, the modeling of systems with multiple phases or axes has been solved with multibond graphs which are vector bond graphs.

The bond graph theory is based on an approach to modeling power transfer through ports called bonds. In this way, a structured approach to modeling dynamic systems is presented in the bond graph.

The main characteristics of the bond graph can be stated below: (1) The bond graph allows the modeling of systems formed by different energy domains (electrical, mechanical, hydraulic, thermal, magnetic); (2) Through the causal information, the relationship between the elements of a system is known, determining mathematical models in transfer function or in state space, likewise, structural properties such as stability, controllability and observability can be directly obtained in the bond graph model without requiring its mathematical model; (3) Linear and nonlinear, invariant and time-varying systems with lumped distributed parameters can be modeled in a bond graph; and (4) Controllers can be designed in a bond graph environment.

The modeling of robots, cars, projectiles or multi-axis systems often leads to complicated mathematical models. Even in bond graphs, these systems can result in models that cannot easily apply the methodology and its applications in the physical domain. Thus, the introduction of multibond graphs as an extension of bond graphs turns out to be a natural way to model multibody systems.

In modeling with multibond graphs, single bonds are grouped into multibonds. Likewise, the generalized power variables of effort and flow in bond graphs are now vectors of effort and flow in multibond graphs whose matrix product determines power.

Some papers on fundamentals and application with multibond graphs have been published, some of which are cited below: the basic concepts in the modeling with multibond graphs of physical systems are proposed in [18]. The causality assignment in vector bond graphs is introduced in [19]. The modeling of mechanical systems with multibond graphs was developed in [20]. The decomposition of multibody elements such as resistors, inertias, capacitors, transformers and gyrators into their equivalent in junctions, bonds and 1-port and 2-port elements was presented in [21].

Recently, some developments with multibond graphs have been published, and the representation of electrical circuits of phasors containing real and imaginary parts with two-dimensional multibond and steady state was proposed in [22]. The linearization of a class of nonlinear systems that can be modeled with multibond graphs was presented in [23]. The direct determination of the steady-state response for LTI systems modeled with multibond graphs with a derivative causality assignment to the storage elements was proposed in [24].

In this paper, the modeling of three-phase electrical systems in coordinates $\left(d,q,0\right)$ is presented. The modeling of an electrical system in coordinates $\left(a,b,c\right)$ determines the systems of time-varying differential equations, and by applying Park’s transformation, an equivalent time-invariant system is obtained. In the analysis of electromagnetic transients to electrical systems in the coordinates $\left(d,q,0\right)$, the differential equations are determined with inductive and capacitive elements as well as the connectivity with the different elements, whilst ascertaining whether the three phases are balanced is difficult and complicated.

Electrical system simulation software allows graphic results to be obtained, but the structural mathematical analysis of the system is generally not its objective. Thus, this paper enables the modeling of model-balanced or -unbalanced three-phase electrical systems in the multibond graphs environment.

Bond graph tools can be applied in multibond graphs. In particular, a lemma to directly obtain the multibond graph in the coordinates $\left(d,q,0\right)$ is proposed and from this, other lemma to determine the mathematical model in state space is presented. Therefore, the advantages of this paper with respect to traditional developments were exposed.

The works developed in bond graphs [25,26,27] that mainly use the Park transformation for the modeling of electrical machines are bond graphs built from the mathematical model in the state space of the system and it is effectively verified that the bond graph is correct. However, general methodologies similar to this proposed paper are not reported. In multibond graphs, practically no papers have been published on the modeling of three-phase electrical systems, and as such, this paper is an interesting proposal on the modeling of three-phase electrical systems in coordinates $\left(a,b,c\right)$ and its transformation in coordinates $\left(d,q,0\right)$.

Therefore, the primary advantages of this paper are the modeling of three-phase electrical systems in coordinates $\left(a,,b,c\right)$ in a direct way, directly obtaining its symbolic representation in state space and its derivation of the model in coordinates $\left(d,q,0\right)$.

Section 2 describes the traditional modeling of a power system from coordinates $\left(a,,b,c\right)$ to coordinates $\left(d,q,0\right)$. The essential elements in modeling systems with multibond graphs are developed in Section 3. In this section, the junction structure and state space of a system modeled in multibond graphs are presented. In Section 4, a lemma and procedure for directly obtaining the multibond graph of an electrical system are proposed. Two examples applying the described methodology are solved, including the simulation results. In Section 6, describes the aplication of the metodology. Finally, Section 7 gives the conclusions.

2. Problem Statement

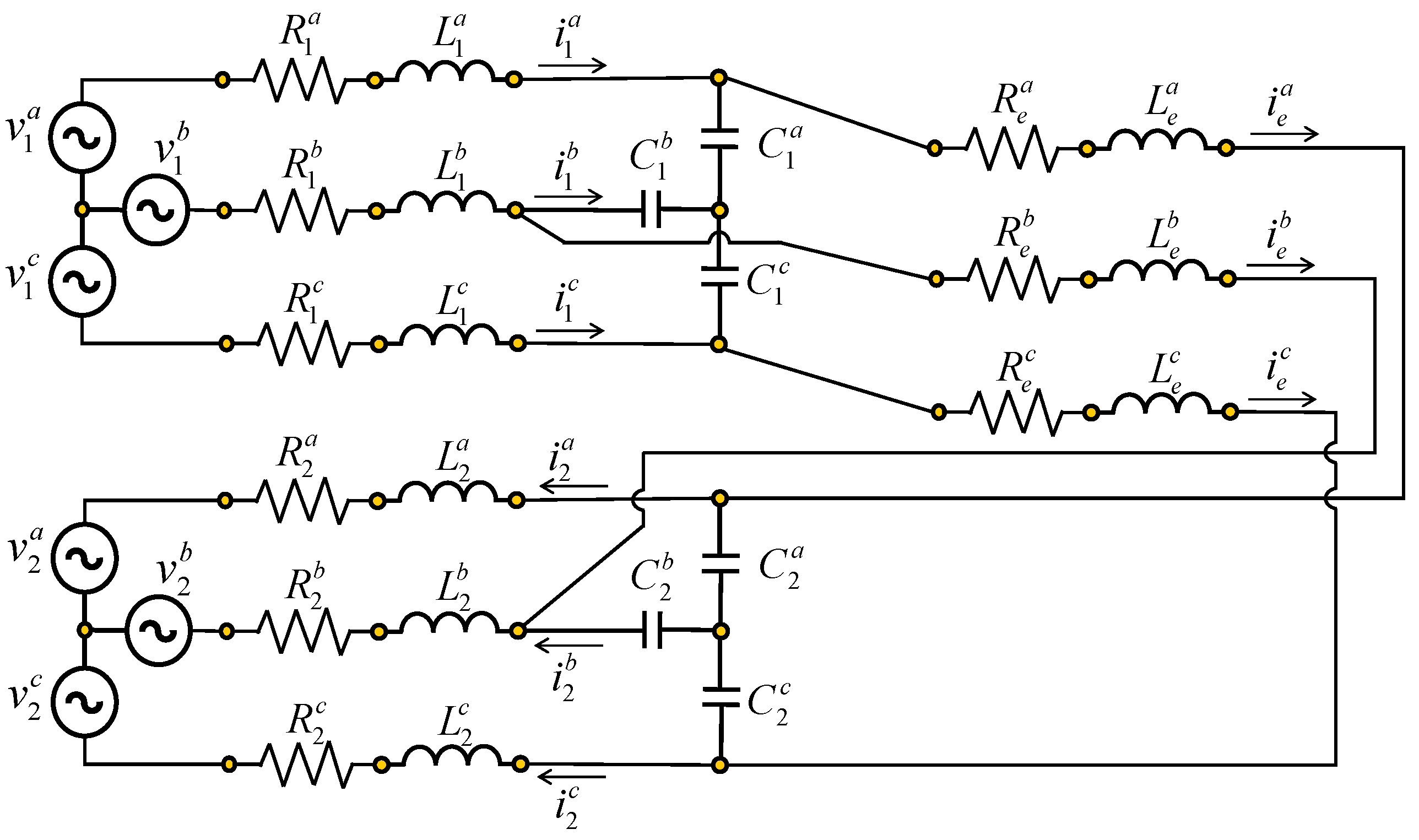
Most commercial electrical power is generated in three-phase systems [28,29]. Consider a simple three-phase circuit formed by two generators and a line transmission which is shown in Figure 1 [30].

With the objective of obtaining the dynamic equations of the system for the analysis of electromagnetic transients, then applying the voltages law to the circuit of Figure 1 gives

$$\begin{array}{ccc}\hfill v_1^{abc}& =& v_{R_1}^{abc}+v_{L_1}^{abc}+v_{C_1}^{abc}\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill v_{C_1}^{abc}& =& v_{R_e}^{abc}+v_{L_e}^{abc}+v_{C_2}^{abc}\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill v_{C_2}^{abc}& =& v_{R_2}^{abc}+v_{L_2}^{abc}+v_2^{abc}\hfill \end{array}$$

(3)

where $v_1^{abc}$ and $v_2^{abc}$ denote the three-phase voltages of supply sources 1 and 2, respectively; $v_{R_1}^{abc},$$v_{R_2}^{abc}$ and $v_{R_e}^{abc}$ denote the three-phase voltages across the resistors $R_1$, $R_2$ and $R_e,$ respectively; $v_{L_1}^{abc},$$v_{L_2}^{abc}$ and $v_{L_e}^{abc}$ denote the three-phase voltages across the inductances $L_1$, $L_2$ and $L_e,$ respectively;$v_{C_1}^{abc}$ and $v_{C_2}^{abc}$ denotes the three-phase voltages across the capacitances $C_1$ and $C_2$, respectively.

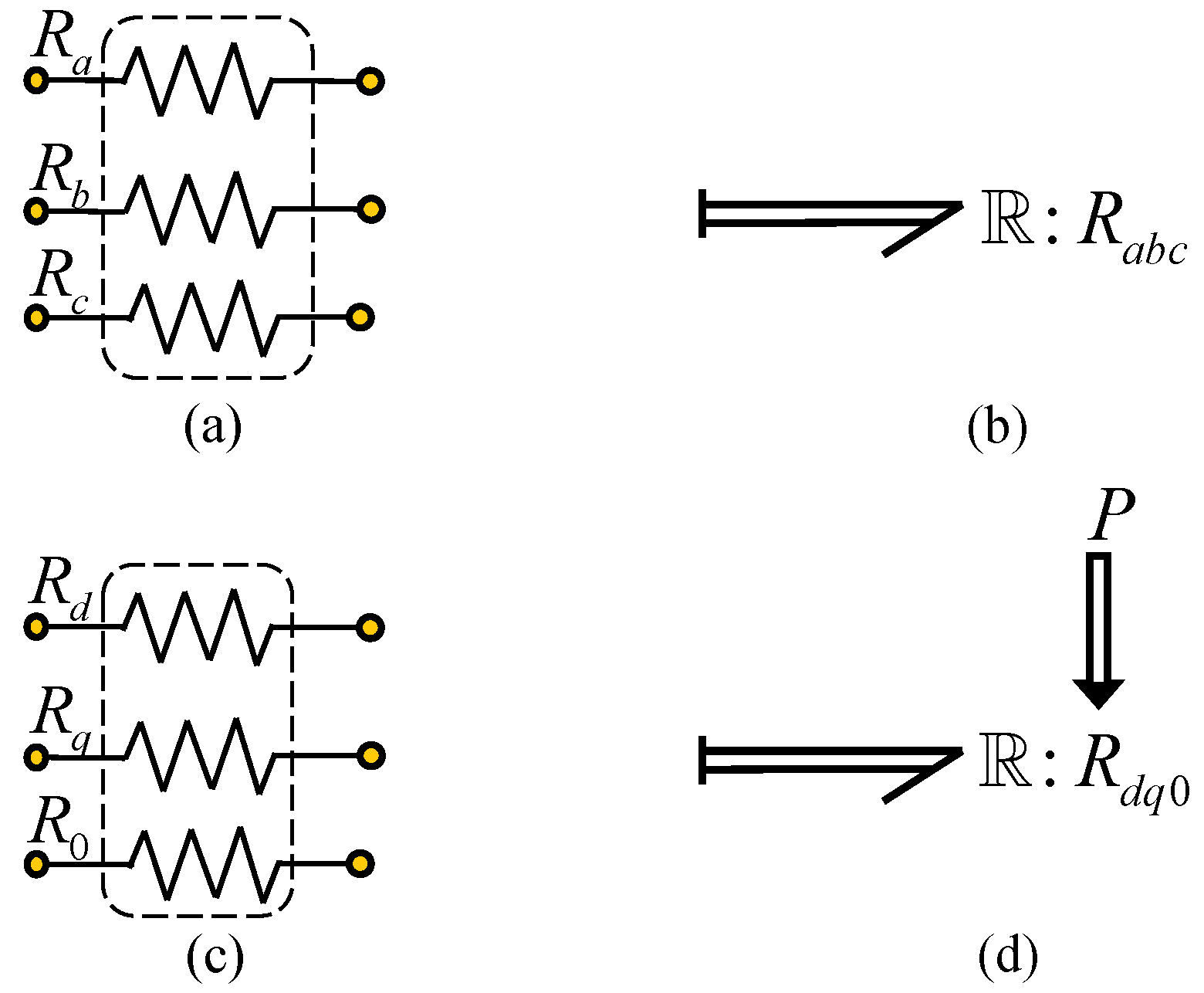
The relationships between the resistors and inductors are

$$v_1^{abc}=\left[\begin{array}{c}{v}_1^a\\ v_1^b\\ v_1^c\end{array}\right];v_2^{abc}=\left[\begin{array}{c}{v}_2^a\\ v_2^b\\ v_2^c\end{array}\right];v_{C_1}^{abc}=\left[\begin{array}{c}{v}_{C_1}^a\\ v_{C_1}^b\\ v_{C_1}^c\end{array}\right];v_{C_2}^{abc}=\left[\begin{array}{c}{v}_{C_2}^a\\ v_{C_2}^b\\ v_{C_2}^c\end{array}\right]$$

where $\left(v_1^a,v_1^b,v_1^c\right)$ and $\left(v_2^a,v_2^b,v_2^c\right)$ are the voltages in each phase $\left(a,b,c\right)$ of supply sources 1 and 2, respectively; $\left(v_{C_1}^a,v_{C_1}^b,v_{C_1}^c\right)$ and $\left(v_{C_2}^a,v_{C_2}^b,v_{C_2}^c\right)$ are the voltages in each phase $\left(a,b,c\right)$ of capacitors 1 and 2, respectively.

$$\begin{array}{ccc}\hfill v_{R_1}^{abc}& =& \left[\begin{array}{c}{v}_{R_1}^a\\ v_{R_1}^b\\ v_{R_1}^c\end{array}\right]=\left[\begin{array}{ccc}{r}_1^a& 0& 0\\ 0& r_1^b& 0\\ 0& 0& r_1^c\end{array}\right]\left[\begin{array}{c}{i}_1^a\\ i_1^b\\ i_1^c\end{array}\right]=R_1^{abc}·i_1^{abc}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill v_{L_1}^{abc}& =& \left[\begin{array}{c}{v}_{L_1}^a\\ v_{L_1}^b\\ v_{L_1}^c\end{array}\right]=\left[\begin{array}{ccc}{l}_1^a& 0& 0\\ 0& l_1^b& 0\\ 0& 0& l_1^c\end{array}\right]\frac{d}{dt}\left[\begin{array}{c}{i}_{L_1}^a\\ i_{L_1}^b\\ i_{L_1}^c\end{array}\right]=L_1^{abc}·\frac{d{i}_1^{abc}}{dt}\hfill \end{array}$$

(5)

where $\left(v_{R_1}^a,v_{R_1}^b,v_{R_1}^c\right)$ and $\left(i_1^a,i_1^b,i_1^c\right)$ are the voltages and currents in each phase $\left(a,b,c\right)$ of resistor 1, respectively; $\left(v_{L_1}^a,v_{L_1}^b,v_{L_1}^c\right)$ and $\left(i_{L_1}^a,i_{L_1}^b,i_{L_1}^c\right)$ are the voltages and currents in each phase $\left(a,b,c\right)$ of inductance 1, respectively; $R_1^{abc}$ is the resistance matrix 1 of the three phases $\left(a,b,c\right);$$r_1^a$, $r_1^b$ and $r_1^c$ are the resistors 1 in each phase $\left(a,b,c\right)$, respectively, and $L_1^{abc}$ is the inductance matrix 1 of the three phases $\left(a,b,c\right);$$l_1^a$, $l_1^b$ and $l_1^c$ denote the inductance 1 in each phase $\left(a,b,c\right)$, respectively.

In the same form, it is established that

$$\begin{array}{ccc}\hfill v_{R_e}^{abc}& =& R_e^{abc}{i}_e^{abc}\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill v_{L_e}^{abc}& =& L_e^{abc}\frac{d{i}_e^{abc}}{dt}\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill v_{R_2}^{abc}& =& R_2^{abc}{i}_2^{abc}\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill v_{L_2}^{abc}& =& L_2^{abc}\frac{d{i}_2^{abc}}{dt}\hfill \end{array}$$

(9)

where $v_{R_e}^{abc}$ and $i_e^{abc}$ denote the three-phase voltages and currents in $R_e^{abc}$, respectively; $v_{R_2}^{abc}$ and $i_2^{abc}$ denote the three-phase voltages and currents in $R_2^{abc}$, respectively; and $v_{L_e}^{abc}$ and $v_{L_2}^{abc}$ denote the three-phase voltages in $L_e^{abc}$ and $L_2^{abc}$, respectively. $R_e^{abc}$ and $R_2^{abc}$ are the resistance matrices of e and 2 of the three phases $\left(a,b,c\right)$, respectively, and $L_e^{abc}$ and $L_2^{abc}$ are the inductance matrices of e and 2 of the three phases $\left(a,b,c\right)$, respectively.

The relationships for the capacitors are

$$\begin{array}{ccc}\hfill i_{C_1}^{abc}& =& \left[\begin{array}{ccc}{c}_1^a& 0& 0\\ 0& c_1^b& 0\\ 0& 0& c_1^c\end{array}\right]\frac{d}{dt}\left[\begin{array}{c}{v}_{C_1}^a\\ v_{C_1}^b\\ v_{C_1}^c\end{array}\right]=C_1^{abc}\frac{d{v}_{C_1}^{abc}}{dt}\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill i_{C_2}^{abc}& =& C_2^{abc}\frac{d{v}_{C_2}^{abc}}{dt}\hfill \end{array}$$

(11)

where $i_{C_1}^{abc}$ and $v_{C_1}^{abc}$ are the three-phase currents and voltages in $C_1^{abc}$, respectively; $i_{C_2}^{abc}$ and $v_{C_2}^{abc}$ are the three-phase currents and voltages in $C_2^{abc}$, respectively, $C_1^{abc}$ and $C_2^{abc}$ are the capacitance matrices 1 and 2 of the three phases $\left(a,b,c\right),$ respectively, and $c_1^a$, $c_1^b$ and $c_1^c$ are the capacitors 1 in each phase $\left(a,b,c\right).$

By substituting from (4) and (9) into (1), (2) and (3)

$$\begin{array}{ccc}\hfill v_1^{abc}& =& R_1^{abc}{i}_1^{abc}+L_1^{abc}\frac{d{i}_1^{abc}}{dt}+v_{C_1}^{abc}\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill v_{C_1}^{abc}& =& R_e^{abc}{i}_e^{abc}+L_e^{abc}\frac{d{i}_e^{abc}}{dt}+v_{C_2}^{abc}\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill v_2^{abc}& =& R_2^{abc}{i}_2^{abc}+L_2^{abc}\frac{d{i}_2^{abc}}{dt}+v_{C_2}^{abc}\hfill \end{array}$$

(14)

in addition, $i_{C_1}^{abc}=i_1^{abc}-i_e^{abc}$ and $i_{C_2}^{abc}=i_e^{abc}-i_2^{abc}$, and the equations for the capacitors are

$$\begin{array}{ccc}\hfill C_1^{abc}\frac{d{v}_{C_1}^{abc}}{dt}& =& i_1^{abc}-i_e^{abc}\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill C_2^{abc}\frac{d{v}_{C_2}^{abc}}{dt}& =& i_e^{abc}-i_2^{abc}\hfill \end{array}$$

(16)

From (12) to (16) represent a fifteenth-order dynamic system for a simple three-phase circuit. However, $v_1^{abc}$ and $v_2^{abc}$ are three-phase voltage sources, these sources are typically balanced and given by

$$\left[\begin{array}{c}{v}^a\\ v^b\\ v^c\end{array}\right]=\left[\begin{array}{c}{V}_{m}sin\left(wt\right)\\ V_{m}sin\left(wt-2\pi /3\right)\\ V_{m}sin\left(wt+2\pi /3\right)\end{array}\right]$$

(17)

where $V_m$ is the maximum value of v and w is the angular frequency such that $w=2\pi f$ being f the frequency in $Hz$.

Hence, considering (17) with (12) to (16), the dynamic system is a linear time-varying (LTV) system of 15 dimensions.

A great simplification in the mathematical description of a three-phase electrical system is obtained from Park’s transformation. The effect of Park’s transformation is simply to transform all stator quantities from phases a, b and c into new variables, the frame of reference of which moves with the rotor [28,29,31]. Electrical systems that have three-phase voltages and currents are complicated to model, analyze and control to determine time-varying systems, so the Park transformation has been applied, which allows obtaining equivalent systems without dependence on time.

In order to remove the time dependence, Park’s transformation can be used. This transformation for voltages is defined by

$$i^{dq0}=P{i}^{abc}$$

(18)

where

$$P=\sqrt{\frac{2}{3}}\left[\begin{array}{ccc}cos\theta & cos\left(\theta -\frac{2\pi }{3}\right)& cos\left(\theta +\frac{2\pi }{3}\right)\\ -sin\theta & sin\left(\theta -\frac{2\pi }{3}\right)& sin\left(\theta +\frac{2\pi }{3}\right)\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]$$

(19)

the angle between the d axis and the rotor is given by

$$\theta =wt+\frac{\pi }{2}$$

where w is the rated angular frequency in $rad/s$.

Park’s transformations for currents and flux linkages are expressed by

$$\begin{array}{ccc}\hfill v^{dcq0}& =& P{v}^{abc}\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\lambda }^{dq0}& =& P{\lambda }^{abc}\hfill \end{array}$$

(21)

Now, representing (12), (13) and (14) by Park’s transformation,

$$\begin{array}{ccc}\hfill P{v}_1^{abc}& =& P{R}_1^{abc}{P}^{-1}P{i}_1^{abc}+P{L}_1^{abc}{P}^{-1}P\frac{d{i}_1^{abc}}{dt}+P{v}_{C_1}^{abc}\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill P{v}_{C_1}^{abc}& =& P{R}_e^{abc}{P}^{-1}P{i}_e^{abc}+P{L}_e^{abc}{P}^{-1}P\frac{d{i}_e^{abc}}{dt}+P{v}_{C_2}^{abc}\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill P{v}_2^{abc}& =& P{R}_2^{abc}{P}^{-1}P{i}_2^{abc}+P{L}_2^{abc}{P}^{-1}P\frac{d{i}_2^{abc}}{dt}+P{v}_{C_2}^{abc}\hfill \end{array}$$

(24)

and from (15) and (16), the equations for the capacitors are

$$\begin{array}{ccc}\hfill P{C}_1^{abc}{P}^{-1}P\frac{d{v}_{C_1}^{abc}}{dt}& =& P{i}_1^{abc}-P{i}_e^{abc}\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill P{C}_2^{abc}{P}^{-1}P\frac{d{v}_{C_2}^{abc}}{dt}& =& P{i}_e^{abc}-P{i}_2^{abc}\hfill \end{array}$$

(26)

in terms of $\left(d,q,0\right)$

$$\begin{array}{ccc}\hfill v_1^{dq0}& =& R_1^{dq0}{i}_1^{dq0}+L_1^{dq0}\left[\frac{d{i}_1^{dq0}}{dt}-\frac{dP}{dt}{P}^{-1}{i}_1^{dq0}\right]+v_{C_1}^{dq0}\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill v_{C_1}^{dq0}& =& R_e^{dq0}{i}_e^{dq0}+L_e^{dq0}\left[\frac{d{i}_e^{dq0}}{dt}-\frac{dP}{dt}{P}^{-1}{i}_e^{dq0}\right]+v_{C_2}^{dq0}\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill v_2^{dq0}& =& R_2^{dq0}{i}_2^{dq0}+L_2^{dq0}\left[\frac{d{i}_2^{dq0}}{dt}-\frac{dP}{dt}{P}^{-1}{i}_2^{dq0}\right]+v_{C_2}^{dq0}\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill i_1^{dq0}-i_e^{dq0}& =& C_1^{dq0}\left[\frac{d{v}_{C_1}^{dq0}}{dt}-\frac{dP}{dt}{P}^{-1}{v}_{C_1}^{dq0}\right]\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill i_e^{dq0}-i_2^{dq0}& =& C_2^{dq0}\left[\frac{d{v}_{C_2}^{dq0}}{dt}-\frac{dP}{dt}{P}^{-1}{v}_{C_2}^{dq0}\right]\hfill \end{array}$$

(31)

where

$$\begin{array}{ccc}\hfill R_1^{dq0}& =& P{R}_1^{abc}{P}^{-1};R_2^{dq0}=P{R}_2^{abc}{P}^{-1};R_e^{dq0}=P{R}_e^{abc}{P}^{-1}\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill L_1^{dq0}& =& P{L}_1^{abc}{P}^{-1};L_2^{dq0}=P{L}_2^{abc}{P}^{-1};L_e^{dq0}=P{L}_e^{abc}{P}^{-1}\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill C_1^{dq0}& =& P{C}_1^{abc}{P}^{-1};C_2^{dq0}=P{C}_2^{abc}{P}^{-1}\hfill \end{array}$$

(34)

under balanced conditions

$$\begin{array}{ccc}\hfill R_1^{dq0}& =& diag\left\{r_1,r_1,r_1\right\};R_2^{dq0}=diag\left\{r_2,r_2,r_2\right\};R_e^{dq0}=diag\left\{r_e,r_e,r_e\right\}\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill L_1^{dq0}& =& diag\left\{l_1,l_1,l_1\right\};L_2^{dq0}=diag\left\{l_2,l_2,l_2\right\};L_e^{dq0}=diag\left\{l_e,l_e,l_e\right\}\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill C_1^{dq0}& =& diag\left\{c_1,c_1,c_1\right\};C_2^{dq0}=diag\left\{c_2,c_2,c_2\right\}\hfill \end{array}$$

(37)

it is well known that ${\displaystyle \frac{d\left[P\right]}{dt}}{\left[P\right]}^{-1}$ is given by

$$\frac{d\left[P\right]}{dt}{\left[P\right]}^{-1}=\left[\begin{array}{ccc}0& -w& 0\\ w& 0& 0\\ 0& 0& 0\end{array}\right]$$

(38)

substituting (38) into (27), (28) and (29)

$$\begin{array}{ccc}\hfill \left[\begin{array}{c}{v}_1^d\\ v_1^q\\ v_1^0\end{array}\right]& =& \left[\begin{array}{c}{v}_{C_1}^d\\ v_{C_1}^q\\ v_{C_1}^0\end{array}\right]+\left[\begin{array}{ccc}{l}_1& 0& 0\\ 0& l_1& 0\\ 0& 0& l_1\end{array}\right]\left[\begin{array}{c}\frac{d{i}_1^d}{dt}\\ \frac{d{i}_1^q}{dt}\\ \frac{d{i}_1^0}{dt}\end{array}\right]-\left[\begin{array}{ccc}-r_1& -w{l}_1& 0\\ w{l}_1& -r_1& 0\\ 0& 0& -r_1\end{array}\right]\left[\begin{array}{c}{i}_1^d\\ i_1^q\\ i_1^0\end{array}\right]\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill \left[\begin{array}{c}{v}_{C_1}^d\\ v_{C_1}^q\\ v_{C_1}^0\end{array}\right]& =& \left[\begin{array}{c}{v}_{C_2}^d\\ v_{C_2}^q\\ v_{C_2}^0\end{array}\right]+\left[\begin{array}{ccc}{l}_e& 0& 0\\ 0& l_e& 0\\ 0& 0& l_e\end{array}\right]\left[\begin{array}{c}\frac{d{i}_e^d}{dt}\\ \frac{d{i}_e^q}{dt}\\ \frac{d{i}_e^0}{dt}\end{array}\right]-\left[\begin{array}{ccc}-r_e& -w{l}_e& 0\\ w{l}_e& -r_e& 0\\ 0& 0& -r_e\end{array}\right]\left[\begin{array}{c}{i}_e^d\\ i_e^q\\ i_e^0\end{array}\right]\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill \left[\begin{array}{c}{v}_{C_2}^d\\ v_{C_2}^q\\ v_{C_2}^0\end{array}\right]& =& \left[\begin{array}{c}{v}_2^d\\ v_2^q\\ v_2^0\end{array}\right]+\left[\begin{array}{ccc}{l}_2& 0& 0\\ 0& l_2& 0\\ 0& 0& l_2\end{array}\right]\left[\begin{array}{c}\frac{d{i}_2^d}{dt}\\ \frac{d{i}_2^q}{dt}\\ \frac{d{i}_2^0}{dt}\end{array}\right]-\left[\begin{array}{ccc}-r_2& -w{l}_2& 0\\ w{l}_2& -r_2& 0\\ 0& 0& -r_2\end{array}\right]\left[\begin{array}{c}{i}_2^d\\ i_2^q\\ i_2^0\end{array}\right]\hfill \end{array}$$

(41)

a ninth-order LTI dynamic system for the inductances is obtained.

Now, substituting (38) into (30) and (31)

$$\begin{array}{ccc}\hfill \left[\begin{array}{c}{i}_1^d\\ i_1^q\\ i_1^0\end{array}\right]& =& \left[\begin{array}{c}{i}_e^d\\ i_e^q\\ i_e^0\end{array}\right]+\left[\begin{array}{ccc}{c}_1& 0& 0\\ 0& c_1& 0\\ 0& 0& c_1\end{array}\right]\left[\begin{array}{c}{\displaystyle \frac{d{v}_{C_1}^d}{dt}}\\ {\displaystyle \frac{d{v}_{C_1}^q}{dt}}\\ {\displaystyle \frac{d{v}_{C_1}^0}{dt}}\end{array}\right]-\left[\begin{array}{ccc}0& -w{c}_1& 0\\ w{c}_1& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{v}_{C_1}^d\\ v_{C_1}^q\\ v_{C_1}^0\end{array}\right]\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill \left[\begin{array}{c}{i}_e^d\\ i_e^q\\ i_e^0\end{array}\right]& =& \left[\begin{array}{c}{i}_2^d\\ i_2^q\\ i_2^0\end{array}\right]+\left[\begin{array}{ccc}{c}_2& 0& 0\\ 0& c_2& 0\\ 0& 0& c_2\end{array}\right]\left[\begin{array}{c}{\displaystyle \frac{d{v}_{C_2}^d}{dt}}\\ {\displaystyle \frac{d{v}_{C_2}^q}{dt}}\\ {\displaystyle \frac{d{v}_{C_2}^0}{dt}}\end{array}\right]-\left[\begin{array}{ccc}0& -w{c}_2& 0\\ w{c}_2& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{v}_{C_2}^d\\ v_{C_2}^q\\ v_{C_2}^0\end{array}\right]\hfill \end{array}$$

(43)

The complete system in terms $\left(d,q,0\right)$ is defined by (39), (40), (41), (42) and (43) representing a 15th order LTI system.

3. Modeling in Multibond Graphs

In the connection of two elements, components or systems, there is always a power transfer $P\left(t\right)$. This power in generalized terms described in bond graph modeling is defined as the product of effort $e\left(t\right)$ and flow $f\left(t\right)$. Likewise, the power link is represented by a power bond that is illustrated in Figure 2 [32].

Bond graph modeling can be applied to systems of different energy domains, that is, to electrical, mechanical, hydraulic, and thermodynamic systems. The generalized variables for these different systems are indicated in

Table 1. Power variables.

System	Effort $\left[\mathit{e}\left(\mathit{t}\right)\right]$	Flow $\left[\mathit{f}\left(\mathit{t}\right)\right]$
Electrical	Voltage $\left[v\left(t\right)\right]$	Current $\left[i\left(t\right)\right]$
Mechanical	Force $\left[F\left(t\right)\right]$ Torque $\left[\tau \left(t\right)\right]$	Velocity $\left[\nu \left(t\right)\right]$ Ang. velocity $\left[\omega \left(t\right)\right]$
Hydraulic	Pressure $\left[P\left(t\right)\right]$	Volume flow rate $\left[Q\left(t\right)\right]$
Thermodynamics	Temperature $\left[T\left(t\right)\right]$	Entropy flow $\left[S\left(t\right)\right]$

.

In bond graph modeling, two additional variables are required to characterize a system, in which variables are called energy variables which are momentum $p\left(t\right)$ and displacement $q\left(t\right)$. The time integral of an effort defines a momentum: $p\left(t\right)=\int e\left(t\right)dt$ and the displacement is the time integral of a flow: $q\left(t\right)=\int f\left(t\right)dt$.

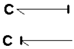
One of the fundamental properties in bond graph models is the causality that is applied to each of the elements that constitute part of a model. With the application of the causal stroke, each bond accurately indicates the input and output signals, as illustrated in Figure 3, which is a power bond with its causality [32].

According to the type of element, it has a given causality, as shown in

Table 2. Causal forms for 1-ports.

Element	Causal Form	Causal Relation
Effort source		$e\left(t\right)=E\left(t\right)$
Flow source		$f\left(t\right)=F\left(t\right)$
Resistance		$e\left(t\right)={\Phi }_R\left(f\left(t\right)\right)$ $f\left(t\right)={\Phi }_R^{-1}\left(e\left(t\right)\right)$
Capacitance		$e\left(t\right)={\Phi }_C(\int f\left(t\right)dt)$ $f\left(t\right)={\Phi }_C^{-1}\left(\frac{de\left(t\right)}{dt}\right)$
Inertia		$e\left(t\right)={\Phi }_I(\int e\left(t\right)dt)$ $f\left(t\right)={\Phi }_I^{-1}\left(\frac{df\left(t\right)}{dt}\right)$

.

Many systems can generally be modeled as multiport power elements. For example, mechatronic systems that are constructed of mechanical, electrical and hydraulic subsystems but in turn have movements in three axes $\left(x,y,z\right)$; electrical power systems can be represented as systems with multiport phases $\left(a,b,c\right)$, likewise, hydraulic and thermal systems with a multiport can be modeled. Therefore, systems modeled with bond graphs can be represented with multibond graph models with the advantages of structural modeling, analysis and control that determine bond graphs which are generalized and extended with multibond graphs [18,20].

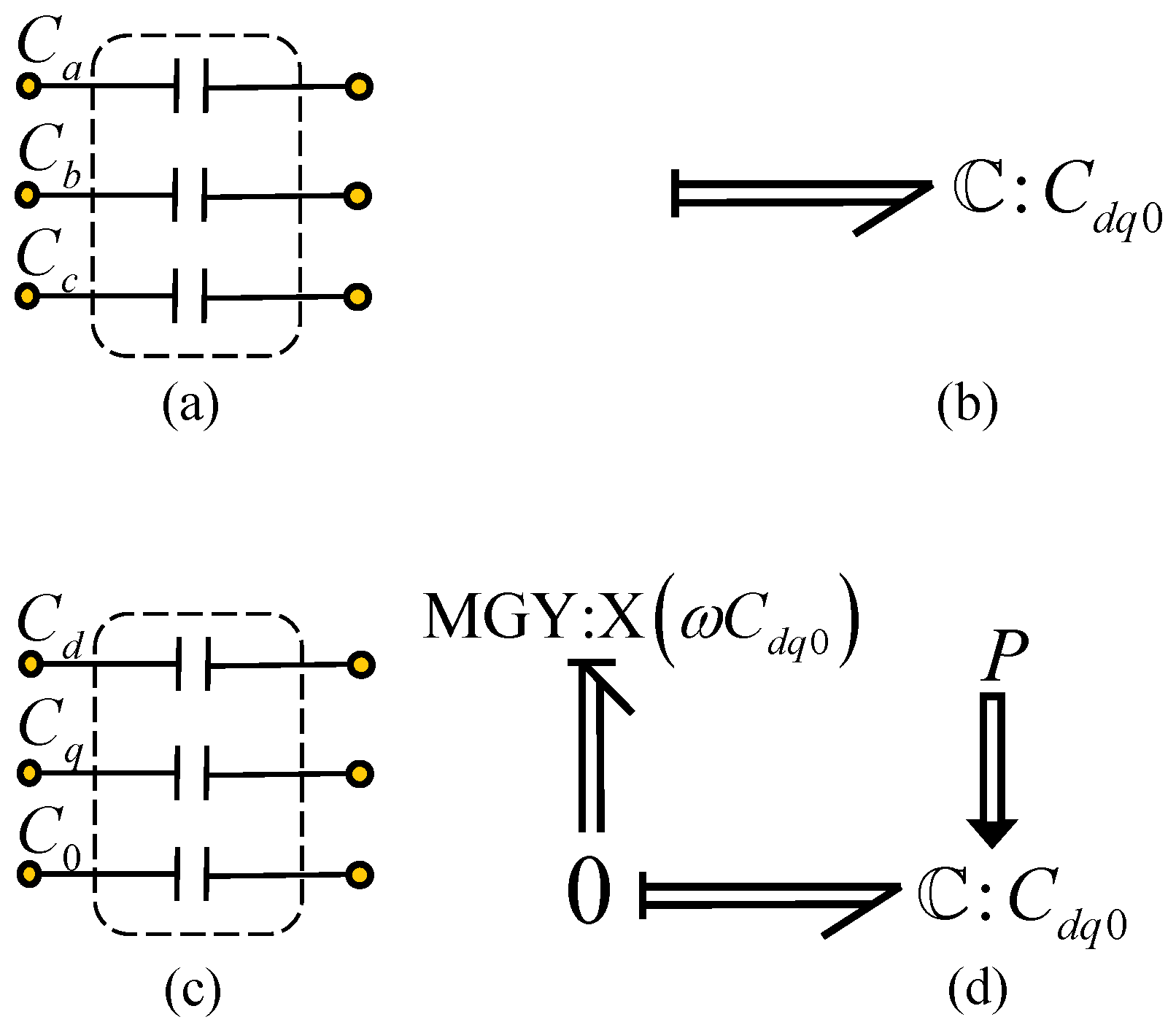
Firstly, the notation of the variables generalized with multibond graphs are efforts $\underline{e}\left(t\right)$ and flows $\underline{f}\left(t\right)$ with an underscore indicating that these variables determine vector bond notation, which is a composition of three bonds corresponding to the three perpendicular axes in a multibond graph. Figure 4 shows a multibond and its equivalent in bonds [18,20].

Modeling with multibond graphs is common for the application to vectors with three elements for physical systems, but this does not limit the fact that it can be extended to higher-order vectors [18]. The power in a multibond is defined by

$$\underline{P}\left(t\right)={\underline{e}}^T\left(t\right)\underline{f}\left(t\right)$$

(44)

where ${\underline{e}}^T\left(t\right)$ is the transpose of the column vector

$$\underline{e}\left(t\right)=\left[\begin{array}{c}{e}^x\left(t\right)\\ e^y\left(t\right)\\ e^z\left(t\right)\end{array}\right]=\left[\begin{array}{c}{e}^a\left(t\right)\\ e^b\left(t\right)\\ e^c\left(t\right)\end{array}\right]$$

(45)

and

$$\underline{f}\left(t\right)=\left[\begin{array}{c}{f}^x\left(t\right)\\ f^y\left(t\right)\\ f^z\left(t\right)\end{array}\right]=\left[\begin{array}{c}{f}^a\left(t\right)\\ f^b\left(t\right)\\ f^c\left(t\right)\end{array}\right]$$

(46)

A general multibond graph indicating the generalized variables in each multibond and the junctions or multiport elements $\left(MP\right)$ is shown in Figure 5 [18].

The essential elements in modeling with multibond graphs are described in Appendix A.

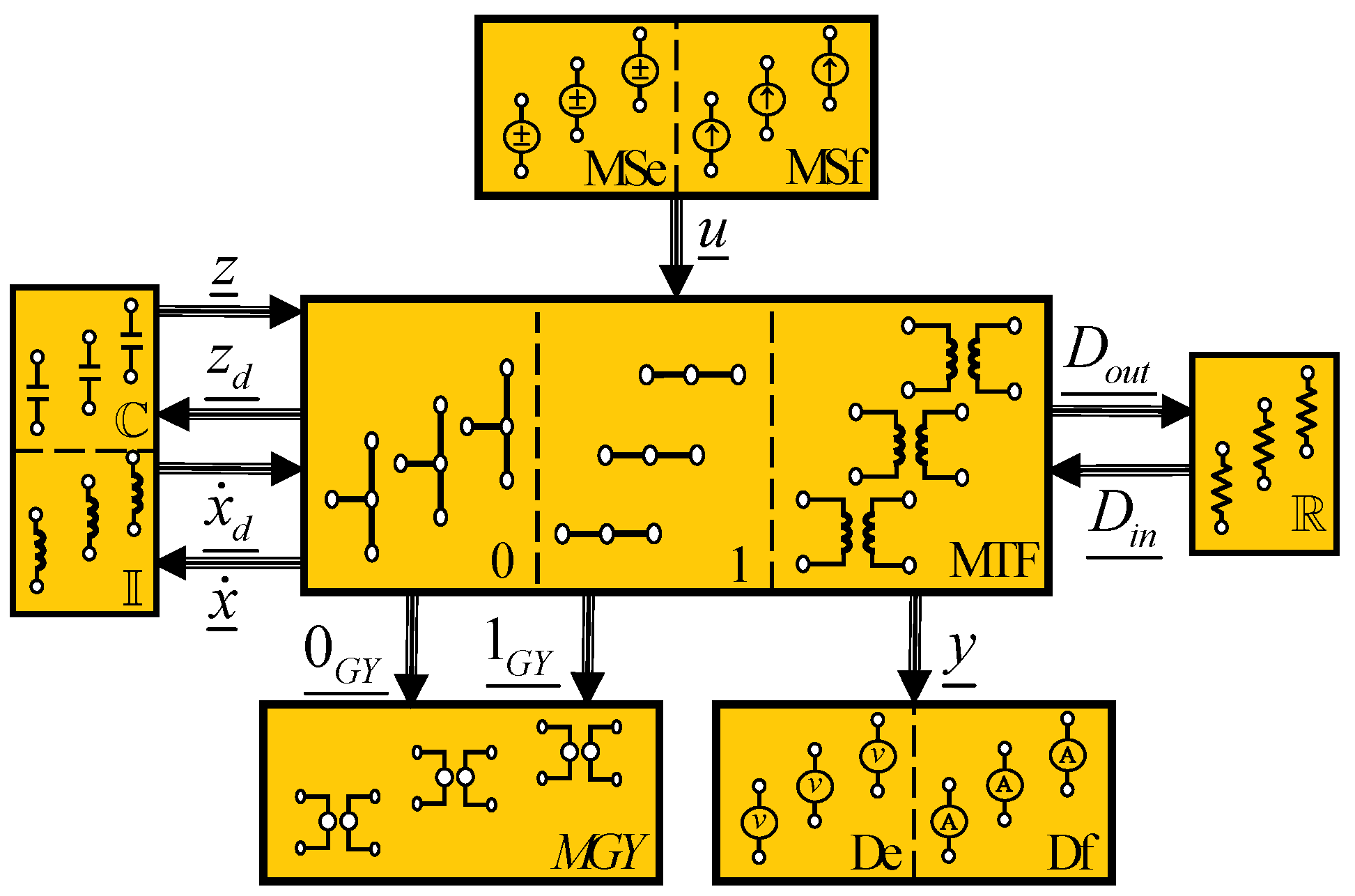
The link of the different elements that are part of a system can be organized into fields as illustrated in Figure 6. Considering a model in a multibond graph with a predefined integral causality assignment, its fields and the key vectors. Figure 6 presents the causal relationships between these elements that describe the system.

The different multiport fields in a multibond graph that are shown in Figure 6 determine:

• System input $\underline{u}\left(t\right)\in {\Re }^{\underline{p}}$ is the power supply through the source multiport field denoted by $\left(\underline{MSe},\underline{MSf}\right)$.
• The power exchange due to the connection in multiport junctions $\underline{0}$ or $\underline{1}$ or in multiport transformers $\underline{MTF}$ are carried out in the multiport junction structure.
• Storage elements $\mathbb{C}$ and $II$ determine the energy storage multiport field denoted by $\left(\mathbb{C},II\right)$ that they are associated with the energy variables $\underline{q}\left(t\right)$ and $\underline{p}\left(t\right)$, variables which derive in the following state variables:

  -

  When the storage elements have integral causality, they determine the linearly independent state variables $\underline{x}\left(t\right)\in {\Re }^{\underline{n}}$ with the co-energy vector $\underline{z}\left(t\right)\in {\Re }^{\underline{n}}$.

  -

  When the storage elements have derivative causality, they determine the linearly dependent state variables $\underline{x_d}\left(t\right)\in {\Re }^{\underline{m}}$ with the co-energy vector $\underline{z_d}\left(t\right)\in {\Re }^{\underline{m}}$.

• The key vectors $\underline{D_{in}}\in {\Re }^{\underline{r}}$ and $\underline{D_{out}}\in {\Re }^{\underline{r}}$ establish the relation between the energy dissipation multiport field denoted by $\left(\mathbb{R}\right)$ and the multiport junction structure through the mixture of power variables $\underline{e}\left(t\right)$ and $\underline{f}\left(t\right)$.
• $\underline{y}\left(t\right)\in {\Re }^{\underline{q}}$ are the system outputs that are obtained from the multiport junction structure to the detectors and are denoted by $\left(\underline{De},\underline{D_f}\right)$.

The mathematical model of a system based on a multibond graph is determined following Lemma 1.

Lemma 1. 

Consider a multibond graph model with a predefined integral causality assignment that represents a system whose block diagrams is shown in Figure 6 and the multiport junction structure is defined by

$$\left[\begin{array}{c}\stackrel{•}{\underline{x}}\left(t\right)\\ \underline{I_{GY}}\left(t\right)\\ \underline{D_{in}}\left(t\right)\\ \underline{y}\left(t\right)\\ \underline{z_d}\left(t\right)\end{array}\right]=\left[\begin{array}{ccccc}{\mathbf{S}}_{11}^{11}\left(z\right)& {\mathbf{S}}_{11}^{12}\left(z\right)& {\mathbf{S}}_{12}^{11}\left(z\right)& {\mathbf{S}}_{13}^{11}\left(z\right)& {\mathbf{S}}_{14}^{11}\left(z\right)\\ {\mathbf{S}}_{11}^{21}\left(z\right)& {\mathbf{S}}_{11}^{22}\left(z\right)& {\mathbf{S}}_{12}^{21}\left(z\right)& {\mathbf{S}}_{13}^{21}\left(z\right)& \mathbf{0}\\ {\mathbf{S}}_{21}^{11}\left(z\right)& {\mathbf{S}}_{21}^{12}\left(z\right)& {\mathbf{S}}_{22}\left(z\right)& {\mathbf{S}}_{23}\left(z\right)& \mathbf{0}\\ {\mathbf{S}}_{31}^{11}\left(z\right)& {\mathbf{S}}_{31}^{12}\left(z\right)& {\mathbf{S}}_{32}\left(z\right)& {\mathbf{S}}_{33}\left(z\right)& \mathbf{0}\\ {\mathbf{S}}_{41}^{11}\left(z\right)& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\underline{z}\left(t\right)\\ \underline{O_{GY}}\left(t\right)\\ \underline{D_{out}}\left(t\right)\\ \underline{u}\left(t\right)\\ \underline{{\stackrel{•}{x}}_d}\left(t\right)\end{array}\right]$$

(47)

where the entries of $\mathbf{S}\left(z\right)$ are in the set $\left\{0,\pm \mathbf{I},\pm {\mathbf{K}}_t\right\}$ and ${\mathbf{K}}_t$ determines the transformer module which are constants or co-energy functions and the constitutive relations for the multiport elements are

$$\begin{array}{ccc}\hfill \underline{z}\left(t\right)& =& \mathbf{F}\underline{x}\left(t\right)\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill {\underline{z}}_d\left(t\right)& =& \mathbf{F}{\underline{x}}_d\left(t\right)\hfill \end{array}$$

(49)

$$\begin{array}{ccc}\hfill \underline{O_{GY}}\left(t\right)& =& {\mathbf{X}}_{GY}\underline{I_{GY}}\left(t\right)\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill \underline{D_{out}}\left(t\right)& =& \mathbf{L}\underline{D_{in}}\left(t\right)\hfill \end{array}$$

(51)

then, a state variable representation in terms of co-energy is defined by

$$\begin{array}{ccc}\hfill \stackrel{•}{\underline{z}}\left(t\right)& =& {\mathbf{E}}^{-1}\left(z\right)\mathbf{A}\left(z\right)\underline{z}\left(t\right)+{\mathbf{E}}^{-1}\left(z\right)\mathbf{B}\left(z\right)\underline{u}\left(t\right)\hfill \end{array}$$

(52)

$$\begin{array}{ccc}\hfill \underline{y}\left(t\right)& =& \mathbf{C}\left(z\right)\underline{z}\left(t\right)+\mathbf{D}\left(z\right)\underline{u}\left(t\right)\hfill \end{array}$$

(53)

where

$$\begin{array}{ccc}\hfill \mathbf{A}\left(z\right)& =& {\mathbf{S}}_{11}^{11}\left(z\right)+{\mathbf{R}}_{11}^{12}\left(z\right){\mathbf{A}}_1\left(z\right)+{\mathbf{R}}_{12}^{11}\left(z\right){\mathbf{A}}_2\left(z\right)+{\mathbf{S}}_{14}^{11}\left(z\right)F_d^{-1}{\stackrel{•}{\mathbf{S}}}_{41}^{11}\left(z\right)\hfill \end{array}$$

(54)

$$\begin{array}{ccc}\hfill \mathbf{B}\left(z\right)& =& {\mathbf{S}}_{13}^{11}\left(z\right)+{\mathbf{R}}_{11}^{12}\left(z\right){\mathbf{B}}_1\left(z\right)+{\mathbf{R}}_{12}^{11}\left(z\right){\mathbf{B}}_2\left(z\right)\hfill \end{array}$$

(55)

$$\begin{array}{ccc}\hfill \mathbf{E}\left(z\right)& =& \mathbf{I}-{\mathbf{S}}_{14}^{11}{\mathbf{F}}_d^{-1}{\mathbf{S}}_{31}^{11}\mathbf{F}\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill \mathbf{C}\left(z\right)& =& {\mathbf{S}}_{31}^{11}\left(z\right)+{\mathbf{R}}_{31}^{12}\left(z\right){\mathbf{A}}_1\left(z\right)+{\mathbf{R}}_{32}\left(z\right){\mathbf{A}}_2\left(z\right)\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill \mathbf{D}\left(z\right)& =& {\mathbf{S}}_{33}\left(z\right)+{\mathbf{R}}_{31}^{12}\left(z\right){\mathbf{B}}_1\left(z\right)+{\mathbf{R}}_{32}\left(z\right){\mathbf{B}}_2\left(z\right)\hfill \end{array}$$

(58)

$$\begin{array}{ccc}\hfill {\mathbf{A}}_1\left(z\right)& =& {\mathbf{S}}_{11}^{21}\left(z\right)+{\mathbf{R}}_{12}^{21}\left(z\right){\mathbf{S}}_{21}^{11}\left(z\right)\hfill \end{array}$$

(59)

$$\begin{array}{ccc}\hfill {\mathbf{A}}_2\left(z\right)& =& {\mathbf{S}}_{21}^{11}\left(z\right)+{\mathbf{R}}_{21}^{12}\left(z\right){\mathbf{S}}_{11}^{21}\left(z\right)\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill {\mathbf{B}}_1\left(z\right)& =& {\mathbf{S}}_{13}^{21}\left(z\right)+{\mathbf{R}}_{12}^{21}\left(z\right){\mathbf{S}}_{23}\left(z\right)\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\hfill {\mathbf{B}}_2\left(z\right)& =& {\mathbf{S}}_{23}\left(z\right)+{\mathbf{R}}_{21}^{12}\left(z\right){\mathbf{S}}_{13}^{21}\left(z\right)\hfill \end{array}$$

(62)

with

$$\begin{array}{ccc}\hfill {\mathbf{Q}}_X\left(z\right)& =& {\mathbf{X}}_{GY}{\left[\mathbf{I}-\left({\mathbf{S}}_{11}^{22}\left(z\right)+{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{12}\left(z\right)\right){\mathbf{X}}_{GY}\right]}^{-1}\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill {\mathbf{Q}}_L\left(z\right)& =& \mathbf{L}{\left[\mathbf{I}-\left({\mathbf{S}}_{12}^{21}\left(z\right)+{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{12}^{21}\left(z\right)\right)\mathbf{L}\right]}^{-1}\hfill \end{array}$$

(64)

$$\begin{array}{ccc}\hfill {\mathbf{M}}_L\left(z\right)& =& \mathbf{L}{\left(\mathbf{I}-{\mathbf{S}}_{22}\left(z\right)\mathbf{L}\right)}^{-1}\hfill \end{array}$$

(65)

$$\begin{array}{ccc}\hfill {\mathbf{M}}_X\left(z\right)& =& {\mathbf{X}}_{GY}{\left(\mathbf{I}-{\mathbf{S}}_{11}^{22}\left(z\right){\mathbf{X}}_{GY}\right)}^{-1}\hfill \end{array}$$

(66)

$$\begin{array}{ccc}\hfill {\mathbf{R}}_{11}^{12}\left(z\right)& =& {\mathbf{S}}_{11}^{12}\left(z\right){\mathbf{Q}}_X\left(z\right)\hfill \end{array}$$

(67)

$$\begin{array}{ccc}\hfill {\mathbf{R}}_{12}^{11}\left(z\right)& =& {\mathbf{S}}_{12}^{11}\left(z\right){\mathbf{Q}}_L\left(z\right)\hfill \end{array}$$

(68)

$$\begin{array}{ccc}\hfill {\mathbf{R}}_{12}^{21}\left(z\right)& =& {\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right)\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\hfill {\mathbf{R}}_{21}^{12}\left(z\right)& =& {\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right)\hfill \end{array}$$

(70)

$$\begin{array}{ccc}\hfill {\mathbf{R}}_{31}^{12}\left(z\right)& =& {\mathbf{S}}_{31}^{12}\left(z\right){\mathbf{Q}}_X\left(z\right)\hfill \end{array}$$

(71)

$$\begin{array}{ccc}\hfill {\mathbf{R}}_{32}\left(z\right)& =& {\mathbf{S}}_{32}\left(z\right){\mathbf{Q}}_L\left(z\right)\hfill \end{array}$$

(72)

Proof. 

From the second and third lines of (47) with (50) and (51)

$$\underline{I_{GY}}\left(t\right)={\left[\mathbf{I}-{\mathbf{S}}_{11}^{22}\left(z\right){\mathbf{X}}_{GY}\right]}^{-1}\left[{\mathbf{S}}_{11}^{21}\left(z\right)\underline{z}\left(t\right)+{\mathbf{S}}_{12}^{21}\left(z\right)\mathbf{L}\underline{D_{in}}\left(t\right)+{\mathbf{S}}_{13}^{21}\left(z\right)\underline{u}\left(t\right)\right]$$

(73)

$$\underline{D_{in}}\left(t\right)={\left(\mathbf{I}-{\mathbf{S}}_{22}\left(z\right)\mathbf{L}\right)}^{-1}\left[{\mathbf{S}}_{21}^{11}\left(z\right)\underline{z}\left(t\right)+{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{X}}_{GY}\underline{I_{GY}}\left(t\right)+{\mathbf{S}}_{23}\left(z\right)\underline{u}\left(t\right)\right]$$

(74)

The solution of (73) and (74) can be expressed by

$$\begin{array}{ccc}\hfill \underline{I_{GY}}\left(t\right)& =& {\left[\mathbf{I}-{\mathbf{S}}_{11}^{22}\left(z\right){\mathbf{X}}_{GY}-{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{X}}_{GY}\right]}^{-1}\left\{\left[{\mathbf{S}}_{11}^{21}\left(z\right)+\right.\right.\hfill \\ & & \left.\left.{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{11}\left(z\right)\right]\underline{z}\left(t\right)+\left[{\mathbf{S}}_{13}^{21}\left(z\right)+{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{23}\left(z\right)\right]\underline{u}\left(t\right)\right\}\hfill \end{array}$$

(75)

with

$${\mathbf{M}}_L\left(z\right)=\mathbf{L}{\left[\mathbf{I}-{\mathbf{S}}_{22}\left(z\right)\mathbf{L}\right]}^{-1}$$

(76)

and

$$\begin{array}{ccc}\hfill \underline{D_{in}}\left(t\right)& =& {\left[\mathbf{I}-{\mathbf{S}}_{22}\left(z\right)\mathbf{L}-{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{12}^{21}\mathbf{L}\right]}^{-1}\left\{\left[{\mathbf{S}}_{21}^{11}\left(z\right)+\right.\right.\hfill \\ & & \left.\left.{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{11}^{21}\left(z\right)\right]\underline{z}\left(t\right)+\left[{\mathbf{S}}_{23}\left(z\right)+{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{13}^{21}\left(z\right)\right]\underline{u}\left(t\right)\right\}\hfill \end{array}$$

(77)

with

$${\mathbf{M}}_X\left(z\right)={\mathbf{X}}_{GY}{\left[\mathbf{I}-{\mathbf{S}}_{11}^{22}\left(z\right){\mathbf{X}}_{GY}\right]}^{-1}$$

(78)

from the fifth line of (47) with (48) and (49) and deriving

$$\underline{{\stackrel{•}{x}}_d}\left(t\right)={\mathbf{F}}_d^{-1}{\stackrel{•}{\mathbf{S}}}_{41}^{11}\left(z\right)\underline{z}\left(t\right)+{\mathbf{F}}_d^{-1}{\mathbf{S}}_{41}^{11}\left(z\right)\mathbf{F}\stackrel{•}{\underline{x}}\left(t\right)$$

(79)

by substituting (75) and (77) into the first line (47) with (50) and (51)

$$\begin{array}{ccc}\hfill \stackrel{•}{\underline{x}}\left(t\right)& =& {\mathbf{S}}_{11}\left(z\right)\underline{z}\left(t\right)+{\mathbf{S}}_{13}^{11}\left(z\right)\underline{u}\left(t\right)+{\mathbf{S}}_{14}^{11}\left(z\right)\underline{{\stackrel{•}{x}}_d}\left(t\right)\hfill \\ & & {\mathbf{S}}_{11}^{12}\left(z\right){\mathbf{X}}_{GY}{\left[\mathbf{I}-{\mathbf{S}}_{11}^{22}\left(z\right){\mathbf{X}}_{GY}-{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{X}}_{GY}\right]}^{-1}\left\{\left[{\mathbf{S}}_{11}^{21}\left(z\right)+\right.\right.\hfill \\ & & \left.\left.{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{11}\left(z\right)\right]\underline{z}\left(t\right)+\left[{\mathbf{S}}_{13}^{21}\left(z\right)+{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{23}\left(z\right)\right]\underline{u}\left(t\right)\right\}+\hfill \\ & & {\mathbf{S}}_{12}^{11}\left(z\right)\mathbf{L}{\left[\mathbf{I}-{\mathbf{S}}_{22}\left(z\right)\mathbf{L}-{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{12}^{21}\left(z\right)\mathbf{L}\right]}^{-1}\left\{\left[{\mathbf{S}}_{21}^{11}\left(z\right)+\right.\right.\hfill \\ & & \left.\left.{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{11}^{21}\left(z\right)\right]\underline{z}\left(t\right)+\left[{\mathbf{S}}_{23}\left(z\right)+{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{13}^{21}\left(z\right)\right]\underline{u}\left(t\right)\right\}\hfill \end{array}$$

(80)

if we expressed

$${\mathbf{Q}}_X\left(z\right)={\mathbf{X}}_{GY}{\left[\mathbf{I}-\left({\mathbf{S}}_{11}^{22}\left(z\right)+{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{12}\left(z\right)\right){\mathbf{X}}_{GY}\right]}^{-1}$$

and

$${\mathbf{Q}}_L\left(z\right)=\mathbf{L}{\left[\mathbf{I}-\left({\mathbf{S}}_{12}^{21}\left(z\right)+{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{12}^{21}\left(z\right)\right)\mathbf{L}\right]}^{-1}$$

(80) can be reduced as

$$\begin{array}{ccc}\hfill \stackrel{•}{\underline{x}}\left(t\right)& =& \left\{{\mathbf{S}}_{11}\left(z\right)+{\mathbf{S}}_{11}^{12}\left(z\right){\mathbf{Q}}_X\left(z\right)\left[{\mathbf{S}}_{11}^{21}\left(z\right)+{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{11}\left(z\right)\right]+\right.\hfill \\ & & \left.{\mathbf{S}}_{12}^{11}\left(z\right){\mathbf{Q}}_L\left(z\right)\left[{\mathbf{S}}_{21}^{11}\left(z\right)+{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{11}^{21}\left(z\right)\right]\right\}\underline{z}\left(t\right)+\hfill \\ & & \left\{{\mathbf{S}}_{13}^{11}\left(z\right)+{\mathbf{S}}_{11}^{12}\left(z\right){\mathbf{Q}}_X\left(z\right)\left[{\mathbf{S}}_{13}^{21}\left(z\right)+{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{23}\left(z\right)\right]\right.\hfill \\ & & \left.{\mathbf{S}}_{12}^{11}\left(z\right){\mathbf{Q}}_L\left(z\right)\left[{\mathbf{S}}_{23}\left(z\right)+{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{13}^{21}\left(z\right)\right]\underline{u}\left(t\right)\right\}+{\mathbf{S}}_{14}^{11}\left(z\right)\underline{{\stackrel{•}{x}}_d}\left(t\right)\hfill \end{array}$$

(81)

and substituting (79) into (81) with (54) to (62), the space state representation defined by (52) is proven. □

For the output, from the fourth line of (47) with (50) and (51)

$$\underline{y}\left(t\right)={\mathbf{S}}_{31}^{11}\left(z\right)\underline{z}\left(t\right)+{\mathbf{S}}_{31}^{12}\left(z\right){\mathbf{X}}_{GY}\underline{I_{GY}}\left(t\right)+{\mathbf{S}}_{32}\left(z\right)\mathbf{L}\underline{D_{in}}\left(t\right)+{\mathbf{S}}_{33}\left(z\right)\underline{u}\left(t\right)$$

(82)

substituting (75) and (77) into (82),

$$\begin{array}{ccc}\hfill \underline{y}\left(t\right)& =& {\mathbf{S}}_{31}^{12}\left(z\right){\mathbf{X}}_{GY}{\left[\mathbf{I}-{\mathbf{S}}_{11}^{22}\left(z\right){\mathbf{X}}_{GY}-{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{X}}_{GY}\right]}^{-1}\left\{\left[{\mathbf{S}}_{11}^{21}\left(z\right)+\right.\right.\hfill \\ & & \left.\left.{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{11}\left(z\right)\right]\underline{z}\left(t\right)+\left[{\mathbf{S}}_{13}^{21}\left(z\right)+{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{23}\left(z\right)\right]\underline{u}\left(t\right)\right\}\hfill \\ & & +{\mathbf{S}}_{32}\left(z\right)\mathbf{L}{\left[\mathbf{I}-{\mathbf{S}}_{22}\left(z\right)\mathbf{L}-{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{12}^{21}\mathbf{L}\right]}^{-1}\left\{\left[{\mathbf{S}}_{21}^{11}\left(z\right)+\right.\right.\hfill \\ & & \left.\left.{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{11}^{21}\left(z\right)\right]\underline{z}\left(t\right)+\left[{\mathbf{S}}_{23}\left(z\right)+{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{13}^{21}\left(z\right)\right]\underline{u}\left(t\right)\right\}+\hfill \\ & & {\mathbf{S}}_{31}^{11}\left(z\right)\underline{z}\left(t\right)+{\mathbf{S}}_{33}\left(z\right)\underline{u}\left(t\right)\hfill \end{array}$$

(83)

with (63) and (64), (83) can be expressed by

$$\begin{array}{ccc}\hfill \underline{y}\left(t\right)& =& {\mathbf{S}}_{31}^{11}\left(z\right)\underline{z}\left(t\right)+{\mathbf{S}}_{33}\left(z\right)\underline{u}\left(t\right)+{\mathbf{S}}_{31}^{12}\left(z\right){\mathbf{Q}}_X\left(z\right)\left\{\left[{\mathbf{S}}_{11}^{21}\left(z\right)+\right.\right.\hfill \\ & & \left.\left.{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{21}^{11}\left(z\right)\right]\underline{z}\left(t\right)+\left[{\mathbf{S}}_{13}^{21}\left(z\right)+{\mathbf{S}}_{12}^{21}\left(z\right){\mathbf{M}}_L\left(z\right){\mathbf{S}}_{23}\left(z\right)\right]\underline{u}\left(t\right)\right\}\hfill \\ & & +{\mathbf{S}}_{32}\left(z\right){\mathbf{Q}}_L\left(z\right)\left\{\left[{\mathbf{S}}_{21}^{11}\left(z\right)+\right.\right.\hfill \\ & & \left.\left.{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{11}^{21}\left(z\right)\right]\underline{z}\left(t\right)+\left[{\mathbf{S}}_{23}\left(z\right)+{\mathbf{S}}_{21}^{12}\left(z\right){\mathbf{M}}_X\left(z\right){\mathbf{S}}_{13}^{21}\left(z\right)\right]\underline{u}\left(t\right)\right\}\hfill \end{array}$$

(84)

from (84), (57) and (58) with (59) to (62), the output equation (53) is proven.

Note that the multibond graph model permits the representation of systems with integral and derivative causality assignments.

In the next section, a procedure to represent electrical power systems in a multibond graph approach is proposed.

4. Modeling of Three-Phase Circuits in the Physical Domain

Considering the basic three-phase circuit of Figure 1 is defined by (39) to (43). A lemma to obtain a multibond graph of a three-phase circuit given in the coordinates $\left(d,q,0\right)$ is proposed.

Lemma 2. 

Consider a three-phase electrical system that is modeled by a multibond graph with a predefined integral causality assignment in coordinates $\left(a,b,c\right)$ according to the multiport junction structure of Figure 6 and then, a multibond graph with a predefined integral causality assignment in coordinates $\left(d,q,0\right)$ can be built if the different elements are connected according to the construction rules of multibond graphs and the multiport inertia in coordinates $\left(a,b,c\right)$ is replaced by a multiport inertia in coordinates $\left(d,q,0\right)$ connected through a $1-$ junction to a multiport gyrator modulated by

$$x\left(-wL\right)=\left[\begin{array}{ccc}0& w{L}_d& 0\\ -w{L}_q& 0& 0\\ 0& 0& 0\end{array}\right]$$

(85)

and the multiport capacitor in coordinates $\left(a,b,c\right)$ is replaced by a multiport capacitor in coordinates $\left(d,q,0\right)$ connected through a $0-$ junction to a multiport gyrator modulated by

$$x\left(-wC\right)=\left[\begin{array}{ccc}0& w{C}_d& 0\\ -w{C}_q& 0& 0\\ 0& 0& 0\end{array}\right]$$

(86)

Proof. 

The basic elements of a three-phase electrical system are described by resistances, inductances and capacitances supplied by electrical currents and voltages. It is known that $v^{dq0}=P{v}^{abc}$ and $i^{dq0}=P{i}^{abc}$ where P is Park’s transformation matrix. The conversion of resistances from $\left(a,b,c\right)$ to $\left(d,q,0\right)$ is defined by

$$v_R^{abc}=R^{abc}{i}_R^{abc}$$

(87)

where $i_R^{abc}$ are the electric currents through the resistors $R^{abc}$ and the voltage across the resistors are $v_R^{abc}$, premultiplying (87) by P, and then

$$P{v}_R^{abc}=P{R}^{abc}{i}_R^{abc}=P{R}^{abc}P{P}^{-1}{i}_R^{abc}$$

in coordinates $\left(d,q,0\right)$

$$v_R^{dq0}=R^{dq0}{i}_R^{dq0}$$

(88)

where

$$R^{dq0}=P{R}^{abc}{P}^{-1}$$

(89)

in multibond graphs, the multiport resistor $R^{abc}$ is changed by $R^{dq0}$ as well as modulated by P and $P^{-1}$ according to (89).

For inductances in coordinates $\left(a,b,c\right)$, the voltage is given by

$$v_L^{abc}=L^{abc}\frac{d{i}_L^{abc}}{dt}$$

(90)

and premultiplying by P

$$P{v}_L^{abc}=P{L}^{abc}\frac{d{i}_L^{abc}}{dt}=P{L}^{abc}{P}^{-1}P\frac{d{i}_L^{abc}}{dt}$$

(91)

the derivative with respect to time $i_L^{dq0}=P{i}_L^{abc}$ determines

$$\frac{d{i}_L^{dq0}}{dt}=\frac{dP}{dt}{i}_L^{abc}+P\frac{d{i}_L^{abc}}{dt}$$

(92)

substituting (92) into (91)

$$v_L^{dq0}=L^{dq0}\frac{d{i}_L^{dq0}}{dt}-L^{dq0}\frac{dP}{dt}{P}^{-1}{i}^{dq0}$$

(93)

however,

$$\frac{dP}{dt}{P}^{-1}=\left[\begin{array}{ccc}0& -w& 0\\ w& 0& 0\\ 0& 0& 0\end{array}\right]$$

(94)

then the term $-L^{dq0}\frac{dP}{dt}{P}^{-1}{i}^{dq0}$ can be represented as a multiport gyrator which is shown in Figure 7.

The constitutive relationship is given by

$$v_{Lp}^{dq0}=X\left(w{L}_{dq0}\right)i^{dq0}$$

(95)

where $X\left(w{L}_{dq0}\right)=L^{dq0}\frac{dP}{dt}{P}^{-1}$ and then (93) is modeled according to Figure 8.

The current through capacitances is defined by

$$i_C^{abc}=C^{abc}\frac{d{V}_C^{abc}}{dt}$$

(96)

premultiplying by P

$$P{i}_C^{abc}=P{C}^{abc}\frac{d{V}_C^{abc}}{dt}=P{C}^{abc}{P}^{-1}P\frac{d{V}_C^{abc}}{dt}$$

(97)

this expression in coordinates $\left(d,q,0\right)$ is reduced to

$$i_C^{dq0}=C^{dq0}\frac{d{V}_C^{abc}}{dt}$$

(98)

where

$$C^{dq0}=P{C}^{abc}{P}^{-1}$$

(99)

differentiating $v_C^{dq0}=P{v}_C^{abc}$ with respect to time

$$\frac{d{V}_C^{dq0}}{dt}=\frac{dP}{dt}{V}_C^{abc}+P\frac{d{V}_C^{abc}}{dt}$$

(100)

substituting (100) into (97)

$$i_C^{dq0}=C^{dq0}\left[\frac{d{V}_C^{dq0}}{dt}-\frac{dP}{dt}{P}^{-1}{V}_C^{dq0}\right]=C^{dq0}\frac{d{V}_C^{dq0}}{dt}-i_{Cp}^{dq0}$$

(101)

where

$$i_{Cp}^{dq0}=C^{dq0}\frac{dP}{dt}{P}^{-1}{V}_C^{dq0}$$

(102)

can be represented by a multiport gyrator as shown in Figure 9.

The constitutive relationship of this gyrator is defined by

$$i_{Cp}^{dq0}=X\left(w{C}_{dq0}\right)V_C^{dq0}$$

where

$$X\left(w{C}_{dq0}\right)=C^{dq0}\frac{dP}{dt}{P}^{-1}$$

then modeling the capacitance in coordinates $\left(d,q,0\right)$ given by (101) is shown in Figure 10.

Finally, Figure 8 and Figure 10 prove Lemma 2. □

Next, a procedure based on Lemma 2 is presented for the direct modeling of three-phase electrical systems in multibond graphs.

Procedure 1

1. The three-phase voltage source is represented by $\underline{M{S}_e}:v^{abc}$ and $\underline{M{S}_e}:v^{dq0}$ is obtained using a modulated multiport transformer $\underline{MTF}$ by P which is Park’transformation matrix according to Figure 11.

2. Three-phase resistances are represented by multiport resistor $R:R_{abc}$ shown in Figure 12 in coordinates $\left(a,b,c\right)$ is given in Figure 5a; for coordinates $\left(d,q,0\right)$, the multiport resistor is modulated by P which is shown in Figure 12d.

3. Three-phase inductances in coordinates $\left(a,b,c\right)$ are shown in Figure 13b by a multiport inertia and in coordinates $\left(d,q,0\right)$ are represented by multiport inertia $I:L_{dq0}$ connected to a multiport gyrator modulated by $x\left(w{L}_{dq0}\right)$ through a one-junction which is shown in Figure 13d.

4. Three-phase capacitance in coordinates $\left(a,b,c\right)$ is modeled by a multiport capacitor shown in Figure 14b in the coordinates $\left(d,q,0\right)$ which is represented by the multiport capacitor $C:C_{dq0}$ connected to a multiport gyrator modulated by $x\left(w{C}_{dq0}\right)$ through a zero-junction according to Figure 14d.

Next, the methodology presented is applied to two examples.

5. Study Cases

1. A basic electrical power system is illustrated in Figure 15. It is built by two three-phase sources linked by a transmission line that is a resistance in series with an inductance.

Applying the modeling methodology with multibond graphs of systems and Lemma 2, the three-phase system in coordinates $\left(d,q,0\right)$ is shown in Figure 16.

Inside the dotted box, we have the multibond graph in coordinates $\left(d,q,0\right)$, and on the outside, we have the supply voltages and the current of the system in coordinates $\left(a,b,c\right)$ connected through multiport transformers modulated by the Park’s transformation matrix. The multibond graph model inside the blue dotted line is a time-invariant model formed by the three-phase series connection of the two power supplies $v_1^{abc}$ and $v_2^{abc}$, the three-phase resistance ${\mathbf{R}}_e$ and the inductance ${\mathbf{L}}_e$ that must be connected to a multiport gyrator.

The key vectors of the multibond graph are expressed by

$$\begin{array}{ccc}\hfill \underline{x}\left(t\right)& =& \underline{p_3};\stackrel{•}{\underline{x}}\left(t\right)=\underline{e_3};\underline{z}\left(t\right)=\underline{f_3}\hfill \\ \hfill \underline{D_{in}}\left(t\right)& =& \underline{e_4};\underline{D_{out}}\left(t\right)=\underline{f_4}\hfill \\ \hfill \underline{I_{GY}}\left(t\right)& =& \underline{f_5};\underline{O_{GY}}\left(t\right)=\underline{e_5}\hfill \\ \hfill \underline{u}\left(t\right)& =& {\left[\begin{array}{cc}\underline{e_1}& \underline{e_2}\end{array}\right]}^T\hfill \end{array}$$

the constitutive relationships of the multiport fields are given by

$$\begin{array}{ccc}\hfill F& =& {\mathbf{L}}_e^{-1}\hfill \end{array}$$

(103)

$$\begin{array}{ccc}\hfill L& =& {\mathbf{R}}_e\hfill \end{array}$$

(104)

$$\begin{array}{ccc}\hfill X_{GY}& =& \mathbf{X}\left(w\mathbf{Le}\right)\hfill \end{array}$$

(105)

where the inductances and resistors is for a balanced system

$$\begin{array}{ccc}\hfill {\mathbf{L}}_e& =& \left[\begin{array}{ccc}{l}_e& 0& 0\\ 0& l_e& 0\\ 0& 0& l_e\end{array}\right]\hfill \\ \hfill {\mathbf{R}}_e& =& \left[\begin{array}{ccc}{r}_e& 0& 0\\ 0& r_e& 0\\ 0& 0& r_e\end{array}\right]\hfill \\ \hfill \mathbf{X}\left(w\mathbf{Le}\right)& =& \left[\begin{array}{ccc}0& -w{l}_e& 0\\ w{l}_e& 0& 0\\ 0& 0& 0\end{array}\right]\hfill \end{array}$$

The multiport junction structure of the multibond graph model is defined by

$$\left[\begin{array}{c}\underline{e_3}\\ \underline{f_5}\\ \underline{f_4}\end{array}\right]=\left[\begin{array}{ccccc}0& -\mathbf{I}& -\mathbf{I}& \mathbf{I}& -\mathbf{I}\\ \mathbf{I}& 0& 0& 0& 0\\ \mathbf{I}& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}\underline{f_3}\\ \underline{e_5}\\ \underline{e_4}\\ \underline{e_1}\\ \underline{e_2}\end{array}\right]$$

(106)

Because there are no elements in derivative causality $\mathbf{E}=\mathbf{I}$. In addition, from (106) ${\mathbf{S}}_{11}^{22}\left(z\right)={\mathbf{S}}_{12}^{21}\left(z\right)={\mathbf{S}}_{21}^{12}\left(z\right)=0$ with (63), (64), (65) and (66),

$$\begin{array}{ccc}\hfill {\mathbf{Q}}_X\left(z\right)& =& {\mathbf{X}}_{GY}\hfill \end{array}$$

(107)

$$\begin{array}{ccc}\hfill {\mathbf{Q}}_L\left(z\right)& =& \mathbf{L}\hfill \end{array}$$

(108)

$$\begin{array}{ccc}\hfill {\mathbf{M}}_X\left(z\right)& =& {\mathbf{X}}_{GY}\hfill \end{array}$$

(109)

$$\begin{array}{ccc}\hfill {\mathbf{M}}_L\left(z\right)& =& \mathbf{L}\hfill \end{array}$$

(110)

From (103) to (105) with (106), the state space of this system in coordinates $\left(d,q,0\right)$ is given by

$$\stackrel{•}{\underline{z}}\left(t\right)={\mathbf{L}}_e^{-1}\left[-{\mathbf{R}}_e-\mathbf{X}\left(w\mathbf{Le}\right)\right]\underline{z}\left(t\right)+{\mathbf{L}}_e^{-1}\left[\underline{e_1}-\underline{e_2}\right]$$

(111)

A developed representation of (111) can be expressed as

$$\left[\begin{array}{c}{\displaystyle \frac{d{f}_3^a\left(t\right)}{dt}}\\ {\displaystyle \frac{d{f}_3^b\left(t\right)}{dt}}\\ {\displaystyle \frac{d{f}_3^c\left(t\right)}{dt}}\end{array}\right]=-\left[\begin{array}{ccc}\frac{R_e}{l_e}& w& 0\\ -w& \frac{R_e}{l_e}& 0\\ 0& 0& \frac{R_e}{l_e}\end{array}\right]\left[\begin{array}{c}{f}_3^a\left(t\right)\\ f_3^b\left(t\right)\\ f_3^c\left(t\right)\end{array}\right]+\left[\begin{array}{ccc}\frac{1}{le}& 0& 0\\ 0& \frac{1}{le}& 0\\ 0& 0& \frac{1}{le}\end{array}\right]\left[\begin{array}{c}{e}_1^a\left(t\right)-e_2^a\left(t\right)\\ e_1^b\left(t\right)-e_2^b\left(t\right)\\ e_1^v\left(t\right)-e_2^v\left(t\right)\end{array}\right]$$

The simulation results shown in this section are based on the 20-Sim software. This software allows the modeling, analysis and simulating systems represented in bond graphs and multibond graphs in a simple and direct way.

For this case study, the system parameters are balanced three-phase voltages $V_1$ and $V_2$ of magnitudes of 200 V and 100 V, respectively; the balanced link impedance of these two voltage sources are with inductances $l_e=0.1$ H and resistances $r_e=5\mathrm{\Omega }$. The behavior of the currents in coordinates $\left(d,q,0\right)$ is shown in Figure 17.

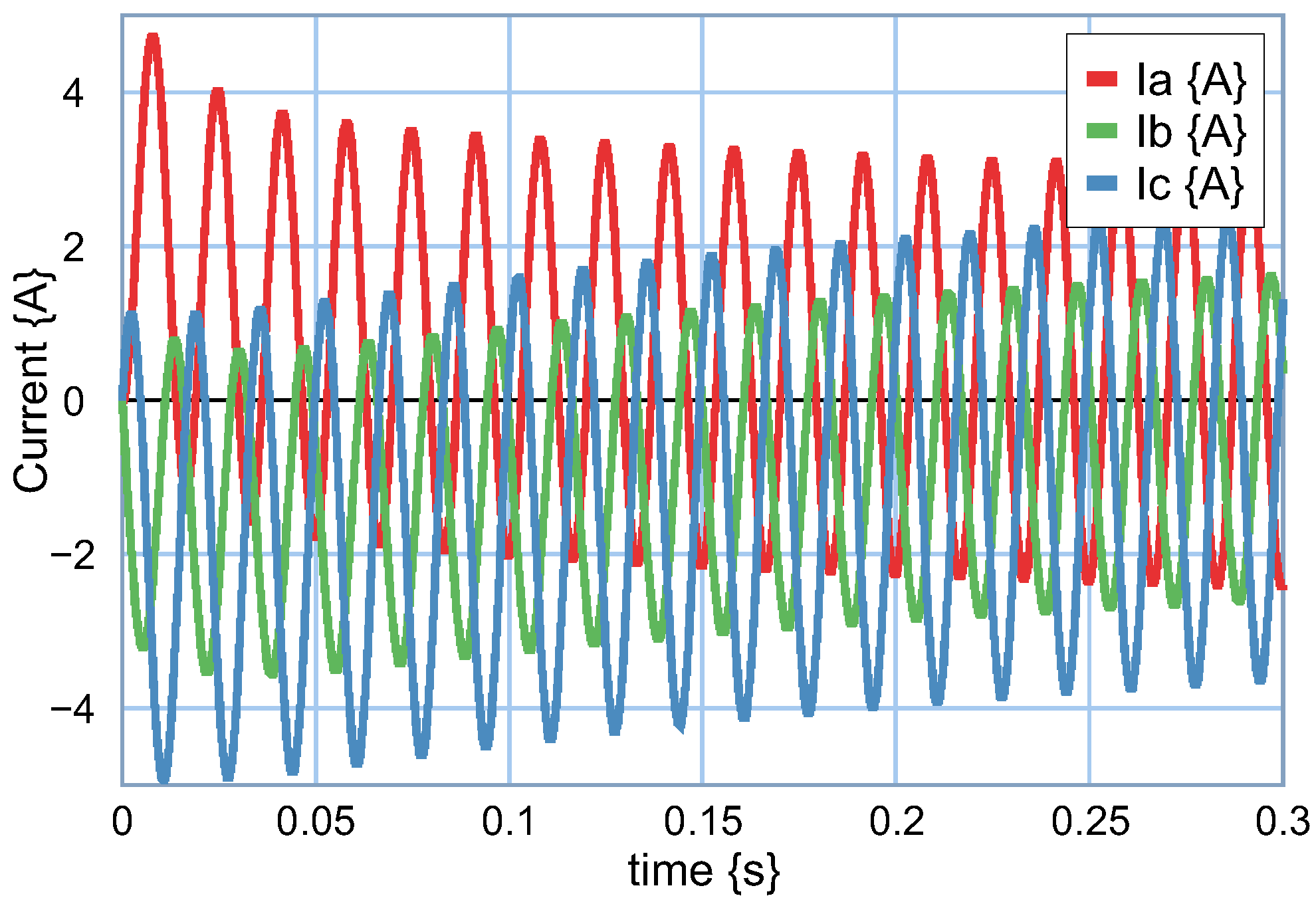
Electrical currents in coordinates $\left(a,b,c\right)$ are shown in Figure 18. It can be noted that the electrical currents in both coordinates are stable after the end of the transient period. The transfer of coordinates $\left(a,b,c\right)$ to $\left(d,q,0\right)$ consists of the use of a modulated transformer with the Park transformation matrix which, in multibond graph, is simple and direct.

The transient response in coordinates $\left(d,q,0\right)$ is illustrated in a clear and evident way due to its characteristic invariance in time, unlike the transient response in coordinates $\left(a,b,c\right)$ that could have relative confusion due to the time variance for balanced systems.

This basic electrical power system can be analyzed under unbalanced conditions for the impedance of the line linking the two supply voltage sources; in this way, the new parameters are given by

$${\mathbf{L}}_e=\left[\begin{array}{ccc}0.1& 0& 0\\ 0& 0.11& 0\\ 0& 0& 0.098\end{array}\right]$$

The behaviors of the current in coordinates $\left(d,q,0\right)$ and $\left(a.b,c\right)$ are illustrated in Figure 19 and Figure 20, showing the flexibility of multibond graphs for modeling and simulating systems in one coordinate or another under balanced or unbalanced conditions.

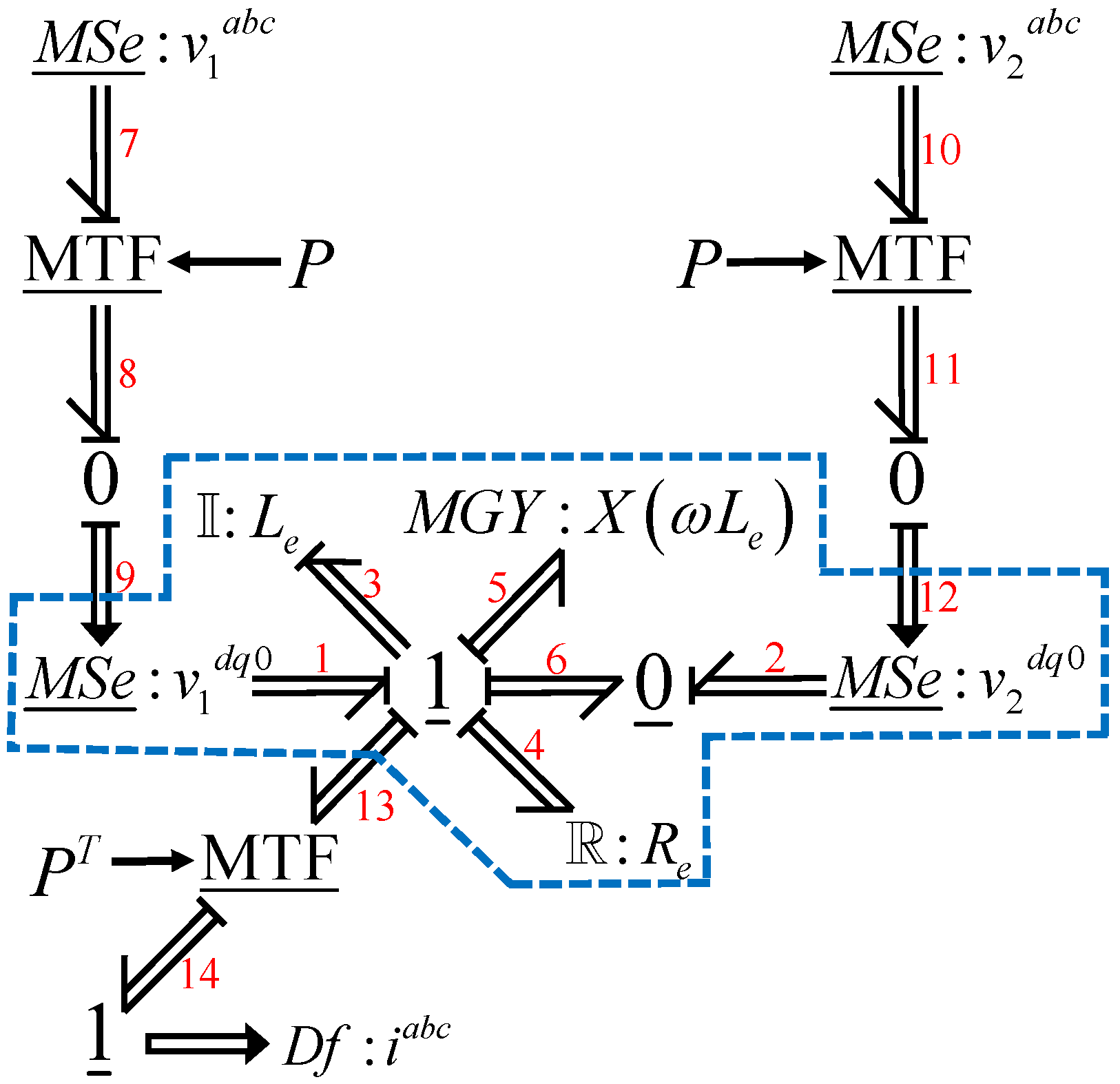
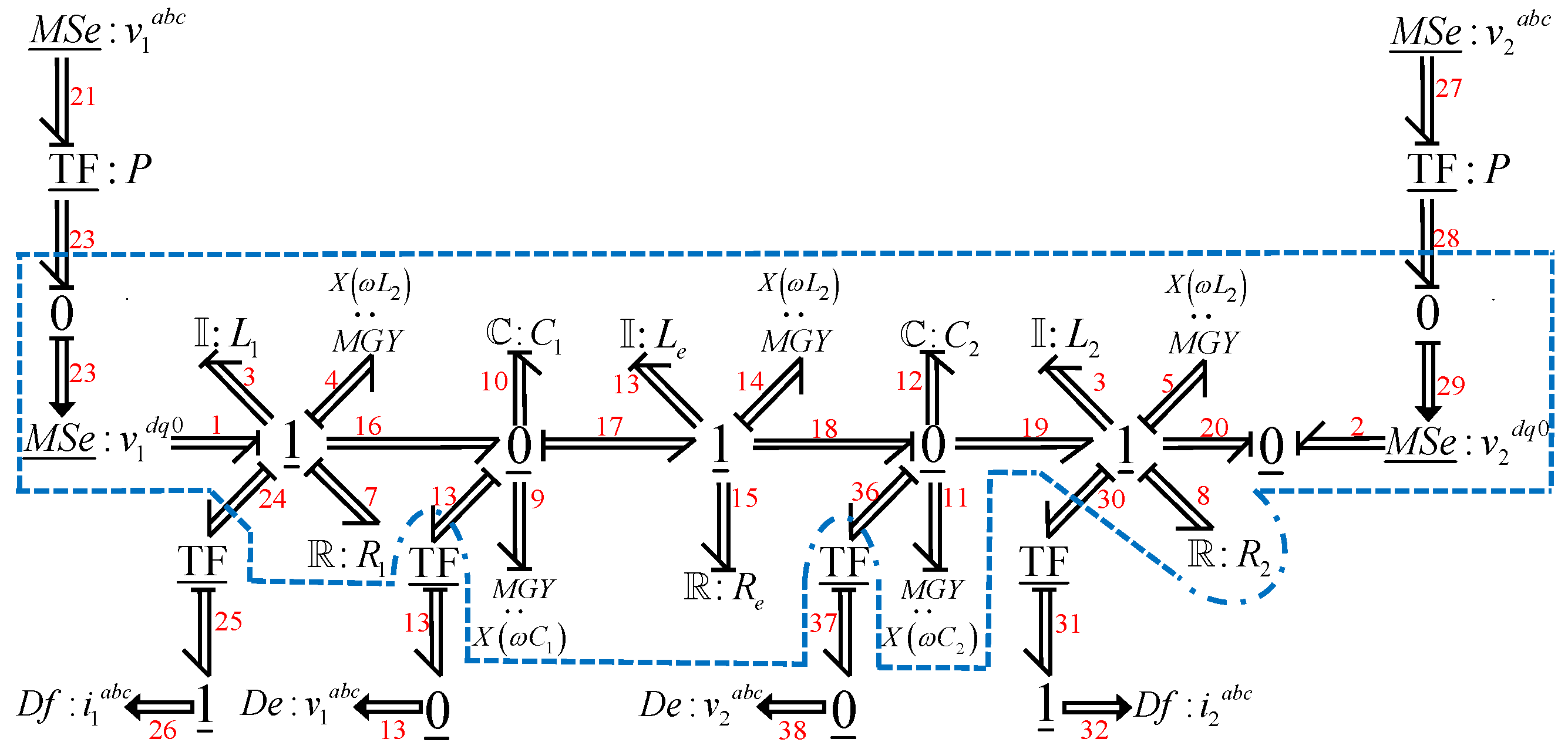
2. A second case study in the modeling of three-phase electrical systems is the one shown in Figure 1 whose multibond graph is illustrated in Figure 21.

The elements of the multibond graph that are inside the dotted box are defined in coordinates $\left(d,q,0\right)$ and those that are outside are the elements in coordinates $\left(a,b,c\right)$ that are the supply voltages and the current measurement. Within the blue dotted line, we have the multibond graph model composed of the source $v_1$ connected in series with the three-phase inductance ${\mathbf{L}}_1$, the three-phase resistance ${\mathbf{R}}_1$ and the multiport gyrator; the same is true for branch 2 and for the central branch e in which it is not connected to any source but to the three-phase capacitors ${\mathbf{C}}_1$ and ${\mathbf{C}}_2$.

The key vectors of the multibond graph for the multiport storage elements are

$$\underline{x}\left(t\right)=\left[\begin{array}{c}\underline{p_3}\\ \underline{p_{13}}\\ \underline{p_5}\\ \underline{q_{10}}\\ \underline{q_{12}}\end{array}\right];\stackrel{•}{\underline{x}}\left(t\right)=\left[\begin{array}{c}\underline{e_3}\\ \underline{e_{13}}\\ \underline{e_5}\\ \underline{f_{10}}\\ \underline{f_{12}}\end{array}\right];\underline{z}\left(t\right)=\left[\begin{array}{c}\underline{f_3}\\ \underline{f_{13}}\\ \underline{f_5}\\ \underline{e_{10}}\\ \underline{e_{12}}\end{array}\right]$$

for the multiport resistors

$$\underline{D_{in}}\left(t\right)=\left[\begin{array}{c}\underline{f_7}\\ \underline{f_{15}}\\ \underline{f_8}\end{array}\right];\underline{D_{out}}\left(t\right)=\left[\begin{array}{c}\underline{e_7}\\ \underline{e_{15}}\\ \underline{e_8}\end{array}\right]$$

and for the multiport gyrators and the multiport sources

$$\underline{I_{GY}}\left(t\right)=\left[\begin{array}{c}\underline{f_4}\\ \underline{f_{14}}\\ \underline{f_6}\\ \underline{e_9}\\ \underline{e_{11}}\end{array}\right];\underline{I_{GY}}\left(t\right)=\left[\begin{array}{c}\underline{e_4}\\ \underline{e_{14}}\\ \underline{e_6}\\ \underline{f_9}\\ \underline{f_{11}}\end{array}\right];u\left(t\right)=\left[\begin{array}{c}\underline{e_1}\\ \underline{e_2}\end{array}\right]$$

The constitutive relationships are given by

$$\begin{array}{ccc}\hfill \mathbf{F}& =& diag\left\{{\mathbf{L}}_1^{-1},{\mathbf{L}}_e^{-1},{\mathbf{L}}_2^{-1},{\mathbf{C}}_1^{-1},{\mathbf{C}}_2^{-1}\right\}\hfill \end{array}$$

(112)

$$\begin{array}{ccc}\hfill \mathbf{L}& =& diag\left\{{\mathbf{R}}_1,{\mathbf{R}}_e,{\mathbf{R}}_2\right\}\hfill \end{array}$$

(113)

$$\begin{array}{ccc}\hfill {\mathbf{X}}_{GY}& =& diag\left\{\mathbf{X}\left(w{L}_1\right),\mathbf{X}\left(w{L}_e\right),\mathbf{X}\left(w{L}_2\right),\mathbf{X}\left(w{C}_1\right),\mathbf{X}\left(w{C}_2\right)\right\}\hfill \end{array}$$

(114)

being

$$\begin{array}{ccc}\hfill {\mathbf{L}}_1& =& diag\left\{l_1,l_1,l_1\right\}\hfill \\ \hfill {\mathbf{L}}_2& =& diag\left\{l_2,l_2,l_2\right\}\hfill \\ \hfill {\mathbf{L}}_e& =& diag\left\{l_e,l_e,l_e\right\}\hfill \\ \hfill {\mathbf{C}}_1& =& diag\left\{c_1,c_1,c_1\right\}\hfill \\ \hfill {\mathbf{C}}_2& =& diag\left\{c_2,c_2,c_2\right\}\hfill \\ \hfill {\mathbf{R}}_1& =& diag\left\{r_1,r_1,r_1\right\}\hfill \\ \hfill {\mathbf{R}}_2& =& diag\left\{r_2,r_2,r_2\right\}\hfill \\ \hfill {\mathbf{R}}_e& =& diag\left\{r_e,r_e,r_e\right\}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \mathbf{X}\left(w{L}_1\right)& =& \left[\begin{array}{ccc}0& -w{l}_1& 0\\ w{l}_1& 0& 0\\ 0& 0& 0\end{array}\right]\hfill \\ \hfill \mathbf{X}\left(w{L}_e\right)& =& \left[\begin{array}{ccc}0& -w{l}_e& 0\\ w{l}_e& 0& 0\\ 0& 0& 0\end{array}\right]\hfill \\ \hfill \mathbf{X}\left(w{L}_2\right)& =& \left[\begin{array}{ccc}0& -w{l}_2& 0\\ w{l}_2& 0& 0\\ 0& 0& 0\end{array}\right]\hfill \\ \hfill \mathbf{X}\left(w{C}_1\right)& =& \left[\begin{array}{ccc}0& -w{c}_1& 0\\ w{c}_1& 0& 0\\ 0& 0& 0\end{array}\right]\hfill \\ \hfill \mathbf{X}\left(w{C}_2\right)& =& \left[\begin{array}{ccc}0& -w{c}_2& 0\\ w{c}_2& 0& 0\\ 0& 0& 0\end{array}\right]\hfill \end{array}$$

The corresponding multiport junction structure is defined by

(115)

For this example, the matrices ${\mathbf{S}}_{22}=0$ and ${\mathbf{S}}_{11}^{22}=0$ then ${\mathbf{M}}_L=L$ and ${\mathbf{M}}_X=X_{GY}$, also, ${\mathbf{S}}_{12}^{21}=0$ and ${\mathbf{S}}_{21}^{12}=0$ then ${\mathbf{Q}}_L=L$ and ${\mathbf{Q}}_X=X_{GY}$.

From (112) to (116) with (54) and (55), the state space model of the system is given by

$$\begin{array}{ccc}\hfill \left[\begin{array}{c}{\mathbf{L}}_1\underline{f_3}\left(t\right)\\ {\mathbf{L}}_e\underline{f_{13}}\left(t\right)\\ {\mathbf{L}}_2\underline{f_5}\left(t\right)\\ {\mathbf{C}}_1\underline{e_{10}}\left(t\right)\\ {\mathbf{C}}_2\underline{e_{12}}\left(t\right)\end{array}\right]& =& \left[\begin{array}{ccccc}-{\mathbf{R}}_1-\mathbf{X}\left({\mathbf{wL}}_1\right)& 0& 0& -\mathbf{I}& 0\\ 0& -{\mathbf{R}}_e-\mathbf{X}\left({\mathbf{wL}}_e\right)& 0& \mathbf{I}& -\mathbf{I}\\ 0& 0& -{\mathbf{R}}_2-\mathbf{X}\left({\mathbf{wL}}_2\right)& 0& \mathbf{I}\\ \mathbf{I}& -\mathbf{I}& 0& -\mathbf{X}\left({\mathbf{wC}}_1\right)& 0\\ \mathbf{I}& \mathbf{I}& -\mathbf{I}& 0& \mathbf{X}\left({\mathbf{wC}}_2\right)\end{array}\right]\left[\begin{array}{c}\underline{f_3}\left(t\right)\\ \underline{f_{13}}\left(t\right)\\ \underline{f_5}\left(t\right)\\ \underline{e_{10}}\left(t\right)\\ \underline{e_{12}}\left(t\right)\end{array}\right]\hfill \\ & & +\left[\begin{array}{cc}\mathbf{I}& 0\\ 0& 0\\ 0& -\mathbf{I}\\ 0& 0\\ 0& 0\end{array}\right]\underline{u}\left(t\right)\hfill \end{array}$$

(116)

It can be seen that there is a great advantage to modeling the system with multibond graphs through which the mathematical model is obtained in a compact way. In order to show the effectiveness of the proposed methodology, the simulation results of this system are obtained using the following numerical parameters: balanced three-phase voltages $V_1$ and $V_2$ of magnitudes of 200 V and 100 V, respectively; inductors $l_1=0.1$ H, $l_2=0.15$ H, $l_e=0.3$ H; capacitors $c_1=0.01$ F, $c_2=0.02$ F and resistors $r_1=10\mathrm{\Omega }$, $r_2=5\mathrm{\Omega }$ and $r_e=15\mathrm{\Omega }$.

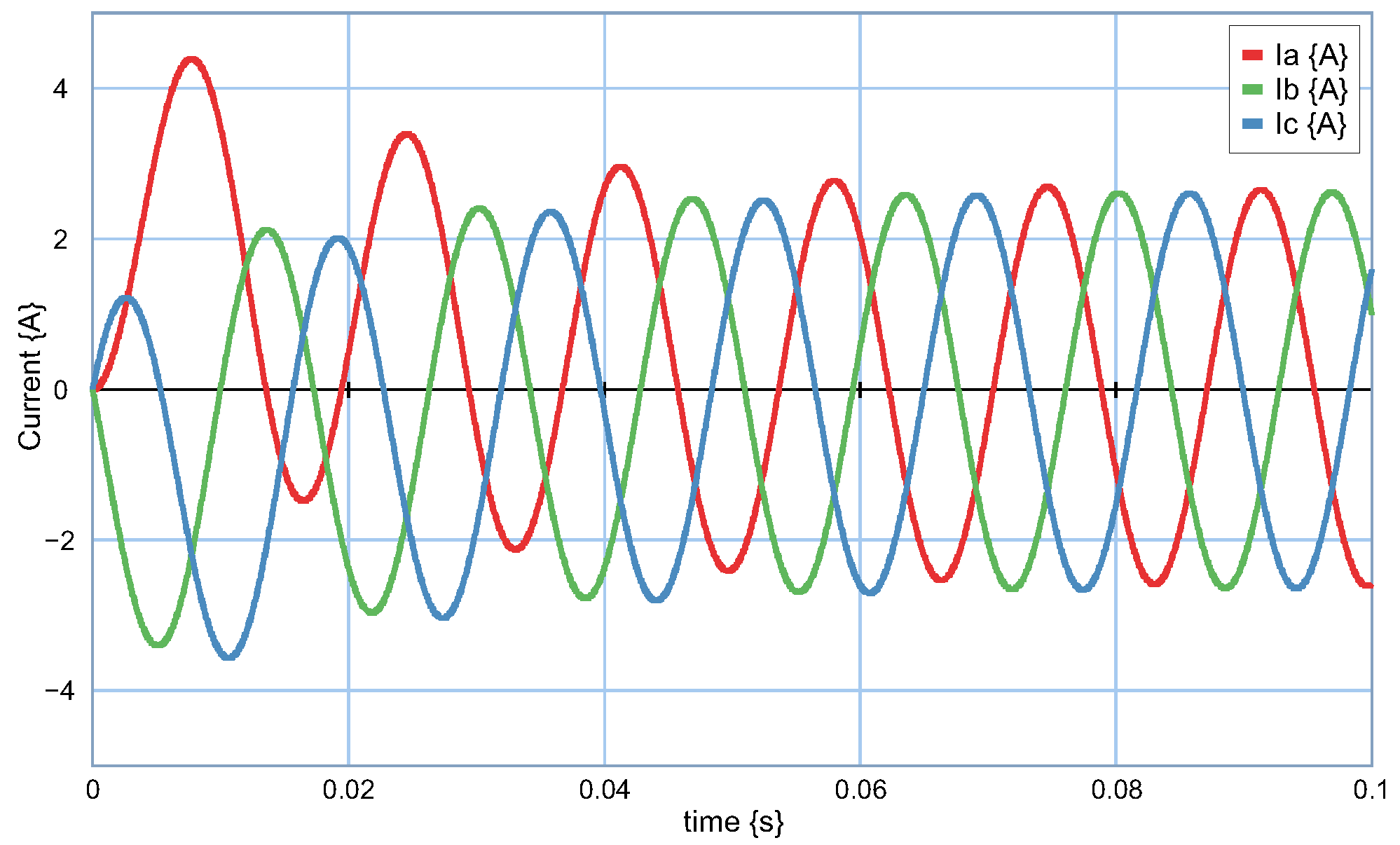
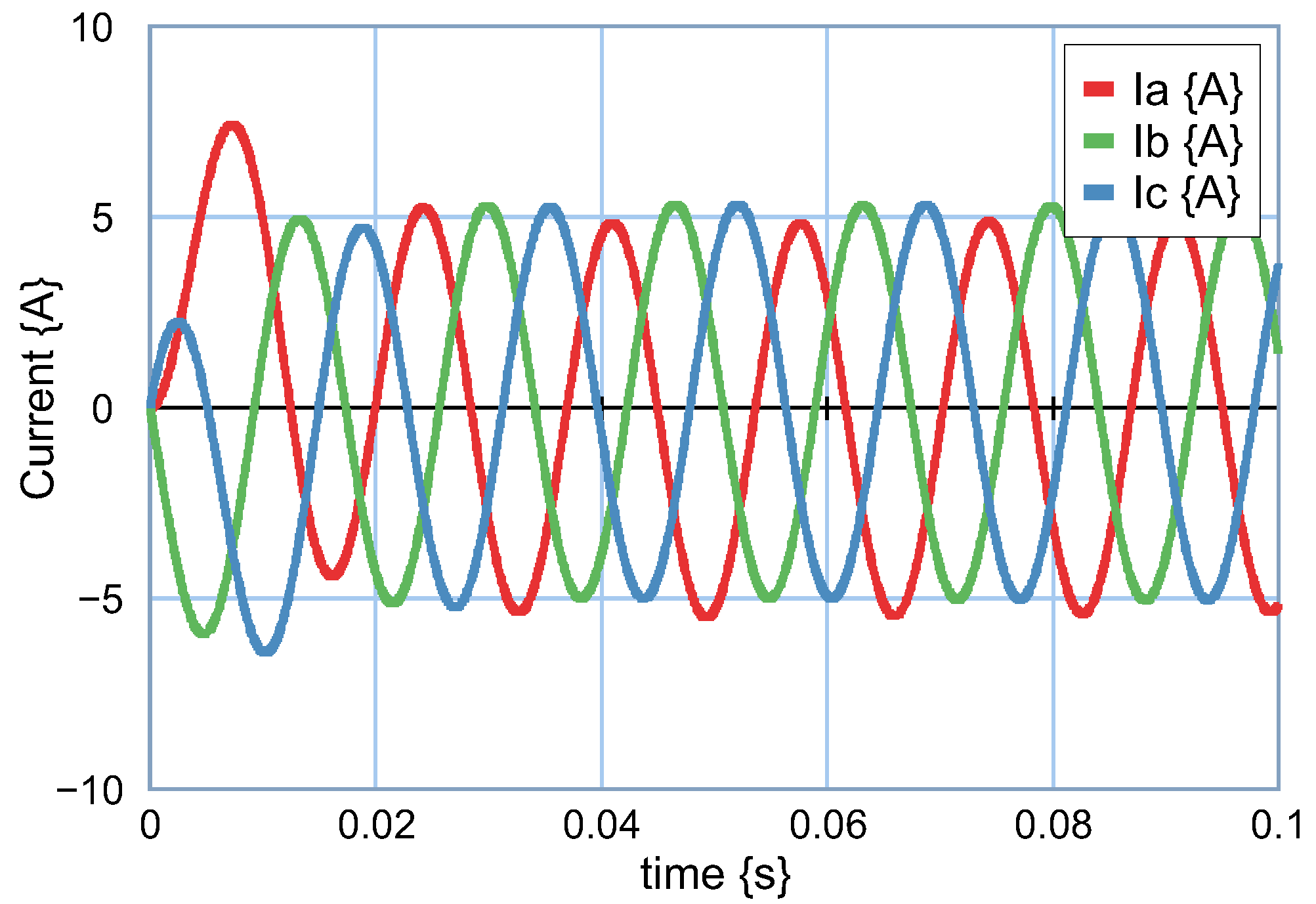
Figure 22 illustrates the behavior of the current in the coordinates $\left(a,b,c\right)$ on the first branch of the resistors ${\mathbf{R}}_1$ and inductors ${\mathbf{L}}_1$. The graphs indicate the behavior of the currents $I_a,$$I_b$ and $I_c$ with respect to time. In this case, the magnitude of the current is due to the voltage $V_1$ and the impedance formed by ${\mathbf{R}}_1$ and ${\mathbf{L}}_1$, and the capacitor ${\mathbf{C}}_1$.

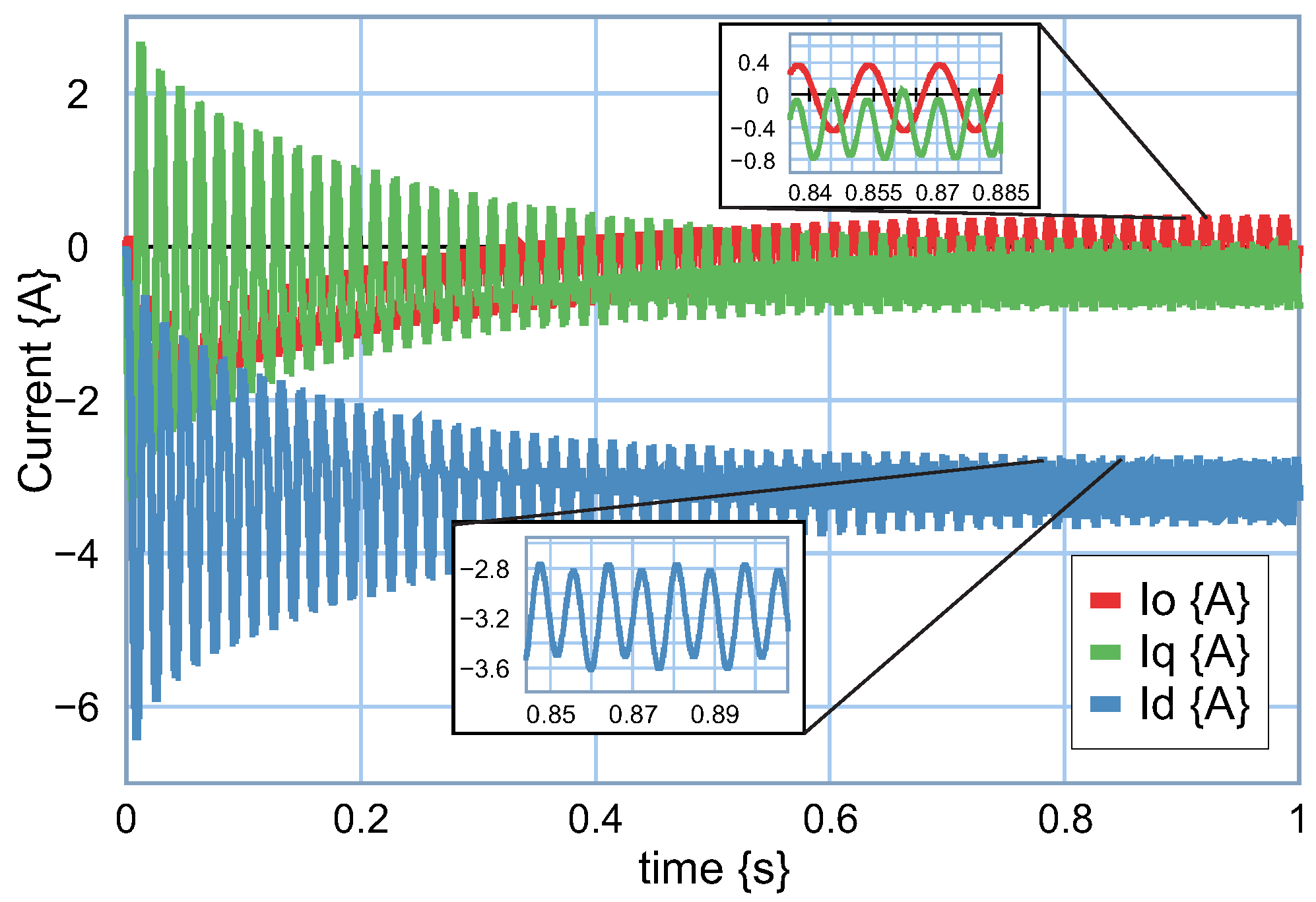
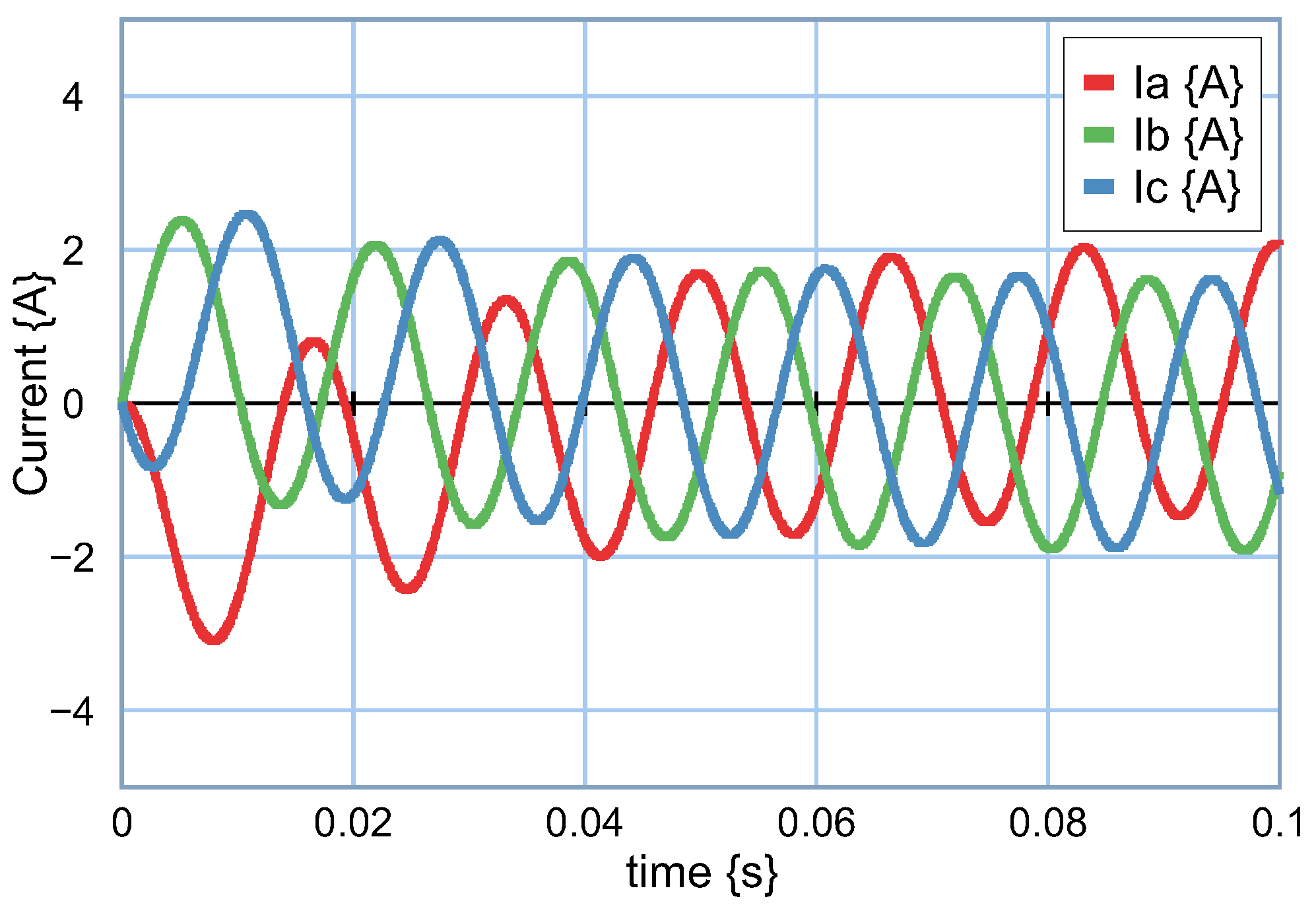
The currents in coordinates $\left(a,b,c\right)$ of the second branch of the elements $R_2$ and $L_2$ are shown in Figure 23, and the currents $I_a$, $I_b$ and $I_c$ with respect to time are shown.

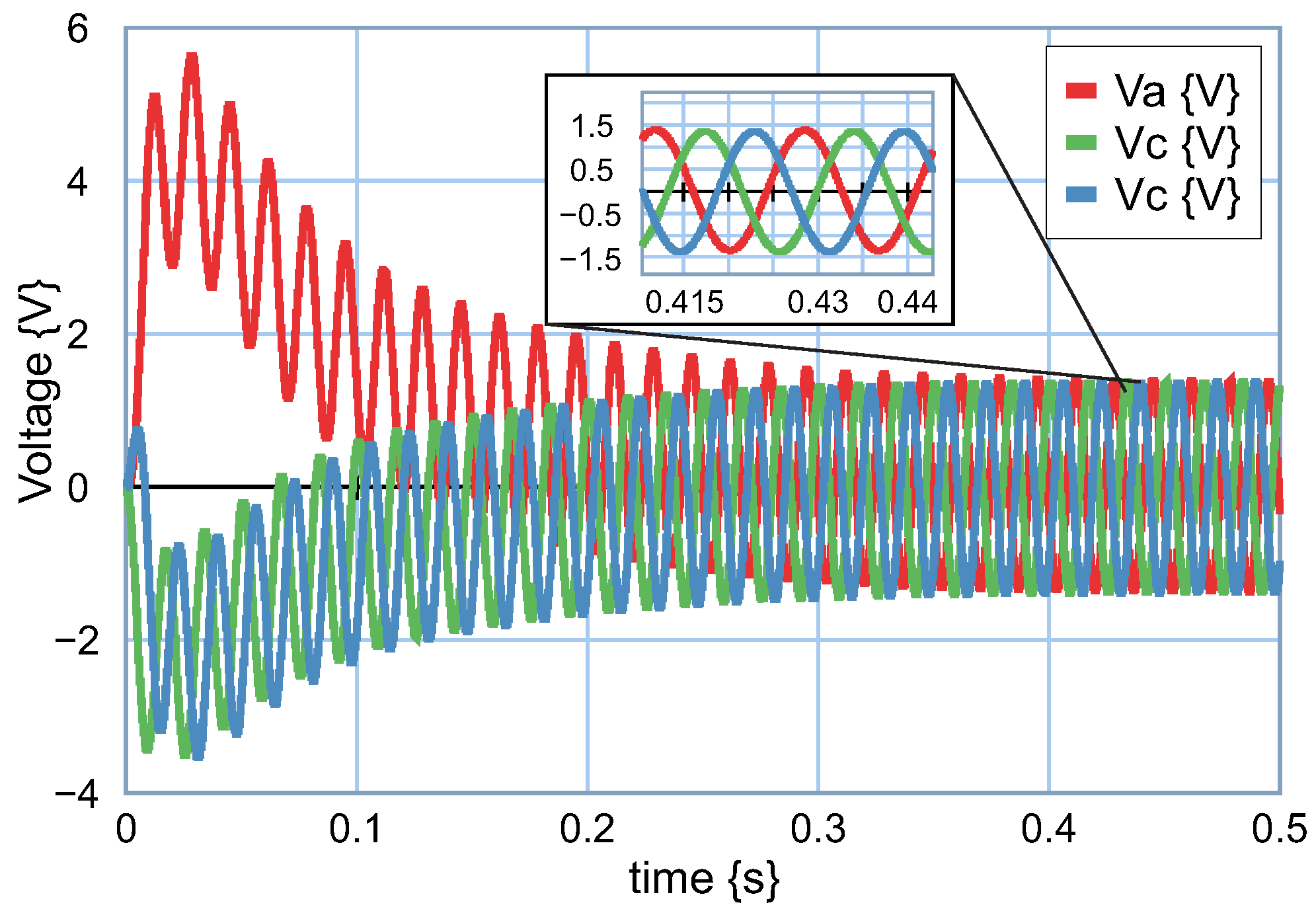
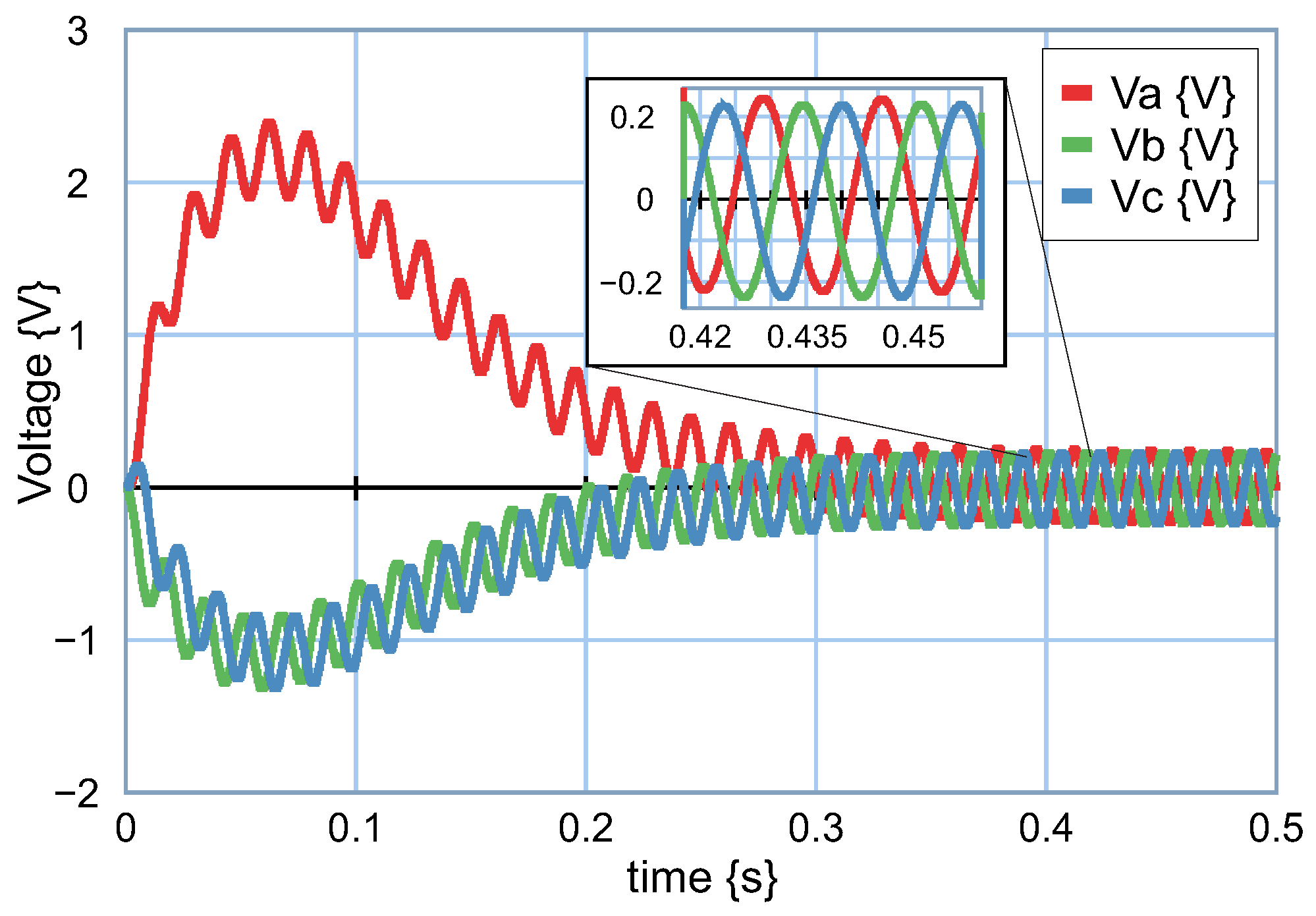
The current in coordinates $\left(a,b,c\right)$ that links the capacitors is shown in Figure 24, and the currents $I_a$, $I_b$ and $I_c$ with respect to time are shown. Furthermore, the magnitude depends on the sources of supply and the capacitances $C_1$ and $C_2$. It can be seen that the currents are stable. The behavior of the capacitor voltages $V_a$, $V_b$ and $V_c$ with respect to time are shown in Figure 25 and Figure 26.

The response in the voltage of $C_1$ indicates that the transient period could represent an unbalanced system; however, in the steady-state period, the response determines a balanced system.

Note that the multibond graph methodology for the modeling and simulation of three-phase electrical systems is presented. Likewise, the application of power electronics to control these systems can be an interesting challenge to extend the results of this paper. Recently, renewable energy sources due to their characteristics require control, and power electronics allows linking this to have control of three-phase systems; as such, this paper can be the beginning of solving this type of control problems.

6. Discussion

This section describes the following comments on multibond graph modeling applied to three-phase electrical systems:

• The traditional approach to modeling three-phase electrical systems consists of obtaining the model in the coordinates $\left(a,b,c\right)$ and applying the Park transformation to determine the model in the coordinates $\left(d,q,0\right)$.
• The approach in bond graph is to build the model according to the properties of the system and with the knowledge of the mathematical model in the coordinates $\left(d,q,0\right)$.
• The approach in multibond graph of this paper is to directly build the model without requiring knowledge of the mathematical model and in a more compact and general way than in bond graphs.
• The multibond graph model of the three-phase electrical system can be for balanced and unbalanced conditions.
• The determination of the model in the coordinates $\left(d,q,0\right)$ with this paper is described through a lemma, allowing to ensure its proper application.
• For very-high-order systems, which depends on the number of elements that store energy, it is not a problem with the approach of this paper, but with other approaches, it can be a complex problem to solve.
• The symbolic determination of the state equation using multibond graphs of the system allows one to analyze stability, controllability and observability as future works.
• The design of controllers of three-phase electrical systems that involve power electronics and that require stages of the closed loop system transformations $\left(a,b,c\right)$ and $\left(d,q,0\right)$ in the multibond graphs approach can be carried out as future works.

7. Conclusions

Multibond graph models of three-phase electrical systems in coordinates $\left(d,q,0\right)$ have been presented. Due to the flexibility of multibond graph modeling, the determination of the signals in coordinates $\left(a,b,c\right)$ can be obtained using multiport transformers modulated with the Park transformation matrix. Starting from an electrical system, the multibond graph associated with this system in coordinates $\left(d,q,0\right)$ using a proposed lemma is obtained. Likewise, the determination of the mathematical model in state space by means of a multibond graph has been proposed. The state equation is expressed in a compact form according to the key vectors in the multibond graph, which allows one to visualize future works in the analysis of three-phase systems in symbolic form and not only through simulations. Therefore, the electromagnetic transients of three-phase electrical systems can be analyzed. Two illustrative examples are modeled and simulated in the multibond graph environment to show the effectiveness of the proposed methodology. A modeled and simulated example is for balanced and unbalanced conditions, which allows one to show the flexibility of the proposal. Furthermore, well-developed methodologies in the analysis and synthesis of bond graph models can be extended to multibond graph models and applied to electrical power systems. Finally, this paper can be the basis for modeling closed-loop electrical systems, which in many cases, involves the Park transformation with the application of power electronics.