Abstract
The process of heavy metals removal by soil washing using chitosan as washing agent is a multivariate problem. According to the experimental data sets obtained during experiments performed at laboratory scale, the main parameters that influenced the efficiency of the soil washing process were the stirring time of the polluted soil with the investigated washing agent, washing solution concentration, and solid/liquid ratio (S/L ratio). This study explores the statistical relationships between the removal efficiency of Cu and Pb from polluted soil by washing with chitosan and factors influencing the soil washing process by use of a non-linear regression model. The non-linear regression model contains a non-linear component and a component of interaction among the two parameters (S/L ratio “X1”, the stirring time “X2”) which influences the efficiency of the Cu and Pb removal from soil by soil washing with the investigated washing agent. The proposed model is useful for predicting and estimating the effectiveness of the soil decontamination process by washing with chitosan. A comparison between the data calculated using the proposed mathematical model and the experimental data was also performed in order to determine the integrity and conformity of the mathematical model obtained. The results showed a good fit of the obtained model to the experimental data.
1. Introduction
Some of the most detrimental soil pollutants are heavy metals. The sorption of heavy metals in soil is an important process governing their availability for uptake by organisms and mobilization out of soil []. Soil contains mineral and organic constituents that carry hydroxyl and carboxylic surface functional groups. The acid–base characteristics of these functional groups contribute to the formation of a surface charge that plays an important role in the retention of heavy metals []. For example, in the case of organic constituents of the soil represented by humic substances, high pH values can cause the deprotonation of humic-carboxylic-COOH groups, becoming negatively charged moieties and thus attracting the positively charged heavy metal ions and protons []. The interaction of heavy metals with soil particles is controlled by reactions on the surfaces of soil minerals and organic matter, i.e., adsorption as outer- and inner-sphere complexes and surface precipitation [], which depend on soil pH, soil sorption capacity, organic matter content, the particle size distribution of the soil, the age of contamination, and the presence of different inorganic contaminants in soil []. There has been increasing concern about the potential toxic effects of heavy metals in the soil. Heavy metals affect soil fertility and thus crop productivity and exert toxic effects on soil microorganism, hence resulting in the change of the soil structure [], diversity, population size, and overall activity of the soil microbial communities [,]. For example, elevated concentrations of Pb in soils may decrease soil productivity, and a very low Pb concentration can inhibit some vital plant processes like photosynthesis, mitosis, and water absorption, producing toxic symptoms as dark green leaves, wilting of older leaves, and brown, short leaves or roots []. Therefore, depending on the concentration, heavy metals can be valuable and beneficial to crops. Crop productivity is linked to the aggregation of the soil. Low crop productivity was observed in low-aggregated soils while higher crop production was noted in well-aggregated soils. Soil aggregation is influenced by the level of heavy metal concentrations present in the soil. It is well known that heavy metals cations make strong bonds with fine clay and soil organic particles. Consequently, the presence of heavy metals that interacted with clay particles affects the aggregation and soil structure, leading to a modification of the hydraulic parameters of the soil [].
On the other hand, heavy metals are persistent, difficult to transform, and cannot be biodegraded [,], leading to their accumulation in living organisms and posing an important threat to human health [,,,].
The surge of industrial activity has intensified soil pollution with heavy metals. Elevated levels of heavy metals were reported in many industrial areas. For example, 231 mgkg−1 Pb, 0.80 mgkg−1 Cd, 335 mgkg−1 Zn, 24 mgkg−1 Cu, 16 mgkg−1 As, 1.1 mgkg−1 Fe, and 669 mgkg−1 Mn were found in soil near the Cabezo Rajao abandoned mine (Spain) []. Extremely elevated contents of metals were also found in Greece near Lavrion Technology and Cultural Park mining and metallurgy complex: 64,195 mgkg−1 Pb, 7540 mgkg−1 As, 4100 mgkg−1 Cu, 55,900 mgkg−1 Zn, and 6500 mgkg−1 Mn [].
For this reasons, various technologies have been developed, tested, and investigated in past decades for the remediation of heavy metal-contaminated soils, e.g., solidification/stabilization [], soil washing [], soil amendment [], phytoremediation [,], and electrokinetic methods []. Among these, soil washing, which involves the extraction of heavy metals by chemical solutions, is one of the few effective, non-time-consuming, and relatively inexpensive treatment technologies for the decontamination of severely heavy metal-polluted soils [,,].
In spite of the fact that various studies have demonstrated the efficiency of using different washing agents (e.g., HCl, H2SO4, HNO3, oxalic acid, citric acid, saponin, ethylenediaminetetraacetic acid-EDTA, nitrilotriacetate, and ethylenediaminedisuccinic acid), adverse effects may result from their use or toxicity, such as the release of additional contaminants into the environment and changes in soil pH, soil structure, soil productivity, soil microorganism activity, or soil microbial heath [,,,,,,].
The key point in the development of remediation technology for heavy metal-contaminated soil is identifying a washing reagent with a high pollutant removal rate, low toxicity, low damage to soil properties [], low cost, and high biodegradability [].
Therefore, for the washing of soils contaminated with heavy metals, it might be attractive to use natural materials that do not pose a secondary risk to the environment.
In this regard, chitosan, which is a common and biodegradable chelating polymer composed of randomly distributed β-(1-4)-linked D-glucosamine (deacetylated unit) and N-acetyl-D-glucosamine (acetylated unit) and which is made by treating shrimp and other crustacean shells from the food processing industry with the alkali sodium hydroxide [], may have the potential of becoming an extracting agent in soil washing technology.
Chitosan contains hydroxyl and amine functional groups which can react with various heavy metal ions [,]. However, the efficiency of heavy metals’ removal by soil washing using chitosan as a washing agent is influenced not only by the interaction between heavy metals and the functional groups of chitosan, but also by other factors affecting the decontamination process, such as the liquid/solid ratio, the concentration of washing solution in chitosan, the duration of soil washing, the pH of the washing solution, the type of pollutants present in the soil, etc. [,,]. Chitosan is an effective adsorbent for the removal of heavy metals from various media []. The maximum adsorption capacity was reported at a pH of 5.0 and 6.0 [] with a removal efficiency of 93.76% [] and 100%, respectively [].
For example, Moutsatsou et al. [] pointed out that Zn, Cu, and Pb were extracted from soil in a higher rate after 4 h of washing with HCl, while As and Fe were better extracted after 8 h. Besides this, all of the studied heavy metals were extracted better from soil at a HCl concentration of 6 molL−1, while As and Cu were extracted better at a HCl concentration of 2 molL−1 and 3 molL−1, respectively []. Also, the removal of Cu and Ni from the soil increased with increasing concentrations of chitosan in the washing solution from 0.10 to 0.40 gL−1 []. Moreover, with the increase of the liquid/solid ratio from 5 to 20, the removal efficiency of Cu increased from 26.34% to 47.22%, while the removal efficiency of Ni increased from 41.75% to 66.13% when the soil was washed with chitosan []. Abumaizar and Khan [] found that the extraction of Pb from millpond sludge did not seem to increase significantly beyond the 0.05 M EDTA concentration, being observed a decrease beyond the 0.10 M EDTA.
Consequently, the elaboration of a mathematical model is essential in order to predict and estimate the effectiveness of the soil decontamination process by soil washing depending on the variables affecting this process. Regression analysis is a widely used statistical technique for modelling the relationships between variables []. Moreover, to our knowledge, so far, no prediction models can be found in the literature for the estimation of the effectiveness of the soil decontamination process using washing with chitosan.
Therefore, the aim of the present paper was to develop a mathematical model for predicting the effectiveness of the soil decontamination process by washing with chitosan depending on the studied variables affecting this process: the stirring time of the polluted soil with the investigated washing agent, washing solution concentration and solid/liquid ratio (S/L ratio). The model was based on the results obtained in a laboratory test regarding the efficacy of using commercial chitosan to extract copper and lead from heavy metal-contaminated soil collected from the abandoned mining perimeter of “Larga de Sus” from Zlatna (Alba County, Romania). During laboratory investigations, a series of soil washing experiments were performed in order to determine the effects of stirring time, washing solution concentration, and solid/liquid ratio (S/L ratio) in decimal fractions (dec. fr.) on the extraction yield of copper and lead. The purpose of the proposed mathematical model was to show the correct layout of the interdependence among the variables of the process with the scope of helping in the estimation, based on the investigated parameters, of the effectiveness of the soil decontamination process by washing with chitosan. Also, the mathematical model can be used as a tool for modelling Cu and Pb removal by soil washing with the studied washing agent.
2. Materials and Methods
2.1. Soil Washing Experiments Using Chitosan
For the laboratory washing experiment using chitosan, a soil sample from 10–90 cm depth was collected from a pasture located about 800 m downstream of the “Larga de Sus” abandoned mining perimeter (GPS coordinates: 46°07′55.2″ N, 23°09′09.2″ E) from Zlatna (Alba County, Romania). The physicochemical properties of the soil sample used in the washing experiments can be found in our previously published studies [,].
The soil washing experiments were performed in order to determine the factors affecting the decontamination efficiency of the collected soil sample using chitosan as washing agent.
A commercial chitosan sample extracted from shrimp shells was investigated as a potential extracting agent for Cu and Pb found in the collected soil. In soil washing experiments, the investigated washing agent was used its natural state and mixed with distilled water.
The decontamination experiments were conducted at laboratory scale on 5 g polluted soil samples in a 100 mL capacity glass flasks in a stirrer with continuous orbital rotation-oscillation stirring at 100 oscillations/min, at different washing solution concentrations (2% and 5%), S/L ratios (0.2; 0.125; 0.1 and 0.0625 dec. fr.) and durations of stirring (0–40 h).
The concentration of copper and lead in the soil before and after washing with chitosan was determined by atomic adsorption spectrometry (AAS). Prior to the AAS analysis, the polluted and decontaminated soil samples were processed as follows: dried at 95 °C for about 10 h, homogenized, crumbled, and milled to pass through a 250 μm sieve. After that, 3 g of previously processed sample, 1 mL of distilled water, 21 mL of concentrated HCl (Hydrochloric Acid), and 7 mL of concentrated HNO3 (Nitric Acid) were combined in a 100 mL glass flask which was heated in a sand bath for about 2 h. The mixture was then filtered through a 0.45 μm pore size filter into a 100 mL volumetric flask, filled to the mark with distilled water, and analysed for Cu and Pb concentration through AAS.
The removal efficiency of Cu and Pb (ƞ) from the collected heavy metal-contaminated soil was determined using the following equation []:
where me is the extracted pollutant concentration (mgkg−1) and mi is the initial pollutant concentration present in the soil (mgkg−1).
The experimental data obtained according to the above methodology which served to develop the mathematical models are presented in Table 1 and Table 2.

Table 1.
Experimental data obtained during soil washing experiments using 2% chitosan solution and used in the elaboration of the mathematical models.

Table 2.
Experimental data obtained during soil washing experiments using a 5% chitosan solution and used in the elaboration of the mathematical models.
All of the experiments and analyses were performed in duplicate at 25 °C, and the average values were used to develop the mathematical model. All reagents were of analytical grade or ultra-pure. The water was distilled using a Technosklo water distiller.
2.2. Data Set and Non-Linear Mathematical Model
The minimization of the differences between the values determined experimentally for the performance of the process and those calculated using the mathematical model is represented by the principle of analysis of linear regression (the method of least squares) and the method of designing statistical mathematical models [].
More precisely, in the most complex situation within this research (the one describing the variation of the removal efficiency of Cu and Pb from soil)—for the quantification of the dependence between the removal efficiency value and the two process parameters—we opted for a nonlinear mathematical model with two variables: stirring time (X2) and S/L ratios (X1). The form of the model is given by Equation (2):
where Y is the removal efficiency of heavy metals from soil (%), X1 is the S/L ratios (in decimal fractions), X2 is the stirring time (in hours), and b0, b1, b2, b12, b11, and b22 are the coefficients of the mathematical model.
In order to determine the values of the b coefficients, the method of least squares was used [] which starts from the premise that for a mathematical equation to be considered as a mathematical model of any process, it is necessary that the differences between the performance values calculated using the mathematical model, , and the values of the same performance experimentally measured, , in a number of “n” points (i = 1 … n) be as small as possible. In other words, the value of the so-called concordance dispersion —defined as the arithmetic average of the square values of the deviations of the values calculated using the mathematical model and the ones experimentally measured in all the “n” points of the experiment—must be minimal:
where n is the number of determinations or the number of values given to the variables of the process, and m is the number of variables of the model.
From a mathematical point of view, finding the minimum point for a given relation implies its derivation and equalizing the value of the first-order derivative with zero, according to the following equation:
where b0 … bk are the coefficients of Equation (2), their values being able to be determined by means of the system of “k” equations with “k” unknowns which is formed in (5), mathematically expressed as follows:
By particularizing this system of equations [] for the analyzed case, a system of 6 equations with 6 unknowns (b0, b1, b2, b12, b11 and b22) results having the following mathematical form:
This system allowed for the determination of statistical mathematical models that link the efficiency of lead and copper removal from the soil by two factors that influence the efficiency of the soil washing process: stirring time and S/L ratio. Models were developed in two variants corresponding to the two investigated concentrations of the washing solution—2% and 5% chitosan content.
3. Results and Discussions
The mathematical equations describing the evolution of the washing process using chitosan solution, which were obtained as a result of the proposed algorithm, are shown in Table 3 as a function of the metal removed from the soil and the two concentrations of the chitosan-containing washing solutions that were investigated: 2% and 5%, respectively. For each mathematical model, the values of the R-squared (R2) and adjusted R-squared coefficients (R2adj) were calculated and included in Table 3.

Table 3.
Mathematical relationships that describe the evolution of the depollution process by washing the soil with chitosan solution.
By analyzing the four equations of the second-degree polynomial mathematical models, it can be observed that the coefficients of the X22 variables have very small values. Therefore, in order to simplify the models, they can be considered as equal to zero. In this case, the b22X22 terms will disappear from the model equations. This approach is also supported by the fact that when the adjusted R-squared coefficients (R2adj) were calculated for the new models (in which the X22 terms no longer appear), the values of these coefficients compared to the initial ones indicate that the influence of the X22 terms was insignificant. This is because the new coefficients R2adj have higher values than the initial ones.
The graphical representation of the obtained mathematical relationships that describe the evolution of the washing process using chitosan solution are indicated in Figure 1 and Figure 2.
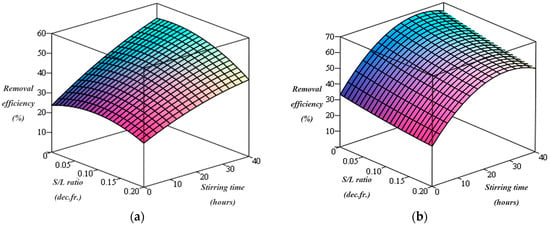
Figure 1.
Cu removal efficiency using chitosan for (a) C = 2% and (b) C = 5%.
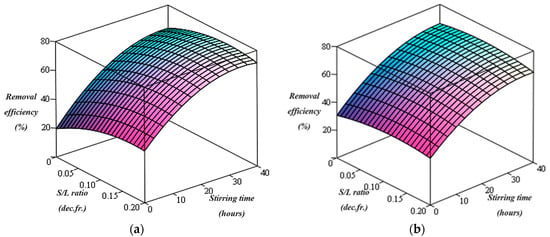
Figure 2.
Pb removal efficiency using chitosan for (a) C = 2% and (b) C = 5%.
Thus, the graphical representation of the dependence of copper removal efficiency on the two variables of the washing process (stirring time and S/L ratios) indicates that the efficiency of copper removal from the soil gradually increases with an increase of the stirring time of the contaminated soil with washing solution containing chitosan (Figure 1). By increasing the chitosan concentration in washing solution from 2% to 5%, a great improvement of the copper removal efficiency could be observed, in agreement with experimental data and the results reported by other researchers []. A previously published work [] reported that high concentrations of washing solution containing chitosan or other chelating agents could provide more binding sites for metals, resulting in an increase in the efficiency of heavy metal removal from the soil.
Furthermore, the highest copper removal efficiencies (52.51% and 62.59% in the case of the 2% and 5% washing solution concentrations, respectively) are obtained at a S/L ratio of 0.0625 dec.fr. Therefore, the removal efficiency of copper increases as the stirring time of the contaminated soil as the washing solution containing 2% chitosan increases, and the S/L ratio decreases from 0.2 to 0.0625 dec.fr. as well as with increase the concentration of the washing solution in chitosan from 2% to 5%.
The graphical representation of the dependence of lead removal efficiency on the two variables of the washing process (stirring time and S/L ratios) obtained from the determined mathematical relations is illustrated in Figure 2a,b in the cases of using 2% and 5% chitosan washing solution, respectively.
The lead removal efficiency gradually increases as the stirring time of the contaminated soil with the chitosan-containing washing solution increases. Also, the highest lead removal efficiency (73.82%) was obtained at a S/L ratio of 0.125 dec.fr. in the case of using 2% chitosan washing solution. Increasing the chitosan content in the washing solution from 2% to 5% and increasing the S/L ratio from 0.0625 to 0.2 (dec.fr) did not significantly improve the lead removal efficiency during the stirring time (Figure 2).
Analyzing the link between the performance of the washing process (the removal efficiency after the removal of lead and copper from the soil by washing with chitosan solution) and the process parameters of S/L ratio (X1) and stirring time (X2)—as shown in the experimental values obtained—an exponential dependency is revealed in which the removal efficiency rapidly increases in the first time intervals, after which the removal phenomena is considerably subdued. This exponential fluctuation means that the widely used linear regression method [,] cannot be used in the case of this paper. For a better approximation of the real phenomena, it was necessary to use a non-linear equation of the mathematical model. In order to determine the coefficients, this equation was corrected to a linear one, first through variable changes [] and afterward using the method of linear regression. The developed mathematical model is in agreement with the results obtained by Lu et al. (2022) [] and Hou et al. (2019) [] that highlight the ability of mathematical models to significantly reduce experiment workload by predicting the removal efficiency according to several parameters [], such as pH, the initial metal concentration [], solid–liquid ratio, and washing time [].
Therefore, the removal efficiency of Cu reaches 55.09% after 6 h of stirring the contaminated soil with the washing solution containing chitosan in a concentration of 5% and at a S/L ratio of 0.0625 dec. r. As can be seen from Figure 1b, extending the stirring time from 6 to 40 h did not affect the removal efficiency significantly, and the removal efficiency of Cu after 40 h of stirring only increased by 18.4% as compared to the value obtained after 6 h of stirring (S/L ratio of 0.0625 dec.fr. and a concentration of 5% chitosan). Considering the economy of the washing process, the optimal stirring time was 6 h in the case of Cu. Higher Cu removal efficiencies at shorter stirring times were also reported by other authors []. It was suggested that the process of extracting heavy metal from the soil using washing with chelating agents included two step adsorptions, in which a rapid desorption within the first hours was followed by a subsequent gradual release that occurred over the following hours [].
In order to verify the integrity and conformity of the mathematical model obtained (Table 3), a comparison was performed between the data calculated using the proposed mathematical model and real experimental data obtained in the laboratory. The comparison is illustrated in Figure 3 and Figure 4. The accuracy of the obtained mathematical models was tested by calculating the concordance dispersion between the experimentally obtained values and those calculated based on the models. The calculated values of the concordance dispersion indicate a good agreement between the developed models and the real process they describe. Moreover, higher values of the R2 coefficients were obtained from the experiments regarding the removal of lead as compared to those obtained from experiments regarding the removal of copper (Table 3), indicating a better agreement between the models and the real phenomenon. This fact can also be observed from the Figure 3 and Figure 4.
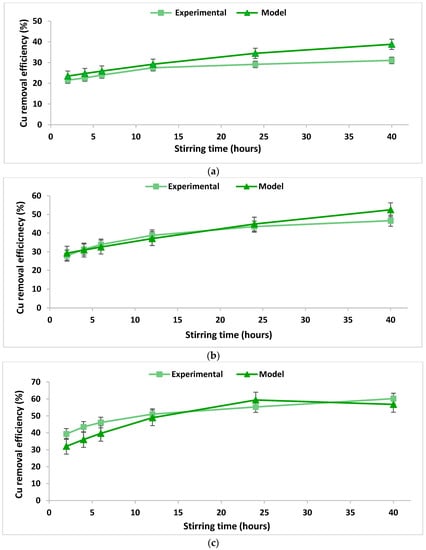
Figure 3.
Copper removal efficiency over the stirring time using 2% chitosan washing solution at a S/L ratio of (a) 0.2 dec.fr. and (b) 0.0625 dec.fr.; copper removal efficiency over the stirring time using 5% chitosan washing solution at a S/L ratio of (c) 0.125 dec.fr.
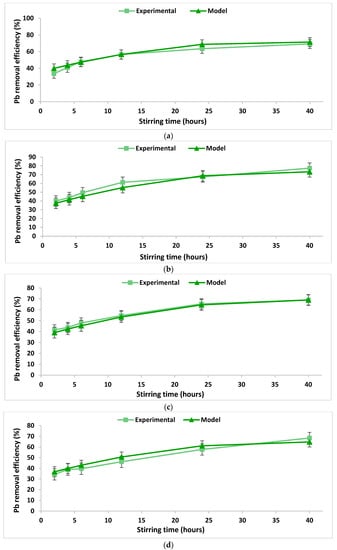
Figure 4.
Lead removal efficiency over the stirring time using 2% chitosan washing solution at a S/L ratio of (a) 0.2 dec.fr. and (b) a S/L ratio of 0.1 dec.fr.; lead removal efficiency over the stirring time using 5% chitosan washing solution at a S/L ratio of (c) 0.1 dec.fr. and (d) 0.2 dec.fr.
The Cu removal efficiency increased with the increase of the chitosan concentration in the washing solution. Thus, in the case of using 2% chitosan solution, 31% to 46% of Cu was removed from the soil, while 39% to 60% Cu was removed when 5% chitosan solution was used. Similar results were obtained by Jiang et al. (2011) [].
By comparing the Cu extraction yields using chitosan obtained in the present research (21.08–74.57%) with the ones obtained in the case of using other washing agents, similar results were reported in the case of using dissolved organic matter (57%) [] and 0.1 N HCl (57.9%) []. Better removal efficiencies of Cu were reported in the case of using soluble humic substances (51–95%) [,,], Ethylenediaminetetraacetic acid (82.5%), and FeCl3 (95.8%) []. By using a chitosan-based washing agent, the Pb removal efficiency reached values between 25.59% and 79.65%. Similar results were reported when soluble humic substances were used (44.8–47.6%) [,,], while higher removal efficiencies were obtained when soluble humic-like substances (86.5–98%) [], FeCl3 (98.7%) [], and Ethylenediaminetetraacetic acid (97.4–99.4%) [] were used. Also, chitosan-based washing agents showed better extraction efficiencies as compared to those obtained when using 0.1 N HCl (28.5%) [].
The mathematical model of the soil washing is valid for all of the studied parameters influencing the washing process (S/L ratio and stirring time). The results of the comparison between the values obtained through the proposed mathematical model and the ones experimentally determined present a good concordance, indicating the integrity of the obtained mathematical relations and the degree of accuracy with which they describe the real experimental conditions.
4. Conclusions
The obtained non-linear regression model allows for the estimation of the efficiency of copper and lead removal from the soil using chitosan as a washing agent and depending on the main variables affecting the washing process (S/L ratio and stirring time), and it can successfully be used to predict and estimate the effectiveness of the decontamination process at certain stirring times and various S/L ratios and concentrations of chitosan in the washing solution.
The mathematical model developed describes with high accuracy the real process of soil depollution by washing with chitosan-containing solution. The results indicated the existence of a good concordance between the experimental data and data calculated using the mathematical model.
However, heavy metal removal through soil washing using chitosan is site-specific and depends upon the physicochemical properties of the soil. Among other variables like initial heavy metal concentration, organic matter content, particle size distribution, etc., the suitability of the current method may be limited by the pH of the studied soil, which influences the charge of the aminic group from the chitosan structure involved in the metal complexation by chitosan. Therefore, the applied decontamination method needs to be tested with different soil types in order to draw conclusions regarding the effectiveness of the current method on various soil types.
Author Contributions
Conceptualization, V.M., G.C.R. and G.E.D.; investigation, G.C.R., G.E.D. and I.M.S.; methodology, G.C.R. and G.E.D.; resources, V.M. and I.M.S.; visualization, V.M., G.C.R., G.E.D. and I.M.S.; writing—original draft preparation, G.C.R. and G.E.D.; writing—review and editing, I.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Strawn, D.G. Sorption Mechanisms of Chemicals in Soils. Soil Syst. 2021, 5, 13. [Google Scholar] [CrossRef]
- Mohanty, B.; Mahindrakar, A.B. Removal of heavy metal by screening followed by soil washing from contaminated soil. Int. J. Technol. Eng. Syst. 2011, 2, 290–293. [Google Scholar]
- Bahemmat, M.; Farahbakhsh, M.; Kianirad, M. Humic substances-enhanced electroremediation of heavy metals contaminated soil. J. Hazard. Mater. 2016, 312, 307–318. [Google Scholar] [CrossRef] [PubMed]
- Moutsatsou, A.; Gregou, M.; Matsas, D.; Protonotarios, V. Washing as a remediation technology applicable in soils heavily polluted by mining metallurgical activities. Chemosphere 2006, 63, 1632–1640. [Google Scholar] [CrossRef] [PubMed]
- Nartowska, E.; Kozłowski, T.; Gawdzik, J. Assessment of the influence of copper and zinc on the microstructural parameters and hydraulic conductivity of bentonites on the basis of SEM tests. Heliyon 2019, 5, e02142. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Li, R.; Peng, S.; Liu, Q.; Zhu, X. Effect of humic acid on transformation of soil heavy metals. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017. [Google Scholar] [CrossRef]
- Ashraf, R.; Ali, T.A. Effect of heavy metals on soil microbial community and mung beans seed germination. Pak. J. Bot. 2007, 39, 629–636. [Google Scholar]
- Bhattacharyya, P.; Chakrabarti, K.; Chakraborty, A.; Tripathy, S.; Powell, M.A. Fractionation and bioavailability of Pb in municipal solid waste compost and Pb uptake by rice straw and grain under submerged condition in amended soil. Geosci. J. 2008, 12, 41–45. [Google Scholar] [CrossRef]
- Angelaki, A.; Dionysidis, A.; Sihag, P.; Golia, E.E. Assessment of Contamination Management Caused by Copper and Zinc Cations Leaching and Their Impact on the Hydraulic Properties of a Sandy and a Loamy Clay Soil. Land 2022, 11, 290. [Google Scholar] [CrossRef]
- Plugaru, S.R.C.; Rusu, T.; Molnar, K.; Fodorpataki, L. Chromium removal from Polluted Water and its influence on biochemical and physiological parameters in algal cells used for phytoremediation. Stud. UBB Chem. 2017, 3, 225–238. [Google Scholar] [CrossRef]
- Boechat, C.L.; Pistoia, V.C.; Ludtke, A.C.; Gianello, C.; Camargo, F.A.O. Solubility of Heavy Metals/Metalloid on Multi-Metal Contaminated Soil Samples from a Gold Ore Processing Area: Effects of Humic Substances. Rev. Bras. Cienc. Solo 2016, 40, 15. [Google Scholar] [CrossRef]
- Karachaliou, T.; Protonotarios, V.; Kaliampakos, D.; Ariamenegaki, M. Using Risk Assessment and Management Approaches to Develop Cost-Effective and Sustainable Mine Waste Management Strategies. Recycling 2016, 1, 328–342. [Google Scholar] [CrossRef]
- Shi, J.; Pang, J.; Liu, Q.; Luo, Y.; Ye, J.; Xu, Q.; Long, B.; Ye, B.; Yuan, X. Simultaneous removal of multiple heavy metals from soil by washing with citric acid and ferric chloride. RSC Adv. 2020, 10, 7432–7442. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.-J.; Li, Q.; Peng, H.; Zhang, J.-X.; Chen, W.-J.; Zhou, B.-C.; Chen, M. Remediation of Heavy Metal-Contaminated Soils with SoilWashing: A Review. Sustainability 2022, 14, 13058. [Google Scholar] [CrossRef]
- Navarro, M.C.; Pérez-Sirvent, C.; Martínez-Sánchez, M.J.; Vidal, J.; Tovar, P.J.; Bech, J. Abandoned mine sites as a source of contamination by heavy metals: A case study in a semi-arid zone. J. Geochem. Explor. 2008, 96, 183–193. [Google Scholar] [CrossRef]
- Scanferla, P.; Marcomini, A.; Pellay, R.; Girotto, P.; Zavan, D.; Fabris, M.; Collina, A. Remediation of a Heavy Metals Contaminated Site with a Botanical Garden: Monitoring Results of the Application of an Advanced S/S Technique. Chem. Eng. Trans. 2012, 28, 235–240. [Google Scholar]
- Sun, L.; Wu, Q.; Liao, K.; Yu, P.; Cui, Q.; Rui, Q.; Wang, D. Contribution of heavy metals to toxicity of coal combustion related fine particulate matter (PM2.5) in Caenorhabditis elegans with wild-type or susceptible genetic background. Chemosphere 2016, 144, 2392–2400. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.; Mishra, R.K.; Sinam, G.; Mallick, S.; Gupta, A.K. Comparative Evaluation of Metal Phytoremediation Potential of Trees, Grasses, and Flowering Plants from Tannery-Wastewater-Contaminated Soil in Relation with Physicochemical Properties. Soil Sediment Contam. Int. J. 2013, 22, 958–983. [Google Scholar] [CrossRef]
- Golia, E.E.; Angelaki, A.; Giannoulis, K.D.; Skoufogianni, E.; Bartzialis, D.; Cavalaris, C.; Vleiora, S. Evaluation of soil properties, irrigation and solid waste application levels on Cu and Zn uptake by industrial hemp. Agron. Res. 2021, 19, 92–99. [Google Scholar] [CrossRef]
- Soleimani, M.; Hajabbasi, M.A.; Afyuni, M.; Akbar, S. Comparison of Natural Humic Substances and Synthetic Ethylenediaminetetraacetic Acid and Nitrilotriacetic Acid as Washing Agents of a Heavy Metal–Polluted Soil. J. Environ. Qual. 2010, 39, 855–862. [Google Scholar] [CrossRef]
- Lestan, D.; Luo, C.; Li, X. The use of chelating agents in the remediation of metal-contaminated soils: A review. Environ. Pollut. 2008, 153, 3–13. [Google Scholar] [CrossRef]
- Gusiatin, Z.M. Novel and Eco-Friendly Washing Agents to Remove Heavy Metals from Soil by Soil Washing. Environ. Anal. Ecol. Stud. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Kim, M.-S.; Koo, N.; Kim, J.-G.; Lee, S.-H. Effects of Washing Solution, Washing Time, and Solid-Solution Rate on the Maximum Heavy Metals Removal Efficiency. Appl. Sci. 2021, 11, 6398. [Google Scholar] [CrossRef]
- Meng, F.; Yuan, G.; Wei, J.; Bi, D.; Ok, Y.S.; Wang, H. Humic substances as a washing agent for Cd-contaminated soils. Chemosphere 2017, 181, 461–467. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Hodson, M.E. Investigating the use of synthetic humic-like acid as a soil washing treatment for metal contaminated soil. Sci. Total Environ. 2019, 647, 290–300. [Google Scholar] [CrossRef] [PubMed]
- Gusiatin, Z.M.; Kulikowsk, D.; Klik, B. New-GenerationWashing Agents in Remediation of Metal-Polluted Soils and Methods for Washing efuent Treatment: A Review. Int. J. Environ. Res. Public Health 2020, 17, 6220. [Google Scholar] [CrossRef]
- Khalid, A.A.; Berhan, A.; Graham, B. Soil Washing Technology for Removing Heavy Metals from a Contaminated Soil: A Case Study. Pol. J. Environ. Stud. 2020, 29, 1029–1036. [Google Scholar] [CrossRef]
- Sumalatha, J.; Naveen, B.P.; Malik, R.K. Efficiency of Washing Techniques for Removal of Heavy Metals from Industrial Sludge. Pollution 2019, 5, 189–198. [Google Scholar] [CrossRef]
- Arafat, A.; Sabrin, A.S.; Shah, M.M.; Mohammad, M. Preparation and Characterization of Chitosan from Shrimp shell waste. Int. J. Sci. Eng. Res. 2015, 6, 538–541. [Google Scholar]
- Kamari, A.; Pulford, I.D.; Hargreaves, J.S.J. Chitosan-assisted Phytoextraction of Heavy Metal from Lead/Zinc Tailings Using Lolium Perenne—A Preliminary Study. In Proceedings of the 15th International Conference on Heavy Metals in the Environment, Gdańsk, Poland, 19–23 September 2010. [Google Scholar]
- Qasem, N.A.A.; Mohammed, R.H.; Lawal, D.U. Removal of heavy metal ions from wastewater: A comprehensive and critical review. Clean Water 2021, 4, 36. [Google Scholar] [CrossRef]
- Lu, C.; Xu, Z.; Dong, B.; Zhang, Y.; Wang, M.; Zeng, Y.; Zhang, C. Machine learning for the prediction of heavy metal removal by chitosan-based flocculants. Carbohydr. Polym. 2022, 285, 119240. [Google Scholar] [CrossRef]
- Hou, T.; Du, H.; Yang, Z.; Tian, Z.; Shen, S.; Shi, Y.; Zhang, L. Flocculation of different types of combined contaminants of antibiotics and heavy metals by thermo-responsive flocculants with various architectures. Sep. Purif. Technol. 2019, 223, 123–132. [Google Scholar] [CrossRef]
- Agarwal, R.M.; Singh, K. Heavy metal removal from wastewater using various adsorbents: A review. J. Water Reuse Desalin. 2017, 7, 387–419. [Google Scholar]
- Herath, B.G.; Crisler, A.; Bridges, G.; Patel, D.; Pittman, S.; Todd, C.M. Cadmium and Copper Removal From Aqueous Solutions Using Chitosan-Coated Gasifier Biochar. Front. Environ. Sci. 2020, 8, 541203. [Google Scholar] [CrossRef]
- Wan, M.W.; Petrisor, I.G.; Lai, H.T.; Kim, D.; Yen, T.F. Copper adsorption through chitosan immobilized on sand to demonstrate the feasibility for in situ soil decontamination. Carbohydr. Polym. 2004, 55, 249–254. [Google Scholar] [CrossRef]
- Hydari, S.; Sharififard, H.; Nabavinia, M.; Reza Parvizi, M. A comparative investigation on removal performances of commercial activated carbon, chitosan biosorbent and chitosan/activated carbon composite for cadmium. Chem. Eng. J. 2012, 193, 276–282. [Google Scholar] [CrossRef]
- Jiang, W.; Tao, T.; Liao, Z. Removal of heavy metal from contaminated soil with chelating agents. Open J. Soil Sci. 2011, 1, 70–76. [Google Scholar] [CrossRef]
- Abumaizar, R.; Khan, L.I. Laboratory Investigation of Heavy Metal Removal by Soil Washing. J. Air Waste Manag. Assoc. 2012, 46, 765–768. [Google Scholar] [CrossRef]
- Chayalakshmi, C.L.; Jangamshetti, D.S.; Sonoli, S. Multiple linear regression analysis for prediction of boiler losses and boiler efficiency. Int. J. Instrum. Control Syst. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Damian, G.E.; Micle, V.; Sur, I.M. Study regarding the pedological properties of the soil in the “Larga de Sus” mining area in order to establish the appropriate soil remediation technology. Pangeea 2021, 52–61. [Google Scholar] [CrossRef]
- Damian, G.E.; Micle, V.; Sur, I.M. Mobilisation of Cu and Pb from multi-metal contaminated soils by dissolved humic substances extracted from Leonardite and factors affecting the process. J. Soils Sediments 2019, 19, 2869–2881. [Google Scholar] [CrossRef]
- Sur, I.M.; Micle, V.; Gabor, T. Heavy metals removal by bioleaching using Thiobacillus ferrooxidans. Rom. Biotechnol. Lett. 2018, 23, 13409–13416. [Google Scholar]
- Rogozan, G.C. Contributions Related to the Use of Mathematical Modeling to Emphasize Spatial Distribution of Heavy Metals in the Soil and Drawing Vulnerability Maps. Ph.D. Thesis, Technical University of Cluj-Napoca, Cluj-Napoca, Romania, 2013. (In Romanian). [Google Scholar]
- Taloi, D. Optimization of Technological Processes; Academia Publishing House: Bucharest, Romania, 1987. [Google Scholar]
- Li, Y.; Lei, M.; Chen, T.; Yang, J.; Zhou, X.; Wang, Y. Optimized EDTA washing procedure to decontaminate heavymetals from soils in iron and steel works sites. Asian J. Chem. 2013, 25, 37. [Google Scholar] [CrossRef]
- Merdun, H.; Çinar, Ö.; Meral, R.; Apan, M. Comparison of artificial neural network and regression pedotransfer functions for prediction of soil water retention and saturated hydraulic conductivity. Soil Tillage Res. 2006, 90, 108–116. [Google Scholar] [CrossRef]
- Rajkai, K.; Kabos, S.; Van Genuchten, M.T. Estimating the water retention curve from soil properties: Comparison of linear, nonlinear and concomitant variable methods. Soil Tillage Res. 2004, 79, 145–152. [Google Scholar] [CrossRef]
- Kulikowska, D.; Gusiatin, Z.M.; Bułkowska, K.; Klik, B. Feasibility of using humic substances from compost to remove heavy metals (Cd, Cu, Ni, Pb, Zn) from contaminated soil aged for different periods of time. J. Hazard. Mater. 2015, 300, 882–891. [Google Scholar] [CrossRef]
- Kulikowska, D.; Gusiatin, Z.M.; Bułkowska, K.; Kierklo, K. Humic substances from sewage sludge compost as washing agent e_ectively remove Cu and Cd from soil. Chemosphere 2015, 136, 42–49. [Google Scholar] [CrossRef]
- Rasmussen, S.B.; Jensen, J.K.; Borggaard, O.K. A laboratory test of NOM-assisted remediation of arsenic and copper contaminated soils. J. Environ. Chem. Eng. 2015, 3, 3020–3023. [Google Scholar] [CrossRef]
- Chen, Y.-M.; Lin, W.-H.; Lin, Y.-A.; Liu, C.-C.; Wang, M.-K. Remediation of lead-contaminated soil using dissolved organic carbon solutions prepared by wine-processing waste sludge. Geoderma 2014, 235–236, 233–239. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).