1. Introduction
Lithium-ion (Li-ion) battery technologies have conquered the current electric vehicle (EV) market as a clear-cut winner. The zero-emission target in the automotive sector is led by a variety of Li-ion systems powering on-road vehicles [
1,
2]. While alternative solutions are still within the development phase, Li-ion batteries that are currently on the market require advanced tools to go beyond the promised performances. Among the critical challenges, the prognosis and diagnosis of battery health are one of the most crucial factors to be tackled during the lifetime of the battery as well as the vehicle [
3,
4]. Though varieties of battery pack-level models can be developed, their reliability and accuracy can be a concern referring to the lack of a standard procedure or guidance [
5]. The pack-level aging models can be derived either from real-life on-road vehicles [
6] or lab-level investigations [
7,
8]. The modeling approach is computationally expensive and lacks multi-factor analysis capability when field data is enabled with advanced methodologies such as machine learning (ML) [
9]. Moreover, big data processing, training of data-driven algorithms, limited operating conditions, and no physical knowledge make the ML methods futile considering safety and reliability [
10]. In contrast, upscaling a cell-level model to pack-level considering relevant electrical and thermal aspects is straightforward and computationally inexpensive for the choice of battery management system (BMS) implementation [
11,
12]. Such an approach also allows for a multi-condition analysis of the operating environment broadening the model boundaries, thus increasing robustness.
This research work proposes an efficient methodological process that would facilitate a pack-level battery lifetime model development strategy. The pathway starts from the cell-level study stretching the boundary limit beyond the possible real-life scenarios including temperature, depth of discharge (DoD), state of charge (SoC) range, current rate (C-rate), and calendar life SoC, temperature, etc., variations. Such studies exist in the literature based on different Li-ion technologies followed by behavioral analysis and modeling [
13,
14]. The lifetime prediction types typically follow an imprecise definition of aging that can be classified as either cycle life and/or calendar life degradation in the form of capacity fade and/or internal resistance increase (IR). The model methodological choice also varies depending on the study type and application requirements where a compromise of model complexity, accuracy, and computational effort is accepted [
15]. The empirical equation-based models fitted to the laboratory experimental data are found to be a good fit that could ensure high accuracy, online applicability, and real-time computing with a less complex flexible framework [
16]. Hence, the representative models are often cell-level demonstrations and only a few researchers have showcased the real-life validation [
17,
18]. Nevertheless, the battery system or pack-level upscaling of a cell-level model is rare, challenging, and requires relevant consideration of pack topology, electrical and thermal properties, etc.
Investigating the aging of a battery pack that is a multi-cell configuration is usually a more complicated phenomenon where non-linear degradation, cell-to-cell variation, cell imbalance, inefficient thermal management, sudden impedance growth, mechanical stresses, etc., worsen the already existing interrelated aging mechanisms. It is extremely challenging to map all the external factors counting their contributions to the total degradation. However, researchers have studied one or more of these elements to investigate pack-level health [
19]. Perhaps, physics-based modeling could solve the puzzle of monitoring battery state of health (SoH), and if linked with data-driven techniques, can precisely forecast the system failure to avoid unprecedented colossal damage [
20,
21]. Thus, Horizon Europe has identified this topic as one of the future scopes of research for batteries in Europe [
22]. Moreover, the electrical and thermal properties of the battery pack directly impact battery aging, thus being the dominant parameters in the lifetime model. The SoC prediction and thermal simulations are usually done at the pack-level to understand the concerning behaviors; however, it is rare to be involved in the aging contribution, which should be the case [
23]. Thus, an efficient electro-thermal coupling framework is proposed to be linked to the aging model. Hence, the impact of an efficient thermal management system (TMS) is undeniable as both the cooling and heating service positively improve the battery pack health. Researchers are continuously developing better thermal management methodologies and materials to extend the pack lifetime; however, that is not the aim of this research [
24,
25].
Generally, 1D electro-thermal models benefit from easy integration into system-level frameworks (e.g., an entire EV model) and fast simulation runtimes, while they provide an acceptable averaged surface temperature of the battery cells [
26]. The baseline of the electro-thermal models can start from an equivalent circuit model [
27] or atomistic level entailing battery physical-chemical phenomena in a multi-scale simulation environment [
28]. On the other hand, 3D thermal models provide higher accuracy in terms of temperature values and temperature distribution patterns alongside every point of the battery geometry, e.g., tabs, sides, inner part, etc. [
29,
30]. These features help determine the hottest and coolest points of the batteries for specific applications for a proper thermal management design. Yet, they require much more computation resources for the computational fluid dynamics (CFD) solver leading to high CPU-to-real-time ratios (i.e., slow simulation runtimes), and they are not inherently implementable into a 1D system-level modeling framework for integration. Researchers have tried to gather the benefits of both model types by replacing the thermal part of the 1D electro-thermal model [
31] with a reduced-order model of the 3D CFD battery model for temperature calculations (for quick computation), while the electrical properties of the battery are achieved by the 1D electrical part [
32]. Thus, an optimal, robust, and precise electro-thermal model can be an integral part of the whole modeling framework where lifetime, safety, and reliability sections work together providing feedback to each other [
33].
The proposed pathway is focused on battery aging that is kicked off with commercial cells’ (LTO technology) cycle life study to generate a high-quality dataset. The detailed investigation results in a thorough understanding of battery aging that leads to the development of a robust empirical lifetime model. The model is validated to a realistic standard profile before being extended to the pack-level following an approved design that has been demonstrated as part of Horizon2020 European project GHOST [
34]. The augmented lifetime model employs an integrated electro-thermal system consideration while simulating the lifetime. This coupled 1D electrical and 3D thermal model is developed and validated within the framework of another Horizon2020 project (Vision xEV) [
35]. Upscaling the pack-level electro-thermal simulation result is generated using commercial AVL advanced simulation technologies (AST) packages and linked to the lifetime model appraising the actual health condition in the remaining life calculation. Hence, the rationality and applicability of such models in the BMS for online use cases are discussed providing perspective-based guidance to the research community.
The proposed pack-level lifetime modeling framework consists of the following series of novel contributions within the scope of this research.
- (1)
A cell-level empirical model is developed from an extensive aging study. The cells were cycled in-house for more than 2 years covering a wide range of operating conditions.
- (2)
The model is validated with a real-life standard profile showing robustness.
- (3)
The cell-level lifetime model is extended to simulate the total lifetime of a series-connected 144S1P architecture battery system.
- (4)
The pack-level lifetime model is connected to a coupled electro-thermal model developed in a commercial platform that provides necessary electrical and thermal inputs.
Further in this article,
Section 2 describes the performed experimental methodology, and
Section 3 presents the aging results with sensitivity analysis identifying the impact factors.
Section 4 includes the modeling framework developed in this work where simulation and the validation results are compared for cell-level.
Section 5 details the development of electro-thermal model coupling.
Section 6 presents the integrated framework and pack-level lifetime simulation results. Finally, discussions and concluding remarks are reported in
Section 7 and
Section 8 stating the model performance and its rationality.
2. Aging Dataset
Any lifetime campaign to generate a degradation dataset and understand aging behavior requires a long-term engagement of resources. Thanks to the research community that many of the aging datasets of Li-ion technology variants are publicly available [
36]. However, an LTO cell database is challenging to find due to barriers such as lack of commercial availability, cost, low energy density, etc. Nonetheless, a commercial TOSHIBA SCiB™ 23 Ah LTO cell is utilized in the Horizon2020 GHOST project considering its safe chemistry, high specific power, long lifetime, etc. The cell has a nominal voltage of 2.3 V, high input/output power (1000 W), compact design (W116 × D22 × H106 mm), and a light weight (0.55 kg). The prismatic-shaped 45 cells have been used to perform a series of electrical, thermal, and lifetime tests. The campaign generates a novel battery aging dataset that facilitates the degradation understanding of the studied battery type and helps to parameterize the lifetime model.
The adapted test methodology for the aging study is focused on both the degradation aspects (cycle life and calendar life). It consists of a series of cycle and calendar aging tests at given stress and/or operating conditions to understand the degradation behavior. Regular performance tests are also performed between the aging rounds to learn the non-linear degradation trend. One can find the details of the test flow in the authors’ previous work that is based on similar test protocols listed in
Table 1 [
37]. As part of an EU project, at least 2 cells per condition are studied and the average result is used for the model development.
As shown in
Table 1, the degradation rate of the cells’ aging performance is targeted to study by 5 stress factors which are DoD, mid-SoC, temperature, charge and discharge current rates or C-Rates for cycle life and 2 stress factors which are storage temperature and SoC for calendar life, respectively. The influence of these factors is investigated separately, and their joint influence corresponds to the actual measured data.
The cycling profile consists of a series of charge and discharge processes until the number of Full Equivalent Cycles (FECs) is reached. An FEC (as in Equation (1)) is calculated based on the charge ampere-hour throughput and it is considered as the cycle count to compare the degradation results. Typically, 300 FEC per round is performed on the investigated cells considering its long lifetime nature specified by the manufacturer. Regular reference performance tests such as capacity test (full DoD with 1C-rate) and hybrid pulse power characterization (HPPC) tests (varying pulses at three SoC points), etc., are performed at cycling temperature to track the degradation. The calendar storage tests are done at the specific condition with a frequency of one month before performing check-up tests. The 1C discharge capacity and the internal resistance from a 10-s 3C discharge pulse are recorded to calculate the SoH of the battery. The battery is considered dead or has reached EoL once the SoH drops below 80% [
38].
To verify the validity of the lifetime model to be developed based on the parameters acquired from the different characterization tests, an independent validation test is required to be conducted. The designed validation test can be used to compare the model output checking the accuracy of the model to a dynamic and realistic condition.
The worldwide harmonized light vehicles test cycle (WLTC) has been selected to perform the validation of the model [
39]. For this research work, a current load profile representing a high-power application has been derived and modified to emulate real-life driving. The Fiat 500X vehicle is used as a reference to generate the current profile and the more stressful sub-urban part is selected for the driving cycle at room temperature. The performed WLTC cycle consists of four repeated sub-urban sections making an hour profile and then the cell is charged. The validation test is performed at 90% SoC and 25 °C. One single cycle is repeated for 12 times to make a day-long WLTC test which is then run continuously 15 times per round before doing the check-up. The discharge current of the WLTC cycle is limited to 100A due to battery cycler channel constraints.
All the mentioned aging tests, validation tests, and check-ups are done using PEC manufactured ACT0550 and CT0550G2 type battery cyclers. The controlled environmental conditions are ensured by performing the tests inside CTS-made climate chambers.
3. Degradation Results
The crucial impact factors that are employed in the cycle and calendar life campaign, had a diverse contribution to total aging. The internal resistance deviation for the studied cells is not analyzed, thoroughly as very slow growth is observed. Thus, the lifetime results are presented in terms of capacity decay in the work. In the following, the impact of the influential parameters is analyzed for the capacity degradation.
The cycling capacity retention is stress factor-dependent among which the DoD and temperature play a major role. The DoD or cycling SoC range may affect battery life heavily at different temperatures along with other operating conditions. The impact of deep and shallow cycling on battery life is observed for the LTO cell which is common for other lithium technologies as well [
40,
41,
42]. The DoD dependency at 45 °C where higher DoD cycling tends to reach the EoL criterion sooner than lower DoD cycling. Although the shallow cycling measurement does not include the full life until 80% SoH, the already existing data reflects the DoD dependency showing the irreversible effect of full DoD cycling. It has been found that the cycle life of this battery cell can be doubled theoretically if cycled at 80% DoD compared to 100% DoD. Further lower DoD cycling can extend lifetime as well.
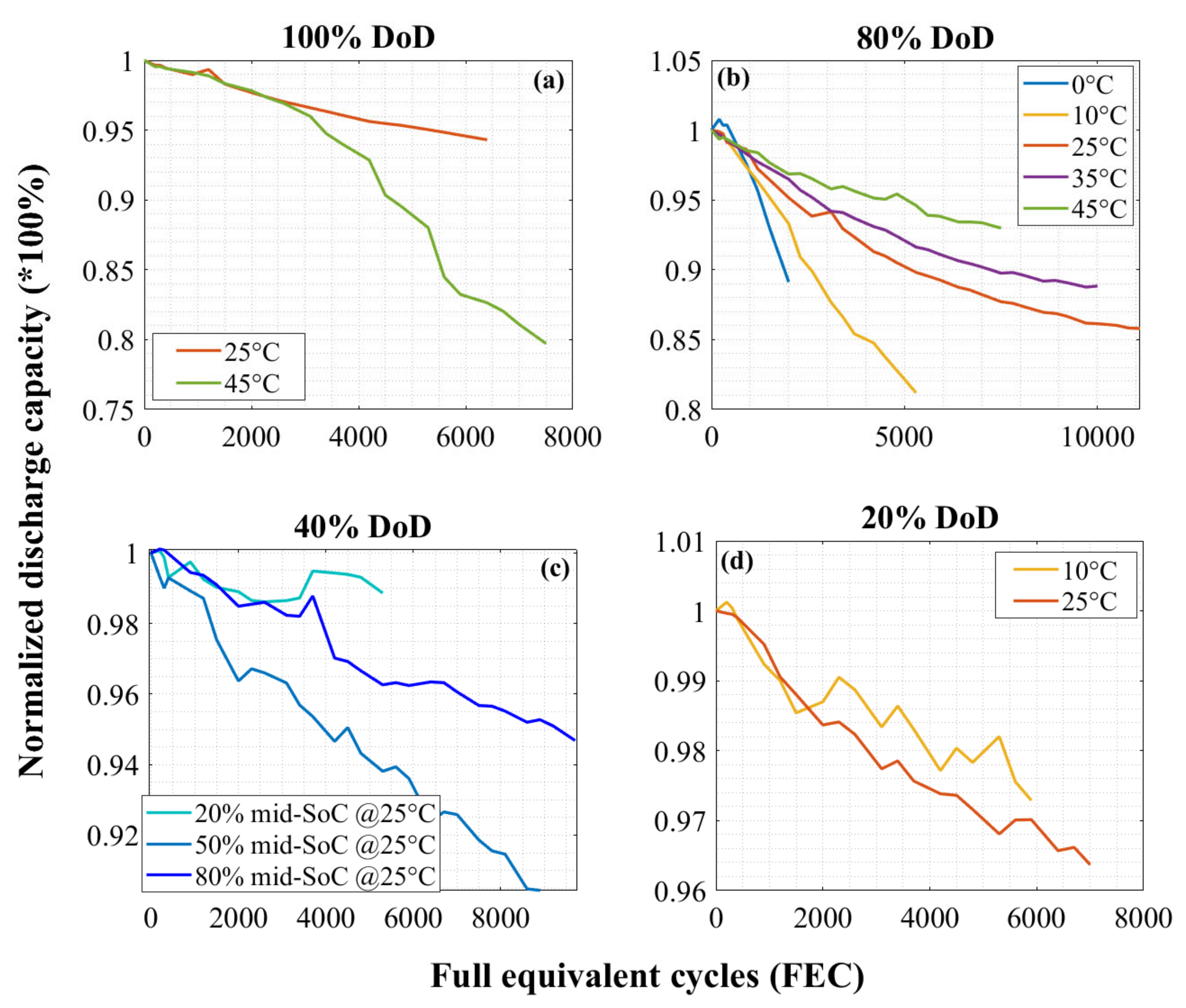
Figure 1 explicitly exhibits dependency for the cells that are cycled at different conditions. When cycled with full DoD range continuously, the higher temperature dependency is significant and clear. The prominent impact of high temperature such as 45 °C cycling degrades the cells to EoL after 7500 FEC, while the room temperature cycling loses 6% of the capacity after 6400 FEC. The shallow 20% DoD (in the 50% mid-SoC region) degrades much slower than full DoD cycling (
Figure 1d) indicating that its usage in a hybrid application or urban driving may make it even last long. The displayed figure also reports a consistent temperature effect in the studied DoD cycling results where it is found that the temperature is inversely proportional to the capacity fade. This means that the studied cell type aging is prone to the lower temperature as shown in
Figure 1b for 80% DoD cycling. At this condition, the cells on average lost 7% of the capacity after 7500 FEC at 45 °C, while the 0 °C cycling condition experienced 11% capacity loss after only 2000 FEC. The temperature effect is found to be the key degradation stress factor that would drive the model parameterization.
The impact of mid-SoC is not found at available lower DoD cycling conditions; however, cycling at 20% mid-SoC (when DoD is 40%) seems to have the least capacity fade as shown in
Figure 1c, but conclusive remarks could only be made with a complete first-life dataset. The minor stress is still considered to be included in the model parametrization to have an integrated impact on this condition.
The charge–discharge cycling rates can significantly contribute to Li-ion batteries capacity degradation if not power-optimized. The charge rates are studied at room temperature and for an 80% DoD cycling scenario. The aim was to obtain the current rate influence; however, the degradation trend is found to be unclear which is a challenge for the modeling work. Due to ambiguous characteristics and lack of discharge variation data, the C-rate impact is neglected in the model parameterization.
Moreover, the calendar life tests as per the designed test matrix have generated trivial information. After 18 months of storage tests, the cells have showcased a robust behavior (up to 2% negative fade) with little or no degradation sign. Thus, the calendar life impact is excluded from the modeling framework due to its negligible contribution over the lifetime. The extremely long life of LTO anode-based cells is acknowledged in the literature as well and in line with the manufacturer’s claim [
43,
44].
4. Performance-Based Lifetime Modeling
The authors have modified their already established framework that is accurate and flexible, thus adapting it to the new LTO aging dataset. The gathered knowledge from the long cycle and calendar life tests is deployed considering the influential parameters. This type of approach is quite simple and common thanks to its quick adaptability, high accuracy, and real-time computational ability. Hence, the model constructed based on a large lab-level measurement dataset should showcase the rationality via real-life profile validation. In this work, the capacity fade model is aimed to achieve less than 1% RMSE with the selected WLTC profile.
4.1. Model Framework
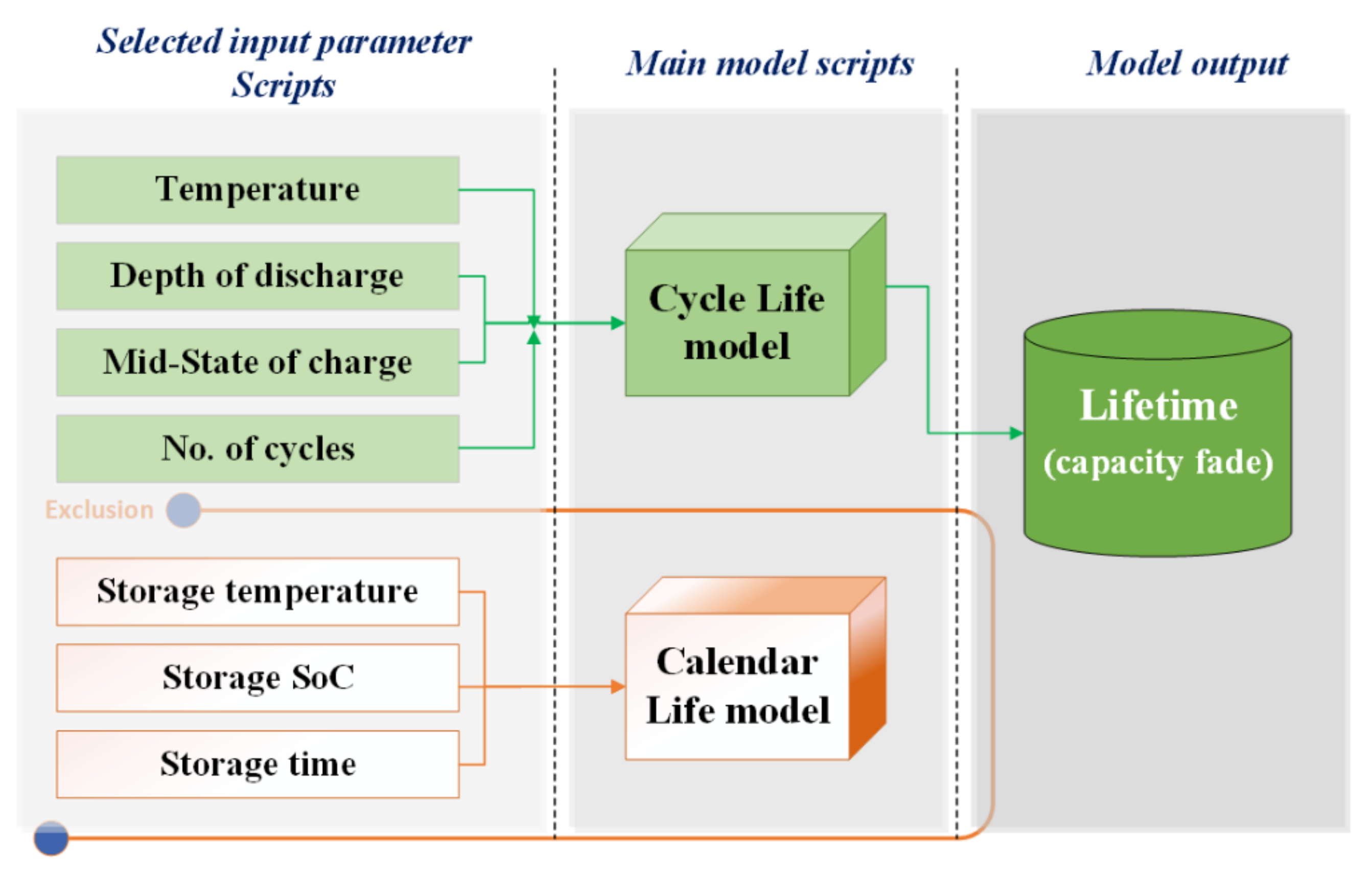
The lifetime model is developed using empirical representations with respective mathematical equations for estimating the cell’s capacity fade resulted from cycling effects. The adapted lifetime model primarily considers the cycling capacity fade consisting of several Matlab scripts referring to the different impact factors. These impact factors are selected from the sensitivity analysis of the results explained in
Section 3. The detailed construction of the framework can be found in the author’s previous publications [
13,
37]. As mentioned in
Section 3, the calendar life imposes a minimal effect; thus, it has been excluded from the model consideration. The corresponding cycle life stress factors which resulted in the capacity loss representations include the temperature, depth of discharge, and mid-state of charge with their respective ratings as indicated in the aging test matrix. The multivariable model is parameterized with the sensitive impact factors and scripted to get a total and single representation. This has been achieved by using the Matlab platform obtaining the overall cycling capacity fade. The adapted modeling framework for this work is shown in
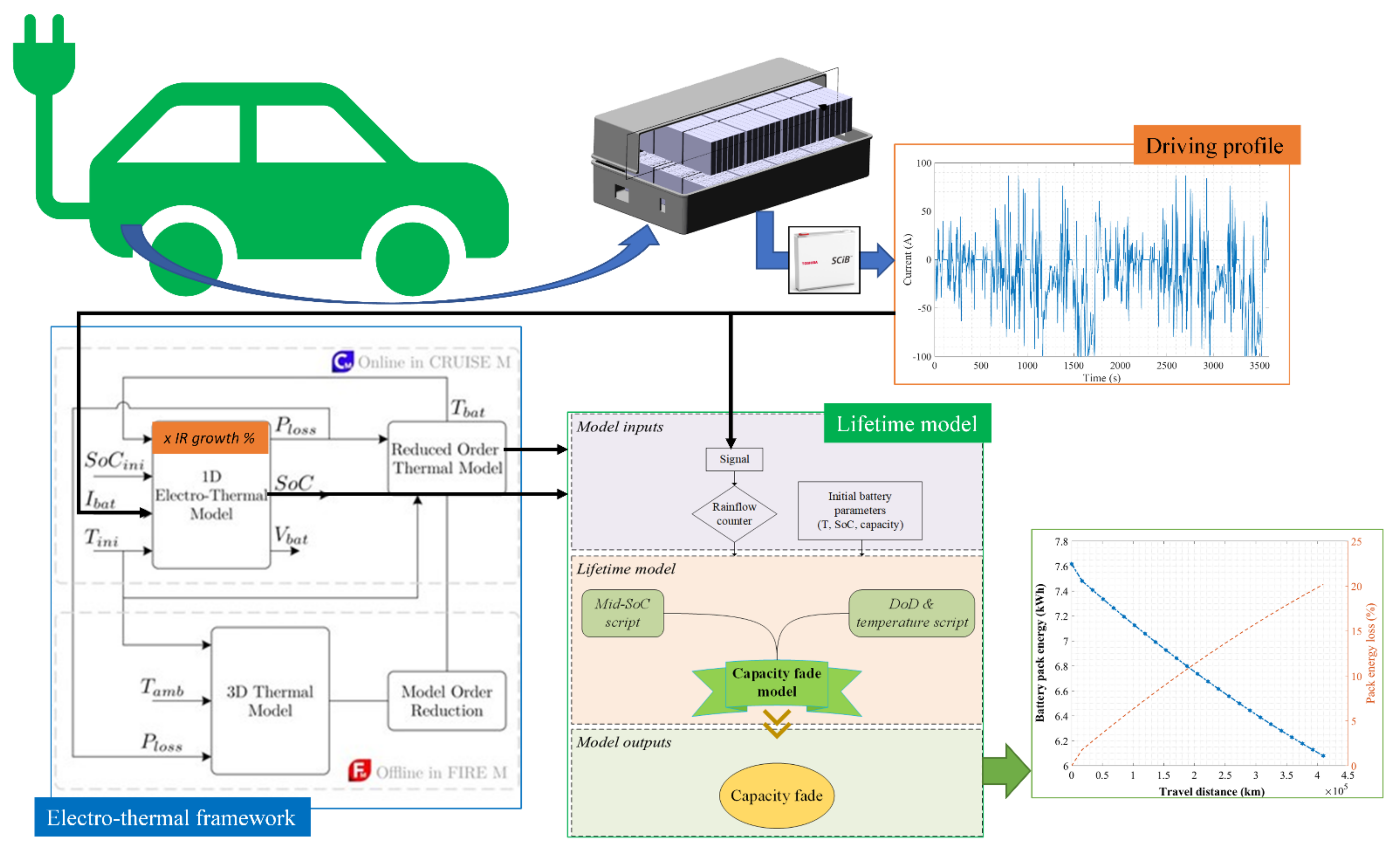
Figure 2.
The result analysis and parameter selection process make the model development smooth covering a wide range of operating conditions. First, the sensitive parameters are identified, and the corresponding data are plotted to the respective FECs. Then, the aging outputs from the sensitive parameters are fitted with mathematical equations to represent the individual influences. All the cycling stress parameters (DoD, temperature, mid-SoC, etc.) effect is scripted, separately but merged for DoD and temperature effect. The following general cycle life equation is used to fit the generated dataset.
In Equation (2), IP refers to the influential parameters for cycle life, A
j and B
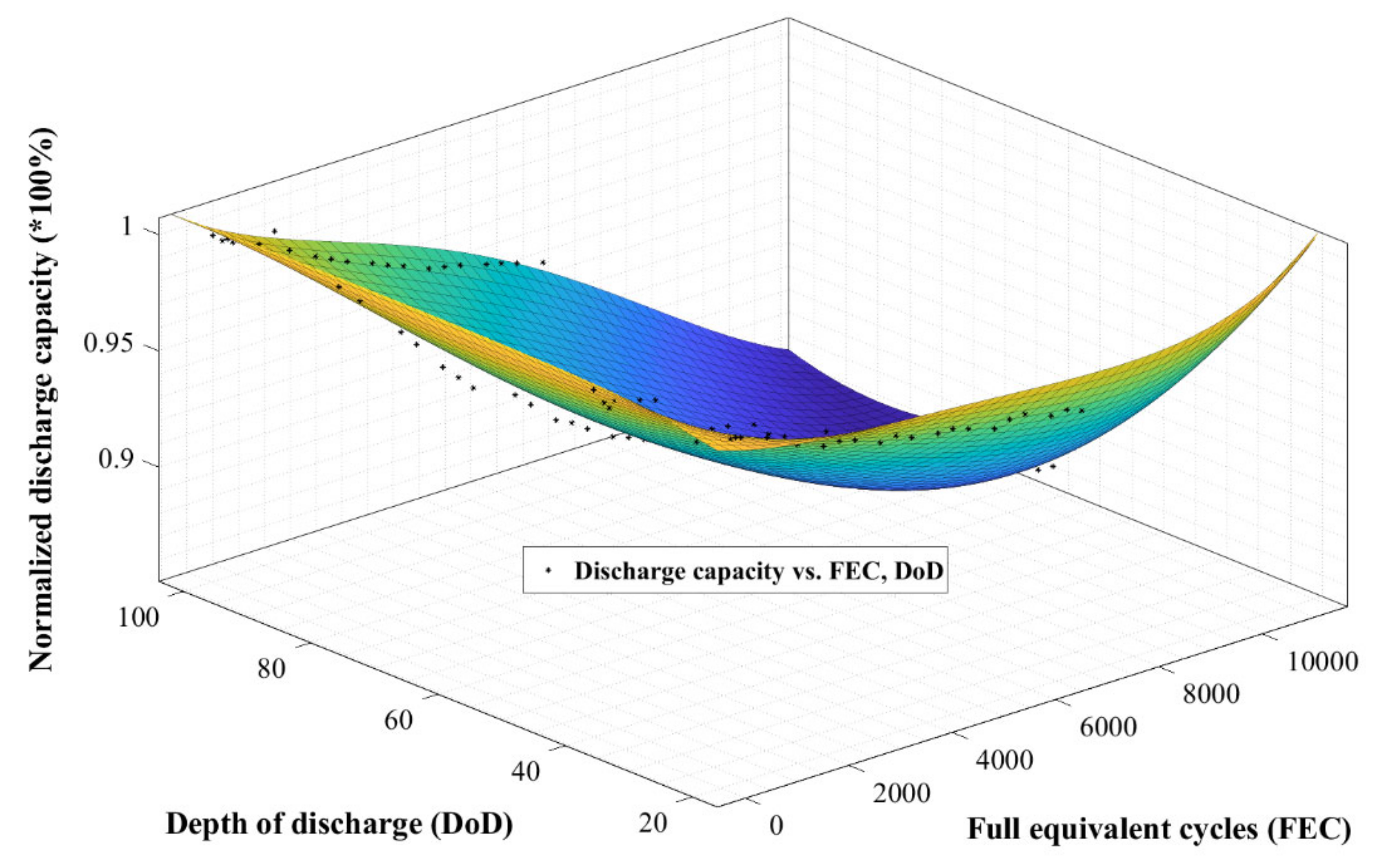
j are constant coefficients, n and m are surface fitting orders, and i and j are polynomial orders to get the best fit. For instance, DoD impact on the cycle life degradation is fitted at every investigated temperature with 4th order polynomials (i = 4, j = 2). A sample of the fitting scenario for the capacity fade in terms of DoD, and FEC is presented in
Figure 3 which illustrates excellent fitting (R
2 = 0.98) based on Equation (2). Similarly, the mid-SoC effect is formulated in a separate script to get the quantified impact. In this way, the total aging corresponds to the necessary degradation scenarios. The Matlab curve fitting toolbox is used for this purpose.
The developed model can intake dynamic or one-dimensional current signal as input together with other initial battery states such as SoC, BoL capacity, and the cycling temperature. The load signal is filtered in the initial section with a rainflow counter that is typically used for fatigue analysis. The rainflow algorithm extracts the crucial information from the dynamic profile and separates the load and no-load (zero current) conditions to be processed, accordingly, to the model scripts. The no-load situations are considered negligible due to the long calendar life of the investigated cell. The current profile is analyzed by a simple battery model (coulomb counting) that makes an SoC profiling and the rainflow counter prepares the DoD profile and cycle numbers for the whole simulated duration.
The developed model can accurately predict the degradation within the boundary conditions of the generated dataset; however, it is also capable of estimating beyond the considered conditions by extrapolations compromising the accuracy. The developed framework is also easily adaptable to other fitting algorithms (corresponding to the diversified aging path) for different Li-ion technologies.
4.2. Model Validation
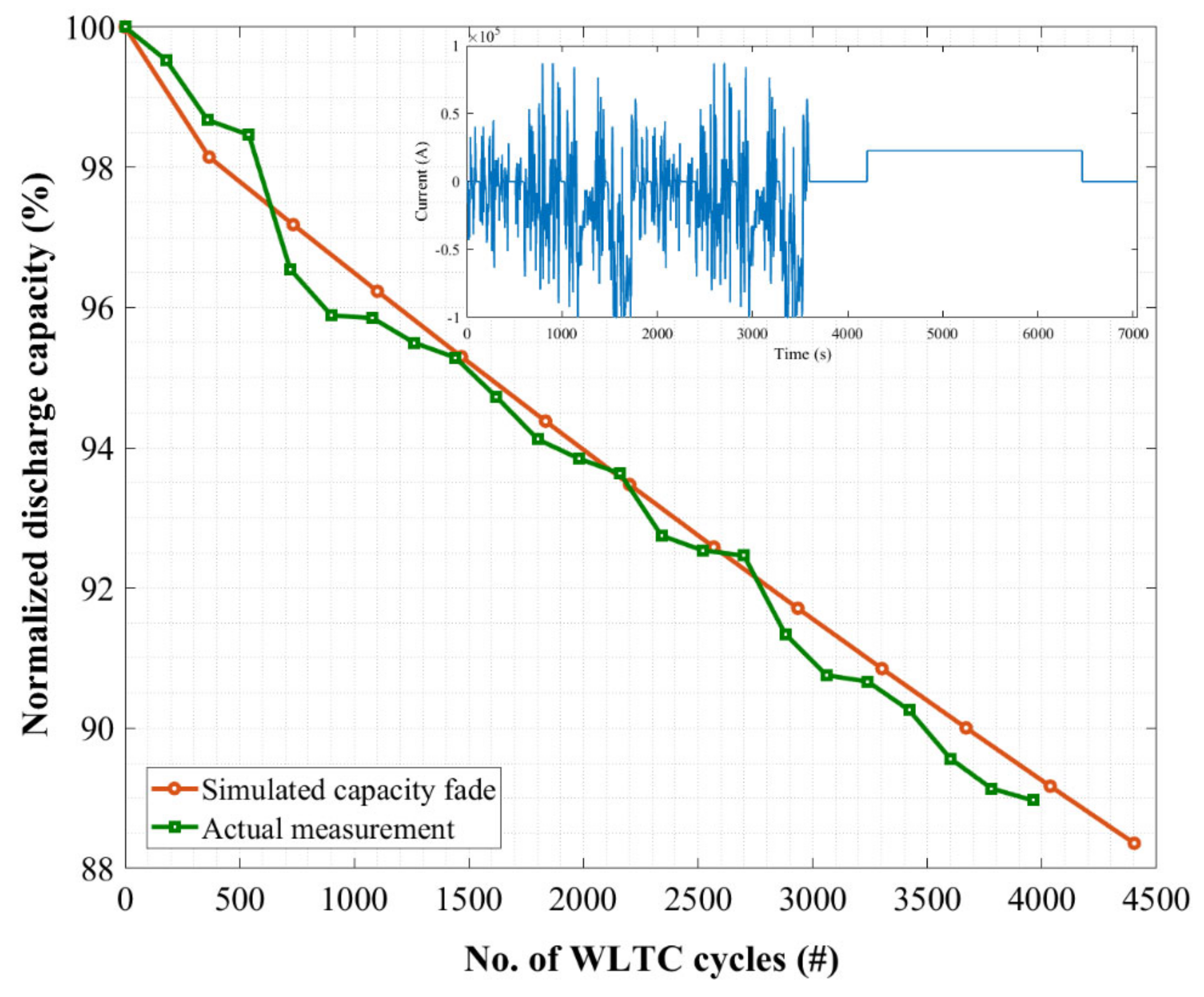
Dynamic WLTC currents are used to testify to the model’s robustness by performing separate cycling tests. The continuous dynamic profile as shown in
Figure 4 (inset), is performed at 90% DoD and room temperature for a standard validation as mentioned in
Section 2. The simulated outputs are evaluated by RMSE, and the metric is expressed as Equation (3).
In this equation, n is the number of measurement points, Ῠ is the model response, and Ỳ is the actual discharge capacity.
Figure 4 presents the simulated result against the measured values showing an excellent agreement providing an RMSE of only 0.45 for the cycling capacity fade. Considering the challenging factors in the measured data, the achieved accuracy scores well compared to models that are available in the literature [
37,
42]. The minimal model error can be attributed to the limitation of the empirical methodology, incomplete dataset, and the non-linear characteristics of the investigated LTO cell.
The cell-level simulated result has been verified reporting an actual measurement of approximately 11% SoH showcasing the developed model’s robustness. If the simulation is continued further until 80% SoH which is the usual first life for an automotive case, then the model could predict the whole life in terms of FECs. The model simulates the first life as 9000 FEC after which the capacity decay goes beyond 20%.
4.3. Lifetime Model Extension to a Pack-Level Use Case
The capacity degradation and such prediction on the pack-level is the aim of this study considering the crucial features. The unit aging factors are already considered while developing the cell-level lifetime model. Thus, the electrical and thermal elements are introduced when the model is expanded for a series-connected 144S1P topology.
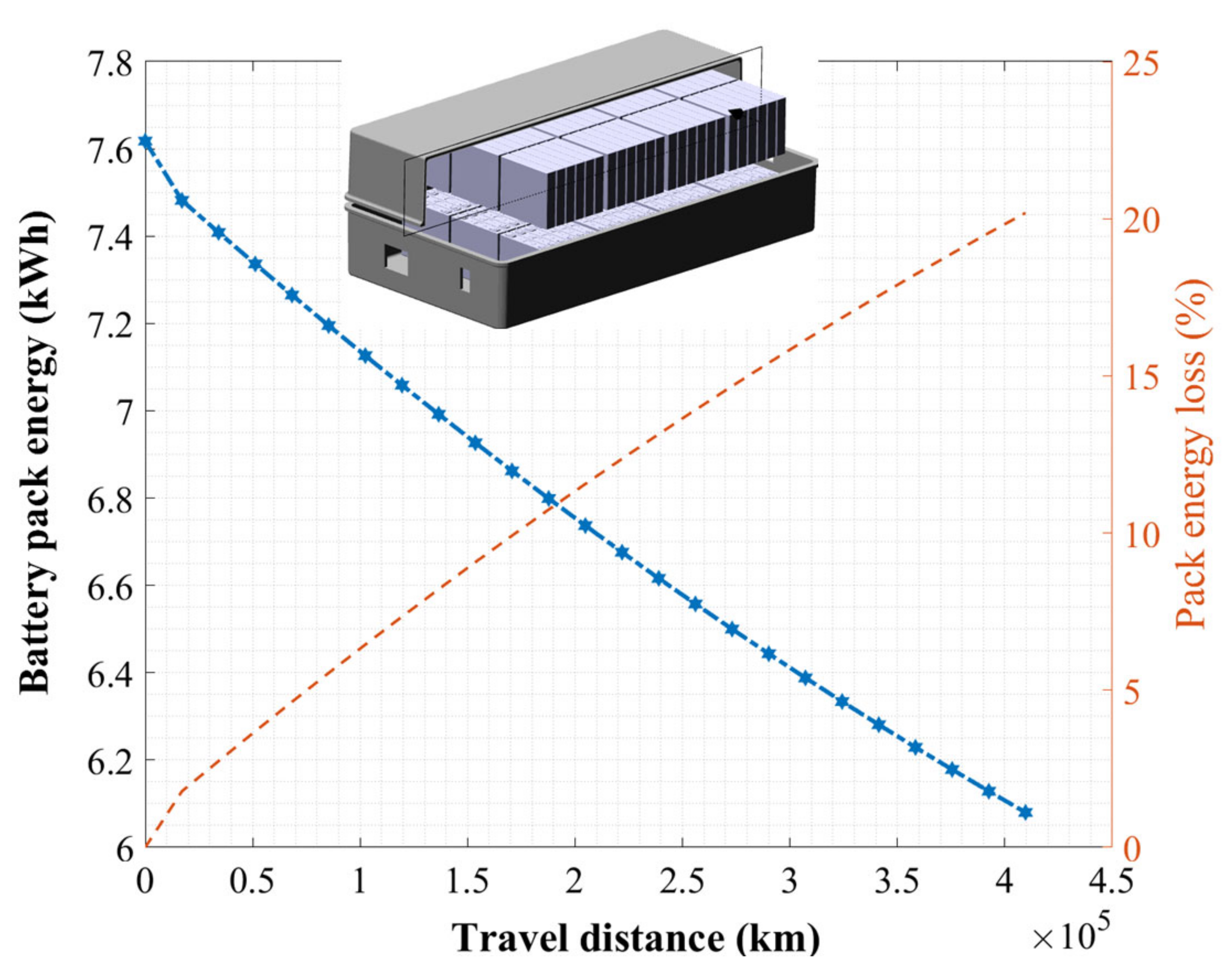
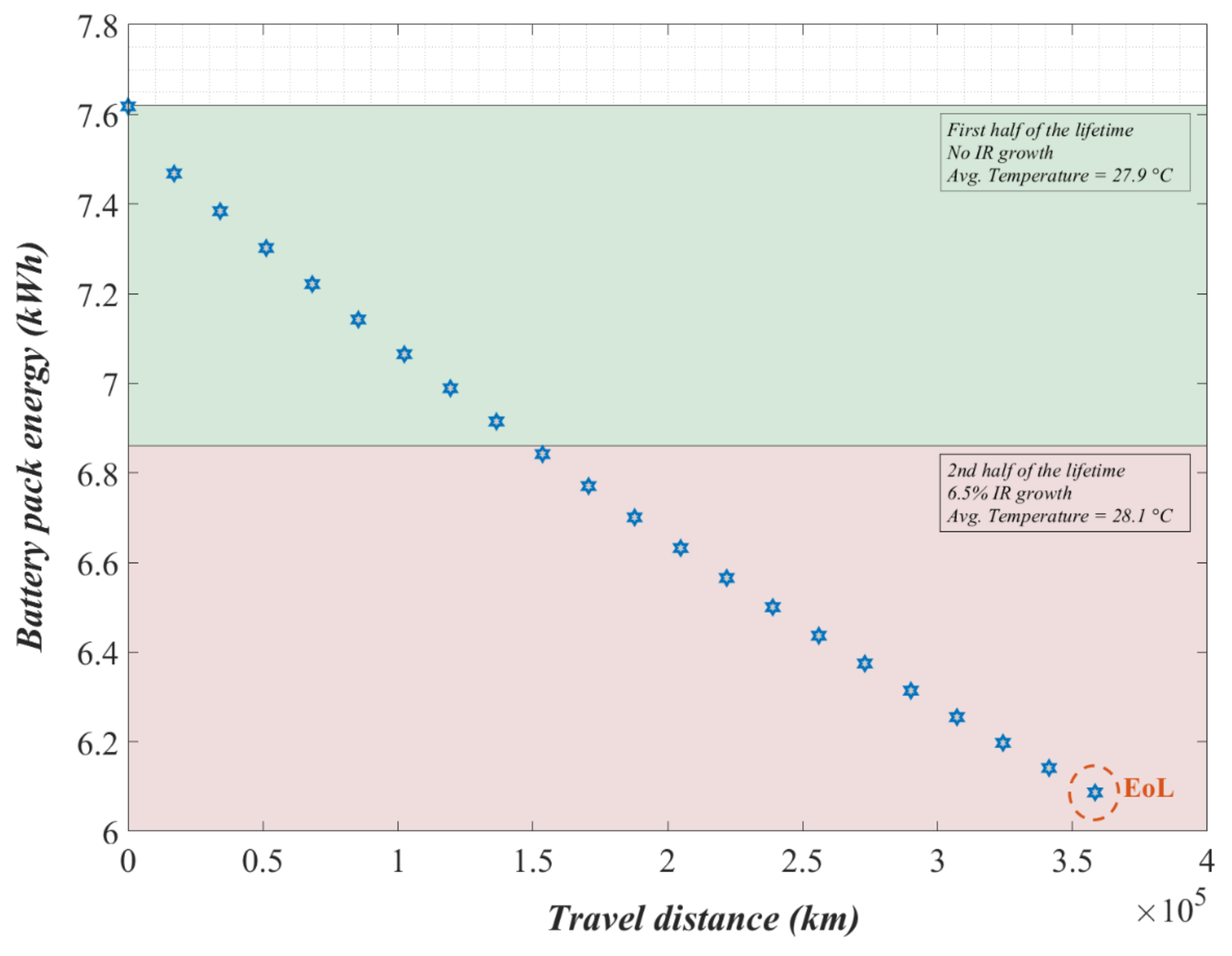
The pack topology of the study case is a series-connected configuration of 144 LTO cells. The assembled configuration has a nominal 7.62 kWh pack energy. The cell-level aging model is scaled up according to the cell specifications to build the pack-level model. The scaling is done by simple multiplication for the multicell configuration. Ideal balancing is considered for the cell-to-cell SoC variation having negligible impact on the lifetime.
Figure 5 displays the pack-level full first life simulation result with the pack CAD (inset). The prediction basis is converted to travel distance against the pack energy loss. The simulation at 25 °C estimates the driving distance to be 409,614 km in the first life, however, without considering the electrical and thermal updates of aspects such as increased IR, TMS, etc. The model considers a 16.5 km travel distance per suburban WLTC section that is used for the validation purpose. This proves that the cell can withstand stressed WLTC cycling and still can give a very long mileage. It can also be assumed that with shallow cycling or with a full WLTC (urban and suburban) profile, the LTO pack would be able to survive even longer.
5. Pack-Level Electro-Thermal Modeling
So far, the constructed pack-level lifetime model can provide an accurate capacity fade prediction only considering the aging stress factors. However, other crucial considerations of electrical and thermal properties are to be integrated as these performances change over the lifetime. Thus, these aspects are unfolded and derived from further developed models in this section. Here, the critical parameters are the pack SoC, IR growth, and heat generation during operation considering the aging state.
The electrical and thermal behavior of the battery pack is modeled by online coupling of an impedance equivalent circuit (EC) model that derives electrical characteristics, and a reduced-order 3D thermal model that demonstrates thermal characteristics. Both model types are implemented separately at cell-level first and upscaled to pack-level. Then, the online coupling process has been done within AST features widely used in the automotive industry. The Following describes the entire pack-level model implementation in the beforementioned steps.
5.1. Lifetime Model Extension to a Pack-Level Use Case
The electrical model is expected to deliver the predictions of electrical parameters of terminal voltage, SoC, overall internal resistances, and conclusively power loss under various environmental and operational conditions. For this work, the authors have used their 2nd order EC reported in [
35], and the characterization results can be found in [
32]. The already validated model development is not repeated to avoid redundancy; however, the governing equations can be found as the following.
The open-circuit voltage
of the cell is assumed as an ideal DC voltage source, connected to an ohmic resistance
, and followed by multiple
loops for simulating battery polarization effect [
45]. For this study, two branches are considered including
,
,
, and
. The Kirchhoffs Voltage Law gives the battery terminal voltage
, where
is the charge/discharge current, and
and
are voltage drops across each
branch. All the beforementioned parameters are a function of instantaneous
(also referred to as C-rate), cell temperature
, SoC, and number of cycles the battery has undergone, i.e., aged. In which the latter is the focus of this study. Coulomb counting method is utilized to estimate SoC as in [
46]. The other important parameter to be achieved through the electrical model is the overall Ohmic power loss
induced by internal resistances of the battery as stated in Equation (5). It is used as volumetric heat input to the 3D model described in the next section.
Once all the required look-up tables are achieved from experimental results, they are loaded to the battery module within the AVL CRUISE™ M commercial platform. Interpolation and extrapolation techniques are used to achieve consistent data series of the parameters within or outside the testing points. Once the cell model is implemented and validated (RMSE = 0.09), it gets upscaled into pack-level by series or parallel connection of multiple individual cells. The considered battery pack at its beginning of life (BoL) state, can store 7.62 kWh energy, and outputs 331 V nominal voltage at its terminals.
5.2. 3D Thermal Model Implementation
It is well-known that temperature plays a crucial role in batteries’ performance, and the model parameters change nonlinearly at various thermal conditions. Therefore, a 3D thermal model that can predict the surface temperature of the batteries as a function of internal power loss, can improve the accuracy of the 1D electrical model [
31] for sensitive designs such as cooling/heating system optimizations, and lifetime predictions. Model order reduction techniques can significantly eliminate this problem while maintaining the accuracy of the 3D thermal model [
47]. In this section, the implementation of a 3D triple adjacent module in the FIRE M platform is described to simulate the heat transfer effect in cell-to-cell and cell-to-environment levels, and then this 3D model order is reduced to 1D to be coupled with the electrical model for online coupling during pack-level simulations in CRUISE M platform.
As shown in
Figure 6, the implementation of this model is summarized in four major steps. The first step consists of designing a proper CAD geometry including every highlighted detail of the three battery cells adjacent to each other. The casing or shell covers the inner parts of the cells. The following step is assigning a domain to each part of the CAD. Each cell has been divided into seven separate domains including the Aluminum casing on six sides and an inner cell part (fill). The advantages of such a multi-domain approach are that the temperature distribution of each can be analyzed separately and there will be control over where to apply the heat input. The third step is conducting a proper and neat meshing process on the model for which AVL FIRE™ M provides a polygonal meshing approach with the flexibility of size and boundary layers adjustments. The quantity and the size of mesh elements define the simulation accuracy and solver precision. On the other hand, a higher number of mesh elements causes a much more computational workload on the CPU. Therefore, a trade-off shall be made between these two factors to achieve the most accurate and efficient simulation. Once the meshing is done, the solver shall be prepared, and every simulation parameter is tuned. The battery power loss under various current profiles is imported from the 1D electrical model as volumetric heat input and it is applied to the inner (fill) domain of the three batteries. After simulation as shown in
Figure 6d, post-processing of the results is performed to extract and demonstrate the model outcome. Such a 3D thermal modeling approach not only provides accurate temperature values but also gives a temperature distribution over the entire geometry which makes it helpful for optimal cooling/heating system designs.
5.3. Thermal Model Order Reduction (3D to 1D)
The lumped-element network generation methodology for the model order reduction process has been thoroughly described in [
47] and it has been applied to the triple-cell module model developed in this work. The resulting 1D thermal model in the CRUISE M environment consists of the three battery cells that are interfaced with each other through their corresponding adjacent domains and heat transfer among them and boundary conditions are translated into differential blocks from the 3D model. Three heat source blocks apply the battery power loss to each cell. Each heat source block is connected to the inner cell (fill) domain of the cells as the heat input is only applied to the inner cell material. In this topology, individual cells are packed as sub-models as they include multiple blocks with interfaces among each other as well.
Each domain of the battery cells is translated into a solid-mass block corresponding to domain specifications defined in the native FIRE M model. Each block contains material characteristics (Aluminum and inner battery), and they are interfaced with each other using differential blocks translating boundary conditions between adjacent domains. It shall be noted that for this study, the average temperature of the inner cell domain has been considered as the reference temperature value signal for lifetime evaluation. Lastly, the triple-cell module thermal model is upscaled as a string of 144 cells to form the 1P144S pack configuration in the 1D environment of the CRUISE M platform to be ready for coupling with the electrical model to have online coupled electro-thermal simulations.
5.4. Overall Electro-Thermal Model Coupling
The combined pack electro-thermal model consisted of the three sub-models presented in this work, their integration, and input/output (I/O) signals are presented in
Figure 7 together with the interlinked lifetime model. The 3D model is simulated in FIRE M in an offline mode to generate the reduced order lumped-element network. It requires ambient temperature
, initial pack temperature
, and power loss
signals during a steady load profile extracted from the 1D electrical model as inputs. This process is done once, and the rest of the simulations could be run in CRUISE M. The reduced order model block is responsible for accurate battery pack temperature
generation which is fed back into the electrical model. This block requires
and
signals for that purpose. The electrical characteristics of the pack (e.g., terminal voltage
,
, etc.) are outputed by the 1D electrical model. The inputs for this block are initialization signals
and
, and the battery current
which could be a constant or dynamic load profile.
7. Discussions and Recommendations
There are certain pros and cons of upscaling a cell-level lifetime model; however, one big advantage is the ability to build a multi-model framework. The constructed base can easily facilitate more models such as electrochemical, mechanical, etc., which could be integrated. The present work makes a comprehensive guideline for the development of a pack-level lifetime modeling structure that can be processed online with a dynamic driving characteristic and other available inputs. The robustness of the framework could be further increased if the IR parameterization is performed more frequently compromising the computational cost. Moreover, the inclusion of thermal management, pressure effect of the cells inside the pack, cell-to-cell variation, balancing, humidity, vibration, etc., could make the model all-inclusive. Nevertheless, the framework can be optimal to study the lifetime impact of different cooling methods, driving characteristics, etc.
7.1. Rationality of Cell-Level Model Expansion
The construction of a pack-level lifetime model from cell-level is certainly more logical but complex than studying real-life pack-level dataset. Field data from on-road vehicles often require challenges such as missing data points, noisy and/or partial data, limited boundary conditions, etc., to be tackled in a black-box approach. However, an extension of a cell-level aging model provides the opportunity to merge several interconnected models such as electrical, thermal, and mechanical. Hence, the 1D electro-aging model gives a clear understanding of the cell’s performance and characteristics for any operating conditions that are required for other pack-level models leading to a merger of collective models.
The cell-level models are usually based on numerous lab-based tests that are almost impossible to replicate at pack-level. The variations in the operating conditions, test setup, various performance tests, etc., give the flexibility to develop models with an extended reach. In situ measurements and/or cell autopsy can also verify the physical link to cell degradation if an appropriate cell-level campaign is designed.
7.2. Feasibility Checks of Model Implementation in BMS
In general, algorithms for estimating lifetime can be divided into two types. The first is based on complex calculations. The advantage of this type is that it requires low experimental data and is relatively accurate, but it also has the obvious disadvantage of consuming a lot of computing resources on the processor. The second type of algorithm is based on a lot of experimental data and this method replaces complex operations with a lot of real experimental logs. For example, the aging of the battery is obtained by interpolating the database based on the current state of the battery, e.g., temperature, SoC, voltage, etc. This approach requires less computational effort and is relatively easy to integrate into a BMS where storage resources are more easily obtained than computational resources when designing the hardware of BMS. The empirical algorithm in this paper is suitable for the second method.
To obtain detailed data to build a comprehensive database, this paper tested many cells meaning that the lifetime of the battery is predicted by interpolation from the multidimensional database. By this method, the algorithms can be imported into BMS. When the lifetime is needed to predict, BMS will first investigate the present battery health status and prepare a driving characteristic from memory. With the inputs, it can quickly simulate the remaining life based on the conditions. Furthermore, the multi-model framework can continuously be optimized if the database is regularly updated (i.e., IR growth). For example, the framework can stay in the cloud continuously collecting battery data from the BMS upon connection.