Abnormal Ship Behavior Detection Based on AIS Data
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. Overview of Study Area and AIS Data Preprocessing
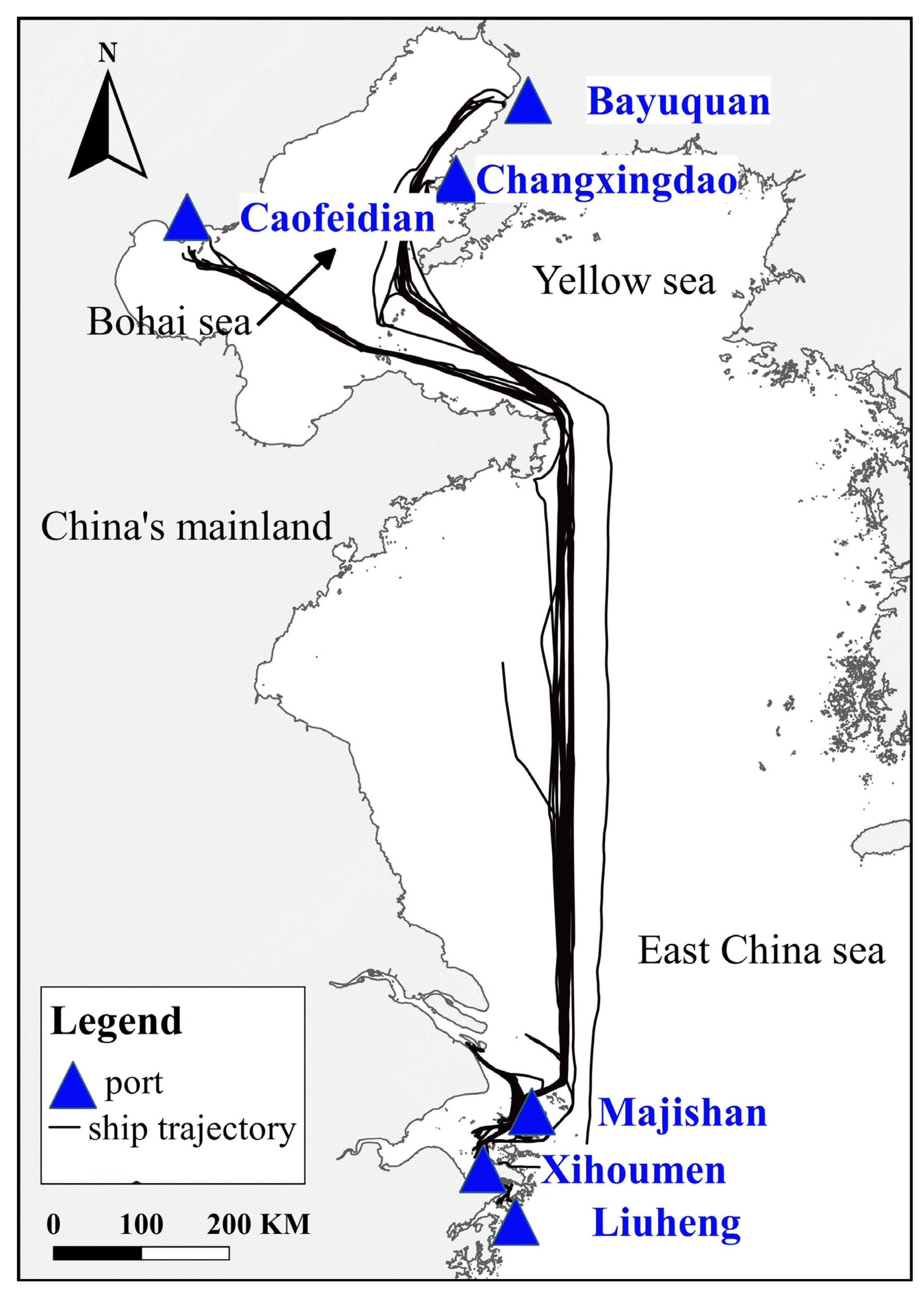
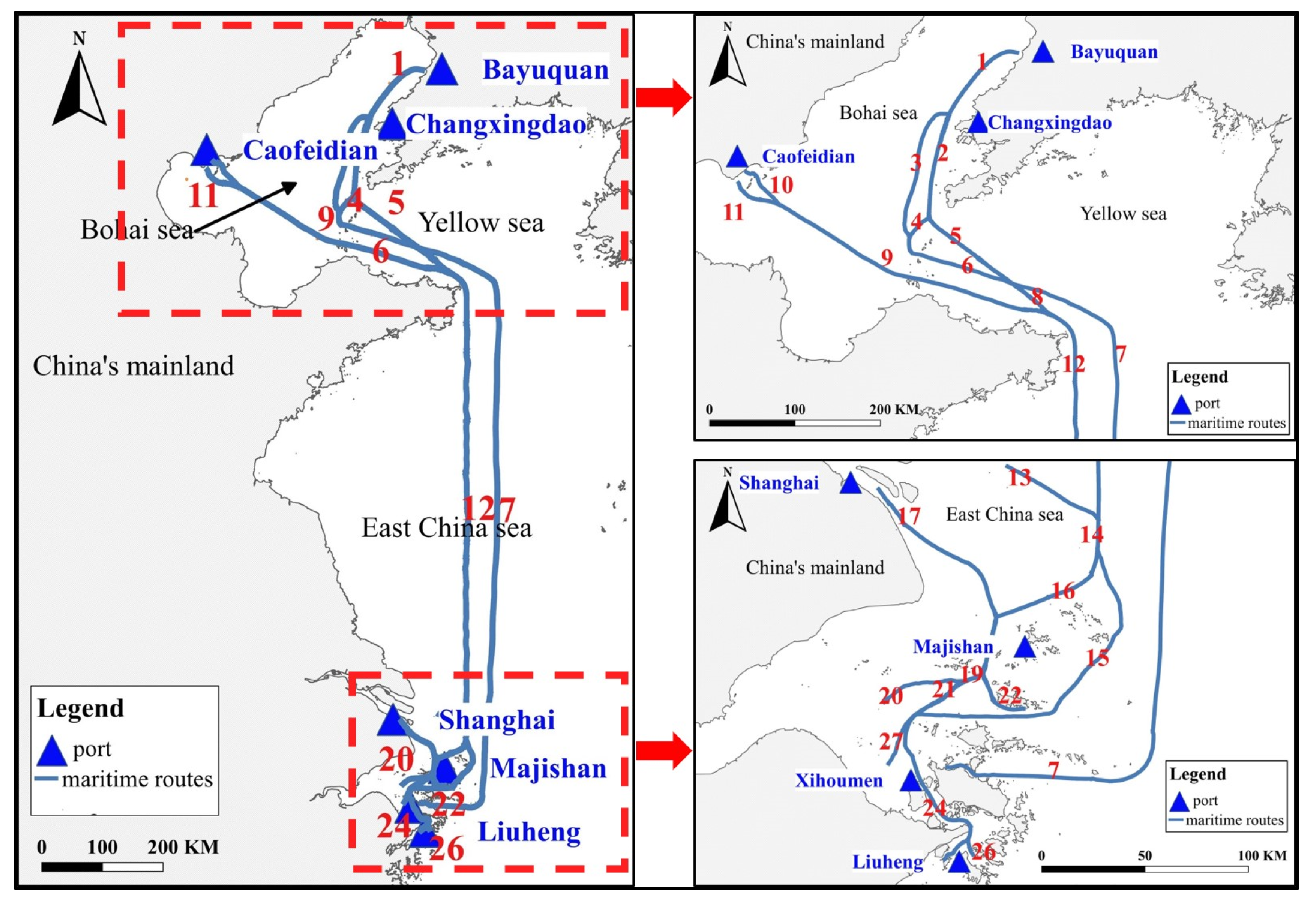
3.1.1. Overview of the Study Area
3.1.2. AIS Data Preprocessing
- Map matching. Map matching is essentially a process of matching trajectory points with maps. The geographic coordinate system for the AIS data is WGS84. However, due to the data encryption problem for the data crawler, we needed to perform artificial offset correction by comparing them with the WGS84 map.
- Data deletion. In order to ensure the accuracy of the research, it was necessary to delete illogical data. We directly deleted data in the following cases: (1) trajectory data whose MMSI was null or whose length was not 9, (2) duplicate AIS data, (2) the trajectory of a vessel sailing in a foreign sea area bordering on China, as the study only considered vessels sailing within China’s sea areas, and (4) the intersection points of the track segments whose lengths of the adjacent track segments were all greater than the average length of all the segments of the target track.
- Data cutting. As the data obtained by the crawler are accidental, it was possible for multiple navigations to mark a single voyage, so we cut the ship track from the spatial and time angle.
- Data completion. (1) After completion of the data cleaning and cutting, since the offshore environment is unstable, and the probability of shore-based satellite dot drift is high, we chose the Kalman filter algorithm for processing the ship trajectory data. on the one hand, it can eliminate abnormal points for the distance offset, and it can effectively smooth the trajectory, making it more in line with the mapping features of the real world. (2) For the continuity of the follow-up study, we then interpolated the trajectory data. For the problem of data completion, we chose the Lagrange first-order interpolation algorithm and the Lagrange second-order interpolation algorithm to complete the trajectory according to the concave–convex trajectory points until the interval condition of the trajectory segment was satisfied. (3) Since some dynamic attributes appeared as null locus points after interpolation, the attributes of the vessel locus points were calculated and completed according to the actual situation.
3.2. Detection of Abnormal Ship Behavior Based on Spatial Attributes
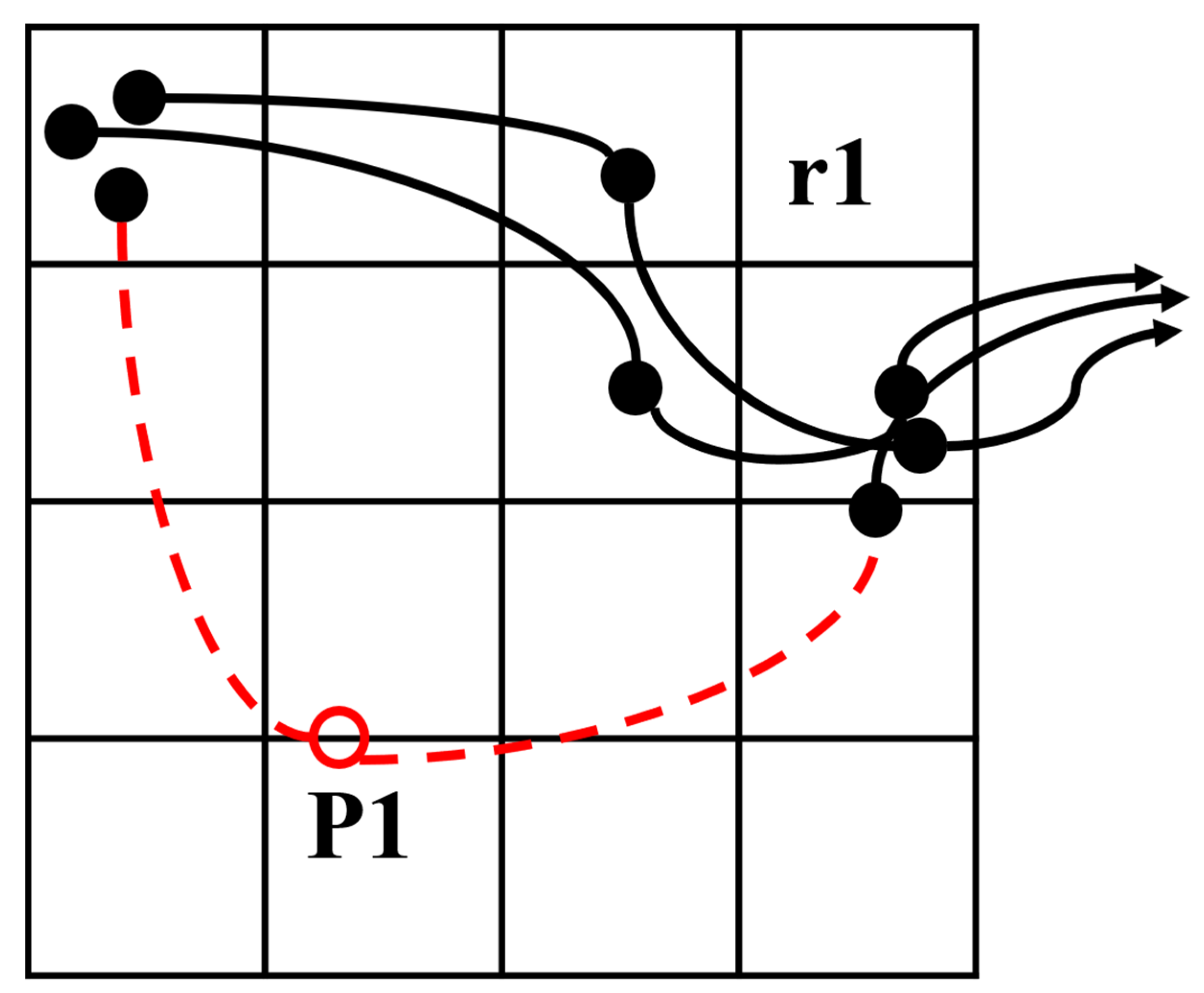
3.2.1. Maritime Route Extraction Based on AIS Data
| Algorithm 1: Principal graph algorithm |
| Input: Trajectory points and parameters: |
| Output: the principal graph: |
|
3.2.2. Detection of Spatial Abnormal Behavior of Ships Based on Rayda’s Criterion
| Algorithm 2: Rayda’s criterion |
| Input: Trajectory points , standard deviation multiple |
| Output: outlier set |
|
| Then, put into y |
3.3. Detection of Abnormal Ship Behavior Based on Thematic Attributes
3.3.1. Nearest Route Matching
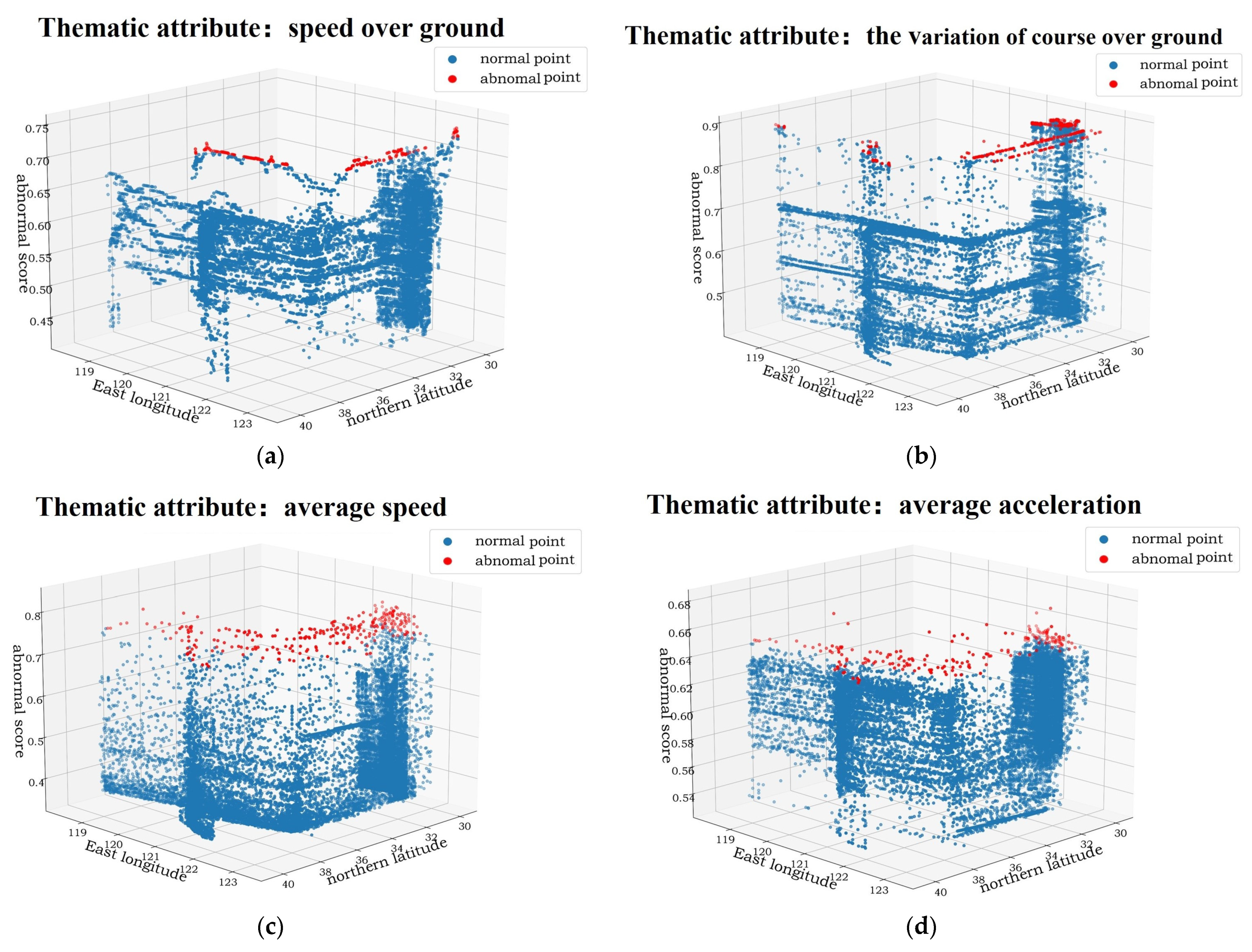
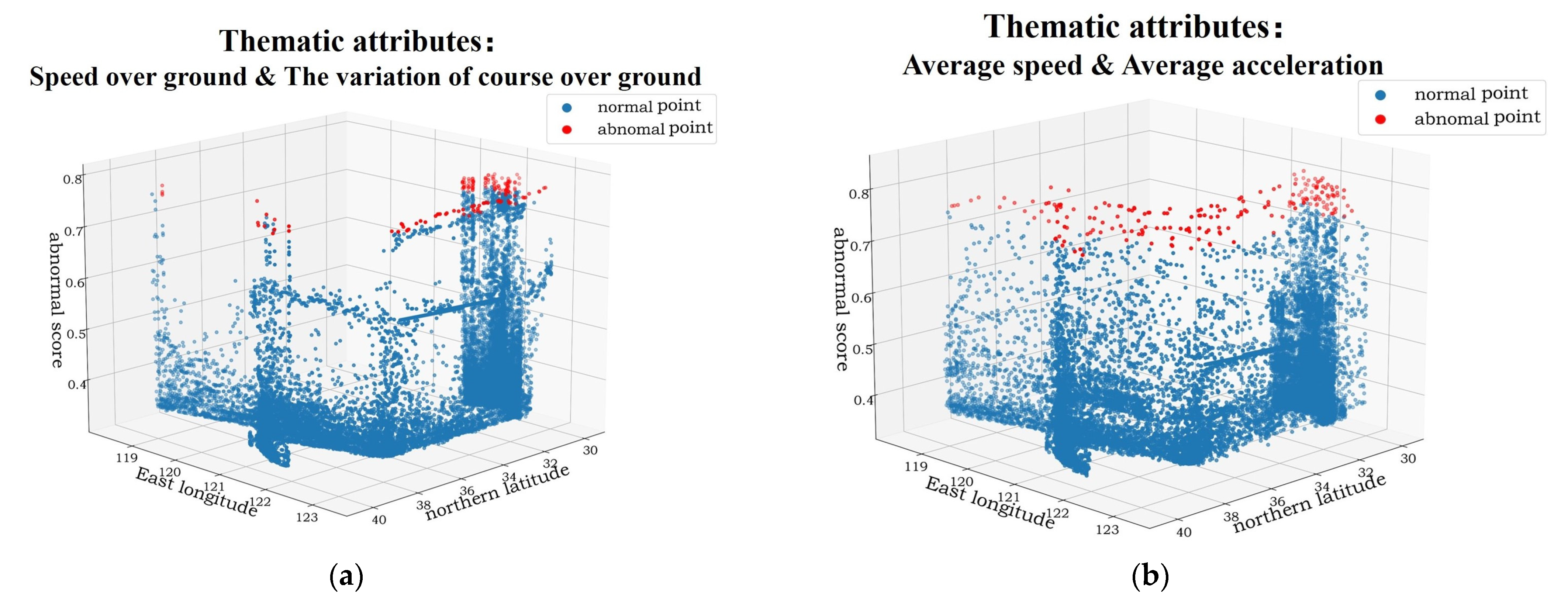
3.3.2. Anomaly Detection Based on the Isolation Forest Algorithm by Using Thematic Attributes
- The data are abnormal when s approaches 1;
- The data are more normal when s is far less than 0.5;
- If the score of the entire set of data is around 0.5, there is no significant outlier in the set of data.
4. Results and Discussion
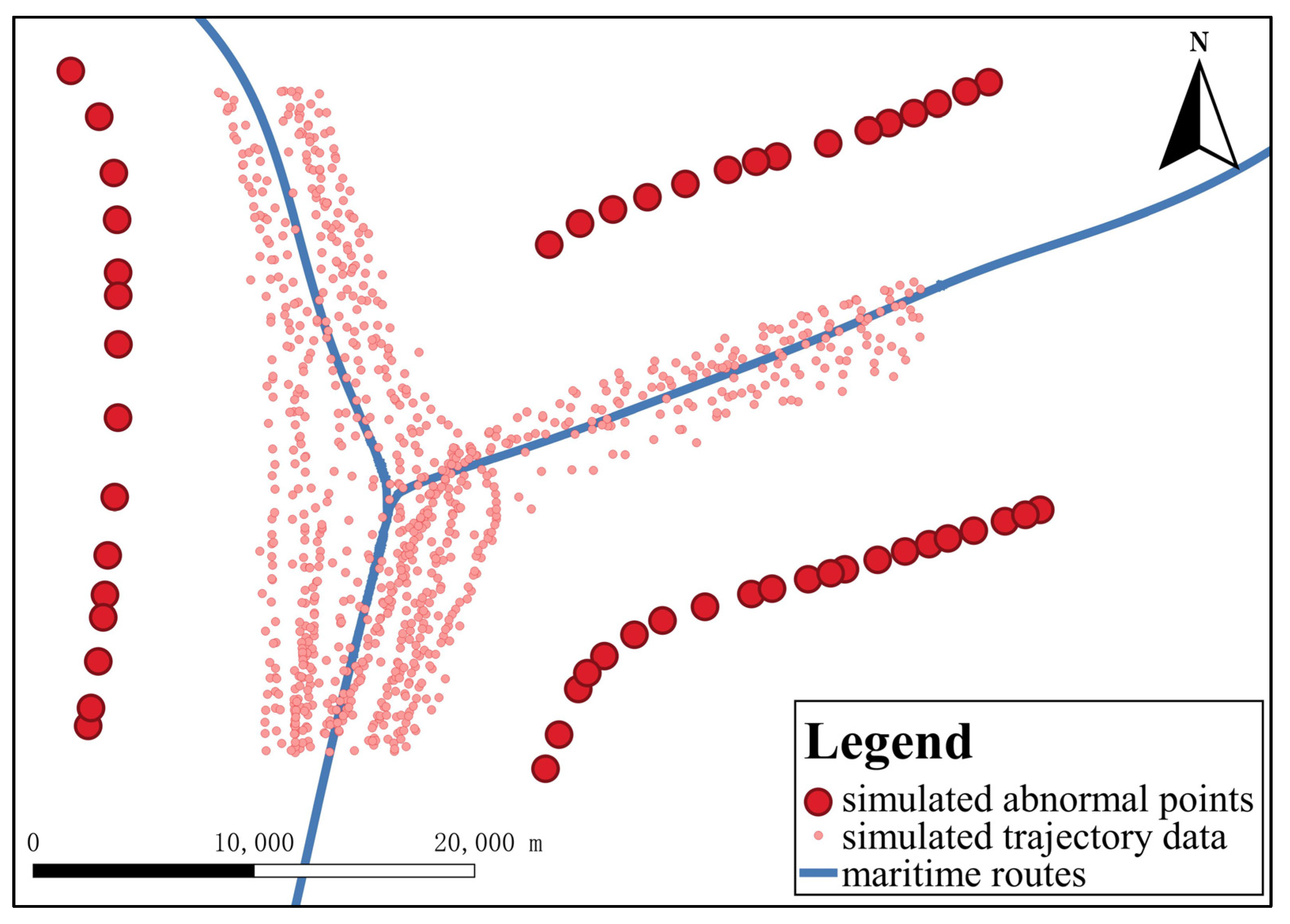
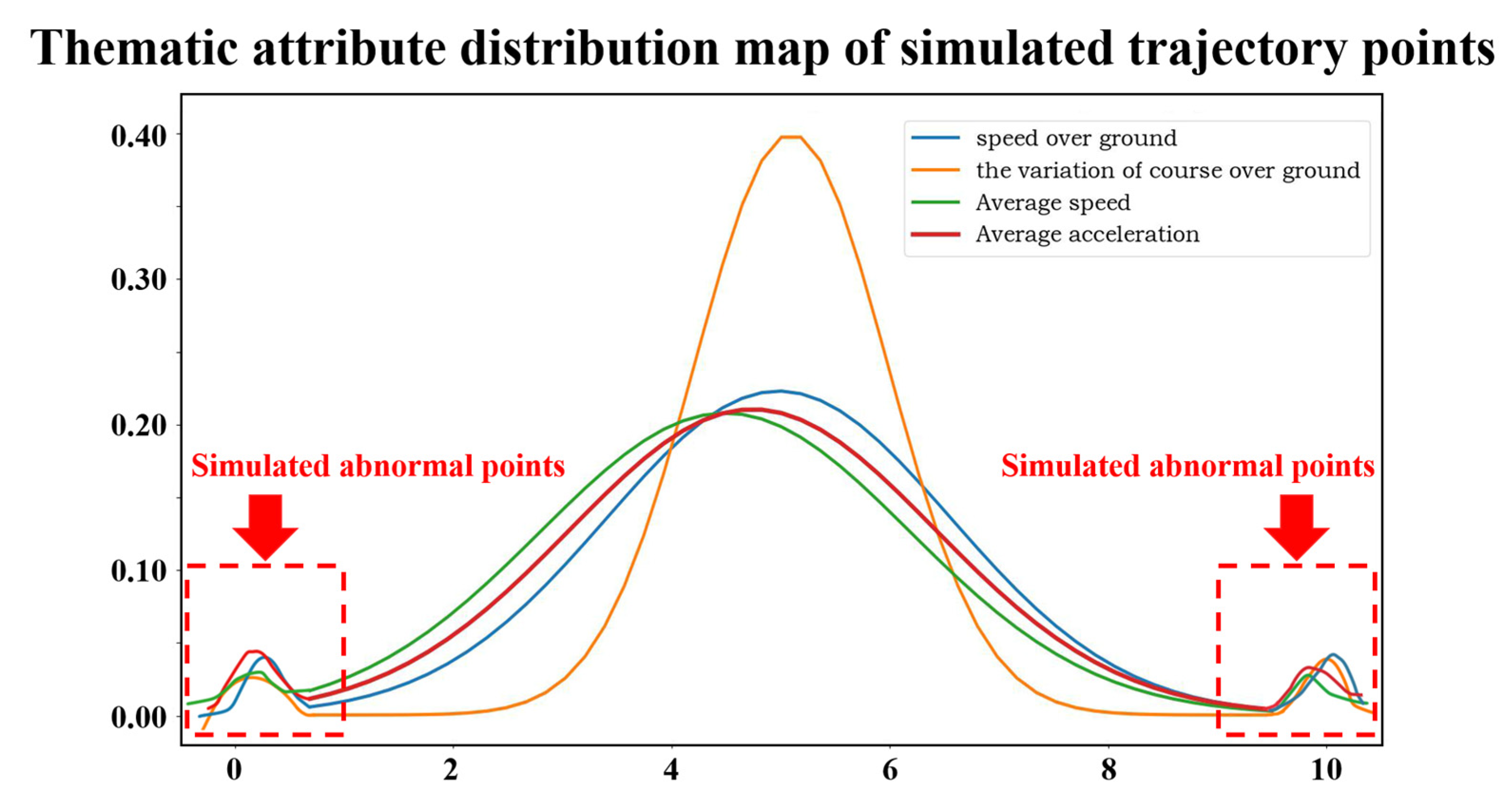
4.1. Simulated Experiments
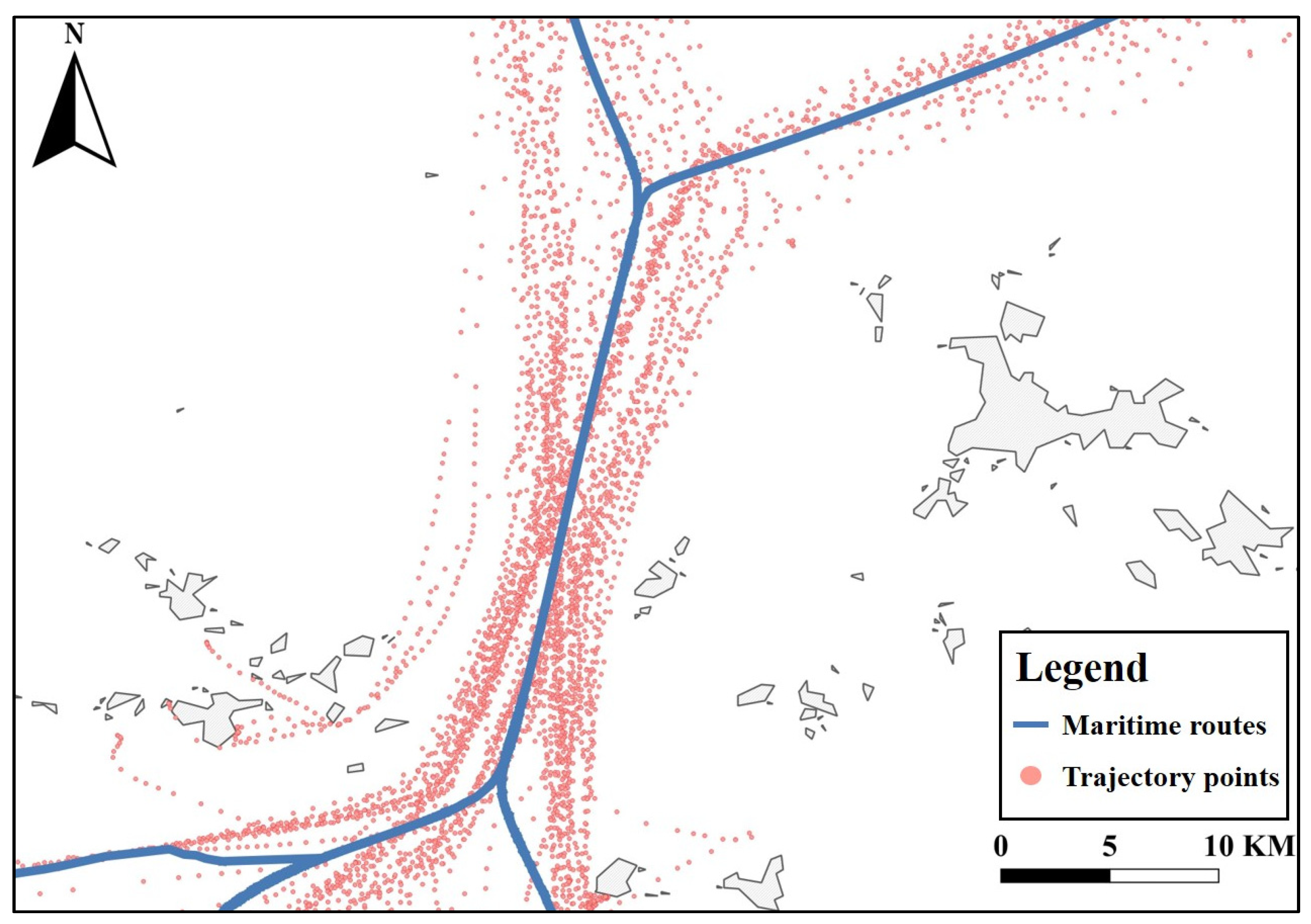
4.2. Experimental Results for Real Datasets
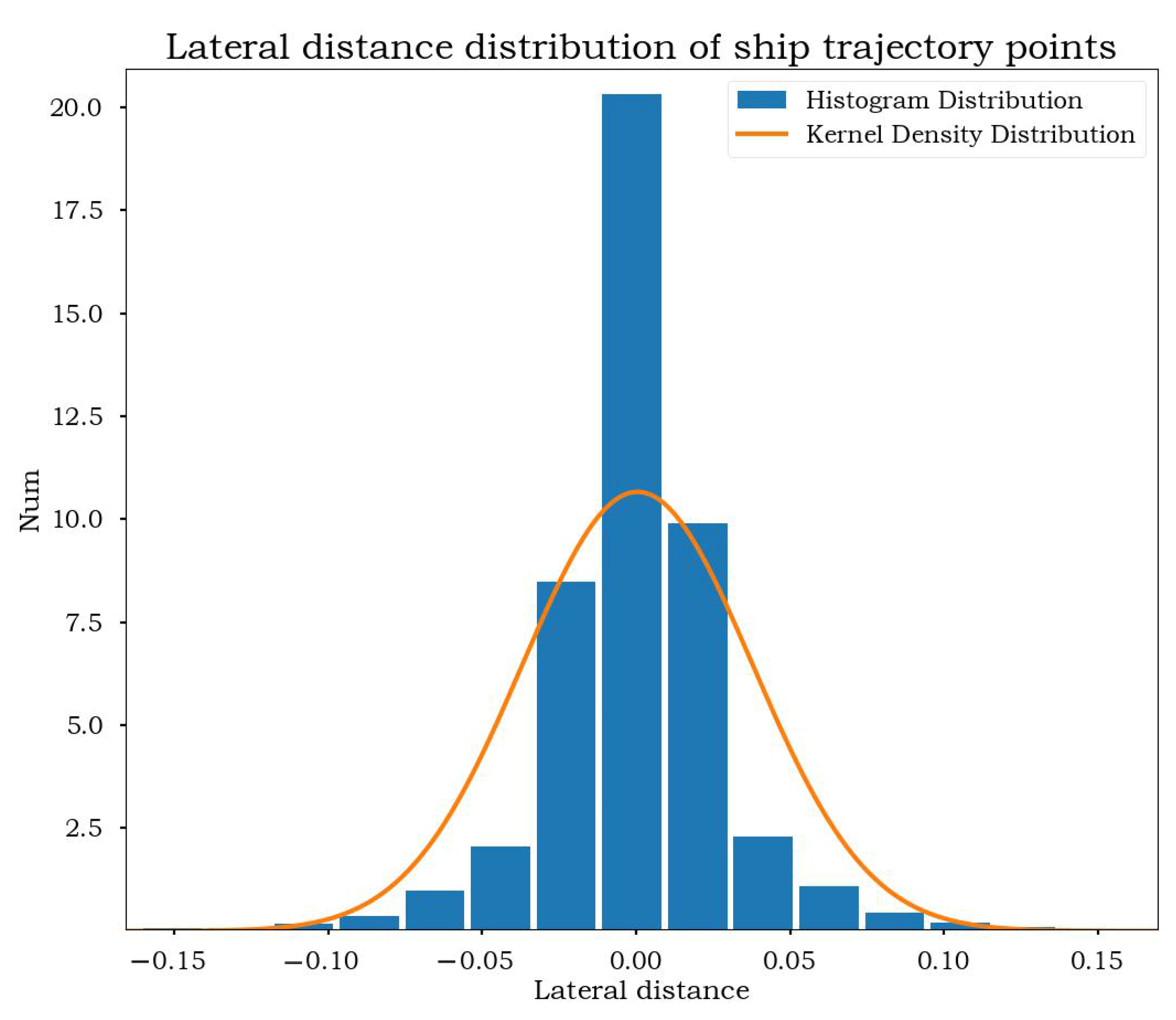
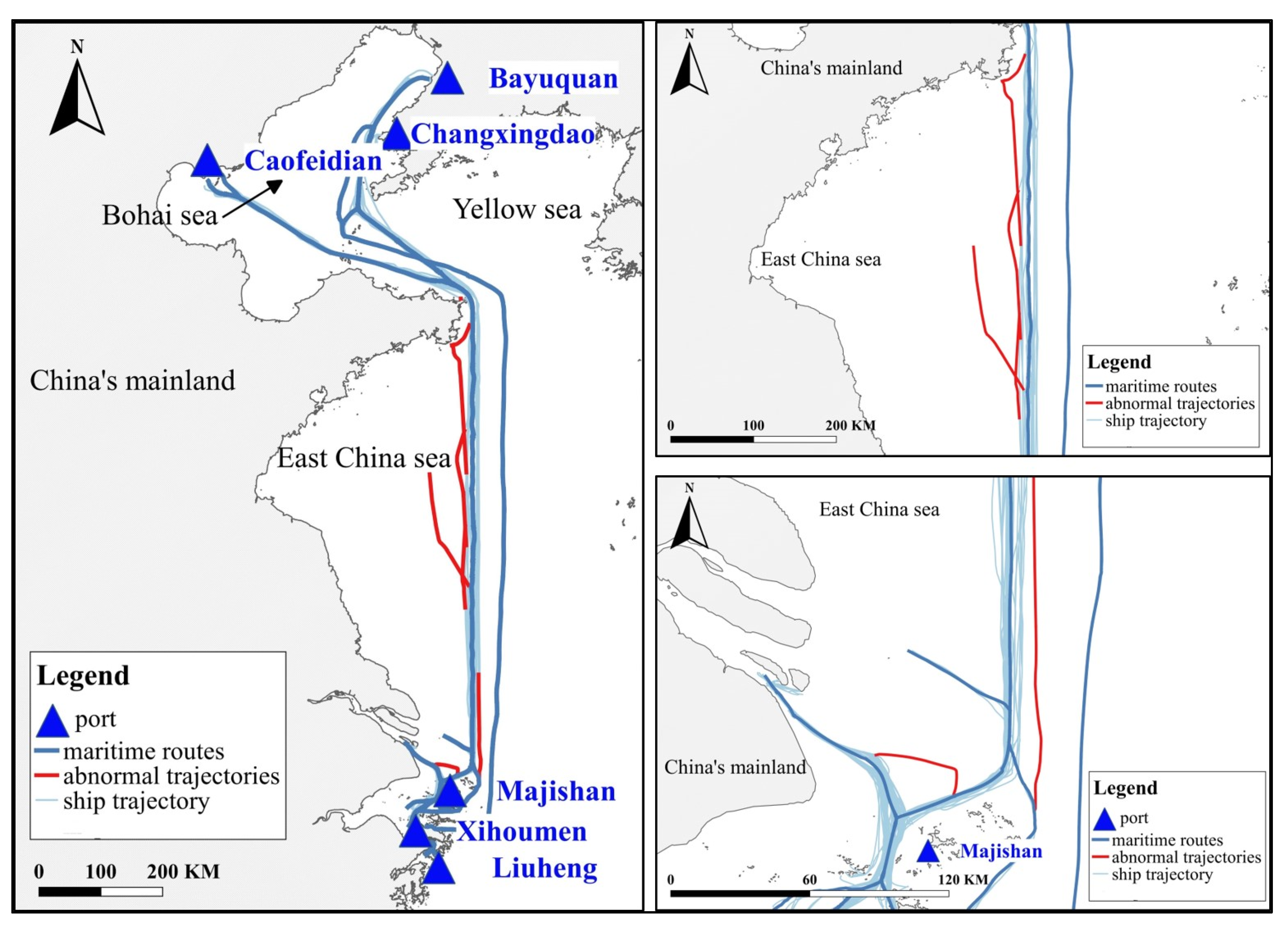
4.2.1. Detection of Abnormal Ship Behavior Based on Spatial Attributes
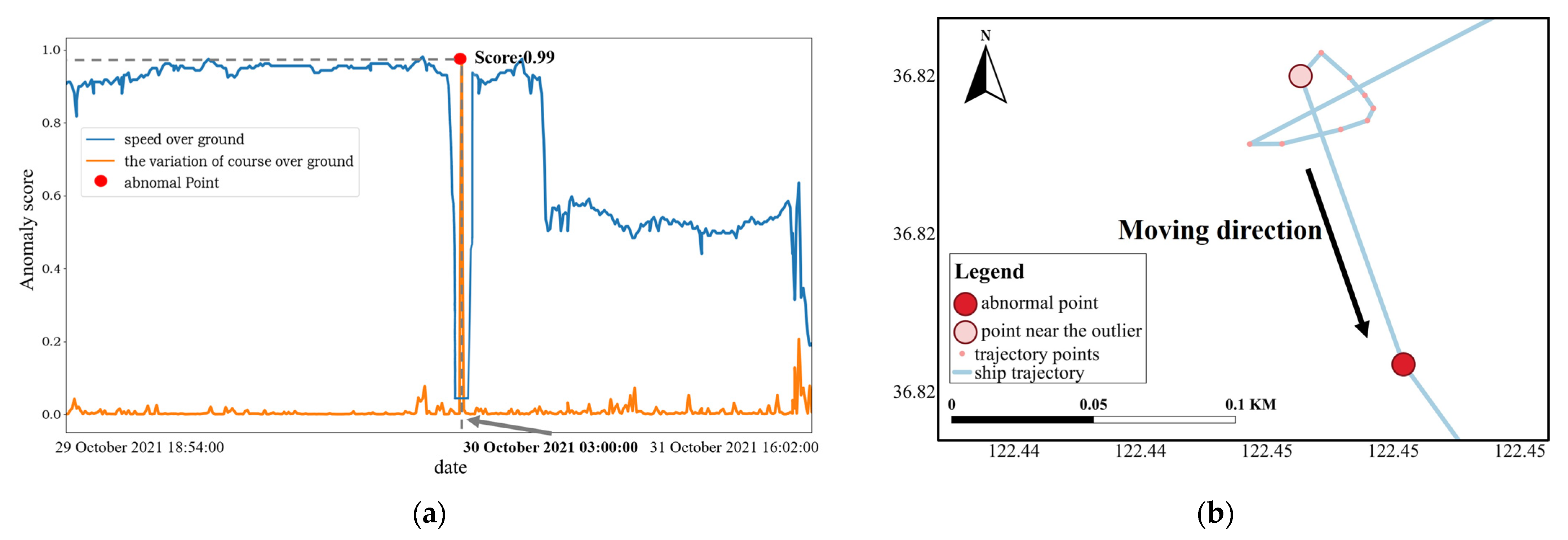
4.2.2. Detection of Abnormal Ship Behavior Based on Thematic Attributes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rong, H.; Teixeira, A.P.; Soares, C.G. Ship trajectory uncertainty prediction based on a Gaussian Process model. Ocean Eng. 2019, 182, 499–511. [Google Scholar] [CrossRef]
- Pallotta, G.; Vespe, M.; Bryan, K. Vessel Pattern Knowledge Discovery from AIS Data: A Framework for Anomaly Detection and Route Prediction. Entropy 2013, 15, 2218–2245. [Google Scholar] [CrossRef]
- Mou, N.; Ren, H.; Zheng, Y.; Chen, J.; Niu, J.; Yang, T.; Zhang, L.; Liu, F. Traffic Inequality and Relations in Maritime Silk Road: A Network Flow Analysis. ISPRS Int. J. Geo-Inf. 2021, 10, 40. [Google Scholar] [CrossRef]
- He, J. ‘One Belt, One Road’: China's New Strategy and Its Impact on FDI. In Asia's Changing International Investment Regime; Springer: Berlin/Heidelberg, Germany, 2017; pp. 163–175. [Google Scholar]
- Lee, E.S.; Mokashi, A.J.; Sang, Y.M.; Kim, G.S. The Maturity of Automatic Identification Systems (AIS) and Its Implications for Innovation. J. Mar. Sci. Eng. 2019, 7, 287. [Google Scholar] [CrossRef]
- Lei, P.R. A framework for anomaly detection in maritime trajectory behavior. Knowl. Inf. Syst. 2016, 47, 189–214. [Google Scholar] [CrossRef]
- Yang, D.; Wu, L.; Wang, S.; Jia, H.; Li, K.X. How big data enriches maritime research—A critical review of Automatic Identification System (AIS) data applications. Transp Rev. 2019, 39, 755–773. [Google Scholar] [CrossRef]
- Ristic, B.; La Scala, B.; Morelande, M.; Gordon, N. Statistical analysis of motion patterns in AIS Data: Anomaly detection and motion prediction. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–7. [Google Scholar]
- Zhaolin, W. Maritime Traffic Engineering; Maritime Traffic Engineering: Liaoning, China, 1993. [Google Scholar]
- Holst, A.; Bjurling, B.; Ekman, J.; Rudström, Å.; Wallenius, K.; Björkman, M.; Fooladvandi, F.; Laxhammar, R.; Trönninger, J. A Joint Statistical and Symbolic Anomaly Detection System: Increasing performance in maritime surveillance. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 1919–1926. [Google Scholar]
- Soleimani, B.H.; De Souza, E.N.; Hilliard, C.; Matwin, S. Anomaly Detection in Maritime Data Based on Geometrical Analysis of Trajectories. In Proceedings of the 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 6–July 2015; pp. 1100–1105. [Google Scholar]
- Rong, H.; Teixeira, A.P.; Soares, C.G. Data mining approach to shipping route characterization and anomaly detection based on AIS data. Ocean. Eng. 2020, 198, 12. [Google Scholar] [CrossRef]
- Xiong, Y.; Xiaohao, Q.U.; Guo, J.; Mou, J.; Navigation, S.O. Monitoring of abnormal movement patterns of ferry based on AIS data. China Saf. Sci. J. 2016, 26, 100–103. [Google Scholar]
- Laxhammar, R. Anomaly detection for sea surveillance. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–8. [Google Scholar]
- Bomberger, N.A.; Rhodes, B.J.; Seibert, M.; Waxman, A.M. Associative learning of vessel motion patterns for maritime situation awareness. In Proceedings of the 9th International Conference on Information Fusion, Florence, Italy, 10 July 2006; pp. 729–736. [Google Scholar]
- Smith, M.; Reece, S.; Roberts, S.; Rezek, I. Online Maritime Abnormality Detection using Gaussian Processes and Extreme Value Theory. In Proceedings of the 12th IEEE International Conference on Data Mining (ICDM), Brussels, Belgium, 10–13 December 2012; pp. 645–654. [Google Scholar]
- Venskus, J.; Treigys, P.; Bernatavičienė, J.; Tamulevičius, G.; Medvedev, V. Real-Time Maritime Traffic Anomaly Detection Based on Sensors and History Data Embedding. Sensors 2019, 19, 3782. [Google Scholar] [CrossRef] [PubMed]
- Shahir, H.Y.; Glässer, U.; Nalbandyan, N.; Wehn, H. Maritime Situation Analysis: A Multi-vessel Interaction and Anomaly Detection Framework. In Proceedings of the 2014 IEEE Joint Intelligence and Security Informatics Conference, The Hague, The Netherlands, 24–26 September 2014; pp. 192–199. [Google Scholar]
- Pallotta, G.; Jousselme, A.L. Data-driven Detection and Context-based Classification of Maritime Anomalies. In Proceedings of the 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 6–9 July 2015; pp. 1152–1159. [Google Scholar]
- Osekowska, E.; Johnson, H.; Carlsson, B. Grid Size Optimization for Potential Field based Maritime Anomaly Detection. Transp. Res. Procedia 2014, 3, 720–729. [Google Scholar] [CrossRef][Green Version]
- Venskus, J.; Kurmis, M.; Andziulis, A.; Lukosius, Z.; Voznak, M.; Bykovas, D. Self-Learning Adaptive Algorithm for Maritime Traffic Abnormal Movement Detection based on Virtual Pheromone Method. In Proceedings of the 2015 International Symposium on Performance Evaluation of Computer and Telecommunication Systems (SPECTS), Chicago, IL, USA, 27–29 July 2015. [Google Scholar]
- Riveiro, M.; Pallotta, G.; Vespe, M. Maritime anomaly detection: A review. Wiley Interdiscip. Rev.-Data Min. Knowl. Discov. 2018, 8, e1266. [Google Scholar] [CrossRef]
- Kraiman, J.B. Automated anomaly detection processor. Proc. SPIE 2002, 4716, 128–137. [Google Scholar]
- Riveiro, M.; Falkman, G.; Ziemke, T. Visual analytics for the detection of anomalous maritime behavior. In Proceedings of the 12th International Conference Information Visualisation 2008, London, UK, 9–11 July 2008; pp. 273–279. [Google Scholar]
- Mascaro, S.; Nicholson, A.; Korb, K. Anomaly detection in vessel tracks using Bayesian networks. Int. J. Approx. Reason. 2014, 55, 84–98. [Google Scholar] [CrossRef]
- Radon, A.N.; Wang, K.; Glässer, U.; Wehn, H.; Westwell-Roper, A. Contextual verification for false alarm reduction in maritime anomaly detection. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 1123–1133. [Google Scholar]
- Jakob, M.; Vanĕk, O.; Pĕchouček, M. Using Agents to Improve International Maritime Transport Security. IEEE Intell. Syst. 2011, 26, 90–96. [Google Scholar] [CrossRef]
- Laxhammar, R.; Falkman, G.; Sviestins, E. Anomaly detection in sea traffic—A comparison of the Gaussian Mixture Model and the Kernel Density Estimator. In Proceedings of the 12th International Conference on Information Fusion, Seattle, WA, USA, 6–9 July 2009; pp. 756–763. [Google Scholar]
- Arguedas, V.F.; Mazzarella, F.; Vespe, M. Spatio-temporal Data Mining for Maritime Situational Awareness. In Proceedings of the Oceans 2015 Genova, Ctr Congressi, Genova, Genova, Italy, 18–21 May 2015. [Google Scholar]
- Jasinevicius, R.; Petrauskas, V. Fuzzy Expert Maps for Risk Management Systems. In Proceedings of the IEEE/OES Us/EU-Baltic International Symposium, Tallinn, Estonia, 27–29 May 2008; pp. 35–38. [Google Scholar]
- Bautista-Sánchez, R.; Barbosa-Santillan, L.I.; Sánchez-Escobar, J. Method for Select Best AIS Data in Prediction Vessel Movements and Route Estimation. Appl. Sci. 2021, 11, 2429. [Google Scholar] [CrossRef]
- Huang, J.; Deng, M.; Tang, J.; Hu, S.; Liu, H.; Wariyo, S.; He, J. Automatic Generation of Road Maps from Low Quality GPS Trajectory Data via Structure Learning. IEEE Access 2018, 6, 71965–71975. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008. [Google Scholar]






| AIS Data Type | AIS Data Message Content |
|---|---|
| Static | Maritime Mobile Service Identification (MMSI), International Maritime Organization (IMO), callsign, ship width, ship type, ship draught, navigation port |
| Dynamic | Position, timestamp, speed over ground (SOG), course over ground (COG) |
| Methods | Accuracy | Recall | Precision | F-Score |
|---|---|---|---|---|
| Our method | 0.988 | 0.780 | 0.975 | 0.867 |
| GMM | 0.733 | 0.820 | 0.142 | 0.243 |
| MT-MAD | 0.984 | 0.740 | 0.949 | 0.831 |
| Methods | Accuracy | Recall | Precision | F-Score |
|---|---|---|---|---|
| Our method | 0.989 | 0.950 | 0.809 | 0.874 |
| DBSCAN | 0.995 | 0.520 | 0.347 | 0.416 |
| Shahir’s method | 0.987 | 0.950 | 0.792 | 0.864 |
| Name of Sea Area | Number of Tracks |
|---|---|
| East China Sea | 10,746 |
| Bohai Sea | 870 |
| Yellow Sea | 820 |
| South China Sea | 206 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Long, C.; Yang, X.; Deng, M. Abnormal Ship Behavior Detection Based on AIS Data. Appl. Sci. 2022, 12, 4635. https://doi.org/10.3390/app12094635
Shi Y, Long C, Yang X, Deng M. Abnormal Ship Behavior Detection Based on AIS Data. Applied Sciences. 2022; 12(9):4635. https://doi.org/10.3390/app12094635
Chicago/Turabian StyleShi, Yan, Cheng Long, Xuexi Yang, and Min Deng. 2022. "Abnormal Ship Behavior Detection Based on AIS Data" Applied Sciences 12, no. 9: 4635. https://doi.org/10.3390/app12094635
APA StyleShi, Y., Long, C., Yang, X., & Deng, M. (2022). Abnormal Ship Behavior Detection Based on AIS Data. Applied Sciences, 12(9), 4635. https://doi.org/10.3390/app12094635








