A Pressure-Based Fully-Coupled Flow Algorithm for the Control Volume Finite Element Method
Abstract
1. Introduction
2. Governing Equations
3. The Control Volume Finite Element Method
4. The Pressure-Based Coupled Solution Procedure
4.1. Discretized Momentum Conservation Equation
4.2. Discretized Mass Conservation Equation
4.3. Discretized Energy Conservation Equation
5. Boundary Conditions
5.1. Boundary Conditions for the Momentum Conservation Equation
5.1.1. No-Slip Wall
5.1.2. Inlet
5.1.3. Outlet
5.1.4. Opening
5.1.5. Symmetry Plane
5.2. Boundary Conditions for the Mass Conservation Equation
5.2.1. No-Slip Walls
5.2.2. Inlet
5.2.3. Outlet
5.2.4. Opening
5.2.5. Symmetry Plane
5.3. Boundary Conditions for the Energy Conservation Equation
5.3.1. No-Slip Wall
5.3.2. Inlet
5.3.3. Outlet
5.3.4. Opening
5.3.5. Symmetry Plane
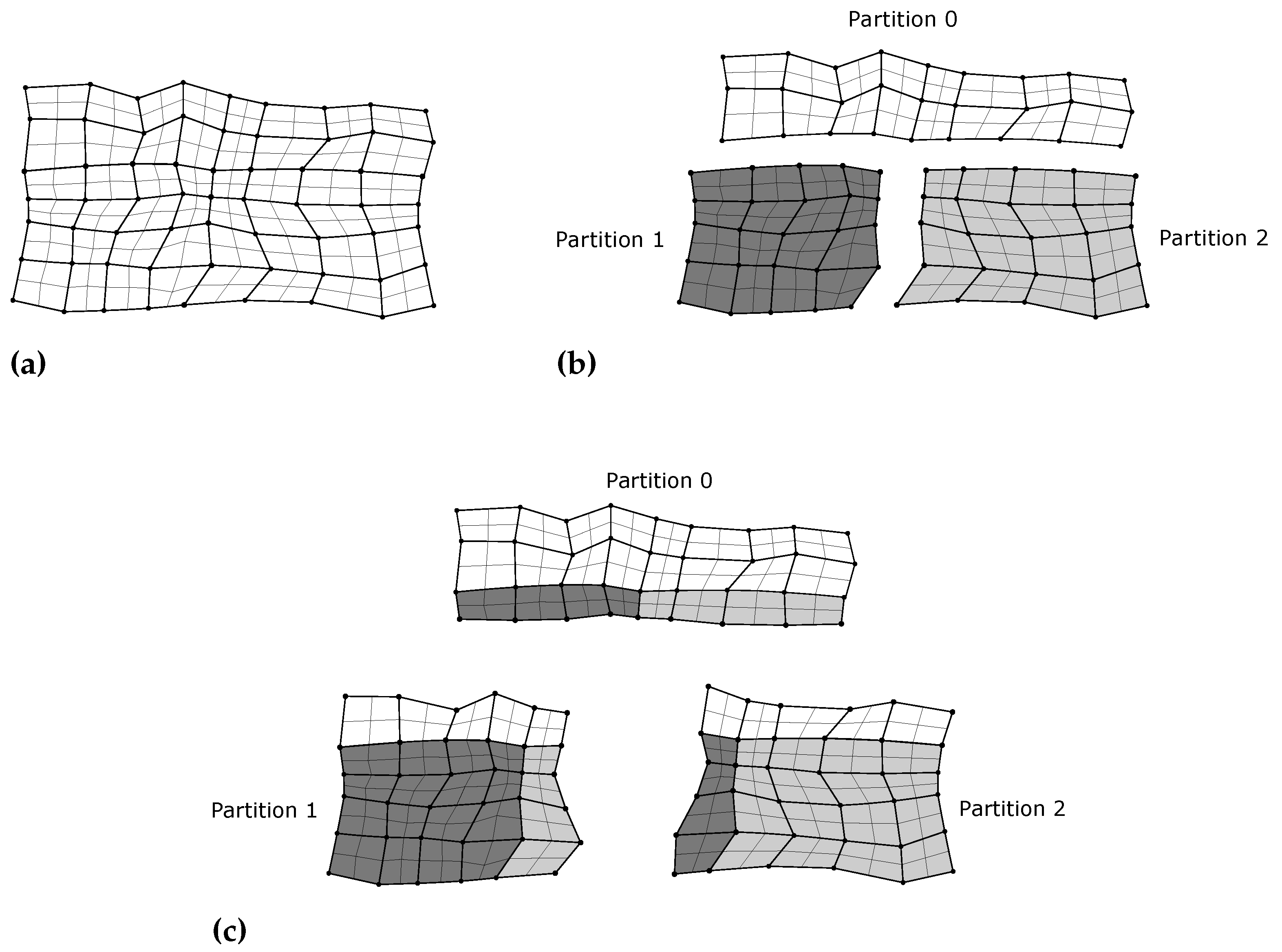
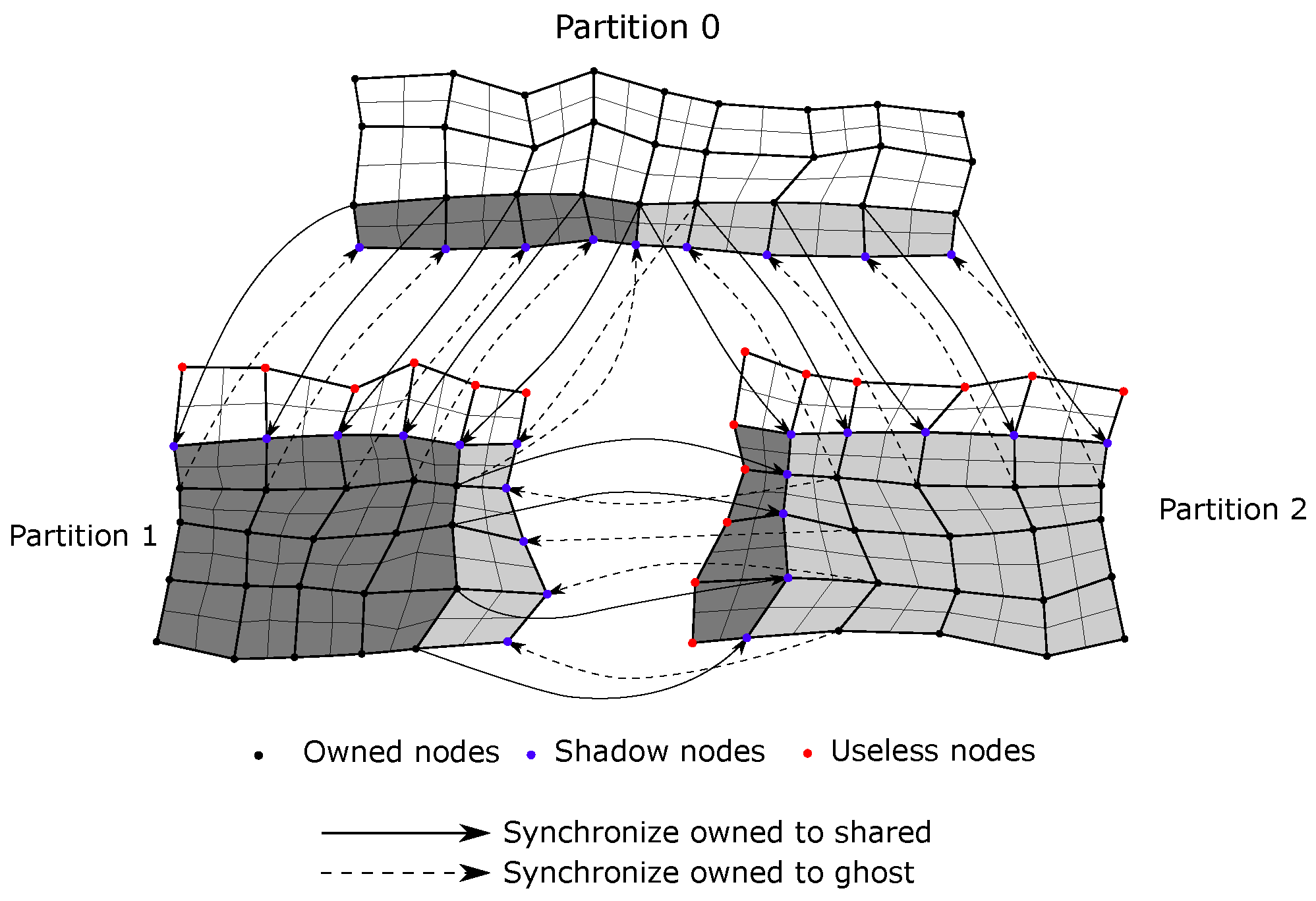
6. Parallelization Strategy
7. Test Cases
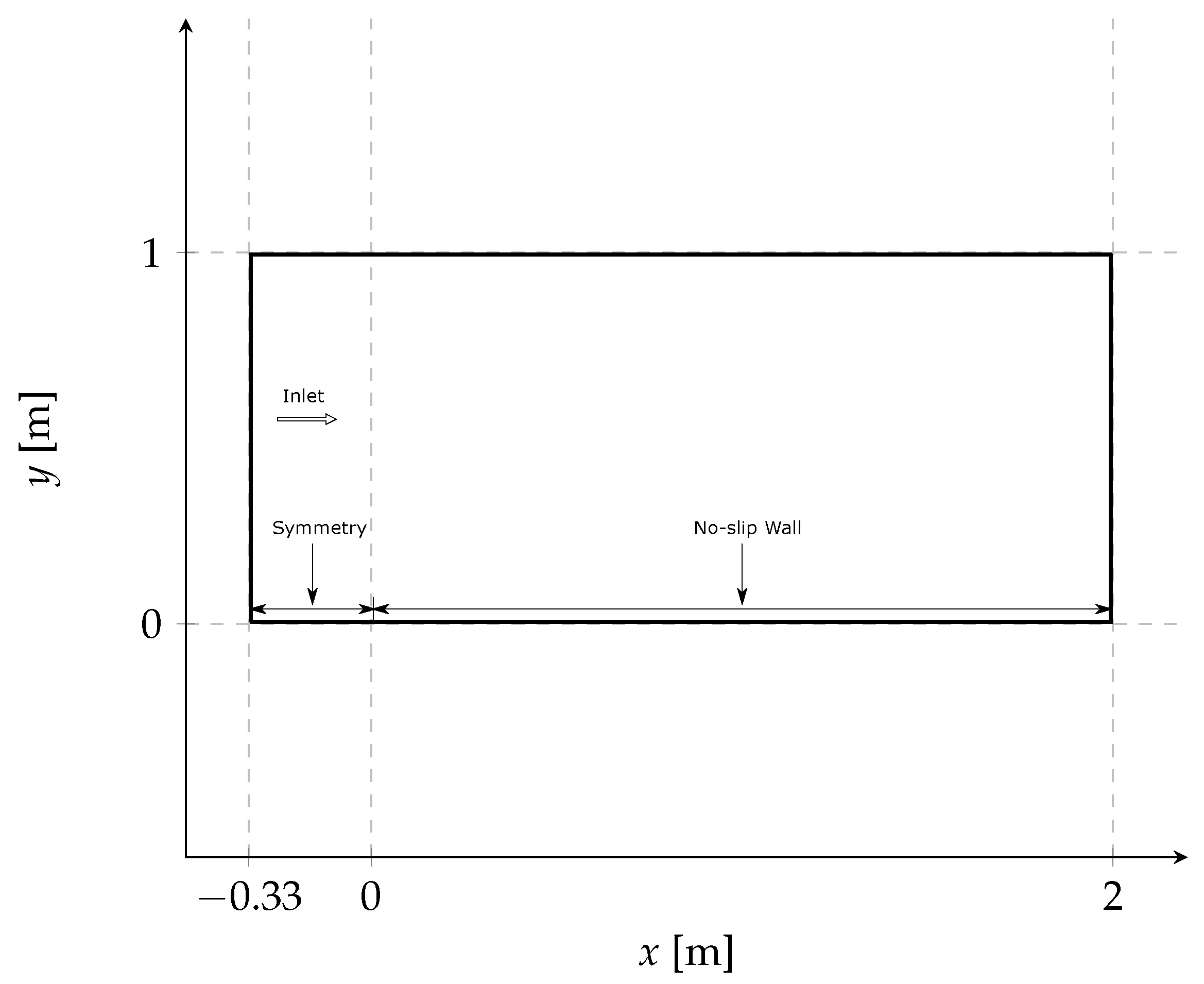
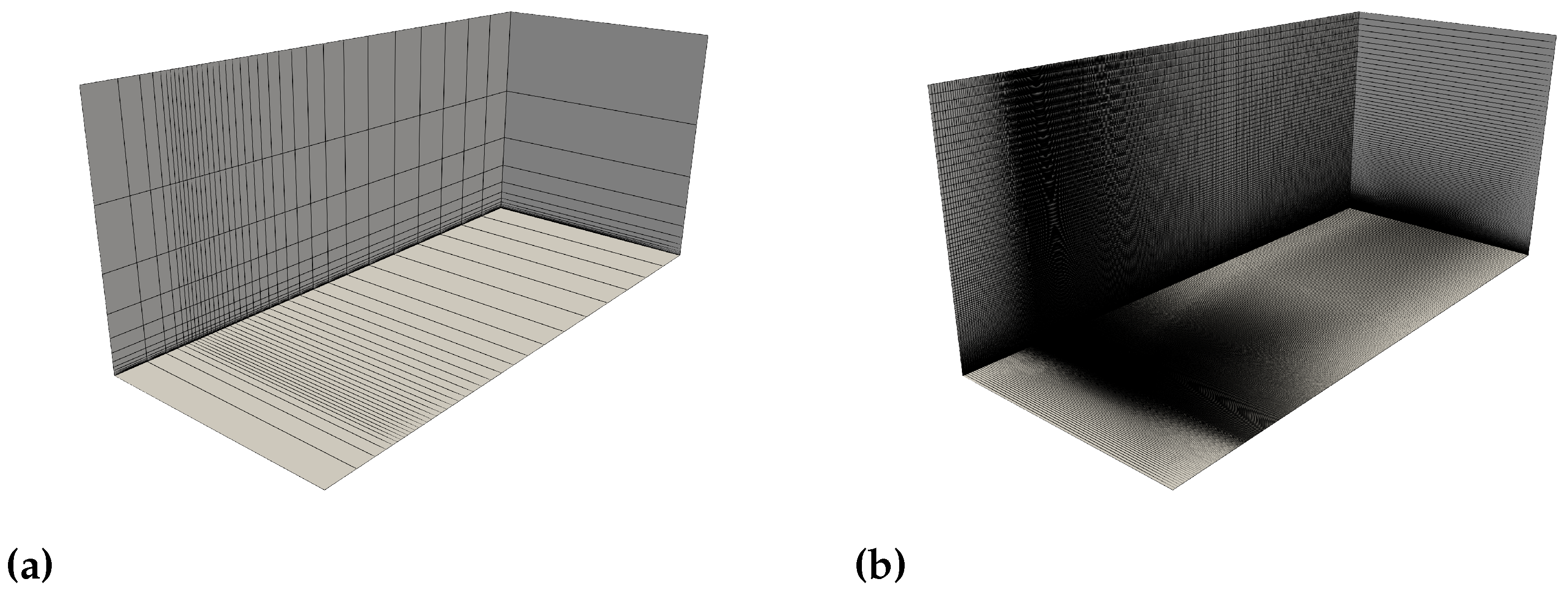
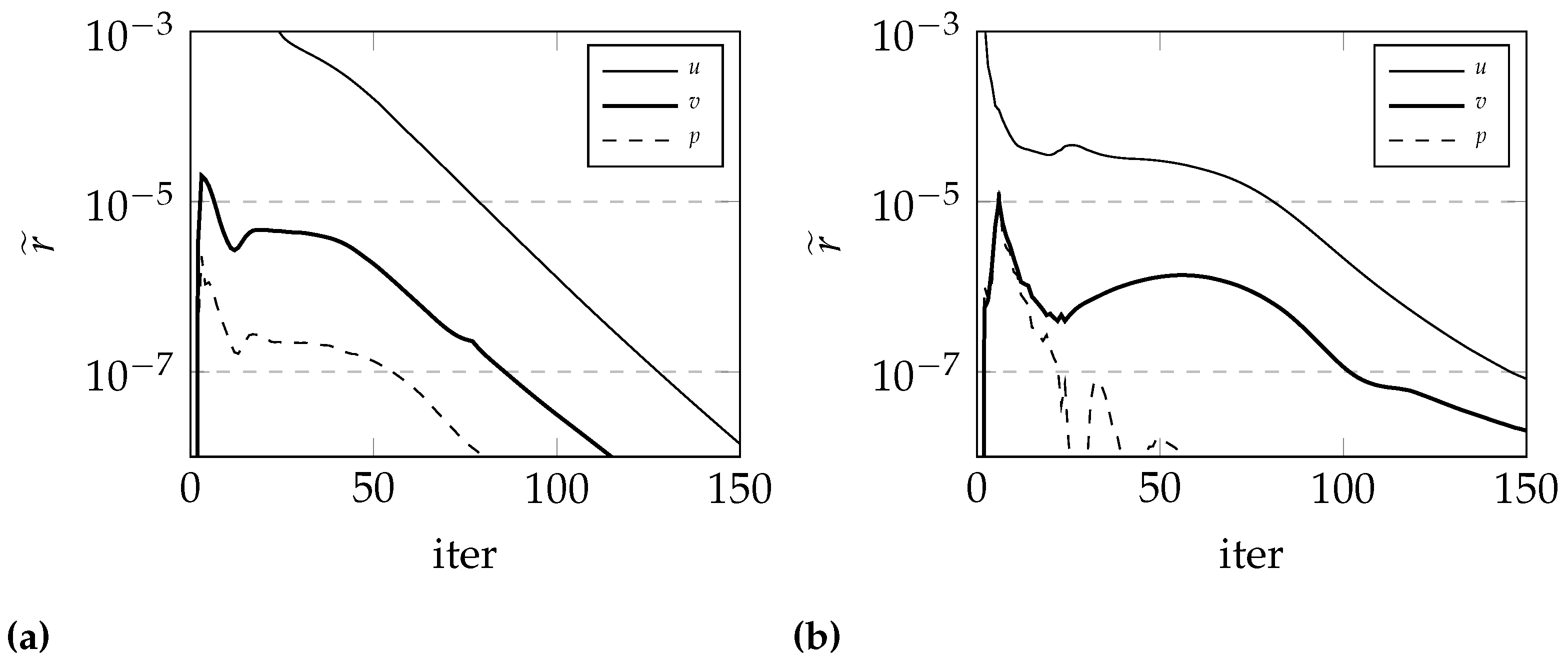
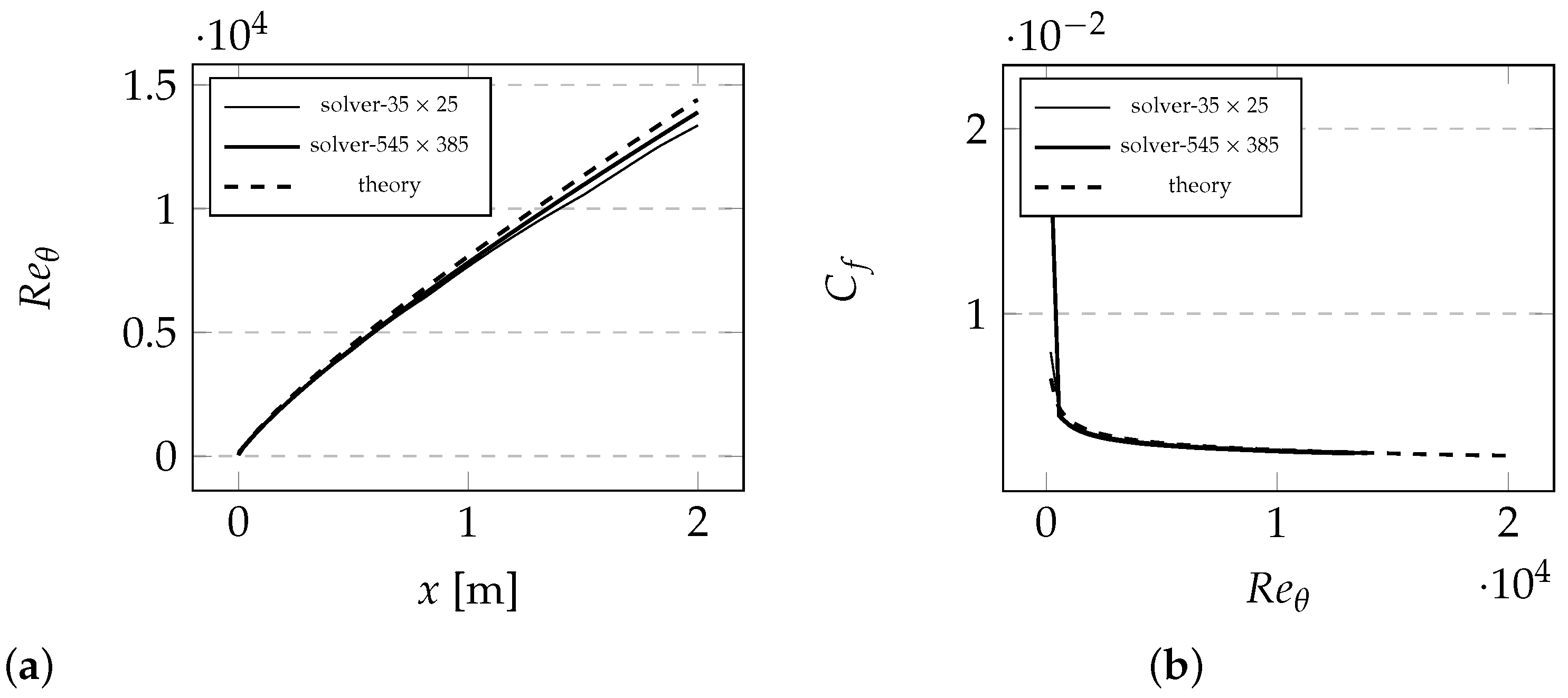
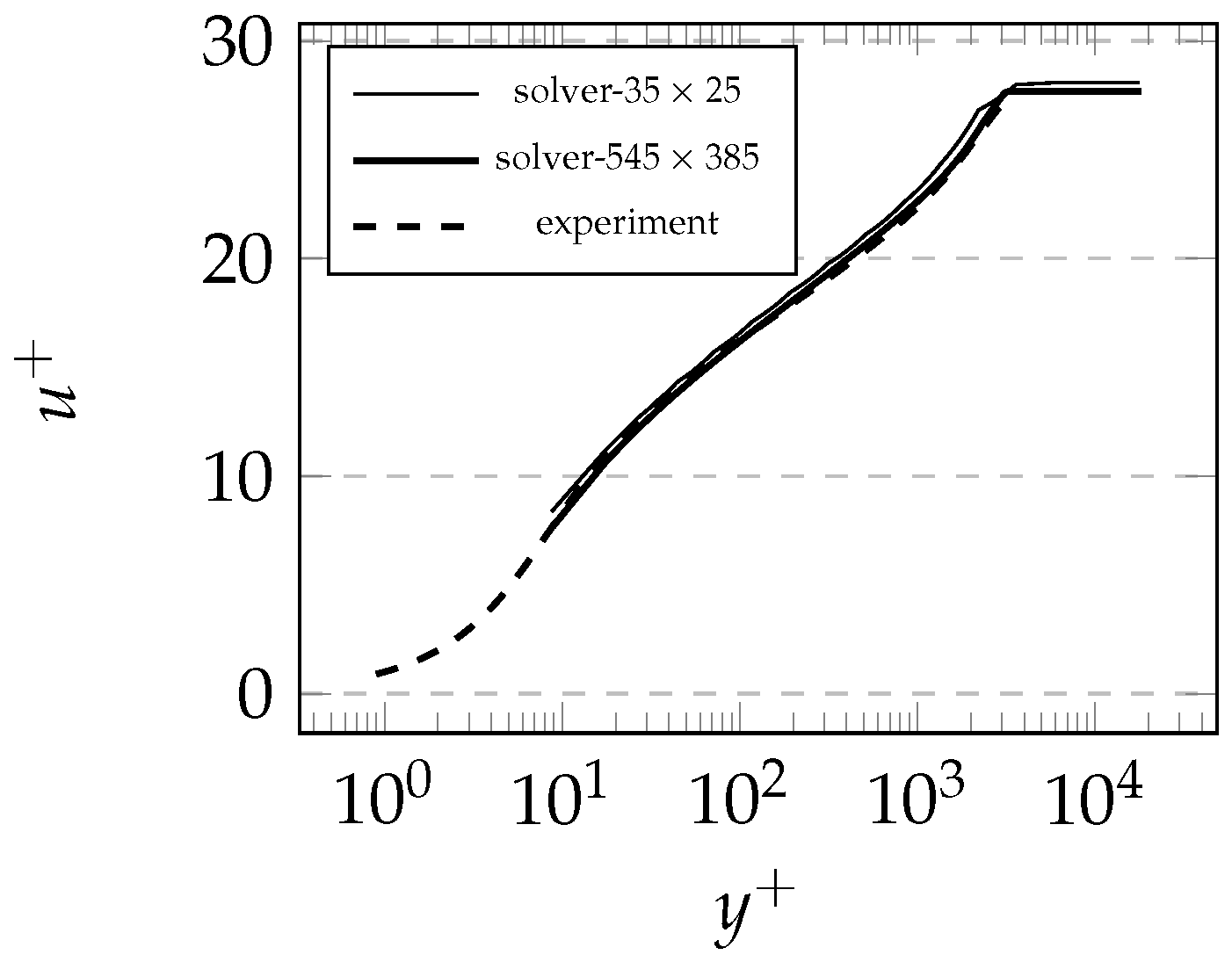
7.1. Turbulent Flow over a Flat Plate
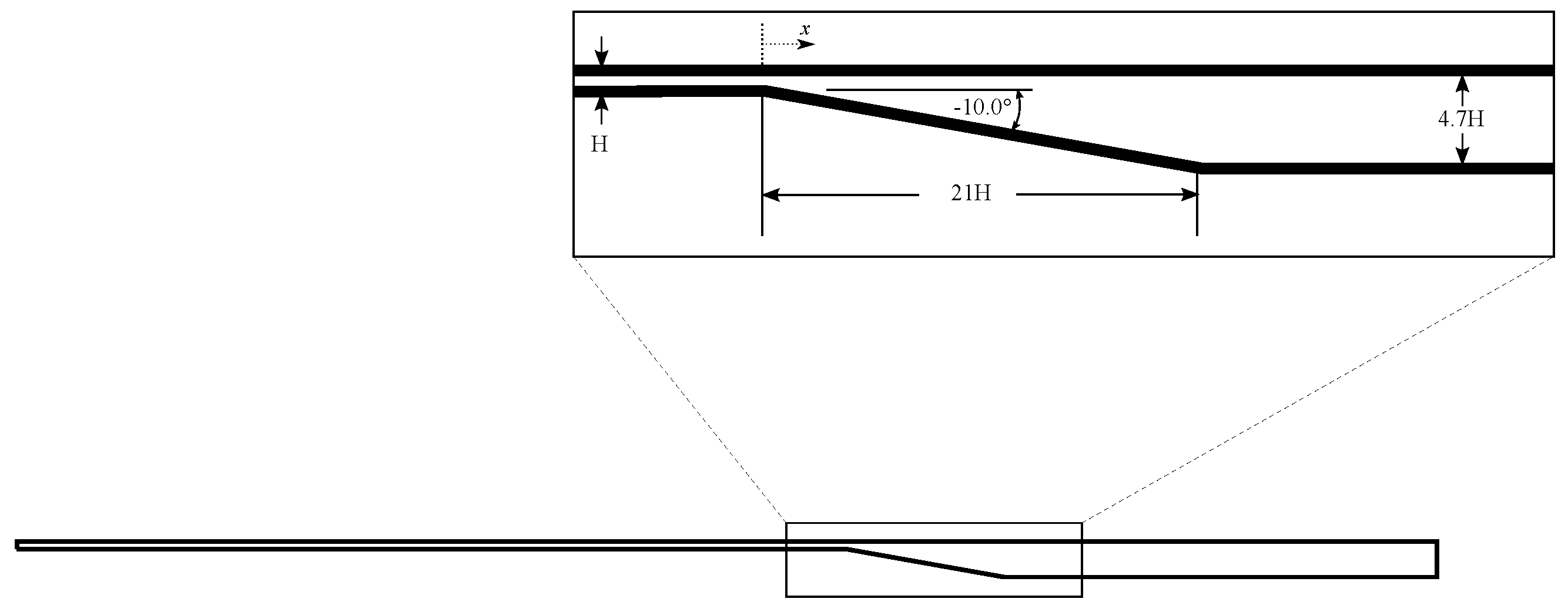
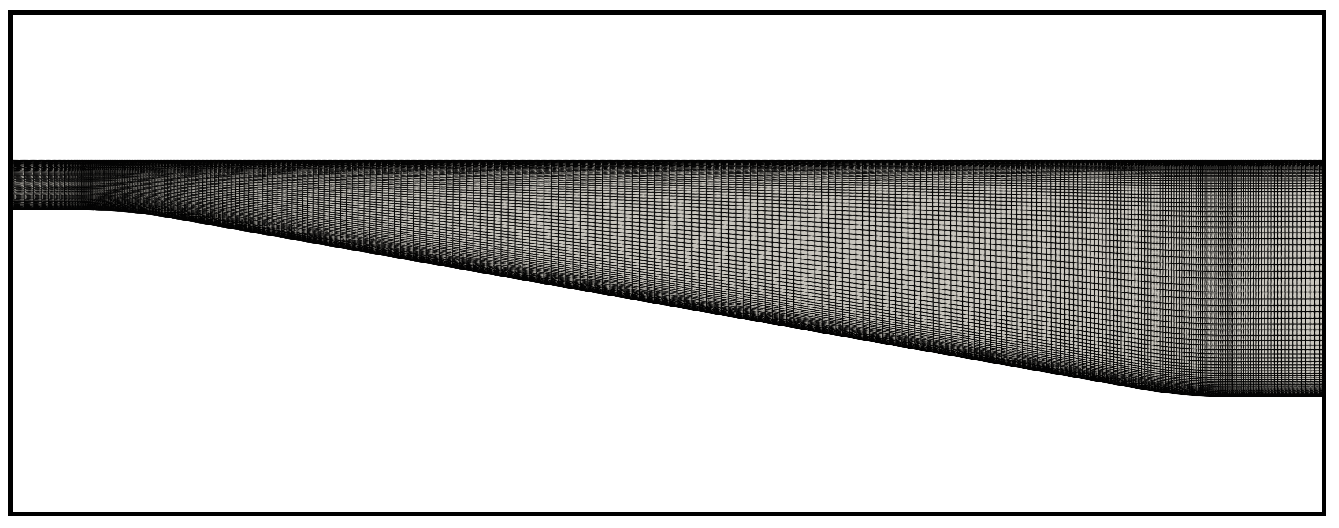
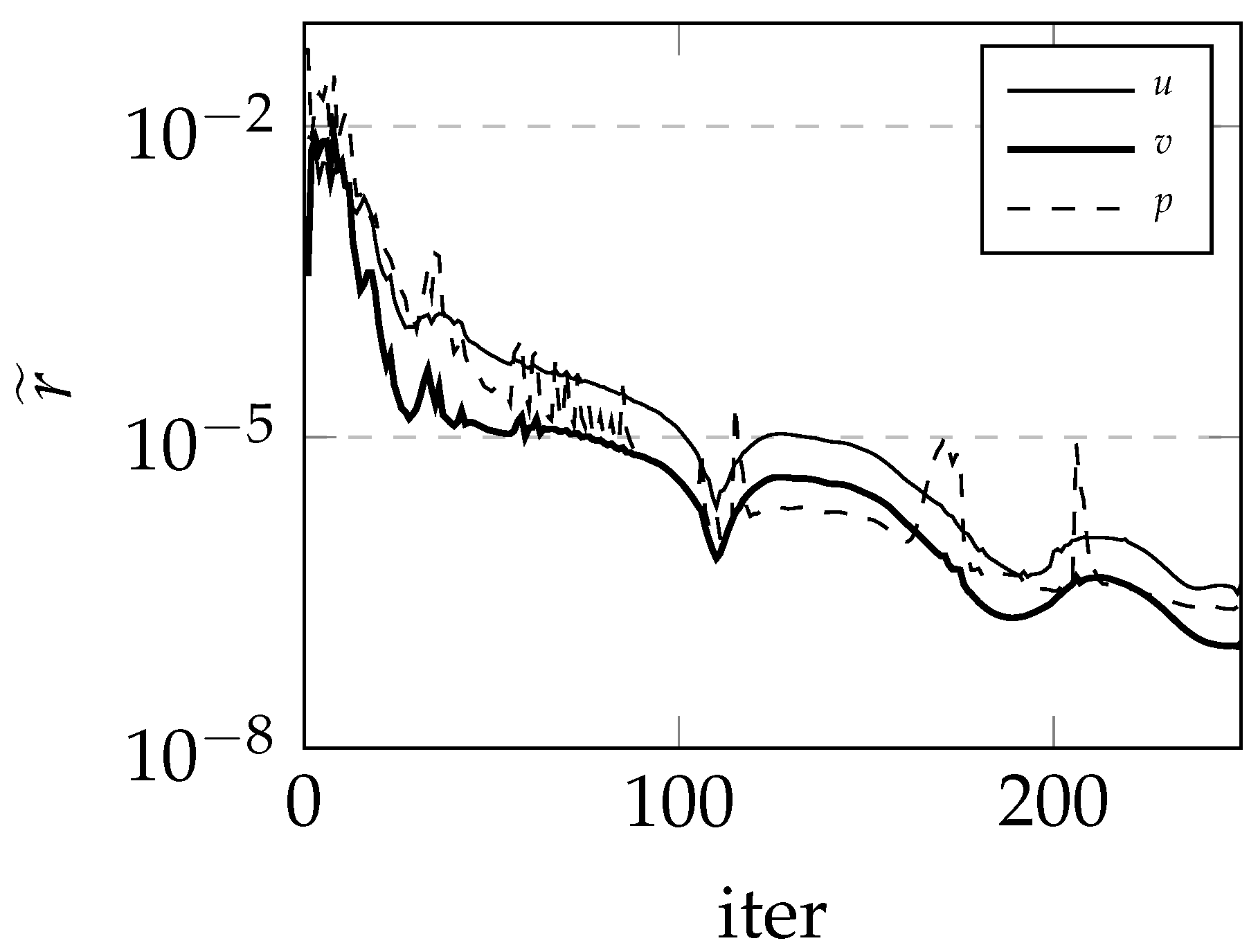
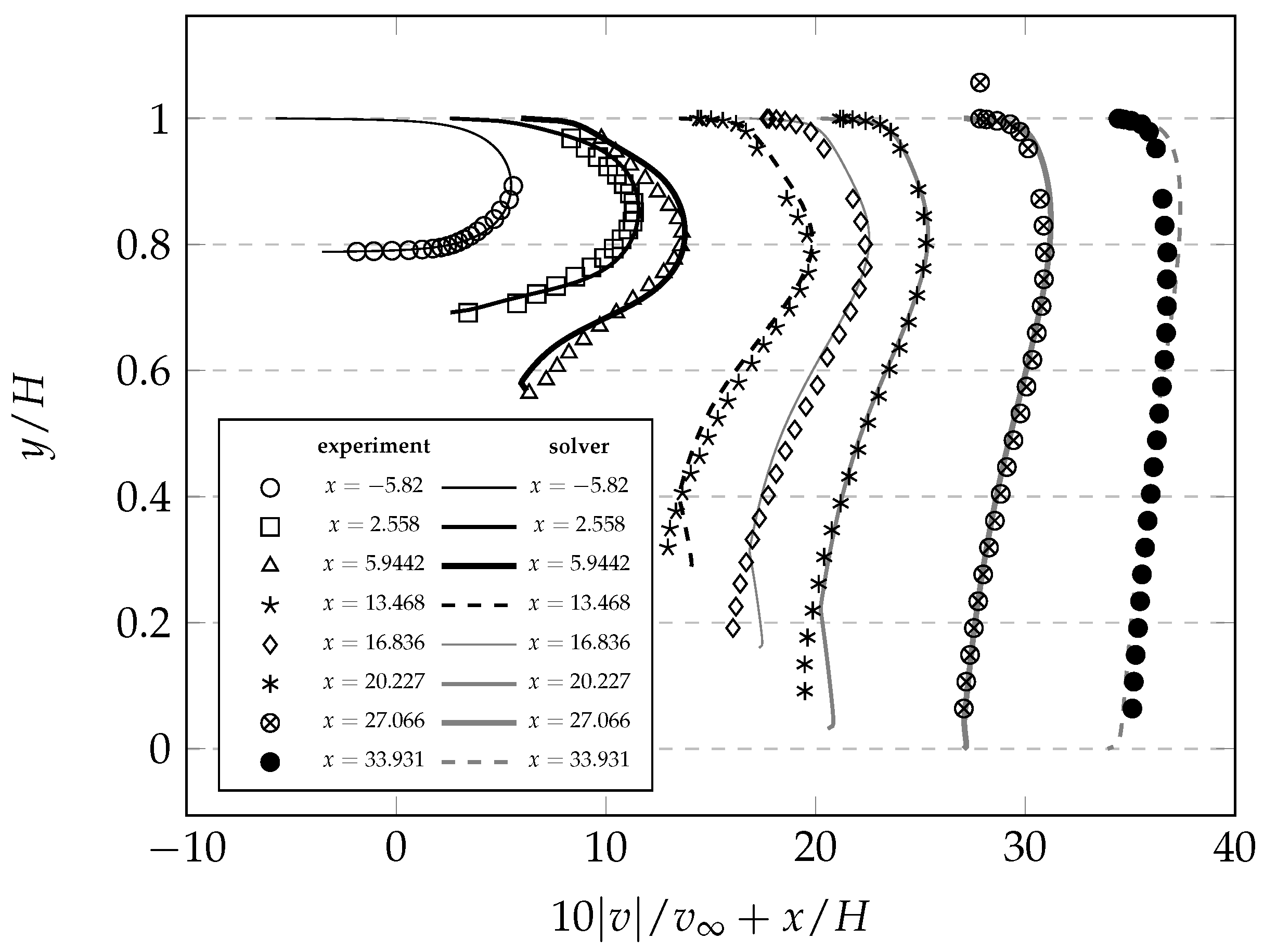
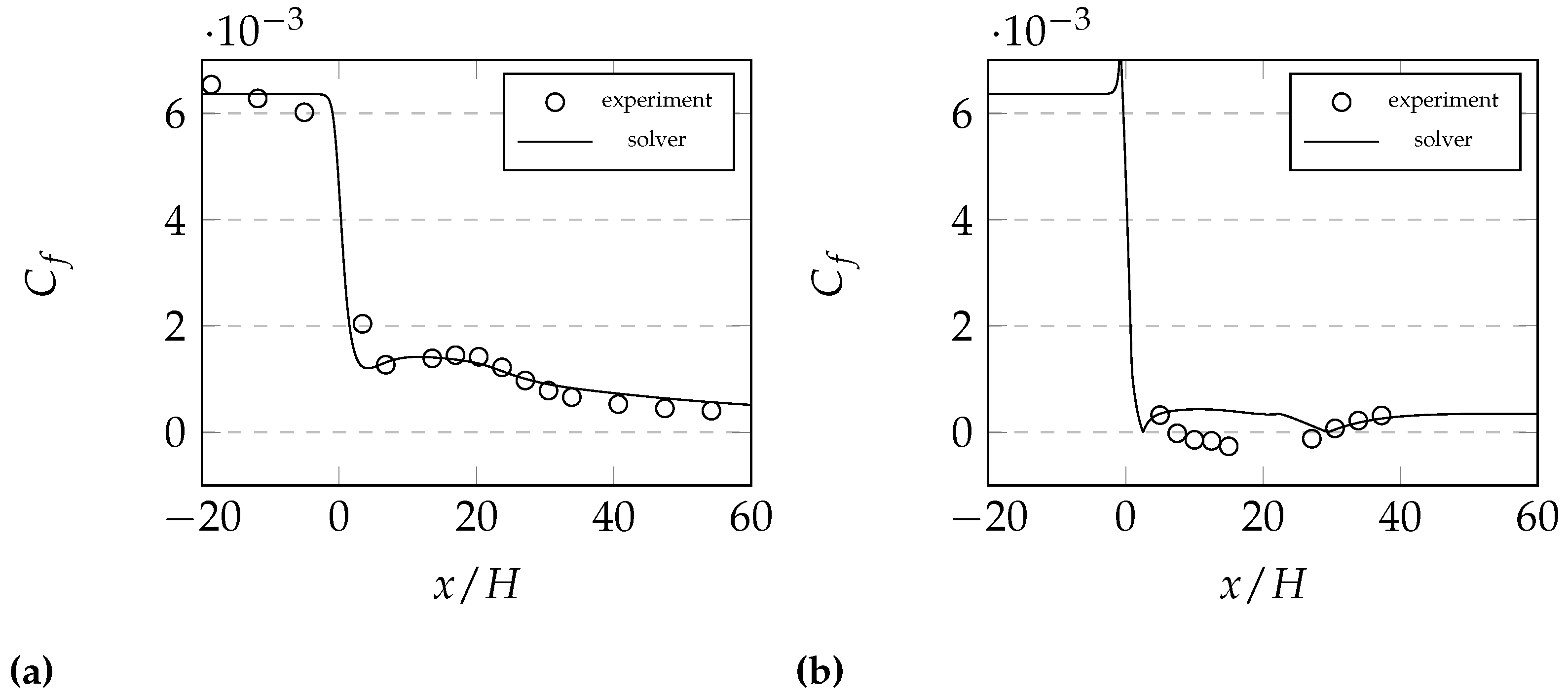
7.2. Buice 2D Diffuser
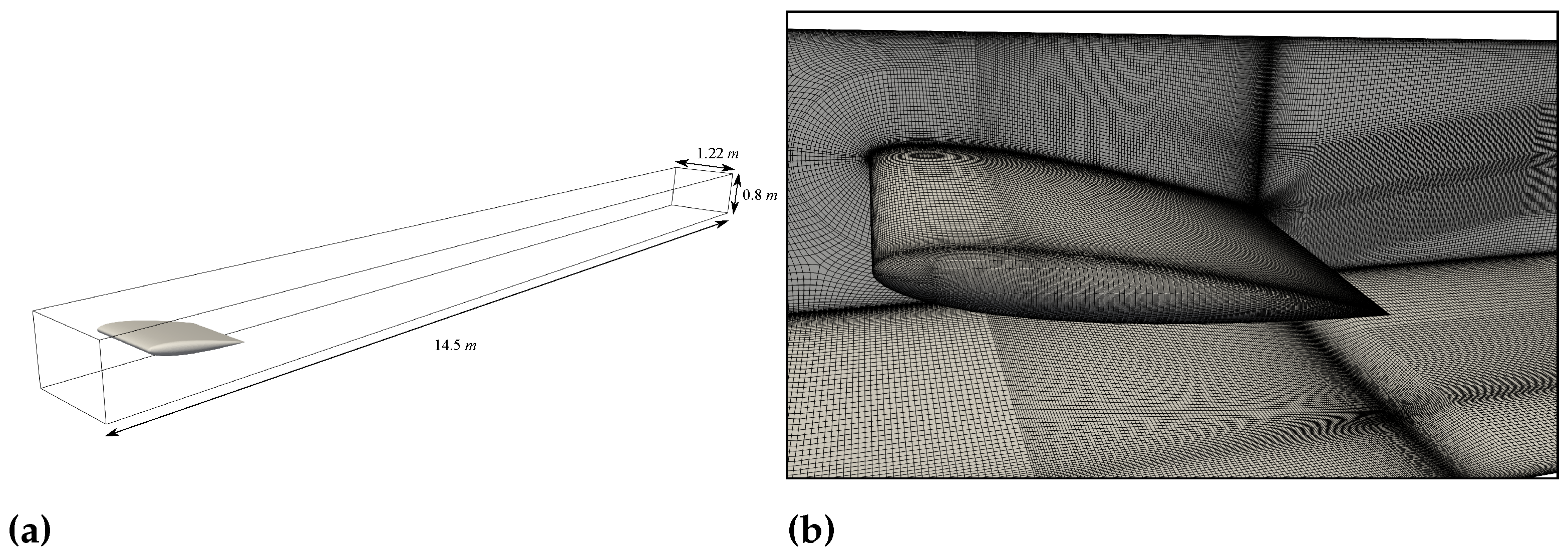
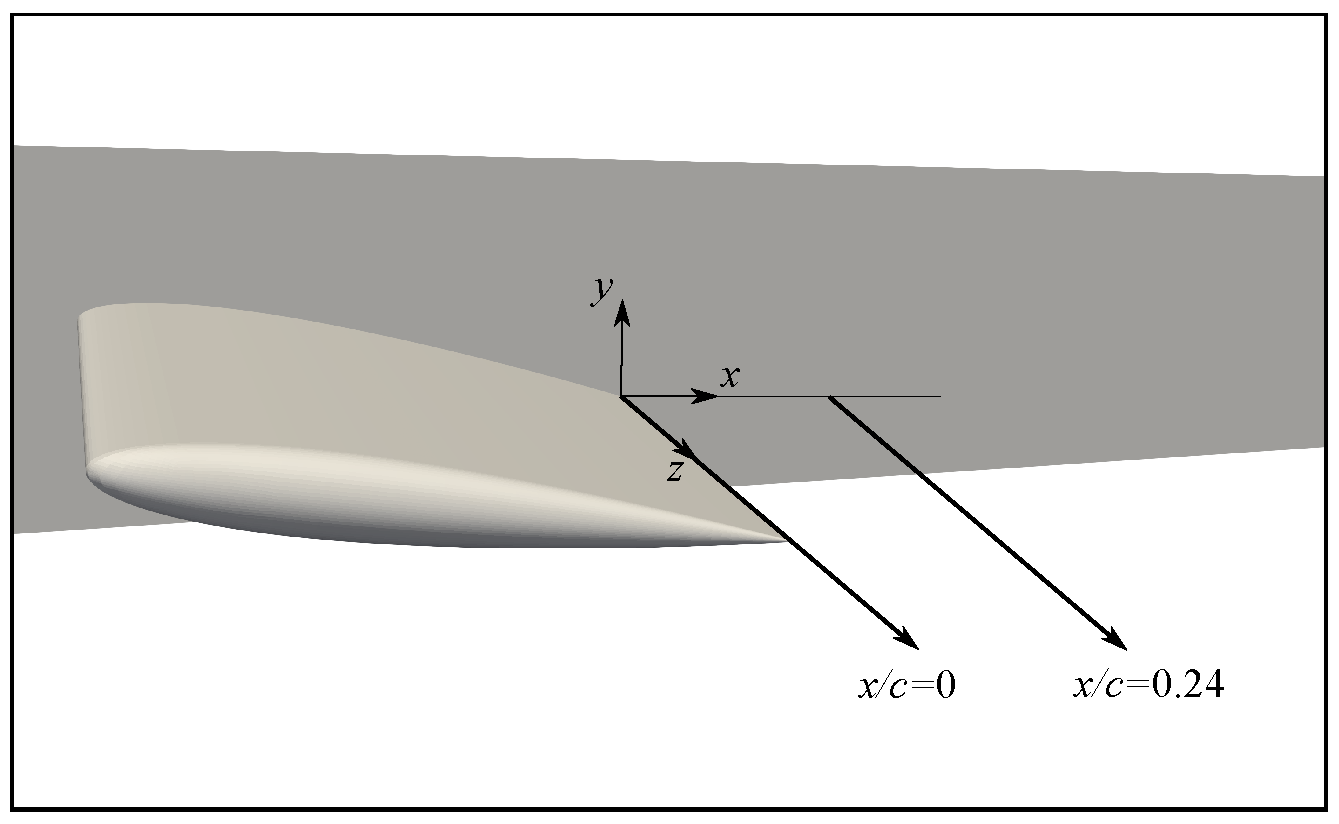
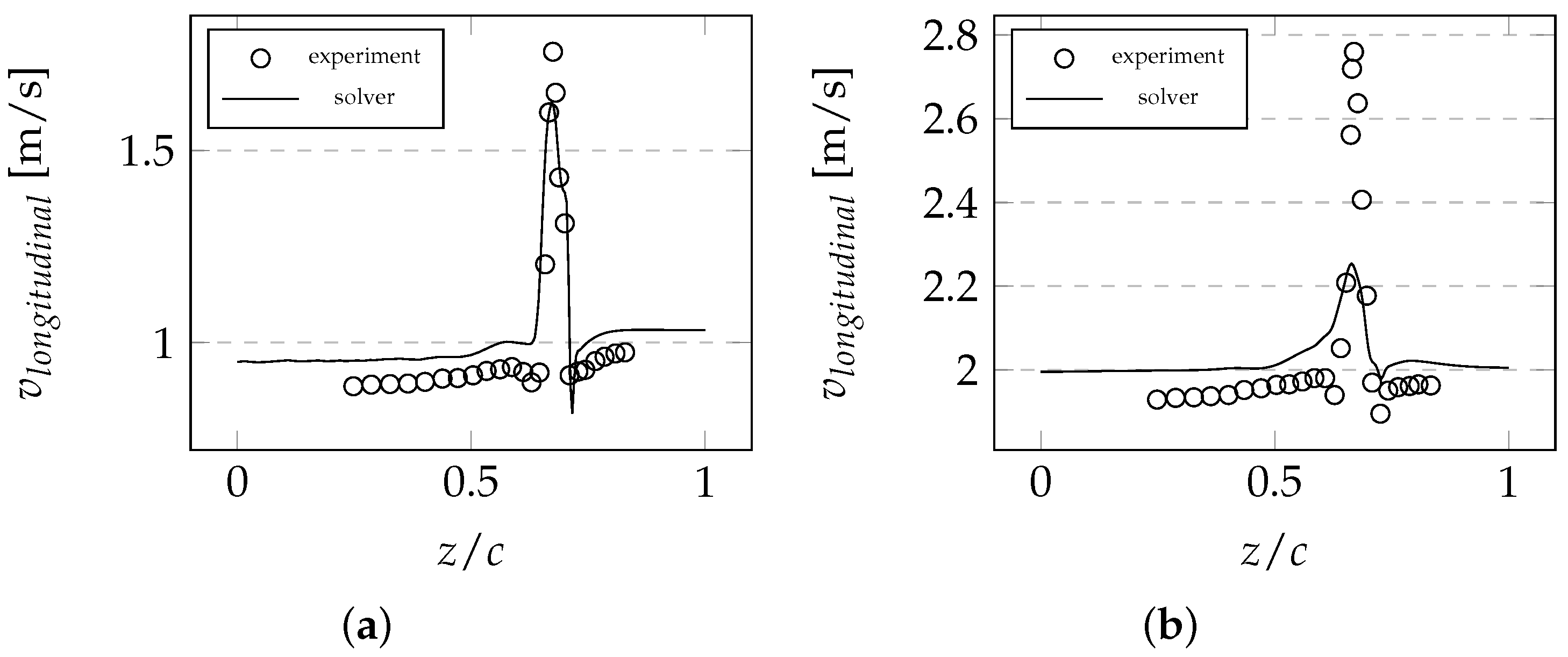
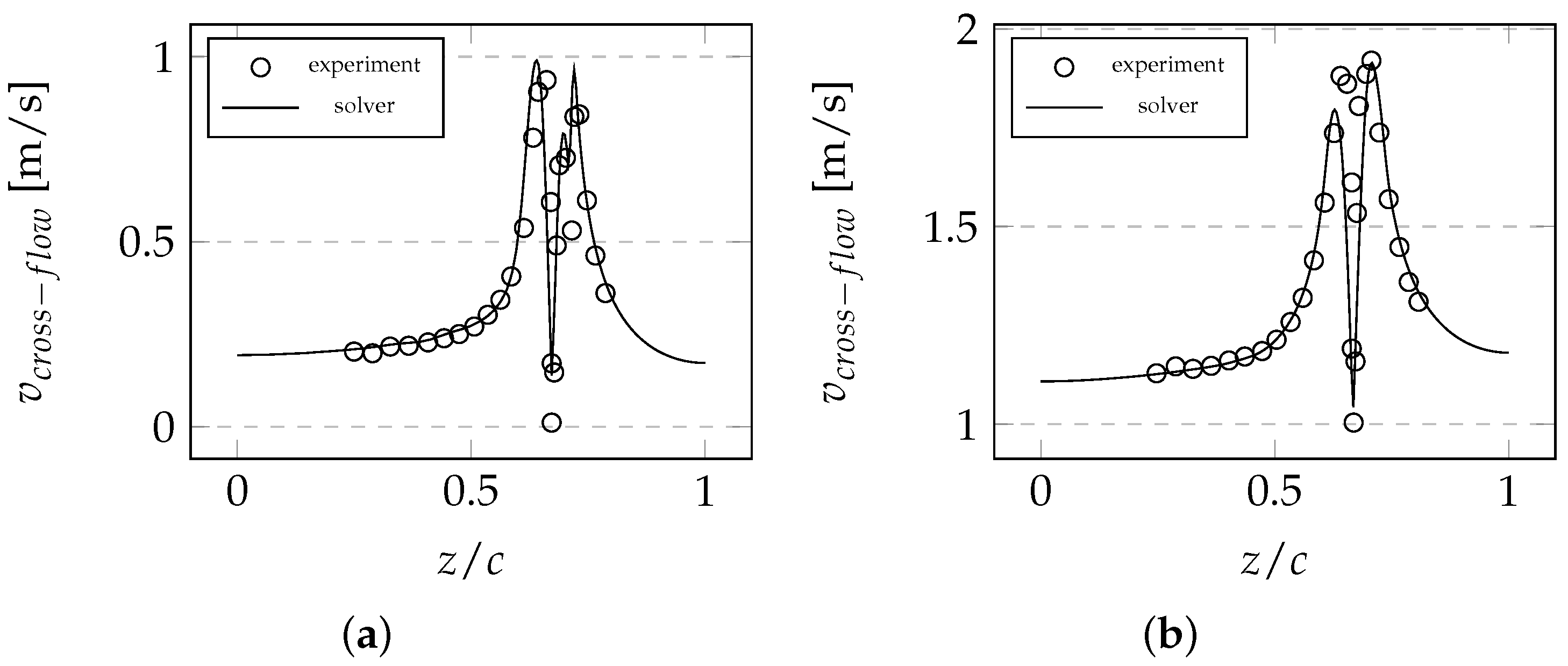
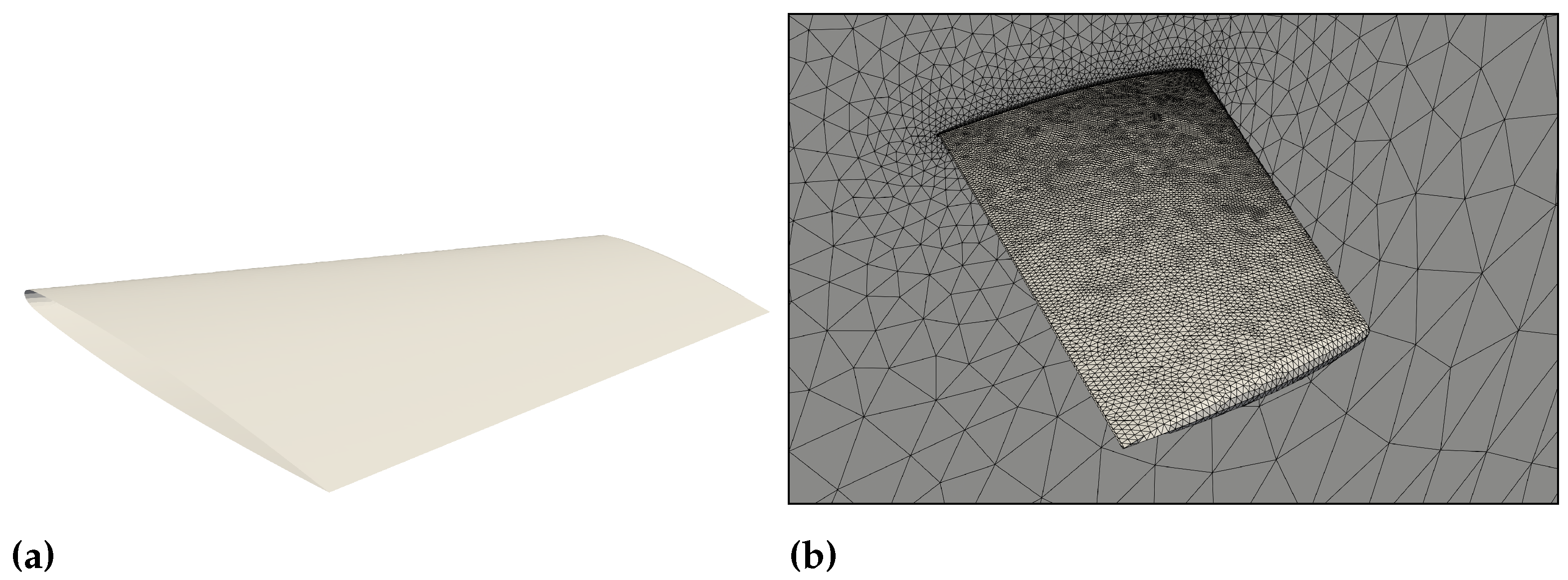
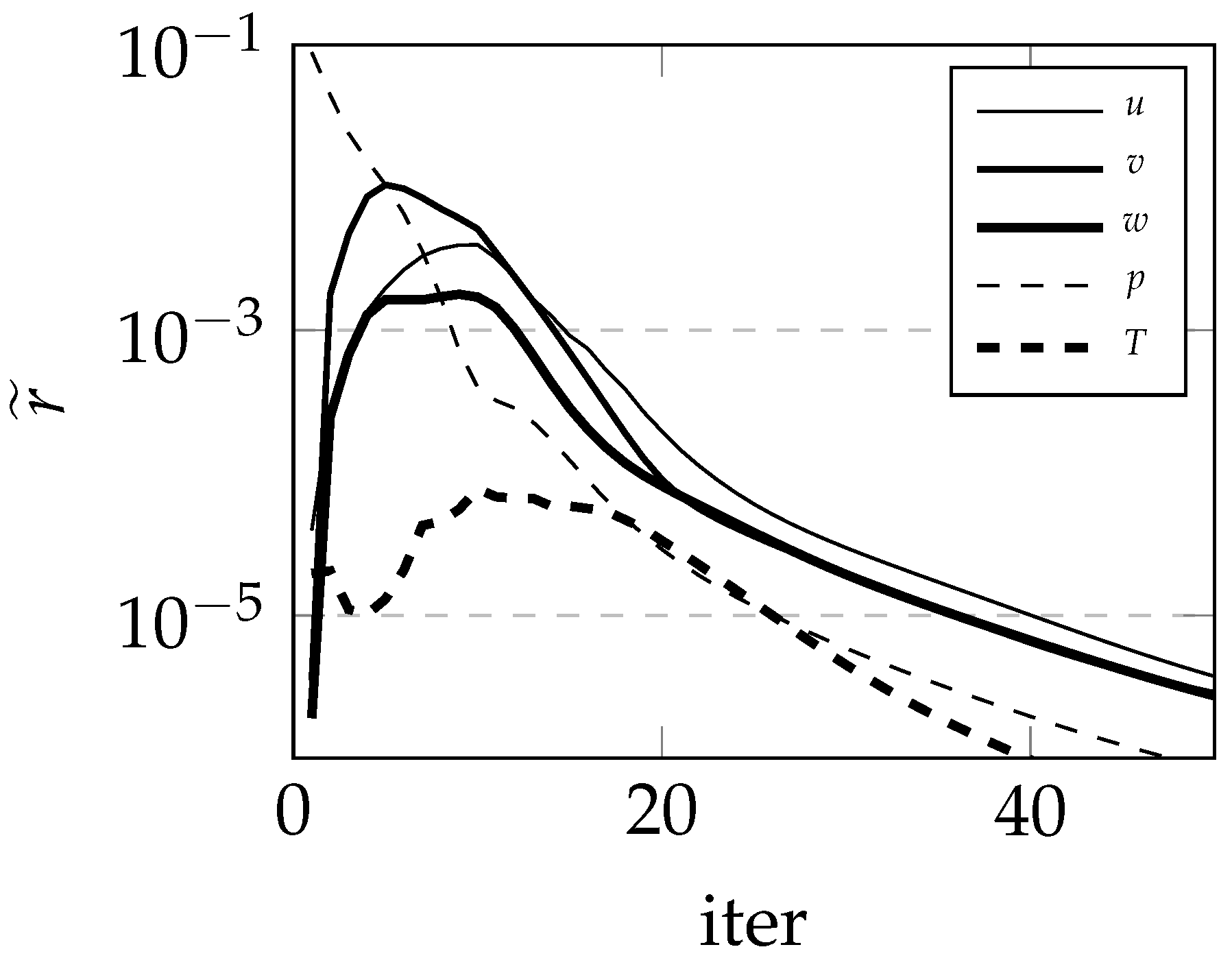
7.3. 3D NACA0012 Wing Wind Tunnel Test
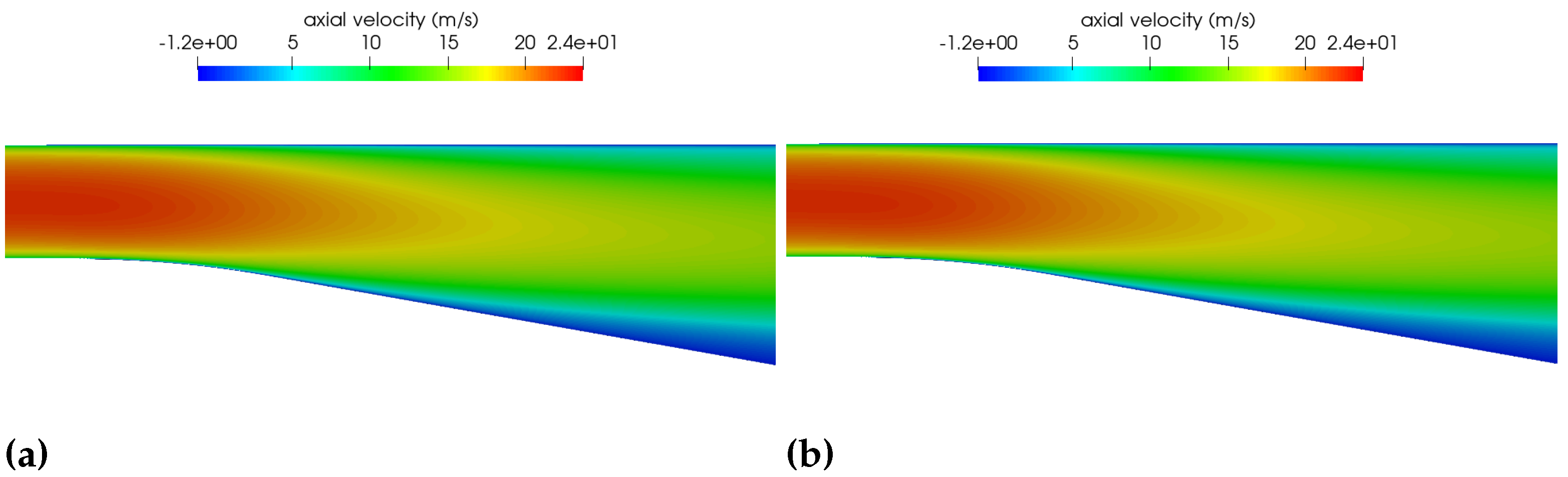
7.4. Transonic Turbulent Flow over ONERA Wing
8. Closing Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Fields and Parameters | |
| Velocity | |
| v | Velocity magnitude |
| p | Pressure |
| Specific total enthalpy | |
| T | Temperature |
| Density | |
| Viscosity | |
| Turbulent viscosity | |
| Effective viscosity | |
| Thermal conductivity | |
| Turbulent thermal conductivity | |
| Effective thermal conductivity | |
| Specific heat at constant pressure | |
| R | Gas constant |
| k | Turbulent kinetic energy |
| Turbulent dissipation frequency | |
| Ratio of specific heats | |
| t | Time |
| Pressure coefficient | |
| Stress tensor | |
| Surface vector | |
| S | Surface area |
| V | Volume |
| N | Shape function |
| Mass flux | |
| Scalar quantity | |
| Distance vector | |
| n | Number of nodes of an element |
| Number of nodes of a side | |
| Number of nodes of the whole mesh | |
| r | Residual |
| Identity matrix | |
| Pressure coefficient | |
| Super- and Subscripts | |
| * | Latest available value |
| ∘ | Previous time step value |
| Cartesian components of a vector | |
| i | Node index |
| j | Neighboring/adjacent node index to i |
| C | Control volume associated with the node of index i |
| F | Neighboring/adjacent control volume to C |
| Neighboring/adjacent control volume to C with no s shared | |
| Integration point | |
| Boundary integration point | |
| k | Index of a node which straddles the integration point |
| Specified | |
| ∞ | Free-stream condition |
References
- Ammara, I.; Masson, C. Development of a fully coupled control-volume finite element method for the incompressible navier–stokes equations. Int. J. Numer. Methods Fluids 2004, 44, 621–644. [Google Scholar] [CrossRef]
- Chandrashekar, P. Finite volume discretization of heat equation and compressible navier–stokes equations with weak dirichlet boundary condition on triangular grids. Int. J. Adv. Eng. Sci. Appl. Math. 2016, 8, 174–193. [Google Scholar] [CrossRef]
- Baliga, B.; Patankar, S. A control volume finite-element method for two-dimensional fluid flow and heat transfer. Numer. Heat Transf. 1983, 6, 245–261. [Google Scholar]
- Schneider, G.E.; Raw, M.J. Control Volume Finite-Element Method for Heat Transfer and Fluid Flow Using Colocated Variables. Numer. Heat Transf. Int. J. Comput. Methodol. 1987, 11, 363–390. [Google Scholar]
- Vogel, A.; Xu, J.; Wittum, G. A generalization of the vertex-centered finite volume scheme to arbitrary high order. Comput. Vis. Sci. 2010, 13, 221–228. [Google Scholar] [CrossRef]
- Asouti, V.; Trompoukis, X.; Kampolis, I.; Giannakoglou, K. Unsteady CFD computations using vertex-centered finite volumes for unstructured grids on graphics processing units. Int. J. Numer. Methods Fluids 2011, 67, 232–246. [Google Scholar] [CrossRef]
- Tombarevic, E.; Voller, V.; Vušanovic, I. Detailed cvfem algorithm for three dimensional advection-diffusion problems. Comput. Model. Eng. Sci. 2013, 96, 1–29. [Google Scholar]
- Zhang, Z.; Zou, Q. Some recent advances on vertex centered finite volume element methods for elliptic equations. Sci. China Math. 2013, 56, 2507–2522. [Google Scholar] [CrossRef]
- Zhang, Z.; Zou, Q. Vertex-centered finite volume schemes of any order over quadrilateral meshes for elliptic boundary value problems. Numer. Math. 2015, 130, 363–393. [Google Scholar] [CrossRef]
- Yang, H.; Harris, R. Development of vertex-centered high-order schemes and implementation in fun3d. AIAA J. 2016, 54, 3742–3760. [Google Scholar] [CrossRef]
- Yang, H.; Harris, R. Vertex-centered, high-order schemes for turbulent flows. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1098. [Google Scholar]
- Domino, S. Design-order, non-conformal low-Mach fluid algorithms using a hybrid CVFEM/DG approach. J. Comput. Phys. 2018, 359, 331–351. [Google Scholar] [CrossRef]
- Setzwein, F.; Ess, P.; Gerlinger, P. An implicit high-order k-exact finite-volume approach on vertex-centered unstructured grids for incompressible flows. J. Comput. Phys. 2021, 446, 110629. [Google Scholar] [CrossRef]
- Knaus, R. A fast matrix-free approach to the high-order control volume finite element method with application to low-Mach flow. Comput. Fluids 2022, 239, 105408. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S. CVFEM simulation for nanofluid migration in a porous medium using Darcy model. Int. J. Heat Mass Transf. 2018, 122, 1264–1271. [Google Scholar] [CrossRef]
- Dogonchi, A.; Waqas, M.; Ganji, D. Shape effects of Copper-Oxide (CuO) nanoparticles to determine the heat transfer filled in a partially heated rhombus enclosure: CVFEM approach. Int. Commun. Heat Mass Transf. 2019, 107, 14–23. [Google Scholar] [CrossRef]
- Xiong, P.; Almarashi, A.; Dhahad, H.; Alawee, W.; Abusorrah, A.; Issakhov, A.; Abu-Hamdeh, N.; Shafee, A.; Chu, Y. Nanomaterial transportation and exergy loss modeling incorporating CVFEM. J. Mol. Liq. 2021, 330, 115591. [Google Scholar] [CrossRef]
- Kutanaei, S.; Choobbasti, A. Effect of the fluid weight on the liquefaction potential around a marine pipeline using CVFEM. EJGE 2013, 18, 633–646. [Google Scholar]
- Milanez, M.; Naterer, G.; Popplewell, N.; Venn, G.; Richardson, G. CVFEM for Multiphase Flow with Disperse and Interface Tracking, and Algorithms Performances. J. Comput. Multiph. Flows 2015, 7, 195–226. [Google Scholar] [CrossRef][Green Version]
- Samier, P. Pressure coupling for geomechanical multi-phase Flow simulation using vertex centered flow elements and unstructured grids. In Proceedings of the SPE Reservoir Simulation Conference, Montgomery, TX, USA, 20–22 February 2017. [Google Scholar]
- Seyyedi, S.; Ghadakpour, M.; Bayat, M.; Pilehvar, M.; Kutanaei, S.; Abdollahtabar, M.; Kardarkolai, M. CVFEM modeling of fluid flow induced by convective heat transfer from a hot pipe buried in soil. J. Therm. Anal. Calorim. 2021, 146, 367–379. [Google Scholar] [CrossRef]
- Li, L.; Lohner, R.; Pandare, A.; Luo, H. A vertex-centered finite volume method with sharp interface capturing for compressible two-phase flows. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 & 19–21 January 2021; p. 0856. [Google Scholar]
- Cunha, F.; Veras, C. Modelling laminar diffusion flames using a fast convergence three-dimensional CVFEM code. Combust. Theory Model. 2021, 25, 460–487. [Google Scholar] [CrossRef]
- SIERRA Solid Mechanics Team. SIERRA Toolkit Manual Version 4.48; Sandia National Laboratories: Livermore, CA, USA, 2018. [Google Scholar]
- Darwish, M.; Sraj, I.; Moukalled, F. A coupled incompressible flow solver on structured grids. Numer. Heat Transf. Part B Fundam. 2007, 52, 353–371. [Google Scholar] [CrossRef]
- Darwish, M.; Sraj, I.; Moukalled, F. A coupled finite volume solver for the solution of incompressible flows on unstructured grids. J. Comput. Phys. 2009, 228, 180–201. [Google Scholar] [CrossRef]
- Mangani, L.; Darwish, M.; Moukalled, F. Development of a pressure-based coupled cfd solver for turbulent and compressible flows in turbomachinery applications. In ASME Turbo Expo 2014: Turbine Technical Conference and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. V02BT39A019. [Google Scholar]
- Darwish, M.; Moukalled, F. A fully coupled navier-stokes solver for fluid flow at all speeds. Numer. Heat Transf. Part B Fundam. 2014, 65, 410–444. [Google Scholar] [CrossRef]
- Darwish, M.; Aziz, A.A.; Moukalled, F. A coupled pressure-based finite-volume solver for incompressible two-phase flow. Numer. Heat Transf. Part B Fundam. 2015, 67, 47–74. [Google Scholar] [CrossRef]
- Mangani, L.; Darwish, M.; Moukalled, F. An openfoam pressure-based coupled cfd solver for turbulent and compressible flows in turbomachinery applications. Numer. Heat Transf. Part B Fundam. 2016, 69, 413–431. [Google Scholar] [CrossRef]
- Xiao, C.-N.; Denner, F.; van Wachem, B.G. Fully-coupled pressure-based finite-volume framework for the simulation of fluid flows at all speeds in complex geometries. J. Comput. Phys. 2017, 346, 91–130. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hughes, T.J. Weak imposition of dirichlet boundary conditions in fluid mechanics. Comput. Fluids 2007, 36, 12–26. [Google Scholar] [CrossRef]
- Nordström, J.; Eriksson, S.; Eliasson, P. Weak and strong wall boundary procedures and convergence to steady-state of the navier–stokes equations. J. Comput. Phys. 2012, 231, 4867–4884. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The finite volume method in computational fluid dynamics. In An Advanced Introduction with OpenFoam® and Matlab®; Springer: New York, NY, USA, 2016; Available online: http://www.gidropraktikum.narod.ru/Moukalled-et-al-FVM-OpenFOAM-Matlab.pdf (accessed on 15 November 2021).
- Darwish, M.; Saad, T.; Hamdan, Z. Parallelization of an additive multigrid solver. Numer. Heat Transf. Part B Fundam. 2008, 54, 157–184. [Google Scholar] [CrossRef]
- Ansys, C. 15.0 User Manual; ANSYS Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Rumsey, C.L. Turbulence modeling verification and validation. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 0201. [Google Scholar]
- Schoenherr, K.E. Resistance of flat surfaces moving through a fluid. Trans. Soc. Nav. Archit. Mar. Eng. 1932, 40, 279–313. [Google Scholar]
- Huang, P.; Bardina, J.; Coakley, T. Turbulence Modeling Validation, Testing, And Development; NASA-TM-110446; National Aeronautics and Space Administrat: Washington, DC, USA, 1997; p. 147. [Google Scholar]
- Buice, C.U. Experimental Investigation of Flow through an Asymmetric Plane Diffuser; Stanford University: Stanford, CA, USA, 1997. [Google Scholar]
- Chow, J.S.; Zilliac, G.G.; Bradshaw, P. Mean and turbulence measurements in the near field of a wingtip vortex. AIAA J. 1997, 35, 1561–1567. [Google Scholar] [CrossRef]
- Schmitt, V. Pressure Distributions on the Onera M6-Wing at Transonic Mach Numbers, Experimental Data Base for Computer Program Assessment; AGARD AR-138; NATO STO: Brussels, Belgium, 1979. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mangani, L.; Alloush, M.M.; Lindegger, R.; Hanimann, L.; Darwish, M. A Pressure-Based Fully-Coupled Flow Algorithm for the Control Volume Finite Element Method. Appl. Sci. 2022, 12, 4633. https://doi.org/10.3390/app12094633
Mangani L, Alloush MM, Lindegger R, Hanimann L, Darwish M. A Pressure-Based Fully-Coupled Flow Algorithm for the Control Volume Finite Element Method. Applied Sciences. 2022; 12(9):4633. https://doi.org/10.3390/app12094633
Chicago/Turabian StyleMangani, Luca, Mhamad Mahdi Alloush, Raphael Lindegger, Lucian Hanimann, and Marwan Darwish. 2022. "A Pressure-Based Fully-Coupled Flow Algorithm for the Control Volume Finite Element Method" Applied Sciences 12, no. 9: 4633. https://doi.org/10.3390/app12094633
APA StyleMangani, L., Alloush, M. M., Lindegger, R., Hanimann, L., & Darwish, M. (2022). A Pressure-Based Fully-Coupled Flow Algorithm for the Control Volume Finite Element Method. Applied Sciences, 12(9), 4633. https://doi.org/10.3390/app12094633





