Software Defect Prediction Using Stacking Generalization of Optimized Tree-Based Ensembles
Abstract
:1. Introduction
2. Background
2.1. Tree-Based Ensembles
- AdaBoost (Ada) [10], or adaptive boosting, is a well-known boosting algorithm introduced by Freund and Schapire. AdaBoost fits a series of base classifiers and then changes the weights of the instances by giving the misclassified ones a higher weight and then fitting the updated weights with a new base learner. The final prediction is calculated by integrating the results from all base classifiers using a weighted majority vote approach, in which each base classifier contributes based on its results (i.e., assigned a greater weight).
- Random forest (RF) [12] is a bagging algorithm that employs a large number of small decision trees, each of which is developed from random dataset subsets. To increase the tree’s diversity, a random subset of features is chosen at each node to produce the best split. Overfitting is less likely due to the randomness of the dataset and features. The majority vote is used in a classification problem to determine the final class label.
- Extra trees (ET) [13], or extremely randomized trees, is similar to the RF algorithm but with additional randomness. ET differs from RF in two ways: (1) each decision tree is constructed using the entire dataset, and (2) it randomly selects the splits at each node (i.e., does not select the best splits).
- Gradient boosting (GB) [14] is a generalization of the AdaBoost ensemble that can be constructed utilizing a variety of loss functions. GB, unlike AdaBoost, fits a new base classifier using gradients rather than the weight of misclassified instances. Using GB will boost the efficiency of fitting the base classifiers, but memory usage and processing time are inefficient.
- Histogram-based gradient boosting (HGB) [15], or histogram-based gradient boosting, is a boosting ensemble that selects the best splits easily and reliably using feature histograms. It is more efficient than GB in terms of processing speed and memory utilization.
- XGBoost (XGB) [16], or extreme gradient boosting, is similar to the GB algorithm, but instead of gradients, it fits a new base classifier using second-order derivatives of the loss function. XGB is thought to be more precise and effective than GB.
- CatBoost (CAT) [17], or categorical boosting, is a boosting ensemble with two key characteristics: (1) it handles categorical features with one-hot encoding, and (2) it produces oblivious decision trees as base classifiers with the same features used as a splitting criterion for all nodes within the same tree level. Oblivious trees are symmetrical; thus, overfitting is minimized and training time is reduced.
2.2. Stacking Ensemble
- Step 1—first-level classifiers: Assume that we have T base classifier. For each base classifier learn and fit the classifier using .
- Step 2—construct new datasets: The outputs of the T base classifiers are used as input to the meta-classifier. To create new datasets, for each instance , construct a new instance such that (1) is a vector of length T and , where is the prediction output of a base classifier t and (2) y represents the original class labels.
- Step 3—a second-level classifier: Using the dataset created in step 2, fit and teach a meta-classifier which produces a final prediction by combining the outputs of all base classifiers.
| Algorithm 1: Stacking ensemble. |
Require: Training data Ensure: An ensemble classifier H 1: Step 1: Learn first-level classifiers 2: for to T do 3: Learn a Tree-based ensemble based on 4: end for 5: Step 2: Construct new data sets from 6: for to m do 7: Construct a new data set that contains where 8: end for 9: Step 3: Learn a second-level classifier 10: Learn a new classifier based on the newly constructed data set 11: return |
3. Literature Review
3.1. Ensemble Learning
| Ref | Dataset | Base Classifiers | Ensembles | Statistical Analysis |
|---|---|---|---|---|
| [20] | KC1 (class) | MLP, RBF, BBN, NB, SVM, DT | Bagging, AdaBoost | no |
| [21] | ar1, ar4, JM1, KC2, MC1, MW1, PC3, PC4 | J48 | Bagging, AdaBoost.M2 | no |
| [23] | CM1, KC1, KC2, KC3, MC1, MC2, PC1, JM1, MW1, PC2, PC3, PC4 | IBK, MLP, SVM, RF, NB, Logistic Boost, PART, JRip, J48, Decision Stump | Voting | Wilcoxon |
| [22] | ant-1.5, ant-1.6, ant-1.7, jedit-4.1, jedit-4.2, tomcat. xalan-2.5, xalan-2.6 | NB, DT, KNN, SMO | Stacking | Wilcoxon |
| [24] | Ant-1.7, Camel-1.6, e-learning, Forrest-0.8, Jedit-4.3, Tomcat, Xalan-2.7, Xerces-1.4, Zuzel, Berek, Pbean2, Velocity-1.6 | NB, LR, J48, VP, SMO | AdaBoostM1, Voting, Stacking | no |
| [25] | CM1, JM1, KC1, KC2, PC1 | J48 | AdaBoost, Bagging, RSM, RF, Voting | no |
| [27] | CM1, KC1, KC2, KC3, MC1, MC2, MW1, PC1, PC2, PC3, PC4, JM1 | Bagging, RF, AdaBoost | Weighted average probabilities | Wilcoxon |
| [26] | KC1, KC2, KC3, PC1, PC2, PC3, PC4, MC1, MC2, CM1, JM1, MW1 | Bagging, RF, AdaBoost | Weighted average probabilities | no |
| [28] | Ant-1.7, Camel-1.6, KC3, MC1, PC2, PC4 | RF, GB, SGD, W-SVMs, LR, M-NB, B-NB | Average probability | no |
| This work | 21 Defect Datasets | Ada, RF, ET, GB, HGB, XGB, CAT | Stacking | Wilcoxon |
3.2. Hyperparameter Optimization
| Ref | Datasets | Optimization Methods | Classifiers | Ensembles |
|---|---|---|---|---|
| [29] | Eclipse JDT Core, Eclipse PDE UI, Equinox, Mylyn, Lucene | opt-aiNet | KNN, SVM, NB, DT, LDA, RF, AdaBoost | Yes |
| [5] | JM11, PC51, Prop-12, Prop-22, Prop-32, Prop-42, Prop-52, Camel 1.22, Xalan 2.52, Xalan 2.62, Platform 2.03, Platform 2.13, Platform 3.03, Debug 3.44, SWT 3.44, JDT5, Mylyn5, PDE5 | Grid search | NB, KNN, LR, NN, PLS, DA, Rule-based, DT, SVM, Bagging, Boosting | Yes |
| [30] | JM11, PC51, Prop-12, Prop-22, Prop-32, Prop-42, Prop-52, Camel 1.22, Xalan 2.52, Xalan 2.62, Platform 2.03, Platform 2.13, Platform 3.03, Debug 3.44, SWT 3.44, JDT5, Mylyn5, PDE5 | Grid search, Random search, Genetic algorithm, Differential evolution | NB, KNN, LR, NN, PLS, DA, Rule-based, DT, SVM, Bagging, Boosting | Yes |
| [6] | Eclipse JDT Core, Eclipse PDE UI, Equinox, Mylyn, Lucene | Grid Search | KNN, SVM | No |
| [31] | antV0, antV1, antV2, camelV0, camelV1, ivy, jeditV0, jeditV1, jeditV2, log4j, lucene, poiV0, poiV1, synapse, velocity, xercesV0, xercesV1 | Differential evolution | Where-based Learner, DT, RF | Yes |
| [32] | ar1, ar3, ar4, ar5, ar6, cm1, jm1, kc1, kc2, kc3, pc1, pc2, pc3, pc4, pc5, Eclipse JDT Core, Eclipse PDE UI, Equinox framework, Lucene, Mylyn | Grid Search | RF, SVM | No |
| This work | 21 Defect Datasets | Grid Search | Ada, RF, ET, GB, HGB, XGB, CAT | Yes |
3.3. Summary
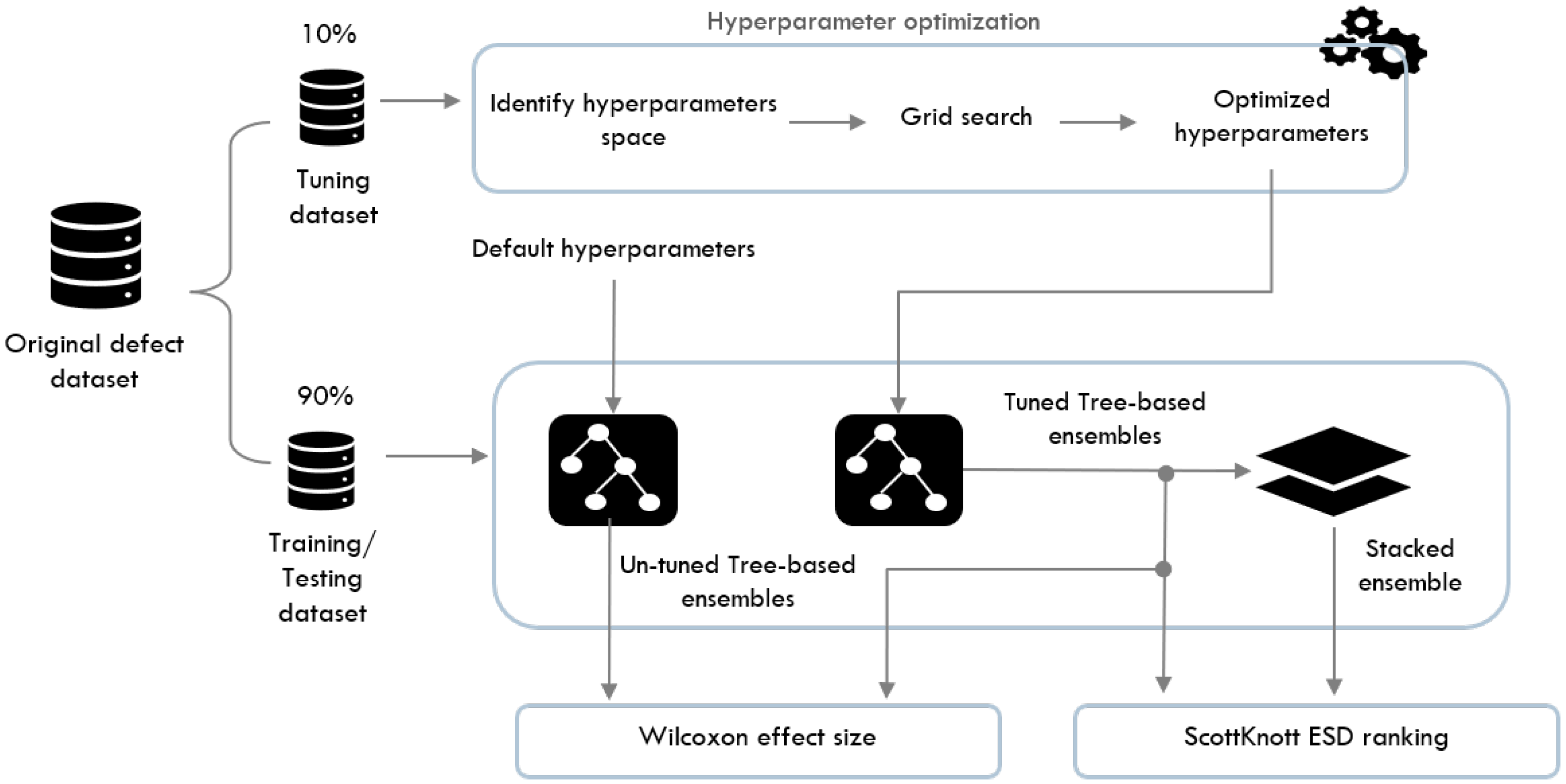
4. Empirical Study
4.1. Goal
- RQ 1. To what extent does hyperparameter optimization increase the prediction performance of an ensemble?
- RQ 2. To what extent does stacking generalization of fine-tuned tree-based ensembles increase defect prediction?
4.2. Datasets
4.3. Hyperparameter Optimization
4.4. Ensemble Models Construction and Validation
- Data transformation. Data transformation is recommended to boost the performances of machine learning models [46]. Therefore, we used a logarithmic data transformation where each value of the independent variables was transformed using , where x is the numerical value of the variable. We selected the log transformation because it has been used previously in software defect prediction [30,46].
- Handling missing values. Missing data can be handled in a variety of ways, including mean imputation, deletion and median imputation [47]. For all datasets, we utilized the mean imputation approach to deal with missing values. The mean of all values belonging to the independent variable was used to fill in the missing values. It is one of the most often used approaches and has been proved to yield good results in supervised learning tasks [48].
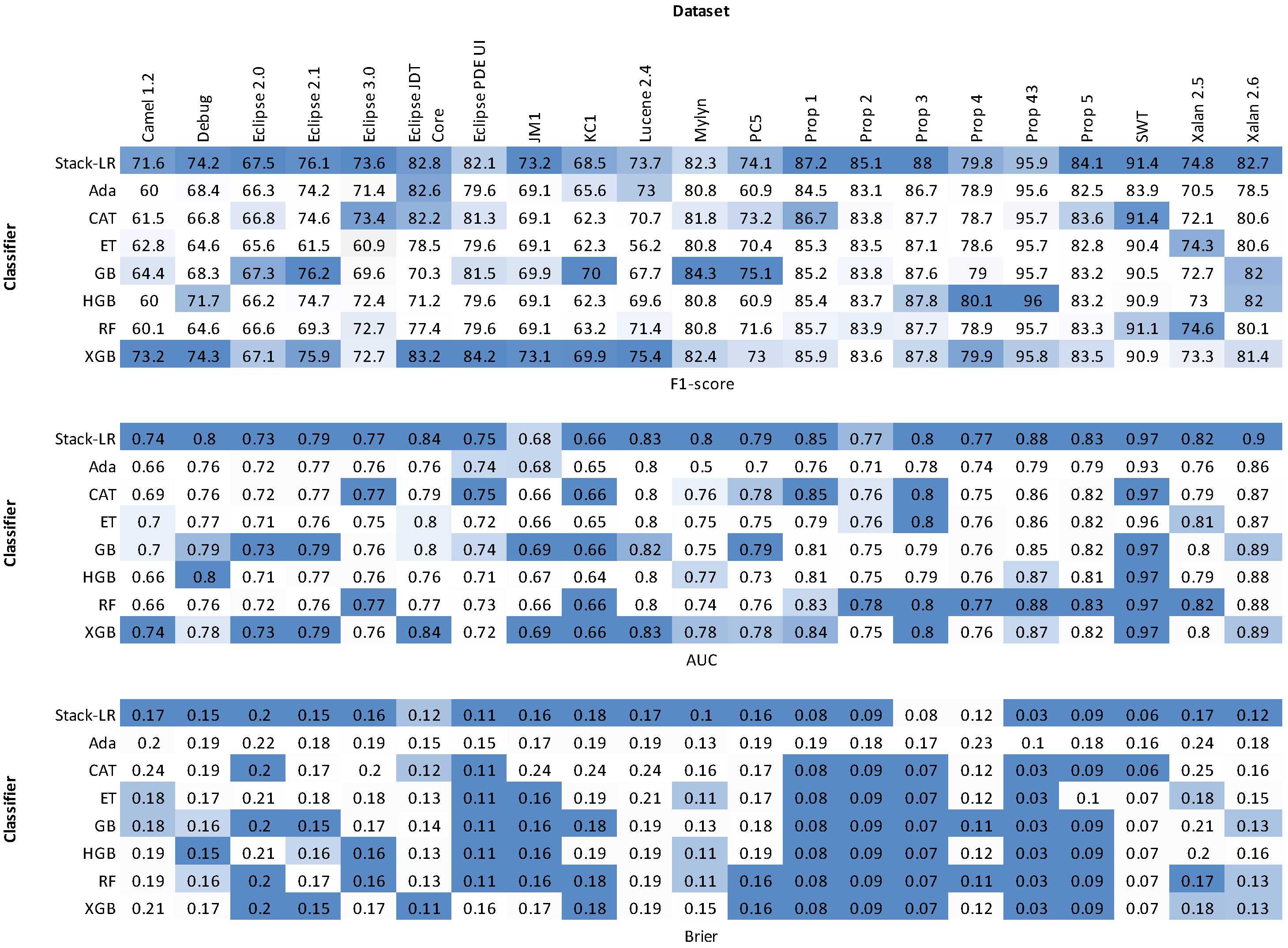
4.5. Evaluation Measures
- F-measurement (F-measure): is the harmonic mean of both precision and recall. F-measurement is calculated as:where true positives (TP) is the number of defective instances correctly classified as defective, false positives (FP) is the number of defective instances incorrectly classified as non-defective and false negatives (FN) is the number of non-defective instances incorrectly classified as defective.
- Area under the curve (AUC): The percentage of the area that is underneath the receiver operator characteristic (ROC) curve. True positive rates are plotted against the false positive rates. The AUC metric calculates the area under the curve, and a large area indicates high performance. AUC can have a value between 0 and 1:1 indicates the best performance and zero is considered the worst performance.
- Brier [51]: The mean squared difference between the predicted probability and the actual outcome. It can be calculated using the following formula:where is the predicted probability and is the actual outcome. Brier has a range of values from 0 to 1, with 0 denoting the highest performance, 1 denoting the worst and 0.5 denoting a random estimate.
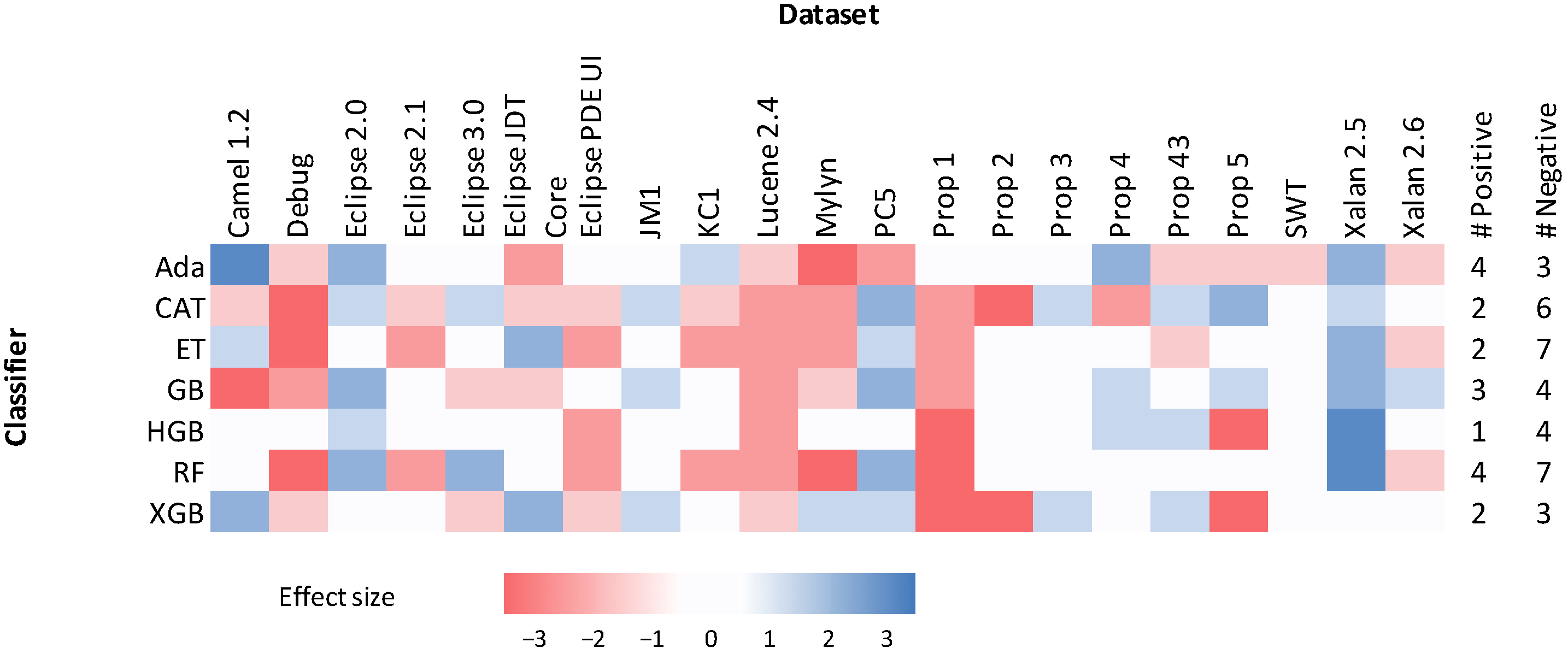
4.6. Effect Size Estimation
4.6.1. Wilcoxon Effect Size
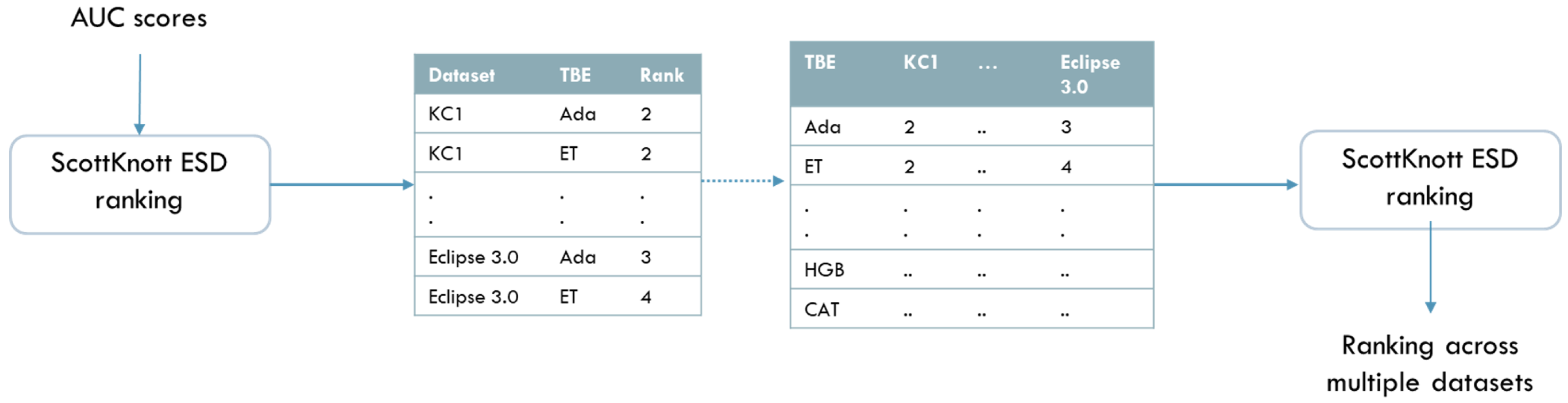
4.6.2. Scott–Knott Effect Size Difference (ESD)
5. Results and Discussion
5.1. Effects of Hyperparameter Optimization on Tree-Based Ensembles
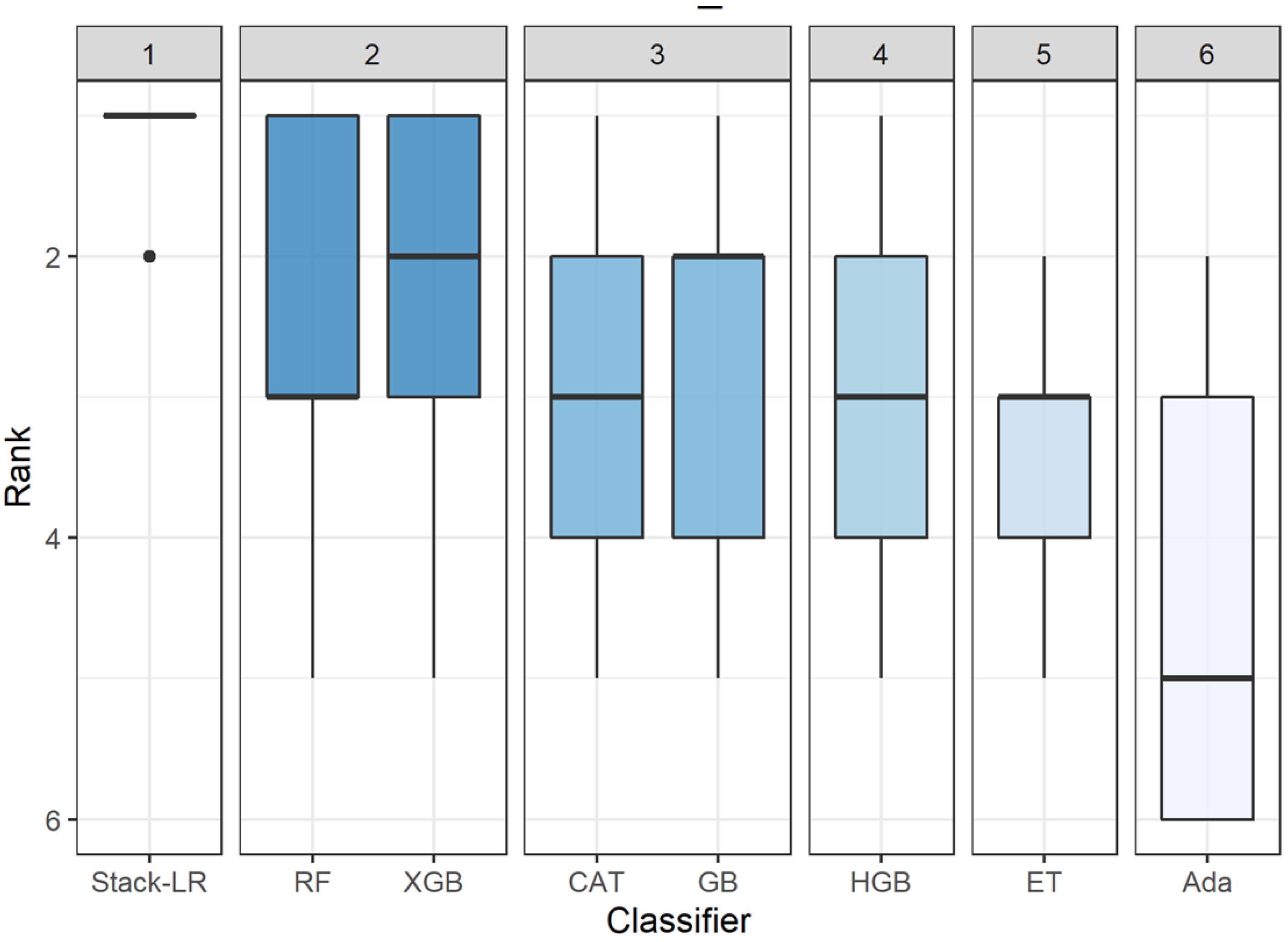
5.2. Stacking Ensembles
5.3. Threats to Validity
5.3.1. Internal Validity
5.3.2. Construct Validity
5.3.3. External Validity
5.3.4. Conclusion Validity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Menzies, T.; Milton, Z.; Turhan, B.; Cukic, B.; Jiang, Y.; Bener, A. Defect prediction from static code features: Current results, limitations, new approaches. Autom. Softw. Eng. 2010, 17, 375–407. [Google Scholar] [CrossRef]
- Malhotra, R. A systematic review of machine learning techniques for software fault prediction. Appl. Soft Comput. 2015, 27, 504–518. [Google Scholar] [CrossRef]
- Aljamaan, H.; Alazba, A. Software defect prediction using tree-based ensembles. In Proceedings of the 16th ACM International Conference on Predictive Models and Data Analytics in Software Engineering, Virtual Event, 8–9 November 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1–10. [Google Scholar]
- Tosun, A.; Bener, A. Reducing false alarms in software defect prediction by decision threshold optimization. In Proceedings of the 2009 3rd International Symposium on Empirical Software Engineering and Measurement, Lake Buena Vista, FL, USA, 15 October 2009; pp. 477–480. [Google Scholar] [CrossRef]
- Tantithamthavorn, C.; McIntosh, S.; Hassan, A.E.; Matsumoto, K. Automated Parameter Optimization of Classification Techniques for Defect Prediction Models. In Proceedings of the 2016 IEEE/ACM 38th International Conference on Software Engineering (ICSE), Austin, TX, USA, 14–22 May 2016; pp. 321–332. [Google Scholar] [CrossRef]
- Osman, H.; Ghafari, M.; Nierstrasz, O. Hyperparameter optimization to improve bug prediction accuracy. In Proceedings of the 2017 IEEE Workshop on Machine Learning Techniques for Software Quality Evaluation (MaLTeSQuE), Klagenfurt, Austria, 21 February 2017; pp. 33–38. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Safavian, S.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y. Boosting a Weak Learning Algorithm by Majority. Inf. Comput. 1995, 121, 256–285. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Guryanov, A. Histogram-Based Algorithm for Building Gradient Boosting Ensembles of Piecewise Linear Decision Trees. In Analysis of Images, Social Networks and Texts; Lecture Notes in Computer Science; van der Aalst, W.M.P., Batagelj, V., Ignatov, D.I., Khachay, M., Kuskova, V., Kutuzov, A., Kuznetsov, S.O., Lomazova, I.A., Loukachevitch, N., Napoli, A., et al., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 39–50. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: San Francisco, CA, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Data Classification: Algorithms and Applications; Google-Books-ID: NwQZCwAAQBAJ; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Aljamaan, H.I.; Elish, M.O. An empirical study of bagging and boosting ensembles for identifying faulty classes in object-oriented software. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence and Data Mining, Nashville, TN, USA, 30 March–2 April 2009; pp. 187–194. [Google Scholar] [CrossRef]
- Yohannese, C.W.; Li, T.; Simfukwe, M.; Khurshid, F. Ensembles based combined learning for improved software fault prediction: A comparative study. In Proceedings of the 2017 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), Nanjing, China, 24–26 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Petrić, J.; Bowes, D.; Hall, T.; Christianson, B.; Baddoo, N. Building an Ensemble for Software Defect Prediction Based on Diversity Selection. In Proceedings of the 10th ACM/IEEE International Symposium on Empirical Software Engineering and Measurement (ESEM ’16), Ciudad Real, Spain, 8–9 September 2016; Association for Computing Machinery: Ciudad Real, Spain, 2016; pp. 1–10. [Google Scholar] [CrossRef] [Green Version]
- Pandey, S.K.; Mishra, R.B.; Tripathi, A.K. BPDET: An effective software bug prediction model using deep representation and ensemble learning techniques. Expert Syst. Appl. 2020, 144, 113085. [Google Scholar] [CrossRef]
- Hussain, S.; Keung, J.; Khan, A.A.; Bennin, K.E. Performance Evaluation of Ensemble Methods For Software Fault Prediction: An Experiment. In Proceedings of the ASWEC 2015 24th Australasian Software Engineering Conference (ASWEC ’15), Adelaide, SA, Australia, 28 September–1 October 2015; Association for Computing Machinery: Adelaide, SA, Australia, 2015; Volume II, pp. 91–95. [Google Scholar] [CrossRef]
- Li, R.; Zhou, L.; Zhang, S.; Liu, H.; Huang, X.; Sun, Z. Software Defect Prediction Based on Ensemble Learning. In Proceedings of the 2019 2nd International Conference on Data Science and Information Technology (DSIT 2019), Seoul, Korea, 19–21 July 2019; Association for Computing Machinery: Seoul, Korea, 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Tran, H.D.; Hanh, L.T.M.; Binh, N.T. Combining feature selection, feature learning and ensemble learning for software fault prediction. In Proceedings of the 2019 11th International Conference on Knowledge and Systems Engineering (KSE), Da Nang, Vietnam, 24–26 October 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Tong, H.; Liu, B.; Wang, S. Software defect prediction using stacked denoising autoencoders and two-stage ensemble learning. Inf. Softw. Technol. 2018, 96, 94–111. [Google Scholar] [CrossRef]
- Laradji, I.H.; Alshayeb, M.; Ghouti, L. Software defect prediction using ensemble learning on selected features. Inf. Softw. Technol. 2015, 58, 388–402. [Google Scholar] [CrossRef]
- Khan, F.; Kanwal, S.; Alamri, S.; Mumtaz, B. Hyper-Parameter Optimization of Classifiers, Using an Artificial Immune Network and Its Application to Software Bug Prediction. IEEE Access 2020, 8, 20954–20964. [Google Scholar] [CrossRef]
- Tantithamthavorn, C.; McIntosh, S.; Hassan, A.E.; Matsumoto, K. The Impact of Automated Parameter Optimization on Defect Prediction Models. IEEE Trans. Softw. Eng. 2019, 45, 683–711. [Google Scholar] [CrossRef] [Green Version]
- Fu, W.; Menzies, T.; Shen, X. Tuning for Software Analytics: Is it Really Necessary? Inf. Softw. Technol. 2016, 76, 135–146. [Google Scholar] [CrossRef] [Green Version]
- Öztürk, M.M. Comparing Hyperparameter Optimization in Cross- and Within-Project Defect Prediction: A Case Study. Arab. J. Sci. Eng. 2019, 44, 3515–3530. [Google Scholar] [CrossRef]
- Basili, V.; Rombach, H. The TAME project: Towards improvement-oriented software environments. IEEE Trans. Softw. Eng. 1988, 14, 758–773. [Google Scholar] [CrossRef]
- Shepperd, M.; Song, Q.; Sun, Z.; Mair, C. Data Quality: Some Comments on the NASA Software Defect Datasets. IEEE Trans. Softw. Eng. 2013, 39, 1208–1215. [Google Scholar] [CrossRef] [Green Version]
- D’Ambros, M.; Lanza, M.; Robbes, R. An extensive comparison of bug prediction approaches. In Proceedings of the 2010 7th IEEE Working Conference on Mining Software Repositories (MSR 2010), Cape Town, South Africa, 2–3 May 2010; pp. 31–41. [Google Scholar] [CrossRef]
- Jureczko, M.; Madeyski, L. Towards identifying software project clusters with regard to defect prediction. In Proceedings of the 6th International Conference on Predictive Models in Software Engineering (PROMISE ’10), Timisoara, Romania, 12–13 September 2010; Association for Computing Machinery: New York, NY, USA, 2010; pp. 1–10. [Google Scholar] [CrossRef] [Green Version]
- Wu, R.; Zhang, H.; Kim, S.; Cheung, S.C. ReLink: Recovering links between bugs and changes. In Proceedings of the 19th ACM SIGSOFT Symposium and the 13th European Conference on Foundations of Software Engineering (ESEC/FSE ’11), Szeged, Hungary, 5–9 September 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 15–25. [Google Scholar] [CrossRef]
- Zimmermann, T.; Premraj, R.; Zeller, A. Predicting Defects for Eclipse. In Proceedings of the Third International Workshop on Predictor Models in Software Engineering (PROMISE ’07), Minneapolis, MN, USA, 20 May 2007; IEEE Computer Society: Minneapolis, MN, USA, 2007; p. 9. [Google Scholar] [CrossRef]
- Kim, S.; Zhang, H.; Wu, R.; Gong, L. Dealing with noise in defect prediction. In Proceedings of the 2011 33rd International Conference on Software Engineering (ICSE), Honolulu, HI, USA, 21–28 May 2011; pp. 481–490. [Google Scholar] [CrossRef]
- Turhan, B.; Menzies, T.; Bener, A.B.; Di Stefano, J. On the relative value of cross-company and within-company data for defect prediction. Empir. Softw. Eng. 2009, 14, 540–578. [Google Scholar] [CrossRef] [Green Version]
- Peduzzi, P.; Concato, J.; Kemper, E.; Holford, T.R.; Feinstein, A.R. A simulation study of the number of events per variable in logistic regression analysis. J. Clin. Epidemiol. 1996, 49, 1373–1379. [Google Scholar] [CrossRef]
- Tantithamthavorn, C.; McIntosh, S.; Hassan, A.E.; Matsumoto, K. An Empirical Comparison of Model Validation Techniques for Defect Prediction Models. IEEE Trans. Softw. Eng. 2017, 43, 1–18. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; pp. 2546–2554. [Google Scholar]
- Dietterich, T.G. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput. 1998, 10, 1895–1923. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Jiang, Y.; Cukic, B.; Menzies, T. Can data transformation help in the detection of fault-prone modules? In Proceedings of the 2008 Workshop on Defects in Large Software Systems (DEFECTS ’08), Seattle, WA, USA, 20 July 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 16–20. [Google Scholar] [CrossRef] [Green Version]
- Young, W.; Weckman, G.; Holland, W. A survey of methodologies for the treatment of missing values within datasets: Limitations and benefits. Theor. Issues Ergon. Sci. 2011, 12, 15–43. [Google Scholar] [CrossRef]
- Mundfrom, D.J.; Whitcomb, A. Imputing Missing Values: The Effect on the Accuracy of Classification; Multiple Linear Regression Viewpoints: Birmingham, UK, 1998; Volume 25. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence-Volume 2 (IJCAI’95), Montreal, QC, Canada, 20–25 August 1995; Morgan Kaufmann Publishers Inc.: Montreal, QC, Canada, 1995; pp. 1137–1143. [Google Scholar]
- Qu, Y.; Zheng, Q.; Chi, J.; Jin, Y.; He, A.; Cui, D.; Zhang, H.; Liu, T. Using K-core Decomposition on Class Dependency Networks to Improve Bug Prediction Model’s Practical Performance. IEEE Trans. Softw. Eng. 2019, 47, 348–366. [Google Scholar] [CrossRef]
- Brier, G.W. Verification of Forecasts Expressed in Terms of Probability. Mon. Weather Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Fritz, C.O.; Morris, P.E.; Richler, J.J. Effect size estimates: Current use, calculations, and interpretation. J. Exp. Psychol. Gen. 2012, 141, 2–18. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J. A power primer. Psychol. Bull. 1992, 112, 155–159. [Google Scholar] [CrossRef]
- Tantithamthavorn, C. ScottKnottESD: The Scott-Knott Effect Size Difference (ESD) Test. 2018. Available online: https://cran.r-project.org/package=ScottKnottESD (accessed on 2 March 2022).
- Scott, A.J.; Knott, M. A Cluster Analysis Method for Grouping Means in the Analysis of Variance. Biometrics 1974, 30, 507–512. [Google Scholar] [CrossRef] [Green Version]

| Authors | Dataset Name | Ind. Variables | Defective | Non- Defective | Instances | EPV | Defective % | Granularity |
|---|---|---|---|---|---|---|---|---|
| Shepperd et al. [34] | JM1 | 21 | 1672 | 6110 | 7782 | 79.6 | 21% | Method |
| KC1 | 21 | 314 | 869 | 1183 | 15.0 | 27% | Method | |
| PC5 | 38 | 471 | 1240 | 1711 | 12.4 | 28% | Method | |
| D’Ambros et al. [35] | Eclipse JDT Core | 15 | 206 | 791 | 997 | 13.7 | 21% | Class |
| Eclipse PDE UI | 15 | 209 | 1288 | 1497 | 13.9 | 14% | Class | |
| Mylyn | 15 | 245 | 1617 | 1862 | 16.3 | 13% | Class | |
| Jureczko et al. [36] | camel 1.2 | 20 | 216 | 549 | 765 | 10.8 | 28% | Class |
| lucene 2.4 | 20 | 203 | 333 | 536 | 10.2 | 38% | Class | |
| prop-1 | 20 | 2436 | 20,622 | 23,058 | 121.8 | 11% | Class | |
| prop-2 | 20 | 1514 | 11,645 | 13,159 | 75.7 | 12% | Class | |
| prop-3 | 20 | 840 | 8027 | 8867 | 42.0 | 9% | Class | |
| prop-4 | 20 | 1299 | 7274 | 8573 | 65.0 | 15% | Class | |
| prop-43 | 20 | 341 | 11,338 | 11,679 | 17.1 | 3% | Class | |
| prop-5 | 20 | 2720 | 17,686 | 20,406 | 136.0 | 13% | Class | |
| xalan 2.5.0 | 20 | 387 | 558 | 945 | 19.4 | 41% | Class | |
| xalan 2.6.0 | 20 | 411 | 759 | 1170 | 20.6 | 35% | Class | |
| Zimmermann et al. [38] | Eclipse 2.0 | 31 | 2610 | 4119 | 6729 | 84.2 | 39% | File |
| Eclipse 2.1 | 31 | 2139 | 5749 | 7888 | 69.0 | 27% | File | |
| Eclipse 3.0 | 31 | 2913 | 7680 | 10,593 | 94.0 | 27% | File | |
| Kim et al. [39] | SWT | 17 | 653 | 832 | 1485 | 38.4 | 44% | File |
| Debug | 17 | 263 | 802 | 1065 | 15.5 | 25% | File |
| Ensemble | Hyperparameter Name | Description | Optimized Value Range |
|---|---|---|---|
| Random Forest (RF) Extra Trees (ET) | n_estimators | Number of trees in the forest. | [100, 50, 40, 30] |
| max_depth | Maximum depth of the tree. | [1, 4, 8] | |
| min_samples_leaf | Minimum number of samples at a leaf node. | RF = [1, 10, 5] ET = [1, 2, 4] | |
| criterion | Measure the quality of a split. | [gini, entropy] | |
| AdaBoost (Ada) | n_estimators | Number of estimators at which boosting is terminated. | [50, 100, 1000] |
| learning_rate | The step size of the loss function. | [1, 0.1, 0.001, 0.01] | |
| Gradient Boosting (GB) | n_estimators | Number of estimators at which boosting is terminated. | [100, 50, 500, 1000] |
| learning_rate | The step size of the loss function. | [0.1, 0.001, 0.01] | |
| min_samples_leaf | Minimum number of samples at a leaf node. | [1, 10, 5] | |
| max_depth | Maximum depth of individual tree. | [3, 7, 9] | |
| loss | The loss function to be optimized in the boosting process. | [deviance, exponential] | |
| Hist Gradient Boosting (HGB) | max_iter | Number of iterations of the boosting process. | [100, 50, 500, 1000] |
| learning_rate | The step size of the loss function. | [0.1, 0.001, 0.01] | |
| min_samples_leaf | Minimum number of samples at a leaf node. | [20, 10, 5] | |
| max_depth | Maximum depth of individual tree. | [None, 1, 3, 5] | |
| loss | The metric to use in the boosting process. | [auto, binary crossentropy, categorical crossentropy] | |
| XGBoost (XGB) | n_estimators | Number of gradient boosted trees. | [100, 50, 500, 1000] |
| learning_rate | The step size of the loss function. | [0.3, 0.1, 0.001, 0.01] | |
| max_depth | Maximum tree depth for base learners. | [6, 3, 4, 5] | |
| CatBoost (CAT) | n_estimators | Number of estimators at which boosting is terminated. | [1000, 100, 50, 500] |
| loss_function | The metric to use in the boosting process. | [Logloss, MultiClass] | |
| learning_rate | The step size of the loss function. | [0.03, 0.001, 0.01, 0.1] | |
| depth | Depth of the tree. | [1, 5, 10] | |
| min_data_in_leaf | Minimum number of samples at a leaf node. | [1, 10] |
| Classifier | Negligible | Small | Medium | Large |
|---|---|---|---|---|
| Ada | 7 | 7 | 5 | 2 |
| CAT | 2 | 11 | 6 | 2 |
| ET | 8 | 4 | 8 | 1 |
| GB | 7 | 6 | 7 | 1 |
| HGB | 13 | 3 | 2 | 3 |
| RF | 9 | 1 | 7 | 4 |
| XGB | 7 | 9 | 2 | 3 |
| Classifier | ET | RF | Ada | GB | HGB | XGB | CAT |
|---|---|---|---|---|---|---|---|
| Camel 1.2 | 13 | 16 | 21 | 138 | 168 | 77 | 1842 |
| Debug | 9 | 12 | 4 | 71 | 78 | 31 | 673 |
| Eclipse 2.0 | 5 | 7 | 13 | 234 | 366 | 62 | 3915 |
| Eclipse 2.1 | 6 | 8 | 15 | 291 | 467 | 80 | 4358 |
| Eclipse 3.0 | 5 | 8 | 15 | 342 | 446 | 72 | 5136 |
| Eclipse JDT Core | 5 | 6 | 10 | 48 | 67 | 30 | 797 |
| Eclipse PDE UI | 5 | 6 | 9 | 59 | 87 | 32 | 918 |
| JM1 | 20 | 27 | 40 | 930 | 634 | 116 | 7318 |
| KC1 | 14 | 23 | 32 | 177 | 260 | 84 | 2907 |
| Lucene 2.4 | 10 | 14 | 17 | 77 | 82 | 37 | 743 |
| Mylyn | 11 | 12 | 16 | 135 | 181 | 46 | 1143 |
| PC5 | 20 | 26 | 35 | 362 | 406 | 112 | 4976 |
| Prop 1 | 6 | 8 | 13 | 414 | 321 | 883 | 4095 |
| Prop 2 | 6 | 8 | 20 | 283 | 287 | 816 | 2126 |
| Prop 3 | 5 | 7 | 13 | 204 | 251 | 750 | 2038 |
| Prop 4 | 5 | 7 | 13 | 216 | 263 | 796 | 1910 |
| Prop 43 | 5 | 7 | 12 | 196 | 231 | 574 | 2023 |
| Prop 5 | 6 | 9 | 16 | 409 | 308 | 896 | 4199 |
| SWT | 10 | 13 | 17 | 116 | 161 | 45 | 1321 |
| Xalan 2.5 | 10 | 14 | 16 | 106 | 131 | 45 | 1239 |
| Xalan 2.6 | 10 | 12 | 16 | 110 | 140 | 42 | 1313 |
| AVG time (ms) | 8.86 | 11.90 | 17.29 | 234.19 | 254.05 | 267.90 | 2618.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alazba, A.; Aljamaan, H. Software Defect Prediction Using Stacking Generalization of Optimized Tree-Based Ensembles. Appl. Sci. 2022, 12, 4577. https://doi.org/10.3390/app12094577
Alazba A, Aljamaan H. Software Defect Prediction Using Stacking Generalization of Optimized Tree-Based Ensembles. Applied Sciences. 2022; 12(9):4577. https://doi.org/10.3390/app12094577
Chicago/Turabian StyleAlazba, Amal, and Hamoud Aljamaan. 2022. "Software Defect Prediction Using Stacking Generalization of Optimized Tree-Based Ensembles" Applied Sciences 12, no. 9: 4577. https://doi.org/10.3390/app12094577
APA StyleAlazba, A., & Aljamaan, H. (2022). Software Defect Prediction Using Stacking Generalization of Optimized Tree-Based Ensembles. Applied Sciences, 12(9), 4577. https://doi.org/10.3390/app12094577







