Abstract
The electron transfer process between pentammineaquacobalt (III) and hexacyanoferrate (II), [Co(NH3)5H2O]3+/Fe(CN)6]4− ion pair was investigated in water/dioctyl sodium sulfosuccinate (AOT)/Isooctane reverse micelles. The study observed that the electron transfer rate depends on the size of the reverse micelles. The concentrations of Fe (II) ions were varied in different-sized (Wo) reverse micelles of Wo = [H2O]/[AOT] = 10 to 30, but the concentration of Co (III) ions was kept constant. The rate of electron transfer in the ion pair [Co(NH3)5H2O]3+/[Fe(CN)6]4− increased with decreasing size (Wo) of reverse micelles. The smallest reverse micelles Wo = 10 demonstrated the fastest electron transfer rate, and the biggest Wo = 30 reverse micelles showed the slowest electron transfer rate. The change of reaction environment and the location of the reactants in the reverse micelles due to confinement are considered the factors responsible for the results.
1. Introduction
Reverse micelles (RMs) have been used in diverse applications, including biological, synthetic, and physical chemistry [1,2,3]. The interior part of RMs contains an aqueous core where various reactions can be carried out, and hence, the study of reactions in RMs has been of considerable attention. RMs have been employed in enzyme separation [1], pharmaceutical application [2], and protein separation and refolding [3]. Due to the possibility of controlling the volume of water pool within RMs, they have been used as a reaction medium to synthesize nanoparticles [4].
RMs are formed by surfactant droplets dispersed in organic solvents. These surfactant droplets confine the water pool and form ternary systems in RMs. The inner core of the reverse micelle confined by the surfactant molecules of RMs forms a water pool (Figure 1). The water pool is nanosized. Depending on the location in the water pool, properties such as polarity, micro fluidity, bonding, viscosity, and pH, vary from those of bulk water [5]. Water changes states from bound at the interface to free at the center in the water pool [5,6]. So, the physicochemical properties of water shells inside the water pool also vary, as the distance changes from interfacial molecules’ heads in RMs [5,7]. These properties at the bound state (interface) and free state (center of the shell) also vary with the size of RMs [6,8]. The RMs size is represented by Wo and is dependent on the molar ratio of water to surfactant concentration, Wo = [H2O]/[Surfactant]. Several parameters control the size and concentration of reverse micelles [9].
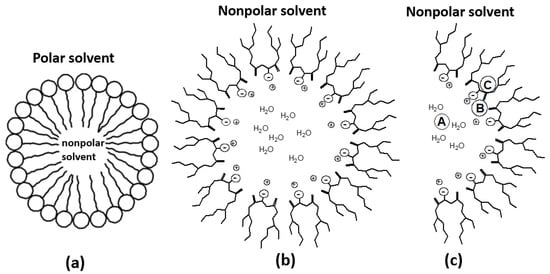
Figure 1.
Schematic representation of (a) a micelle (b) a reverse micelle and (c) a part of reverse micelles with different locations. Plus represents Na+ ions [6,10].
Though different types of surfactants can be used to prepare RMs, dioctyl sodium sulfosuccinate (AOT) is the most used. AOT in isooctane reverse micelles is characterized as spherical in shape in which Na+ ions remain inside the reverse micelles surrounding the counterions, especially at the interface, as shown in Figure 1b,c. A spherical RM formed by water and NaAOT in isooctane can be divided into three parts [11], including (1) the water pool, A (2) the aqueous interface, B (3) the hydrophobic interface region, C (shown in Figure 1c) [6]. Since each of these three regions differs in their locations in an RM, a solute can experience different physical and chemical environments in these three regions [6,8]. Metal complexes (solutes) can occupy any of these three regions. The location of the metal complexes in RMs affects the rate of electron transfer. The collision of the solvated coordination sphere is required for an outer sphere electron transfer process between transition metal complexes [12]. An outer sphere electron transfer rate depends on the reorganizational energy of the solvent molecules around the reactants and the activated complex [13]. The general rate law for outer sphere electron transfer can be represented by [14]
where ket is the electron transfer rate constant, and KIP is the ion-pairing constant.
If one reactant is in excess in experiments of the pseudo-first order, the pseudo-first-order rate constant or the observed rate constant, kobs can be measured, and it depends on the concentration of excess reagent [14]. If the reductant is in excess, the relation follows as
When both partners in an electron transfer are substitution inert, and there is no change in the coordination sphere during the reaction, an outer sphere electron transfer reaction takes place. When an outer sphere electron transfer takes place between two reactants, an ion pair is formed by the association of the ions due to electrostatic interactions. Ion pairing is affected by many factors, such as ionic strength, the size of electrical charge on the ions, the size of the solvent dielectric constant, and the size of the ions. The Bjerrum theory [15,16] of ion pairing states that ion pairing (1) decreases with the increasing ionic strength of the solvent, (2) increases with increasing magnitude of electric charge on the ions, (3) increases with decreasing solvent dielectric constant [17], and (4) increases with decreasing ionic size [17].
Transition metal hexacyanoferrates and pentaaminecobalt (III) complexes are extremely stable coordination compounds [18,19]. Both the hexacyanoferrates and pentaaminecobalt (III) complexes are water soluble and exhibit redox properties [20]. So, transition metal hexacynoferrate complexes have attracted attention due to their structural attributes and various properties, such as electrochemical and ion-exchanging properties [18].
In this paper, we discuss the results of the investigation of the effect of the size of the reverse micelles on the outer sphere electron transfer rate constant (ket) and ion-pairing constant KIP in the following reaction.
[Co(NH3)5(H2O)]3+ + [Fe(CN)6]4− → [Co(NH3)5(H2O)]]2+ + [Fe(CN)6]3−
Co (III) Fe (II) Co (II) Fe (III)
2. Experimental Section
2.1. Reagents
[Co(NH3)5Cl]Cl2, [Co(NH3)5CO3]NO3, and [Co(NH3)5trf]trf2, complexes were prepared in the laboratory following the previously reported procedure. Docusate sodium salt (NaAOT), HCl, NH3, AgNO3, ether, ethylenediamminetetraacetic acid disodium salt dehydrate, and 2,2,4-trimethyl pentane were purchased from Sigma Aldrich (St. Louis, MO, USA). Cobalt (II) ammonium carbonate, H2O2, and acetone were purchased from Fisher Scientific. Co (II) nitrate hexahydrate and trifluoromethane sulfonic acid were purchased from Acros, and K4[Fe(CN)6] was purchased from J T Baker Chemicals.
2.2. Synthesis of Metal Complexes
2.2.1. Synthesis of [Co(NH3)5CO3]NO3
Three different solutions of Co(NO3)2·6H2O, ammonium carbonate, and ammonium hydroxide were first prepared. The solution of cobalt nitrate hexahydrate, Co(NO3)2·6H2O, was prepared by dissolving 5.0 g of it in 10 mL of deionized water. In a separate 1000 mL beaker, 7.0 g of solid ammonium carbonate was dissolved in 20 mL of water. Then, 20 mL of concentrated aqueous ammonium hydroxide was added carefully to the ammonium carbonate solution. First, the whole cobalt nitrate solution was transferred to the resulting solution. Then, 3 mL of 30% H2O2 was slowly added to it. The solution was placed on a hot plate, maintaining the temperature at 70–80 °C for slow water evaporation. Once the volume of the solution decreased to about 40 mL, an additional 2.0 g of solid ammonium carbonate was slowly added. Carbon dioxide gas started evolving with the addition of ammonium carbonate. When the evolution of CO2 gas ceased, the beaker was transferred to an ice bath for cooling. Dark-red shiny crystals of [Co(NH3)5CO3]NO3 precipitated as the solution cooled. These crystals were rinsed with 15–20 mL of acetone and finally air-dried.
2.2.2. Synthesis of [Co(NH3)5Cl]Cl2
The solution of [Co(NH3)5CO3]NO3 was prepared by dissolving 1.0 g of it in 50 mL of water. An amount of 5 mL of concentrated HCl was added to it to expel carbonate ions. The solution was made basic by adding a concentrated aqueous ammonia solution. The basic nature was tested by exposing the vapor to red litmus paper, which turned blue. An additional 5 mL of aqueous ammonia solution was then added. The solution was warmed for 20 min but not boiled. The solution was cooled slightly and slowly added to the 15 mL of concentrated HCl. The solution was then reheated, avoiding boiling, for 20–30 min. The solution was then cooled to room temperature. Once the purple-red crystals were precipitated, they were recovered using a suction funnel and washed with several mL of acetone. They were dried in the air.
2.2.3. Synthesis of [Co(NH3)5trf]trf2
The compound [Co(NH3)5trf]trf2 was synthesized following the process developed by Dixon and Sargeson. Ten grams of [Co(NH3)5Cl]Cl2 was taken in a perfectly dry three-necked round-bottom 2 L flask. Two side necks of the flask were fitted with two separate pipettes: one for the outlet and the other for the inlet of argon gas. The middle mouth was fitted with a dropping funnel. The dropping funnel had a stopper at the mouth. An amount of 50 mL of triflic acid (CF3SO3H) was carefully added through this funnel. As the triflic acid dropped down, the argon gas was bubbled through the solution. The reaction also produced HCl gas. The reaction was maintained at 90–100 °C, and a steady stream of argon was passed through the resulting solution. The other pipette of the other side neck (outlet) was dipped in water to dissolve the outcoming gas. After approximately 1 h, the outcoming gas was passed through a silver nitrate (AgNO3) solution to check whether HCl gas generation had ceased. Once finished, the flask was cooled in an ice bath to 0 °C. 70 mL of diethyl ether was then added dropwise with vigorous stirring.
Additionally, 150 mL of ether was added to dilute the solution. It had two layers: upper pink and lower dark red layer. The mixture was sediment, and the clear supernatant pink liquid was decanted and thrown away. Again, ether was added to repeat the decantation and washing process until the upper solution of ether was clear. The transparent upper liquid was decanted, and the dark-red liquid was kept in the refrigerator for one whole night. Gleaming dark-red crystals were formed. The crystals were dried in a vacuum desiccator.
2.3. Preparation of Standard Solutions
The metal complexes solutions were prepared in an Argon environment of 0.01 M EDTA solution.
2.3.1. Preparation of Standard Solution of [Co(NH3)5OH2]3+
UV-Vis spectra were monitored using Hewlett Packard HP 8452 A Diode array spectrophotometer with a standard 1 cm path length quartz cuvette to measure the concentration of [Co(NH3)5OH2]3+ solution. This solution was prepared by dissolving the [Co(NH3)5trf]trf2 complex in water. [Co(NH3)5trf]trf2 complex readily undergoes hydrolysis in water to produce [Co(NH3)5OH2]3+. The concentration of [Co(NH3)5OH2]3+ was measured using its molar absorption extinction coefficient, ε492 = 47.2 M−1 cm−1 using Beer–Lambert’s law, where the path length was 1 cm. The absorption for 0.001 M aqueous solution at λmax 492 nm was 0.0472. To prepare a Wo = 30 RM solution, 0.363 mL of 0.001 M solution was mixed in 3 mL of AOT/isooctane solution to obtain a total volume of 3.363 mL of 0.00093 M [Co(NH3)5OH2]3+ solution.
2.3.2. Preparation of Standard Solution of [Fe(CN)6]4−
A solution of 0.05 M was prepared by dissolving 105.6 mg of K4[Fe(CN)6] in 5 mL of 0.01 M EDTA solution. For the preparation of wo = 30 RMs, 926 μL of the solution was diluted to 5 mL with 0.01 M EDTA solution to obtain 0.0093 M solution. Then, 0.363 mL of this solution was added to 3 mL of 0.2 M AOT/isooctane to obtain a total volume of 3.363 mL of 10−3 M [Fe(CN)6]4− solution in AOT/isooctane.
2.4. Kinetic Studies
The kinetics of the electron transfer was investigated between [Fe(CN)6]4− and [Co (NH3)5OH2]3+ complexes using a UV-Vis spectrophotometer. RMs solutions of Fe (II) and Co (III) complexes were mixed in 1:1 proportion (1 mL each). This mixture was used in a 1 cm path length quartz cuvette using a micropipette. These cuvettes were placed in the diode spectrophotometer immediately to observe the reaction. As the reaction seemed to be very slow, the time in the spectrophotometer was set for 2 h for dilute and 1 h for concentrated solutions. When the two complexes react, [Fe(CN)6]3− is produced. The absorption maxima (λmax) for [Fe(CN)6]3− was 420 nm [21,22]. As Fe (II) was oxidized to Fe (III) by Co (III) ion, the absorbance increased with time as the concentration of Fe (III) increased, as shown in Figure 2.
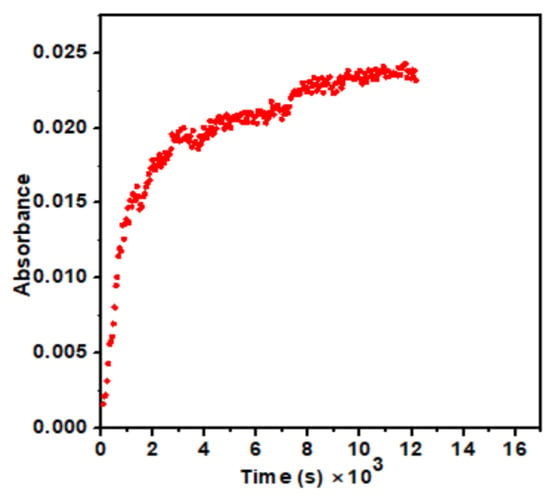
Figure 2.
Representative plot of absorbance (at 420 nm) against time illustrating the formation of [Fe(CN)6]3−.
The absorbance of [Fe(CN)6]3− versus time was measured in aqueous medium under pseudo-first-order conditions of [Fe(CN)6]4− ≫ [Co(NH3)5OH2]3+ and in different RMs small sizes (Wo = 10, 15, 20, and 30). The representative absorbance data for Wo = 30 are shown in Figure 2. It was fitted well to a single exponential growth equation to obtain the observed pseudo-first-order rate constant (kobs).
The plot of kobs versus [Fe(CN)64−] gave a saturation curve, whereas the double reciprocal plot of 1/obs−1 and [Fe(CN)64−] gave a straight line with positive y-intercept and slope, as shown in Figure 3. Here, the y-intercept was equal to 1/ket, and the slope was equal to 1/ket × 1/KIP. Thus, the ket and KIP values were determined from the y-intercept and slope, respectively. The equation for the observed rate constant is given below:
where ket is the electron transfer rate constant, KIP is the ion-pairing constant.
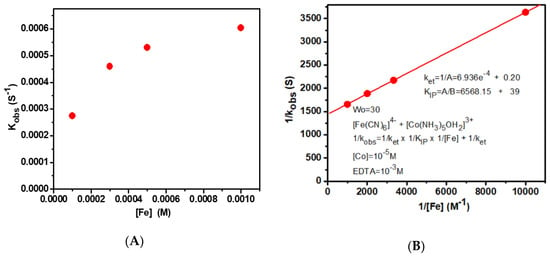
Figure 3.
Plots of (A) kobs versus [Fe(CN)6]4− and (B) 1/kobs versus 1/[Fe(CN)6]4− where Intercept = 1/ket and slope = 1/KIP × 1/ket.
K4[Fe(CN)6] solutions used were 1 × 10−3 M, 2 × 10−3 M, 5 × 10−3 M, and 1 × 10−2 M at a constant concentration of 10−4 M of [Co(NH3)5H2O]3+. UV-Vis spectra were monitored to obtain the kinetic data. All the measurements were determined at pseudo-first-order conditions at room temperature and pH 7–8, where
[Fe (CN) 6]4− >> [Co (NH3)5OH2]3+
3. Discussion
When AOT RM solutions of [Co(NH3)5OH2]3+ and [Fe(CN)6]4− are mixed, the precipitation of Co (II) hexacyanoferrate (II) occurs. When EDTA is added, soluble EDTA complexes of Co (II) are formed as soon as Co (II) is produced. So, EDTA is added to the reaction mixture to prevent the formation of the precipitate. In such a case, the electron transfer takes place, resulting in the ion pair of [Co(NH3)5OH2]2+/[Fe(CN)6]3−. Linear plots of the inverse of kobs versus the inverse of the concentrations of hexacyanoferrite (III) ions give the ion-pairing constant (KIP) and the electron transfer rate constant (ket). Table 1 shows the ket and KIP values for the reaction between [Co(NH3)5OH2]3+ and [Fe(CN)6]4−.

Table 1.
Rate constants and ion-pairing constant at different RMs size.
It can be observed in Table 1 that the electron transfer rates become faster in smaller reverse micelles, and the ion-pairing constant is more significant for larger RMs.
The faster electron transfer rate in smaller RMs can be rationalized based on the solvent reorganization energy and dielectric constant. According to the Marcus theory, the outer sphere electron transfer rates increase with decreasing solvent reorganization energies. The equations for the Marcus theory are as follows [23]
where ΔG* is the activation free energy, λi and λo are the inner and outer sphere solvent reorganization energies, respectively. Z is the collision frequency, e is the charge on the electron, R is the universal gas constant, and T is the temperature.
ΔG* = λi + λo + ΔGo
ket = Ze(−ΔG*/R)
The inner sphere reorganization energy (λi) is assumed to be the same in the aqueous and RMs system:
Δλi(aq/RMs) = 0
Thus, the electron transfer rate constant (ket) is related to the solvent reorganization energy. Solvent reorganization energy increases with the increase in solvent (water) volume inside RMs; therefore, the electron transfer rate decreases with increasing RMs size. The research of Gebbiki and Lidia has supported this result [11]. They found a higher rate of electron self-exchange rate (kex) in smaller RMs. This result can also be discussed in terms of ionic strength variation with the change in the size of reverse micelles. As previously determined, the ionic strength increases as RMs size decreases. Pellizetti et al. clearly showed the effect of ionic strength (μ) on the electron transfer rate [24]. They showed that the electron transfer rate increases with the increase in ionic strength. Thus, the rate of electron transfer increases as the RMs size decreases.
This result can be rationalized in the RMs of dielectric constant variation with the change in the size of reverse micelles. It has already been discussed in relation to electron transfer in nonaqueous solvents that electron transfer rate increases with the decrease in dielectric constant. Durocher reported that the dielectric constant decreases with the decrease in the size of RMs [25]. He measured the effective dielectric constant in reverse micelles of n-heptane/AOT/water. Chamorovsky studied the correlation of electron transfer rate in photosynthetic reaction centers with intraprotein dielectric properties [26]. He found that the rate of the electron transfer correlated with the value of dielectric constant; the faster electron transfer reaction occurred in low dielectric constant. Thus, the smaller the reverse micelles, the lower the dielectric constant and the higher the electron transfer rate.
Larger ion-pairing constants for bigger RMs can be discussed on the basis of ionic strength. The ratio of free water to bound water increases as Wo increases. Similarly, ionic strength decreases with Wo. The relationship between ionic strength and RMs size can be shown by a simple mathematical expression:
where, the volume of RMs is 4/3πr3 and the number of AOT is equal to the number of Na+. “r” is the radius of an RMs, and navg represents the average aggregation number, which is the molar ratio of AOT concentration to reverse micelle (RMs) concentration.
navg = [AOT]/[RM]
According to this expression, the average number of [Na+] increases with the decrease in “r” value or the decrease in RMs size, and the ionic strength is greater for smaller RMs size. The effective charge of each of the complex ions reduces with increasing ionic strength. The coulombic interactions between the counter ions become relatively less effective, resulting in less ion pair formation. Increasing ionic strength decreases the ion-pair formation [15]. Thus, smaller RMs with higher ionic strength have smaller ion-pair constants. The ion-pairing constant has also been expressed mathematically by Debye–Huckel relating to a dielectric constant of the solvent and the charges on the ions as follows:
KIP = 4пNɑ3/3000exp(−U/κT)
U= z1z2e2/ε × [1/ɑ(1+κɑ)]
Here, ɑ is the distance of the closest approach of the ions (cm), N is Avogadro’s number (6.022 × 1023), κ is Boltzmann’s constant (1.38 × 10−16 erg·K−1), e is the charge of electrons (4.803 × 10−10 eu), ε is the bulk solvent dielectric constant, μ is the ionic strength, and z1 and z2 are the charges on the ions.
According to this expression, the value of U decreases with increasing distance between positive and negative ions and with increasing ε value. When U decreases, the KIP value increases. The literature reports lower dielectric constants in smaller reverse micelles. So, these facts support the hypothesis that the KIP value increases from smaller to bigger reverse micelles.
4. Conclusions
Due to the difference in the volume of water in different-sized reverse micelles, the reaction environments are different. Similarly, the reaction environment is different in water compared to RMs. Metal complexes may remain in different locations in different RMs. Due to the variation of environments, the rate of the electron transfer varies in different RMs and bulk water. Because of the variation of physicochemical properties of water in water-pool with RMs size, the ion-pairing constants and the electron transfer rate constants also vary with RMs size. The ion-pairing constants of [Fe(CN)6]4−/[Co(NH3)5OH2]3+ in AOT/water/isooctane RMs were found to increase with growing RMs size. The KIP value is found lower for smaller RMs. This may be ascribed to higher ionic strength and lower dielectric constant in smaller RMs. The electron transfer rate increases from smaller to bigger RMs. This may be ascribed to less solvent reorganization energy, higher ionic strength in smaller RMs, and lower dielectric constant.
Author Contributions
Data collection and analysis, R.K.H. Manuscript writing and review, R.T. Funding acquisition and resources, G.S.D. All authors have read and agreed to the published version of the manuscript.
Funding
The co-author Gurjot S. Dhaliwal was supported in this research by the National Science Foundation (HRD 1839895).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tonova, K.; Lazarova, Z. Reversed micelle solvents as tools of enzyme purification and enzyme-catalyzed conversion. Biotechnol. Adv. 2008, 26, 516–532. [Google Scholar] [CrossRef]
- Jones, M.C.; Gao, H.; Leroux, J.C. Reverse polymeric micelles for pharmaceutical applications. J. Control. Release 2008, 132, 208–215. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Dong, X.; Sun, Y. New Development of Reverse Micelles and Applications in Protein Separation and Refolding. Chin. J. Chem. Eng. 2008, 16, 949–955. [Google Scholar] [CrossRef]
- Eastoe, J.; Hollamby, M.J.; Hudson, L. Recent advances in nanoparticle synthesis with reversed micelles. Adv. Colloid Interface Sci. 2006, 128–130, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.L.; Gunderson, W.A.; Weitz, A.C.; Hendrich, M.P.; Ryabov, A.D.; Collins, T.J. Activation of Dioxygen by a TAML Activator in Reverse Micelles: Characterization of an FeIIIFeIV Dimer and Associated Catalytic Chemistry. J. Am. Chem. Soc. 2015, 137, 9704–9715. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silber, J.J.; Biasutti, A.; Abuin, E.; Lissi, E. Interactions of small molecules with reverse micelles. Adv. Colloid Interface Sci. 1999, 82, 189–252. [Google Scholar] [CrossRef]
- Volkova, O.I.; Kuleshova, A.A.; Saletsky, A.M. The Effect of Nanoscale Reverse Micelles on the Photophysical Properties of Fluorescein Molecules. Mosc. Univ. Phys. Bull. 2020, 75, 605–610. [Google Scholar] [CrossRef]
- Moulik, S.P.; Paul, B.K. Structure, dynamics and transport properties of microemulsions. Adv. Colloid Interface Sci. 1998, 78, 99–195. [Google Scholar] [CrossRef]
- Maitra, A. Determination of size parameters of water-Aerosol OT-oil reverse micelles from their nuclear magnetic resonance data. J. Phys. Chem. 1984, 88, 5122–5125. [Google Scholar] [CrossRef]
- Pang, Y.; Deàk, J.C.; Huang, W.; Lagutchev, A.; Pakoulev, A.; Patterson, J.E.; Sechler, T.D.; Wang, Z.; Dlott, D.D. Vibrational energy in molecules probed with high time and space resolution. Intl. Rev. Phys. Chem. 2007, 26, 223–248. [Google Scholar] [CrossRef]
- Gebicki, J.L.; Gebicka, L. Radical reactions in reverse micelles studied by pulse radiolysis. Radiat. Phys. Chem. 2020, 177, 109105. [Google Scholar] [CrossRef]
- Jordan, R.B. Reaction Mechanisms of Inorganic and Organometallic Systems; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Atkins, P.; de Paula, J. Physical Chemistry, 7th ed.; Oxford University Press: Oxford, UK, 2002; pp. 1015–1018. [Google Scholar]
- Gaus, P.L.; Villanueva, J.L. Direct determinations of the ion pairing equilibrium constant and first-order rate constant for outer sphere electron transfer reactions. J. Am. Chem. Soc. 1980, 102, 1934–1938. [Google Scholar] [CrossRef]
- Bjerrum, N.; Danske, V.S. Mat. Fys. Medd.; Selected Papers; Einar Munksgaard: Copenhagen, Denmark, 1949. [Google Scholar]
- Schellman, J.A. The Application of the Bjerrum Ion Association Theory to the Binding of Anions by Proteins. J. Phys. Chem. 1953, 57, 472–475. [Google Scholar] [CrossRef]
- Nielson, R.M.; Wherland, S. Electron self-exchange by hexakis (cyclohexyl isocyanide) manganese (I/II): Solvent, electrolyte and temperature dependences. Inorg. Chem. 1984, 23, 1338–1344. [Google Scholar] [CrossRef]
- Jassal, V.; Shanker, U.; Shankar, S. Synthesis, Characterization and Applications of Nano-structured Metal Hexacyanoferrates: A Review. J. Environ. Anal. Chem. 2015, 2, 1–14. [Google Scholar] [CrossRef]
- Schlessinger, G.G.; Britton, D.; Rhodes, T.; Ng, E. Chloropentaamminecobalt(III) Chloride. Inorg. Synth. 1967, 9, 160–163. [Google Scholar]
- Van Eldik, R.; Kelm, H. Concerning the pressure dependence of outer-sphere electron-transfer reactions: The reduction of Co(NH3)5OH3+2 by Fe(CN)4−6 in aqueous acidic solution. Inorg. Chim. Acta 1983, 73, 91–94. [Google Scholar] [CrossRef]
- Bera, A.K.; Pal, B.; Sen Gupta, K.K. Outer-sphere reduction of hexacyanoferrate(III) by enolizable and nonenolizable aldehydes in alkaline medium. Int. J. Chem. Kinet. 2012, 44, 494–505. [Google Scholar] [CrossRef]
- Rajchel-Mieldzioć, P.; Tymkiewicz, R.; Sołek, J.; Secomski, W.; Litniewski, J.; Fita, P. Reaction kinetics of sonochemical oxidation of potassium hexacyanoferrate(II) in aqueous solutions. Ultrason. Sonochem. 2020, 63, 104912. [Google Scholar] [CrossRef]
- Marcus, R.A. Transfer reactions in chemistry. Theory and experiment. Pure Appl. Chem. 1997, 69, 13–30. [Google Scholar] [CrossRef]
- Pelizzetti, E.; Mentasti, E.; Pramauro, E. Outer-sphere oxidation of ascorbic acid. Inorg. Chem. 1978, 17, 1181–1186. [Google Scholar] [CrossRef]
- Belletete, M.; Lachapelle, M.; Durocher, G. Polarity of AOT micellar interfaces: Use of the preferential solvation concepts in the evaluation of the effective dielectric constants. J. Phys. Chem. 1990, 94, 5337–5341. [Google Scholar] [CrossRef]
- Chamorovsky, S.K.; Cherepanov, D.A.; Chamorovsky, C.S.; Semenov, A.Y. Correlation of electron transfer rate in photosynthetic reaction centers with intraprotein dielectric properties. Biochim. Biophys. Acta 2007, 1767, 441–448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).