Abstract
Recently, increasing interest in managing pedestrian and bicycle flows has been demonstrated by cities and transportation professionals aiming to reach community goals related to health, safety, and the environment. Precise forecasting of pedestrian and bicycle traffic flow is crucial for identifying the potential use of bicycle and pedestrian infrastructure and improving bicyclists’ safety and comfort. Advances in sensory technology enable collecting massive traffic flow data, including road traffic, bicycle, and pedestrian traffic flow. This paper introduces a novel deep hybrid learning model with a fully guided-attention mechanism to improve bicycles and pedestrians’ traffic flow forecasting. Notably, the proposed approach extends the modeling capability of the Variational Autoencoder (VAE) by merging a long short-term memory (LSTM) model with the VAE’s decoder and using a self-attention mechanism at multi-stage of the VAE model (i.e., decoder and before data resampling). Specifically, LSTM improves the VAE decoder’s capacity in learning temporal dependencies, and the guided-attention units enable selecting relevant features based on the self-attention mechanism. This proposed deep hybrid learning model with a multi-stage guided-attention mechanism is called GAHD-VAE. Proposed methods were validated with traffic measurements from six publicly available pedestrian and bicycle traffic flow datasets. The proposed method provides promising forecasting results but requires no assumptions that the data are drawn from a given distribution. Results revealed that the GAHD-VAE methodology can efficiently enhance the traffic forecasting accuracy and achieved better performance than the deep learning methods VAE, LSTM, gated recurrent units (GRUs), bidirectional LSTM, bidirectional GRU, convolutional neural network (CNN), and convolutional LSTM (ConvLSTM), and four shallow methods, linear regression, lasso regression, ridge regression, and support vector regression.
1. Introduction
University of Science and Technology of Oran-Mohamed Boudiaf (USTO-MB), Computer Science Department Signal, Image and Speech Laboratory (SIMPA) Laboratory, El Mnaouar, BP 1505, Bir El Djir 31000, Oran, Algeria
Continued growth in road traffic demand generates numerous challenges, such as traffic congestion, pollution, and road traffic accidents, which could cause severe injuries and even deaths [1,2,3]. In recent years, growing attention has been paid to the correlation between health and cities to mitigate obesity, pollution, climate change, and road traffic injuries. Hence, governments are more engaged in creating safer, more comfortable, and more connected bicycling and walking environments. While walking and bicycling are beneficial to both the city environment and its citizens’ health, there is not much research focusing on modeling and forecasting pedestrian and bike traffic flow compared to motorized vehicle-based traffic flow [4]. For cities attempting to encourage walking and bicycling activities (i.e., nonmotorized travel), it is essential to quantify the need for facilities supporting active transportation [5]. Importantly, pedestrian and bicycle traffic flows are characterized by their sensitivity to environmental conditions (e.g., weather situations and topography) and are more dynamic. A timely and accurate forecast of nonmotorized traffic flow (walking and bicycling) is essential in developing walkable cities [4]. Due to the high dynamic behavior of motorized-based traffic flow, modeling and predicting pedestrian and bicycle traffic flows become a challenging task. Deep recurrent neural networks have recently gained great success in modeling the time-dependence in time series data. Thus, this work attempted to develop an innovative deep learning-driven approach to forecasting bicycle and pedestrian traffic flows.
Short and long-term forecasting techniques represent helpful tools for efficiently managing road traffic flow. In the last decades, much effort has been made to develop and improve traffic flow forecasting [6,7,8]. Time-series methods, such as autoregressive integrated moving average (ARIMA) and its extensions, are widely exploited in modeling and forecasting traffic flow [7,9,10]. Crucially, parametric models provide generally reasonable performance in the case of traffic flow with regular variations, but the forecasting quality can be degraded when the traffic flow exhibits irregular variations [11]. Several non-parametric techniques have been designed in the literature to mitigate this challenge. As data-driven methods, machine learning methods, such as support vector machine [12] and neural network [13], have been widely used to enhance forecasting of traffic flow. The central feature of data-based methods is their capacity to model complex data without an analytical model formulation. For example, Chun et al. in [14] introduced an approach for forecasting road traffic speed by coupling a radial basis function neural network and the aid of the Fuzzy system. They showed that the coupled model reduced the mean absolute percentage error to 6.4% and provided performance superior than the time series and simplex prediction methods. In [15], Cai et al. considered a hybrid learning-based approach by merging the benefit of support vector regression (SVR) and the gravitational search algorithm (GSA). They applied GSA to determine the optimal values of the SVR parameters and showed that the SVR-GSA provides better results than SVR-particle swarm optimization (PSO). In [16], Chen et al. presented an innovative approach by constructing multiple base forecasting models, each with different time lag and performance. More specifically, they employed the least-squares SVR (LSSVR) and investigated the influence of time lag on forecasting quality. In [17], Wenqi et al. introduced an approach to forecast lane-level traffic flow by integrating extreme gradient boosting and complete ensemble empirical mode decomposition. Results revealed the suitable performance of this approach in modeling the complex volatility of traffic flow at different types of lane sections. The study conducted in [18] focused on passenger flow forecasting based on automatic fare collection (AFC) data in metro transportation. To this end, different models, including ARIMA, linear regression, and SVR, have been employed to forecast passenger flow. It has been shown that incorporating information from temporal, spatial, and weather features improves forecasting accuracy. In [19], a stacking model is introduced to predict the variation of public bicycle traffic flow. This model combines numerous base models, and they are trained using distinct combinations of features to improve prediction. The XGBoost algorithm is employed to train the models. Results using datasets from Hangzhou and New York City showed the promising performance of this stacked model compared to the standalone models.
Over the last decade, city and transportation professionals have shown increasing interest in managing pedestrian and bicycle flows to reach community goals related to health, safety, and the environment [20,21]. Precise traffic forecasting of pedestrian and bicycle traffic flows is crucial to improve conditions for pedestrians and bicycles and in providing crucial information to road users and decision managers for improved decision making [22]. However, few research studies have been proposed in the literature to forecast the potential use of bicycle and pedestrian infrastructure. Besides, most of the methods mentioned above need a large amount of labeled data for supervised learning, exhibit high computation cost, and have a complex architecture that limits online forecasting applications. This study developed a guided-attention hybrid deep learning architecture for improved forecasting of different types of traffic flows.
This work aims to develop a forecasting method from traffic flow data, which leverages pedestrian and bicycle traffic flow complexity and produces accurate results. The major contributions of this work are summarized as follows.
- In this study, we first introduce a proficient hybrid approach for traffic flow forecasting. The primary elements of the proposed guided-attention hybrid deep learning architecture (termed GAHD-VAE) are the VAE model, the self-attention mechanism, and LSTM. As we know, this is the first study using a hybrid deep learning model to improve the forecasting of pedestrian and bicycle traffic flows. This approach improves the traditional VAE model to capture potential temporal dependencies by using the self-attention unit at a multi-level of the VAE model and including an LSTM model in the VAE encoder. The self-attention mechanism that mimics the human brain is adapted in the GAHD-VAE to uncover the most relevant traffic flow data features. Indeed, self-attention allows attention-driven long-range dependency modeling for time-series. On the other hand, the hybrid LSTM-VAE is employed to automatically learn time dependence in traffic data without feature engineering. Employing all these advanced statistical tools is beneficial in the sense that it has the potential to enhance short-term forecasting of pedestrian and bicycle traffic flows. The forecasting performance of the GAHD-VAE method has been compared to that of the traditional VAE and some powerful deep recurrent neural networks, namely LSTM, gated recurrent units (GRUs), BiLSTM, bidirectional GRU (BiGRU), convolutional neural network (CNN), and convolutional LSTM (ConvLSTM), and four shallow methods, linear regression (LR), lasso regression, ridge regression (RR), and support vector regression (SVR).
- The second contribution consists of investigating the impact of using different configurations of the self-attention module on the forecasting quality of the GAHD-VAE. Crucially, we examined the influence of the adopted activation functions in the attention mechanism, such as Rectified Linear Unit (ReLU), Hyperbolic Tangent (tanh), and Logistic Sigmoid, on the proposed approach’s forecasting quality. Moreover, the influence of the attention type, including multiplicative and additive, on the forecasting accuracy has been investigated.
- Finally, this study investigated both single- and multi-step-ahead forecasting. Data sets from six pedestrians and bicycle traffic flows are utilized to evaluate the forecasting quality of the considered methods. Results reveal that the proposed GAHD-VAE method offers satisfying performance to forecast different types of traffic flows and consistently performed better than the other methods.
The rest of the paper consists of three sections. Section 2 highlights literature reviews on the related works. Section 3 describes preliminary material and the proposed GAHD-VAE methodology. Section 4 presents the forecasting results and discussion based on six pedestrians and bicycle traffic flow datasets. Lastly, Section 5 summarizes the paper and provides future directions for possible improvements.
2. Related Works
Deep learning techniques are powerful in discovering layer-by-layer complex non-linearity in multivariate data and automatically extracting hidden and relevant complex patterns from data. They achieved remarkable success in modeling and forecasting time series data in academia and industry [11,23,24,25]. Numerous deep methodologies have been employed in the literature to address traffic flow forecasting [26]. In [23], a temporal convolutional network (TCN) is proposed for traffic flow, and the Taguchi method is utilized to optimize the TCN structure. Lv et al. in [27] employed a stacked auto-encoder (SAE) model to predict traffic flow. They used a greedy layerwise approach to train the model and showed the superior performance of the SAE compared to the backpropagation neural network, SVM, and random walk forecast approach. In [26], Yang et al. proposed an approach using the exponential smoothing and extreme learning machine approach to forecast traffic flow. The configuration of this approach has been optimized using the Taguchi method. Results revealed that this approach exhibited satisfactory performance in traffic flow forecasting by achieving 91% and 88% accuracy rates in freeways and highways. In [28], Dai et al. introduced a deep learning approach to predict traffic flow by combining a Gated Recurrent Unit (GRU) with the spatio-temporal analysis. To this end, the GRU model is applied to process the spatio-temporal feature information obtained from the time and spatial correlation analyses. Results showed the superior performance of this combined approach compared to the convolutional neural network (CNN) model and the GRU model. By using a deep belief network and kernel extreme learning machine, a short-term method for the traffic flow prediction is proposed in [29].
During recent years, attention-driven methods have shown good efficacy for vision-based multiple-object localization and recognition, despite the training performed using labeled samples of each object [30]. Essentially, attention-based methods mimic the human vision system to recognize objects by focusing only on the object’s relevant areas. However, it is worth noticing that, until recently, only a very few studies reported in the literature focused on attention-driven methods for time-series data modeling and prediction. For instance, in [31] a traffic flow prediction framework is introduced using a complex architecture including a combination of LSTM and CNN with a wide attention module. This architecture comprises dual paths: The wide attention module preprocesses input data via linear transformation followed by a self-attention layer in the first path. The second path contains a composite model formed by staking LSTM and CNN models; the two paths’ outputs are also concatenated in one layer. In this approach, the feature extraction is performed via interactions between a linear model and a self-attention mechanism to predict traffic flow. The authors in [32] design a hybrid deep learning-driven model based on CNN and LSTM (called Conv-LSTM) for traffic flow forecasting. The Conv-LSTM is applied to uncover spatial-temporal features in traffic data efficiently. A bidirectional LSTM (Bi-LSTM) is employed to extract long-term temporal features. It has been shown that incorporating the attention mechanism in this approach improves forecasting performance.
3. Methods
This section is dedicated to providing the basic concept of the investigated attention, self-attention mechanisms, and VAE employed in this study. Then, the introduced GAHD-VAE forecasting methodology is presented.
3.1. Attention Mechanism
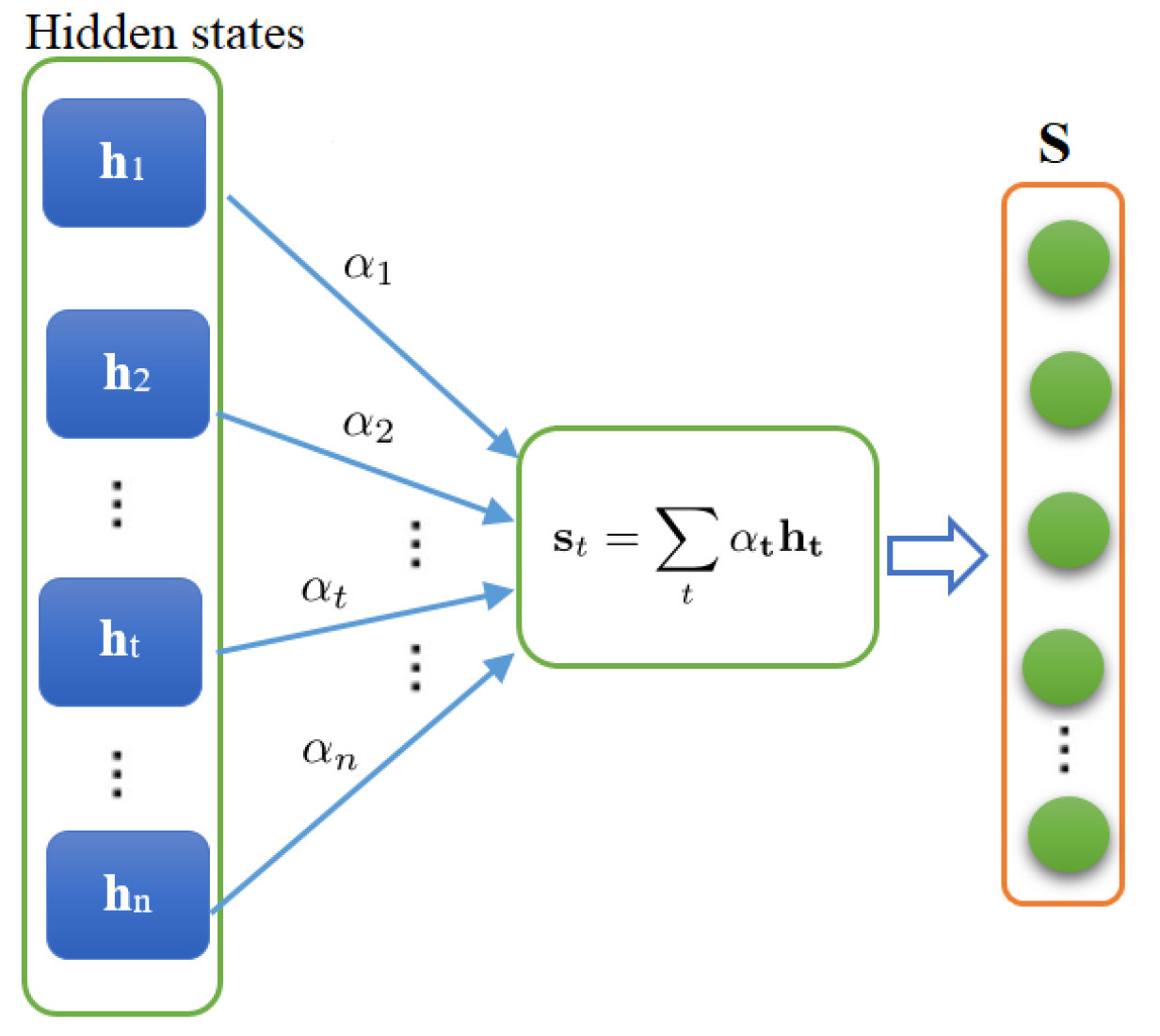
The attention mechanism, also called soft attention, was primarily designed to improve machine translation in [33]. Importantly, it is designed to mimic the human brain by targeting the most relevant information in a sentence or some specific regions in images where the most important information is given rather than memorizing all the input data. In recent years, attention mechanisms are becoming a necessary component of neural network construction [34]. It has been widely exploited in image processing [35] and neural machine translation [33]. Essentially, the attention mechanism aims to identify the importance of every feature and attribute weight coefficients to highlight the important and unimportant features. To this end, in the training phase, the main purpose is to focus on particular features by a weighted sum procedure described by an attention vector. Specifically, the attention vector at time t, , is calculated as,
Here, denotes the hidden states from the model (e.g., a recurrent network) feeding the attention model. refers to the normalized attention model weights calculated by:
where denotes the attention model weights, also known as alignment score; it is usually calculated using a feed-forward neural network [33], conditioned on the past hidden state (Figure 1):
and represent, respectively, weight matrix and bias vector of the attention model calculated in the training stage. Essentially, the attention vector of the attention model is a dynamic representation of the pertinent portion of the data at time t.
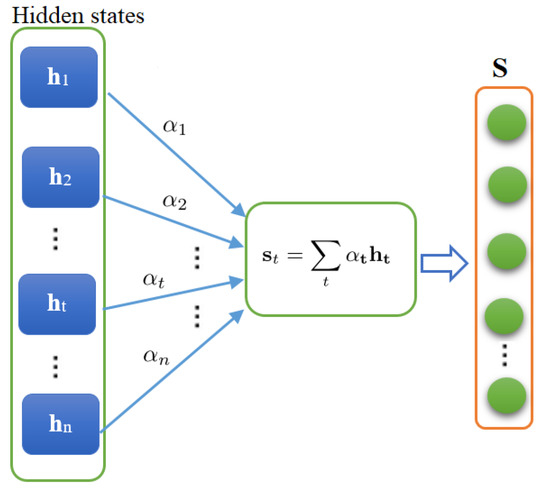
Figure 1.
Schematic representation of attention layer.
This mechanism uses a weighted sum for highlighting the important and unimportant data based on the normalized attention model weights that could be explained as a probability (Figure 1). Of course, the idea behind the attention mechanism is inspired by humans’ brain functionality that focuses on the distinctive and relevant pieces in case of handling large amounts of information. The attention unit provides the model the ability to concentrate on relevant features. Specifically, it supports the learning to identify a distinctive part of the data sequence by evaluating its memory at prediction. In this study, not all features contribute equitably to traffic flow forecasting. Hence, we should assign more attention to more relevant features.
Note that the two widely employed attention types are additive [33] (Equation (3)) and multiplicative [36] attentions. The principal distinction between then consists in the way of computing the alignment score:
Additive attention, also called Bahdanau attention, is essentially based on a single-hidden layer feed-forward network with tanh activation function for computing the attention alignment score. The alignment score in the multiplicative attention is obtained by reducing the hidden states using matrix multiplications [37].
3.2. Self-Attention Mechanism
The self-attention, also called intra-attention, can be viewed as an extension of the attention mechanism with the ability to reduce external information dependency and model dependencies within the input data [37]. In recent years, deep learning models incorporating the self-attention mechanisms demonstrated improved performance in different applications, including machine translation and image description generation [37,38,39]. For instance, the authors in [40] demonstrated that the attention mechanism improves the capacity of both the generator and the discriminator (i.e., neural network models) to capture the long-range dependencies in the feature maps. One of the key properties of the self-attention concept consists of its flexibility to be employed in any layer that represents a data sequence like a time series, which enhances the internal input structure’s learning by concentrating on the relation within observations of the same sequence. Notably, the key concept of self-attention is generating weights (termed score) between observation in position i and j of input data sequence as [37]:
The weight of the self-attention, , is obtained in the training stage. In (5), the division by is employed to make the convergence faster. High weights are an indicator of high relevance, whereas low weights indicate lower relevancy. The weights, , are then passed via a softmax function. The normalization of the weights can make them be seen as a probability (the sum of weight values is 1).
The output of the self-attention unit is given by,
This output effectively enhances the extracted features’ quality and explicitly describes the internal correlation of the input data. Of course, self-attention quantifies the level of relevance between the actual observation and any other observation previously seen in the sequence.
3.3. Variational Autoencoder
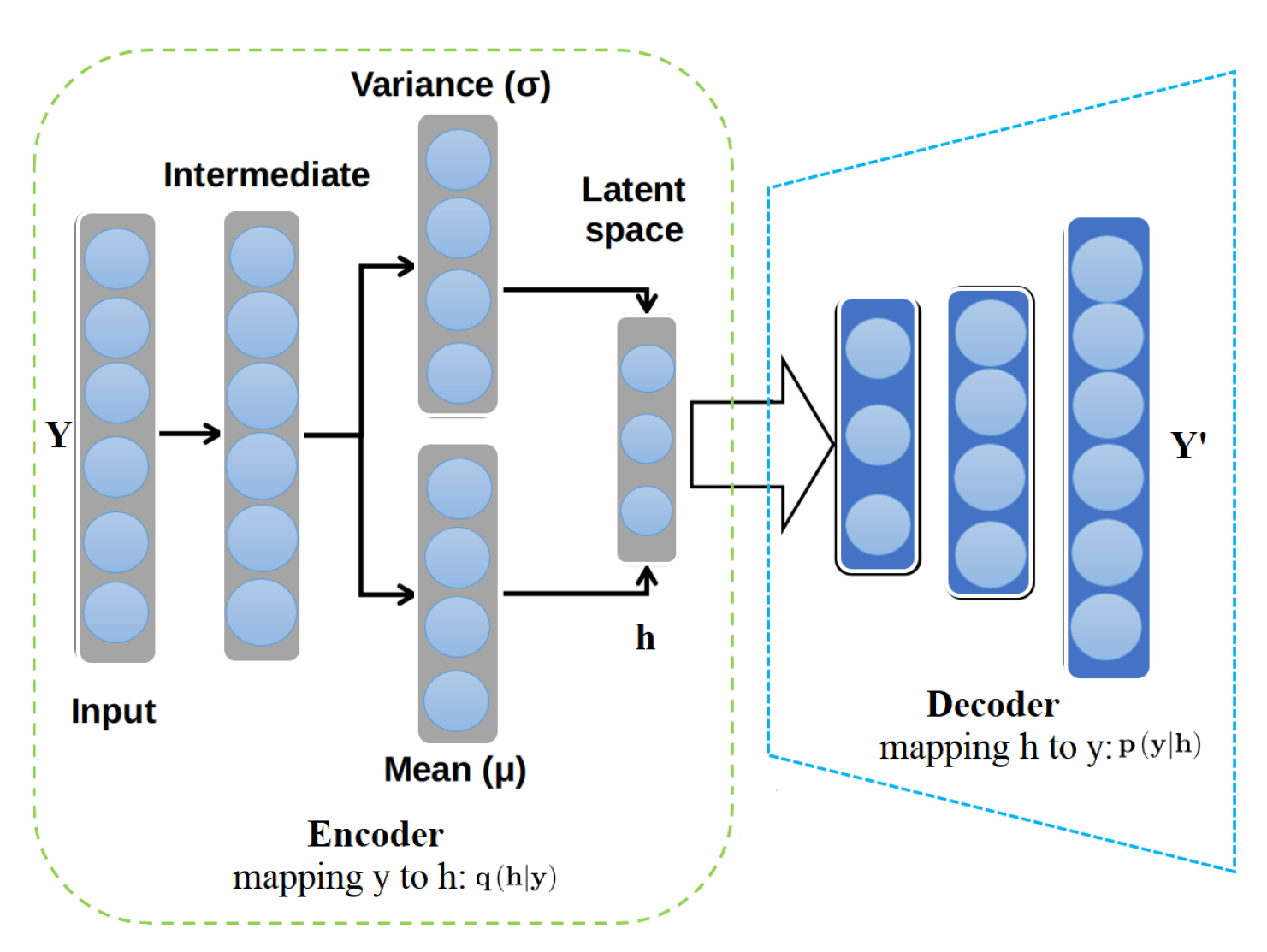
Variational autoencoders represent one of the most effective and proficient classes of deep generative methods [41]. Recently, VAE-based models have been shown good performance in different applications, including forecasting of photovoltaic solar power [42], desertification detection [43], overcrowding forecasting [44], air pollution forecasting [45], and COVID-19 time series forecasting [46,47]. The primary components of the VAE architecture are two neural networks: An encoder and a decoder (Figure 2). The encoder maps the data into a latent representation to get more compacted and informative data with a reduced dimension compared to the input data. Crucially, the decoder’s principal mission is to learn a data distribution (i.e., the distribution parameters) over the latent variables. In other words, the decoder attempts to rebuild the input data based on the sampled data provided by the encoder. The encoder is usually computed via a posterior approximation of , whereas the decoder is derived via a likelihood , where and denote, respectively, the parameters of the VAE encoder and decoder.
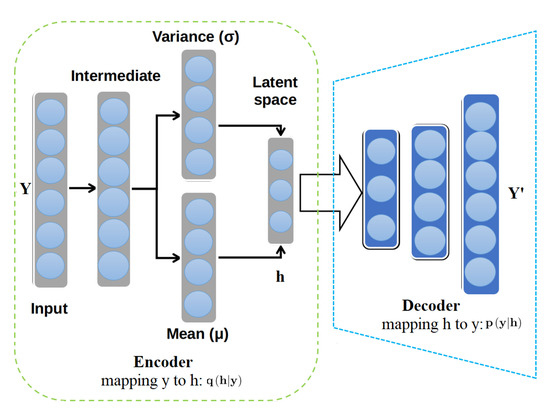
Figure 2.
Variational autoencoder architecture.
The VAE tries to find the appropriate assignments of latent variables that would have resulted in input data . More specifically, is considered following a prior distribution , usually Gaussian distribution ; the VAE encoder tries to estimate the parameters of this distribution. Analytically, the purpose is to determine
It should be noted that this is challenging to compute because the left-hand side in (8) includes , which is intractable. Precisely, it could be calculated through the marginalization out of the latent variables:
Regrettably, this integral is not easy to calculate. To bypass this difficulty, VAE treats it as an optimization problem [48]. More specifically, we can solve this based on the variational inference procedure by finding an approximation posterior [48,49]
Here, and refer to the standard deviation and the mean of , respectively, obtained using the VAE encoder.
Given , we can compute the evidence lower bound (ELBO) as [48,49]:
where denotes the Kulback–Leibler divergence separating the true posterior and the approximate , and the first term denotes the ELBO. Since , it can be deduced that
The term on the right-hand side of (13) (i.e., the ELBO term) represents that the lower bound of needs to be maximized. Therefore, for the maximization of , we concentrate on the maximization of the ELBO term, which is equivalent and computationally tractable. The VAE cost function can be expressed as:
Note that during the construction of the VAE approach using training data, the Stochastic Gradient Variational Bayes procedure has been usually implemented for optimizing the ELBO to compute the values of the encoder and decoder parameters [48,50,51].
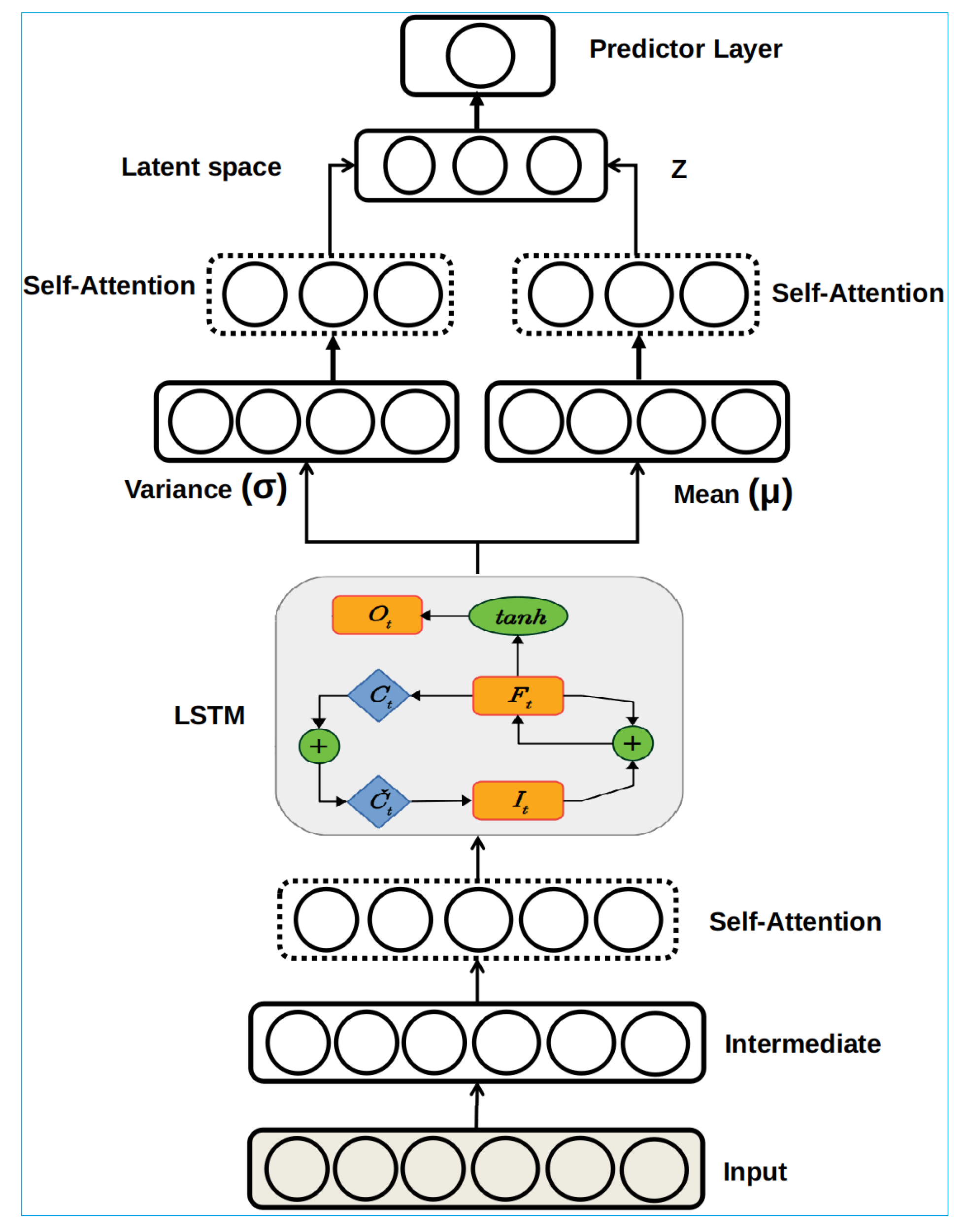
3.4. The Proposed Approach
This paper proposes a novel guided-attention hybrid deep learning framework (called GAHD-VAE) for traffic flow forecasting. The GAHD-VAE stretches the VAE model’s ability, enhances forecasting quality, and outperforms traditional neural network models. This study introduces the self-attention unit into the VAE at multi-levels, specifically in the encoder part with a recurrent neural network (Figure 3), to improve modeling and forecasting quality. As discussed above, the attention’s integration was most commonly used in the decoder parts [33,35], where the objective is to map the sequence (image or text) to a sequence of text. However, the forecasting task aims to map a sequence of numerical values to a single data point, which is the next value in this sequence. The key idea behind VAE is to learn the probability distribution of the input without any data labeling via an unsupervised method. It is anticipated that integrating the robust variation inference method, a robust regularization, and the attention mechanism will increase forecasting accuracy.
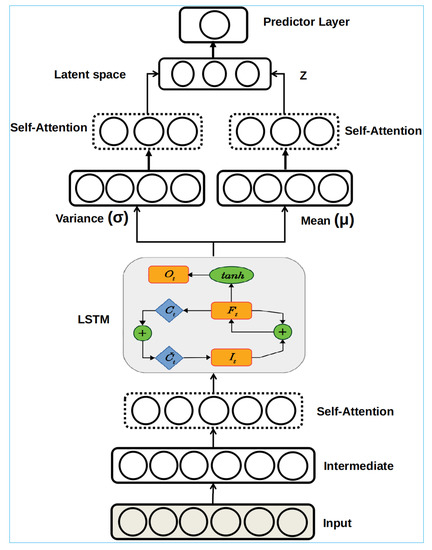
Figure 3.
The flowchart of the GAHD-VAE forecasting procedure.
First, the input (data sequence in our case) is processed via a non-linear transformation using a dense layer. Next, a self-attention layer is applied to dense layer output to highlight interactions between sequence data points by computing the context vector (i.e., a weighted sum of features). The regularization procedure ensures the diversification of the weighted sum; we applied regularization optimization methods to weights normalization based on the kernel-regularizer: and bias extenuation via bias-regularizer: [52]. Moreover, regularization aims to avoid over-fitting during traffic flow training. The third step consists of feeding the LSTM using the self-attention output, which starts extracting the long-term dependencies learning and capturing the temporal sequential dependency embedded in traffic flow input (time-series). LSTM output is obtained after several non-linear transformations supported by a complex gating mechanism; this output serves as input to regularize the covariance matrix and the mean of the distributions returned by LSTM. More specifically, the regularization is realized by imposing that the distributions be similar to a standard Gaussian distribution and enforcing the covariance matrix close to the identity. Next, the latent space is obtained after double self-attention of the regularized mean and variance; both are concatenated to form an enhanced input for the encoder output layer. Data points are sampled from the latent space to be reconstructed using the decoder model; only generative models can generate new data. The decoder in the proposed approach is a deep, fully connected neural network; it represents the reverse path, where the sampled data points are reconstructed. Kullback–Leibler (KL) is used to measure the loss, which is the divergence between the learned probability distribution and the true data; this step is repeated until the convergence of the model parameters, especially when the divergence becomes small, ideally close to zero. The reconstruction error is back-propagated over the whole neural network structure, and the model parameters are updated accordingly. To be concise, the forecasting is accomplished at the level of the encoding space. The training procedure of the GA-HD-VAE algorithm is given in Algorithm 1.
The effectiveness of the proposed model was verified through experiments of large-scale datasets. A comparison with the baseline deep learning methods, including GRU, LSTM, BiLSTM, and BiGRU, is performed to show the proposed approach’s forecasting capacity.
| Algorithm 1: The training procedure of the GA-HD-VAE algorithm |
 |
4. Model Testing and Results Analysis
This section presents the used pedestrian and bicycle traffic flow datasets and evaluates the forecasting performance of the proposed method. At first, we verify the one-step forecasting performance of the proposed GAHD-VAE model and compare its improvement with the traditional VAE model. Then, we provide a comparison against the baseline deep learning models, namely LSTM, GRU, BiLSTM, and BiGRU. Furthermore, the impact of using different configurations of the attention model, namely, attention type and activation function at a different level of the proposed architecture, is analyzed. Finally, we evaluate the effectiveness of the considered methods for multi-step forecasting.
4.1. Measurements of Effectiveness
To evaluate the forecasting results, the following scores were adopted: The root-mean-square error (RMSE), the mean absolute error (MAE), the coefficient of determination (), and the explained variance (EV).
where are the actual values, are the corresponding forecasted values, and n is the number of measurements.
4.2. Data Description
This study uses six actual pedestrian and bicycle traffic flow datasets to verify the investigated deep learning methods’ forecasting performance. These hourly traffic flow datasets are created and maintained by the Seattle Department of Transportation in the USA. The data is gathered using sensors that record people riding bikes and pedestrians from 2014 until now in different Seattle locations (Table 1). In our experiment, the training is conducted using 90% of each dataset. The k-fold cross-validation technique has been considered in constructing these models based on the training data as recommended in [53,54]. Specifically, we applied a five-fold cross-validation technique in training the investigated models.

Table 1.
Traffic datasets used to evaluate the considered models.
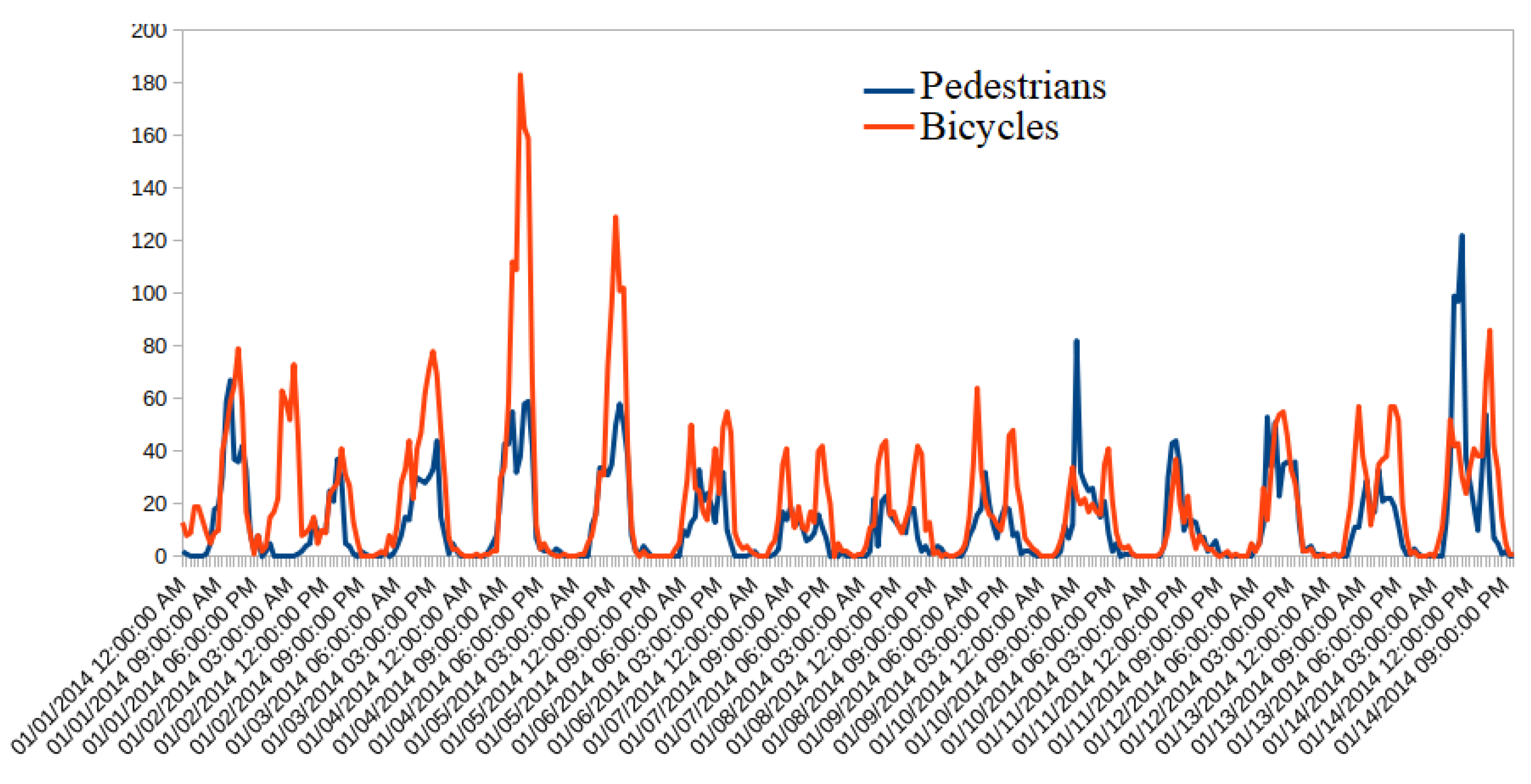
Figure 4 displays an example of the time evolution of bicycle and pedestrian traffic flows recorded over two weeks. The descriptive statistics of the six traffic flow datasets are given in Table 2. Table 2 indicates that the pedestrian and bicycle traffic datasets are non-Gaussian distributed with positive support and exhibit different intervals of variability.
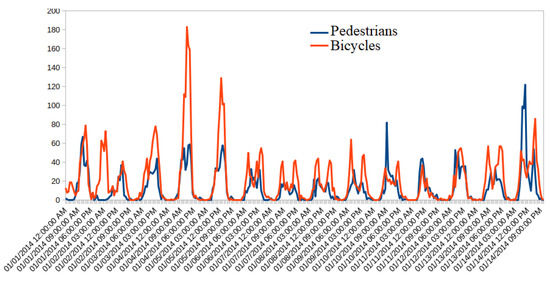
Figure 4.
A week of traffic data from Data 1 and Data 2.

Table 2.
Statistics summary of the pedestrian and bicycle traffic flow datasets.
4.3. Results Analysis and Comparison
This section first shows the improvement introduced to the traditional VAE by incorporating the self-attention mechanism at the VAE encoder. We compare it with well known recurrent neural networks, LSTM, GRU, BiLSTM, BiGRU, CNN, and ConvLSTM, as well as baseline methods, namely LR, RR, SVR, and Lasso regression, to forecast pedestrian and bicycle traffic flows. The LSTM and GRU are equipped with memory-cell and gating mechanisms, making them powerful models for time-series modeling and suitable for a comparison study. In these experimentations, the set of hyperparameters is fixed for all considered model-based training datasets: optimizer = ‘rmsprop’, loss function = ‘Cross-Entropy’, batch size = 250, epochs = 500, and learning rate = 0.001, activation function = ‘Rectified Linear Unit (ReLU)’. The configuration of the proposed approach is: [Input: 3, Intermediate: 6, Self-Attention: 6, LSTM: 16, Variance: 16, Mean: 16, Z: 16, Self-Attention: 4, Self-Attention: 4, Predictor: 1]. For the considered models GRU, LSTM, BiLSTM, BiGRU, and ConvLSTM, we set the hidden units to 32. Here, deep recurrent neural networks are built by stacking two recurrent layers as deep temporal feature extractors and a dense layer used for the forecasting task. For example, for LSTM, we have a stacked-LSTM network containing two LSTM layers with 32 hidden units for each layer and a fully connected layer. All hyper-parameters are determined based on a grid search approach. Similarly, the same architecture is used for BiLSTM and BiGRU models: Deep bidirectional temporal feature extractors and a dense layer used for the forecasting task. Generally, the bidirectional models allow the input to be processed in the forward and backward direction, making it possible to extract more complex hidden features. We used a linear kernel for the SVR model, with the regularization parameter and gamma = ‘scale’. For the Lasso regression, we set the constant that multiplies the L1 term, , the maximum number of iterations is 1000, and the tolerance for the optimization is . For RR, the value of the regularization strength is chosen as 1, the maximum number of iterations is 1000, and the precision of the solution is chosen to be .
To show the advantage of the proposed GAHD-VAE compared to the traditional VAE, we applied them to the six traffic flow datasets (Table 3). The proposed approach scored the lowest RMSE for the six considered datasets () compared to results achieved by the VAE (). Furthermore, the averaged and EV values for the GAHD-VAE are (0.963, 0.968) and for the VAE are (0.919, 0.94), respectively. Results demonstrate the significant improvement attributed to the high learning quality and capability of GAHD-VAE, brought by the deep self-attention mechanism and the deep hybrid architecture that incorporates recurrent neural networks. Results in Table 3 also revealed that the GAHD-VAE model exhibited superior prediction performance compared to four shallow methods, linear regression, Lasso regression, ridge regression, and support vector regression. This could be attributed to the ability of a deep learning structure to learn complicated patterns from data. Indeed, deep models’ structure enables transforming data multiple times to get the final output, allowing to learn deeper information. On the other hand, shallow methods generally can transform the data only one or two times to reach the output, limiting their ability to learn complicated patterns from input data.

Table 3.
Performance comparison of the proposed GAHD-VAE, traditional VAE, SVR, LR, RR, and Lasso.
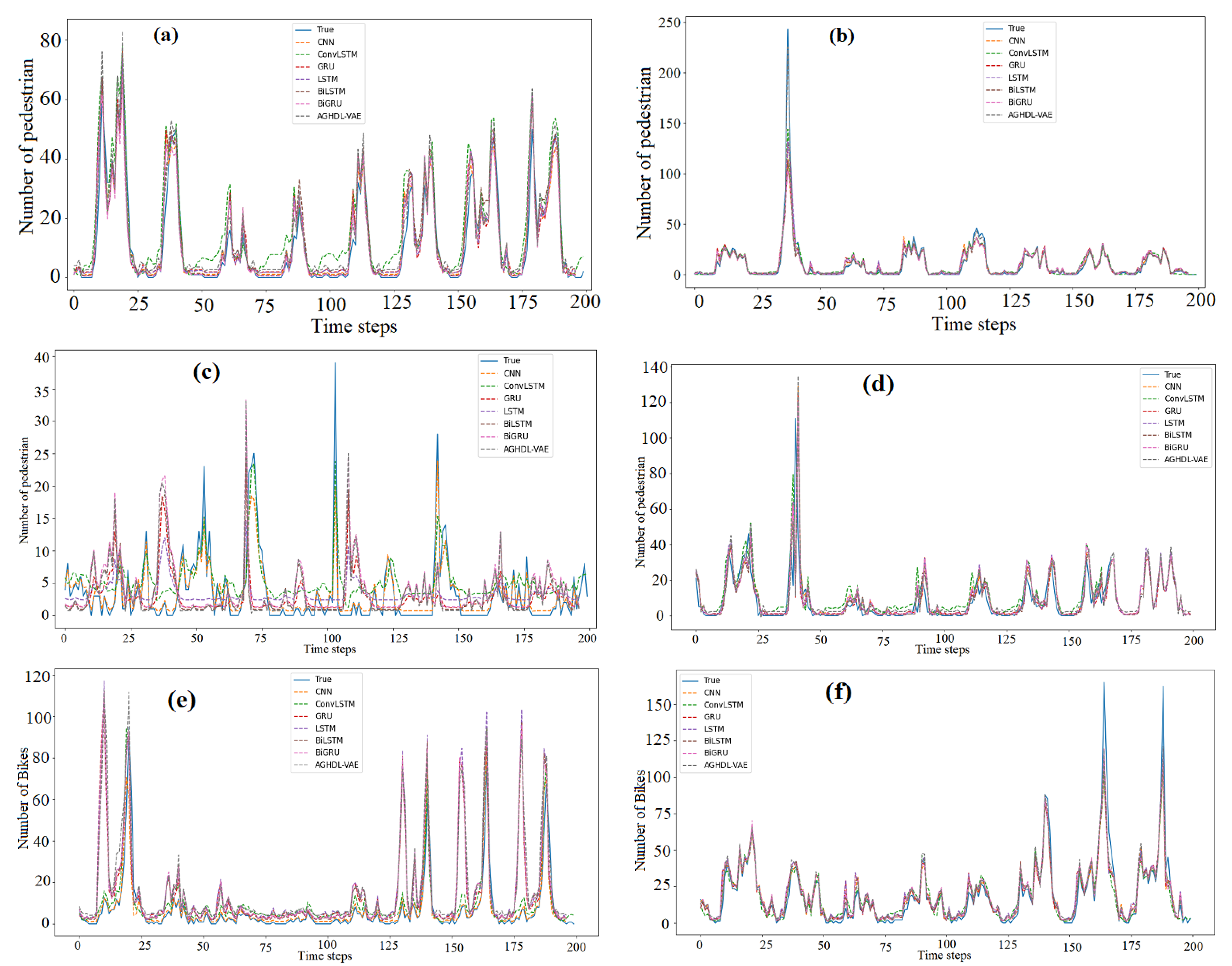
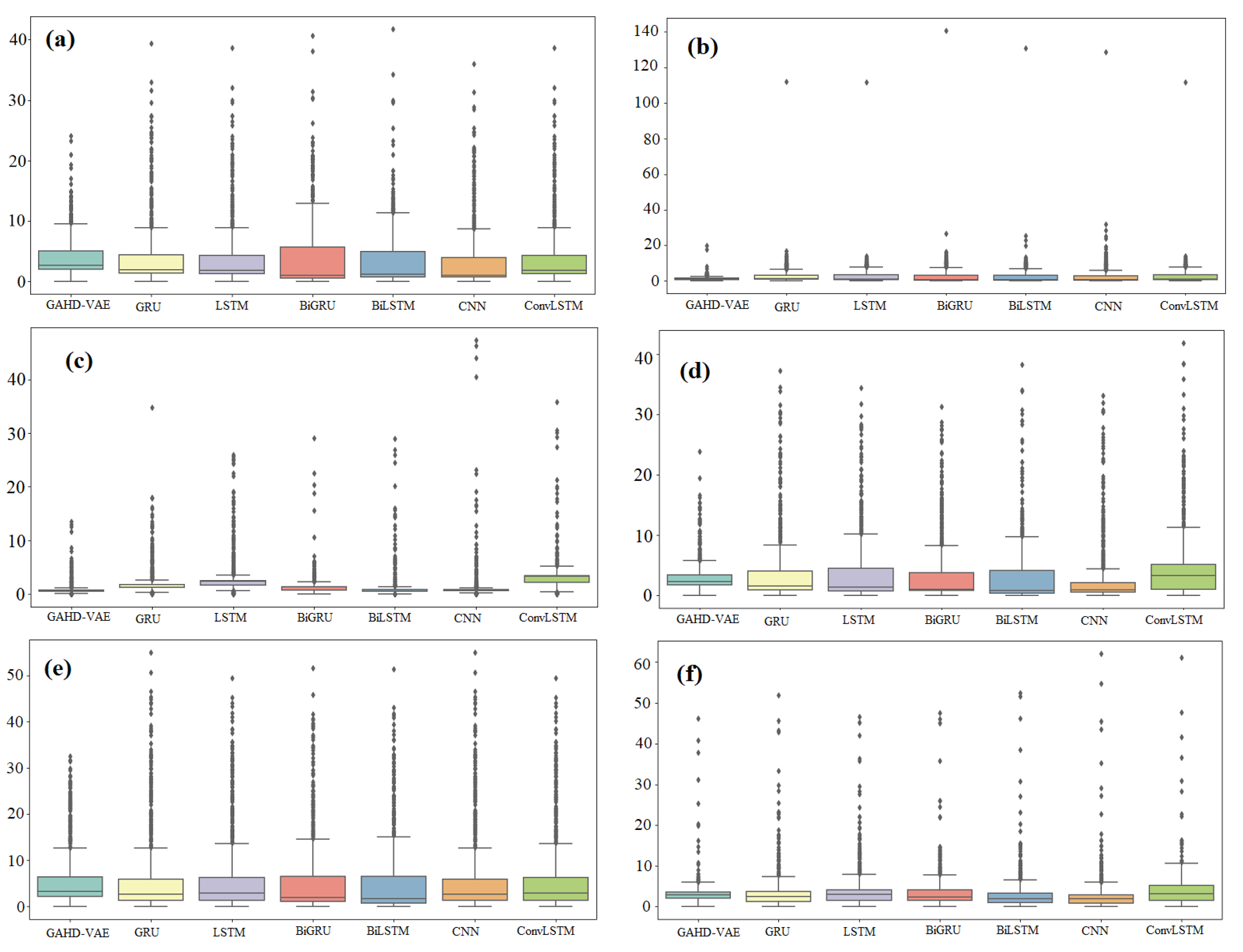
In the next numerical experiments, we compared the performance of the proposed GAHD-VAE approach to that of GRU, LSTM, BiLSTM, BiGRU, CNN, and ConvLSTM models because of their popularity in modeling and forecasting time-series data. Figure 5a–f displays the measured and the forecasted traffic flow obtained by the proposed GAHD-VAE and the six considered deep learning models when applied to the six traffic datasets. From Figure 5a–f, we observe that the forecasted traffic flows from the seven models closely followed the measured traffic flow data (solid line) for all test datasets. Figure 6a–f present the boxplots of forecasting errors, which is the deviation between the forecasted and the measured traffic flow values. The more the boxplot’s median tends to zero, and the boxplot is compact, the more the model is accurate. As a consequence, Figure 6 indicates that the GAHD-VAE provides better performance than all the other models.
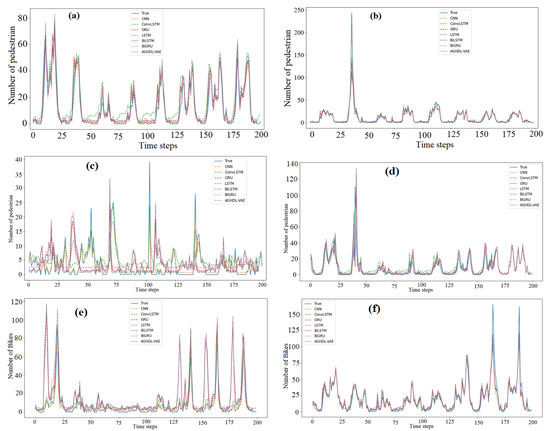
Figure 5.
Measured and forecasted, (a) Data Set 1, (b) Data Set 2, (c) Data Set 3, (d) Data Set 4, (e) Data Set 5 and (f) Data Set 6.
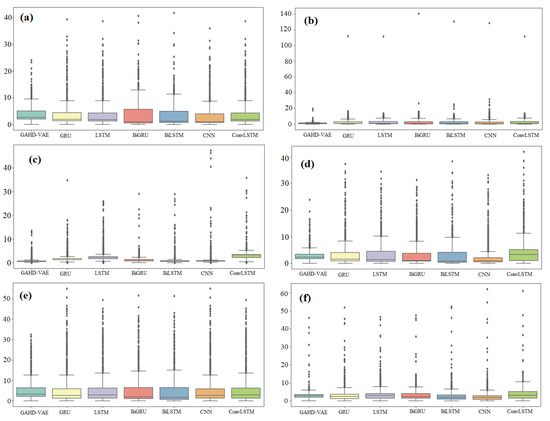
Figure 6.
Boxplot of forecasting errors obtained by the seven considered methods based on the six datasets: (a) Data Set 1, (b) Data Set 2, (c) Data Set 3, (d) Data Set 4, (e) Data Set 5 and (f) Data Set 6.
The obtained forecasting results are tabulated in Table 4. Results in Table 4 show that the quality of the forecast of pedestrian and bicycle traffic flows from the seven trained models is promising. Table 4 indicates that the proposed approach exhibited improved forecasting performance compared to other deep learning methods by achieving the lowest RMSE and MAE values and the highest and EV values (close to 1). The averaged metrics by datasets of the proposed approach are RMSE of 3.35 and MAE of 2.54; the proposed model has reached a high fitting score with low forecasting error for pedestrians, and bicycle traffic flows using six datasets. This could be attributed to the GAHD-VAE capacity in handling nonlinearity. On the other hand, results demonstrate that bidirectional methods (i.e., BiLSTM and BiGRU) improved the quality of forecasting compared to the uni-directional models (i.e., LSTM and GRU). Moreover, the overall performance of BiLSTM is slightly better than BiGRU. Notably, the GAHD-VAE method shows promising capability for modeling complex temporal features in different datasets, especially pedestrian traffic flow (datasets 2 and 3), which is highly dynamic and nonlinear.

Table 4.
One-step ahead forecasting of pedestrian and bicycle traffic flows using the seven deep learning models.
Table 5 summarizes the aggregated performances of each approach. implies that all deep learning approaches are providing good forecasting. In terms of all metrics computed, the proposed GAHD-VAE approach achieves the best forecasting with high efficiency and satisfying accuracy (i.e., , RMSE = ). It is followed by BiGRU and BiLSTM, which achieve . Notice that a significant forecasting improvement was obtained using the GAHD-VAE approach compared to the other deep learning models. This could be attributed to its capacity to capture relevant information and dynamics from traffic flow time series.

Table 5.
Averaged measurements of effectiveness per model.
To further assess the performance of the GAHD-VAE, we investigate the impact of the attention mechanism setting used in the proposed GAHD-VAE model on the forecasting accuracy. An important point to highlight is that the activation function changes how data is transformed (or processed) at the layer unit level and significantly impacts the neural network’s overall performance. Mainly, we evaluate the impact of the used activation function in the attention mechanism on the proposed approach’s forecasting performance. Table 6 shows the forecasting results obtained through different configurations of the activation function used on each attention layer: Rectified Linear Unit (ReLU), Hyperbolic Tangent (tanh), and Logistic Sigmoid. We also evaluate the impact of the attention type, namely multiplicative and additive, on the forecasting accuracy. Moreover, these experiments are based on four traffic flow datasets for the proposed approach with a self-attention mechanism (Table 6). Note here that the highlighted rows in Table 6 represent the results obtained with default attention configuration (activation function: Tanh; attention type: Additive), while the results in bold are the enhanced forecasting metrics. The term ’None’ in Table 6 represents the case where the multiplicative self-attention is based only on matrix multiplications without the activation function.

Table 6.
Evaluation of the forecasting performance of the GAHD-VAE under different configurations of the attention mechanism. ⨁ is the additive attention mode, while ⨂ is the multiplicative attention mode.
Results in Table 6 show that the GAHD-VAE model with the Sigmoid activation function, when applied to dataset 1, provides the best results for both attention types (i.e., multiplicative and additive). Specifically, it achieves the lowest RMSE and MAE values (i.e., 1.812 and 1.224, respectively) and describes 98.8% of the traffic flow variance. We also observe that adjusting the attention layer significantly improves the forecasting quality by reducing RMSE from 3.336 to 1.812 and MAE from 2.81 to 1.224 and improving to more than 0.98. Moreover, Table 6 shows that the multiplicative type with Tanh and additive with Sigmoid offers the most favorable result for the traffic data set 4 (i.e., RMSE = 1.18, MAE = 0.761, and = 0.986). The best forecasting accuracy when applying GAHD-VAE to Data Set 5 is obtained by using multiplicative type with Sigmoid activation function, where RMSE was reduced from 5.641 to 2.743 and MAE from 4.853 to 1.969, compared to the additive type with Tanh (i.e., default configuration). From Table 6, we also observe that there is no improvement on Dataset 6; the default configuration scored the best results. Overall, it is not obvious to automatically decide the best attention configuration for any dataset. On average, the use of GAHD-VAE with the Sigmoid activation function provides suitable forecasting performance.
Table 7 displays the aggregated performances of GAHD-VAE per configurations of the attention mechanism (i.e., additive attention mode and multiplicative attention mode). implies that the use of the two configurations in the GAHD-VAE approach results in good forecasting performance. Overall, forecasts based on the additive attention mode outperform those based on the multiplicative attention mode.

Table 7.
Averaged validation metrics per configurations of the attention mechanism. ⨁ is the additive attention mode, while ⨂ is the multiplicative attention mode.
The following experiments are devoted to assessing the proposed approach’s daily forecasting performance against the other recurrent models. Table 8 summarized the results of forecasting daily pedestrian and bicycle traffic flows using the seven deep learning models based on the six datasets. Results indicate that the proposed approach scored the lowest averaged forecasting error (i.e., RMSE = 42 and MAE = 32) and the highest determination factor (i.e., = 0.9 and EV = 0.9). Moreover, results in Table 8 indicate that the bi-directional recurrent neural networks (BiLSTM and BiGRU) exhibit higher accuracy compared to the uni-directional (LSTM, GRU). This could be due to the capability of BiLSTM and BiGRU in processing data in the forward and backward direction, which enable them to discover more complex features. We also observe that BiLSTM outperforms BiGRU slightly; however, LSTM and GRU recorded mostly the same score. Results confirm the superiority of the proposed GAHD-VAE approach in modeling long-term temporal dependencies and the attention mechanism’s efficiency to highlight the internal correlation between elements. In summary, results in this study showed that the proposed model achieved an improved forecasting quality for both one-step and multi-step pedestrians and bicycle traffic flow forecasting.

Table 8.
Performance evaluation of the seven models for daily forecasting of pedestrian and bicycle traffic flows.
To summarize the assessments, the averaged metrics of effectiveness per model computed from Table 8 are listed in Table 9. The results support that the GAHD-VAE forecasting approach has higher accuracy overall than the other deep learning models (i.e., VAE, LSTM, GRU, BiLSTM, BiGRU, CNN, and ConvLSTM). Overall, the results indicate that the GAHD-VAE approach has high forecasting accuracy due to the robustness of variational inferences in approximating data probability distribution of traffic flow time-series, in addition to the promising capability of a self-attention mechanism to learn implicit information within data points of a given sequence.

Table 9.
Averaged measurements of effectiveness per model for daily forecasting of pedestrian and bicycle traffic flows.
5. Conclusions and Future Directions
5.1. Conclusions
This paper introduced the guided-attention hybrid deep learning architecture (called GAHD-VAE) and showed its capacity for pedestrian and bicycle traffic flow modeling and forecasting. Notably, the proposed approach improves the VAE capacity to learn temporal dependencies in time-series data by adding the self-attention mechanism at different levels in the VAE structure and including a recurrent neural network (LSTM) in the VAE encoder side. The role of the self-attention mechanism in the GAHD-VAE is to uncover the most relevant part of features. LSTM is embedded in the VAE encoder to enable modeling the time-dependence in time series data. Results based on six traffic flow datasets demonstrated that the GAHD-VAE could generate high accurate traffic flow forecasting (one-step and multi-step) and outperform the traditional VAE model and the state-of-the-art models, namely LSTM, GRU, BiGRU, and BiLSTM, as well as four shallow models (i.e., LR, SVR, RR, Lasso regression). Furthermore, we investigated the impact of using the attention module’s multi-configuration on the forecasting quality of the GAHD-VAE. It has been shown that results could be improved by changing the attention mechanism’s internal data processing (activation function) and the attention mode.
5.2. Future Directions
Despite the satisfactory traffic flow forecasting results using the GAHD-VAE methodology, future works will be aimed at improving the robustness of the GAHD-VAE model to noisy traffic flow measurements by developing a wavelet-based GAHD-VAE approach. Another direction of improvement is to incorporate explanatory variables, such as meteorological measurements and spatial information, in constructing the deep learning models to further improve forecasting quality. Moreover, this deep learning approach ignores the spatiotemporal correlation in the traffic network. Thus, we plan to develop a more flexible forecasting approach that considers spatiotemporal correlations of the traffic network and captures spatiotemporal features. We will also investigate the capacity of applying the GAHD-VAE approach in other applications that need forecasting like environment, health, energy, big data, and many others. We also plan to improve the robustness of the GAHD-VAE model to noisy measurements by developing a wavelet-based GAHD-VAE forecasting model. Moreover, it will be interesting to investigate the forecasting capability of this deep learning method in other applications, such as predicting bike-sharing demand.
Author Contributions
F.H.: Conceptualization, Formal analysis, Investigation, Methodology, Software, Writing-original draft, Writing-review & editing. A.D.: Conceptualization, Formal analysis, Investigation, Methodology, Software, Supervision, Writing-original draft, Writing-review & editing. A.Z.: Investigation, Conceptualization, Formal analysis, Methodology, Writing-original draft. Y.S.: Investigation, Conceptualization, Formal analysis, Methodology, Writing-review & editing, Funding acquisition, Supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by funding from King Abdullah University of Science and Technology (KAUST), Office of Sponsored Research (OSR) under Award No: OSR-2019-CRG7-3800.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xie, Y.; Zhao, K.; Sun, Y.; Chen, D. Gaussian processes for short-term traffic volume forecasting. Transp. Res. Rec. 2010, 2165, 69–78. [Google Scholar] [CrossRef] [Green Version]
- Zeroual, A.; Harrou, F.; Sun, Y.; Messai, N. Integrating Model-Based Observer and Kullback–Leibler Metric for Estimating and Detecting Road Traffic Congestion. IEEE Sens. J. 2018, 18, 8605–8616. [Google Scholar] [CrossRef] [Green Version]
- Harrou, F.; Zeroual, A.; Sun, Y. Traffic congestion monitoring using an improved kNN strategy. Measurement 2020, 156, 107534. [Google Scholar] [CrossRef]
- Bongiorno, C.; Santucci, D.; Kon, F.; Santi, P.; Ratti, C. Comparing bicycling and pedestrian mobility: Patterns of non-motorized human mobility in Greater Boston. J. Transp. Geogr. 2019, 80, 102501. [Google Scholar] [CrossRef]
- Lee, K.; Sener, I.N. Emerging data for pedestrian and bicycle monitoring: Sources and applications. Transp. Res. Interdiscip. Perspect. 2020, 4, 100095. [Google Scholar] [CrossRef]
- Xu, C.; Li, Z.; Wang, W. Short-term traffic flow prediction using a methodology based on autoregressive integrated moving average and genetic programming. Transport 2016, 31, 343–358. [Google Scholar] [CrossRef] [Green Version]
- Alghamdi, T.; Elgazzar, K.; Bayoumi, M.; Sharaf, T.; Shah, S. Forecasting Traffic Congestion Using ARIMA Modeling. In Proceedings of the 2019 15th International Wireless Communications Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 1227–1232. [Google Scholar] [CrossRef]
- Harrou, F.; Zeroual, A.; Hittawe, M.M.; Sun, Y. Road Traffic Modeling and Management: Using Statistical Monitoring and Deep Learning; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Voort, M.V.D.; Dougherty, M.; Watson, S. Combining kohonen maps with arima time series models to forecast traffic flow. Transp. Res. Part C Emerg. Technol. 1996, 4, 307–318. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.V.; Vanajakshi, L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data. Eur. Transp. Res. Rev. 2015, 7, 21. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.Y.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Gu, X.; Li, T.; Wang, Y.; Zhang, L.; Wang, Y.; Yao, J. Traffic fatalities prediction using support vector machine with hybrid particle swarm optimization. J. Algorithms Comput. Technol. 2018, 12, 20–29. [Google Scholar] [CrossRef]
- Karlaftis, M.; Vlahogianni, E. Statistical methods versus neural networks in transportation research: Differences, similarities and some insights. Transp. Res. Part C Emerg. Technol. 2011, 19, 387–399. [Google Scholar] [CrossRef]
- Ai, C.; Jia, L.; Hong, M.; Zhang, C. Short-term road speed forecasting based on hybrid RBF neural network with the aid of fuzzy system-based techniques in urban traffic flow. IEEE Access 2020, 8, 69461–69470. [Google Scholar] [CrossRef]
- Cai, L.; Chen, Q.; Cai, W.; Xu, X.; Zhou, T.; Qin, J. SVRGSA: A hybrid learning based model for short-term traffic flow forecasting. IET Intell. Transp. Syst. 2019, 13, 1348–1355. [Google Scholar] [CrossRef]
- Chen, X.; Cai, X.; Liang, J.; Liu, Q. Ensemble Learning Multiple LSSVR with Improved Harmony Search Algorithm for Short-Term Traffic Flow Forecasting. IEEE Access 2018, 6, 9347–9357. [Google Scholar] [CrossRef]
- Lu, W.; Rui, Y.; Yi, Z.; Ran, B.; Gu, Y. A Hybrid Model for Lane-Level Traffic Flow Forecasting Based on Complete Ensemble Empirical Mode Decomposition and Extreme Gradient Boosting. IEEE Access 2020, 8, 42042–42054. [Google Scholar] [CrossRef]
- Tang, L.; Zhao, Y.; Cabrera, J.; Ma, J.; Tsui, K.L. Forecasting short-term passenger flow: An empirical study on shenzhen metro. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3613–3622. [Google Scholar] [CrossRef]
- Lin, F.; Jiang, J.; Fan, J.; Wang, S. A stacking model for variation prediction of public bicycle traffic flow. Intell. Data Anal. 2018, 22, 911–933. [Google Scholar] [CrossRef]
- Xu, H.; Ying, J.; Wu, H.; Lin, F. Public bicycle traffic flow prediction based on a hybrid model. Appl. Math. Inf. Sci. 2013, 7, 667–674. [Google Scholar] [CrossRef]
- Yang, Y.; Heppenstall, A.; Turner, A.; Comber, A. Using graph structural information about flows to enhance short-term demand prediction in bike-sharing systems. Comput. Environ. Urban Syst. 2020, 83, 101521. [Google Scholar] [CrossRef]
- Brookshire, K.; Blank, K.; Redmon, T.; Blackburn, L. Decision making support for bikeway selection. ITE J. 2020, 90, e1. [Google Scholar]
- Zhao, W.; Gao, Y.; Ji, T.; Wan, X.; Ye, F.; Bai, G. Deep Temporal Convolutional Networks for Short-Term Traffic Flow Forecasting. IEEE Access 2019, 7, 114496–114507. [Google Scholar] [CrossRef]
- Cheng, T.; Harrou, F.; Kadri, F.; Sun, Y.; Leiknes, T. Forecasting of Wastewater Treatment Plant Key Features using Deep Learning-Based Models: A Case Study. IEEE Access 2020, 8, 184475–184485. [Google Scholar] [CrossRef]
- Harrou, F.; Cheng, T.; Sun, Y.; Leiknes, T.O.; Ghaffour, N. A Data-Driven Soft Sensor to Forecast Energy Consumption in Wastewater Treatment Plants: A Case Study. IEEE Sens. J. 2020, 21, 4908–4917. [Google Scholar] [CrossRef]
- Yang, H.; Dillon, T.S.; Chang, E.; Phoebe Chen, Y. Optimized Configuration of Exponential Smoothing and Extreme Learning Machine for Traffic Flow Forecasting. IEEE Trans. Ind. Inform. 2019, 15, 23–34. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F. Traffic Flow Prediction with Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Dai, G.; Ma, C.; Xu, X. Short-Term Traffic Flow Prediction Method for Urban Road Sections Based on Space–Time Analysis and GRU. IEEE Access 2019, 7, 143025–143035. [Google Scholar] [CrossRef]
- Han, L.; Huang, Y. Short-term traffic flow prediction of road network based on deep learning. IET Intell. Transp. Syst. 2020, 14, 495–503. [Google Scholar] [CrossRef]
- Ba, J.; Mnih, V.; Kavukcuoglu, K. Multiple object recognition with visual attention. arXiv 2014, arXiv:1412.7755. [Google Scholar]
- Zhou, J.; Dai, H.; Wang, H.; Wang, T. Wide-Attention and Deep-Composite Model for Traffic Flow Prediction in Transportation Cyber-Physical Systems. IEEE Trans. Ind. Inform. 2020, 17, 3431–3440. [Google Scholar] [CrossRef]
- Zheng, H.; Lin, F.; Feng, X.; Chen, Y. A Hybrid Deep Learning Model with Attention-Based Conv-LSTM Networks for Short-Term Traffic Flow Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 22, 6910–6920. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhudinov, R.; Zemel, R.; Bengio, Y. Show, attend and tell: Neural image caption generation with visual attention. In Proceedings of the International conference on machine learning, Lille, France, 6–11 July 2015; pp. 2048–2057. [Google Scholar]
- Luong, M.T.; Pham, H.; Manning, C.D. Effective approaches to attention-based neural machine translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; 2017. pp. 5998–6008. Available online: https://www.bibsonomy.org/bibtex/c9bf08cbcb15680c807e12a01dd8c929 (accessed on 20 April 2022).
- Parikh, A.P.; Täckström, O.; Das, D.; Uszkoreit, J. A decomposable attention model for natural language inference. arXiv 2016, arXiv:1606.01933. [Google Scholar]
- Lin, Z.; Feng, M.; Santos, C.N.D.; Yu, M.; Xiang, B.; Zhou, B.; Bengio, Y. A structured self-attentive sentence embedding. arXiv 2017, arXiv:1703.03130. [Google Scholar]
- Zhang, H.; Goodfellow, I.; Metaxas, D.; Odena, A. Self-attention generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 7354–7363. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. Stat 2014, 1050, 1. [Google Scholar]
- Dairi, A.; Harrou, F.; Sun, Y.; Khadraoui, S. Short-term forecasting of photovoltaic solar power production using variational auto-encoder driven deep learning approach. Appl. Sci. 2020, 10, 8400. [Google Scholar] [CrossRef]
- Zerrouki, Y.; Harrou, F.; Zerrouki, N.; Dairi, A.; Sun, Y. Desertification Detection using an Improved Variational AutoEncoder-Based Approach through ETM-Landsat Satellite Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 14, 202–213. [Google Scholar] [CrossRef]
- Harrou, F.; Dairi, A.; Kadri, F.; Sun, Y. Forecasting emergency department overcrowding: A deep learning framework. Chaos Solitons Fractals 2020, 139, 110247. [Google Scholar] [CrossRef]
- Dairi, A.; Harrou, F.; Khadraoui, S.; Sun, Y. Integrated multiple directed attention-based deep learning for improved air pollution forecasting. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar] [CrossRef]
- Zeroual, A.; Harrou, F.; Dairi, A.; Sun, Y. Deep learning methods for forecasting COVID-19 time-Series data: A Comparative study. Chaos Solitons Fractals 2020, 140, 110121. [Google Scholar] [CrossRef] [PubMed]
- Dairi, A.; Harrou, F.; Sun, Y. Deep Generative Learning-based 1-SVM Detectors for Unsupervised COVID-19 Infection Detection Using Blood Tests. IEEE Trans. Instrum. Meas. 2021, 71, 2500211. [Google Scholar] [CrossRef]
- Doersch, C. Tutorial on variational autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar]
- Chen, T.; Liu, X.; Xia, B.; Wang, W.; Lai, Y. Unsupervised anomaly detection of industrial robots using sliding-window convolutional variational autoencoder. IEEE Access 2020, 8, 47072–47081. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Cortes, C.; Mohri, M.; Rostamizadeh, A. L2 regularization for learning kernels. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009; AUAI Press: Arlington, VA, USA, 2009; pp. 109–116. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).