Prediction of Lithium-Ion Battery Capacity by Functional Principal Component Analysis of Monitoring Data
Abstract
1. Introduction
2. Literature Review
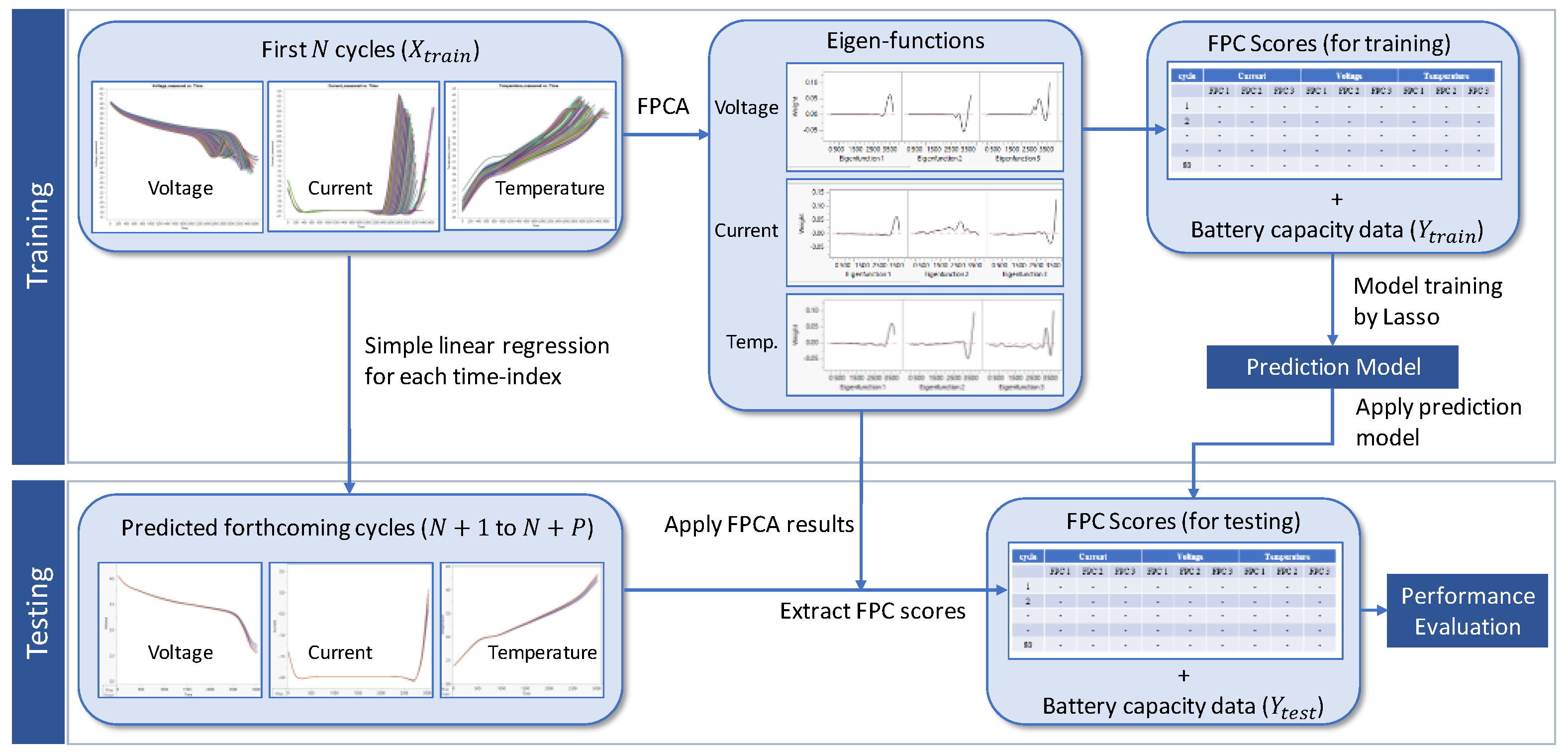
3. Methodology
3.1. Functional Principal Component Analysis (fPCA)
3.2. Prediction Model Building and Testing
- (a).
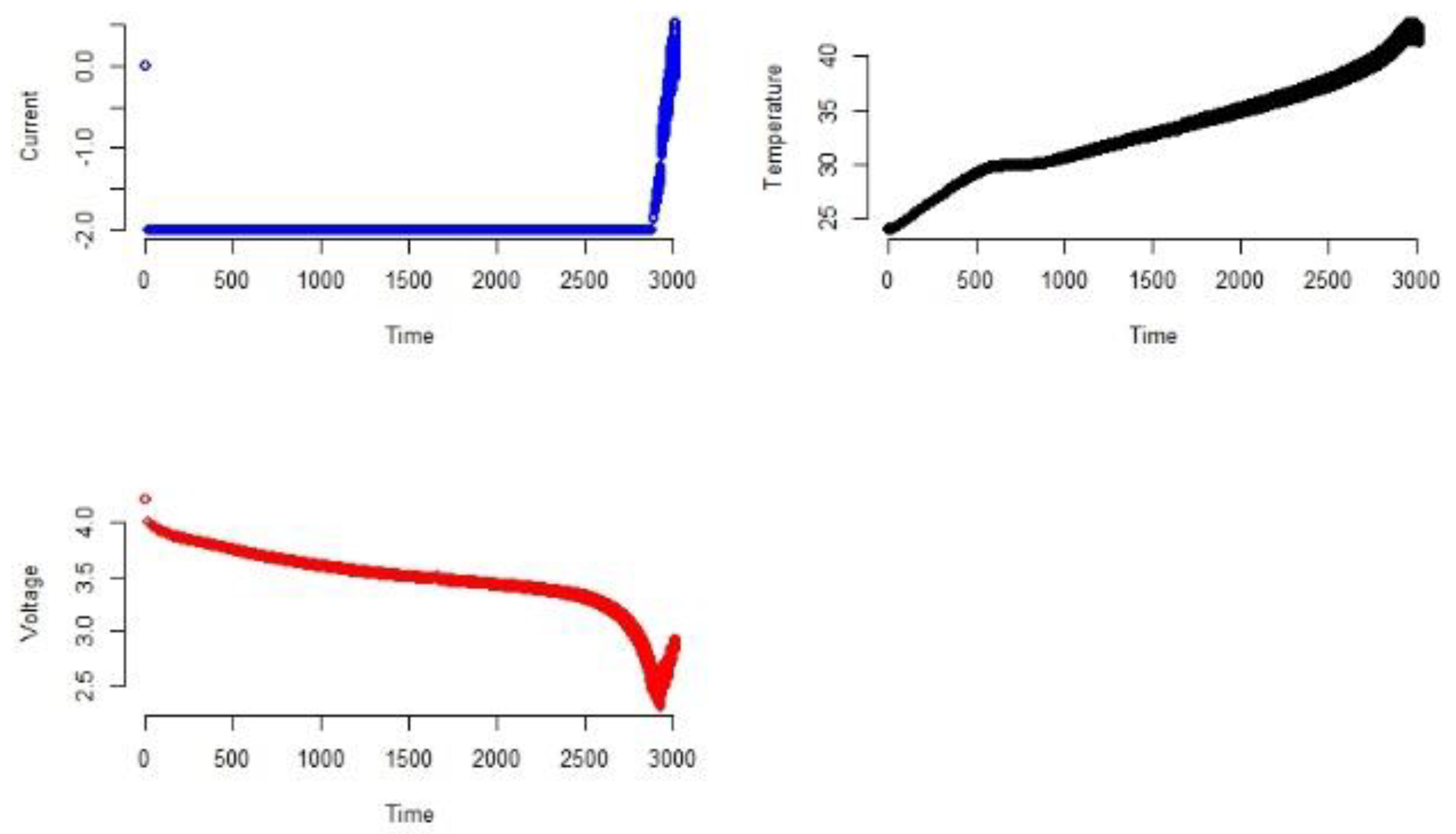
- The monitoring data of the Li-ion battery comprise 168 cycles of voltage, current, and temperature. To begin, we considered the initial cycles as training data to build a prediction model.
- (b).
- The original discretized measurements are transformed to smooth curves by applying the B-spline basis expansion. The number of knots is chosen, for each of voltage, current, and temperature, such that the fitted model has the lowest BIC value.
- (c).
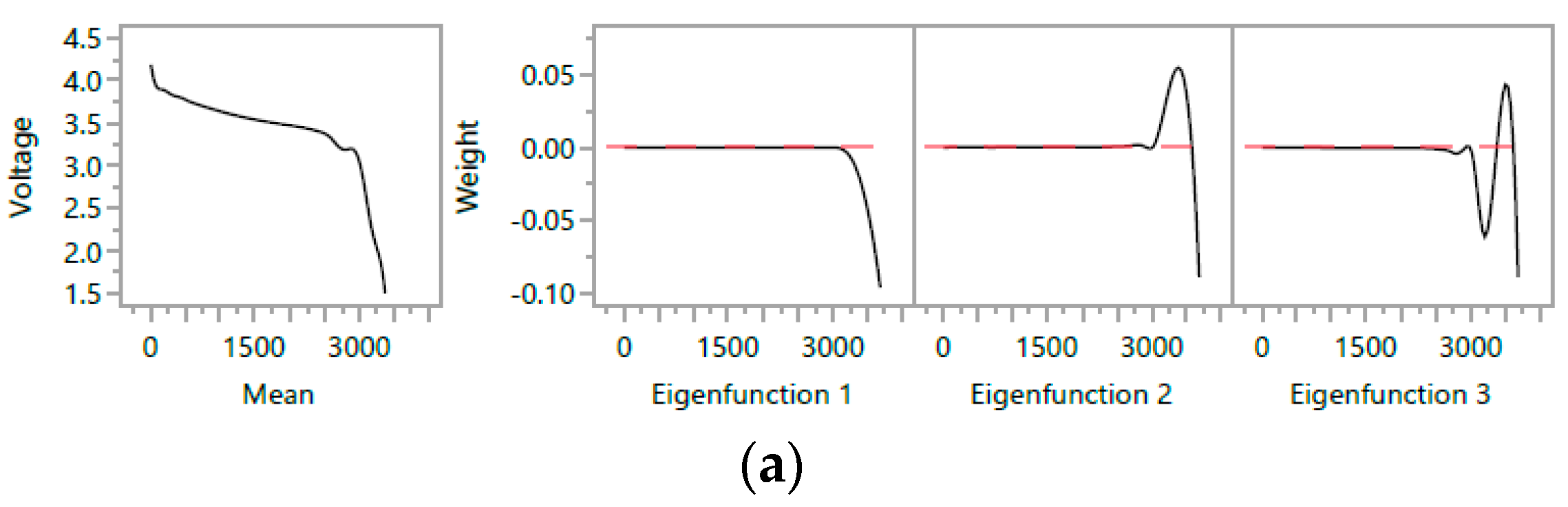
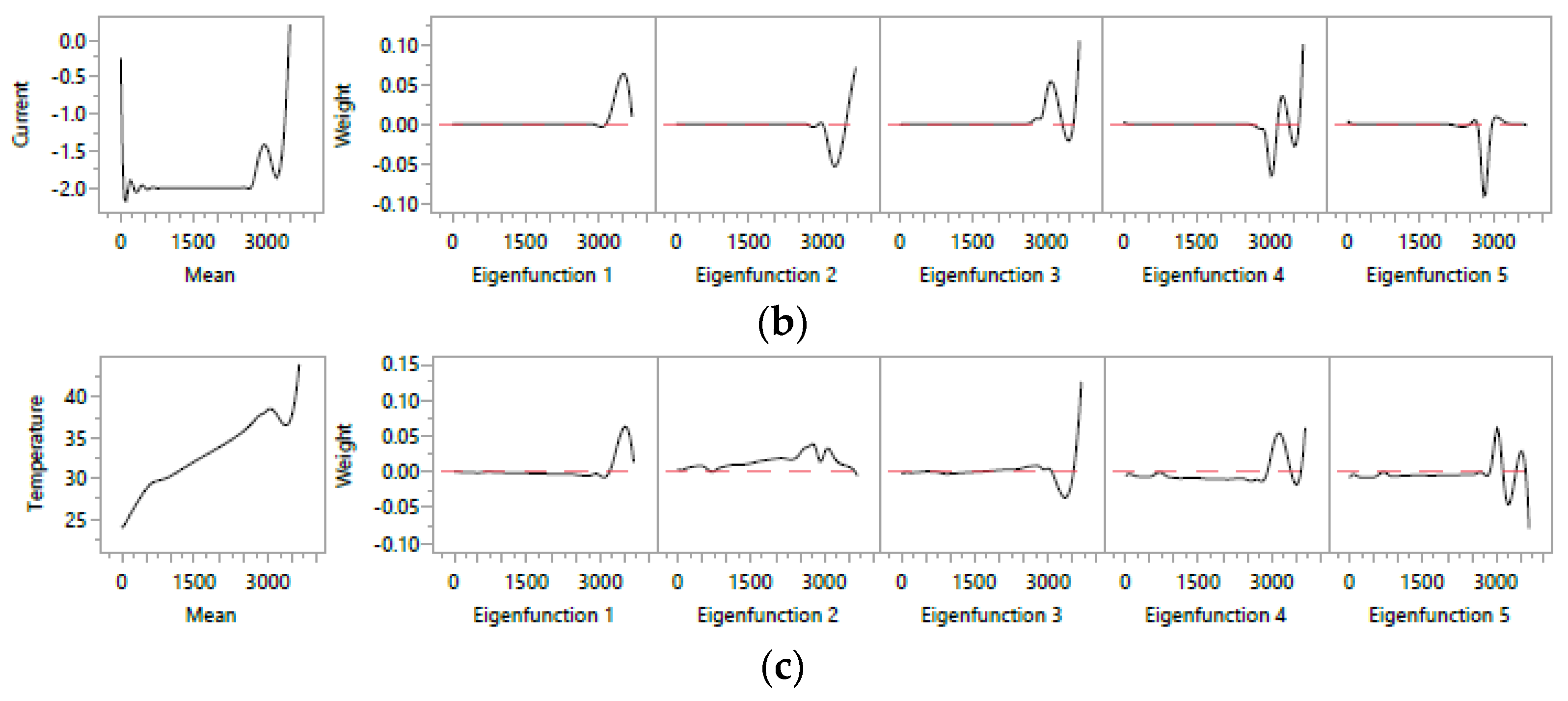
- The fPCA technique is performed on each monitoring variable, and the mean function , fPC scores , and corresponding eigenfunctions are obtained for each predictor. These fPC scores characterize the status of the battery at the corresponding cycle.
- (d).
- The LASSO regression model is trained based on fPC scores. The LASSO complexity parameter is chosen by the -fold cross-validation with 5 folds.
- (e).
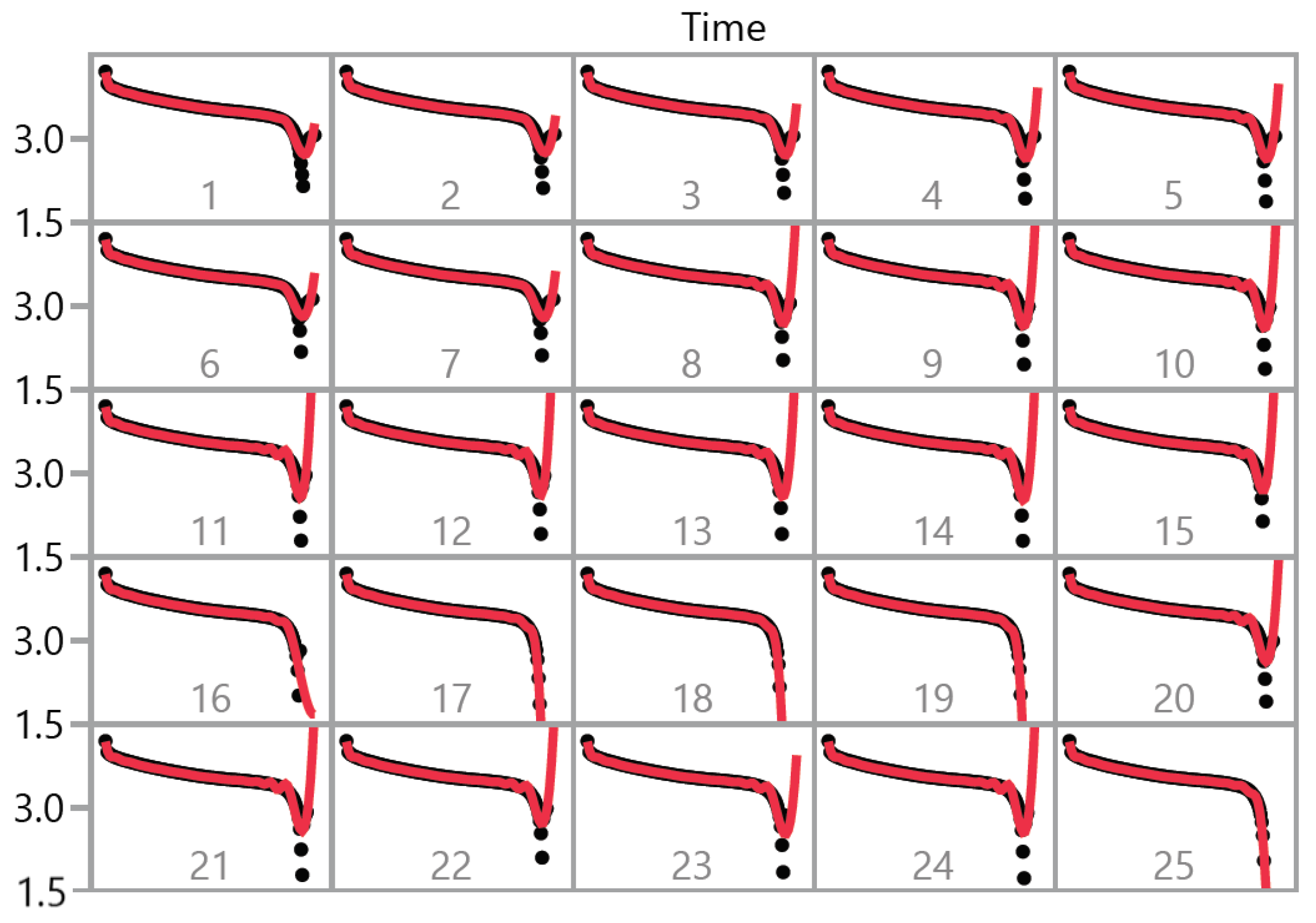
- To test the model, the monitoring variables’ measurements for the forthcoming cycles are predicted. Simple linear regression was used for this task for each time point. For the voltage measurements for a time point of , for example, we fit the following model to the initial 100 cycles of data:
- (f).
- Using the eigenfunctions obtained from the training phase, the fPC scores are extracted from each predicted curve.
- (g).
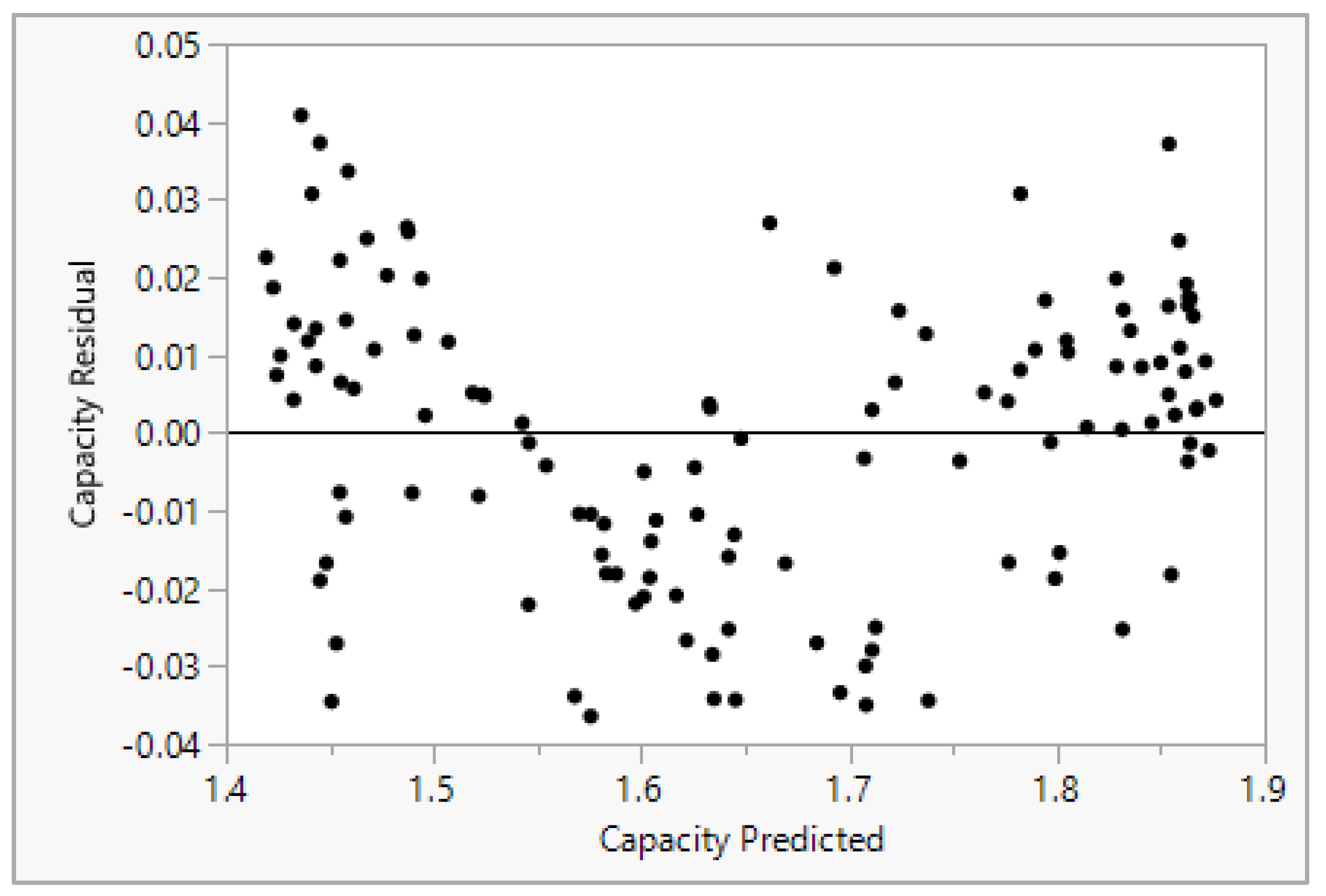
- The prediction of are obtained by LASSO model obtained in (d) and compared with the true battery capacity values to evaluate the model performance.
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, L.; Fu, X.; Guan, Y. Review of the remaining useful life prognostics of vehicle lithium-ion batteries using data-driven methodologies. Appl. Sci. 2016, 6, 166. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Alvi, M.J.; Kim, H.J. Towards a smarter battery management system for electric vehicle applications: A critical review of lithium-ion battery state of charge estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Zhang, J.; Lee, J. A review on prognostics and health monitoring of Li-ion battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Cheng, Y.; Lu, C.; Li, T.; Tao, L. Residual lifetime prediction for lithium-ion battery based on functional principal component analysis and Bayesian approach. Energy 2015, 90, 1983–1993. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Wang, F.; Mamo, T. A hybrid model based on support vector regression and differential evolution for remaining useful lifetime prediction of lithium-ion batteries. J. Power Sources 2018, 401, 49–54. [Google Scholar] [CrossRef]
- Escabias, M.; Aguilera, A.M.; Valderrama, M.J. Modeling environmental data by functional principal component logistic regression. Environmetrics 2005, 16, 95–107. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, H.; Yang, J.; Miller, D.J. A stock market forecasting model combining two-directional two-dimensional principal component analysis and radial basis function neural network. PLoS ONE 2015, 10, e0122385. [Google Scholar] [CrossRef]
- Viviani, R.; Grön, G.; Spitzer, M. Functional principal component analysis of fMRI data. Hum. Brain Mapp. 2005, 24, 109–129. [Google Scholar] [CrossRef] [PubMed]
- Kipp, K.; Johnson, S.T.; Hoffman, M.A. Functional principal component analysis of H-reflex recruitment curves. J. Neurosci. Methods 2011, 197, 270. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ma, S.; Dai, Y. Principal component analysis-based methods in bioinformatics studies. Brief. Bioinform. 2011, 12, 714. [Google Scholar] [CrossRef] [PubMed]
- Yao, F.; Müller, H.G.; Wang, J.L. Functional data analysis for sparse longitudinal data. J. Am. Stat. Assoc. 2005, 100, 577–590. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Ramsay, J.O.; Dalzell, C.J. Some tools for functional data analysis. J. R. Stat. Soc. Ser. B (Methodol.) 1991, 53, 539–561. [Google Scholar] [CrossRef]
- Kayano, M.; Konishi, S. Functional principal component analysis via regularized Gaussian basis expansions and its application to unbalanced data. J. Stat. Plan. Inference 2009, 139, 2388–2398. [Google Scholar] [CrossRef]
- Coffey, N.; Harrison, A.J.; Donoghue, O.A.; Hayes, K. Common functional principal components analysis: A new approach to analyzing human movement data. Hum. Mov. Sci. 2011, 30, 1144–1166. [Google Scholar] [CrossRef]
- Guo, J.; Li, Z. Prognostics of Lithium ion battery using functional principal component analysis. In Proceedings of the 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA, 19–21 June 2017; pp. 14–17. [Google Scholar]
- Hu, X.; Jiang, J.; Cao, D.; Egardt, B. Battery health prognosis for electric vehicles using sample entropy and sparse Bayesian predictive modeling. IEEE Trans. Ind. Electron. 2016, 63, 2645–2656. [Google Scholar] [CrossRef]
- Patil, M.A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.; Doo, S. A novel multistage support vector machine based approach for Li ion battery remaining useful life estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Wang, G.; Lu, D.D.C.; He, T. Differential voltage analysis based state of charge estimation methods for lithium-ion batteries using extended Kalman filter and particle filter. Energy 2018, 158, 1028–1037. [Google Scholar] [CrossRef]
- Mavroforakis, M.E.; Georgiou, H.V.; Dimitropoulos, N.; Cavouras, D.; Theodoridis, S. Mammographic masses characterization based on localized texture and dataset fractal analysis using linear, neural and support vector machine classifiers. Artif. Intell. Med. 2006, 37, 145–162. [Google Scholar] [CrossRef] [PubMed]
- Long, B.; Xian, W.; Jiang, L.; Liu, Z. An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 821–831. [Google Scholar] [CrossRef]
- Kirk, M. Thoughtful Machine Learning: A Test-Driven Approach; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2014. [Google Scholar]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Qin, T.; Zeng, S.; Guo, J. Robust prognostics for state of health estimation of lithium-ion batteries based on an improved PSO–SVR model. Microelectron. Reliab. 2015, 55, 1280–1284. [Google Scholar] [CrossRef]
- Zhao, Q.; Qin, X.; Zhao, H.; Feng, W. A novel prediction method based on the support vector regression for the remaining useful life of lithium-ion batteries. Microelectron. Reliab. 2018, 85, 99–108. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Gaussian process regression for forecasting battery state of health. J. Power Sources 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Xian, W.; Long, B.; Li, M.; Wang, H. Prognostics of lithium-ion batteries based on the verhulst model, particle swarm optimization and particle filter. IEEE Trans. Instrum. Meas. 2014, 63, 2–17. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, M.; Yin, X.; Guo, J.; Li, Z. Evaluation of Lithium Batteries Based on Continuous Hidden Markov Model. In Proceedings of the 2017 IEEE International Conference on Software Quality, Reliability and Security Companion, Prague, Czech Republic, 25–29 July 2017; pp. 221–225. [Google Scholar]
- NASA Ames Prognostics Data Repository. Available online: https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository (accessed on 20 April 2022).
- JMP Pro®, Version 14; SAS Institute Inc.: Cary, NC, USA, 1989–2022. Available online: http://jmp.com (accessed on 20 April 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 20 April 2022).

| Authors | Data-Driven Models | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bayesian Regression | Gaussian Process | Kalman Filter | Particle Filter | Particle Swarm Optimization | Autoregressive Based | Neural Network | Support Vector Machine | Relevance Vector Machine | Functional PCA | LASSO Regression | |
| Hu et al., 2016 [20] | ✓ | ||||||||||
| Patil et al., 2015 [21] | ✓ | ✓ | |||||||||
| Zheng et al., 2018 [22] | ✓ | ✓ | |||||||||
| Mavroforakis et al., 2006 [23] | ✓ | ✓ | |||||||||
| Long et al., 2013 [24] | ✓ | ✓ | |||||||||
| Kirk, 2014 [25] | ✓ | ✓ | |||||||||
| Nuhic et al., 2013 [26] | ✓ | ✓ | |||||||||
| Qin et al., 2015 [27] | ✓ | ✓ | |||||||||
| Zhao et al., 2018 [28] | ✓ | ✓ | |||||||||
| Richardson et al., 2017 [29] | ✓ | ✓ | |||||||||
| Xian et al., 2014 [30] | ✓ | ✓ | |||||||||
| Cheng et al., 2015 [6] | ✓ | ✓ | |||||||||
| Lin et al., 2017 [31] | ✓ | ||||||||||
| Criteria | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Training cycle | Training cycle | Training cycle | |
| 1–100 | 1–120 | 1–140 | |
| Testing cycle | Testing cycle | Testing cycle | |
| 101–120 | 121–140 | 141–160 | |
| RMSE | 0.009 | 0.02 | 0.04 |
| MAPE (%) | 0.44 | 1.74 | 3.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shoriat Ullah, M.; Seo, K. Prediction of Lithium-Ion Battery Capacity by Functional Principal Component Analysis of Monitoring Data. Appl. Sci. 2022, 12, 4296. https://doi.org/10.3390/app12094296
Shoriat Ullah M, Seo K. Prediction of Lithium-Ion Battery Capacity by Functional Principal Component Analysis of Monitoring Data. Applied Sciences. 2022; 12(9):4296. https://doi.org/10.3390/app12094296
Chicago/Turabian StyleShoriat Ullah, MD, and Kangwon Seo. 2022. "Prediction of Lithium-Ion Battery Capacity by Functional Principal Component Analysis of Monitoring Data" Applied Sciences 12, no. 9: 4296. https://doi.org/10.3390/app12094296
APA StyleShoriat Ullah, M., & Seo, K. (2022). Prediction of Lithium-Ion Battery Capacity by Functional Principal Component Analysis of Monitoring Data. Applied Sciences, 12(9), 4296. https://doi.org/10.3390/app12094296







