Throughput/Area Optimized Architecture for Elliptic-Curve Diffie-Hellman Protocol
Abstract
:1. Introduction
1.1. Related Work
1.2. Need for a High-Speed and Low-Area Key-Exchange Design
1.3. Contributions
- (i)
- An ECDH architecture is presented, with a focus on high-speed with low-area utilization, over on FPGA.
- (ii)
- The high-speed is achieved with the use of: (a) a two-stage pipelining and (b) a bit parallel Karatsuba multiplier. To deal with the pipelining, an efficient rescheduling of PAdd and PDbl operations for PM computation is proposed. The use of pipelining increases the clock frequency and reduces the critical path. Moreover, the proposed rescheduling and the employed Karatsuba multiplier reduce clock cycles, where m is the key length. Further details are illustrated in Section 3.4.
- (iii)
- Apart from the high-speed, the low-area is achieved with the use of one adder and a Karatsuba multiplier. It implies that the squaring and inversion computations are operated with the same hardware resources (Karatsuba multiplier) which eventually reduces the overall implementation resources.
- (iv)
- Finally, the two dedicated finite state machine (FSM) based controllers are used for controlling PM and ECDH operations respectively.
1.4. Novelty
1.5. Outcomes and Significance
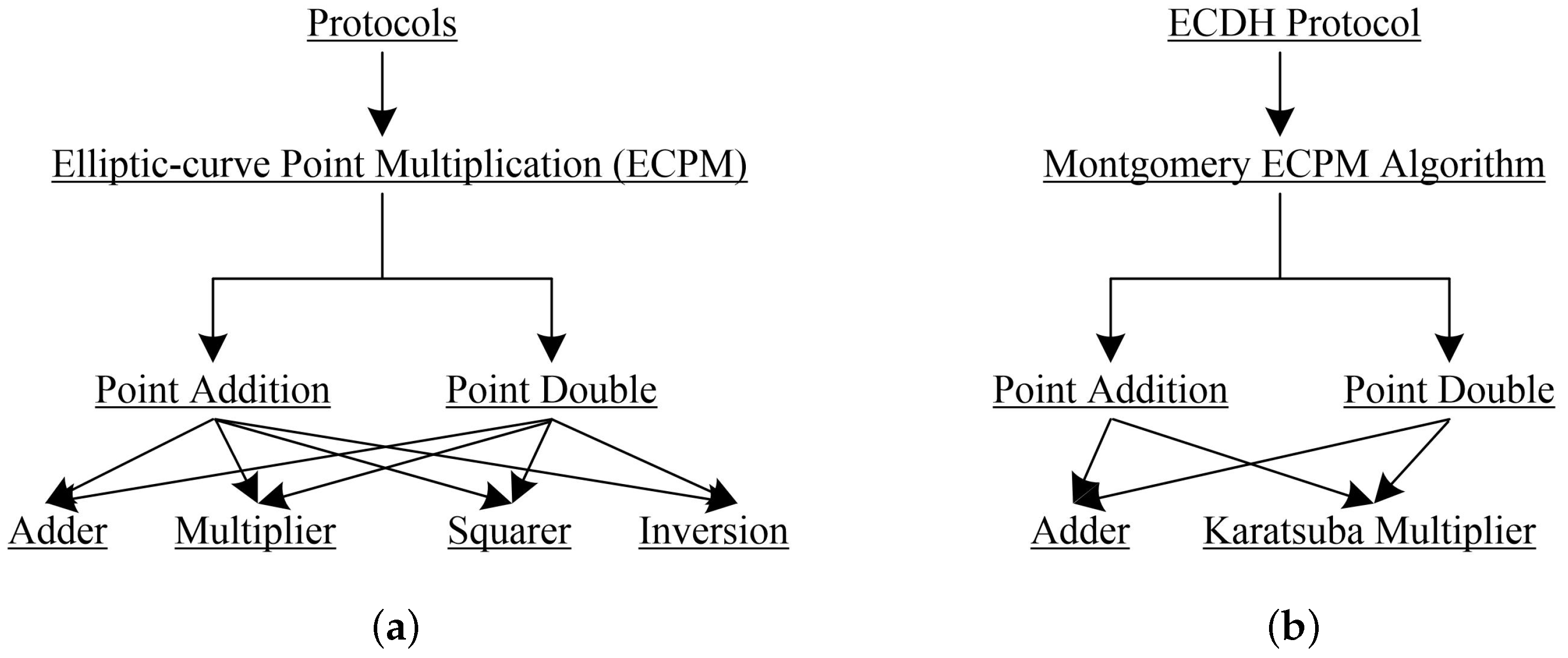
2. Related Mathematical Background
| Algorithm 1: Montgomery ECPM Algorithm [12]. |
 |
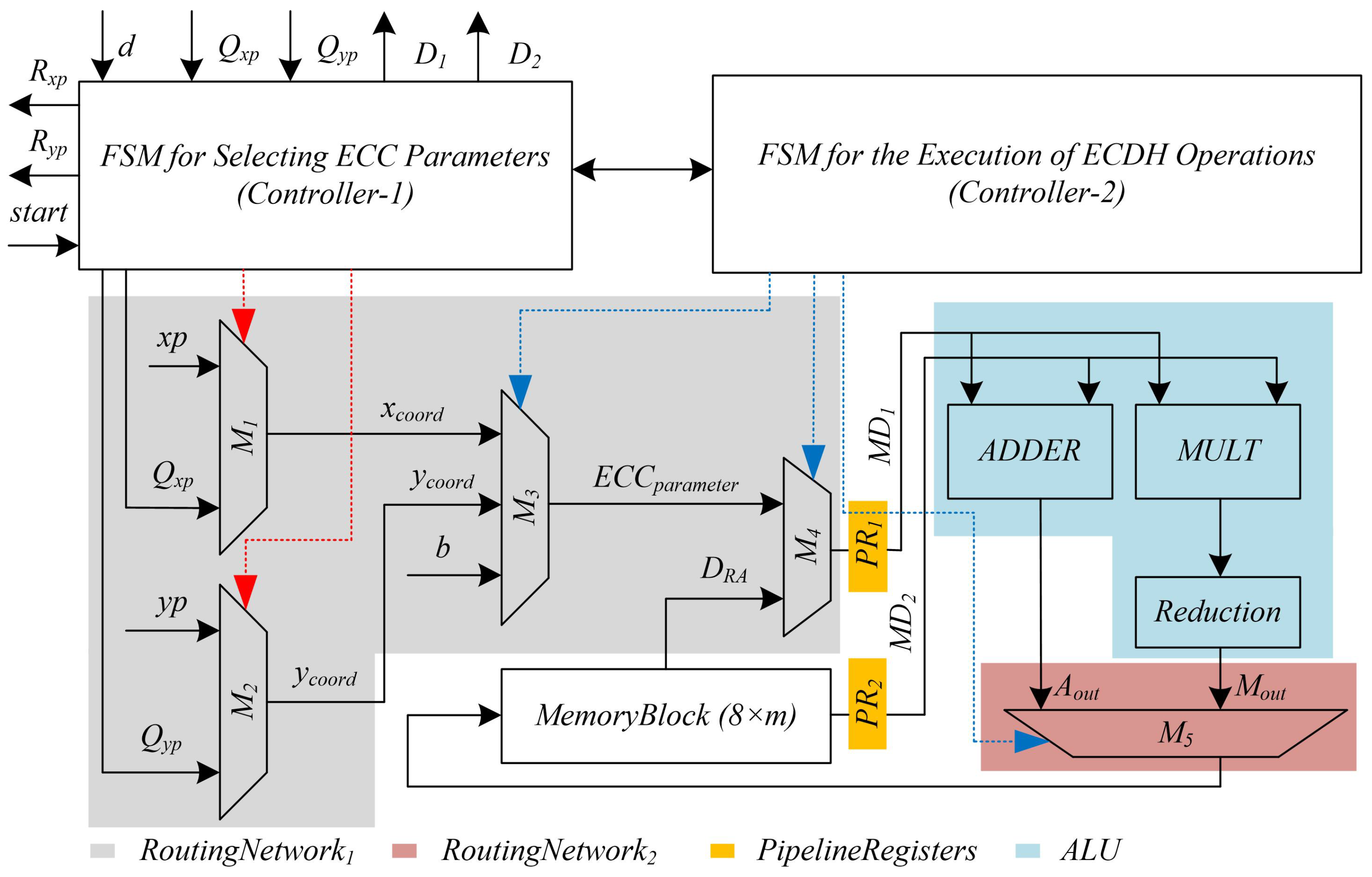
3. Proposed ECDH Architecture
3.1. Routing Networks (RoutingNetwork1 and RoutingNetwork2)
3.2. Memory Block
3.3. Arithmetic and Logic Unit (ALU)
3.4. Pipeline Registers and Scheduling
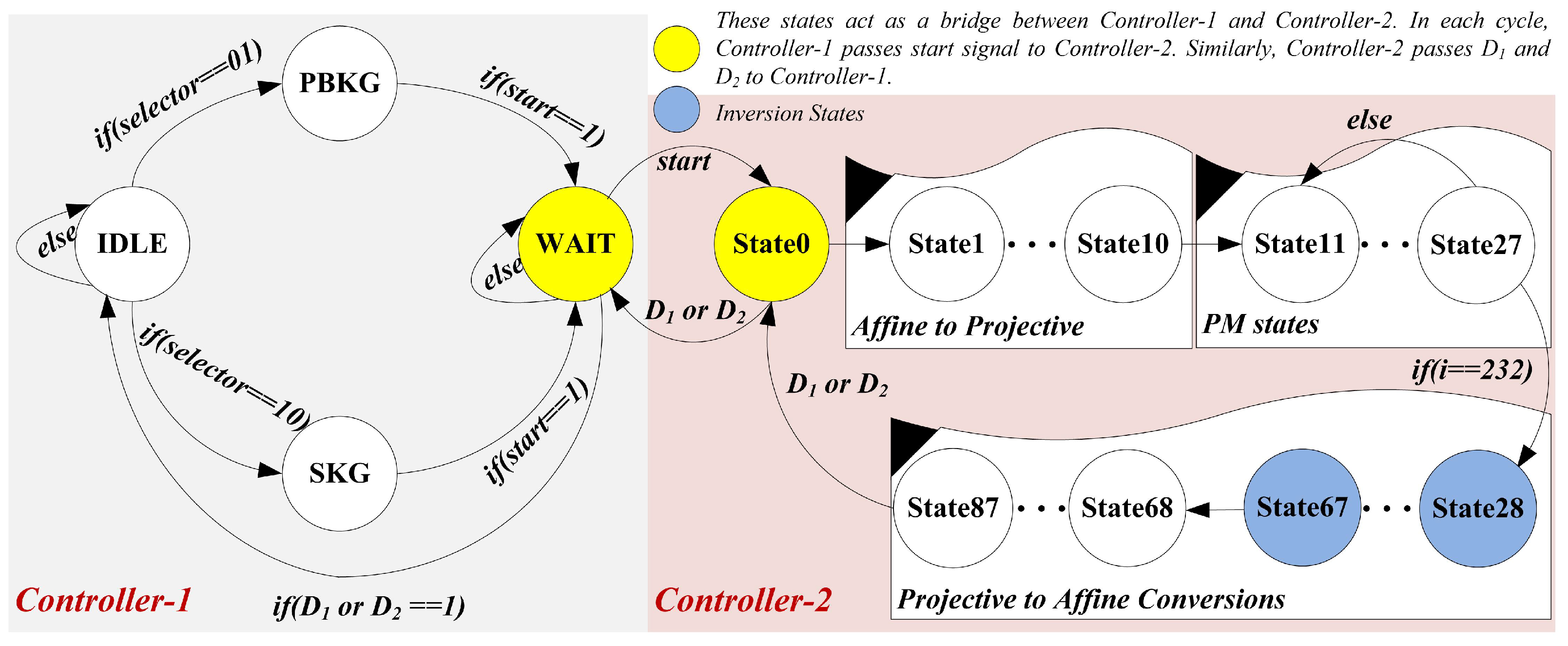
3.5. Dedicated FSM Controllers
3.5.1. Controller-1
- (i)
- State one is an state. Based on the signal (not shown in Figure 3), the processor shifts from state to either in or . Otherwise, the processor remains in the state.
- (ii)
- In the state, the processor checks the signal. Once it becomes true, the Controller-1 generates the control signals to select and coordinates of initial point P.
- (iii)
- Similarly, the processor checks the signal in state three (). Once it becomes true, it generates the control signals to choose and coordinates of a public key Q.
- (iv)
- After generating control signals either in-state or , the next state becomes state four (). The state determines that the processor is now waiting for the done signals (either for or ) from Controller-2. Whenever the processor switches its state from to , it implies that the processor is generating coordinates for a public key. Whenever the processor changes its state from to , it denotes that the processor is computing coordinates for a shared key. It is important to note that the transformation, either from to or from to , the proposed architecture consumes one clock cycle. The clock cycles for the state depends on the required cycles for Controller-2 to set the or signals. Therefore, Equation (1) provides the total number of clock cycles for our ECDH architecture.
3.5.2. Controller-2
- (i)
- The initial state (state 0) is idle. When Controller-2 receives the signal (as 1) from Controller-1, it starts generating the control signals for projective to affine conversions. It requires 10 states from state 1 to 10 such that each state takes one clock cycle for computation. In other words, the proposed ECDH architecture takes 10 clock cycles for affine to projective conversions.
- (ii)
- Fourteen instructions of (seven) and (seven) functions of Algorithm 1 are operated in seventeen states (state 11 to 27). The reason for more states is the two-stage pipelining. The details of pipelining are given in Table 1 of Section 3.4). During each state, the value for an inspected key bit, i.e., , is checked. When the inspected value for becomes 1, the part from Algorithm 1 is implemented. Otherwise, the part is operated. These 17 states are operated in 17 clock cycles and are repeated until the condition for the statement of Algorithm 1 becomes true. When it becomes true, the processor switches control from PM to the reconversions step.
- (iii)
- The states from 28 to 87 are responsible for projective to affine conversions. In states 28 to 67, a polynomial inversion is computed. For one inversion computation, our ECDH design takes clock cycles. As shown in Algorithm 1, the projective to affine conversions require two inversion computations. Therefore, the cost for two inversion operations is . Moreover, some additional states are needed (from 68 to 87) to accomplish the remaining operations of projective to affine conversions.
4. Results and Comparisons
4.1. Results
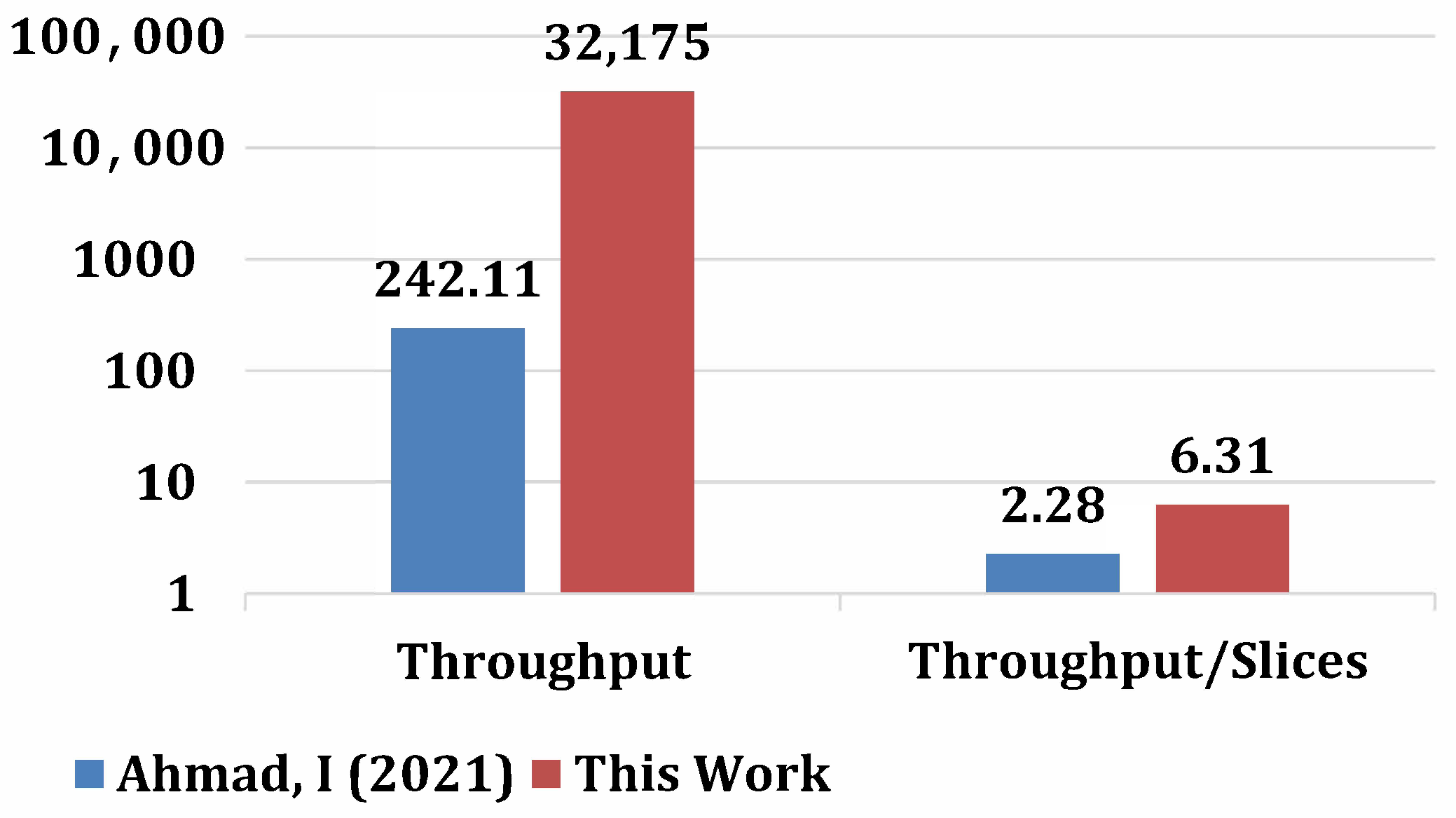
4.2. Comparisons with State-of-the-Art
4.3. Significance of This Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ding, D.; Conti, M.; Solanas, A. A smart health application and its related privacy issues. In Proceedings of the 2016 Smart City Security and Privacy Workshop (SCSP-W), Vienna, Austria, 11 April 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Kornaros, G.; Tomoutzoglou, O.; Mbakoyiannis, D.; Karadimitriou, N.; Coppola, M.; Montanari, E.; Deligiannis, I.; Gherardi, G. Towards holistic secure networking in connected vehicles through securing CAN-bus communication and firmware-over-the-air updating. J. Syst. Archit. 2020, 109, 101761. [Google Scholar] [CrossRef]
- Mun, H.; Han, K.; Lee, D.H. Ensuring Safety and Security in CAN-Based Automotive Embedded Systems: A Combination of Design Optimization and Secure Communication. IEEE Trans. Veh. Technol. 2020, 69, 7078–7091. [Google Scholar] [CrossRef]
- Xie, G.; Li, R.; Hu, S. Security-Aware Obfuscated Priority Assignment for CAN FD Messages in Real-Time Parallel Automotive Applications. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 4413–4425. [Google Scholar] [CrossRef]
- Chandramouli, R.; Lee, P. Infrastructure Standards for Smart ID Card Deployment. IEEE Secur. Priv. 2007, 5, 92–96. [Google Scholar] [CrossRef]
- Premila Bai, T.D.; Raj, K.M.; Rabara, S.A. Elliptic Curve Cryptography Based Security Framework for Internet of Things (IoT) Enabled Smart Card. In Proceedings of the 2017 World Congress on Computing and Communication Technologies (WCCCT), Tiruchirappalli, India, 2–4 February 2017; pp. 43–46. [Google Scholar] [CrossRef]
- Vinoth, R.; Deborah, L.J.; Vijayakumar, P.; Kumar, N. Secure Multifactor Authenticated Key Agreement Scheme for Industrial IoT. IEEE Internet Things J. 2021, 8, 3801–3811. [Google Scholar] [CrossRef]
- Srinivas, J.; Das, A.K.; Wazid, M.; Kumar, N. Anonymous Lightweight Chaotic Map-Based Authenticated Key Agreement Protocol for Industrial Internet of Things. IEEE Trans. Dependable Secur. Comput. 2020, 17, 1133–1146. [Google Scholar] [CrossRef]
- Sahu, A.K.; Sharma, S.; Puthal, D. Lightweight Multi-Party Authentication and Key Agreement Protocol in IoT-Based E-Healthcare Service. ACM Trans. Multimedia Comput. Commun. Appl. 2021, 17, 64. [Google Scholar] [CrossRef]
- Rahman, M.S.; Hossam-E-Haider, M. Quantum IoT: A Quantum Approach in IoT Security Maintenance. In Proceedings of the 2019 International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 10–12 January 2019; pp. 269–272. [Google Scholar] [CrossRef]
- Rashid, M.; Imran, M.; Jafri, A.R.; Al-Somani, T.F. Flexible Architectures for Cryptographic Algorithms—A Systematic Literature Review. J. Circuits Syst. Comput. 2019, 28, 1930003. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M.; Jafri, A.R.; Kashif, M. Throughput/area optimised pipelined architecture for elliptic curve crypto processor. IET Comput. Digit. Tech. 2019, 13, 361–368. [Google Scholar] [CrossRef] [Green Version]
- Bansal, M.; Gupta, S.; Mathur, S. Comparison of ECC and RSA Algorithm with DNA Encoding for IoT Security. In Proceedings of the 2021 6th International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 20–22 January 2021; pp. 1340–1343. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer: New York, NY, USA, 2004; pp. 1–311. Available online: https://link.springer.com/book/10.1007/b97644 (accessed on 13 August 2021).
- Liusvaara, I. CFRG Elliptic Curve Diffie-Hellman (ECDH) and Signatures in JSON Object Signing and Encryption (JOSE). RFC 8037. 2017. Available online: https://www.rfc-editor.org/info/rfc8037 (accessed on 7 January 2022).
- Rashidi, B. Low-Cost and Fast Hardware Implementations of Point Multiplication on Binary Edwards Curves. In Proceedings of the Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 8–10 May 2018; pp. 17–22. [Google Scholar] [CrossRef]
- Khan, Z.U.A.; Benaissa, M. High-Speed and Low-Latency ECC Processor Implementation Over GF(2m) on FPGA. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 165–176. [Google Scholar] [CrossRef] [Green Version]
- Khan, Z.U.A.; Benaissa, M. Low area ECC implementation on FPGA. In Proceedings of the 2013 IEEE 20th International Conference on Electronics, Circuits, and Systems (ICECS), Abu Dhabi, United Arab Emirates, 8–11 December 2013; pp. 581–584. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M.; Shafi, I. Lopez Dahab based elliptic crypto processor (ECP) over GF(2163) for low-area applications on FPGA. In Proceedings of the 2018 International Conference on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, 22–23 February 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Batina, L.; Mentens, N.; Ors, S.; Preneel, B. Serial multiplier architectures over GF(2/sup n/) for elliptic curve cryptosystems. In Proceedings of the 12th IEEE Mediterranean Electrotechnical Conference (IEEE Cat. No.04CH37521), Dubrovnik, Croatia, 12–15 May 2004; Volume 2, pp. 779–782. [Google Scholar] [CrossRef]
- Kodali, R.K.; Gomatam, P.; Boppana, L. FPGA implementation of multipliers for ECC. In Proceedings of the 2014 2nd International Conference on Emerging Technology Trends in Electronics, Communication and Networking, Surat, India, 26–27 December 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Imran, M.; Abideen, Z.U.; Pagliarini, S. An Open-source Library of Large Integer Polynomial Multipliers. In Proceedings of the 2021 24th International Symposium on Design and Diagnostics of Electronic Circuits Systems (DDECS), Vienna, Austria, 7–9 April 2021; pp. 145–150. [Google Scholar] [CrossRef]
- Heidarpur, M.; Mirhassani, M. An Efficient and High-Speed Overlap-Free Karatsuba-Based Finite-Field Multiplier for FGPA Implementation. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, 29, 667–676. [Google Scholar] [CrossRef]
- Lee, C.Y.; Zeghid, M.; Sghaier, A.; Ahmed, H.Y.; Xie, J. Efficient Hardware Implementation of Large Field-Size Elliptic Curve Cryptographic Processor. IEEE Access 2022, 10, 7926–7936. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M. Architectural review of polynomial bases finite field multipliers over GF(2m). In Proceedings of the 2017 International Conference on Communication, Computing and Digital Systems (C-CODE), Islamabad, Pakistan, 8–9 March 2017; pp. 331–336. [Google Scholar] [CrossRef]
- Gaudry, P. Index Calculus for Abelian Varieties and the Elliptic Curve Discrete Logarithm Problem. Cryptology ePrint Archive, Report 2004/073. 2004. Available online: https://ia.cr/2004/073 (accessed on 4 January 2022).
- Petit, C.; Quisquater, J.J. On Polynomial Systems Arising from a Weil Descent. Cryptology ePrint Archive, Report 2012/146. 2012. Available online: https://ia.cr/2012/146 (accessed on 19 January 2022).
- Chen, L.; Moody, D.; Regenscheid, A. Recommendations for Discrete Logarithm-Based Cryptography: Elliptic Curve Domain Parameters. Available online: https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-186-draft.pdf (accessed on 4 April 2022).
- Raso, O.; Mlynek, P.; Fujdiak, R.; Pospichal, L.; Kubicek, P. Implementation of Elliptic Curve Diffie Hellman in ultra-low power microcontroller. In Proceedings of the 2015 38th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 9–11 July 2015; pp. 662–666. [Google Scholar] [CrossRef]
- Fujdiak, R.; Misurec, J.; Mlynek, P.; Leonard, J. Cryptograph key distribution with elliptic curve Diffie-Hellman algorithm in low-power devices for power grids. Rev. Roum. Sci. Tech. 2016, 61, 84–88. [Google Scholar]
- Hossain, M.S.; Saeedi, E.; Kong, Y. High-performance FPGA Implementation of Elliptic Curve Cryptography Processor over Binary Field GF(2163). In Proceedings of the 2nd International Conference on Information Systems Security and Privacy (ICISSP 2016), Rome, Italy, 19–21 February 2016; pp. 415–422. [Google Scholar] [CrossRef] [Green Version]
- Turan, F.; Verbauwhede, I. Compact and Flexible FPGA Implementation of Ed25519 and X25519. ACM Trans. Embed. Comput. Syst. 2019, 18, 24. [Google Scholar] [CrossRef]
- Azarderakhsh, R.; Khatib, R.E.; Koziel, B.; Langenberg, B. Hardware Deployment of Hybrid PQC. Cryptology ePrint Archive, Report 2021/541. 2021. Available online: https://ia.cr/2021/541 (accessed on 24 December 2021).
- Ionita, D.M.; Simion, E. FPGA Offloading for Diffie-Hellman Key Exchange Using Elliptic Curves. Cryptology ePrint Archive, Report 2021/065. 2021. Available online: https://ia.cr/2021/065 (accessed on 26 December 2021).
- Ahmad, I.; Morales-Sandoval, M.; Flores, L.A.R.; Cumplido, R.; Garcia-Hernandez, J.J.; Feregrino, C.; Algredo, I. A Compact FPGA-Based Accelerator for Curve-Based Cryptography in Wireless Sensor Networks. J. Sens. 2021, 2021, 8860413. [Google Scholar] [CrossRef]
- Yang, P.; Xiong, N.; Ren, J. Data Security and Privacy Protection for Cloud Storage: A Survey. IEEE Access 2020, 8, 131723–131740. [Google Scholar] [CrossRef]
- Rawal, B.S.; Vivek, S.S. Secure Cloud Storage and File Sharing. In Proceedings of the 2017 IEEE International Conference on Smart Cloud (SmartCloud), New York, NY, USA, 3–5 November 2017; pp. 78–83. [Google Scholar] [CrossRef]
- Fournaris, A.P.; Zafeirakis, I.; Koulamas, C.; Sklavos, N.; Koufopavlou, O. Designing efficient elliptic Curve Diffie-Hellman accelerators for embedded systems. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 2025–2028. [Google Scholar] [CrossRef]
- NIST. Recommended Elliptic Curves for Federal Government Use. 1999. Available online: https://csrc.nist.gov/csrc/media/publications/fips/186/2/archive/2000-01-27/documents/fips186-2.pdf (accessed on 19 September 2021).
- Zode, P.; Deshmukh, R.B.; Samad, A. Fast Architecture of Modular Inversion Using Itoh-Tsujii Algorithm. In International Symposium on VLSI Design and Test; Kaushik, B.K., Dasgupta, S., Singh, V., Eds.; Springer: Singapore, 2017; pp. 48–55. Available online: https://www.springerprofessional.de/fast-architecture-of-modular-inversion-using-itoh-tsujii-algorit/15326436 (accessed on 11 December 2021).
- Wilson, P. Chapter 22—Finite State Machines in VHDL and Verilog. In Design Recipes for FPGAs, 2nd ed.; Wilson, P., Ed.; Newnes: Oxford, UK, 2016; pp. 305–309. [Google Scholar] [CrossRef]
- XILINX. 7 Series FPGAs Data Sheet: Overview. Available online: https://www.mouser.ee/pdfDocs/Virtex-7-ds180_7Series_Overview.pdf (accessed on 17 October 2021).
- Khan, S.Z.; Le Moullec, Y.; Alam, M.M. An NB-IoT-Based Edge-of-Things Framework for Energy-Efficient Image Transfer. Sensors 2021, 21, 5929. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.M.Z.; Alam, M.M.; Le Moullec, Y.; Kuusik, A.; Pärand, S.; Verikoukis, C. An Empirical Modeling for the Baseline Energy Consumption of an NB-IoT Radio Transceiver. IEEE Internet Things J. 2021, 8, 14756–14772. [Google Scholar] [CrossRef]

| CCs | Instructions of PAdd and PDbl | Status of Instructions of Algorithm 1 in 2-Stage Pipelining | |||||
|---|---|---|---|---|---|---|---|
| Without Scheduling | Proposed Scheduling | ||||||
| [R] | [EWB] | Hazard | [R] | [EWB] | Hazard | ||
| 1 | – | – | – | – | |||
| 2 | – | – | |||||
| 3 | – | – | |||||
| 4 | – | – | – | ||||
| 5 | – | – | |||||
| 6 | – | – | |||||
| 7 | – | – | |||||
| 8 | – | – | – | ||||
| 9 | – | – | |||||
| 10 | – | – | – | ||||
| 11 | – | – | |||||
| 12 | – | – | |||||
| 13 | – | – | – | – | |||
| 14 | – | – | |||||
| 15 | – | – | – | – | |||
| 16 | – | – | – | – | |||
| 17 | – | – | – | – | |||
| 18 | – | – | – | – | – | – | |
| 19 | – | – | – | – | – | ||
| 20 | – | – | – | – | – | ||
| 21 | – | – | – | – | – | – | |
| 22 | – | – | – | – | – | – | |
| Device | Utilized Area | Freq (in MHz) | Public Key | Shared Key | FoM | ||||
|---|---|---|---|---|---|---|---|---|---|
| Slices | LUTs | FFs | CCs | Lat (in μs) | CCs | Lat (in μs) | |||
| Virtex-7 | 5102 | 12,339 | 2459 | 318 | 4942 | 15.54 | 9886 | 31.08 | 6.30 |
| Spartan-7 | 5634 | 12,891 | 2463 | 312 | 4942 | 15.83 | 9886 | 31.68 | 5.60 |
| Artix-7 | 5957 | 13,105 | 2461 | 316 | 4942 | 15.63 | 9886 | 31.28 | 5.36 |
| Kintex-7 | 6102 | 13,258 | 2466 | 304 | 4942 | 16.25 | 9886 | 32.51 | 5.04 |
| Ref #. | /Algorithm | Device | FPGA Slices | Freq. (in MHz) | Latency (in μs) |
|---|---|---|---|---|---|
| Designs for specific to Elliptic-curve Point Multiplication computation | |||||
| [17] | /Montgomery | Virtex-7 | 11657 | 159 | 2.83 |
| [19] | /Montgomery | Virtex-7 | 3657 | 135 | 25.30 |
| [31] | /Double and Add | Kintex-7 | 2253 (7963 LUTs) | 306 | 1060 |
| [12] | /Montgomery | Virtex-7 | 5120 | 357 | 15.78 |
| This work | /Montgomery | Virtex-7 | 5102 | 318 | 15.54 |
| This work | /Montgomery | Kintex-7 | 6102 | 304 | 16.25 |
| Designs for shared key generation | |||||
| [35] | /Montgomery | Virtex-7 | 1809 | 62 | 4130.00 |
| [33] | ECDH + SIKEX434/– | Artix-7 | 1663 | 195 | 6200 |
| [32] | Ed25519 + X25519/– | Artix-7 | 3204 | 82 | – |
| This work | /Montgomery | Virtex-7 | 5102 | 318 | 31.08 |
| This work | /Montgomery | Artix-7 | 5957 | 316 | 15.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, M.; Kumar, H.; Khan, S.Z.; Bahkali, I.; Alhomoud, A.; Mehmood, Z. Throughput/Area Optimized Architecture for Elliptic-Curve Diffie-Hellman Protocol. Appl. Sci. 2022, 12, 4091. https://doi.org/10.3390/app12084091
Rashid M, Kumar H, Khan SZ, Bahkali I, Alhomoud A, Mehmood Z. Throughput/Area Optimized Architecture for Elliptic-Curve Diffie-Hellman Protocol. Applied Sciences. 2022; 12(8):4091. https://doi.org/10.3390/app12084091
Chicago/Turabian StyleRashid, Muhammad, Harish Kumar, Sikandar Zulqarnain Khan, Ismail Bahkali, Ahmed Alhomoud, and Zahid Mehmood. 2022. "Throughput/Area Optimized Architecture for Elliptic-Curve Diffie-Hellman Protocol" Applied Sciences 12, no. 8: 4091. https://doi.org/10.3390/app12084091
APA StyleRashid, M., Kumar, H., Khan, S. Z., Bahkali, I., Alhomoud, A., & Mehmood, Z. (2022). Throughput/Area Optimized Architecture for Elliptic-Curve Diffie-Hellman Protocol. Applied Sciences, 12(8), 4091. https://doi.org/10.3390/app12084091








