Featured Application
Semantic dependency parsing could be applied in many downstream tasks of natural language processing, including named entity recognition, information extraction, machine translation, sentiment analysis, question generation, question answering, etc.
Abstract
Higher-order information brings significant accuracy gains in semantic dependency parsing. However, modeling higher-order information is non-trivial. Graph neural networks (GNNs) have been demonstrated to be an effective tool for encoding higher-order information in many graph learning tasks. Inspired by the success of GNNs, we investigate improving semantic dependency parsing with higher-order information encoded by multi-layer GNNs. Experiments are conducted on the SemEval 2015 Task 18 dataset in three languages (Chinese, English, and Czech). Compared to the previous state-of-the-art parser, our parser yields 0.3% and 2.2% improvement in average labeled F1-score on English in-domain (ID) and out-of-domain (OOD) test sets, 2.6% improvement on Chinese ID test set, and 2.0% and 1.8% improvement on Czech ID and OOD test sets. Experimental results show that our parser outperforms the previous best one on the SemEval 2015 Task 18 dataset in three languages. The outstanding performance of our parser demonstrates that the higher-order information encoded by GNNs is exceedingly beneficial for improving SDP.
Dataset:https://doi.org/10.18653/v1/s15-2153.
1. Introduction
Semantic dependency parsing (SDP) attempts to identify semantic relationships between words in a sentence by representing the sentence as a labeled directed acyclic graph (DAG), also known as the semantic dependency graph (SDG). In an SDG, not only can semantic predicates have multiple or zero arguments, but also words from the sentence can be attached as arguments to more than one head word (predicate), or they can be outside the SDG (being neither a predicate nor an argument). SDP has been successfully applied in many downstream tasks of natural language processing, including named entity recognition [1], information extraction [2], machine translation [3], sentiment analysis [4], question generation [5], question answering [6], etc. SDP originates from syntactic dependency parsing which aims to represent the syntactic structure of a sentence by means of a labeled tree.
Higher-order information is generally helpful for improving the performance of syntactic and semantic dependency parsing [7,8,9] because it contains not only the information about the head and modifier tokens but also the information about higher-order parts (head tokens, modifier tokens, and other tokens linked to them together form the higher-order parts). Here is a straightforward example (as in Figure 1). For the sentence “They read Mickey Spillane and talk about Groucho and Harpo”, its semantic dependency representation is shown in Figure 1a; the higher-order parts that appear in this sentence are shown in Figure 1b. When considering the semantic dependency relationship between talk and Harpo (dotted edge), if we know (1) Groucho and Harpo are included in the second-order part (siblings) and (2) there is a dependency edge labeled PAT-arg between talk and Groucho (blue edges), it is obvious that there is also a dependency edge labeled PAT-arg between talk and Harpo.
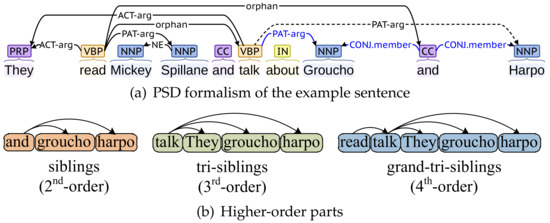
Figure 1.
Second-order, third-order, and fourth-order parts that appear in the example sentence.
Several semantic dependency parsers have been presented in recent years. Most of them are first-order parsers that utilize the information about first-order parts [10,11,12,13,14]; the rest are second-order parsers that utilize the information about second-order parts [8,15,16]. They have demonstrated that second-order information could bring significant accuracy gains in SDP. However, the second-order parts used in these second-order parsers are limited to specific types, including siblings, grandparent, and co-parents. Utilizing more types of higher-order parts (e.g. tri-siblings, great-grandparents, grand-tri-siblings, etc.) in SDP still remains under-explored. The reason for this issue is that modeling higher-order parts is non-trivial [8]. Higher-order parts have been exploited in syntactic dependency parsing [7,9,17,18,19]. However, algorithms for higher-order syntactic dependency parsing aim to generate a dependency tree rather than a dependency graph, therefore they are not applicable to SDP.
Graph neural networks (GNNs) have been demonstrated to be an effective tool for encoding higher-order information in many graph learning tasks [7,20]. GNNs aggregate higher-order information in a similar incremental manner: One GNN layer encodes information about immediate neighbors and K layers encode K-order neighborhoods (i.e., information about nodes at most K hops away).
This study aims to exploit GNNs’ powerful ability of representation learning in SDP. Inspired by the success of GNNs, we investigate using GNNs to encode higher-order information to improve the accuracy of SDP. Instead of encoding higher-order information of specific types of higher-order parts extracted from intermediate parsing graphs, we aggregate higher-order information by stacking multiple GNN layers. We extend the biaffine parser [12] and employ it as the vanilla parser to produce an initial adjacency matrix (close to gold) since there is no graph structure available during testing. Two GNN variants, Graph Convolutional Network (GCN) [21] and Graph Attention Network (GAT) [22], have been investigated in our model (GNNSDP: GNN-based Semantic Dependency Parser).
GNNSDP has been evaluated on the SemEval 2015 Task 18 dataset which covers three languages (Chinese, English, and Czech) and contains three semantic dependency formalisms (DM, PAS, and PSD). Compared to the previous best one, our parser yields 0.3% and 2.2% improvement in average labeled F1-score on English in-domain (ID) and out-of-domain (OOD) test sets, 2.6% improvement on Chinese ID test set, and 2.0% and 1.8% improvement on Czech ID and OOD test sets. Experimental results show that GNNSDP outperforms the previous state-of-the-art parser in three languages. In addition, GNNSDP shows greater advantage over the baseline in the longer sentence and PSD formalism (appearing linguistically most fine grained). To the best of our knowledge, this work is the first study to apply GNNs in semantic dependency parsing. Our code is publicly available at https://github.com/LiBinNLP/GNNSDP (accessed on 16 April 2022).
2. Related Work
In this section, the studies on higher-order syntactic dependency parsing, semantic dependency parsing, and GNNs will be summarized.
2.1. Higher-Order Syntactic Dependency Parsing
Higher-order parsing has received a lot of attention in the syntactic dependency parsing. McDonald and Pereira [23] presented a second-order parser which extended the maximum spanning tree parsing framework to incorporate second-order siblings parts. Carreras [17] presented a second-order parser which incorporated grand-parental relationships in the dependency structure. Koo and Collins [18] developed a third-order parser. They introduced grand-siblings and tri-siblings parts. Ma and Zhao [19] developed a forth-order parser which utilized grand-tri-siblings parts for fourth-order dependency parsing. Ji et al. [7] used GNNs to capture higher-order information for syntactic dependency parsing, which was closely related to our work. The core difference between their method and ours is that they integrated three types of high-order information (grandparent, grandchild, and siblings), and ours is not limited to any specific types of higher-order parts. Zhang et al. [9] presented a second-order TreeCRF extension to the biaffine parser.
Higher-order parts have been exploited in syntactic dependency parsing. However, approaches for higher-order syntactic dependency parsing aim to generate a dependency tree rather than a dependency graph. Therefore, they are not applicable to semantic dependency parsing.
2.2. Semantic Dependency Parsing
Several SDP models have been presented in recent years. Their parsing mechanisms are either transition based or graph based. Most of them are first-order parsers. Wang et al. [13] presented a neural transition-based parser, using a variant of the list-based arc-eager transition algorithm for dependency graph parsing. Lindemann et al. [24] developed a transition-based parser for Apply-Modify dependency parsing. They extended the stack-pointer model to predict transitions. Fernández-González and Gómez-Rodríguez [14] developed a transition-based parser, using the Pointer Network to choose a transition between Attach-p and Shift. More recently, there has been a predominance of purely graph-based SDP models. Dozat and Manning [12] extended the LSTM-based syntactic parser of Dozat et al. [25] to train on and generate SDG. Kurita and Søgaard [26] developed a reinforcement learning-based approach that iteratively applied the syntactic dependency parser to build a DAG structure sequentially. Jia et al. [27] presented a semi-supervised model based on the Conditional Random Field Autoencoder to learn a dependency graph parser. He and Choi [28] significantly improved the performance by introducing contextual string embeddings (called Flair).
Higher-order SDP has received less attention. Martins et al. [15] developed a second-order parser which employed a feature-rich linear model to incorporate first and second-order parts (arcs, siblings, grandparent, and co-parents). The algorithm was employed for approximate decoding. Cao et al. [16] presented a quasi-second-order parser and used a dynamic programming algorithm (called Maximum Subgraph) for exact decoding. Wang et al. [8] extended the parser [12] and managed to add the information about three types of second-order parts (siblings, grandparent, and co-parents) for score computation and then applied either mean-field variational inference or loopy belief propagation for approximate decoding.
These second-order parsers demonstrated that second-order information could bring significant accuracy gains in SDP. However, the second-order parts used in these second-order parsers are limited to specific types, including siblings, grandparent, and co-parents. Utilizing more types of higher-order parts (e.g., tri-siblings, great-grandparent, grand-tri-siblings, etc.) in SDP still remains under-explored. The reason for this issue is that modeling higher-order parts is non-trivial [8].
2.3. Graph Neural Networks
Recent years have witnessed great success from GNNs [21,22,29] in graph learning. GNNs follow a message-passing mechanism, where the node embedding is obtained by aggregating and transforming the embeddings of its neighbors. Due to the powerful ability to learn effective representations of graphs, GNNs have been applied to various downstream tasks including node classification, link prediction, and graph classification.
Two main families of GNNs have been proposed, i.e., spectral methods and spatial methods. The first family learns node representation based on graph spectral theory [21,30,31]. The second family defines graph convolutions in the spatial domain as aggregating and transforming local information [22,29]. GCNs [21] is a spectral-based method, which learns node representation based on graph spectral theory. GAT [22] is a spatial-based method, which introduces the multi-head attention mechanism to learn different attention scores for neighbors when aggregating information.
GNNs have been demonstrated to be an effective tool for encoding higher-order information in many graph learning tasks [7,20]. Marcheggiani and Titov [20] utilized GNNs to capture higher-order information from the syntactic dependency tree for semantic role labeling. Ji et al. [7] utilized GNNs to encode specific types of higher-order parts for syntactic dependency parsing.
Inspired by the success of GNNs, we investigate using GNNs to encode higher-order information for improving semantic dependency parsing.
3. GNN-Based Semantic Dependency Parser
GNNSDP is a parser that extends the biaffine parser [12]. An overview of GNNSDP is shown in Figure 2. Given sentence s with n words , there are three steps to parse it as an SDG. Firstly, the sentence will be parsed with a vanilla SDP parser, producing an initial SDG. Secondly, the contextualized word representations output by long short-term memory (BiLSTM) and adjacency matrix obtained from the initial SDG will be fed into the GNN encoder to obtain node representations which contain higher-order information. Finally, Multi-Layer Perceptron (MLP) will be used to get the hidden state representation, and then decoded by the biaffine classifier to predict edge and label.
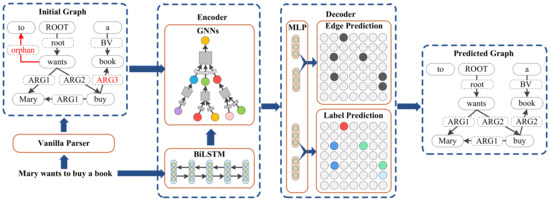
Figure 2.
Overall architecture of the proposed GNNSDP.
3.1. Vanilla Parser
We use the biaffine parser [12] as the vanilla parser. Sentence s will be parsed by the vanilla parser to obtain the initial adjacency matrix.
where is the initial adjacency matrix; is the initial SDG; W denotes n words and F denotes features of words.
3.2. Embeddings
Word embeddings and feature embeddings are used to represent the embedding of each token in GNNSDP.
3.2.1. Word Embeddings
Pretrained word embeddings of three languages are downloaded from the internet:
- For English, the 100-dimension English word embeddings from GloVe [32] are used.
- For Chinese, the 300-dimension Chinese word embeddings from SGNS [33] are used.
- For Czech, the 300-dimension Czech word embeddings from fasttext [34] are used.
3.2.2. Feature Embeddings
Four types of features are used in GNNSDP. The dimension of each feature embedding is denoted as d ():
- Part-of-speech (POS) tag embeddings: POS tag embeddings are randomly generated. , where n is the number of POS tags.
- Lemma embeddings: A lemma is the base form of a word; lemma embeddings are also randomly generated. , where l is the number of lemmas. Lemmas that occurred seven times or more are included in the lemma embedding matrix.
- Character embeddings: Character embeddings summarize the information of characters in each token, which are generated using a one-layer unidirectional LSTM (CharLSTM) that convolves over three character embeddings at a time, whose end state is linearly transformed to be d-dimensional.
- Bidirectional Encoder Representation from Transformer (BERT) embeddings: BERT embeddings are extracted from the pretrained BERT model.
3.3. Encoder
We concatenate word embeddings and feature embeddings, and feed them into a BiLSTM to obtain contextualized representations.
Specifically, BiLSTM is a sequence processing model that consists of two reversed unidirectional LSTM networks: One taking the input in a forward direction to capture forward information, and another in a backward direction to capture backward information. BiLSTM can integrate both forward and backward information by concatenating bidirectional information.
where is the concatenation (⊕) of the word embeddings and feature embeddings of word , X represents . is the contextualized representations of sequence X.
Then we employ K-layer GNNs to capture higher-order information by aggregating the representation of K-order neighborhoods. The node embedding matrix in the kth-layer is computed as Equation (6):
When the GNNLayer is implemented in the GCN, the representation of node i in the kth layer is computed as Equation (7)
where W and B are parameter matrices; are neighbors of node i; is the active function (ReLU is used); .
When GNNLayer is implemented in GAT, is computed as Equation (8):
where is the attention coefficient of node i to its neighbour j in attention head m at the th layer.
While higher-order information is important, GNNs would suffer from the over-smoothing problem when the number of layer is excessive. Therefore we stack three layers with the past experience.
3.4. Decoder
The decoder has two modules: The edge existence prediction module and the edge label prediction module. For each of the two modules, we use MLP to split the final node representation into two parts—a head representation, and a dependent representation, as shown in Equations (9)–(12):
We can then use two biaffine classifiers (as Equation (13)), which are generalizations of linear classifiers to include multiplicative interactions between two vectors—to predict edges and labels, as Equations (14) and (15):
where and are scores of edge existence and edge label between words and . U, W, and b are learned parameters of the biaffine classifier. For the edge existence prediction module, U will be -dimensional, so that the will be a scalar. For edge label prediction, if the parser is unlabeled, U will be -dimensional, so that the will be a scalar. If the parser is labeled, U will be -dimensional, where c is the number of labels, so that the is a vector that represents the probability distributions of each label.
The unlabeled parser scores each edge between pairs of words in the sentence—these scores can be decoded into a graph by keeping only edges that received a positive score. The labeled parser scores every label for each pair of words, so we simply assign each predicted edge its highest-scoring label and discard the rest.
3.5. Learning
We can train the model by summing the losses from the two modules, back propagating the error to the parser. The cross entropy function is used as as the loss function, which is computed as Equation (18):
The loss functions of the edge existence prediction module and the edge label prediction module are defined as:
where and are the parameters of two modules.
Then the adaptive moment estimation (Adam) method is used to optimize the summed loss function :
where is a tunable interpolation constant .
4. Experiments
In this section, the dataset, hyper-parameters, and experimental results are shown as follows.
4.1. Dataset
In order to test the proposed approach, we conducted experiments on the SemEval 2015 Task 18 dataset [35], which covers three languages (English, Chinese, and Czech) and contains three different formalisms (DELPH-IN MRS (DM) [36], Predicate-Argument Structure (PAS) [37], and Prague Semantic Dependencies (PSD) [38]). For English, three formalisms (DM, PAS, and PSD) are all available; for Chinese, only PAS formalism is available; for Czech, only PSD formalism is available.
The dataset split of three languages is shown as Table 1. For English, we use the same dataset split as in previous approaches [10,39], with 33,964 training sentences from Sections 00-19 of the Wall Street Journal corpus [40], 1692 development sentences from Section 20, 1410 sentences from Section 21 as in-domain (ID) test data, and 1849 sentences sampled from the Brown Corpus [41] as the out-of-domain (OOD) test data. For Chinese, we use the top 3000 sentences as the development data, the remaining 25,336 sentences as the training data, and 8976 sentences as the ID test data. For Czech, we use the top 3000 sentences as the development data, the remaining 39,057 sentences as the training data, 1670 sentences as the ID test data, and 316 sentences as the OOD test data.

Table 1.
The number of sentences contained in each divided dataset of three languages. Only the in-domain test set is available for Chinese; the in-domain and out-of-domain test sets are available for English and Czech.
For the evaluation, we use the evaluation script used in Wang et al. [8], reporting labeled F-measure scores (LF1) (including ROOT arcs) on the ID and OOD test sets for each formalism as well as the macro-average over the three of them.
4.2. Experimental Environments
The main hardware and software used in our experimental environments are shown as Table 2. GPU is utilized to do the computation of neural networks, to speed up the process of training and prediction.

Table 2.
Hardware and software used in our experimental environments.
4.3. Hyper-Parameters
The hyper-parameter configuration for our final system is given in Table 3. Following Wang et al. [8], we use Adam to optimize our model, annealing the learning rate by 0.5 for every 10,000 steps, and switch the optimizer to AMSGrad after 5000 steps without improvement. We train the model for 100,000 iterations with batch sizes of 6000 tokens and terminate the training early after 10,000 iterations with no improvement on the development set.

Table 3.
Final hyper-parameter configuration.
4.4. Baseline Approaches
We compare GNNSDP with previous state-of-the-art parsers in Table 4 and Table 6. Turku is from Kanerva et al. [42]. Riga is from Barzdins et al. [43]. Peking is a hybrid model from Du et al. [10]. Lisbon is from Almeida and Martins [39]. WCGL [13] is a neural transition-based model. PTS17 is proposed by Peng et al. [11] and Basic is single task parsing, while Freda3 is a multitask parser across three formalisms. D&M [12] is a first-order graph-based model. MF and LBP [8] are a second-order model using mean field variational inference or loopy belief propagation. Lindemann et al. [44] and Lindemann et al. [24] are a compositional semantic parser for SDP and abstract meaning representation. SemPointer [14] is a transition-based model using the Pointer Network. Jia et al. [27] is a semi-supervised parser, only the full-supervised result on DM formalism is shown in their paper. He and Choi [28] uses not only BERT but also contextual string embeddings (called Flair).

Table 4.
Comparison of labeled F1 scores achieved by our model and previous state-of-the-art in the English dataset. The bold numbers indicate the current best scores. The F1 scores of baseline and our models are averaged over five runs. ID denotes the in-domain (WSJ) test set and OOD denotes the out-of-domain (Brown) test set. +Char, +Lemma, +BERT, and +Flair mean augmenting the token embeddings with character-level, lemma embeddings, BERT embeddings, and Flair embeddings. Semi-SDP only shows the full-supervised result on DM formalism.
4.5. Experimental Results
We group SDP models into three blocks depending on the embeddings provided to the models: (1) just basic pre-trained word embeddings and POS tag embeddings (Basic), (2) character and pre-trained lemma embeddings augmentation (+Char+Lemma), and (3) pre-trained BERT embedding augmentation (+Char+Lemma+BERT).
4.5.1. Results on English
Table 4 presents the comparison of GNNSDP and previous approaches on the test sets of the SemEval 2015 Task 18 English dataset. From the results, we have the following observations:
- In the basic settings, GNNSDP achieves 1.8 and 1.3 averaged LF1 improvements on the ID and OOD test set over the previous best parsers.
- Adding both the character-level and the lemma embeddings, most models improve performance quite a bit generally. GNNSDP leads to 1.9 and 1.9 averaged LF1 improvements over the previous best parsers on the ID and OOD test sets.
- Adding BERT embeddings pushes performance even higher generally. GNNSDP outperforms the previous best parsers by 0.3 and 2.2 average LF1 improvements on the ID and OOD test sets, respectively.
- GNNSDP makes significant improvements on the PSD formalism, with 4.6 and 4.7 LF1 improvements in the basic settings, 4.6 and 5.1 LF1 improvements when character-level and lemma embeddings are added, 0.9 and 5.3 LF1 improvements when BERT embeddings are added on the ID and OOD test sets, respectively.
- The LF1 scores of all parsers on the PSD is lower than the other two formalisms. Table 5 shows part of contrastive statistics of three formalisms. We have noticed that the PSD formalism appears linguistically most fine-grained because it contains the most semantic labels and frames [35]. This makes PSD more challenging to predict. However, GNNSDP performs better than other first-order and second-order parsers, suggesting that higher-order information is beneficial for improving SDP.
 Table 5. Contrastive statistics of three semantic formalisms.
Table 5. Contrastive statistics of three semantic formalisms. - The performances of GNNSDP(GCN) and GNNSDP(GAT) are close in three embedding settings, demonstrating that both GCN and GAT are capable of capturing higher-order information.
4.5.2. Results on Chinese and Czech
Table 6 shows the comparison of GNNSDP and previous studies on the SemEval 2015 Task 18 Chinese and Czech datasets. From the results, we have observed that:

Table 6.
Comparison of labeled F1 scores achieved by our model and previous state-of-the-art on Chinese and Czech datasets. The bold numbers indicate the current best scores. The results of D&M on Chinese and Czech are not reported in their paper; therefore, we reproduce it. The F1 scores of baseline and our models are averaged over five runs. Only the PAS formalism and in-domain test set is available for Chinese; the PSD formalism, in-domain, and out-of-domain test sets are available for Czech.
- GNNSDP(GCN) and GNNSDP(GAT) outperform the previous parsers on Chinese and Czech.
- The LF1 scores of GNNSDP(GCN) and GNNSDP(GAT) are relatively close on Chinese and Czech.
In summary, GNNSDP outperforms the previous state-of-the-art parser in three languages and three semantic dependency formalisms. Outstanding performances of GNNSDP have demonstrated that higher-order information can bring considerable accuracy gains in SDP. In addition, GNNs are capable of capturing higher-order information.
5. Experimental Analysis
In this section, we analyse the experimental results from three perspectives, including performance on different sentence length, ablation study, and case study.
5.1. Performance on Different Sentence Length
We want to study the impact of sentence lengths. The ID and OOD test sets of the three formalisms are split with 10 tokens range. The ID test set has six groups and OOD has seven groups. GNNSDP(GCN) and biaffine parser are evaluated on them. The results for different groups are shown in Figure 3.
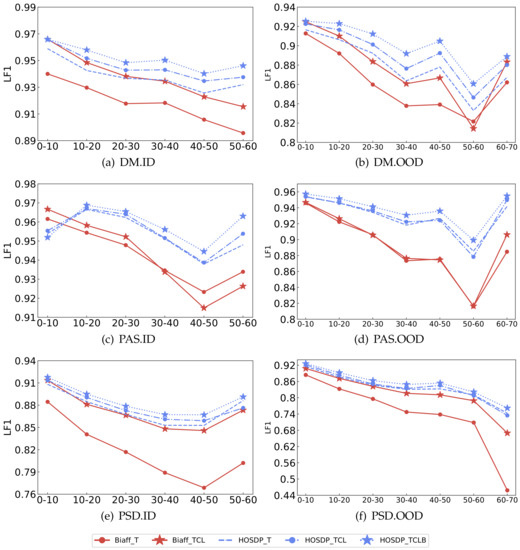
Figure 3.
LF1 score of different sentence lengths in three formalisms. ★-T represents that only the POS tag is used as feature. ★-TCL represents that the POS tag, character-level, and lemma embeddings are used as features. ★-TCLB represents that the POS tag, character-level, lemma, and BERT embeddings are used as features.
The results show that GNNSDP outperforms the biaffine parser on different groups with the same embedding settings, except for being slightly lower on the first group (0–10 tokens) on ID test set of PAS formalism. Furthermore, GNNSDP that only uses POS tag embeddings outperforms the biaffine parser that uses POS tag, character-level, and lemma embeddings when sentences get longer, especially when sentences are longer than 30. It turns out that higher-order information is favorable for longer sentences since higher-order dependency relationships are more prevalent in longer sentences.
5.2. Ablation Study
We investigate how the number of GNN layers affects the performance of our parser. We train and test the GNNSDP(GCN) in PSD formalism datasets of English and Czech. The number of GCN layers increases from 1 to 3.
Table 7 shows the results of GNNSDP(GCN) with different numbers of GCN layers in basic embedding settings. From the results, we can see that:

Table 7.
LF1 scores of GNNSDP with different GNN layers on ID and OOD test set of Chinese and Czech. The bold numbers indicate the current best scores.
- GNNSDP(GCN) with only one GCN layer still performs better than the biaffine parser, demonstrating that higher-order information is beneficial for improving SDP.
- The performance of GNNSDP(GCN) is gradually improved when the number of GCN layers is increased, demonstrating that stacking more GNN layers is able to capture better higher-order information.
5.3. Case Study
We provide a parsing example to show why GNNSDP benefits from higher-order information. Figure 4 shows the parsing results of the biaffine parser (Figure 4a) and GNNSDP(GCN) (Figure 4b) for the English sentence (sent_id = 40504035, in OOD of PSD formalism) “There is never enough corn, peas or strawberries”. Both parsers are trained in the basic embedding settings.
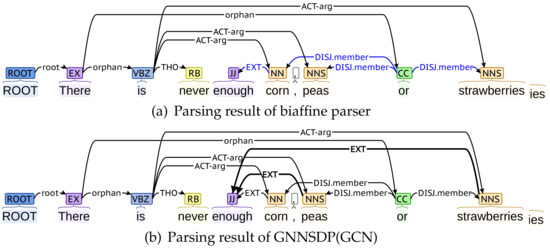
Figure 4.
Parsing results of the biaffine parser and GNNSDP, for the sentence (sent_id = 40504035 in OOD of PSD formalism). Some irrelevant dependency edges are hidden.
In the gold annotation, three words corn, peas, and strawberries are three members of the disjunctive word or. In addition, the word enough has three dependency edges labeled EXT with them. In the results of the biaffine parser, only the dependency edge between enough and corn is identified; the remaining two are not. In GNNSDP(GCN), given the initial SDG predicted by the biaffine parser, the words corn, peas, and strawberries aggregate the higher-order information of or and is (first-order), there (second-order), and ROOT (third-order). The word enough aggregates the higher-order information of the corn (first-order), is and or (second-order), there (third-order), and ROOT (fourth-order). The dependent word enough and three head words corn, peas, and strawberries aggregate information of four common words (ROOT, There, is and or). Therefore, the representations of them with higher-order information bring more evidence into decoders’ final decisions. As a result, it is effortless for GNNSDP to identify that there are also two dependency edges labeled EXT between the dependent word enough and the head words peas and strawberries.
6. Conclusions
This paper aims to exploit GNNs’ powerful ability of representation learning in SDP. GNNs are utilized to encode higher-order information to improve the accuracy of semantic dependency parsing. Experiments are conducted on the SemEval 2015 Task 18 dataset in three languages (Chinese, English, and Czech). Compared to the previous state-of-the-art parser, our parser yields 0.3% and 2.2% improvement in the average labeled F1-score on English in-domain (ID) and out-of-domain (OOD) test sets, 2.6% improvement on Chinese ID test set, and 2.0% and 1.8% improvement on the Czech ID and OOD test sets. Experimental results show that our parser outperforms the previous best one on the SemEval 2015 Task 18 dataset in three languages. In addition, our parser shows greater advantage in longer sentence and complex semantic formalism. Outstanding performances of our parser demonstrates that higher-order information encoded by GNNs is exceedingly beneficial for improving SDP.
Despite that significant improvement has been made, the initial graph structure output by the vanilla parser may be noisy, resulting in a performance penalty to some extent. In the future, we would like to apply graph structure learning models to jointly learn graph structure and graph representation, rather than depending on the initial dependency graph output by the vanilla parser.
Author Contributions
Conceptualization, B.L. and Z.G.; Methodology, B.L. and Y.F.; Writing—original draft, B.L.; Writing—review & editing, Y.F., Y.S., Z.G. and Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research is sponsored by the Foundation of Jiangsu Provincial Double-Innovation Doctor Program (Grant No. JSSCBS20210507) and NUPTSF (Grant No. NY220176).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Our experiment is conducted on SemEval 2015 Task 18 dataset [35]. The description of this dataset is shown in https://alt.qcri.org/semeval2015/task18/ (accessed on 7 May 2021). Trial data has been provided in https://alt.qcri.org/semeval2015/task18/index.php?id=data-and-tools (accessed on 7 May 2021), full data is available in LDC official site https://catalog.ldc.upenn.edu/LDC2016T10 (accessed on 7 May 2021).
Acknowledgments
Our code extends this github repository https://github.com/yzhangcs/parser (accessed on 15 October 2021), thanks to it very much.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| SDP | Semantic Dependency Parsing |
| SDG | Semantic Dependency Graph |
| GNNs | Graph Neural Networks |
| GCN | Graph Convolutional Network |
| GAT | Graph Attention Network |
| DM | DELPH-IN MRS |
| PAS | Predicate-Argument Structure |
| PSD | Prague Semantic Dependencies |
| BERT | Bidirectional Encoder Representation from Transformers |
| BiLSTM | Bidirectional Long Short-Term Memory Networks |
| MLP | Multi-Layer Perceptron |
References
- Sun, X.; Zhou, J.; Wang, S.; Li, X.; Zheng, B.; Liu, D. Linguistic Dependency Guided Graph Convolutional Networks for Named Entity Recognition. In International Conference on Advanced Data Mining and Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 237–248. [Google Scholar]
- Ali, S.; Mousa, H.; Hussien, M. A Review of Open Information Extraction Techniques. IJCI Int. J. Comput. Inf. 2019, 6, 20–28. [Google Scholar] [CrossRef][Green Version]
- Zhang, M. A survey of syntactic-semantic parsing based on constituent and dependency structures. Sci. China Technol. Sci. 2020, 63, 1898–1920. [Google Scholar] [CrossRef]
- Barnes, J.; Kurtz, R.; Oepen, S.; Øvrelid, L.; Velldal, E. Structured sentiment analysis as dependency graph parsing. arXiv 2021, arXiv:2105.14504. [Google Scholar]
- Anuranjana, K.; Rao, V.A.; Mamidi, R. Hindi question generation using dependency structures. arXiv 2019, arXiv:1906.08570. [Google Scholar]
- Fu, B.; Qiu, Y.; Tang, C.; Li, Y.; Yu, H.; Sun, J. A survey on complex question answering over knowledge base: Recent advances and challenges. arXiv 2020, arXiv:2007.13069. [Google Scholar]
- Ji, T.; Wu, Y.; Lan, M. Graph-based dependency parsing with graph neural networks. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 2475–2485. [Google Scholar]
- Wang, X.; Huang, J.; Tu, K. Second-Order Semantic Dependency Parsing with End-to-End Neural Networks. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 4609–4618. [Google Scholar]
- Zhang, Y.; Li, Z.; Zhang, M. Efficient Second-Order TreeCRF for Neural Dependency Parsing. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 3295–3305. [Google Scholar]
- Du, Y.; Zhang, F.; Zhang, X.; Sun, W.; Wan, X. Peking: Building semantic dependency graphs with a hybrid parser. In Proceedings of the 9th International workshop on Semantic Evaluation (Semeval 2015), Denver, CO, USA, 4–5 June 2015; pp. 927–931. [Google Scholar]
- Peng, H.; Thomson, S.; Smith, N.A. Deep multitask learning for semantic dependency parsing. arXiv 2017, arXiv:1704.06855. [Google Scholar]
- Dozat, T.; Manning, C.D. Simpler but More Accurate Semantic Dependency Parsing. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), Melbourne, Australia, 15–20 July 2018; pp. 484–490. [Google Scholar]
- Wang, Y.; Che, W.; Guo, J.; Liu, T. A neural transition-based approach for semantic dependency graph parsing. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Fernández-González, D.; Gómez-Rodríguez, C. Transition-based semantic dependency parsing with pointer networks. arXiv 2020, arXiv:2005.13344. [Google Scholar]
- Martins, A.F.; Almeida, M.S. Priberam: A turbo semantic parser with second order features. In Proceedings of the 8th International Workshop on Semantic Evaluation (SemEval 2014), Dublin, UK, 23–24 August 2014; pp. 471–476. [Google Scholar]
- Cao, J.; Huang, S.; Sun, W.; Wan, X. Quasi-second-order parsing for 1-endpoint-crossing, pagenumber-2 graphs. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 7–11 September 2017; pp. 24–34. [Google Scholar]
- Carreras, X. Experiments with a higher-order projective dependency parser. In Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning (EMNLP-CoNLL), Prague, Czech Republic, 28–30 June 2007; pp. 957–961. [Google Scholar]
- Koo, T.; Collins, M. Efficient third-order dependency parsers. In Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics, Uppsala, Sweden, 11–16 July 2010; pp. 1–11. [Google Scholar]
- Ma, X.; Zhao, H. Fourth-order dependency parsing. In Proceedings of the 24th International Conference on Computational Linguistics, Mumbai, India, 8–15 December 2012; pp. 785–796. [Google Scholar]
- Marcheggiani, D.; Titov, I. Encoding sentences with graph convolutional networks for semantic role labeling. arXiv 2017, arXiv:1703.04826. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- McDonald, R.; Pereira, F. Online learning of approximate dependency parsing algorithms. In Proceedings of the 11th Conference of the European Chapter of the Association for Computational Linguistics, Trento, Italy, 19–23 April 2006; pp. 81–88. [Google Scholar]
- Lindemann, M.; Groschwitz, J.; Koller, A. Fast semantic parsing with well-typedness guarantees. arXiv 2020, arXiv:2009.07365. [Google Scholar]
- Dozat, T.; Qi, P.; Manning, C.D. Stanford’s graph-based neural dependency parser at the conll 2017 shared task. In Proceedings of the CoNLL 2017 Shared Task: Multilingual Parsing from Raw Text to Universal Dependencies, Vancouver, BC, Canada, 3–4 August 2017; pp. 20–30. [Google Scholar]
- Kurita, S.; Søgaard, A. Multi-task semantic dependency parsing with policy gradient for learning easy-first strategies. arXiv 2019, arXiv:1906.01239. [Google Scholar]
- Jia, Z.; Ma, Y.; Cai, J.; Tu, K. Semi-supervised semantic dependency parsing using CRF autoencoders. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 6795–6805. [Google Scholar]
- He, H.; Choi, J. Establishing strong baselines for the new decade: Sequence tagging, syntactic and semantic parsing with BERT. In Proceedings of the Thirty-Third International Flairs Conference, North Miami Beach, FL, USA, 17–18 May 2020. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 3844–3852. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Li, S.; Zhao, Z.; Hu, R.; Li, W.; Liu, T.; Du, X. Analogical Reasoning on Chinese Morphological and Semantic Relations. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), Melbourne, Australia, 15–20 July 2018; pp. 138–143. [Google Scholar]
- Grave, E.; Bojanowski, P.; Gupta, P.; Joulin, A.; Mikolov, T. Learning Word Vectors for 157 Languages. In Proceedings of the International Conference on Language Resources and Evaluation (LREC 2018), Miyazaki, Japan, 7–12 May 2018. [Google Scholar]
- Oepen, S.; Kuhlmann, M.; Miyao, Y.; Zeman, D.; Cinková, S.; Flickinger, D.; Hajic, J.; Uresova, Z. Semeval 2015 task 18: Broad-coverage semantic dependency parsing. In Proceedings of the 9th International Workshop on Semantic Evaluation (SemEval 2015), Denver, CO, USA, 4–5 June 2015; pp. 915–926. [Google Scholar]
- Flickinger, D.; Zhang, Y.; Kordoni, V. DeepBank. A dynamically annotated treebank of the Wall Street Journal. In Proceedings of the 11th International Workshop on Treebanks and Linguistic Theories, Lisbon, Portugal, 30 November–1 December 2012; pp. 85–96. [Google Scholar]
- Miyao, Y.; Tsujii, J. Deep linguistic analysis for the accurate identification of predicate-argument relations. In Proceedings of the COLING 2004: Proceedings of the 20th International Conference on Computational Linguistics, Geneva, Switzerland, 23–27 August 2004; pp. 1392–1398. [Google Scholar]
- Hajic, J.; Hajicová, E.; Panevová, J.; Sgall, P.; Bojar, O.; Cinková, S.; Fucíková, E.; Mikulová, M.; Pajas, P.; Popelka, J.; et al. Announcing prague czech-english dependency treebank 2.0. In Proceedings of the Eighth International Conference on Language Resources and Evaluation (LREC’12), Istanbul, Turkey, 21–27 May 2012; pp. 3153–3160. [Google Scholar]
- Almeida, M.S.; Martins, A.F. Lisbon: Evaluating Turbo Semantic Parser on multiple languages and out-of-domain data. In Proceedings of the 9th International Workshop on Semantic Evaluation (SemEval 2015), Denver, CO, USA, 4–5 June 2015; pp. 970–973. [Google Scholar]
- Marcus, M.; Santorini, B.; Marcinkiewicz, M.A. Building a large annotated corpus of English: The Penn Treebank. In Using Large Corpora; MIT Press: Cambridge, MA, USA, 1993; Volume 273. [Google Scholar]
- Francis, W.N.; Kucera, H. Frequency Analysis of English Usage: Lexicon and Usage; Houghton Mifflin: Boston, MA, USA, 1982. [Google Scholar]
- Kanerva, J.; Luotolahti, J.; Ginter, F. Turku: Semantic dependency parsing as a sequence classification. In Proceedings of the 9th International Workshop on Semantic Evaluation (SemEval 2015), Denver, CO, USA, 4–5 June 2015; pp. 965–969. [Google Scholar]
- Barzdins, G.; Paikens, P.; Gosko, D. Riga: From FrameNet to Semantic Frames with C6. 0 Rules. In Proceedings of the 9th International Workshop on Semantic Evaluation (SemEval 2015), Denver, CO, USA, 4–5 June 2015; pp. 960–964. [Google Scholar]
- Lindemann, M.; Groschwitz, J.; Koller, A. Compositional semantic parsing across graphbanks. arXiv 2019, arXiv:1906.11746. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).