Design of Third-Order Dispersion Compensation for the SG PW Laser System Using a Birefringent Crystal
Abstract
:1. Introduction
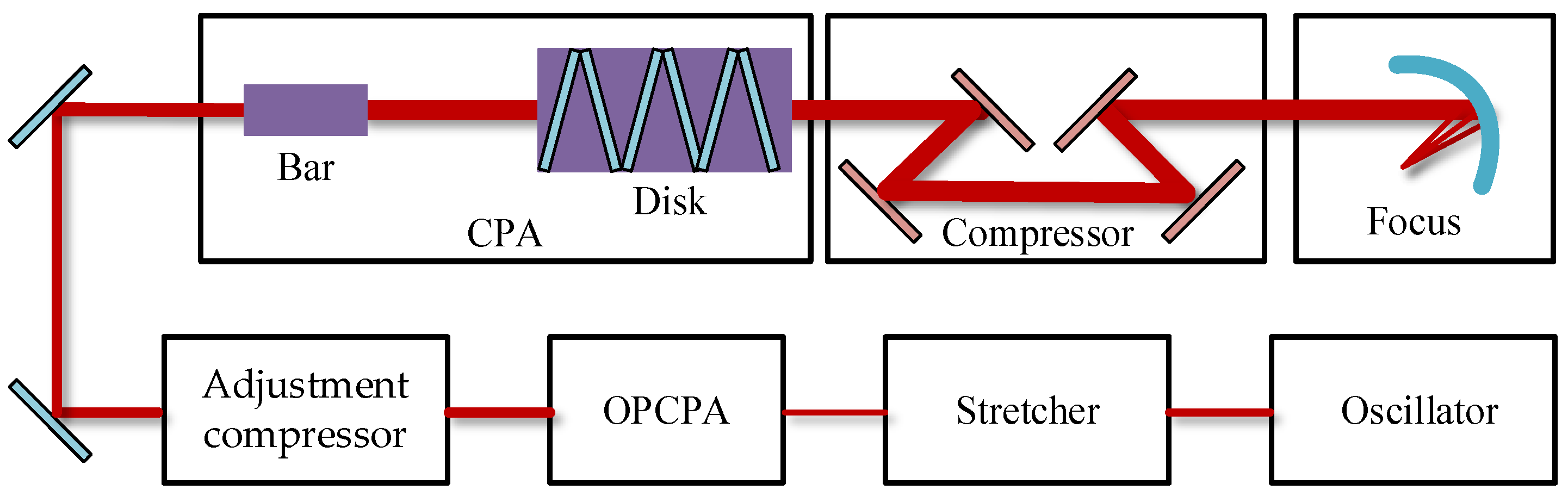
2. Numerical Method
3. Results and Discussion
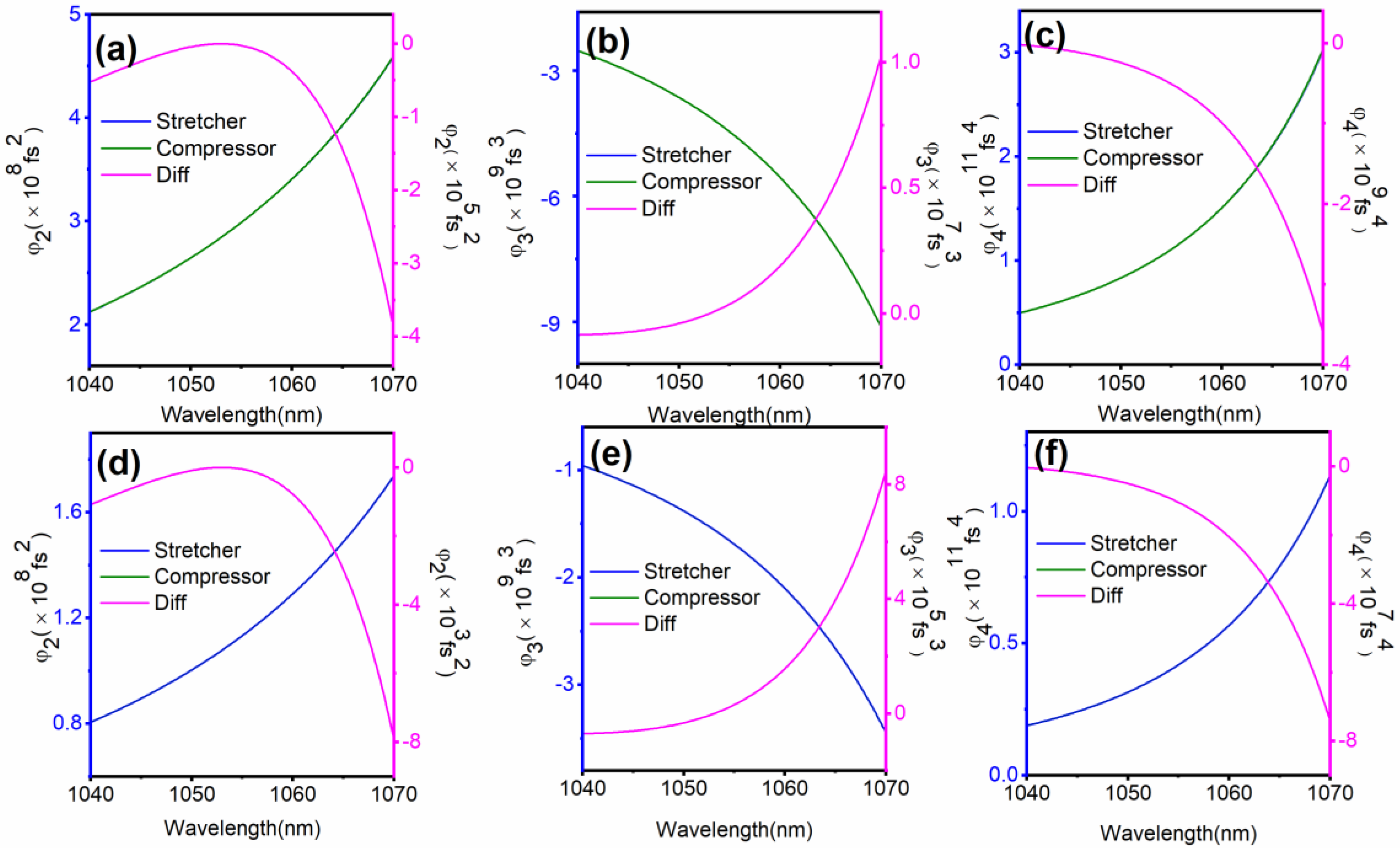
3.1. Residual TOD and FOD and Influence on the Multi-PW Design
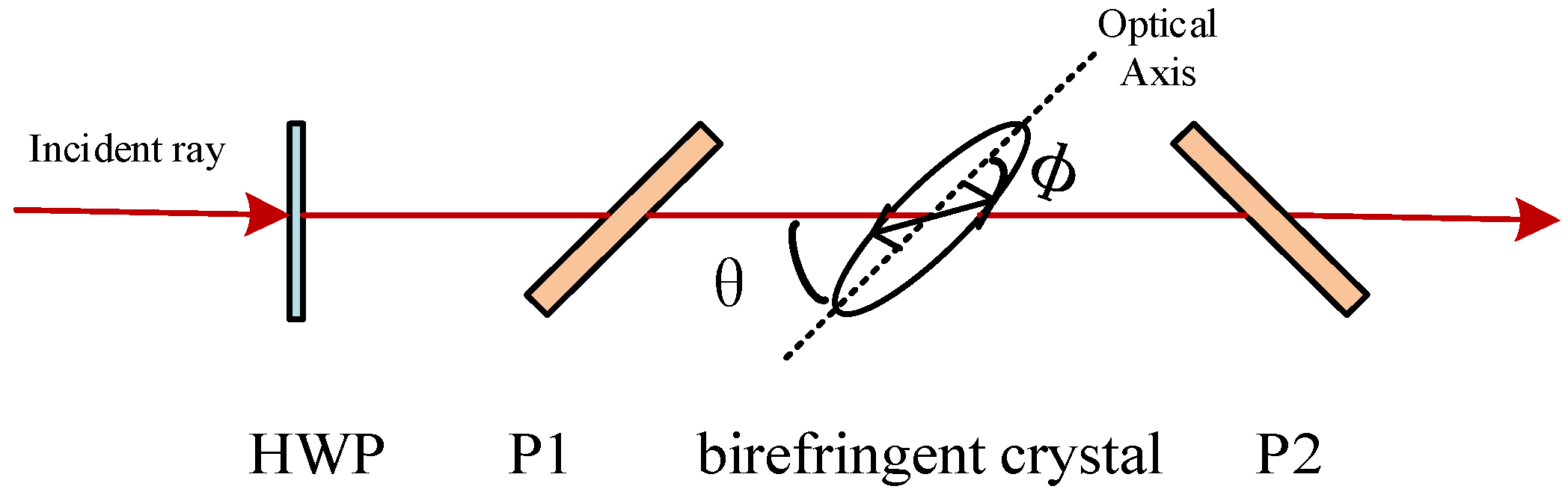
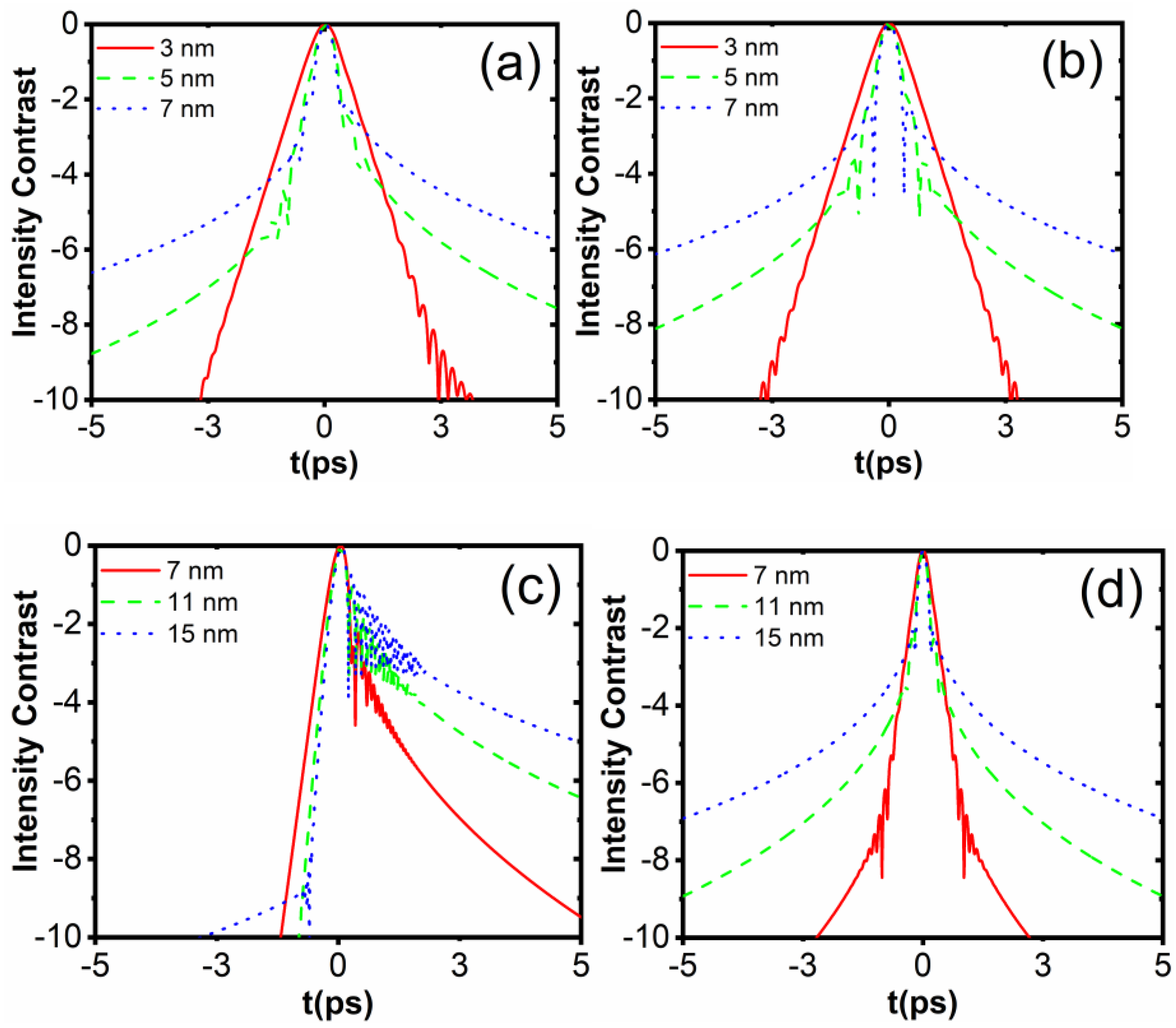
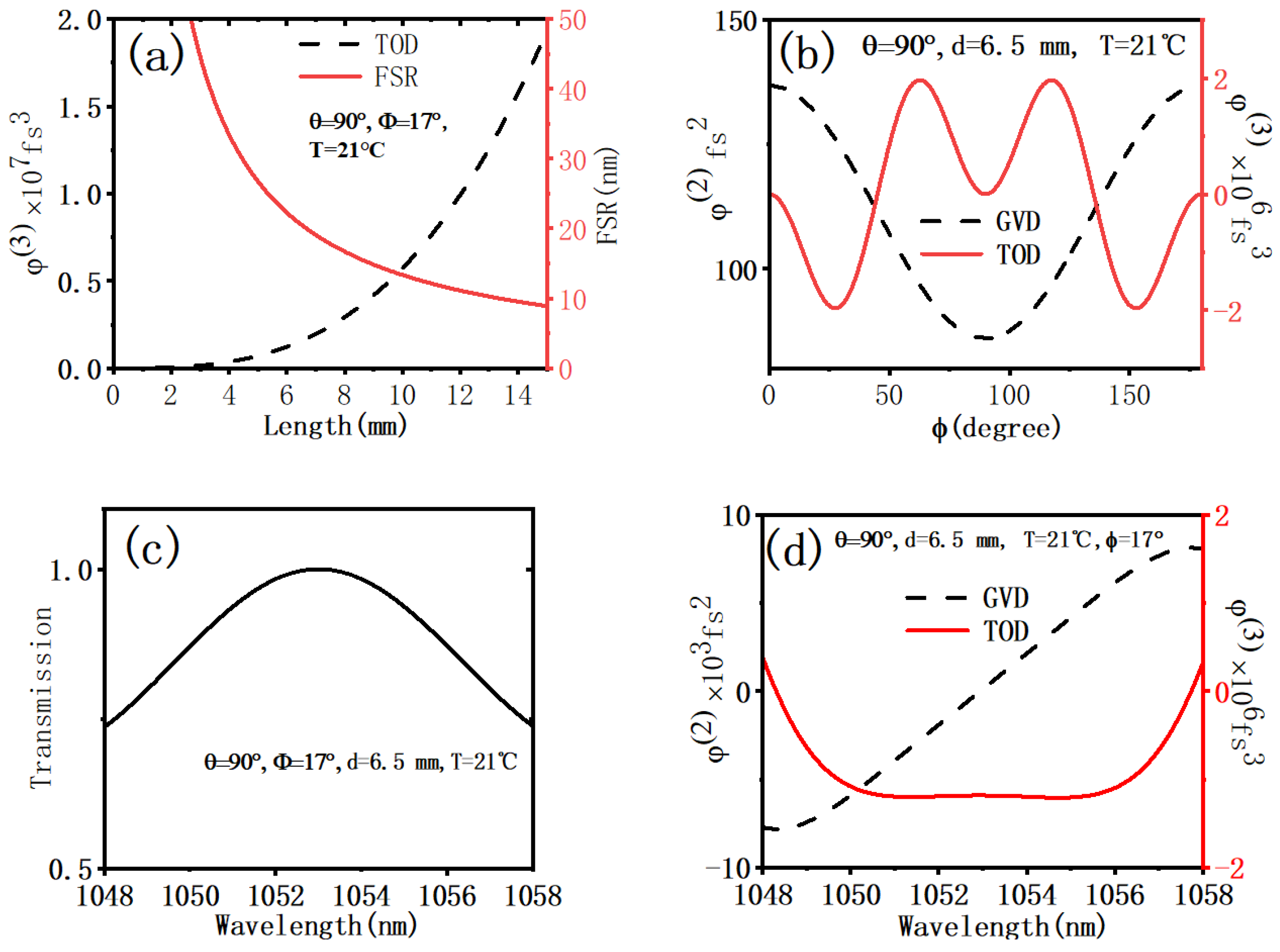
3.2. Design of TOD Compensation Using the Birefringent Plate
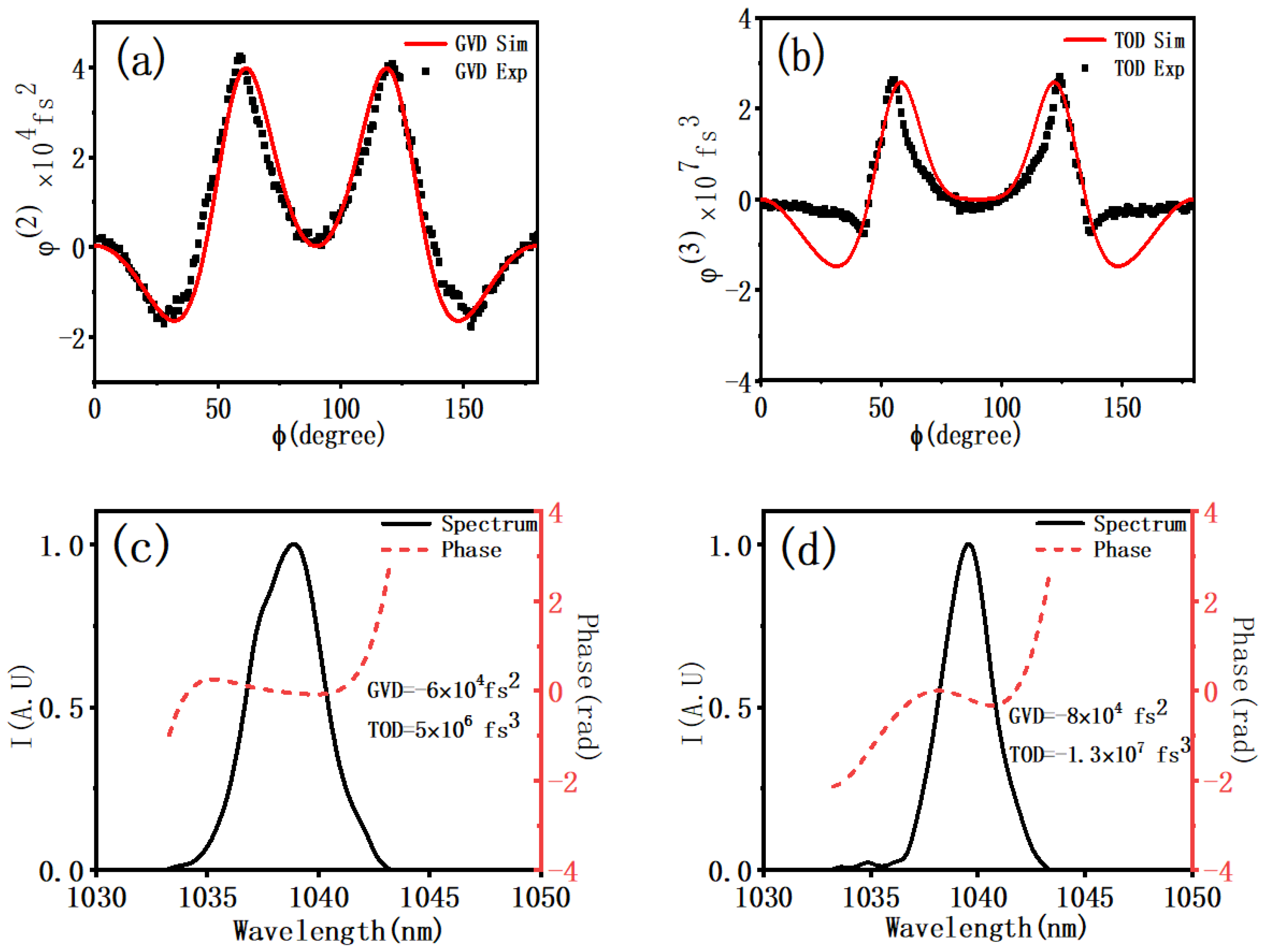
3.3. Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moses, E.I.; Lindl, J.D.; Spaeth, M.L.; Patterson, R.W.; Sawicki, R.H.; Atherton, L.J.; Baisden, P.A.; Lagin, L.J.; Larson, D.W.; MacGowan, B.J.; et al. Overview: Development of the National Ignition Facility and the Transition to a User Facility for the Ignition Campaign and High Energy Density Scientific Research. Fusion Sci. Technol. 2017, 69, 1–24. [Google Scholar] [CrossRef]
- Galletti, M.; Oliveira, P.; Galimberti, M.; Ahmad, M.; Archipovaite, G.; Booth, N.; Dilworth, E.; Frackiewicz, A.; Winstone, T.; Musgrave, I.; et al. Ultra-broadband all-OPCPA petawatt facility fully based on LBO. High Power Laser Sci. Eng. 2020, 8, e31. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.M.; Yang, X.H.; Wu, D.; Ma, Y.Y.; Jiao, J.L.; Zhang, Z.; Wu, F.Y.; Yuan, X.H.; Li, Y.T.; et al. Double-cone ignition scheme for inertial confinement fusion. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2020, 378, 20200015. [Google Scholar] [CrossRef] [PubMed]
- Mariscal, D.; Ma, T.; Wilks, S.C.; Kemp, A.J.; Williams, G.J.; Michel, P.; Chen, H.; Patel, P.K.; Remington, B.A.; Bowers, M.; et al. First demonstration of ARC-accelerated proton beams at the National Ignition Facility. Phys. Plasmas 2019, 26, 43110. [Google Scholar] [CrossRef]
- Hornung, J.; Zobus, Y.; Boller, P.; Brabetz, C.; Eisenbarth, U.; Kuhl, T.; Major, Z.; Ohland, J.B.; Zepf, M.; Zielbauer, B.; et al. Enhancement of the laser-driven proton source at PHELIX. High Power Laser Sci. Eng. 2020, 8, e24. [Google Scholar] [CrossRef]
- Li, Z.; Rao, D.; Leng, Y.; Chen, L.; Dai, Y. Third-order dispersion compensation for petawatt-level lasers employing object-image-grating self-tiling. Quantum Electron. 2015, 45, 891. [Google Scholar]
- Zaouter, Y.; Papadopoulos, D.N.; Hanna, M.; Druon, F.; Cormier, E.; Georges, P. Third-order spectral phase compensation in parabolic pulse compression. Opt. Express 2007, 15, 9372. [Google Scholar] [CrossRef]
- Marhic, M.E.; Kagi, N.; Chiang, T.K.; Kazovsky, L.G. Cancellation of third-order nonlinear effects in amplified fiber links by dispersion compensation, phase conjugation, and alternating dispersion. Opt. Lett. 1995, 20, 863. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Liu, X. Mutual compensation of the higher-order nonlinearity and the third-order dispersion. Phys. Lett. A 1997, 225, 67. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, X.; Cai, Y.; Hu, W.; Zhang, Z. Residual third-order dispersion compensation in femtosecond pulses transmission using a phase modulator. In Proceedings of the Optical Transmission, Switching, and Subsystems VI, Hangzhou, China, 26–30 October 2008; Volume 7136. [Google Scholar]
- Niu, H.L.; Shen, W.D.; Li, C.S.; Zhang, Y.G.; Xie, C.; Yu, P.; Yuan, W.J.; Liu, B.W.; Hu, M.L.; Wang, Q.Y.; et al. Dispersive mirrors for high third-order dispersion compensation in femtosecond amplification fiber laser system. Appl. Phys. B 2012, 108, 609. [Google Scholar] [CrossRef]
- Kane, S.; Squier, J. Grating Compensation of Third-Order Material Dispersion in the Normal Dispersion Regime: Sub- 100-fs Chirped-Pulse Amplification Using a Fiber Stretcher and Grating-Pair Compressor. IEEE JQE 1995, 31, 2052. [Google Scholar] [CrossRef]
- Yang, Q.; Xie, X.; Kang, J.; Zhu, H.; Guo, A.; Gao, Q. Independent and continuous third-order dispersion compensation using a pair of prisms. High Power Laser Sci. Eng. 2014, 2, e38. [Google Scholar] [CrossRef] [Green Version]
- Verluise, F.; Laude, V.; Cheng, Z.; Spielmann, C.; Tournois, P. Amplitude and phase control of ultrashort pulses by use of an acousto-optic programmable dispersive filter: Pulse compression and shaping. Opt. Lett. 2000, 25, 575. [Google Scholar] [CrossRef] [PubMed]
- Lureau, F.; Matras, G.; Chalus, O.; Derycke, C.; Morbieu, T.; Radier, C.; Casagrande, O.; Laux, S.; Ricaud, S.; Rey, G.; et al. High-energy hybrid femtosecond laser system demonstrating 2 × 10 PW capability. High Power Laser Sci. Eng. 2020, 8, 8. [Google Scholar] [CrossRef]
- Tsuda, H.; Okamoto, K.; Ishii, T.; Naganuma, K.; Inoue, Y.; Takenouchi, H.; Kurokawa, T. Second- and third-order dispersion compensator using a high-resolution arrayed-waveguide grating. IEEE Photonics Technol. Lett. 1999, 11, 569. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, J.; Li, X.; Zhu, B.; Ma, W.; Lu, X.; Fan, W.; Liu, Z.; Zhou, S.; Xu, G.; et al. Status and development of high-power laser facilities at the NLHPLP. High Power Laser Sci. 2018, 6, 6. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.; Wang, T.; Li, Z.; Dai, Y.; Lin, Z.; Gu, Y.; Zhu, J. 1 kJ Petawatt Laser System for SG-II-U Program. Rev. Laser Eng. 2008, 36, 1172. [Google Scholar] [CrossRef] [Green Version]
- Gaul, E.; Cheriaux, G.; Antipenkov, R.; Batysta, F.; Borger, T.; Friedman, G.; Greene, J.T.; Hammond, D.; Heisler, J.; Hidinger, D.; et al. Hybrid OPCPA/Glass 10 PW laser at 1 shot a minute. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 13–18 May 2018. [Google Scholar]
- Gaul, E.W.; Martinez, M.; Blakeney, J.; Jochmann, A.; Ringuette, M.; Hammond, D.; Borger, T.; Escamilla, R.; Douglas, S.; Henderson, W.; et al. Demonstration of a 1.1 petawatt laser based on a hybrid optical parametric chirped pulse amplification/mixed Nd:glass amplifier. Appl. Opt. 2010, 49, 1676. [Google Scholar] [CrossRef] [PubMed]
- Cheriaux, G.; Antipenkov, R.; Batysta, F.; Borger, T.; Friedman, G.; Greene, J.T.; Hammond, D.; Heisler, J.; Jochmann, A.; Kepler, M.; et al. Progress on ELI-Beamlines 10 PW Laser System. Rev. Laser Eng. 2018, 46, 125. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, Y.; Sun, D.; Chai, L.; Sun, H.; Wang, C. Compact and material-dispersion-compatible Offner stretcher for chirped pulse amplifications. Opt. Commun. 2002, 206, 7. [Google Scholar] [CrossRef]
- Heebner, J.E.; Acree, R.J.; Alessi, D.A.; Barnes, A.I.; Bowers, M.W.; Browning, D.F.; Budge, T.S.; Burns, S.; Chang, L.S.; Christensen, K.S.; et al. Injection laser system for Advanced Radiographic Capability using chirped pulse amplification on the National Ignition Facility. Appl. Opt. 2019, 58, 8501. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Li, D.; Wang, T.; Cui, Y.; Zhang, T.; Wang, L.; Zhang, J.; Xu, G. Spectral shaping of picosecond petawatt laser system based on lithium niobate birefringent crystal. Acta Phys. Sin. 2021, 70, 084202. [Google Scholar] [CrossRef]
- Preuss, D.R.; Gole, J.L. Three-stage birefringent filter tuning smoothly over the visible region: Theoretical treatment and experimental design. Appl. Opt. 1980, 19, 702. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X. Explicit Jones transformation matrix for a tilted birefringent plate with its optic axis parallel to the plate surface. Appl. Opt. 1994, 33, 3502. [Google Scholar] [CrossRef]
- Burneau, A.; Humbert, B. Temperature effect on a tilted birefringent filter in a tunable laser: A limitation for Raman spectroscopy. J. Appl. Phys. 1989, 66, 5702. [Google Scholar] [CrossRef]
- Batysta, F.; Antipenkov, R.; Borger, T.; Kissinger, A.; Green, J.T.; Kananavicius, R.; Cheriaux, G.; Hidinger, D.; Kolenda, J.; Gaul, E.; et al. Spectral pulse shaping of a 5 Hz, multi-joule, broadband optical parametric chirped pulse amplification frontend for a 10 PW laser system. Opt. Lett. 2018, 43, 3866. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, H. Calculation and evaluation of dispersions in a femtosecond pulse amplification system. Acta Phys. Sin. 2001, 50, 1080. [Google Scholar] [CrossRef]
- Tian, J.; Sun, J.; Wei, Z.; Wang, Z.; Ling, W.; Huang, X.; Liu, L.; Wei, X.; Zhang, J. Theoretical and experimental studies on large-ratio stretching of femtosecond pulse with Offner triplet stretcher. Acta Phys. Sin. 2005, 54, 1200. [Google Scholar] [CrossRef]
- Treacy, E. Optical pulse compression with diffraction gratings. IEEE JQE 1969, 5, 454. [Google Scholar] [CrossRef]
- Liu, X.; Wang, C.; Wang, X.; Lu, X.; Bai, P.; Liu, Y.; Li, Y.; Liu, K.; Yu, L.; Leng, Y.; et al. Dispersion Management in 10-PW Laser Front End. Optics 2020, 1, 191–201. [Google Scholar] [CrossRef]
- Brown, M. Increased spectral bandwidths in nonlinear conversion processes by use of multicrystal designs. Opt. Lett. 1998, 23, 1591. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Wang, T.; Yin, X.; Li, J.; Yu, H.; Wang, L.; Lu, X.; Xu, G. Design of Third-Order Dispersion Compensation for the SG PW Laser System Using a Birefringent Crystal. Appl. Sci. 2022, 12, 4078. https://doi.org/10.3390/app12084078
Li D, Wang T, Yin X, Li J, Yu H, Wang L, Lu X, Xu G. Design of Third-Order Dispersion Compensation for the SG PW Laser System Using a Birefringent Crystal. Applied Sciences. 2022; 12(8):4078. https://doi.org/10.3390/app12084078
Chicago/Turabian StyleLi, Dawei, Tao Wang, Xiaolei Yin, Jiamei Li, Hui Yu, Li Wang, Xingqiang Lu, and Guang Xu. 2022. "Design of Third-Order Dispersion Compensation for the SG PW Laser System Using a Birefringent Crystal" Applied Sciences 12, no. 8: 4078. https://doi.org/10.3390/app12084078
APA StyleLi, D., Wang, T., Yin, X., Li, J., Yu, H., Wang, L., Lu, X., & Xu, G. (2022). Design of Third-Order Dispersion Compensation for the SG PW Laser System Using a Birefringent Crystal. Applied Sciences, 12(8), 4078. https://doi.org/10.3390/app12084078




