Translation-Based Embeddings with Octonion for Knowledge Graph Completion
Abstract
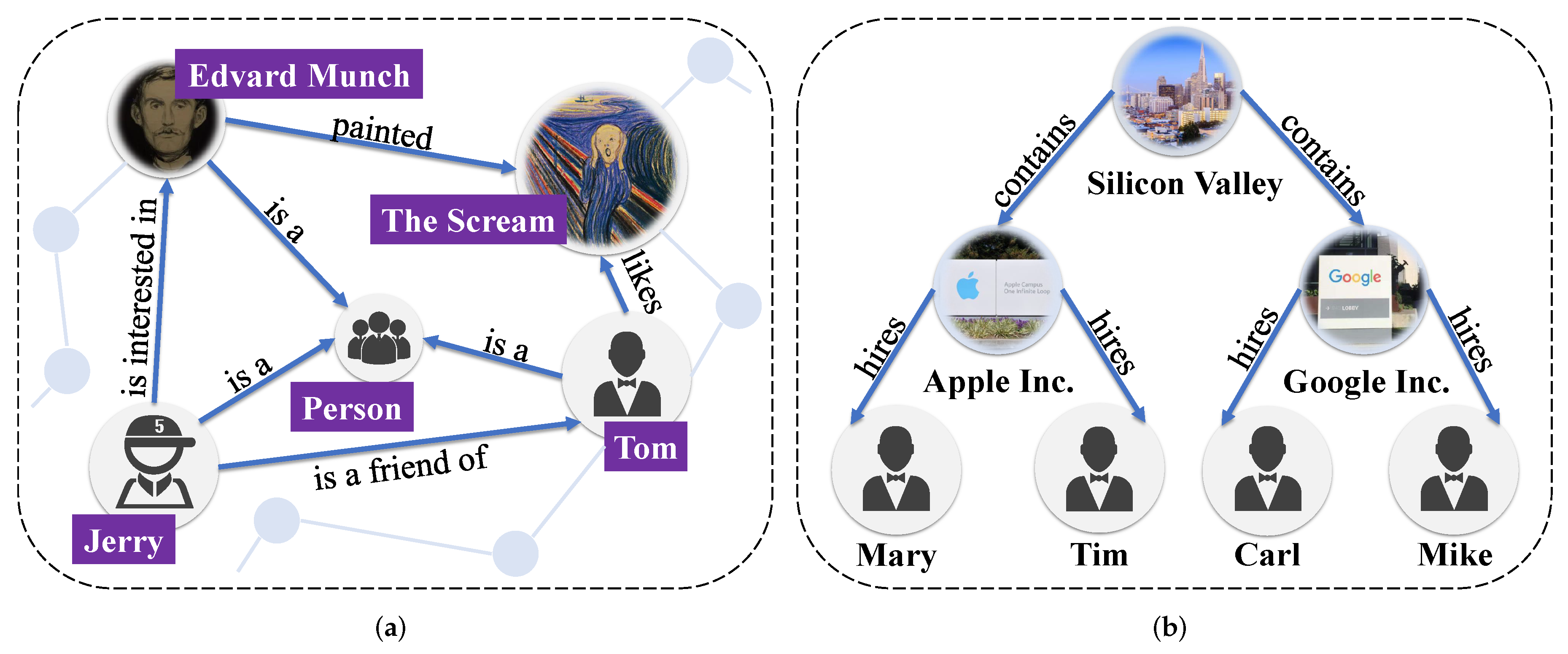
1. Introduction
- Using the mathematical theories of octonion in the field of linear algebra, we propose to introduce octonion into the translation-based KGC method for the first time, which maintains the light weight and high efficiency of the translation-based KGC framework. We realize the compact interaction between entities and relations depending on the multiplication with grouping rules between octonion matrices and vectors, which fully exploits the internal correlations and dependencies of the octonion structure, and enhances the capability to model latent dependencies in KGs.
- We attempt to transfer our model from Euclidean space to hyperbolic Poincaré space, transforming the octonion coordinate vectors into hyperbolic embeddings and integrating the Euclidean-based translation thoughts into hyperbolic space. On the premise of maintaining the processing superiority of octonion on latent dependencies, we further enhance the modeling capability to hierarchical data in KGs.
- We analyze and confirm that our models are superior to the previous approaches on the standard benchmark datasets WN18, WN18RR, and FB15k-237. By ablation experiments, we analyze the performance of our models on (1) different types of relations and (2) different dimensions, demonstrating (1) the advantages of octonion and hyperbolic geometry in KGC tasks and (2) the respective suitable application scenarios.
2. Related Work
2.1. Translation-Based Methods
2.2. Semantics-Based Methods
2.3. Neural Network-Based Methods
3. Methodology
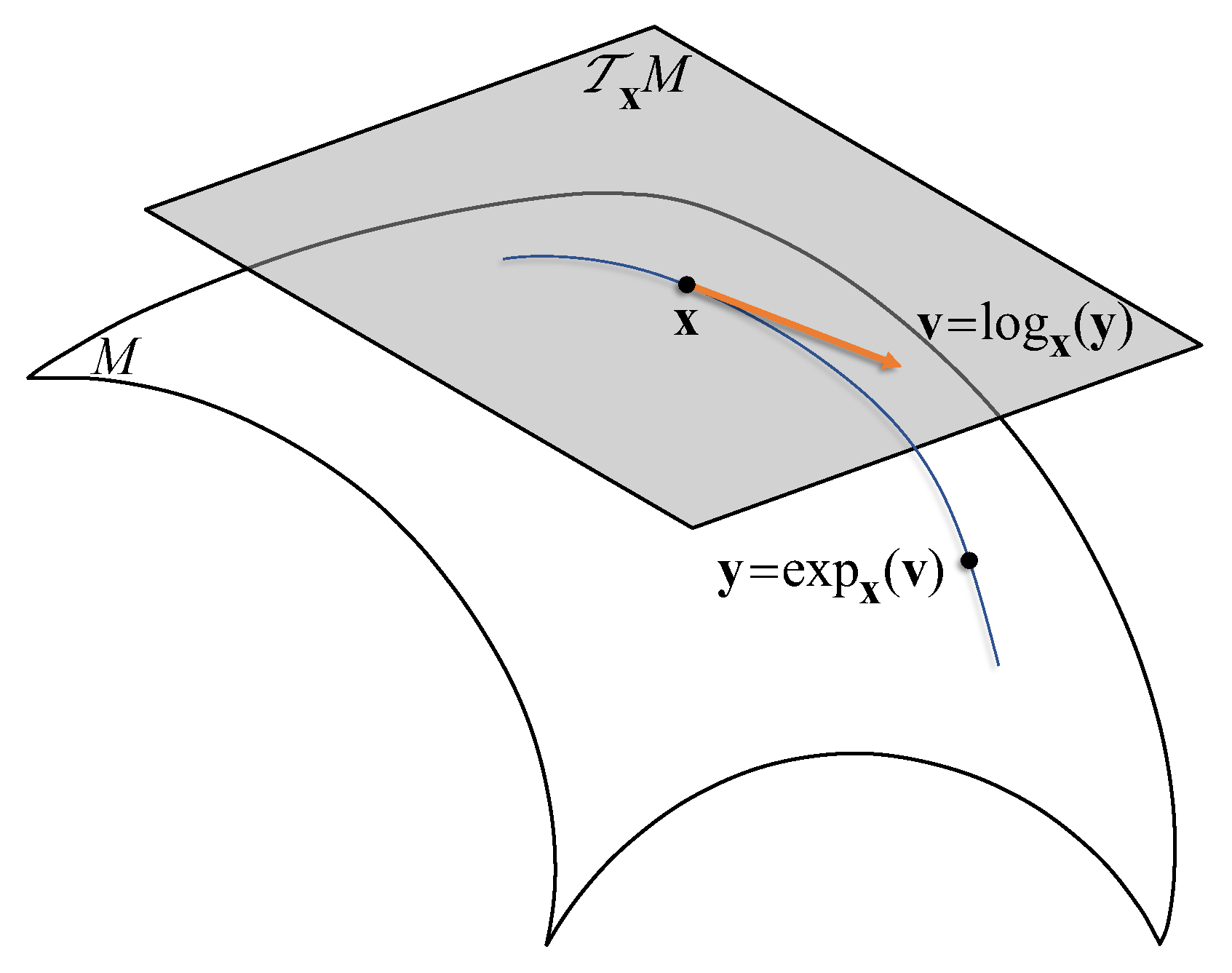
3.1. Preliminaries
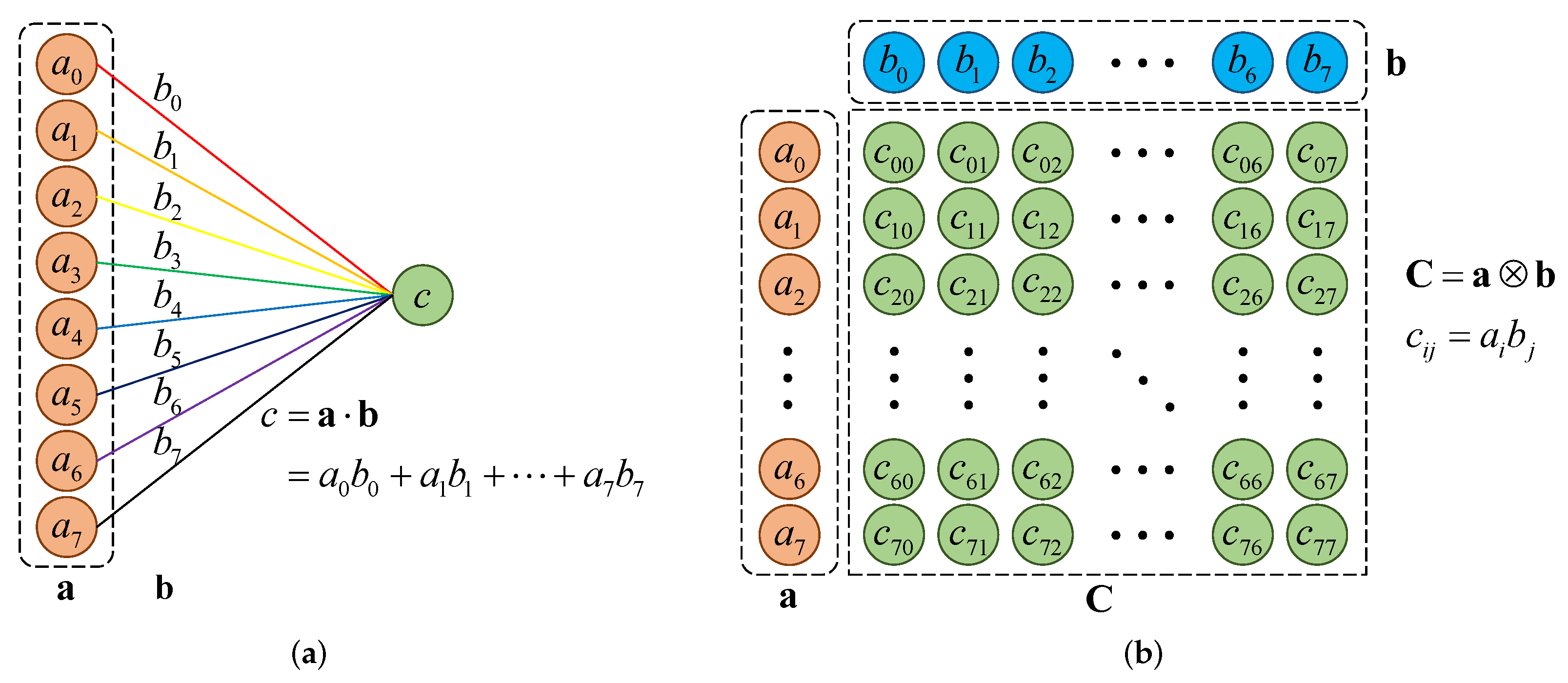
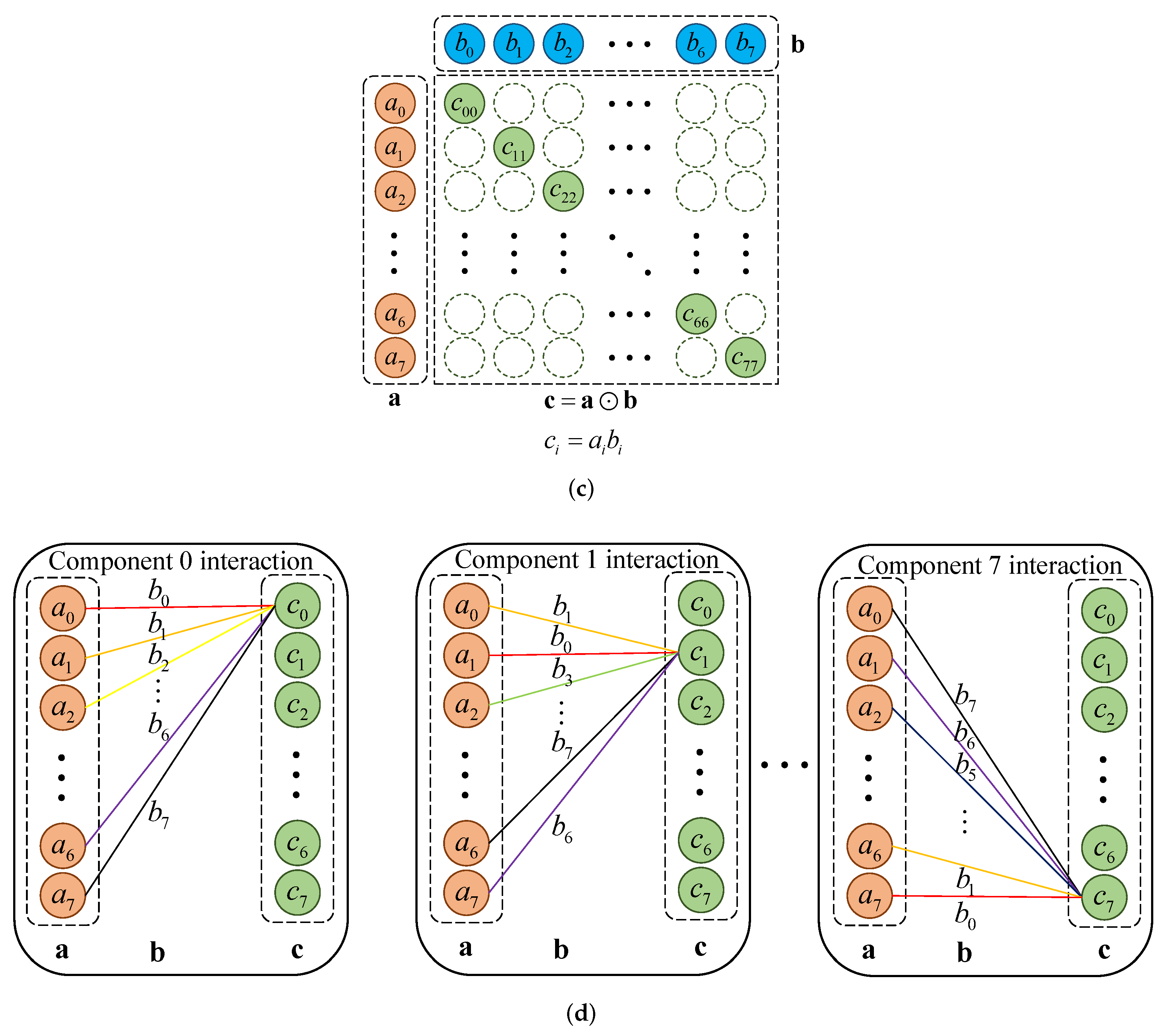
3.1.1. Background and Calculation Rules of Octonion
- As the generalized form of complex number and quaternion, octonion is the only normed division algebra except real number, complex number, and quaternion [36], which can define norm and multiplicative inverse, and can also perform inner product operation, with rich algebraic definitions.
- In geometric space, octonions can represent the combination of rotation and translation [37], which has good geometric significance, while the quaternion, which is also one of the hypercomplex numbers, can only represent rotation. Consequently, compared with the complex number and quaternion, octonion has higher degrees of freedom and more flexible expressive capability.
- The representation of octonion has internal correlations and dependencies among its constituent elements [38]. On the premise of not increasing the amount of parameters, octonion can add additional information capacity and interactive features to the graph data. When performing mathematical operations, octonion can encourage the compact interaction between the objects being calculated.
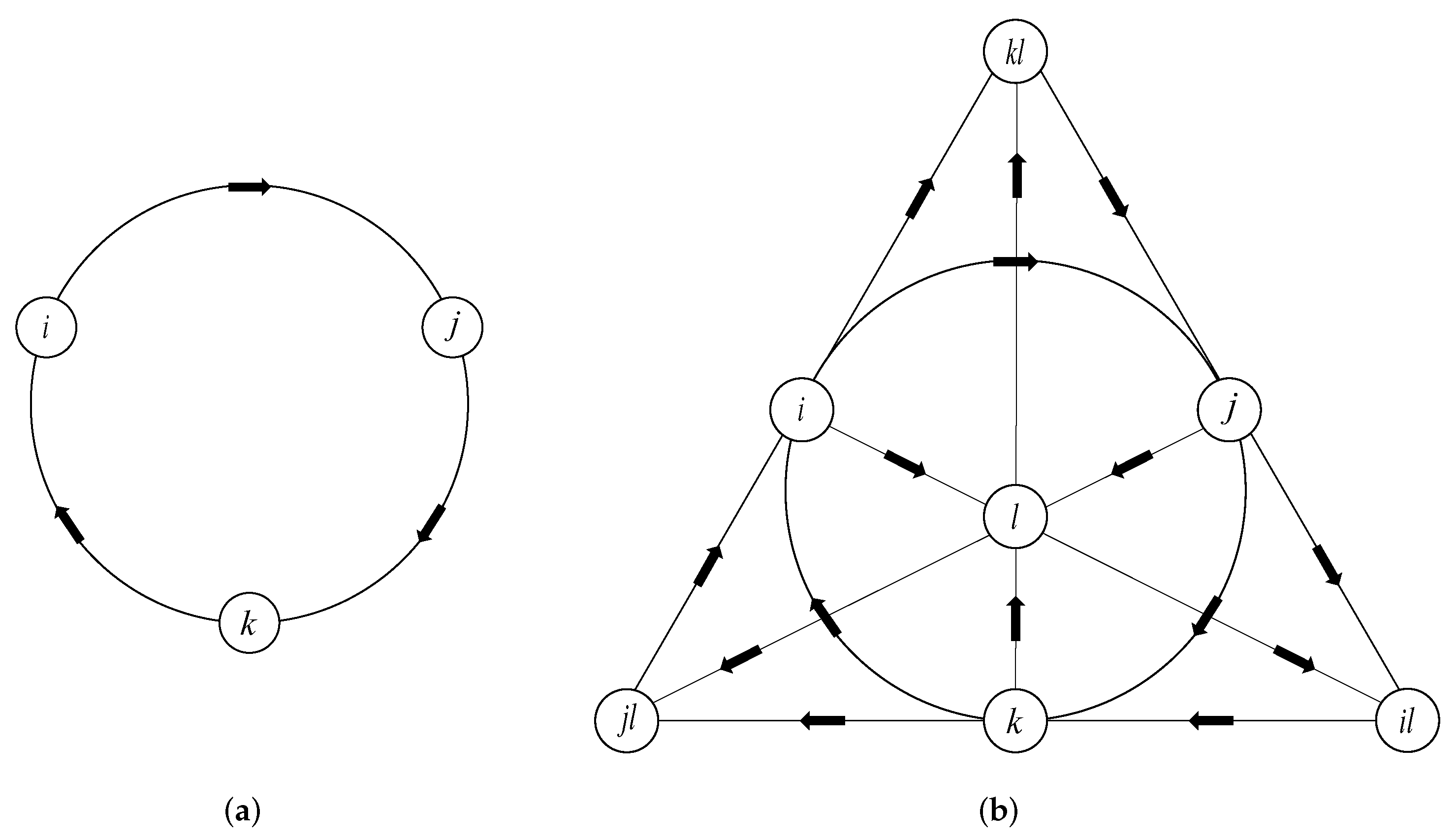
3.1.2. Hyperbolic Geometry of Poincaré Model
- 1.
- Hyperbolic space has fine capabilities of information representation, modeling, and restoration for tree-like structures. A point in the Poincaré disk shown in the figure forms a natural tree-like hierarchical structure in the process of connecting other points step by step to one side of the disk boundary. When the data being modeled also have a tree structure, hyperbolic space can more easily capture and restore the hierarchical features of the data than Euclidean space. In KGs, there are abundant tree-like hierarchical features. Thus, hyperbolic geometric space has natural consistency with the hierarchical information in KGs.
- 2.
- Hyperbolic space is an infinite metric space with higher information capacity. The Poincaré disk shown in the figure has a quantity of hyperbolic spatial triangles with the same shape and different sizes, but for the Poincaré disk, the sizes of these triangles are regarded as the same, only because the visualization gives the impression that the triangles are shrinking as they approach the boundary of the Poincaré model. In fact, the closer to the boundary of the Poincaré model, the capacity of information that the space can accommodate will increase exponentially. In KGs, since hierarchical information has a tree-like structure, the number of nodes in each layer also reflects an exponential growth trend relative to the previous layer. Traditional Euclidean geometry space is unable to model the KGs with a large amount of hierarchical information, and the spatial dimension of the embedded vectors has to be further increased to meet the exponential information growth. However, for hyperbolic space, since it has less information distortion than Euclidean space with lower dimensions and fewer parameters, it is theoretically more suitable for modeling KGs with hierarchical information.
3.2. TransO: A Translation-Based KGC Model with Octonion
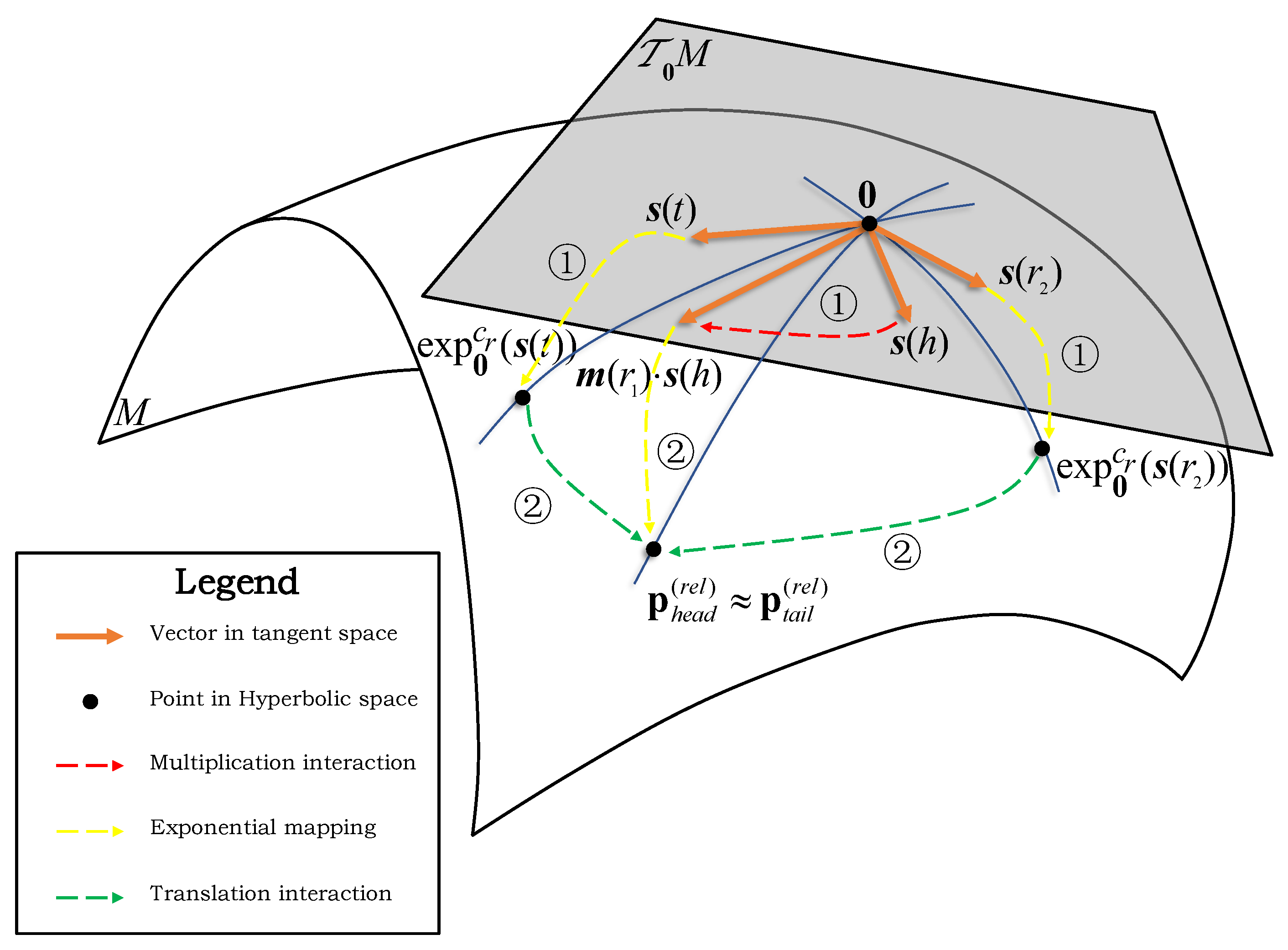
3.3. PTransO: Poincaré-Extended TransO Model
- 1.
- Make the multiplication interaction-related relation component matrix interact with the head entity coordinate vector in the tangent space;
- 2.
- Transfer the interaction result to the hyperbolic Poincaré space by exponential mapping .
- 1.
- Transfer the tail entity coordinate vector and translation interaction-related relation coordinate vector to hyperbolic Poincaré space by exponential mapping ;
- 2.
- Add these two transferred vectors by Möbius addition .
3.4. Training and Optimization
4. Experiments and Discussion
4.1. Link Prediction Experiment
- 1.
- Make a list of all the entities in the dataset, and place this list in the position of the empty entity in the triple;
- 2.
- Traverse each entity from the list in the position of empty entity, and form complete triples with the entity and relation in the non-empty positions;
- 3.
- Use the experimental model to evaluate the scores of these triples, and sort the entities in the list according to the order of scores from high to low.
4.2. Experimental Setup
4.3. Experimental Results
4.4. Results in Modeling Different Types of Relations
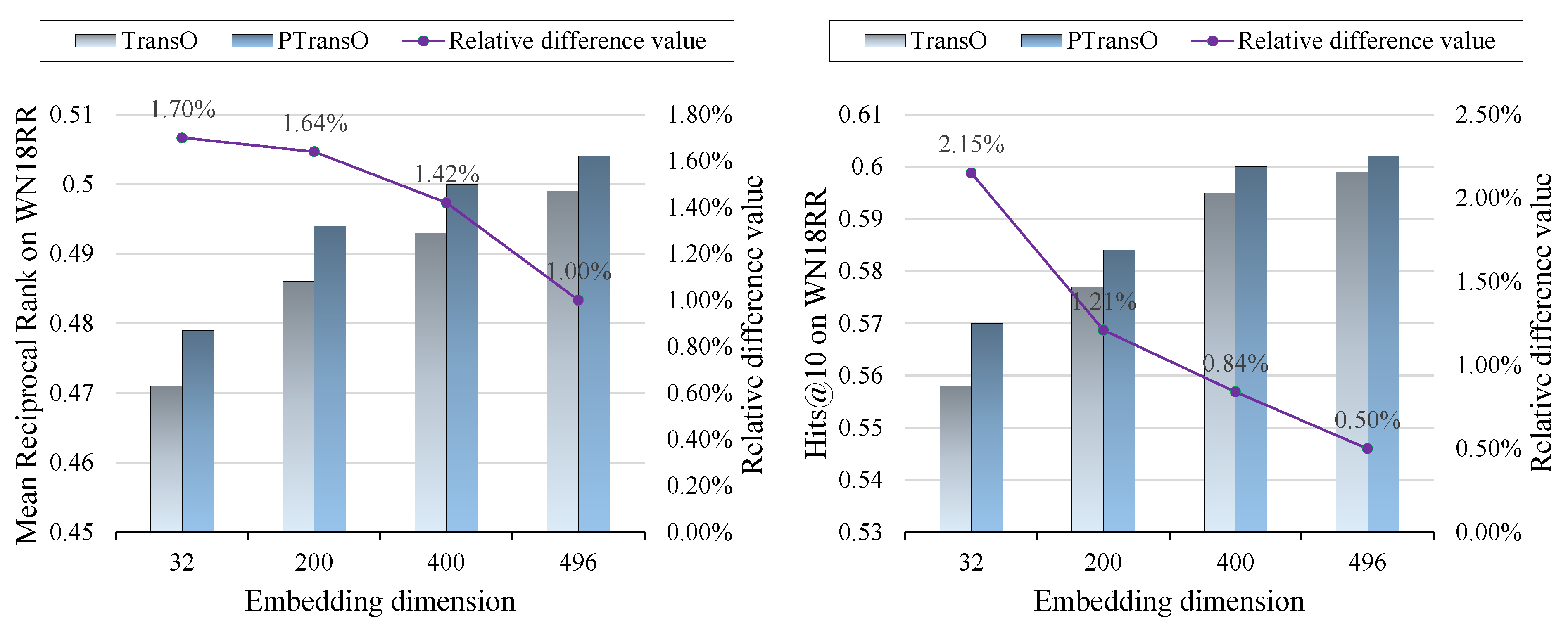
4.5. Euclidean or Poincaré?
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, X.; Huan, Z.; Zhai, Y.; Lin, T. Research of Personalized Recommendation Technology Based on Knowledge Graphs. Appl. Sci. 2021, 11, 7104. [Google Scholar] [CrossRef]
- Introducing the Knowledge Graph: Things, Not Strings. Available online: https://www.blog.google/products/search/introducing-knowledge-graph-things-not/ (accessed on 16 May 2012).
- Xiong, C.; Power, R.; Callan, J. Explicit Semantic Ranking for Academic Search via Knowledge Graph Embedding. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 1271–1279. [Google Scholar]
- Wang, X.; He, X.; Cao, Y.; Liu, M.; Chua, T.-S. KGAT: Knowledge Graph Attention Network for Recommendation. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 950–958. [Google Scholar]
- Saha, A.; Pahuja, V.; Khapra, M.M.; Sankaranarayanan, K.; Chandar, S. Complex Sequential Question Answering: Towards Learning to Converse Over Linked Question Answer Pairs with a Knowledge Graph. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 705–713. [Google Scholar]
- Song, H.-J.; Kim, A.-Y.; Park, S.-B. Learning Translation-Based Knowledge Graph Embeddings by N-Pair Translation Loss. Appl. Sci. 2020, 10, 3964. [Google Scholar] [CrossRef]
- Choi, S.J.; Song, H.-J.; Park, S.-B. An Approach to Knowledge Base Completion by a Committee-Based Knowledge Graph Embedding. Appl. Sci. 2020, 10, 2651. [Google Scholar] [CrossRef]
- Ji, S.; Pan, S.; Cambria, E.; Marttinen, P.; Yu, P.S. A Survey on Knowledge Graphs: Representation, Acquisition, and Applications. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 494–514. [Google Scholar] [CrossRef]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-relational Data. In Advances in Neural Information Processing Systems 26 (NIPS 2013); Curran Associates, Inc.: Red Hook, NY, USA, 2013; pp. 2787–2795. [Google Scholar]
- Nickel, M.; Tresp, V.; Kriegel, H.-P. A Three-Way Model for Collective Learning on Multi-Relational Data. In Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 809–816. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2D Knowledge Graph Embeddings. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 1811–1818. [Google Scholar]
- Nguyen, D.Q.; Nguyen, T.D.; Nguyen, D.Q.; Phung, D. A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, New Orleans, LA, USA, 1–6 June 2018; pp. 327–333. [Google Scholar]
- Popa, C.A. Octonion-Valued Neural Networks. In Proceedings of the 25th International Conference on Artificial Neural Networks, Barcelona, Spain, 6–9 September 2016; pp. 435–443. [Google Scholar]
- Huang, G.; Li, X. Color Palmprint Feature Extraction and Recognition Algorithm Based on Octonion. Comput. Eng. 2012, 38, 28–33. [Google Scholar]
- Daboul, J.; Delbourgo, R. Matrix representation of octonions and generalizations. J. Math. Phys. 1999, 40, 4134–4150. [Google Scholar] [CrossRef][Green Version]
- Cariow, A.; Cariowa, G. Algorithm for multiplying two octonions. Radioelectron. Commun. Syst. 2012, 55, 464–473. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, C. The Real Representation of Octonion Vector and Matrix. J. Xianyang Norm. Univ. 2013, 4, 9–12. [Google Scholar]
- Ungar, A.A. Hyperbolic Trigonometry and its Application in the Poincaré Ball Model of Hyperbolic Geometry. Comput. Math. Appl. 2001, 41, 135–147. [Google Scholar] [CrossRef]
- Balažević, I.; Allen, C.; Hospedales, T. Multi-relational Poincaré Graph Embeddings. In Advances in Neural Information Processing Systems 32 (NeurIPS 2019); Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 4463–4473. [Google Scholar]
- Chami, I.; Wolf, A.; Juan, D.-C.; Sala, F.; Ravi, S.; Ré, C. Low-Dimensional Hyperbolic Knowledge Graph Embeddings. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online. 5–10 July 2020; pp. 6901–6914. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge Graph Embedding by Translating on Hyperplanes. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; pp. 1112–1119. [Google Scholar]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning Entity and Relation Embeddings for Knowledge Graph Completion. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 2181–2187. [Google Scholar]
- Ji, G.; He, S.; Xu, L.; Liu, K.; Zhao, J. Knowledge Graph Embedding via Dynamic Mapping Matrix. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing, Beijing, China, 26–31 July 2015; pp. 687–696. [Google Scholar]
- Nguyen, D.Q.; Sirts, K.; Qu, L.; Johnson, M. STransE: A novel embedding model of entities and relationships in knowledge bases. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, USA, 12–17 June 2016; pp. 460–466. [Google Scholar]
- Ji, G.; Liu, K.; He, S.; Zhao, J. Knowledge Graph Completion with Adaptive Sparse Transfer Matrix. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 985–991. [Google Scholar]
- Qian, W.; Fu, C.; Zhu, Y.; Cai, D.; He, X. Translating Embeddings for Knowledge Graph Completion with Relation Attention Mechanism. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 4286–4292. [Google Scholar]
- Yang, B.; Yih, W.-T.; He, X.; Gao, J.; Deng, L. Embedding Entities and Relations for Learning and Inference in Knowledge Bases. In Proceedings of the 2nd International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Kazemi, S.M.; Poole, D. SimplE Embedding for Link Prediction in Knowledge Graphs. In Advances in Neural Information Processing Systems 31 (NeurIPS 2018); Curran Associates, Inc.: Red Hook, NY, USA, 2018; pp. 4284–4295. [Google Scholar]
- Balažević, I.; Allen, C.; Hospedales, T.M. TuckER: Tensor Factorization for Knowledge Graph Completion. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, Hong Kong, China, 3–7 November 2019; pp. 5185–5194. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex Embeddings for Simple Link Prediction. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 2071–2080. [Google Scholar]
- Sun, Z.; Deng, Z.; Nie, J.; Tang, J. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zhang, S.; Tay, Y.; Yao, L.; Liu, Q. Quaternion Knowledge Graph Embeddings. In Advances in Neural Information Processing Systems 32 (NeurIPS 2019); Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 2735–2745. [Google Scholar]
- Nguyen, D.Q.; Vu, T.; Nguyen, T.D.; Nguyen, D.Q.; Phung, D. A Capsule Network-based Embedding Model for Knowledge Graph Completion and Search Personalization. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; pp. 2180–2189. [Google Scholar]
- Vashishth, S.; Sanyal, S.; Nitin, V.; Agrawal, N.; Talukdar, P. InteractE: Improving Convolution-based Knowledge Graph Embeddings by Increasing Feature Interactions. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 3009–3016. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; van den Berg, R.; Titov, I.; Welling, M. Modeling Relational Data with Graph Convolutional Networks. In Proceedings of the 15th European Semantic Web Conference, Heraklion, Greece, 3–7 June 2018; pp. 593–607. [Google Scholar]
- Knarr, N.; Stroppel, M.J. Subforms of norm forms of octonion fields. Arch. Math. 2018, 110, 213–224. [Google Scholar] [CrossRef]
- Conway, J.H.; Smith, D.A.; Dixon, G. On quaternions and octonions: Their geometry, arithmetic, and symmetry. Math. Intell. 2004, 26, 75–77. [Google Scholar]
- Kaplan, A. Quaternions and octonions in Mechanics. Rev. Union Mat. Argent. 2008, 49, 45–53. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of the 19th International Conference on Computational Statistics, Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar]
- Li, K.; Gu, S.; Yan, D. A Link Prediction Method Based on Neural Networks. Appl. Sci. 2021, 11, 5186. [Google Scholar] [CrossRef]
- Toutanova, K.; Chen, D. Observed versus latent features for knowledge base and text inference. In Proceedings of the 3rd Workshop on Continuous Vector Space Models and their Compositionality, Beijing, China, 31 July 2015; pp. 57–66. [Google Scholar]
- Miller, G.A.; Beckwith, R.; Fellbaum, C.; Gross, D.; Miller, K. Introduction to WordNet: An On-line Lexical Database. Int. J. Lexicogr. 1990, 3, 235–244. [Google Scholar] [CrossRef]
- Bollacker, K.D.; Evans, C.; Paritosh, P.K.; Sturge, T.; Taylor, J. Freebase: A collaboratively created graph database for structuring human knowledge. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 10–12 June 2008; pp. 1247–1249. [Google Scholar]
- Lacroix, T.; Usunier, N.; Obozinski, G. Canonical Tensor Decomposition for Knowledge Base Completion. In Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; pp. 2863–2872. [Google Scholar]
- Zhang, Y.; Yao, Q.; Shao, Y.; Chen, L. NSCaching: Simple and Efficient Negative Sampling for Knowledge Graph Embedding. In Proceedings of the 35th IEEE International Conference on Data Engineering, Macao, China, 8–11 April 2019; pp. 614–625. [Google Scholar]


| Dataset | Entites | Relations | Triples | #Training | #Validation | #Test |
|---|---|---|---|---|---|---|
| WN18 | 40,943 | 18 | 151k | 141,442 | 5000 | 5000 |
| WN18RR | 40,943 | 11 | 93k | 86,835 | 3034 | 3134 |
| FB15k-237 | 14,951 | 237 | 310k | 272,115 | 17,535 | 20,466 |
| Model | MR | MRR | Hits@10 | Hits@3 | Hits@1 |
|---|---|---|---|---|---|
| TransE (Bordes et al., 2013) [9] | 251 | 0.454 | 0.934 | 0.823 | 0.089 |
| TransH (Wang et al., 2014) [21] | 388 | 0.485 | 0.936 | 0.916 | 0.060 |
| TransR (Lin et al., 2015) [22] | 225 | 0.605 | 0.940 | 0.876 | 0.335 |
| TransD (Ji et al., 2015) [23] | 212 | 0.580 | 0.942 | 0.923 | 0.241 |
| STransE (Nguyen et al., 2016) [24] | 206 | 0.657 | 0.934 | - | - |
| TransSparse (Ji et al., 2016) [25] | 211 | - | 0.932 | - | - |
| TransAT (Qian et al., 2018) [26] | 157 | - | 0.950 | - | - |
| DistMult (Yang et al., 2014) [27] | 902 | 0.822 | 0.934 | 0.914 | 0.728 |
| TransO | 98 | 0.918 | 0.962 | 0.942 | 0.889 |
| Model | WN18RR | FB15k-237 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MR | MRR | Hits@10 | Hits@3 | Hits@1 | MR | MRR | Hits@10 | Hits@3 | Hits@1 | |
| TransE (Bordes et al., 2013) [9] | 3384 | 0.226 | 0.501 | - | - | 357 | 0.294 | 0.465 | - | - |
| DistMult (Yang et al., 2014) [27] | 5110 | 0.430 | 0.490 | 0.440 | 0.390 | 254 | 0.241 | 0.419 | 0.263 | 0.155 |
| TuckER (Balažević et al., 2019) [29] | - | 0.470 | 0.526 | 0.482 | 0.443 | - | 0.358 | 0.544 | 0.394 | 0.266 |
| ComplEx-N3 (Lacroix et al., 2018) [45] | - | 0.480 | 0.572 | 0.495 | 0.435 | - | 0.357 | 0.547 | 0.392 | 0.264 |
| RotatE (Sun et al., 2019) [31] | 3340 | 0.476 | 0.571 | 0.492 | 0.428 | 177 | 0.338 | 0.533 | 0.375 | 0.241 |
| QuatE (Zhang et al., 2019) [32] | 2314 | 0.488 | 0.582 | 0.508 | 0.438 | 87 | 0.348 | 0.550 | 0.382 | 0.248 |
| ConvE (Dettmers et al., 2018) [11] | 4187 | 0.430 | 0.520 | 0.440 | 0.400 | 244 | 0.325 | 0.501 | 0.356 | 0.237 |
| MuRE (Balažević et al., 2019) [19] | 2108 | 0.475 | 0.554 | 0.487 | 0.436 | 171 | 0.336 | 0.521 | 0.370 | 0.245 |
| AttE (Chami et al., 2020) [20] | - | 0.490 | 0.581 | 0.508 | 0.443 | - | 0.351 | 0.543 | 0.386 | 0.255 |
| MuRP (Balažević et al., 2019) [19] | 2306 | 0.481 | 0.566 | 0.495 | 0.440 | 172 | 0.335 | 0.518 | 0.367 | 0.243 |
| AttH (Chami et al., 2020) [20] | - | 0.486 | 0.573 | 0.499 | 0.443 | - | 0.348 | 0.540 | 0.384 | 0.252 |
| TransO | 2269 | 0.499 | 0.599 | 0.519 | 0.445 | 169 | 0.347 | 0.534 | 0.383 | 0.253 |
| PTransO | 2416 | 0.504 | 0.602 | 0.524 | 0.455 | 169 | 0.345 | 0.531 | 0.381 | 0.251 |
| Model | WN18RR | FB15k-237 | ||||||
|---|---|---|---|---|---|---|---|---|
| MRR | Hits | MRR | Hits | |||||
| @10 | @3 | @1 | @10 | @3 | @1 | |||
| TransE (Bordes et al., 2013) [9] | 0.182 | 0.419 | 0.266 | 0.053 | 0.147 | 0.259 | 0.158 | 0.089 |
| DistMult (Yang et al., 2014) [27] | 0.327 | 0.379 | 0.351 | 0.293 | 0.178 | 0.332 | 0.197 | 0.100 |
| ComplEx-N3 (Lacroix et al., 2018) [45] | 0.420 | 0.460 | 0.420 | 0.390 | 0.294 | 0.463 | 0.322 | 0.211 |
| RotatE (Sun et al., 2019) [31] | 0.387 | 0.491 | 0.417 | 0.330 | 0.290 | 0.458 | 0.316 | 0.208 |
| ConvE (Dettmers et al., 2018) [11] | 0.395 | 0.476 | 0.420 | 0.350 | 0.307 | 0.476 | 0.335 | 0.222 |
| MuRE (Balažević et al., 2019) [19] | 0.458 | 0.525 | 0.471 | 0.421 | 0.313 | 0.489 | 0.340 | 0.226 |
| RotE (Chami et al., 2020) [20] | 0.463 | 0.529 | 0.477 | 0.426 | 0.307 | 0.482 | 0.337 | 0.220 |
| AttE (Chami et al., 2020) [20] | 0.456 | 0.526 | 0.471 | 0.419 | 0.311 | 0.488 | 0.339 | 0.223 |
| MuRP (Balažević et al., 2019) [19] | 0.465 | 0.544 | 0.484 | 0.420 | 0.323 | 0.501 | 0.353 | 0.235 |
| RotH (Chami et al., 2020) [20] | 0.472 | 0.553 | 0.490 | 0.428 | 0.314 | 0.497 | 0.346 | 0.223 |
| AttH (Chami et al., 2020) [20] | 0.466 | 0.551 | 0.484 | 0.419 | 0.324 | 0.501 | 0.354 | 0.236 |
| TransO | 0.471 | 0.558 | 0.493 | 0.421 | 0.324 | 0.501 | 0.356 | 0.235 |
| PTransO | 0.479 | 0.570 | 0.500 | 0.430 | 0.325 | 0.503 | 0.357 | 0.235 |
| Relation Name | RotatE | QuatE | TransO | PTransO |
|---|---|---|---|---|
| hypernym | 0.148 | 0.173 | 0.206 | 0.207 |
| derivationally_related_form | 0.947 | 0.953 | 0.941 | 0.950 |
| instance_hypernym | 0.318 | 0.364 | 0.397 | 0.405 |
| also_see | 0.585 | 0.629 | 0.656 | 0.636 |
| member_meronym | 0.232 | 0.232 | 0.258 | 0.261 |
| synset_domain_topic_of | 0.341 | 0.468 | 0.427 | 0.420 |
| has_part | 0.184 | 0.233 | 0.239 | 0.246 |
| member_of_domain_usage | 0.318 | 0.441 | 0.400 | 0.373 |
| member_of_domain_region | 0.200 | 0.193 | 0.397 | 0.368 |
| verb_group | 0.943 | 0.924 | 0.874 | 0.888 |
| similar_to | 1.000 | 1.000 | 1.000 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Bai, C.; Yu, J.; Zhao, M.; Xu, T.; Liu, H.; Li, X.; Yu, R. Translation-Based Embeddings with Octonion for Knowledge Graph Completion. Appl. Sci. 2022, 12, 3935. https://doi.org/10.3390/app12083935
Yu M, Bai C, Yu J, Zhao M, Xu T, Liu H, Li X, Yu R. Translation-Based Embeddings with Octonion for Knowledge Graph Completion. Applied Sciences. 2022; 12(8):3935. https://doi.org/10.3390/app12083935
Chicago/Turabian StyleYu, Mei, Chen Bai, Jian Yu, Mankun Zhao, Tianyi Xu, Hongwei Liu, Xuewei Li, and Ruiguo Yu. 2022. "Translation-Based Embeddings with Octonion for Knowledge Graph Completion" Applied Sciences 12, no. 8: 3935. https://doi.org/10.3390/app12083935
APA StyleYu, M., Bai, C., Yu, J., Zhao, M., Xu, T., Liu, H., Li, X., & Yu, R. (2022). Translation-Based Embeddings with Octonion for Knowledge Graph Completion. Applied Sciences, 12(8), 3935. https://doi.org/10.3390/app12083935





