Study on Vibration Reduction Performance of Gear Pairs Made by a High-Strength Fe-Mn Damping Alloy
Abstract
:1. Introduction
- (1)
- A nonlinear constitutive model of Fe-Mn damping alloy materials based on viscoelastic theory is constructed and extended to a three-dimensional state using tensor theory. The time increment step form of the constitutive model is derived.
- (2)
- The user subroutine UMAT of the nonlinear constitutive model of the Fe-Mn damping alloy material is written, and the accuracy of the proposed constitutive model in representing the mechanical behavior of the Fe-Mn damping alloy is verified.
- (3)
- The transient dynamic of a gearbox is analyzed by using the LS-Dyna damping alloy material user subroutine, in which the spur gear pair of the gearbox is fabricated by Fe-Mn damping alloy.
2. Preparation of High-Strength Fe-Mn Alloy
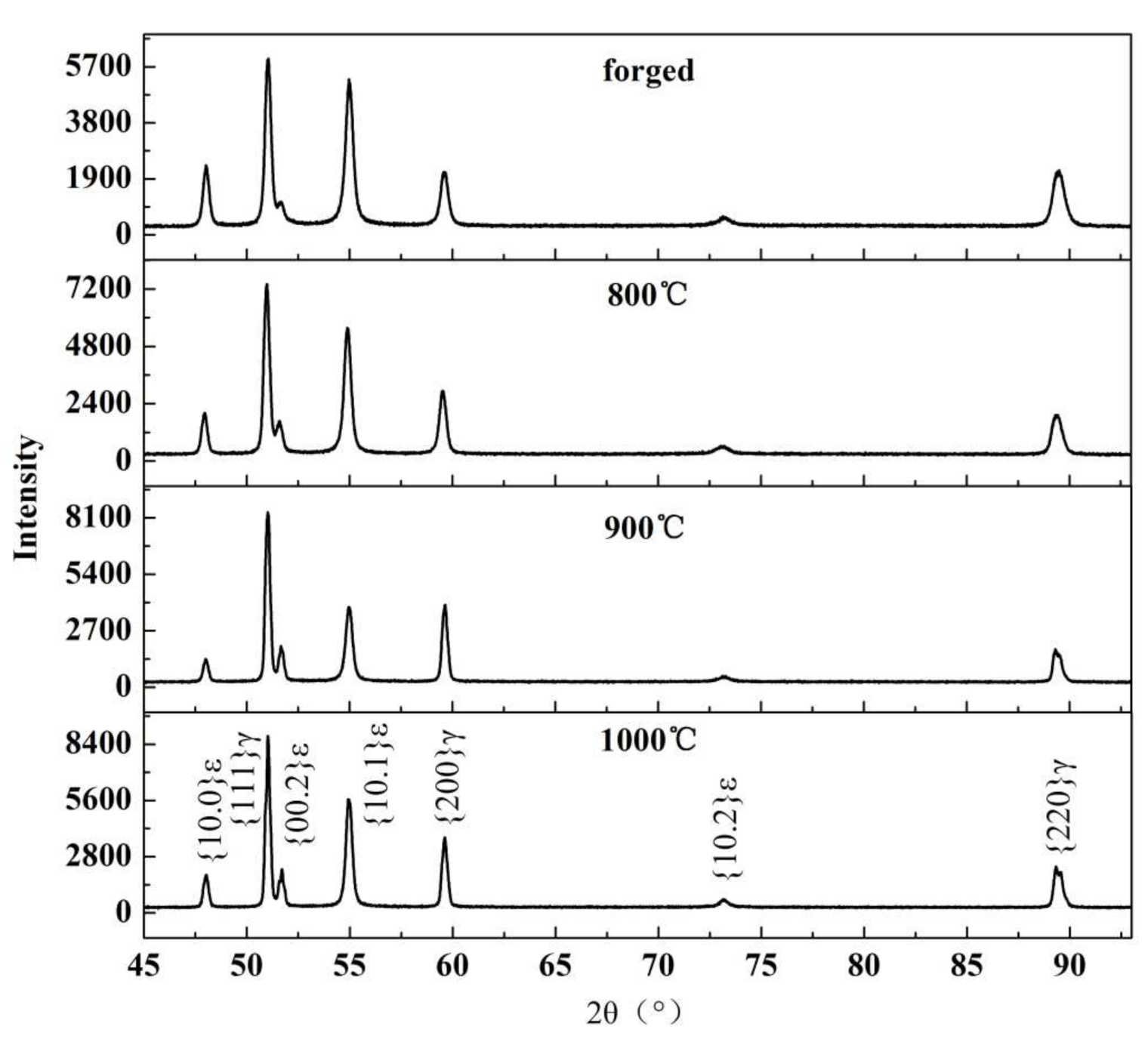
2.1. Phase Analysis of Fe-Mn Alloy
2.2. Phase Transformation Point Test of Fe-Mn Alloy
3. Experimental Properties of Fe-Mn Alloy Specimens
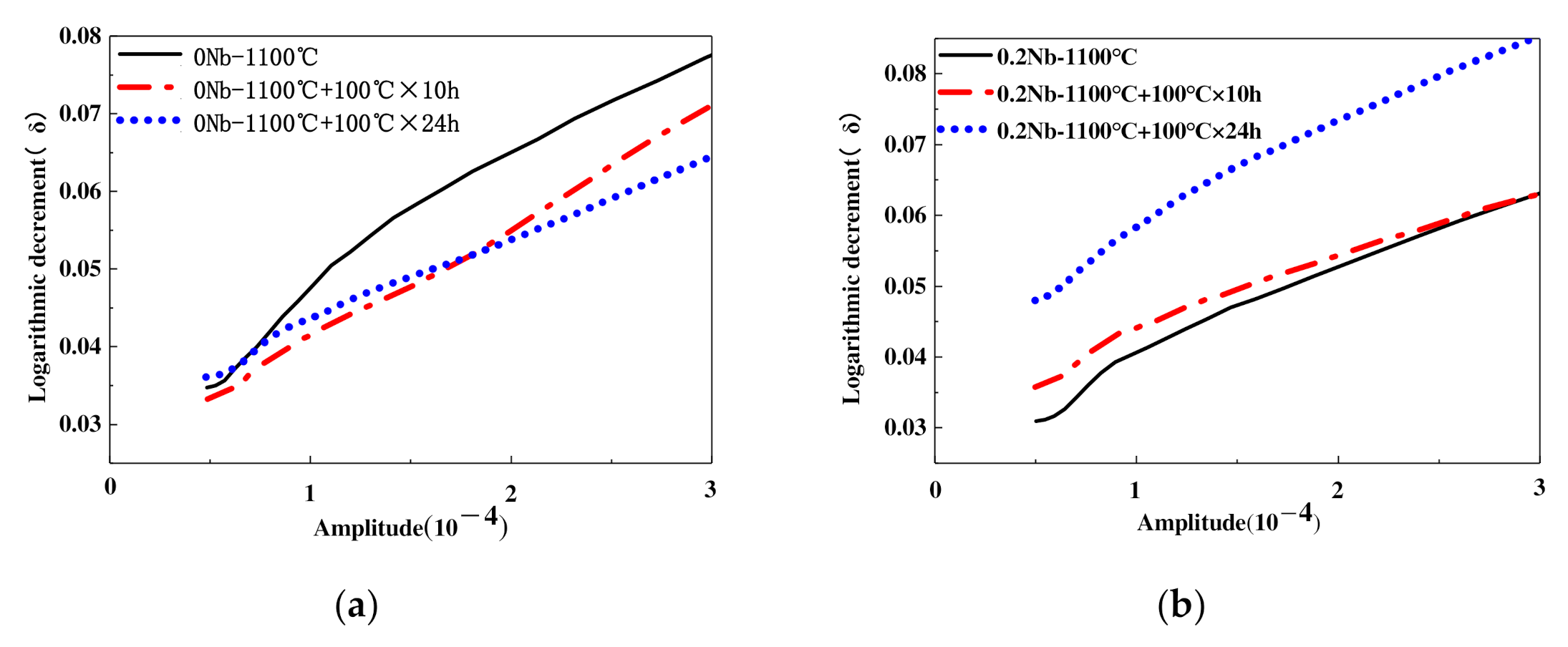
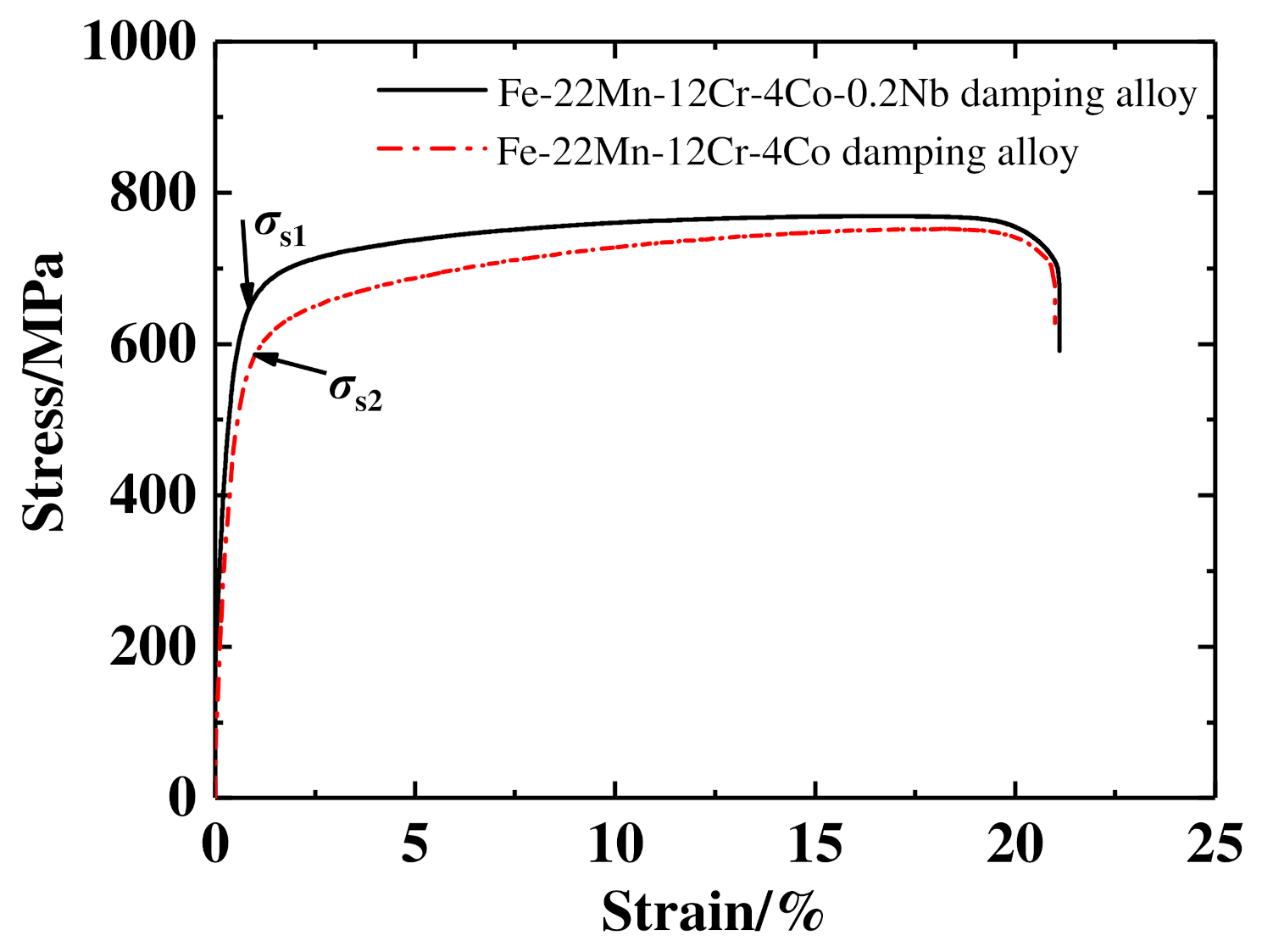
3.1. Experimental Properties of Annealed Fe-Mn Alloy Specimens
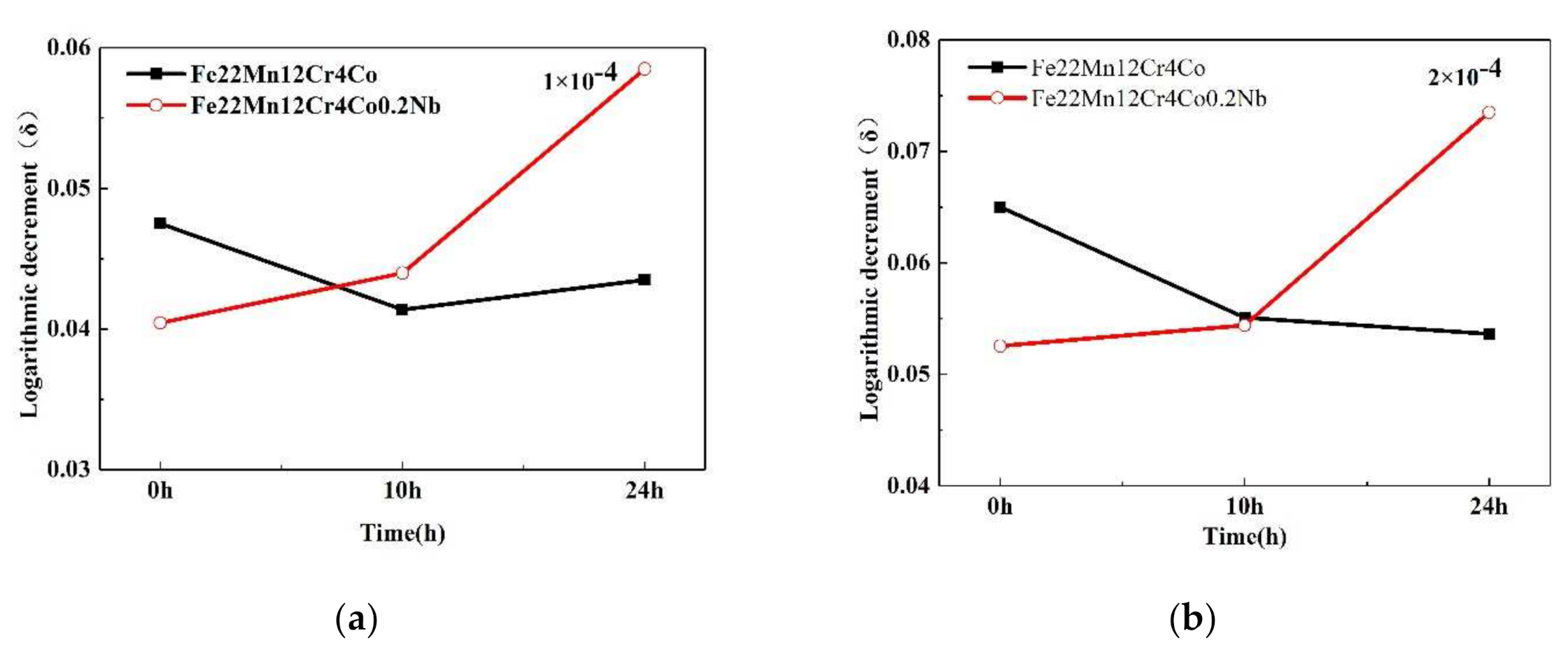
3.2. Effect of Annealing Temperature on Fe-22Mn-12Cr-4Co-0.2Nb Alloy
3.3. Effect of Annealing Temperature on the Microstructure of the Alloy
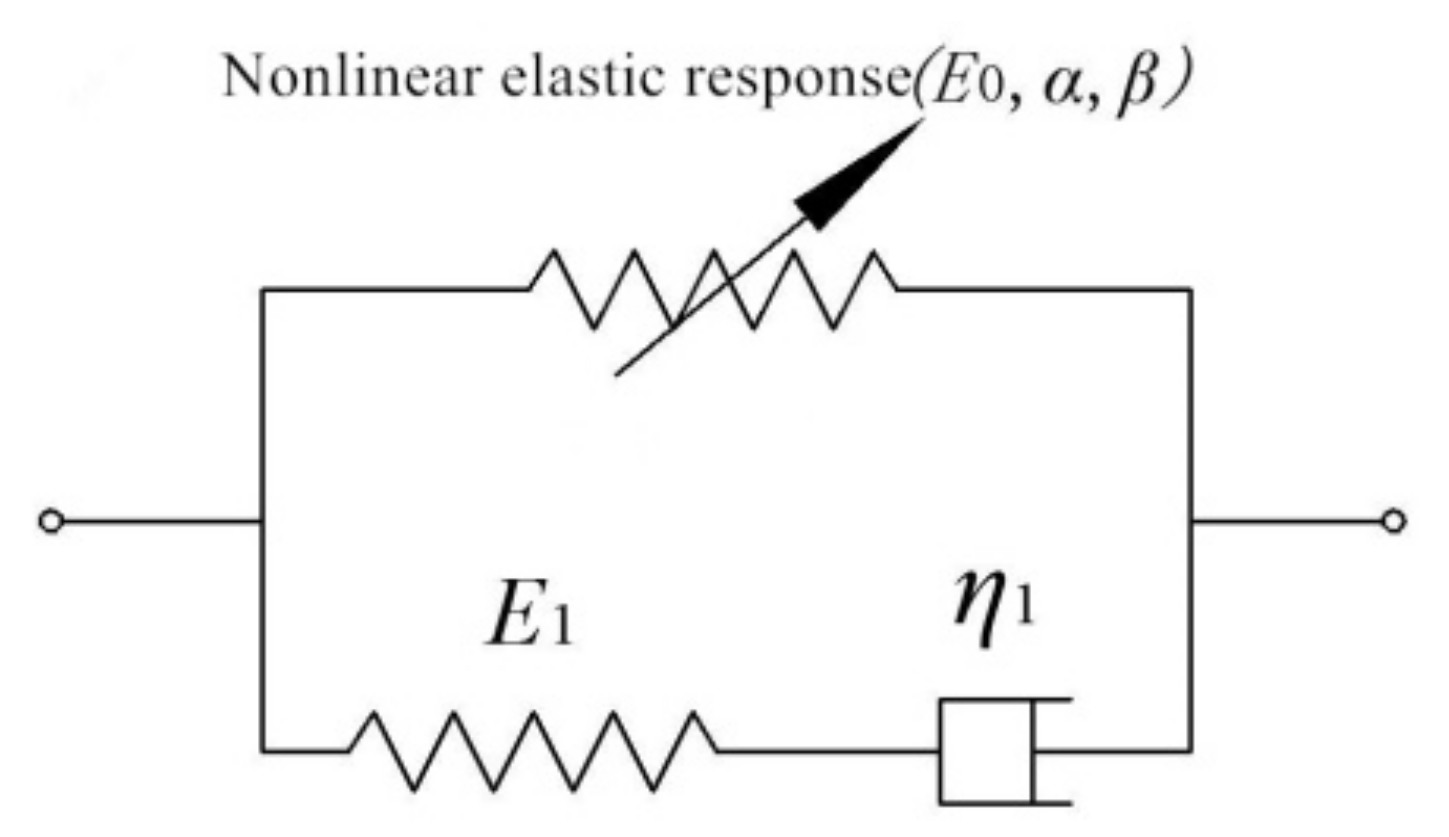
4. Constitutive Model of a New Type of Fe-Mn Damping Alloy Material
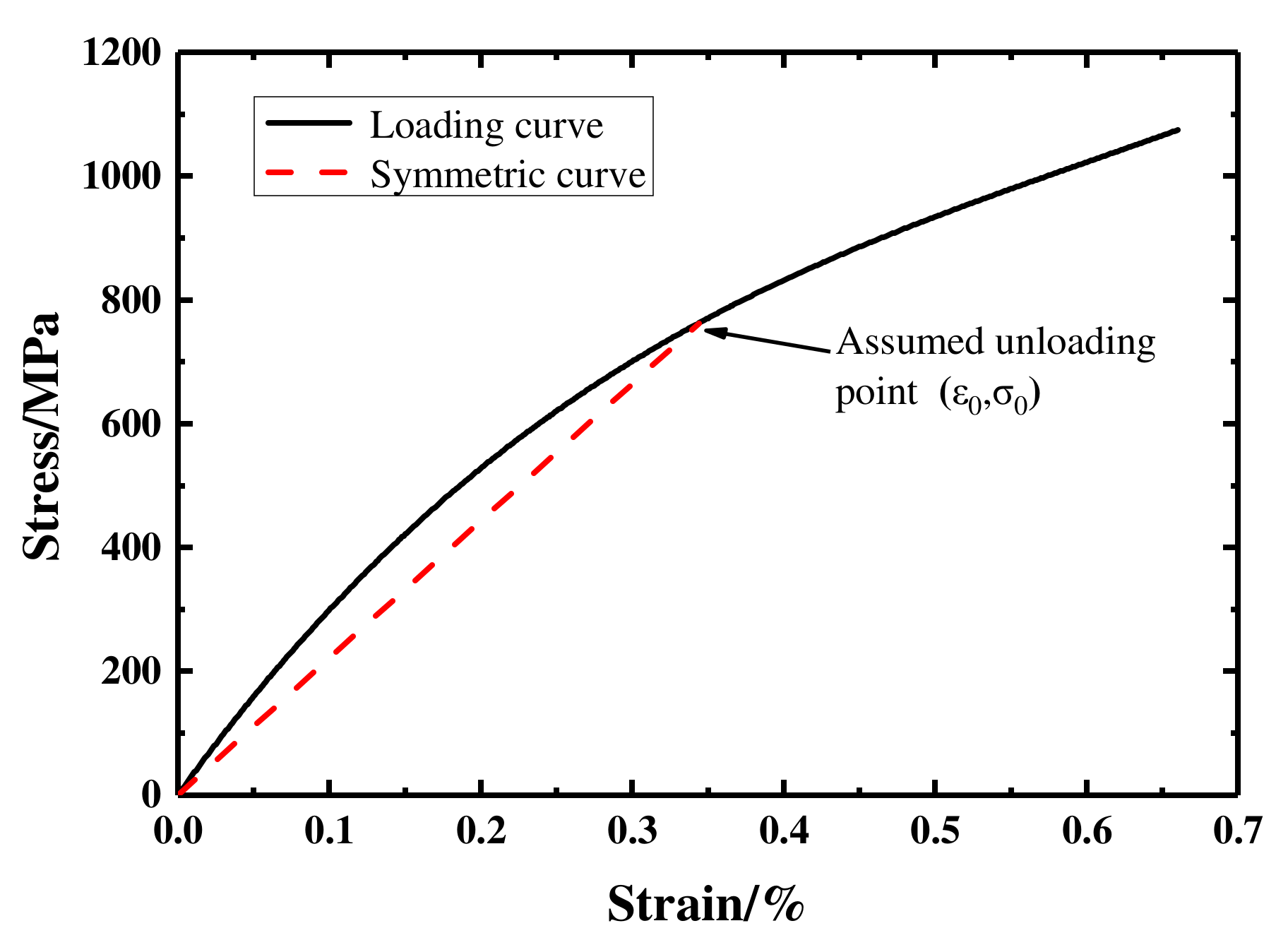
4.1. The Constitutive Equation for Loading
4.2. The Constitutive Equation for Unloading
5. The User Subprogram of LS-Dyna Software for the Constitutive Model of the Damping Alloy Material
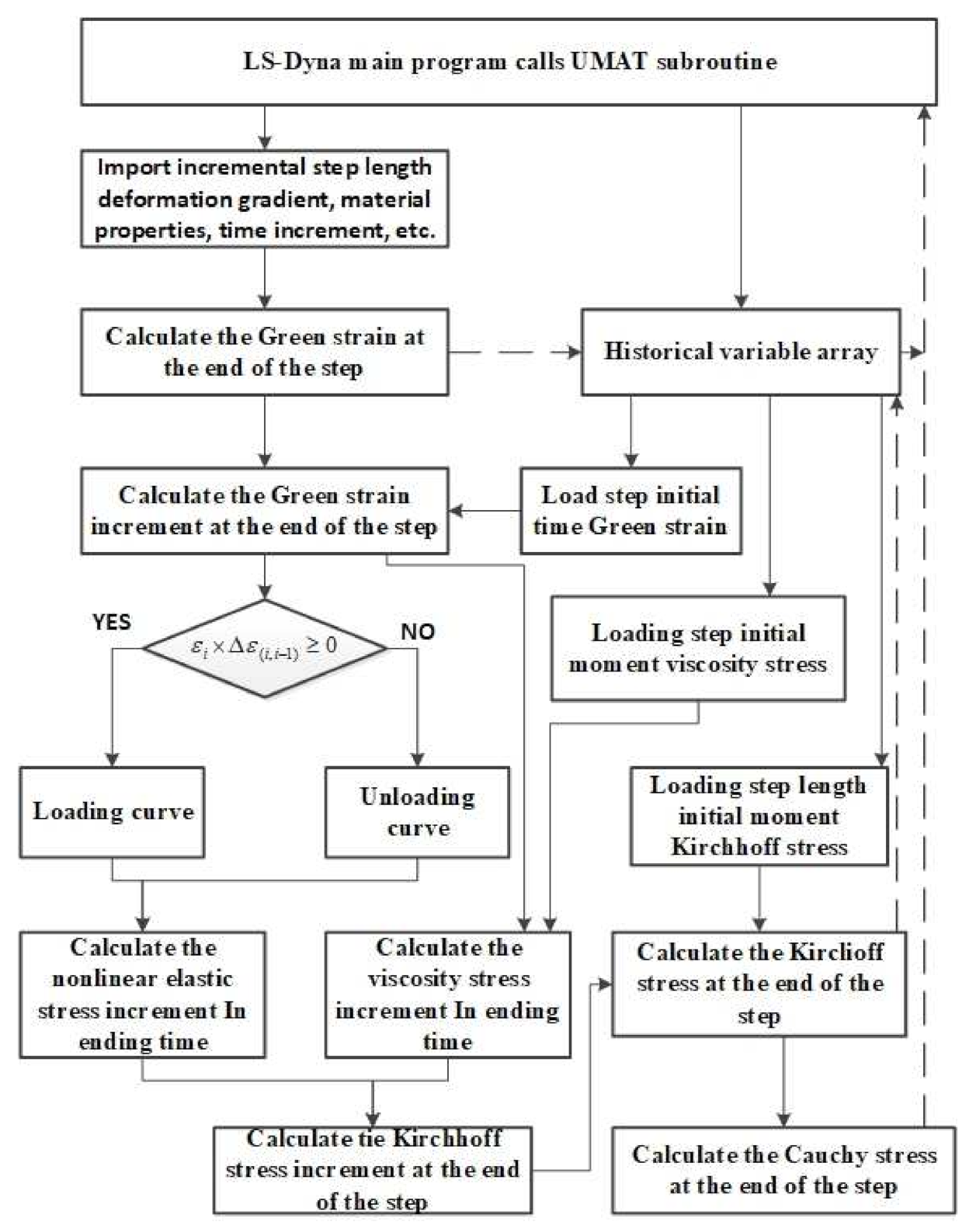
5.1. Calculation Process
- We first imported the material attributes , , , , , , and from the LS-Dyna main program, with the variables at the beginning of the time step being the deformation gradient tensor , time increment , and an array of historical variables;
- We then loaded the strain tensor , the stress tensor and the viscous response stress of the previous step from the user-defined array of historical variables;
- We calculated the strain tensor and the increment of the strain tensor of the current step length;
- We calculated the nonlinear elastic stress increment and viscoelastic stress increment ;
- We calculated the increment of the stress tensor ;
- We calculated the stress tensor ;
- We calculated and returned the Cauchy stress tensor at the end of the incremental step;
- We then updated the state variables , , , etc.
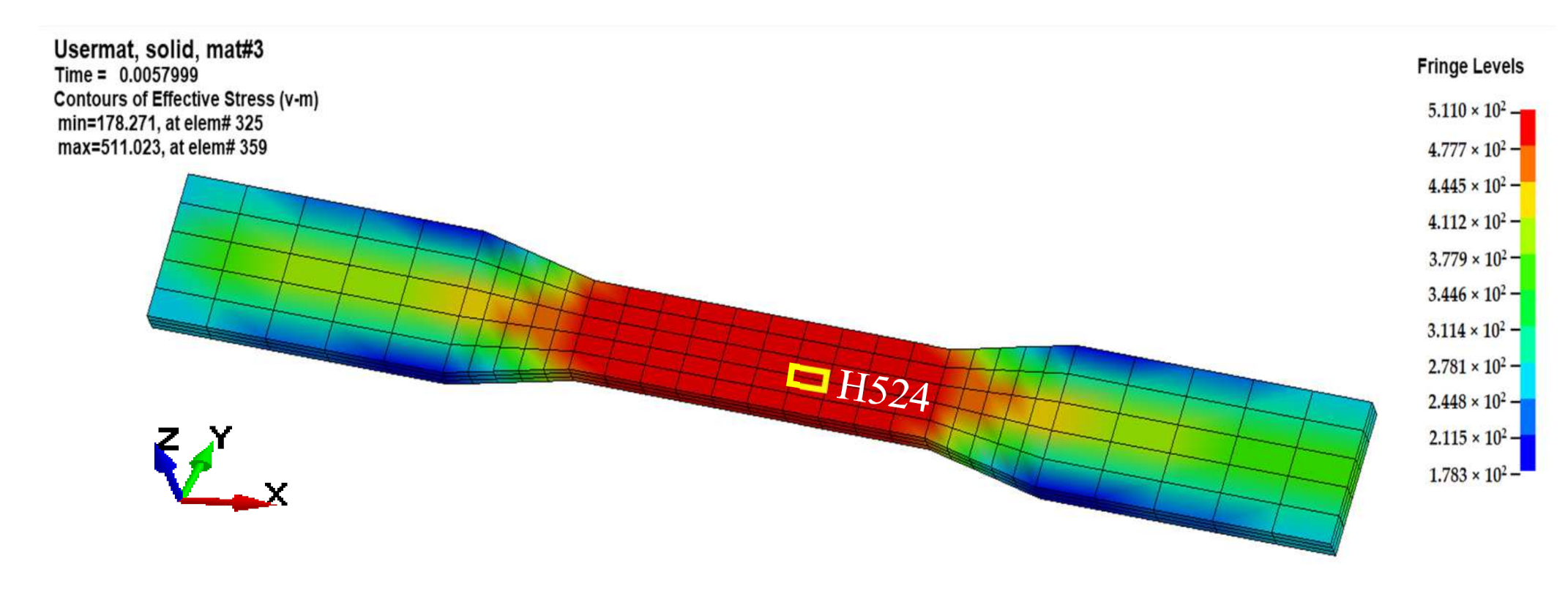
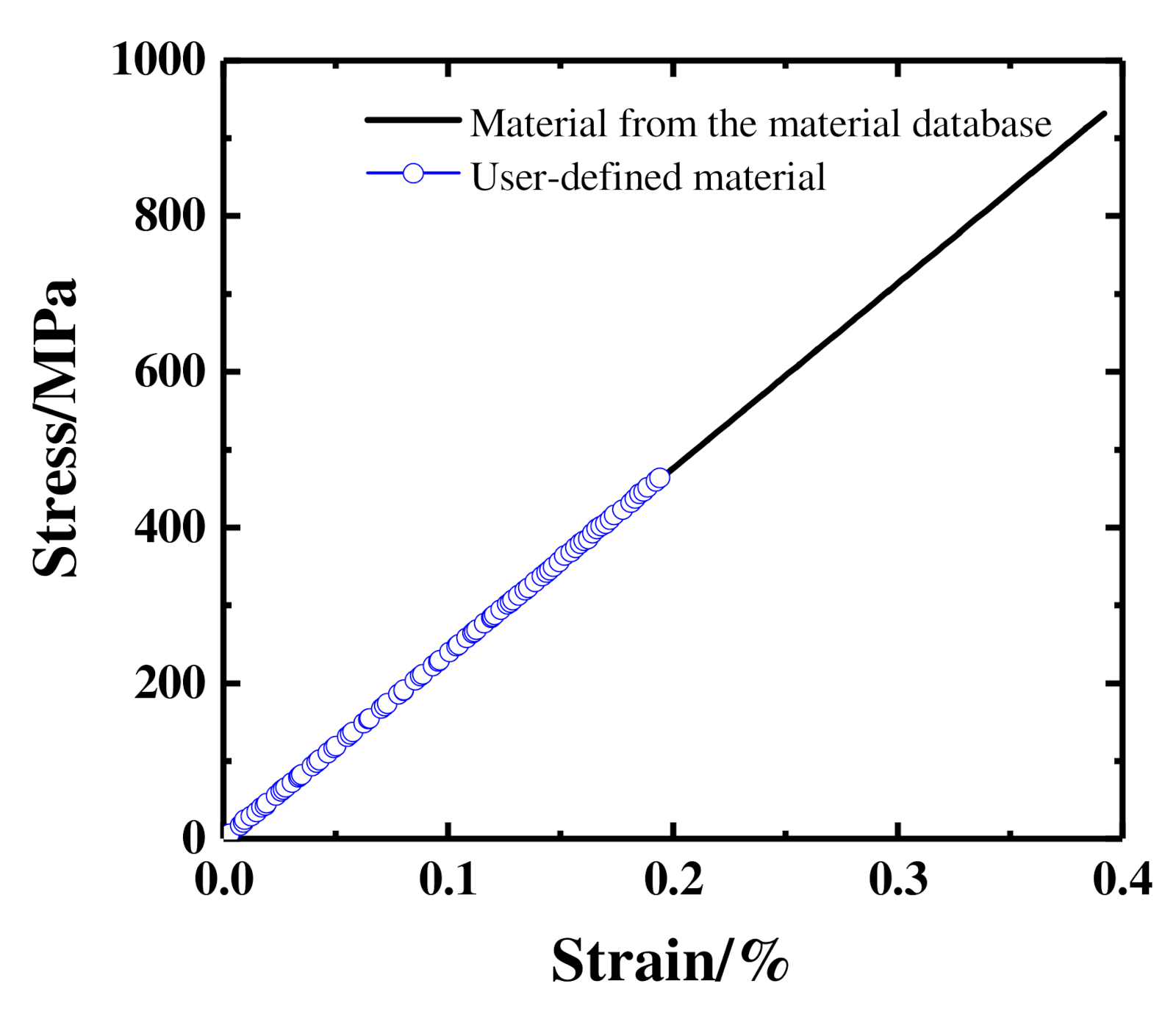
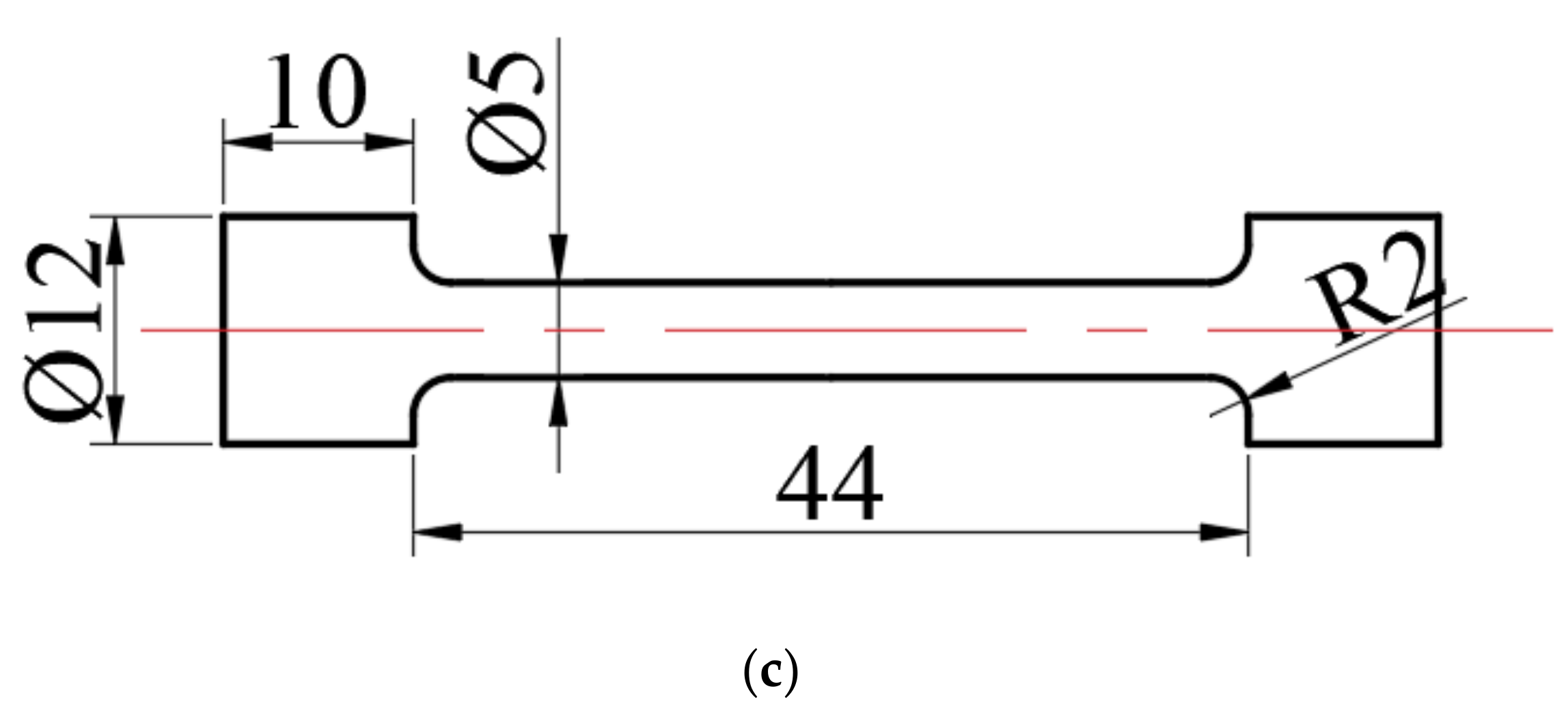
5.2. Example Verification
6. Transient Dynamic Analysis of Gears Made by Damping Alloy Materials
6.1. Numerical Simulation of Damping Alloy Materials
6.2. Simulation Results of Different Damping Alloy Materials and 40Cr Materials
7. Gearbox Vibration Experiment
7.1. Experiment Objects
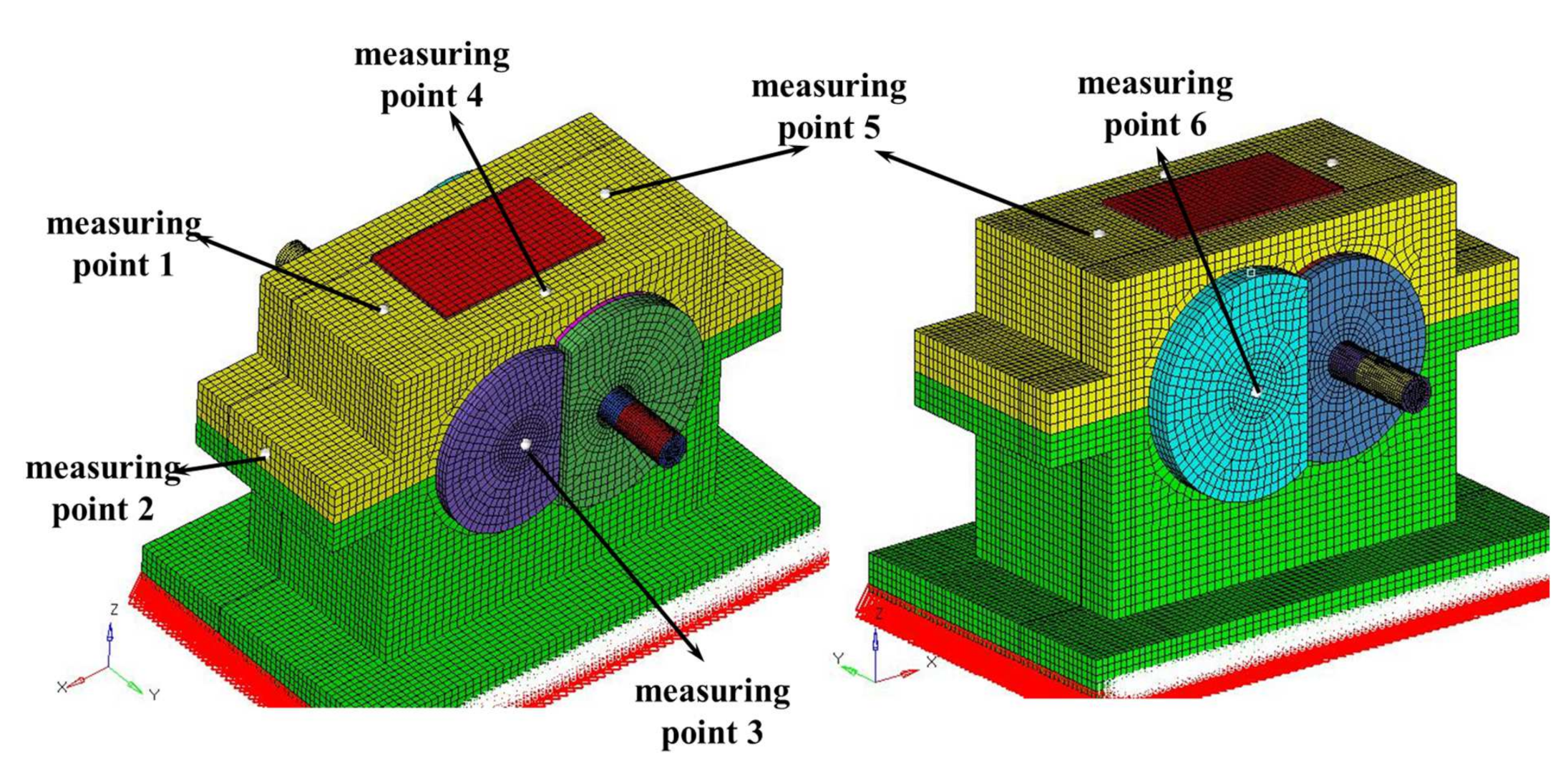
7.2. Vibration Test System for Reduction Gearbox
7.3. Vibration Test Results and Analysis of Gearbox
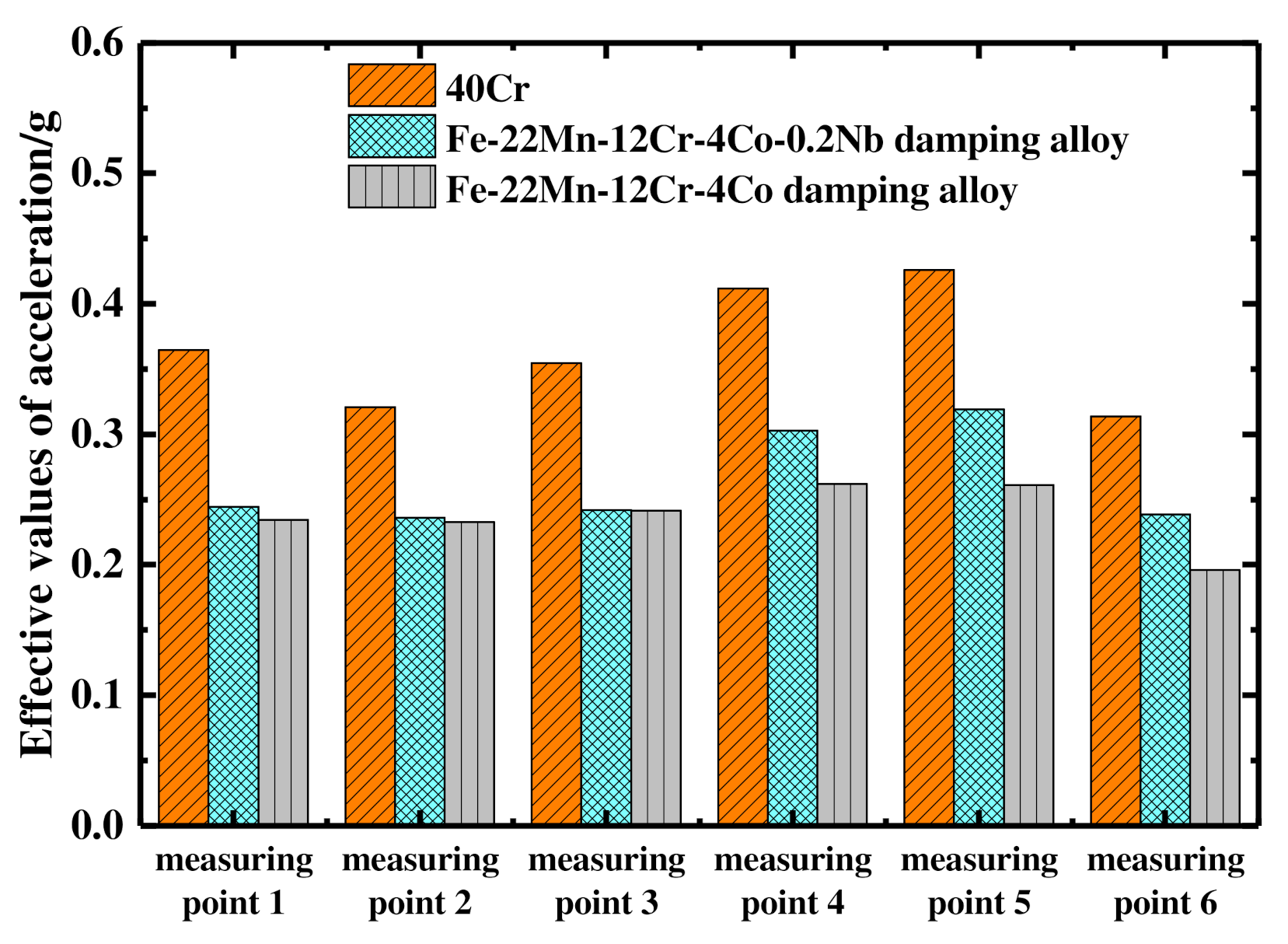
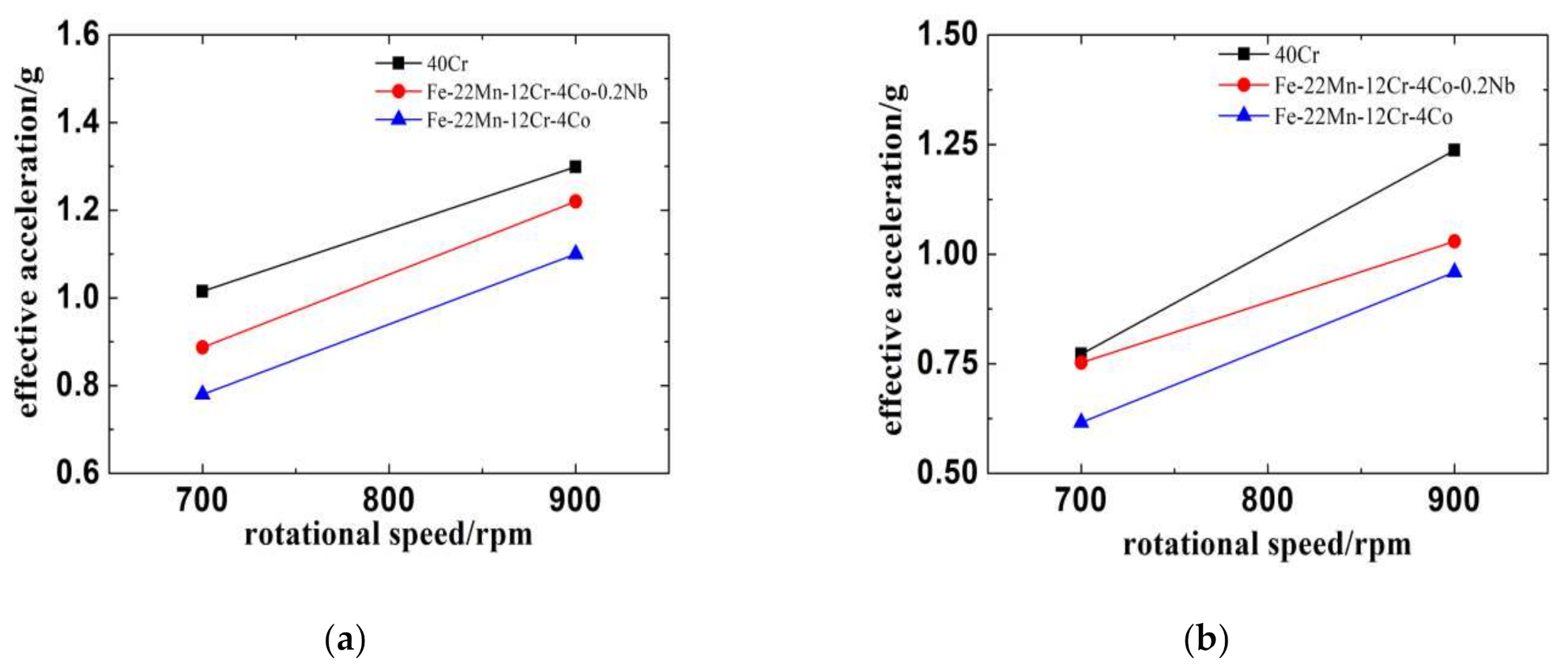
7.3.1. Comparison of Effective Values of Vibration Acceleration of Gears with Different Materials under 700 rpm and 10 N·m Working Conditions
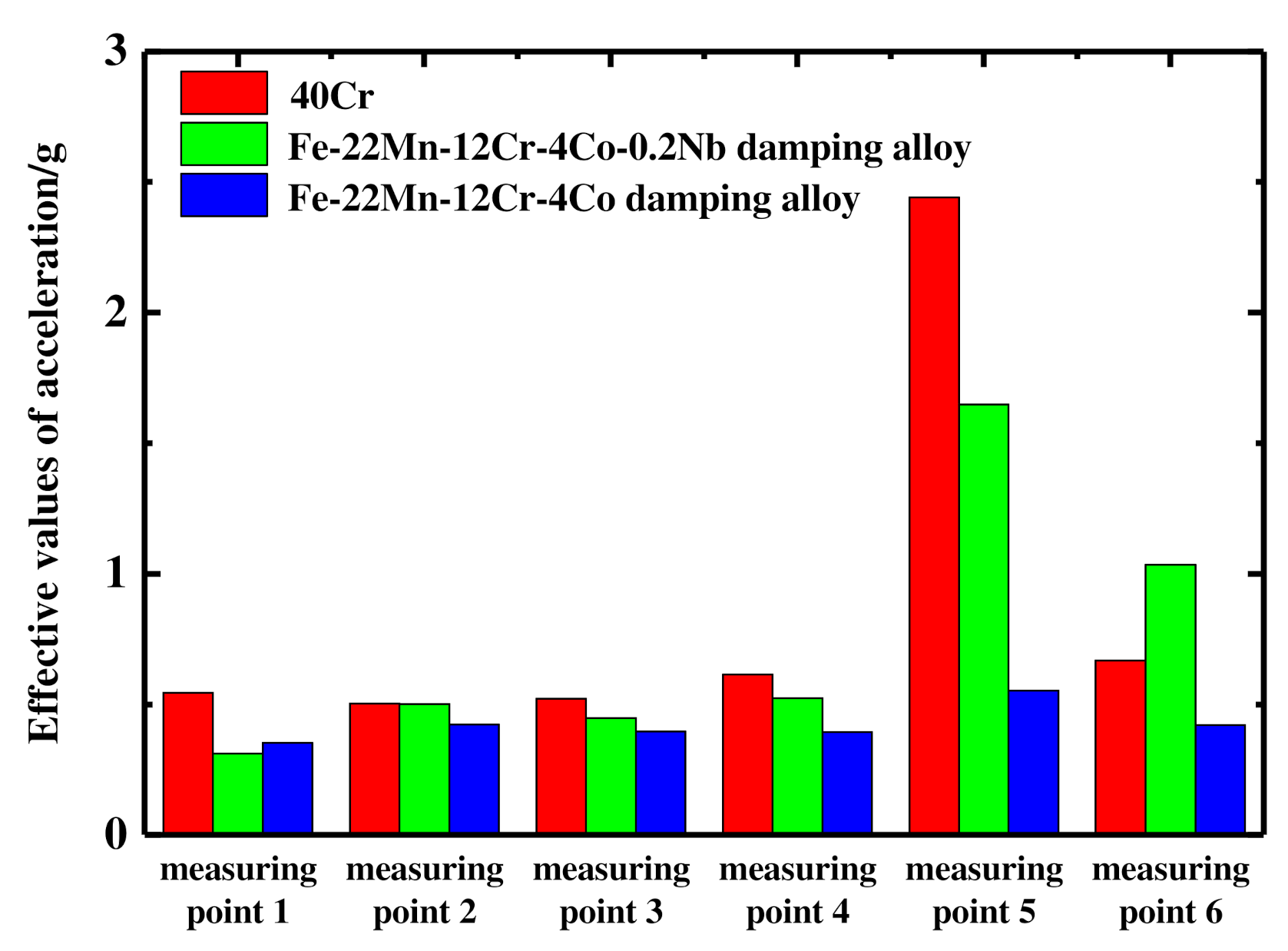
7.3.2. Comparison of Effective Values of Vibration Acceleration of Gears with Different Materials under 900 rpm 10 N·m Working Conditions
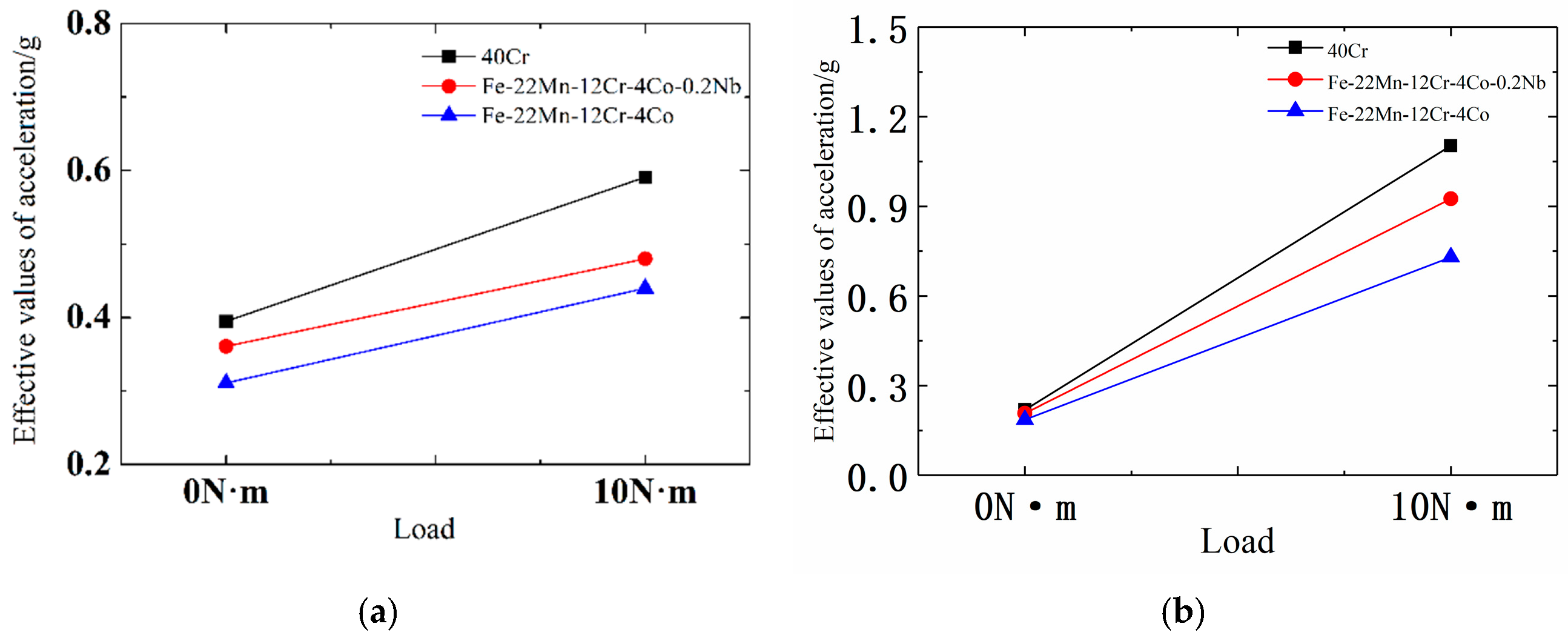
7.3.3. Comparison of Vibration Acceleration Results of Different Gear Materials under Different Working Conditions
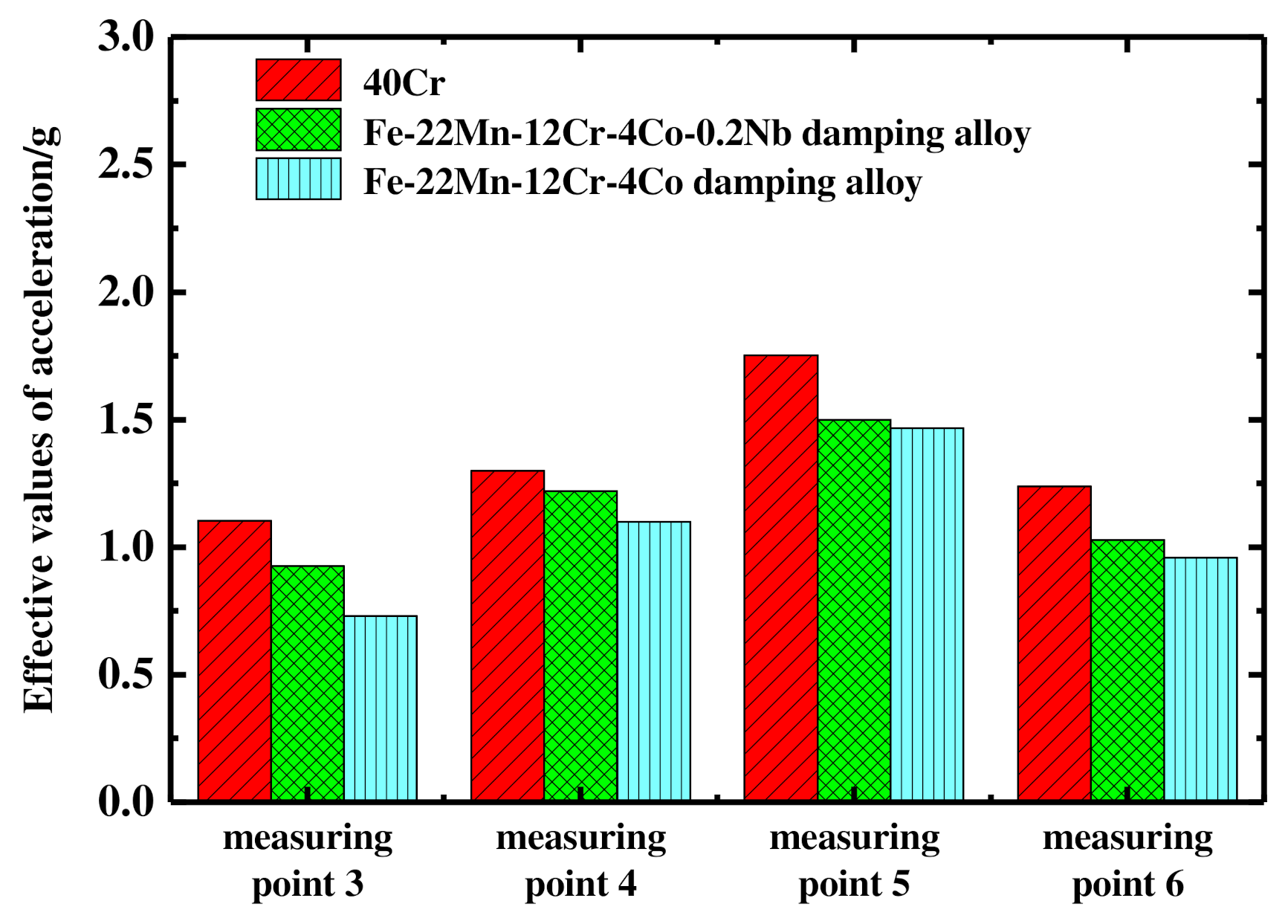
7.3.4. Comparison between Test Results and Simulation Results of Acceleration Effective Values of Different Gear Materials
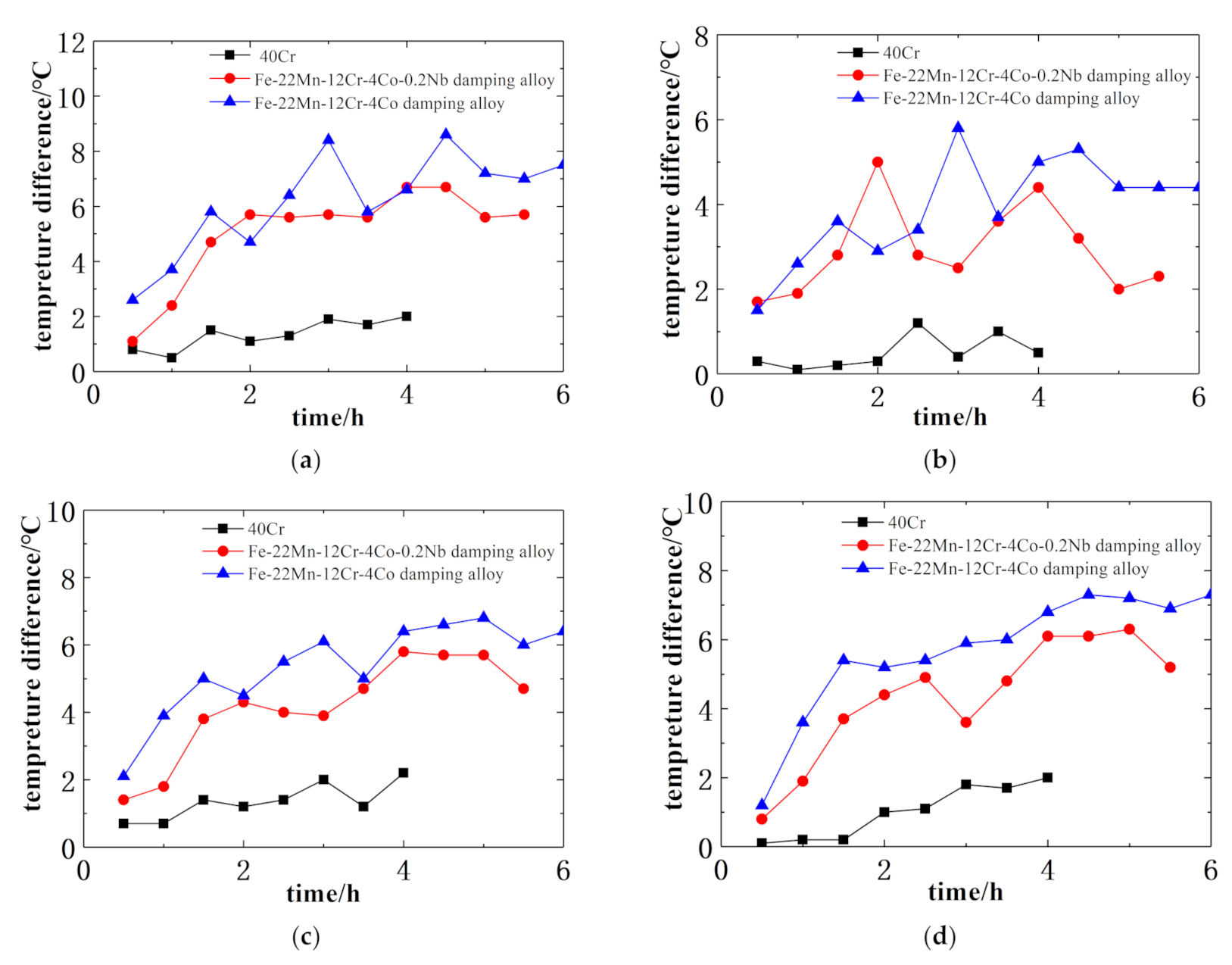
7.4. Comparison of Temperature Changes in Different Parts of the Gearbox during Gear Operation with Different Materials
8. Conclusions
- (1)
- A nonlinear constitutive model of Fe-Mn damping alloy materials based on viscoelastic theory was constructed and extended to a three-dimensional state using tensor theory, and the time increment step form of the constitutive model was derived;
- (2)
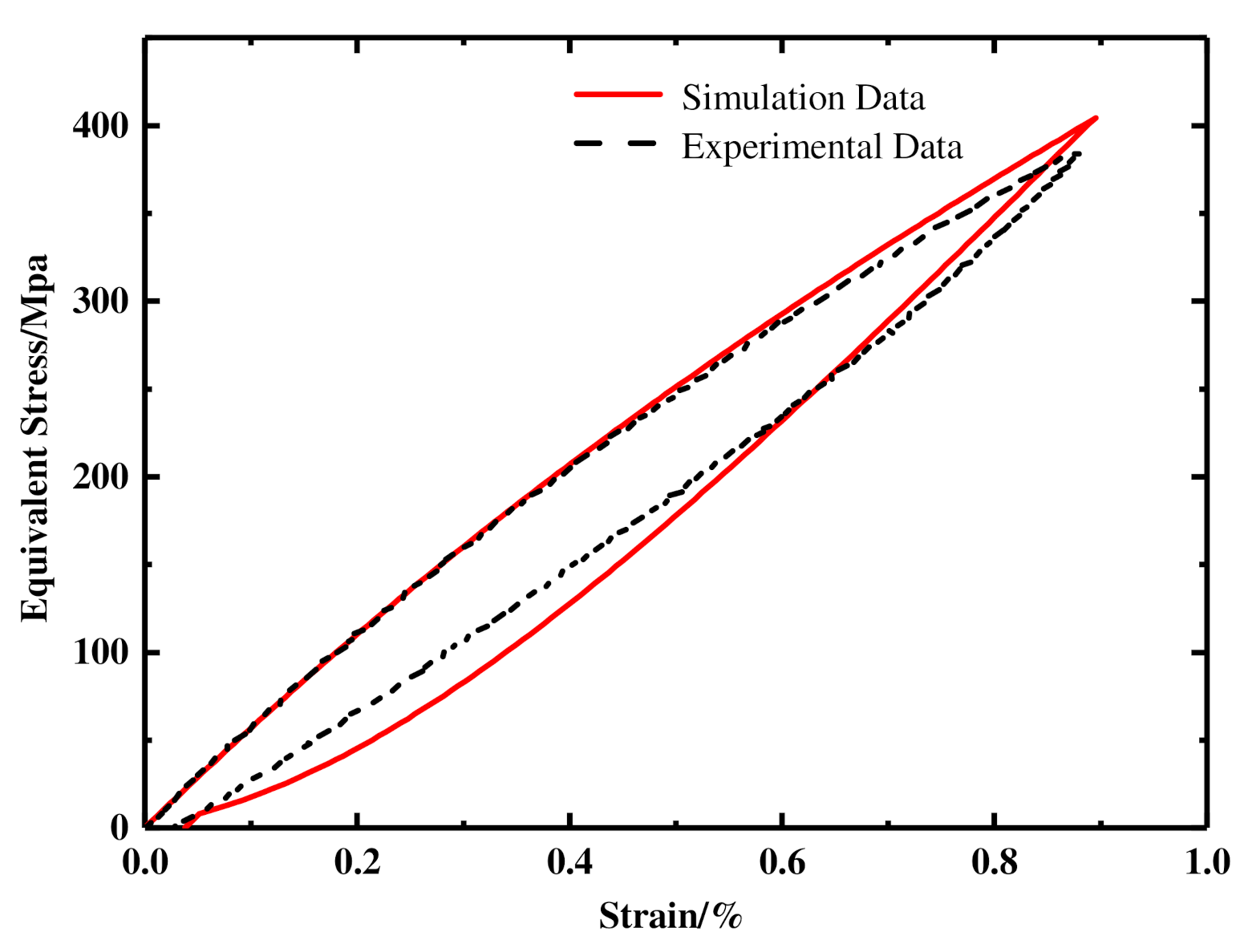
- Using the three-dimensional stress-strain expression of the nonlinear constitutive model of the damping alloy material and the stress recurrence relationship under the time increment step, the user subroutine UMAT of the nonlinear constitutive model of the Fe-Mn damping alloy materials was compiled, and the tensile test simulation of an Fe-Mn damping alloy rod was carried out. The experimental data of the Fe-Mn damping alloy tensile specimen are consistent with the simulation result. It was proved that the proposed constitutive model can accurately describe the mechanical behavior of the Fe-Mn damping alloy.
- (3)
- A transient dynamic analysis of the gearbox, in which spur gear pairs were fabricated by Fe-Mn damping alloys, was achieved using an LS-Dyna damping alloy material user subroutine. It can effectively and quantitatively evaluate the vibration damping performance of Fe-Mn alloys;
- (4)
- By comparing the time domain effective values of vibration acceleration between two kinds of damping alloy materials and 40Cr materials under different working conditions, it can be concluded that two kinds of damping alloy materials have an obvious damping effect. The damping effect of Fe-22Mn-12Cr-4Co alloy materials is better.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, M.H.; Brennan, M.J. Active control of gear vibration using specially configured sensors and actuators. Smart Mater. Struct. 2000, 9, 342–350. [Google Scholar] [CrossRef]
- Guan, Y.H.; Lim, T.C.; Shepard, W.S. Experimental study on active vibration control of a gearbox system. J. Sound Vib. 2005, 282, 713–733. [Google Scholar] [CrossRef]
- Okamura, H.; Suzuki, Y.; Nakano, N. Experiments and analysis of sound-damping rings for gears: Application of snap rings. In Proceedings of the Power Transmission and Gearing Conference, San Diego, CA, USA, 6–9 October 1996; pp. 345–349. [Google Scholar]
- Hume-Rothery, W. Elasticity and Anelasticity of Metals. Nature 1949, 164, 84–85. [Google Scholar] [CrossRef]
- Worrell, F.T. Twinning in tetragonal alloys of copper and manganese. J. Appl. Phys. 1948, 19, 929–933. [Google Scholar] [CrossRef]
- Bacon, G.E.; Dunmur, I.W.; Smith, J.H.; Street, R. The Antiferromagnetism of Manganese Copper Alloys. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 223–238. [Google Scholar]
- Lee, Y.K.; Jun, J.H.; Choi, C.S. Damping capacity in Fe-Mn binary alloys. ISIJ Int. 1997, 37, 1023–1030. [Google Scholar] [CrossRef] [Green Version]
- Baik, S.H. High damping Fe-Mn martensitic alloys for engineering applications. Nucl. Eng. Des. 2000, 198, 241–252. [Google Scholar] [CrossRef]
- Baik, S.H.; Kim, J.C.; Han, D.W.; Kim, T.H.; Back, J.H.; Lee, Y.K. Fe-Mn martensitic alloys for control of noise and vibration in engineering applications. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Proc. 2006, 438, 1101–1105. [Google Scholar] [CrossRef]
- Shariyat, M.; Mozaffari, A.; Pachenari, M.H. Damping sources interactions in impact of viscoelastic composite plates with damping treated SMA wires, using a hyperbolic plate theory. Appl. Math. Model. 2017, 43, 421–440. [Google Scholar] [CrossRef]
- Igata, N. Applications of High Damping Stainless Alloy (HIDAS). Key Eng. Mater. 2006, 319, 209–216. [Google Scholar] [CrossRef]
- Ha, K.; Schapery, R.A. A three-dimensional viscoelastic constitutive model for particulate composites with growing damage and its experimental validation. Int. J. Solids Struct. 1998, 35, 3497–3517. [Google Scholar] [CrossRef]
- Muliana, A.; Rajagopal, K.R.; Tscharnuter, D.; Pinter, G. A nonlinear viscoelastic constitutive model for polymeric solids based on multiple natural configuration theory. Int. J. Solids Struct. 2016, 100, 95–110. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, F.; Yu, C.; Kang, G. A Rate-Type Nonlinear Viscoelastic-Viscoplastic Cyclic Constitutive Model for Polymers: Theory and Application. Polym. Eng. Sci. 2016, 56, 1375–1381. [Google Scholar] [CrossRef]
- De Lima, A.M.G.; Guaraldo-Neto, B.; Sales, T.P.; Rade, D.A. A time-domain modeling of systems containing viscoelastic materials and shape memory alloys as applied to the problem of vibration attenuation. Eng. Struct. 2014, 68, 85–95. [Google Scholar] [CrossRef]
- Peultier, B.; Ben Zineb, T.; Patoor, E. A simplified micromechanical constitutive law adapted to the design of shape memory applications by finite element methods. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Proc. 2008, 481, 384–388. [Google Scholar] [CrossRef]
- Svobodnik, A.J.; Bohm, H.J.; Rammerstorfer, F.G. Elastic-Plastic Behavior of Metal Matrix Composites with a Special Emphasis on Finite Element Analysis. In Advances in Plasticity 1989; Khan, A.S., Tokuda, M., Eds.; Pergamon: Oxford, UK, 1989; pp. 137–140. [Google Scholar]
- Haghdoust, P.; Lo Conte, A.; Cinquemani, S.; Lecis, N. A Numerical Method to Model Non-linear Damping Behaviour of Martensitic Shape Memory Alloys. Materials 2018, 11, 2178. [Google Scholar] [CrossRef] [Green Version]
- Zhou, A.G.; Basu, S.; Friedman, G.; Finkel, P.; Yeheskel, O.; Barsoum, M.W. Hysteresis in kinking nonlinear elastic solids and the Preisach-Mayergoyz model. Phys. Rev. B 2010, 82, 094105. [Google Scholar] [CrossRef]
- Mahi, A.E.; Assarar, M.; Sefrani, Y.; Berthelot, J.M. Damping analysis of orthotropic composite materials and laminates. Compos. Part. B Eng. 2008, 39, 1069–1076. [Google Scholar] [CrossRef]
- Yun, K.S.; Park, J.B.; Jung, G.D.; Youn, S.K. Viscoelastic constitutive modeling of solid propellant with damage. Int. J. Solids Struct. 2016, 80, 118–127. [Google Scholar] [CrossRef]
- Peultier, B.; Zineb, T.B.; Patoor, E. Macroscopic constitutive law for SMA: Application to structure analysis by FEM. Mater. Sci. Eng. A 2018, 438, 454–458. [Google Scholar] [CrossRef]
- Haghdoust, P.; Conte, A.L.; Cinquemani, S.; Lecis, N. Experimental and Numerical Characterization of High Damping Martensitic CuAlMn Sheets. Materials. 2020, 13, 529. [Google Scholar] [CrossRef] [Green Version]
- Muravskii, G. On description of hysteretic behaviour of materials. Int. J. Solids Struct. 2005, 42, 2625–2644. [Google Scholar] [CrossRef]
- Toolabi, M.; Fallah, A.S.; Baiz, P.M.; Louca, L.A. Dynamic analysis of a viscoelastic orthotropic cracked body using the extended finite element method. Eng. Fract. Mech. 2013, 109, 17–32. [Google Scholar] [CrossRef]
- Sun, T.S.; Yu, C.G.; Wang, Q.; Zhong, J.L. Creep Prediction of GFRP Directors in Multiple Launch Rocket System under Long-term Stacking Storage. Trans. Can. Soc. Mech. Eng. 2020, 45, 147–158. [Google Scholar] [CrossRef]
- Abu Al-Rub, R.K.; Tehrani, A.H.; Darabi, M.K. Application of a large deformation nonlinear-viscoelastic viscoplastic viscodamage constitutive model to polymers and their composites. Int. J. Damage Mech. 2014, 24, 198–244. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Luo, Q.; Peng, H.; Wen, Y. Designing damping capacity in high strength Fe–Mn based alloys by controlling crystal defect configurations. J. Philos. Mag. 2021, 101, 1765–1781. [Google Scholar] [CrossRef]
- Wen, Y.; Xiao, H.; Peng, H.; Li, N.; Raabe, D. Relationship Between Damping Capacity and Variations of Vacancies Concentration and Segregation of Carbon Atom in an Fe-Mn Alloy. Metall. Mater. Trans. A 2015, 46, 4828–4833. [Google Scholar] [CrossRef]









| Alloy | Chemical Compound (wt.%) | ||||
|---|---|---|---|---|---|
| Mn | Cr | Co | Nb | C | |
| FeMnCrCo | 22 | 12 | 4 | 0 | 0.02 |
| FeMnCrCoNb | 22 | 12 | 4 | 0.2 | 0.02 |
| γ Austenite (f.c.c.) a = 3.60 Å | ε Martensite (h.c.p.) a = 2.54 Å, c = 4.14 Å | α’ Martensite (b.c.c.) a = 2.866 Å | ||||||
|---|---|---|---|---|---|---|---|---|
| hkl | d (Å) | 2θ (°) | hkl | d (Å) | 2θ (°) | hkl | d (Å) | 2θ (°) |
| 111 | 2.08 | 50.85 | 100 | 2.195 | 48.14 | 110 | 2.027 | 52.19 |
| 200 | 1.8 | 58.72 | 002 | 2.071 | 51.07 | 200 | 1.433 | 72.15 |
| 220 | 1.27 | 78.53 | 101 | 1.94 | 54.54 | 211 | 1.17 | 81.58 |
| 311 | 1.083 | 82.61 | 102 | 1.506 | 69.25 | 220 | 1.013 | 81.20 |
| 222 | 1.037 | 81.99 | 110 | 1.268 | 78.60 | 310 | 0.906 | 71.03 |
| 103 | 1.169 | 81.60 | ||||||
| 200 | 1.098 | 82.60 | ||||||
| 112 | 1.079 | 82.59 | ||||||
| 201 | 1.062 | 82.46 | ||||||
| Material Type | α/MPa | β/MPa | |||
|---|---|---|---|---|---|
| Fe-Mn damping alloy material | 5.953 × 104 | −2.297 × 106 | 6.147 × 107 | 1078 | 0.067 |
| Material Type | a/MPa | b/MPa | c/MPa | ||
|---|---|---|---|---|---|
| Fe-Mn damping alloy material | 3.662 × 104 | −3.745 × 105 | 1.334 × 108 | 1078 | 0.067 |
| Equipment | Main Parameters |
|---|---|
| Three-phase induction motor | Type: Y2VP132M-4, rated power: 7.5 kW, rated voltage: 380 V, frequency: 50 Hz, electricity: 26.2 A, rated speed: 1445 r/min, rated torque: 47.7 N·m, connection: Y, protection class of enclosure: IP54 |
| Torque and speed sensor | Type: JC1A, rated torque(range): 50 N·m accuracy class: 0.2, calibration temperature: 21 °C, working speed: 0~6000 r/min |
| Magnetic powder brake | Type: CZ-5, rated torque: 50 N·m, magnetizing current: 0.8 A, slip power: 4kW, weight: 20 kg, cooling method: single water cooling |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, P.; Yang, W.; Jiang, K.; Yang, J.; Shi, W. Study on Vibration Reduction Performance of Gear Pairs Made by a High-Strength Fe-Mn Damping Alloy. Appl. Sci. 2022, 12, 3925. https://doi.org/10.3390/app12083925
Xiao P, Yang W, Jiang K, Yang J, Shi W. Study on Vibration Reduction Performance of Gear Pairs Made by a High-Strength Fe-Mn Damping Alloy. Applied Sciences. 2022; 12(8):3925. https://doi.org/10.3390/app12083925
Chicago/Turabian StyleXiao, Ping, Wei Yang, Kongming Jiang, Jiafeng Yang, and Wankai Shi. 2022. "Study on Vibration Reduction Performance of Gear Pairs Made by a High-Strength Fe-Mn Damping Alloy" Applied Sciences 12, no. 8: 3925. https://doi.org/10.3390/app12083925
APA StyleXiao, P., Yang, W., Jiang, K., Yang, J., & Shi, W. (2022). Study on Vibration Reduction Performance of Gear Pairs Made by a High-Strength Fe-Mn Damping Alloy. Applied Sciences, 12(8), 3925. https://doi.org/10.3390/app12083925





