A New Maximum Power Point Tracking Framework for Photovoltaic Energy Systems Based on Remora Optimization Algorithm in Partial Shading Conditions
Abstract
:1. Introduction
2. PV Cell and PSC Modeling
2.1. PV Cell Modeling
2.2. MPPT and the Effect of PSC
3. The Proposed ROA Based MPPT
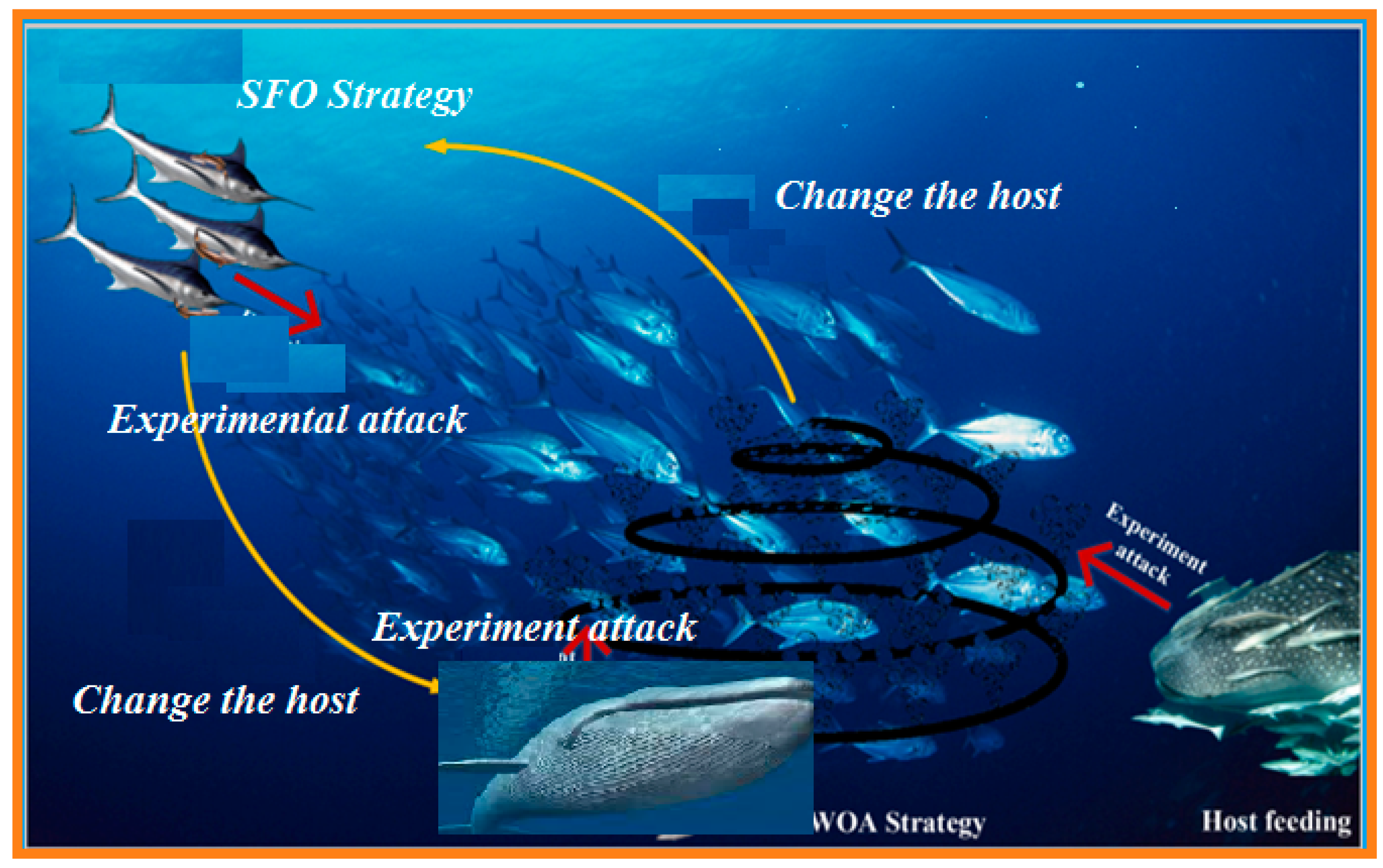
3.1. Overview of ROA
3.1.1. Preparation (Initialization)
3.1.2. Free Travel (Exploration)
- Swordfish optimization strategy
- Attack experience
3.1.3. Thoughtful Nutrition (Exploitation)
- Whale Optimization Algorithm (WOA) Strategy
- Host nutrition
| Algorithm 1 Pseudo-code of the ROA |
| 1: Initiate the population and memory location Ri and Rpre; 2: Initiate the RBest as optimal solution and f(RBest) as its optimal fitness; 3: While t < T do 4: Compute the fitness value of each ROA population; 5: Investigate if any remora goes beyond the search space and amend it; 6: Update a,α and V; 7: For each remora indexed by i do 8: If H(i) = 0 then 9: Based on Equation (6), update the whales position; 10: Elseif H(i) = 1 then 11: Based on Equation (2) update the Sailfishes position; 12: Endif 13: Make a prediction via Equation (3); 14: Calculate the H(i) value via Equations (4) and (5) to evaluate whether host replacement is vital; 15: In case of non-replacement of the host, Equation (10) is applied as the host feeding state; 16: End for 17: End while |
3.2. Application of the ROA for MPPT
4. Simulation Results
- Pattern (1) STC with uniform radiation of 1000 W/m2;
- Pattern (2) PSC with non-uniform radiation of 1000 and 700 W/m2;
- Pattern (3) PSC with non-uniform radiation of 900 and 600 W/m2.
4.1. Results of Pattern 1
4.2. Results of Pattern 2
4.3. Results of Pattern 3
4.4. Results Comparison of Patterns 1–3
- The implementation of the ROA in MPPT solving is easy, its complexity is low, and it is also not trapped in the local optimal solution.
- The ROA achieved global power in all patterns with desirable exploration power.
- The ROA extracted more PV maximum power in all patterns than the MRFO and PSO methods. The PSO algorithm is an optimization method that may be involved in premature convergence and trapped with a local optimal solution in solving the optimization problem. The random selection of reference points in the early iterations weakens the exploitation capability of MRFO. Furthermore, hain foraging tends to lead the algorithm into local optimum. However, the ROA has high exploitative, exploratory, and local optimal avoidance capabilities. Therefore, these cases increase the accuracy of tracking and reduce state steady errors in a shorter time than other methods. The above cases are the reasons for the superiority of the ROA over other methods.
- The ROA with highly competitive capability has been able to solve the PV MPPT problem for different patterns with higher efficiency and tracking rate.
4.5. Results of Pattern 4
4.6. Results of Temperature Variations
4.7. Results Comparison with Previous Studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arabi-Nowdeh, S.; Nasri, S.; Saftjani, P.B.; Naderipour, A.; Abdul-Malek, Z.; Kamyab, H.; Jafar-Nowdeh, A. Multi-criteria optimal design of hybrid clean energy system with battery storage considering off-and on-grid application. J. Clean. Prod. 2021, 290, 125808. [Google Scholar] [CrossRef]
- Nasri, S.; Nowdeh, S.A.; Davoudkhani, I.F.; Moghaddam, M.J.H.; Kalam, A.; Shahrokhi, S.; Zand, M. Maximum Power Point Tracking of Photovoltaic Renewable Energy System Using a New Method Based on Turbulent Flow of Water-Based Optimization (TFWO) Under Partial Shading Conditions. In Fundamentals and Innovations in Solar Energy, 1st ed.; Singh, S.N., Tiwari, P., Tiwari, S., Eds.; Springer: Singapore, 2021; pp. 285–310. [Google Scholar]
- Davoodkhani, F.; Nowdeh, S.A.; Abdelaziz, A.Y.; Mansoori, S.; Nasri, S.; Alijani, M. A new hybrid method based on gray wolf optimizer-crow search algorithm for maximum power point tracking of photovoltaic energy system. In Modern Maximum Power Point Tracking Techniques for Photovoltaic Energy Systems; E-Book; Eltamaly, A.M., Abdelaziz, A.Y., Eds.; Springer: Cham, Switzerland, 2020; pp. 421–438. [Google Scholar]
- Rezk, H.; Eltamaly, A.M. A comprehensive comparison of different MPPT techniques for photovoltaic systems. Sol. Energy 2015, 112, 1–11. [Google Scholar] [CrossRef]
- Shaiek, Y.; Smida, M.B.; Sakly, A.; Mimouni, M.F. Comparison between conventional methods and GA approach for maximum power point tracking of shaded solar PV generators. Sol. Energy 2013, 90, 107–122. [Google Scholar] [CrossRef]
- Li, S. A MPPT control strategy with variable weather parameter and no DC/DC converter for photovoltaic systems. Sol. Energy 2014, 108, 117–125. [Google Scholar] [CrossRef]
- Salas, V.; Olias, E.; Barrado, A.; Lazaro, A. Review of the maximum power point tracking algorithms for stand-alone photovoltaic systems. Sol. Energy Mater. Sol. Cells 2006, 90, 1555–1578. [Google Scholar] [CrossRef]
- Nowdeh, S.A.; Moghaddam, M.J.H.; Babanezhad, M.; Davoodkhani, I.F.; Kalam, A.; Ahmadi, A.; Abdelaziz, A.Y. A novel maximum power point tracking method for photovoltaic application using secant incremental gradient based on Newton Raphson. In Solar Photovoltaic Power Plants; E-Book; Precup, R.-E., Kamal, T., Hassan, S.Z., Eds.; Springer: Singapore, 2019; pp. 71–96. [Google Scholar]
- Pan, J.S.; Tian, A.Q.; Snášel, V.; Kong, L.; Chu, S.C. Maximum power point tracking and parameter estimation for multiple-photovoltaic arrays based on enhanced pigeon-inspired optimization with Taguchi method. Energy 2022, 123865. [Google Scholar] [CrossRef]
- Nowdeh, S.A.; Moghaddam, M.J.H.; Nasri, S.; Abdelaziz, A.Y.; Ghanbari, M.; Faraji, I. A New Hybrid Moth Flame Optimizer-Perturb and Observe Method for Maximum Power Point Tracking in Photovoltaic Energy System. In Modern Maximum Power Point Tracking Techniques for Photovoltaic Energy Systems; E-Book; Eltamaly, A.M., Abdelaziz, A.Y., Eds.; Springer: Cham, Switzerland, 2020; pp. 401–420. [Google Scholar]
- Carannante, G.; Fraddanno, C.; Pagano, M.; Piegari, L. Experimental performance of MPPT algorithm for photovoltaic sources subject to inhomogeneous insolation. IEEE Trans. Ind. Electron. 2009, 56, 4374–4380. [Google Scholar] [CrossRef]
- Kobayashi, K.; Takano, I.; Sawada, Y. A study on a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 4, pp. 2612–2617. [Google Scholar]
- Ahmed, N.A.; Miyatake, M. A novel maximum power point tracking for photovoltaic applications under partially shaded insolation conditions. Electr. Power Syst. Res. 2008, 78, 777–784. [Google Scholar] [CrossRef]
- Renaudineau, H.; Houari, A.; Martin, J.P.; Pierfederici, S.; Meibody-Tabar, F.; Gerardin, B. A new approach in tracking maximum power under partially shaded conditions with consideration of converter losses. Sol. Energy 2011, 85, 2580–2588. [Google Scholar] [CrossRef]
- Lei, P.; Li, Y.; Seem, J.E. Sequential ESC-based global MPPT control for photovoltaic array with variable shading. IEEE Trans. Sustain. Energy 2011, 2, 348–358. [Google Scholar]
- Karatepe, E.; Hiyama, T. Artificial neural network-polar coordinated fuzzy controller based maximum power point tracking control under partially shaded conditions. IET Renew. Power Gener. 2009, 3, 239–253. [Google Scholar]
- Femia, N.; Lisi, G.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Distributed maximum power point tracking of photovoltaic arrays: Novel approach and system analysis. IEEE Trans. Ind. Electron. 2008, 55, 2610–2621. [Google Scholar] [CrossRef] [Green Version]
- Mathi, D.K.; Chinthamalla, R. Enhanced leader adaptive velocity particle swarm optimisation based global maximum power point tracking technique for a PV string under partially shaded conditions. IET Renew. Power Gener. 2020, 14, 243–253. [Google Scholar] [CrossRef]
- Kaced, K.; Larbes, C.; Ramzan, N.; Bounabi, M.; elabadine Dahmane, Z. Bat algorithm based maximum power point tracking for photovoltaic system under partial shading conditions. Sol. Energy 2017, 158, 490–503. [Google Scholar] [CrossRef] [Green Version]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A new MPPT design using grey wolf optimization technique for photovoltaic system under partial shading conditions. IEEE Trans. Sustain. Energy 2016, 7, 181–188. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Rezk, H. Global MPPT based on flower pollination and differential evolution algorithms to mitigate partial shading in building integrated PV system. Sol. Energy 2017, 157, 171–186. [Google Scholar] [CrossRef]
- Abadi, I.; Uyuniyah, Q.; Fitriyanah, D.N.; Jani, Y.; Abdullah, K. Performance Study of Maximum Power Point Tracking (MPPT) Based on Type-2 Fuzzy Logic Controller on Active Dual Axis Solar Tracker. In Proceedings of the E3S Web of Conferences, Padang, Indonesia, 12–14 November 2019; EDP Sciences: Les Ulis, France, 2020; Volume 190, p. 00016. [Google Scholar]
- Yang, B.; Zhang, M.; Zhang, X.; Wang, J.; Shu, H.; Li, S.; He, T.; Yang, L.; Yu, T. Fast atom search optimization based MPPT design of centralized thermoelectric generation system under heterogeneous temperature difference. J. Clean. Prod. 2020, 248, 119301. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H.; Yousri, D. A robust global MPPT to mitigate partial shading of triple-junction solar cell-based system using manta ray foraging optimization algorithm. Sol. Energy 2020, 207, 305–316. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Lang, C. Remora optimization algorithm. Expert Syst. Appl. 2021, 185, 115665. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A.; Abdelaziz, A.Y. A comparison of different global MPPT techniques based on meta-heuristic algorithms for photovoltaic system subjected to partial shading conditions. Renew. Sustain. Energy Rev. 2017, 74, 377–386. [Google Scholar] [CrossRef]
- Dileep, G.; Singh, S.N. An improved particle swarm optimization based maximum power point tracking algorithm for PV system operating under partial shading conditions. Sol. Energy 2017, 158, 1006–1015. [Google Scholar] [CrossRef]
- Premkumar, M.; Sowmya, R. An effective maximum power point tracker for partially shaded solar photovoltaic systems. Energy Rep. 2019, 5, 1445–1462. [Google Scholar] [CrossRef]




















| Method | Control Item | Value |
|---|---|---|
| Particle swarm optimization [18] | Social parameters | (C1 = 2, C2 = 2) |
| Weights of inertia | 0.1–0.9 | |
| Velocity | 10% of dimension value | |
| Multi-verse optimizer [25] | Exploitation accuracy (p) | 6 |
| Grey wolf optimizer [20] | Convergence control, a | From 0 to 2 |
| Bat algorithm [19] | Qmin and Qmax | 0 and 2 |
| A and r | 0.5 and 0.5 | |
| Flower pollution algorithm [21] | Probability parameter, p | 0.8 |
| Crow search algorithm [3] | pa | 0.25 |
| Moth flame optimizer [10] | a | [−2, −1] |
| b | 1 | |
| Manta ray foraging optimizer [25] | a | [0, 1] |
| w | [0, 1] | |
| r1, r2 and r3 | [0, 1] | |
| Atom search optimization [23] | Mining capability p | 1/6 |
| Random parameters r1, r2, r3 & r4 | [0, 1] | |
| Contrast parameter H | 0.5 | |
| Remora optimization algorithm (ROA) | Remora factor C | [0, 0.3] |
| Item | Value |
|---|---|
| Maximum of PV power | 56.75 W |
| Voltage of open circuit | 21 V |
| Maximum of PV voltage | 14.56 V |
| Current of short circuit | 5 A |
| Maximum of PV current | 3.898 A |
| Coefficient of voltage temperature | −0.085 V/°C |
| Coefficient of current temperature | 0.0051 A/°C |
| Item | Value |
|---|---|
| Frequency of switching | 50 kHz |
| C | 440 × 10−6 6 F |
| L | 2.5 × 10−³ H |
| R | 50 Ohm |
| Parameter/Method | ROA | MFRO | PSO |
|---|---|---|---|
| Global power (W) | 113.42 | 113.42 | 113.42 |
| Extracted power (W) | 113.39 | 113.36 | 113.32 |
| Tracking efficiency (%) | 99.97 | 99.94 | 99.91 |
| Tracking rate (S) | 0.66 | 1.12 | 3.01 |
| Parameter/Method | ROA | MFRO | PSO |
|---|---|---|---|
| Global power (W) | 90.54 | 90.54 | 90.54 |
| Extracted power (W) | 90.52 | 90.47 | 90.45 |
| Tracking efficiency (%) | 99.97 | 99.92 | 99.90 |
| Tracking rate (S) | 1.08 | 2.25 | 2.78 |
| Parameter/Method | ROA | MFRO | PSO |
|---|---|---|---|
| Global power (W) | 79.72 | 79.72 | 79.72 |
| Extracted power (W) | 79.69 | 79.65 | 79.61 |
| Tracking efficiency (%) | 99.96 | 99.91 | 99.86 |
| Tracking rate (S) | 0.90 | 2.20 | 3.10 |
| Parameter/Method | ROA | MFRO | PSO |
|---|---|---|---|
| Global power (W) | 80.62 | 80.62 | 80.62 |
| Extracted power (W) | 80.37 | 80.25 | 79.68 |
| Tracking efficiency (%) | 99.68 | 99.54 | 98.83 |
| Tracking rate (S) | 0.70 | 0.91 | 1.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alanazi, A.; Alanazi, M.; Arabi, S.; Sarker, S. A New Maximum Power Point Tracking Framework for Photovoltaic Energy Systems Based on Remora Optimization Algorithm in Partial Shading Conditions. Appl. Sci. 2022, 12, 3828. https://doi.org/10.3390/app12083828
Alanazi A, Alanazi M, Arabi S, Sarker S. A New Maximum Power Point Tracking Framework for Photovoltaic Energy Systems Based on Remora Optimization Algorithm in Partial Shading Conditions. Applied Sciences. 2022; 12(8):3828. https://doi.org/10.3390/app12083828
Chicago/Turabian StyleAlanazi, Abdulaziz, Mohana Alanazi, Saber Arabi, and Shiplu Sarker. 2022. "A New Maximum Power Point Tracking Framework for Photovoltaic Energy Systems Based on Remora Optimization Algorithm in Partial Shading Conditions" Applied Sciences 12, no. 8: 3828. https://doi.org/10.3390/app12083828
APA StyleAlanazi, A., Alanazi, M., Arabi, S., & Sarker, S. (2022). A New Maximum Power Point Tracking Framework for Photovoltaic Energy Systems Based on Remora Optimization Algorithm in Partial Shading Conditions. Applied Sciences, 12(8), 3828. https://doi.org/10.3390/app12083828








