Ultra-Wideband Bandpass Filters Using Tapered Resonators
Abstract
:1. Introduction
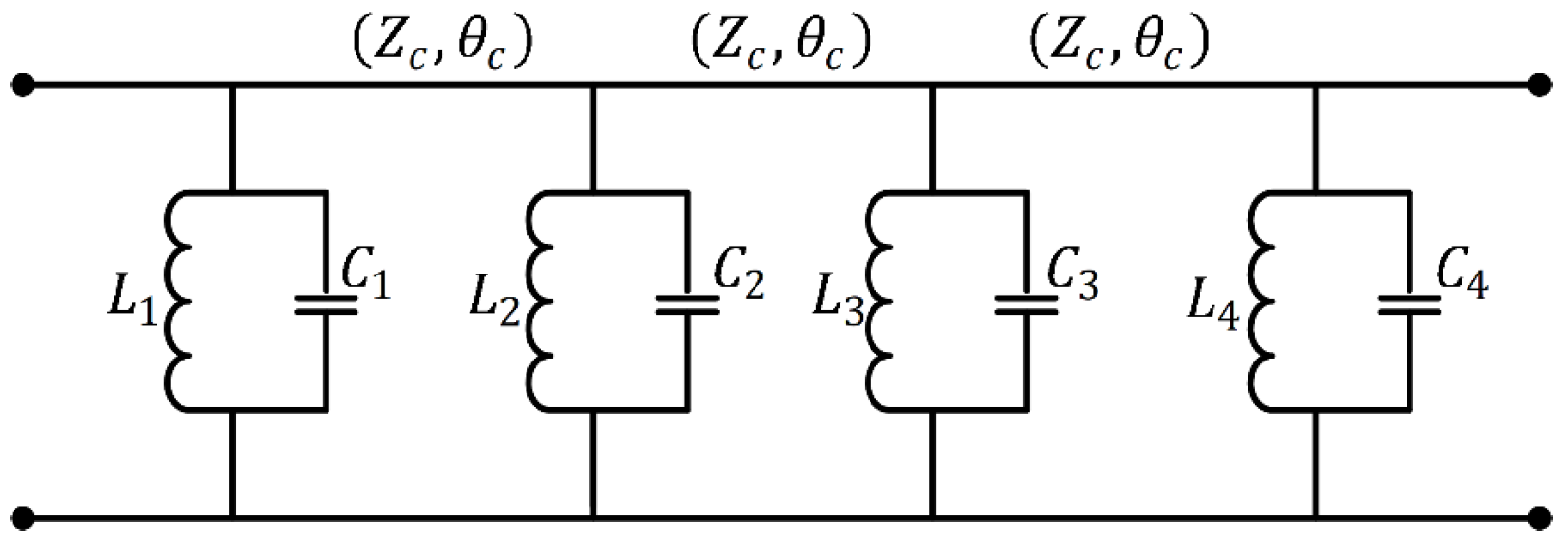
2. Analysis
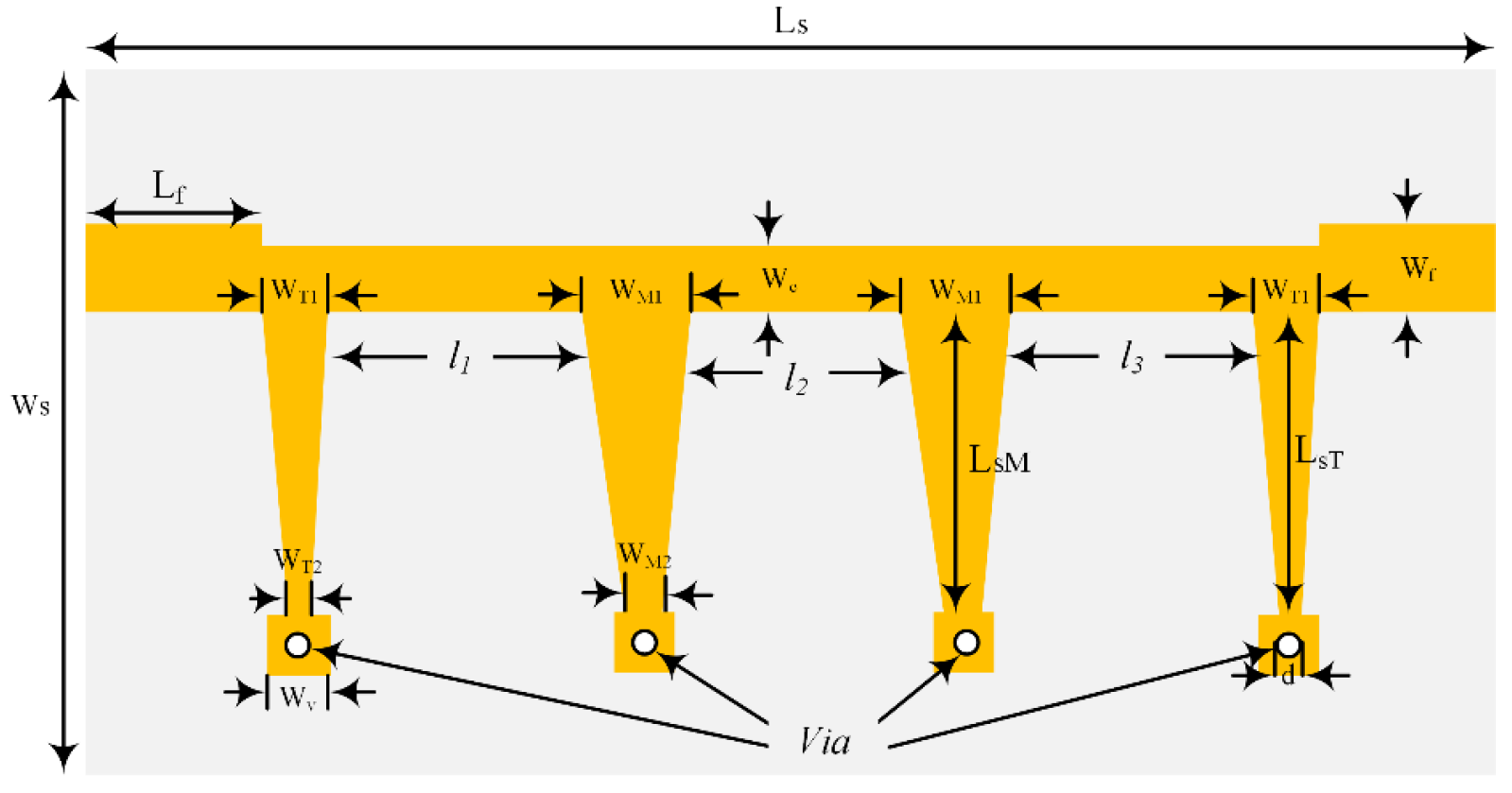
3. Design of Tapered Resonators
4. UWB Bandpass Filter Design
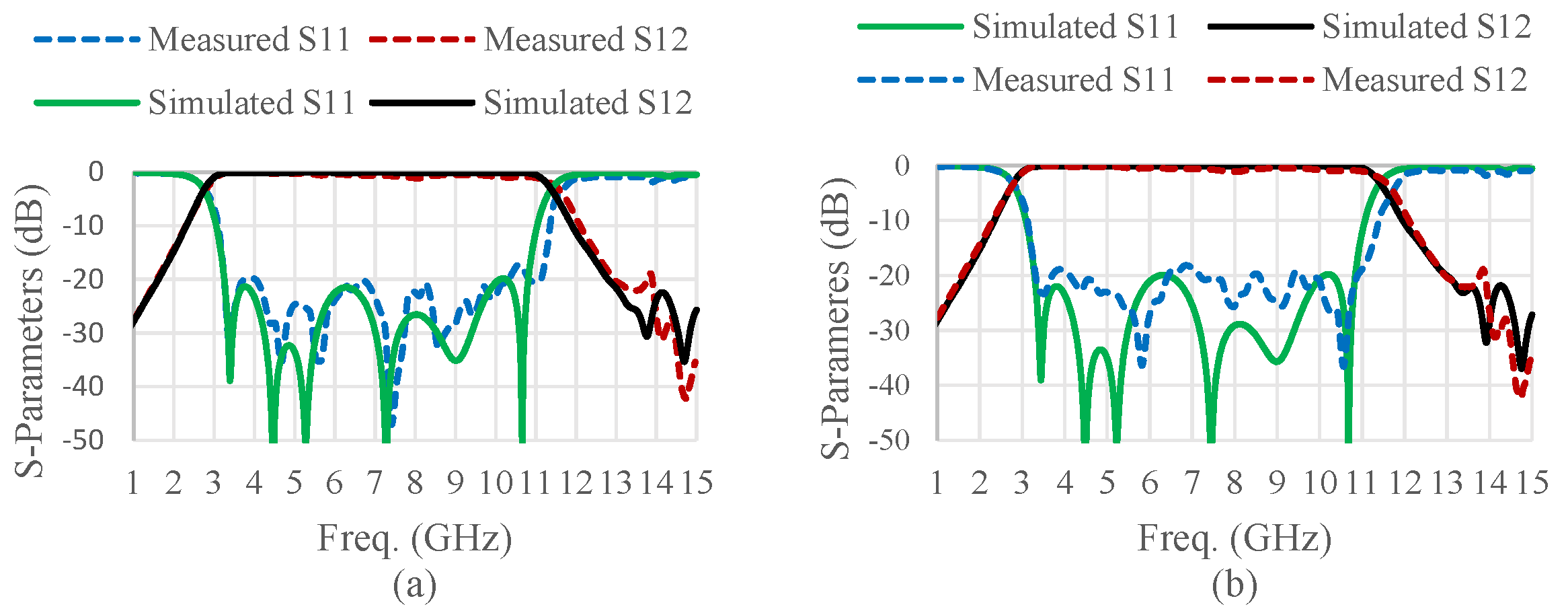
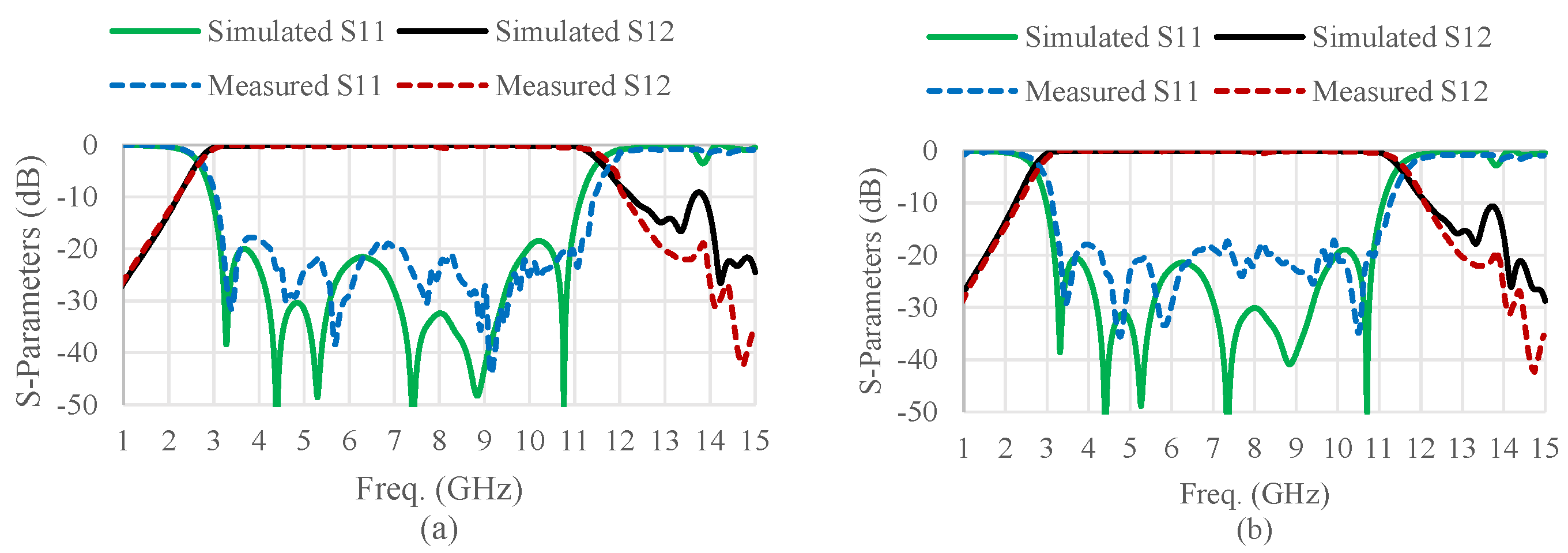
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Federal Communications Commission. Federal Communications Commission Revision of Part 15 of the Commission’s Rules Regarding Ultra-Wideband Transmission System from 3.1 to 10.6 GHz; Federal Communications Commission: Washington, DC, USA, 2002. [Google Scholar]
- Hao, Z.-C.; Hong, J.-S. Ultrawideband filter technologies. IEEE Microw. Mag. 2010, 11, 56–68. [Google Scholar] [CrossRef]
- Jamsai, M.; Angkawisittpan, N.; Nuan-On, A. Design of a compact ultra-wideband bandpass filter using inductively compensated parallel-coupled lines. Electronics 2021, 10, 2575. [Google Scholar] [CrossRef]
- Shome, P.P.; Khan, T.; Koul, S.K.; Antar, Y.M. Two Decades of UWB Filter Technology: Advances and Emerging Challenges in the Design of UWB Bandpass Filters. IEEE Microw. Mag. 2021, 22, 32–51. [Google Scholar] [CrossRef]
- Sun, S.; Zhu, L. Multiple-resonator-based bandpass filters. IEEE Microw. Mag. 2009, 10, 88–98. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, S.; Menzel, W. Ultra-wideband (UWB) bandpass filters using multiple-mode resonator. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 796–798. [Google Scholar]
- Li, R.; Zhu, L. Compact UWB bandpass filter using stub-loaded multiple-mode resonator. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 40–42. [Google Scholar] [CrossRef]
- Song, K.; Fan, Y. Compact ultra-wideband bandpass filter using dual-line coupling structure. IEEE Microw. Wirel. Compon. Lett. 2008, 19, 30–32. [Google Scholar] [CrossRef]
- Shaman, H.; Hong, J.-S. A novel ultra-wideband (UWB) bandpass filter (BPF) with pairs of transmission zeroes. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 121–123. [Google Scholar] [CrossRef]
- Shahrazel Razalli, M.; Ismail, A.; Adzir Mahdi, M.; Nizar Hamidon, M. Ultra-wide band microwave filter utilizing quarter-wavelength short-circuited stubs. Microw. Opt. Technol. Lett. 2008, 50, 2981–2983. [Google Scholar] [CrossRef]
- Razalli, M.S.; Ismail, A.; Mahdi, M.A.; bin Hamidon, M.N. Novel compact microstrip ultra-wideband filter utilizing short-circuited stubs with less vias. Prog. Electromagn. Res. 2008, 88, 91–104. [Google Scholar] [CrossRef] [Green Version]
- Hong, J.-S. Microstrip Filters for RF/Microwave Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Thomson, N.; Hong, J.-S. Compact ultra-wideband microstrip/coplanar waveguide bandpass filter. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 184–186. [Google Scholar] [CrossRef]
- Kuo, T.-N.; Lin, S.-C.; Chen, C.H. Compact ultra-wideband bandpass filters using composite microstrip–coplanar-waveguide structure. IEEE Trans. Microw. Theory Tech. 2006, 54, 3772–3778. [Google Scholar] [CrossRef]
- Tang, C.-W.; Chen, M.-G. A microstrip ultra-wideband bandpass filter with cascaded broadband bandpass and bandstop filters. IEEE Trans. Microw. Theory Tech. 2007, 55, 2412–2418. [Google Scholar] [CrossRef]
- Shaman, H.; Hong, J.-S. Ultra-wideband (UWB) bandpass filter with embedded band notch structures. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 193–195. [Google Scholar] [CrossRef]
- Guan, X.; Gui, P.; Xiong, T.; Ren, B.; Zhu, L. Hybrid microstrip/slotline ultra-wideband bandpass filter with a controllable notch band. Int. J. Antennas Propag. 2017, 2017, 2398610. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Jiang, T. Realization of dual notch bands in UWB bandpass filter using two T-shaped resonators. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium-Italy (ACES), Firenze, Italy, 26–30 March 2017; pp. 1–2. [Google Scholar]
- Womack, C.P. The use of exponential transmission lines in microwave components. IRE Trans. Microw. Theory Tech. 1962, 10, 124–132. [Google Scholar] [CrossRef]
- Holt, A. General principle of electrical equivalence for nonuniform transmission lines. Electron. Lett. 1969, 5, 143–144. [Google Scholar] [CrossRef]
- Rustogi, O. Linearly Tapered Transmission Line and Its Application in Microwaves (Correspondence). IEEE Trans. Microw. Theory Tech. 1969, 17, 166–168. [Google Scholar] [CrossRef]
- Mathur, S.; Sinha, A.K.; Sinha, A. Design of microstrip exponentially tapered lines to match helical antennas to standard coaxial transmission lines. IETE Tech. Rev. 1988, 5, 426–429. [Google Scholar] [CrossRef]
- Shome, P.P.; Khan, T. A compact design of circular ring-shaped MMR based bandpass filter for UWB applications. In Proceedings of the 2019 IEEE Asia-Pacific Microwave Conference (APMC), Singapore, 10–13 December 2019; pp. 962–964. [Google Scholar]
- Shaman, H.; Hong, J.-S. An optimum ultra-wideband (UWB) bandpass filter with spurious response suppression. In Proceedings of the 2006 IEEE Annual Wireless and Microwave Technology Conference, Clearwater Beach, FL, USA, 4–5 December 2006; pp. 1–5. [Google Scholar]
- Djeddi, T.; Elsaadany, M.; Shams, S.; Hamouda, W. Compact ultra-wideband printed bandpass filter based on coupled-line resonator loading. In Proceedings of the 2018 18th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), Waterloo, ON, Canada, 19–22 August 2018; pp. 1–2. [Google Scholar]
- Ye, J.-D.; He, L.; Zhong, X.-J.; Qu, D.-X. Design of ultra-wideband bandpass (UWB) filter with enhanced couplings by using lumped capacitors. In Proceedings of the 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Chengdu, China, 7–11 May 2018; pp. 1–3. [Google Scholar]
- Jhariya, D.K.; Mohan, A.; Sinha, M. Design of two-stage fish spear-shaped UWB bandpass filter with sharp selectivity and good out-of-band performances. Int. J. Microw. Wirel. Technol. 2017, 9, 1821–1826. [Google Scholar] [CrossRef]
- Ghazali, A.N.; Sazid, M.; Virdee, B. A compact UWB-BPF based on microstrip-to-CPW transition with multiple transmission zeros. Microw. Opt. Technol. Lett. 2018, 60, 1925–1928. [Google Scholar] [CrossRef]
- Xie, J.; Tang, D.; Shu, Y.; Luo, X. Compact UWB BPF With Broad Stopband Based on Loaded-Stub and C-Shape SIDGS Resonators. IEEE Microw. Wirel. Compon. Lett. 2021, 1–4. [Google Scholar] [CrossRef]
- Shome, P.P.; Khan, T. A quintuple mode resonator based bandpass filter for ultra-wideband applications. Microsyst. Technol. 2020, 26, 2295–2304. [Google Scholar] [CrossRef]
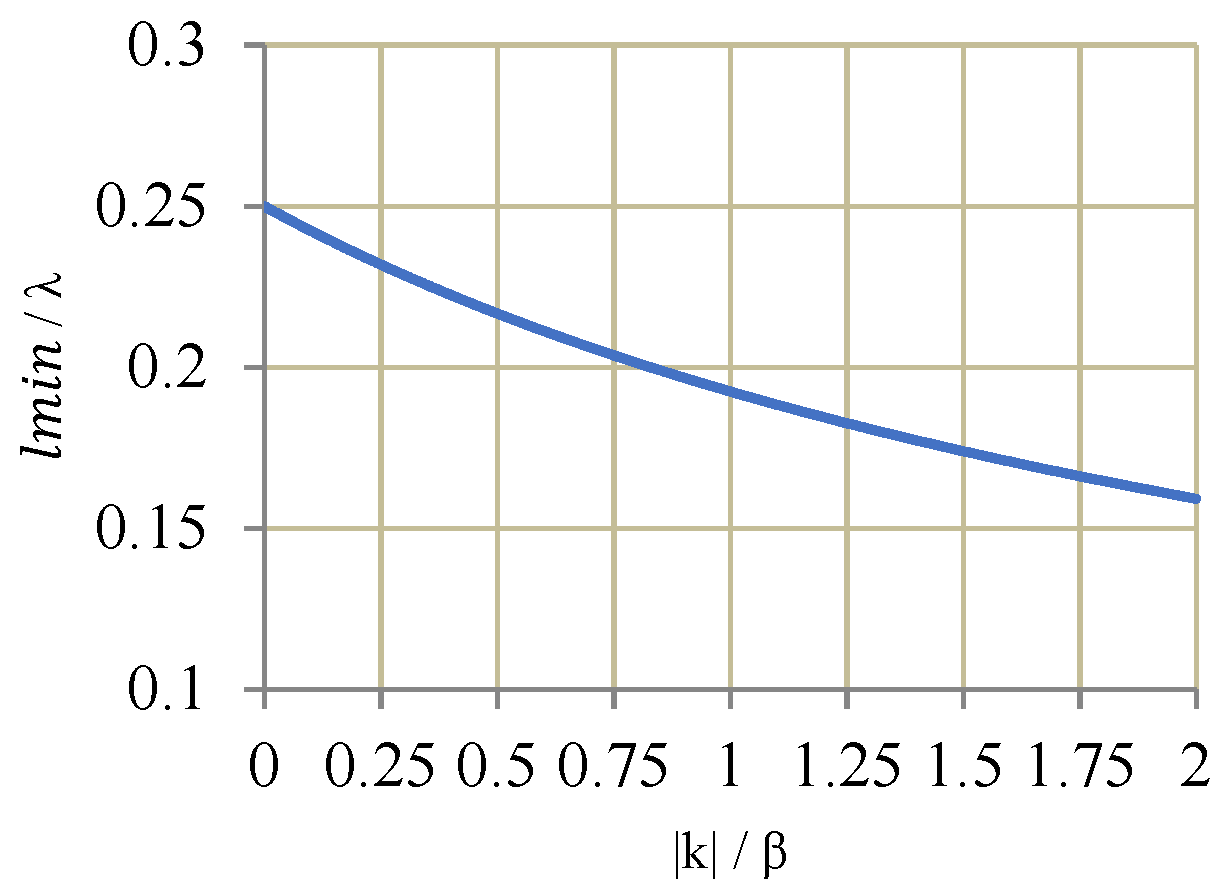
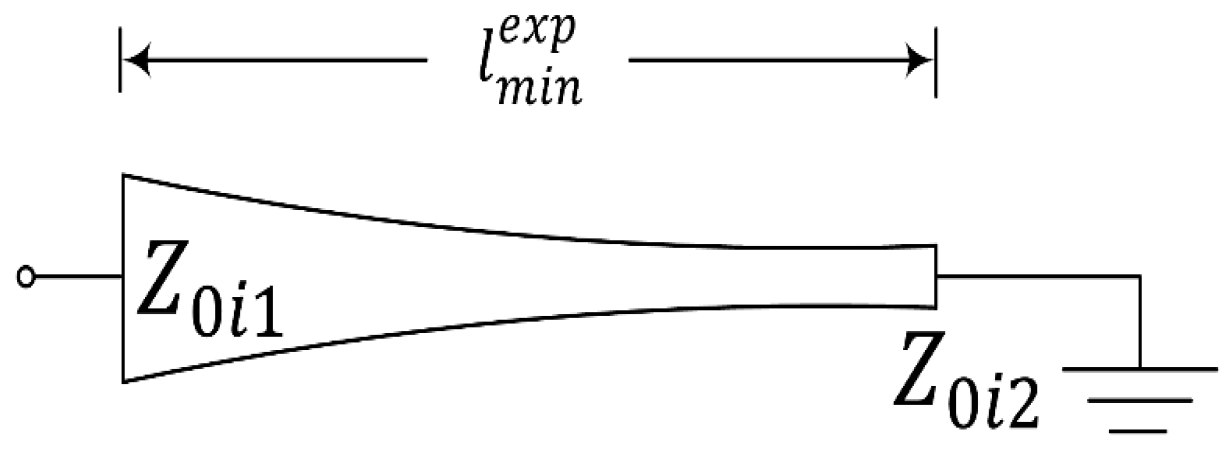
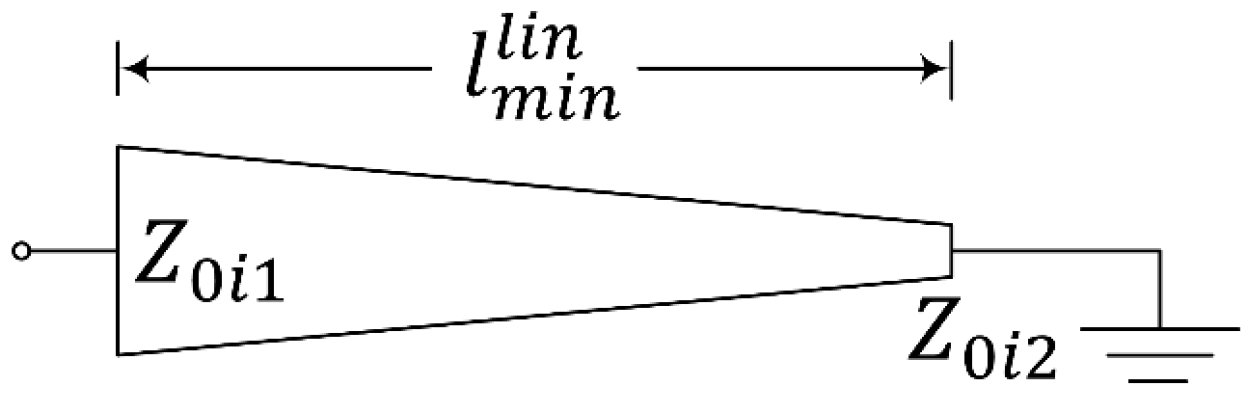
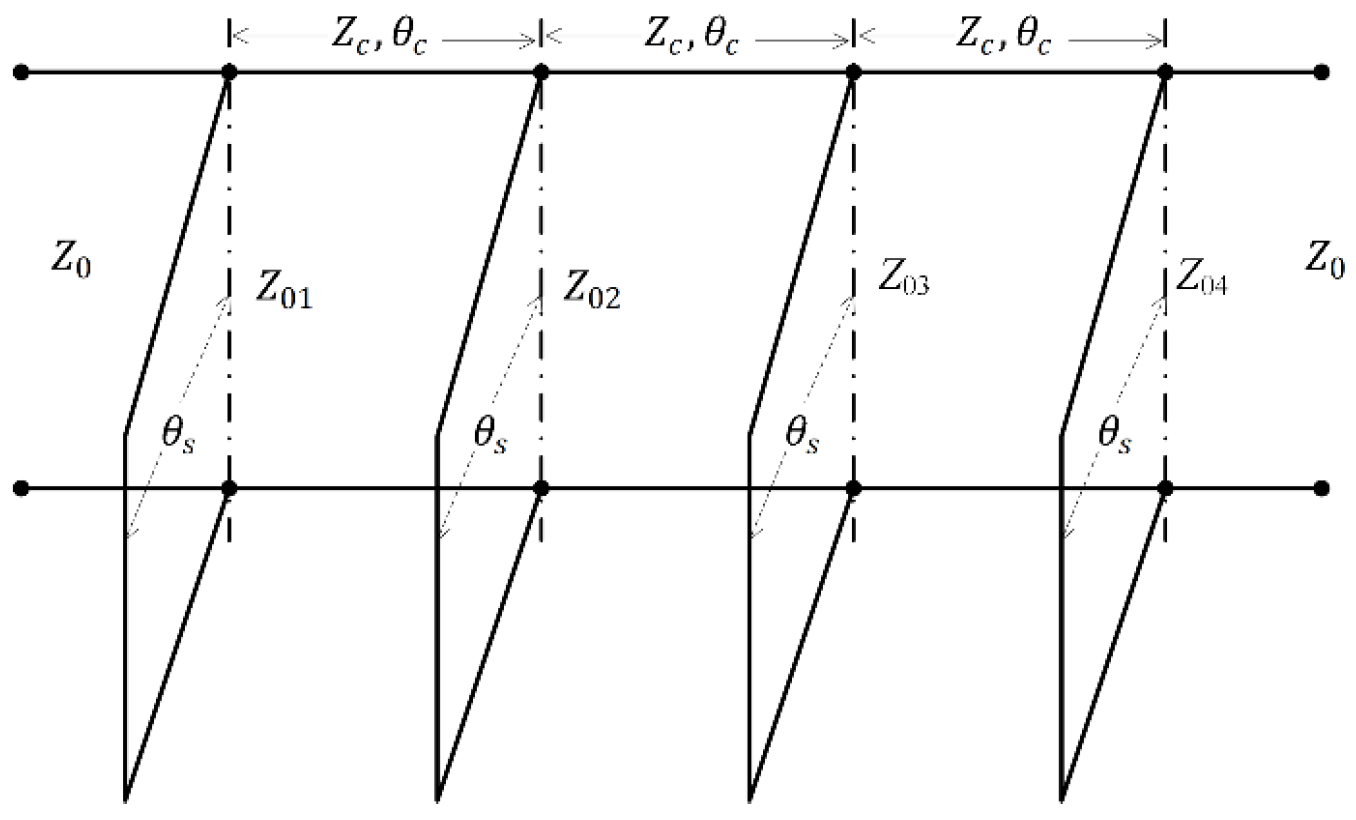





| k/β0 | 0.25 | 0.375 | 0.50 |
| lmin | 0.232 λ | 0.224 λ | 0.212 λ |
| Z0i2 | 1.44 Z0i1 | 1.695 Z0i1 | 1.98 Z0i1 |
| k/β0 | 0.25 | 0.375 | 0.50 | |
| l1 | 14.92 | 14.92 | 14.92 | |
| l2 | 14.17 | 14.17 | 14.17 | |
| l3 | 14.92 | 14.92 | 14.92 | |
| Terminal stub widths | WT1 | 0.51 | 0.51 | 0.51 |
| WT2 | 0.16 | 0.08 | 0.03 | |
| Middle stub widths | WM1 | 2.00 | 2.00 | 2.00 |
| WM2 | 1.10 | 0.80 | 0.53 | |
| Lengths of the terminal stubs (LsT) | 7.27 | 6.86 | 6.51 | |
| Lengths of the middle stubs (LsM) | 7.03 | 6.63 | 6.28 | |
| Wc | 2.07 | |||
| Wv | 0.7 | |||
| Wf | 2.4 | |||
| Radius of vias | 0.25 | |||
| Ws | 20 | |||
| Ls | 59.03 | |||
| Lf | 5 | |||
| k/β0 | 0.25 | 0.375 | 0.50 |
| L1 = L4 (nH) | 3.85 | 4.14 | 4.44 |
| L2 = L3 (nH) | 1.93 | 2.07 | 2.22 |
| C1 = C4 (pF) | 0.14 | 0.13 | 0.12 |
| C2 = C3 (pF) | 0.28 | 0.26 | 0.24 |
| Reference | Passband (GHz) | Bandwidth (GHz) | Insertion Loss (dB) | Return Loss (dB) | Techniques | |
|---|---|---|---|---|---|---|
| [3] | 2.92–10.95 | 8.03 (107.0%) | −0.49 | −12.0 | ICPCL | |
| [15] | 3.06–10.0 | 6.94 (106.3%) | −1.00 | −13.0 | Cascaded bandpass and bandstop filters | |
| [23] | 3.05–10.62 | 7.57 (100.9%) | −1.50 | −13.0 | MMR | |
| [24] | 3.1–10.6 | 7.5 (110.0%) | No data | −11.0 | Short-circuited stubs | |
| [25] | 2.50–7.00 | 4.5 (60.0%) | No Data | −23.0 | CLR | |
| [26] | 3.00–10.2 | 7.20 (96.0%) | −2.00 | −14.9 | Lumped capacitors | |
| [27] | 3.20–11.70 | 8.50 (114.0%) | −1.50 | −12.0 | MMR | |
| [28] | 3.12–10.69 | 7.57 (109.6%) | −1.20 | −12.7 | MMR | |
| [29] | 2.95–10.75 | 7.80 (113.9%) | −0.60 | −14.0 | SIDGS | |
| [30] | 3.21–10.77 | 7.56 (109.4%) | −0.80 | No Data | MMR | |
| This work | 3.24–10.88 | 7.64 (108.22%) | −1.25 | −17.5 | Short-circuited tapered resonators | |
| 3.11–10.95 | 7.84 (111.52%) | −1.00 | −17.3 | |||
| 3.09–10.99 | 7.90 (112.22%) | −0.80 | −17.0 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razzaz, F.; Saeed, S.M.; Alkanhal, M.A.S. Ultra-Wideband Bandpass Filters Using Tapered Resonators. Appl. Sci. 2022, 12, 3699. https://doi.org/10.3390/app12073699
Razzaz F, Saeed SM, Alkanhal MAS. Ultra-Wideband Bandpass Filters Using Tapered Resonators. Applied Sciences. 2022; 12(7):3699. https://doi.org/10.3390/app12073699
Chicago/Turabian StyleRazzaz, Faroq, Saud M. Saeed, and Majeed A. S. Alkanhal. 2022. "Ultra-Wideband Bandpass Filters Using Tapered Resonators" Applied Sciences 12, no. 7: 3699. https://doi.org/10.3390/app12073699
APA StyleRazzaz, F., Saeed, S. M., & Alkanhal, M. A. S. (2022). Ultra-Wideband Bandpass Filters Using Tapered Resonators. Applied Sciences, 12(7), 3699. https://doi.org/10.3390/app12073699






