Modeling of Swab and Surge Pressures: A Survey

Abstract

Swab and surge pressure fluctuations are decisive during drilling for oil. The axial movement of the pipe in the wellbore causes pressure fluctuations in wellbore fluid; these pressure fluctuations can be either positive or negative, corresponding to the direction of the movement of the pipe. For example, if the drill string is lowering down in the borehole, the drop is positive (surge pressure), and if the drill string is pulling out of the hole, the drop is negative (swab pressure). The intensity of these pressure fluctuations depends on the speed of the lowering down (tripping in) or withdrawing the pipe out (tripping out). High tripping speed corresponds to higher pressure fluctuations and can lead to fracturing the well formation. Low tripping speed leads to a slow operation, causing non-productive time, thus increasing the overall well budget. Researchers used mathematical equations and physics to understand the phenomena and have provided many empirical, mathematical, and physics-based models. This paper starts with a literature study on the swab and surge pressures. After that, this paper concludes with a proposal for a new approach. The new approach proposes developing new models that are more robust, using field data, as we have access to field data from drilling operations. Research using field data would provide data-driven methodologies as new solutions for the rate of penetration, reservoir management, and drilling optimization. The expected outcome will improve the performance of the tripping in and tripping out process within drilling and well construction, and will further reduce the risk related to swab and surge pressures.

1. Introduction

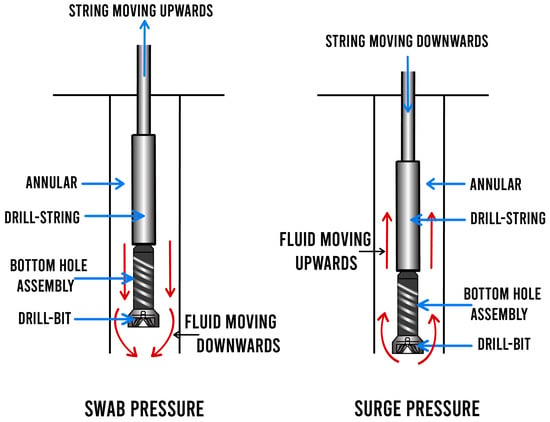
Swab and surge is a well-known problem for drilling and well construction operations. Researchers have been investigating this problem since the 19th century. Swab and surge refer to pressure fluctuations due to lowering or withdrawing the pipe from the hole. See Figure 1.

Swab and surge pressure fluctuations are either positive or negative. They are positive when lowering down the pipe and negative when withdrawing the pipe. The intensity of these pressure fluctuations depends on the speed of the lowering down (tripping in) or withdrawing the pipe out (tripping out). If the tripping speed is very high, the corresponding pressure fluctuation is high, and in some cases, this can be higher than the fracture pressure of the formation. This will cause fracturing the formation, partial or in some cases full losses, and in a worst-case scenario well collapse can occur. If the tripping speed is too low, this leads to a slow tripping operation, which is considered non-productive time (NPT), increasing the overall well budget.

The reverse of positive pressure fluctuation is also true. If the pipe is withdrawn very fast from the hole, this will lead to negative pressure in the wellbore and well inflow and can cause kick. In a worst-case scenario well incident or blowout can happen.

Researchers over the years have looked into swab and surge, utilizing mathematical equations and physics to understand the phenomena. As a result, some empirical, mathematical, and physics-based models are available for swab and surge simulations. This paper looks into some literature on the swab and surge in wellbore pressures. The literature study presented in Section 2 presents a thorough analysis of five prominent works. The models given in these works were developed when pressure measurements were unavailable during the tripping in or tripping out operations. However, measuring the downhole pressure and temperature is possible with the emergence of high-speed telemetry. Hence, it is now possible to build newer models for the processes using data-driven techniques on top of mathematical equations and physics with these new technologies; Section 3 presents a new proposal.

2. Literature Review of Five Prominent Works on Swab and Surge Models

The oil and gas industry has historically relied on empirical and numerical models to understand the physical phenomena. Many high-fidelity models in the literature estimate the swab and surge in wellbore pressures. However, each model has its assumptions and limitations. The most well know work is by Burkhardt [1], published in 1961. This work compared the measured values from a model with the predicted ones. The model considered ideal Bingham plastic fluids with the concentric annulus and uniform wellbore.

In 1964, Schuh [2] developed a model based on Burkhardt’s assumption for the power-law fluid and steady-state conditions. Mitchell [3] developed a dynamic model based on the existing swab and surge model but added factors of formation, cement, and pipe elasticity, mud properties changes with temperature and viscous forces.

The following subsections present a thorough analysis of five prominent works on the swab and surge.

2.1. Surge and Swab Modeling for Dynamic Pressures and Safe Trip Velocities

In this work by Lal [4], the authors present a new dynamic swab and surge model based on the physics of the transient nature of the phenomenon. The authors wanted a model that not only predicts the maximum swab and surge pressures or their variation with time at the bottom of the hole, casing-shoe, or at any other point in the borehole for a given trip speed, but also that computes the maximum safe trip speed for a specified pressure margin or effective circulating density (ECD). The presented model treats friction as a distributed parameter and considers various parameters in hole geometry, hole expansion, varying trip velocity, return area for tricone and diamond drill bits, plugged jets, and mud properties.

2.1.1. Lal’s Model

Unsteady transient flow in the borehole due to pipe movement generates pressure surges that propagate at the sound velocity, C. For a given set of initial boundary conditions, the transient nature of a pipe movement in the borehole with a certain cross-section area, A, depends on the fluid density, fluid compressibility, conduit expansion ability, and friction (resistance to flow).

The model of this work [4] is shown in Equations (1) to (6). This model shows the fundamental equations for the transient pressure and average flow rate in a vertical well with a constant area of cross-section were obtained from the momentum balance, flow continuity, and equations of state.

$$\frac{\partial p}{\partial z}+\frac{p}{A}\frac{\partial g}{\partial t}+h_f\left(q,v_p\right)=0$$

(1)

$$\frac{\partial p}{\partial t}+s·c\frac{\partial q}{\partial z}=0$$

(2)

$$S=Pc/A$$

(3)

$$c=\sqrt{g/\rho (\alpha +\beta )}$$

(4)

$$\mathsf{\Delta }P=\frac{1}{\alpha }\frac{\partial V}{V}$$

(5)

$$\mathsf{\Delta }P=\frac{1}{\alpha }\frac{A_p·\mathsf{\Delta }L}{A_h·L}$$

(6)

This work solved the first two equations for the known initial and the boundary conditions at the endpoints, considering every section in a borehole filled with drilling fluid and in communication with the other sections. Also, the endpoints boundary conditions were determined from pressure variations and the flow continuity.

The impedance of surge is given by Equation (3). The sonic speed of propagation, C, is given by Equation (4). For calculating acoustic speed, C, a compressibility factor $2.7\times {10}^{-6}$ (psi) of water at 122 deg F and 7255 psi was used. The expansibility factor for various conduits is derived from the theory of elasticity.

This work computed the friction pressure term by utilizing the Power-Law drilling fluid model. In addition, the frictional pressure loss term in the Power-Law model for the static pipe and fluid in the annulus was modified for incorporating the moving pipe effect on the average cross-section fluid speed and flow rate.

For the turbulent fluid, the Equation (1) becomes non-linear due to the nature of the friction term. This work also employed the characteristic popular numerical technique used for computing problems of unsteady flow. This method essentially converts Equations (1) and (2) to ordinary differential equations while using the finite difference scheme for converting these equations to algebraic form.

The effect of initial pressure required to break the mud gel were computed from the fluid compressibility. According to the definition of fluid compressibility if a fluid of volume is compressed by a small volume, this can result in an increase in the pressure and is given by Equation (3).

Suppose a pipe with a cross-section area, $A_p$, is moved a small distance $\mathsf{\Delta }L$, in an open hole with cross-section area, $A_h$, and length L, from the bottom of the pipe to the wellbore. The resulting increase in pressure $\mathsf{\Delta }P$ due to compressing the fluid below the pipe is given by Equation (4).

From the computed result, the model assumes that the effect of gel breaking the mud on the initial pressure is insignificant. Therefore, the initial conditions are taken as zero.

The calculated pressures and flow rates along the fluid line (pipe moving the hole) at $t=\mathsf{\Delta }t$ are used as the initial inputs to calculate the pressures and flow rates at time $t=2\mathsf{\Delta }t$. This computation is continued to calculate the pressures and the flow rates at a different time span along the pipe and the borehole.

2.1.2. Analysis of the Work by Lal

The main feature of the work [4] is the computer program to predict the maximum swab and surge pressures, the variations of swab and surge in the time domain at the bottom wellbore, and casing when running a casing, liner, or drill pipe stand. The computer program also generates warnings of lost circulation for surge or influx for the swab.

This work presents the main features of the theory for the model and a computer program. Based on the theoretical development of the dynamic swab and surge model, the computer program has been written, tested, and validated to some extent based on limited measured data. It simulates conditions in boreholes with fairly complex geometries, considering casing, liner, open hole, tricone or diamond bits, and the return area around the bit, drill collars, special pipe, or top drill collars, and drill pipe. The computer program has the following main features:

• It predicts the maximum surge or swab pressure or their variation with time at the bottomhole and casing-shoe when running a casing joint, liner, or a drill pipe stand;
• It warns about the danger of lost circulation for the surge (or kick for the swab) when the computed maximum pressure (or minimum pressure for swab) exceeds (or falls below) the specified pressure margin or the maximum (or minimum for swab) equivalent mud weight. For each case, it computes the maximum safe trip speed in order to avoid the lost circulation or the kick problem. These answers can be obtained while running in or pulling out the pipe at various distances from the bottom of the hole.

Based on the computer program runs, the authors had the following conclusions regarding swab and surge pressures:

• The computations of swab and surge pressures based on steady-state flow are generally incorrect given the unsteady nature of the flow;
• As far as the effect of various parameters on the swab and surge pressures is concerned, these parameters can be listed, in order of their importance, as follows.

The most critical parameters are the maximum trip speed and various parameters in hole geometry, such as the size of the hole and various pipes, and the depth of the well and the relative depth at which a pipe is being run. From the given example, one may run a pipe at a higher trip speed when running at large distances from the bottom, but one must carefully note the increase in surge pressure at the casing shoe when the pipe is close to it. The effect of the expansion of the hole and other conduits is also significant. In the case of the drill string, the plugging of the jet nozzles in tricone bits (or crowfoot area in diamond bits) and the constriction of the annulus return area can also significantly affect the swab and surge pressures. Regarding the effect of mud parameters, the increase in yield value has a maximum. However, not as many preceding parameters affect the surge pressure, followed by the plastic viscosity and mud weight. The mud weight appears to have a relatively small effect on the surge pressures.

The computer program written for the model includes almost all the significant parameters. It is user-friendly and has fast run times. It accurately predicts not only the maximum surge pressure or its time-variation at any point in the well but also computes the safe maximum trip speed when running a casing, liner, or drill string at a given depth in the borehole.

2.2. Bottomhole Pressure Surges While Running Pipe

The work by Clark [5] suggests a method of calculating bottomhole pressure surges due to the movement of tubular goods in a wellbore and the use of these values in predicting their effect on further drilling and completion. The work explains formulas for calculating and predicting various factors working behind the scenes during drilling and how they are used.

This work started an investigation of pressure surges by analyzing the factors that go into their calculations and then developing a set of formulas that predict the pressure surges. The work makes several assumptions in order to develop such formulas. One of the important assumptions is that the fluid and the borehole walls are incompressible. The second assumption this work makes is that the tubing being lowered is concentric with the borehole all the time. This means the hole is perfectly engaged for its complete length.

Ormsby [6] reorganized the equations for pressure drop due to friction for the plastic fluids in steady laminar flow in the fixed boundaries developed by Beck et al. [7] from the Bingham fluid model.

2.2.1. Clark’s Model

The model [5] is shown in Equations (7) to (21).

Table 1. The variables used in the model by Clark [5].

Notation	Variable	Equations
P	Pressure drop in psi over the length being computed.	(7), (8), (14), (18), (20), (21)
l	Total length in feet of the diameter being considered.	(7), (8), (14), (18), (21)
$t_Y$	Mud yield point in lbs./100 sq.ft.	(7), (10)
n	Plastic viscosity of the mud in Centipoise.	(7), (18), (19)
V	Mean fluid mud velocity in ft.per sec.	(7), (9), (11)–(13)
D	Pipe ID in inches for internal flow, or, bit size minus pipe OD in inches for annular flow.	(7)–(10), (18)–(20)
f	Pigott friction factor.	(8), (20)
$rho$	Mud weight in lbs./cu.ft.	(8), (9), (10), (14), (19)–(21)
V	Mean fluid mud velocity in ft.per sec.	(8)
R	appropriate Reynolds number in turbulent flow.	(8), (19)
$V_{L}C$	Lower critical fluid velocity in ft.per.sec.	(10)
$Q_A$	Observed mean annulus displacement rate in cu.ft/sec.	(11)–(13), (15), (16)
$Q_P$	Observed mean internal displacement rate in cu.ft/sec.	(11)–(13)
$A_A$	Annulus area in sq.ft alongside the considered diameter.	(11)–(13), (18)–(21)
$A_P$	Area of internal section being considered in sq.ft.	(11)–(14)
$V_P$	Pipe speed in ft./sec.	(11)–(13), (15), (16), (18), (19)
A	Square feet area of the section being considered.	(14)
$\frac{dQ}{dt}$	Rate of change of flow rate in cu-ft/sec./sec.	(14)
$S_{J}T$	Total volume displaced in cu. up in the annulus for the joint under consideration.	(15)–(21)
$L_{J}T$	Joint total length in ft. under consideration.	(15)–(21)
$Q_G$	Average rate of displacement in cu.ft/sec. at any given point in the annulus.	(16)
$Q_L$	Local annulus displacement rate in cu.ft/sec.	(16)
$A_{PR}$	Sq.ft. area that projects outside the basic pipe size on the under consideration.	(16), (17)–(21)
$\frac{d{Q}_G}{dt}$	Acceleration of annulus flow rate at any point in the annulus in cu.ft/sec./sec.	(17)
$a_P$	Acceleration of pipe in ft/sec./sec.	(17), (21)
$t_Y$	Yield point of the mud in Ibs. $/100$ sq. ft.	(18)
$K_L$	Constant from clinging effect in laminar flow (0.39 For drill pipe AND 0.46 for casing).	(18)
$K_T$	Constant from clinging effect in turbulent flow (0.166 for drill pipe and 0.181 for casing).	(19), (20)

summarizes the variables involved in the model.

$$P=\frac{l{t}_Y}{225D}+\frac{nlV}{1500D^2}$$

(7)

$$P=\frac{0.001296f{l}_{\rho }{V}^2}{D}$$

(8)

$$R=\frac{396D_{\rho }V}{n}$$

(9)

$$V_{LC}=\frac{8.07n+8.07\sqrt{n^2+1.65p{t}_X{D}^2}}{\rho D}$$

(10)

$$V=-\frac{Q_A}{A_A}+\left\{\begin{array}{c}0.46V_P\left(\mathrm{for}\mathrm{casing}\right)\hfill \\ \mathrm{or}\hfill \\ 0.39V_P\left(\mathrm{for}\mathrm{drill}\mathrm{pipe}\right)\hfill \end{array}\right.$$

(11)

$$V=-\frac{Q_A}{A_A}+\left\{\begin{array}{c}0.181V_P\left(\mathrm{for}\mathrm{casing}\right)\hfill \\ \mathrm{or}\hfill \\ 0.166V_P\left(\mathrm{for}\mathrm{drill}\mathrm{pipe}\right)\hfill \end{array}\right.$$

(12)

$$V=-\frac{Q_P}{A_P}+V_P$$

(13)

$$P=-0.0002155\frac{\rho l}{A}\frac{dQ}{dt}$$

(14)

$$Q_A=-V_P\times \frac{S_{JT}}{L_{JT}}$$

(15)

$$Q_G=Q_A+Q_L=-V_P\left(\frac{S_{JT}}{L_{JT}}+A_{PR}\right)$$

(16)

$$\frac{d{Q}_G}{dt}=-a_P\left(\frac{S_{JT}}{L_{JT}}+A_{PR}\right)$$

(17)

$$P=\frac{l{t}_Y}{225D}+\frac{nl{V}_P}{1500D^2}\left[\frac{S_{JT}}{L_{JT}{A}_A}+\frac{A_{PR}}{A_A}+K_L\right]$$

(18)

$$R=\frac{396D_{\rho }{V}_P}{n}\left[\frac{S_{JT}}{L_{JT}{A}_A}+\frac{A_{PR}}{A_A}+K_T\right]$$

(19)

$$P=\frac{0.001296f{l}_P{V}_P^2}{D}{\left[\frac{S_{JT}}{L_{JT}{A}_A}+\frac{A_{PR}}{A_A}+K_T\right]}^2$$

(20)

$$P=0.{0002155}_{\rho }l{a}_P\left[\frac{S_{JT}}{L_{JT{A}_A}}+\frac{A_{PR}}{A_A}\right]$$

(21)

Equation (7) is the friction drop in Laminar Flow for Plastic Fluids. Equation (8) is the friction drop in Turbulent Flow. Equation (9) is the Reynolds Number in Turbulent Flow. Equation (10) is used for computing the lower critical velocity value (based on R = 2000 in Laminar Flow) at which the flow changes from laminar to turbulent.

Equations (7) to (10) can be implemented to calculate the bottom hole pressure provided the equivalent velocity formed of served displacement and clinging velocity. For different conditions, the equivalent velocity can be calculated from Equations (11)–(13). These three equations are calculations of Turbulent Annulus Flow, Laminar Annulus Flow, and either laminar or turbulent flow inside the pipe, respectively.

Acceleration Pressure: The pipe goes from zero speed to a maximum speed and then back to zero when dropping downpipe in the hole. Since the pipe movement makes the fluid move from rest to a peak and then return to static, there must be an increase and decrease in pressure with respect to the dropping cycle. The value of these respective increase and decrease in pressure between any two points can be calculated from Equation (14).

Conversion into Measurable Values: Due to the difficulties of measuring the fluid flow variables, these should convert mostly the available values of speed and acceleration of the pipe. For buoyancy in an incompressible fluid, this relationship is given by Equation (15). Equation (15) is strictly not true when the float is not included in the bottom hole assembly; this allows the fluid to find its own path of minimum energy loss.

Local Displacement: Where an expanded diameter exists on a pipe string, at these locations, there must be a movement over and above the surface-recorded displacement. This is evident, since as the projection falls, a local fluid movement must occur from the forecast to fill the gap produced behind the projection. The amount of these local fluid displacements is equal to the projection area multiplied by the pipe speed. Equation (16) would be used to obtain the general terms of displacement at any point in the string.

A simple derivation of this flow rate will give the fluid flow acceleration in terms of measurable pipe acceleration and is given in Equation (17).

Completed Formulas For Analyzing Annulus Flow: Each flow equations can now be written in its final form with its components, which can be directly monitored. Equation (18) yields a loss of pressure at any given pipe velocity value due to laminar flow.

Equation (19) can be used to find the Reynolds number for finding the friction factor for the turbulent flow. However, this should not be used for critical speed as this value is only approximated. However, it is sufficiently accurate enough to find friction factors.

The pressure drop due to the turbulent flow at any pipe speed can be calculated with Equation (20). Finally, Equation (21) is the general equation for acceleration pressure in the Annulus. In this equation, downward pipe movement with reference to earth is taken as positive.

2.2.2. Analysis of the Work by Clark

This work [5] also explains (using various graphs) what happens during various drilling in which a velocity and acceleration curve of a typical 90-foot stand of drill pipe is lowered into the hole. The work concludes that drill pipe or casing velocity acceleration and deceleration can and should be minimized without markedly changing the drilling time. Through such action, the resulting savings in “trouble” costs will pay a thousand times over the few dollars extra per round trip. In drilling, mud should be mixed and weighted in such a manner as to maintain the plastic viscosity and yield strength at the lowest possible value consistent with other problems. Also, during casing jobs in “tight holes”, particular care must be taken with dropping time, or displacements should be relieved by fill-up devices to prevent the bottom-hole pressure from causing excessive amounts of damage.

This work had the following recommendations on practices to be instituted as standard procedure:

• Increase running or pulling times sufficiently to keep pressures safely above zonal hydrostatic pressure, but below the formation strength at all times;
• Decrease the rate of acceleration or deceleration of the pipe through smoother brake handling and earlier use of a hydromatic brake;
• Use bottom fill devices to relieve annulus volumes by internal filling;
• Increase clearances wherever possible;
• Care should be used with projections above pipe size such as oversized drill collars and drill pipe protectors, or improperly designed centering and scratching equipment run on the casing;
• The practice of spudding back through previously drilled formations, using high rates of pumping as well as high rates of pipe acceleration and deceleration, should definitely be controlled.

2.3. Automatic Prediction of Downhole Pressure Surges in Tripping Operations

In this work by Gjerstad et al. [8], the authors implemented an Ensemble Kalman Filter (EnKF) to predict the downhole pressure surges in a tripping operation based on the proposed medium-order dynamic model.

Equations (22) to (37) represent the conceptual model. Different parts of the drill string with different outer and inner diameters are used in these equations.

Table 2. The variables used in the model by Gjerstad et al. [8].

Notation	Variable	Equations
$Q_n$	Flow through the bit nozzle.	(22)–(24)
$V_I$	String inside volume.	(22)–(24)
$A_{IM}$	String internal cross-section.	(22)–(24)
$\rho$	Mud density.	(26)
$A_n$	Total cross-section of all nozzles.	(26)
$C_n$	Discharge coefficient to account for unmodeled effects.	(26)
$A_{u1\left(j\right)}$, $A_{u2\left(j\right)}$	The boundary surface areas.	(31), (34)
${\tau }_{w1\left(j\right)}$, ${\tau }_{w2\left(j\right)}$	Wall share stress that were calculated from respective radius, $R_{1\left(j\right)}$ or $R_{2\left(j\right)}$.	(31), (34)
$L_{2\left(j\right)}$	Length of secondary part.	(32)
$h_{2\left(j\right)}$	Annular gap of secondary part.	(32)
$m_{1\left(j\right)}$	Mass of main part.	(33), (36)
$m_{2\left(j\right)}$	Mass of secondary part.	(33), (36)

summarizes the variables involved in the model.

$${\dot{P}}_{\left(j\right)}=\frac{K}{V_{\left(j\right)}}\left(Q_{(j+1)}-Q_{\left(j\right)}\right),j=1,2,\dots \left(n_s-2\right)$$

(22)

$${\dot{P}}_{\left(j\right)}=\frac{K}{V_{\left(j\right)}}\left(Q_{(j+1)}-Q_{\left(j\right)}-v_s\left(A_M-A_C\right)\right),j=n_s-1$$

(23)

$${\dot{P}}_{\left(j\right)}=\frac{K}{V_{\left(j\right)}}\left(-Q_n-Q_{\left(j\right)}-v_s{A}_C\right),j=n_s$$

(24)

$${\dot{P}}_I=\frac{K}{V_I}\left(Q_n-Q_I+v_s{A}_{IM}\right)$$

(25)

$$Q_n=min\left\{0,C_n{A}_n\sqrt{2\left(P_I-P_{\left(n_s\right)}\right)/\rho }\right\}$$

(26)

$$R_{1\left(j\right)}=D_M/2,j=1,\dots ,\left(n_s-1\right)$$

(27)

$$R_{1\left(j\right)}=D_C/2,j=n_s$$

(28)

$$R_{2\left(j\right)}=D_J/2,j=1,\dots ,\left(n_s-1\right)$$

(29)

$$R_{2\left(j\right)}=D_B/2,j=n_s$$

(30)

$$F_{f\left(j\right)}=A_{u1\left(j\right)}{\tau }_{w1\left(j\right)}+A_{u2\left(j\right)}{\tau }_{w2\left(j\right)},j=1,\dots n_s$$

(31)

$$F_{P\left(j\right)}=\left(P_{\left(j\right)}-P_{(j-1)}\right)A_{f1\left(j\right)}+2{\tau }_{w2\left(j\right)}\frac{L_{2\left(j\right)}}{h_{2\left(j\right)}}\left(A_{f2\left(j\right)}-A_{f1\left(j\right)}\right)$$

(32)

$${\dot{Q}}_{\left(j\right)}=\frac{1}{M_{\left(j\right)}}\left(F_{f\left(j\right)}+F_{P\left(j\right)}\right),M_{\left(j\right)}=\frac{m_{1\left(j\right)}}{A_{f1\left(j\right)}}+\frac{m_{2\left(j\right)}}{A_{f2\left(j\right)}}$$

(33)

$$F_{fl}=A_{uI1}{\tau }_{w/1}+A_{ul2}{\tau }_{w/2}$$

(34)

$$F_{PI}=\left(P_I-P_{I0}\right)\pi R_{IeP}^2\iff F_{PI}=\left(P_I-P_{I0}\right)A_{I\rho P},A_{IfP}=\pi R_{IeP}^2$$

(35)

$${\dot{Q}}_I=\frac{1}{M_I}\left(F_{If}+F_{IP}\right),M_I=\frac{m_{I1}}{A_{f11}}+\frac{m_{I2}}{A_{f12}}$$

(36)

$$\mathsf{\Delta }{P}_{bha}=P_{\left(n_s\right)}+\mathsf{\Delta }{P}_{HS},\mathsf{\Delta }{P}_{HS}=-\rho g\mathsf{\Delta }zcos\left(I_{\left(n_s\right)}\right)$$

(37)

Since there are several uncertain and/or slowly changing parameters in this model, some sort of calibration of the model is necessary to achieve good agreement with the data. A problem in tripping operations is that measuring data is often unavailable in real-time because the mud-pulse telemetry system is not transmitting when circulation is off. However, if circulation is turned on while running the string before a tripping operation, measuring data for calibrating the model for consecutive runs can be achieved.

Conservation of Mass: This work defined $Q_{(j+1)}$ as the output flow at top of element $j+1$, and into element j. $V_{\left(j\right)}$ is the volume of fluid of element j, and K is the mud bulk modulus. $A_M$ and $A_C$ are the outer cross-section of the drill string and collars with their respective diameters as $D_M$ and $D_C$. The conservation of mass is presented as Equations (22) to (24).

Because of the check valves in the string, the flow through the bit nozzle is always negative or zero. Therefore, it is given by the static expression, Equation (26).

Conservation of Momentum in the Annulus: This work divided every segment in the elements into two parts as primary and secondary part. For the main part, the radius is defined by Equations (27) and (28). Equations (29) and (30) are for the secondary part.

The outer diameter/surface is not homogeneous as the outer diameter in the real BHA is not homogeneous. For model simplification, this work uses a normal averaging of the outer diameter of the BHA. This work separately computes the viscous friction forces in each segment of the primary and the secondary part. Their basic equation for friction forces is given by Equation (31).

For precise computation of the transient pressure forces on the fluid, the pressure at the position where the cross-sectional area changes must be known. This work assumes steady-state conditions. The resultant pressure force obtained from the main part of the cross-section area was modified by an additional term dependent on the share wall stress. The resultant pressure force is given by Equation (32).

As the authors treated the volumetric flow rates as state variables, they therefore presented the momentum as Equation (33).

Conservation of Momentum in the string: The whole surrounding wall of the drill string moves uniformly. Therefore, the theory for calculating the viscous friction force is simpler than the annulus one. As the diameters $D_{IM},D_{IJ},D_{IC},D_{IB}$ across the drill string are not uniform, to deal the diameters non-uniformity, the authors derived an effective radius. This work first calculated the approximated values of the respective radii and obtained $R_{IMFL},R_{IJFL},R_{ICFL},R_{IBFL}$ for laminar flow and $R_{IMFT},R_{IJFT},R_{ICFT},R_{IBFT}$ for turbulent flow. Similarly, they computed the effective radii representing the secondary part of the entire volume inside the drill string.

This work expressed the friction forces as given in Equation (34).

This work also computed the pressure forces by Equation (35), and the momentum equation inside the drill string is given by Equation (36).

Changes in Hydrostatic Pressure: As the BHA moves in the annulus, the pressure sensors also follow the BHA. The authors computed the change in hydrostatic pressure caused by the BHA movement. They left out the initial component of hydrostatic pressure in their computations. The change in hydrostatic pressure is given by Equation (37), in which the string position is give by $\frac{d}{dt}\left(\mathsf{\Delta }z\right)=v_s$.

The Automatic Pressure Estimation: Since there are a lot of uncertainties in their model, to achieve a good agreement with the data, it is important to have some calibration of the model. One of the problems the authors pointed out is that during tripping operations, no real-time measurements are often available due to limitations imposed by mud pulse telemetry, which cannot measure the pressures when the pumps are off. However, the model can be calibrated for consecutive runs if pumps are turned on before tripping operations. The authors employed the Ensemble Kalman Filter for the downhole pressure prediction. In addition, they computed the change in hydrostatic pressure caused by the BHA movement. They left out the initial component of hydrostatic pressure in our computations. The change in hydrostatic pressure is given by Equation (37), in which the string position is give by $\frac{d}{dt}\left(\mathsf{\Delta }z\right)=v_s$.

Analysis of the Work by Gjerstad et al.

By discretization, the authors supposed that the non-linear, time-invariant system [8] can be described as:

$$x(t+1)=f\left(x\right(t),u(t\left)\right)+w\left(t\right)$$

$$y\left(t\right)=h\left(x\right(t\left)\right)+v\left(t\right)$$

where $x\in R^{n_x}$ is the state of the system, $u\in R^{n_u}$ is the input, and $y\in R^{n_y}$ is the output.

The objective of their EnKF is to obtain the estimate $\widehat{x}\left(t\right)$ of the true state $x\left(t\right)$ using the measurements $y\left(t\right)$ so that $tr\left(E\left[(x\left(t\right)-\widehat{x}\left(t\right)){(x\left(t\right)-\widehat{x}\left(t\right))}^T\right]\right)$ is minimized.

This work assumed that at initial time t, there is an ensemble of N forecasted state estimates with random sample error. This ensemble is denoted as $X^f\left(t\right)=\left\{x^{f_1}\left(t\right),\dots ,x^{f_N}\left(t\right)\right\}$. The obtained estimated state is:

$${\widehat{x}}_i\left(t\right)=x^{f_i}\left(t\right)+K^e\left(t\right)\left(y\left(t\right)+v_i\left(t\right)-h\left(x^{f_i}\left(t\right)\right)\right)$$

$$\widehat{x}\left(t\right)=1/N\sum _{i=1}^N{\widehat{x}}_i\left(t\right)$$

A more detailed summary of the EnKF algorithm is given in the paper.

During the ensemble, Kalman Filter for Automatic Parameter Estimation, the largest uncertainties in the model were related to the viscous friction losses. Therefore, most of the parameters chosen to estimate were related to calculating frictional forces.

This work provides the algorithm for the model and a MATLAB program for simulation to test the model. The authors had very limited field data, but they achieved satisfactory estimations with their models.

2.4. Wellbore Pressure Surges by Pipe Movement

This work by Burkhardt [1] has created a theory to successfully predict the sequence and magnitudes of these positive and negative surges and has established a basis for understanding how they occur. The research described in this work was undertaken to supplement that described, and overcame some of the difficulties noted. The model of this work is summarized with Equations (38) to (52).

Table 3. The variables used in the model by Brukhardt [1].

Notation	Variable	Equations
P	Pressure, psi.	(38), (39)
L	Length of pipe section, ft.	(38), (39)
$\zeta$	Mud gel strength, lb/100 $f{t}^2$.	(38), (39)
$D_i$	Internal diameter, in.	(38), (39)
$D_p$	Pipe outside diameter, in.	(38), (39), (42)–(46), (48)
$D_h$	Hole inside diameter, in.	(38), (39), (42)–(46), (48)
$a_p$	Pipe acceleration.	(40), (41)
$\rho$	Mud density.	(40), (41), (45), (46)
L	Length of pipe section, ft.	(40), (41)
g	Acceleration of gravity.	(40), (41)
$V_{d_u}$	Annulus competent of velocity due to displacement, ft/min.	(42)
$V_p$	Velocity of pipe, ft/min, in.	(42), (43), (48)
$V_{a_e}$	Effective annular mud velocity, ft/min.	(43), (45), (48)
K	Proportionality constant.	(43), (48)
$T_0$	Mud yield point, lb/100 $f{t}^2$.	(44)
${\mu }_p$	Plastic viscosity, cp.	(44)
$R_e$	Reynolds number.	(45)
$\frac{\mathsf{\Delta }P}{L}$	Pressure gradient, psi/ft.	(46)
f	Friction factor.	(46)
$q_a$	Mud flow in annulus measured with respect to the fixed borehole wall, $f{t}^3$/min.	(48)
$V_{be}$	Effective pipe bore mud velocity, ft/min.	(49)
$q_b$	Mud flow in pipe bore measured with respect to pipe walls, $f{t}^3$/min.	(49)
$D_i$	Inside diameter of pipe, in.	(49)

presents the variables involved in the model.

$$P=\frac{4L\zeta }{D_i}$$

(38)

$$P=\frac{4L\zeta }{D_h-D_p}$$

(39)

$$P=\frac{L\rho a_p{D}_p^2}{g\left(D_h^2-D_p^2\right)}$$

(40)

$$P=\frac{L\rho a_p\left(D_p^2-D_i^2\right)}{g\left(D_h^2-D_p^2+D_i^2\right)}$$

(41)

$$V_{du}=-\frac{D_p^2}{D_h^2-D_p^2}{V}_p\left[\frac{\mathrm{ft}}{min}\right]$$

(42)

$$V_{ae}=-\left(\frac{D^2{}_p}{D_h^2-D_p^2}+K\right)V_p\left[\frac{\mathrm{ft}}{min}\right]$$

(43)

$$S=2394\frac{\left(D_h-D_p\right){\tau }_n}{{\mu }_p{V}_{a\theta }}$$

(44)

$$R_e=15.44\frac{\left(D_h-D_p\right)V_{ae}\rho }{{\mu }_p}$$

(45)

$$\frac{\mathsf{\Delta }P}{L}=\frac{f{V}_{ae}^2\rho }{9.282\times {10}^4\left(D_h-D_p\right)}\left(\frac{\mathrm{psi}}{\mathrm{ft}}\right)$$

(46)

$$P_b=P_a$$

(47)

$$V_{ac}=-\left(\frac{-576q_a}{\pi \left(D_h^2-D_p^2\right)}+K{V}_p\right)\left[\frac{\mathrm{ft}}{min}\right]$$

(48)

$$V_{be}=\frac{576\left\{q_b\right\}}{\pi D_i^2}\left[\frac{\mathrm{ft}}{\min }\right]$$

(49)

$$S=\frac{2394\left(D_i\right){\tau }_o}{{\mu }_p{V}_{be}}$$

(50)

$$R_e=\frac{15.44\left(D_i\right)V_{be}\rho }{{\mu }_p}$$

(51)

$$\frac{\mathsf{\Delta }P}{L}=\frac{f{V}_{be}^2\rho }{9.282\times {10}^4{D}_i}(\frac{\mathrm{psi}}{\mathrm{ft}})$$

(52)

The research was done in three parts:

• A valid theory useful in all field situations was developed. This theory must be based upon realistic assumptions, must be formulated rigorously, and should lead to clear concepts whereby the nature of pressure surges can be easily understood;
• The theory, however complex and involved, must ultimately be presented in a simplified form for convenient field use. This may involve extensive machine computations and the use of figures and empirical equations;
• The accuracy of the simplified equations must be established by comparing measured pressure surges with those predicted by the theory. These must agree both in their characteristic nature and in magnitude. This means that careful measurements of surges occurring in actual field operations must be made.

Pressure Generated by Breaking the Mud Gel: Melrose et al. [9] developed a formulation for the pressure needed to break the mud gel and start circulation. The important parameters are hole diameter, the out and inside diameter of the pipe, the length of the pipe in the hole, and the mud gel strength. Equation (38) is for the pressure to break the mud gel inside the pipe, whereas Equation (39) is inside the annulus.

Pressure Generated by Inertia of The Mud Column: Newton’s motion law described the inertial pressure surge component due to the shift of the mud column to oppose a change in motion. Inertial pressure surge component is expressed in Equations (40) and (41). Equation (40) is for closed pipe string, and Equation (41) is for open pipe string.

Theoretically, the viscus drag for the open and closed-end strings are similar; however, the equations are conceptual and in form differ considerably. Therefore, it is worth discussing them separately. Closed-end pipe strings are considered in this section. Closed-end pipe strings usually have a float sub, which prevents the mud flux from the borehole to pipe string.

Determination of the Effective Annular Mud Velocity: Besides the effective velocity component because of the mud clinging effect, there is also an annulus mud velocity component as displacing pipe generates volumetric mudflow. This effective velocity component can be determined from the relative area of the cross-section of the annulus and the closed-end pipe, as shown in Equation (42).

The effective annular mud velocity is given by Equation (43).

The mean of the effective annular mud velocity is the mud velocity that creates the surge pressure’s viscus drag with reference to the wellbore wall.

Pressure Generated Due to the Mud Flow in an Annulus: For the Bingham plastic fluid, the plasticity for an annulus is defined by Equation (44).

The Reynolds number of Bingham plastic fluid for annular flow is defined by Equation (45).

By finding the friction factor using this Reynolds number, the pressure surge generated in the annulus by moving a closed-end pipe in the borehole is given by Equation (46).

The contribution to pressure gradients due to change in borehole or geometry of the pipe, specifically for each geometry, should be computed. Then, the total pressure would be the sum of the separate component.

Viscus Drag Pressure Surges with Open Pipe Strings: The open pipe strings are defined, the strings have openings to the annulus, and the pipe bore at the string bottom, e.g., the drill string without the float sub in the assembly or a fill-up shoe in the casing string.

A statement must be made regarding how the extra pipe borer mudflow channel is associated with the annular mud flow path to calculate the effective annular mud velocity, creating the viscose drag pressure-surge components. The criterion utilized to characterize this connection was that the total pressure surge created in the pipe bore must be equal to the total pressure surge generated in the annulus. The total pressure surge is given by Equation (47). In Equation (47), $P_b$ is the pipe bore pressure, psi., and $P_a$ is annulus pressure, psi.

This equality of pressure is achieved by separating the mudflow from the two pathways in different ratios until the same pressure is created in each flow path. The ultimate pressure should be the same as the pressure that really occurred; hence, the surge pressure.

Effective Mud Velocities for Pressure-Surge Generation: The effective mean mud annulus mud velocity is the total of mud displacement and the moving pipe walls. Thus, Equation (48) presents effective annulus mud velocity.

The effective mean mud velocity in the pipe bore with reference to the pipe bore walls is given by Equation (49).

The flow rate of the mud pipe walls $q_b$ generates pressure in the pipe bore regardless of which is considered to be moving.

Pressure Generated in the Annulus and Pipe Bore: The pressure generated in the annulus of the open-end string is calculated the same as computed for the closed-end pipe except for $V_{ae}$. The same method is used to calculate the pressure generated in the pipe bore and the annulus. For the changed geometry, the fluid plasticity, Reynolds number, and pressure gradient equations are given in Equations (50)–(52).

The pressure gradient for each change in the diameter of the pipe bore and the annulus will vary, with the pressure created by each flow route being the total of each diameter change.

Analysis of the Work by Burkhardt

This work [1] presents figures for the several positive and negative pressure fluctuations produced when a single casing joint was lowered into a mud-filled borehole. This work also presents tables that show the Mud Properties during pressure surge measurements during various scenarios. The comparisons listed in some tables confirm the theory as a quantitative means of predicting pressure surges. Although several large deviations are present in the comparisons, the deviations are generally well within the experimental accuracy. The agreement is especially good in the case of viscous-drag pressures, which are the largest and therefore most important pressure peaks of the pressure-surge pattern.

The contribution of this work can be summarized as follows:

• A quantitative, theoretical description of surge pressures generated by pipe movement in a mud-filled wellbore has been developed and verified by experimentation;
• The theory correctly predicts the existence and magnitude of various positive and negative peaks due to gel breaking, inertia, and viscous drag of the mud;
• When running a drill pipe, or a casing without fill-up devices, the surge due to viscous drag is usually the largest and, therefore, the most important;
• Simple, approximate equations were developed to predict the viscous-drag surge, and the predictions were found to be within experimental accuracy.

2.5. Experimental Study of Swab and Surge Pressures in Horizontal and Inclined Wells

The main objective of this study by Srivastav et al. [10] is to examine the effects of different drilling parameters such as trip speed, fluid rheology, and eccentricity on swab and surge pressures. The model is summarized in Equations (53) to (67).

Table 4. The variables used in the model by Srivastav et al. [10].

Notation	Variable	Equations
$d_p$	Pipe diameter.	(53), (54)
$d_h$	Hole/casing diameter.	(53), (54)
n	Fluid behavior index.	(53), (54), (56)
R	Reduction factor.	(53), (54)
$h\left(\theta \right)$	Element slot thickness.	(55)–(58)
$r_o$	Inner radius of outer pipe.	(55)
$r_i$	Outer radius of inner pipe.	(55)
E	Fractional eccentricity.	(55)
C	Radius clearance $(r_o-r_i)$.	(55)
$V_p$	Pipe velocity.	(56)
k	Consistency Index.	(56)
${\pi }_2$	Dimensionless plug thickness.	(57)–(59), (62)
$y_1$	Lower limit of region II.	(57)
$y_2$	Upper limit of region II.	(57)
${\overline{y}}_1$	Dimensionless lower boundary limit of region II.	(57), (59), (62)
${\overline{y}}_2$	Dimensionless upper boundary limit of region II.	(57)
${\tau }_o$	Yield stress.	(58)
$\mathsf{\Delta }L$	Slot length/hole depth.	(58)
$\mathsf{\Delta }P$	Pressure drop.	(58)
${\pi }_1$	Dimensionless pressure.	(59), (62)
b	Constant.	(59), (62)
${\overline{q}}_t$	dimensionless total flow rate.	(60)–(62)
q	Actual flow rate.	(61), (63)
W	Slot width.	(61), (64)
$V_p$	Pipe velocity.	(61), (63)
H	Slot thickness.	(61), (64)
$d_p$	Pipe diameter.	(63), (64)
$d_h$	Wellbore diameter.	(64)
K	Diameter ratio $\left(\mathrm{K}=d_p/d_h\right)$	(67)
$\epsilon$	Fractional eccentricity.	(67)

presents the symbols used in these equations.

$${\left(\frac{dp}{dl}\right)}_e=R\times {\left(\frac{dp}{dl}\right)}_c$$

(53)

$$R=1-0.72\frac{e}{n}{\left[\frac{d_p}{d_h}\right]}^{0.8454}-1.5e^2\sqrt{n}{\left[\frac{d_p}{d_h}\right]}^{0.1852}+0.96e^3\sqrt{n}{\left[\frac{d_p}{d_h}\right]}^{0.2527}$$

(54)

$$h\left(\theta \right)={\left(r_o^2-{\epsilon }^2{c}^2{sin}^2\theta \right)}^{0.5}-r_i+\epsilon ccos\theta$$

(55)

$${\pi }_1=\left(\frac{n}{n+1}\right)\left(\frac{h}{V_p}\right){\left(\frac{\mathsf{\Delta }P}{\mathsf{\Delta }L}\frac{h}{k}\right)}^{\frac{1}{n}}$$

(56)

$${\pi }_2={\overline{y}}_2-{\overline{y}}_1\mathrm{where}{\overline{y}}_1=\frac{y_1}{h}\mathrm{and}{\overline{y}}_2=\frac{y_2}{h}$$

(57)

$${\pi }_2=\frac{2{\tau }_o/h}{\mathsf{\Delta }P/\mathsf{\Delta }L}$$

(58)

$${(1-{\overline{y}}_1-{\pi }_2)}^b-{\left({\overline{y}}_1\right)}^b-\frac{1}{{\pi }_1}=0$$

(59)

$${\overline{q}}_t={\int }_0^1(\overline{V_1}d\overline{y}+{\overline{V}}_{2}d\overline{y}+{\overline{V}}_{3}d\overline{y})$$

(60)

$${\overline{q}}_t=\frac{-q}{WH{V}_p}$$

(61)

$$\begin{array}{c}\hfill {\overline{q}}_t=-{\overline{q}}_{tA}-{\overline{q}}_{tB}+{\overline{q}}_{tC}-{\overline{q}}_{tD},\mathrm{where};\\ \hfill {\overline{q}}_{tA}={\pi }_1\left[\left(\frac{b}{b+1}\right){\overline{y}}_1^{b+1}\right]\\ \hfill {\overline{q}}_{tB}=\left[{\pi }_1{\left(1-{\overline{y}}_1-{\pi }_2\right)}^b-1\right][1-\left.{\overline{y}}_1-{\pi }_2\right]\\ \hfill {\overline{q}}_{tC}={\pi }_1\left(\frac{1}{b+1}\right){\left(1-{\overline{y}}_1-{\pi }_2\right)}^{b+1}\\ \hfill {\overline{q}}_{tD}={\pi }_1{\left({\overline{y}}_1\right)}^b{\pi }_2\end{array}$$

(62)

$$q=\frac{\pi }{4}{d}_p^2{V}_p$$

(63)

$$h=\frac{\left(d_h-d_p\right)}{2}W=\frac{\left(d_h-d_p\right)}{2}$$

(64)

$$\begin{array}{c}\hfill d_h\left(\theta \right)=2h\left(\theta \right)+d_p\\ \hfill {\pi }_1\left(\theta \right)=\left(\frac{n}{n+1}\right)\left(\frac{h\left(\theta \right)}{V_p}\right){\left(\frac{\mathsf{\Delta }P}{\mathsf{\Delta }L}\frac{h\left(\theta \right)}{k}\right)}^{\frac{1}{n}}\\ \hfill {\pi }_2\left(\theta \right)=\frac{2{\tau }_o/h\left(\theta \right)}{\mathsf{\Delta }P/\mathsf{\Delta }L}\\ \hfill \begin{array}{c}{\overline{q}}_t\left(\theta \right)=-{\pi }_{1\left(\theta \right)}\left[\left(\frac{b}{b+1}\right){\overline{y}}_1^{b+1}\right]-\left[{\pi }_1\left(\theta \right)\left(1-{\overline{y}}_1-\right.\right.\\ \left.{\left.{\pi }_2\left(\theta \right)\right)}^b-1\right]\left[1-{\overline{y}}_1-{\pi }_2\left(\theta \right)\right]+{\pi }_1\left(\theta \right)\left(\frac{1}{b+1}\right)\left(1-{\overline{y}}_1-\right.\\ {\left.{\pi }_2\left(\theta \right)\right)}^{b+1}-{\pi }_1\left(\theta \right){\left({\overline{y}}_1\right)}^b{\pi }_2\left(\theta \right)\end{array}\end{array}$$

(65)

$${\overline{q}}_{total}=2\times \sum _1^{\theta =180}{\overline{q}}_t\left(\theta \right)$$

(66)

$${\left(\frac{dp}{dl}\right)}_{\mathrm{corrected}}=\frac{1}{K^{0.27\epsilon }}{\left(\frac{dp}{dl}\right)}_{\mathrm{model}}$$

(67)

Haciislamoglu and Langlinais [11] developed an accurate numerical model to calculate the pressure loss due to the eccentricity reduction factor (R).The reduction factor is dependent on the diameter pipe ratio (K) and fluid behavior index (n).Their study also includes the axial pipe and yield stress. Their study reveals that the tripping speed has a minor impact on the pressure loss for yield stress fluids. For static inner pipe, the pressure loss in the eccentric annulus is calculated for a pressure drop of the concentric annulus by Equation (53) and the reduction factor by Equation (54).

Concept of Narrow-Slot Model: For simplification of mathematical analysis of annular flow, numerous approximations have been developed which consider different mud rheology, for example, Newtonian, Bingham Plastic, Power land, and yield power law. A commonly used model in the industry is a narrow-slot model, in which a rectangular slot represents the concentric annulus can.

Model Formulation: In this study, the narrow-slot modeling technique developed Iyoho and Azar [12] has been adopted to predict swab and surge pressures. The eccentric annulus is divided into numerous concentric annuli with a variable annular clearance. Each concentric annulus is treated separately and is represented by its annular clearance, which is a function of pipe eccentricity and angular position.

Flow is determined in every discrete element as a narrow slot with a constant slot height h depending on angular location $\theta$ and eccentricity. The slot height expression [12] is given by Equation (55).

The dimensionless surge pressure $\left({\pi }_1\right)$ and dimensionless exponent ($b=\frac{n+1}{n}$) in model development are given in Equation (56).

The dimensionless plug thickness $\left({\pi }_2\right)$ is determined from the dimensionless plug-boundary limits (${\overline{y}}_1$ and ${\overline{y}}_2$) is given by Equation (57).

For the momentum balance, a relationship between dimensionless plug thickness and surge pressure gradient is given by Equations (58) and (59).

Flowrate Analysis is given by the Equation (60), in which ${\overline{q}}_t$ is a dimensionless total flowrate and is given by Equation (61). By putting the quantities of dimensionless velocities integrating the equation, Crespo and Ahmed [13] developed a dimensionless expression, Equation (62), to compute the flow rate.

In the case of the closed-end pipe string, the flow rate in the annular is equal to the displaced fluid during the tripping operation. Ignoring the effects of ballooning and loss circulation, the fluid displaced rate can be expressed as in Equation (63).

For the representation of wellbore geometry, the annular clearance $h\left(\theta \right)$ and the mean slot width (W) is defined in Equation (64).

Modeling Flow in Eccentric Annulus: Eccentric annulus is represented by many narrow, variable-range slots (h) from earlier discussions. The annulus is split into 360 segments of 1 degree each at the center-point of each segment with a clearance determined (Equation (54)). By rearranging Equation (65), the outer diameter is computed using the estimated height (h). The dimensionless flow rate is calculated by (Equation (63)). Because of the symmetry, half of the annulus was calculated. For each segment computations, the equations are updated (Equation (65)). The technique for the iteration of a certain pressure gradient systematically varies to alter after slot height computation.

The total annular flow in dimensionless form can be expressed as in Equation (66), where ${\overline{q}}_t\left(\theta \right)$ is the total dimensionless flowrate for the segment.

The maximum possible value for $y_2$ is equal to the slot thickness, which equals 1 in the dimensionless form. In the model development phase, they recognize that with an increase in eccentricity values, the error in $\overline{y_2}$ is considerable. Therefore, they made a check to the maximum value of $\overline{y_2}$ and maintained it at 1. The maximum value of $\overline{y_1}$ is set to 0.

Therefore, by using the expression ${\pi }_{2,max}={\overline{y}}_{2,max}-{\overline{y}}_{1,min}$, it is obvious that the maximum possible value of ${\pi }_{2,max}$ is 1.

Circumferential Wall Shear Stress Variation: Luo and Peden [14] developed an eccentric model on the basis of many concentric annuli with varying outer radii. This method only takes into account the change in shear stress readily. Therefore, with increasing eccentricity, each segment’s circumferential share stress change becomes significant. Duan et al. [15] accounted for the radial shear stress variations and made a correction factor as in Equation (67).

The following assumptions were presumed during the model formulation:

• The fluid is incompressible (constant density);
• Steady state and isothermal Couette flow conditions;
• Laminar flow;
• Drill pipe moving at a constant speed, Vp;
• Negligible wall slippage effects.

Analysis of the Work by Srivastav et al.

Since the whole point of the models was to do experimental studies, the authors [10] used an existing small-scale setup. The setup is explained in detail, and the figures compare the experimental results with their models’ predictions. The authors then moved on to parametric study between two hypothetical fluids, power-law fluid, and yield-power law fluid.

The figures also show surge pressure predictions as a function of pipe velocity for both concentric and eccentric annulus. These figures show that the surge pressure increases with the diameter ratio due to decreased annular clearance. The numerical model developed in this study precisely predicts swab and surge pressures, simulating downhole pressure fluctuations that occur during tripping in inclined and horizontal wells. The model utilizes the existing variable narrow-slot approximation technique to account for pipe eccentric in surge pressure calculation.

The conclusions of this work are:

• The present model predicts swab and surge pressures of a yield power-law fluid in the eccentric annulus (i.e., eccentricity ranging from 0 to 90%) with reasonable accuracy (maximum discrepancy of 14%);
• Eccentricity has considerable effects on swab and surge pressures. Both experimental and theoretical results show surge pressure reduction of up to 40% as a result of eccentricity;
• Results show that for highly shear-thinning fluids, a small decrease in surge pressure can considerably increase the safe tripping speed limit;
• Surge pressure predictions for the concentric and eccentric model can be considered for the boundary limits for the expected surge pressures. In real field conditions, due to lateral pipe movement, the pipe does not maintain the concentric or fully eccentric geometry throughout, resulting in surge pressure variations between these limits;
• In general, fluid rheological parameters, tripping speeds, and diameter ratios considerably affect the generated pressure surges.

2.6. Recent Works

Crespo et al. [16] presented a new steady-state model for power-law fluids, which includes fluid and formation compressibility and pipe elasticity. Krishna et al. [17] performed laboratory experiments to investigate the effect of centric and eccentric on the swab and surge pressure. This work confirms that in the investigation, swab and surge pressures are greatly affected by the tripping speed, mud properties, clearance between pipe and annular, and the eccentricity of the tube. Gjerstad et al. [18] developed a model for Herschel-Bulkley fluids based on ordinary differential equations to predict swab and surge in real-time.

2.7. Summary of the Literature Study

Table 5. Summary of five prominent works on the swab and surge pressure model.

Model Name	Impact	Assumptions	Strengths	Weaknesses	Focus	Fluid Model
Srivastav et al. [10]	Horizontal and extended reach well.	Constant tripping speed. Flow approximation in eccentric annulus.	Eccentricity effect. Model validation with experiments. Good agreement between model and experiments.	Constant tripping speed. Experiments under controlled laboratory environment.	Eccentricity effect. Mud rheology effect.	Herschel Buckley.
Clark [5]	Simple formulation.	Incompressible fluid and bore hole wall.	Pipe motion effect. Acceleration pressure.	Neglected the effect of eccentricity. Neglected the bore hole conditions.	Pressure surges caused by moving pipe in wellbore.	Bingham Plastic.
Gjerstad et al. [8]	Automatic prediction of swab and surge pressures during tripping operations.	Non-Newtonian fluid.	Fast and robust automatic down hole pressure predictions. Coupling ability with modern control for tripping speed.	To tune the model, circulation of the well prior to tripping.	Developing an automatic prediction of down hole pressure for real-time application.	Herschel Bulkley.
Burkhardt et al. [1]	Theoretical prediction of surge and swab pressures.	Closed and open-end pipe string.	Rigorously formulation for swab and surge pressures. Presentation of formulation with simplified graphs.	Measurements of pressure pulses generated by moving pipe in wellbore. Computation of transient pressure surges due to moving pipe in borehole.	Approximations of theory of viscus drag by a simplified graph for field application	Bingham Plastic.
Lal [4]	Interactive and user-friendly swab and surge pressures predictions.	Friction as a “lumped parameter”.	Non-Newtonian fluid Dynamic model.	Friction as a “lumped parameter”.	Dynamic modeling.	Power Law.

below summarizes the above models with their impact, weaknesses, assumptions, strengths, focus, and fluid models utilized in the different models.

3. Data-Driven Modeling in Drilling in Well Operations

Many researchers have recently made a paradigm in drilling and well operations and implemented data-driven techniques to improve operational performance and reduce risks. Traditionally, the oil and gas industry, especially drilling, heavily relied on the analytical modeling approach. However, recent advancements such as big data, data analytics, machine learning modeling, and AI modeling have tremendous value creation in other industries. Hence, the oil and gas industry and drilling are also implementing these techniques to create value through performance improvements and reduce risks.

The oil and gas industry’s decision-making process revolves around quantifying uncertainty, limiting risk, and maximizing profit, as well as speed. The ever-increasing amount of data collected due to technological advancements can drastically improve the intuitive judgments made in numerous day-to-day operations. However, the data’s potential advantages can only be realized if the correct tools are used to combine various forms of data and translate it into valuable information that can be used to draw wise conclusions.

3.1. Applications of Data-Driven Techniques in Oil and Gas

Data-driven approaches are effective instruments for transforming information into knowledge. Due to a lack of well-organized data, historical data has not been used effectively in assessing operations. However, there is an enormous potential for turning terabytes of data into knowledge. Data-driven models have become increasingly commonly employed in the analysis, predictive modeling, control, and optimization of numerous processes due to improvements and implementation of data-driven approaches. Even though physics and geology are frequently included in this technique, the industry as a whole is still cautious of the adoption of data-driven methods since they are data-based solutions rather than traditional physics-based approaches [19].

3.2. Subsurface Characterization and Petrophysics

In the oil and gas industry, mathematical models are commonly employed. For example, Taner et al. [20] created a mathematical model that describes how complicated trace analysis is applied to seismic data and how it might be used in geologic interpretation. On the other hand, mathematical models have severe constraints and are more difficult to mimic. Therefore, several researchers in the oil and gas industry have also employed data-driven methodologies. Specifically, reservoir management and simulation, production and drilling optimization, real-time drilling automation, and facility maintenance are the key application areas [21]. This section will look at some of the applications of the stated data-driven methodologies in various industries.

Ouenes [22] investigated the usefulness of fuzzy logic and neural networks in fractured reservoir characterization, using three phases to compare the performance of two alternative models. Ouenes [22] showed that by employing fuzzy curves, the influence of each model input on fractures can be characterized, and the factors that may have a high link with fractures can be determined [23]. Al-Anazi et al. [24] presented research that used support vector regression (an SVM extension) to accurately estimate the porosity and permeability values for a field. Hosseini et al. [25] demonstrated how a random forest tree algorithm supported by a naive Bayesian operation might be utilized to analyze field permeability.

For intersecting and near-well fracture corridors, Ozkaya [26] demonstrated the use of decision trees. Chamkalani et al. [27], El-Sebakhy [28], Tohidi-Hosseini [29], and Ahmadi et al. [30] have used SVM and decision trees to predict gas PVT characteristics as well as oil–gas interaction. Analyzing logs and generating missing log tracts are two of the most common artificial intelligence applications. For example, to produce a sonic log to assess over-pressured zones at the Anardarko Basin, Cranganu et al. [31] used a Support Vector Regression technique.

Akande et al. [32] created a support Vector Regression approach supported by an evolutionary algorithm to generate the best hydrocarbon estimations from logs acquired from logs from a reservoir. Another use of machine learning was estimating a reservoir’s Total Organic Content using log data [33]. Masoudi et al. [34] created a supervised Dymanic Bayseian Network (DBN) algorithm that learned from logs to produce a model for identifying reservoirs without the need for user-defined cut-offs. Anifowose et al. [35] suggested an ensemble SVM approach for predicting porosity and permeability values comparable to the random forest tree algorithm.

3.3. Drilling

Drilling has made significant progress, particularly in risk control, regulated rate of penetrations, and so on. Ahmadi et al. [30] utilized SVM to model the rheology of many drilling fluids under various environmental circumstances. Cross-verification also revealed a strong agreement between the forecast and the test data. Fatehi et al. [36] used deposition information to construct a transductive support vector machine system for mapping possible drilling targets during exploration. Zhang et al. [23] developed a Dynamic Bayesian Network (DBN) to efficiently analyze risk and uncertainty in controlled pressure drilling. This approach takes into account several elements to calculate uncertainty utilizing additional probability parameters. DBN was also utilized by Al-Yami et al. [37] to create a drilling expert system based on reservoir and fluid data. Bhandari et al. [38] developed a technique to anticipate the conditions that lead to an offshore blow-out, particularly during conducted measured pressure drilling and unbalanced drilling, as well as risk analysis. Sule et al. [39] conducted a similar study that looked at the robustness of system controls after recreating kick circumstances used in measured pressure drilling. Chang et al. [40] also used DBN algorithms to examine emergency riser disconnection modules. Six disconnected module criteria linked the DBN system and the failure tree investigation. Cai et al. [41] used a DBN to investigate the dependability of Blowout Preventer redundancy in deep-sea wells. Principal component analysis was utilized by Kormaksson et al. [42] to find economically viable sites for new wells. Bakshi [43] developed a unique nonlinear regression model to predict shale oil well performance, including optimal well sites and completion parameters. Temizel et al. [44] investigated the factors that impact vertical and horizontal well performance in confined reservoirs.

4. Proposal for New Research on Surge and Swab Pressure Modeling

New research on swab and surge Pressure Modeling is proposed in this section, based on the literature review. The literature in Section 2 presented a thorough analysis of five works. The models given in these works were developed when pressure measurements were unavailable during the tripping in or tripping out operations. However, with the emergence of high-speed telemetry (NOV wired drill pipe) and data while tripping tool (NOV DWT), measuring the downhole pressure and temperature is possible when tripping in or tripping out of hole [45,46]. Therefore, NOV wired drill pipe and data while tripping tool made it possible to look into swab and surge to understand the phenomena better. With these new technologies, it is now possible to build a new model for the processes using data-driven techniques on top of mathematical equations and physics.

4.1. The Role of Sensors and Data Acquisition (Logging Data)

This section presents an overview of different sensors used to understand a well’s physical properties, from the surface to the final depth.

The sensors and the sensor recording systems are classified into different categories based on the physical attributes to be measured:

• Depth tracking sensor;
• Flow in and out tracking sensors;
• Measurement while drilling (MWD) and Logging-While-Drilling (LWD) tool;
• Electromagnetic-Wave Resistivity (EWR) tool;
• Electronic Drilling Recorder (EDR) system.

The depth tracking sensor provides instantaneous or an average rate of penetration (ROP) based on the amount of work done by draw works or change in hydrostatic pressure in a column of water.

The flow in and out tracking sensors are used to monitor the fluid-flow rate being applied downhole and the flow rate coming out of the annulus; these sensors provide an early warning of either a kick condition or a loss of circulation. The surface revolutions-per-minute (RPM), rotary torque, and hook load are obtained using Drill-monitor sensors, used for efficient drilling and minimizing downhole failures like stick-slip or stuck-pipe. Several other sensors are used to measure the drilling mud level, surface pressure, and gases present in the formation, which helps to understand downhole conditions better.

Measurement while drilling (MWD) is a type of Logging-While-Drilling (LWD), in which tools are encompassed in a single module in the steering tool. This tool is with the drill string at the end of the drilling apparatus, providing wellbore position, drill bit information, and directional data, as well as real-time drilling information.

In the rig site software system, MWD and LWD are the most comprehensive data-acquisition systems present at the rig site. Real-time data-acquisition systems typically connected to a surface and downhole sensor enable live monitoring of the rig-equipment operation and the well-construction process. The obtained surface measurements are stored in an electronic drilling recorder (EDR) system in the form of electronic tour-sheet applications.

4.2. The Steps Involved in New Research

With the availability of real-time drilling data, we propose developing newer models for swab and surge pressures. The following steps are involved:

• Preparing the data;
• Validating the existing models with the data and improving the model;
• Testing the new model.

Research with field data also demands the development of newer algorithms for the automated processing of tripping in, tripping out, and the drilling data of an actual well. During the tripping in and tripping out process in drilling operations, E&P companies are implementing the Data While Tripping tool to obtain internal, annular Pressure, and temperature while using Pressure While Drilling and Enhance Measurement System. However, Pressure While Drilling Tool and Enhance Measurement Systems are usually from different vendors, and the sensors mounted on these tools are of varying quality. Therefore, it is essential to determine the agreement between the measurements of the same variables from different methods. For example, Bland Altman Plot Analysis theory, which is utilized in health sciences [47]) could be implemented on the Pressure While Drilling and Enhance Measurement System measurements obtained via data while the tripping tool through wired drill pipe telemetry system.

5. Conclusions

The paper proposes developing newer and more robust models for the swab and surge pressures involving actual data from tripping in, tripping out, and drilling operations. Oil companies must facilitate this research by providing field data while tripping tools (e.g., NOV DWT) and wired drill pipe telemetry systems (e.g., NOV Wired Drill Pipe Telemetry Network. For example, these field data could belong to one of the fields in the Barents Sea, Norway. In this way, actual field problems that are encountered relating to tripping in and tripping out can be investigated, and potential data-driven solutions can be delivered. Several researchers have implemented data-driven methodologies to find new solutions within ROP modeling, reservoir management, drilling optimization, and data processing, and have already achieved promising results.

Using field data to improve the models further develops a solid relationship between academics and industry by finding new solutions to drilling and well construction operations challenges. For example, in Norce—the research institution in Norway—several projects on drilling automation are ongoing.