The Failure Intensity Estimation of Repairable Systems in Dynamic Working Conditions Considering Past Effects
Abstract
1. Introduction
2. Cumulative Damage and Failure Intensity
2.1. The Cumulative Damage Interpretation of Failure Probability
2.2. Equal Damage Model of Failure Intensity
3. Improved PIM under Dynamic Conditions
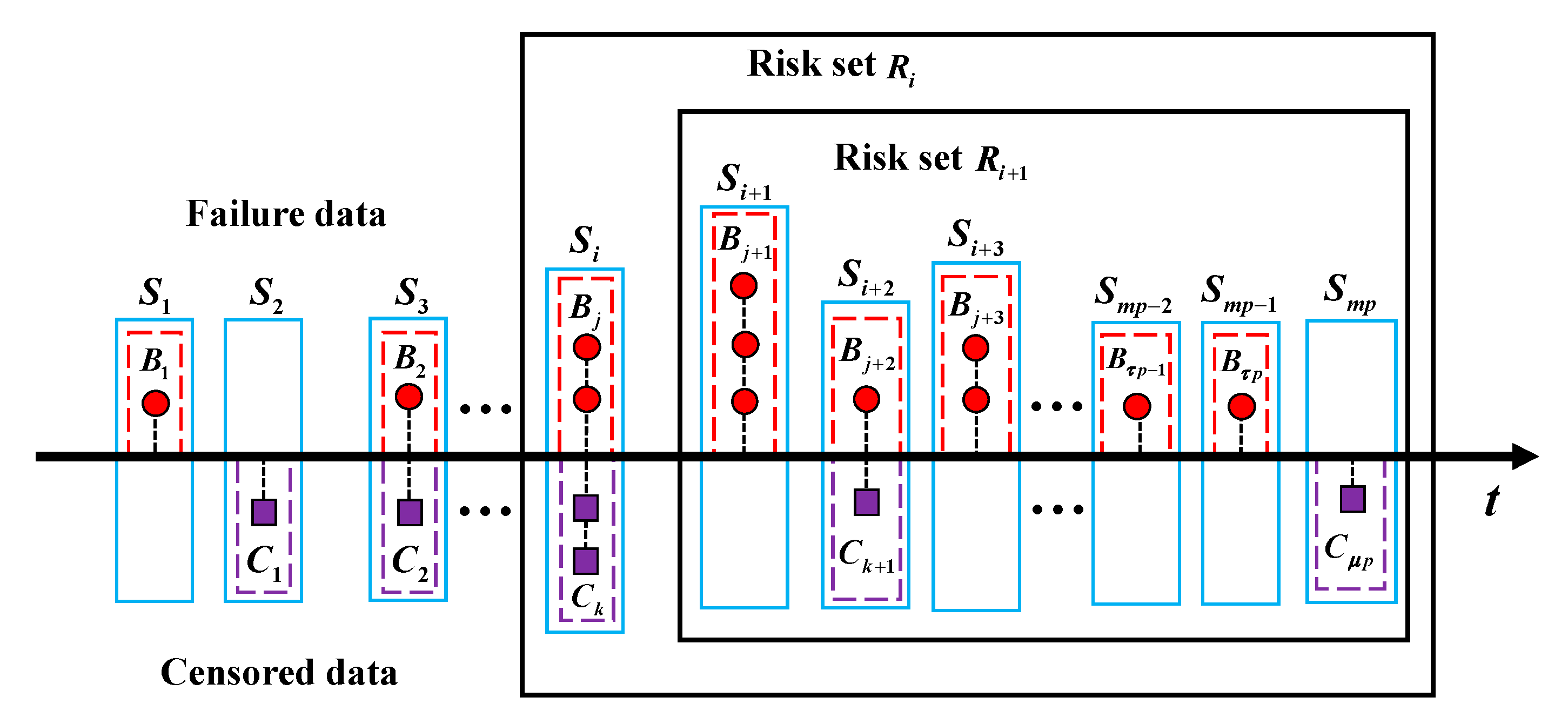
3.1. Traditional PIM and Its Limitations
3.2. Improved PIM Which Considers Past Effects
3.3. Model Estimation
4. Case Study
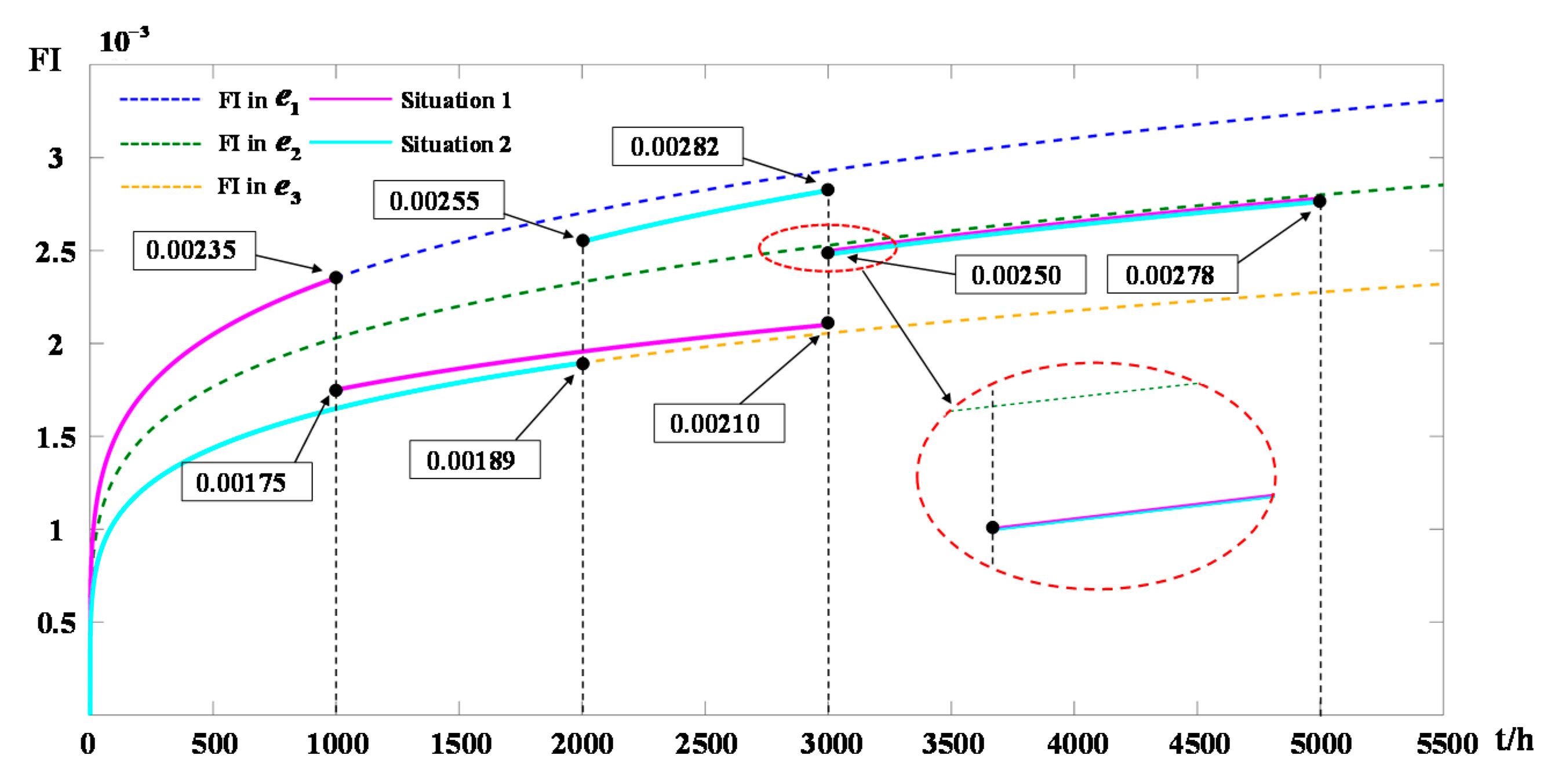
4.1. Numerical Cases
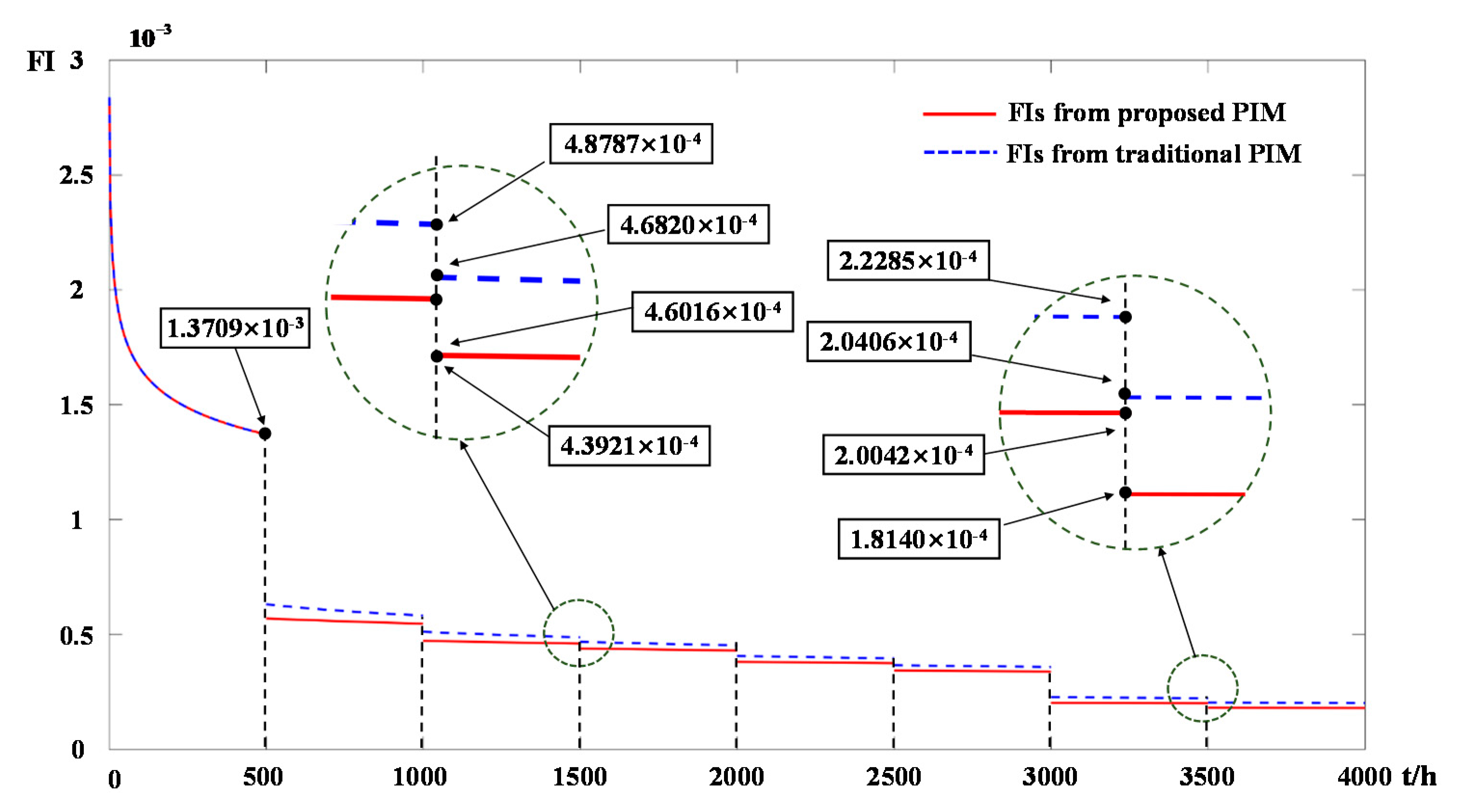
4.2. Real-World Cases
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, T.; Yang, L.; Ma, X.; Zhang, Z.; Zhao, Y. Dynamic maintenance strategy with iteratively updated group information. Reliab. Eng. Syst. Saf. 2020, 197, 106820. [Google Scholar] [CrossRef]
- Fan, D.; Zhang, A.; Feng, Q.; Cai, B.; Liu, Y.; Ren, Y. Group maintenance optimization of subsea Xmas trees with stochastic dependency. Reliab. Eng. Syst. Saf. 2021, 209, 107450. [Google Scholar] [CrossRef]
- Dao, C.; Zuo, M. Optimal selective maintenance for multi-state systems in variable loading conditions. Reliab. Eng. Syst. Saf. 2017, 166, 171–180. [Google Scholar] [CrossRef]
- Li, H.; Deng, Z.M.; Golilarz, N.A.; Soares, C.G. Reliability analysis of the main drive system of a CNC machine tool including early failures. Reliab. Eng. Syst. Saf. 2021, 215, 107846. [Google Scholar] [CrossRef]
- Li, H.; Soares, C.G.; Huang, H.Z. Reliability analysis of a floating offshore wind turbine using Bayesian Networks. Ocean Eng. 2020, 217, 107827. [Google Scholar] [CrossRef]
- Jia, X.; Cui, L.; Xing, L. New insights into reliability problems for supply chains management based on conventional reliability model. Eksploat. I Niezawodn. 2018, 20, 465–470. [Google Scholar] [CrossRef]
- Niu, X.; Wang, R.; Liao, D.; Zhu, S.; Zhang, X.; Keshtegar, B. Probabilistic modeling of uncertainties in fatigue reliability analysis of turbine bladed disks. Int. J. Fatigue 2021, 142, 105912. [Google Scholar] [CrossRef]
- Hu, W.; Westerlund, P.; Hilber, P.; Chen, C.; Yang, Z. A general model, estimation, and procedure for modeling recurrent failure process of high-voltage circuit breakers considering multivariate impacts. Reliab. Eng. Syst. Saf. 2022, 220, 108276. [Google Scholar] [CrossRef]
- Cheng, Q.; Qi, B.; Liu, Z.; Zhang, C.; Xue, D. An accuracy degradation analysis of ball screw mechanism considering time-varying motion and loading working conditions. Mech. Mach. Theory 2019, 134, 1–23. [Google Scholar] [CrossRef]
- Jia, X.; Xing, L.; Song, X. Aggregated Markov-based reliability analysis of multi-state systems under combined dynamic environments. Qual. Reliab. Eng. Int. 2020, 36, 846–860. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, Y.; Ma, X.; Zhou, K. Reliability assessment in dynamic field environment incorporating multiple environmental effects. Proc. Inst. Mech. Eng. Part O J. Risk. Reliab. 2020, 234, 3–14. [Google Scholar] [CrossRef]
- Dong, Q.; Cui, L. Reliability analysis of a system with two-stage degradation using Wiener processes with piecewise linear drift. IMA J. Manag. Math. 2021, 32, 3–29. [Google Scholar] [CrossRef]
- Hong, L.; Zhai, Q.; Wang, X.; Ye, Z. System reliability evaluation under dynamic operating conditions. IEEE Trans. Reliab. 2018, 68, 800–809. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, B.; Ge, T.; Feng, H.; Tao, W. Small-Sample accelerated life test method based on the inverse power law model. Appl. Math. Inform. Sci. 2014, 8, 1725. [Google Scholar] [CrossRef][Green Version]
- Escobar, L.; Meeker, W. A review of accelerated test models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Chen, C.; Zhao, H.; Yang, D.; Guo, J.; Luo, W. Reliability assessment of the spindle systems with a competing risk model. Proc. Inst. Mech. Eng. Part O J. Risk. Reliab. 2019, 233, 226–234. [Google Scholar] [CrossRef]
- Li, H.; Yang, Z.; Xu, B.; Chen, C.; Kan, Y.; Liu, G. Reliability evaluation of NC machine tools considering working conditions. Math. Probl. Eng. 2016, 206, 9842607. [Google Scholar] [CrossRef]
- Pike, M. A method of analysis of a certain class of experiments in carcinogenesis. Biometrics 1966, 22, 142–161. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and Life-Tables. J. R. Stat. Soc. Ser. B Stat. Methodol. 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Bokoro, P.; Doorsamy, W. Reliability analysis of low-voltage metal-oxide surge arresters using accelerated failure time model. IEEE Trans. Power Syst. 2018, 33, 3139–3146. [Google Scholar] [CrossRef]
- Bagdonavičius, V.; Levulienė, R. On accelerated life testing when the AFT model fails. IEEE Trans. Reliab. 2019, 68, 1311–1319. [Google Scholar] [CrossRef]
- Su, S. Flexible parametric accelerated failure time model. J. Biopharm. Stat. 2021, 31, 650–667. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; He, W.; Li, H. A semiparametric approach for accelerated failure time models with covariates subject to measurement error. Commun. Stat. Simul. Comput. 2014, 43, 329–341. [Google Scholar] [CrossRef]
- Zhu, W.; Fouladirad, M.; Bérenguer, C. Condition-based maintenance policies for a combined wear and shock deterioration model with covariates. Comput. Ind. Eng. 2015, 85, 268–283. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Shahidehpour, M.; Wu, L.; Guo, C.; Zhu, B. Stochastic co-optimization of midterm and short-term maintenance outage scheduling considering covariates in power systems. IEEE Trans. Power Syst. 2016, 31, 4795–4805. [Google Scholar] [CrossRef]
- Yuan, F.; Kumar, U. Kernelized proportional intensity model for repairable systems considering piecewise operating conditions. IEEE Trans. Reliab. 2012, 61, 618–624. [Google Scholar] [CrossRef]
- Hu, W.; Yang, Z.; Chen, C.; Wu, Y.; Xie, Q. A Weibull-based recurrent regression model for repairable systems considering double effects of operation and maintenance: A case study of machine tools. Eng. Syst. Saf. 2021, 213, 107669. [Google Scholar] [CrossRef]
- Lu, X.; Lin, M. Hazard rate function in dynamic environment. Reliab. Eng. Syst. Saf. 2014, 130, 50–60. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, Z.; Liao, H. Preventive maintenance of a batch production system under time-varying operational condition. Int. J. Prod. Res. 2017, 55, 5681–5705. [Google Scholar] [CrossRef]
- Pang, M.; Platt, R.; Schuster, T.; Abrahamowicz, M. Flexible extension of the accelerated failure time model to account for nonlinear and time-dependent effects of covariates on the hazard. Stat. Methods Med. Res. 2021, 30, 2526–2542. [Google Scholar] [CrossRef]
- Solomon, P. Effect of misspecification of regression model in the analysis of survival data. Biometrika 1984, 71, 291–298. [Google Scholar] [CrossRef]
- Syamsundar, A.; Naikan, V. Imperfect repair proportional intensity models for maintained systems. IEEE Trans. Reliab. 2011, 60, 782–787. [Google Scholar] [CrossRef]
- Xu, B. Study on Reliability Modeling and Analysis of CNC Machine Tools Based on Maintenance Degree. Ph.D. Thesis, Jilin University, Changchun, China, 2011. [Google Scholar]
- Cox, D. Partial likelihood. Biometrika 1975, 62, 269–276. [Google Scholar] [CrossRef]
- Wen, F. Numerical study of likelihood-ratio-test-based single change point estimation. Electron. Lett. 2012, 48, 1532–1533. [Google Scholar] [CrossRef]


| Working Conditions | ||||
|---|---|---|---|---|
| 0.25 | 2200 | 1 | 10 | |
| 0.23 | 3500 | 0 | 12 | |
| 0.39 | 2800 | 1 | 6 | |
| 0.42 | 1800 | 1 | 6 | |
| 0.26 | 4200 | 0 | 2 | |
| 0.13 | 3500 | 1 | 9 | |
| 0.51 | 3000 | 1 | 6 | |
| 0.60 | 3600 | 1 | 8 |
| Covariate Number | Working Conditions Covariates | |||||
|---|---|---|---|---|---|---|
| 4 | −0.510233 | 0.000505 | 0.012975 | −0.080421 | 7.603 | 9.488 |
| 3 | −0.493228 | 0.000500 | 0 | −0.080318 | 7.602 | 7.815 |
| 2 | 0 | 0.000536 | 0 | −0.075618 | 7.503 | 5.991 |
| Working Condition | ||||||||
|---|---|---|---|---|---|---|---|---|
| Time | 0 | 500 | 500 | 1000 | 1000 | 1500 | 1500 | 2000 |
| Proposed PIM | 0 | 13.7089 10−4 | 5.6969 10−4 | 5.4697 10−4 | 4.7250 10−4 | 4.6016 10−4 | 4.3921 10−4 | 4.3022 10−4 |
| Traditional PIM | 0 | 13.7089 10−4 | 6.3138 10−4 | 5.8216 10−4 | 5.1159 10−4 | 4.8787 10−4 | 4.6820 10−4 | 4.5270 10−4 |
| Working Condition | ||||||||
| Time | 2000 | 2500 | 2500 | 3000 | 3000 | 3500 | 3500 | 4000 |
| Proposed PIM | 3.8103 10−4 | 3.7510 10−4 | 3.4319 10−4 | 3.3885 10−4 | 2.0183 10−4 | 2.0042 10−4 | 1.8140 10−4 | 1.8032 10−4 |
| Traditional PIM | 4.0668 10−4 | 3.9619 10−4 | 3.6628 10−4 | 3.5854 10−4 | 2.2691 10−4 | 2.2285 10−4 | 2.0406 10−4 | 2.0090 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Tian, H.; Deng, F.; Dong, L.; Li, J. The Failure Intensity Estimation of Repairable Systems in Dynamic Working Conditions Considering Past Effects. Appl. Sci. 2022, 12, 3434. https://doi.org/10.3390/app12073434
Zhou X, Tian H, Deng F, Dong L, Li J. The Failure Intensity Estimation of Repairable Systems in Dynamic Working Conditions Considering Past Effects. Applied Sciences. 2022; 12(7):3434. https://doi.org/10.3390/app12073434
Chicago/Turabian StyleZhou, Xinda, Hailong Tian, Fuqin Deng, Luntao Dong, and Jieli Li. 2022. "The Failure Intensity Estimation of Repairable Systems in Dynamic Working Conditions Considering Past Effects" Applied Sciences 12, no. 7: 3434. https://doi.org/10.3390/app12073434
APA StyleZhou, X., Tian, H., Deng, F., Dong, L., & Li, J. (2022). The Failure Intensity Estimation of Repairable Systems in Dynamic Working Conditions Considering Past Effects. Applied Sciences, 12(7), 3434. https://doi.org/10.3390/app12073434






