Interval Analysis of Vibro-Acoustic Systems by the Enclosing Interval Finite-Element Method
Abstract
:1. Introduction
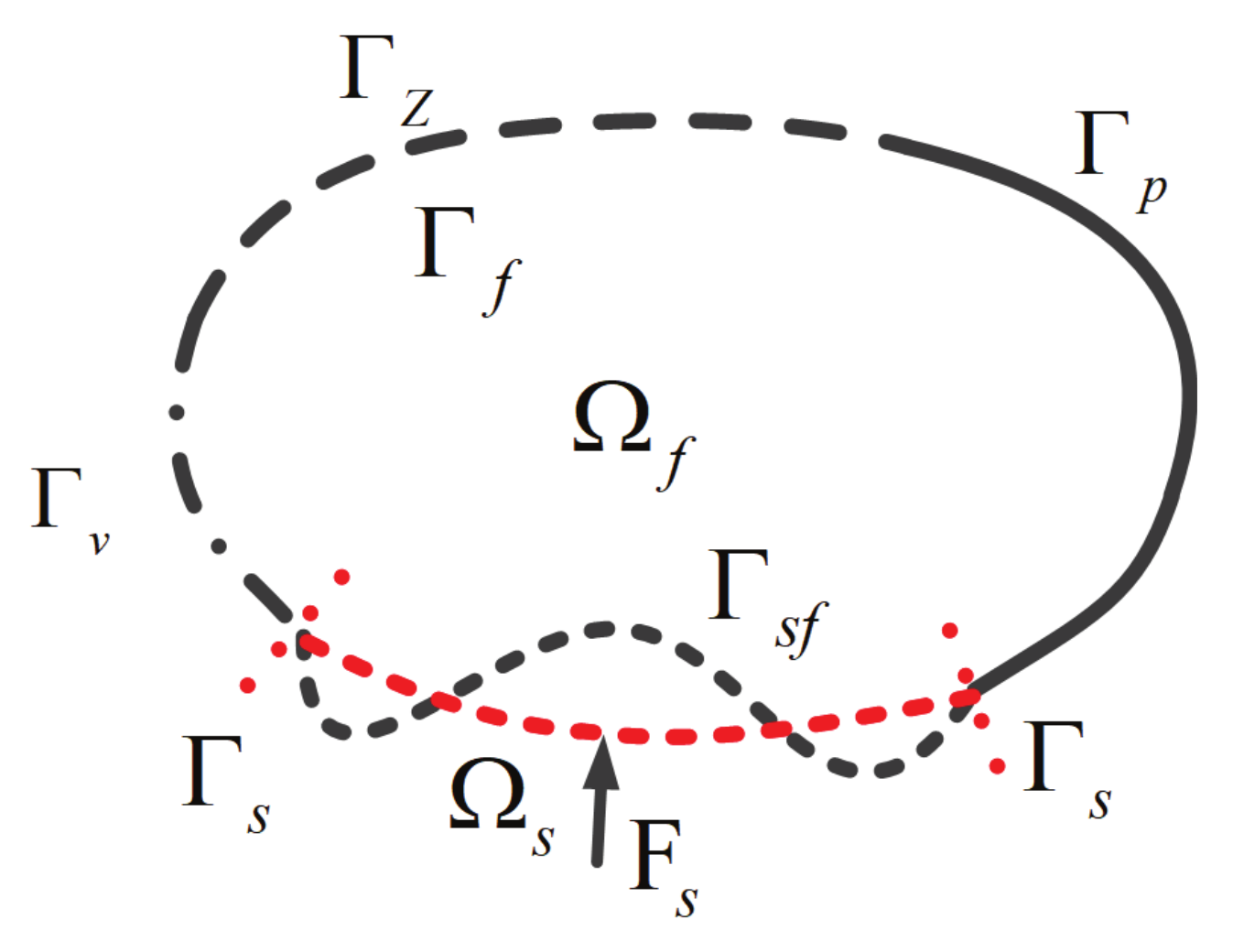
2. Formulation of Vibro-Acoustic Coupling System with Uncertain-But-Bounded Parameters
2.1. Interval Vibro-Acoustic Coupling Equation
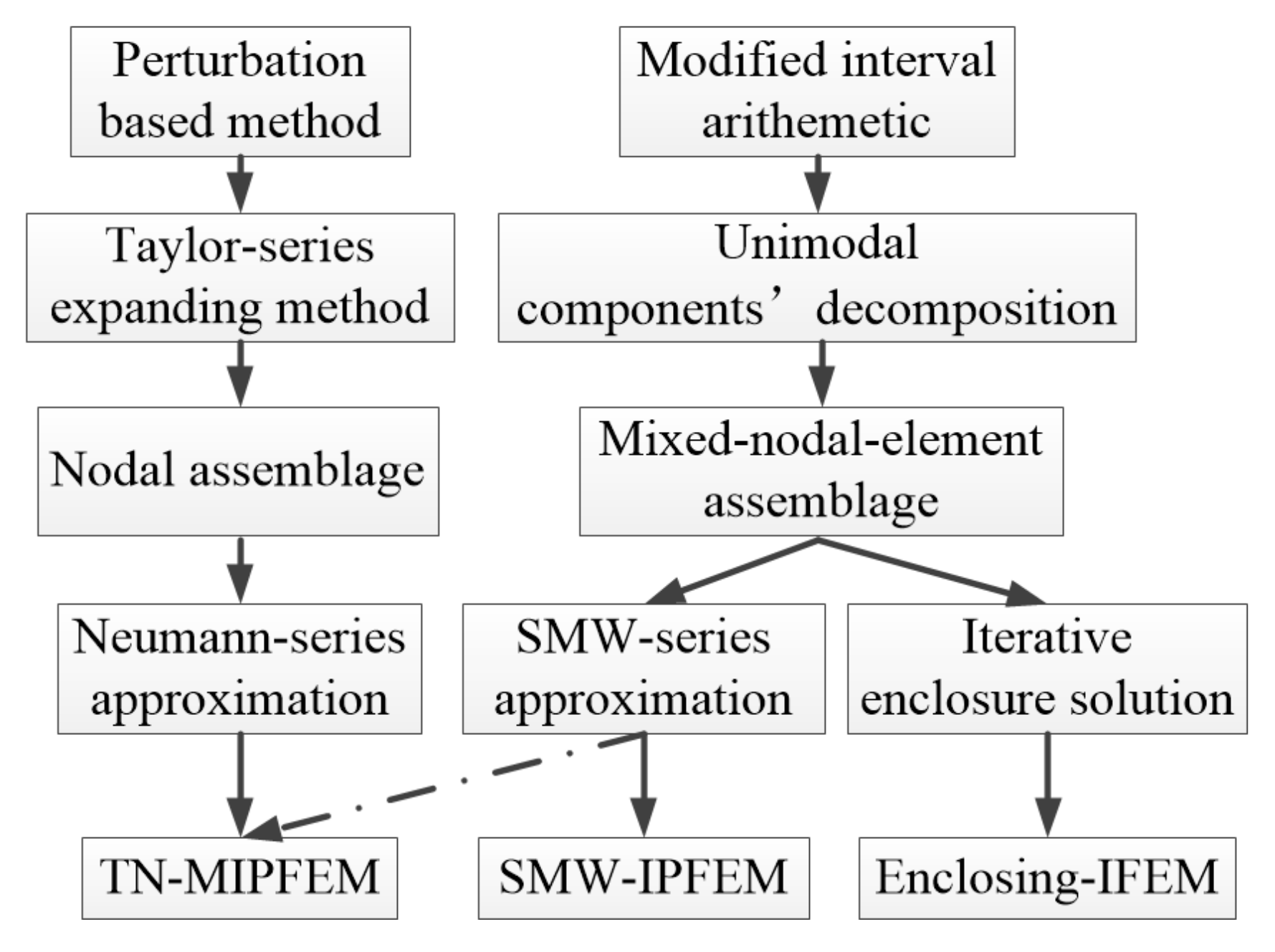
2.2. Unimodal Components’ Decomposition for Uncertain Structures
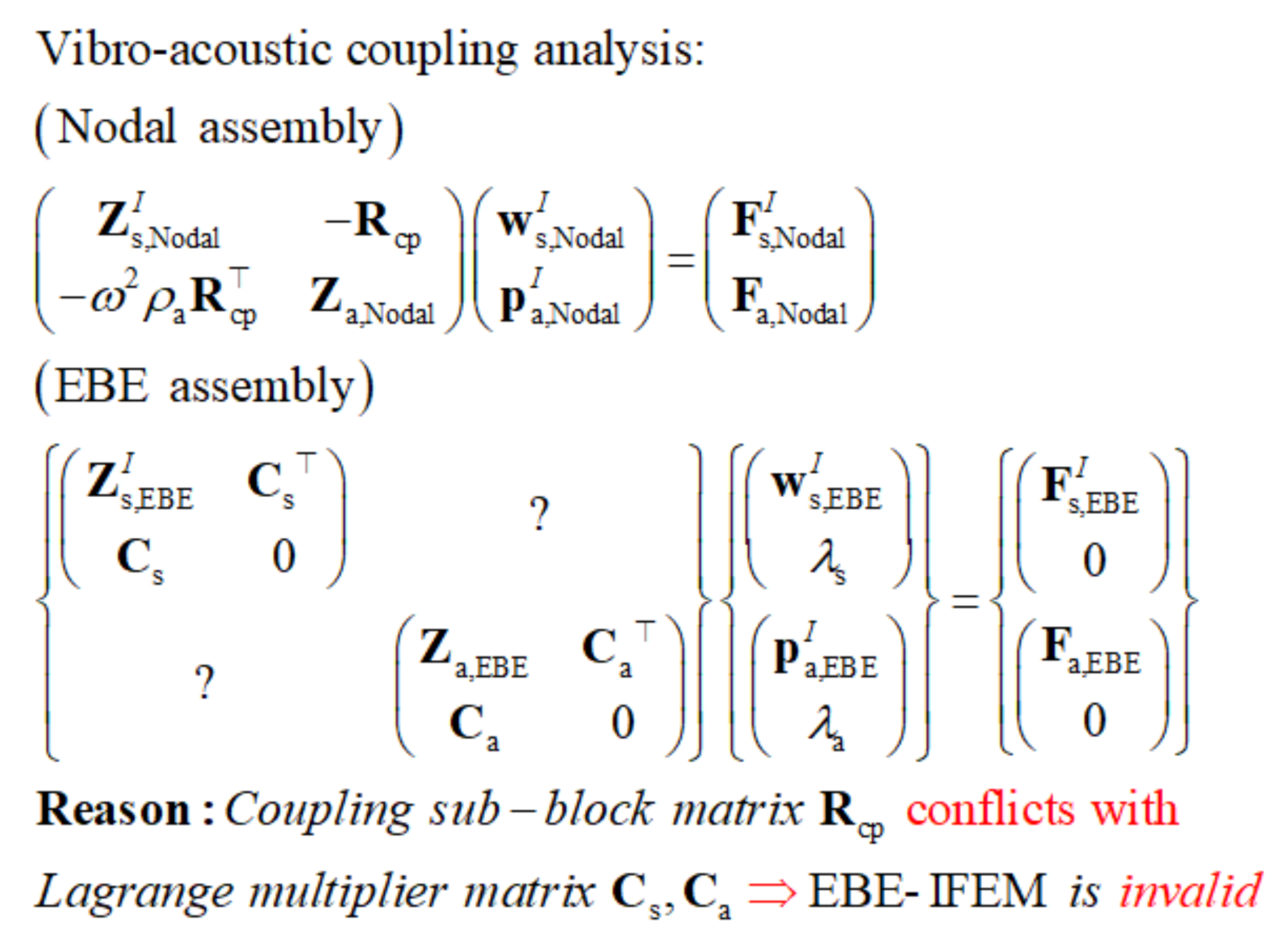
2.3. Different Assembly Strategies for Interval Coupling System
2.4. The Construction of the Interval Coupling Governing Equations
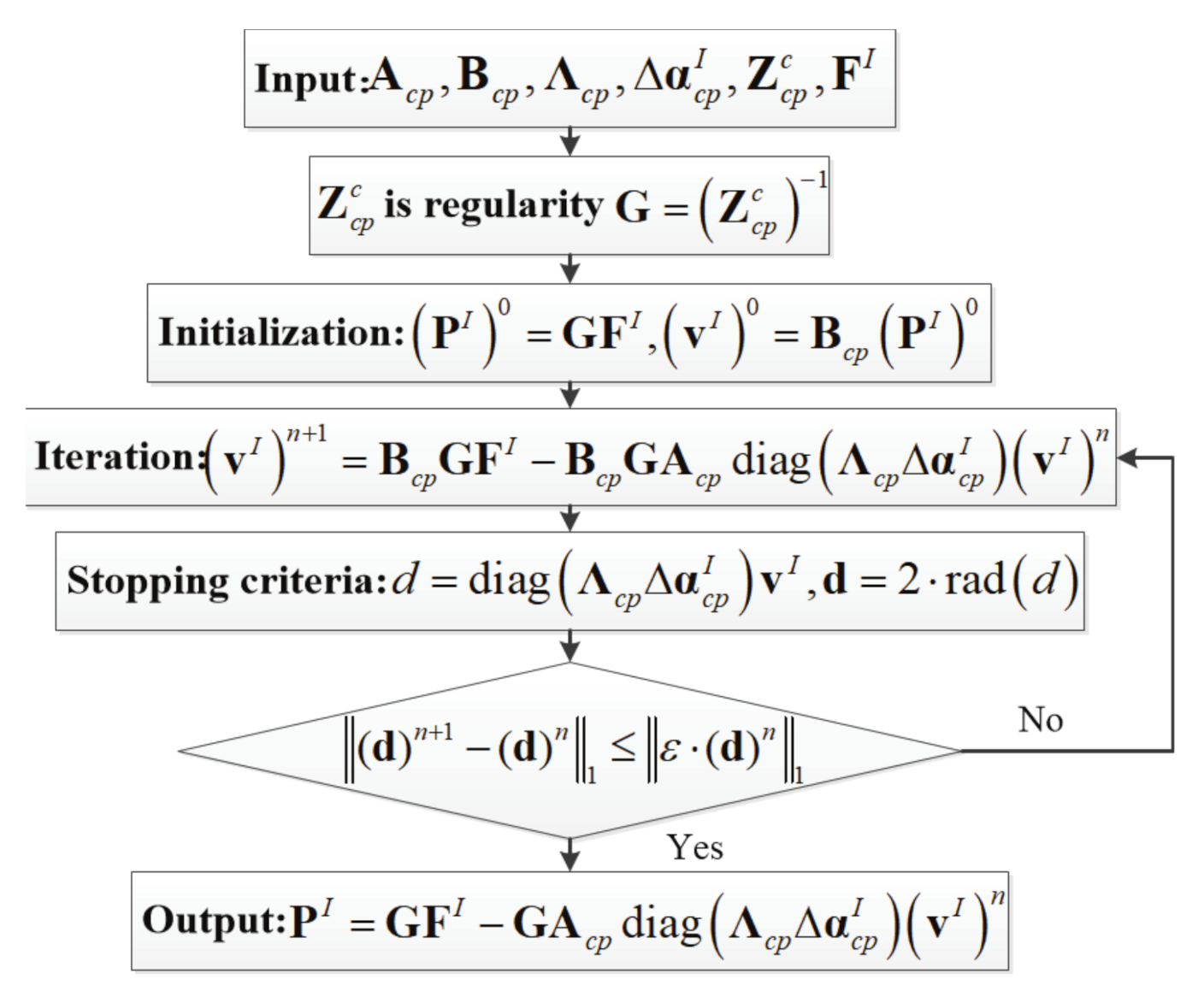
2.4.1. The Iterative Enclosure Formula of Interval Coupling Governing Equations
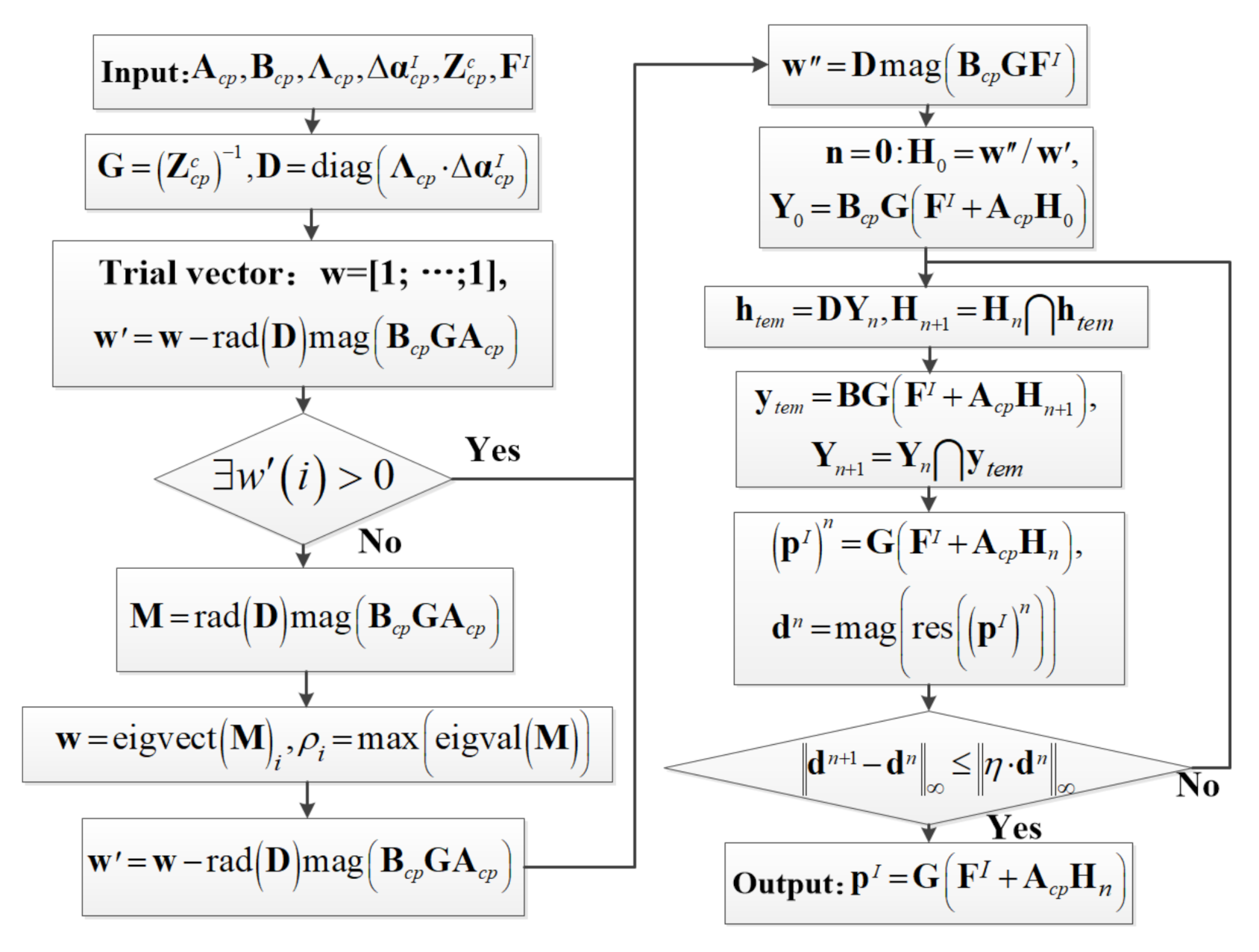
2.4.2. The Dyadic-Product Formula of Interval Coupling Governing Equation for the Dynamic Extended SMW-IPFEM
3. Enclosing Interval Finite-Element Method for Coupling Problem
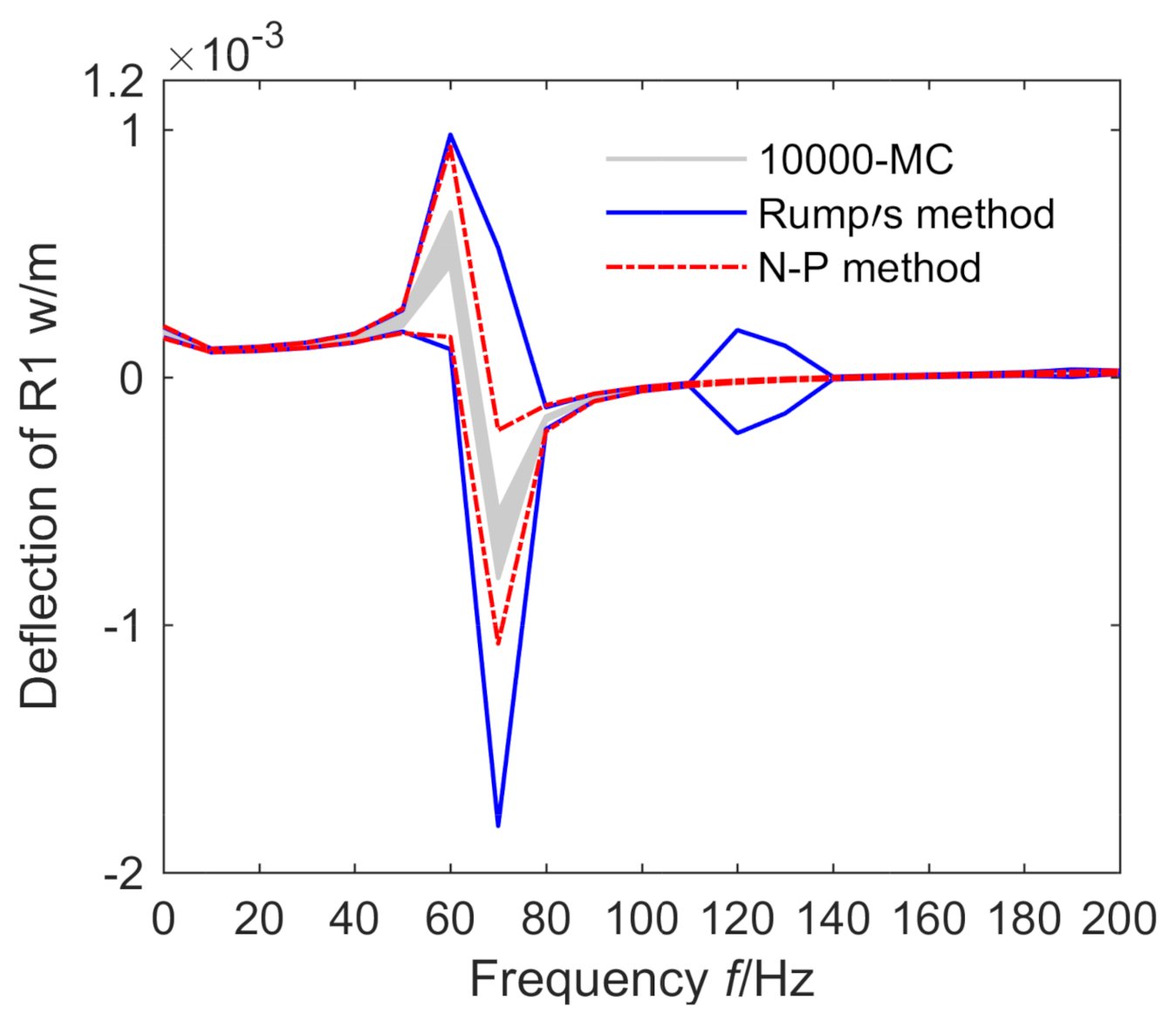
3.1. Rump’s Inclusion Method in Vibro-Acoustic Coupling Problem
3.2. Neumaier–Pownuk Method in Vibro-Acoustic Coupling Problem
4. Numerical Applications in Vibro-Acoustic Coupling Problem
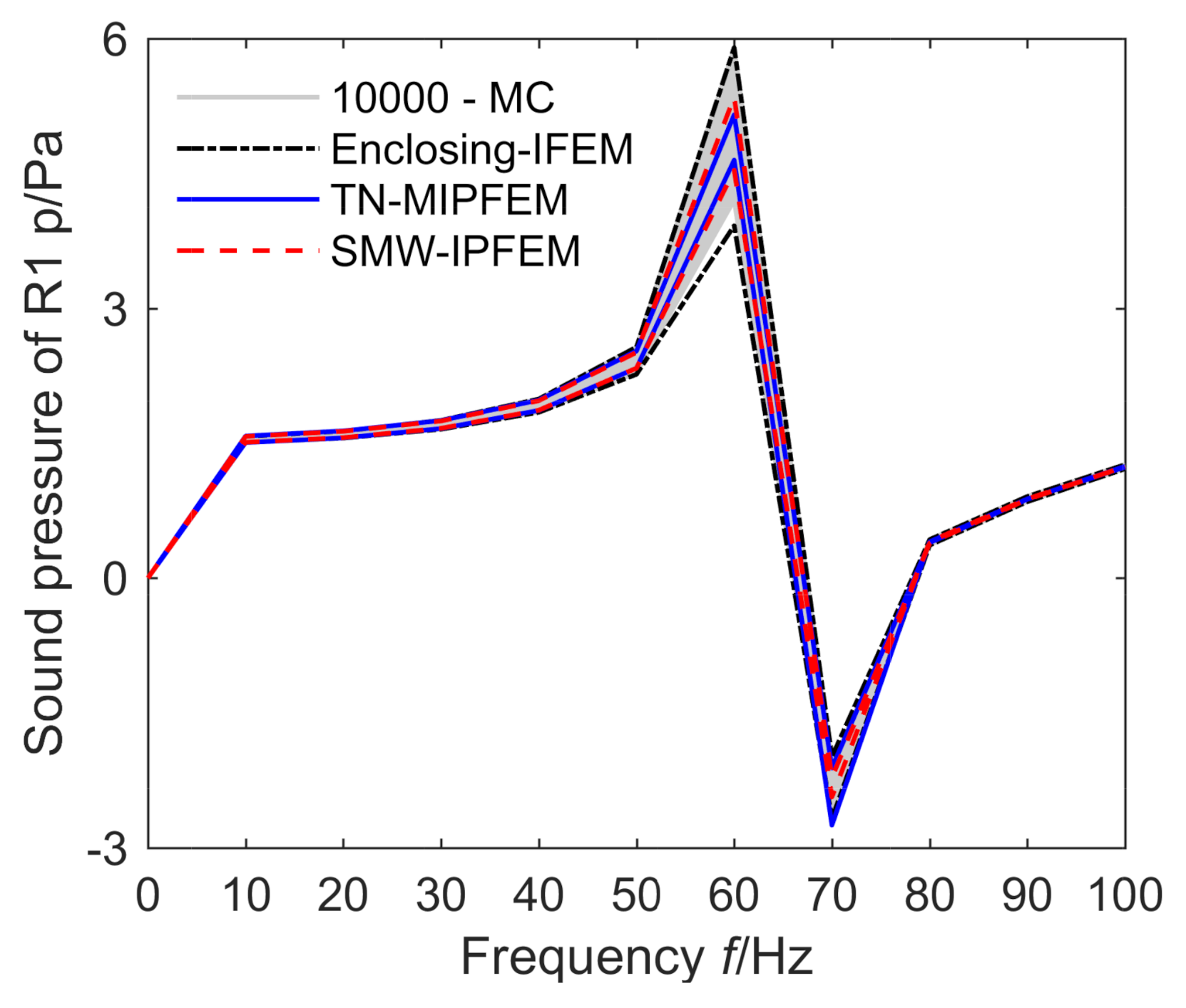
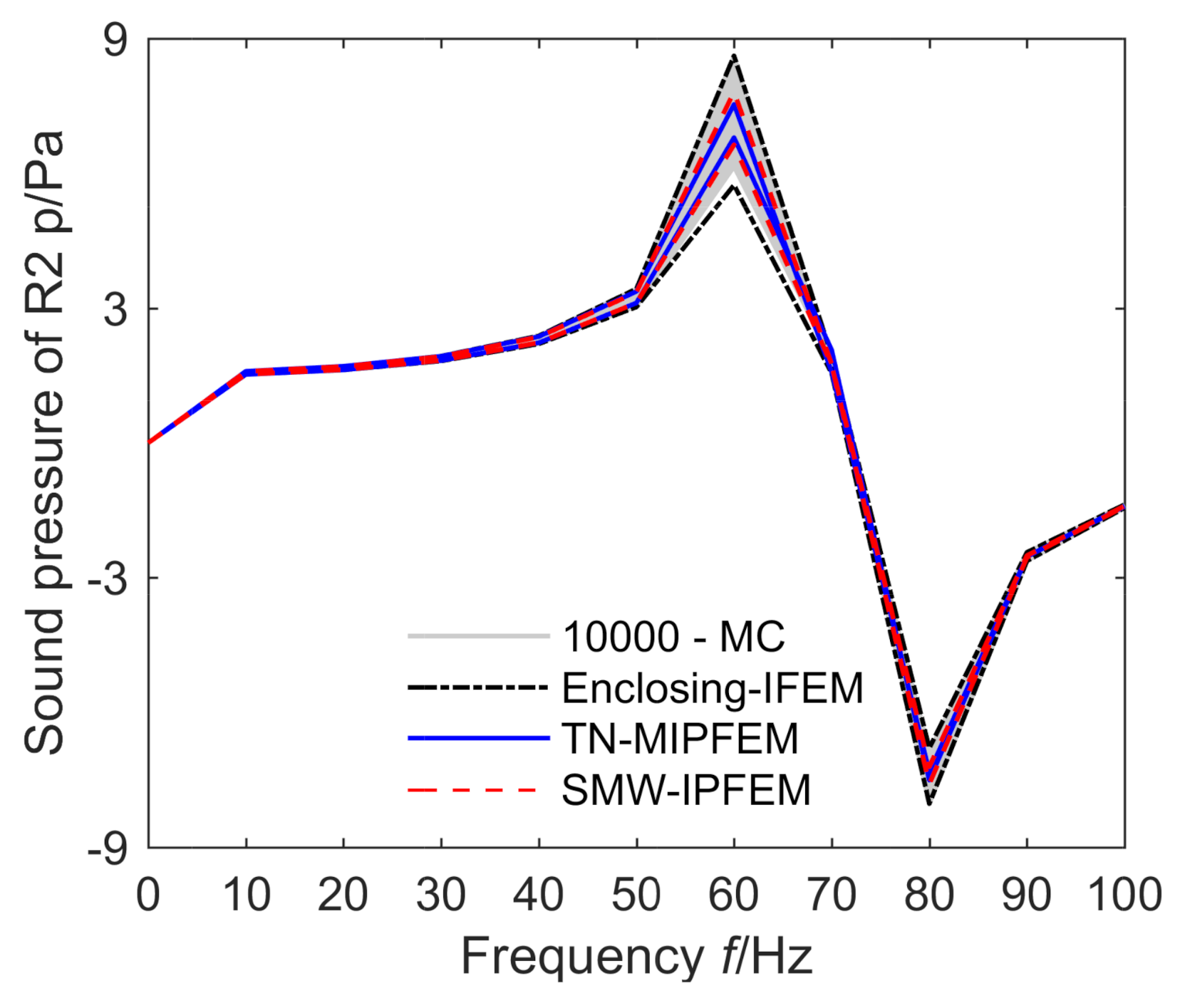
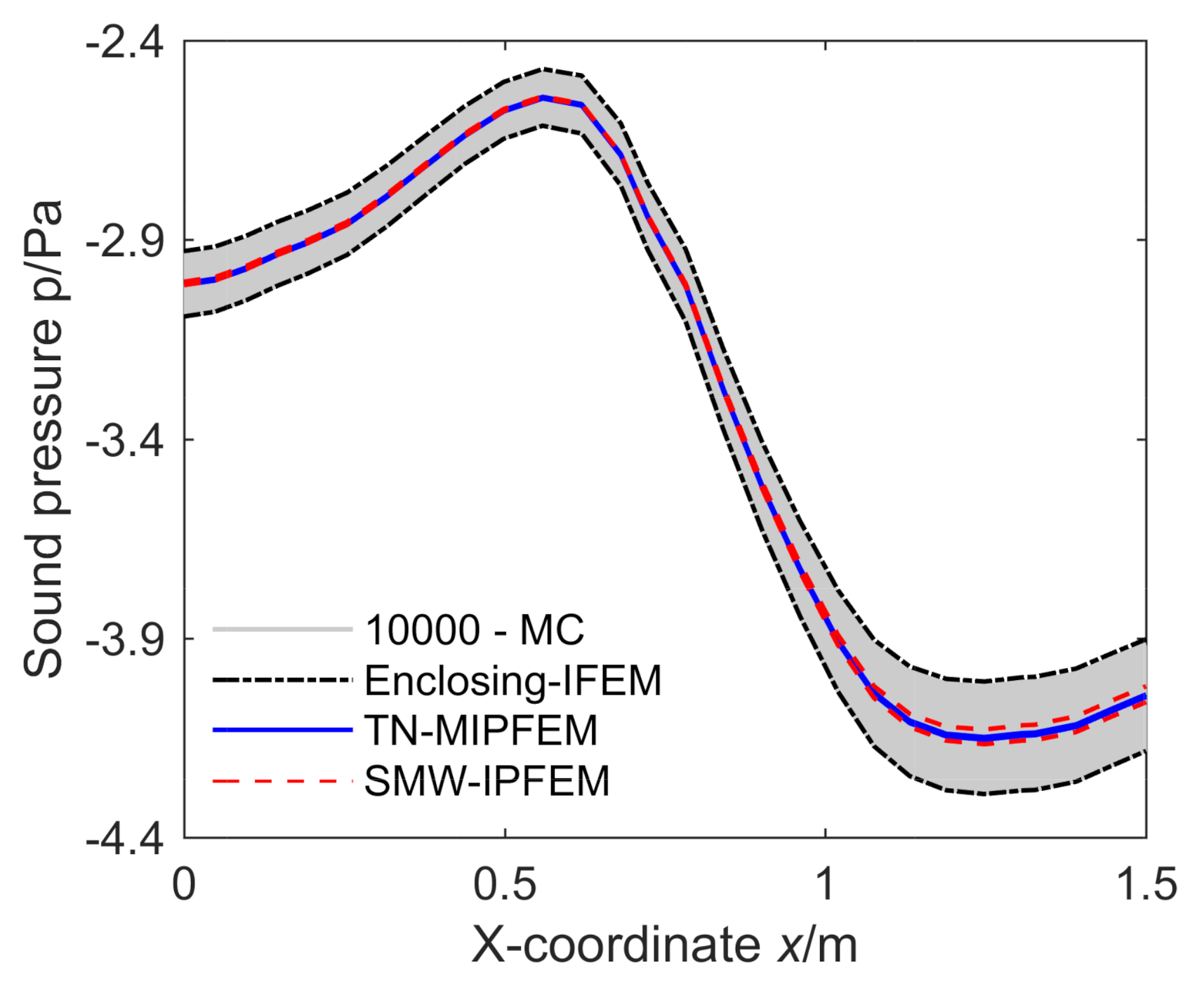
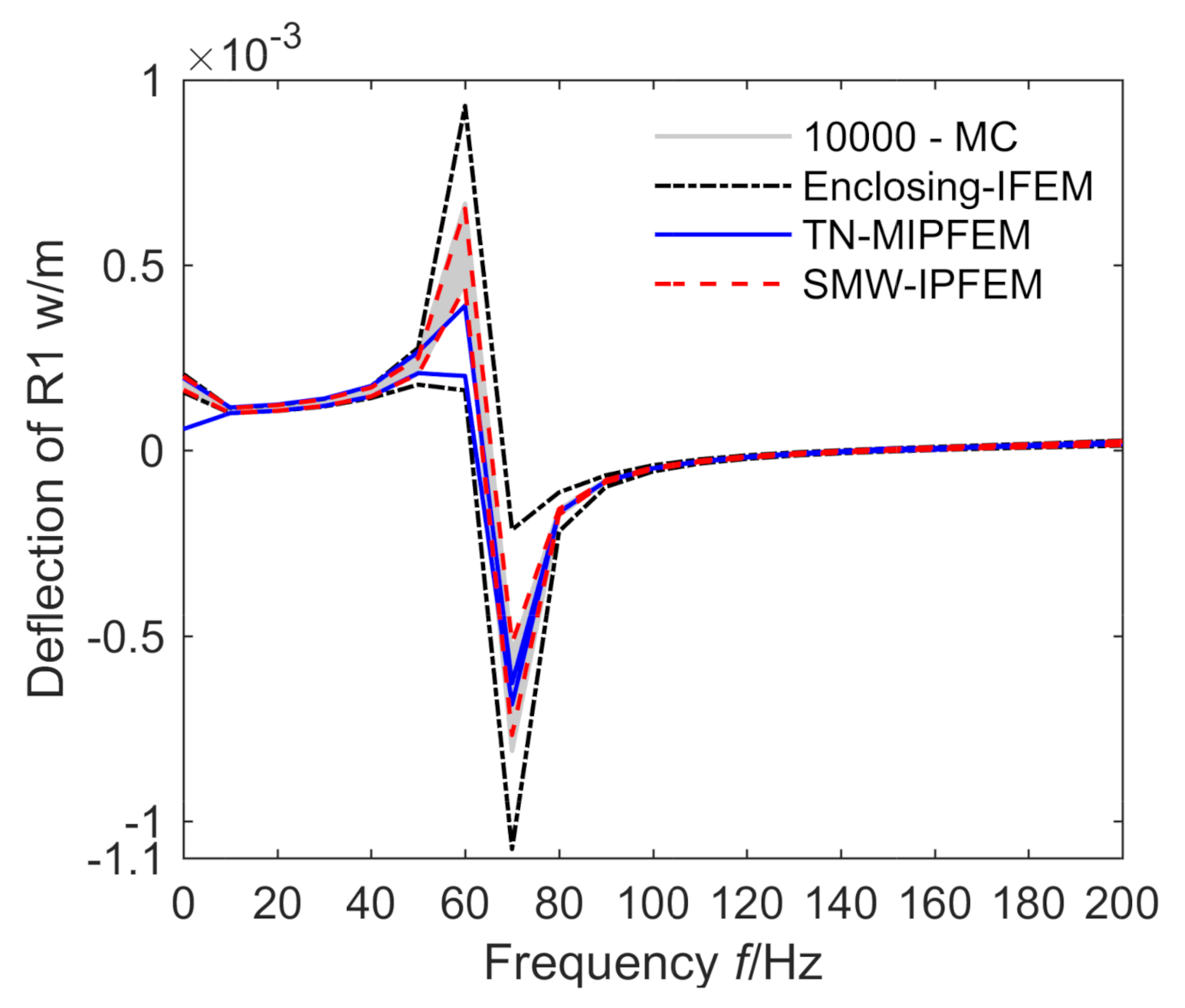
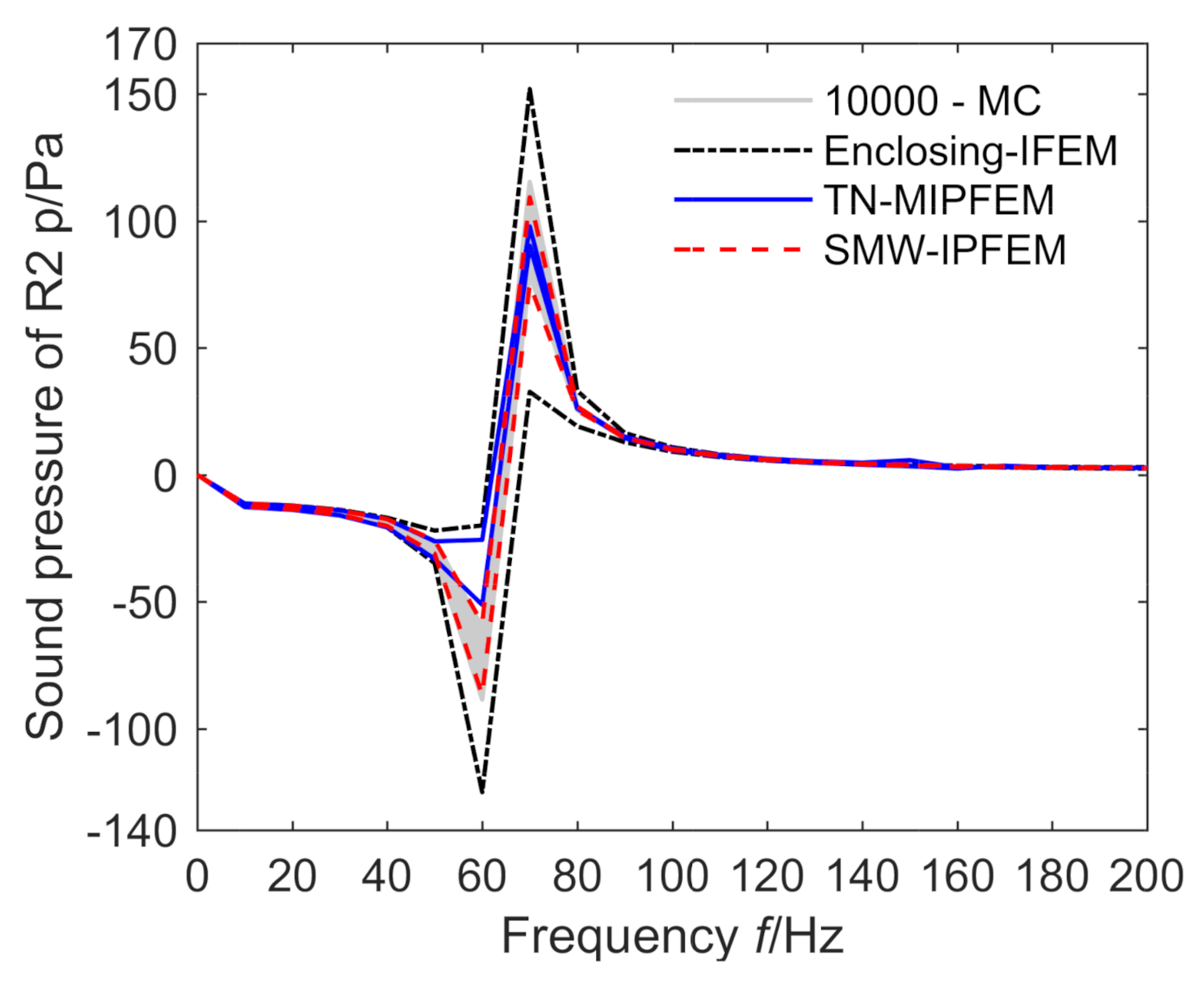
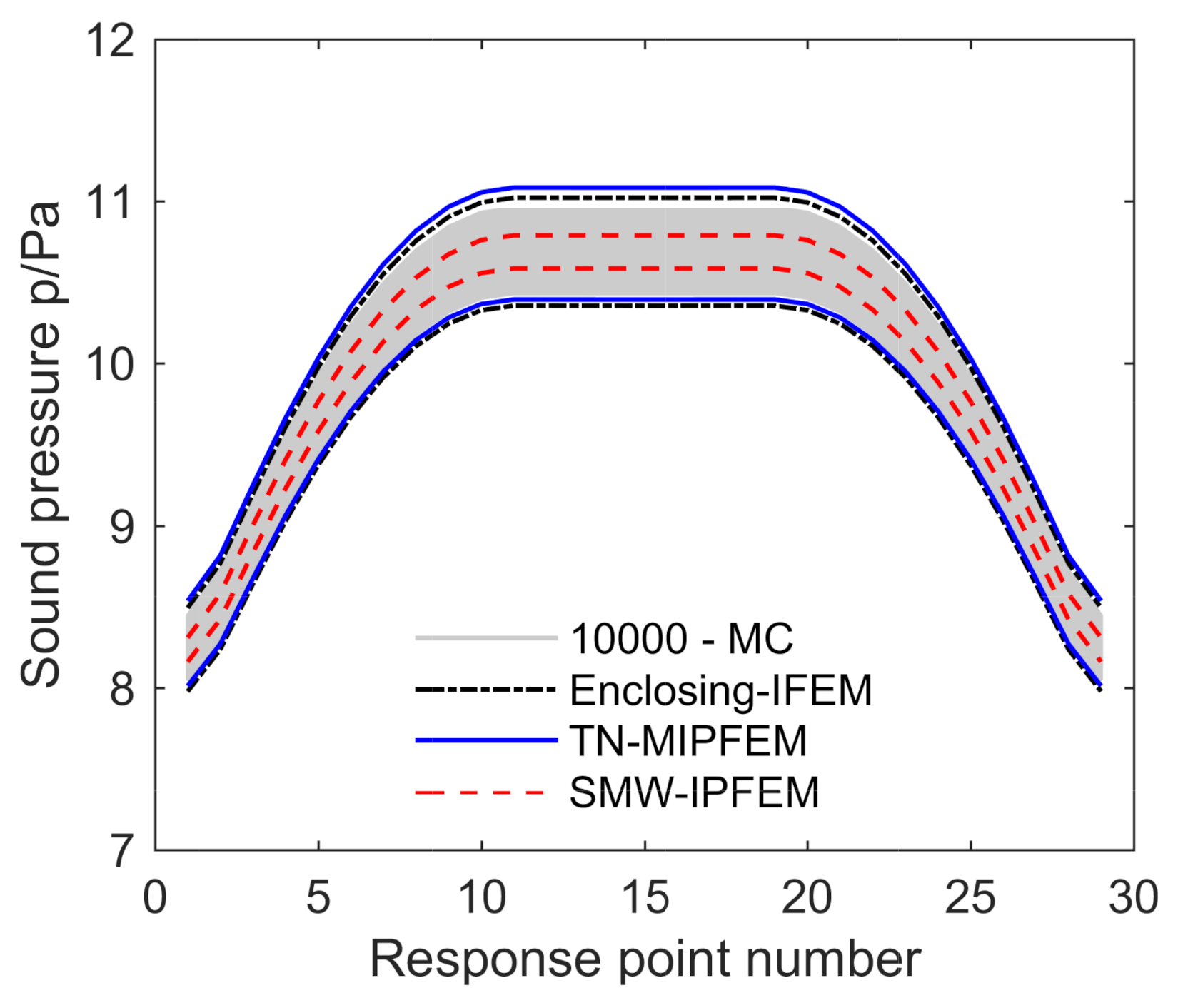
4.1. Numerical Analysis of a 2D Interior-Car Vibro-Acoustic Coupling Model
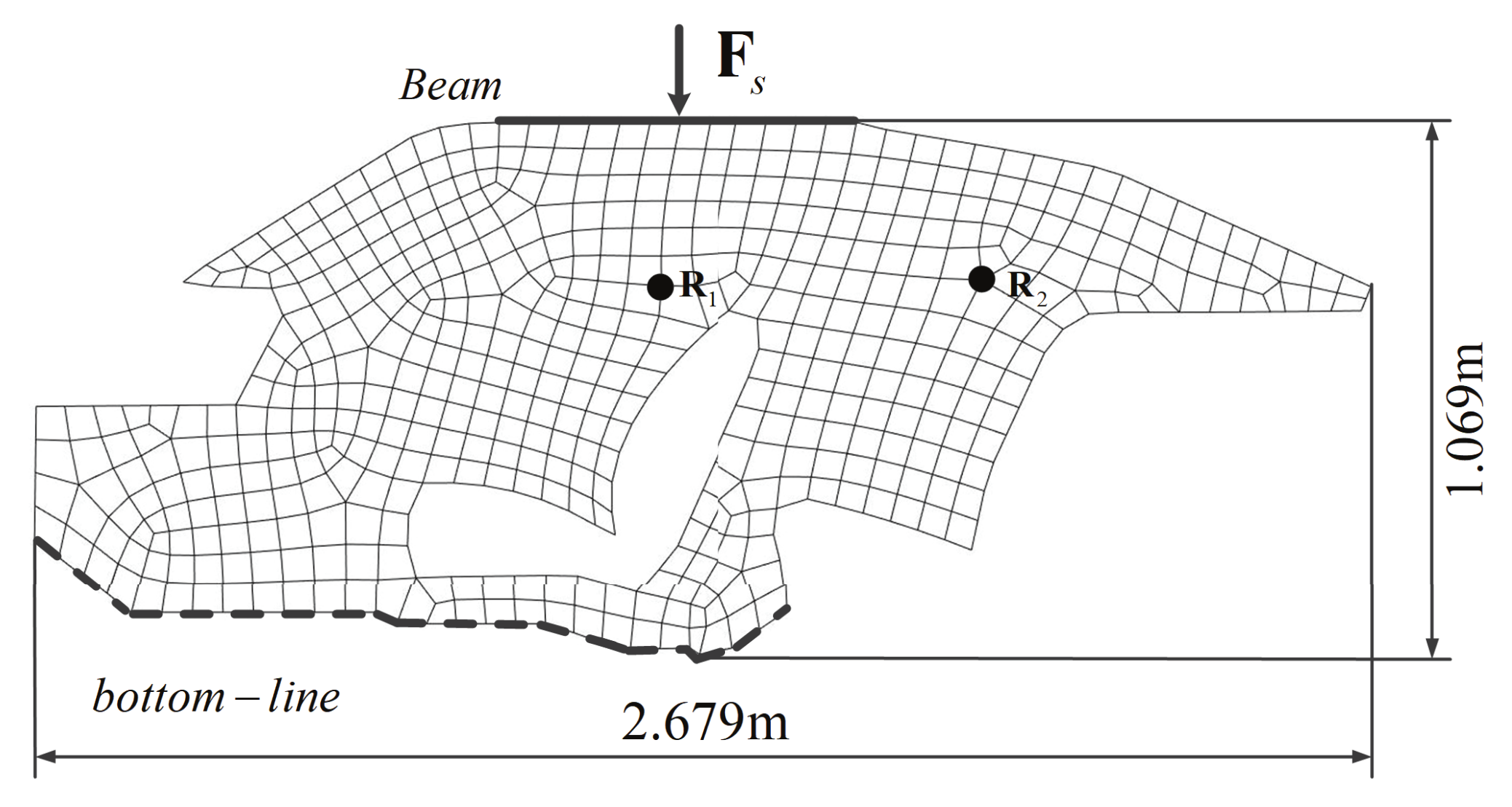
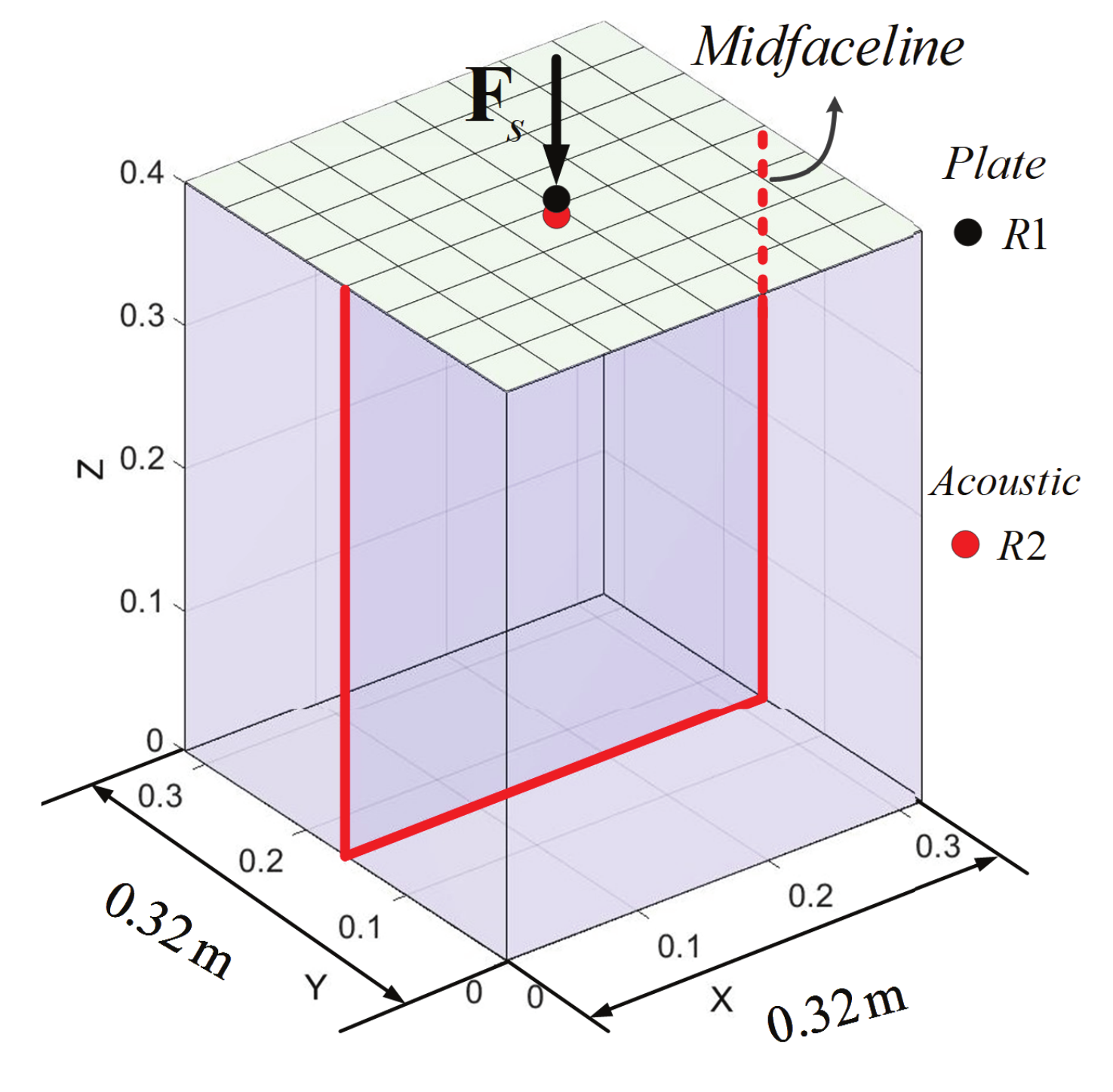
4.2. Numerical Analysis of a 3D Classical Vibro-Acoustic Coupling Model
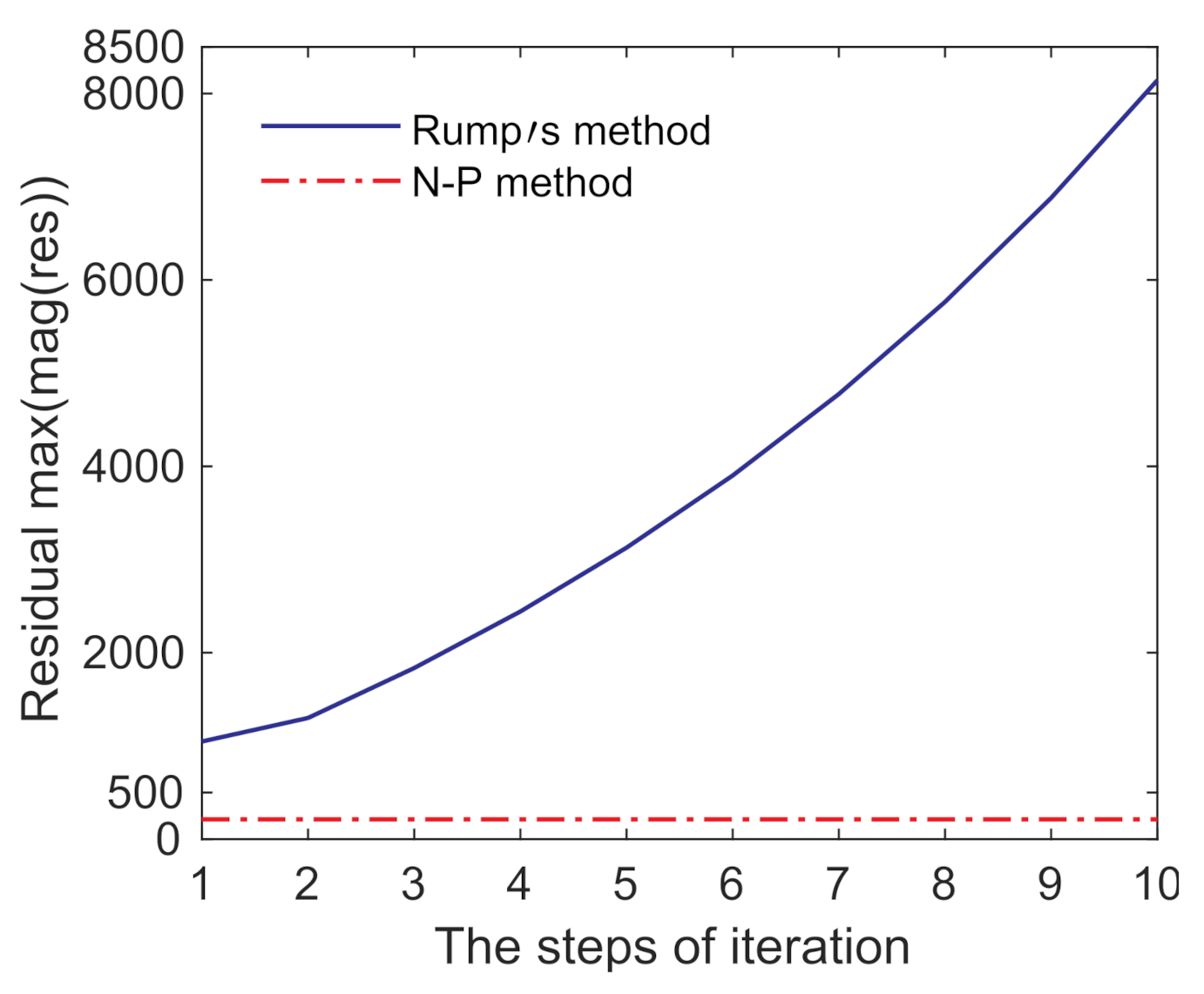
4.3. Convergence of Residual between Two Iterative Methods
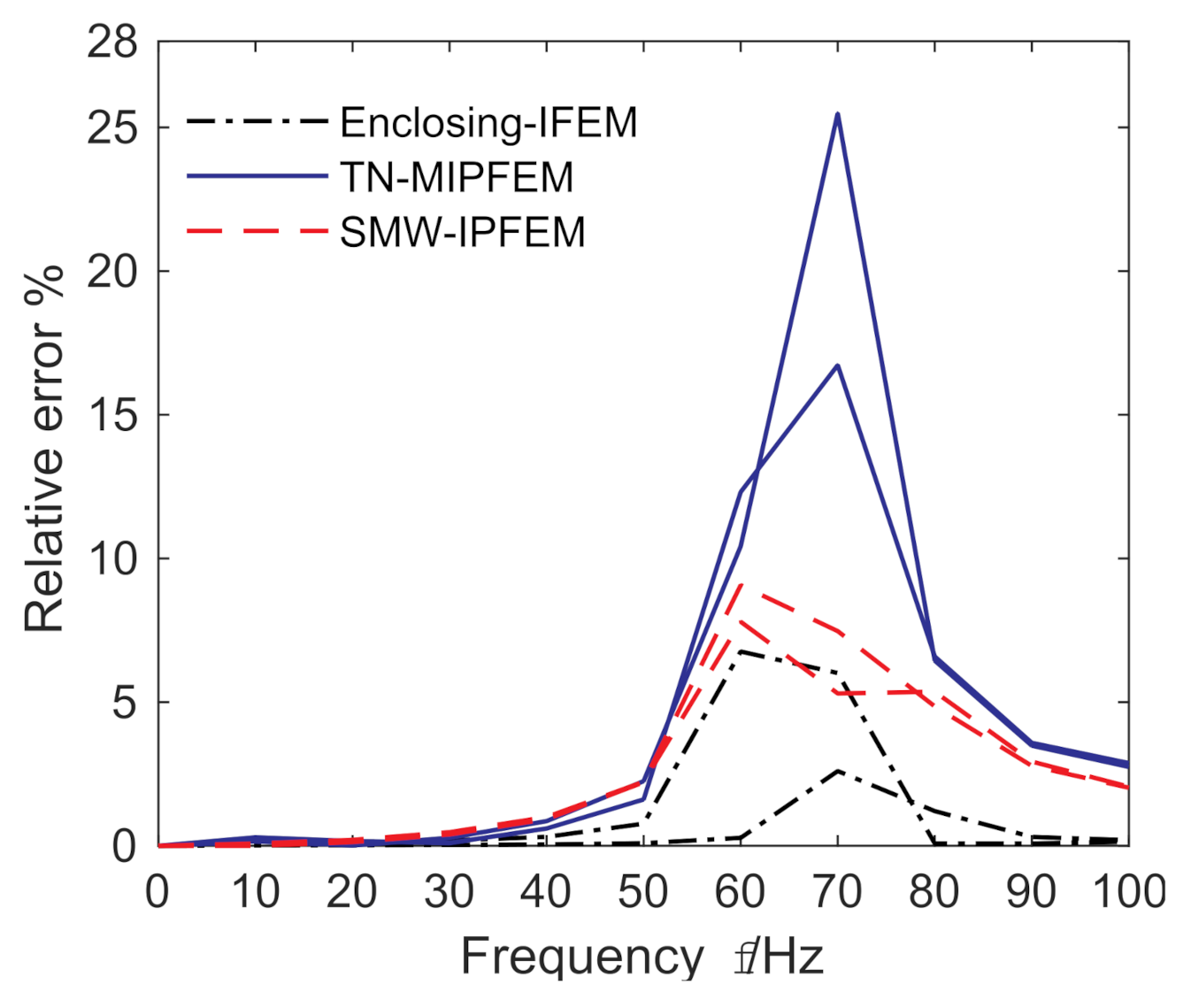
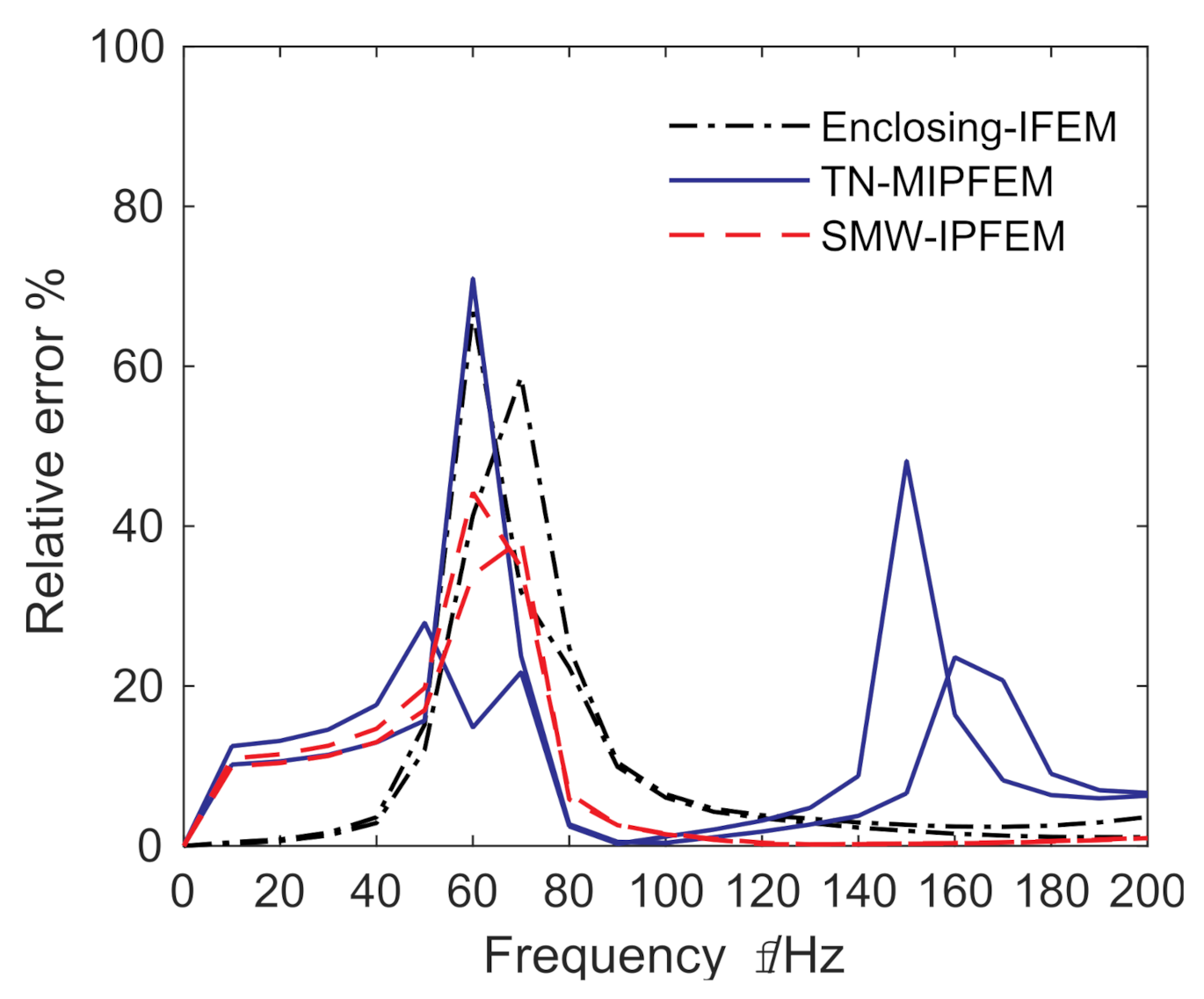
4.4. Analysis of the Relative Error
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atalla, N.; Sgard, F. Finite Element and Boundary Methods in Structural Acoustics and Vibration; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Chen, Q.; Fei, Q.; Wu, S.; Li, Y. Uncertainty propagation of the energy flow in vibro-acoustic system with fuzzy parameters. Aerosp. Sci. Technol. 2019, 94, 105367. [Google Scholar]
- Faes, M.; Moens, D. Recent trends in the modeling and quantification of non-probabilistic uncertainty. Arch. Comput. Methods Eng. 2020, 27, 633–671. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Liu, Y. An inverse method for distributed dynamic load identification of structures with interval uncertainties. Adv. Eng. Softw. 2019, 131, 77–89. [Google Scholar]
- Wang, L.; Liu, J.; Yang, C.; Wu, D. A novel interval dynamic reliability computation approach for the risk evaluation of vibration active control systems based on PID controllers. Appl. Math. Model. 2021, 92, 422–446. [Google Scholar]
- Moens, D.; Hanss, M. Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: Recent advances. Finite Elem. Anal. Des. 2011, 47, 4–16. [Google Scholar]
- Dessombz, O.; Thouverez, F.; Laîné, J.P.; Jézéquel, L. Analysis of mechanical systems using interval computations applied to finite element methods. J. Sound Vib. 2001, 239, 949–968. [Google Scholar]
- Xia, B.; Yu, D. Interval analysis of acoustic field with uncertain-but-bounded parameters. Comput. Struct. 2012, 112, 235–244. [Google Scholar] [CrossRef]
- Xia, B.; Yu, D.; Liu, J. Interval and subinterval perturbation methods for a structural-acoustic system with interval parameters. J. Fluids Struct. 2013, 38, 146–163. [Google Scholar] [CrossRef]
- Moore, R.E. Interval Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1966; Volume 4. [Google Scholar]
- Muhanna, R.L.; Mullen, R.L. Uncertainty in mechanics problems—Interval–based approach. J. Eng. Mech. 2001, 127, 557–566. [Google Scholar]
- Fuchs, M. Unimodal formulation of the analysis and design problems for framed structures. Comput. Struct. 1997, 63, 739–747. [Google Scholar] [CrossRef]
- Impollonia, N. A method to derive approximate explicit solutions for structural mechanics problems. Int. J. Solids Struct. 2006, 43, 7082–7098. [Google Scholar] [CrossRef] [Green Version]
- Neumaier, A.; Pownuk, A. Linear systems with large uncertainties, with applications to truss structures. Reliab. Comput. 2007, 13, 149–172. [Google Scholar] [CrossRef]
- Yaowen, Y.; Zhenhan, C.; Yu, L. Interval analysis of frequency response functions of structures with uncertain parameters. Mech. Res. Commun. 2013, 47, 24–31. [Google Scholar] [CrossRef]
- Xiang, Y.; Shi, Z. Interval Analysis of Interior Acoustic Field with Element-By-Element-Based Interval Finite-Element Method. J. Eng. Mech. 2021, 147, 04021085. [Google Scholar] [CrossRef]
- Chen, Q.; Fei, Q.; Wu, S.; Li, Y. Statistical energy analysis for the vibro-acoustic system with interval parameters. J. Aircr. 2019, 56, 1869–1879. [Google Scholar] [CrossRef]
- Dong, J.; Ma, F.; Hao, Y.; Gu, C. An interval statistical energy method for high-frequency analysis of uncertain structural–acoustic coupling systems. Eng. Optim. 2020, 52, 2100–2124. [Google Scholar] [CrossRef]
- Baklouti, A.; Dammak, K.; El Hami, A. Uncertainty Analysis Based on Kriging Meta-Model for Acoustic-Structural Problems. Appl. Sci. 2022, 12, 1503. [Google Scholar] [CrossRef]
- Qiu, Z.; Chen, S.; Elishakoff, I. Bounds of eigenvalues for structures with an interval description of uncertain-but-non-random parameters. Chaos Solitons Fractals 1996, 7, 425–434. [Google Scholar] [CrossRef]
- Xia, B.; Yu, D. Modified sub-interval perturbation finite element method for 2D acoustic field prediction with large uncertain-but-bounded parameters. J. Sound Vib. 2012, 331, 3774–3790. [Google Scholar] [CrossRef]
- Xia, B.; Yu, D. Modified interval perturbation finite element method for a structural-acoustic system with interval parameters. J. Appl. Mech. 2013, 80, 041027. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, Z.; Wang, X.; Wu, D. Interval finite element analysis and reliability-based optimization of coupled structural-acoustic system with uncertain parameters. Finite Elem. Anal. Des. 2014, 91, 108–114. [Google Scholar] [CrossRef]
- Wu, F.; Gong, M.; Ji, J.; Peng, G.; Yao, L.; Li, Y.; Zeng, W. Interval and subinterval perturbation finite element-boundary element method for low-frequency uncertain analysis of structural-acoustic systems. J. Sound Vib. 2019, 462, 114939. [Google Scholar] [CrossRef]
- Wu, F.; Gong, M.; Yao, L.; Hu, M.; Jie, J. High precision interval analysis of the frequency response of structural-acoustic systems with uncertain-but-bounded parameters. Eng. Anal. Bound. Elem. 2020, 119, 190–202. [Google Scholar] [CrossRef]
- Xu, M.; Du, J.; Wang, C.; Li, Y. A dimension-wise analysis method for the structural-acoustic system with interval parameters. J. Sound Vib. 2017, 394, 418–433. [Google Scholar] [CrossRef]
- Xu, M.; Du, J.; Wang, C.; Li, Y. Hybrid uncertainty propagation in structural-acoustic systems based on the polynomial chaos expansion and dimension-wise analysis. Comput. Methods Appl. Mech. Eng. 2017, 320, 198–217. [Google Scholar] [CrossRef]
- Xu, M.; Du, J.; Wang, C.; Li, Y.; Chen, J. A dual-layer dimension-wise fuzzy finite element method (DwFFEM) for the structural-acoustic analysis with epistemic uncertainties. Mech. Syst. Signal Process. 2019, 128, 617–635. [Google Scholar] [CrossRef]
- Chen, N.; Xia, S.; Yu, D.; Liu, J.; Beer, M. Hybrid interval and random analysis for structural-acoustic systems including periodical composites and multi-scale bounded hybrid uncertain parameters. Mech. Syst. Signal Process. 2019, 115, 524–544. [Google Scholar] [CrossRef]
- Impollonia, N.; Muscolino, G. Interval analysis of structures with uncertain-but-bounded axial stiffness. Comput. Methods Appl. Mech. Eng. 2011, 200, 1945–1962. [Google Scholar] [CrossRef]
- Sandberg, G.; Wernberg, P.A.; Davidsson, P. Fundamentals of fluid-structure interaction. In Computational Aspects of Structural Acoustics and Vibration; Springer: Berlin/Heidelberg, Germany, 2008; pp. 23–101. [Google Scholar]
- Desmet, W.; Vandepitte, D. Finite element modeling for acoustics. In ISAAC13-International Seminar on Applied Acoustics; Citesee: Leuven, Belgium, 2005; pp. 37–85. [Google Scholar]
- Chen, S.H.; Wu, J. Interval optimization of dynamic response for structures with interval parameters. Comput. Struct. 2004, 82, 1–11. [Google Scholar] [CrossRef]
- Chen, N.; Yu, D.; Xia, B.; Liu, J.; Ma, Z. Homogenization-based interval analysis for structural-acoustic problem involving periodical composites and multi-scale uncertain-but-bounded parameters. J. Acoust. Soc. Am. 2017, 141, 2768–2778. [Google Scholar] [CrossRef]
- Köylüoğlu, H.U.; Çakmak, Ş.A.; Nielsen, S.R. Interval algebra to deal with pattern loading and structural uncertainties. J. Eng. Mech. 1995, 121, 1149–1157. [Google Scholar] [CrossRef]
- Xiao, N.; Muhanna, R.L.; Fedele, F.; Mullen, R.L. Interval finite element analysis of structural dynamic problems. SAE Int. J. Mater. Manuf. 2015, 8, 382–389. [Google Scholar] [CrossRef]
- Katili, I.; Batoz, J.L.; Maknun, I.J.; Lardeur, P. A comparative formulation of DKMQ, DSQ and MITC4 quadrilateral plate elements with new numerical results based on s-norm tests. Comput. Struct. 2018, 204, 48–64. [Google Scholar] [CrossRef]
- Xiao, N. Interval Finite Element Approach for Inverse Problems under Uncertainty. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2015. [Google Scholar]
- Popova, E.D. Rank one interval enclosure of the parametric united solution set. BIT Numer. Math. 2019, 59, 503–521. [Google Scholar] [CrossRef]
- Rump, S.M. INTLAB—Interval laboratory. In Developments in Reliable Computing; Springer: Berlin/Heidelberg, Germany, 1999; pp. 77–104. [Google Scholar]
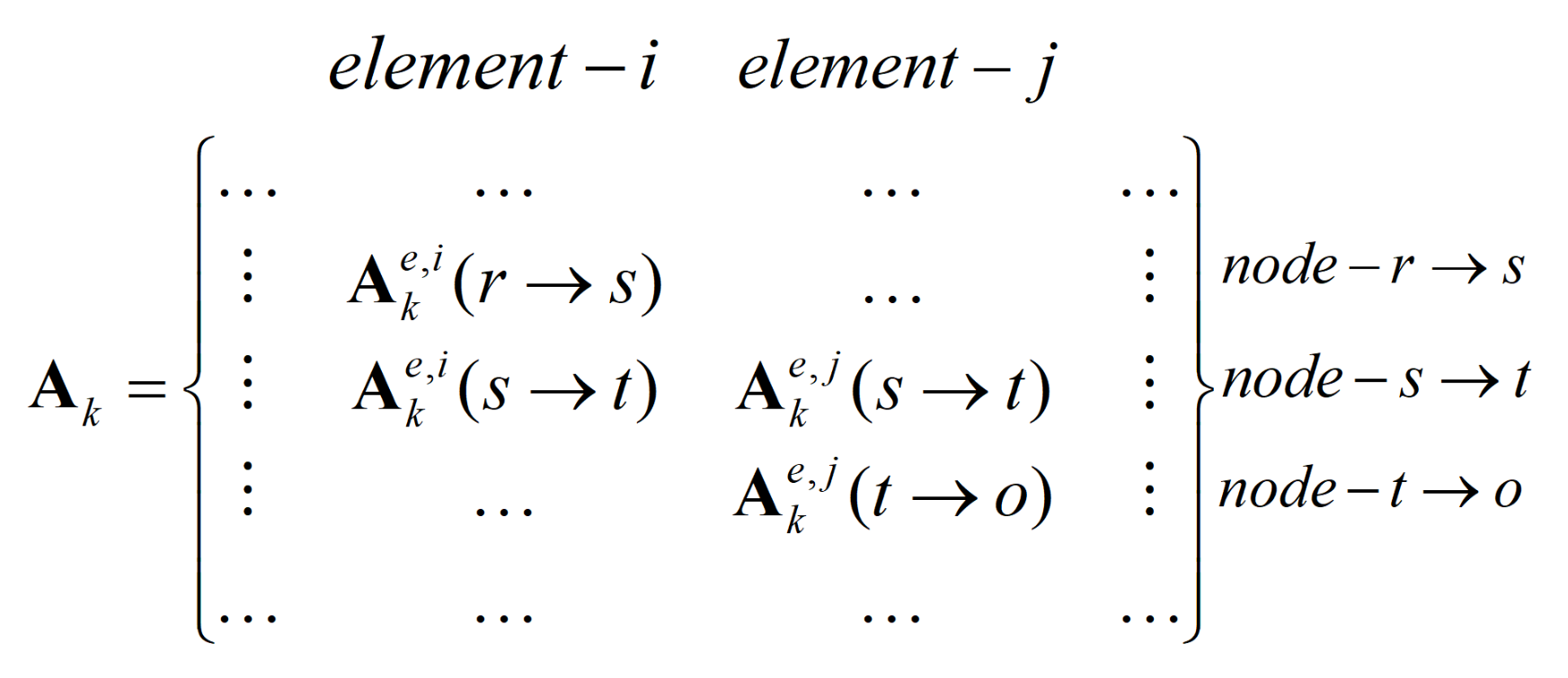


| MC | TN-MIPFEM | SMW-IPFEM | Enclosing-IFEM | |||
|---|---|---|---|---|---|---|
| 9667.2 s | 3.7 s | 10.1 s | 4.6 s | |||
| MC | TN-MIPFEM | SMW-IPFEM | Enclosing-IFEM | |||
|---|---|---|---|---|---|---|
| 4855.6 s | 16.5 s | 1422.8 s | 35.8 s | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Y.; Shi, Z. Interval Analysis of Vibro-Acoustic Systems by the Enclosing Interval Finite-Element Method. Appl. Sci. 2022, 12, 3061. https://doi.org/10.3390/app12063061
Xiang Y, Shi Z. Interval Analysis of Vibro-Acoustic Systems by the Enclosing Interval Finite-Element Method. Applied Sciences. 2022; 12(6):3061. https://doi.org/10.3390/app12063061
Chicago/Turabian StyleXiang, Yujia, and Zhiyu Shi. 2022. "Interval Analysis of Vibro-Acoustic Systems by the Enclosing Interval Finite-Element Method" Applied Sciences 12, no. 6: 3061. https://doi.org/10.3390/app12063061
APA StyleXiang, Y., & Shi, Z. (2022). Interval Analysis of Vibro-Acoustic Systems by the Enclosing Interval Finite-Element Method. Applied Sciences, 12(6), 3061. https://doi.org/10.3390/app12063061





