Approximation Method for Stress–Strain Using Metamodel Parameter Updating
Abstract
1. Introduction
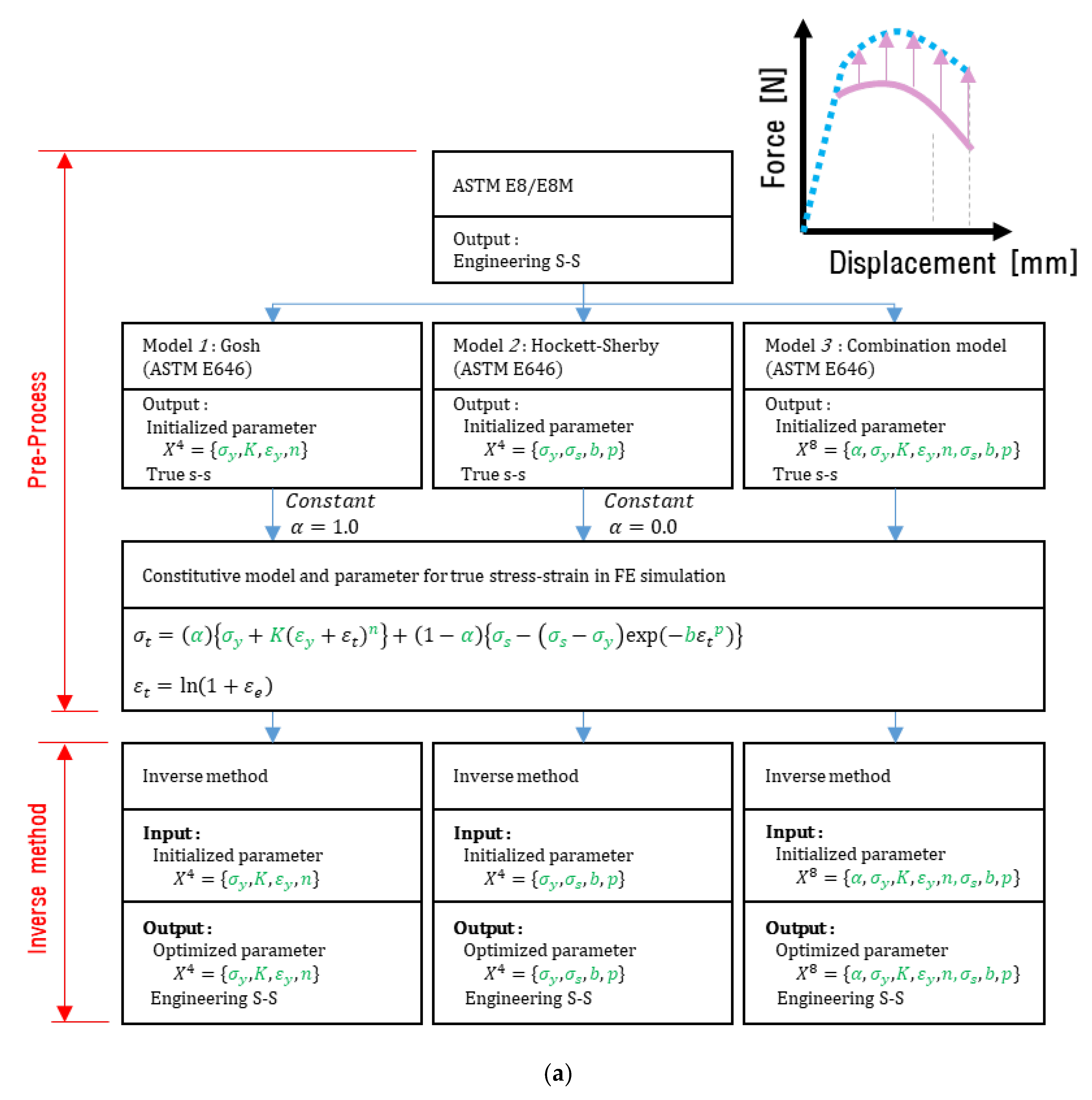
2. Pre-Processing of the Constitutive Model
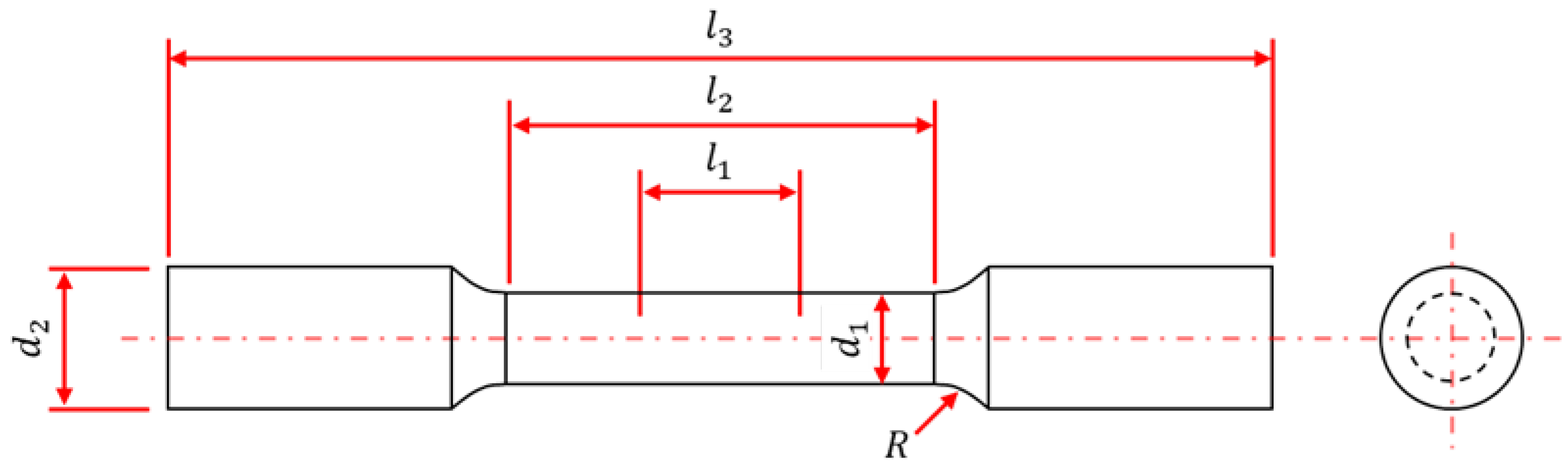
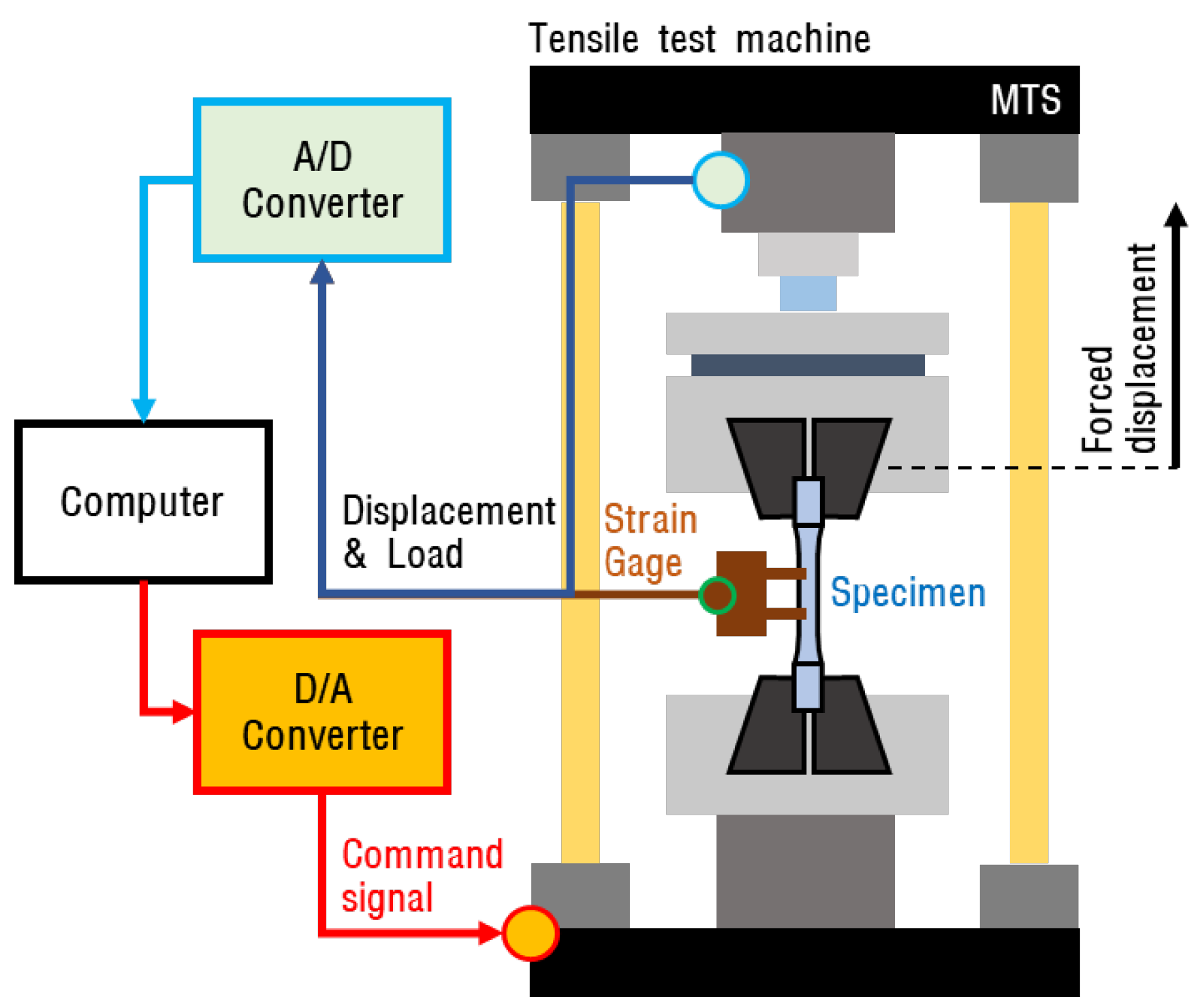
2.1. Tensile Test
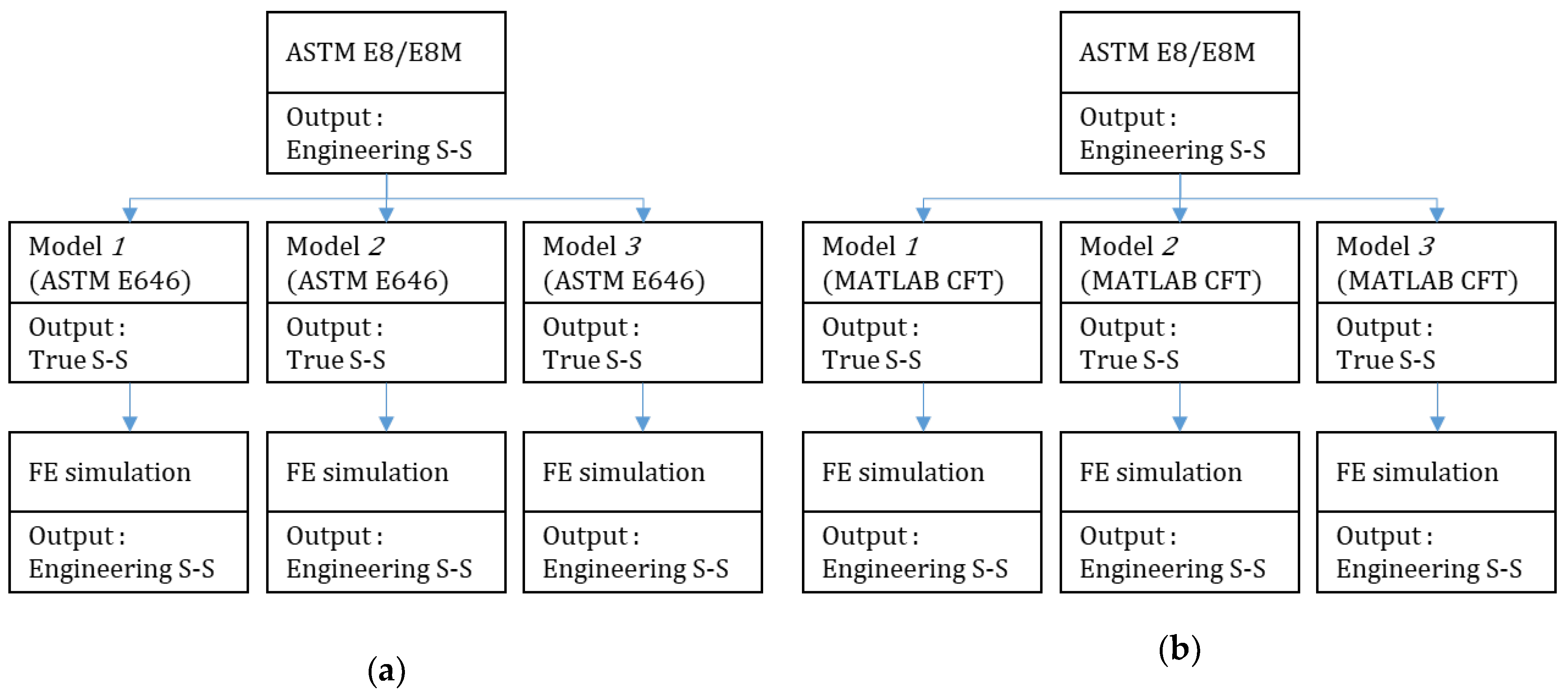
2.2. Initialization of Constitutive Model Parameters for True Stress–Strain Curve
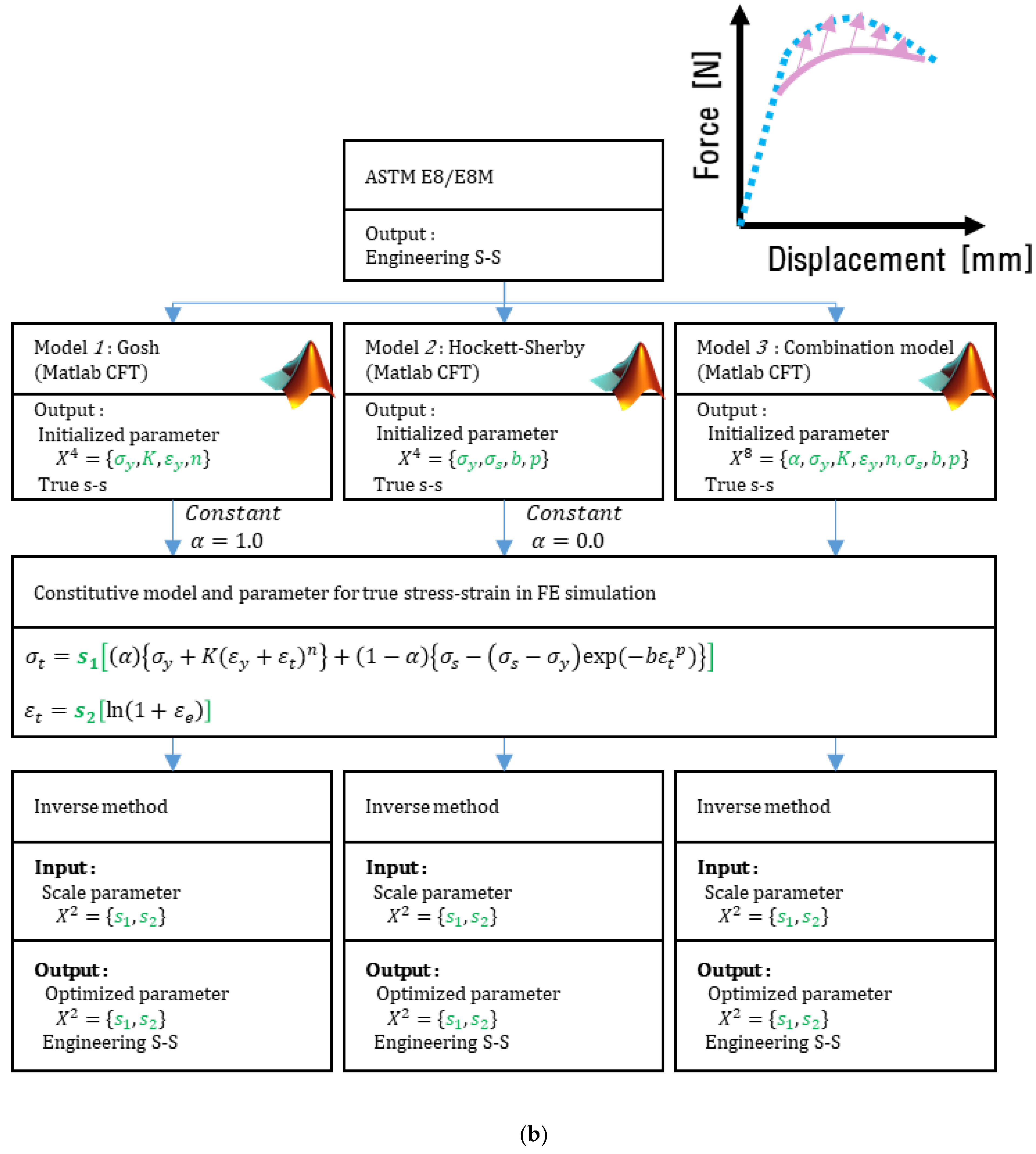
2.3. CFT Method for Constitutive Model of the True Stress–Strain Curve
3. FE Simulation
3.1. Material Model
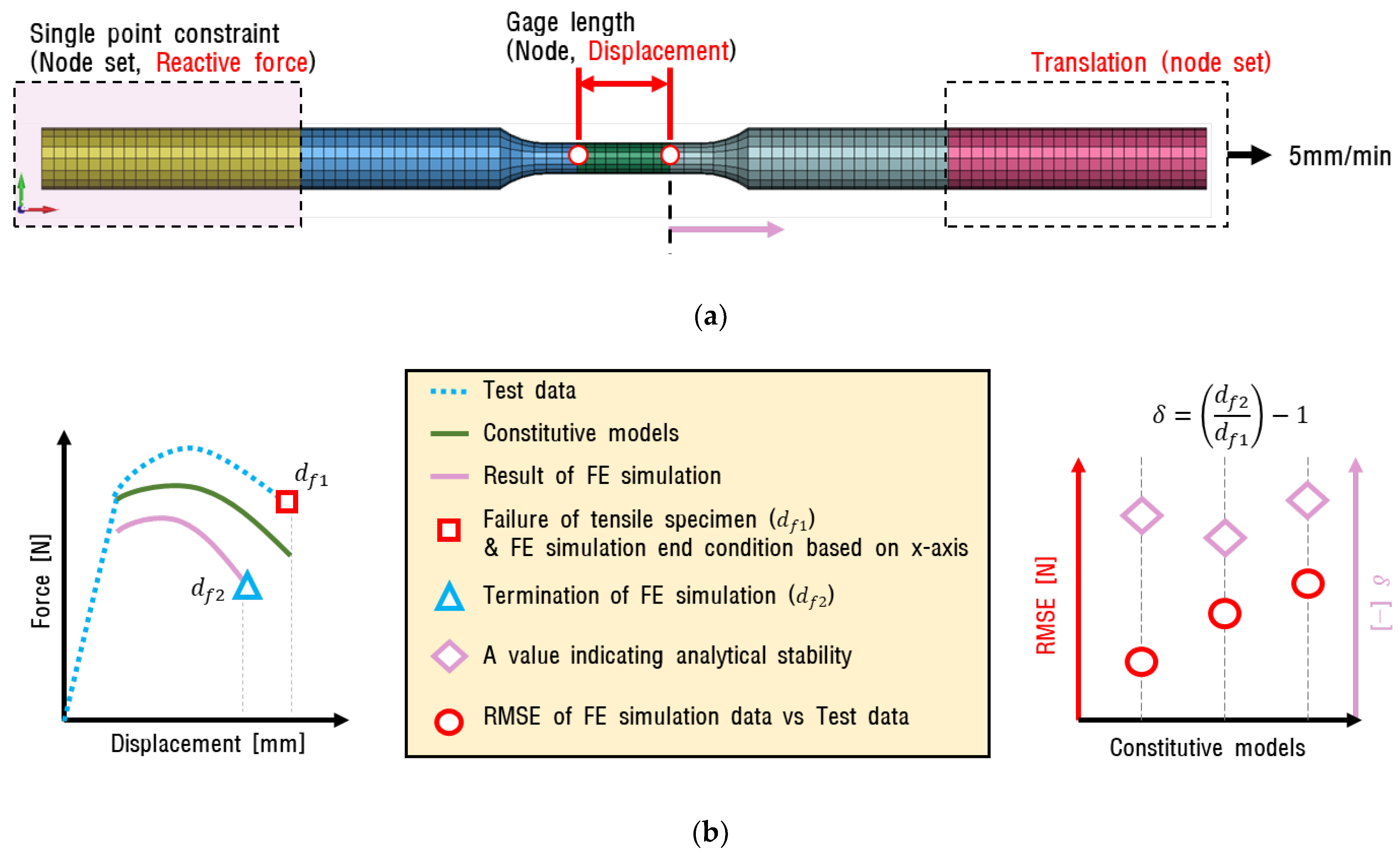
3.2. FE Modeling
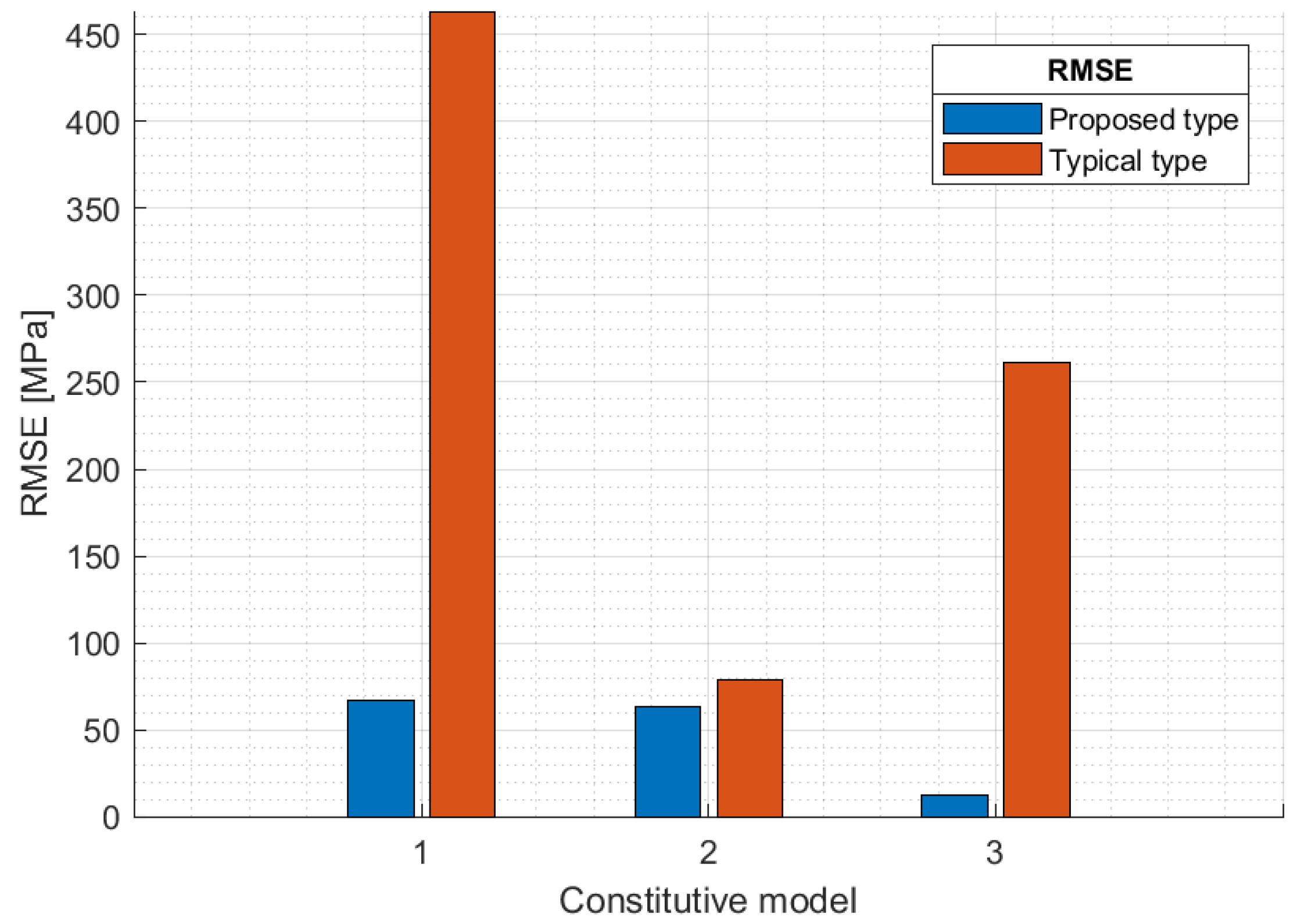
3.3. Results of FE Simulation
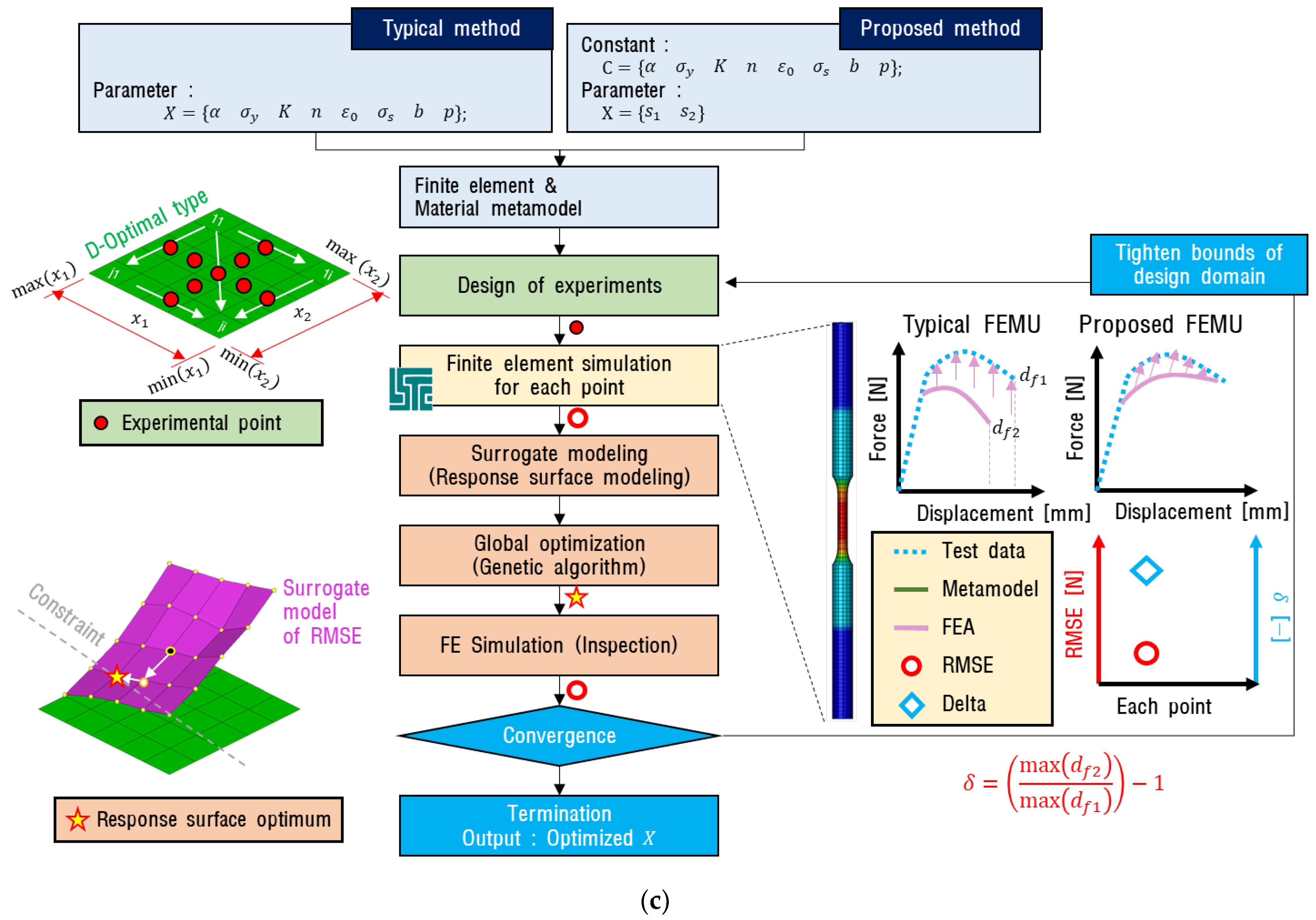
4. Inverse Method
4.1. Metamodel-Based Simulation Optimization
4.2. Inverse Method Using Metamodel-Based Simulation Optimization
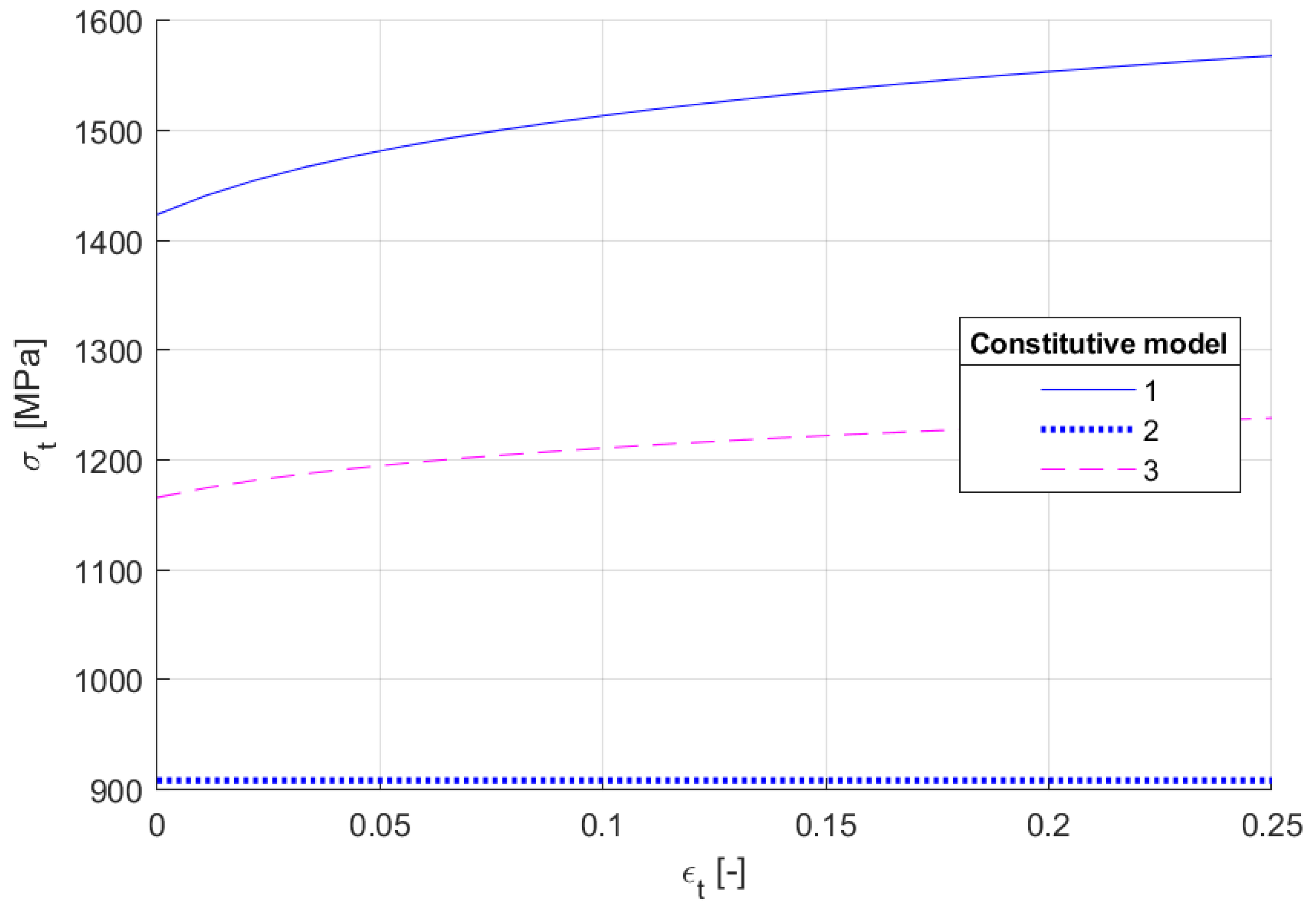
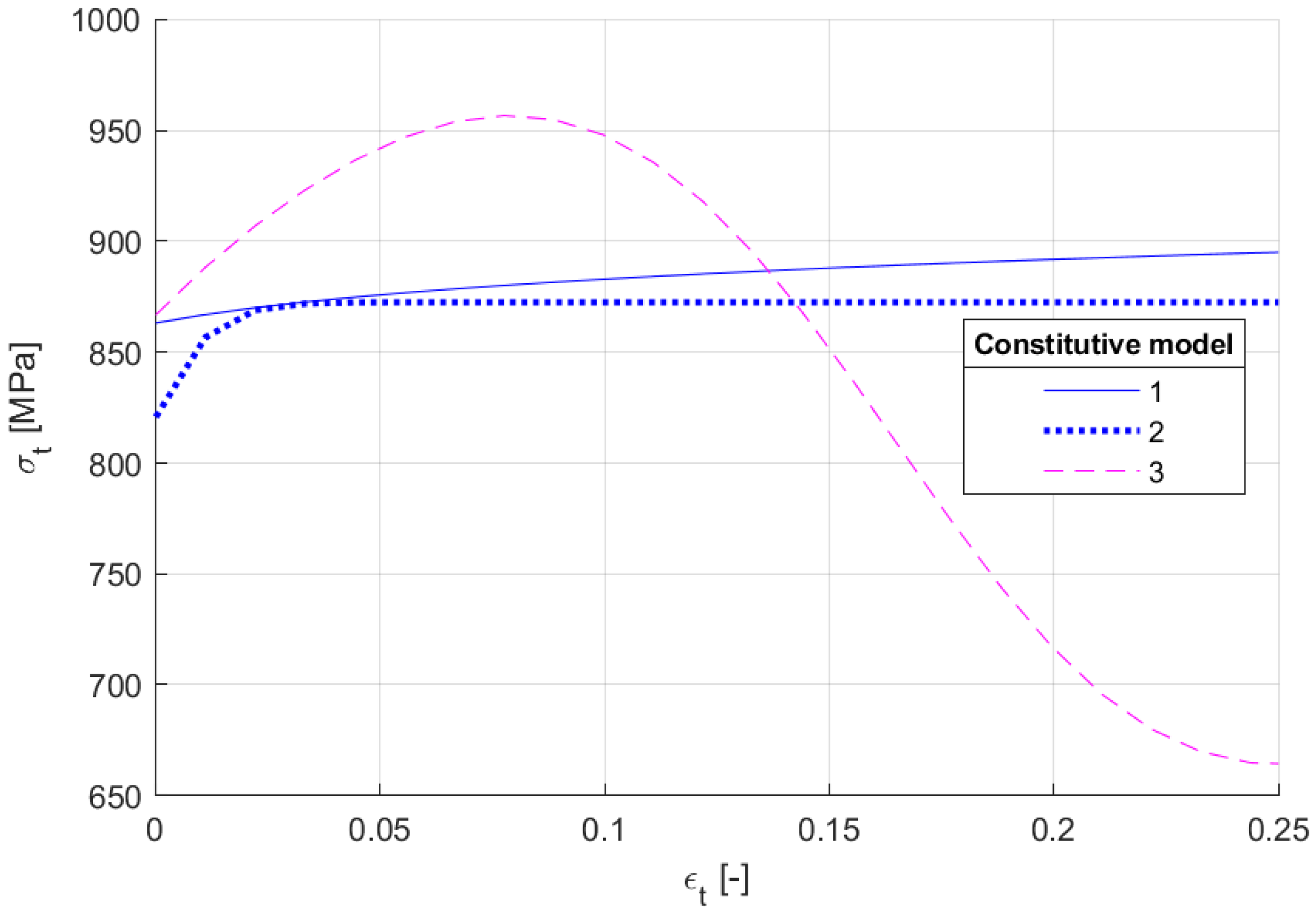
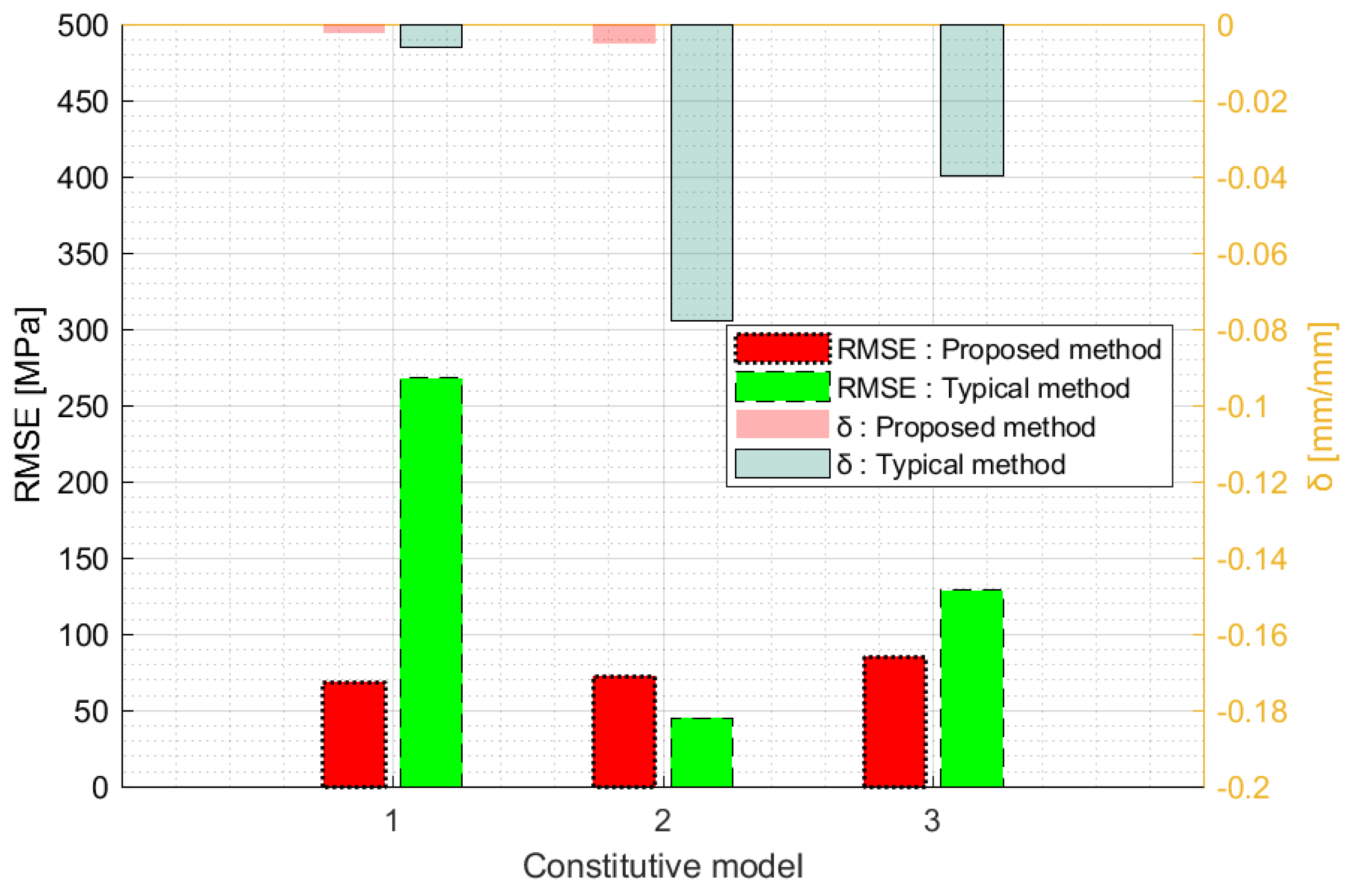
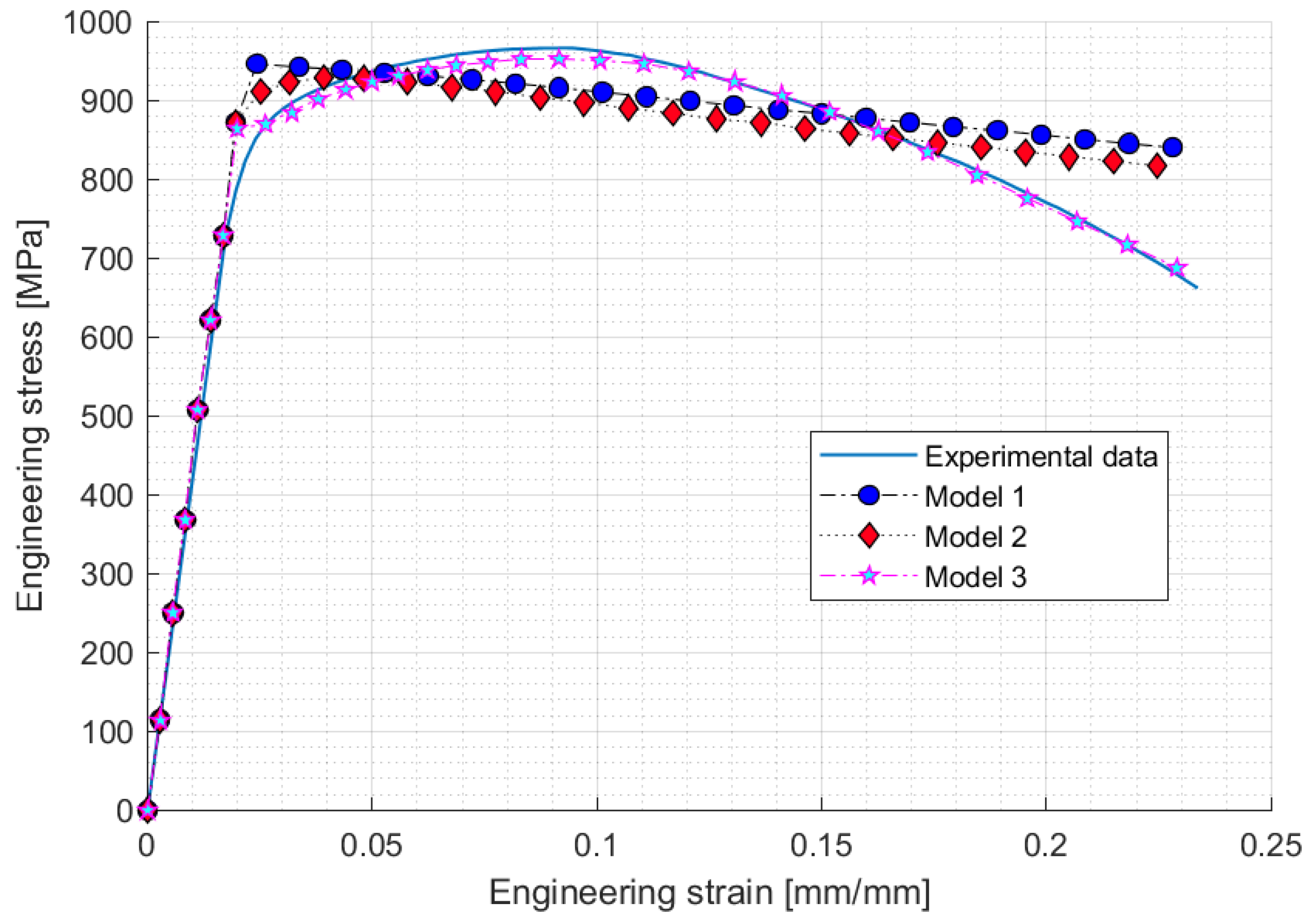
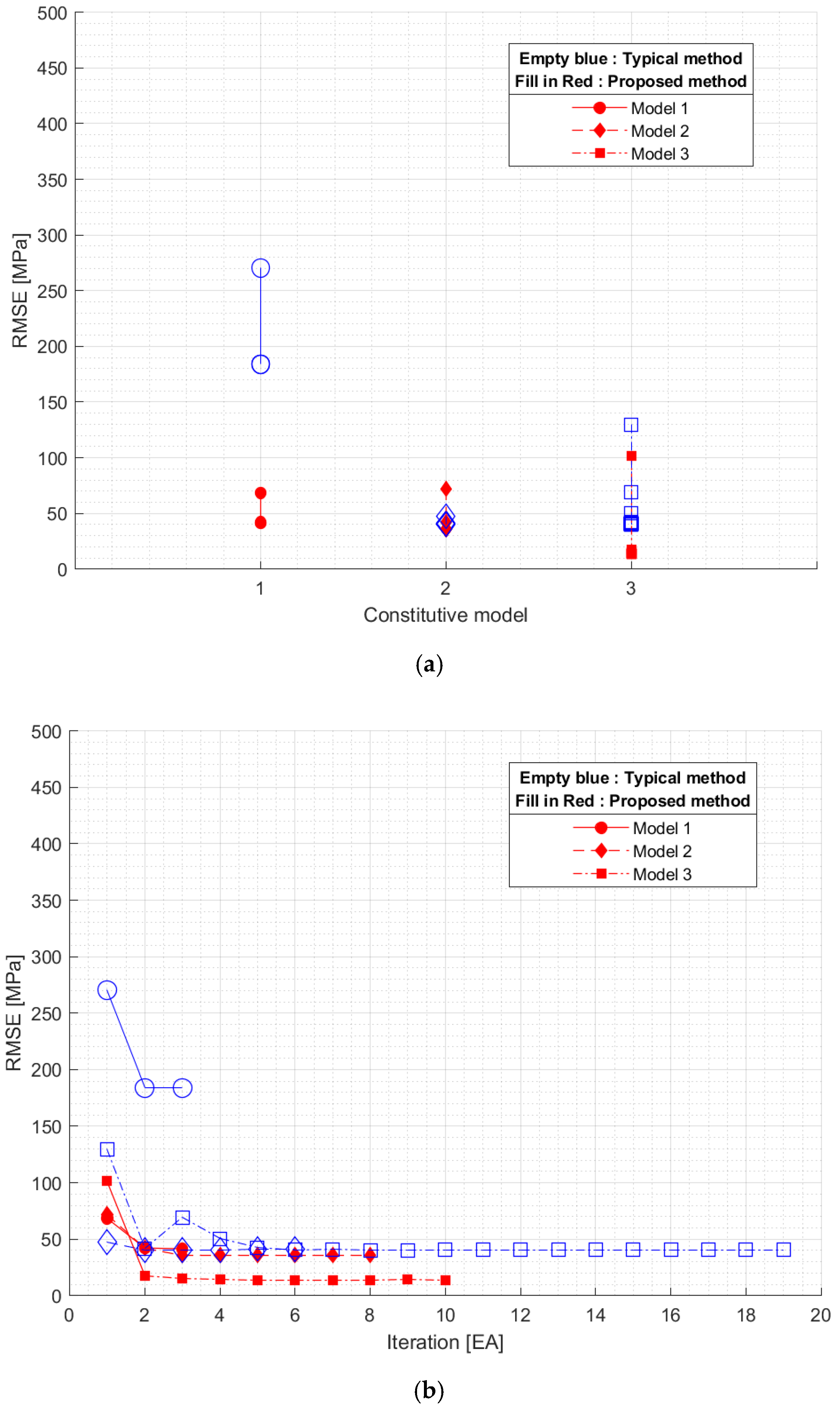
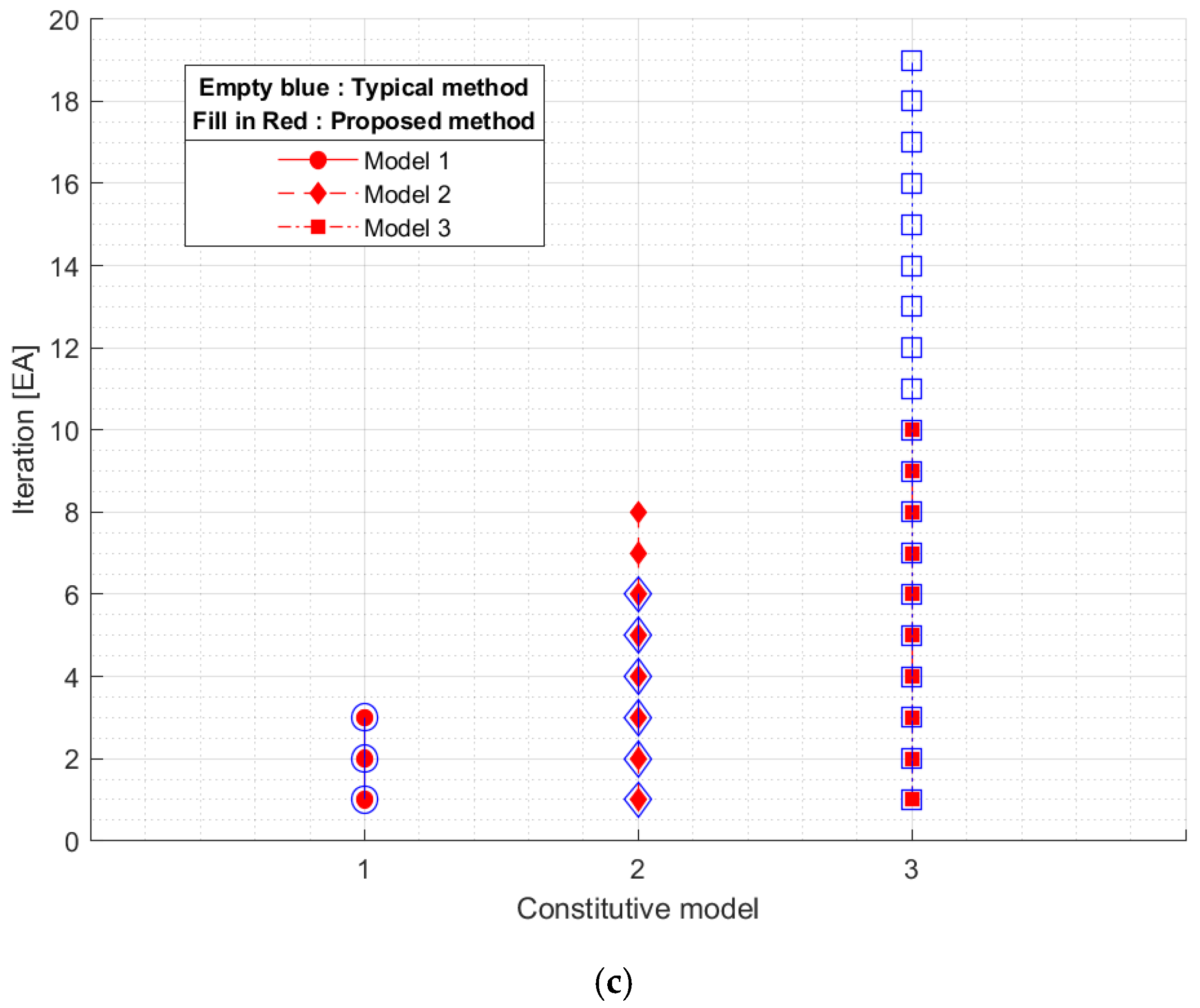
4.3. Results of the Inverse Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J.H.; Serpantié, A.; Barlat, F.; Pierron, F.; Lee, M.G. Characterization of the Post-Necking Strain Hardening Behavior Using the Virtual Fields Method. Int. J. Solids Struct. 2013, 50, 3829–3842. [Google Scholar] [CrossRef]
- Niutta, C.B.; Tridello, A.; Ciardiello, R.; Belingardi, G.; Paolino, D.S. Assessment of Residual Elastic Properties of a Damaged Composite Plate with Combined Damage Index and Finite Element Methods. Appl. Sci. 2019, 9, 2579. [Google Scholar] [CrossRef]
- Mazzon, E.; Habas-Ulloa, A.; Habas, J.P. Lightweight Rigid Foams from Highly Reactive Epoxy Resins Derived from Vegetable Oil for Automotive Applications. Eur. Polym. J. 2015, 68, 546–557. [Google Scholar] [CrossRef]
- Joun, M.S.; Eom, J.G.; Lee, M.C. A New Method for Acquiring True Stress-Strain Curves over a Large Range of Strains Using a Tensile Test and Finite Element Method. Mech. Mater. 2008, 40, 586–593. [Google Scholar] [CrossRef]
- Seon, G.; Makeev, A.; Schaefer, J.D.; Justusson, B. Measurement of Interlaminar Tensile Strength and Elastic Properties of Composites Using Open-Hole Compression Testing and Digital Image Correlation. Appl. Sci. 2019, 9, 2647. [Google Scholar] [CrossRef]
- Enami, K. The Effects of Compressive and Tensile Prestrain on Ductile Fracture Initiation in Steels. Eng. Fract. Mech. 2005, 72, 1089–1105. [Google Scholar] [CrossRef]
- ASTM E8/E8M -21 Standard Test Methods for Tension Testing of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2021. [CrossRef]
- Ling, Y. Uniaxial True Stress-Strain after Necking. AMP J. Technol. 1996, 5, 37–48. [Google Scholar]
- Cabezas, E.E.; Celentano, D.J. Experimental and Numerical Analysis of the Tensile Test Using Sheet Specimens. Finite Elem. Anal. Des. 2004, 40, 555–575. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Hauge, M.; Ødegård, J.; Thaulow, C. Determining Material True Stress-Strain Curve from Tensile Specimens with Rectangular Cross-Section. Int. J. Solids Struct. 1999, 36, 3497–3516. [Google Scholar] [CrossRef]
- Tvergaard, V. Effect of Kinematic Hardening on Localized Necking in Biaxially Stretched Sheets. Int. J. Mech. Sci. 1978, 20, 651–658. [Google Scholar] [CrossRef]
- Needleman, A.; Tvergaard, V. Necking of Biaxially Stretched Elastic-Plastic Circular Plates. J. Mech. Phys. Solids 1977, 25, 159–183. [Google Scholar] [CrossRef]
- Tvergaard, V.; van der Giessen, E. Effect of Plastic Spin on Localization Predictions for a Porous Ductile Material. J. Mech. Phys. Solids 1991, 39, 763–781. [Google Scholar] [CrossRef][Green Version]
- Dziallach, S.; Bleck, W.; Blumbach, M.; Hallfeldt, T. Sheet Metal Testing and Flow Curve Determination under Multiaxial Conditions. Adv. Eng. Mater. 2007, 9, 987–994. [Google Scholar] [CrossRef]
- Liu, X.; Ma, H.; Fan, F. Modified Johnson–Cook Model of SWRH82B Steel under Different Manufacturing and Cold-Drawing Conditions. J. Constr. Steel Res. 2021, 186, 106894. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, X.; Chen, H.; Yang, X.; Wang, F.; Zeng, L. Modified Johnson-Cook Constitutive Model of Metallic Materials under a Wide Range of Temperatures and Strain Rates. Results Phys. 2021, 27, 104498. [Google Scholar] [CrossRef]
- Qian, X.; Peng, X.; Song, Y.; Huang, J.; Wei, Y.; Liu, P.; Mao, X.; Zhang, J.; Wang, L. Dynamic Constitutive Relationship of CuCrZr Alloy Based on Johnson-Cook Model. Nucl. Mater. Energy 2020, 24, 100768. [Google Scholar] [CrossRef]
- Yue, N.; Li, L.; Morandi, A.; Zhao, Y. A Metamodel-Based Multi-Objective Optimization Method to Balance Thermal Comfort and Energy Efficiency in a Campus Gymnasium. Energy Build. 2021, 253, 111513. [Google Scholar] [CrossRef]
- Mastrippolito, F.; Aubert, S.; Ducros, F. Kriging Metamodels-Based Multi-Objective Shape Optimization Applied to a Multi-Scale Heat Exchanger. Comp. Fluids 2021, 221, 104899. [Google Scholar] [CrossRef]
- Francisco, M.B.; Pereira, J.L.J.; Oliver, G.A.; da Silva, F.H.S.; da Cunha, S.S.; Gomes, G.F. Multiobjective Design Optimization of CFRP Isogrid Tubes Using Sunflower Optimization Based on Metamodel. Comp. Struct. 2021, 249, 106508. [Google Scholar] [CrossRef]
- Dai, Y.; Li, Y.; Xu, X.; Zhu, Q.; Yin, Y.; Ge, S.; Huang, A.; Pan, L. Characterization of Tensile Failure Behaviour of Magnesia Refractory Materials by a Modified Dog-Bone Shape Direct Tensile Method and Splitting Tests. Ceram. Int. 2020, 46, 6517–6525. [Google Scholar] [CrossRef]
- Rauchs, G.; Bardon, J.; Georges, D. Identification of the Material Parameters of a Viscous Hyperelastic Constitutive Law from Spherical Indentation Tests of Rubber and Validation by Tensile Tests. Mech. Mater. 2010, 42, 961–973. [Google Scholar] [CrossRef]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture, with Special Emphasis on the Effects of Hydrostatic Pressure; McGraw-Hill: New York, NY, USA, 1952. [Google Scholar]
- Mirone, G. A New Model for the Elastoplastic Characterization and the Stress-Strain Determination on the Necking Section of a Tensile Specimen. Int. J. Solids Struct. 2004, 41, 3545–3564. [Google Scholar] [CrossRef]
- Da Fonseca, J.Q.; Mummery, P.M.; Withers, P.J. Full-Field Strain Mapping by Optical Correlation of Micrographs Acquired during Deformation. J. Microsc. 2005, 218, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Tang, Z.; Hong, X. Inverse Parameter Identification for Hyperelastic Model of a Polyurea. Polymers 2021, 13, 2253. [Google Scholar] [CrossRef]
- Kamaya, M.; Kawakubo, M. A Procedure for Determining the True Stress-Strain Curve over a Large Range of Strains Using Digital Image Correlation and Finite Element Analysis. Mech. Mater. 2011, 43, 243–253. [Google Scholar] [CrossRef]
- Denys, K.; Coppieters, S.; Seefeldt, M.; Debruyne, D. Multi-DIC Setup for the Identification of a 3D Anisotropic Yield Surface of Thick High Strength Steel Using a Double Perforated Specimen. Mech. Mater. 2016, 100, 96–108. [Google Scholar] [CrossRef]
- Pham, Q.T.; Lee, M.G.; Kim, Y.S. New Procedure for Determining the Strain Hardening Behavior of Sheet Metals at Large Strains Using the Curve Fitting Method. Mech. Mater. 2021, 154, 103729. [Google Scholar] [CrossRef]
- Boyer, G.; Molimard, J.; ben Tkaya, M.; Zahouani, H.; Pericoi, M.; Avril, S. Assessment of the In-Plane Biomechanical Properties of Human Skin Using a Finite Element Model Updating Approach Combined with an Optical Full-Field Measurement on a New Tensile Device. J. Mech. Behav. Biomed. Mater. 2013, 27, 273–282. [Google Scholar] [CrossRef][Green Version]
- Guery, A.; Hild, F.; Latourte, F.; Roux, S. Identification of Crystal Plasticity Parameters Using DIC Measurements and Weighted FEMU. Mech. Mater. 2016, 100, 55–71. [Google Scholar] [CrossRef]
- Bresolin, F.L.; Vassoler, J.M. A Numerical Study of the Constitutive Characterization of Thermoplastic Materials Submitted to Finite Strain. Int. J. Solids Struct. 2020, 206, 456–471. [Google Scholar] [CrossRef]
- ASTM E646-16 Standard Test Method for Tensile Strain-Hardening Exponents (n-Values) of Metallic Sheet Materials; ASTM International: West Conshohocken, PA, USA, 2016.
- Husain, A.; Sehgal, D.K.; Pandey, R.K. An Inverse Finite Element Procedure for the Determination of Constitutive Tensile Behavior of Materials Using Miniature Specimen. Comput. Mater. Sci. 2004, 31, 84–92. [Google Scholar] [CrossRef]
- Aksen, T.A.; Sener, B.; Firat, M. Failure Prediction Capability of Generalized Plastic Work Criterion. Proc. Manuf. 2020, 47, 1235–1240. [Google Scholar] [CrossRef]
- Zhang, H.; Coppieters, S.; Jiménez-Peña, C.; Debruyne, D. Inverse Identification of the Post-Necking Work Hardening Behaviour of Thick HSS through Full-Field Strain Measurements during Diffuse Necking. Mech. Mater. 2019, 129, 361–374. [Google Scholar] [CrossRef]
- Chen, J.J.; Lian, C.W.; Lin, J.P. Validation of Constitutive Models for Experimental Stress-Strain Relationship of High-Strength Steel Sheets under Uniaxial Tension. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Beijing, China, 19–22 August 2019; Institute of Physics Publishing: Bristol, UK, 2019; Volume 668, p. 1. [Google Scholar] [CrossRef]
- Pham, Q.T.; Lee, B.H.; Park, K.C.; Kim, Y.S. Influence of the Post-Necking Prediction of Hardening Law on the Theoretical Forming Limit Curve of Aluminium Sheets. Int. J. Mech. Sci. 2018, 140, 521–536. [Google Scholar] [CrossRef]
- Sener, B.; Yurci, M.E. Comparison of Quasi-Static Constitutive models and Modeling of Flow Curves for Austenitic 304 and Ferritic 430 Stainless Steels. In Proceedings of the 6th International Congress & Exhibition (APMAS2016), Istanbul, Turkey, 1–3 June 2016; Acta Physica Polonica Series A. 2017; Volume 131, pp. 605–607. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic Instability under; Pergamon Press Ltd.: London, UK, 1952; Volume 1. [Google Scholar]
- Hockett, J.E.; Sherby, D. Large Strain Deformation of Polycrystalline Metals at Low Homologous Temperatures. J. Mech. Phys. Solids 1975, 23, 87–98. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, L.; Chang, Y.; Yan, J. Identification of Post-Necking Stress-Strain Curve for Sheet Metals by Inverse Method. Mech. Mater. 2016, 92, 107–118. [Google Scholar] [CrossRef]
- Kim, Y.S.; Pham, Q.T.; Kim, C.I. New Stress-Strain Model for Identifying Plastic Deformation Behavior of Sheet Materials. J. Korean Soc. Precis. Eng. 2017, 34, 273–279. [Google Scholar] [CrossRef]
- Tang, B.; Wu, F.; Wang, Q.; Li, C.; Liu, J.; Ge, H. Numerical and Experimental Study on Ductile Fracture of Quenchable Boron Steels with Different Microstructures. Int. J. Lightweight Mater. Manuf. 2020, 3, 55–65. [Google Scholar] [CrossRef]
- Ghosh, A.K. Tensile Instability and Necking in Materials with Strain Hardening and Strain-Rate Hardening. Acta Met. 1977, 25, 1413–1424. [Google Scholar] [CrossRef]
- Hollomon, J.H.; Lubahn, J.D. Plastic Flow of Metals. Phys. Rev. 1946, 70, 775. [Google Scholar] [CrossRef]
- Ludwik, P. Elemente der Technologischen Mechanik; Springer: Berlin/Heidelberg, Germany, 1909. [Google Scholar]
- Kweon, H.D.; Kim, J.W.; Song, O.; Oh, D. Determination of True Stress-Strain Curve of Type 304 and 316 Stainless Steels Using a Typical Tensile Test and Finite Element Analysis. Nucl. Eng. Technol. 2021, 53, 647–656. [Google Scholar] [CrossRef]
- Sainath, G.; Choudhary, B.K.; Christopher, J.; Isaac Samuel, E.; Mathew, M.D. Applicability of Voce Equation for Tensile Flow and Work Hardening Behaviour of P92 Ferritic Steel. Int. J. Press. Vess. Piping 2015, 132–133, 1–9. [Google Scholar] [CrossRef]
- Knitel, S.; Spätig, P.; Seifert, H.P. An Inverse Method Based on Finite Element Model to Derive the Plastic Flow Properties from Non-Standard Tensile Specimens of Eurofer97 Steel. Nucl. Mater. Energy 2016, 9, 311–316. [Google Scholar] [CrossRef]
- Doh, J.; Lee, J. Approximate Multi-Objective Optimization of a Wall-Mounted Monitor Bracket Arm Considering Strength Design Conditions. Trans. Korean Soc. Mech. Eng. A 2015, 39, 535–541. [Google Scholar] [CrossRef]
- Rikards, R.; Auzins, J. Response Surface Method for Solution of Structural Identification Problems. In Inverse Problems in Science and Engineering; Taylor and Francis Inc.: London, UK, 2004; Volume 12, pp. 59–70. [Google Scholar] [CrossRef]



| Symbol | Description | Value |
|---|---|---|
| l1 | Gauge length | 62.5 mm |
| l2 | Length of reduced section | 75 mm |
| l3 | Total length | 145 mm |
| d1 | Diameter of reduced section | 12.5 mm |
| d2 | Diameter of grip | 12.5 mm |
| R | Radius of fillet | 10 mm |
| No. | Description | Constitutive Models (εy ≤ ε) | Number of Variables |
|---|---|---|---|
| - | Engineering data | - | |
| - | ASTM E646 | - | |
| 1 | Gosh | 4 | |
| 2 | Hockett–Sherby | 4 | |
| 3 | Gosh and Hockett–Sherby | 8 |
| Symbol | Unit | ASTM & Experience Value | Matlab CFT | ||||
|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||
| εy | mm/mm | 0.018 | 0.018 | 0.018 | 0.018 | 0.018 | 0.018 |
| σy | MPa | 208 | 208 | 208 | 735.708 | 735.708 | 735.708 |
| σs | MPa | 908 | 908 | 908 | - | 872.42 | 1249.410 |
| b | - | 2.9725 | 2.9725 | 2.9725 | - | 600.00 | 12.000 |
| p | - | 1 | 1 | 1 | - | 1.575 | 0.905 |
| n | - | −0.0063 | −0.0063 | −0.0063 | 0.120 | - | 0.596 |
| K | MPa | 938 | 938 | 938 | 187.766 | - | 1983.170 |
| - | 1.0 | 0.0 | 0.5 | - | - | 2.633 | |
| Symbol | Unit | ASTM & Experience Value | Matlab CFT | ||||
|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||
| εy | mm/mm | 0.018 | 0.018 | 0.018 | 0.018 | 0.018 | 0.018 |
| σy | MPa | 735.708 | 735.708 | 735.708 | 735.708 | 735.708 | 735.708 |
| σs | MPa | - | 966.129 | 831.348 | - | 872.42 | 1249.410 |
| b | - | - | 33.005 | 28.754 | - | 600.00 | 12.000 |
| p | - | - | 0.0782 | 0.094 | - | 1.575 | 0.905 |
| n | - | 0.108 | - | 0.083 | 0.120 | - | 0.596 |
| K | MPa | 751.1 | - | 855.197 | 187.766 | - | 1983.170 |
| α | - | - | - | 0.765 | - | - | 2.633 |
| s1 | - | - | - | - | 1.142 | 1.133 | 1.094 |
| s2 | - | - | - | - | 1.100 | 1.100 | 1.412 |
| No. | Number of Variables in the Inverse Method [EA] | Maximum Iteration [EA] | Total Experiment Points [EA] | Converged RMSE [MPa] | ||||
|---|---|---|---|---|---|---|---|---|
| A | B | A | B | A | B | A | B | |
| 1 | 4 | 2 | 4 | 3 | 16 | 11 | 194.6 | 41.5 |
| 2 | 4 | 2 | 6 | 8 | 36 | 36 | 41.2 | 35.9 |
| 3 | 8 | 2 | 18 | 10 | 325 | 61 | 37.0 | 14.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, D.-S.; Jeon, E.-S.; Kim, Y.-S. Approximation Method for Stress–Strain Using Metamodel Parameter Updating. Appl. Sci. 2022, 12, 2868. https://doi.org/10.3390/app12062868
Shin D-S, Jeon E-S, Kim Y-S. Approximation Method for Stress–Strain Using Metamodel Parameter Updating. Applied Sciences. 2022; 12(6):2868. https://doi.org/10.3390/app12062868
Chicago/Turabian StyleShin, Dong-Seok, Euy-Sik Jeon, and Young-Shin Kim. 2022. "Approximation Method for Stress–Strain Using Metamodel Parameter Updating" Applied Sciences 12, no. 6: 2868. https://doi.org/10.3390/app12062868
APA StyleShin, D.-S., Jeon, E.-S., & Kim, Y.-S. (2022). Approximation Method for Stress–Strain Using Metamodel Parameter Updating. Applied Sciences, 12(6), 2868. https://doi.org/10.3390/app12062868






