NMR in Metabolomics: From Conventional Statistics to Machine Learning and Neural Network Approaches
Abstract
:1. Introduction
2. Conventional Approaches
2.1. Unsupervised Methods
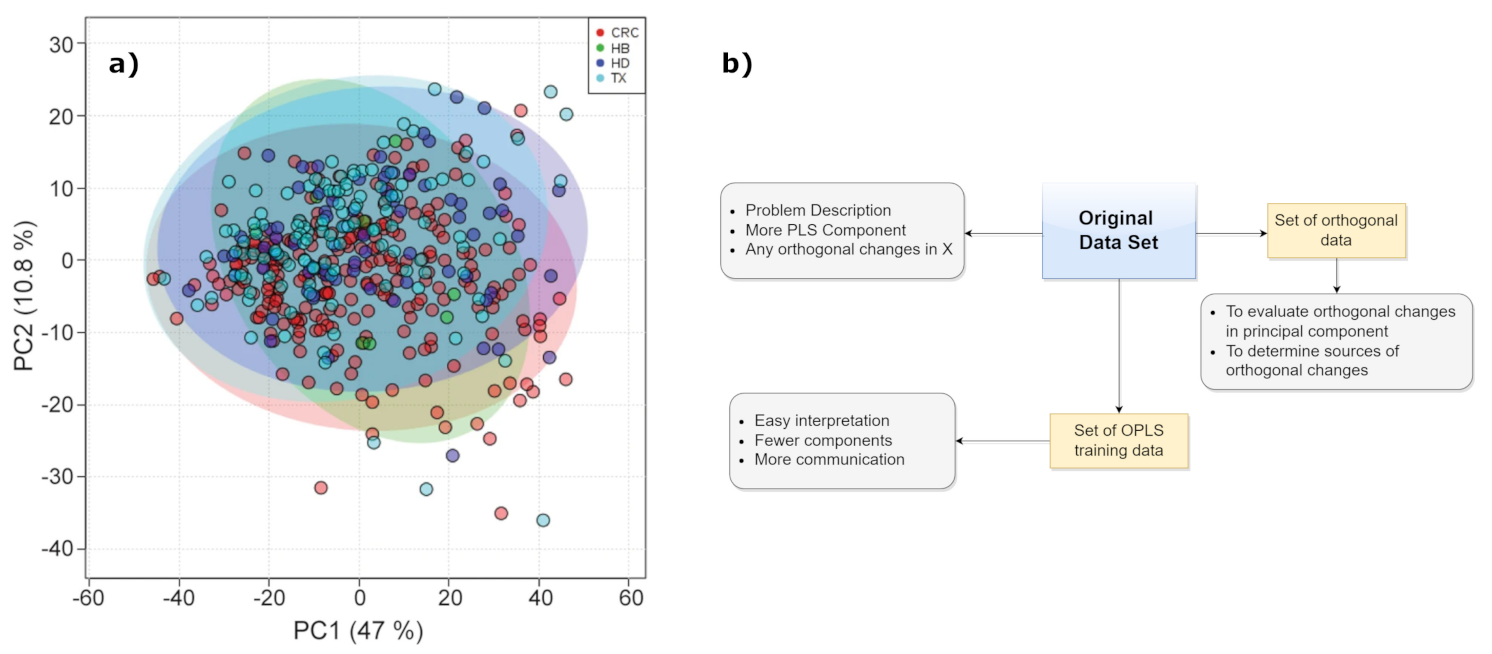
2.1.1. Principal Component Analysis (PCA)
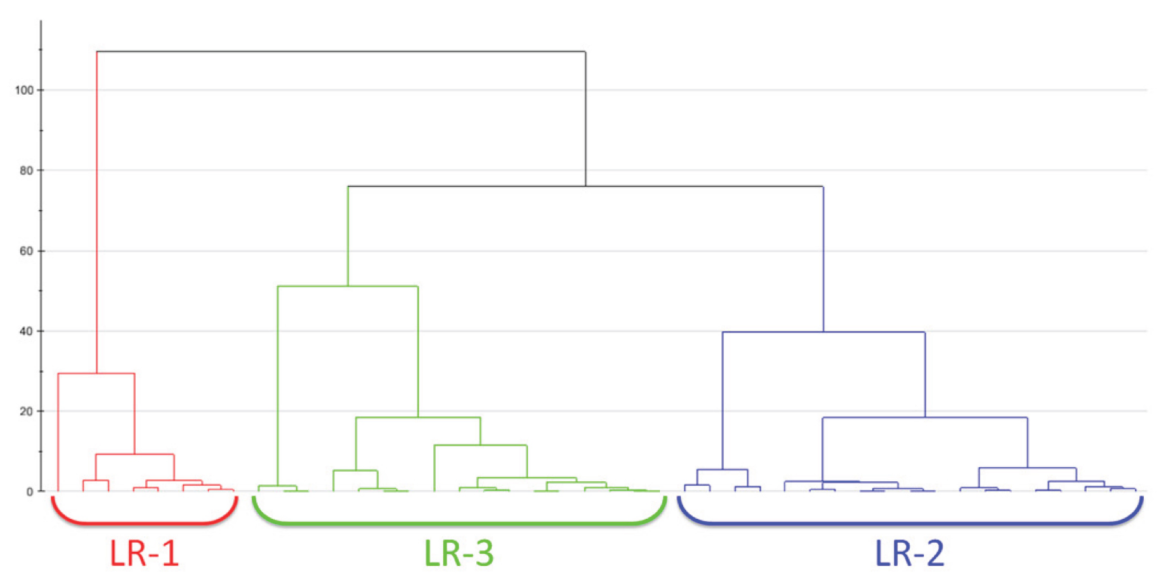
2.1.2. Clustering
2.1.3. Self-Organizing Maps (SOMs)
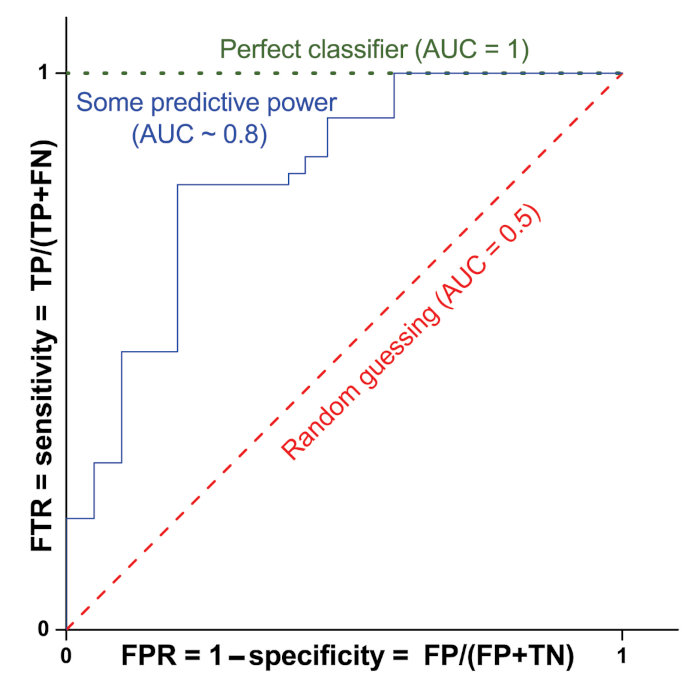
2.2. Supervised Methods
- The filter method marks subgroups of variables by calculate “easy to compute” quantities ahead of the model training.
- The wrapper method marks subgroups of variables by applying the chosen trained models on the testing dataset with the aim to determine the achieving the optimal performance.
- The embedded method is able to ascertain simultaneously the feature selection and model structure.
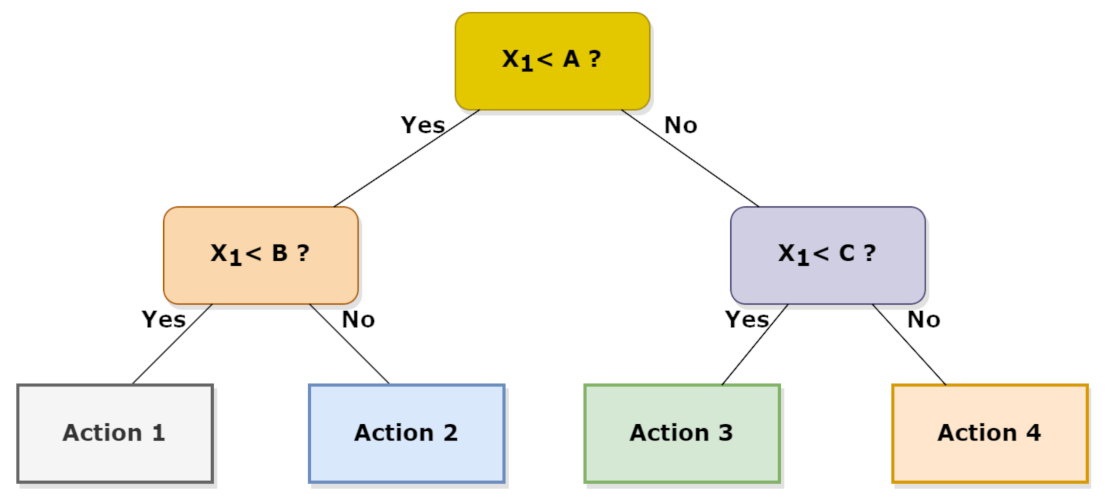
2.2.1. Random Forest (RF) and k-Nearest Neighbors (KNN)
2.2.2. Principal Component Regression (PCR) and Partial Least Squares (PLS)
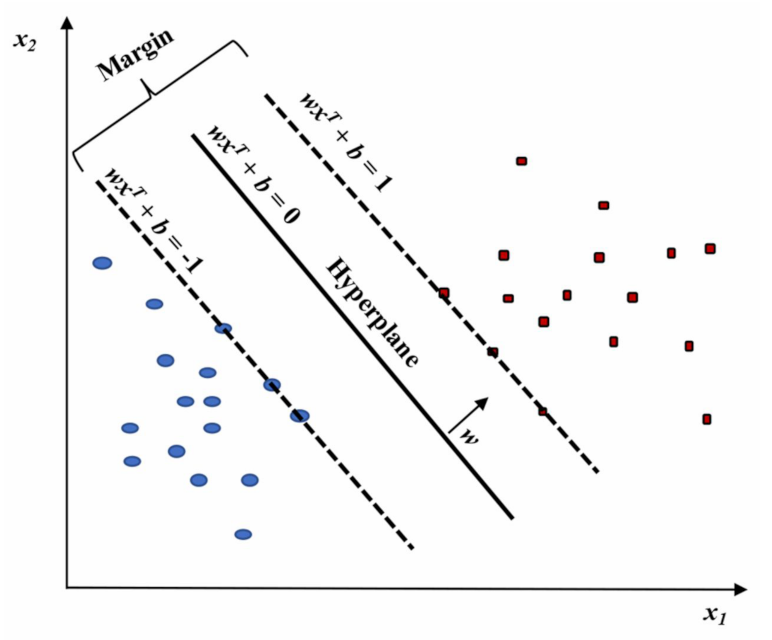
2.2.3. Support Vector Machine (SVM)
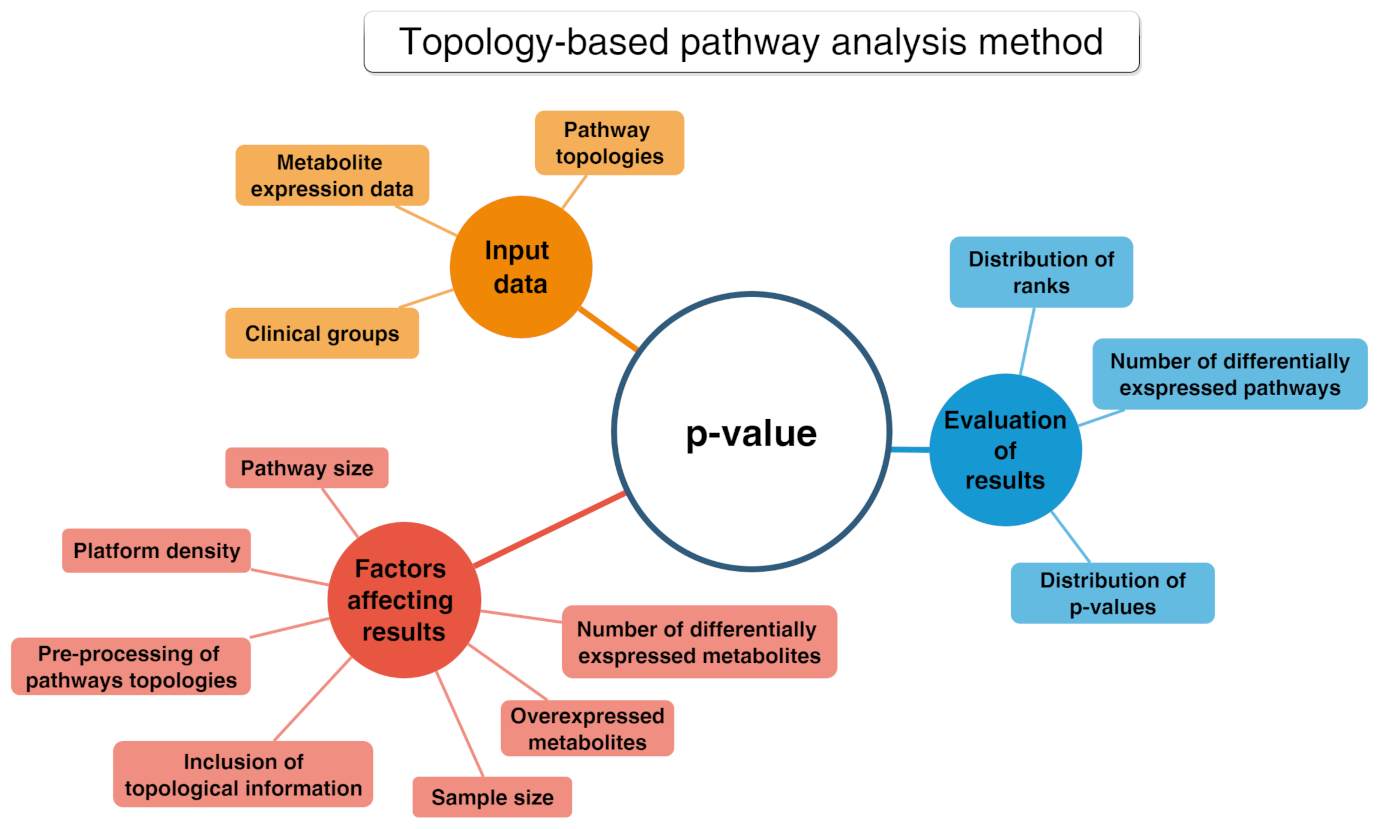
2.3. Pathway Analysis Methods
2.3.1. Over-Representation Analysis (ORA)
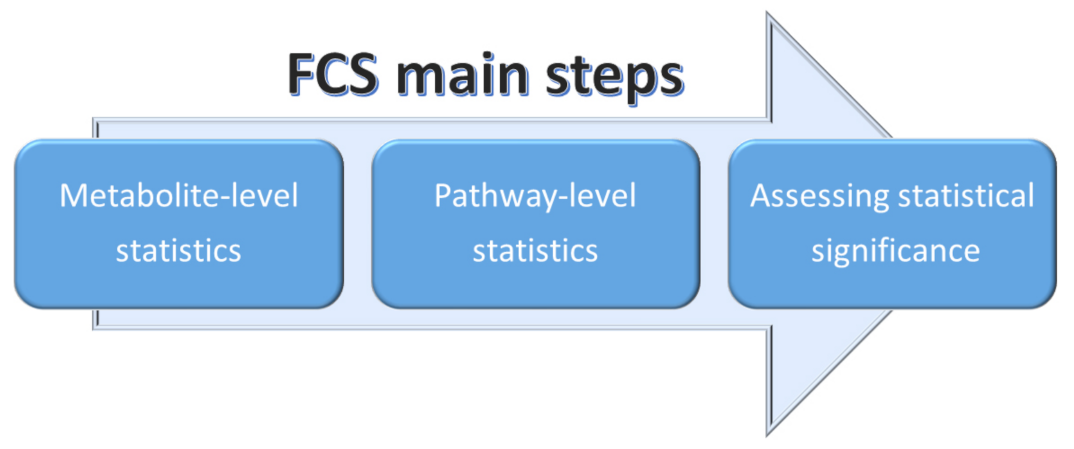
2.3.2. Functional Class Scoring (FCS)
- A statistical approach is applied to compute differential expression of individual metabolites (metabolite-level statistics), looking for correlations of molecular measurements with phenotype [87]. Those mostly used consider the analysis of variance (ANOVA) [88], Q-statistic [89], signal-to-noise ratio [90], t-test [91], and Z-score [92]. The choice of the most suitable statistical approach may depend on the number of biological replicates and on the effect of the metabolites set on a specific pathway [93].
- Initial statistics for all metabolites of a given pathway are combined into statistics on different pathways (pathway-level statistics) that can consider interdependencies among metabolites (multivariate) [94] or not (univariate) [91]. The pathway-level statistics usually is performed in terms of the Kolmogorov–Smirnov statistics [90], mean or median of metabolite-level statistics [93], the Wilcoxon rank sum [95], and the maxmean statistics [96]. Note that, although multivariate statistics should have more statistical significance, univariate statistics provide the best results if applied to the data of biologic systems (p≤ 0.001) [97].
- The last FCS step corresponds to estimating the significance of the so-called pathway-level statistics. In detail, the null hypothesis can be tested into two different ways: (i) by permuting metabolite labels for every pathways, so comparing the set of metabolites in that pathway with a set of metabolites not included in that pathway (competitive null hypothesis) [75] and (ii) by permuting class labels for every sample, so comparing the collection of metabolites in a considered pathway with itself, whereas the metabolites excluded by that pathway are not considered (self-contained null hypothesis) [91].
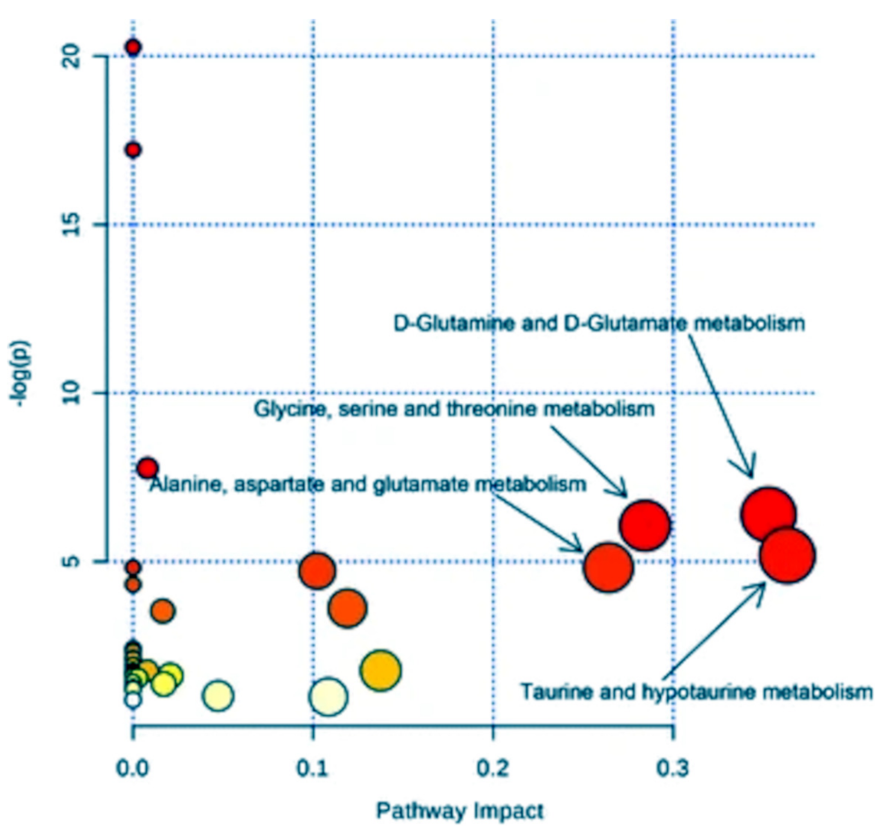
2.3.3. Metabolic Pathway Reconstruction and Simulation
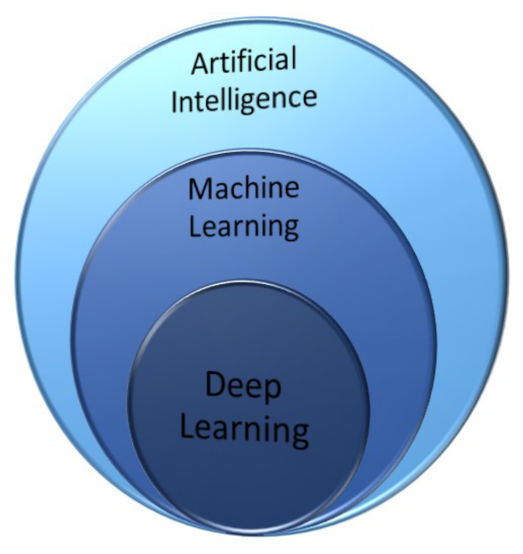
3. Artificial Intelligence toward Learning Techniques
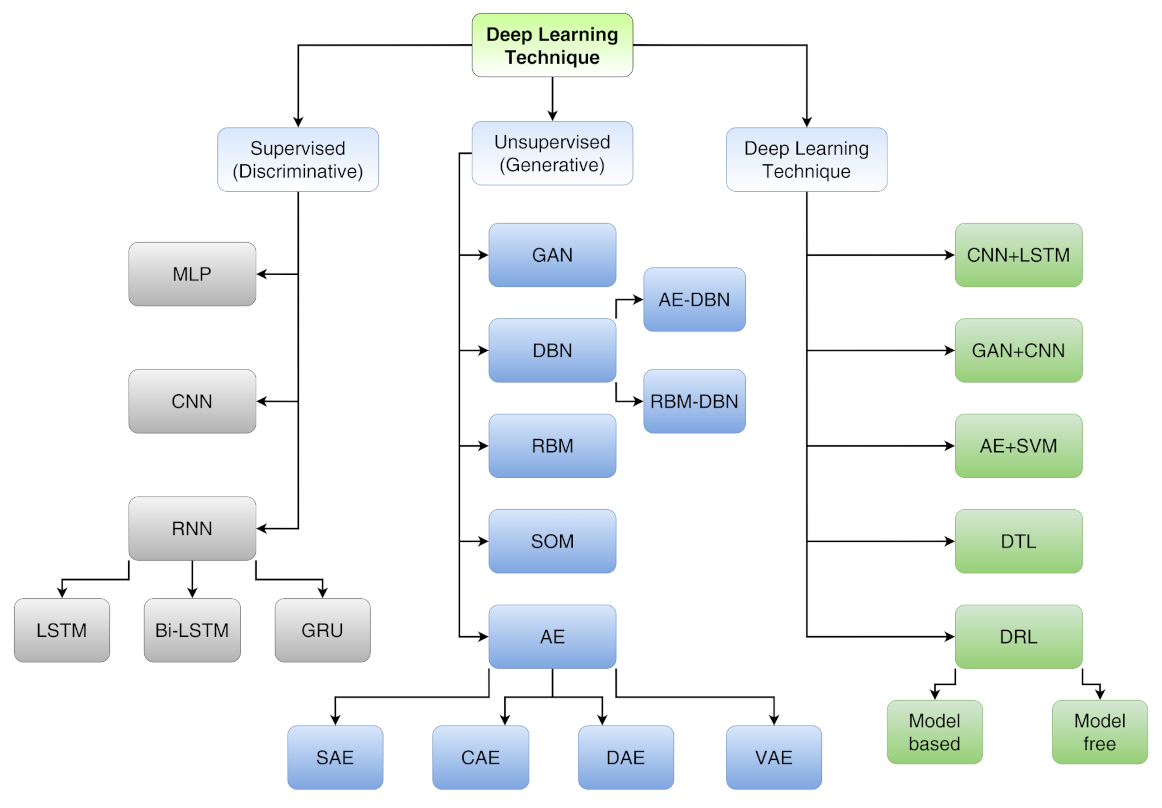
Machine Learning, Neural Networks and Deep Learning
- Supervised learning (discriminative) includes multi-layer perceptron (MLP), convolutional neural network (CNN), long short-term memory (LSTM) and gated recurrent unit (GRU);
- Unsupervised learning (generative) includes generative adversarial network (GAN), autoencoder (AE), sparse autoencoder (SAE), denoising autoencoder (DAE), contractive autoencoder (CAE), variational autoencoder (VAE), self-organizing map (SOM), restricted Boltzmann machine (RBM) and deep belief network (DBN);
- Hybrid learning (both discriminative and generative) includes models composed by both supervised and unsupervised algorithms other than deep transfer learning (DTL) and deep reinforcement learning (DRL).
- 1.
- Classic neural networks encompass linear and non-linear functions which, in turn, include S-shaped functions ranging from 0 to 1 (sigmoid) or from −1 to 1 (hyperbolic tangent, tanh) and rectified linear unit (ReLU), which gives 0 for input lower than the set value or evaluates a linear multiple for bigger input.
- 2.
- Convolutional neural networks (CNN) take into high consideration the neuron organization found in the visual cortex of an animal brain. It is particularly suited for high complexity and allows for optimal pre-processing. Four stages can be considered for CNN building (see Figure 17):
- (a)
- Deduce feature maps from input after applying a proper function (convolution);
- (b)
- Reveal an image after given changes (max-pooling);
- (c)
- Flatten the data for the CNN analysis (flattening);
- (d)
- Compiling the loss function by a hidden layer (full connection).
- 3.
- Recurrent neural networks (RNN) are exploited when the objective is the prediction of a sequence. They are a subset of ANN for sequential or time series data, usually applied for language translation, speech recognition, and son on. Their peculiar feature is that the outcome of the output node is a function of the output of previous elements within the sequence (see Figure 18a).
- 4.
- Generative adversarial networks (GAN) combine generator networks for providing artificial data and discriminator networks for distinguishing real and fake data.
- 5.
- Self-organizing maps (SOMs) have a fixed bi-dimensional output since each synapse joins its input and output nodes, and usually take advantage of data reduction performed by unsupervised approaches.
- 6.
- Boltzmann machine is a stochastic model exploited for yielding proper parameters defined in the model.
- 7.
- Deep reinforcement learning are mainly used to understand and so predict the effect of every action executed in a defined state of the observation.
- 8.
- Autoencoders work directly on the considered inputs, without taking into account the effect of activation functions. Among the autoencoders, we mention the following:
- (a)
- Sparse autoencoders have more hidden than input layers for reducing overfitting.
- (b)
- Denoising autoencoders are able to reconstruct corrupted data by randomly assigning 0 to some inputs.
- (c)
- Contractive autoencoders include a penalty factor to the loss function to prevent overfitting and data repetition when the network has more hidden than input layers.
- (d)
- Stacked autoencoders perform two stages of encoding by the inclusion of an additional hidden layer.
- 9.
- Backpropagation (BP) are neural networks that use the flux of information going from the output to input for learning about the errors corresponding to the achieved prediction. An architecture of the BP network is shown in Figure 18b.
- 10.
- Gradient descent are neural networks that identify a slope corresponding to a relation among variables (for example, the error produced in the neural network and data parameter: small data changes provoke errors variations).
4. Applications of Deep Learning Approaches for NMR-Based Metabolomics
4.1. Food
4.2. Biomedical
5. Conclusions and Future Perspective
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NMR | Nuclear Magnetic Resonance |
| MS | Mass Spectrometry |
| AI | Artificial Intelligence |
| ML | Machine Learning |
| DL | Deep Learning |
| NN | Neural Network |
| ANN | Artificial Neural Network |
| DNN | Deep Neural Network |
| PCA | Principal Component Analysis |
| PLS | Partial Least Squares |
| ORA | Over Representation Analysis |
| FCS | Functional Class Scoring |
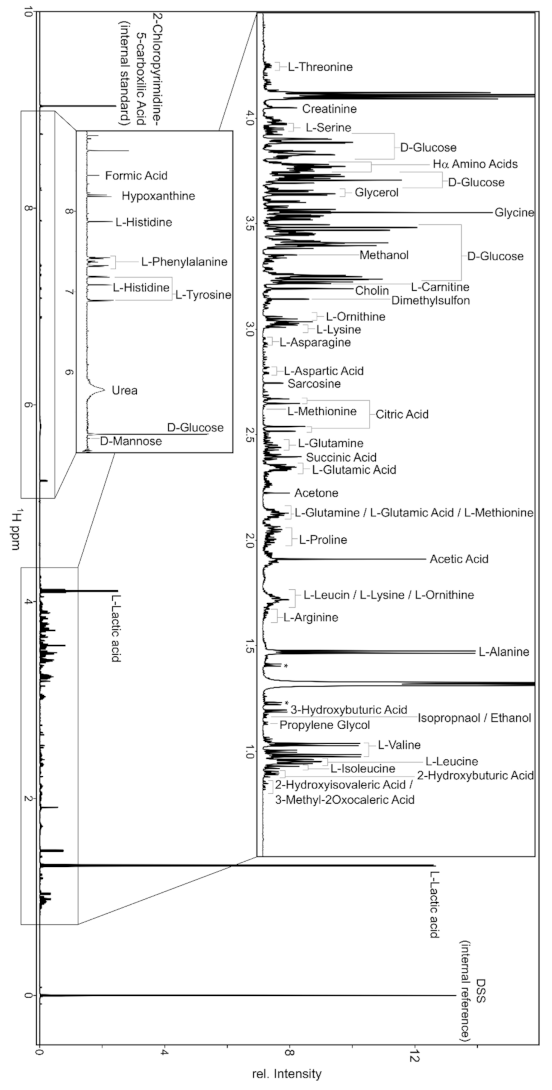
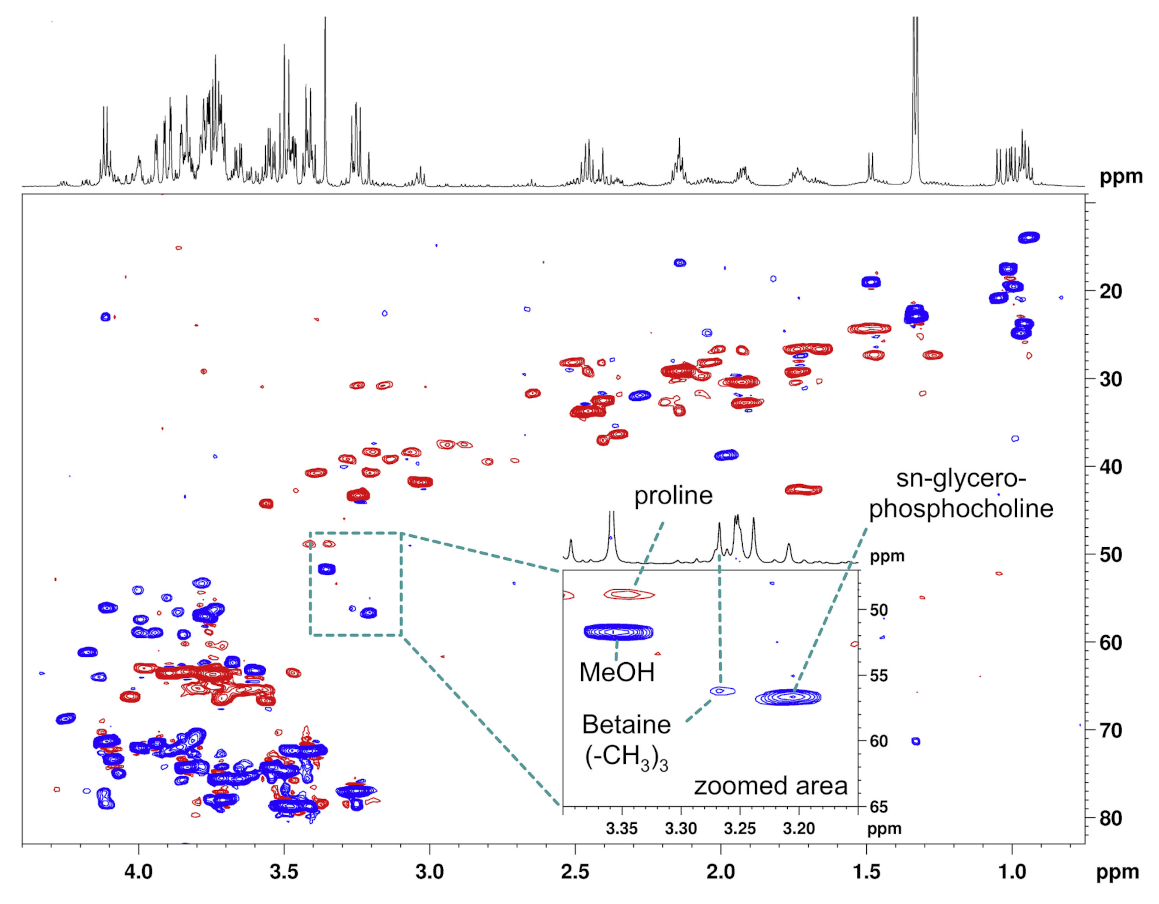
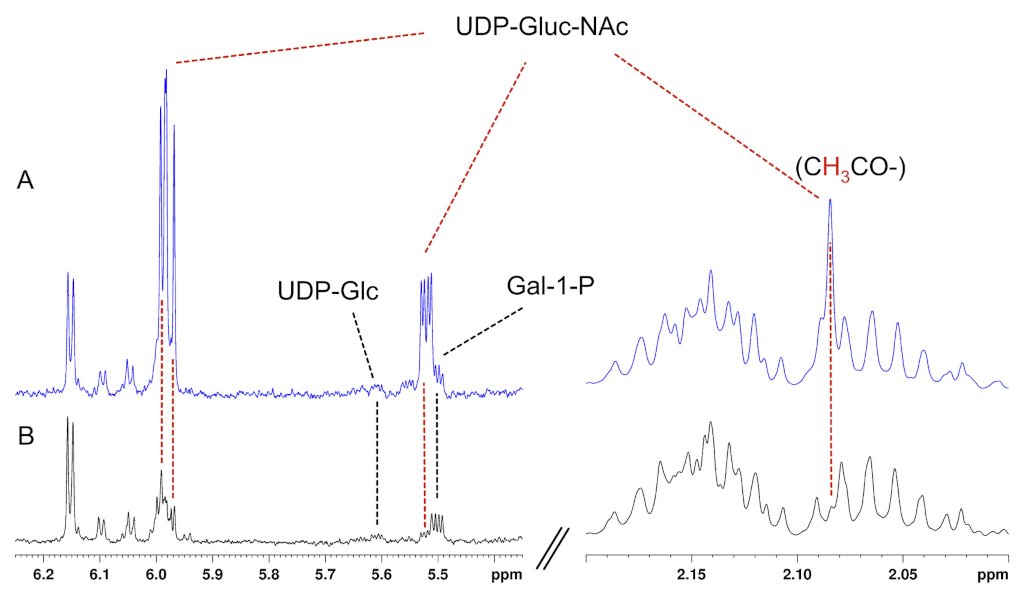
Appendix A. Technical Aspects

References
- Muthubharathi, B.C.; Gowripriya, T.; Balamurugan, K. Metabolomics: Small molecules that matter more. Mol. Omics 2021, 17, 210–229. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Du, X.; Xu, H.; Yang, S.; Wang, C.; Zhu, Y.; Zhang, T.; Zhao, W. Metabolic profiling of liver and faeces in mice infected with echinococcosis. Parasites Vectors 2021, 14, 324. [Google Scholar] [CrossRef] [PubMed]
- Emwas, A.H.; Roy, R.; McKay, R.T.; Tenori, L.; Saccenti, E.; Gowda, G.A.N.; Raftery, D.; Alahmari, F.; Jaremko, L.; Jaremko, M.; et al. NMR Spectroscopy for Metabolomics Research. Metabolites 2019, 9, 123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Onuh, J.O.; Qiu, H. Metabolic Profiling and Metabolites Fingerprints in Human Hypertension: Discovery and Potential. Metabolites 2021, 11, 687. [Google Scholar] [CrossRef]
- Caspani, G.; Sebők, V.; Sultana, N.; Swann, J.R.; Bailey, A. Metabolic phenotyping of opioid and psychostimulant addiction: A novel approach for biomarker discovery and biochemical understanding of the disorder. Br. J. Pharmacol. 2021, 1–29. [Google Scholar] [CrossRef]
- Wishart, D.S.; Guo, A.; Oler, E.; Wang, F.; Anjum, A.; Peters, H.; Dizon, R.; Sayeeda, Z.; Tian, S.; Lee, B.L.; et al. HMDB 5.0: The Human Metabolome Database for 2022. Nucleic Acids Res. 2022, 50, D622–D631. [Google Scholar] [CrossRef]
- Ulrich, E.L.; Akutsu, H.; Doreleijers, J.F.; Harano, Y.; Ioannidis, Y.E.; Lin, J.; Livny, M.; Mading, S.; Maziuk, D.; Miller, Z.; et al. BioMagResBank. Nucleic Acids Res. 2007, 36, D402–D408. [Google Scholar] [CrossRef] [Green Version]
- Goodacre, R.; Broadhurst, D.; Smilde, A.K.; Kristal, B.S.; Baker, J.D.; Beger, R.; Bessant, C.; Connor, S.; Capuani, G.; Craig, A.; et al. Proposed minimum reporting standards for data analysis in metabolomics. Metabolomics 2007, 3, 231–241. [Google Scholar] [CrossRef]
- Claridge, T.D. High-Resolution NMR Techniques in Organic Chemistry; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Oyedeji, A.B.; Green, E.; Adebiyi, J.A.; Ogundele, O.M.; Gbashi, S.; Adefisoye, M.A.; Oyeyinka, S.A.; Adebo, O.A. Metabolomic approaches for the determination of metabolites from pathogenic microorganisms: A review. Food Res. Int. 2021, 140, 110042. [Google Scholar] [CrossRef]
- Letertre, M.P.M.; Giraudeau, P.; de Tullio, P. Nuclear Magnetic Resonance Spectroscopy in Clinical Metabolomics and Personalized Medicine: Current Challenges and Perspectives. Front. Mol. Biosci. 2021, 8, 698337. [Google Scholar] [CrossRef]
- Emwas, A.H.; Alghrably, M.; Al-Harthi, S.; Poulson, B.G.; Szczepski, K.; Chandra, K.; Jaremko, M. New Advances in Fast Methods of 2D NMR Experiments. In Nuclear Magnetic Resonance; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef] [Green Version]
- Deaton, A.; Cartwright, N. Understanding and misunderstanding randomized controlled trials. Soc. Sci. Med. 2018, 210, 2–21. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.M.; Holmes, M.V.; Davey Smith, G. Reading Mendelian randomisation studies: A guide, glossary, and checklist for clinicians. BMJ 2018, 362, k601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teumer, A. Common Methods for Performing Mendelian Randomization. Front. Cardiovasc. Med. 2018, 5, 51. [Google Scholar] [CrossRef] [PubMed]
- Mishra, P.; Biancolillo, A.; Roger, J.M.; Marini, F.; Rutledge, D.N. New data preprocessing trends based on ensemble of multiple preprocessing techniques. TrAC Trends Anal. Chem. 2020, 132, 116045. [Google Scholar] [CrossRef]
- Augustijn, D.; de Groot, H.J.M.; Alia, A. HR-MAS NMR Applications in Plant Metabolomics. Molecules 2021, 26, 931. [Google Scholar] [CrossRef]
- Xu, X.; Xie, Z.; Yang, Z.; Li, D.; Xu, X. A t-SNE Based Classification Approach to Compositional Microbiome Data. Front. Genet. 2020, 11, 1633. [Google Scholar] [CrossRef]
- Worley, B.; Powers, R. Generalized adaptive intelligent binning of multiway data. Chemom. Intell. Lab. Syst. 2015, 146, 42–46. [Google Scholar] [CrossRef] [Green Version]
- Emwas, A.H.; Saccenti, E.; Gao, X.; Mckay, R.; Martins dos Santos, V.; Roy, R.; Wishart, D. Recommended strategies for spectral processing and post-processing of 1D 1H-NMR data of biofluids with a particular focus on urine. Metabolomics 2018, 14, 31. [Google Scholar] [CrossRef] [Green Version]
- Anderson, P.; Reo, N.; Delraso, N.; Doom, T.; Raymer, M. Gaussian binning: A new kernel-based method for processing NMR spectroscopic data for metabolomics. Metabolomics 2008, 4, 261–272. [Google Scholar] [CrossRef]
- Puchades-Carrasco, L.; Palomino-Schätzlein, M.; Pérez-Rambla, C.; Pineda-Lucena, A. Bioinformatics tools for the analysis of NMR metabolomics studies focused on the identification of clinically relevant biomarkers. Brief. Bioinform. 2015, 17, 541–552. [Google Scholar] [CrossRef]
- Hu, J.M.; Sun, H.T. Serum proton NMR metabolomics analysis of human lung cancer following microwave ablation. Radiat. Oncol. 2018, 13, 40. [Google Scholar] [CrossRef]
- Dieterle, F.; Ross, A.; Schlotterbeck, G.; Senn, H. Probabilistic Quotient Normalization as Robust Method to Account for Dilution of Complex Biological Mixtures. Application in 1H NMR Metabonomics. Anal. Chem. 2006, 78, 4281–4290. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Abbas, A.; Jing, B.Y.; Gao, X. WaVPeak: Picking NMR peaks through wavelet-based smoothing and volume-based filtering. Bioinformatics 2012, 28, 914–920. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- MacDonald, R.; Sokolenko, S. Detection of highly overlapping peaks via adaptive apodization. J. Magn. Reson. 2021, 333, 107104. [Google Scholar] [CrossRef] [PubMed]
- Dona, A.C.; Kyriakides, M.; Scott, F.; Shephard, E.A.; Varshavi, D.; Veselkov, K.; Everett, J.R. A guide to the identification of metabolites in NMR-based metabonomics/metabolomics experiments. Comput. Struct. Biotechnol. J. 2016, 14, 135–153. [Google Scholar] [CrossRef] [Green Version]
- Khalili, B.; Tomasoni, M.; Mattei, M.; Mallol Parera, R.; Sonmez, R.; Krefl, D.; Rueedi, R.; Bergmann, S. Automated Analysis of Large-Scale NMR Data Generates Metabolomic Signatures and Links Them to Candidate Metabolites. J. Proteome Res. 2019, 18, 3360–3368. [Google Scholar] [CrossRef] [Green Version]
- Jaadi, Z. A Step-by-Step Explanation of Principal Component Analysis (PCA). Available online: https://builtin.com/data-science/step-step-explanation-principal-component-analysis (accessed on 8 January 2022).
- AG, S. What Is Principal Component Analysis (PCA) and How It Is Used? Available online: https://www.sartorius.com/en/knowledge/science-snippets/what-is-principal-component-analysis-pca-and-how-it-is-used-507186 (accessed on 8 January 2022).
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Parsons, H.M.; Ludwig, C.; Günther, U.L.; Viant, M.R. Improved classification accuracy in 1- and 2-dimensional NMR metabolomics data using the variance stabilising generalised logarithm transformation. BMC Bioinform. 2007, 8, 234. [Google Scholar] [CrossRef] [Green Version]
- Izquierdo-Garcia, J.L.; del Barrio, P.C.; Campos-Olivas, R.; Villar-Hernández, R.; Prat-Aymerich, C.; Souza-Galvão, M.L.D.; Jiménez-Fuentes, M.A.; Ruiz-Manzano, J.; Stojanovic, Z.; González, A.; et al. Discovery and validation of an NMR-based metabolomic profile in urine as TB biomarker. Sci. Rep. 2020, 10, 22317. [Google Scholar] [CrossRef]
- Shiokawa, Y.; Date, Y.; Kikuchi, J. Application of kernel principal component analysis and computational machine learning to exploration of metabolites strongly associated with diet. Sci. Rep. 2018, 8, 3426. [Google Scholar] [CrossRef]
- Halouska, S.; Powers, R. Negative impact of noise on the principal component analysis of NMR data. J. Magn. Reson. 2006, 178, 88–95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rutledge, D.N.; Roger, J.M.; Lesnoff, M. Different Methods for Determining the Dimensionality of Multivariate Models. Front. Anal. Sci. 2021, 1, 754447. [Google Scholar] [CrossRef]
- Smilde, A.K.; Jansen, J.J.; Hoefsloot, H.C.J.; Lamers, R.J.A.N.; van der Greef, J.; Timmerman, M.E. ANOVA-simultaneous component analysis (ASCA): A new tool for analyzing designed metabolomics data. Bioinformatics 2005, 21, 3043–3048. [Google Scholar] [CrossRef]
- Lemanska, A.; Grootveld, M.; Silwood, C.J.L.; Brereton, R.G. Chemometric variance analysis of NMR metabolomics data on the effects of oral rinse on saliva. Metabolomics 2012, 8, 64–80. [Google Scholar] [CrossRef]
- Puig-Castellví, F.; Alfonso, I.; Piña, B.; Tauler, R. 1H NMR metabolomic study of auxotrophic starvation in yeast using Multivariate Curve Resolution-Alternating Least Squares for Pathway Analysis. Sci. Rep. 2016, 6, 30982. [Google Scholar] [CrossRef] [Green Version]
- Trepalin, S.V.; Yarkov, A.V. Hierarchical Clustering of Large Databases and Classification of Antibiotics at High Noise Levels. Algorithms 2008, 1, 183–200. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, P.; Madabhushi, A.; Rosen, M. A Hierarchical Unsupervised Spectral Clustering Scheme for Detection of Prostate Cancer from Magnetic Resonance Spectroscopy (MRS). In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2007; Ayache, N., Ourselin, S., Maeder, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 278–286. [Google Scholar]
- Čuperlović Culf, M.; Belacel, N.; Culf, A.S.; Chute, I.C.; Ouellette, R.J.; Burton, I.W.; Karakach, T.K.; Walter, J.A. NMR metabolic analysis of samples using fuzzy K-means clustering. Magn. Reson. Chem. 2009, 47, S96–S104. [Google Scholar] [CrossRef] [Green Version]
- Zou, X.; Holmes, E.; Nicholson, J.K.; Loo, R.L. Statistical HOmogeneous Cluster SpectroscopY (SHOCSY): An Optimized Statistical Approach for Clustering of 1H NMR Spectral Data to Reduce Interference and Enhance Robust Biomarkers Selection. Anal. Chem. 2014, 86, 5308–5315. [Google Scholar] [CrossRef]
- Gülseçen, S.; Sharma, S.; Akadal, E. Who Runs the World: Data; Istanbul University Press: Istanbul, Turkey, 2020. [Google Scholar] [CrossRef]
- Schonlau, M. Visualizing non-hierarchical and hierarchical cluster analyses with clustergrams. Comput. Stat. 2004, 19, 95–111. [Google Scholar] [CrossRef]
- Yim, O.; Ramdeen, K.T. Hierarchical Cluster Analysis: Comparison of Three Linkage Measures and Application to Psychological Data. Quant. Methods Psychol. 2015, 11, 8–21. [Google Scholar] [CrossRef]
- Zhang, Z.; Murtagh, F.; Poucke, S.V.V.; Lin, S.; Lan, P. Hierarchical cluster analysis in clinical research with heterogeneous study population: Highlighting its visualization with R. Ann. Transl. Med. 2017, 5, 75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richard, V.; Conotte, R.; Mayne, D.; Colet, J.M. Does the 1H-NMR plasma metabolome reflect the host-tumor interactions in human breast cancer? Oncotarget 2017, 8, 49915–49930. [Google Scholar] [CrossRef] [PubMed]
- Selvaratnam, R.; Chowdhury, S.; VanSchouwen, B.; Melacini, G. Mapping allostery through the covariance analysis of NMR chemical shifts. Proc. Natl. Acad. Sci. USA 2011, 108, 6133–6138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kohonen, T. Self-Organizing Maps, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Kaski, S. Data exploration using self-organizing maps. In Acta Polytechnica Scandinavica: Mathematics, Computing and Management in Engineering Series no. 82; Finnish Academy of Technology: Espoo, Finland, 1997. [Google Scholar]
- Zheng, H.; Ji, J.; Zhao, L.; Chen, M.; Shi, A.; Pan, L.; Huang, Y.; Zhang, H.; Dong, B.; Gao, H. Prediction and diagnosis of renal cell carcinoma using nuclear magnetic resonance-based serum metabolomics and self-organizing maps. Oncotarget 2016, 7, 59189–59198. [Google Scholar] [CrossRef] [Green Version]
- Akdemir, D.; Rio, S.; Isidro y Sánchez, J. TrainSel: An R Package for Selection of Training Populations. Front. Genet. 2021, 12, 607. [Google Scholar] [CrossRef]
- Migdadi, L.; Lambert, J.; Telfah, A.; Hergenröder, R.; Wöhler, C. Automated metabolic assignment: Semi-supervised learning in metabolic analysis employing two dimensional Nuclear Magnetic Resonance (NMR). Comput. Struct. Biotechnol. J. 2021, 19, 5047–5058. [Google Scholar] [CrossRef]
- Alonso-Salces, R.M.; Gallo, B.; Collado, M.I.; Sasía-Arriba, A.; Viacava, G.E.; García-González, D.L.; Gallina Toschi, T.; Servili, M.; Ángel Berrueta, L. 1H–NMR fingerprinting and supervised pattern recognition to evaluate the stability of virgin olive oil during storage. Food Control 2021, 123, 107831. [Google Scholar] [CrossRef]
- Suppers, A.; Gool, A.J.v.; Wessels, H.J.C.T. Integrated Chemometrics and Statistics to Drive Successful Proteomics Biomarker Discovery. Proteomes 2018, 6, 20. [Google Scholar] [CrossRef] [Green Version]
- Biswas, S.; Bordoloi, M.; Purkayastha, B. Review on Feature Selection and Classification using Neuro-Fuzzy Approaches. Int. J. Appl. Evol. Comput. 2016, 7, 28–44. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef] [Green Version]
- Venkatesan, P.; Dharuman, C.; Gunasekaran, S. A Comparative Study of Principal Component Regression and Partial least Squares Regression with Application to FTIR Diabetes Data. Indian J. Sci. Technol. 2011, 4, 740–746. [Google Scholar] [CrossRef]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The Collinearity Problem in Linear Regression. The Partial Least Squares (PLS) Approach to Generalized Inverses. SIAM J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef] [Green Version]
- Lee, L.C.; Liong, C.Y.; Jemain, A.A. Partial least squares-discriminant analysis (PLS-DA) for classification of high-dimensional (HD) data: A review of contemporary practice strategies and knowledge gaps. Analyst 2018, 143, 3526–3539. [Google Scholar] [CrossRef]
- Song, W.; Wang, H.; Maguire, P.; Nibouche, O. Nearest clusters based partial least squares discriminant analysis for the classification of spectral data. Anal. Chim. Acta 2018, 1009, 27–38. [Google Scholar] [CrossRef]
- Traquete, F.; Luz, J.; Cordeiro, C.; Sousa Silva, M.; Ferreira, A.E.N. Binary Simplification as an Effective Tool in Metabolomics Data Analysis. Metabolites 2021, 11, 788. [Google Scholar] [CrossRef]
- Jiménez-Carvelo, A.M.; Martín-Torres, S.; Ortega-Gavilán, F.; Camacho, J. PLS-DA vs sparse PLS-DA in food traceability. A case study: Authentication of avocado samples. Talanta 2021, 224, 121904. [Google Scholar] [CrossRef]
- Gabrielsson, J.; Jonsson, H.; Airiau, C.; Schmidt, B.; Escott, R.; Trygg, J. OPLS methodology for analysis of pre-processing effects on spectroscopic data. Chemom. Intell. Lab. Syst. 2006, 84, 153–158. [Google Scholar] [CrossRef]
- Embade, N.; Cannet, C.; Diercks, T.; Gil-Redondo, R.; Bruzzone, C.; Ansó, S.; Echevarría, L.R.; Ayucar, M.M.M.; Collazos, L.; Lodoso, B.; et al. NMR-based newborn urine screening for optimized detection of inherited errors of metabolism. Sci. Rep. 2019, 9, 13067. [Google Scholar] [CrossRef]
- Huang, S.; Cai, N.; Pacheco, P.P.; Narrandes, S.; Wang, Y.; Xu, W. Applications of Support Vector Machine (SVM) Learning in Cancer Genomics. Cancer Genom. Proteom. 2018, 15, 41–51. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, T.; Zhang, W.; Ghosh, D.; Kechris, K. Predictive Modeling for Metabolomics Data. In Computational Methods and Data Analysis for Metabolomics; Li, S., Ed.; Springer: New York, NY, USA, 2020; pp. 313–336. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, C.; Xie, K.; Wang, J.; Pan, Z. Current State of Metabolomics Research in Meat Quality Analysis and Authentication. Foods 2021, 10, 2388. [Google Scholar] [CrossRef] [PubMed]
- Broadhurst, D.I.; Kell, D.B. Statistical strategies for avoiding false discoveries in metabolomics and related experiments. Metabolomics 2006, 2, 171–196. [Google Scholar] [CrossRef] [Green Version]
- Westerhuis, J.A.; Hoefsloot, H.C.J.; Smit, S.; Vis, D.J.; Smilde, A.K.; van Velzen, E.J.J.; van Duijnhoven, J.P.M.; van Dorsten, F.A. Assessment of PLSDA cross validation. Metabolomics 2008, 4, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Wehrens, R.; Putter, H.; Buydens, L.M. The bootstrap: A tutorial. Chemom. Intell. Lab. Syst. 2000, 54, 35–52. [Google Scholar] [CrossRef]
- Wieder, C.; Frainay, C.; Poupin, N.; Rodríguez-Mier, P.; Vinson, F.; Cooke, J.; Lai, R.P.; Bundy, J.G.; Jourdan, F.; Ebbels, T. Pathway analysis in metabolomics: Recommendations for the use of over-representation analysis. PLoS Comput. Biol. 2021, 17, e1009105. [Google Scholar] [CrossRef]
- Khatri, P.; Sirota, M.; Butte, A.J. Ten Years of Pathway Analysis: Current Approaches and Outstanding Challenges. PLoS Comput. Biol. 2012, 8, e1002375. [Google Scholar] [CrossRef]
- Marco-Ramell, A.; Palau, M.; Alay, A.; Tulipani, S.; Urpi-Sarda, M.; Sánchez-Pla, A.; Andres-Lacueva, C. Evaluation and comparison of bioinformatic tools for the enrichment analysis of metabolomics data. BMC Bioinform. 2018, 19, 1. [Google Scholar] [CrossRef]
- Karnovsky, A.; Li, S. Pathway Analysis for Targeted and Untargeted Metabolomics. Methods Mol. Biol. 2020, 2104, 387–400. [Google Scholar]
- Nguyen, T.M.; Shafi, A.; Nguyen, T.; Draghici, S. Identifying significantly impacted pathways: A comprehensive review and assessment. Genome Biol. 2019, 20, 203. [Google Scholar] [CrossRef]
- García-Campos, M.A.; Espinal-Enríquez, J.; Hernández-Lemus, E. Pathway Analysis: State of the Art. Front. Physiol. 2015, 6, 383. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Xu, X.; Deng, L.; Cheng, K.K.; Xu, J.; Raftery, D.; Dong, J. A Novel Network Modelling for Metabolite Set Analysis: A Case Study on CRC Metabolomics. IEEE Access 2020, 8, 106425–106436. [Google Scholar] [CrossRef]
- Mitrea, C.; Taghavi, Z.; Bokanizad, B.; Hanoudi, S.; Tagett, R.; Donato, M.; Voichita, C.; Draghici, S. Methods and approaches in the topology-based analysis of biological pathways. Front. Physiol. 2013, 4, 278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ihnatova, I.; Popovici, V.; Budinska, E. A critical comparison of topology-based pathway analysis methods. PLoS ONE 2018, 13, e0191154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, J.; Shojaie, A.; Michailidis, G. A comparative study of topology-based pathway enrichment analysis methods. BMC Bioinform. 2019, 20, 546. [Google Scholar] [CrossRef] [Green Version]
- Chagoyen, M.; Pazos, F. Tools for the functional interpretation of metabolomic experiments. Brief. Bioinform. 2012, 14, 737–744. [Google Scholar] [CrossRef] [Green Version]
- Huang, D.W.; Sherman, B.T.; Lempicki, R.A. Bioinformatics enrichment tools: Paths toward the comprehensive functional analysis of large gene lists. Nucleic Acids Res. 2008, 37, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Emwas, A.H.M. The Strengths and Weaknesses of NMR Spectroscopy and Mass Spectrometry with Particular Focus on Metabolomics Research. In Methods in Molecular Biology; Springer: New York, NY, USA, 2015; pp. 161–193. [Google Scholar] [CrossRef]
- Pavlidis, P.; Qin, J.; Arango, V.; Mann, J.J.; Sibille, E. Using the Gene Ontology for Microarray Data Mining: A Comparison of Methods and Application to Age Effects in Human Prefrontal Cortex. Neurochem. Res. 2004, 29, 1213–1222. [Google Scholar] [CrossRef]
- Al-Shahrour, F.; Díaz-Uriarte, R.; Dopazo, J. Discovering molecular functions significantly related to phenotypes by combining gene expression data and biological information. Bioinformatics 2005, 21, 2988–2993. [Google Scholar] [CrossRef] [Green Version]
- Goeman, J.J.; van de Geer, S.A.; de Kort, F.; van Houwelingen, H.C. A global test for groups of genes: Testing association with a clinical outcome. Bioinformatics 2004, 20, 93–99. [Google Scholar] [CrossRef] [Green Version]
- Subramanian, A.; Tamayo, P.; Mootha, V.K.; Mukherjee, S.; Ebert, B.L.; Gillette, M.A.; Paulovich, A.; Pomeroy, S.L.; Golub, T.R.; Lander, E.S.; et al. Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA 2005, 102, 15545–15550. [Google Scholar] [CrossRef] [Green Version]
- Tian, L.; Greenberg, S.A.; Kong, S.W.; Altschuler, J.; Kohane, I.S.; Park, P.J. Discovering statistically significant pathways in expression profiling studies. Proc. Natl. Acad. Sci. USA 2005, 102, 13544–13549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, S.Y.; Volsky, D.J. PAGE: Parametric Analysis of Gene Set Enrichment. BMC Bioinform. 2005, 6, 144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, Z.; Gentleman, R. Extensions to gene set enrichment. Bioinformatics 2006, 23, 306–313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kong, S.W.; Pu, W.T.; Park, P.J. A multivariate approach for integrating genome-wide expression data and biological knowledge. Bioinformatics 2006, 22, 2373–2380. [Google Scholar] [CrossRef]
- Barry, W.T.; Nobel, A.B.; Wright, F.A. Significance analysis of functional categories in gene expression studies: A structured permutation approach. Bioinformatics 2005, 21, 1943–1949. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. On testing the significance of sets of genes. Ann. Appl. Stat. 2007, 1, 107–129. [Google Scholar] [CrossRef] [Green Version]
- Glazko, G.V.; Emmert-Streib, F. Unite and conquer: Univariate and multivariate approaches for finding differentially expressed gene sets. Bioinformatics 2009, 25, 2348–2354. [Google Scholar] [CrossRef] [Green Version]
- Koza, J.R.; Mydlowec, W.; Lanza, G.; Yu, J.; Keane, M.A. Reverse Engineering of Metabolic Pathways From Observed Data Using Genetic Programming. Pac. Symp. Biocomput. 2001, 434–445. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, M.D.; Vallabhajosyula, R.R.; Jenkins, J.W.; Hood, J.E.; Soni, A.S.; Wikswo, J.P.; Lipson, H. Automated refinement and inference of analytical models for metabolic networks. Phys. Biol. 2011, 8, 055011. [Google Scholar] [CrossRef]
- Qi, Q.; Li, J.; Cheng, J. Reconstruction of metabolic pathways by combining probabilistic graphical model-based and knowledge-based methods. BMC Proc. 2014, 8, S5. [Google Scholar] [CrossRef] [Green Version]
- Xia, J.; Wishart, D.S. Web-based inference of biological patterns, functions and pathways from metabolomic data using MetaboAnalyst. Nat. Protoc. 2011, 6, 743–760. [Google Scholar] [CrossRef] [PubMed]
- Damiani, C.; Gaglio, D.; Sacco, E.; Alberghina, L.; Vanoni, M. Systems metabolomics: From metabolomic snapshots to design principles. Curr. Opin. Biotechnol. 2020, 63, 190–199. [Google Scholar] [CrossRef]
- Kim, H.I.; Han, K.Y. Urban Flood Prediction Using Deep Neural Network with Data Augmentation. Water 2020, 12, 899. [Google Scholar] [CrossRef] [Green Version]
- Sarker, I.H. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef] [PubMed]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An Introduction to Deep Reinforcement Learning. Found. Trends® Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef] [Green Version]
- Le, T.L.; Huynh, T.T.; Hong, S.K.; Lin, C.M. Hybrid Neural Network Cerebellar Model Articulation Controller Design for Non-linear Dynamic Time-Varying Plants. Front. Neurosci. 2020, 14, 695. [Google Scholar] [CrossRef] [PubMed]
- Arabasadi, Z.; Alizadehsani, R.; Roshanzamir, M.; Moosaei, H.; Yarifard, A.A. Computer aided decision making for heart disease detection using hybrid neural network-Genetic algorithm. Comput. Methods Programs Biomed. 2017, 141, 19–26. [Google Scholar] [CrossRef]
- Fan, X.; Wang, X.; Jiang, M.; Pei, Z.; Qiao, S. An Improved Stacked Autoencoder for Metabolomic Data Classification. Comput. Intell. Neurosci. 2021, 2021, 1051172. [Google Scholar] [CrossRef]
- Zhu, L.; Spachos, P.; Pensini, E.; Plataniotis, K.N. Deep learning and machine vision for food processing: A survey. Curr. Res. Food Sci. 2021, 4, 233–249. [Google Scholar] [CrossRef]
- Sakib, S.; Ahmed, N.; Kabir, A.J.; Ahmed, H. An Overview of Convolutional Neural Network: Its Architecture and Applications. Preprints 2018, 2018110546. [Google Scholar] [CrossRef]
- Gil-Solsona, R.; Álvarez-Muñoz, D.; Serra-Compte, A.; Rodríguez-Mozaz, S. (Xeno)metabolomics for the evaluation of aquatic organism’s exposure to field contaminated water. Trends Environ. Anal. Chem. 2021, 31, e00132. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, C.; Cheng, S.; Li, G.; Griebel, J.; Neuhaus, J. Novel Metabolic Signatures of Prostate Cancer Revealed by 1H-NMR Metabolomics of Urine. Diagnostics 2021, 11, 149. [Google Scholar] [CrossRef] [PubMed]
- Mandrone, M.; Chiocchio, I.; Barbanti, L.; Tomasi, P.; Tacchini, M.; Poli, F. Metabolomic Study of Sorghum (Sorghum bicolor) to Interpret Plant Behavior under Variable Field Conditions in View of Smart Agriculture Applications. J. Agric. Food Chem. 2021, 69, 1132–1145. [Google Scholar] [CrossRef]
- Nunes, C.A.; Alvarenga, V.O.; de Souza Sant’Ana, A.; Santos, J.S.; Granato, D. The use of statistical software in food science and technology: Advantages, limitations and misuses. Food Res. Int. 2015, 75, 270–280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Class, L.C.; Kuhnen, G.; Rohn, S.; Kuballa, J. Diving Deep into the Data: A Review of Deep Learning Approaches and Potential Applications in Foodomics. Foods 2021, 10, 1803. [Google Scholar] [CrossRef] [PubMed]
- Greer, M.; Chen, C.; Mandal, S. Automated classification of food products using 2D low-field NMR. J. Magn. Reson. 2018, 294, 44–58. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.Q.; Venkataramanan, L.; Hürlimann, M.; Flaum, M.; Frulla, P.; Straley, C. T1–T2 Correlation Spectra Obtained Using a Fast Two-Dimensional Laplace Inversion. J. Magn. Reson. 2002, 154, 261–268. [Google Scholar] [CrossRef]
- Date, Y.; Kikuchi, J. Application of a Deep Neural Network to Metabolomics Studies and Its Performance in Determining Important Variables. Anal. Chem. 2018, 90, 1805–1810. [Google Scholar] [CrossRef]
- Wang, D.; Greenwood, P.; Klein, M.S. Deep Learning for Rapid Identification of Microbes Using Metabolomics Profiles. Metabolites 2021, 11, 863. [Google Scholar] [CrossRef]
- Ebrahimnejad, H.; Ebrahimnejad, H.; Salajegheh, A.; Barghi, H. Use of Magnetic Resonance Imaging in Food Quality Control: A Review. J. Biomed. Phys. Eng. 2018, 8, 127–132. [Google Scholar] [CrossRef]
- Caballero, D.; Pérez-Palacios, T.; Caro, A.; Amigo, J.M.; Dahl, A.B.; Ersbll, B.K.; Antequera, T. Prediction of pork quality parameters by applying fractals and data mining on MRI. Food Res. Int. 2017, 99, 739–747. [Google Scholar] [CrossRef] [PubMed]
- Teimouri, N.; Omid, M.; Mollazade, K.; Mousazadeh, H.; Alimardani, R.; Karstoft, H. On-line separation and sorting of chicken portions using a robust vision-based intelligent modelling approach. Biosyst. Eng. 2018, 167, 8–20. [Google Scholar] [CrossRef]
- Ribeiro, F.D.S.; Caliva, F.; Swainson, M.; Gudmundsson, K.; Leontidis, G.; Kollias, S. An adaptable deep learning system for optical character verification in retail food packaging. In Proceedings of the 2018 IEEE Conference on Evolving and Adaptive Intelligent Systems (EAIS), Kallithea Rhodes, Greece, 25–27 May 2018. [Google Scholar] [CrossRef]
- Grapov, D.; Fahrmann, J.; Wanichthanarak, K.; Khoomrung, S. Rise of Deep Learning for Genomic, Proteomic, and Metabolomic Data Integration in Precision Medicine. OMICS J. Integr. Biol. 2018, 22, 630–636. [Google Scholar] [CrossRef] [Green Version]
- Cao, C.; Liu, F.; Tan, H.; Song, D.; Shu, W.; Li, W.; Zhou, Y.; Bo, X.; Xie, Z. Deep Learning and Its Applications in Biomedicine. Genom. Proteom. Bioinform. 2018, 16, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.W.; Zhang, C.; Cottrell, G.W.; Gerwick, W.H. SMART-Miner: A convolutional neural network-based metabolite identification from 1H-13C HSQC spectra. Magn. Reson. Chem. 2021. [Google Scholar] [CrossRef] [PubMed]
- Brougham, D.F.; Ivanova, G.; Gottschalk, M.; Collins, D.M.; Eustace, A.J.; O’Connor, R.; Havel, J. Artificial Neural Networks for Classification in Metabolomic Studies of Whole Cells Using1H Nuclear Magnetic Resonance. J. Biomed. Biotechnol. 2011, 2011, 158094. [Google Scholar] [CrossRef] [Green Version]
- Di Donato, S.; Vignoli, A.; Biagioni, C.; Malorni, L.; Mori, E.; Tenori, L.; Calamai, V.; Parnofiello, A.; Di Pierro, G.; Migliaccio, I.; et al. A Serum Metabolomics Classifier Derived from Elderly Patients with Metastatic Colorectal Cancer Predicts Relapse in the Adjuvant Setting. Cancers 2021, 13, 2762. [Google Scholar] [CrossRef]
- Encyclopedia of Spectroscopy and Spectrometry; Elsevier: Amsterdam, The Netherlands, 2017. [CrossRef]
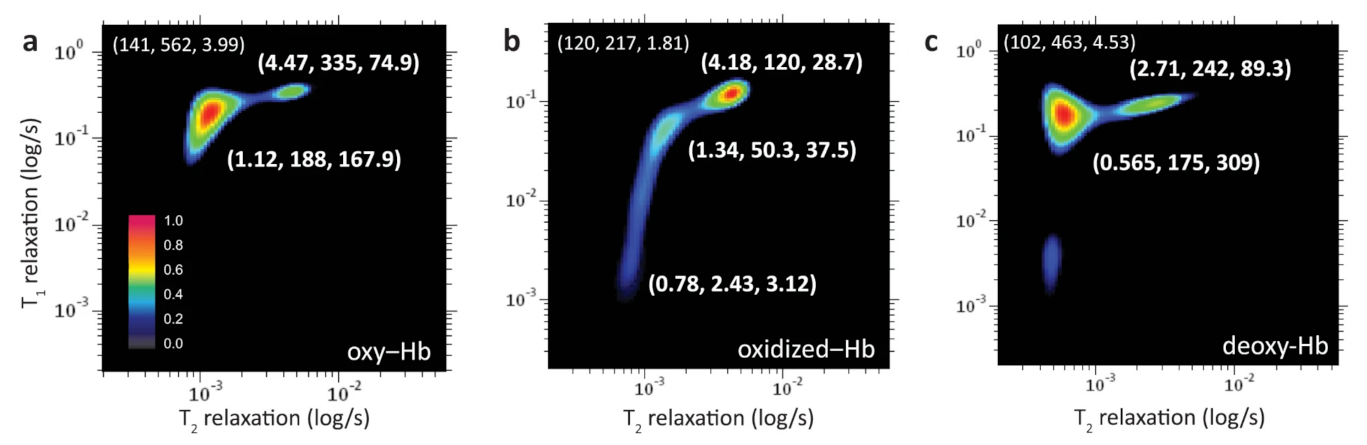
- Peng, W.K.; Ng, T.T.; Loh, T.P. Machine learning assistive rapid, label-free molecular phenotyping of blood with two-dimensional NMR correlational spectroscopy. Commun. Biol. 2020, 3, 535. [Google Scholar] [CrossRef]
- Corsaro, C.; Mallamace, D.; Neri, G.; Fazio, E. Hydrophilicity and hydrophobicity: Key aspects for biomedical and technological purposes. Phys. A Stat. Mech. Its Appl. 2021, 580, 126189. [Google Scholar] [CrossRef]
- Chandra, K.; Al-Harthi, S.; Sukumaran, S.; Almulhim, F.; Emwas, A.H.; Atreya, H.S.; Jaremko, Ł.; Jaremko, M. NMR-based metabolomics with enhanced sensitivity. RSC Adv. 2021, 11, 8694–8700. [Google Scholar] [CrossRef]
- Crook, A.A.; Powers, R. Quantitative NMR-Based Biomedical Metabolomics: Current Status and Applications. Molecules 2020, 25, 5128. [Google Scholar] [CrossRef] [PubMed]
- Salmerón, A.M.; Tristán, A.I.; Abreu, A.C.; Fernández, I. Serum Colorectal Cancer Biomarkers Unraveled by NMR Metabolomics: Past, Present, and Future. Anal. Chem. 2021, 94, 417–430. [Google Scholar] [CrossRef] [PubMed]
- Corsaro, C.; Cicero, N.; Mallamace, D.; Vasi, S.; Naccari, C.; Salvo, A.; Giofrè, S.V.; Dugo, G. HR-MAS and NMR towards Foodomics. Food Res. Int. 2016, 89, 1085–1094. [Google Scholar] [CrossRef]
- Corsaro, C.; Fazio, E.; Mallamace, D. Direct Analysis in Foodomics: NMR approaches. In Comprehensive Foodomics; Elsevier: Amsterdam, The Netherlands, 2021; pp. 517–535. [Google Scholar] [CrossRef]
- Chen, D.; Wang, Z.; Guo, D.; Orekhov, V.; Qu, X. Review and Prospect: Deep Learning in Nuclear Magnetic Resonance Spectroscopy. Chem.—A Eur. J. 2020, 26, 10391–10401. [Google Scholar] [CrossRef] [Green Version]
- Cobas, C. NMR signal processing, prediction, and structure verification with machine learning techniques. Magn. Reson. Chem. 2020, 58, 512–519. [Google Scholar] [CrossRef]
- Helin, R.; Indahl, U.G.; Tomic, O.; Liland, K.H. On the possible benefits of deep learning for spectral preprocessing. J. Chemom. 2022, 26, e3374. [Google Scholar] [CrossRef]
- Silverstein, R.M.; Webster, F.X.; Kiemle, D.J.; Bryce, D.L. Spectrometric Identification of Organic Compounds, 8th ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Bisht, B.; Kumar, V.; Gururani, P.; Tomar, M.S.; Nanda, M.; Vlaskin, M.S.; Kumar, S.; Kurbatova, A. The potential of nuclear magnetic resonance (NMR) in metabolomics and lipidomics of microalgae- a review. Arch. Biochem. Biophys. 2021, 710, 108987. [Google Scholar] [CrossRef]
- Holmes, E.; Nicholls, A.W.; Lindon, J.C.; Connor, S.C.; Connelly, J.C.; Haselden, J.N.; Damment, S.J.P.; Spraul, M.; Neidig, P.; Nicholson, J.K. Chemometric Models for Toxicity Classification Based on NMR Spectra of Biofluids. Chem. Res. Toxicol. 2000, 13, 471–478. [Google Scholar] [CrossRef]
- Lindon, J.C.; Nicholson, J.K.; Holmes, E.; Everett, J.R. Metabonomics: Metabolic processes studied by NMR spectroscopy of biofluids. Concepts Magn. Reson. 2000, 12, 289–320. [Google Scholar] [CrossRef]
- Giraudeau, P.; Silvestre, V.; Akoka, S. Optimizing water suppression for quantitative NMR-based metabolomics: A tutorial review. Metabolomics 2015, 11, 1041–1055. [Google Scholar] [CrossRef]
- Kostidis, S.; Addie, R.D.; Morreau, H.; Mayboroda, O.A.; Giera, M. Quantitative NMR analysis of intra- and extracellular metabolism of mammalian cells: A tutorial. Anal. Chim. Acta 2017, 980, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Wider, G.; Dreier, L. Measuring Protein Concentrations by NMR Spectroscopy. J. Am. Chem. Soc. 2006, 128, 2571–2576. [Google Scholar] [CrossRef] [PubMed]
- Akoka, S.; Barantin, L.; Trierweiler, M. Concentration Measurement by Proton NMR Using the ERETIC Method. Anal. Chem. 1999, 71, 2554–2557. [Google Scholar] [CrossRef] [PubMed]
- Bharti, S.K.; Roy, R. Quantitative 1H NMR spectroscopy. TrAC Trends Anal. Chem. 2012, 35, 5–26. [Google Scholar] [CrossRef]
- Farrant, R.D.; Hollerton, J.C.; Lynn, S.M.; Provera, S.; Sidebottom, P.J.; Upton, R.J. NMR quantification using an artificial signal. Magn. Reson. Chem. 2010, 48, 753–762. [Google Scholar] [CrossRef]
- Crockford, D.J.; Keun, H.C.; Smith, L.M.; Holmes, E.; Nicholson, J.K. Curve-Fitting Method for Direct Quantitation of Compounds in Complex Biological Mixtures Using 1H NMR: Application in Metabonomic Toxicology Studies. Anal. Chem. 2005, 77, 4556–4562. [Google Scholar] [CrossRef]
- Singh, A.; Prakash, V.; Gupta, N.; Kumar, A.; Kant, R.; Kumar, D. Serum Metabolic Disturbances in Lung Cancer Investigated through an Elaborative NMR-Based Serum Metabolomics Approach. ACS Omega 2022, 7, 5510–5520. [Google Scholar] [CrossRef]






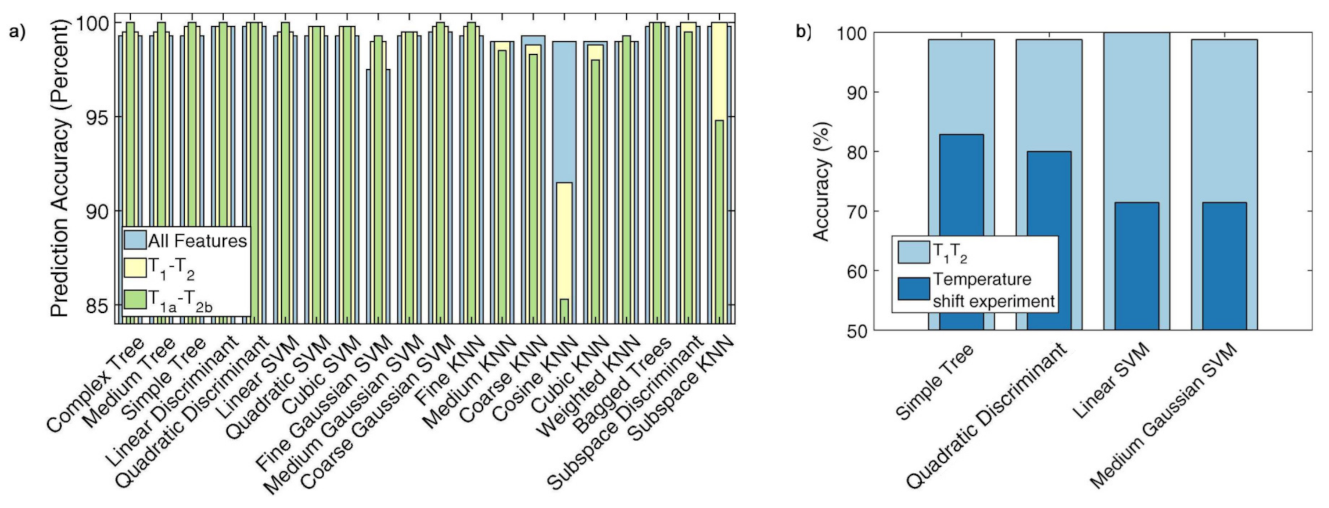


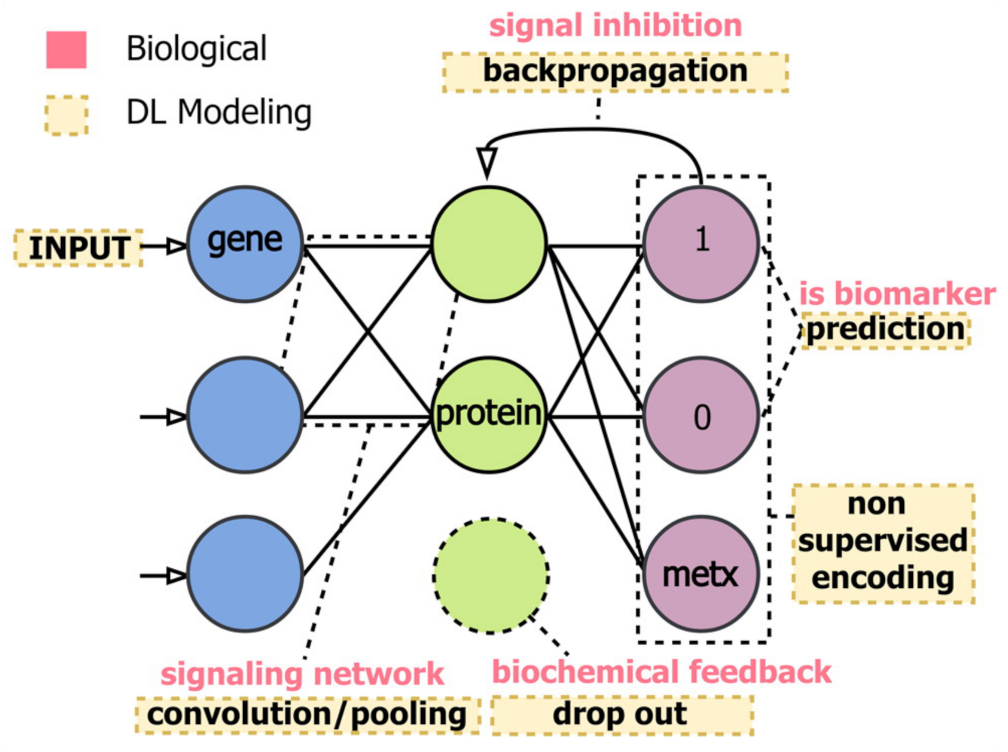
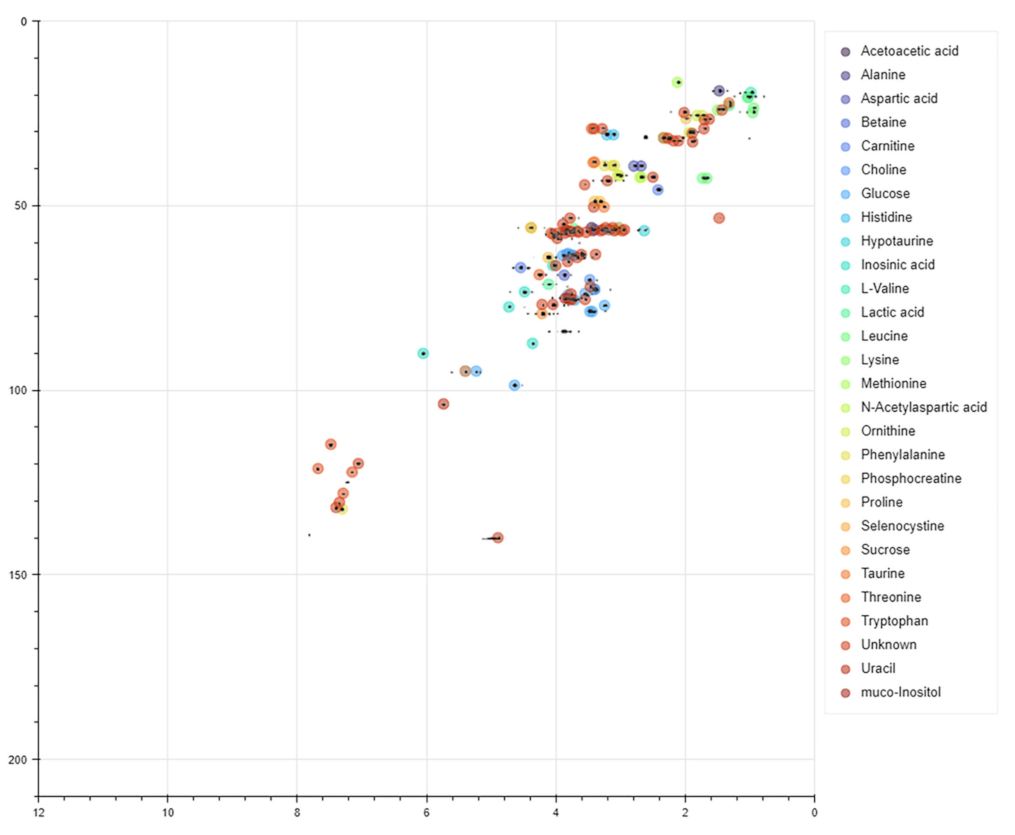
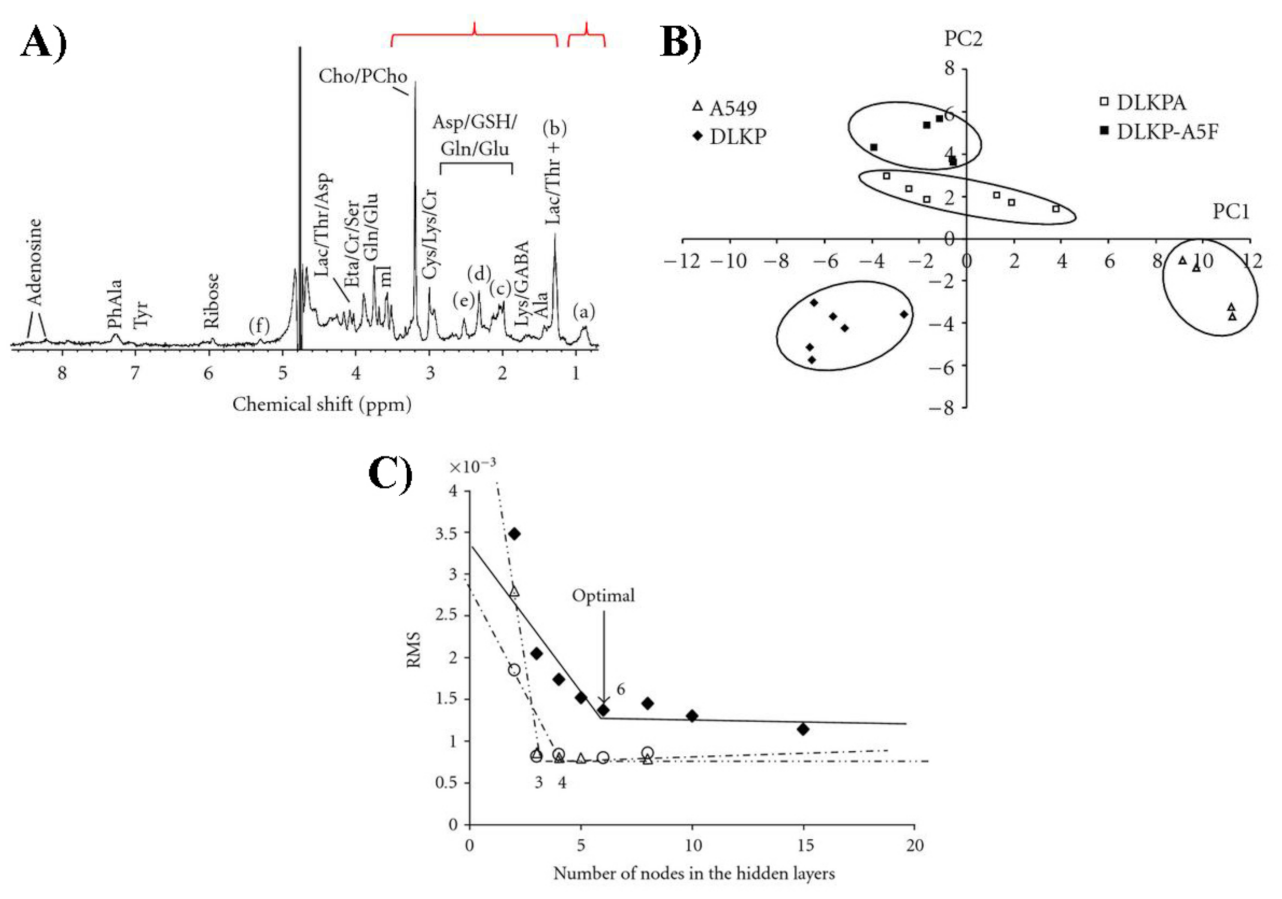
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corsaro, C.; Vasi, S.; Neri, F.; Mezzasalma, A.M.; Neri, G.; Fazio, E. NMR in Metabolomics: From Conventional Statistics to Machine Learning and Neural Network Approaches. Appl. Sci. 2022, 12, 2824. https://doi.org/10.3390/app12062824
Corsaro C, Vasi S, Neri F, Mezzasalma AM, Neri G, Fazio E. NMR in Metabolomics: From Conventional Statistics to Machine Learning and Neural Network Approaches. Applied Sciences. 2022; 12(6):2824. https://doi.org/10.3390/app12062824
Chicago/Turabian StyleCorsaro, Carmelo, Sebastiano Vasi, Fortunato Neri, Angela Maria Mezzasalma, Giulia Neri, and Enza Fazio. 2022. "NMR in Metabolomics: From Conventional Statistics to Machine Learning and Neural Network Approaches" Applied Sciences 12, no. 6: 2824. https://doi.org/10.3390/app12062824
APA StyleCorsaro, C., Vasi, S., Neri, F., Mezzasalma, A. M., Neri, G., & Fazio, E. (2022). NMR in Metabolomics: From Conventional Statistics to Machine Learning and Neural Network Approaches. Applied Sciences, 12(6), 2824. https://doi.org/10.3390/app12062824










