Sensitivity Analysis for Transient Thermal Problems Using the Complex-Variable Finite Element Method

Abstract

Solving transient heat transfer equations is required to understand the evolution of temperature and heat flux. This physics is highly dependent on the materials and environmental conditions. If these factors change with time and temperature, the process becomes nonlinear and numerical methods are required to predict the thermal response. Numerical tools are even more relevant when the number of parameters influencing the model is large, and it is necessary to isolate the most influential variables. In this regard, sensitivity analysis can be conducted to increase the process understanding and identify those variables. Here, we combine the complex-variable differentiation theory with the finite element formulation for transient heat transfer, allowing one to compute efficient and accurate first-order sensitivities. Although this approach takes advantage of complex algebra to calculate sensitivities, the method is implemented with real-variable solvers, facilitating the application within commercial software. We present this new methodology in a numerical example using the commercial software Abaqus. The calculation of sensitivities for the temperature and heat flux with respect to temperature-dependent material properties, boundary conditions, geometric parameters, and time are demonstrated. To highlight, the new sensitivity method showed step-size independence, mesh perturbation independence, and reduced computational time contrasting traditional sensitivity analysis methods such as finite differentiation.

1. Introduction

The physics of transient heat transfer allows one to evaluate the dynamics of energy movements for bodies subjected to changes in temperature, enabling the analysis of the heat flux, temperature history, and temperature rate of different processes. Transient heat transfer problems have significant applications in food processing [1,2], alternative energies [3,4], oil and gas [5], metallurgical processes [6,7], metallography [8,9], infrastructure materials [10,11], and electronics and semiconductor cooling [12,13,14], among others. These applications require analysis of multiple parameters, e.g., time-dependent boundary conditions [15], temperature-dependent thermo-mechanical properties [16,17], and evolving geometries [18] to guide the design of components.

Experimental, analytical, and numerical approaches have been proposed to model transient heat transfer processes. In the experimental approach, level values of the inputs are set to generate random and independent experimental runs. This approach allows the empirical models to capture the dynamic characteristics of a thermal problem regardless of its complexity [19]. It has been used to optimize operational parameters of radiation heat exchange materials [20], induction heating [21], heat treatments [22], sensor design and calibration [23,24], cooling devices [25,26], and electronics refrigeration [27]. However, when the processes of interest involve many parameters, and the factors are prone to uncontrollable changes (e.g., uncontrolled room conditions), the experimental approach becomes time-consuming and expensive, limiting its application.

Approximations for specific processes can be obtained using simplified analytical solutions for the heat diffusion equation for plates [28], walls [29], cylinders [30,31], or spheres [32] under temperature, heat flux, or periodic heating [29]. For instance, predictions in the thermal profile of a plate due to a moving heat source can be approximated by this method [33]. However, explicit analytical solutions are uncommon when systems are large, complex, and time-dependent. The approximations based on simplified models lead to significant errors. As a result, numerical models such as the finite element method (FEM), finite-difference methods, and boundary element methods are popular for solving transient heat transfer problems due to their flexibility and versatility. These numerical methods have been used to approximate the solution of the heat diffusion equation in large and complex problems such as the analysis of fractal piping design [34], phase change materials [35], enhanced surfaces [36], heat exchangers [37], heat sinks [38] and additive manufacturing [39,40], among others. In addition, these and other numerical techniques have been used to study the rate of change of temperature to time in crystallization [2,41], microstructural evolution [42], and superconducting devices [43].

Regardless of the modeling technique, the more elaborate the model, the more challenging it is to track the effects of the input variables on the outputs of the models. Sensitivity analysis is a technique to determine the interactions among the input parameters in a model. For instance, an output could be insensitive to a specific input but highly sensitive to a combination of that input with other parameters in the model. Sensitivity analysis is also used to quantify the influence of these parameters on the model response [44]. In sensitivity analysis, each of the inputs is represented by sensitivity coefficients given by the partial derivative of the output of interest with respect to each input [19,23,24,45,46,47,48,49,50]. The traditional methods to obtain sensitivities are hand-coded analytical differentiation [44], symbolic differentiation [51], automatic differentiation [52], and finite differentiation (FD) [44]. Hand-coded analytical and symbolic differentiation are similar methods as both are exact and rely on analytical models. However, in the hand-code differentiation, the sensitivities are obtained by hand procedures and typed directly in the code. These make the method error-prone, time-consuming to develop and code, and challenging for implicit models. In contrast, symbolic differentiation generates explicit symbolic expressions of explicit analytical models and uses computational symbolic packages to obtain the sensitivities automatically [53]. Automatic differentiation or algorithmic differentiation takes advantage of the chain rule and function composition to sequentially decompose a function in the root variables and its operations in the function. Then the recurrent evaluation of the decomposition in the chain rule of the function allows the algorithm to recover the sensitivity using forward, backward, or adjoint schemes. The formulation of the method makes the algorithm slow and memory demanding [52,53,54]. Another traditional method for obtaining the sensitivities of a model is the numerical FD. This technique has been widely applied in sensitivity analysis in many fields because it is easy to implement as it only requires multiple model evaluations with a small step size for the analyzed variable. Nevertheless, when the model becomes nonlinear, obtaining high precision sensitivities using FD is challenging because the method is subject to computational subtraction cancellation errors and truncation errors [55,56]. In addition, the step size for each input to the model is problem dependent and usually requires a convergence analysis to select it for each of the inputs. Moreover, multiple evaluations of the model are required to calculate each parameter sensitivity of interest, making the technique disk memory intensive and time demanding [54].

An alternative approach for the numerical calculation of sensitivities is the Complex Taylor Series Expansion Method (CTSE) [57]. Unlike finite differencing, CTSE does not require the difference of two analyses. Instead, the derivatives are computed using a small perturbation along the imaginary axis of the input parameters, evaluating the function, extracting the imaginary part of the outputs, and dividing by the perturbation magnitude (more details shown in Section 2.2). In this context, since no subtraction operations are needed, no subtractive error is generated, and the computed sensitivity is highly accurate [56]. CTSE can be incorporated in partial differential equation solvers based on techniques such as the finite-differences method [58], the boundary element method [59], and the FEM [60,61].

The combination between CTSE and analytical modeling has been successfully applied to transient heat transfer analysis. For instance, Jayapragasam et al. [53] showed a sensitivity study for a 1D transient heat conduction problem. The authors compared analytical differentiation, FD, and CTSE methodologies for calculating sensitivities and concluded that CTSE provides certain advantages over other methods, such as near analytical accuracy, step size independency, reduction of computing time, and elimination of the subtractive cancelation problem. Similarly, CTSE has been applied to calculate sensitivities to solve inverse heat transfer problems using the finite-differences method. In this application, the sensitivities calculated using CTSE were used to guide the optimization algorithms to recover the values of temperature-dependent thermal properties and thermal boundary conditions [62,63,64]. Moreover, some authors have reported improved computational times and convergence rates in the minimization algorithms when CTSE is used over other numerical differentiation algorithms [65,66,67].

This work presents and verifies a methodology that integrates CTSE and the transient heat transfer FEM. We call this method the transient heat transfer complex-variable finite element method or Transient Thermal ZFEM. This methodology allows the calculation of faster and more accurate sensitivities of heat flux and temperature history with respect to constant and temperature-dependent thermo-physical properties, boundary conditions, initial conditions, time, and geometry than FD. Moreover, although the essence of the method takes advantage of complex variable operations to calculate sensitivities, it is demonstrated how this method can also be applied in real-variable solvers. A sensitivity analysis for a fin problem under 1D transient thermal conditions was performed to demonstrate our methodology. This device, as represented in Figure 1a, was selected due to the availability of an analytical solution with constant parameters and the relevance of the problem in thermal systems. Fins are present in almost all heat transfer applications such as engines, computers and electronics, and cooling systems. It is worth highlighting that ZFEM has been verified in a number of application areas such as elastic analysis [60], fatigue [68,69], fracture mechanics [61,70,71,72,73], plasticity [74], residual stresses [75], creep [76], variance estimates [77], reliability-based design optimization [78], steady-state thermo-elasticity [79], structural dynamics [80], and periodic material design [81]. However, this is the first demonstration of ZFEM in transient heat transfer problems.

The outline for the rest of the paper is as follows: Section 2 presents the background related to the transient heat transfer FEM and CTSE. Section 3 presents our new methodology that integrates FEM and CTSE to form the Transient Thermal ZFEM methodology. Section 4 demonstrates the application of the methodology on the analysis of the fin problem considering thermal transient conditions for constant parameters (e.g., constant material properties and boundary conditions, see Figure 1). The results are compared against analytical equations. Subsequently, we analyzed the case of temperature-dependent specific heat, and the results were compared against FD. Finally, the conclusions and future work are presented in Section 5.

2. Background

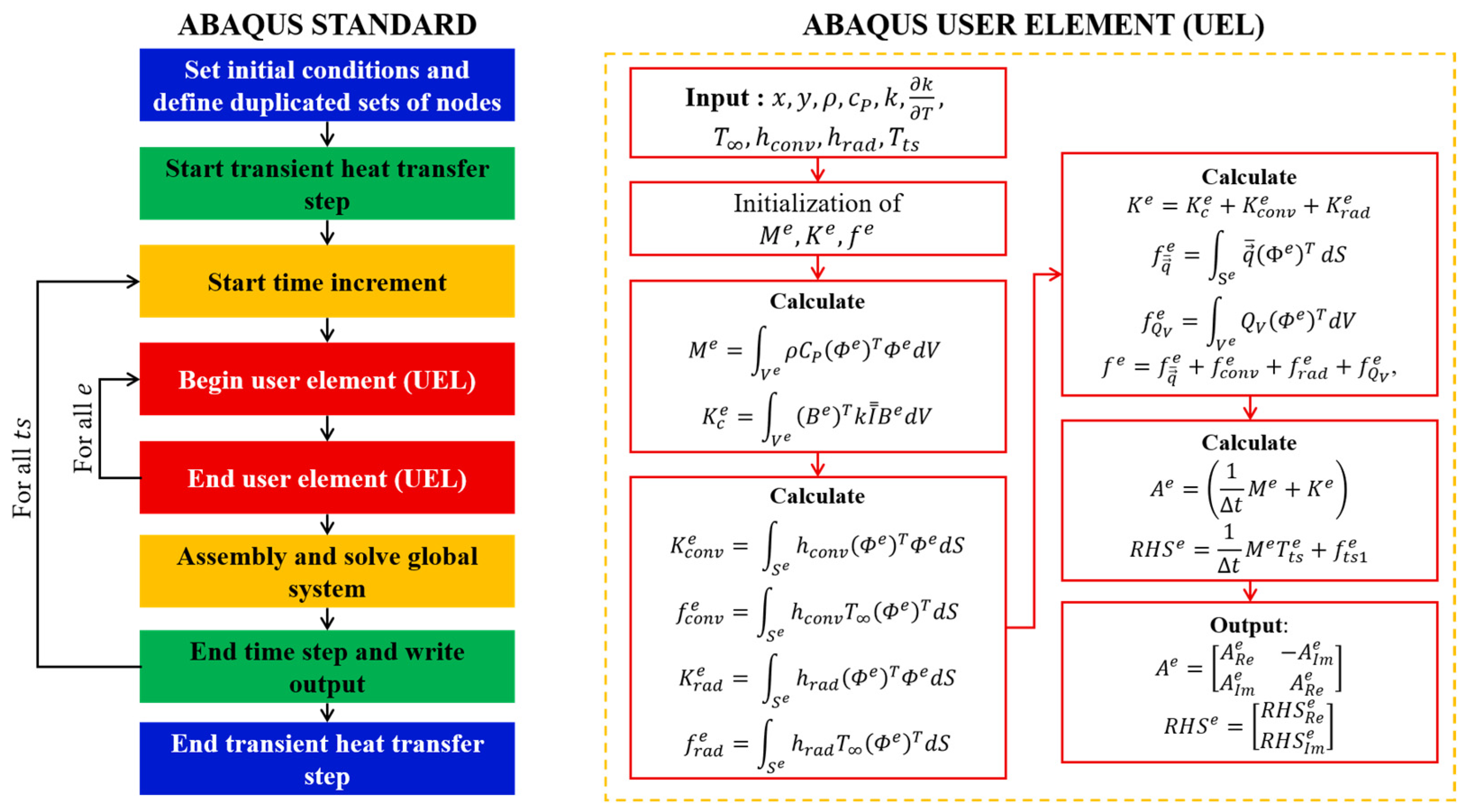
2.1. Finite Element Method Formulation for Transient Heat Transfer Problems

The governing equation for transient heat transfer for a solid body with unit length, isotropic thermal conductivity $k\left[\mathrm{W}/\mathrm{mK}\right]$, is presented in Equation (1), where $\rho \left[\mathrm{kg}/{\mathrm{m}}^3\right]$ corresponds to the density, $C_P\left[\mathrm{J}/\mathrm{kg}\mathrm{K}\right]$ the specific heat, $\dot{Q_V}\left[\mathrm{W}/{\mathrm{m}}^3\right]$ is the volumetric internal heat generation rate, $I$ corresponds to the identity matrix, and $\nabla$ is the nabla differential operator.

$$\rho C_P\frac{\partial T\left(x,y,z,t\right)}{\partial t}=-kI{\nabla }^T\nabla T\left(x,y,z,t\right)+\dot{Q_V}$$

(1)

$$T\left(x,y,z,0\right)=T_0$$

(2)

$$T\left(x_S,y_S,z_S,t\right)=T_S=\overline{T}$$

(3)

$$\nabla T\left(x_S,y_S,z_S,t\right)=\nabla T_S=\overline{\overrightarrow{q}}$$

(4)

$$\begin{gathered} \nabla T\left(x_S,y_S,z_S,t\right)=\nabla T_S=h_U\left(T_{\infty }-T_S\right) \\ {h}_U=h_{conv}+h_{rad} \\ {h}_{rad}=ϵ\sigma \left(T_{\infty }^2+T_S^2\right)\left(T_{\infty }+T_S\right) \end{gathered}$$

(5)

This equation allows one to find a solution for the temperature $T\left(x,y,z,t\right)\left[\mathrm{K}\right]$ at time $t\left[\mathrm{s}\right]$ and any position $\left(x,y,z\right)\left[\mathrm{m}\right]$ in a geometric domain. To solve Equation (1), a time-dependent temperature condition, e.g., the initial temperature ($T_0\left[\mathrm{K}\right]$) in Equation (2), and surface boundary conditions are required. Surface conditions are denoted by the sub-index $S$ in Equations (3)–(5). The surface boundary conditions are predefined temperatures ($\overline{T}\left[\mathrm{K}\right]$, in Equation (3)) and predefined heat fluxes ($\overline{\overrightarrow{q}}\left[\mathrm{W}/{\mathrm{m}}^2\right]$, in Equation (4)). For example, Figure 1a represents a fin with a predefined wall temperature ($\overline{T}=T_W$), and insulation at the tip ($\overline{\overrightarrow{q}}=0\mathrm{W}/{\mathrm{m}}^2$). Heat fluxes can be position-dependent, time-dependent, or surface temperature-dependent, as in convection and radiation conditions (Equation (5)). Here, $ϵ$ is the material’s surface emissivity, $\sigma =5.67\times {10}^{-8}\mathrm{W}/{\mathrm{m}}^2{\mathrm{K}}^4$ is the Stefan-Boltzmann constant. If there are multiple boundary conditions on the same surface, superposition is used for the analysis. For instance, if radiation and convection boundary conditions are applied over the same surface, the global heat transfer coefficient $h_U\left[\mathrm{W}/{\mathrm{m}}^2\mathrm{K}\right]$ is used to represent the contribution from both heat transfer mechanisms, as shown in Equation (5). Here, $T_{\infty }\left[\mathrm{K}\right]$ is the room temperature, $h_{conv}\left[\mathrm{W}/{\mathrm{m}}^2\mathrm{K}\right]$ is the convection heat transfer coefficient, and $h_{rad}$ is the radiation heat transfer. When $T_0$ and $T_{\infty }$ are similar, $h_{rad}\left[\mathrm{W}/{\mathrm{m}}^2\mathrm{K}\right]$ can be treated as a constant by replacing the surface temperature ($T_S$) in Equation (5) by the average temperature among $T_0$ and $T_{\infty }$ [29,32].

Using the finite element method, the representation of the nodal temperatures, $T^e$, in the element is specified by the shape functions, ${\Phi }^e$, given by:

$$T\left(x,y,z,t\right)={\Phi }^e{T}^e={\displaystyle \sum }_{j=1}^n{T}_j^e\cdot {\Phi }_j^e\left(x,y,z,t\right)$$

(6)

where $n$ represents the number of nodes of the element [82]. Combining Equations (1)–(6), we obtain Equation (7), which represents the transient heat transfer FEM formulation for any time step ($ts$). In this equation, $M^e\left[\mathrm{J}/\mathrm{K}\right]$ is the element capacitance matrix, $K_c^e$ $\left[\mathrm{W}/\mathrm{K}\right]$ is the symmetric element conductivity matrix, $K_{h_{conv}}^e\left[\mathrm{W}/\mathrm{K}\right]$ and $K_{h_{rad}}^e\left[\mathrm{W}/\mathrm{K}\right]$ are the asymmetric convective and radiative flux matrixes, respectively. The right-hand side terms include the heat flux vectors $f_{\overline{\overrightarrow{q}}}^e\left[\mathrm{W}\right]$, $f_{conv}^e$ $\left[\mathrm{W}\right]$, $f_{rad}^e$ $\left[\mathrm{W}\right]$, and the volumetric heat generation vector $f_{Q_V}^e$ $\left[\mathrm{W}\right]$ for the element $e$.

$$M^e{\dot{T}}^e+\left(K_c^e+K_{conv}^e+K_{rad}^e\right)T^e=f_{\overline{\overrightarrow{q}}}^e+f_{conv}^e+f_{rad}^e+f_{Q_V}^e$$

(7)

To obtain the temperature history from Equation (7), the generalized Crank-Nicholson method for the time integration recurrence scheme is applied. This integration scheme is obtained by a trapezoidal approximation of the elemental temperature rate ${\dot{T}}^e$ and solving for $T_{ts+1}^e$. Using the substitutions $K^e=K_c^e+K_{conv}^e+K_{rad}^e$ and $f^e=f_{\overline{\overrightarrow{q}}}^e+f_{conv}^e+f_{rad}^e+f_{Q_V}^e$, the time integration scheme is given by [82]:

$$\left(\frac{1}{\mathsf{\Delta }t}{M}^e+\beta K^e\right)T_{ts+1}^e=\left(\frac{1}{\mathsf{\Delta }t}{M}^e-\left(1-\beta \right)K^e\right)T_{ts}^e+\left(1-\beta \right)f_{ts}^e+\beta f_{ts+1}^e$$

(8)

where $\mathsf{\Delta }t$ is the time increment and the temperature of the time $ts+1$ is obtained based on the values of $M^e$, $K^e$, $T^e$, and $f_{ts}^e$, and the next value of $f_{ts+1}^e$. For linear problems, $f_{\overline{\overrightarrow{q}}}^e,f_{conv}^e,f_{rad}^e,f_{Q_V}^e$ are constant, then the flux vectors $f_{ts}^e=f_{ts+1}^e$, therefore $\left(1-\beta \right)f_{ts}^e+\beta f_{ts+1}^e=f_{ts}^e$. Setting $\beta =1$ in Equation (8) minimizes numerical integration problems, prevents spurious oscillations, and ensures stability for the solution [82,83]. With this condition, the system of equations becomes the fully implicit system $A^e{T}_{ts+1}^e=RH{S}^e$, where the coefficient matrix for the time increment ($A^e\left[\mathrm{W}/\mathrm{K}\right]$) and the right-hand side of the equation ($RH{S}^e\left[\mathrm{W}\right]$) are defined in Equations (9) and (10), respectively.

$$A^e=\left(\frac{1}{\mathsf{\Delta }t}{M}^e+K^e\right)$$

(9)

$$RH{S}^e=\frac{1}{\mathsf{\Delta }t}{M}^e{T}_{ts}^e+f_{ts}^e$$

(10)

It is noted that when 2D conditions are assumed, the FEM formulation for 2D elements considers that the temperature gradient in the out-of-plane direction is null. For instance, if the problem is modeled in the $xy$ plane, then $\partial \mathrm{T}/\partial \mathrm{z}=0$. This implies that the heat flux in the $\mathrm{z}$-direction is zero, and the element is insulated along with the front and back faces. To overcome this issue, Morville et al. [84] and La Batut et al. [85] proposed the use of the volumetric sink term ($Q_V$ in Equation (1)) to enhance the heat transfer in a 2D model. $Q_V$ is defined in Equation (11) with $U_V\left[\left(\mathrm{W}/\left({\mathrm{m}}^2\mathrm{K}\right)\right)/\mathrm{m}\right]$ corresponding to the heat transfer coefficient per unit of thickness. In this equation, the temperature-dependent heat sink dissipates more heat as the temperature difference increases. This is similar to having surface convection/radiation heat transfer in the out-of-plane direction. In addition, $U_V$ should be tuned to minimize the error of the temperature response of the FEM and a reference solution.

$$Q_V=-U_V\left(T-T_{\infty }\right)$$

(11)

2.2. Numerical Differentiation by CTSE

CTSE is used to calculate the numerical sensitivities of any function $g\left(\varphi \right)$ with respect to any input parameter $\varphi$. To obtain the sensitivity $g^{\left(1\right)}\left(\varphi \right)=\partial g/\partial \varphi$, where the superscript indicates the order of differentiation, $\varphi$ is perturbed by a small amount $h$ (i.e., $h\le {10}^{-10}$ [61]) in the imaginary axis. Then, the evaluation of the function with the complex input, $g\left(\varphi +ih\right)$, is obtained by considering a Taylor’s series expansion as shown in Equation (12). Truncating the infinite series to the first-order term of $h$ and solving for the first-order sensitivity $g^{\left(1\right)}\left(\varphi \right)$, Equation (13) presents the formulation for the numerical sensitivity of the function $g$ for the parameter of interest $\varphi$ [56]. If $h$ is small enough, the truncation of the higher-order terms is accurate because the powers of $h$ of order two and higher will be approximately zero. Moreover, the original response of the solution variable is returned unchanged in the real component.

$$g\left(\varphi +ih\right)\approx g\left(\varphi \right)+g^{\left(1\right)}\left(\varphi \right)\frac{ih}{1!}+g^{\left(2\right)}\left(\varphi \right)\frac{{\left(ih\right)}^2}{2!}+\dots$$

(12)

$$g^{\left(1\right)}\left(\varphi \right)=\frac{\partial g\left(\varphi \right)}{\partial \varphi }\approx \frac{Im\left[g\left(\varphi +ih\right)\right]}{h}$$

(13)

The sensitivities obtained from Equation (13) have the units of the output parameter ($g$) divided by the perturbed parameter ($\varphi$). To simplify the analysis of sensitivities, it is recommended to transform them into relative coefficients [45]. The calculation of these relative coefficients can be achieved by the application of Equation (14), where the relative sensitivities of $g$ with respect to the parameter of interest $\varphi$ or $S_{\varphi }^g$, have the same units of $g$.

$$S_{\varphi }^g\left(x,y,z,t\right)=\left|\varphi \right|\frac{\partial g\left(x,y,z,t\right)}{\partial \varphi }$$

(14)

On the other hand, when analyzing sensitivities regarding $T_{\infty },T_0$, and $\overline{T}$ in heat transfer problems, it is common to normalize these sensitivities using the maximum temperature difference in the system ($\mathsf{\Delta }{T}_{max}\left[\mathrm{K}\right]$) instead of the values of $T_{\infty },T_0$, or $\overline{T}$. For example, in the extended surface of Figure 1a, $\left|\varphi \right|=\left|\mathsf{\Delta }{T}_{max}\right|=\left|T_W-T_{\infty }\right|$ [32]. This is commonly used to normalize temperature differences in thermal systems because the sensitivity to those temperatures can be explained as the change of the output $g$ due to a small change Δ in $T_{\infty },T_0$, or $\overline{T}$.

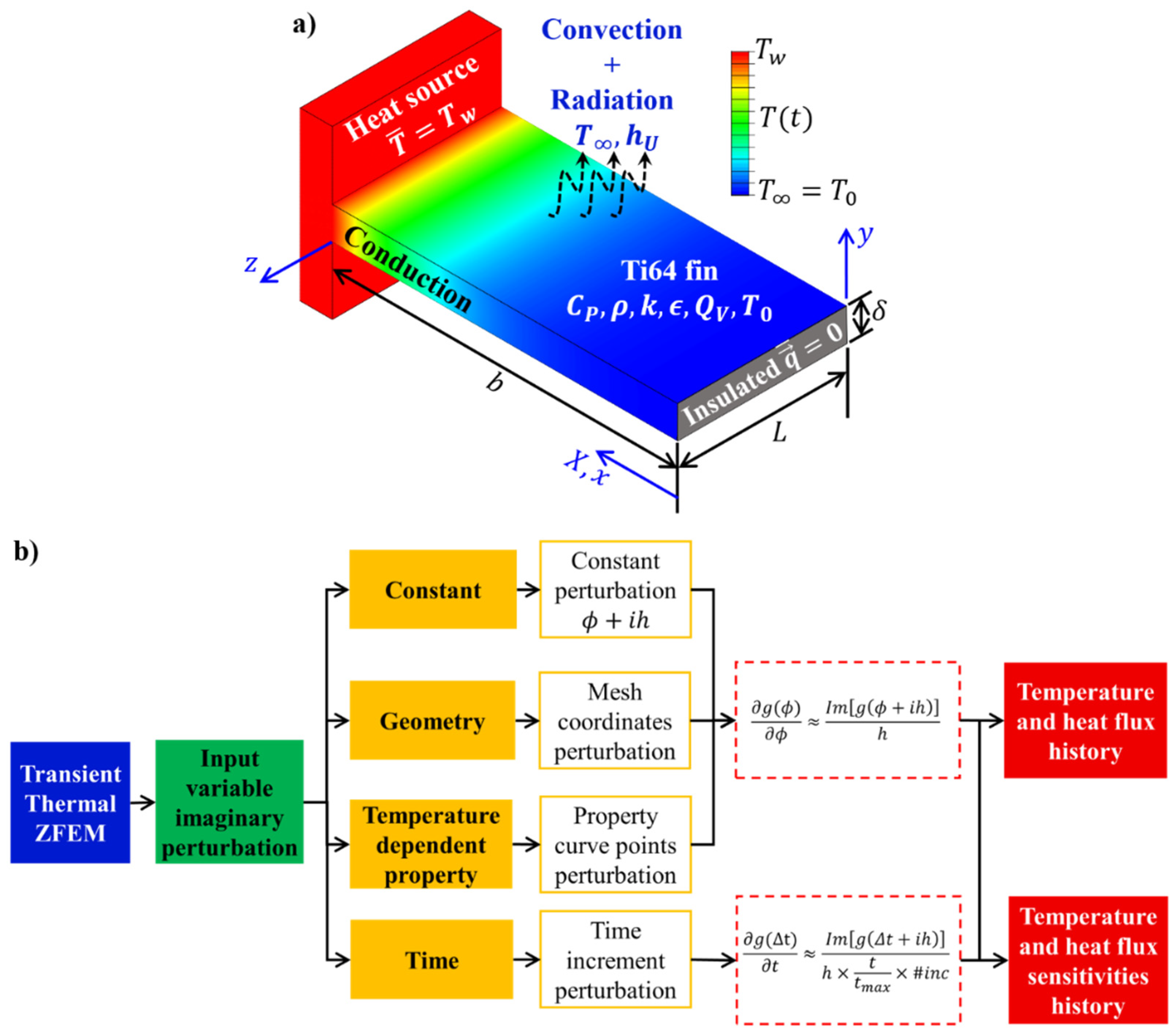
3. Sensitivity Analysis in Transient Heat Transfer Problems Using Transient Thermal ZFEM

To obtain sensitivity information for transient heat transfer problems, we propose a methodology that combines the solution of the transient heat transfer equation using the finite element method with the Complex Taylor Series Expansion. We call this methodology Transient Thermal ZFEM, and the main concepts are presented in Figure 1b. To begin, all of the components in the FEM formulation, such as nodal coordinates, material properties, and boundary conditions, become complex-valued variables [79]. Then, to obtain sensitivities of $T$ or any other output of the Transient Thermal ZFEM model with respect to the input parameters $\varphi$, different perturbation schemes for $\varphi$ should be followed depending on the kind of input, as follows:

• Constant inputs: to obtain sensitivities with respect to the input variables in the model that are constant, the procedure presented in Equation (13) can be applied with only a small imaginary perturbation $h$ applied to the variable of interest. For instance, to obtain sensitivities with respect to $T_{\infty }$, we evaluated the model is evaluated with a value of $T_{\infty }^{*}=T_{\infty }\left(1+hi\right)$.
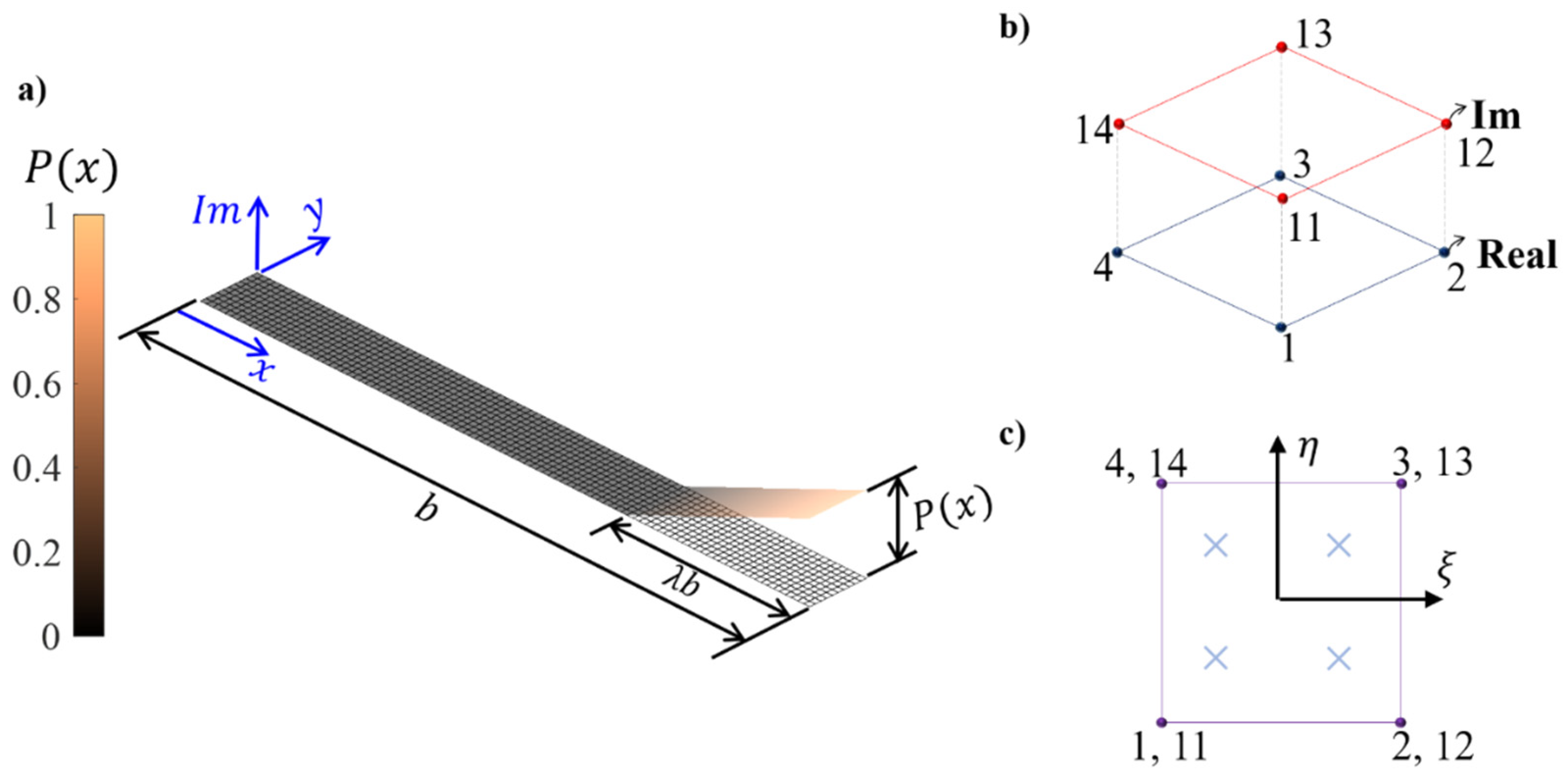
• Geometry sensitivities: to obtain sensitivities with respect to geometric shapes, perturbations to the geometry are required. In Transient Thermal ZFEM, the domain shape is represented by the nodal coordinates. As previously mentioned, the nodal coordinates are converted to complex-variable. For reference, Figure 2a shows a mesh where the nodal coordinates are in the plane xy, and the out of plane represents the imaginary component $Im$. Moreover, Figure 2b shows the representation of a planar element with real and imaginary coordinates. To obtain sensitivities with respect to the geometry, the imaginary component of the nodal coordinates should be perturbed according to the following guidelines: First, the direction of the perturbation should be selected. For instance, considering sensitivities with respect to the length $b\left[\mathrm{m}\right]$ in the fin problem (see Figure 2a), as $b$ is parallel to the $x\text{-}\mathrm{axis}$ and its boundaries normal to that axis, the perturbation should be applied by translating the imaginary nodal coordinates along the direction of positive $Im$ axis. Second, a fraction of the nodes ($\lambda$) should be selected in the mesh to be perturbed. As presented in Figure 2a, $\lambda$ can take values from zero to one. The selected value for this fraction depends on the balance between precision and computational time. This parameter is problem-dependent and could be determined with convergence analysis. However, previous works have shown that considering a value of $\lambda$ large enough to perturb at least two elements normal to the boundary is enough for most problems [60,71,86,87]. Next, a perturbation function $P\left(x\right)$ is selected. In Figure 2a a linear $P\left(x\right)$ is considered. This function has a minimum value of zero and a maximum value of one. The maximum and minimum values of $P\left(x\right)$ are located along the geometric boundaries of dimension $\lambda b$. Finally, the fraction of the imaginary coordinates of the nodes are shifted in the selected imaginary direction, a magnitude $h\times P\left(x\right)$, and the sensitivity is obtained following Equation (13). An example of this perturbation scheme is presented in Figure 2a, where the wireframe mesh presents the real components of the nodal coordinates and surface pointing out of the plane, representing the perturbation on the imaginary axis.
• Temperature-dependent properties: to obtain sensitivities with respect to temperature-dependent properties, the properties should be defined for any given temperature; therefore, fitting or interpolating from experimental values is necessary. After fitting, the perturbation is applied by shifting $h$ units in the imaginary axis of the resulting temperature-dependent curve, and the perturbed function is used to perform the calculations as usual. This procedure is analogous to the perturbation of a constant parameter. Finally, Equation (13). is used to obtain the numerical sensitivities. An example of the fin problem is presented in Section 4.3.
• Time sensitivities: to obtain sensitivities with respect to time, the time increment $\mathsf{\Delta }t$ is perturbed by a value $h$ in the imaginary component. Then the standard solution method is applied. After the model is solved, the time sensitivities are calculated using Equation (15). The time function in the denominator of Equation (15) compared to Equation (13) is a consequence of the numerical time integration of the imaginary perturbation associated $\mathsf{\Delta }t$ where $\#inc$ is the total number of converged times increments in the solution. A convergence study should be performed on the time increment to determine the correct balance between computational time and accuracy.

  $$\frac{\partial g}{\partial t}\approx \frac{Im\left[g\left(\mathsf{\Delta }t+hi\right)\right]}{h\times \frac{t}{t_{max}}\times \#inc}$$

  (15)

Solution of Complex-Valued System of Equations: Cauchy-Riemann Matrix Notation

As most numerical packages do not support complex variable linear algebra operations, it is possible to take advantage of the multicomplex algebra isomorphism to represent any complex number as a matrix with all real numbers [79]. This representation of complex numbers is known as the Cauchy-Riemann (CR) matrix notation and allows for the use of matrix functions and arithmetic operations as homologous of the operations between complex numbers [88].

Consider the complex-variable $A^e$ matrix and $RH{S}^e$ vector in Equations (9) and (10), respectively, these quantities can be represented as the CR matrices following Equation (16) and CR vectors following Equation (17). This representation implies the addition of extra degrees of freedom in the Transient Thermal ZFEM model. Consequently, a duplicated mesh approach is used to consider the extra degrees of freedom provided by the sensitivity information in the imaginary components. In Figure 2b, a 2D Transient Thermal ZFEM element with the duplicated mesh approach is presented. In this case, the original mesh of the FEM (nodes 1 to 4) will carry the real information, while the secondary or imaginary mesh (nodes 11 to 14) contains the sensitivity of the output with respect to the perturbed input. A four-node—four-quadrature point complex 2D isoparametric element is shown in Figure 2c.

$$A^e=A_{Re}^e+i{A}_{Im}^e=\left[\begin{array}{cc}{A}_{Re}^e& -A_{Im}^e\\ A_{Im}^e& A_{Re}^e\end{array}\right]$$

(16)

$$RH{S}^e=RH{S}_{Re}^e+iRH{S}_{Im}^e=\left[\begin{array}{c}RH{S}_{Re}^e\\ RH{S}_{Im}^e\end{array}\right]$$

(17)

4. Numerical Example: Transient Fin Problem

We implemented the method in 2D User Element Subroutine (UEL) within the commercial finite element analysis software Abaqus to demonstrate the performance of the Transient Thermal ZFEM method. Abaqus cannot solve systems with complex variables directly because its built-in equation solver is made for real-valued components. As a result, the complex-variable right-hand side of the element ($RH{S}^e$), and the complex-variable coefficient matrix for the element ($A^e$) are transformed to the Cauchy-Riemann form of all real numbers before returning the results to Abaqus. Then, the global system of equations is assembled internally by Abaqus and solved for each time increment. This process is presented in the flowchart of Figure 3, and the full version of the UEL is presented in the Supplementary Material.

The method was verified by analyzing the heat transfer behavior for the thin fin shown in Figure 1a. The geometry of the fin is characterized by the length $b$, height $\delta$, and thickness $L$, and it is made from a material with conductivity $k$, density $\rho$, and specific heat $C_P$. The results computed using ZFEM were compared with the analytical solution using symbolic differentiation and Abaqus simulation with 2D DC2D4 elements and finite differentiation. The errors were measured using the Normalized Root Mean Square Error (NRMSE) metric as described in Equation (18). In this equation, $o$ corresponds to the order of the sensitivity of $g$, $\overline{g^{\left(o\right)}}$ is the reference results, and $\#inc$ is the total number of sampling points which is coincident with the total number of increments in the transient thermal problem.

$$\mathrm{NRMSE}=\frac{1}{\max \left(\overline{g^{\left(o\right)}}\right)-\min \left(\overline{g^{\left(o\right)}}\right)}\sqrt{\frac{{\displaystyle \sum }{\left(\overline{g^{\left(o\right)}}-g^{\left(o\right)}\right)}^2}{\#inc}}$$

(18)

The analytical solution for the temperature as a function of time for the fin problem was obtained by considering the dimensionless parameters for the position $X$ in Equation (19), the time $\tau$ in Equation (20), $N^2$ in Equation (21), ${\lambda }_n$ in Equation (22), the temperature $\theta$ in Equation (23), and by adding the steady-state ${\theta }_{ss}\left({\rm X}\right)$ and the transient solutions ${\theta }_{\tau }\left({\rm X},\tau \right)$ as shown in Equations (24) and (25), respectively [28]. For this solution, it was also assumed that the axis $x$ and $X$ were aligned with the length of the fin, and the fin had an adiabatic tip.

$${\rm X}=\frac{x}{b}$$

(19)

$$\tau =\frac{tk}{b^2\rho C_P}$$

(20)

$$N^2=\frac{2h_U{b}^2}{k\delta }$$

(21)

$${\lambda }_n=\frac{2n-1}{2}\pi$$

(22)

$$\theta =\frac{T-T_{\infty }}{T_W-T_{\infty }}={\theta }_{ss}\left({\rm X}\right)+{\theta }_{\tau }\left({\rm X},\tau \right)$$

(23)

$${\theta }_{ss}\left({\rm X}\right)=\frac{\cosh \left(N{\rm X}\right)}{\cosh \left(N\right)}$$

(24)

$${\theta }_{\tau }\left({\rm X},\tau \right)=2{\displaystyle \sum }_{n=1}^{\infty }{\left(-1\right)}^{n+1}\left(\frac{{\theta }_0}{{\lambda }_n}-\frac{{\lambda }_n^2}{N^2+{\lambda }_n^2}\right)cos\left({\lambda }_n{\rm X}\right)e^{-(N^2+{\lambda }_n^2)\tau }$$

(25)

In this problem, the fin was in thermal equilibrium with the environment at $t=0\mathrm{s}$, meaning that the room temperature ($T_{\infty }$) was equal to the initial temperature ($T_0$). Then, a prescribed temperature $T_w$ was applied at the base of the fin, i.e., $x=b$. As soon as the fin started to heat, energy dissipation occurred due to the film conditions in the top, bottom, back, and front surfaces determined by $T_{\infty }$ and the global heat transfer coefficient $h_U$. In the case of ZFEM and Abaqus built-in models, combined convection and radiation boundary conditions were applied on the top and bottom edges, and $T_w$ was applied to the left edge as depicted in Figure 1a. In addition, enhanced dissipation was considered to obtain the effects of out-of-plane dissipation. The convergence analysis for $U_V$ is presented in Figure 4a, where the optimal was found at $735\left(\mathrm{W}/\left({\mathrm{m}}^2\mathrm{K}\right)\right)/\mathrm{m}$ and is highlighted with the blue marker. The temperature and sensitivity information were extracted from the node located in the centerline of the fin’s tip. For reference, the analytical solution at that point is presented as a solid black line in Figure 4b. The mesh was discretized along with the height, $\delta \left[\mathrm{m}\right]$, using 10 equally spaced elements, and 1000 elements along the length, $b$, and the time increment for the solver was set to $\mathsf{\Delta }t=1\mathrm{s}$. We used convergence analyses to set the values of discretization in space and time. We varied the number of elements in the domain by one order of magnitude up to ${10}^5$ elements. A similar approach was followed for the time discretization up to a maximum of ${10}^4$ time increments. Full details about the convergence analyses are presented in the Supplementary Material.

Using the parameters in

Table 1. Parameters involved in the transient thermal fin problem.

Parameter Type	Parameter of Interest $\left(\mathit{\varphi }\right)$	Value	Units
Material Properties	$k$	$7.1$	$\mathrm{W}/\left(\mathrm{m}\cdot \mathrm{K}\right)$
	$C_p$	$580$	$\mathrm{J}/\left(\mathrm{kg}\cdot \mathrm{K}\right)$
	$\rho$	$4430$	$\mathrm{kg}/{\mathrm{m}}^3$
Boundary Conditions	$h_U$	$114$	$\mathrm{W}/\left({\mathrm{m}}^2\cdot \mathrm{K}\right)$
	$T_{\infty }$	$283$	$\mathrm{K}$
	$T_w$	$389$	$\mathrm{K}$
Initial Conditions	$T_0$	$283$	$\mathrm{K}$
Geometry	$b$	$51$	$\mathrm{mm}$
	$L$	$1$	$\mathrm{m}$
	$\delta$	$4.75$	$\mathrm{mm}$

(obtained from [28]), the analytical dimensionless temperature history, $\left(\theta \right)$, at the fin’s tip $(X=0$) is presented in Figure 4b. In this figure, the analytical $\theta$ history is presented as a solid black line, ${\theta }_{SS}$ as a dashed red line, and the results using the Transient Thermal ZFEM UEL and the built-in Abaqus functions are overlaid using a yellow star and a blue square, respectively. This convention will be preserved for the rest of the results presented in this work. The sampling rate for the figures was every 14 time steps for visualization purposes. From the results presented in Figure 4b, it is noted that as the temperature approaches the steady-state (approximately at $t=350\mathrm{s}$), and the simulations using the Transient Thermal ZFEM UEL and the built-in Abaqus functions match the temperature history of the analytical solution.

Although the Transient Thermal ZFEM method for obtaining sensitivities can be applied to any input variable in the models, out of briefness, the next sections will focus on obtaining sensitivities for the transient behavior of a material property ($k$), a boundary condition ($T_{\infty }$), a geometric parameter ($b$), a temperature dependent-property ($C_P\left(T\right)$), and for the calculation of heating rates ($\partial \theta /\partial t$), which will cover all the perturbation cases described in Section 3. The results for the remaining parameters affecting the fin’s thermal transient behavior are relegated to the Supplementary Material.

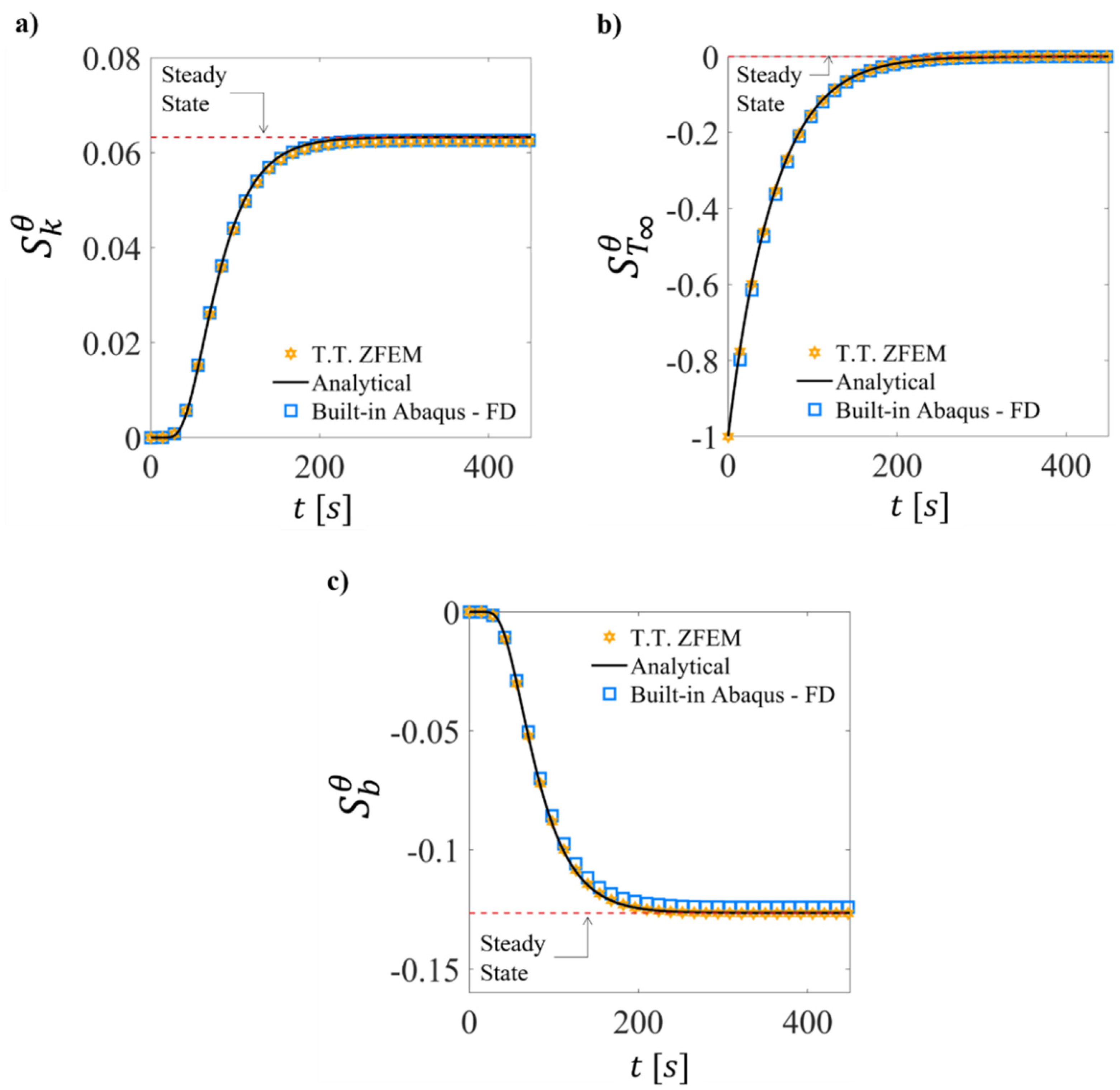
4.1. Sensitivity Analysis of Temperature History

As stated in Section 3, the first step to obtain sensitivities using Transient Thermal ZFEM is to apply a perturbation, h, to the variable of interest. While many other references have shown the step size independence for CTSE when applied in other fields, a step size analysis was conducted for transient thermal analysis to verify previous findings. In addition, the optimal step size for FD was also computed for comparison purposes.

Considering the analytical equations as a reference for the calculation of the error, the NRMSE for the responses as a function of the step size for Transient Thermal ZFEM and FD calculated with built-in Abaqus functions is presented in Figure 5a, using continuous and dashed lines, respectively. All the FD results were obtained by using a forward differentiation scheme and first-order accuracy, which is analogous to applying a positive imaginary perturbation in the CTSE method integrated into Transient Thermal ZFEM. In agreement with previous literature about numerical sensitivities [89], for values above $h\times \varphi$ with $h={10}^{-4}$, the truncation error completely cancels the precision of the sensitivity response in the FD method. However, the Transient Thermal ZFEM is completely insensitive to the step size for the analyzed input parameters. The change in the trend for the dashed red and dashed green lines in FD is related to a shift in the dominance of the truncation error to round-off error. This analysis highlights one of the main advantages of the Transient Thermal ZFEM over the regular FD in that CTSE is dramatically less prone to step size inaccuracies. Based on the perturbation step analysis study, the rest of the results presented herein were calculated using $h={10}^{-10}\varphi$ for the Transient Thermal ZFEM and $h=1\%\varphi$ for FD.

For geometrical perturbations, it is required to perturb a fraction of nodes in the mesh. Besides using the rule of thumb for this parameter, a convergence for study for $\lambda$ was performed. Figure 5b, shows the NRMSE for the sensitivity with respect to b, $S_b^{\theta }$, as a function of $\lambda$. In this figure, the top insert shows the rule of thumb suggested $\lambda$, and the bottom inset shows a completely perturbed mesh. For the transient thermal fin problem, the precision of $S_b^{\theta }$ is insensitive to $\lambda$, as shown by the almost flat line of Figure 5b. Therefore, the rule of thumb and the case when $\lambda =1$ have almost the same precision. For illustration purposes in the fin problem, we picked $\lambda =1$ for the sensitivity analysis of the fin length. This means that all the imaginary coordinates of the mesh have non-zero values as shown in the bottom right inset in Figure 5b.

The sensitivities history of $\theta$ concerning the thermal conductivity, $S_k^{\theta }$, the room temperature, $S_{T_{\infty }}^{\theta },$ and the fin’s height, $S_b^{\theta }$, are shown in Figure 6a–c, respectively. A negative relative sensitivity predicts a decreasing trend for the temperature with an increment of the input parameter and vice versa. Overall, a good agreement between analytical differentiation, FD, and Transient Thermal ZFEM is observed. The solutions from the simulations using Transient Thermal ZFEM had a better match than built-in Abaqus functions with FD match when compared with the analytical values, as could be seen by error measurements in

Table 2. NRMSE of $\theta$ and the selected sensitivities compared to the analytical solution.

	NRMSE
	$\mathit{\theta }$	${\mathit{S}}_{\mathit{k}}^{\mathit{\theta }}$	${\mathit{T}}_{\mathit{\infty }}$	${\mathit{S}}_{\mathit{b}}^{\mathit{\theta }}$
ZFEM	0.003	0.011	0.002	0.003
FD	0.003	0.009	0.009	0.019

. These errors are on the same order as the NRMSE for $\theta$; therefore, we attribute the good agreement among methodologies to the enhanced dissipation implemented to counter the lack of heat transfer in the out-of-plane direction in the 2D FEM and Transient Thermal ZFEM elements.

From the time-dependent sensitivity analysis in Figure 6, it can be stated that $T_{\infty }$ is only influential in the transient state, since $S_{T_{\infty }}^{\theta }\approx 0$ at steady state while $k$ and $b$ are not influential at the beginning, but they are influential in steady-state given that $S_k^{\theta }\ne 0$ and $S_b^{\theta }\ne 0$ at $425$. Based on the information provided by Figure 6a, a less conductive fin will reduce $\theta$ given that $S_k^{\theta }\left(t\right)\ge 0$. On the other hand, Figure 6b,c show that longer fins exposed to higher room temperatures will reduce the fin’s tip temperature. This is explained by the inverse relation of $\theta$, $S_b^{\theta }\left(t\right)$, and $S_{T_{\infty }}^{\theta }\left(t\right)$. In the current application, reducing the fin’s tip is desired because it means that more energy can be dissipated in the system before reaching the tip.

Computational Efficiency of Transient Thermal ZFEM

For the numerical solutions to the transient fin problem, the computational system used consisted of an Intel Xeon W-2265 at 3.50 GHz, 128 Gb of RAM, Abaqus 2021 Hot Fix 5, and Ubuntu 20.04 Long Term Support. In this specific case, the total CPU time of three pairs of sequential and independent simulation runs made with ZFEM and FD were conducted and averaged. The results showed that on average, ZFEM required $45\%$ less total CPU time to solve the Transient Thermal ZFEM model and obtain sensitivities compared to using built-in Abaqus functions and FD. This contrasts with that reported in the ZFEM literature for more complicated physics, where 2.5 to 4 times longer computational times were obtained for equivalent real variable runs [71,74,87]. This behavior shows another advantage of using CTSE for the transient thermal linear problem as it requires only one evaluation of the model to obtain sensitivities. In contrast, at least two evaluations of the models are required for FD, assuming the optimal step size is known a priori.

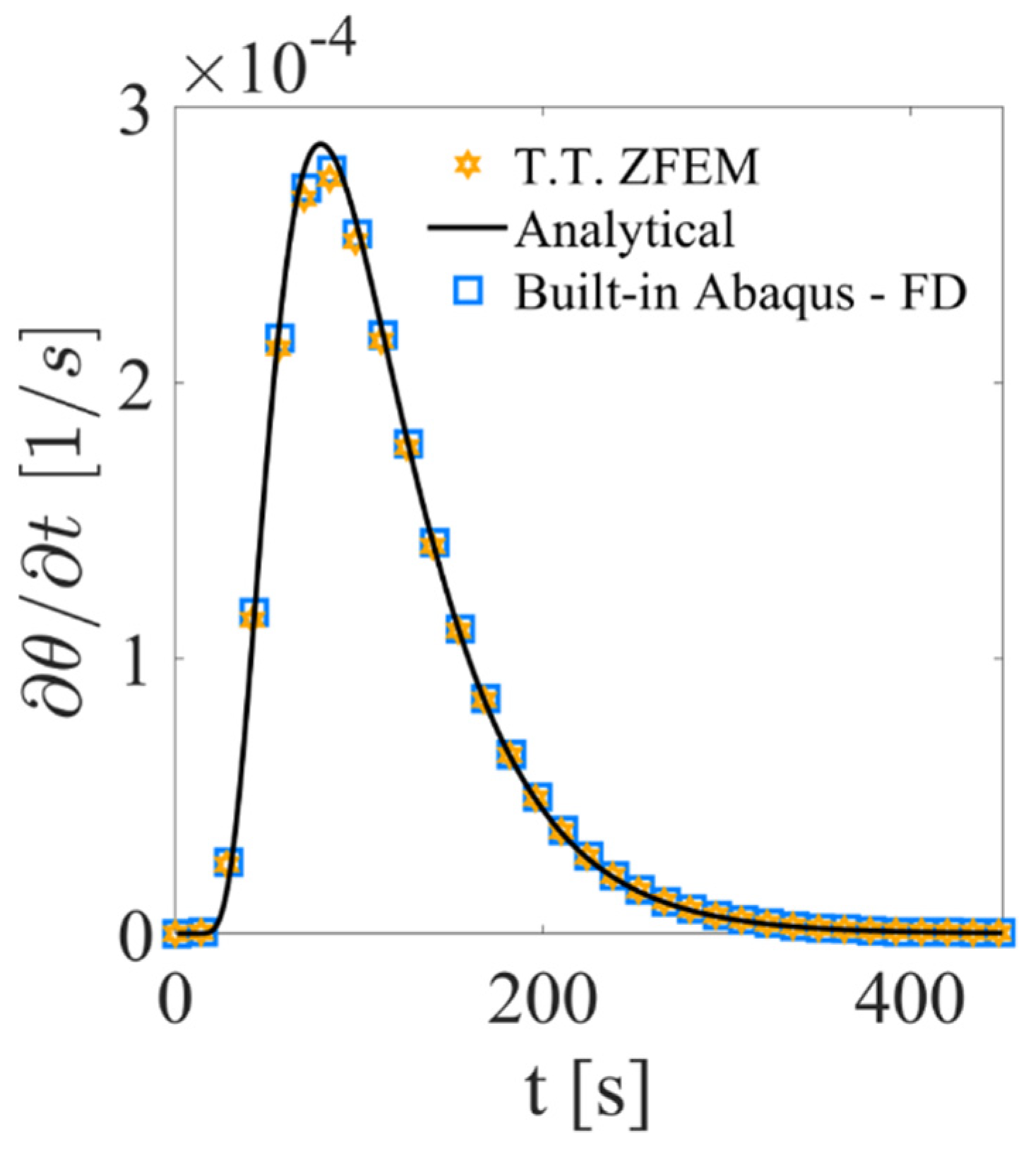
4.2. Heating Rate

Figure 7 shows the results for the heating rate, $\partial \theta /\partial t$, at the fin’s tip. This rate was obtained by directly evaluating the Transient Thermal ZFEM model and applying the methodology shown in Section 3. In contrast, one is required to post-process the built-in Abaqus solutions by computing FD using the time domain to obtain the heating rate. The NRMSE for Transient Thermal ZFEM and Abaqus built-in functions with FD is 0.012 and 0.010, respectively. The small deviations with respect to the analytical solutions can be attributed to the time increment used in the simulations. A detail about the influence of the time incrementation in the heating rate can be seen in the Supplementary Material.

4.3. Sensitivity Analysis of Temperature History for a Fin with Temperature-Dependent Specific Heat

When any coefficient of Equation (1) is temperature-dependent, the transient heat transfer problem becomes nonlinear and analytical equations are no longer available [82]. To test the capacity of Transient Thermal ZFEM to handle nonlinearities, a model containing temperature-dependent specific heat was created and solved. For this analysis, the specific heat was selected as the variable of interest because it is temperature-dependent in the model and it directly modifies the thermal capacitance of the material. Moreover, according to Equations (1) and (7), this property is expected only to affect the process in the transient state. The values for $C_P\left(T\right)$ used in the model are presented in Figure 8a and correspond to Ti64 alloy [90]. Due to the lack of analytical equations, the response obtained from built-in Abaqus functions combined with FD was used as a reference to calculate the NRMSE. To calculate the reference response for $S_{C_p}^{\theta }$ with FD, one model was run with the nominal parameters from the curve shown in Figure 8a, and for the second model, all the values in the curve defining $C_P\left(T\right)$ were shifted $5.5\mathrm{J}/\mathrm{Kg}\mathrm{K}$ which corresponds to 1% of the minimum value of the specific heat. The convergence analysis for these models is presented in the Supplementary Material. For the calculation of the sensitivities using Transient Thermal ZFEM, the procedure described in Section 3 was followed as: (a) first interpolating the experimental values for $C_P\left(T\right)$ in the temperature range of the solution, and then (b) applying an imaginary perturbation, $h={10}^{-10}$ to all values as shown in the inset of Figure 8a. Finally, to normalize the sensitivity results, we used $\left|\varphi \right|=580\mathrm{J}/\mathrm{Kg}\mathrm{K}$ for Equation (10) which corresponds to the specific heat reported in Table 1.

The $\theta$ response for Transient Thermal ZFEM and built-in Abaqus functions is reported in Figure 8b, and the sensitivity response is presented in Figure 8c. A good agreement was found between both models with an NRMSE of 0.003 for $\theta$, and $0.007$ for $S_{C_p}^{\theta }$. These results show that the Transient Thermal ZFEM can accurately determine sensitivities considering material nonlinearities and temperature-dependent parameters.

4.4. Sensitivity Analysis of the Heat Flux History: Defining the Fin’s Performance

Using the heat flux output, two measurements of performance were calculated for the fin: heat transfer effectiveness, $\epsilon$, calculated using Equation (26), and the thermal efficiency, $\eta$, defined in Equation (27). The heat transfer effectiveness corresponds to the ratio of the heat flux ($\overrightarrow{q}$) from a wall with a fin to the heat flux of the same wall without a fin, and the efficiency is the relationship of effective heat transfer from the fin to the room regarding the heat transfer of an ideal fin kept at the initial temperature ${\theta }_0$ [24]. The sensitivity analysis of these two performance indices represents useful information for improving the design of fins since it can identify which variables positively affect their performance. In this regard, the main idea is to reduce the values of parameters with negative sensitivities and increase the importance of parameters with positive sensitivities.

$$\epsilon \left(t\right)=\frac{\overrightarrow{q}\left(\theta \left({\rm X}=1,t\right)\right)}{\overrightarrow{q}\left({\rm X}=1\right)}$$

(26)

$$\eta \left(t\right)=\frac{\dot{Q}\left(\theta \left({\rm X},t\right)\right)}{\dot{Q}\left(\theta \left({\rm X}\right)={\theta }_0\right)}=\epsilon \left(t\right)\frac{\delta }{2b}$$

(27)

To calculate the performance parameters using Transient Thermal ZFEM and built-in Abaqus functions, the heat flux was obtained at the wall-fin interface ($x\approx b$). The evolution of $\epsilon$ and $\eta$ are presented in Figure 9a,b, respectively, showing good agreement between the Transient Thermal ZFEM and the Abaqus built-in element response and with NRMSE values of 0.052 and 0.052, respectively, when compared with the analytical equations. $\eta$ and $\epsilon$ quickly reach the steady-state value with an asymptotic behavior tending to positive infinity in $t=0\mathrm{s}$. This behavior is explained by the discontinuity of the temperature profile at the wall-fin interface at that time. In addition, this is similar to the behavior of the transient heat transfer coefficient studied in similar problems [30,31].

A comprehensive sensitivity analysis of the fin performance parameters involving all of the parameters affecting the model was performed. The time history evolutions for all sensitivities are shown in the Supplementary Material, and only the results for $k$, $T_{\infty }$, and $b$, are included in Figure 10 for $\epsilon$ and Figure 11 for $\eta$. The maximum error for the sensitivities corresponded to 0.048 for $S^{\epsilon }$ and 0.048 for $S^{\eta }$ when compared to the analytical solution. As observed in the time history for the sensitivities, the values quickly stabilized to the steady-state. Therefore, pie charts were developed showing the values of the contribution of the individual sensitivities to the total sum of the sensitivities for all variables in the model after steady-state conditions have been reached. Figure 10d and Figure 11d show the sensitivities for $\epsilon$ and $\eta$, respectively. In the pie charts, the $(+)$ symbol inside each of the colored sections implies a direct relationship between the output and the input variable while the $(-)$ implies an inverse relationship.

From Figure 10d, it is possible to identify that $\delta$, $h_U,$ and $k$ are the most influential parameters to modify $\epsilon$. Each of these variables accounts for nearly a third of the total sensitivity of the effectiveness. Based on Equation (14), if $\delta$, $h_U,$ or $k$ are duplicated, an equivalent thermal effectiveness increment (or reduction) in the fin at steady-state will occur. In this regard, the $(-)$ inside the pie sections for $\delta$ and $h_U$ means that they should be reduced to increase the effectiveness. The other parameters, e.g., b, $\rho ,C_P,T_{\infty }$, and $T_0$ influence the effectiveness less than the 1% compared to the sum of all relative sensitivities. This means that an increment or reduction of these five variables will not produce a significant change in the effectiveness of the fin.

Similarly, from Figure 11d, it is possible to identify that $\delta$, $b$, $h_U$, and $k$ are the most influential parameters to modify the thermal efficiency. Therefore, increments in $\delta$ and $k$ will increase this index. For the efficiency, the weights are not equally split as in the case of the effectiveness. For instance, the fin length is almost twice more influential than $h_U$, and $k$. Moreover, the fin thickness is approximately 2.4 times less influential in $\eta$ than the length of the fin. This means that larger geometries will reduce the thermal efficiency of the fin while enhancing the heat transfer with more conductive materials larger heat transfer coefficients are beneficial for $\eta$.

From these results, some guidelines for the fin’s design can be stated: To cool a heated wall, it is preferred to have a fin with a low aspect ratio made of a material with high conductivity and low heat transfer coefficient. This boundary condition requirement is counterintuitive because larger heat transfer coefficients typically improve the heat exchange from the external surfaces to the room. However, this also means that the heat will be transferred only at the beginning of the fin. Therefore, according to the first-order sensitivity information, a shorter and thicker fin made of more conductive materials is preferred to increase the dissipation performance.

It is worth highlighting that although we show the Transient Thermal ZFEM methodology in a simple thermal problem, the methodology is general. For instance, we have included an additional verification of the capabilities of the Transient Thermal ZFEM in the Supplementary Material for a 2D problem corresponding to a rotating disk under nonconstant initial temperature.

5. Conclusions

In this work, the complex Taylor series expansion method was integrated with the transient heat transfer FEM to create the Transient Thermal ZFEM methodology. This methodology enables the calculation of high precision sensitivities regarding geometrical parameters, boundary conditions, time, and material properties. Although the method takes advantage of complex algebra to obtain the sensitivities, we do not require complex variable solvers. Instead, the system of equations is solved using the Cauchy-Reimann matrix representation of a complex number. This transformation allows the solution of the FEM equations in any real-variable solver facilitating the implementation of the new method within commercial finite element software.

We verified the Transient Thermal ZFEM method against the analytical solution for a fin with an insulated tip. Our methodology accurately computed temperature and temperature sensitivity history regarding specific heat, thermal conductivity, ambient temperature, and fin geometry. Good agreement with the reference solutions was obtained for the numerical example. Similarly, the thermal performance of the fin based on the fin’s heat flux presented a good agreement with the analytical solution. The sensitivities using Transient Thermal ZFEM were compared with FD using built-in Abaqus elements. Overall, we found a reduction of 45% in the computational time compared with FD. Moreover, we demonstrated that the Transient Thermal ZFEM is step-size independent and mesh perturbation independent for the transient thermal linear problem. On the other hand, the time derivative obtained by Transient Thermal ZFEM is highly dependent on the number of increments of time but only limited by the computing hardware.

Implementing the Transient Thermal ZFEM in finite element analysis programs will enable the sensitivity analysis of heat transfer models with a fraction of the computational cost and higher precision than sensitivity analysis using the traditional finite differentiation method. Moreover, Transient Thermal ZFEM can improve the convergence rates and computational times on gradient-based optimizations, especially in inverse heat transfer problems. These improvements are possible because the Transient Thermal ZFEM methodology allows one to obtain a more precise and computationally efficient calculation of partial derivatives than the traditional methods.

Given the advantages of Transient Thermal ZFEM over the traditional sensitivity analysis methodologies, our methodology is especially attractive for complicated systems in alternative energies, petroleum engineering, chemical, agriculture, materials, and metallurgical industries. Accurate sensitivity information in transient thermal problems allows one to understand the system’s thermal behavior better. For instance, in the numerical example, using Transient Thermal ZFEM, the variables can be sorted by their influence in the transient state and steady states. Then, it was possible to effectively filter the variables that affect the processes after reaching the steady-state, even if the parameters of the systems are temperature dependent.

As future work, this method will be extended to calculate higher-order sensitivities and to explore other multiphysics problems such as thermo-mechanical, microstructural evolution, crystal plasticity, heat treatments, and thermo-electrical. Moreover, we will explore the use of sensitivities to perform a derivative-based approximation of functions that enable predictions in complicated problems or to evaluate models with output uncertainty related to the input parameters for uncertainty quantification. In addition, these sensitivities could guide semiempirical techniques that rely on simulations to recover basic parameters of the process as the Nusselt numbers, Biot numbers, or Prandtl numbers.