Improving Entity Linking by Introducing Knowledge Graph Structure Information

Abstract

Entity linking involves mapping ambiguous mentions in documents to the correct entities in a given knowledge base. Most of the current methods are a combination of local and global models. The local model uses the local context information around the entity mention to independently resolve the ambiguity of each entity mention. The global model encourages thematic consistency across the target entities of all mentions in the document. However, the known global models calculate the correlation between entities from a semantic perspective, ignoring the correlation information between entities in nature. In this paper, we introduce knowledge graphs to enrich the correlation information between entities and propose an entity linking model that introduces the structural information of the knowledge graph (KGEL). The model can fully consider the relations between entities. To prove the importance of the knowledge graph structure, extensive experiments are conducted on multiple public datasets. Results illustrate that our model outperforms the baseline and achieves superior performance.

1. Introduction

The named entity linking (NEL) task refers to correctly linking entity mentions in text to entities in a structured knowledge base (such as Wikipedia, Freebase [1], or YAGO [2]), which can solve the ambiguity of mentions in natural language processing. In Figure 1, for example, a mention of “Michael Jordan” may correspond to entity entries in the knowledge base (KB) such as “Michael Jordan”, “Michael I. Jordan”, “Michael Jordan (footballer)”, “Michael B. Jordan”, etc. The entity linking (EL) involves linking the mention “Michael Jordan” to the correct entity “Michael I. Jordan” in the KB. Entity linking is also the basis of many other natural language processing tasks, such as knowledge base question and answer [3], information retrieval [4], and content analysis [5].

Figure 1. An example of NEL whose goal is to link each mention to an entity in the KB (e.g., “Michael Jordan” is linked to Michael I. Jordan; “Artificial intelligence” is linked to Artificial intelligence). Note that there are various relations between entities in the KB.

Given a document, the named entity mentions are recognized in advance by a named entity recognition (NER) method. Generally speaking, a typical entity linking system consists of two steps: (1) candidate entity generation, in which a model retrieves a set of candidate entities, which contains the entities that the mention may refer to; and (2) candidate entity ranking, in which a model ranks the entities in the candidate set and selects the entity that the mention is most likely to link to. Recently, some methods such as techniques based on a named dictionary and techniques based on surface form expansion have achieved high candidate recalls, and thus most work focuses on methods for downstream candidate entity ranking, as described in this paper.

In early work, prior distribution and local contexts played important roles in disambiguating different candidate entities. However, in many cases, local features alone cannot provide sufficient information for disambiguation. Therefore, many global models have emerged to solve the task of entity linking. For example, Ganea and Hofmann [6] combine local and global information. First, the word-entity co-occurrence counts are used to train the entity embeddings, then the local scores between contexts of mentions and the entity embeddings are calculated in the local model, and the scores between candidate entities of all mentions in the document are calculated in the global model. On the basis of [6], Le and Titov [7] model the latent relations between mentions. Based on [7], Hou et al. [8] inject fine-grained semantic information into entity embeddings. In addition, Yang et al. [9] propose the dynamic context augmentation method, which uses the entity embedding in [6].

However, the above methods still have some shortcomings. They essentially calculate the similarity between entity embeddings when obtaining global scores, which only consider the semantic proximity between entities. While there are real relations between some entity mentions in a document, these relations are contained in some knowledge graphs, and comprise the so-called knowledge graph structural information. As shown in Figure 1, there is an association relation of “colleague” between entity “Michael I. Jordan” and entity “Xiandong Jing” in the knowledge base. In addition, although there are also some works [10,11,12,13] that involve knowledge graphs, this is because their target knowledge base is a knowledge graph, and our method is different from them essentially. For example, Cetoli et al. [12] use bi-directional long short-term memory (Bi-LSTM) to encode graph triplets. Mulang et al. [13] develop a context-aware attentive neural network approach on Wikidata. Instead, on the basis of Wikipedia, we introduce the structural information of other knowledge graphs to complement the semantic information of Wikipedia, which is somewhat similar to the fusion of information from different knowledge bases.

To address the limitations of existing methods, we propose an entity linking model that introduces knowledge graph structural information (KGEL). First, under the premise that the target knowledge base is Wikipedia, we obtain the entities and triples in the knowledge graph Wikidata corresponding to the candidate entities. Then, the knowledge graph embedding method is used to train entity embeddings and relation embeddings. Finally, according to the different characteristics of local and global models, we use the previously trained entity embeddings and relation embeddings only for the global model of entity linking; that is, the global scores are computed from the perspective of the graph structure and fused with the Ment–Norm [7] model. Existing methods have been able to achieve more than 90% F1 on the standard AIDA-CoNLL dataset; for example, Ment–Norm achieves 93.07% F1. Our KGEL method achieves an improvement of 0.4% F1 on the basis of Ment–Norm, and the average result of KGEL on the five out-of-domain datasets is also 0.2% higher than Ment–Norm, which indicates that our model also has better generalization. Our method can also further improve the performance when using a more superior baseline.

The main contributions of our paper can be summarized as follows. (1) We propose to introduce knowledge graph structure information into the entity linking model, so as to complement the semantic information. (2) We obtain the Wikipedia–Wikidata mappings of entities and the required triples, and then obtain the entity and relation embeddings containing the graph structure through the knowledge graph embedding method. This provides a new idea for information fusion between different knowledge bases (graphs). (3) Extensive experiments on multiple datasets show the excellent performance of our method and demonstrate the effectiveness of the knowledge graph structure for entity linking.

2. Background and Related Work

2.1. Problem Definition

Given a knowledge base containing a set of entities $E_s=\{e_1,\dots ,e_t\}$ and a set of entity mentions $M=\{m_1,\dots ,m_n\}$ in corpus $\mathcal{D}$, the goal of entity linking is to map each entity mention $m_i\in M$ in the text to its corresponding entity $e_i^{*}\in E_s$. Because a KB may contain a large number of entities, in order to reduce complexity, we usually use a heuristic to choose potential candidates, thus obtaining candidate set $C_i=(e_{i1},\dots ,e_{i{l}_i})$, which is the candidate entity generation we mentioned earlier. Then, we select gold entities on the candidate set in the candidate entity ranking stage.

2.2. Entity Linking

As it is an important task in natural language processing, there is a lot of work in the field of entity linking. Most of the early work comprises methods based on manually designed features and rule-based methods, which are not enough to capture the potential dependence and interaction in the data. With the rapid development of deep learning, a large number of deep-learning-based methods have appeared in the field of entity linking, and they have achieved better results than previous methods. Topics related to the work of this article are as follows.

Local model. The local model uses the local text context information around the entity mention to independently resolve the ambiguity of each entity mention. He et al. [14] were early adopters of deep learning for entity linking. They learned distributed representations of entities to measure similarity, avoiding manually designed features, so that words and entities could be in the joint semantic space, and then candidate entities could be sorted based on vector similarity. Subsequently, Sun et al. [15] used neural networks to encode mentions, contexts of mentions, and entities. Among them, contexts of mentions are encoded by convolutional neural networks (CNN), which are combined with representations of the mention titles to obtain the final mention representations. The entity representations are obtained from the entity titles and entity categories. Finally, the similarities between the mention representations and the entity representations are calculated to obtain local scores. Based on [15], Francis-Landau et al. [16] used CNN and stacked denoising auto-encoders to encode different granular information of mentions and entities to enhance the representation. In addition, Gupta et al. [17] cascaded the output of two long short-term memory (LSTM) [18] networks. The two LSTM networks independently encode the left and right context of the entity mention, including the entity mention itself. Kolitsas et al. [19] expressed entity mention as a combination of LSTM hidden states contained in the span of entity mention. Eshel et al. [20] used a variant of LSTM-GRU [21]. Ganea and Hofmann [6] introduced an attention mechanism in the local model. They assumed that a context word was important if it was strongly related to at least one candidate entity, and the context words were hard pruned. The local model in this paper is based on Ganea and Hofmann [6].

Global model. The global model links all the mentions in a document at the same time and considers that the target entities of all the mentions are consistent on the subject. The previous global methods usually executed RandomWalk [22] or PageRank [23] algorithms on the graph containing candidate entities. Another solution is to maximize the conditional random field [24], but the problem is NP-hard. Ganea and Hofmann [6] used loopy belief propagation (LBP) [25] to iteratively propagate entity scores to reduce complexity. Based on [6], Le and Titov [7] modeled the latent relations between mentions and added them to the global model in the form of features, achieving better results. Some recent studies have defined the global entity linking problem as a sequential decision task, where the linking of the new entity is based on the already linked entity. Fang et al. [26] used LSTM to maintain long-term memory for previous decisions; Yang et al. [9] proposed a dynamic context integration method that uses previous decisions as dynamic context to improve subsequent decisions; Yamada et al. [27] calculated the confidence scores based on the previous decisions. In addition, graph neural networks (GNNs) can also be used for the global model of entity linking. Wu et al. [28] proposed a dynamic graph convolutional network model, in which the graph structure is dynamically calculated and changed during training, and fusion of knowledge through dynamically linked nodes can effectively obtain the theme consistency in the document. Fang et al. [29] proposed a sequential graph attention network to synthesize the advantages of the graph model and the sequence model, which dynamically encodes the preceding and following entity mentions, and assigns different weights to these entity mentions. The global model of this article refers to the work of [7].

Entity embedding. Entity embedding is a key component in entity linking to avoid manual features and enhance model effects. There is also a lot of work for entity embedding. Yamada et al. [30] proposed to map words and entities to the same continuous vector space. They used two models to extend the skip-gram model. The KB graph model uses the link structure in the KB to learn the relevance of entities. The anchor context model aims to use KB anchor text and context words to align vectors so that similar words and entities are close in the vector space. Yamada et al. [31] further proposed to jointly learn distributed representations of text and entities. Given a piece of text in the knowledge base, a model is trained to predict entities related to the text; that is, using a large amount of text extracted from Wikipedia and their entity annotations to train the model. Ganea and Hofmann [6] used pre-trained word embeddings and word-entity co-occurrence counts to obtain entity embeddings so that words and entities were represented in the same low-dimensional vector space. Ling et al. [32] proposed a fill-in-the-blank task to learn context-independent entity representations from the text context. Hou et al. [8] proposed incorporating fine-grained semantic information into entity embedding to reduce uniqueness and promote the learning of contextual commonality. Yamada et al. [27] used the pre-trained model BERT [33] to generate the representation of words and entities, and the results were greatly improved compared to the previous method. This paper also uses the entity embeddings of [6].

2.3. Knowledge Graph Embedding

The knowledge graph is a multi-relational graph composed of entities (nodes) and relations (edges), and each edge is in the form of a triple (head entity, relation, tail entity). The existing knowledge graphs include Freebase [1], DBpedia [34], Wikidata, etc. Knowledge graph embedding [35] involves embedding the entities and relations in the knowledge graph into a continuous vector space. In general, knowledge graph embedding methods can be divided into two groups: translational distance models and semantic matching models [36,37,38]. The former use distance-based scoring functions, and the latter similarity-based ones. Among translational distance models, TransE [39] is the most representative. The main idea is to give a triple $\left(h,r,t\right)$, the goal is $\mathbf{h}+\mathbf{r}\approx \mathbf{t}$, where $h,r,t$ are the head entity, relation, and tail entity, respectively, and $\mathbf{h},\mathbf{r},\mathbf{t}$ are, respectively, vector representations. To solve the limitations of the TransE model in dealing with 1-to-N, N-to-1, and N-to-N complex relations, TransH [40] introduces relation-specific hyperplanes that allow an entity to have different representations under different relations. In order to further improve the representation ability, TransR [41] introduces relation-specific spaces, rather than hyperplanes. TransD [42] simplifies TransR by further decomposing the projection matrix into a product of two vectors. TransM [43] assigns specific relation weight to each triple $\left(h,r,t\right)$.

There are also recent knowledge graph embedding methods with better performance. Zhang et al. [44] proposed the hierarchy-aware knowledge graph embedding model (HAKE), which maps entities into a polar coordinate system. PairRE [45] has paired vectors for each relation representation, which can adaptively adjust the margin in a loss function to fit for complex relations. Additionally, PairRE can encode three relation patterns: symmetry/antisymmetry, inverse, and composition. DualE [46] introduces dual quaternions into knowledge graph embedding, where a dual quaternion is similar to a “complex quaternion” with its real and imaginary part all being quaternar. DualE universally models relations as the combination of a series of translation and rotation operations. EIGAT [47] allows correct incorporation of global information into the graph attention network (GAT) family of models by using scaled entity importance, which is computed by an attention-based global random walk algorithm. In order to focus on the importance of the knowledge graph structure for the entity linking task, the knowledge graph embedding method used in this article is the most basic TransE model.

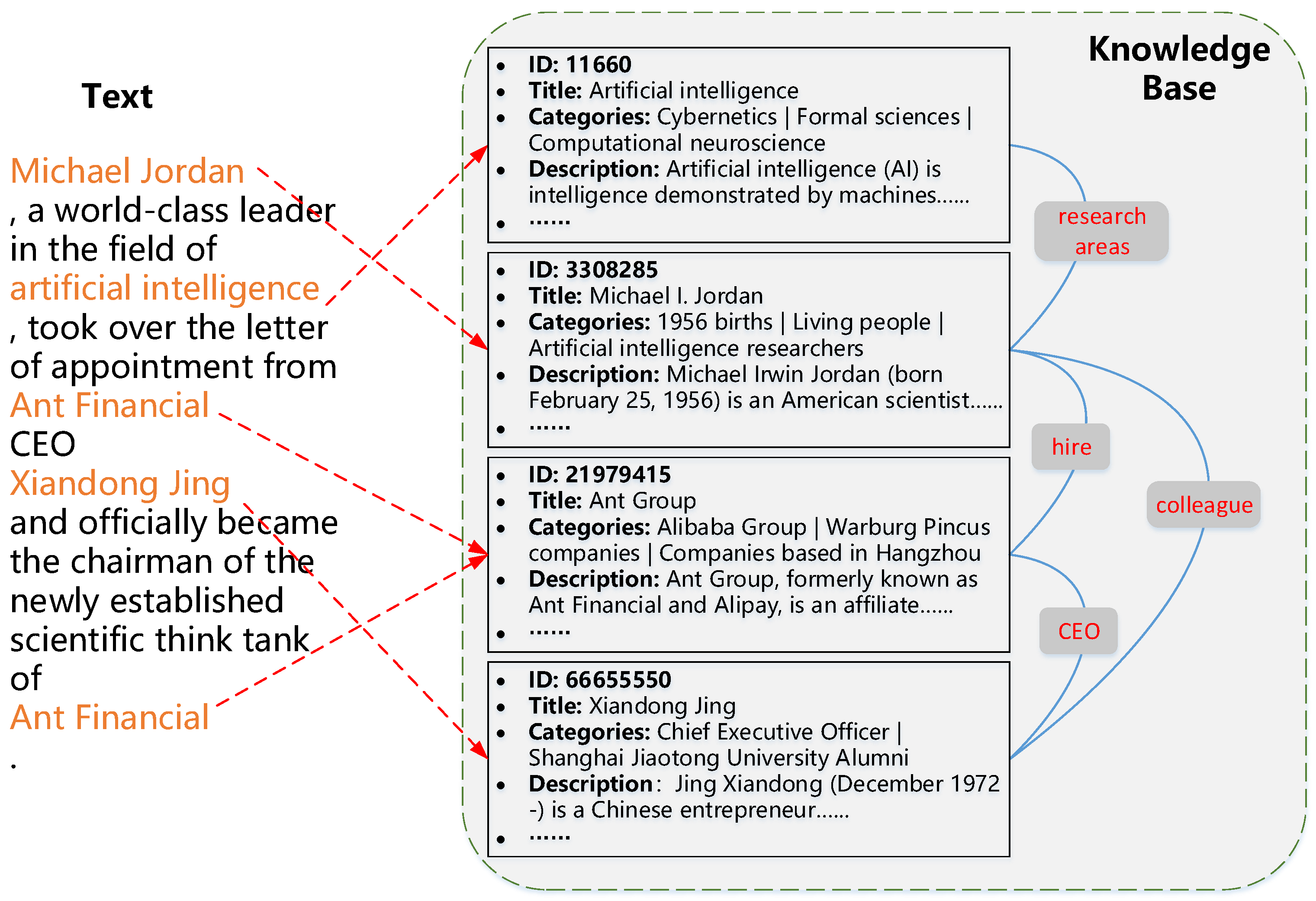
3. Learning Entity Embeddings KGEmbs

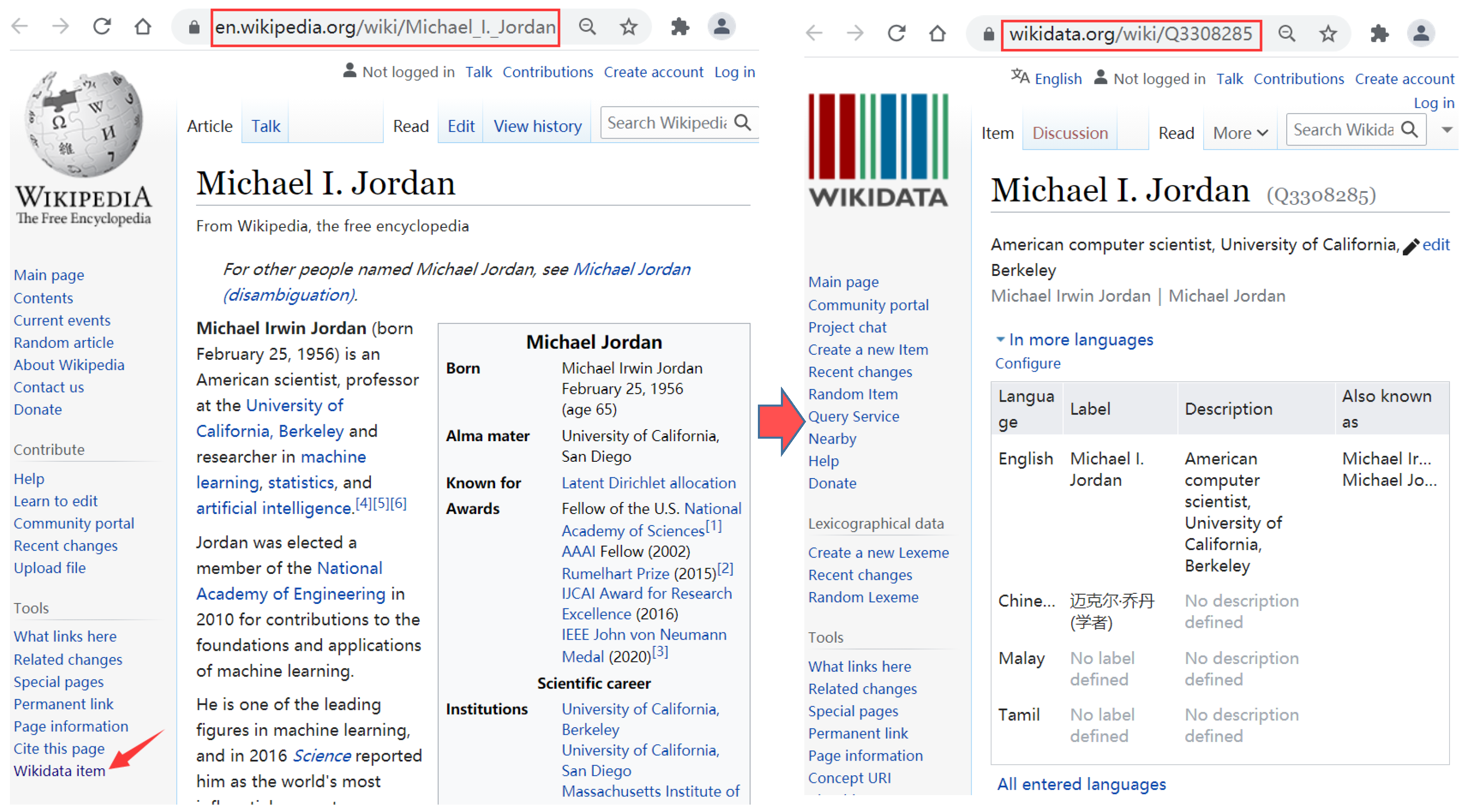
3.1. Wikipedia–Wikidata Mappings

Since the target knowledge base of the dataset we use is Wikipedia, and we want to introduce the structural information of other knowledge graphs, for the Wikipedia entities used, we need to obtain their corresponding Wikidata entities, i.e., obtain the Wikipedia–Wikidata mappings. In the entity’s Wikipedia page, there is a corresponding Wikidata hyperlink, as shown in Figure 2. Therefore, we can obtain the Wikidata ID of the Wikipedia entity through the crawler. Examples of the Wikipedia–Wikidata mappings are shown on the left side of Table 1.

Figure 2. Example for the Wikipedia–Wikidata mapping. We can obtain the corresponding Wikidata ID through the entity’s Wikipedia page.

Table 1. Examples of Wikipedia–Wikidata mappings and triples.

Wikipedia–Wikidata Mappings		Triples
en.wikipedia.org/wiki/Universe	Q1	Q1	P2670	Q523
en.wikipedia.org/wiki/Star	Q523	Q1	P2184	Q136407
en.wikipedia.org/wiki/Big_Bang	Q323	Q1	P793	Q323
en.wikipedia.org/wiki/Happiness	Q8	Q8	P31	Q331769
en.wikipedia.org/wiki/Mood_(psychology)	Q331769	Q8	P31	Q9415
…		…
en.wikipedia.org/wiki/Toledo, _Minas_Gerais	Q22065023	Q22065023	P131	Q39109
en.wikipedia.org/wiki/Minas_Gerais	Q39109	Q22065023	P17	Q155

3.2. Triple Knowledge

We can obtain the triple knowledge of Wikidata from OpenKE: http://139.129.163.161/index/toolkits (accessed on 1 March 2022), including 20,982,733 entities, 594 relations, and 68,904,773 triples. According to the work of [7], we obtain 274,474 entities in the candidate entity generation stage to filter relations and triples, and finally obtain 486 relations and 807,587 triples. The triple format is shown on the right side of Table 1. For example, (Q1, P2670, Q523) is a triple, where Q1 is the head entity and its corresponding entity is “universe”, Q523 is the tail entity and its corresponding entity is “star”, and P2670 is the relation between entities Q1 and Q523; that is, “instance has part(s) of the class”. Therefore, the triple can be represented as (universe, instance has part(s) of the class, star).

3.3. Entity and Relation Embeddings

In order to demonstrate more intuitively the effectiveness of the knowledge graph structure for entity linking, and also considering the speed differences of each model, we use the TransE model to train entity and relation embeddings on triples, where $h,t\in E$ (the set of entities) and $r\in R$ (the set of relations). The main idea is that the functional relation obtained from the edges labeled by r corresponds to the translation of the embedding; that is, we hope that $h+r\approx t$ when $\left(h,r,t\right)$ holds, while $h+r$ should be far away from t otherwise.

In order to learn entity and relation embeddings, we minimize the following loss:

$$\mathcal{L}=\sum _{(h,r,t)\in S}\sum _{(h^{\prime },r,t^{\prime })\in S_{(h,r,t)}^{\prime }}{\left[{\gamma }_1+d\left(\mathbf{h}+\mathbf{r},\mathbf{t}\right)-d\left({\mathbf{h}}^{\prime }+\mathbf{r},{\mathbf{t}}^{\prime }\right)\right]}_{+}$$

(1)

where ${\left[x\right]}_{+}$ denotes the positive part of x, $\gamma >0$ is a margin hyperparameter, and $d\left(\mathbf{h}+\mathbf{r},\mathbf{t}\right)$ is an indicator to measure similarity. Here we use the $L_1$-norm, and

$$S_{(h,r,t)}^{\prime }=\left\{\left\{h^{\prime },r,t\right\}|h^{\prime }\in E\right\}\cup \left\{\left(h,r,t^{\prime }\right)|t^{\prime }\in E\right\}$$

(2)

The optimization is performed by stochastic gradient descent, and an additional constraint is that the $L_2$-norm of the embeddings of the entities is 1.

4. Model

The entity linking model in this paper integrates local and global features and is a conditional random field model in form. Figure 3 provides an overview of our model. Specifically, a scoring function g is defined to evaluate the mappings from entity mentions $m_1,\dots ,m_n$ to the entities $e_1,\dots ,e_n$ in a document D:

$$g(e_1,...,e_n)=\sum _{i=1}^n\mathsf{\Psi }\left(e_i\right)+\sum _{i\ne j}\mathsf{\Phi }(e_i,e_j,D)$$

(3)

where n represents the number of entity mentions in the document. The first part of Equation (3) is the local score, which is the matching score between the local context of the entity mention and the candidate entity, and the second part is the global score, which is the score between entities in the document. The local model and the global model are described below.

Figure 3. The architecture of the proposed KGEL model. It contains three parts: Local model, WikiEmbs Global model, and KGEmbs Global model. Specifically, in the Local model, the similarity calculated by context embedding and entity embedding is used as the local score. In the Global model, the scores between the candidate entities of all mentions in the document are taken as the global score. Among them, in the WikiEmbs Global model, entity embedding is obtained through word-entity co-occurrence counts, which consider the semantic information. In the KGEmbs Global model, entity embedding is obtained through triples, considering the structural information of the knowledge graph.

4.1. Local Model

According to Ganea and Hofmann [6], this paper takes the local model as an attention model based on entity embedding. For an entity mention m, if a word in the context is strongly related to at least one candidate entity, the word is considered important.

In the candidate generation stage, we can obtain the candidate entity set $C_i=(e_{i1},\dots ,e_{i{l}_i})$. Then we calculate the score of each candidate entity $e\in C_i$ according to the P-word window local context $c=\{w_1,...,w_p\}$ around m. First, we calculate the unnormalized support score of each word in the context; that is, the weight of each word

$$u\left(w\right)=\underset{e\in C_i}{max}{\mathbf{e}}^T\mathbf{A}\mathbf{w}$$

(4)

where $\mathbf{A}$ is a parameterized diagonal matrix, $\mathbf{w}$ is the word embedding (we use the pre-trained word2vec word embedding), and e is the candidate entity embedding, which is trained based on the co-occurrence counts of the word-entity in Wikipedia [6]. If the word is strongly related to at least one candidate entity, its weight score is relatively high. In addition, it is observed that some words with insufficient information will introduce noise to the local model, so the hard pruning method is used to select $Q\le P$ words with the highest weight scores:

$$\stackrel{-}{c}=\left\{w\in c|u\left\{w\right\}\in topQ\left\{\mathbf{u}\right\}\right\}$$

(5)

Therefore, the final attention weight is:

$$\beta \left(w\right)=\left\{\begin{array}{ccc}\hfill \frac{exp\left[u\left[w\right]\right]}{{\displaystyle \sum _{v\in \stackrel{-}{c}}}exp\left[u\left[v\right]\right]}& & ifw\in \stackrel{-}{c}\hfill \\ \hfill 0& & otherwise\hfill \end{array}\right.$$

(6)

Finally, we can obtain the local scores of the candidate entities:

$$\mathsf{\Psi }\left(e\right)=\sum _{w\in \stackrel{-}{c}}\beta \left(w\right){\mathbf{e}}^T\mathbf{B}\mathbf{w}$$

(7)

where $\mathbf{B}$ is another diagonal matrix that can be trained.

4.2. Global Model

Ganea and Hofmann [6] mainly considered the consistency between entities. However, Le and Titov [7] proposed that there is not only consistency between entities, but there are also some latent relations that can support the constraints on entities. Assuming that there are K latent relations, each relation k corresponds to a pair $(m_i,m_j)$, so the second term of Equation (3) can be written as:

$$\mathsf{\Phi }\left(e_i,e_j,D\right)=\sum _{k=1}^K{\alpha }_{ijk}{\mathsf{\Phi }}_k\left(e_i,e_j,D\right)$$

(8)

That is, the paired score $(m_i,m_j)$ is the weighted sum of the corresponding scores of each relation, and ${\alpha }_{ijk}$ is the weight corresponding to the relation k. Here, each relation k is a diagonal matrix ${\mathbf{R}}_k\in {\mathbb{R}}^{d\times d}$, and

$${\mathsf{\Phi }}_k\left(e_i,e_j,D\right)={\mathbf{e}}_i^T{\mathbf{R}}_k{\mathbf{e}}_j$$

(9)

The weight ${\alpha }_{ijk}$ is the normalized score:

$${\alpha }_{ijk}=\frac{1}{Z_{ijk}}exp\left\{\frac{f^T(m_i,c_i){\mathbf{D}}_{k}f(m_j,c_j)}{\sqrt{d}}\right\}$$

(10)

where $Z_{ijk}$ is the normalization factor, ${\mathbf{D}}_k\in {\mathbb{R}}^{d\times d}$ is a diagonal matrix, and $f(m_i,c_i)$ is a single-layer neural network, which is used to obtain the local context representation of the mention $m_i$. For $c_i$, we first obtain the average $c_l$ of the word embeddings of the context words on the left of the mention $m_i$, then obtain the average $c_r$ of the word embeddings of the context words on the right, and finally take the concatenation of $c_l$ and $c_r$. In addition, Le and Titov [7] proposed two normalization methods of $Z_{ijk}$: normalization over relations and normalization over mentions. We adopt the method of normalization over mentions, then

$$Z_{ijk}=\sum _{\begin{array}{c}{j}^{{}^{\prime }}=1\\ j^{{}^{\prime }}\ne i\end{array}}^{n}exp\left\{\frac{f^T(m_i,c_i){\mathbf{D}}_{k}f(m_{j^{{}^{\prime }}},c_{j^{{}^{\prime }}})}{\sqrt{d}}\right\}$$

(11)

Now ${\sum }_{j=1,j\ne i}^n{\alpha }_{ijk}=1$, which means that for each relation k and mention $m_i$, we want to find another mention that has a relation k with the mention $m_i$. The entity embeddings ${\mathbf{e}}_i,{\mathbf{e}}_j$ here are obtained by training using word-entity co-occurrence counts in Wikipedia, so the global model is called the WikiEmbs model, and there is ${\mathsf{\Phi }}_{wiki}\left(e_i,e_j,D\right)=\mathsf{\Phi }\left(e_i,e_j,D\right)$. The WikiEmbs model essentially only uses the semantic information of the entities; that is, the more semantically related entities have a greater probability of appearing in the same document. However, the structural information in the knowledge graph is ignored, so we propose the KGEmbs model, which explicitly uses the knowledge graph structure information in the global model. Our motivation is that the knowledge graph structure should be maintained when the entity mentions in a document are mapped to the knowledge base. Assuming that there are $R_n$ relations (Section 3.2), the second term in Equation (3) can be written as:

$${\mathsf{\Phi }}_{KG}\left(e_i,e_j,D\right)=\underset{r\in R_n}{max}{f}_{KG}\left(e_i,e_j,r\right)$$

(12)

where $f_{KG}\left(e_i,e_j,r\right)$ is the scoring function of the knowledge graph embedding method; that is, for all relations R, the score of $(e_i,e_j)$ must be calculated, and then the maximum value is taken. The TransE [39] model is used here, and because the head entity and tail entity in $(e_i,e_j)$ cannot be distinguished, there is:

$$f_{KG}\left(e_i,e_j,r\right)=max\left({\gamma }_1-d\left(e_i+r,e_j\right),{\gamma }_1-d\left(e_j+r,e_i\right)\right)$$

(13)

where ${\gamma }_1$ is consistent with ${\gamma }_1$ in Equation (1), and

$$d\left(h+r,t\right)={∥\mathbf{h}+\mathbf{r}-\mathbf{t}∥}_1$$

(14)

Among them, the smaller $d(h+r,t)$, the greater the probability that the entities h and t have the relation r. In addition, $\mathbf{h},\mathbf{t}$ are the entity embeddings obtained by the TransE model, and $\mathbf{r}$ is the relation embedding. Finally, we combine the two global scores obtained above:

$$\mathsf{\Phi }\left(e_i,e_j,D\right)=f_{global}\left({\mathsf{\Phi }}_{wiki}\left(e_i,e_j,D\right),{\mathsf{\Phi }}_{KG}\left(e_i,e_j,D\right)\right)$$

(15)

where $f_{global}$ is a two-layer neural network.

4.3. Model Training

The solution of Equation (3) is NP-hard. Following Le and Titov [7], we also adopt max-product loopy belief propagation (LBP) to estimate the max-marginal probability:

$${\widehat{g}}_i\left(e|D\right)\approx \underset{\begin{array}{c}{e}_1,\dots ,e_{i-1}\\ e_{i+1},\dots ,e_n\end{array}}{max}g\left(e_1,\dots ,e_n\right)$$

(16)

Then we obtain the final score of mention $m_i$

$${\rho }_i\left(e\right)=f_{final}\left({\widehat{g}}_i\left(e|D\right),\widehat{p}\left(e|m_i\right)\right)$$

(17)

The one with the highest score is the candidate entity to be linked to, $f_{final}$ is another two-layer neural network, and $\widehat{p}\left(e|m\right)$ is the mention-entity prior. We optimize the parameters in the model by minimizing the ranking loss as follows:

$$L\left(\theta \right)=\sum _{D\in \mathcal{D}}\sum _{m_i\in D}\sum _{e\in C_i}h\left(m_i,e\right)$$

(18)

$$h\left(m_i,e\right)=max\left(0,{\gamma }_2-{\rho }_i\left(e_i^{*}\right)+{\rho }_i\left(e\right)\right)$$

(19)

where $\theta$ denotes the model parameters, $\mathcal{D}$ is the training corpus, D is a document, and $e_i^{*}$ is the gold entity.

5. Experiments

5.1. Datasets

To prove the effectiveness of our method, we conducted experiments on six popular open-source datasets, including an in-domain dataset and five out-domain datasets. For the in-domain dataset, we used the AIDA-CoNLL dataset [48], which contains AIDA-train, AIDA-A, and AIDA-B, which were used for training, verification, and testing, respectively. For out-domain datasets, we used MSNBC (MSB), AQUAINT (AQ), and ACE2004 (ACE), which are cleaned and updated by Guo and Barbosa [22]; and WNED-WIKI (WW) and WNED-CWEB (CWEB), which are automatically extracted from ClueWeb and Wikipedia corpora by Guo and Barbosa [22]. Among them, the latter two datasets are larger in scale and noisier, making linking of entities more difficult. Statistics of these datasets are summarized in Table 2. The target knowledge base is Wikipedia. Based on previous work [6,7], we do not consider mentions that have no corresponding entities in the KB.

Table 2. Statistics of experiment datasets. Gold recall is the probability that the candidate sets of mentions contain the ground truth entities.

Dataset	Number Mentions	Number Docs	Mentions per Doc	Gold Recall
AIDA-train	18,448	946	19.5	-
AIDA-A	4791	216	22.1	97.3
AIDA-B	4485	231	19.4	98.3
MSNBC	656	20	32.8	98.5
AQUAINT	727	50	14.5	94.2
ACE2004	257	36	7.1	90.6
CWEB	11,154	320	34.8	91.1
WIKI	6821	320	21.3	92.4

5.2. Candidate Entity Generation

To ensure fairness and comparable results, we use the candidate generation method of Le and Titov [7]. First, we select the top 30 candidate entities for each mention $m_i$ based on the prior $\widehat{p}\left(e|m_i\right)$, and then select 7 from them. Among them, the top 4 entities are selected based on $\widehat{p}\left(e|m_i\right)$, and the top 3 entities are selected based on the score ${\mathbf{e}}^T\left({\sum }_{w\in d_i}\mathbf{w}\right)$, where $\mathbf{e},\mathbf{w}\in {\mathbb{R}}^d$ are entity and word embeddings, respectively, and $d_i$ is the 50-word local context surrounding $m_i$. The quality of the candidate set obtained by the above method is shown in Table 2.

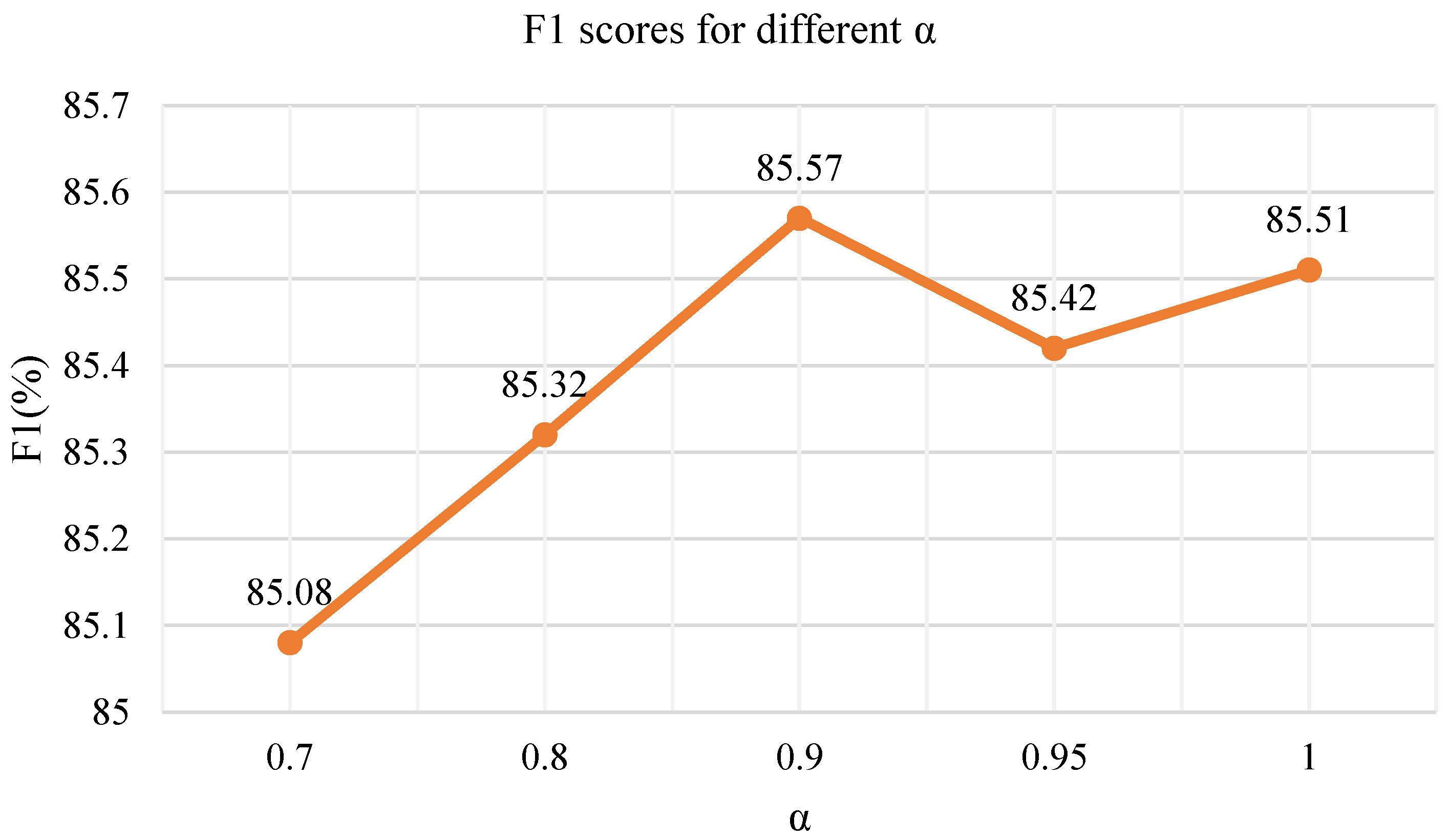
5.3. Hyper-Parameter Setting

Our models are implemented in the Pytorch framework. For the Local model, according to Ganea and Hofmann [6], we use the following hyper-parameters: $P=100,Q=25$ (Equation (5)). We set the dimensions of word embedding and entity embedding to 300, where word embedding and entity embedding are from [6]. For the WikiEmbs Global model, when calculating f (Equation (10)), we use the word embedding in Le and Titov [7] and the entity embedding in [6], both of which have a dimension of 300. In addition, according to [7], the number of LBP loops is set to 10, the dropout rate for f is set to 0.3, the window size $c_i$ of the local context used when calculating pairwise score functions is 6, and the number of relations in Ment-norm is 3. For the KGEmbs Global model, we use the TransE model to train entity embeddings and relation embeddings, where learning rate $\lambda =0.0001$, margin ${\gamma }_1=24$ (Equation (1)), batch size is 1024, hidden size is 300, and the dimensions of entity embedding and relation embedding are 300. When training the model, we set ${\gamma }_2=0.01$ (Equation (19)). When the F1 score of the model on the validation set reaches 91%, we adjust the learning rate from $1\times {10}^{-4}$ to $1\times {10}^{-5}$, and we stop learning if the F1 on the validation set does not improve after 20 epochs.

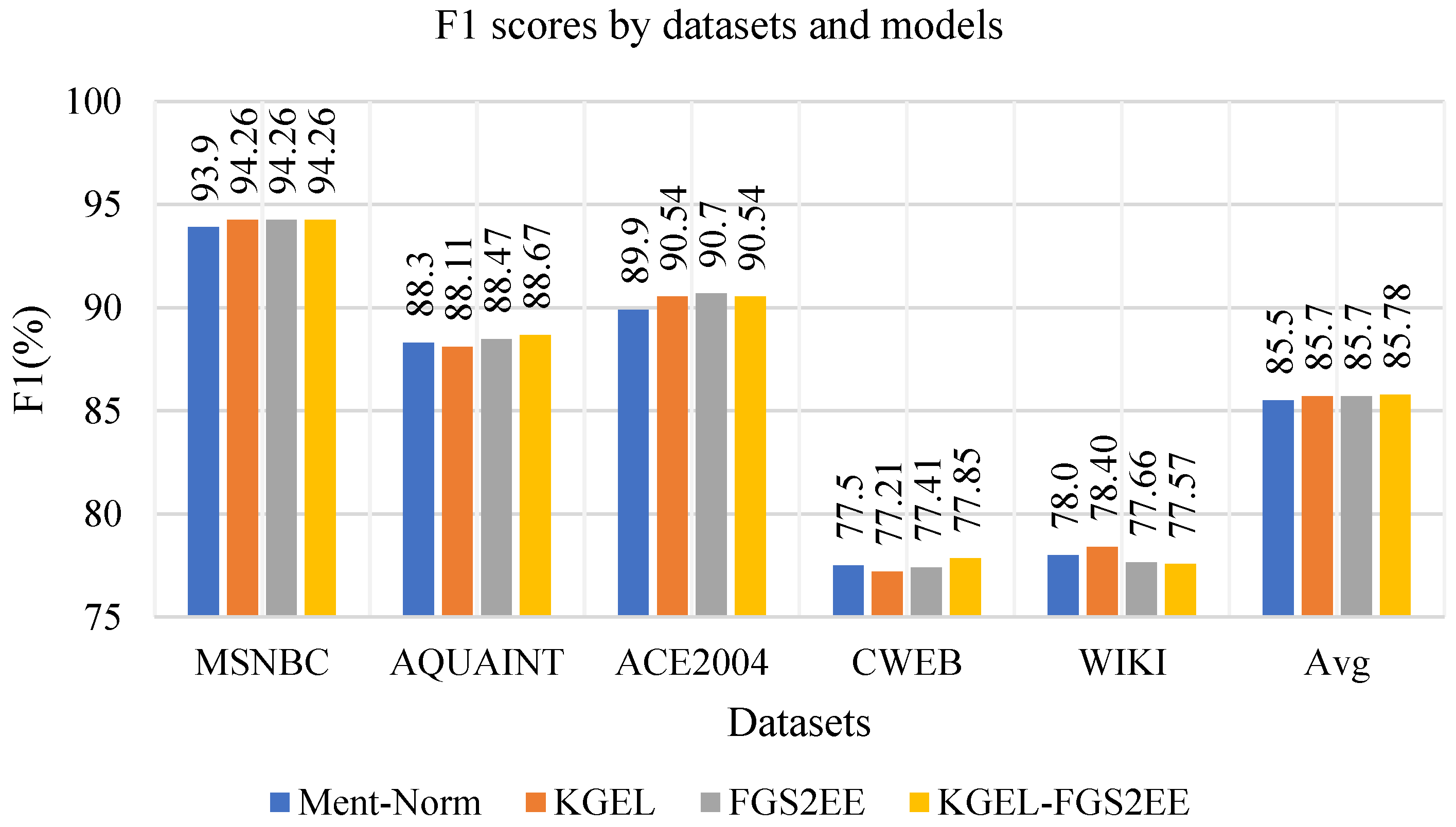
5.4. Main Results

The following methods are selected as baselines.

• AIDA [48] combines the previous methods into a comprehensive framework that contains three measures: the prior probability of an entity being mentioned, the similarity between the context of mention and the candidate entity, and the consistency among candidate entities for all mentions. It constructs a weighted graph whose nodes are mentions and candidate entities and calculates a dense subgraph to obtain an approximately optimal mention-entity mapping.
• GLOW is a global entity disambiguation system proposed by [49], which formulates the entity disambiguation task as an optimization problem with local and global variants.
• RI [50] combines statistical methods to perform richer relational analysis on the text. It proposes a modular formulation that includes the entity-relation inference problem. It also proves that the recognition of relations in the text is not only helpful for candidate entities, but also the subsequent ranking stage.
• PBoH [51] uses a graphical model to perform global entity disambiguation. It simultaneously disambiguates mentions in a document by using the co-occurrence probability between entities in the document and the local context information of the mentions. It uses LBP to perform approximate inference.
• Deep-ED [6] introduces an attention mechanism into the local model, and the context words of mentions are hard pruned. Its global model is a fully-connected pairwise conditional random field. Because the problem is NP-hard, it uses LBP to iteratively propagate entity scores to reduce complexity.
• Ment-Norm [7] models the latent relations between mentions and adds them to the global model in the form of features. There are two options for normalization, where it is normalization over mentions.
• DCA-SL [9] regards entity linking as a sequence decision task and uses the previous decision as dynamic contexts to improve the later decisions. It explores supervised learning strategies for learning the DCA model.
• DCA-RL [9] involves the use of reinforcement-learning strategies to learn the DCA model.

Table 3 shows micro F1 scores on AIDA-B and five out-domain test sets. Compared with Deep-ED [6], our method achieves a substantial improvement on both the in-domain dataset AIDA-B and the average result on five out-domain datasets. Moreover, KGEL’s F1 score is still 0.4% higher than Ment–Norm on the AIDA-B dataset, and for the average result on the five out-domain datasets, KGEL also has an improvement of 0.2% F1 on Ment–Norm. It should be noted that although the DCA-SL model has good results on the datasets AIDA-B and MSNBC, it has poor results on the dataset CWEB, so its average result on the out-domain datasets is not good. The same is true for DCA-RL. This indicates that our method has better generalization. Therefore, overall, our method achieves very competitive results on the AIDA-B dataset. Moreover, KGEL achieves higher F1 scores than previous methods on the ACE2004 dataset as well as on the average of out-domain datasets. This fully demonstrates the effectiveness of our method, i.e., the importance of knowledge graph structure for entity linking.

Table 3. F1 scores on AIDA-B and five out-domain test sets. The last column is the average of F1 scores on the five out-domain datasets. The best results are in bold.

Model	AIDA-B	MSNBC	AQUAINT	ACE2004	CWEB	WIKI	Avg
AIDA	-	79	56	80	58.6	63	67.32
GLOW	-	75	83	82	56.2	67.2	72.68
RI	-	90	90	86	67.5	73.4	81.38
PBoH	87.6	91	89.2	88.7	-	-	-
Deep-ED	92.22	93.7	88.5	88.5	77.9	77.5	85.22
Ment–Norm	93.07	93.9	88.3	89.9	77.5	78	85.5
DCA-SL	94.64	94.57	87.38	89.44	73.47	78.16	84.6
DCA-RL	93.73	93.80	88.25	90.14	75.59	78.84	85.32
KGEL(ours)	93.47	94.26	88.11	90.54	77.21	78.40	85.7

5.5. Ablation Study

In order to study the role of each module of the model, an ablation study was also performed in this research, and the experimental results are shown in Table 4. We utilize the following variants:

Table 4. F1 scores of the ablation experiments.

Model	AIDA-B	MSNBC	AQUAINT	ACE2004	CWEB	WIKI	Avg
KGEL	93.47	94.26	88.11	90.54	77.21	78.40	85.7
- KGEmbs	93.07	93.9	88.3	89.9	77.5	78.0	85.5
- WikiEmbs	87.16	92.12	81.54	87.73	72.84	68.96	80.64
- local	84.86	91.05	79.16	86.92	70	64.46	78.32
- WikiEmbs

• KGEL is our proposed method, which includes three modules: Local model, WikiEmbs Global model, and KGEmbs Global model.
• -KGEmbs represents the results on each dataset after removing the KGEmbs global model.
• -WikiEmbs represents the experimental results after removing the WikiEmbs global model.
• -local-WikiEmbs is the result of removing the Local model and WikiEmbs Global model at the same time.

As can be seen in Table 4, when the KGEmbs Global model is removed, the results on four datasets and the average result on the out-domain datasets drop dramatically. This proves the validity of the KGEmbs Global model, i.e., the necessity of introducing knowledge graph structural information. Similarly, we can find that the results on each dataset drop more significantly when the WikiEmbs Global model is removed, indicating that using only the structural information in the knowledge graph is insufficient because there is a certain sparsity in the knowledge graph, i.e., not every pair of entities has a clear relationship with each other, so the structural information of the knowledge graph has a certain guiding effect on the linking of entities, but cannot be used independently. After removing the Local model based on -WikiEmbs, we find that the results on each dataset have further decreased, which illustrates the necessity of the local model. Thus, the entire ablation experiment shows that all modules of the model are valid.

5.6. Other Ways of Using KG Structure

In addition to using knowledge graph embedding methods such as TransE on triples, we also try to use triples directly. We consider two entities to be related if there is a relation between them, i.e., two entities that can form a triple are related. Therefore, for entity $e_1$, we obtain the entity set $E_r$ related to it from the triples. For example, in Table 1, the related entity set of entity Q1 is {Q523, Q136407, Q323}. To incorporate information about its related entities in the representation of entity $e_1$, we perform the following operations:

$${\mathbf{e}}_r=\frac{1}{a}\sum _{i=1}^a{\mathbf{e}}_i$$

(20)

$$\mathbf{e}=\alpha {\mathbf{e}}_1+\left(1-\alpha \right){\mathbf{e}}_r$$

(21)

where ${\mathbf{e}}_i\in E_r$ is the entity associated with entity $e_1$, a is the size of the entity set $E_r$, ${\mathbf{e}}_r$ is the average embedding of entities associated with entity $e_1$, ${\mathbf{e}}_1$ is the original embedding of entity $e_1$, $\mathbf{e}$ is the embedding of entity $e_1$ after fusing information, and $\alpha$ is a hyperparameter. This operation is equivalent to using 1-hop information of the knowledge graph.

In order to determine the optimal value of $\alpha$, we performed a lot of experiments for different $\alpha$; that is, directly replacing the original entity embedding with the entity embedding after fusion, and the model structure is consistent with Le and Titov [7]. The experimental results are shown in Figure 4.

Figure 4. F1 scores for different $\alpha$, where F1 is the average result on five out-domain datasets.

From the figure, it is clear that the best results are obtained when $\alpha =0.9$. In addition, we also tried some other variants:

• Ment-Norm is the model of Le and Titov [7] and also our basic model.
• KGEL is our main model; that is, the entity and relation embeddings obtained by the knowledge graph embedding method are used in the global model of entity linking.
• Related-Fixed refers to the method of using related entities mentioned in this section, in which the parameter $\alpha$ is fixed at 0.9.
• Related-Vari means that the parameter $\alpha$ is variable; that is, it changes during training.
• Based on Related-Vari, Related-Vari-diff makes the $\alpha$ in the global model and the local model different.
• Related-nn indicates the use of a neural network to fuse ${\mathbf{e}}_1$ and ${\mathbf{e}}_r$.

From the Table 5, it can be seen that the parameter $\alpha$ fixed to 0.9 is the optimal result when using related entities. The result of Related-Fixed is slightly better than that of Ment–Norm, indicating that the knowledge graph structure is beneficial for the effect of entity linking. However, the result of Related-Fixed is worse than that of KGEL, which shows that how the knowledge graph structure is used is also very important. Obviously, it is better for us to use the entity embedding obtained by the knowledge graph embedding for the characteristics of the global model considering the correlations between entities.

Table 5. F1 scores of different variants on out-domain datasets.

Model	MSNBC	AQUAINT	ACE2004	CWEB	WIKI	Avg
Ment–Norm	93.9	88.3	89.9	77.5	78.0	85.5
KGEL	94.26	88.11	90.54	77.21	78.40	85.7
Related-Fixed	94.26	88.39	89.74	77.41	78.06	85.57
Related-Vari	93.65	88.25	88.13	77.07	77.82	84.98
Related-Vari-diff	93.8	87.41	87.73	77.01	77.39	84.67
Related-nn	92.58	86.43	88.13	74.87	71.67	82.74

5.7. Better Baseline

To further prove the importance of the knowledge graph structure to the entity linking, we used the KGEmbs module for a better baseline. FGS2EE [8] is an improvement of Ment–Norm [7], which introduces fine-grained semantic information into the original entity embedding to improve the model performance. KGEL-FGS2EE adds the KGEmbs module on the basis of FGS2EE. The experimental results are shown in Figure 5. We can find that for the average F1 score, KGEL-FGS2EE can further improve the performance based on FGS2EE. This shows that the KGEmbs module we proposed is effective. Similarly, the KGEmbs module can also be used in other methods. In other words, it should be useful to introduce knowledge graph structure based on other methods.

Figure 5. F1 scores of different baselines on out-domain datasets.

5.8. Case Study

Table 6 shows the mentions and their real entities, as well as the results predicted by the model. Examples of incorrect model predictions are shown in red, e.g., “Scotland” is predicted to be “Scotland_national_cricket_team”. This shows that in some cases, only semantic information cannot complete the link to the entity. We note that a document contains a knowledge graph structure. As shown in Figure 6, there is a certain connection between the entities “Scotland” and “England”. When calculating the global score, the score between “Scotland” and “England” will be higher than the scores between other entities, indicating that mentions “English” and “Scotland” are more likely to refer to entities “England” and “Scotland”, respectively. Therefore, we can guide the prediction of mention “Scotland” based on this connection. Similarly, we can use the knowledge graph structure between “Edgbaston” and “Birmingham” to guide the prediction of “Edgbaston”. In summary, the introduction of the knowledge graph structure solves the problem of incorrect prediction of some mentions.

Table 6. The examples predicted by the baseline model. The bold font in the first column denotes the mention, the second column is the entity predicted by the model, and the last column is the real entity corresponding to the mention.

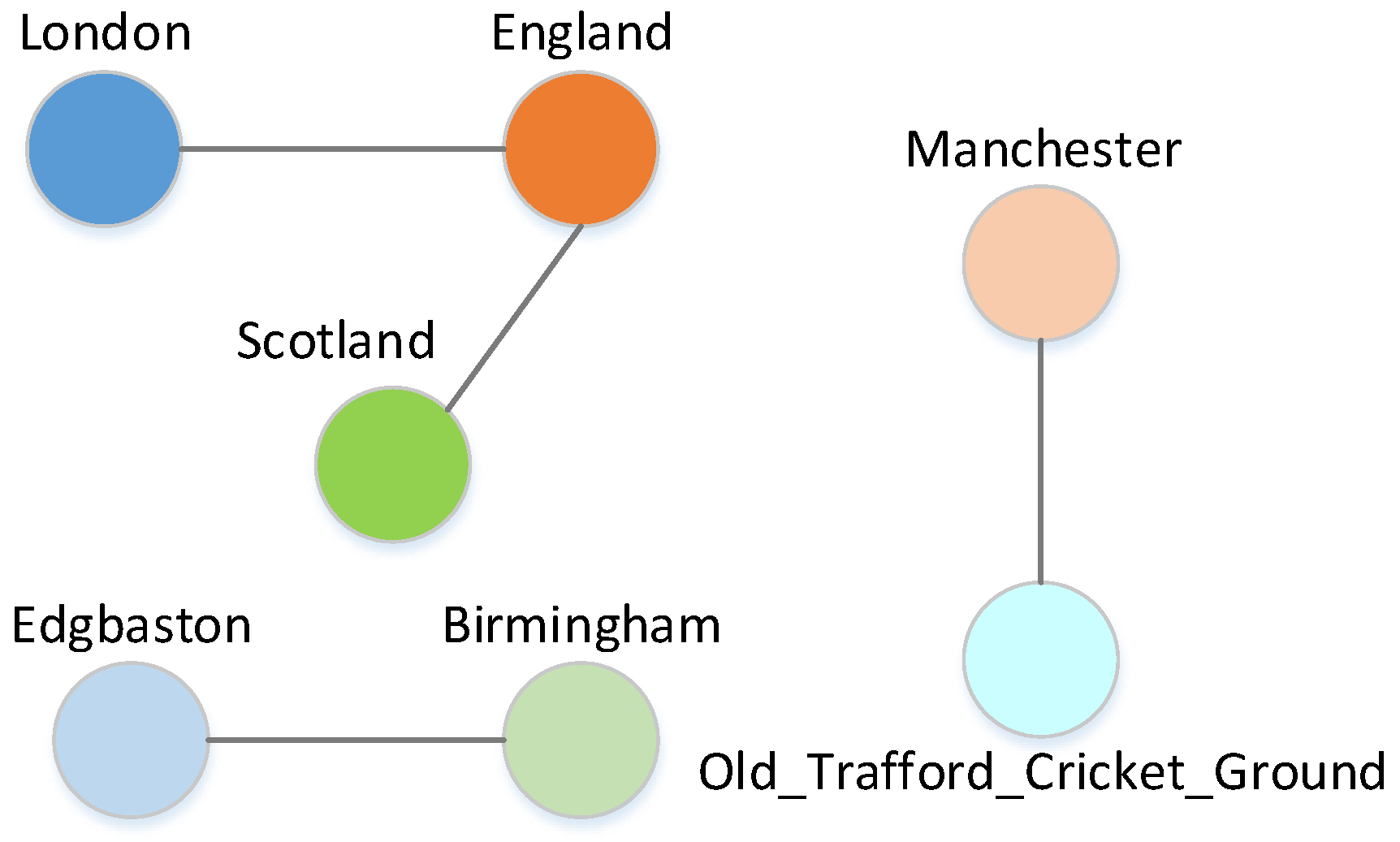
Mention	Pred	Gold
…Arrive in London May 14…	London	London
…matches against English county sides…	England	England
…Counties and Scotland Tour itinerary…	Scotland_national_cricket_team	Scotland
…match (at Edgbaston,Birmingham)…	Edgbaston_Cricket_Ground	Edgbaston
…Edgbaston, Birmingham) June…	Birmingham	Birmingham
…international (at The Oval, London)…	The_Oval	The_Oval
…Sussex or Surrey (three days)…	Surrey_County_Cricket_Club	Surrey_County_Cricket_Club

Figure 6. The knowledge graph structure contained in the example.

5.9. Execution Times of the Models

To investigate the complexity of the method, we conducted experiments on the training and inference time of the model. Among them, the model was trained on the AIDA-train dataset and inference was performed on AIDA-B and five out-of-domain datasets. The results are shown in Table 7, where the second column indicates the time spent for one epoch during model training, and the third column indicates the total time spent by the model for inference on several datasets. As can be seen from the table, under the same experimental conditions, our proposed model KGEL is close to the model Ment–Norm [7] in both training and inference time, because we calculated the scores between entities in the KGEmbs Global model offline. In addition, the epochs required for KGEL and Ment–Norm to converge are similar, so the introduced knowledge graph structure does not have much impact on the execution times.

Table 7. The execution times of the models.

Model	Train Time/Epoch	Inference Time
Ment-Norm	23 s	9 s
KGEL	25 s	10 s

6. Conclusions

In this work, we proposed a simple but effective method, KGEL, to introduce knowledge graph structure information into entity linking. In addition to considering the relevance of entities at the semantic level, the relations between entities were also considered from the perspective of structure. We first obtained the triples and then trained them using the knowledge graph embedding method to obtain the entity embeddings and relation embeddings that contained the graph structure. Finally, the entity embeddings and relation embeddings obtained above were used in the calculation of the global score. Extensive experiments on multiple datasets prove the effectiveness of our method; that is, the knowledge graph structure is useful for entity linking tasks. In addition, KGEmbs can be used as a module to enhance the effects of other baseline models.

In future work, we will solve the sparsity problem of the knowledge graph. Not every entity has a corresponding triple, nor is there a relation between every pair of entities. In addition, we will try to use better methods to utilize the knowledge graph structure, such as other knowledge graph embedding methods. As introduced in Section 2.3, some recent knowledge graph embedding methods such as HAKE [44], PairRE [45], DualE [46], and EIGAT [47] can better encode entities and relations in knowledge graphs, and theoretically they should further improve the performance of entity linking.