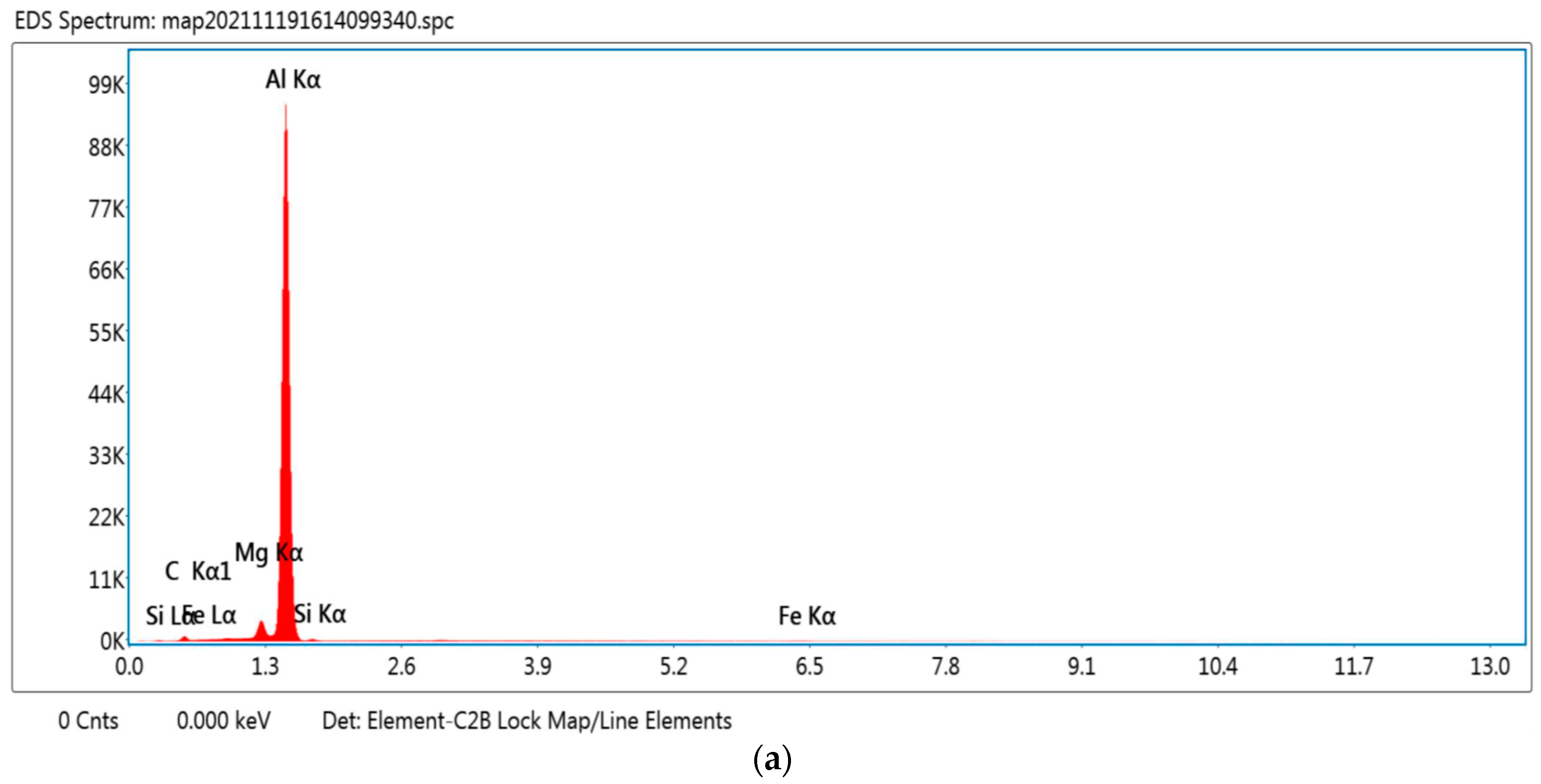
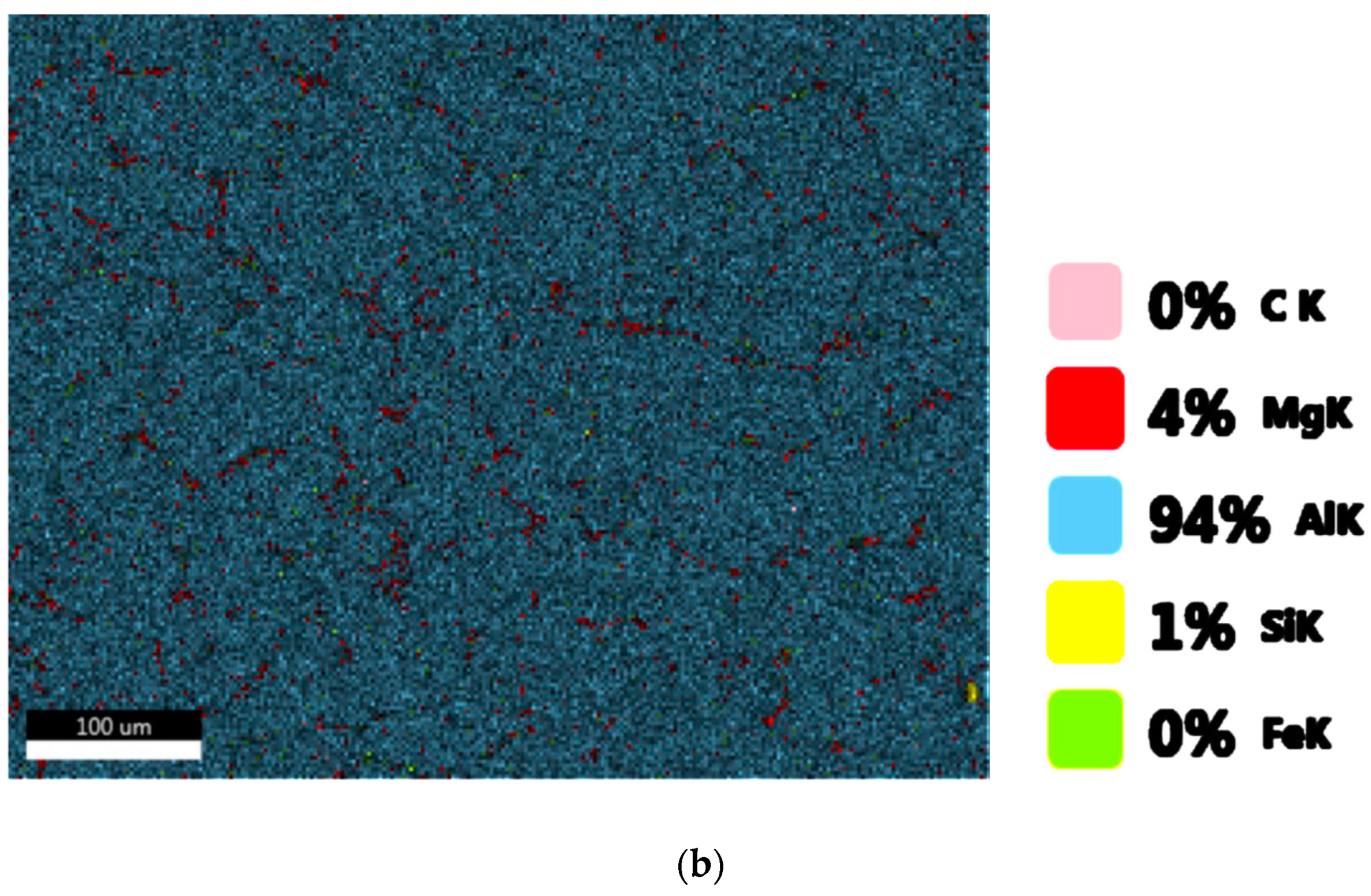
1. Introduction
The requirement of improved strength-to-weight ratio materials has led to the introduction of composite materials in many applications such as structural, automotive, space, manufacturing, etc. The major challenges while switching over to composite materials from conventional metals or alloys is the machining of the material to the required size and shape. Obtaining the materials of near-net shape requires a machining process. Therefore, machining becomes necessary for the manufacturing of a part using composite materials. This leads to the use of nonconventional machining processes where the tool and workpiece will never have physical contact and the machining is carried out by using a spark or chemical process or by using a water jet. In the nonconventional machining process, recent trends have inclined towards EDM due to its cost effectiveness and the capability to handle various composites effectively. These reasons have persuaded a lot of manufacturers to opt for EDM as a machining process for hard-to-machine composite material, mainly metal matrix composites for manufacturing different components.
Natraj and Ramesh [
1] worked on optimising the parameters of Al6061-5% Al
2O
3-3% SiC-2% E-glass in EDM. The work identified current and pulse-on time as the major contributors in surface roughness and MRR. It was also identified, using the Box–Behnken design of experiments of response surface methodology (RSM) that optimum current was 12.4 A, pulse-on time was 30 µs and pulse-off time was 7 µs. The work also identified that the addition of E-glass did not affect the properties of the material. Murugesan and Balamurugan [
2] developed an experimental analysis using the grey relation method for Al6061 reinforced with 15% SiC. The experiment was also conducted using a change of polarity of the workpiece. It was identified that the current was the significant contributor in the output parameters of MRR and surface roughness. It was also identified that the pulse-on time and the pressure of lubricant also plays a significant role in the output parameters. The identified optimal values for current, pressure of dielectric and pulse-on time were 4 A, 0.5 kg/cm
2 and 400 µs, respectively. The work also identified that a negative polarity of the electrode provided better results
Balbir Singh et al. [
3] experimented to identify the contributing parameters for Al6061 with 10% SiC. The work concluded that the higher current increases the MRR and tool wear rate, but diminishes the surface roughness. The increase in pulse-on time increases the MRR as well as the surface roughness. The optimum values of pulse-on time and pulse-off time were identified to be in the range of 90 to 200 μs for better output parameters. Dey, S Debnath and Pandey [
4] used grey relation analysis (GRA) along with the response surface methodology (RSM) approach to optimise the Al6061 cenosphere composite. It was identified that the hybrid approach is able to provide an improved result when compared with the initial experimental results. The optimum values identified were a pulse current of 9.9126 A, pulse-on time of 210.002 μs, reinforcement content of 3.6936% and flushing pressure of 0.5999 MPa. Wuyi Ming et al. [
5] worked on optimising the parameters for Al6061, Inconel and SKD11. The work identified that the percentage of energy transferred to the workpiece was small for all three materials. The range of energy transfer to the workpiece was identified to be between 8 and 12% for Al6061 and between 3 and 4% for Inconel and SKD 11. It was also identified that for difficult-to-cut materials, the increase in discharge current reduced specific discharge energy, but the energy distribution to the workpiece was found to be constant.
Narendra Singh et al. [
6] conducted ANOVA-based analysis on Al6061 with 10% SiC. The work identified that the increase in current and pulse-on time increased the parameters considered, which were mainly MRR and surface roughness. By using RSM, the MRR was improved by 30.13% in powder-mixed EDM and 24.27% in normal EDM. Rajkumar et al. [
7] worked on Al6061 reinforced with boron carbide and graphite, manufactured using stir casting and heat-treated through two different processes, which were conventional and microwave-based heat treatment. The work also identifies current and pulse-on time as the major parameters contributing to MRR and surface roughness. The design values were identified to be 9 A current and 46 μs pulse-on time for the optimum results. Nandakumar and Kanakaraj [
8] studied the mechanical properties of two different aluminium-based composites. It was concluded that the increase in the addition of graphite and SiC had enhanced the tensile strength and hardness, whereas addition of graphite in alumina-reinforced aluminium metal matrix composite does not provide any variation in tensile strength. Arunkumar and Swamy [
9] carried out the study on the mechanical properties of the Al6061–fly ash-E-glass fibre composites. The work concluded that the addition of fly ash had improved the hardness and tensile strength by nearly 60–70%, whereas the addition of E-glass fibre had not shown any significant influence in the properties of the composite. Prasanth et al. [
10] worked on comparing the mechanical properties of Al6061 mixed with SiC and graphite as the reinforcements. It was observed in the work that the addition of 12% SiC as the reinforcement increased hardness by 50% and tensile strength by 60%, whereas the addition of the same percentage of graphite reduced the hardness by 25% but increased the tensile strength by 60%. Nagendran et al. [
11] studied the mechanical properties of Al6061 reinforced with SiC and titanium dioxide. The work identified that the tensile strength dropped when the addition of the reinforcement was more than 4% each in the matrix. However, hardness continued to increase with the increased reinforcement percentage. The hardness improvement was observed to be nearly 5.5% when 6% SiC and TiO
2 was added to the base matrix. Nagendra Maurya et al. [
12] studied the mechanical property of the Al6061 composite with different percentages of SiC. The work concluded that the hardness, as well as tensile strength of the composite, improved by 12.5% with 5% inception of SiC into the composite. Uthayakumar et al. [
13] worked on functionally graded aluminium matrix composites for machining parameters of surface roughness, electrode wear rate, overcut and power consumption in EDM. The work aimed for the application of the material in a disc-brake rotor. The work identified that the pulse current plays a major role in the output parameters. The optimised values of current and pulse-on time were identified to be 5 A and 50 μs. Marafona and Araujo [
14] conducted studies on the influence of the workpiece hardness on the EDM process for different alloys. It was identified in the work that the workpiece hardness and related parameters have significant influence on the surface roughness and MRR of the EDM process. The work aimed at developing a model based on the input data for steel, and identified that the derived model is able to predict the values with a maximum error of 5.2% for MRR and 0.8% for surface roughness to the experimental values. Raza et al. [
15] conducted a study on Al6061-SiC composite using different electrodes on its performance variation for MRR and surface roughness. It was identified that brass electrode provided a better MRR and surface finish when compared to copper and steel electrodes. The brass electrode provided 23.2% higher MRR and 20.3% better surface finish when compared with copper electrode. Steel electrode provided 35.3% and 32.3% less MRR and surface finish, respectively. S. Singh [
16] conducted a study on Al6061 with Al
2O
3 as the reinforcement using grey relational analysis. The work identified that pulse current is the major factor in determining the MRR and surface roughness of the composite. Kashif Ishfaq et al. [
17] conducted an experimental study for the machining of Al6061-7.5% SiC composite using wire EDM. The work indicated on the challenges in the machining of Al6061-based composites. The work evaluated the magnitude of errors due to the wire vibrations and lag. The work evaluated the corner variations and errors in cutting orientations. These variations were expected due to the presence of SiC as the reinforcement element in the composite. The work identified that the lower current with a lower pulse-on time and a higher voltage provided low variations in the considered parameters. Doresamy et al. [
18] worked on the optimization and modelling of wire EDM of Al6061-based composite reinforced with Silicon Carbide particles. The work identified the optimum parameters of current, pulse-on time, pulse-off time, voltage and wire speed for the MRR of the specimens. It was also identified that current is the major contributor for the considered parameter. A regression model was also developed for predicting the MRR for different compositions in this work. The optimum values were identified as current—5 A, ton—40 µs, toff—10 μs and voltage—90 V. H. Singh et al. [
19] worked on the MRR and tool wear rate of Al6061 with copper and brass electrodes. The work identified that the MRR was maximal at a peak current of 15 A for both the electrodes, and that tool wear was minimal for copper electrode when compared to brass electrode.
Mythili and Thanigaivelan [
20] carried out a study of wire EDM in Al6061-Al
2O
3 composite with reinforcement weight fractions of 6 and 8%. The influence of the input parameters of current, gap voltage, wire tension and dielectric pressure were considered for this work. The work concluded that the current is the major contributor for the variation in MRR and surface roughness. The optimum values were identified using TOPSIS analysis. N. Velmurugan et al. [
21] worked on the development of a prediction tool using ANFIS to identify the surface quality of an Al6061-based composite by identifying current, wire feed, pulse-on time and pulse-off time. The work was able to predict the behaviour with very close proximity to the experimental results. The average error rate was observed to be 1.67%. Singh et al. [
22] worked on Al6061 composites with SiC and graphite reinforcement with the independent variables of current, voltage, pulse duration and tool material. The study was carried out using ANOVA. The output parameters determined were MRR and R
a. The work identified that current is the major contributing factor and that an increase in current and pulse duration increased the MRR, but reduced surface finish. Meanwhile, the increase in voltage reduced MRR and surface finish. The work also identified that the electrode material has a significant contribution to the output parameters. Kareem et al. [
23] studied the characteristics of Al6061 composites manufactured using stir casting and compared the material properties with the base alloy. It was identified in the work that the material properties were enhanced with the addition of reinforcement in the base alloys and that stir casting is an economic and efficient technique for the development of Al6061 composites. Amruth Babu and Gurupavan [
24] worked on the wire EDM machining of Al6061 composite with various percentages of SiC added to it. The work was conducted with the input parameters of current, pulse-on time, pulse-off time and wire feed rate. It was identified that the surface roughness reduced with the addition of SiC in the base alloy. The work also identified that the increase in the percentage of SiC reduced the surface roughness. Thiagarajan et al. [
25] carried out a study of the machining of Al6061 composite with nano SiC and nano ZrO
2 as reinforcements using wire EDM, using ANOVA and multiresponse optimisation. The work identified that second-order mathematical equations are required to identify the influencing parameters for kerf width and surface roughness. The work also illustrated that there was a linear correlation between surface roughness and pulse-on time. The kerf width showed an exponential increase with increase in pulse-on time. The pulse-off time showed a directly opposite phenomenon when compared to pulse-on time. The increase in gap voltage showed a decrease in the kerf width as well as the surface roughness. Using multiresponse optimisation, the optimum values were identified—while keeping the input parameters—as 6.11 µs as pulse-on time, 6.52 µs as pulse-off time and 67.8 V as gap voltage. Anjani Srivastava et al. [
26] worked on the optimisation of the EDM of the Al6061 composite with 8% SiC. The work applied response surface methodology (RSM) for the mathematical model, and the Box–Behnken Design (BBD) approach was employed for the experimental design. The input parameters employed were current, pulse-on time and duty cycle. The work evaluated the material removal rate (MRR), electrode wear rate (EWR) and surface roughness of the machined specimen. The variation in MRR was dominated by the current. The variation in EWR was dominated by pulse-on time and the surface roughness was dominated by current as well as pulse-on time. The optimum parameters for MRR were identified to be 8 A peak current, 183.84 msec T
on and 8.67 duty cycle using the theory of desirability. Bindya Devi et al. [
27] carried out a comprehensive review on the recent trends in the machining of aluminum-based metal matrix composites in the recent scenario. The review covered the importance of EDM in the machining of difficult-to-machine composites of aluminum and identified the need for the prediction of the output parameters of an EDM process based on material properties and the input parameters. Shyn et al. [
28] worked on the optimisation of major and minor process parameters in obtaining the MRR, EWR and R
a for Al6061-6% B
4C metal matrix composites (MMC). Extensive work was carried out with the input parameters as current, spark-on time, spark-off time, pulse-on time, gap voltage, duty factor and flushing pressure. The work used RSM to optimise the parameters. The MRR showed the output value at the error level of 0.167%, the surface roughness showed an error rate of 2.31% and the electrode wear rate showed an error in the range of 9.31% with the experimental value. Ishfaq et al. [
29] worked on the machining of Al6061-7.5% SiC composite in high-speed wire EDM. The work aimed at optimizing the kerf width, surface roughness and cutting rate based on the input parameters of current, voltage and pulse-on time. The voltage was identified to be the dominating factor for surface roughness. Current was identified to be the dominating factor for kerf width and the pulse-on time was the dominating factor in cutting rate. A better surface finish was achieved with lower current and voltage. The Scanning Electron Microscope (SEM) images revealed that narrow craters are produced when the machining is carried out at lower voltage and current. RSM was used to predict the error levels in the corner accuracy as well as the cutting orientations. The model was able to predict the values within 5% error. M Singh and S Maharana [
30] worked on EDM machining of Al6061 composite reinforced with SiC and graphite. The work was carried out with the input parameters, current, pulse-on time, pulse-off time and gap voltage and the output parameter was set as MRR. The work identified that voltage has very low significance in the MRR of the material. It was also identified that the current and pulse-on time are the major contributors to the MRR. Increased pulse-off time reduced the MRR. Golshan et al. [
31] carried out an optimisation study of the Al/SiC composites using the nondominated sorting genetic algorithm, which is a multiresponse algorithm for identifying the optimum MRR and Ra of the composite. Since both output parameters are contrasting, the work chose a multiresponse algorithm to optimise both the parameters. Two different algorithms, the single genetic algorithm (SGA) and nondominated sorting genetic algorithm (NSGA-II) were identified for the optimisation, and the author finalised the work based on NSGA-II. The input parameters considered were current, pulse-on time, gap voltage and the volume fraction of SiC in the composite. The work identified that the optimisation in both MRR and Ra can be achieved by keeping the current and pulse-on time constant and varying the voltage and the volume fraction of SiC. This algorithm, once developed, can provide a proper optimised condition for the specified input parameters. Jithin and Suhas [
32] carried out an extensive review on electric discharge texturing (EDT) which is a modified EDM used for different applications. The work discussed the diverse level of applications of EDT and different types of EDT adopted for these applications. The work elaborated on the different parameters which controls the output surface topology in EDT. The variation of the surface roughness due to the variation in the parameters was also detailed in the review paper. The development of deliberate surface modifications using EDM and EDT was also discussed. Various modelling methods with the comparison of the output models were carried out in this work. The work identified that 3D multicrater analysis is required for the proper modelling of EDT. Peta et al. [
33] carried out research work on the surface topology of an EDM machining of Al6060 alloy with discharge energy as the only input parameter. The study identified the strong influence of discharge energy in the surface topology and the parameters linked with the discharge energy were managed automatically by the EDM machine. The work identified that the generated model failed at finer scales below 11 μm. The best results on the relationship of surface topology with discharge energy were identified to have occurred in the values ranging from 36 μm to 41 μm. Peta et al. [
34] conducted investigative studies to identify the relationship between wettability and surface microgeometry of Al6060 alloy. The work was able to identify a strong correlation between parameters pertaining to surface texture and the wettability of the alloy. The size and shape of the surface created due to EDM was identified to have a direct link with the discharge energy and the contact angle, which is the inverse of wettability of the material. Joshi et al. [
35] carried out machining of stainless-steel surfaces using copper electrode, employing dry EDM with a pulsating magnetic field. The pulsating magnetic field provided a rotating magnetic wave around the spark, thereby improving the spark density. It was identified that the MRR improved by 130% with zero electrode wear when dry EDM with a pulsating magnetic field was used for the machining. Dhadda et al. [
36] worked on the enhancement of pool-boiling heat transfer of Al6061 alloy during EDM. The input parameters which were considered for the study were discharge current and pulse-on time. A data-dependant system was employed to identify the relation between the surface topology and boiling performance during the machining process. The average roughness parameter was identified to have a greater correlation with the crater diameter. Golshan et al. [
37] carried out studies on the optimisation of parameters for drilling of Al7075 alloy which has been extensively used in the aerospace industry. The NSGA-II algorithm was used for the development of optimised surface roughness and the dimensional error of the drilled hole. The cutting speed, feed rate and drill diameter were taken as the important input parameters for the model. A linear pattern was observed for the relations between the dimensional error and the surface roughness. The algorithm was able to successfully identify the dimensional error for the required surface roughness or vice versa. Saravanan et.al. [
38] carried out numerical and finite-element analysis (FEA) for simulating drilling in CFRP laminates and the results were compared with the experimental result. The numerical analysis was carried out using a genetic algorithm. The results indicate that the variations observed using the FEA showed 20% variation and the genetic-algorithm-based mathematical model showed a variation in the range of 10%. The numerical analysis also identified the optimised condition for the input parameters for the improved output parameters.
Identification of the optimum input parameters had been a major challenge in the machining of the composites using EDM. In an EDM process, a spark between the tool and the workpiece through a dielectric medium leads to material removal from the workpiece. The process of material removal is very complex, as the phase change from a solid to plasma state of the material of the workpiece and the removal of material by the flowing dielectric also plays a vital part in the proper material removal and the surface roughness of the final component. Proper removal of the materials from the workpiece due to sparks reduces the chance of formation of a white layer on the surface of the workpiece. The re-solidification of the molten metal during the pulse-off time leads to the formation of a white layer on the surface of the workpiece. This formation of white layers on the machined surface of workpiece due to resolidification of the melted material also adds to the uncertainty of the output parameters such as MRR and surface roughness.
The referred works indicate that the material property of the workpiece had a vital role in the output parameters of the machining. This work aims to predict the output parameters linking it with hardness, which is identified to be one of the major properties of a composite material [
14]. This work aims to provide a prediction of the different output parameters based on the experimental values obtained by Singh [
16], Raza [
15], Murugesan [
2] and Nataraj [
1] in the machining of different combinations of Al6061 composites and to compare the mathematical models to identify and predict the output parameters based on the variation of these parameters. The mathematical model was validated by carrying out experiments on a different combination of Al6061 composite, viz. Al6061-1% SiC metal matrix composite.
The objectives of the present work are:
To identify the optimum mathematical model for Al6061 metal matrix composite with different combinations of reinforcements, mainly SiC;
To identify the pattern of variation of coefficients of different input parameters used in the mathematical model based on the hardness of each material;
To create an equation for each coefficient, thereby predicting the mathematical model for a new combination once the hardness of the material is obtained;
To verify the derived equations by carrying out experiments on Al6061-1% SiC MMC and comparing the model results with the experimental results.
3. Results and Discussion
The work was conducted based on Al6061 with different compositions of SiC. The input parameters considered were current (A), pulse-on time (Ton) and pulse-off time (Toff). The developed ANOVA considered ONE degree of freedom for all the terms.
The ANOVA table and the mathematical formulation were prepared.
Table 2 and
Table 3 provide the summary of the ANOVA for the materials considered for the work. The first four material data were taken from the already published manuscripts [
1,
2,
15,
16] and the last three materials were developed and experimented to obtain a satisfactory regression equation to enable the extrapolation.
The characteristic equations obtained were:
The first set of material taken was Al6061-15% SiC based on the work by Murugesan and Balamurugan [
2]. The work included 18 experiments, out of which 9 experimental values were adopted, ignoring the 9 values tabulated with a different polarity of electrode and workpiece. The input values considered for the experiment were: A (4, 8 and 12 A), T
on (200, 400 and 600 μs) and T
off (20, 40 and 60 μs). The equations obtained are provided as Equations (1) and (2). The second material considered was Al6061-20% Al
2O
3. The input for this work was taken from Singh [
16]. A total of 18 experiments in his work were used for this ANOVA. The values of A were 10, 15 and 20 A; the values of T
on were 50, 100 and 200 μs; and the values of Toff were calculated based on the duty cycles of 0.4, 0.5 and 0.7. The equations obtained are provided as Equations (3) and (4). The third material considered for the work was Al6061-5% Al
2O
3-3% SiC-2% E-glass [
1]. The ANOVA was generated with 15 experimental values provided by the author. The experiment was carried out for three values of A (5, 10 and 15 A), T
on (30, 40 and 50 μs) and T
off (7, 8 and 9 μs). The equations for MRR and surface roughness is provided in Equations (5) and (6).The fourth material considered was Al6061-7.5% SiC. The values were taken from the work of Raza et al. [
15]. The work consisted of 15 experimental values. The input values of A were 3, 6 and 9; the values of T
on were 10, 20 and 30 μs; and the values of T
off were calculated based on the duty cycle of 0.7, 0.8 and 0.9. The equations obtained are provided in Equations (7) and (8).
The work pertaining to the Al6061 composites with the considered parameters was much smaller. Most of the works of Al6061 were identified to be in the area of wire EDM. Therefore, for the regression model, three composites were developed and EDM machining was carried out for these composites to identify a proper regression model. The composites developed were Al6061 with 3%, 5% and 9% SiC added to it with the average hardness value of 65, 69 and 75 HRB, respectively. Nine experiments each were carried out, with the values of current taken as 6, 9 and 12 A; the pulse-on times were taken as 36, 48 and 56 μs; and the pulse-off times were taken as 7, 8 and 9 μs. The characteristic equations for Al6061-3% SiC are provided as Equations (9) and (10), those of Al6061-5% SiC is provided as Equations (11) and (12) and for the Al6061-9% SiC composite are Equations (13) and (14).
The hardness of the considered composites is consolidated in
Table 4.
Based on these inputs, graphs were plotted for the variations of each coefficient for the considered output parameters were plotted. The variation of each coefficient based on the hardness of the material is ascertained and the pattern of variation is identified by plotting graphs. The details of the graphs plotted for MRR are provided from
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12,
Figure 13 and
Figure 14 and those of surface roughness are provided from
Figure 15,
Figure 16,
Figure 17,
Figure 18,
Figure 19,
Figure 20,
Figure 21,
Figure 22 and
Figure 23.
The coefficients of equations of MRR in tabular form is given in
Table 5.
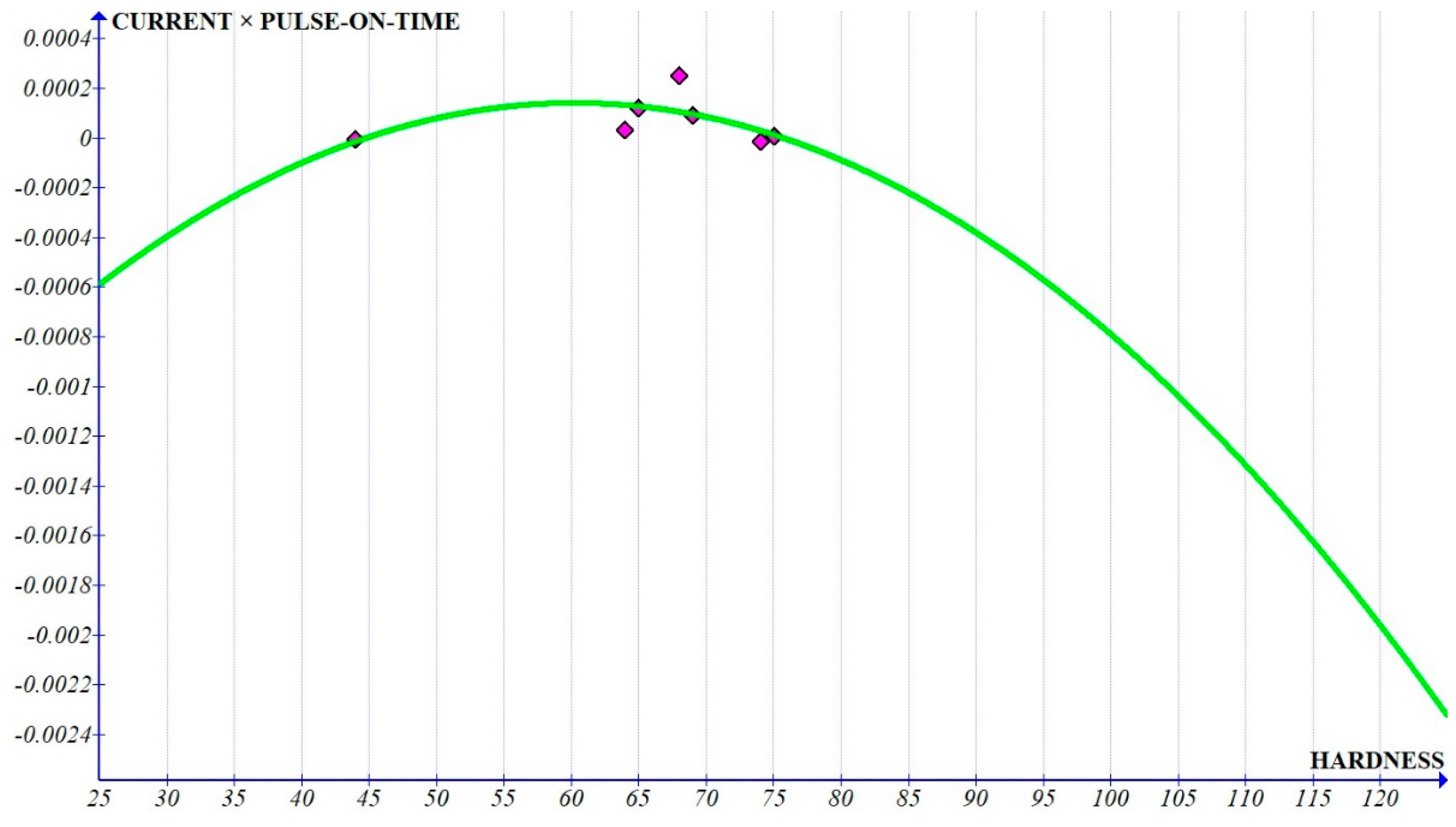
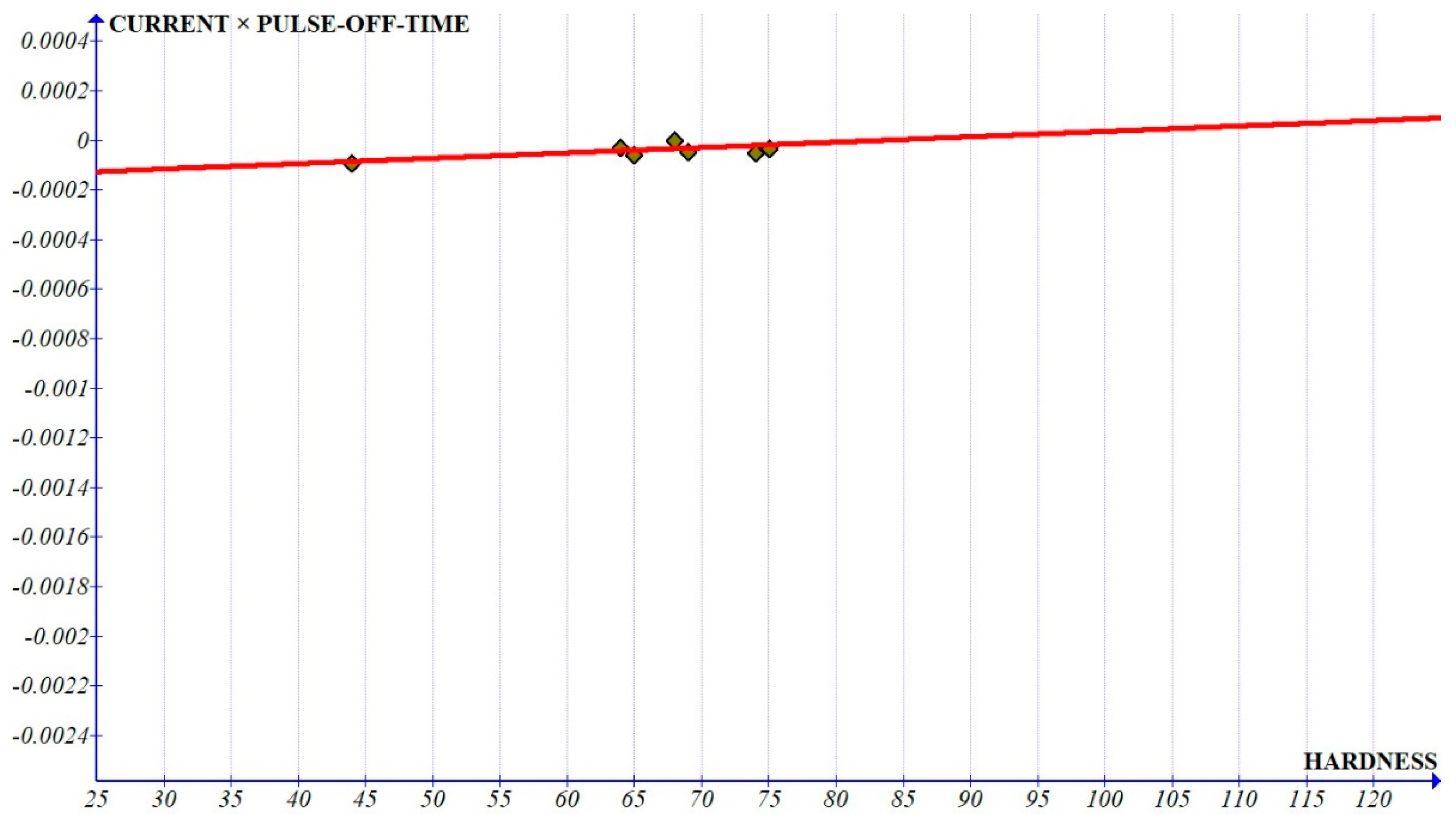
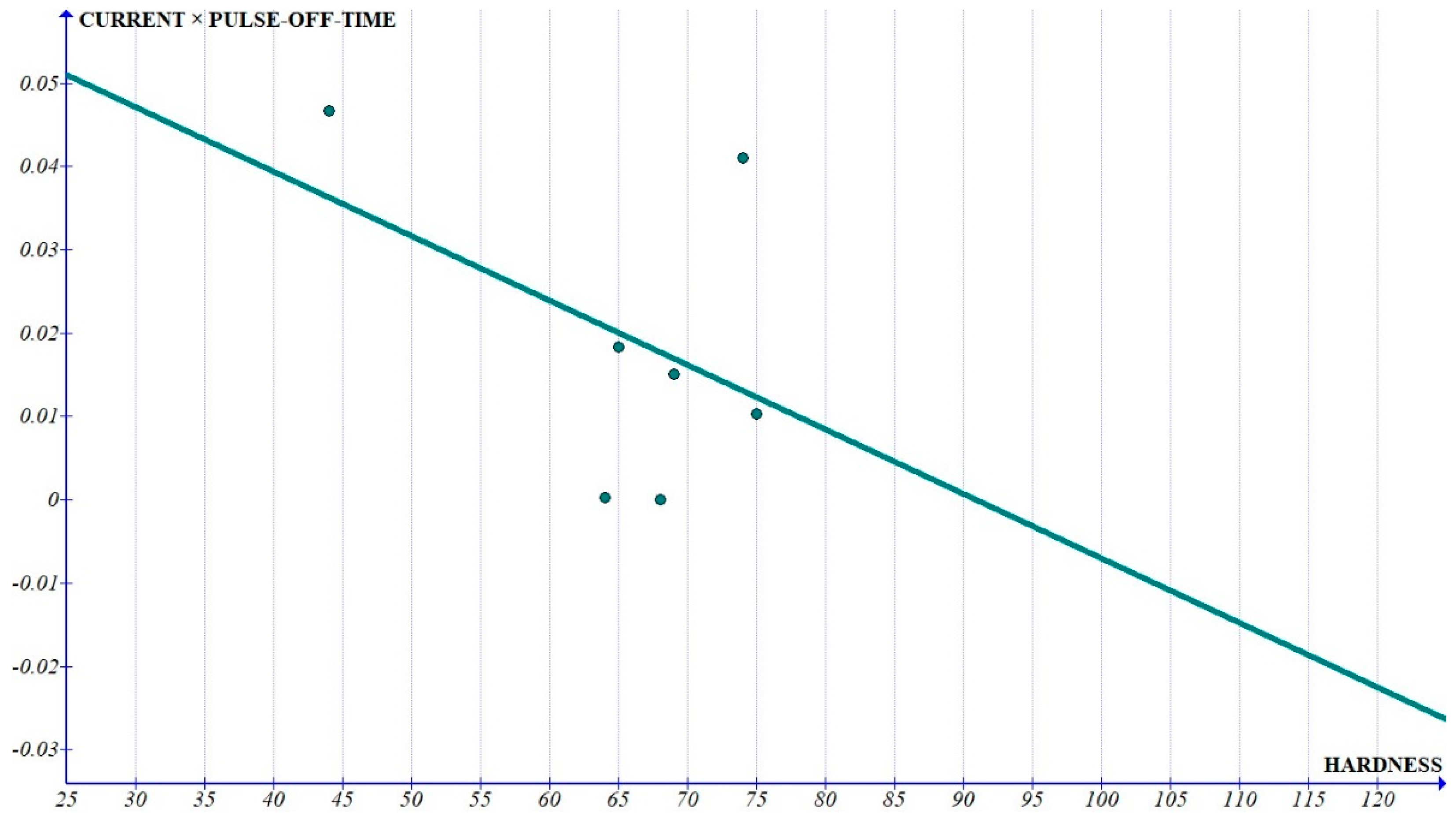
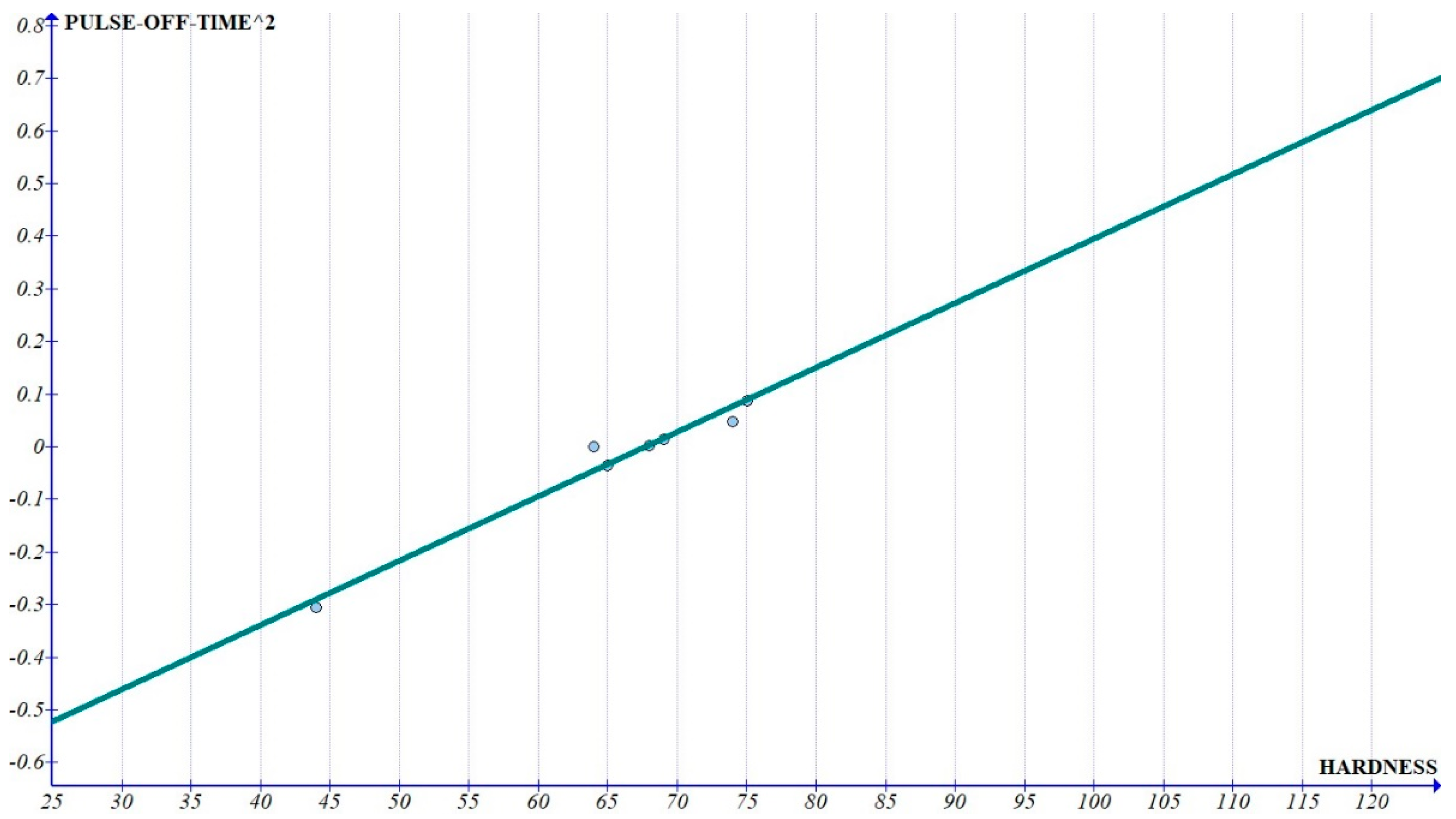
The curves of the interactions (
Figure 10 and
Figure 11) show a very small slope (in the range of 10
−6) which implies that these coefficients can be considered as constants with respect to the hardness.
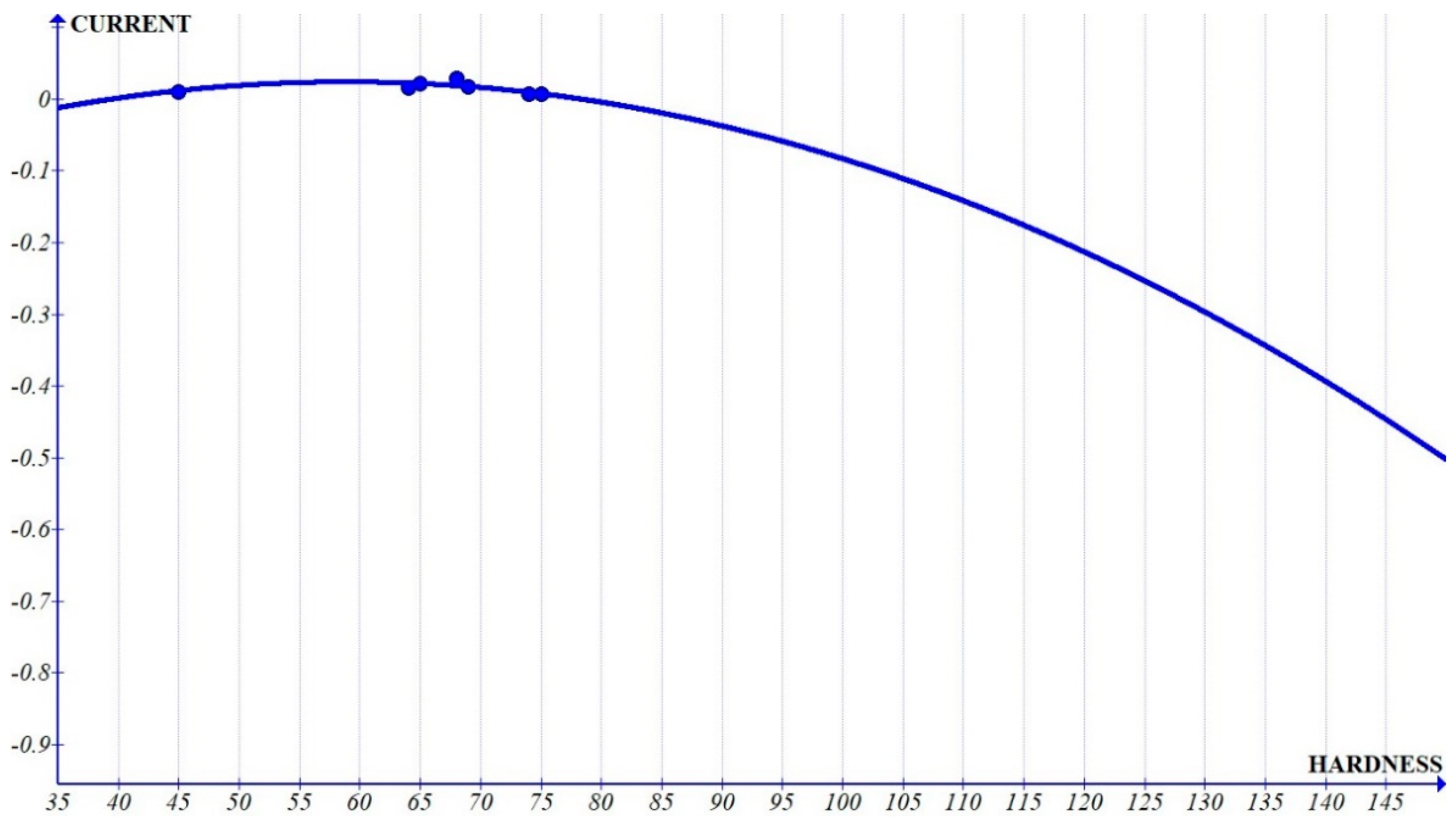
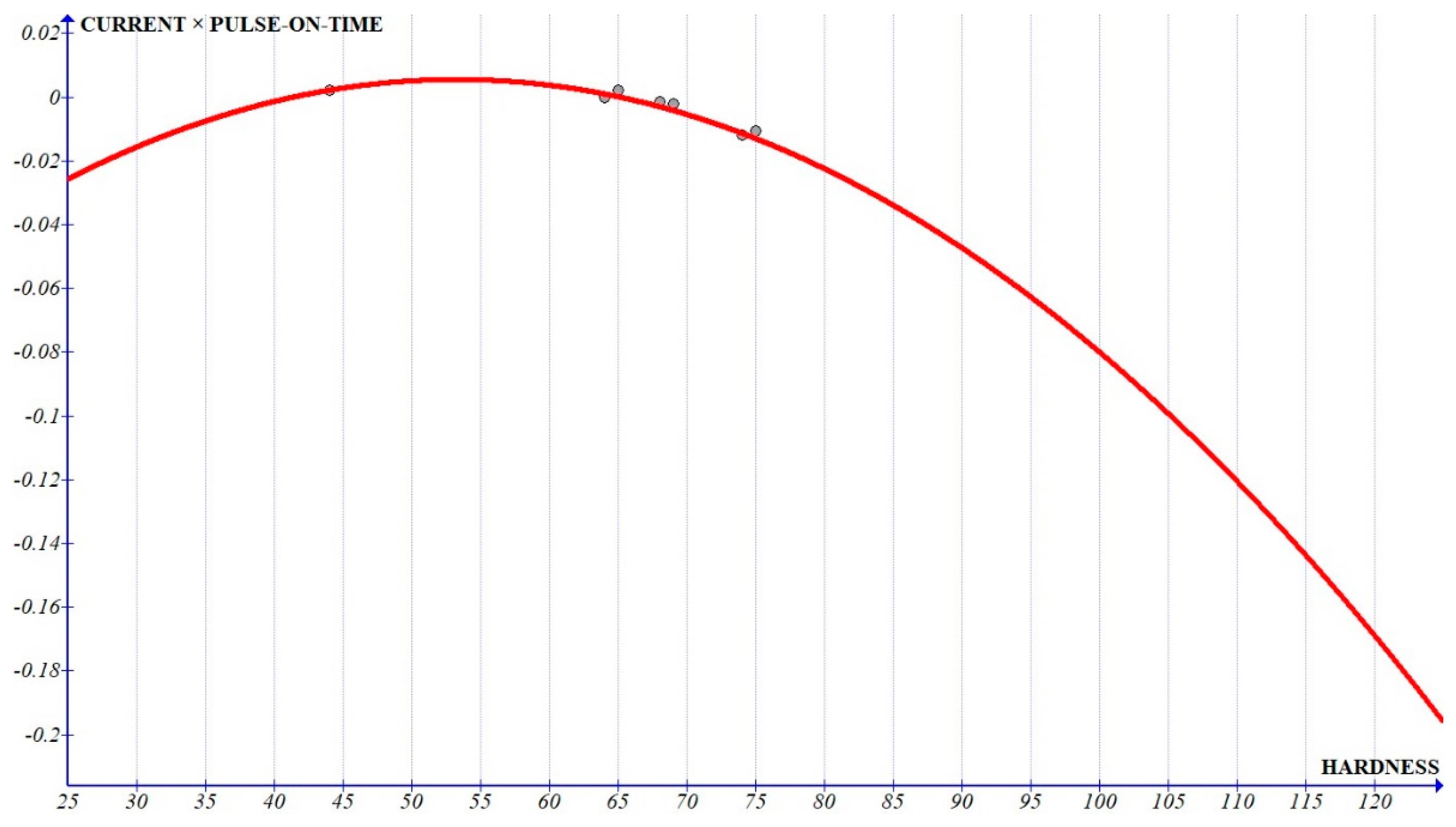
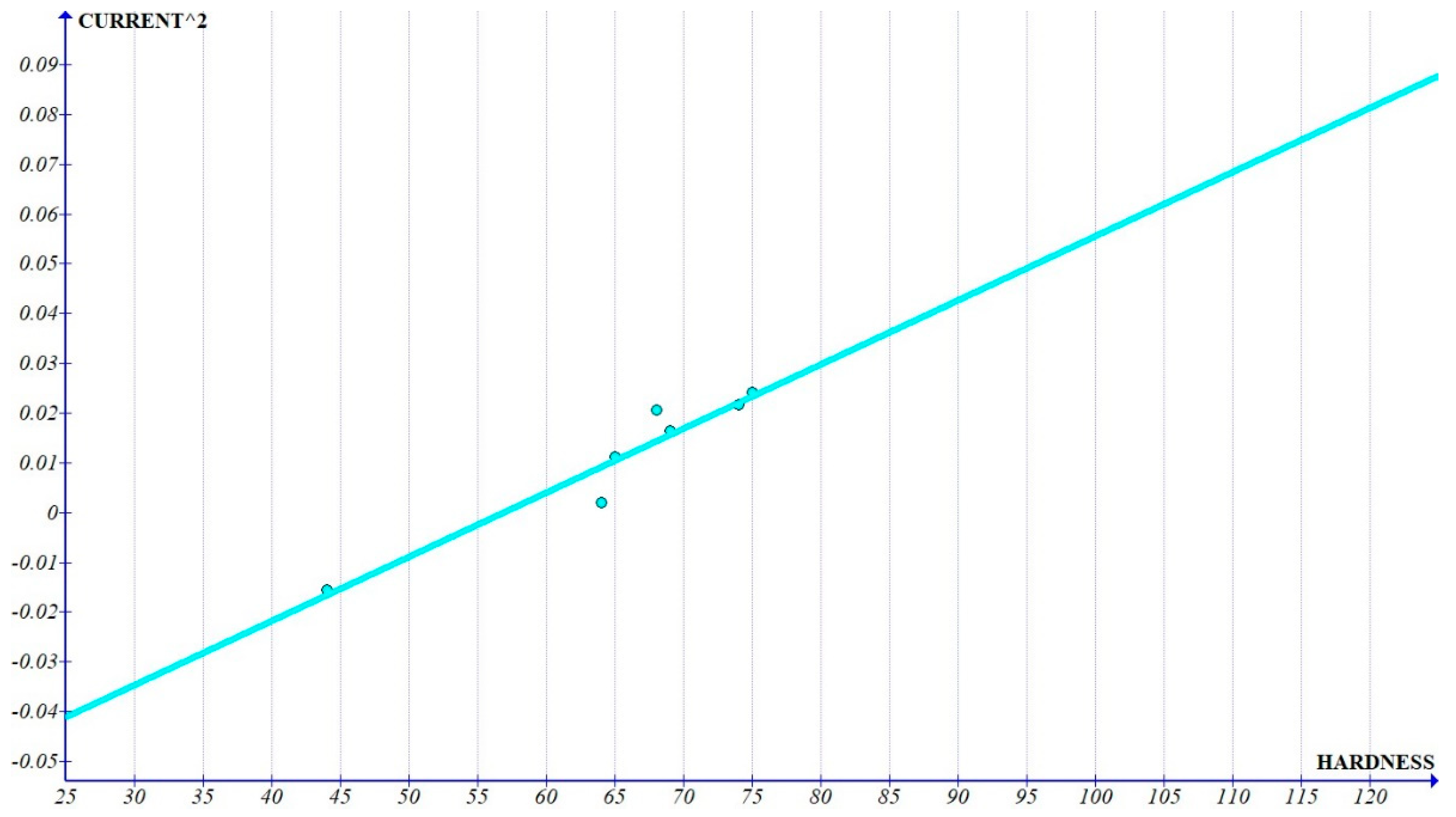
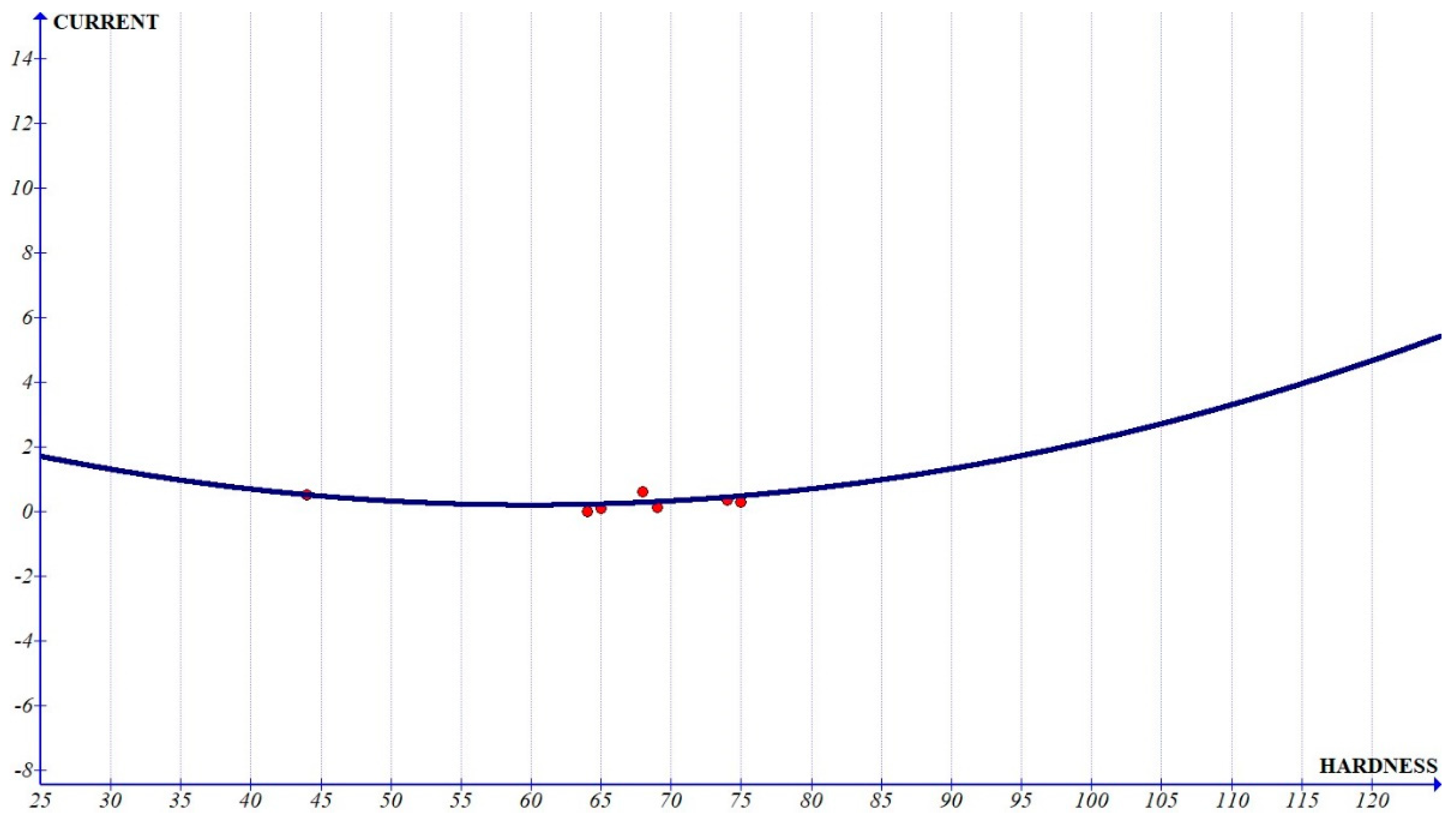
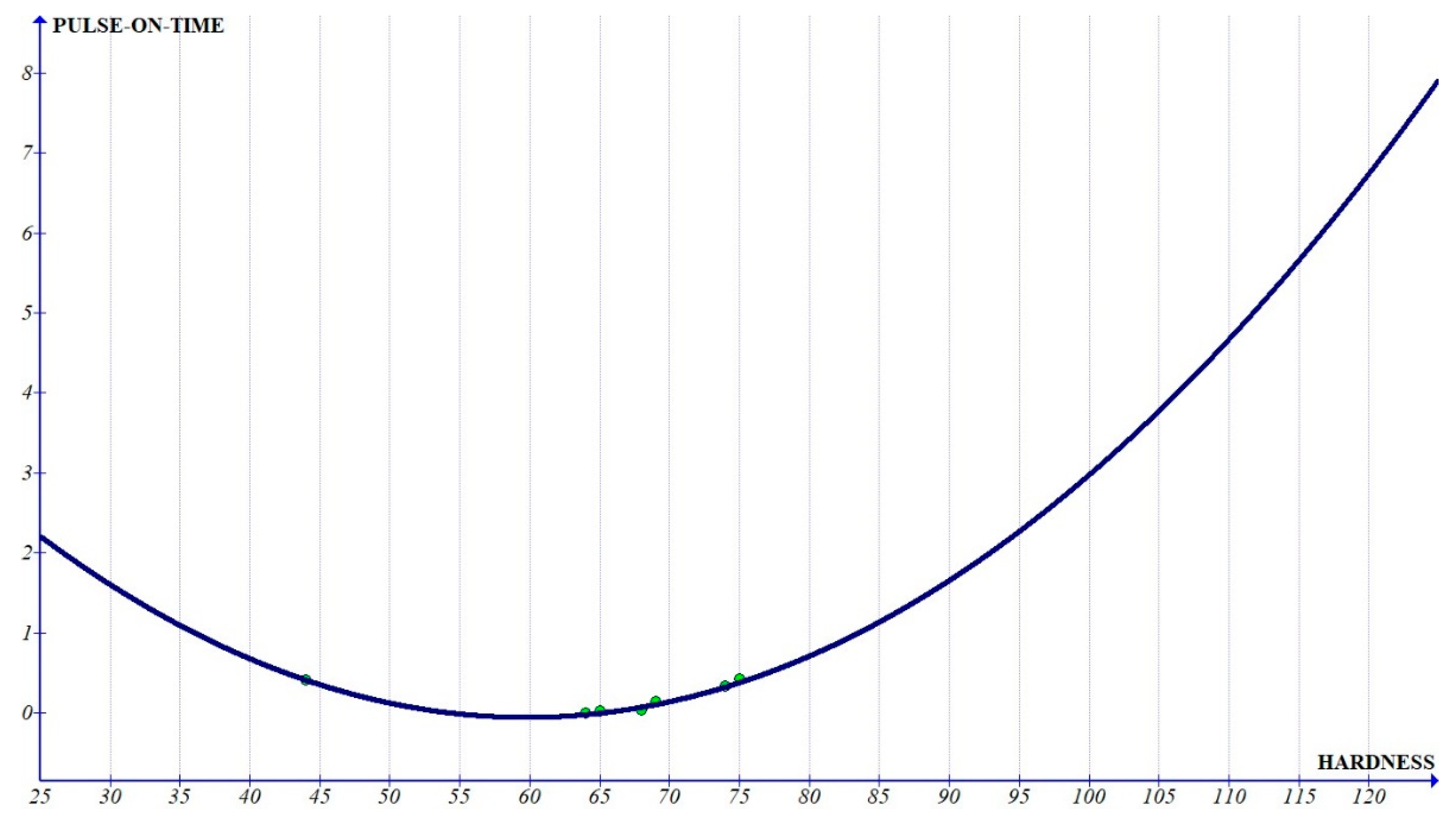
Figure 6,
Figure 8 and
Figure 9, which show the interactions with independent parameters, show that the current was showing a quadratic variation, whereas T
on and T
off show a linear variation (
Figure 8 and
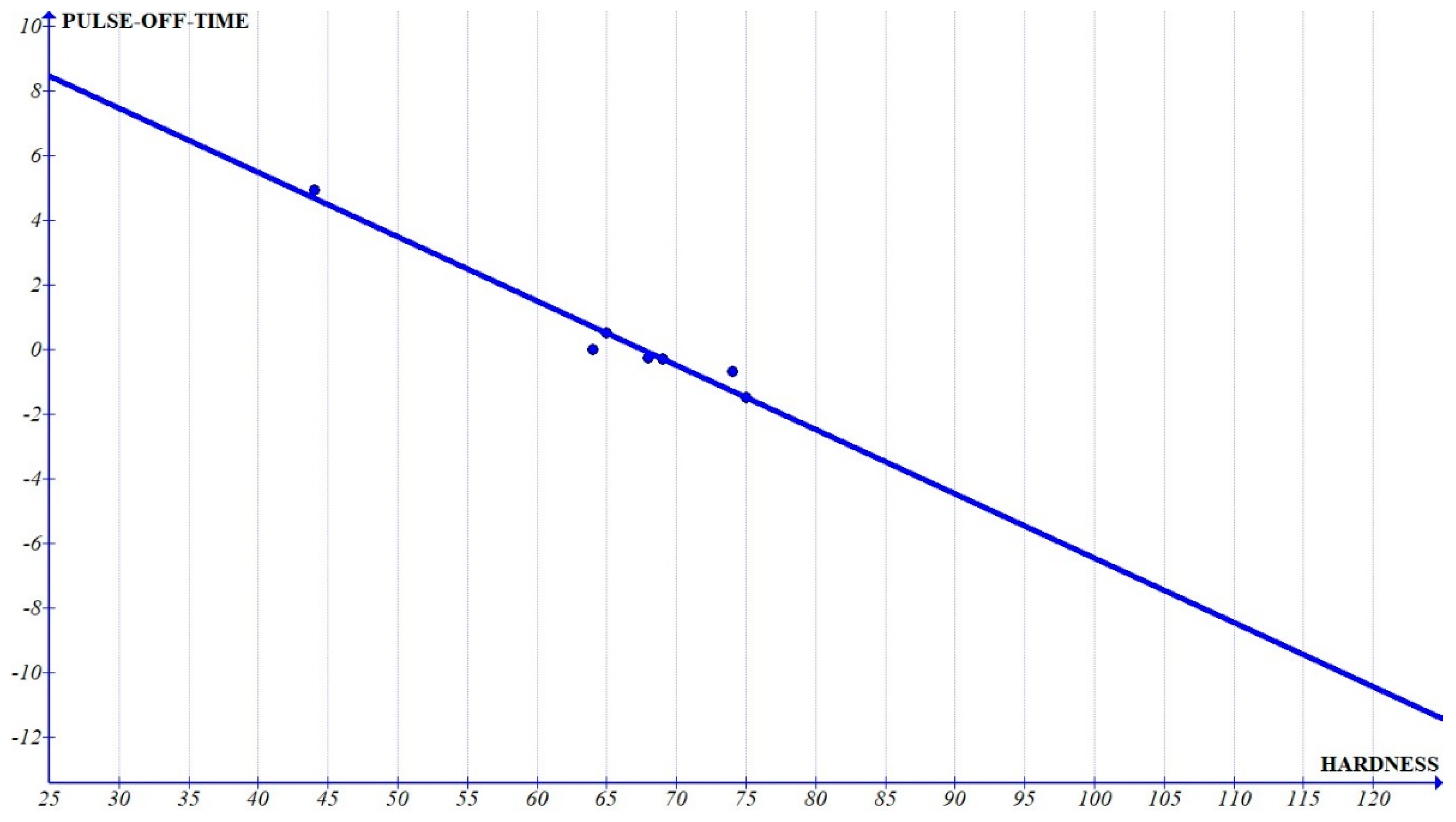
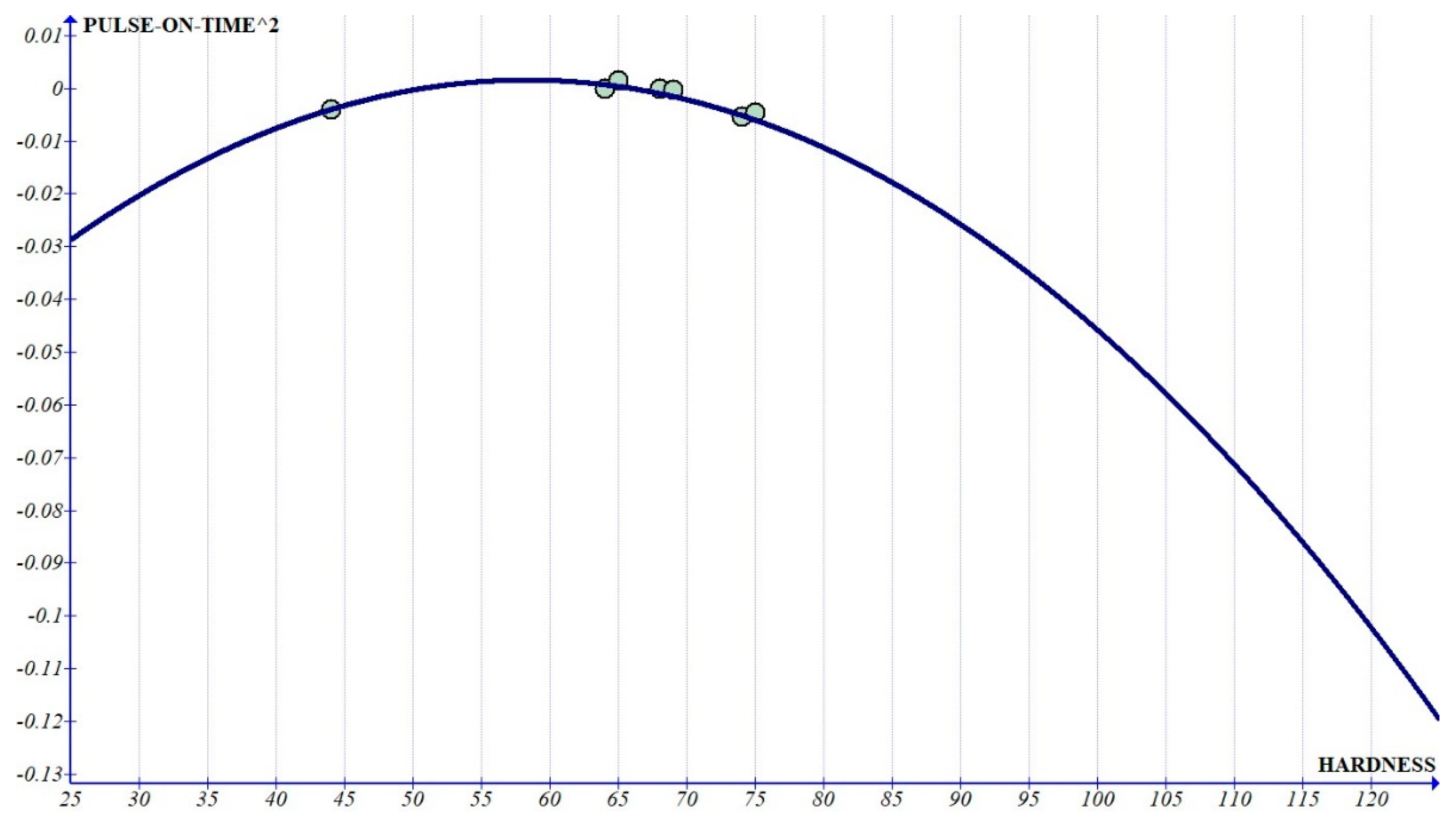
Figure 9). The graph clearly shows that the coefficient of pulse-off time reduces with increased hardness. This can be attributed to the fact that the solidification of the molten metal is quicker as the hardness of the material increases, leading to lower MRR. The increasing slope of pulse-on time with increased hardness, leading to increased MRR can be due to the nature of the composite to exist as two different components. The melting of the base matrix leads to the removal of the reinforcement, leading to increased MRR with increased percentage of the reinforcements, which increases the hardness. Since the slope of the graph of pulse-on time
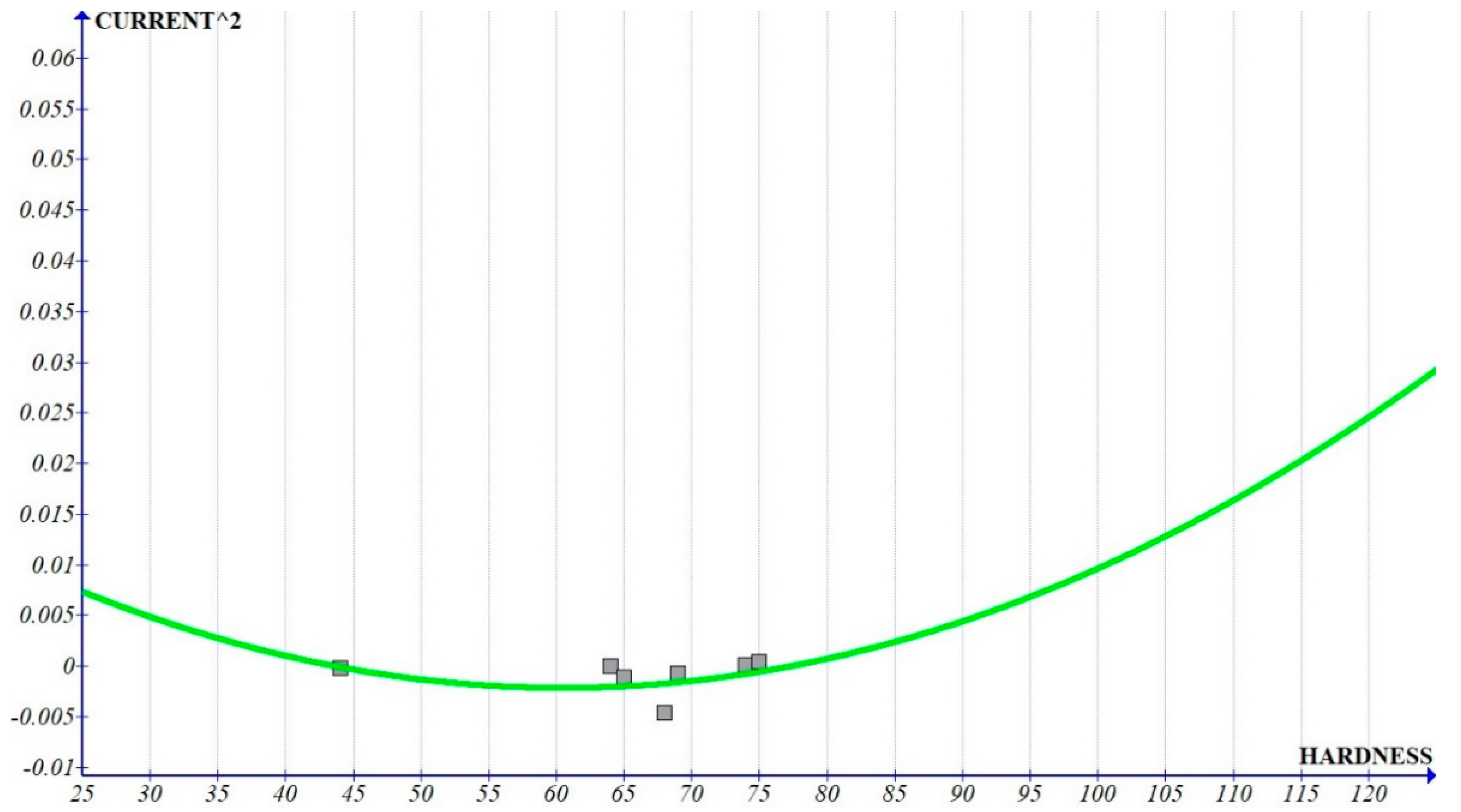
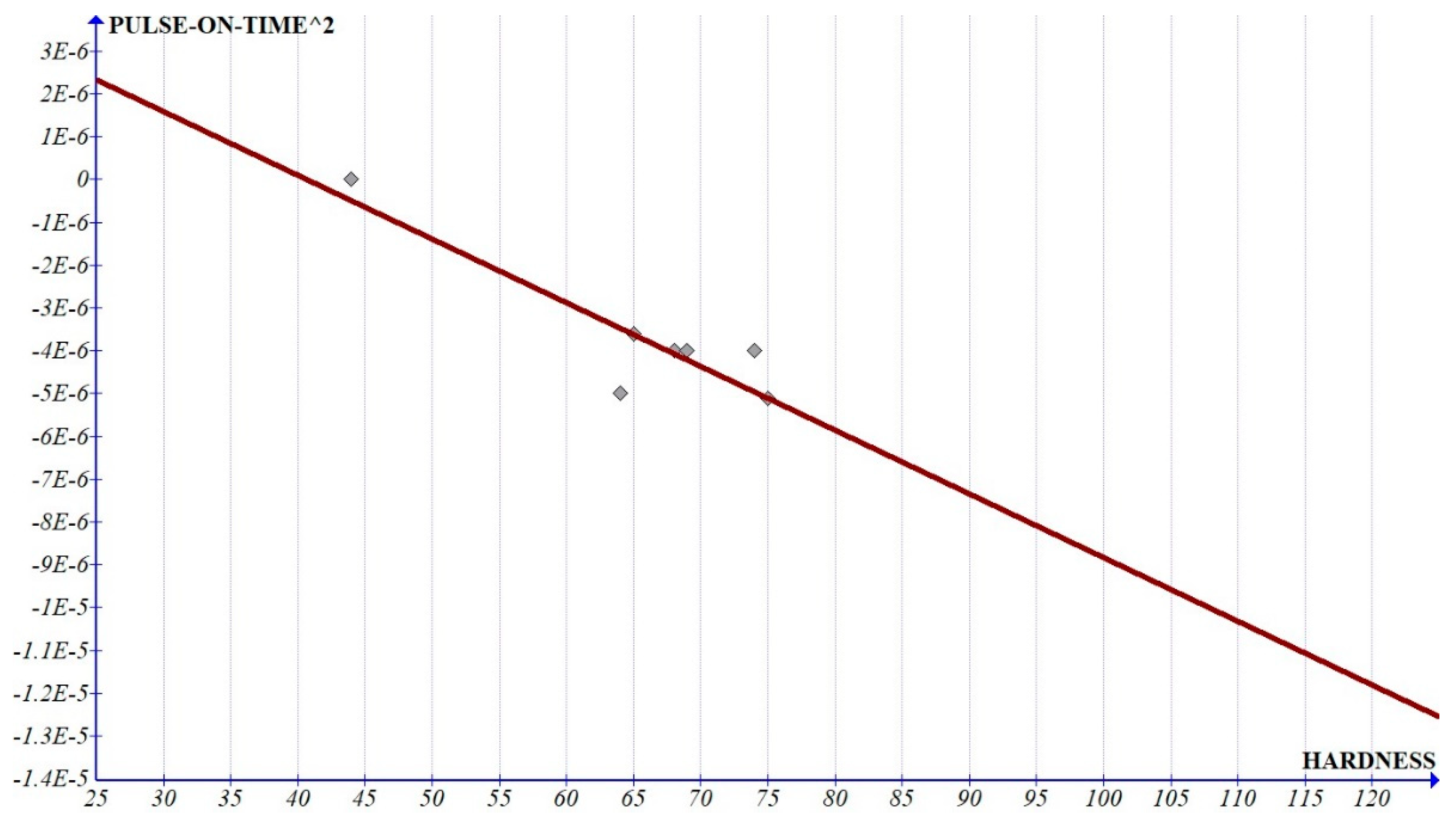
2 as well as pulse-off time
2 (
Figure 13 and
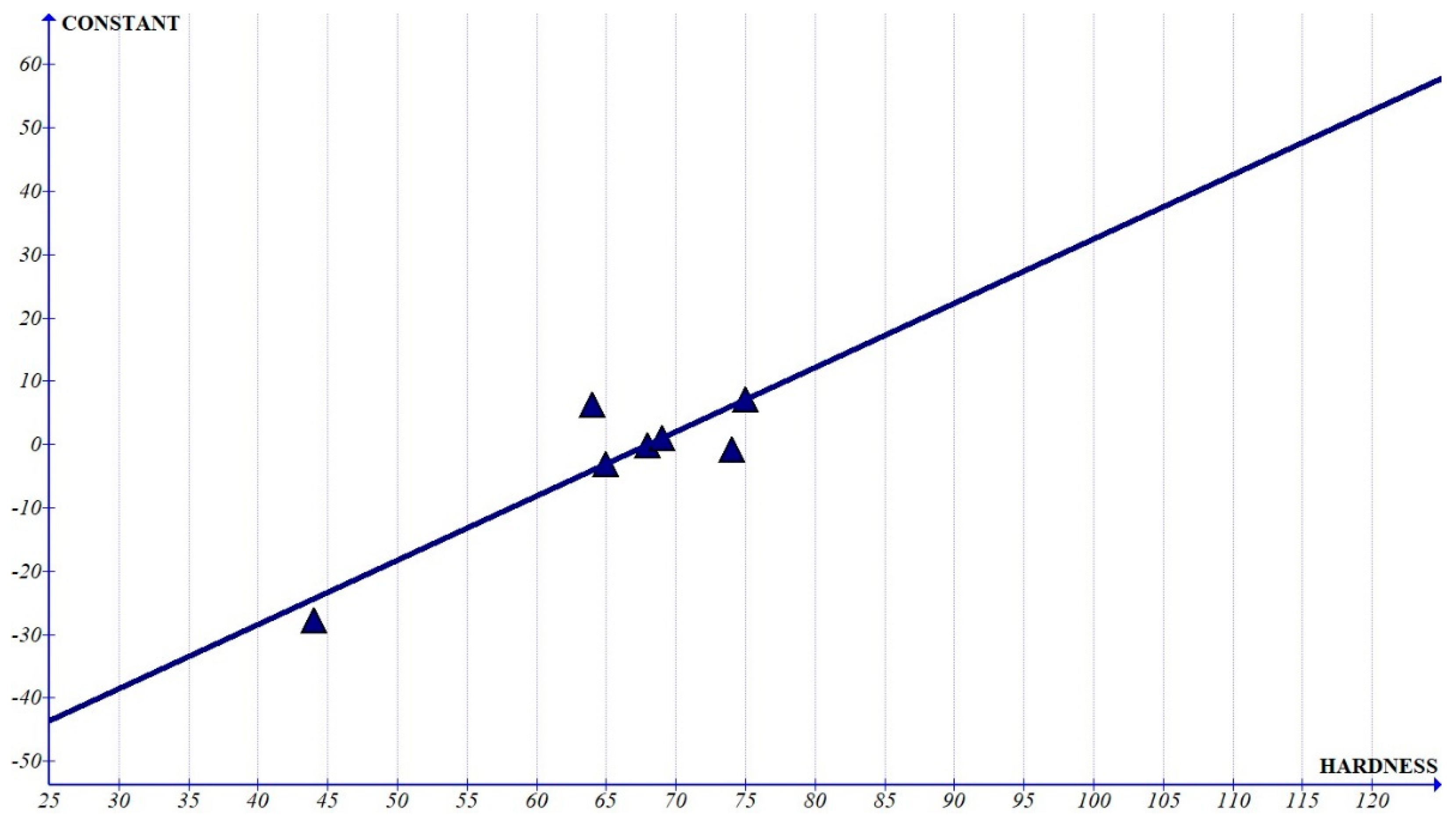
Figure 14) is less than 1% of the graph of pulse-on time and pulse-off time, we can consider that the variation is dominated by single-degree parameters when compared to its higher power. The value of the constant shows a quadratic variation (
Figure 12). It can be observed that the value of the constant has an increasing trend at the zone related to Al6061 composites, which implies that it has more prominent influence as the hardness increases.
From the ANOVA, it can be found that current is the major contributor for the MRR for most of the composites. Next prominent factor was identified as the pulse-on time. The other parameters were found to be less significant for the Al6061 composites if we observe the summarised ANOVA table (
Table 2).
A similar study was carried out for surface roughness, and the following graphs and equations were obtained:
The ANOVA of surface roughness also indicate that the equations obtained for the coefficients of surface roughness taking the hardness in HRB are:
The set of Equations are abbreviated in
Table 6.
The graph of the interactions for surface roughness also shows a very small slope (in the range of 10
−3) and can be considered to be constant for the evaluation (
Figure 15 and
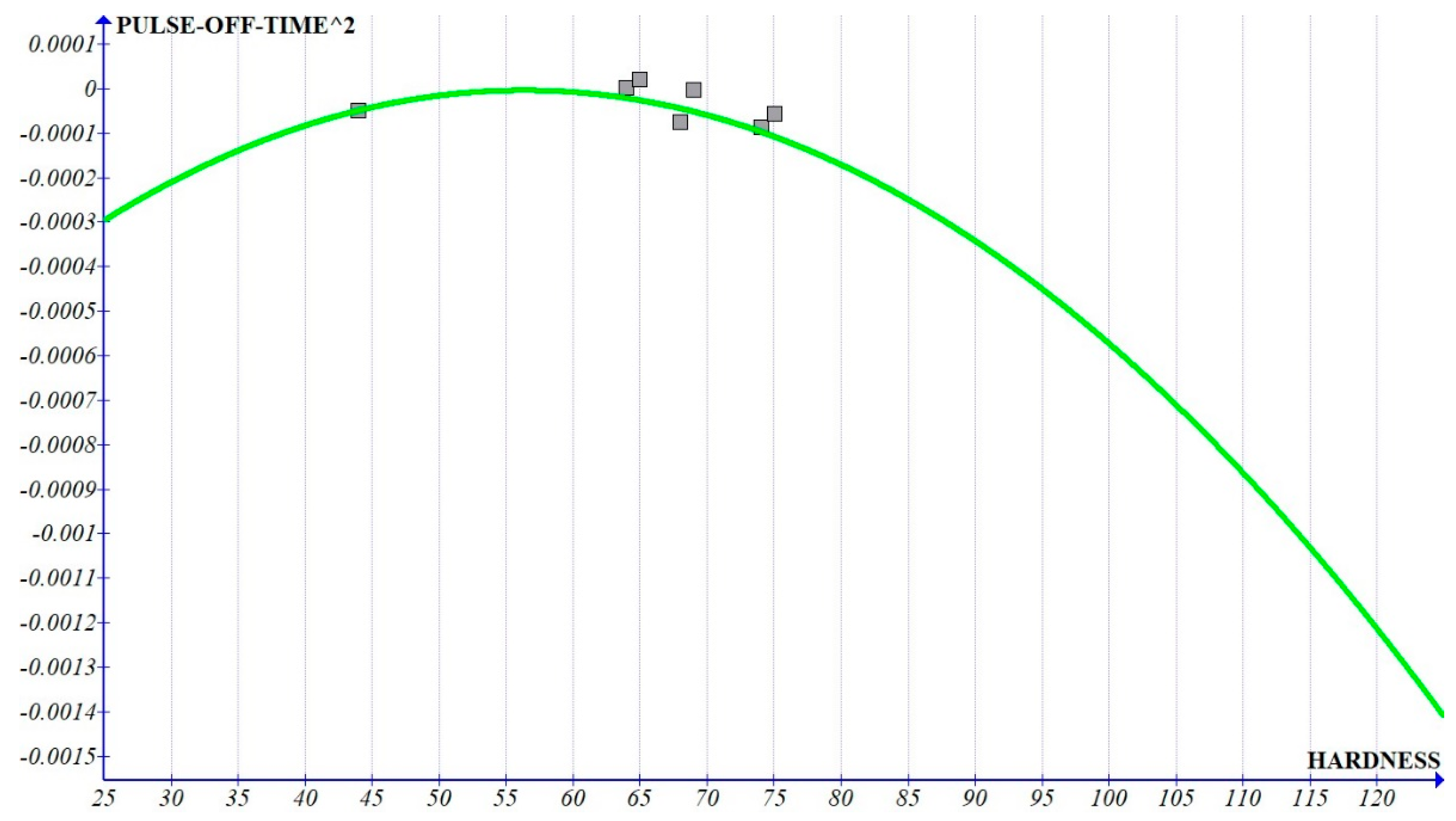
Figure 16). The higher order coefficients also show a very small slope, except for the graph of pulse-off time
2 (
Figure 22), which shows that the higher-order terms can be ignored if a very precise prediction based on the hardness is not required. The graph of pulse-off time (
Figure 20) shows a negative slope, indicating that the increase in hardness improves the surface finish. The trend could be due to white-layer formation and reduced craters while machining higher-hardness composite. The constant shows the maximum slope (
Figure 17) which indicates that the variation in surface roughness has a larger contribution from this term if the values of the input parameters are low. For higher values, the significance of this term reduces. The coefficient of pulse-on time increases with hardness (
Figure 21) which shows that the higher pulse-on time increases surface roughness whereas higher pulse-off time provides a better surface finish.